Evaluation of an Analytical Model in the Prediction of Machining Temperature of AISI 1045 Steel and AISI 4340 Steel
Abstract
1. Introduction
2. Methodology
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
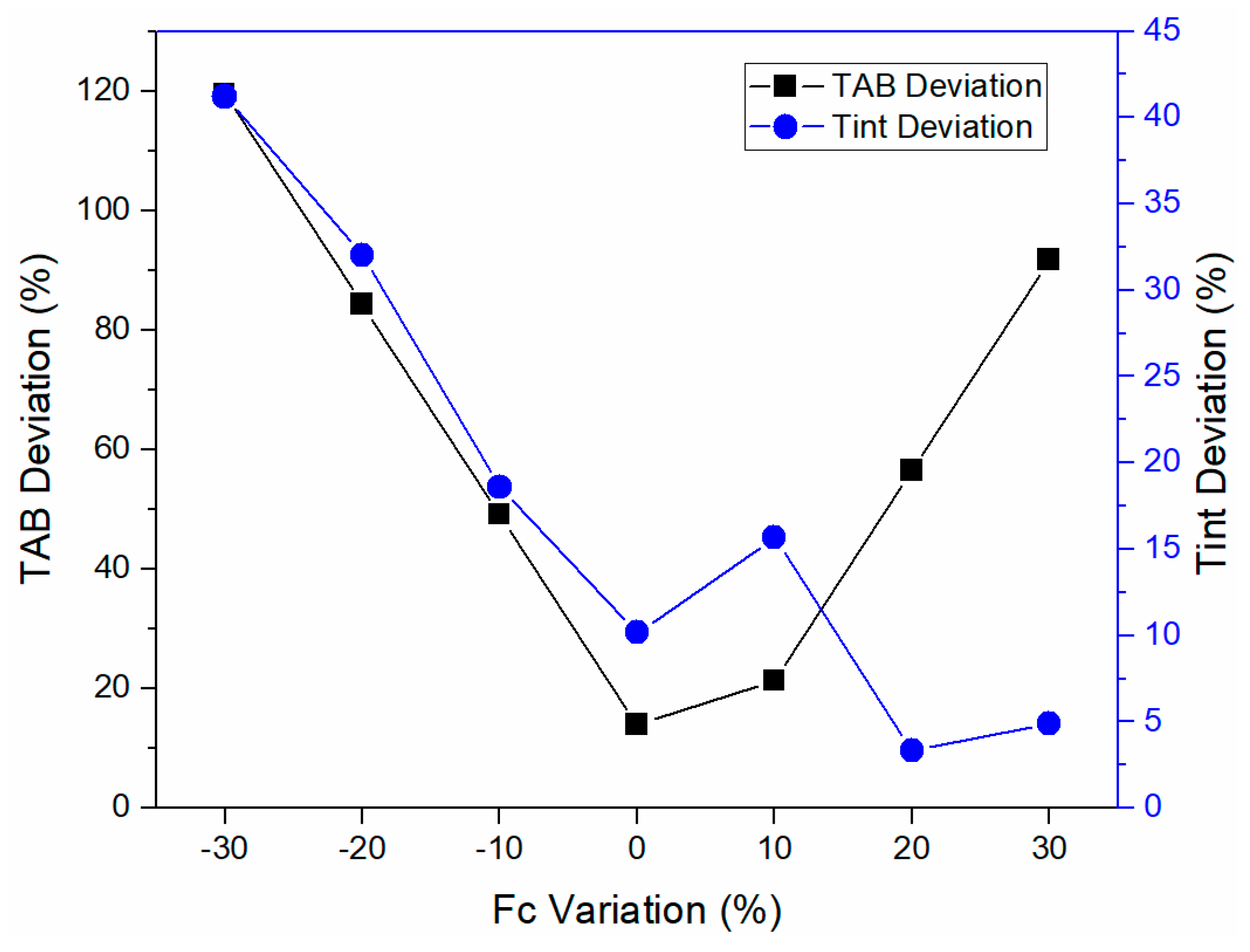
| Fc Variation (%) | TAB (°C) | Tint (°C) | TAB Deviation (%) | Tint Deviation (%) | ϕ (degs) | C0 | δ |
|---|---|---|---|---|---|---|---|
| 30 | 26.15 | 775.91 | 91.65 | 4.88 | 25.61 | 4.65 | 0.08 |
| 20 | 136.22 | 842.72 | 56.49 | 3.31 | 25.61 | 4.65 | 0.07 |
| 10 | 246.44 | 943.44 | 21.29 | 15.65 | 25.61 | 4.65 | 0.03 |
| 0 | 356.66 | 898.56 | 13.91 | 10.15 | 25.61 | 4.65 | 0.18 |
| −10 | 466.74 | 967.37 | 49.06 | 18.59 | 25.61 | 4.65 | 0.12 |
| −20 | 576.96 | 1077.07 | 84.26 | 32.04 | 25.61 | 4.65 | 0.04 |
| −30 | 687.18 | 1151.86 | 119.46 | 41.20 | 25.61 | 4.65 | 0.02 |
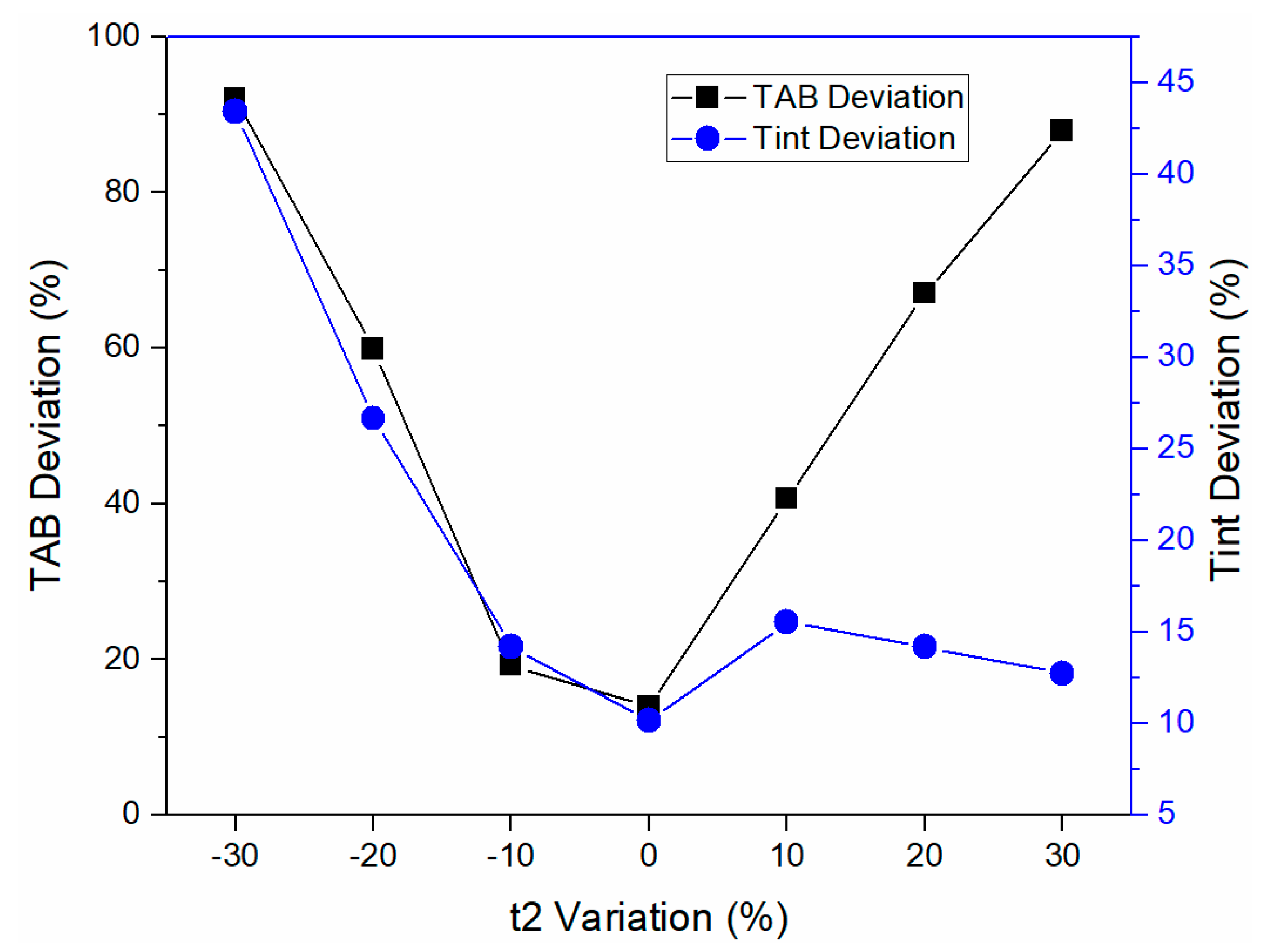
| t2 Variation (%) | TAB (°C) | Tint (°C) | TAB Deviation (%) | Tint Deviation (%) | ϕ (degs) | C0 | δ |
|---|---|---|---|---|---|---|---|
| 30 | 588.29 | 919.51 | 87.88 | 12.72 | 19.95 | 5.35 | 0.13 |
| 20 | 522.85 | 931.47 | 66.98 | 14.19 | 21.57 | 5.15 | 0.08 |
| 10 | 440.33 | 942.44 | 40.63 | 15.53 | 23.59 | 4.90 | 0.06 |
| 0 | 356.66 | 898.56 | 13.91 | 10.15 | 25.61 | 4.65 | 0.18 |
| −10 | 253.04 | 931.47 | 19.19 | 14.19 | 28.03 | 4.37 | 0.15 |
| −20 | 125.60 | 1033.19 | 59.89 | 26.66 | 30.86 | 4.08 | 0.07 |
| −30 | 25.00 | 1169.81 | 92.02 | 43.40 | 34.49 | 3.77 | 0.07 |
| J-C Constants Set | TAB (°C) | Tint (°C) | TAB Deviation (%) | Tint Deviation (%) | ϕ (degs) | C0 | δ |
|---|---|---|---|---|---|---|---|
| 1 | 356.66 | 898.56 | 13.91 | 10.15 | 25.61 | 4.65 | 0.18 |
| 2 | 331.55 | 947.43 | 5.88 | 16.14 | 25.61 | 4.69 | 0.18 |
| 3 | 367.43 | 910.53 | 17.34 | 11.62 | 25.61 | 4.99 | 0.15 |
| 4 | 336.86 | 892.58 | 7.58 | 9.42 | 25.61 | 5.04 | 0.10 |
References
- Rashid, R.R.; Sun, S.; Wang, G.; Dargusch, M.S. An investigation of cutting forces and cutting temperatures during laser-assisted machining of the Ti–6Cr–5Mo–5V–4Al beta titanium alloy. Int. J. Mach. Tools Manuf. 2012, 63, 58–69. [Google Scholar] [CrossRef]
- Egea, A.J.; Rojas, H.A.; Montaña, C.A.; Echeverri, V.K. Effect of electroplastic cutting on the manufacturing process and surface properties. J. Mater. Process. Technol. 2015, 222, 327–334. [Google Scholar] [CrossRef]
- Hameed, S.; Rojas, H.A.; Egea, A.J.; Alberro, A.N. Electroplastic cutting influence on power consumption during drilling process. Int. J. Adv. Manuf. Technol. 2016, 87, 1835–1841. [Google Scholar] [CrossRef]
- Hameed, S.; González Rojas, H.A.; Perat Benavides, J.I.; Nápoles Alberro, A.; Sánchez Egea, A.J. Influence of the Regime of Electropulsing-Assisted Machining on the Plastic Deformation of the Layer Being Cut. Materials 2018, 11, 886. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, M.B.; Wallbank, J. Cutting temperature: Prediction and measurement methods—A review. J. Mater. Process. Technol. 1999, 88, 195–202. [Google Scholar] [CrossRef]
- Longbottom, J.M.; Lanham, J.D. Cutting temperature measurement while machining—A review. Aircr. Eng. Aerosp. Technol. 2005, 77, 122–130. [Google Scholar] [CrossRef]
- Umbrello, D.; Filice, L.; Rizzuti, S.; Micari, F.; Settineri, L. On the effectiveness of finite element simulation of orthogonal cutting with particular reference to temperature prediction. J. Mater. Process. Technol. 2007, 189, 284–291. [Google Scholar] [CrossRef]
- Gonzalo, O.; Jauregi, H.; Uriarte, L.G.; de Lacalle, L.L. Prediction of specific force coefficients from a FEM cutting model. Int. J. Adv. Manuf. Technol. 2009, 43, 348–356. [Google Scholar] [CrossRef]
- Özel, T.; Zeren, E. Finite element modeling the influence of edge roundness on the stress and temperature fields induced by high-speed machining. Int. J. Adv. Manuf. Technol. 2007, 35, 255–267. [Google Scholar] [CrossRef]
- Attia, M.H.; Kops, L. A new approach to cutting temperature prediction considering the thermal constriction phenomenon in multi-layer coated tools. CIRP Ann.-Manuf. Technol. 2004, 53, 47–52. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, C.M. A study of cutting force and preheating-temperature prediction for laser-assisted milling of Inconel 718 and AISI 1045 steel. Int. J. Heat Mass Transf. 2014, 71, 264–274. [Google Scholar] [CrossRef]
- Shi, B.; Attia, H.; Vargas, R.; Tavakoli, S. Numerical and experimental investigation of laser-assisted machining of Inconel 718. Mach. Sci. Technol. 2008, 12, 498–513. [Google Scholar] [CrossRef]
- Yang, J.; Sun, S.; Brandt, M.; Yan, W. Experimental investigation and 3D finite element prediction of the heat affected zone during laser assisted machining of Ti6Al4V alloy. J. Mater. Process. Technol. 2010, 210, 2215–2222. [Google Scholar] [CrossRef]
- Lamikiz, A.; López de Lacalle, L.N.; Sanchez, J.A.; Bravo, U. Calculation of the specific cutting coefficients and geometrical aspects in sculptured surface machining. Mach. Sci. Technol. 2005, 9, 411–436. [Google Scholar] [CrossRef]
- Calleja, A.; Alonso, M.A.; Fernández, A.; Tabernero, I.; Ayesta, I.; Lamikiz, A.; López de Lacalle, L.N. Flank milling model for tool path programming of turbine blisks and compressors. Int. J. Prod. Res. 2015, 53, 3354–3369. [Google Scholar] [CrossRef]
- Oxley, P.L. The Mechanics of Machining: An Analytical Approach to Assessing Machinability; Ellis Horwood: Chichester, UK, 1989; ISBN 9780745800073. [Google Scholar]
- Radulescu, R.; Kapoor, S.G. An analytical model for prediction of tool temperature fields during continuous and interrupted cutting. J. Eng. Ind. 1994, 116, 135–143. [Google Scholar] [CrossRef]
- Stephenson, D.A.; Jen, T.C.; Lavine, A.S. Cutting tool temperatures in contour turning: Transient analysis and experimental verification. J. Manuf. Sci. Eng. 1997, 119, 494–501. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal modeling of the metal cutting process—Part III: Temperature rise distribution due to the combined effects of shear plane heat source and the tool–chip interface frictional heat source. Int. J. Mech. Sci. 2001, 43, 89–107. [Google Scholar] [CrossRef]
- Hahn, R.S. On the temperature developed at the shear plane in the metal cutting process. J. Appl. Mech.-Trans. ASME 1951, 18, 323. [Google Scholar]
- Jaeger, C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959; ISBN 9780198533689. [Google Scholar]
- Huang, Y.; Liang, S.Y. Cutting temperature modeling based on non-uniform heat intensity and partition ratio. Mach. Sci. Technol. 2005, 9, 301–323. [Google Scholar] [CrossRef]
- Korkut, I.; Acır, A.; Boy, M. Application of regression and artificial neural network analysis in modelling of tool–chip interface temperature in machining. Expert Syst. Appl. 2011, 38, 11651–11656. [Google Scholar] [CrossRef]
- Ning, J.; Liang, S.Y. Prediction of Temperature Distribution in Orthogonal Machining Based on the Mechanics of the Cutting Process Using a Constitutive Model. J. Manuf. Mater. Process. 2018, 2, 37. [Google Scholar] [CrossRef]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. Sect. B 1949, 62, 676. [Google Scholar] [CrossRef]
- Shrot, A.; Bäker, M. Determination of Johnson–Cook parameters from machining simulations. Comput. Mater. Sci. 2012, 52, 298–304. [Google Scholar] [CrossRef]
- Agmell, M.; Ahadi, A.; Ståhl, J.E. Identification of plasticity constants from orthogonal cutting and inverse analysis. Mech. Mater. 2014, 77, 43–51. [Google Scholar] [CrossRef]
- Ning, J.; Liang, S.Y. Model-driven determination of Johnson-Cook material constants using temperature and force measurements. Int. J. Adv. Manuf. Technol. 2018, 97, 1053–1060. [Google Scholar] [CrossRef]
- Ning, J.; Nguyen, V.; Huang, Y.; Hartwig, K.T.; Liang, S.Y. Inverse determination of Johnson–Cook model constants of ultra-fine-grained titanium based on chip formation model and iterative gradient search. Int. J. Adv. Manuf. Technol. 2018, 99, 1131–1140. [Google Scholar] [CrossRef]
- Urbikain, G.; Campa, F.J.; Zulaika, J.J.; De Lacalle, L.N.; Alonso, M.A.; Collado, V. Preventing chatter vibrations in heavy-duty turning operations in large horizontal lathes. J. Sound Vib. 2015, 340, 317–330. [Google Scholar] [CrossRef]
- Urbicain, G.; Palacios, J.A.; Fernández, A.; Rodríguez, A.; de Lacalle, L.L.; Elías-Zúñiga, A. Stability prediction maps in turning of difficult-to-cut materials. Procedia Eng. 2013, 63, 514–522. [Google Scholar] [CrossRef]
- Ivester, R.W.; Kennedy, M.; Davies, M.; Stevenson, R.; Thiele, J.; Furness, R.; Athavale, S. Assessment of machining models: Progress report. Mach. Sci. Technol. 2000, 4, 511–538. [Google Scholar] [CrossRef]
- Aydın, M. Cutting temperature analysis considering the improved Oxley’s predictive machining theory. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 2435–2448. [Google Scholar] [CrossRef]
- Naik, P.; Naik, A. Determination of flow stress constants by Oxley’s theory. Int. J. Latest Technol. Eng. Manag. Appl. Sci. 2015, 4, 110–116. [Google Scholar]
- Özel, T.; Zeren, E. A methodology to determine work material flow stress and tool-chip interfacial friction properties by using analysis of machining. J. Manuf. Sci. Eng. 2006, 128, 119–129. [Google Scholar] [CrossRef]
- Özel, T.; Karpat, Y. Identification of constitutive material model parameters for high-strain rate metal cutting conditions using evolutionary computational algorithms. Mater. Manuf. Process. 2007, 22, 659–667. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, J.; Gan, Y.; Li, B.; Fang, N. Improvement of algorithm and prediction precision of an extended Oxley’s theoretical model. Int. J. Adv. Manuf. Technol. 2015, 77, 1–3. [Google Scholar] [CrossRef]
- Karpat, Y.; Özel, T. Predictive analytical and thermal modeling of orthogonal cutting process—Part I: Predictions of tool forces, stresses, and temperature distributions. J. Manuf. Sci. Eng. 2006, 128, 435–444. [Google Scholar] [CrossRef]
- M’saoubi, R.; Chandrasekaran, H. Investigation of the effects of tool micro-geometry and coating on tool temperature during orthogonal turning of quenched and tempered steel. Int. J. Mach. Tools Manuf. 2004, 44, 213–224. [Google Scholar] [CrossRef]
- Chandrasekaran, H.; M’saoubi, R.; Chazal, H. Modelling of material flow stress in chip formation process from orthogonal milling and split Hopkinson bar tests. Mach. Sci. Technol. 2005, 9, 131–145. [Google Scholar] [CrossRef]
- Gibson, A. Tool life and cutting forces when machining XC 45 steel. Int. J. Prod. Res. 1971, 9, 409–421. [Google Scholar] [CrossRef]
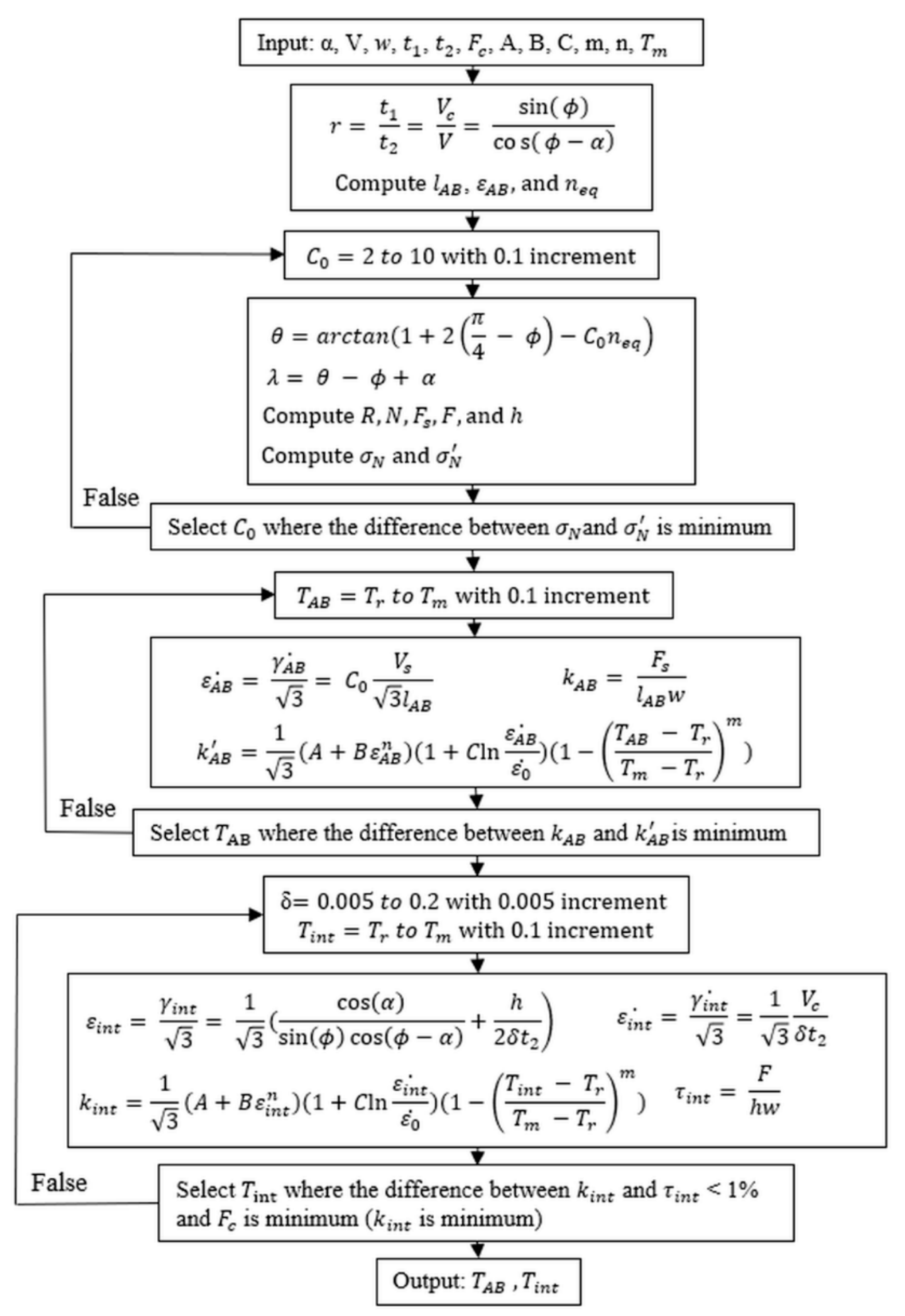

| Material | Test | α (degs) | V (m/min) | w (mm) | t1 (mm) | t2 (mm) | ||
|---|---|---|---|---|---|---|---|---|
| AISI1045 | 1 | 5 | 200 | 1.6 | 0.15 | 0.31 | 433 | 171 |
| [32,33] | 2 | 5 | 200 | 1.6 | 0.30 | 0.54 | 773 | 233 |
| 3 | 5 | 300 | 1.6 | 0.15 | 0.28 | 406 | 136 | |
| 4 | 5 | 300 | 1.6 | 0.30 | 0.69 | 899 | 366 |
| Approach | A (MPa) | B (MPa) | C | m | n |
|---|---|---|---|---|---|
| SHPB [25] | 553.1 | 600.8 | 0.0134 | 1 | 0.234 |
| Naik P. [34] | 552 | 604 | 0.0131 | 0.95 | 0.231 |
| Özel T. [35] | 451.6 | 819.5 | 0.0000009 | 1.0955 | 0.1736 |
| Özel T. CPSO [36] | 546.83 | 609.35 | 0.01376 | 0.94053 | 0.2127 |
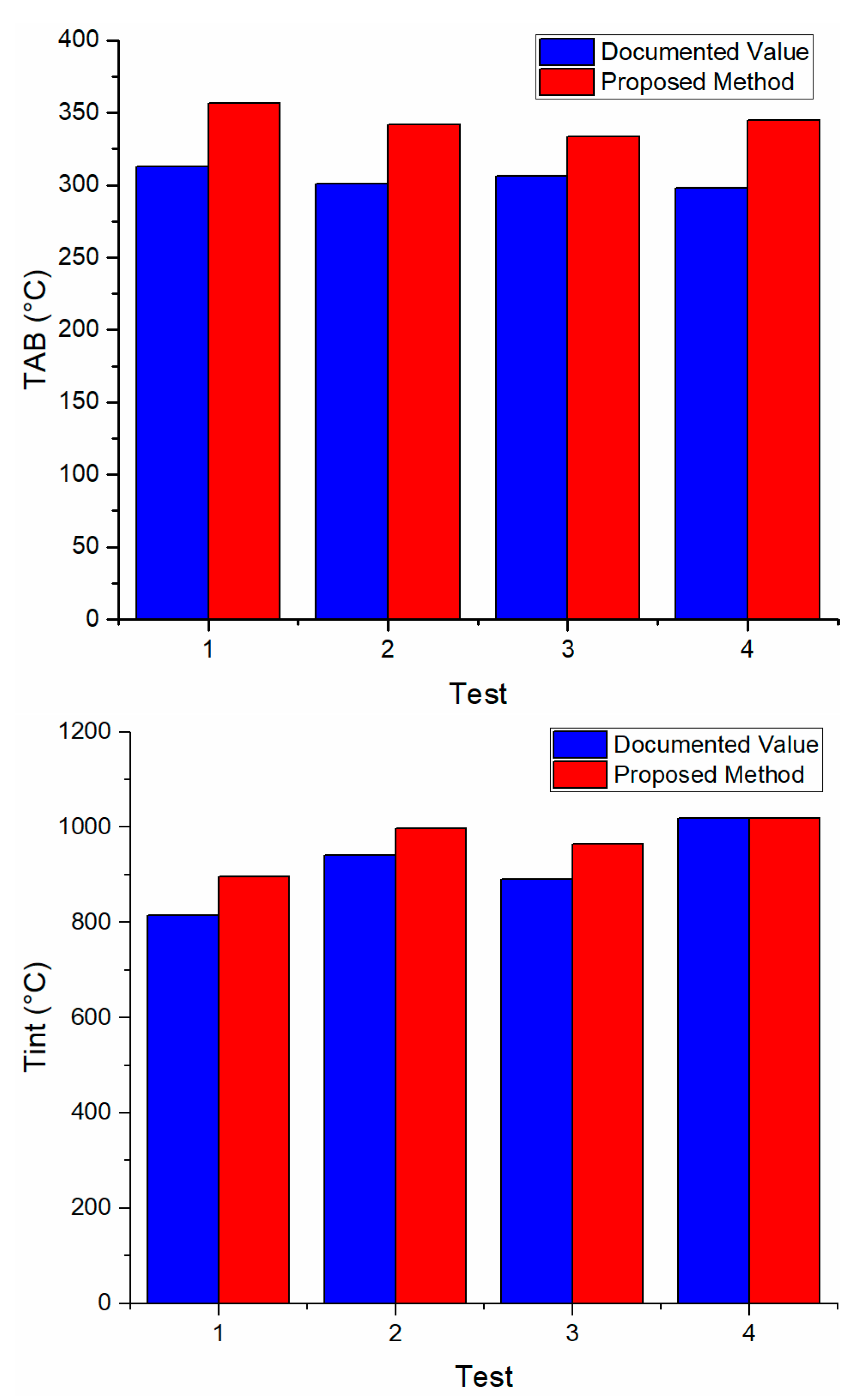
| Test | TAB (°C) R | TAB (°C) | Tint (°C) R | Tint (°C) | ϕ (degs) | C0 | δ |
|---|---|---|---|---|---|---|---|
| 1 | 313.12 | 356.66 | 815.74 | 895.57 | 25.61 | 4.65 | 0.18 |
| 2 | 300.77 | 341.59 | 941.15 | 997.29 | 28.84 | 4.28 | 0.15 |
| 3 | 306.30 | 333.56 | 891.20 | 964.38 | 28.03 | 4.37 | 0.16 |
| 4 | 297.80 | 345.07 | 1018.00 | 1018.23 | 30.12 | 3.77 | 0.02 |
| Material | A (MPa) | B (MPa) | C | m | n | Tm |
|---|---|---|---|---|---|---|
| AISI 4340 | 850 | 356 | 0.072 | 0.513 | 0.304 | 1427 |
| Tool | Edge Preparation | Edge Radius (μm) | PVD Coating |
|---|---|---|---|
| S | Sharp | 2 ± 0.7 | Uncoated |
| R | Round | 25 ± 4 | Uncoated |
| F | Flank Land | 2 ± 0.7 | Uncoated |
| SC | Sharp | 5 ± 3 | TiN (5 μm) |
| RC | Round | 28 ± 3 | TiN (5 μm) |
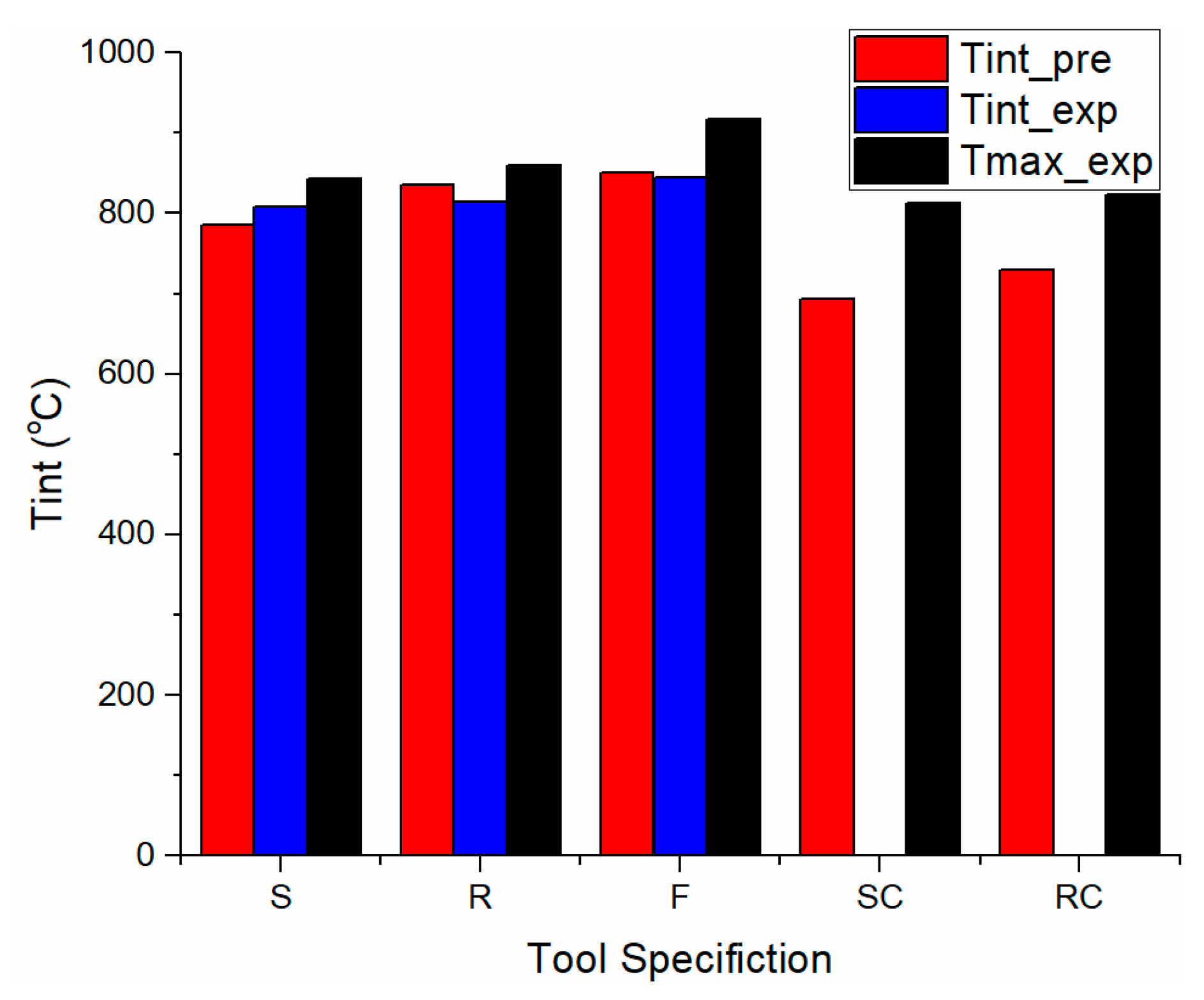
| Tool | t2 (mm) | Fc (N) | Ft (N) | TAB (°C) | Tint (°C) | (°C) | (°C) | ϕ (degs) | C0 | δ |
|---|---|---|---|---|---|---|---|---|---|---|
| S | 0.17 | 1085.03 | 537.01 | 171.6 | 785.39 | 807.88 | 843.2 | 31.67 | 5.04 | 0.04 |
| R | 0.17 | 1175.9 | 812.39 | 123.84 | 834.96 | 813.96 | 859.93 | 31.67 | 5.05 | 0.01 |
| F | 0.17 | 1310.84 | 793.12 | 69.9 | 850.86 | 844.51 | 917.83 | 31.67 | 5.05 | 0.01 |
| SC | 0.2 | 1032.7 | 484.68 | 295.2 | 692.80 | - | 812.32 | 27.22 | 5.89 | 0.12 |
| RC | 0.17 | 1104.3 | 713.25 | 160.69 | 729.27 | - | 823.9 | 31.67 | 5.04 | 0.07 |
| Model | Presented Temperature Model [24] | Oxley’s Chip Formation Model [16] | Komanduri’s Temperature Model [19] |
|---|---|---|---|
| Input | Cutting condition parameters; J-C constants; cutting force; chip thickness. | Cutting condition parameters; J-C constants; workpiece thermal-physical properties; heat partition ratios at PSZ and SSZ respectively. | Cutting condition parameters; cutting forces; workpiece and tool thermal-physical properties; geometry including lengths and angles of PSZ and SSZ. |
| Output | The average temperatures at PSZ and SSZ respectively. | The uniform temperatures at PSZ and SSZ respectively. | Temperature distribution at chip formation zone. |
| Assumption | Constant material flow rate at chip formation zone; steady state and plain strain condition. | Perfect sharp cutting tool; uniform strain and temperature at two shear zones; steady state and plain strain condition. | Moving band heat source in the chip; stationary rectangular heat source in the tool; Imaginary heat source for boundary conditions. |
| Difficulty and limitation | Prediction of average temperature at PSZ and SSZ respectively. | Determination of heat partition ratios at PSZ and SSZ respectively; Prediction of uniform temperatures at PSZ and SSZ respectively. | Determination of geometry including lengths and angles of PSZ and SSZ. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, J.; Liang, S.Y. Evaluation of an Analytical Model in the Prediction of Machining Temperature of AISI 1045 Steel and AISI 4340 Steel. J. Manuf. Mater. Process. 2018, 2, 74. https://doi.org/10.3390/jmmp2040074
Ning J, Liang SY. Evaluation of an Analytical Model in the Prediction of Machining Temperature of AISI 1045 Steel and AISI 4340 Steel. Journal of Manufacturing and Materials Processing. 2018; 2(4):74. https://doi.org/10.3390/jmmp2040074
Chicago/Turabian StyleNing, Jinqiang, and Steven Y. Liang. 2018. "Evaluation of an Analytical Model in the Prediction of Machining Temperature of AISI 1045 Steel and AISI 4340 Steel" Journal of Manufacturing and Materials Processing 2, no. 4: 74. https://doi.org/10.3390/jmmp2040074
APA StyleNing, J., & Liang, S. Y. (2018). Evaluation of an Analytical Model in the Prediction of Machining Temperature of AISI 1045 Steel and AISI 4340 Steel. Journal of Manufacturing and Materials Processing, 2(4), 74. https://doi.org/10.3390/jmmp2040074






