Fractal Analysis Application Outlook for Improving Process Monitoring and Machine Maintenance in Manufacturing 4.0

Abstract

Industry 4.0 has been advertised for a decade as the next disruptive evolution for production. It relies on automation growth and particularly on data exchange using numerous sensors in order to develop faster production with tight monitoring. The huge amount of data generated by clouds of sensors during production is often used to feed machine learning systems in order to detect faults, monitor and find possible ways for improvement. However, the artificial intelligence within machine learning requires finding and selecting key features, such as average and root mean square. While current machine learning has already proven its use in diverse applications, its efficiency could be further improved by generating better characteristics such as fractal parameters. In this paper, fractal analysis concept is presented and its current and future applications in machining are discussed. This sensitive and robust technique is already extracting high performance key features that could fill in monitoring and prediction systems. On top of improving features selection and, thus, improving the overall performance of monitoring and predictive systems in machining, this could lead to a more rapid artificial intelligence implementation into manufacturing.

1. Introduction

For nearly a decade, the industry has been evolving into a manufacturing 4.0 environment. This new industrial revolution brings current automation and data management to a global and decentralization scale. To achieve this, internet-of-things, control process systems and advanced decision-making systems are set. Industrial internet-of-things allows bringing global connectivity to devices and machines by embedding sensors and actuators. Control process systems such as SCADA (Supervisory Control And Data Acquisition) command actuators based on decisions made from multiple sensors signal combined information [1]. In the artificial intelligence domain, machine learning is a strategic asset to develop advanced decision-making systems. In the end, the progress in the machine shop could be leading to improvements in various areas such as process analysis and optimization, prescriptive maintenance, process monitoring and machining quality prediction.

Machine learning algorithms rely on characteristic features extracted from sensor signals. Those signal key characteristics are usually statistically parameters such as average and standard deviation. Determining and optimizing key features is then crucial for the machine learning performance and thus, the associated control system reliability. Fractal parameters may be of interest to feed artificial intelligence systems with peculiar yet decisive information.

Fractals, such as snowflakes and cauliflower, are most commonly known objects. Those entities are singular in the way that their geometric patterns are self-repeated at different scales. Those patterns and, thus, their homothetic characteristics can be described using very few scalar variables in order to generate the object. Fractal analysis allows for estimating those quantities from an object. Nowadays, fractal analysis is known to be an efficient noise estimator and quantifier. Despite often being filtered out and left aside, noise carries relevant information that should be considered.

Fractal analysis has been successfully used for several years in finance trading and bioengineering. Fractal analysis and algorithms originated from chaos theory. They have been implemented since the beginning of the century to forecast stocks and financial products trends [2,3]. In medicine, fractal analysis is used in detection of multiple cancer types using data from computerized tomography (CT), positron emission tomography (PET), Positron Emission Tomography/Computed Tomography (PET-CT), magnetic resonance imaging (MRI) and ultrasound scans [4]. A major progress had also been made possible several years ago on cardiac issues. For example, a few days ahead of cardiac arrest, the heart pulse pattern changes. Fractal analysis allows identifying the changing point, allowing the patient to be treated in time and reducing aftermath problems.

Despite performing results and outstanding possibilities, fractal analysis remains largely underused in many fields, including manufacturing. Setting up this form of analysis may be one of the reasons [5]. Other reasons of the disregard for fractal analysis may be:

• the difficulty of comprehending the fractal analysis concept;
• the relatively complex adaptation of this technique to, e.g., machining monitoring.

The implementation of fractal analysis either in a standalone model or embedded within a control system could drastically improve the diagnosis capabilities of a manufacturing process or machine.

This manuscript presents an example of fractal analysis in order to fully comprehend the different pros and cons of such technique. That approach is indeed needed to see possible performing applications. Then, examples of fractal analysis applications are presented.

2. Fractal Analysis Method

Fractal analysis is a calculation technique allowing the user, among other things, to extract a fractal dimension from a set or an object [6]. The fractal dimension is linked to the topological dimension also called covering dimension which has positive integer values. The covering dimension of a curve in a 2-dimensional space and a curve in a 3-dimensional space admits, respectively, 2 and 3 as values. The fractal dimension can have positive real values, which are between the covering dimension of the object and the covering dimension below. For example, the fractal dimension of a curve in an X-Y graph has a value between one and two. For a fractal dimension close to one, the set tends to be a linear curve. For a fractal dimension close to two, the curve tends to have so much high disturbance, it could nearly be filling the whole window of observation [7].

In practice, the fractal dimension can be associated with the signal complexity. Other parameters can be extracted from fractal analysis providing different type of information such as the signal auto-scale regularity and the ruggedness.

To evaluate the fractal dimension and other parameters, the fractal analysis relies on screening of the object at different scales. The first disclosed technique, introduced in the 1960s, is the ‘stick’ fractal analysis.

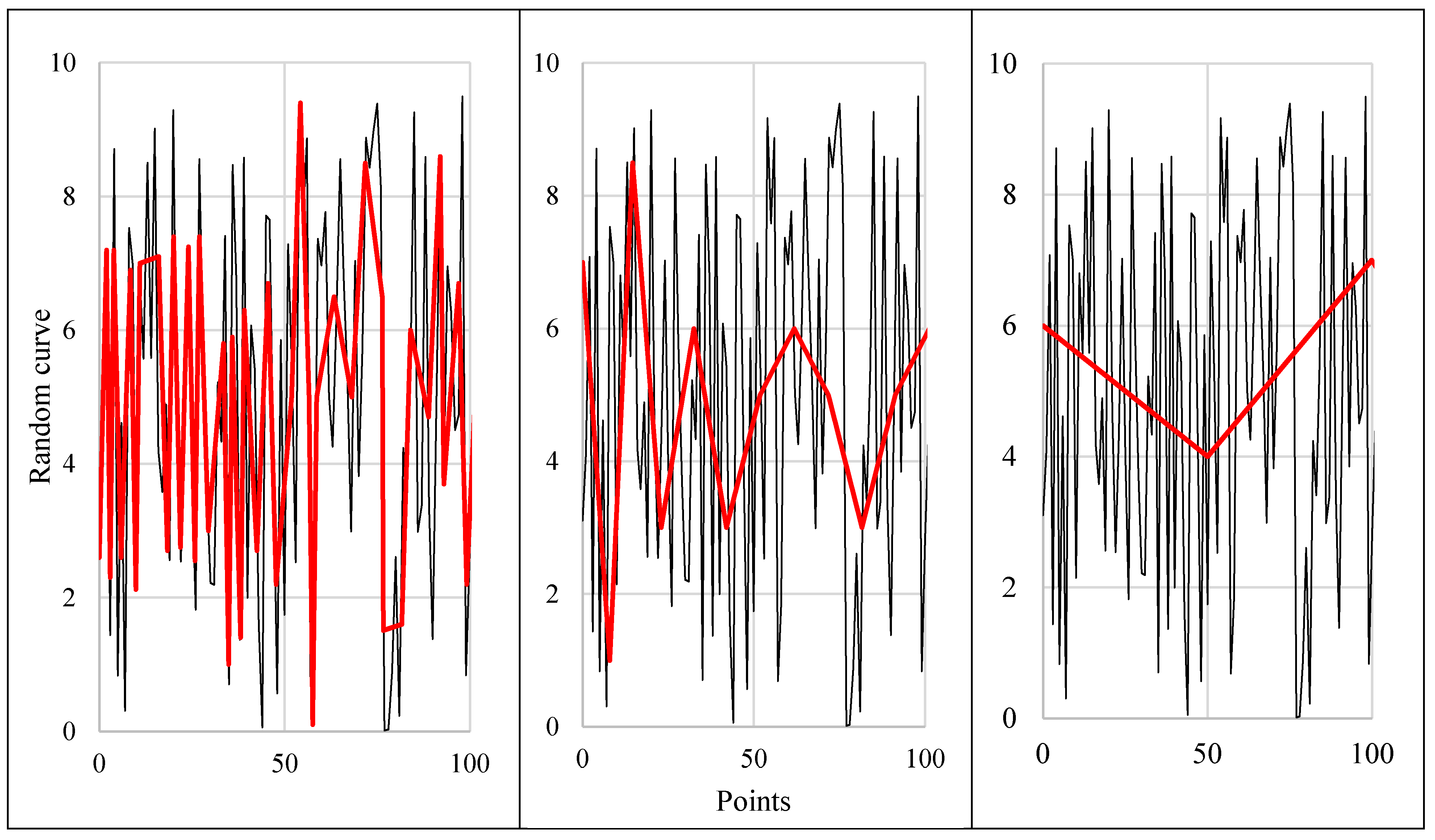
The stick analysis of a 2-dimension curve consists in approximating the curve using different stick sizes (Figure 1). The curve to be analyzed is built by linear approximations of 100 random points. For each stick size, the curve length is calculated using the approximation as the number of sticks times the stick length.

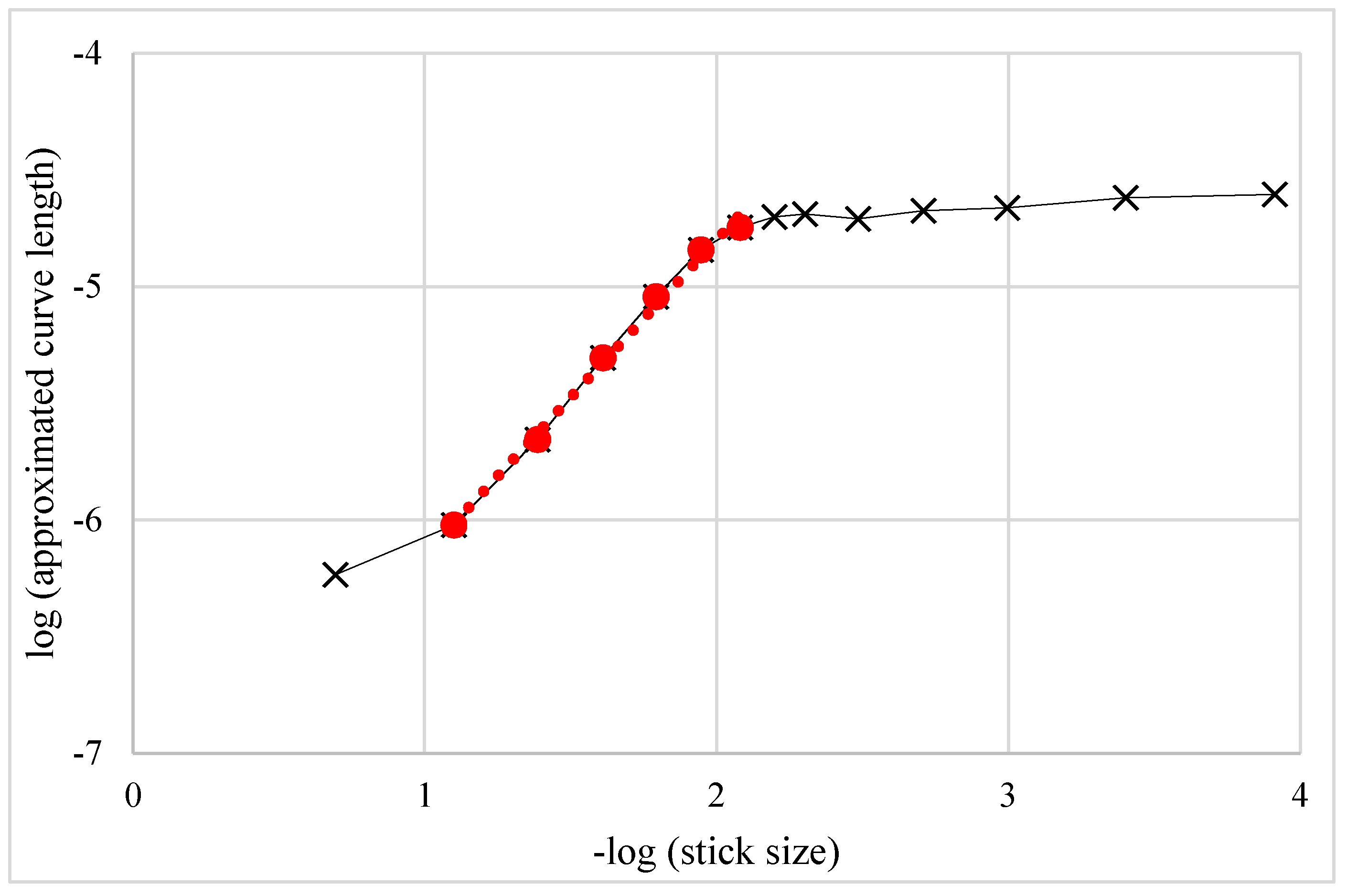
Then, a log-log graph is plotted (Figure 2). The log of the curve length l_a (approximated with a-length sticks) in regards with the log the stick length a (5 stick, 10 stick and 50 stick length from left to right).

In Figure 2, a region of interest is selected where the fractal dimension is to be calculated as the linear regression slope. The region of interest is traditionally the curve section for the smallest stick lengths (so lowest a values) where the log-log graph has no major oscillations or drastic variations. In this example, the assessed fractal dimension is 1.35.

This example illustrates the fractal analysis concept, but its stick analysis admits different drawbacks such as the strong edge effect and a relatively high result deviation. Different types of fractal analysis include box-counting, correlation, power-spectrum and wavelet transform. For instance, box-counting fractal analysis is very similar type of analysis to the stick analysis previously shown. It consists in meshing an object using different size box elements. The number of boxes containing the object is then evaluated vs the box to calculate the fractal dimension [8]. The fractal analysis computed using power-spectrum consists of evaluating the fractal dimension using different frequencies of the power-spectrum [9]. The wavelet transform fractal analysis uses the length estimation of the product of the wavelet transform and the curve [10].

Few of those fractal analysis have been studied to analyze cutting force signals acquired while machining composite plates [11]. One of them, the regularization fractal analysis, produced the best results in terms of calculation time and performance to evaluate the tool wear.

3. Limitations of Fractal Analysis Use

As previously stated, fractal analysis is an excellent noise quantifier. However, fractal analysis suffers from different drawbacks that curbed research and development in various domains. The first obstacle is related to the difficulty of comprehending the fractal analysis concept [5].

The second point is the lack of a link to the application due to the relatively complex adaptation of this technique. Most researchers use fractal analysis as an end and not a mean. This prevented any interest emerging from industrials because it therefore lacked a connection to their problems.

Another point also relies on the lack of comprehension of the use of the technique in regard to the application. For example, a monitoring and control system is often set to ensure manufacturing deviation and scrapped parts are pinpointed and reduced. Before handing the task over to data analysis, engineers need to investigate occurring or possible problems. Typical techniques are FMEA and/or DIVE processes.

Finally, another limitation of fractal analysis use remains in the characteristic differences amongst existing fractal analyses. Because of the lack of knowledge in this subject, researchers tend to use the most known form of fractal analysis, which is often box-counting. However, severe drawbacks have already been highlighted [5].

4. Sample of Applications of Fractal Analysis in the Machine Shop

Thanks to its good characterization of noise, fractal analysis has been regularly used in advanced surface roughness evaluation [12]. However, in machining process and in manufacturing, its use mainly remains for academic research purposes. As previously mentioned, the relative complexity of fractal analysis and unfamiliar approach of the chaos theory is a major obstacle towards its use in the industry. Nevertheless, the already proven strong performance of this technique in other fields shows the gains that could be brought in an industry 4.0 environment.

Different fractal analysis or chaotic analysis were investigated for research purposes but very few are used in production. Hereafter, a few applications in the machine shop have been already explored and will be further investigated for future implementations. Process monitoring and machine maintenance are two fields where fractal analysis could excel as a key features generator.

4.1. Application to the Machining Process Monitoring

Up to now, studies have mainly been limited to tool wear estimation. Bukkapatnam et al. proposed fractal analysis using attractors to extract information such as the dimension [13]. This technique was associated with neural network in order to estimate the flank in turning for different types of steel alloys. However, precursor, this study resulted in relatively high error in the tool wear estimation in regards with the model complexity. Aside automatization limitations, the proposed model based on attractors requires a fairly large amount of time and extensive experience and expertise with chaos theory and applications.

Rimpault et al. applied the regularization fractal analysis for cutting force and acoustic emission signals in composite trimming, drilling and milling as well as multimaterial stack drilling [11,14,15,16]. In total, different materials were tested: Hand lay-up and automated fiber placed pre-preg carbon epoxy composite, Ti-6Al-4V titanium alloy and 2 types of aluminium alloy. Results differ depending on the setup but, at this early stage, fractal analysis outcomes in this area are promising. Current results of evaluating tool wear using fractal analysis of cutting force signals show a root-mean-square error value reaching 0.0005 mm and outperforming traditional statistical models more than 75% of the time [17].

Even though fractal parameters are well performing and could be already used as key features in the industry, the full potential of fractal analysis is yet to be discovered and further improved upon.

4.2. Application to the Machine Maintenance

On the shop floor, machine maintenance is a crucial and constant activity in order to avoid or reduce costly machine downtime. In machines such as CNCs, maintenance concerns the support of physical items such as drives and spindles but also regards the control of machine errors and their fluctuation in time [18]. In the latter, the use of indirect method to evaluate volumetric errors using an artefact and the machine itself. Volumetric errors could be characterized using fractal analysis to evaluate a drift in the machine accuracy.

Secondly, the CNC machine spindle is a strong maintenance concern. Due to high stresses imposed upon it, the spindle is one of the first causes of machine failure. Repetitive mechanical loads from the contact tool-workpiece are transmitted to spindle bearings. A broken bearing often results in replacing the complete spindle head due to tight tolerances. Current research studies introduced fractal analysis to evaluate the health of a bearing [19,20]. After adapting the method to machine spindle head specificities and further optimization, the maintenance department could better assess the frequency of spindle change.

Monitoring key mechanical components of machine tools is crucial in order to prevent a manufacturing line downtime. Fractal analysis is also a research matter for evaluating the machine geometric errors and proceeding to its calibration.

4.3. Application to the Sensor Fault Diagnosis

Monitoring machining processes, machine tool mechanical devices and machine tool geometric errors are all important elements of manufacturing 4.0. All types of manufacturing monitoring rely on army of sensors. However, sensors may suffer downtime as well.

Environmental contamination, mechanical impact or a sensor old age might be causes of failure [21]. Since the concept of industry 4.0 relies on clusters of sensors, their possible failure has to take into consideration the risk assessment during their aggregation in the control system. Increasing the sensors’ number in the aggregate for a control unit or process could reduce the impact of such failure. However, time response of the system would then be increased due to the higher number of data to treat. In addition, increasing the number of sensors for a predefined acquiring role does not address the issue of the false data contamination into the database and the control system. Ensuring that the data acquired is accurate is vital. The risk of sensor failure can be reduced using planned maintenance. Such action will also lead to cost growth and increase the environmental footprint.

In practice, sensor failures are difficult to spot. Noticing a physical degradation of the sensor may be challenging since they are often physically difficult to reach because of their deep integration into a machine or device.

Identifying a failure using its signal is complex as well. The failed sensor signal can be affected under different forms such as high residual noise, systematic error and signal drifting. Additionally, those alterations can be permanent, triggered or randomly intermittent. Thus, detecting such a variety of possible failure consequences is difficult and traditional approaches such as statistics may be blind to those changes.

In this study, fractal analysis was successfully applied to extract information related to the health status of a position sensor [22]. The failure cause could not be found but the consequence was a low factor and distorted signal by intermittence. In the measurement cycles, the fractal analysis was proven to be efficient in detecting the fault signal parts either in stationary and dynamic position or in a random selection of the signal.

5. Suggestions for Fractal Analysis Implementation

However efficient fractal analysis is to extract key features, its implementation for a process or sensor monitoring is relatively complex. Firstly, the engineer should evaluate beforehand if other approaches may fit his/her needs such as statistical parameters. Traditional key features still remain valid and would reduce the implementation time.

If further improvement is required, different elements are to taken into consideration. The type of fractal analysis has to be carefully selected. As previously stated, the most well-known fractal analysis technique is the box-counting method. Nevertheless, this method has numerous drawbacks and the reader is advised to favor more robust techniques such as regularization [11].

Once the fractal analysis technique is carefully chosen, the analysis needs to be adapted to the application and the need. Two ways can be followed. The first consists in evaluating the need and potentiality for the feature extraction. For example, surface roughness characterization relies on surface roughness profile or surface. Using fractal parameters to describe the complexity of a surface is a perfect fit. In the recorded data from the surface profile, the roughness information is associated with the relatively high frequency variations and so the range for the fractal analysis is quite easy to evaluate.

The second way is more empirical and requires a higher level of expertise but produces significantly better results. It consists in observing the fractal dimension determination log-log graph along with the raw data being scrutinized and estimating the ranges for the fractal dimension keeping in mind the application requirements.

Besides the adaptation of the analysis to an application, the efficiency and reliability of the key feature extraction mainly remains on the quality of the signals for a particular use. Contrary to evaluating the average of the signal, the average reliability assessment is relatively not impacted by the signal frequency.

6. Conclusions

Fractal analysis has been underused for the past decades in the industry, particularly in manufacturing. The good results proven in other domains can be reproduced in the machine shop. With the progression of the industry 4.0 philosophy among machining centers, fractal analysis could be applied to provide machine learning and control systems with non-traditional information from sensor signals. Its use could be implemented in processes to monitor and/or optimize them. Machine maintenance and diagnosis could be strongly improved as well.

Regarding fractal analysis, a guide or manual should be proposed in order to have a relatively easy step-by-step tutorial for fractal analysis use and implementation. A comparison of various types of fractal analysis should also be presented in order to help engineers and scientists make a more informed selection of the fractal analysis type they could use for their application.