Intra- and Inter-Repeatability of Profile Deviations of an AlSi10Mg Tooling Component Manufactured by Laser Powder Bed Fusion
Abstract
1. Introduction
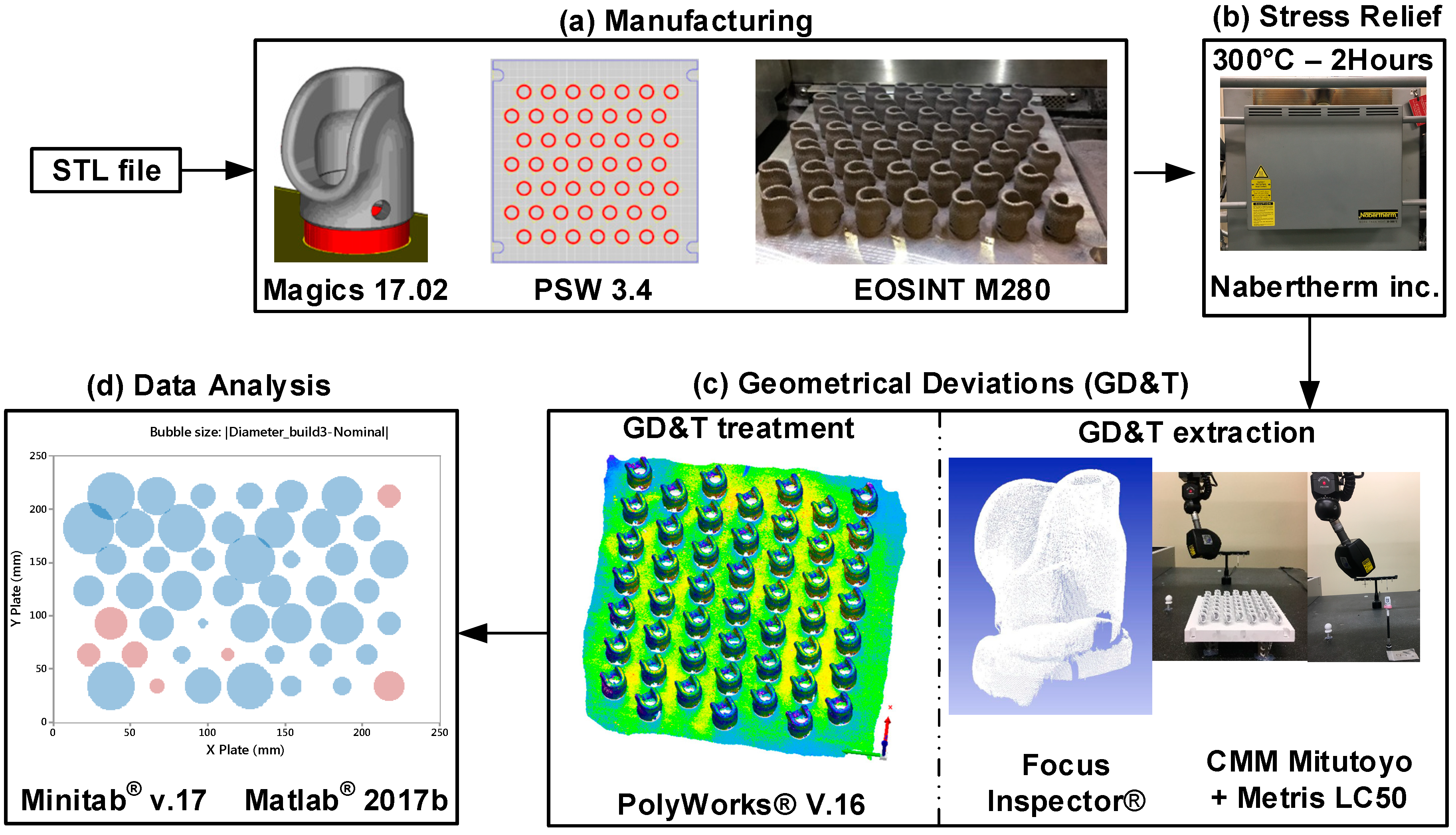
2. Experimental Protocol
2.1. Intra-Build Variations Study
2.2. Inter-Build Variations Study
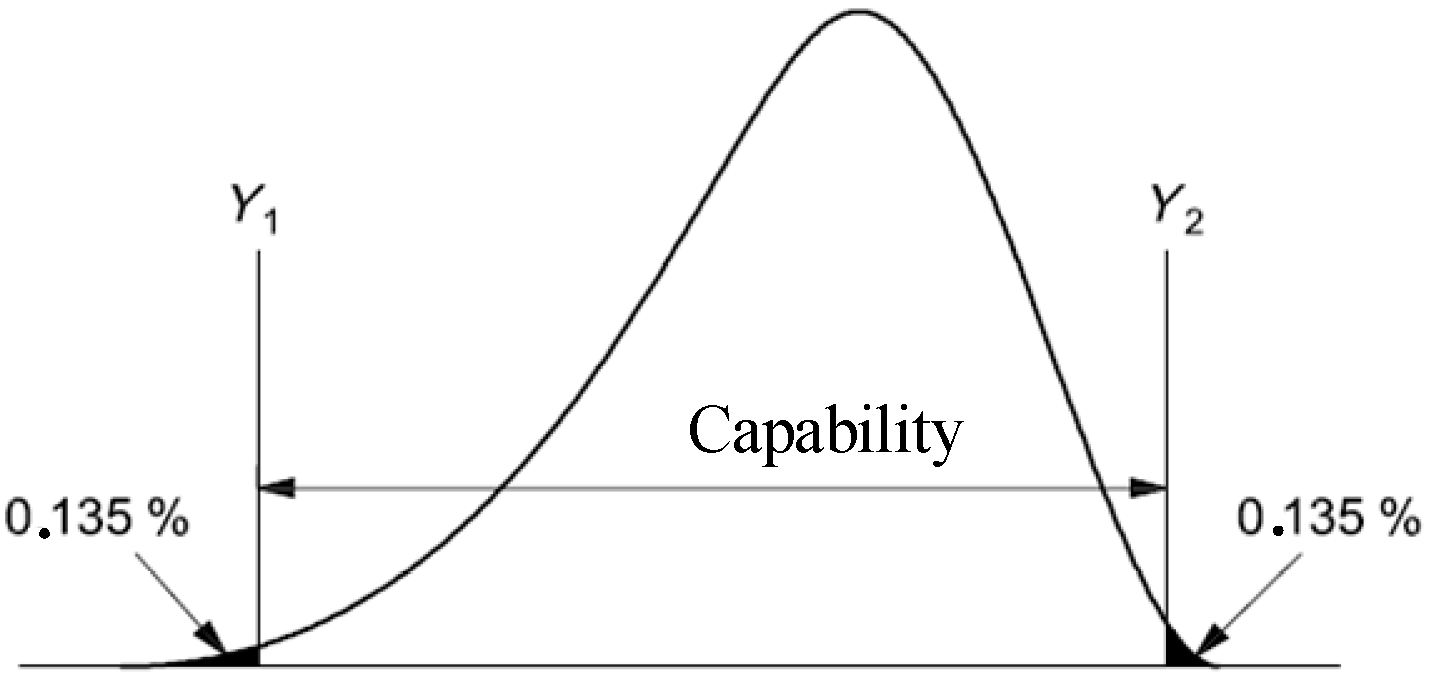
2.3. Capability Study
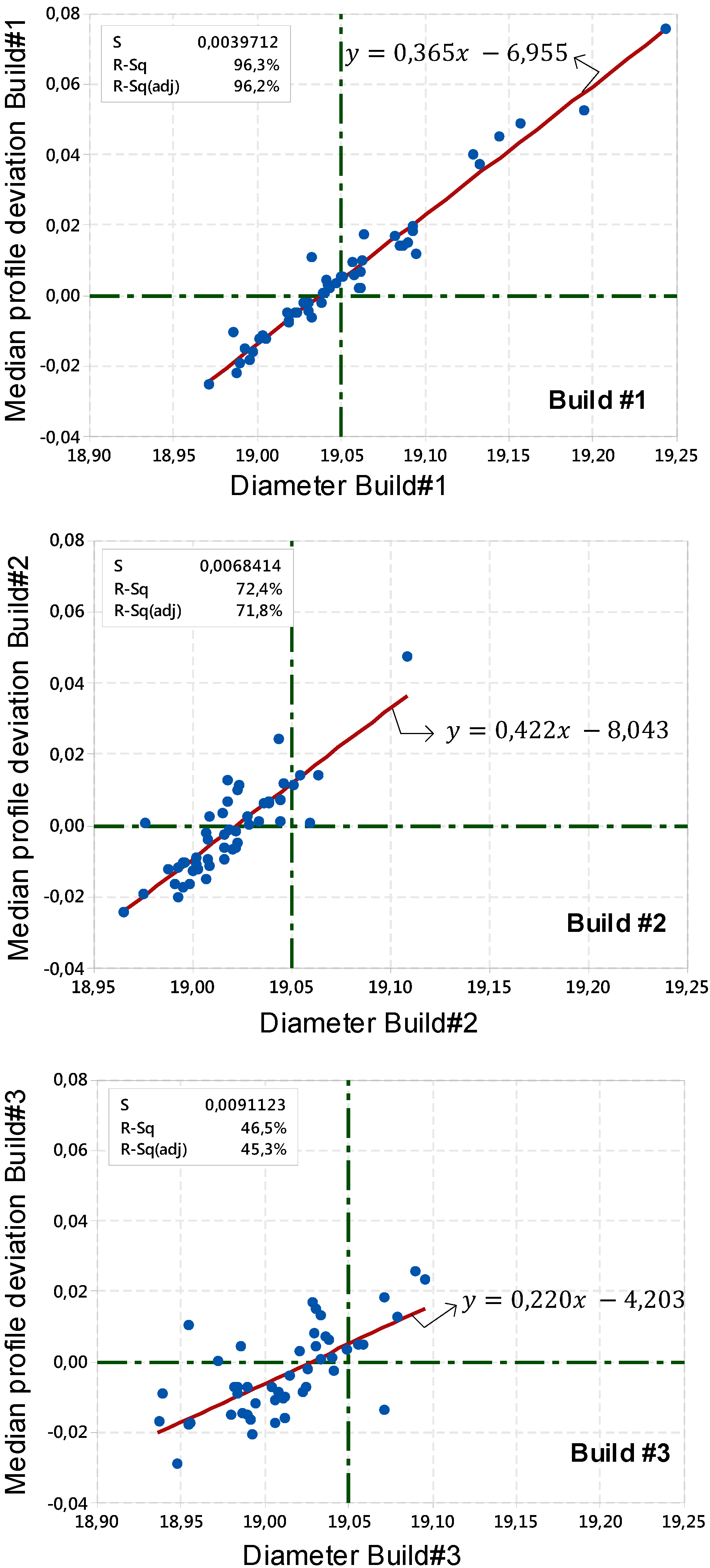
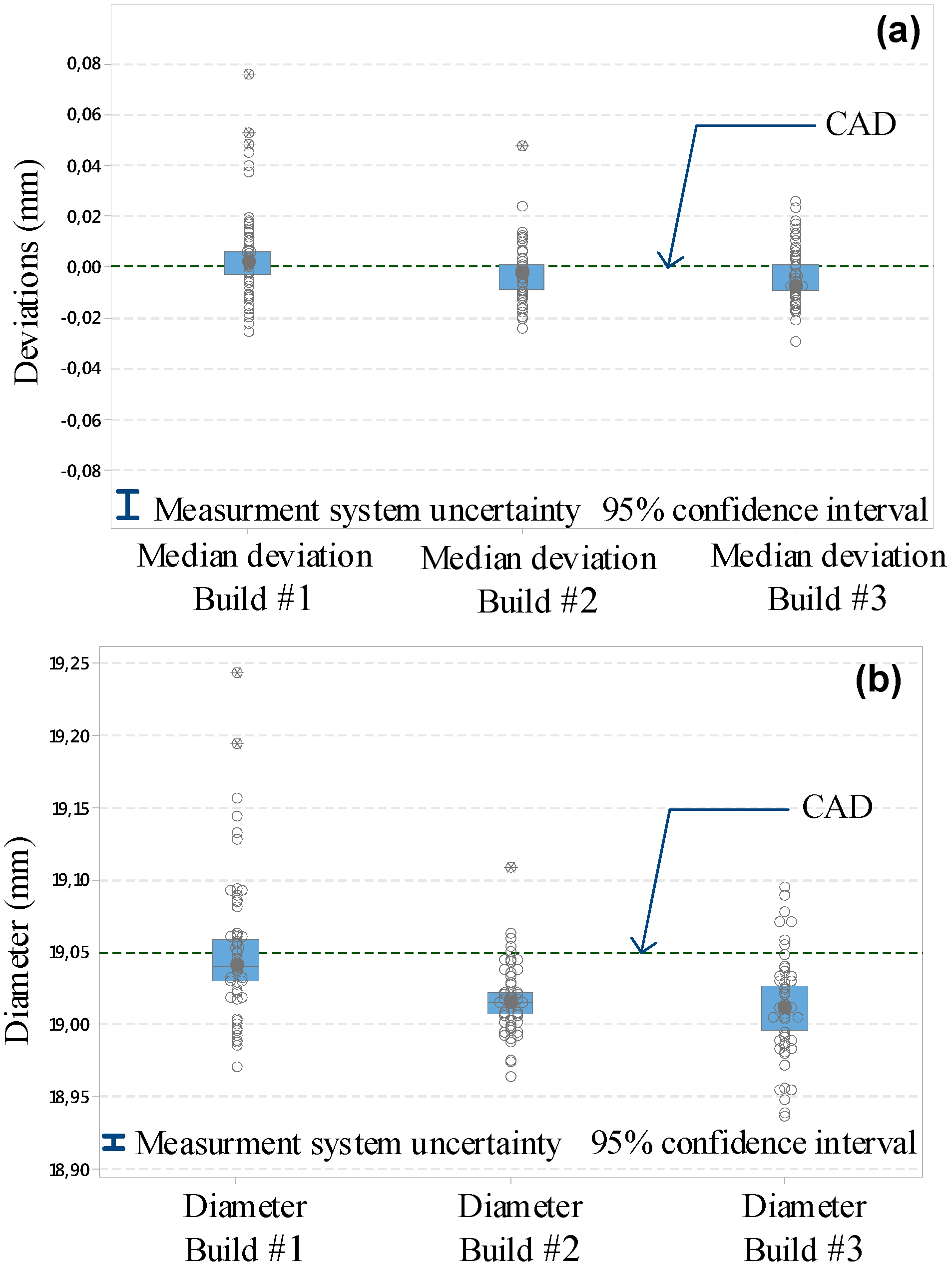
3. Results
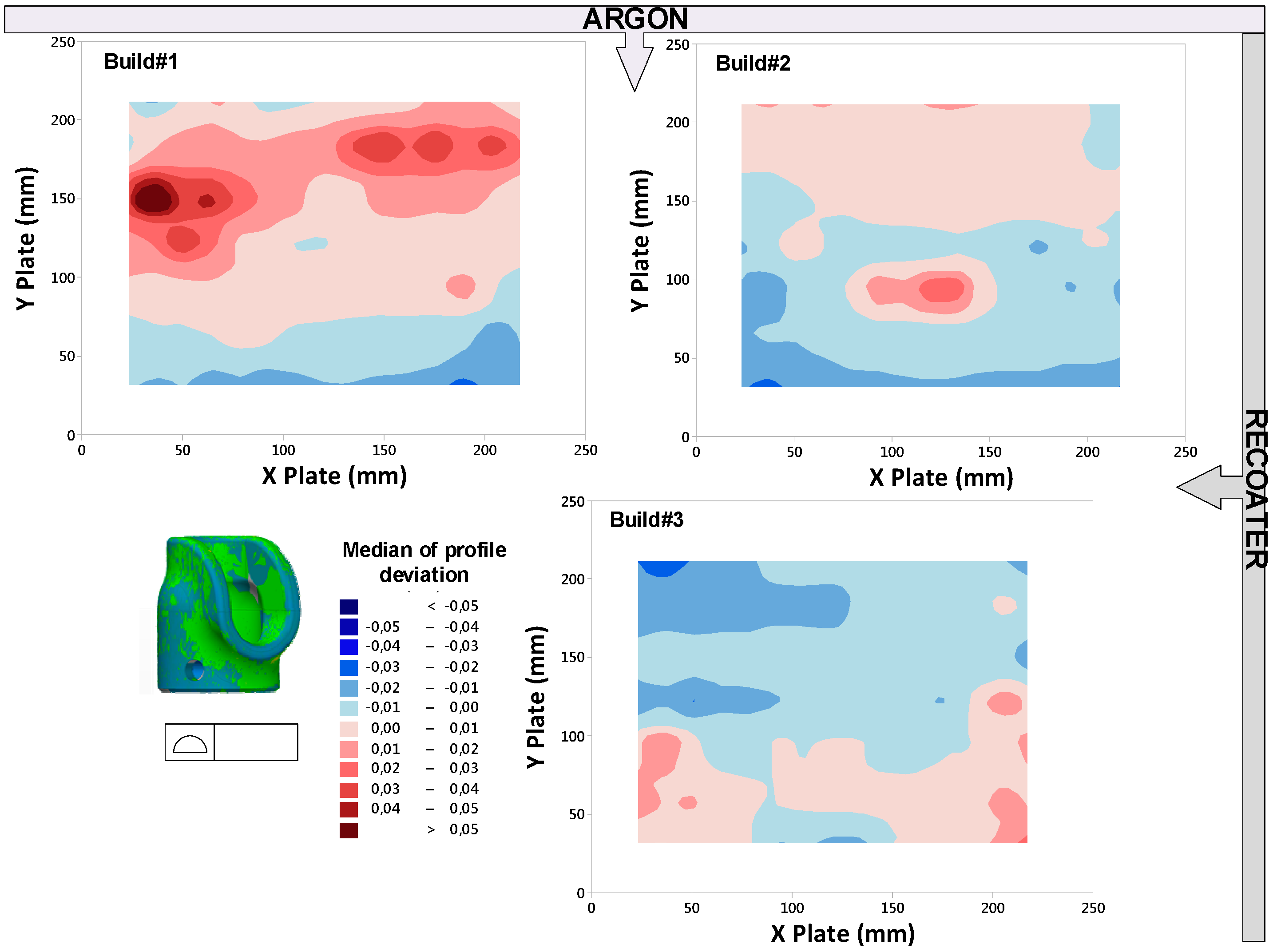
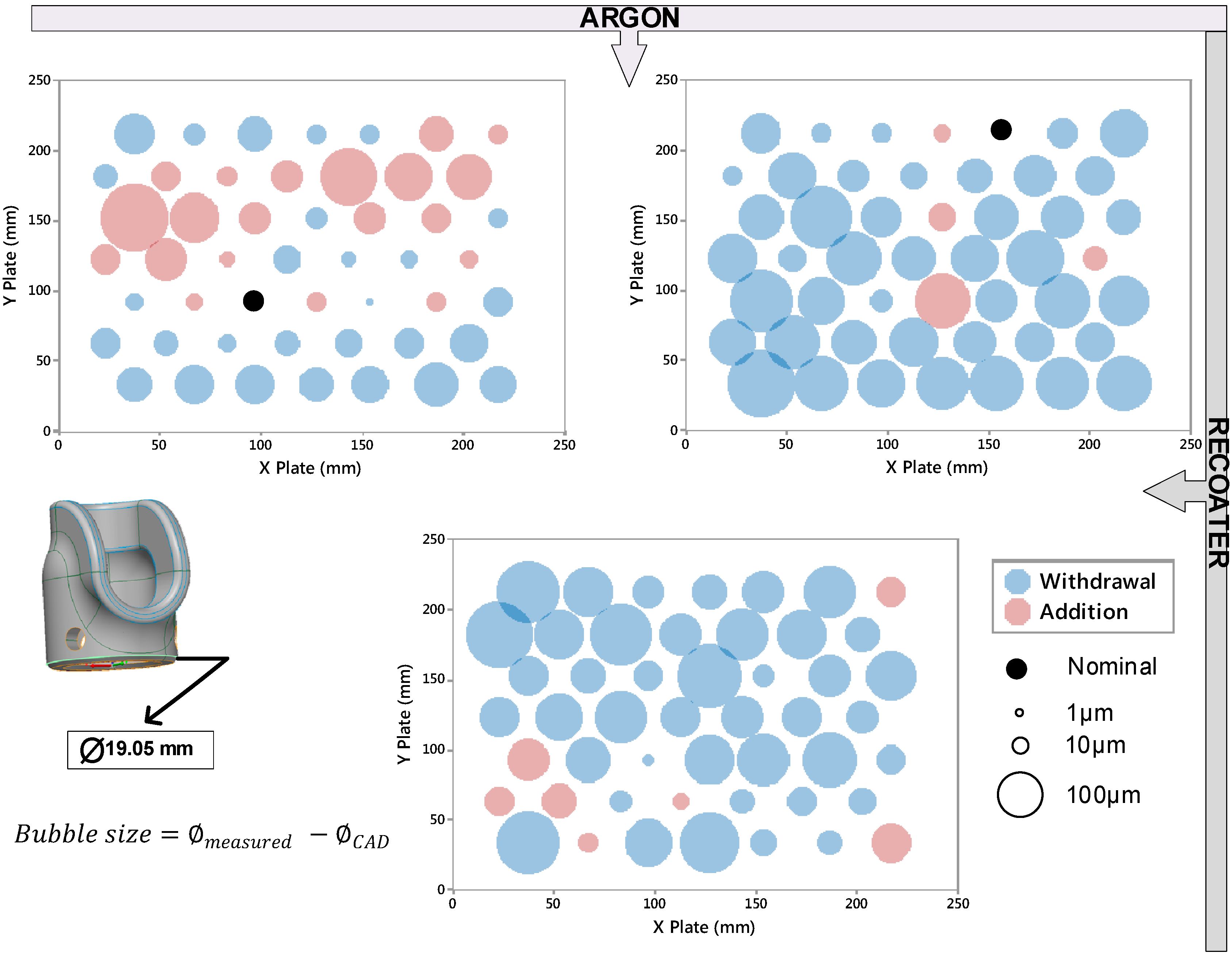
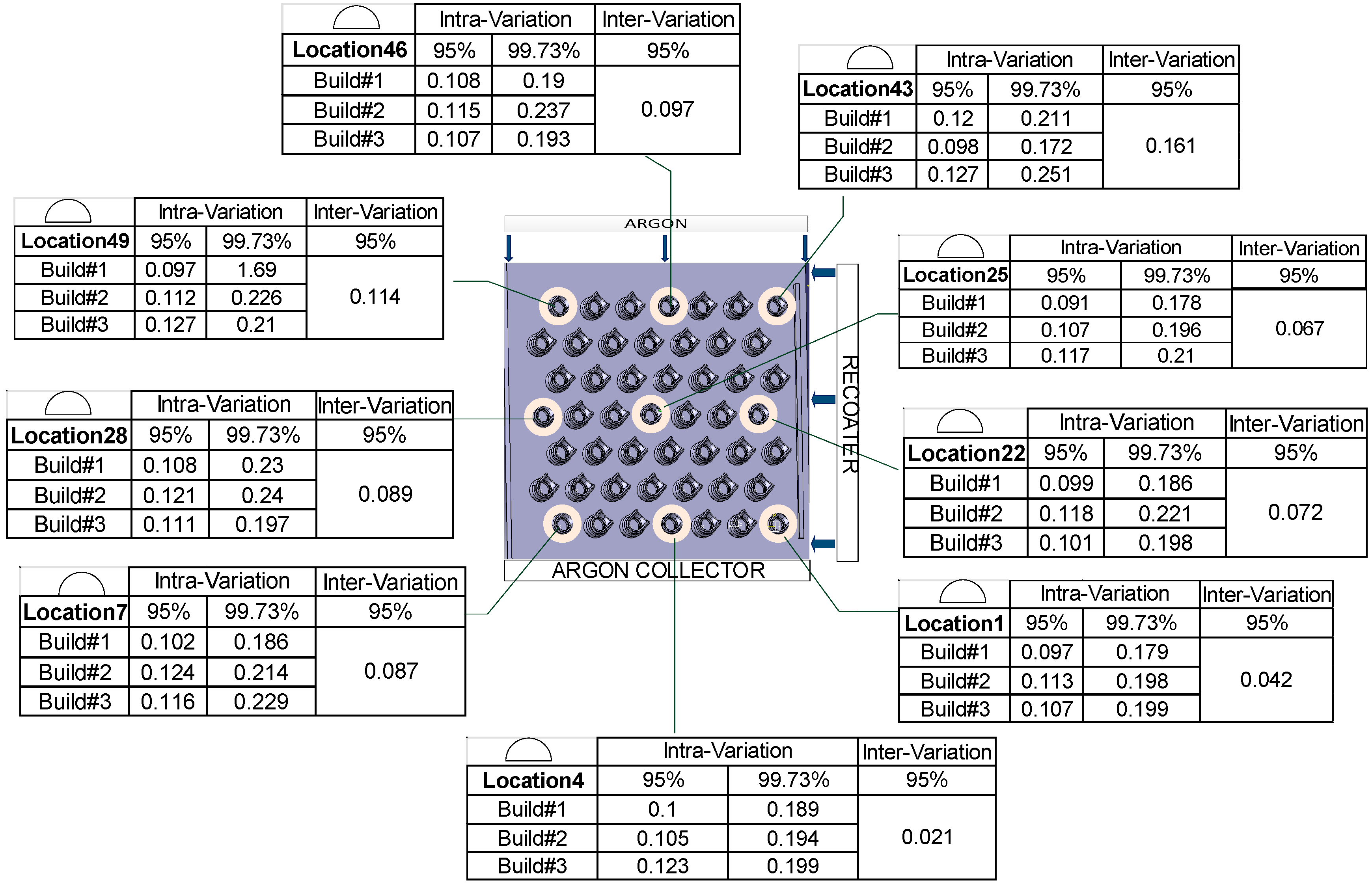
3.1. Intra-Build Variations
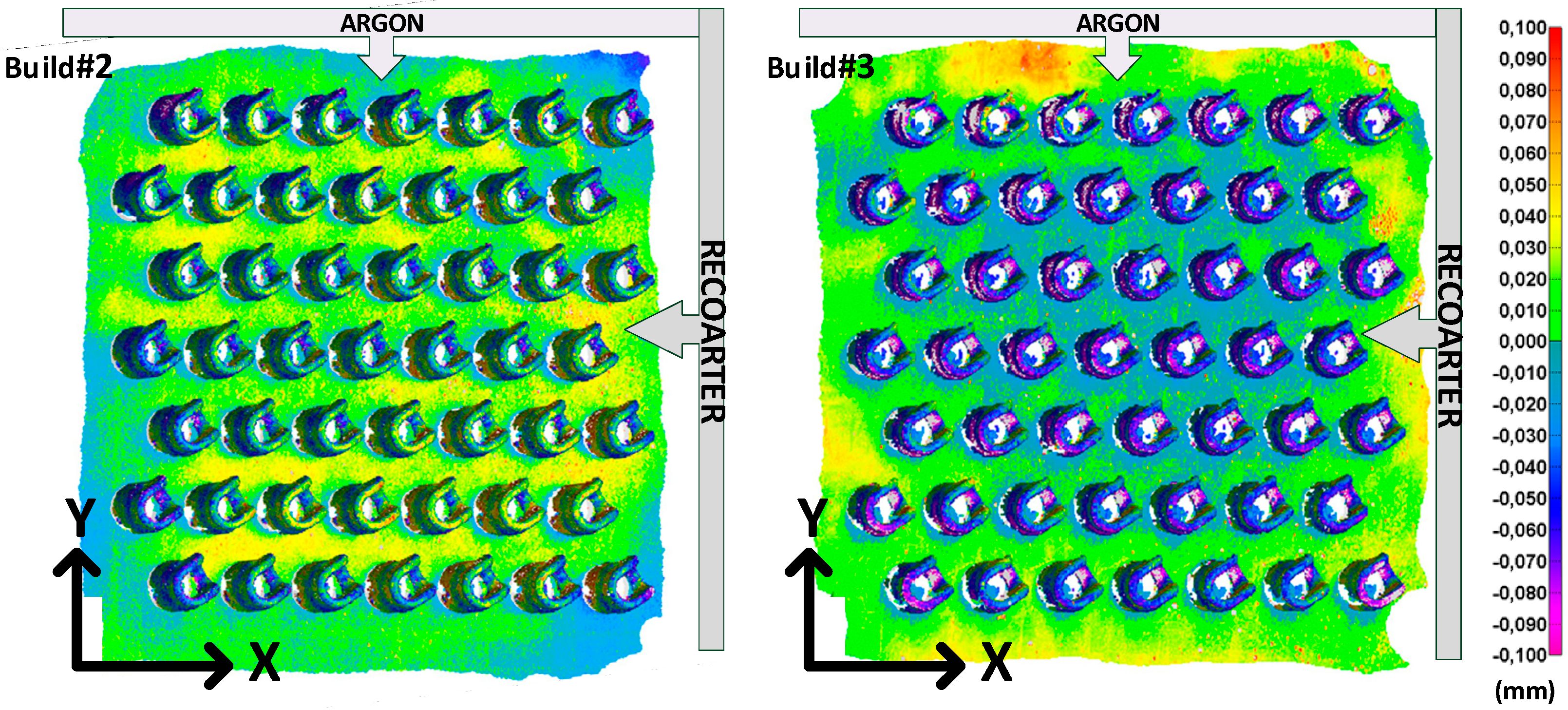
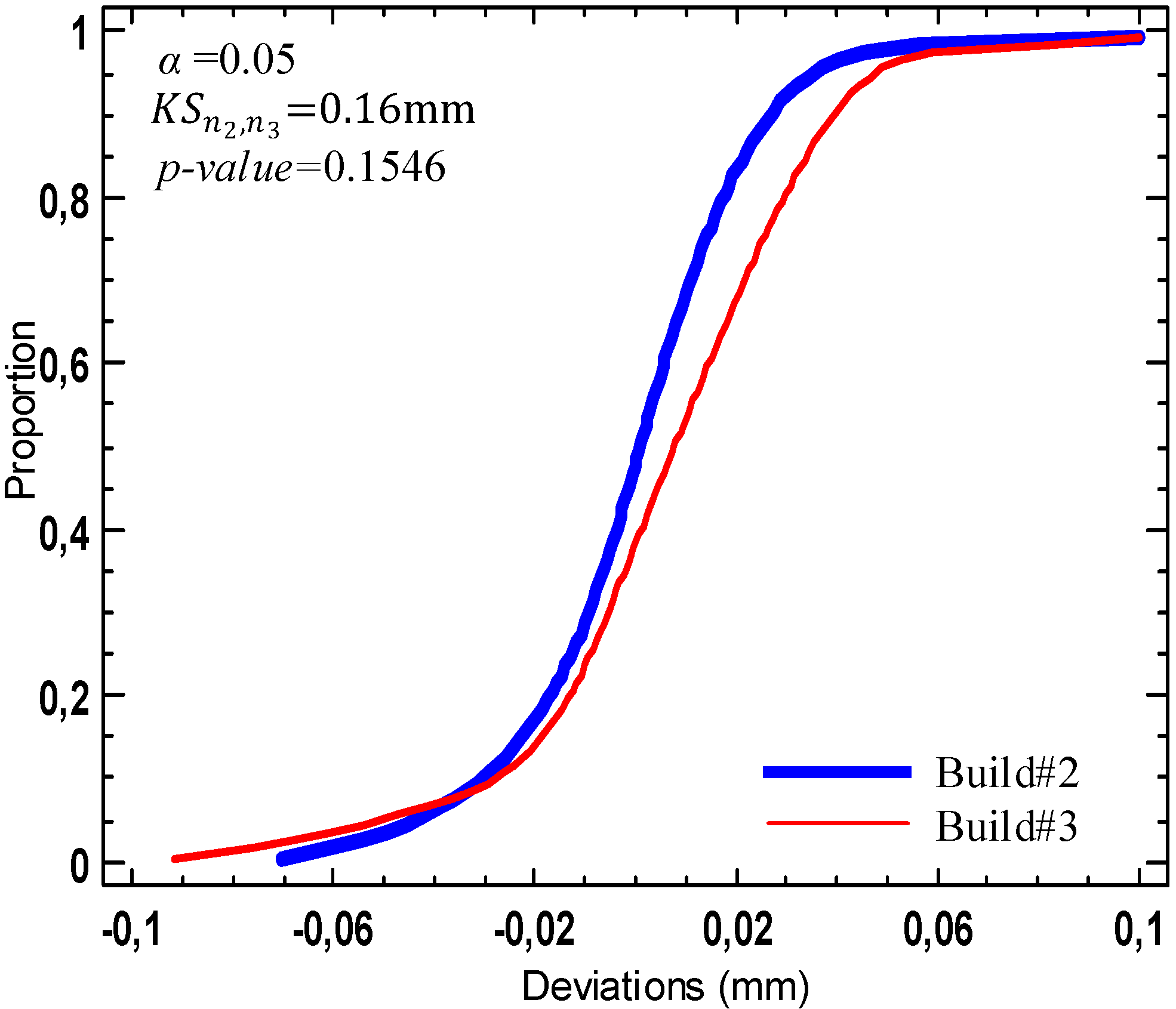
3.2. Inter-Build Variations
3.3. Capability
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ASTM-ISO. Standard Guide for Additive Manufacturing—General Principles—Requirements for Purchased AM Parts; ASTM52901-16; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- ASTM-ISO. ISO/ASTM 52900: 2015 Additive Manufacturing—General Principles—Terminology; ASTM F2792-10e1; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Wohlers, T.; Caffrey, T. Wohlers Report 2014: Additive Manufacturing and 3D Printing State of the Industry; Annual Worldwide Progress Report; Wohlers Associates Inc.: Fort Collins, CO, USA, 2017. [Google Scholar]
- Shiomi, M.; Osakada, K.; Nakamura, K.; Yamashita, T.; Abe, F. Residual stress within metallic model made by selective laser melting process. CIRP Ann. Manuf. Technol. 2004, 53, 195–198. [Google Scholar] [CrossRef]
- Wang, X. Calibration of shrinkage and beam offset in SLS process. Rapid Prototyp. J. 1999, 5, 129–133. [Google Scholar] [CrossRef]
- Zhu, H.; Lu, L.; Fuh, J. Study on shrinkage behaviour of direct laser sintering metallic powder. Proc. Inst. Mech. Eng. Part B 2006, 220, 183–190. [Google Scholar] [CrossRef]
- Raghunath, N.; Pandey, P.M. Improving accuracy through shrinkage modelling by using Taguchi method in selective laser sintering. Int. J. Mach. Tools Manuf. 2007, 47, 985–995. [Google Scholar] [CrossRef]
- Islam, M.N.; Sacks, S. An experimental investigation into the dimensional error of powder-binder three-dimensional printing. Int. J. Adv. Manuf. Technol. 2016, 82, 1371–1380. [Google Scholar] [CrossRef]
- Senthilkumaran, K.; Pandey, P.M.; Rao, P. New model for shrinkage compensation in selective laser sintering. Virtual Phys. Prototyp. 2009, 4, 49–62. [Google Scholar] [CrossRef]
- Galovskyi, B.H.T. Testing Workpieces for Selective Laser Sintering. In Proceedings of the ASPE 2015 Spring Topical Meeting, Golden, CO, USA, 8–10 July 2015; pp. 89–94. [Google Scholar]
- Van Bael, S.; Kerckhofs, G.; Moesen, M.; Pyka, G.; Schrooten, J.; Kruth, J.-P. Micro-CT-based improvement of geometrical and mechanical controllability of selective laser melted Ti6Al4V porous structures. Mater. Sci. Eng. A 2011, 528, 7423–7431. [Google Scholar] [CrossRef]
- Silva, D.N.; De Oliveira, M.G.; Meurer, E.; Meurer, M.I.; da Silva, J.V.L.; Santa-Bárbara, A. Dimensional error in selective laser sintering and 3D-printing of models for craniomaxillary anatomy reconstruction. J. Cranio-Maxillo-Fac. Surg. 2008, 36, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Vanderesse, N.; Ky, I.; González, F.Q.; Nuño, N.; Bocher, P. Image analysis characterization of periodic porous materials produced by additive manufacturing. Mater. Des. 2016, 92, 767–778. [Google Scholar] [CrossRef]
- Kruth, J.-P. Material incress manufacturing by rapid prototyping techniques. CIRP Ann. Manuf. Technol. 1991, 40, 603–614. [Google Scholar] [CrossRef]
- Lart, G. Comparison of rapid prototyping systems. In Proceedings of the First European Conference on Rapid Prototyping, University of Nottingham, Nottingham, UK, 6–7 July 1992; pp. 6–7. [Google Scholar]
- Grimm, T. Fused deposition modelling: A technology evaluation. Time Compress. Technol. 2003, 11, 1–6. [Google Scholar]
- Castillo, L. Study about the Rapid Manufacturing of Complex Parts of Stainless Steel and Titanium; TNO Report with the Collaboration of AIMME; TNO: Delft, The Netherlands, 2005. [Google Scholar]
- Abdel Ghany, K.; Moustafa, S. Comparison between the products of four RPM systems for metals. Rapid Prototyp. J. 2006, 12, 86–94. [Google Scholar] [CrossRef]
- Dimitrov, D.; Van Wijck, W.; Schreve, K.; De Beer, N. Investigating the achievable accuracy of three dimensional printing. Rapid Prototyp. J. 2006, 12, 42–52. [Google Scholar] [CrossRef]
- Hanumaiah, N.; Ravi, B. Rapid tooling form accuracy estimation using region elimination adaptive search based sampling technique. Rapid Prototyp. J. 2007, 13, 182–190. [Google Scholar] [CrossRef]
- Cooke, A.L.; Soons, J.A. Variability in the geometric accuracy of additively manufactured test parts. In Proceedings of the 21st Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 9–11 August 2010; pp. 1–12. [Google Scholar]
- Moylan, S.; Slotwinski, J.; Cooke, A.; Jurrens, K.; Donmez, M.A. Proposal for a standardized test artifact for additive manufacturing machines and processes. In Proceedings of the 2012 Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2012; pp. 6–8. [Google Scholar]
- Minetola, P.; Iuliano, L.; Marchiandi, G. Benchmarking of FDM machines through part quality using IT grades. Procedia CIRP 2016, 41, 1027–1032. [Google Scholar] [CrossRef]
- Fahad, M.; Hopkinson, N. A new benchmarking part for evaluating the accuracy and repeatability of Additive Manufacturing (AM) processes. In Proceedings of the 2nd International Conference on Mechanical, Production and Automobile Engineering (ICMPAE 2012), Singapore, 28–29 April 2012; pp. 28–29. [Google Scholar]
- Teeter, M.G.; Kopacz, A.J.; Nikolov, H.N.; Holdsworth, D.W. Metrology test object for dimensional verification in additive manufacturing of metals for biomedical applications. Proc. Inst. Mech. Eng. Part H 2015, 229, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Ferrar, B.; Mullen, L.; Jones, E.; Stamp, R.; Sutcliffe, C. Gas flow effects on selective laser melting (SLM) manufacturing performance. J. Mater. Process. Technol. 2012, 212, 355–364. [Google Scholar] [CrossRef]
- Aidibe, A.; Tahan, A.; Brailovski, V. Metrological investigation of a selective laser melting additive manufacturing system: A case study. IFAC-PapersOnLine 2016, 49, 25–29. [Google Scholar] [CrossRef]
- Rebaioli, L.; Fassi, I. A review on benchmark artifacts for evaluating the geometrical performance of additive manufacturing processes. Int. J. Adv. Manuf. Technol. 2017, 93, 2571–2598. [Google Scholar] [CrossRef]
- Sing, S.L.; Wiria, F.E.; Yeong, W.Y. Selective laser melting of lattice structures: A statistical approach to manufacturability and mechanical behavior. Robot. Comput. Integr. Manuf. 2018, 49, 170–180. [Google Scholar] [CrossRef]
- Calignano, F. Investigation of the accuracy and roughness in the laser powder bed fusion process. Virtual Phys. Prototyp. 2018, 13, 97–104. [Google Scholar] [CrossRef]
- Wilcox, R. Kolmogorov–Smirnov Test. In Encyclopedia of Biostatistics; John Wiley & Sons, Ltd.: New York, NY, USA, 2005. [Google Scholar]
- Mooney, C.Z. Monte Carlo Simulation; Sage Publications: Thousand Oaks, CA, USA, 1997; Volume 116. [Google Scholar]
- American Society of Mechanical Engineers. Mathematical Definition of Dimensioning and Tolerancing Principles: ASME Y14. 5.1 M-1994; American Society of Mechanical Engineers: New York, NY, USA, 1995. [Google Scholar]


| Build | |||||
|---|---|---|---|---|---|
| #1 | 19.053 | 0.054 | 18.970 | 19.041 | 19.243 |
| #2 | 19.017 | 0.025 | 18.964 | 19.015 | 19.108 |
| #3 | 19.012 | 0.038 | 18.936 | 19.011 | 19.095 |
 for 49 parts (dimensions in mm).
for 49 parts (dimensions in mm).| Build | 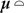 |  | 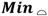 | 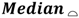 | 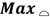 |
|---|---|---|---|---|---|
| #1 | 0.148 | 0.058 | 0.108 | 0.131 | 0.501 |
| #2 | 0.152 | 0.023 | 0.124 | 0.149 | 0.276 |
| #3 | 0.147 | 0.014 | 0.116 | 0.148 | 0.181 |
| Build | 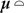 |  | 95% | 97.73% |
|---|---|---|---|---|
| #1 | 0.005 | 0.034 | 0.136 | 0.240 |
| #2 | 0.000 | 0.032 | 0.127 | 0.225 |
| #3 | −0.002 | 0.030 | 0.121 | 0.191 |
| Overall | 0.001 | 0.032 | 0.128 (IT 11) | 0.228 (IT 12) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zongo, F.; Tahan, A.; Aidibe, A.; Brailovski, V. Intra- and Inter-Repeatability of Profile Deviations of an AlSi10Mg Tooling Component Manufactured by Laser Powder Bed Fusion. J. Manuf. Mater. Process. 2018, 2, 56. https://doi.org/10.3390/jmmp2030056
Zongo F, Tahan A, Aidibe A, Brailovski V. Intra- and Inter-Repeatability of Profile Deviations of an AlSi10Mg Tooling Component Manufactured by Laser Powder Bed Fusion. Journal of Manufacturing and Materials Processing. 2018; 2(3):56. https://doi.org/10.3390/jmmp2030056
Chicago/Turabian StyleZongo, Floriane, Antoine Tahan, Ali Aidibe, and Vladimir Brailovski. 2018. "Intra- and Inter-Repeatability of Profile Deviations of an AlSi10Mg Tooling Component Manufactured by Laser Powder Bed Fusion" Journal of Manufacturing and Materials Processing 2, no. 3: 56. https://doi.org/10.3390/jmmp2030056
APA StyleZongo, F., Tahan, A., Aidibe, A., & Brailovski, V. (2018). Intra- and Inter-Repeatability of Profile Deviations of an AlSi10Mg Tooling Component Manufactured by Laser Powder Bed Fusion. Journal of Manufacturing and Materials Processing, 2(3), 56. https://doi.org/10.3390/jmmp2030056





