Reinforcement Learning-Based PD Controller Gains Prediction for Quadrotor UAVs

Abstract

This paper presents a reinforcement learning (RL)-based methodology for the online fine-tuning of PD controller gains, with the goal of bridging the gap between simulation-trained controllers and real-world quadrotor applications. As a first step toward real-world implementation, the proposed approach applies a Deep Deterministic Policy Gradient (DDPG) algorithm—an off-policy actor–critic method—to adjust the gains of a quadrotor attitude PD controller during flight. The RL agent was initially trained offline in a simulated environment, using MATLAB/Simulink 2024a and the UAV Toolbox Support Package for PX4 Autopilots v1.14.0. The trained controller was then validated through both simulation and experimental flight tests. Comparative performance analyses were conducted between the hand-tuned and RL-tuned controllers. Our results demonstrate that the RL-based tuning method successfully adapts the controller gains in real time, leading to improved attitude tracking and reduced steady-state error. This study constitutes the first stage of a broader research effort investigating RL-based PID, LQR, MRAC, and Koopman-integrated RL-based PID controllers for real-time quadrotor control.

1. Introduction

Unmanned aerial vehicles (UAVs) have experienced tremendous growth in recent decades. They have been used in various civilian and public domain applications, such as power line inspection [1], mining area monitoring [2], wildlife conservation and monitoring [3], border protection [4], infrastructure and building inspection [5], and precision agriculture [6], among others. Multirotor UAVs and, in particular, quadrotors have become the most widely used aerial platforms, due to their vertical take-off and landing (VTOL) capabilities, efficient hovering, and overall flight effectiveness.

Although several conventional control techniques have been developed, implemented, and tested effectively for quadrotor navigation and control (via simulation studies, simulated experiments, and in real time), learning-based methodologies and algorithms have recently gained significant momentum, because it has been shown that using them improves platform modeling, thus subsequently enhancing navigation and control effectiveness. A learning-based methodology offers alternatives to parameter tuning and estimation and to learning and understanding the working environment. To this end, several representative surveys on developing and adopting machine learning (ML), deep learning (DL), or reinforcement learning (RL) algorithms for UAV modeling and control have been published. Carrio et al. [7] focus on DL methods and their applications to UAVs. The studies covered in this survey show that DL is effectively used to solve control and navigation problems for UAVs. Also, various controller methods are used to collect the data for the training of the DL agents. Polydoros and Nalpantidis [8] cover model-based reinforcement learning applications in the robotics field, but they also provide a section for RL applications on UAVs. Their survey underscores how model-based approaches can improve control performance in UAV systems by enabling faster adaptation to dynamic environments with fewer real-world interactions. Choi and Cha [9] cover ML techniques on UAVs for autonomous flight. By examining both control mechanisms and perception components, such as object recognition, the authors highlight the substantial progress made in enabling UAVs to execute designated tasks more efficiently and resiliently in dynamic settings. Azar et al. [10] focus on deep reinforcement learning approaches for control and navigation tasks on drones. Brunke et al. [11] study learning-based control in robotic fields. They cover UAVs in their research, and they provide studies comparing learning-based controller and conventional controller performances. The authors’ most recent survey [12] focuses on multirotor navigation and control based on online learning. On a more specific note, Yoo et al. [13] use hybrid RL controllers for a quadrotor. They implement PD-RL and LQR-RL low and high gains for trajectory tracking, maintaining constant gains and deploying the policy on a micro quadrotor platform. Mosweu et al. [14] employ a DDPG-based approach to adjust PD controller gains within a cascaded control structure for a simulated multirotor UAV. The approach in [14] is not deeply explained but appears similar to the author’s prior work [15], which was published shortly beforehand, and which demonstrated the feasibility of RL-based PID parameter tuning and estimation for UAVs. Contrary to the existing literature, this work expands on [14,15] by proposing a training framework that allows for training of the RL agent offline and deploying it on a physical quadrotor UAV in outdoor flights for online controller gain fine-tuning.

The focus of this research was on the real-world implementation and evaluation of a reinforcement learning (RL)-based method for online tuning of PD controller gains, as originally proposed in [15]. This study serves as the first step in a broader research effort that aims to transition various RL-trained controllers—including the PID, LQR, MRAC, and Koopman-integrated PID approaches—from simulation to hardware deployment. Unlike previous simulation-based studies, this work validated the RL-tuned PD controller experimentally on a physical quadrotor UAV. The test platform used an “X” configuration quadrotor, differing from the less conventional “+” configuration adopted in [15], and tracking accuracy was assessed using a circular trajectory rather than the previously tested helix trajectory, due to the safety constraint of the available experimental facility. Accordingly, the RL agent was retrained to account for the updated quadrotor configuration and the new tracking task. While the implementation, at this stage of the research, employed a PD structure to avoid increased controller complexity due to integral windup, the underlying framework is applicable to both PD and PID controllers, and further investigation on full PID implementation with anti-windup strategies, as well as other adaptive control methods, will be the subject of future work.

This research makes four main contributions: (i) It demonstrates the real-world implementation of an RL-based method for fine-tuning the gains of a PD controller on a quadrotor UAV, where the agent is trained in simulation and deployed on hardware without requiring a high-fidelity model that includes drag, gyroscopic effects, or sensor noise. This simplifies the training process while still enabling online adaptation. (ii) The study validates the RL-tuned controller across simulation and real-world outdoor flight tests, highlighting its capacity to adjust control gains in response to external disturbances and model mismatches during flight. (iii) It provides an effective training and development framework for RL-based UAV control strategies, which can be deployed on real hardware flight controller boards (e.g., the Pixhawk flight control unit) and does not require the use of companion computers. Moreover, in doing so, it features a realistic assessment of the challenges faced during sim-to-real transfer, such as the effects of unmodeled dynamics, limited sensor accuracy, and quantized actuator inputs, offering practical insights for future deployments. (iv) The results show that the RL-based control framework is adaptable and effective under different quadrotor configurations and task conditions (e.g., “X” configuration, circular trajectory), thus laying the groundwork for generalizable, platform-independent learning-based control strategies.

Section 2 provides notation and background information related to the mathematical model of the quadrotor, the PD controller with feedback linearization that is implemented, and the RL-based technique. Section 3 introduces the proposed RL-based fine-tuning strategy. Section 4 presents the RL agent environment setup and its implementation in real hardware. The training phase, numerical simulations, and experimental results are provided in Section 5. Section 6 presents our results analysis, and Section 7 concludes the paper.

2. Notation and Background Information

2.1. Quadrotor Mathematical Model

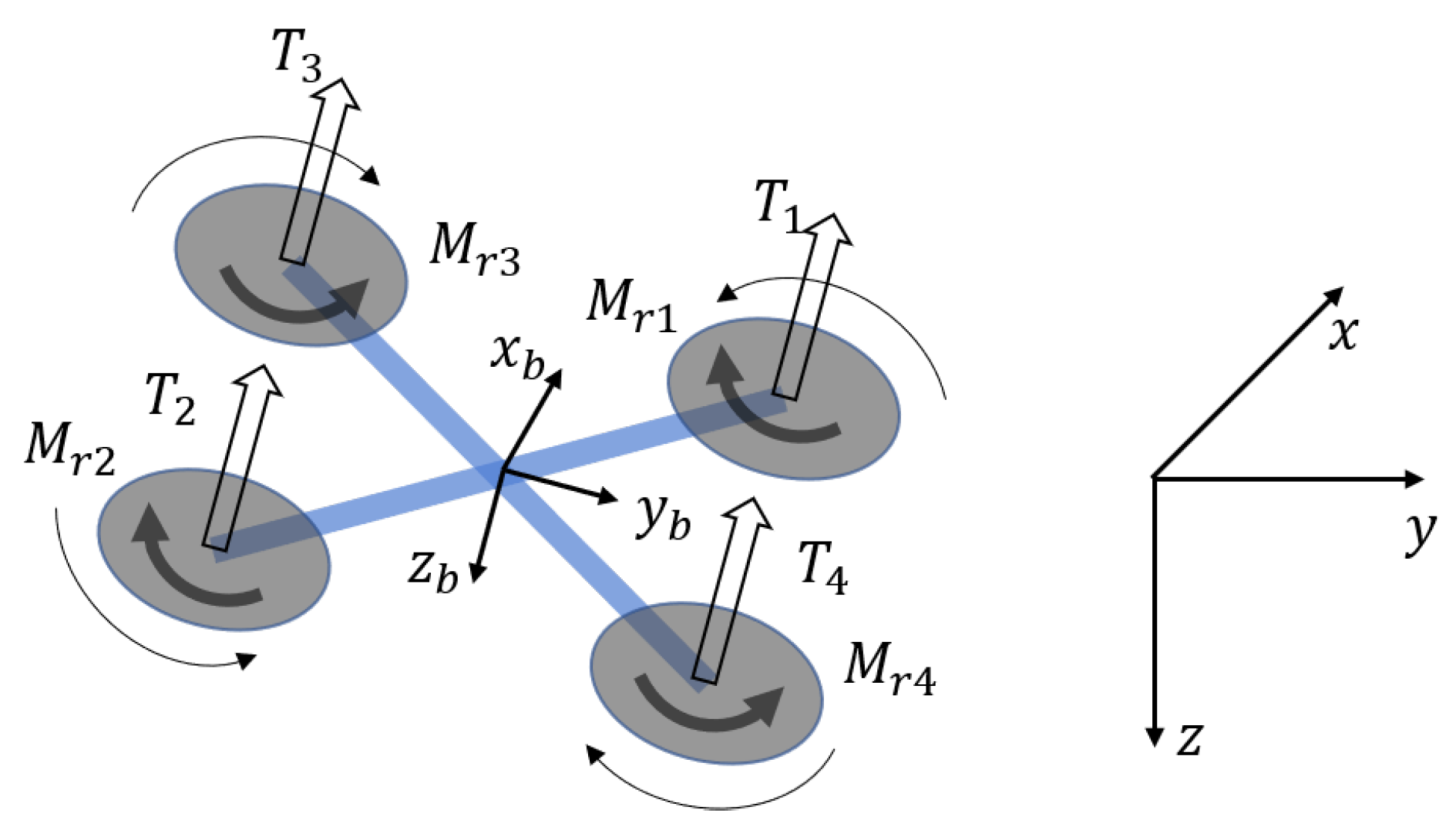
Figure 1 describes the quadrotor structure and reference frame adopted in this work, which is aligned to the PX4 Autopilot convention.

Given two vectors, $a={\left[a_1,a_2,a_3\right]}^{\top }$ and $b={\left[b_1,b_2,b_3\right]}^{\top }$, the matrix $S\left(a\right)$ denotes the skew-symmetric matrix

$$S\left(a\right)=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]$$

(1)

for which the following relation holds: $S\left(a\right)b=a\times b$.

The mathematical model of a quadrotor is derived by considering the “X” configuration, as opposed to the “+” configuration adopted in [15]. The Newton–Euler (N–E) equations of motion are given as follows:

$$\ddot{p}=g\widehat{z}-{\displaystyle \frac{1}{m}}T\mathrm{R}\widehat{\mathrm{z}}$$

(2a)

$$\dot{R}=RS\left({\omega }^B\right)$$

(2b)

$$I_f{\dot{\omega }}^B=-{\omega }^B\times \left(I_f{\omega }^B\right)+M_B$$

(2c)

Let $p={(x,y,z)}^T$ express the position of the body-fixed frame B with respect to the inertial frame E. Gravitational acceleration and mass are defined by g and m, respectively. The unit vector along the z-axis is represented by $\widehat{z}={(0,0,1)}^T$. The rotation matrix $R\in SO\left(3\right)$ maps vectors from the body-fixed frame to the inertial reference frame, and it is parameterized using Euler angles $\eta ={\left[\phi ,\theta ,\psi \right]}^{\top }$ as in [16],

$$R=\left[\begin{array}{ccc}{c}_{\theta }{c}_{\psi }& s_{\varphi }{s}_{\theta }{c}_{\psi }-c_{\varphi }{s}_{\psi }& c_{\varphi }{s}_{\theta }{c}_{\psi }+s_{\varphi }{s}_{\psi }\\ c_{\theta }{s}_{\psi }& s_{\varphi }{s}_{\theta }{s}_{\psi }+c_{\varphi }{c}_{\psi }& c_{\varphi }{s}_{\theta }{s}_{\psi }-s_{\varphi }{c}_{\psi }\\ -s_{\theta }& s_{\varphi }{c}_{\theta }& c_{\varphi }{c}_{\theta }\end{array}\right]$$

(3)

where $c_{\alpha }=cos\alpha$, $s_{\alpha }=sin\alpha$, and $\alpha \in \{\varphi ,\theta ,\psi \}$; ${\omega }^B={\left[p,q,r\right]}^{\top }$ represents angular velocities in the body-fixed frame, the relationship of which to the Euler rates is expressed by

$$\left[\begin{array}{c}\dot{\phi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]=\underset{W^{-1}}{\underbrace{\left[\begin{array}{ccc}1& {\displaystyle \frac{s\left(\phi \right)s\left(\theta \right)}{c\left(\theta \right)}}& {\displaystyle \frac{c\left(\phi \right)s\left(\theta \right)}{c\left(\theta \right)}}\\ 0& c\left(\phi \right)& -s\left(\phi \right)\\ 0& {\displaystyle \frac{s\left(\phi \right)}{c\left(\theta \right)}}& {\displaystyle \frac{c\left(\phi \right)}{c\left(\theta \right)}}\end{array}\right]}}\left[\begin{array}{c}p\\ q\\ r\end{array}\right]$$

(4)

where W is defined as in [16]. I is the symmetric and positive-definite inertia matrix, which is computed with respect to the airframe’s center of mass and expressed in the body-fixed frame. Finally, $M_B={[M_p,M_q,M_r]}^T$ is the external torque expressed in the body-fixed frame.

Following [17], the quadrotor’s model forcing terms are the results of a linear combination of each propeller thrust $T_i$,

$$\begin{array}{cc}\hfill T& =(T_1+T_2+T_3+T_4)\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill M_p& ={\displaystyle \frac{\sqrt{2}}{2}}l(T_2+T_3-T_1-T_4)\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill M_q& ={\displaystyle \frac{\sqrt{2}}{2}}l(T_1+T_3-T_2-T_4)\hfill \end{array}$$

(5c)

$$\begin{array}{cc}\hfill M_r& ={\displaystyle \frac{c_D}{c_L}}(T_1+T_2-T_3-T_4)\hfill \end{array}$$

(5d)

where l, $c_D$, and $c_L$ denote the quadrotor arm length, the linear friction coefficient, and the angular friction coefficient, respectively. The thrust $T_i$ is obtained through the spinning of the i-th propeller and controlled by a PWM signal to be sent to the electronic speed controller (ESC) following the control interface presented in [17]. To this end, it is desirable to express the forcing signals in terms of adimensional virtual control inputs ${\tau }_T,{\tau }_R,{\tau }_P$, and ${\tau }_Y$, which are dependent on the maximum input thrust $T_{max}$ according to the following relations:

$$\begin{array}{cc}\hfill T& =4T_{max}({\tau }_T-1)\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill M_p{\displaystyle \frac{2}{l\sqrt{2}}}& =-4T_{max}{\tau }_R\hfill \end{array}$$

(6b)

$$\begin{array}{cc}\hfill M_q{\displaystyle \frac{2}{l\sqrt{2}}}& =-4T_{max}{\tau }_P\hfill \end{array}$$

(6c)

$$\begin{array}{cc}\hfill M_r{\displaystyle \frac{c_L}{c_D}}& =4T_{max}{\tau }_Y\hfill \end{array}$$

(6d)

2.2. Quadrotor Position and Attitude Controller

Quadrotors are treated as underactuated nonlinear systems, since position and attitude control (six generalized coordinates) are achieved through the four propellers’ input thrust. A hierarchical control architecture has been followed for trajectory tracking tasks [18] that is composed of an outer position-control loop and an inner attitude-control loop, respectively.

2.2.1. Outer-Loop Control

The outer-loop control law is formulated independently for the z axis and x, y axis, respectively. The control law is achieved by inverting the position dynamics of (2a), and it has been slightly modified with respect to the one proposed in [17,19], since the drag effects have not been considered. To this end, the altitude control law is designed as

$${\tau }_T=1-{\displaystyle \frac{m}{4T_{max}(cos\phi )(cos\theta )}}(-g+v_z)$$

(7)

with $v_z$ being the altitude virtual control law to be designed. Additionally, the desired Euler angles to achieve $x,y$-axis position control are computed as

$$\left[\begin{array}{c}{\phi }_r\hfill \\ {\theta }_r\hfill \end{array}\right]={F_B^{*}}^{-1}{V}_{xy}$$

(8)

with

$$F_B^{*}=-{\displaystyle \frac{4T_{max}({\tau }_T-1)}{m}}\left[\begin{array}{cc}sin\psi & cos\psi \\ -cos\psi & sin\psi \end{array}\right]$$

(9)

and $V_{xy}={\left[v_x,v_y\right]}^{\top }$ being the $x,y$-position virtual control law to be designed.

The outer-loop outputs are ${\tau }_T$, ${\phi }_r$, ${\theta }_r$. The ${\tau }_T$ goes to the PWM conversion block, while ${\phi }_r$ and ${\theta }_r$ along with the desired yaw angle ${\psi }_r$ will be used as references for the inner-loop.

The proposed control laws are formulated as follows:

$$\begin{array}{cc}\hfill e_{\dot{x}}& =k_{P1,x}(x_r-x)-\dot{x}\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill e_{\dot{y}}& =k_{P1,y}(y_r-y)-\dot{y}\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill e_{\dot{z}}& =k_{P1,z}(z_r-z)-\dot{z}\hfill \end{array}$$

(10c)

$$\begin{array}{cc}\hfill v_x& =k_{P2,x}{e}_{\dot{x}}+k_{D,x}{\dot{e}}_{\dot{x}}\hfill \end{array}$$

(10d)

$$\begin{array}{cc}\hfill v_y& =k_{P2,y}{e}_{\dot{y}}+k_{D,y}{\dot{e}}_{\dot{y}}\hfill \end{array}$$

(10e)

$$\begin{array}{cc}\hfill v_z& =k_{P2,z}{e}_{\dot{z}}\hfill \end{array}$$

(10f)

Given the symmetry of the quadrotor system, the controller gains related to the x and y positions are set such that $k_{P1,x}=k_{P1,y}=k_{P1,xy}$, $k_{P2,x}=k_{P2,y}=k_{P2,xy}$, $k_{D,x}=k_{D,y}=k_{D,xy}$.

2.2.2. Inner-Loop

The inner-loop control law is designed by enhancing with feedback linearization the linear attitude controller presented in the Mathworks documentation regarding the UAV Toolbox Support Package for PX4 Autopilots [20]. The feedback linearization strategy is used to exactly linearize the quadrotor nonlinear dynamics and, thereby, to guarantee stability away from the equilibrium points. The following implementation exploits the Euler–Lagrange modeling formulation, which, in its correct form, can be used interchangeably with the N–E mathematical model, as shown in [16],

$$M^{\prime }=W^{-T}[Bv+C\dot{\eta }]$$

(11)

where B and C are two $3\times 3$ matrices defined as in [21], and where $v={\left[v_{\phi },v_{\theta },v_{\psi }\right]}^{\top }$ is a virtual control signal resulting from the inner-loop PD controller presented below. Compared to the one presented in [20], the inner-loop PD controller is designed using Euler rates instead of angular velocities, and it is formulated as follows:

$$\begin{array}{cc}\hfill e_{\dot{\phi }}& =k_{P1,\phi }({\phi }_r-\phi )-\dot{\phi }\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill e_{\dot{\theta }}& =k_{P1,\theta }({\theta }_r-\theta )-\dot{\theta }\hfill \end{array}$$

(12b)

$$\begin{array}{cc}\hfill e_{\dot{\psi }}& =k_{P1,\psi }({\psi }_r-\psi )-\dot{\psi }\hfill \end{array}$$

(12c)

$$\begin{array}{cc}\hfill v_{\phi }& =k_{P2,\phi }{e}_{\dot{\phi }}+k_{D,\phi }{\dot{e}}_{\dot{\phi }}\hfill \end{array}$$

(12d)

$$\begin{array}{cc}\hfill v_{\theta }& =k_{P2,\theta }{e}_{\dot{\theta }}+k_{D,\theta }{\dot{e}}_{\dot{\theta }}\hfill \end{array}$$

(12e)

$$\begin{array}{cc}\hfill v_{\psi }& =k_{P2,\psi }{e}_{\dot{\psi }}\hfill \end{array}$$

(12f)

where $k_{P1,\phi }$, $k_{P1,\theta }$, $k_{P1,\psi }$, $k_{P2,\phi }$, $k_{P2,\theta }$, $k_{P2,\psi }$, $k_{D,\phi }$, and $k_{D,\theta }$ are controller gains to be tuned. Given the symmetry of the quadrotor system, the controller gains related to the roll and pitch angles are set such that $k_{P1,\phi }=k_{P1,\theta }=k_{P1,\phi \theta }$, $k_{P2,\phi }=k_{P2,\theta }=k_{P2,\phi \theta }$, $k_{D,\phi }=k_{D,\theta }=k_{D,\phi \theta }$.

2.3. Reinforcement Learning

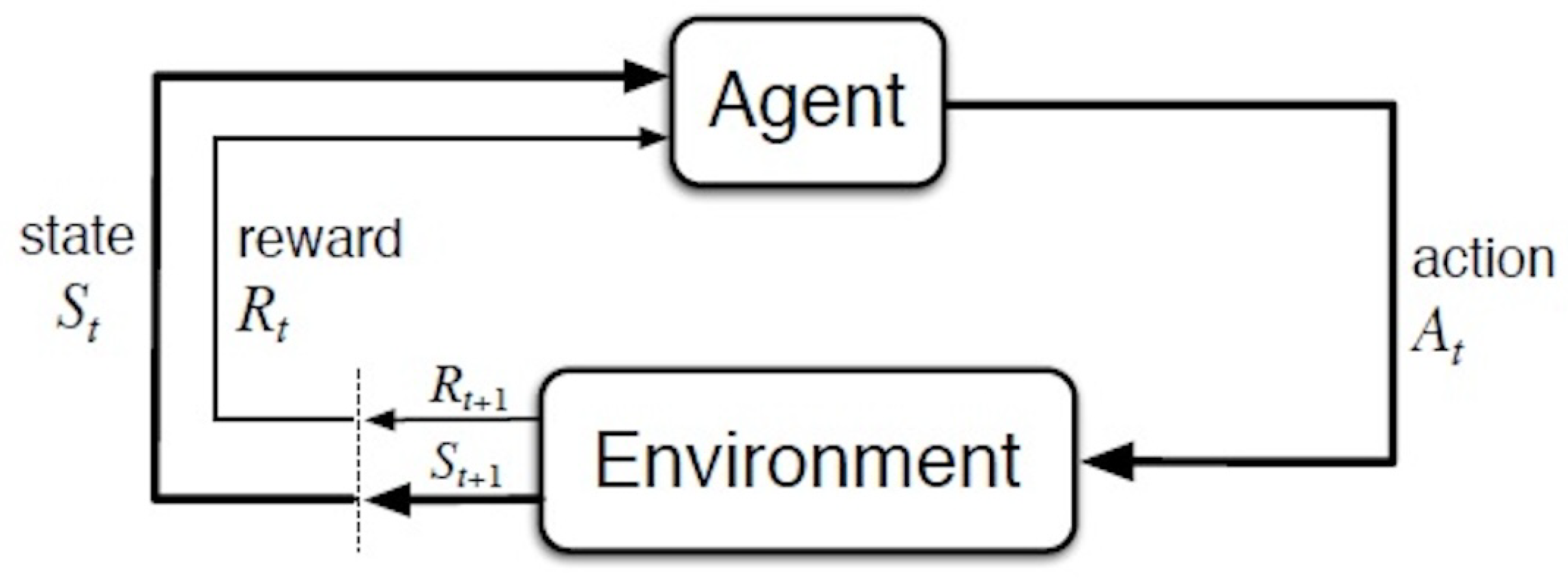
RL centers on training an agent that decides about taking actions by maximizing a long-term benefit through trial and error. RL is generally described by a Markov Decision Process (MDP). The agent–environment interaction in an MDP is illustrated in Figure 2. Agent, environment, and action represent the controller, controlled system, and control signal in engineering terms, respectively [22].

A DDPG algorithm is adopted, and it is designed to handle high-dimensional action spaces. It is an off-policy actor–critic algorithm that works based on the expected gradient of the action-value function that is given by

$$q_{\pi }(s,a)={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s,A_t=a\right]$$

(13)

where $q_{\pi }(s,a)$ denotes the action-value function for policy $\pi$ at state s and action a; where ${\mathbb{E}}_{\pi }[·]$ represents the expected value under policy $\pi$; where ${\sum }_{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$ is the sum of discounted future rewards starting from time t in state s and represents the expected discounted return; and where $\gamma$ is the discount rate, $0\le \gamma \le 1$ [12,22,23].

The DDPG algorithm finds a deterministic target policy using an exploratory behavior policy. Thus, it outputs a specific action rather than a probability distribution over actions.

The actor–critic approach includes both a value function-based and a policy search-based method. While the actor refers to the policy search-based method and chooses actions in the environment, the critic refers to the value function-based method and evaluates the actor using the value function.

3. Proposed RL-Based Fine-Tuning

The main contribution of this work is the introduction, along with the first experimental results, of an RL policy to dynamically adapt control gains during flight. In fact, when considering a ’traditional’ PD attitude controller, the main limitation is that the control gains, which have been set during the offline tuning phase, remain unchanged throughout the outdoor flight. By enhancing the controller with an adaptive law, such as the one that is here presented, the control gain can be fine-tuned during the flight to account for unmodeled dynamics and parameter uncertainties.

Given the online fine-tuning nature of the proposed RL method, a baseline controller tuning is performed as a first step. It is essential to properly adjust the controller parameters, as this directly impacts performance. Given a PD controller, an excessively high proportional gain may lead to overshooting, and a very high derivative gain may lead to instabilities. Thus, achieving a balance among controller gains is crucial to ensure a PD controller’s accurate and stable response.

The MATLAB/Simulink 2024a environment was used for the presented simulation studies. While Simulink offers numerical automatic tools for PD controller tuning, this approach is only effective for linear plants or locally linearized plants. Consequently, manual tuning of PD parameters is performed, which consists in adjusting the control gains to minimize position and attitude error while avoiding excessive oscillations. Considering the authors’ experience in UAV controller tuning, and as shown from the satisfactory results in Section 5, no alternative automatic tuning method (such as genetic algorithm) is deemed necessary at this stage.

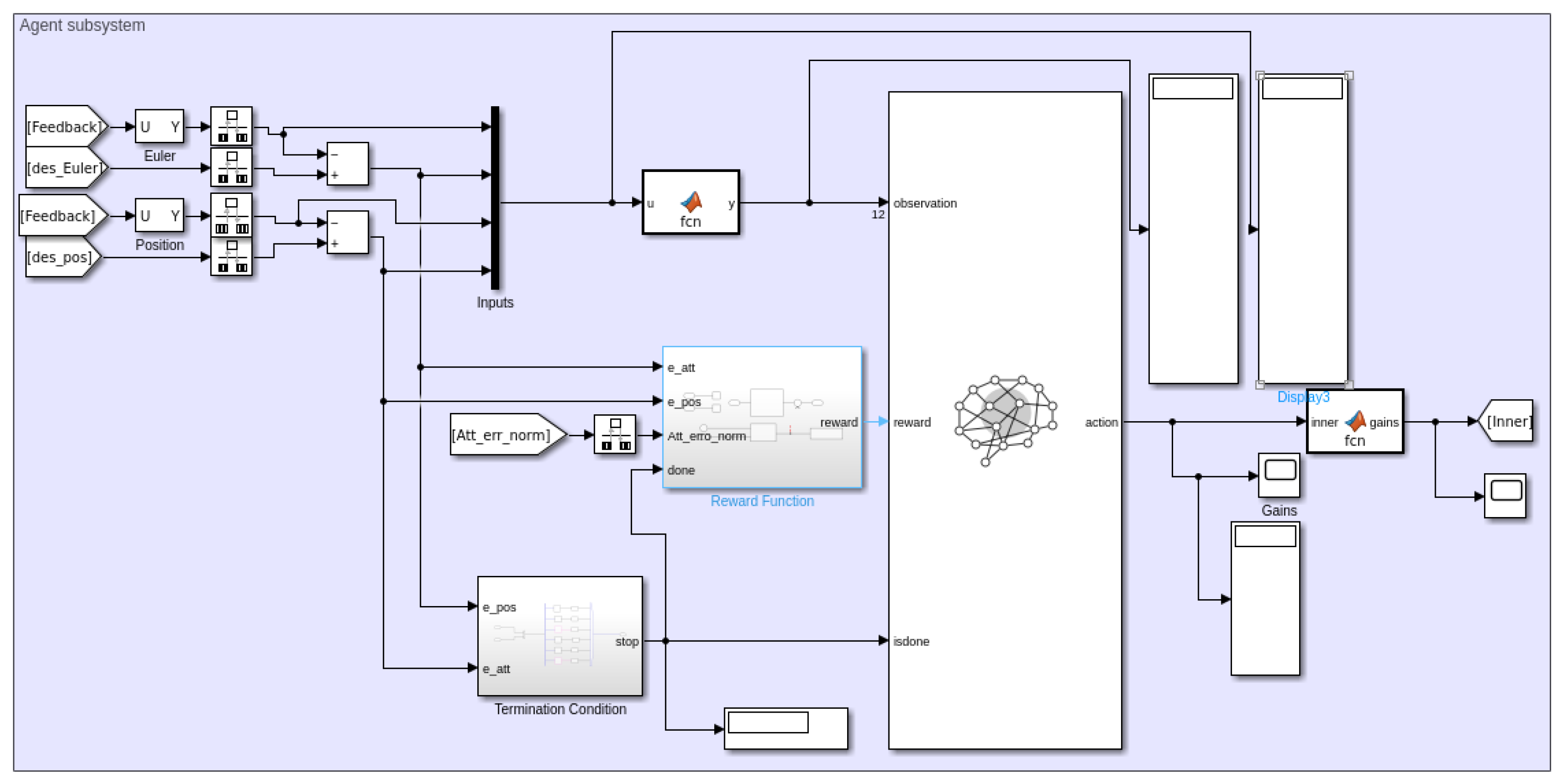
Next, the RL-based controller parameter fine-tuning is implemented, which is illustrated as a block diagram configuration in Figure 3. The overall system consists of three components: controller, plant (the quadrotor in Figure 1), and agent (the RL component). The configuration of Figure 3 includes a trajectory planner, the linear transformation, and the parameter tuning parts. MATLAB/Simulink 2024a is utilized to train the agent for the RL-based fine-tuning of the inner-loop (attitude) controller. The notation has already been explained.

The state space S (for tuning) includes the positions (p) along the x, y, and z axes, as well as the Euler angles ($\eta$). It also includes the position errors ($e_p$) along the x, y, and z axes and the errors on the Euler angles ($e_{\eta }$). The agent learns to adjust dynamically the normalized weights ($n_{P_{\psi 2}}$, $n_{P_{\phi \theta 1}}$, $n_{P_{\psi 1}}$, $n_{P_{\phi \theta 0}}$, $n_{D_{\phi \theta 0}}$), which creates the action space ($A\in {\mathbb{R}}^5$) within the range of [−1, 1] for all the controller parameters. The state and action spaces are denoted as follows:

$$\begin{array}{c}S=[p,\eta ,e_p,e_{\eta }]\in {\mathbb{R}}^{12}\\ A=[n_{P1,\phi \theta },n_{P1,\psi },n_{P1,\phi \theta },n_{P2,\psi },n_{D,\phi \theta }]\in {\mathbb{R}}^5\end{array}$$

(14)

Considering the normalized weights, the corresponding parameter tuning equations, related to the gains in (12a–f), are

$$\left\{\begin{array}{c}{k}_{P1,\phi \theta ,new}=k_{P1,\phi \theta }(1+a{n}_{P1,\phi \theta })\hfill \\ k_{P1,\psi ,new}=k_{P1,\psi }(1+a{n}_{P1,\psi })\hfill \\ k_{P2,\phi \theta ,new}=k_{P2,\phi \theta }(1+a{n}_{P2,\phi \theta })\hfill \\ k_{P2,\psi ,new}=k_{P2,\psi }(1+a{n}_{P2,\psi })\hfill \\ k_{D,\phi \theta ,new}=k_{D,\phi \theta }(1+a{n}_{D,\phi \theta })\hfill \end{array}\right.$$

(15)

where a represents the search rate, and where $k_{P1,\phi \theta ,new}$, $k_{P1,\psi ,new}$, $k_{P2,\phi \theta ,new}$, $k_{P2,\psi ,new}$, and $k_{D,\phi \theta ,new}$ are the new control parameters fine-tuned by the trained RL agent. The manually tuned inner-loop controller parameters serve as the starting gain values for the training, while a combination of the search rate and normalized weights contribute to the tuning within an assigned interval relative to the initial controller gains.

The reward function is defined as a piece-wise function of the attitude error norm,

$$R\left(\right||e_{\eta }\left|\right|)=\left\{\begin{array}{cc}{r}_1,\hfill & {\alpha }_1\le \left|\right|e_{\eta }\left|\right|\hfill \\ r_2,\hfill & {\alpha }_2\le \left|\right|e_{\eta }\left|\right|<{\alpha }_1\hfill \\ r_3,\hfill & {\alpha }_3\le \left|\right|e_{\eta }\left|\right|<{\alpha }_2\hfill \\ r_4,\hfill & {\alpha }_4\le \left|\right|e_{\eta }\left|\right|<{\alpha }_3\hfill \\ r_5,\hfill & {\alpha }_5<\left|\right|e_{\eta }\left|\right|<{\alpha }_4\hfill \\ r_6,\hfill & \left|\right|e_{\eta }\left|\right|\le {\alpha }_5\hfill \end{array}\right.$$

(16)

where $r_i$ ($i=1,\dots ,6$) are the reward values, and where ${\alpha }_i$ ($i=1,\dots ,5$) represents the thresholds for the norm of the attitude errors, $\left|\right|e_{\eta }\left|\right|$. These thresholds define the conditions under which each reward value, $r_i$, is assigned.

The actor and critic neural networks (NNs) are designed as feed-forward NNs, the structures of which are depicted in Figure 4 and Figure 5, respectively. The tanh activation function is chosen for the actor’s output, giving the agent’s output the value from the probability distribution between $[-1,1]$.

4. Agent Environment Setup for Controller Testing

The selected target hardware is the Pixhawk 2.1 Cube Black (ProfiCNC, Black Hill, Victoria, Australia) flight control unit, which supports PX4-Autopilot firmware. The controller is developed in MATLAB/Simulink 2024a, and the deployment process involves overwriting the PX4-Autopilot flight controller v1.14.0 with the one resulting from the C++ code generation of the Simulink model. However, challenges arise when certain blocks in the Simulink model are incompatible with the code generation process, as they may not be supported. This limitation can prevent successful code generation, necessitating the modification or replacement of unsupported blocks to achieve a functional executable.

For the proposed controller, the RL agent Simulink block in Figure 6 is not supported for code generation.

To overcome these limitations, an alternative approach is implemented: the weights and biases are extracted from the trained action model and the NN is reconstructed within the Simulink workspace. These trained weights and biases, represented as large matrices, are used to replicate the hidden layers of the action model. By applying the same series of mathematical operations of the hidden layers, and by utilizing the same observation function employed during the training phase, the original action can be identically reconstructed for the code generation.

In a reinforcement learning agent, the biases and weights within the neural network are fundamental components that allow the model to approximate intricate functions, such as policies or value functions. These parameters are iteratively updated during the training process to optimize the network’s performance. The adjustments aim to reduce prediction errors while improving the agent’s ability to maximize cumulative rewards, enabling it to learn effective strategies for decision-making in complex environments. By learning to minimize the position and attitude error, we expect the RL agent to approximate a control parameters nonlinear adaptation law to effectively compensate for discrepancies between the simulated and real external environment (such as sensor delays, unmodeled disturbances, and parameter uncertainties), consecutively increasing robustness. To this end, the neural network must have a sufficient number of neurons; however, in order to deploy the RL agent directly on the Pixhawk flight control unit, the flash memory limitations of the target hardware need to be taken into account. To balance performance and memory constraints, a neural network configuration of $128\times 128$ neurons is selected. This setup provides satisfactory results while ensuring feasible memory utilization on the hardware.

Reconstruction of the Action Layer

The activation function $tanh$ is applied to the output of the hidden layers in the network, as represented by the following equation:

$$hiddenLayerOutput=tanh(weightsLayer\ast observation+biasesLayer)$$

(17)

where $weightsLayer$ and $biasesLayer$ are the parameters specific to this layer, as the equation operates directly on the input observation. These parameters are responsible for determining the transformation of the input data before the nonlinear activation is applied.

For the final layer, the network uses a clipped ReLU function, defined as

$$action=min(N,max(Q,weightsLayer\ast hiddenLayerOutput+biasesLayer\left)\right)$$

(18)

where N and Q are the maximum and minimum allowable action values, respectively. These bounds are determined during the agent’s training phase to ensure the output remains within a feasible range. In the case of RL-based fine-tuning of PD controller gains, the values of N and Q are set to 1 and $-1$, respectively, reflecting the permissible range for the controller’s actions. This setup ensures that the network’s outputs are appropriately scaled for the control task.

5. Results

In this research, the focus was on the problem of tracking a circular trajectory, also considering take-off and landing tasks. Since the RL agent was implemented for the attitude controller fine-tuning, only the attitude results are presented here, while the position results are listed in Appendix A for completeness. The trajectory under study was divided as follows: 10 s take-off, $2.5$ s hovering, 20 s circumference (one lap), $2.5$ s hovering, and 10 s landing for a total of 45 s. The real quadrotor’s parameters were manually measured and the motors’ characteristics were computed from the relative data-sheet. The resulting values are shown in

Table 1. Quadcopter measured parameters.

Parameter	Value	Unit Measurement
$m_{tot}$	$1.2$	kg
$m_{prop}$	$0.01$	kg
$m_m$	$0.045$	kg
$m_{cg}$	$0.98$	kg
$r_{cg}$	$0.0625$	m
$h_{cg}$	$0.13$	m
$r_m$	$0.015$	m
$h_m$	$0.45$	m
r	$0.125$	m
l	$0.225$	m
T	$8.43$	N
$\tau$	$0.1056$	Nm
$I_{xx}$	$0.0131$	kg m2
$I_{yy}$	$0.0131$	kg m2
$I_{zz}$	$0.0234$	kg m2
$k_{motor}$	$1.4422\times {10}^{-3}$	${\displaystyle \frac{\mathrm{kg}\mathrm{m}}{{\mathrm{rad}}^2}}$
${\displaystyle \frac{c_D}{c_L}}$	$0.0237$	-
b	$3.1427\times {10}^{-7}$	${\displaystyle \frac{\mathrm{kg}\mathrm{m}}{{\mathrm{rad}}^2}}$

, and they were used during the training and numerical simulations.

5.1. Agent Training Phase

As outlined in Section 3, before starting the RL training phase, the flight controller was manually tuned to achieve satisfactory tracking performance. After an iterative trial-and-error tuning process, the controller gain values in

Table 2. Gains table.

Gain	Value	Name
$k_{P1,z}$	$8.9$	Position proportional gain on z-axis
$k_{P2,z}$	$19.8$	Velocity proportional gain on z-axis
$k_{P1,xy}$	$0.6$	Position proportional gain on $xy$-axis
$k_{P2,xy}$	$3.9$	Velocity proportional gain on $xy$-axis
$k_{D,xy}$	$0.29$	Velocity derivative gain on $xy$-axis
$k_{P1,\psi }$	2	Attitude proportional gain for yaw angle
$k_{P2,\psi }$	$5.4801$	Angular rate proportional gain for yaw angle
$k_{P1,\phi ,\theta }$	4	Attitude proportional gain for roll and pitch angles
$k_{P2,\phi ,\theta }$	$11.467$	Angular rate proportional gain for roll and pitch angles
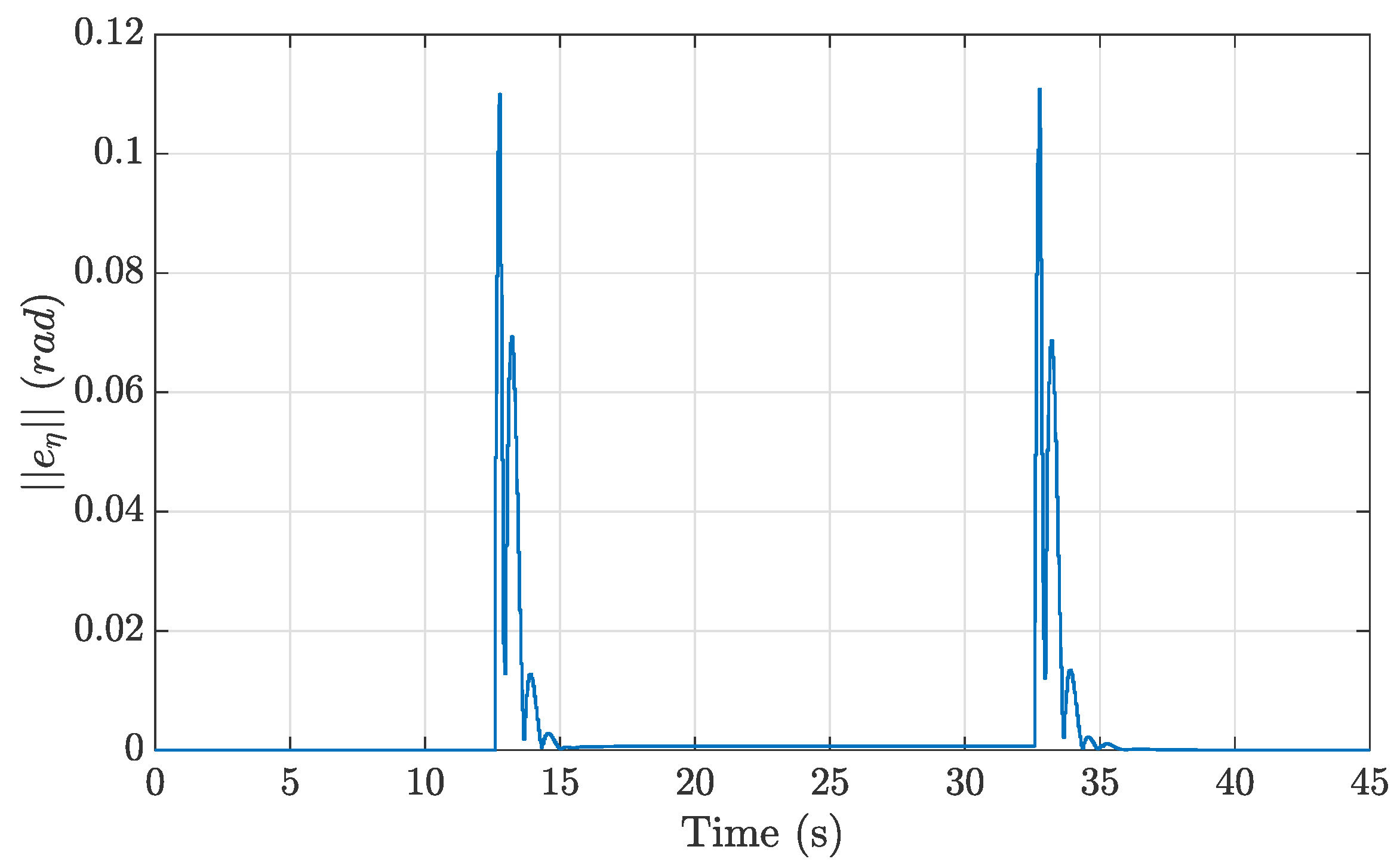
$k_{D,\phi ,\theta }$	$0.81905$	Angular rate derivative gain for roll and pitch angles

were found and the resulting numerical simulation attitude error norm was computed. The plot of the attitude error norm in Figure 7 highlights two main areas with higher spikes that correspond to the quadrotor’s change of direction at $12.5$ s and $32.5$ s; hence, at the beginning and the end of the circular trajectory. In the hovering condition, the attitude was null; then, when starting the circular segment of the trajectory the attitude underwent a sudden change, which caused the spikes. The training of the agent aimed to reduce these high spikes in the attitude error norm.

According to the proposed methodology in Section 3, RL was then applied to further fine-tune the inner-loop controller gains. By heuristically assigning a value of $a=0.4$ to (15), the following updating law was selected:

$$\left\{\begin{array}{c}{k}_{P1,\phi \theta ,new}=k_{P1,\phi \theta }(1+0.4n_{P1,\phi \theta })\hfill \\ k_{P1,\psi ,new}=k_{P1,\psi }(1+0.4n_{P1,\psi })\hfill \\ k_{P2,\phi \theta ,new}=k_{P2,\phi \theta }(1+0.4n_{P2,\phi \theta })\hfill \\ k_{P2,\psi ,new}=k_{P2,\psi }(1+0.4n_{P2,\psi })\hfill \\ k_{D,\phi \theta ,new}=k_{D,\phi \theta }(1+0.4n_{D,\phi \theta })\hfill \end{array}\right.$$

(19)

In this work, the same reward function proposed in [15] was implemented, where the reward is defined as a function of the norm of the attitude error. Considering the simulation studies after the manually tuned controller gains, we observed that the norm of the attitude error ranged from ${10}^{-4}$ to $1.1\times {10}^{-1}$ rad, as shown in Figure 7. Given this relatively wide range, the reward function was set as the following piece-wise function of the attitude error:

$$R\left(\right||e_{\eta }\left|\right|)=\left\{\begin{array}{cc}-25,\hfill & 0.04\le \left|\right|e_{\eta }\left|\right|\hfill \\ -15,\hfill & 0.01\le \left|\right|e_{\eta }\left|\right|<0.04\hfill \\ -10,\hfill & 0.001\le \left|\right|e_{\eta }\left|\right|<0.01\hfill \\ -5,\hfill & 0.0005\le \left|\right|e_{\eta }\left|\right|<0.001\hfill \\ -1,\hfill & 0.0001\le \left|\right|e_{\eta }\left|\right|<0.0005\hfill \\ 10,\hfill & \left|\right|e_{\eta }\left|\right|\le 0.0001\hfill \end{array}\right.$$

(20)

The training phase was carried on in Matlab/Simulink 2024a, using the Deep Learning and Reinforcement Learning Toolbox; the simulation plant was modeled according to (2a–c); and the selected training hyperparameters were found heuristically and are displayed in

Table 3. Hyperparameters.

Parameters	Value
Sampling time	$0.05$
Reward discount factor $\gamma$	$0.99$
Learning rate for actor	${10}^{-3}$
Learning rate for critic	${10}^{-3}$
$L_2$ regularization factor	${10}^{-5}$
Optimizer parameter $ϵ$	${10}^{-8}$
Minimum batch size	1024
Experience buffer length	${10}^6$

. The sampling time for updating the control parameters was selected as a conservative rate that was one order of magnitude larger relative to the 5 ms attitude controller rate. Both of these sampling times were lower than the maximum admissible PWM signal rate of 2.5 ms of the adopted Pixhawk board and combination. The criterion for completion of training was based on achieving a target average reward, the value of which was determined by analyzing the distribution of the step counts across the error intervals shown in (20) relative to the norm of the attitude error observed with the manually tuned parameters.

According to (20) and the selected sampling time, the step count distribution yielded the following values: $[28,24,41,350,143,345]$. The baseline reward value obtained from the piecewise function (20) was calculated as

$$-25·28-15·24-10·41-5·350-1·143+10·345=117.$$

This reward value serves as a reference point. To achieve better results, an improved reward value is required, necessitating adjustments to surpass this baseline value and drive enhanced performance in the training process.

5.2. Simulation Results

Once the training phase was completed, the RL agent-based controller was tested through numerical simulations. The attitude error norms for both the manually tuned controller and the RL-based fine-tuned controller are presented in Figure 8. The results demonstrate that the application of the fine-tuning method reduced overshoots and peak errors while enabling the system to reach steady-state conditions more quickly. This improvement is attributable to the RL agent, which optimized the controller by generating a refined set of gains compared to the manually tuned values. These adjustments resulted in the enhanced performance and stability of the control framework.

Table 4. Numerical simulation RMSE of attitude error norm.

Numerical Simulation	Manually Tuned	Fine-Tuned
$|e_{\eta }{|}_{RMSE}$	$12.75\times {10}^{-3}$	$11.17\times {10}^{-3}$

presents the RMSE values for the attitude errors norm, providing a clear and quantitative comparison between the performance of the manually tuned controller and the RL fine-tuned one. A significant improvement in training performance is not expected in the simulation environment, as no external disturbances and unmodeled dynamics are present during the training and simulation phases.

Additionally, as shown in Figure 9, the RL agent set the fine-tuned controller gains differently from the initial manually tuned values right from the start of the simulation. Given the lack of disturbances in the numerical simulations, the fine-tuned gains remained constant and bounded throughout the simulation.

5.3. Experimental Results

The proposed methodology was deployed on quadrotor hardware to further test whether the RL agent-based controller performance improvements could be carried out in real outdoor flight conditions. To this end, the C++ code was uploaded to the Pixhawk 2.1 Cube Black flight control unit, following the procedure in Section 4.

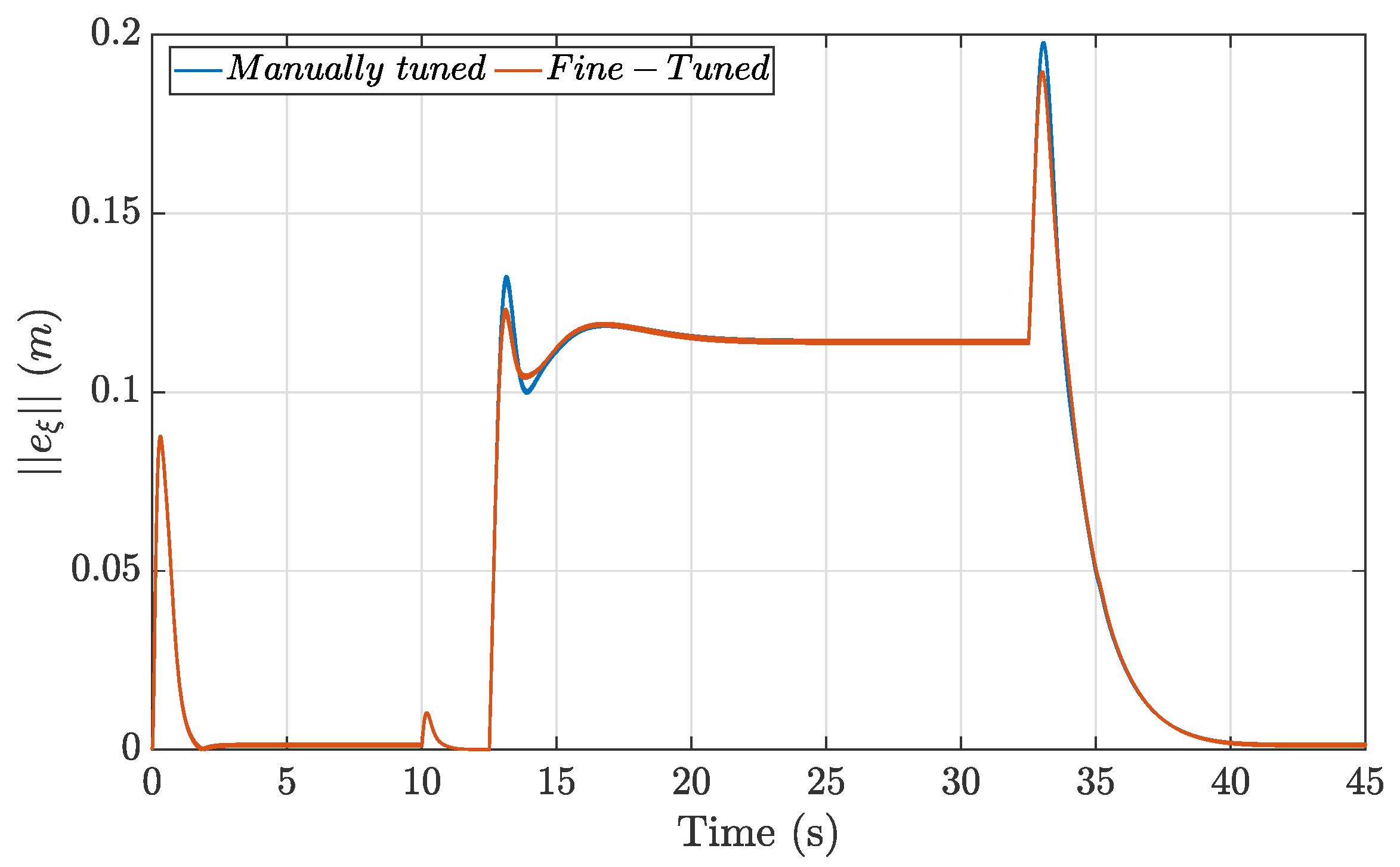
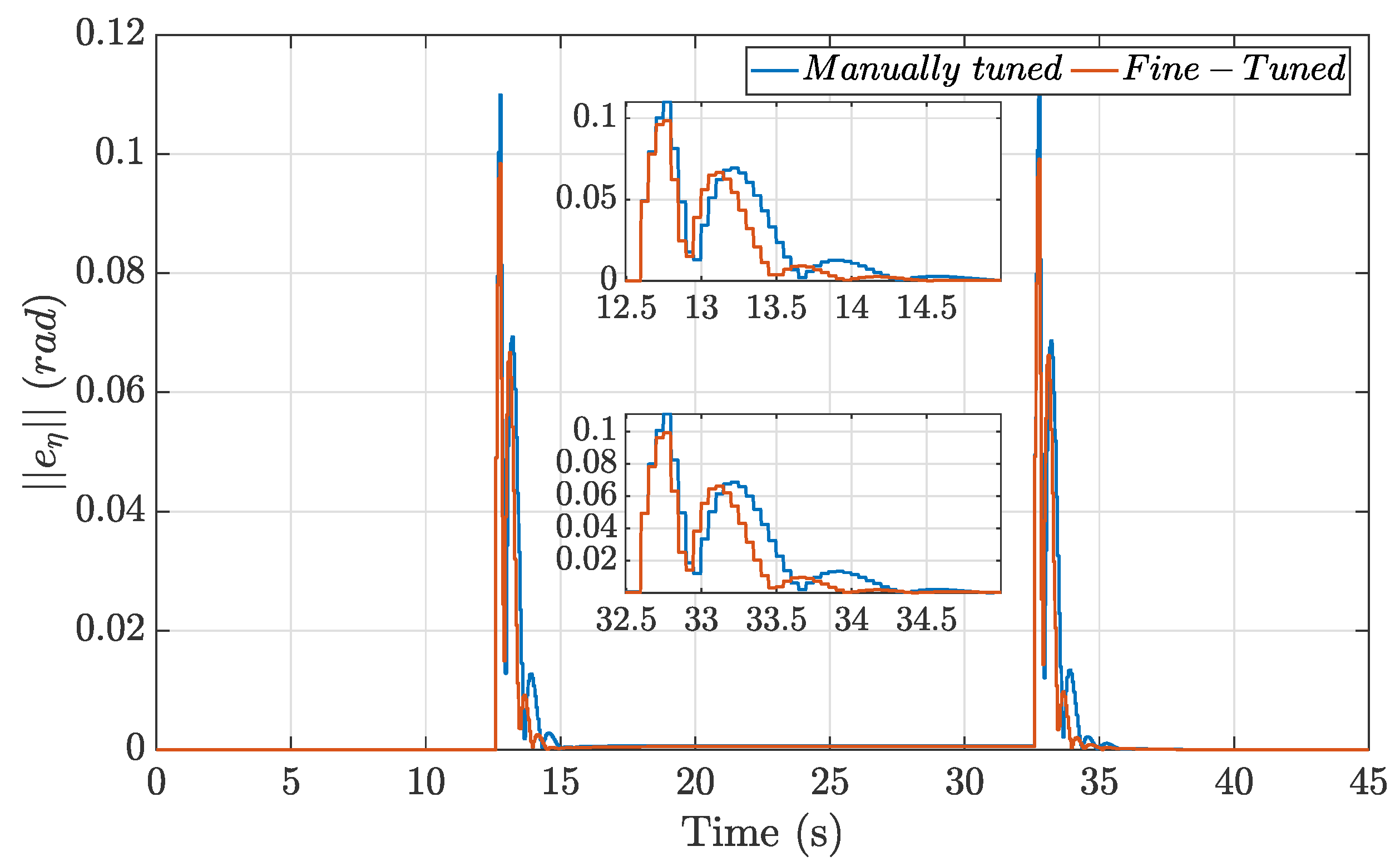
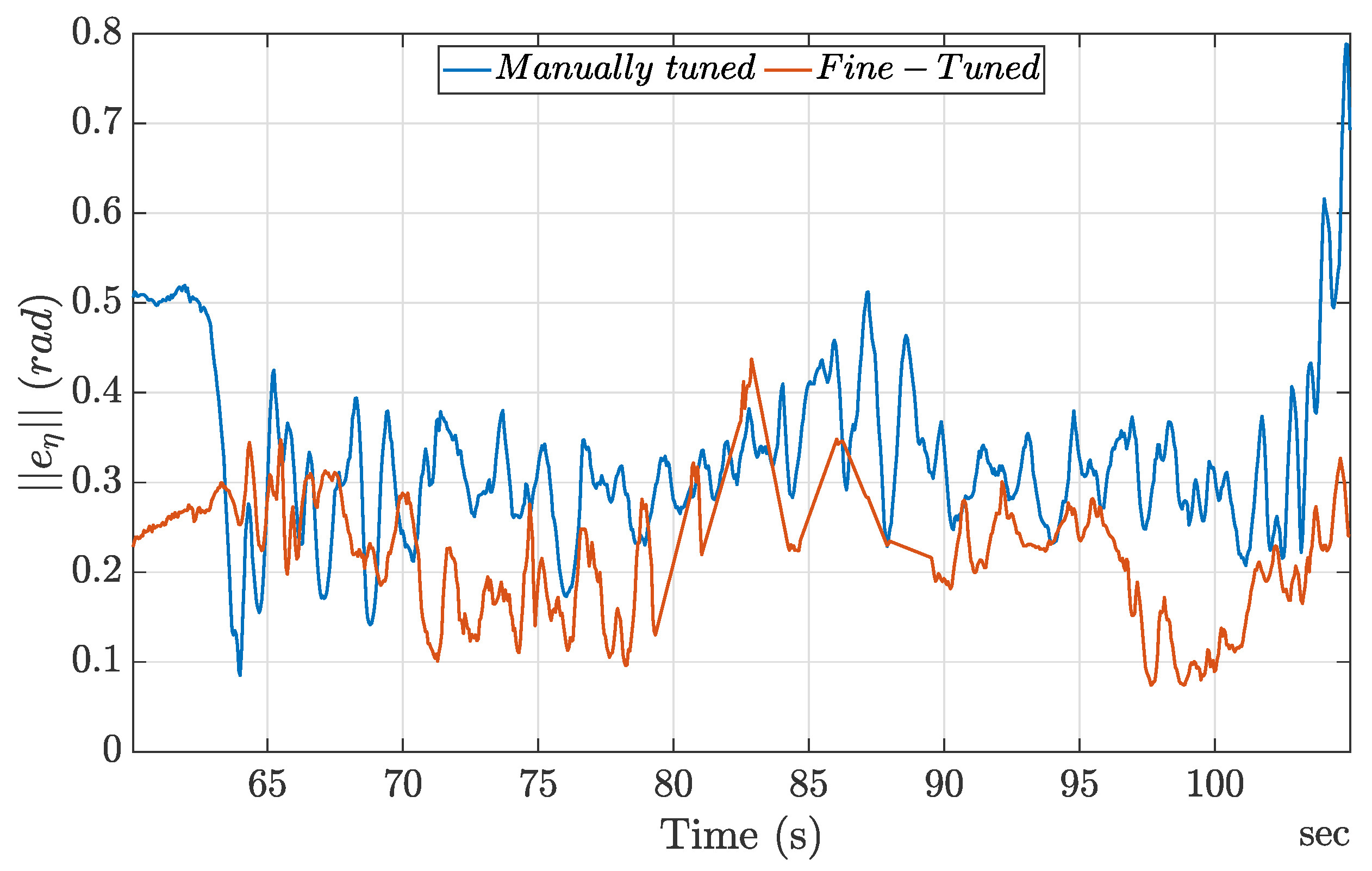
As in the previous section, the performances were compared, in terms of the norm of the attitude errors. Figure 10 compares the performance of the manually tuned gains with that of the fine-tuned gains, highlighting the differences in error magnitudes and response characteristics between the two approaches.

Overall, the observed behavior for the trajectory showed noticeable performance enhancement, with the fine-tuned gains outperforming the manually tuned ones. This highlights the RL agent’s ability to adapt and optimize control performance, even in the presence of real-world disturbances. These results can be further verified by comparing the respective RMSE values presented in

Table 5. RMSE of attitude error norm in the outdoor flight.

Outdoor Flight	Manually Tuned	Fine-Tuned
$|e_{\eta }{|}_{RMSE}$	$33.93\times {10}^{-2}$	$22.55\times {10}^{-2}$

. In the outdoor flight, since the RL agent learned to adapt the controller parameter, the performance improvement was more prevalent, at around 33%.

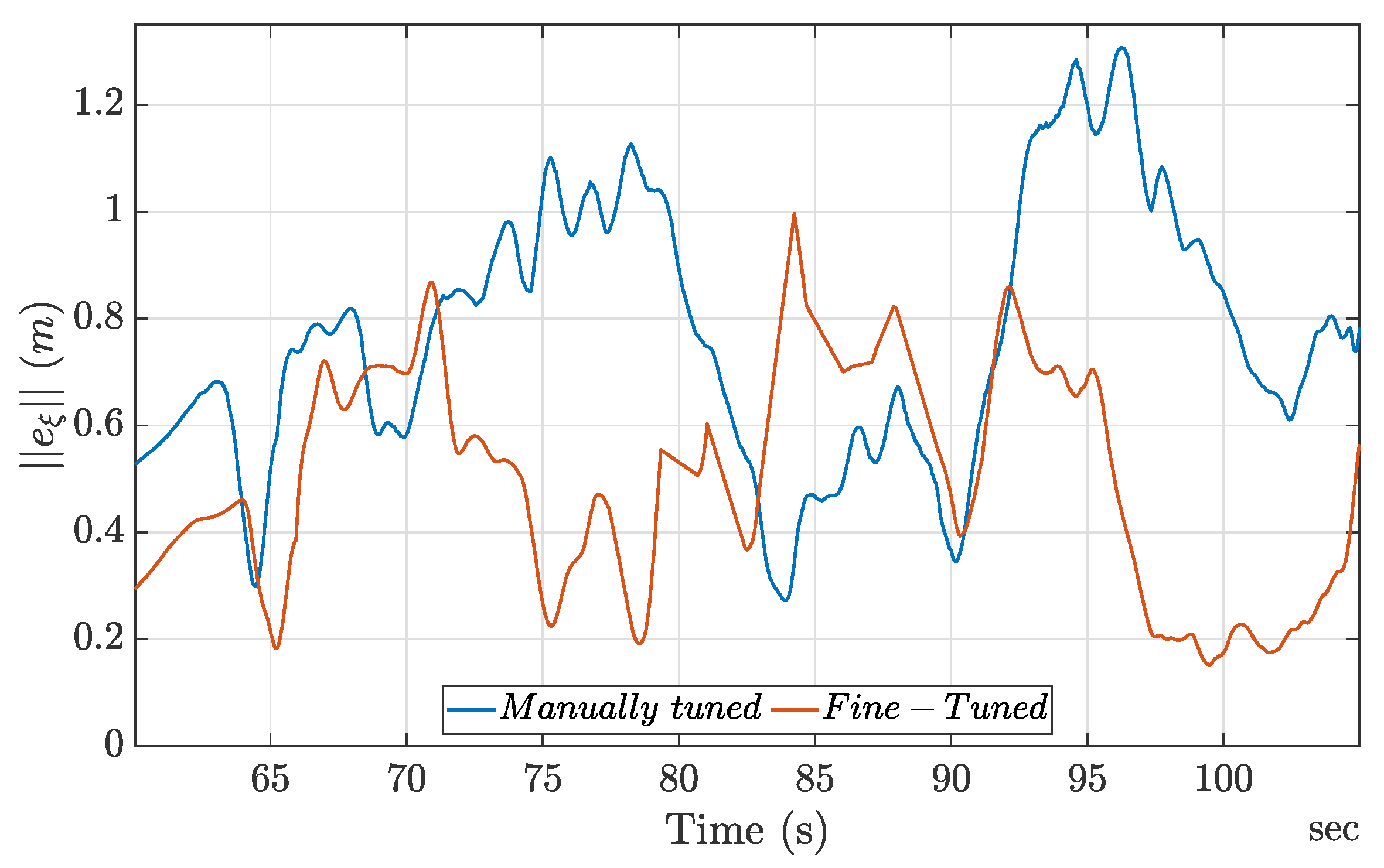
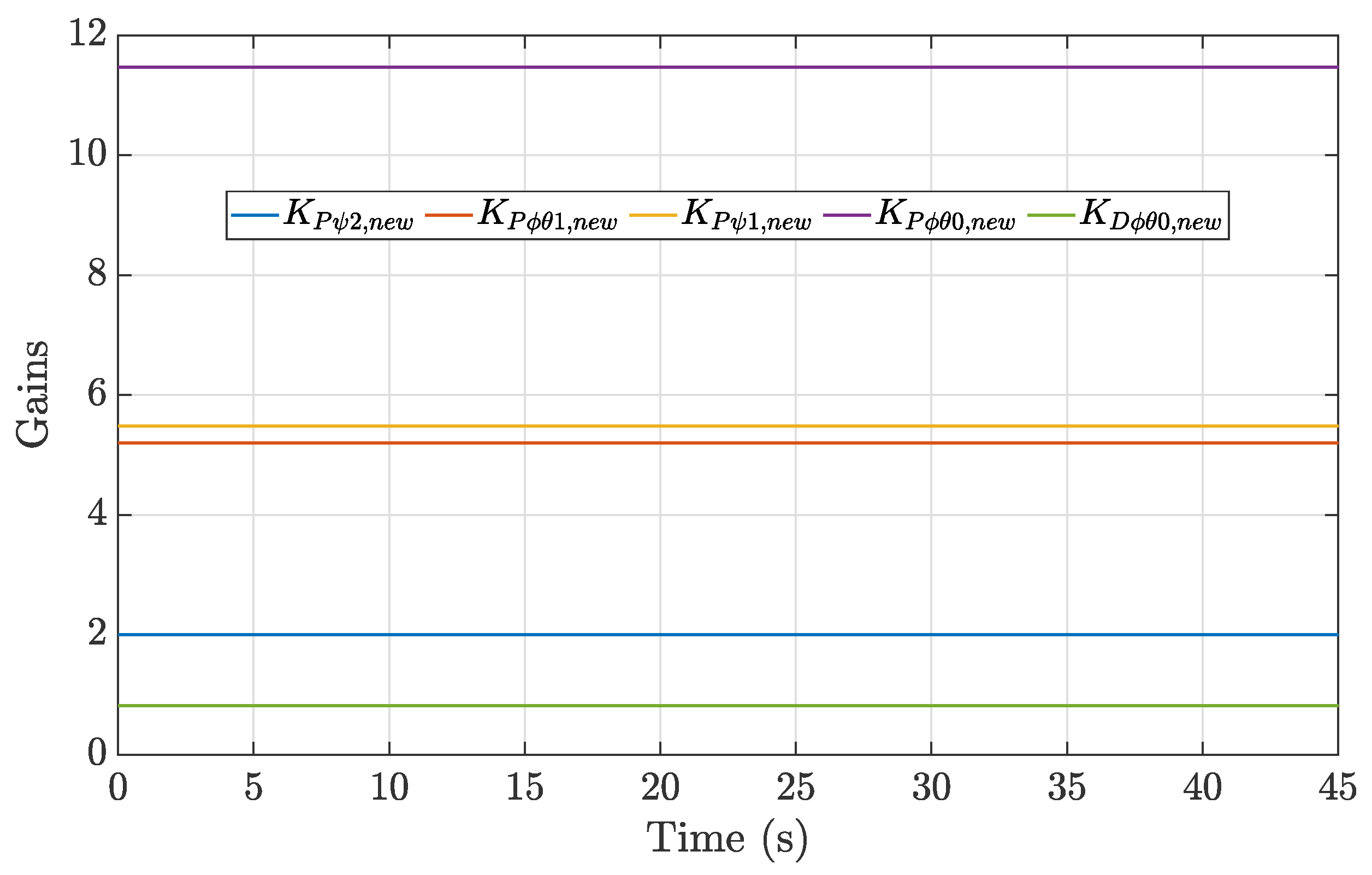
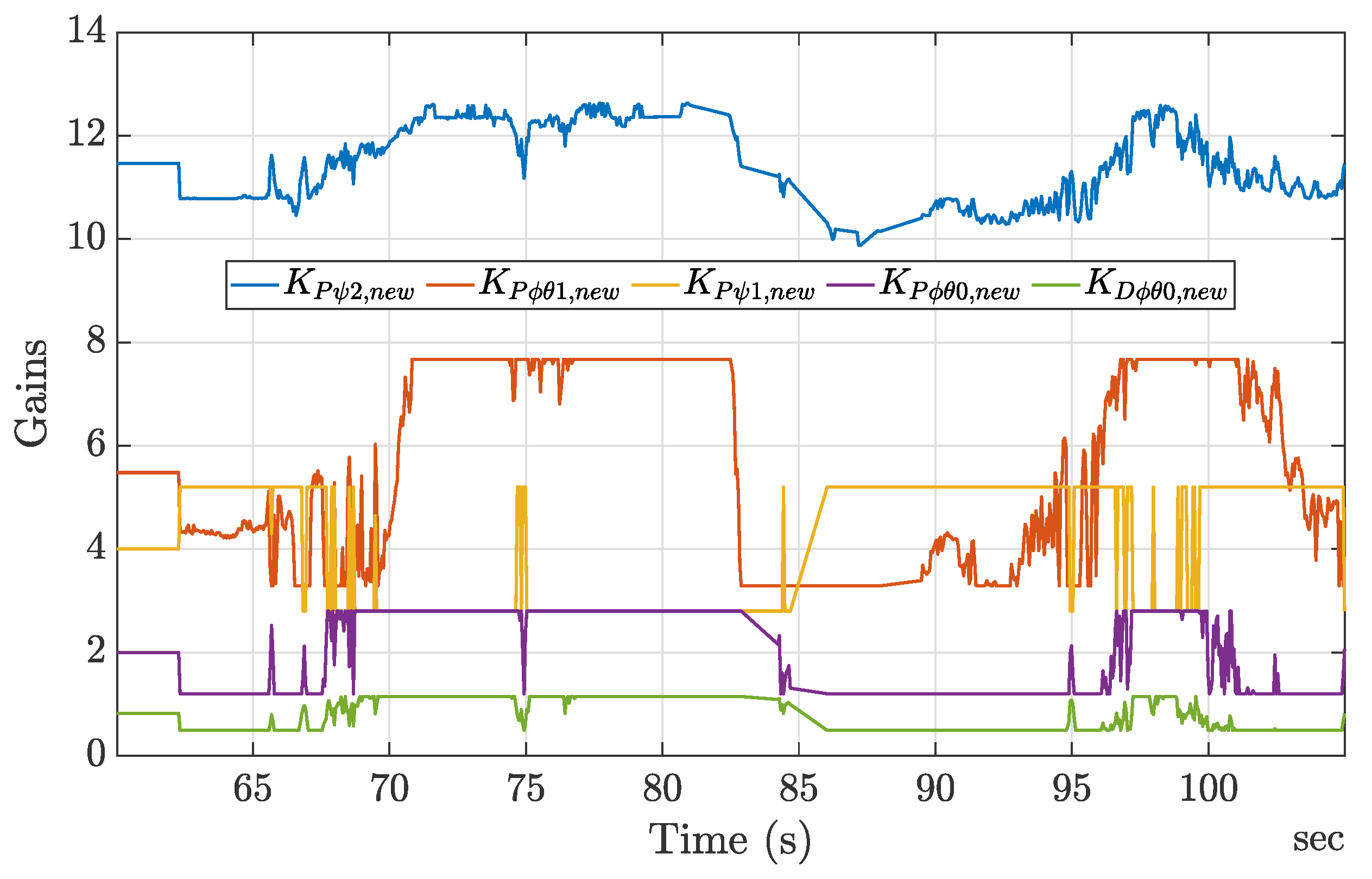
As a further impressive result, the RL agent-based controller was able to adapt online to the controller gains. This behavior shows that, even if not necessary during numerical simulation ideal conditions, the agent had learned how to adapt the controller parameters in case of disturbances. The evolution of the RL-fine-tuned controller gains is shown in Figure 11, and, although initialized to match the manually tuned values, after approximately 2 s the gains began to adjust dynamically. These changes were moderate, avoiding extreme values, and they demonstrate the agent’s ability to refine the control parameters in response to the system’s requirements without overextending them. This behavior reflects a balanced adaptation aimed at maintaining system stability and performance.

The agent operated without prior knowledge of the outdoor environment and had to contend with external factors, such as wind gusts and ground effects. Throughout the flight test, the agent’s adaptive behavior was evident as it attempted to mitigate these disturbances. In some instances, the gains reached their maximum or minimum allowable values, reflecting the system’s efforts to stabilize under challenging conditions. In addition, a few sudden spikes in the gains were observed, indicating rapid adjustments made by the agent to counteract abrupt changes in the environment. This behavior highlights the agent’s responsiveness and the challenges posed by dynamic and unpredictable external forces. Overall, the application of the RL strategy improved the performances of flight outmatching those of the manually tuned gains.

6. Analysis

The results presented highlight both the potential and the challenges of applying reinforcement learning (RL)-based fine-tuning for PD controllers in real-world scenarios. The RL-based controller demonstrated improved tracking performance compared to the manually tuned PD controller, showcasing its ability to adapt and optimize controller parameters in challenging outdoor conditions.

The DDPG-based RL algorithm, an off-policy actor–critic approach, proved effective for fine-tuning the inner-loop gains of the controller. By leveraging this methodology, an adaptation law was achieved, capable of handling complex trajectories involving both circular paths and hovering segments, which mirrors realistic flight scenarios. It is worth noting that drag and gyroscopic effects were omitted during the training phase, but they were inevitably present in the outdoor flight conditions. Despite these simplifications during training, the RL-enhanced controller learned to adapt the PD control gains to external disturbances, and it consistently outperformed the manually tuned PD controller in the simulations and outdoor flight tests.

One of the key practical challenges in transferring an RL agent from simulation to a real-world system involves the deployment constraints of embedded hardware. In this study, the neural network architecture had to be designed to fit within the limited flash memory available on the Pixhawk flight controller. In doing so, the resulting memory requirements and computational complexity remained relatively constrained. Furthermore, the transition from RL simulation training to online agent deployment was partially enabled by the adopted development framework, which carried out RL training on the quadrotor dynamical model adopted in successful hardware in the loop (HIL) studies [17]. Although the training environment did not fully capture all real-world quadrotor dynamics, a relatively detailed nonlinear model was used. A critical factor enabling successful sim-to-real transfer was the manual tuning of the PID controller on a model that incorporated PWM signal data type conversion (UINT16). Including this quantization effect proved essential, as it significantly influenced the resolution of the control inputs and the real-world behavior of the controller.

Ultimately, the findings of this study highlight the transformative potential of RL-based fine-tuning as a relatively computationally efficient solution for enhancing traditional UAV control strategies.

7. Conclusions and Future Works

This study successfully demonstrates the viability and effectiveness of a DDPG-based RL algorithm for fine-tuning PD controller parameters. The proposed method achieved substantial performance improvements in various test environments, including realistic outdoor scenarios. The RL-tuned controller exhibited enhanced adaptability, precise trajectory tracking, and robustness in the face of environmental disturbances. These results underscore the potential of RL-based approaches to bridge the gap between simulation and real-world applications in UAV control.

This study represents the initial stage in a broader research effort aimed at deploying reinforcement learning (RL)-based controllers on real-world quadrotors. While the present work focuses on the online fine-tuning of a PD controller using a DDPG-based RL agent and demonstrates successful implementation on real hardware, several important research directions remain open.

One of the key next steps is to conduct a formal robustness-and-stability analysis of the RL-tuned control system. The RL agent adapts controller gains online in response to changing conditions; however, ensuring consistent stability given real-world uncertainties—such as parameter variations, sensor noise, and external disturbances—requires theoretical validation. Future work will explore Lyapunov-based or other formal approaches to assess the closed-loop stability and robustness of the RL-based control system.

Additional future work will involve real-world deployment and evaluation of the presented approach to several UAV controllers, some of which have partially been explored in the authors’ previous simulation-based works (such as RL-based PID, LQR, MRAC, and Koopman-integrated RL-based PID controllers), assessing their adaptability, performance, and practical challenges in experimental flight tests.

The current benchmark is limited to a comparison with a manually tuned PD controller on a single circular trajectory. To broaden the context, future studies will compare the RL-based method with other adaptive and optimal control strategies, such as MRAC, fuzzy-PID, genetic algorithm-based tuning, and Model Predictive Control (MPC) along several realistic trajectories. This will help quantify the performance trade-offs, training requirements, and applicability of each approach under varying conditions.

The current reward function uses a piecewise-constant structure based on attitude error thresholds, as adopted from the prior work [15]. While effective for initial implementation, this design may limit learning efficiency, due to discontinuous gradients. Future work will explore continuous reward shaping strategies that can promote smoother convergence and more optimal policy learning.

While the training model includes nonlinear dynamics and realistic features, such as actuator quantization (e.g., PWM type conversion), it omits certain aerodynamic effects like air resistance and gyroscopic torques. Future research will investigate the influence of these factors and whether including them in simulation improves real-world transferability. Further analysis will also examine how the RL agent compensates for these unmodeled dynamics during flight.

The framework developed in this paper has been validated on a quadrotor platform. We aim to evaluate its generalizability by applying it to additional aerial vehicles, including fixed-wing UAVs and other multirotor configurations, or unmanned surface vehicles (USVs), thereby testing the scalability and platform-agnostic nature of the proposed methodology.