Secrecy Rate Maximization via Joint Robust Beamforming and Trajectory Optimization for Mobile User in ISAC-UAV System

Abstract

Unmanned aerial vehicles (UAVs) have emerged as a promising platform for integrated sensing and communication (ISAC) due to their mobility and deployment flexibility. By adaptively adjusting their flight trajectories, UAVs can maintain favorable line-of-sight (LoS) communication links and sensing angles, thus enhancing overall system performance in dynamic and complex environments. However, ensuring physical layer security (PLS) in such UAV-assisted ISAC systems remains a significant challenge, particularly in the presence of mobile users and potential eavesdroppers. This manuscript proposes a joint optimization framework that simultaneously designs robust transmit beamforming and UAV trajectories to secure downlink communication for multiple ground users. At each time slot, the UAV predicts user positions and maximizes the secrecy sum-rate, subject to constraints on total transmit power, multi-target sensing quality, and UAV mobility. To tackle this non-convex problem, we develop an efficient optimization algorithm based on successive convex approximation (SCA) and constrained optimization by linear approximations (COBYLA). Numerical simulations validate that the proposed framework effectively enhances the secrecy performance while maintaining high-quality sensing, achieving near-optimal performance under realistic system constraints.

1. Introduction

With the rapid advancement of wireless communication technologies, the demand for ubiquitous, reliable, and high-capacity wireless services has surged to meet the requirements of emerging applications, including autonomous driving, smart cities, and the Internet of Things (IoT) [1].

Integrated sensing and communication (ISAC) has recently emerged as a groundbreaking framework that facilitates the concurrent design and operation of communication and sensing functions over a shared wireless infrastructure and spectrum [2]. By enabling the reuse of hardware components and spectral resources, ISAC substantially improves spectral efficiency, reduces latency, and simplifies system architecture. This integrated approach is expected to empower diverse applications such as high-accuracy localization, environmental sensing, and secure vehicular communication. Concurrently, unmanned aerial vehicles (UAVs) have attracted significant interest from both research and industry sectors owing to their distinctive advantages, including high mobility, flexible deployment capabilities, and inherent LoS links [3]. UAVs are particularly advantageous in dynamic or remote environments where traditional ground-based infrastructure is unavailable or suboptimal.

The convergence of ISAC and UAV technologies opens up promising opportunities for enhancing system-level performance across multiple dimensions. On one hand, UAVs can serve as mobile base stations or airborne sensors to improve the coverage and reliability of wireless networks [4]. On the other hand, the mobility of UAVs can be intelligently exploited to optimize sensing geometry, reduce communication blockage, and dynamically adjust service provisioning. Despite its advantages, the realization of UAV-enabled ISAC systems also entails significant technical challenges [5]. These include accurate user tracking in dynamic environments, robust and secure communication under uncertain channel conditions, and the design of efficient algorithms for trajectory planning, beamforming, and power allocation [6]. Addressing these challenges is essential to fully unlock the potential of UAV-assisted ISAC and to meet the stringent performance requirements of future wireless ecosystems.

In the field of ISAC, numerous studies have investigated the joint design of radar and communication functionalities to enhance overall system performance [7,8,9,10,11,12]. For instance, Ref. [7] examined a dual-function multi-input multi-output (MIMO) system that serves both radar sensing and multi-user communication, where a unified beamforming strategy was developed to simultaneously meet the requirements of both tasks. In terms of sensing performance, Ref. [8] focused on MIMO beamforming design under joint radar and communication constraints, employing the Cramér–Rao bound (CRB) as the key metric for target estimation accuracy, considering both point and extended targets. Moreover, energy-efficient beamforming for ISAC was studied in [9], where the waveform was optimized to support multi-user communication and sensing within power and performance limits. A Pareto-based optimization framework was introduced to balance communication-centric and sensing-centric energy efficiency, providing insights into the trade-off between these competing objectives.

Extending ISAC paradigms to UAV-enabled platforms, numerous studies have explored the integrated design of UAV trajectory planning and beamforming to simultaneously enhance communication quality and sensing accuracy. For example, Wang et al. [13] formulated a network utility maximization framework in a multi-UAV system supporting dual radar–communication functionality. To manage the complexity of joint UAV positioning, user association, and power allocation, a decomposition-based solution was proposed. Similarly, Zhang et al. [14] designed a comprehensive strategy integrating UAV trajectory planning, user association, and beamforming to maximize the weighted communication sum-rate while meeting radar detection constraints. In another contribution, Cheng et al. [15] investigated a coordinated approach to UAV trajectory optimization and transmit beamforming in networked ISAC scenarios tailored to low-altitude economic environments. Meng et al. [16] further developed a throughput-oriented optimization algorithm for UAV-assisted ISAC systems by jointly refining UAV flight paths and allocating communication resources efficiently. In the broader context of space–air–ground integrated networks, Mao et al. [17] studied UAV-assisted communication strategies aimed at mobile user tracking and dynamic beamforming. Meanwhile, Li et al. [18] tackled the challenge of covert communications under stringent energy constraints in ISAC systems by proposing a deep reinforcement learning-based framework, which jointly optimized UAV trajectory and bandwidth allocation. Furthermore, Pan et al. [19] formulated a joint optimization problem for UAV path planning and resource distribution, with the objective of minimizing the Cramér–Rao lower bound for target localization while maintaining user-specific quality-of-service requirements. To solve this, they proposed a pattern search algorithm for UAV path tracking and utilized the Hungarian algorithm for dynamic user association. Additionally, an alternating optimization framework, combined with successive convex approximation, was introduced to iteratively adjust power and bandwidth allocation. Likewise, Al-habob et al. [20] presented a predictive beamforming architecture tailored for secure ISAC in environments with multiple mobile aerial eavesdroppers. They designed a maximum likelihood-based channel estimation technique that leverages echo signals to jointly infer the parameters of each UAV, effectively addressing physical-layer security risks.

Ensuring physical layer security in the presence of eavesdroppers remains a pivotal challenge in UAV-assisted ISAC systems [21]. For example, Ref. [22] developed a secure joint transmit beamforming scheme for ISAC to maximize the secrecy sum-rate while adhering to radar signal-to-noise ratio (SNR) requirements. However, their study did not take into account the mobility of users, which restricts its effectiveness in time-varying or dynamic application scenarios. Likewise, Ref. [23] addressed PLS enhancement where the sensing target may act as a potential eavesdropper. Yet, their work is limited to a single-eavesdropper context, lacking investigation into more generalized or multi-adversary conditions. Moreover, Ref. [24] presented a real-time UAV trajectory optimization method for secure ISAC communication, but assumed omnidirectional transmission, thereby neglecting the additional secrecy and efficiency gains that can be achieved through directional beamforming strategies and detailed modeling of antenna radiation characteristics.

To address the limitations observed in prior studies, this work explores a dynamic scenario involving mobile users and introduces a unified optimization framework that jointly designs robust beamforming and UAV trajectory for an ISAC-enabled UAV system. The objective is to enhance the secrecy rate of communications between the UAV and multiple legitimate users, while simultaneously suppressing the risk of information leakage to potential eavesdroppers. The proposed optimization problem incorporates several practical constraints, including UAV mobility restrictions, total transmission power limitations, and sensing accuracy requirements for multiple targets. Due to the non-convex nature of the formulated problem, an efficient alternating optimization algorithm is proposed. In this framework, the robust beamforming component is addressed using a successive convex approximation approach, whereas the UAV trajectory is refined via constrained optimization by a linear approximation technique. This hybrid method facilitates the convergence toward a high-quality, near-optimal solution. Extensive simulation results validate the effectiveness and superiority of the proposed approach in comparison with existing benchmark schemes.

In this work, we use the following notation conventions. The symbols ${(·)}^T$ and ${(·)}^H$ represent the transpose and Hermitian transpose (conjugate transpose) of a matrix, respectively. The operator $|·|$ stands for the absolute value when applied to a scalar, and the modulus when applied to a complex number. The Euclidean norm (${\ell }_2$-norm) and Frobenius norm of vectors or matrices are denoted as ${\parallel ·\parallel }_2$ and ${\parallel ·\parallel }_F$, respectively. For a square matrix, its trace is indicated by $tr(·)$. The set of all complex-valued matrices of dimension $m\times n$ is expressed as ${\mathbb{C}}^{m\times n}$. The real part of a complex variable is written as $\Re (·)$. The expectation operator in the statistical sense is denoted by $\mathbb{E}[·]$.

2. System Model

As illustrated in Figure 1, we consider a UAV-enabled secure ISAC system, where a UAV transmits communication signals and simultaneously receives echo signals from the sensing targets, while simultaneously mitigating signal exposure to the eavesdropper. This dual-functional operation leverages the UAV’s mobility and flexible deployment capabilities to meet both performance and security requirements in dynamic wireless environments.

The UAV is assumed to fly at a fixed altitude H, whereas all ground nodes, including users, targets, and the eavesdroppers, are located at ground level (i.e., height zero). At time slot t, the UAV’s position is given by $\mathbf{q}\left[t\right]=\left(x^q\left[t\right],y^q\left[t\right],H\right)$, and the location of user $k\in \mathcal{K}=\{1,2,\dots ,K\}$ is denoted as ${\mathbf{g}}_k\left[t\right]=\left(x_k^g\left[t\right],y_k^g\left[t\right],0\right)$. For simplicity, the positions of the target $m\in \mathcal{M}=\{1,2,\dots ,M\}$ and eavesdropper $e\in \mathcal{E}=\{1,2,\dots ,E\}$ are assumed to be static, denoted by ${\mathbf{g}}_m=\left(x_m^g,y_m^g,0\right)$ and ${\mathbf{g}}_e=\left(x_e^g,y_e^g,0\right)$, respectively.

The total operation time T is divided into Q equal time slots, each with duration $\Delta t={\displaystyle \frac{T}{Q}}$. This duration is assumed to be short enough to ensure that the channel state information (CSI) for both radar sensing and communication remains approximately constant and can be accurately estimated using pilot signals.

2.1. Mobility Model of UAV

At time slot t, the UAV is allowed to maneuver freely in the horizontal plane, with a displacement distance denoted by $d\left[t\right]\in [0,d_{max}]$, where $d_{max}$ represents the maximum displacement that the UAV can achieve within one time slot. This maximum displacement is determined by the UAV’s maximum flight speed and the duration of each time slot. Accordingly, the UAV’s trajectory can be modeled as a cumulative sum of its successive horizontal displacements, which is mathematically expressed as follows:

$$\mathbf{q}\left[t\right]=\mathbf{q}\left[0\right]+\sum _{\tau =1}^t\nabla \mathbf{q}\left[\tau \right],$$

(1)

where $\nabla \mathbf{q}\left[t\right]=\left(d^x\left[t\right],d^y\left[t\right]\right)$ denotes the horizontal displacement vector at time slot t, with $d^x\left[t\right]$ and $d^y\left[t\right]$ representing the movement components along the x- and y-axes, respectively. The magnitude of the horizontal displacement satisfies the following constraint:

$$d\left[t\right]=\sqrt{{\left(d^x\left[t\right]\right)}^2+{\left(d^y\left[t\right]\right)}^2}.$$

(2)

2.2. Transmit Antenna Model

The UAV is equipped with a uniform planar array (UPA) deployed on the XOY plane for signal transmission. The array consists of $N_x$ antenna elements along the x-axis and $N_y$ antenna elements along the y-axis, resulting in a total of $N=N_x\times N_y$ elements. The corresponding steering vector is denoted by $\mathbf{a}(\varphi ,\theta )\in {\mathbb{C}}^{N\times 1}$, which characterizes the spatial response of the antenna array towards the target direction. Specifically, the steering vector is parameterized by the elevation angle ${\theta }_k\left[t\right]=\theta \left(\mathbf{q}\left[t\right],{\mathbf{g}}_k\left[t\right]\right)$ and the azimuth angle ${\varphi }_k\left[t\right]=\varphi \left(\mathbf{q}\left[t\right],{\mathbf{g}}_k\left[t\right]\right)$, which are determined by the relative positions of the UAV located at $\mathbf{q}\left[t\right]$ and the k-th user located at ${\mathbf{g}}_k\left[t\right]$.

The direction-of-arrival (DoA) information, including both elevation and azimuth angles, is calculated based on the relative geometry between the UAV and the k-th target as follows:

$$\theta \left(\mathbf{q}\left[t\right],{\mathbf{g}}_k\left[t\right]\right)=arcsin{\displaystyle \frac{H}{\sqrt{H^2+{\parallel \mathbf{q}\left[t\right]-{\mathbf{g}}_k\left[t\right]\parallel }^2}}},$$

(3)

$$\varphi \left(\mathbf{q}\left[t\right],{\mathbf{g}}_k\left[t\right]\right)=arctan{\displaystyle \frac{x^q\left[t\right]-x_k^g\left[t\right]}{y^q\left[t\right]-y_k^g\left[t\right]}}.$$

(4)

The steering vector of the UPA can be expressed as the Kronecker product of the steering vectors along the x- and y-axes, given by the following:

$$\mathbf{a}(\varphi ,\theta )={\mathbf{a}}_x(\varphi ,\theta )\otimes {\mathbf{a}}_y(\varphi ,\theta ),$$

(5)

$${\mathbf{a}}_x\left(\varphi ,\theta \right)={\left[e^{-2j\pi \Delta dcos\theta cos\varphi },\dots ,e^{-2j\pi (N_x-1)\Delta dcos\theta cos\varphi }\right]}^T,$$

(6)

$${\mathbf{a}}_y\left(\varphi ,\theta \right)={\left[e^{-2j\pi \Delta dcos\theta sin\varphi },\dots ,e^{-2j\pi (N_y-1)\Delta dcos\theta sin\varphi }\right]}^T,$$

(7)

where $\Delta d$ denotes the inter-element spacing normalized by the carrier wavelength, ensuring phase coherence across the array elements.

2.3. Channel Model

In this work, the air-to-ground (A2G) channel between the UAV and the k-th ground user is modeled based on a widely-adopted probabilistic framework, following the methodology presented in [25]. This model jointly considers both Line-of-Sight and Non-Line-of-Sight (NLOS) propagation conditions, which are critical for accurately capturing the characteristics of UAV-ground communications under various environments.

At each time slot t, the average path loss $\Lambda \left[t\right]$ is expressed as a weighted combination of the LOS and NLOS path losses, given by the following:

$$\Lambda \left[t\right]=P_{LOS}\left[t\right]{\Lambda }_{LOS}\left[t\right]+(1-P_{LOS}\left[t\right]){\Lambda }_{NLOS}\left[t\right],$$

(8)

where ${\Lambda }_{\mathrm{LOS}}\left[t\right]$ and ${\Lambda }_{\mathrm{NLOS}}\left[t\right]$ represent the instantaneous path loss under LOS and NLOS conditions, respectively. Specifically, these path losses can be formulated as follows:

$${\Lambda }_{LOS}\left[t\right]=(\parallel \mathbf{q}\left[t\right]-{\mathbf{g}}_k\left[t\right]{{\parallel }^2{\varsigma }_{LOS})}^{-1},$$

(9)

$${\Lambda }_{NLOS}\left[t\right]=(\parallel \mathbf{q}\left[t\right]-{\mathbf{g}}_k\left[t\right]{{\parallel }^2{\varsigma }_{NLOS})}^{-1},$$

(10)

where ${\varsigma }_{\mathrm{LOS}}$ and ${\varsigma }_{\mathrm{NLOS}}$ denote the additional attenuation factors accounting for shadowing, scattering, and other environment-specific losses beyond the free-space path loss.

The probability of establishing an LOS link is modeled as a function of the UAV’s elevation angle using a modified sigmoid function, which effectively captures the statistical variation in LOS probability with respect to different propagation conditions:

$$\begin{array}{c}\hfill P_{LOS}\left[t\right]={(1+c_1{e}^{-c_2(\theta \left[t\right]-c_1)})}^{-1},\end{array}$$

(11)

$$\begin{array}{c}\hfill P_{NLOS}\left[t\right]=1-P_{LOS}\left[t\right],\end{array}$$

(12)

where $\theta \left[t\right]$ denotes the elevation angle at time slot t, while $c_1$ and $c_2$ are environment-dependent constants that characterize the urban, suburban, or rural scenarios.

Consequently, the A2G channel vector between the UAV and the k-th ground user at time slot t can be expressed as follows:

$${\mathbf{h}}_k\left[t\right]={\Lambda }_k\left[t\right]\mathbf{a}({\varphi }_k\left[t\right],{\theta }_k\left[t\right]),$$

(13)

where $\mathbf{a}({\varphi }_k\left[t\right],{\theta }_k\left[t\right])$ denotes the steering vector corresponding to the current azimuth and elevation angles, as previously defined.

2.4. ISAC Model

Following the ISAC beamforming matrix modeling approach proposed in [7], we adopt a unified framework in which the joint transmitter solely employs precoded communication symbols for simultaneous sensing and communication operations.

Under this modeling paradigm, as illustrated in Figure 2, the transmitted signals are pre-processed by a carefully designed beamforming matrix that serves both communication and sensing functionalities, thereby enabling efficient resource utilization while maintaining the integrated system performance.

$$\mathbf{X}=\mathbf{W}\mathbf{S},$$

(14)

where $\mathbf{S}={\left[{\mathbf{s}}_1\left[n\right],{\mathbf{s}}_2\left[n\right],\dots ,{\mathbf{s}}_K\left[n\right]\right]}^T\in {\mathbb{C}}^{K\times L}$ contains K unit-power data streams intended for the users with ${\displaystyle \frac{1}{L}}\mathbb{E}\left[\mathbf{S}{\mathbf{S}}^H\right]={\mathbf{I}}_K$. The matrix $\mathbf{W}=\left[{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_K\right]\in {\mathbb{C}}^{N\times K}$ is the beamformer for communication and radar sensing, where ${\mathbf{w}}_i$ represents the i-th column of matrix W.

2.4.1. Communication Metrics

Based on the aforementioned communication channel model, the received signal of the k-th user can be written as follows:

$${\mathbf{y}}_k\left[t\right]={\mathbf{h}}_k^H\left[t\right]\mathbf{W}\left[t\right]\mathbf{S}\left[t\right]+{\mathbf{n}}_k\left[t\right],$$

(15)

where ${\mathbf{n}}_k\left[t\right]\sim \mathcal{CN}(0,{\sigma }_k^2{\mathbf{I}}_N)$ denotes the additive white Gaussian noise (AWGN). Thus, the Signal-to-Interference-plus-Noise ratio (SINR) of the k-th communication user can be calculated as

$${\gamma }_k\left[t\right]={\displaystyle \frac{|{\mathbf{h}}_k^H\left[t\right]{\mathbf{w}}_k{\left[t\right]|}^2}{{\sum }_{i=1,i\ne k}^K{\left|{\mathbf{h}}_k^H\left[t\right]{\mathbf{w}}_i\left[t\right]\right|}^2+{\sigma }_k^2}}.$$

(16)

And the communication rate for the k-th ground user can be calculated as

$$R_k\left[t\right]={log}_2(1+{\gamma }_k\left[t\right]).$$

(17)

In addition to reliably serving legitimate GUs, the UAV-enabled wireless communication system must also address potential security vulnerabilities posed by passive eavesdroppers attempting to intercept confidential information. Assuming that the spatial location of an eavesdropper is known or can be estimated, the A2G channel from the UAV to the eavesdropper can be modeled in a manner analogous to that of legitimate users. Specifically, the channel vector between the UAV and the eavesdropper at time slot t is represented as follows:

$${\mathbf{h}}_e\left[t\right]={\Lambda }_e\left[t\right]\mathbf{a}({\varphi }_e\left[t\right],{\theta }_e\left[t\right]).$$

(18)

Let ${\mathbf{w}}_k\left[t\right].$ denote the beamforming vector designed for ground user k. The SINR at the eavesdropper when attempting to decode the message intended for user k can be expressed as follows:

$${\gamma }_{e,k}\left[t\right]={\displaystyle \frac{|{\mathbf{h}}_e^H\left[t\right]{\mathbf{w}}_k{\left[t\right]|}^2}{{\sum }_{i=1,i\ne k}^K{\left|{\mathbf{h}}_e^H\left[t\right]{\mathbf{w}}_i\left[t\right]\right|}^2+{\sigma }_e^2}},$$

(19)

where ${\sigma }_e^2$ denotes the AWGN power at the eavesdropper. The numerator represents the power of the confidential signal as received by the eavesdropper, while the denominator accounts for the total interference from other users’ signals as well as background noise.

Based on this SINR, the eavesdropper’s achievable data rate for decoding the signal of user k is given by the following:

$$R_{e,k}\left[t\right]={log}_2(1+{\gamma }_{e,k}\left[t\right]).$$

(20)

To measure the communication security performance, the instantaneous secrecy rate of ground user k at time t is defined as the difference between the legitimate communication rate and the maximum achievable rate at the eavesdroppers:

$$R_k^{+}\left[t\right]=R_k\left[t\right]-\sum _{e=1}^E{R}_{e,k}\left[t\right],$$

(21)

where the positive secrecy rate implies successful protection of confidential information, while a non-positive secrecy rate indicates a potential breach of communication privacy. In the subsequent analysis, we will demonstrate that this secrecy rate formulation provides an effective and tractable performance metric for constraining the information leakage to potential eavesdroppers.

2.4.2. Sensing Metric

In the considered ISAC-UAV system, a dual-functional transmit waveform is employed to simultaneously support both communication and radar sensing tasks. The transmitted signal is exploited to illuminate the target region of interest, requiring sufficient directional energy to ensure reliable detection performance. To characterize this energy distribution, we define the transmit signal covariance matrix as follows:

$$\mathbf{R}\left[t\right]=\mathbb{E}\left[\mathbf{X}\left[t\right]{\left(\mathbf{X}\left[t\right]\right)}^H\right]=\mathbf{W}\left[t\right]{\left(\mathbf{W}\left[t\right]\right)}^H,$$

(22)

where the matrix $\mathbf{R}\left[t\right]$ captures the spatial power distribution of the transmitted signal and plays a key role in shaping the sensing beam pattern. To evaluate the system’s sensing performance toward the m-th target, the beam pattern gain at time slot t is defined as follows [14,26,27]:

$$\mathbf{P}(\mathbf{q}\left[t\right],{\mathbf{g}}_m\left[t\right],\mathbf{W}\left[t\right])={\mathbf{a}}^H\left({\varphi }_m\left[t\right],{\theta }_m\left[t\right]\right)\mathbf{R}\left[t\right]\mathbf{a}\left({\varphi }_m\left[t\right],{\theta }_m\left[t\right]\right),$$

(23)

where $\mathbf{a}({\varphi }_m\left[t\right],{\theta }_m\left[t\right])$ represents the steering vector toward the direction of the m-th target. The resulting beampattern gain quantifies the amount of energy directed along the target’s direction, serving as a fundamental indicator of radar detection capability in the integrated sensing and communication framework.

3. Problem Formulation and Joint Optimization Framework

3.1. Problem Formulation

In this section, we formulate a joint robust beamforming and UAV trajectory optimization problem tailored for secure ISAC systems. At each discrete time slot t, the UAV is equipped with onboard sensing modules—such as visual-inertial odometry or LiDAR systems—which are utilized to estimate the positions of the ground mobile users. The positions of the eavesdroppers are assumed to be known in advance, thereby satisfying the prerequisites for secrecy rate optimization. Based on the estimated relative positions between the UAV and the users, and by employing the standardized 3GPP channel modeling approach for UAV communications as introduced earlier, the downlink CSI can be obtained accordingly.

However, due to inevitable estimation errors introduced by imperfect sensing hardware and dynamic environments, the obtained user positions are inherently uncertain, leading to potential deviations in the channel estimation. To ensure reliable and secure communication under such uncertainty, a robust beamforming strategy is required to mitigate the impact of channel estimation errors. Furthermore, it is crucial to jointly optimize the UAV’s trajectory and its corresponding transmit beamforming matrix in order to maximize system performance.

The overall objective is to maximize the cumulative secrecy sum-rate achieved by all legitimate users over a given time horizon. Specifically, the robust design seeks to optimize the expected secrecy sum-rate under user location uncertainty modeled by a normal distribution over the estimation error $\Delta {\mathbf{g}}_k$. The optimization problem is formulated as follows:

$$\begin{array}{cc}\hfill \left(\mathcal{P}1\right):\underset{\mathbf{q}\left[t\right],\mathbf{W}\left[t\right]}{max}& \sum _{t=1}^T\sum _{k=1}^K{\mathbb{E}}_{\Delta {\mathbf{g}}_k}{\left[R_k(\mathbf{q}\left[t\right],\mathbf{W}\left[t\right])-\sum _{e=1}^E{R}_{e,k}(\mathbf{q}\left[t\right],\mathbf{W}\left[t\right])\right]}^{+}\hfill \end{array}$$

(24a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \left(\mathrm{C}1\right):d\left[t\right]\le d^{max},\hfill \end{array}$$

(24b)

$$\begin{array}{cc}\hfill & \left(\mathrm{C}2\right):tr\left(\mathbf{W}\left[t\right]{\left(\mathbf{W}\left[t\right]\right)}^H\right)\le P_T,\hfill \end{array}$$

(24c)

$$\begin{array}{cc}\hfill & \left(\mathrm{C}3\right):\mathbf{P}(\mathbf{q}\left[t\right],{\mathbf{g}}_m\left[t\right])\ge \Gamma ,\forall m\in \mathcal{M}\hfill \end{array}.$$

(24d)

In the above formulation, Constraint $\left(\mathrm{C}1\right)$ ensures that the UAV’s movement is limited by its maximum flying distance per time slot. Constraint $\left(\mathrm{C}2\right)$ imposes the total transmit power budget $P_T$. Constraint $\left(\mathrm{C}3\right)$ enforces the minimum required sensing quality Γ, characterized by the power of the signal reflected from each sensing target m.

3.2. Joint Optimization Framework

As shown in Figure 3, the initial positions of the legitimate users are estimated using the onboard sensors. Based on these estimates, channel conditions are characterized using a sample average approximation (SAA) method to derive robust channel parameters. These estimations serve as the foundational inputs for subsequent optimization. To address the challenges associated with the joint design of UAV trajectory and robust beamforming in secure ISAC systems, we decompose the original problem $\left(\mathcal{P}1\right)$ into two interrelated yet tractable sub-problems: (i) robust beamforming matrix design under uncertain channel conditions, total transmit power budget and sensing constraints, and (ii) UAV trajectory optimization subject to mobility. This decomposition enables the use of an alternating optimization framework that iteratively updates the beamforming strategy and the UAV position at each time slot.

3.2.1. Design of Robust Beamforming

In practical UAV-enabled ISAC systems, the accuracy of channel state information is often compromised due to uncertainties in the UAV’s localization process. For instance, measurement errors from LiDAR-based positioning systems may result in inaccurate estimations of the UAV’s position, thereby leading to imperfect knowledge of the communication channels. This imperfection in CSI severely degrades the performance of conventional beamforming strategies, which typically rely on precise user location information.

To mitigate the detrimental effects of such uncertainties, we model the user position prediction error as a two-dimensional Gaussian distribution in the spatially orthogonal x- and y-axes. This probabilistic representation, as shown in Figure 4, captures the prior uncertainty in location estimation and provides a statistical foundation for robust beamforming design.

$$f\left(\mathbf{x}\right)={\displaystyle \frac{1}{2\pi \sqrt{|\Sigma |}}}exp\left(-{\displaystyle \frac{1}{2}}{(\mathbf{x}-\mathit{\mu })}^{\top }{\Sigma }^{-1}(\mathbf{x}-\mathit{\mu })\right),$$

(25)

where $\mathbf{x}={[x,y]}^T$ denotes the perturbed user location, $\mathit{\mu }={[x_0,y_0]}^T$ is the predicted mean position, and $\Sigma$ is the covariance matrix expressed as follows:

$$\Sigma =\left[\begin{array}{cc}{\sigma }_x^2& \rho {\sigma }_x{\sigma }_y\\ \rho {\sigma }_x{\sigma }_y& {\sigma }_y^2\end{array}\right],$$

(26)

where ${\sigma }_x$ and ${\sigma }_y$ represent the standard deviations along the x and y directions, respectively, and $\rho$ is the correlation coefficient between the two axes.

By leveraging this uncertainty model, we employ the Sample Average Approximation (SAA) method to incorporate the effects of user location perturbations into the beamforming design process. The SAA framework enables the evaluation of the average channel behavior over multiple error realizations, thereby ensuring that the actual CSI deviations are statistically reflected in the beamforming optimization. This robust design significantly enhances communication reliability in the presence of localization noise.

Since the beamforming optimization process at each time slot is decoupled from the UAV’s trajectory design, the time slot index t is omitted in the subsequent formulation for notational clarity. Consequently, the robust beamforming subproblem at a given time slot can be expressed as follows:

$$\begin{array}{cc}\hfill \left(\mathcal{P}2\right):\underset{\mathbf{W}}{max}& \sum _{k=1}^K{\mathbb{E}}_{\Delta {\mathbf{g}}_k}{\left[R_k(\mathbf{q},\mathbf{W})-R_{e,k}(\mathbf{q},\mathbf{W})\right]}^{+}\hfill \end{array}$$

(27a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \left(\mathrm{C}{2}^{*}\right):tr\left(\mathbf{W}{\mathbf{W}}^H\right)\le P_T,\hfill \end{array}$$

(27b)

$$\begin{array}{cc}\hfill & \left(\mathrm{C}{3}^{*}\right):{\mathbf{P}}_m\left(\mathbf{q},{\mathbf{g}}_m,\mathbf{W}\right)\ge \Gamma ,\forall m\in \mathcal{M}\hfill \end{array}.$$

(27c)

The optimization problem introduced in the previous section is inherently non-convex, primarily due to the presence of logarithmic functions and fractional terms in the secrecy rate expressions. These nonlinearities make direct optimization intractable. To overcome this challenge, we adopt a convex approximation strategy that combines the Successive Convex Approximation method with Semi-Definite Relaxation (SDR). In this context, the beamforming covariance matrices are defined as ${\mathbf{R}}_i={\mathbf{W}}_i{\mathbf{W}}_i^H,\forall i\in \mathcal{K}$, and the secrecy rate of the k-th legitimate user is rewritten as follows:

$$R_k={\Phi }_{k1}\left({\mathbf{R}}_i\right)-{\Phi }_{k2}\left({\mathbf{R}}_i\right),$$

(28)

where

$${\Phi }_{k1}\left({\mathbf{W}}_i\right)={log}_2\left(1+{\sigma }_k^{-2}\sum _{i=1}^K{\mathbf{h}}_k^H{\mathbf{R}}_i{\mathbf{h}}_k\right),$$

(29)

$${\Phi }_{k2}\left({\mathbf{W}}_i\right)={log}_2\left(1+{\sigma }_k^{-2}\sum _{i=1,i\ne k}^K{\mathbf{h}}_k^H{\mathbf{R}}_i{\mathbf{h}}_k\right).$$

(30)

Similarly, the information leakage rate to the eavesdropper is defined as follows:

$$R_{e,k}={\Phi }_{e,k1}\left({\mathbf{R}}_i\right)-{\Phi }_{e,k2}\left({\mathbf{R}}_i\right),$$

(31)

where

$${\Phi }_{e,k1}\left({\mathbf{W}}_i\right)={log}_2\left(1+{\sigma }_e^{-2}\sum _{i=1}^K{\mathbf{h}}_e^H{\mathbf{R}}_i{\mathbf{h}}_e\right),$$

(32)

$${\Phi }_{e,k2}\left({\mathbf{W}}_i\right)={log}_2\left(1+{\sigma }_e^{-2}\sum _{i=1,i\ne k}^K{\mathbf{h}}_e^H{\mathbf{R}}_i{\mathbf{h}}_e\right).$$

(33)

It can be observed that the non-convexity primarily arises from ${\Phi }_{k2}\left({\mathbf{R}}_i\right)$ and ${\Phi }_{e,k1}\left({\mathbf{R}}_i\right)$, which are concave functions subtracted from other concave functions. To convexify the problem, we apply the first-order Taylor expansion to approximate these non-convex terms around a given point ${\tilde{\mathbf{R}}}_i$:

$${\Phi }_{k2}\left({\mathbf{W}}_i\right)\approx {\Phi }_{k2}\left({\tilde{\mathbf{W}}}_i\right)+{\zeta }_{k2}\sum _{i=1,i\ne k}^K\left({\mathbf{h}}_k^H\left({\mathbf{W}}_i-{\tilde{\mathbf{W}}}_i\right){\mathbf{h}}_k\right),$$

(34)

where the linearization coefficients are defined as follows: ${\zeta }_{k2}={\displaystyle \frac{1}{\left({\sum }_{i=1,i\ne k}^K{\mathbf{h}}_k^H{\tilde{\mathbf{W}}}_i{\mathbf{h}}_k+{\sigma }_k^2\right)ln2}}$.

$${\Phi }_{e,k1}\left({\mathbf{W}}_i\right)\approx {\Phi }_{e,k1}\left({\tilde{\mathbf{W}}}_i\right)+{\zeta }_{e,k1}\sum _{i=1}^K\left({\mathbf{h}}_e^H\left({\mathbf{W}}_i-{\tilde{\mathbf{W}}}_i\right){\mathbf{h}}_e\right),$$

(35)

where ${\zeta }_{e,k1}={\displaystyle \frac{1}{\left({\sum }_{i=1,i\ne k}^K{\mathbf{h}}_e^H{\tilde{\mathbf{W}}}_i{\mathbf{h}}_e+{\sigma }_e^2\right)ln2}}$.

Substituting these approximations into the original secrecy rate expression yields the following convexified surrogate functions:

$${\tilde{R}}_k={\Phi }_{k1}\left({\mathbf{W}}_i\right)-{\Phi }_{k2}\left({\tilde{\mathbf{W}}}_i\right)-{\zeta }_{k2}\sum _{i=1,i\ne k}^K{\mathbf{h}}_k^H\left({\mathbf{W}}_i-{\tilde{\mathbf{W}}}_i\right){\mathbf{h}}_k,$$

(36)

$${\tilde{R}}_{e,k}={\Phi }_{e,k1}\left({\tilde{\mathbf{W}}}_i\right)+{\zeta }_{e,k1}\sum _{i=1}^K{\mathbf{h}}_k^H\left({\mathbf{W}}_i-{\tilde{\mathbf{W}}}_i\right){\mathbf{h}}_k-{\Phi }_{e,k2}\left({\mathbf{W}}_i\right).$$

(37)

Accordingly, the robust beamforming subproblem can be reformulated as follows:

$$\begin{array}{cc}\hfill \left(\mathcal{P}3\right):\underset{\mathbf{W}}{max}& \sum _{k=1}^K{\mathbb{E}}_{\Delta {\mathbf{g}}_k}{\left[{\tilde{R}}_k(\mathbf{q},\mathbf{W})-\sum _{e=1}^E{\tilde{R}}_{e,k}(\mathbf{q},\mathbf{W})\right]}^{+}\hfill \end{array}$$

(38a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \left(\mathrm{C}{2}^{*}\right):tr\left(\mathbf{W}{\mathbf{W}}^H\right)\le P_T,\hfill \end{array}$$

(38b)

$$\begin{array}{cc}\hfill & \left(\mathrm{C}{3}^{*}\right):{\mathbf{P}}_m\left(\mathbf{q},{\mathbf{g}}_m,\mathbf{W}\right)\ge \Gamma ,\forall m\in \mathcal{M}\hfill \end{array}.$$

(38c)

The reformulated problem $\left(\mathcal{P}3\right)$ is a standard semi-definite programming (SDP) problem that can be efficiently solved using off-the-shelf convex optimization solvers such as CVX. As the procedure has a tendency to reduce interference and noise components, initializing the auxiliary optimization variables ${\tilde{\mathbf{R}}}_i$ as zero matrices provides an effective starting point, often requiring only one calculation. Consequently, the computational complexity of the interior-point method for beamforming design is on the order of $\mathcal{O}\left(K^{3.5}\right)$.

3.2.2. Design of Trajectory

Given the current beamforming design, the UAV trajectory optimization subproblem aims to determine the optimal UAV locations at t-th time slot to further enhance the system’s secrecy performance. The problem can be formulated as follows:

$$\begin{array}{cc}\hfill \left(\mathcal{P}4\right):\underset{\mathbf{q}\left[t\right]}{max}& \sum _{t=1}^T\sum _{k=1}^K{\mathbb{E}}_{\Delta {\mathbf{g}}_k}{\left[R_k\left(\mathbf{q}\left[t\right]\right)-\sum _{e=1}^E{R}_{e,k}\left(\mathbf{q}\left[t\right]\right)\right]}^{+}\hfill \end{array}$$

(39a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \left(\mathrm{C}1\right):d\left[t\right]\le d_{max}.\hfill \end{array}$$

(39b)

This subproblem remains highly non-convex due to the nonlinear dependence of the secrecy rate on the UAV’s position $\mathbf{q}\left[t\right]$, the probabilistic nature of the CSI model, and the absence of closed-form gradients. Additionally, the time-varying characteristics of wireless channels and the UAV’s mobility constraints further complicate trajectory planning.

To address this challenge, we adopt the COBYLA algorithm, a derivative-free trust-region method suitable for solving non-convex problems with nonlinear constraints and unknown gradient information. COBYLA iteratively approximates both the objective and constraint functions via linear models constructed in a local neighborhood around the current solution.

Specifically, at the s-th iteration, the algorithm solves the following local trust-region subproblem:

$$\begin{array}{cc}\hfill \left(\mathcal{P}5\right):\underset{\mathbf{d}\in {\mathbb{R}}^2}{min}& \tilde{f}({\mathbf{q}}^{\left(s\right)}+\mathbf{d})=f^{\left(s\right)}+\nabla f^{\left(s\right)}\mathbf{d}\hfill \end{array}$$

(40a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& {\tilde{c}}_i({\mathbf{q}}^{\left(s\right)}+\mathbf{d})=c_i^{\left(s\right)}+\nabla c_i^{\left(s\right)}\mathbf{d}\ge 0,\hfill \end{array}$$

(40b)

$$\begin{array}{cc}\hfill & {\parallel \mathbf{d}\parallel }_2\le {\rho }^{\left(s\right)},\hfill \end{array}$$

(40c)

where $f^{\left(s\right)}=f\left({\mathbf{q}}^{\left(s\right)}\right)$ and $c_i^{\left(s\right)}=c_i\left({\mathbf{q}}^{\left(s\right)}\right)$ denote the values of the objective and constraint functions at the current iterate ${\mathbf{q}}^{\left(s\right)}$. The gradients $\nabla f^{\left(s\right)}$ and $\nabla c_i^{\left(s\right)}$ are estimated using finite-difference approximations or polynomial interpolation.

Based on the solution of this subproblem, the UAV’s position is iteratively updated as ${\mathbf{q}}^{(s+1)}={\mathbf{q}}^{\left(s\right)}+{\mathbf{d}}^{\left(s\right)}$, where ${\mathbf{d}}^{\left(s\right)}$ denotes the search direction. The trust-region radius ${\rho }^{\left(s\right)}$ is adaptively adjusted depending on constraint feasibility and the improvement in the objective function. This iterative process continues until the convergence criteria are met, ensuring a locally optimal solution for UAV trajectory planning. The worst-case computational complexity of COBYLA is considered to scale as $\mathcal{O}(2^2·\mu )$, where μ is the maximum number of iterations. Since the beamforming matrix must be optimized at each iteration of trajectory optimization, the overall algorithm exhibits a computational complexity of $\mathcal{O}(2^2·\mu ·K^{3.5})$. And the whole steps of the proposed optimization procedure are summarized in Algorithm 1.

Algorithm 1 Proposed algorithm for joint robust beamforming and trajectory optimization

1: Input: Initial UAV position $\mathbf{q}\left[0\right]$, total transmit power $P_T$, sensing threshold $\Gamma$, time horizon T, number of time slots Q, maximum flight distance $d_{max}$, predicted user positions $\left\{{\mathbf{g}}_k\left[t\right]\right\}$, target positions $\left\{{\mathbf{g}}_m\left[t\right]\right\}$, eavesdropper positions $\left\{{\mathbf{g}}_e\left[t\right]\right\}$, convergence tolerance $ϵ$ 2: Output: Optimized UAV trajectory ${\left\{\mathbf{q}\left[t\right]\right\}}_{t=1}^T$ and beamforming matrices ${\left\{\mathbf{W}\left[t\right]\right\}}_{t=1}^T$ 3: for $t=1$ to T do 4:       Solve the trajectory subproblem (39) using COBYLA 5:       Inner step – Beamforming Optimization: 6:          Given UAV position $\mathbf{q}\left[t\right]$ and predicted user positions ${\mathbf{g}}_k\left[t\right]$ 7:          Solve the robust beamforming problem (38) via SCA and SDR to obtain $\mathbf{W}\left[t\right]$ 8: end for 9: return Final UAV trajectory ${\left\{\mathbf{q}\left[t\right]\right\}}_{t=1}^T$ and beamforming matrices ${\left\{\mathbf{W}\left[t\right]\right\}}_{t=1}^T$

4. Simulation Results

To validate the performance of the proposed secure ISAC-UAV framework, extensive simulations are carried out using the system parameters detailed in

Table 1. Simulation parameters.

Parameter	Description	Value
K	Number of ground users	1/3/4
M	Number of targets	1/2
E	Number of eavesdroppers	1/2
$N_x$	Number of x-axis antennas	4
$N_y$	Number of y-axis antennas	4
T	Total flight time of UAV	30 s
Q	Number of time slots	30
H	Height of UAV	100 m
$f_c$	Carrier frequency	5 GHz
$P_T$	Transmit power budget	30 dBm
${\sigma }_k^2$	Communication noise power	80 dB
$d_{max}$	Maximum displacement within one time slot	10 m
Γ	Minimum threshold for radar detection	5 dB
$\Delta d$	Antenna spacing	0.5
${\varsigma }^L$, ${\varsigma }^{NL}$	Path loss factors	1 dB, 20 dB
$c_1$, $c_2$	Environment parameters	9.61, 0.16
ϵ	Convergence threshold	10−4
$\mu$	Maximum number of iterations	50

. The UAV is configured with a 4 × 4 uniform planar antenna array and maintains a constant flight altitude of 100 m throughout a mission duration of 30 s. This time span is uniformly divided into 30 discrete intervals for analysis.

System performance is evaluated in terms of the achievable secrecy sum-rate under various conditions, including transmit power, number of users, radar sensing thresholds, and key statistical characteristics such as the mean and standard deviation.

The initial UAV position is randomly assigned but constrained to be within a reasonable distance from legitimate users. If the initial location is set too far from the users, the secrecy sum-rate may fall below zero during the initial time slots, indicating the inability to establish effective secure communication due to significant signal leakage to eavesdroppers. To facilitate a more comprehensive performance analysis, three scenarios with different numbers of users are designed. All optimization procedures are reproducible using either CVX solvers in MATLAB 2020b or CVXPY in Python 3.11.0.

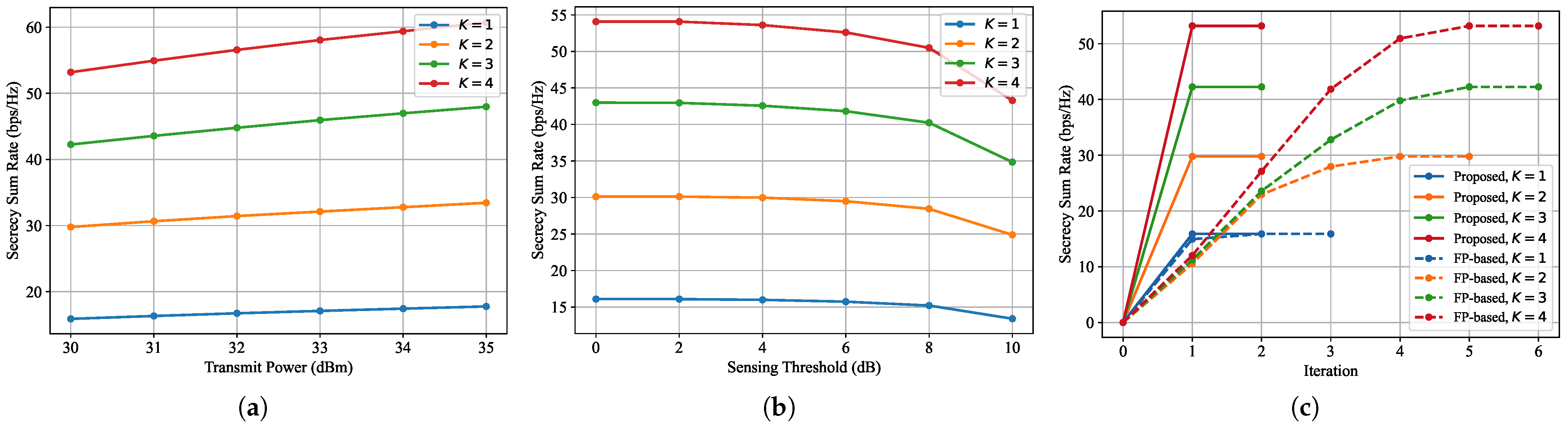
To investigate the performance of the beamforming optimization stage, we first consider a single time slot scenario in which only the beamforming matrix is optimized. Multiple legitimate users are placed at a horizontal distance of 50 m from the UAV, while sensing targets and eavesdroppers are positioned at a horizontal distance of 150 m. The performance of the beamforming algorithm is analyzed by varying the transmit power and the radar sensing threshold constraints.

Figure 5a illustrates the relationship between the total transmit power and the achievable secrecy sum-rate under different numbers of legitimate users ($K=1,2,3,4$). The transmit power ranges from 30 dBm to 35 dBm, and the secrecy performance is evaluated using the proposed joint robust beamforming optimization algorithm. It can be observed that the secrecy sum-rate increases monotonically with the transmit power across all cases. This is because higher transmit power enhances the signal strength at the legitimate users, thereby improving the achievable communication rates. Additionally, the performance is significantly influenced by the number of ground users. When $K=1$, the system achieves the lowest sum-rate due to limited degrees of freedom in beamforming. As K increases, the sum-rate rises steadily, with the case of $K=4$ achieving the highest throughput. This is attributed to multi-user diversity, where more users provide greater flexibility in beam allocation. However, this also introduces additional challenges in interference management and secrecy protection. The results in this figure verify the scalability and robustness of the proposed framework, demonstrating its ability to support an increasing number of users without significant degradation in secrecy performance, especially when sufficient power is provisioned.

Figure 5b illustrates the impact of the radar sensing threshold Γ on the achieved secrecy sum-rate under different numbers of legitimate users. As the sensing requirement becomes increasingly stringent, the system is compelled to allocate greater transmit power and beamforming resources toward the sensing direction. Consequently, it becomes essential to configure the minimum transmit beamforming gain according to specific scene requirements to achieve a balanced trade-off between sensing quality and communication performance. The figure reveals a clear trend: as Γ increases from 0 to 10 dB, the secrecy sum-rate degrades gradually across all user configurations. This is due to the increased power and spatial focus required to satisfy the sensing constraint, which in turn limits the degrees of freedom available for optimizing secure communication. Notably, the performance degradation is more pronounced when the number of users K is larger. For instance, in the case of $K=4$, the secrecy sum-rate drops from approximately 54 bps/Hz at Γ = 0 dB to around 44 bps/Hz at Γ = 10 dB. Similarly, for $K=1$, the sum-rate drops from about 16 bps/Hz to below 14 bps/Hz over the same range. This trend underscores the trade-off between sensing reliability and communication security in UAV-enabled ISAC systems. Overall, the results highlight the importance of jointly optimizing sensing and communication under practical constraints. The proposed algorithm effectively balances both objectives, maintaining robust secrecy rates even under tightening sensing requirements.

Figure 5c depicts the convergence performance of the proposed robust beamforming algorithm in comparison to the traditional fractional programming (FP)-based method, which is detailed in Appendix A. The results are shown for varying numbers of ground users $K=\{1,2,3,4\}$, with the secrecy sum-rate (in bps/Hz) plotted over successive iterations. It can be observed that the proposed algorithm achieves rapid and stable convergence within two iterations across all tested user configurations. For instance, when $K=4$, the proposed method converges to a secrecy sum-rate of approximately 54 bps/Hz after just one step. Similarly, for $K=1$, the performance stabilizes at around 16 bps/Hz. In contrast, the FP-based scheme requires more iterations to achieve convergence. The rapid convergence of the proposed algorithm can be attributed to the application of the SCA method, which linearizes a part of the objective function via first-order Taylor expansion to construct a convex lower bound. Moreover, since the iterative process progressively reduces the interference and noise terms, initializing the intermediate optimization variables as zero vectors provides a favorable starting point, further accelerating convergence. The figure underscores the fast convergence and robustness of the proposed algorithm, making it suitable for real-time UAV-enabled ISAC deployments, especially in dynamic environments.

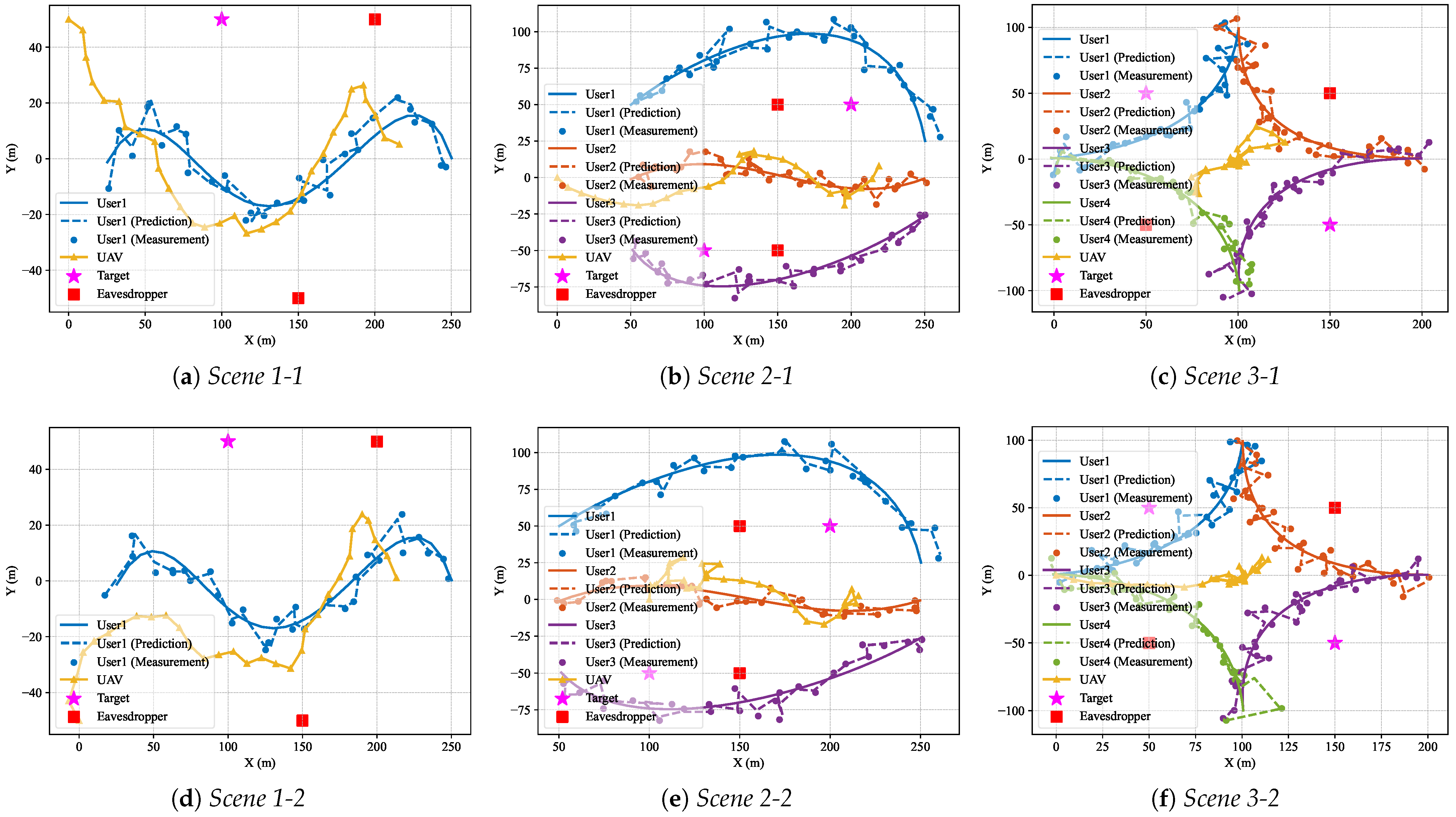
Figure 6 illustrates the UAV flight trajectories and user movements in three secure ISAC scenarios. The system aims to maximize the secrecy sum-rate while guaranteeing radar sensing performance and minimizing exposure to the eavesdropper.

Figure 6a illustrates the actual trajectory of a single user (solid line), the predicted positions (dashed line), and the measured positions (scattered markers) in Scene 1. The UAV trajectory, initialized at (0, 50, 100) and depicted by a yellow line with triangular markers, dynamically adapts to the user’s predicted positions. It hovers near optimal locations that enhance secure communication while minimizing signal leakage to the eavesdropper (red square) and maintaining sufficient sensing performance for the designated target (magenta star). It can be observed that the UAV gradually moves closer to the legitimate user during the optimization process to improve the overall secrecy rate. Eventually, the UAV’s trajectory tends to align with the user’s movement pattern.

Figure 6d presents another UAV trajectory in Scene 1, where the UAV starts from a different randomly initialized position (0, −50, 100). Despite this variation, the optimization process over time leads to a similar trajectory in the final time slots, demonstrating the robustness of the proposed approach to different initializations.

Figure 6b illustrates the UAV trajectory in Scene 2, where three legitimate users are located at (50, −50, 0), (50, 0, 0), and (50, 50, 0). The UAV is initialized at (0, 0, 100) and optimizes its trajectory to serve all users fairly while maintaining secure communication in the presence of two eavesdroppers and ensuring sufficient sensing quality for two targets. The UAV adaptively balances its position between the three users, as reflected in its curved flight path, which avoids proximity to the eavesdroppers (red squares) and remains within effective sensing range of the targets (magenta stars).

Figure 6e presents the same scenario as in Figure 6b, but with a different UAV initialization at (100, 0, 100). Although the initial trajectory differs significantly, the UAV eventually converges to a similar serving pattern, positioning itself closer to the users and away from high-risk regions. This again demonstrates the adaptability and robustness of the proposed trajectory optimization method under varying initial conditions.

Figure 6c corresponds to Scene 3, where four users are located at (0, 0, 0), (100, 100, 0), (100, −100, 0), and (200, 0, 0). The UAV starts from (100, 0, 100) and is required to jointly serve all users while satisfying security and sensing constraints. Compared with previous scenarios, the UAV path in this case exhibits more dynamic and distributed movement due to the wider spatial distribution of users. The trajectory is shaped to prioritize both the central users and those located at the edges, ensuring balanced performance.

Figure 6f shows the result of Scene 3 with a different UAV initial position at (0, 0, 100). Similar to previous observations, although the UAV starts from a suboptimal location, the optimization algorithm quickly adjusts its path, steering the UAV towards more favorable positions that optimize the secrecy sum-rate and radar sensing performance. The final trajectory aligns closely with the distribution of user positions, confirming the effectiveness of the proposed approach under complex and asymmetrical user layouts.

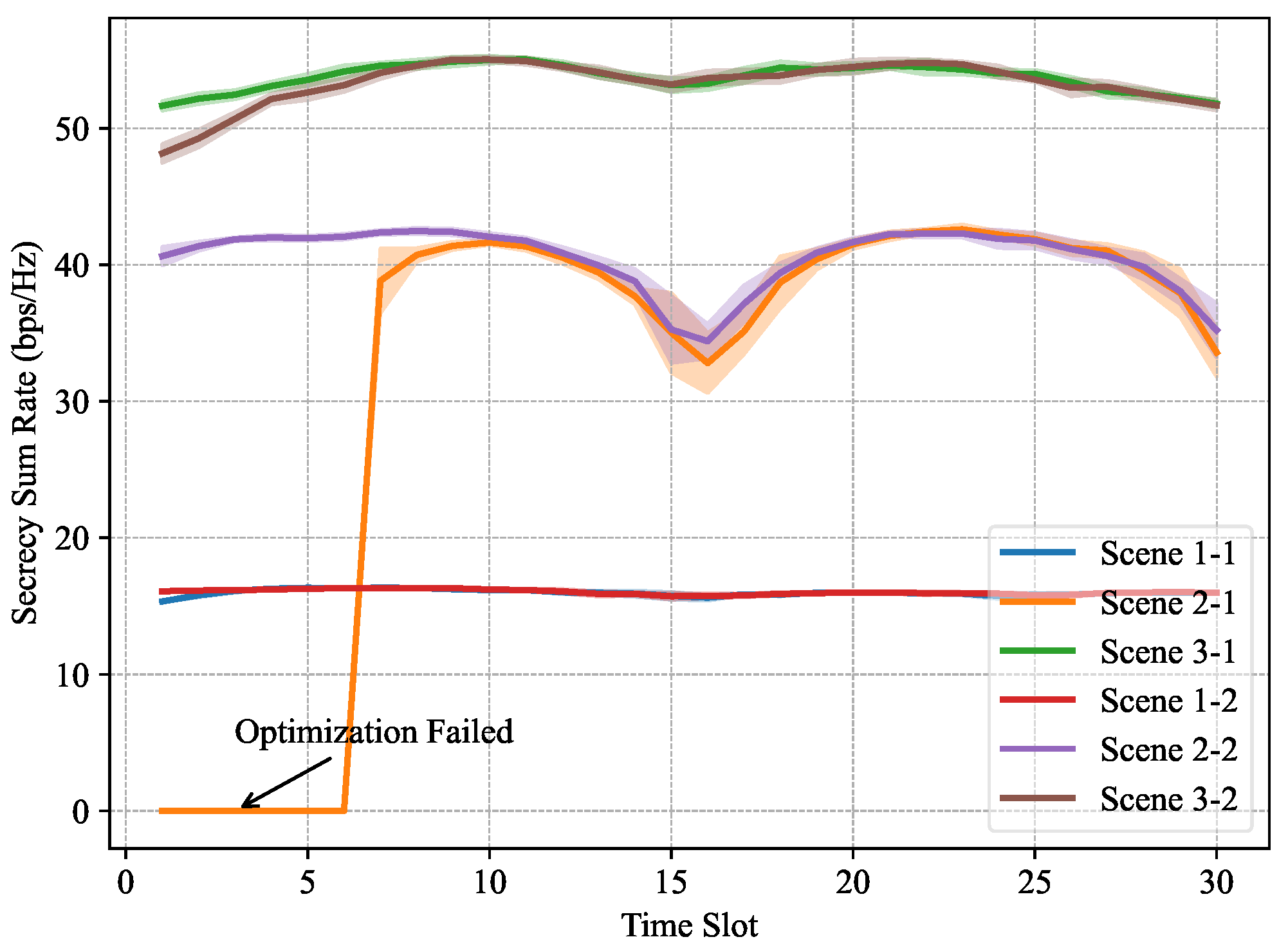
Figure 7 presents the secrecy sum-rate evolution across all 30 time slots under six different configurations, covering three scene settings and two UAV initial positions per scene. The figure highlights the strong correlation between the UAV’s proximity to legitimate users and the achieved secrecy rate: scenarios where the UAV quickly converges toward users (e.g., Scene 3-1 and Scene 3-2) consistently yield higher secrecy performance. In Scene 2-1, the secrecy rate is initially negative due to suboptimal UAV positioning, resulting in excessive signal leakage to eavesdroppers. This phase is labeled as “Optimization Failed” in the figure. However, the algorithm effectively learns a secure trajectory over subsequent slots, and the performance stabilizes to a competitive level. This behavior demonstrates the resilience of the proposed framework, even under poor initial conditions. Additionally, it is evident that differences in the UAV’s initial position only affect the early stage of the optimization. As time progresses, the optimized trajectories across the two variants of each scene converge to similar secrecy performance levels, indicating that the proposed method consistently finds effective flight paths regardless of initialization.

5. Conclusions

In this article, we present a novel unified optimization framework that jointly addresses robust beamforming and UAV trajectory planning for a secure ISAC-UAV system involving mobile users. The overall optimization is decoupled into two interrelated subproblems: the robust beamforming subproblem is tackled using the SCA combined with the SDR approach, while the UAV trajectory subproblem is handled by employing the derivative-free COBYLA algorithm. Simulation results reveal that the proposed approach substantially outperforms conventional benchmark schemes in terms of secrecy sum-rate and convergence efficiency, all while satisfying both radar sensing requirements and UAV mobility constraints. Furthermore, numerical evaluations confirm that the proposed framework achieves near-optimal performance under practical system limitations, offering considerable improvements in secrecy capabilities while preserving high-fidelity sensing performance.

While this study presents promising results, it is currently limited to simulations based on synthetic data and idealized channel models. Future work should validate the proposed framework under real-world deployment conditions, considering practical factors such as hardware impairments and channel measurement noise. The current model also does not account for dynamic parameters, such as user velocity, propagation delay, and Doppler shifts, all of which are critical in high-mobility environments. Incorporating these parameters into the mobility and sensing models would improve the realism and practical relevance of the proposed ISAC-UAV system design.

In particular, the proposed framework holds significant potential for real-world applications in scenarios requiring secure communications and high-accuracy sensing. For example, it can be deployed in military surveillance missions to support covert information transmission and precise target detection in contested environments; in border patrol operations to simultaneously monitor intrusion activities and maintain encrypted communication links and in disaster response scenarios to ensure confidential data exchange and environmental sensing under infrastructure-damaged conditions. These applications highlight the importance of integrated, secure, and adaptive ISAC-UAV designs in future wireless systems.