A Two-Stage Optimization Framework for UAV Fleet Sizing and Task Allocation in Emergency Logistics Using the GWO and CBBA
Abstract
1. Introduction
1.1. Context and Motivation
1.2. State of the Art and Research Gap
1.2.1. Centralized and Distributed Task Allocation Methods
1.2.2. The Disconnect Between Fleet Sizing and Task Allocation
1.3. Our Contribution and Paper Organization
2. Problem Analysis
2.1. Constraint Establishment
2.2. Single UAV Objective Function
2.3. UAV Cluster Objective Function
3. Integrated UAV Scheduling Modeling
3.1. Model for Optimizing the Number of UAVs
Model Assumptions and Symbolic Definitions
3.2. Objective Function
3.3. Define Each Subfunction
3.4. Constraints
3.5. Optimization Problems
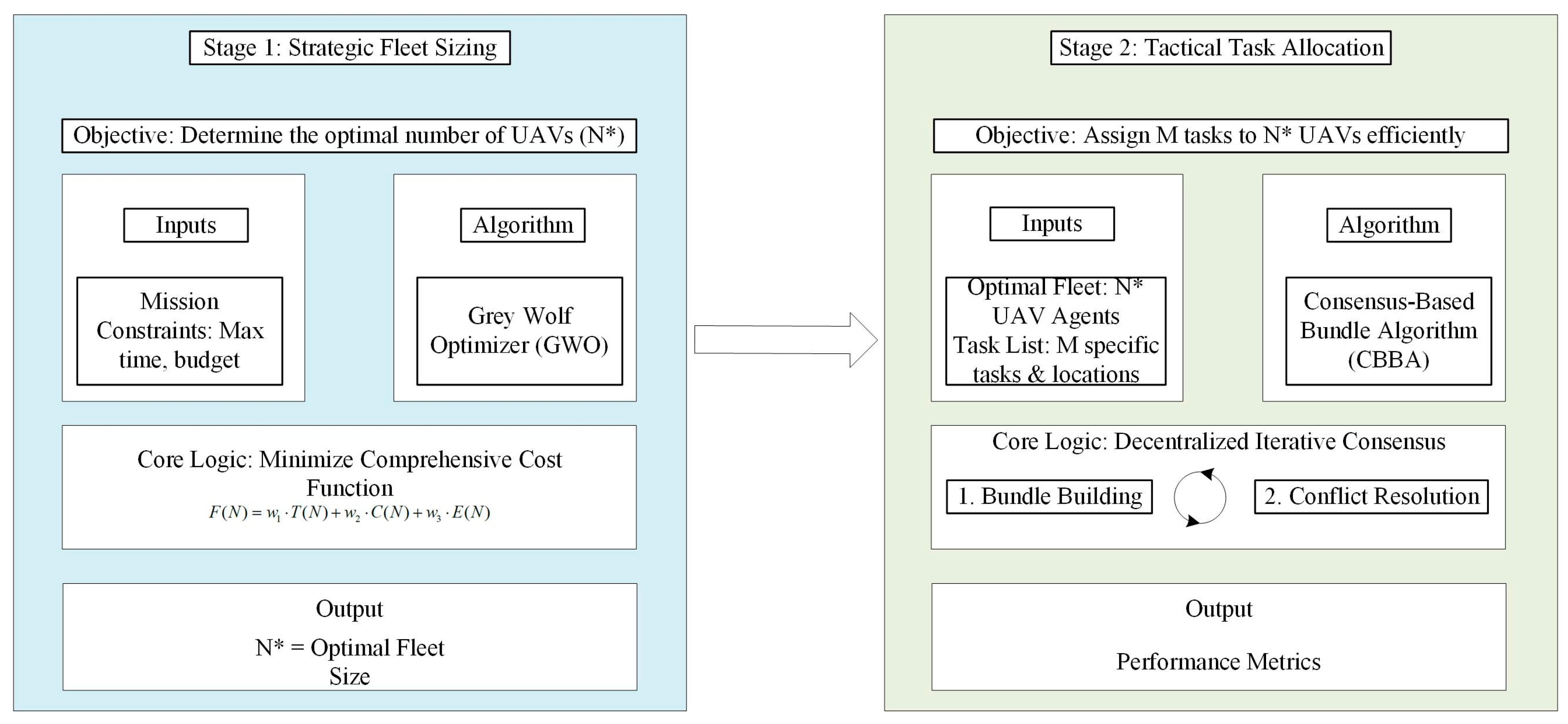
4. The Proposed Two-Stage GWO-CBBA Framework
4.1. Stage 1: GWO for Optimal Fleet Sizing
4.2. Stage 2: CBBA for Distributed Task Allocation
4.2.1. Communication Model
4.2.2. CBBA Execution
4.3. Algorithmic Implementation
| Algorithm 1: GWO-CBBA Framework for UAV Scheduling |
| // Stage 1: GWO Fleet Size Optimization 1: Initialize GWO parameters (population size, max iterations) and search space for N. 2: Initialize a population of wolves with random N values. 3: Repeat until max iterations or convergence: 4: For each wolf (candidate N): 5: Calculate fitness F(N) using Equation (9). 6: End For 7: Update Alpha, Beta, and Delta wolf positions (best N values). 8: Update all other wolf positions based on Alpha, Beta, and Delta. 9: End Repeat 10: Output optimal fleet size N* (position of the Alpha wolf). // Stage 2: CBBA Task Allocation 11: Initialize N* UAV agents and the set of M tasks. 12: Repeat until task allocation is stable: 13: // Bundle Building Phase (local to each agent) 14: For each agent i from 1 to N*: 15: Agent i selects the best task to add to its bundle based on score U_ij. 16: End For 17: // Conflict Resolution Phase (communication) 18: Agents broadcast their bundles to neighbors. 19: Agents update their bundles to resolve conflicts according to consensus rules. 20: End Repeat 21: Output final, conflict-free task assignments for all N* agents. |
5. Simulation Verification
5.1. Experimental Setup
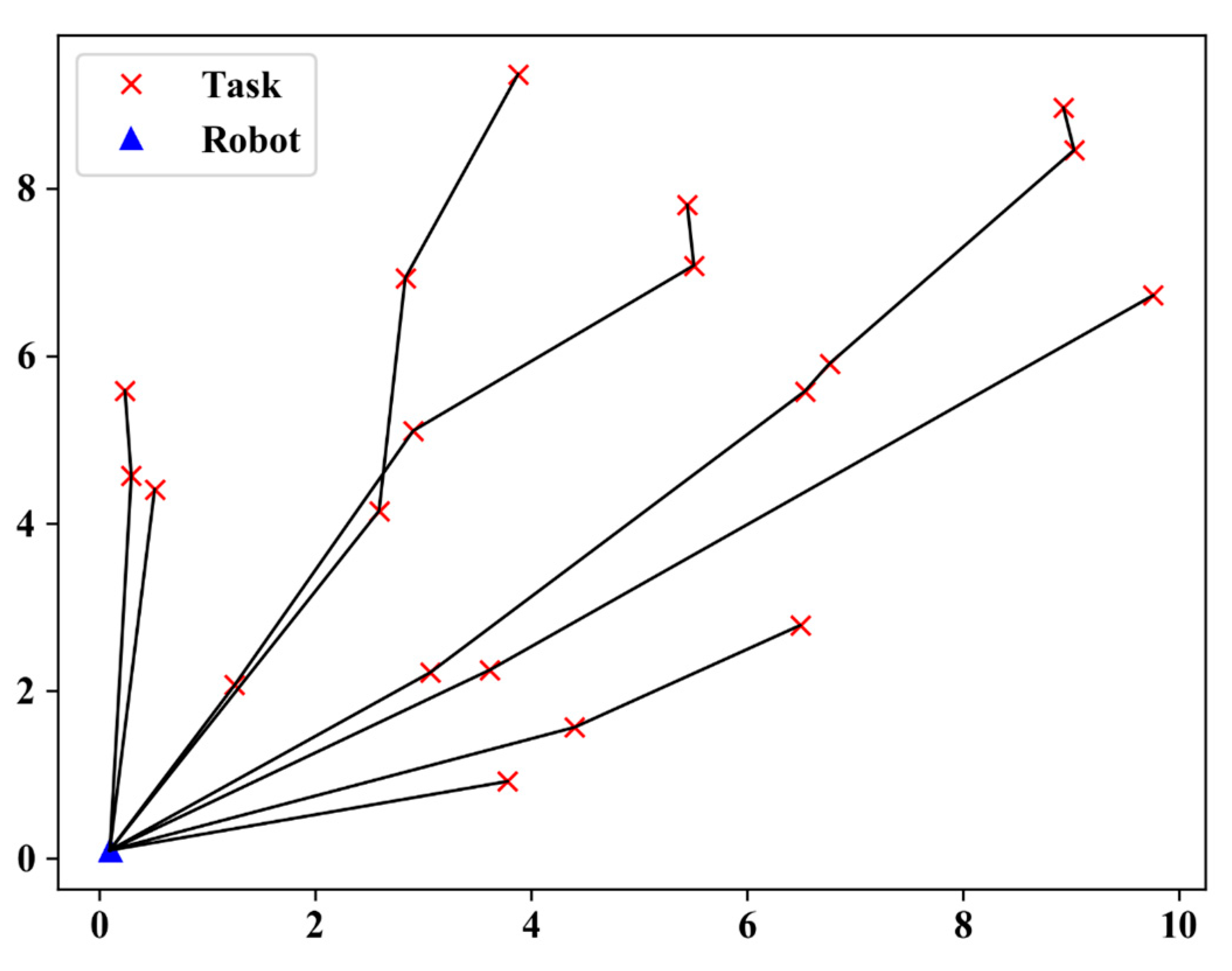
5.1.1. Scenario Definition
5.1.2. Model and Algorithm Parameters
5.1.3. Baseline Methods for Comparison
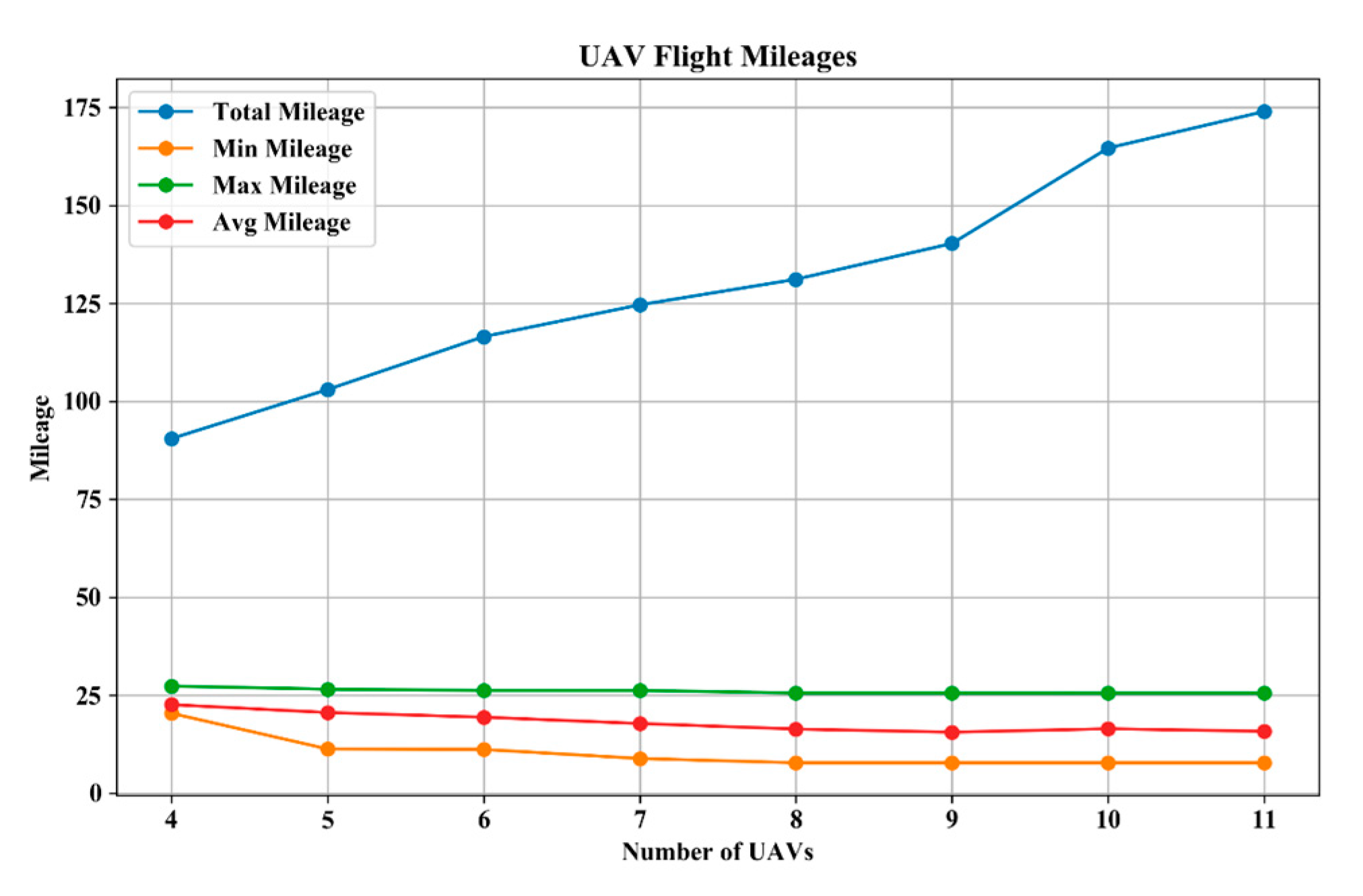
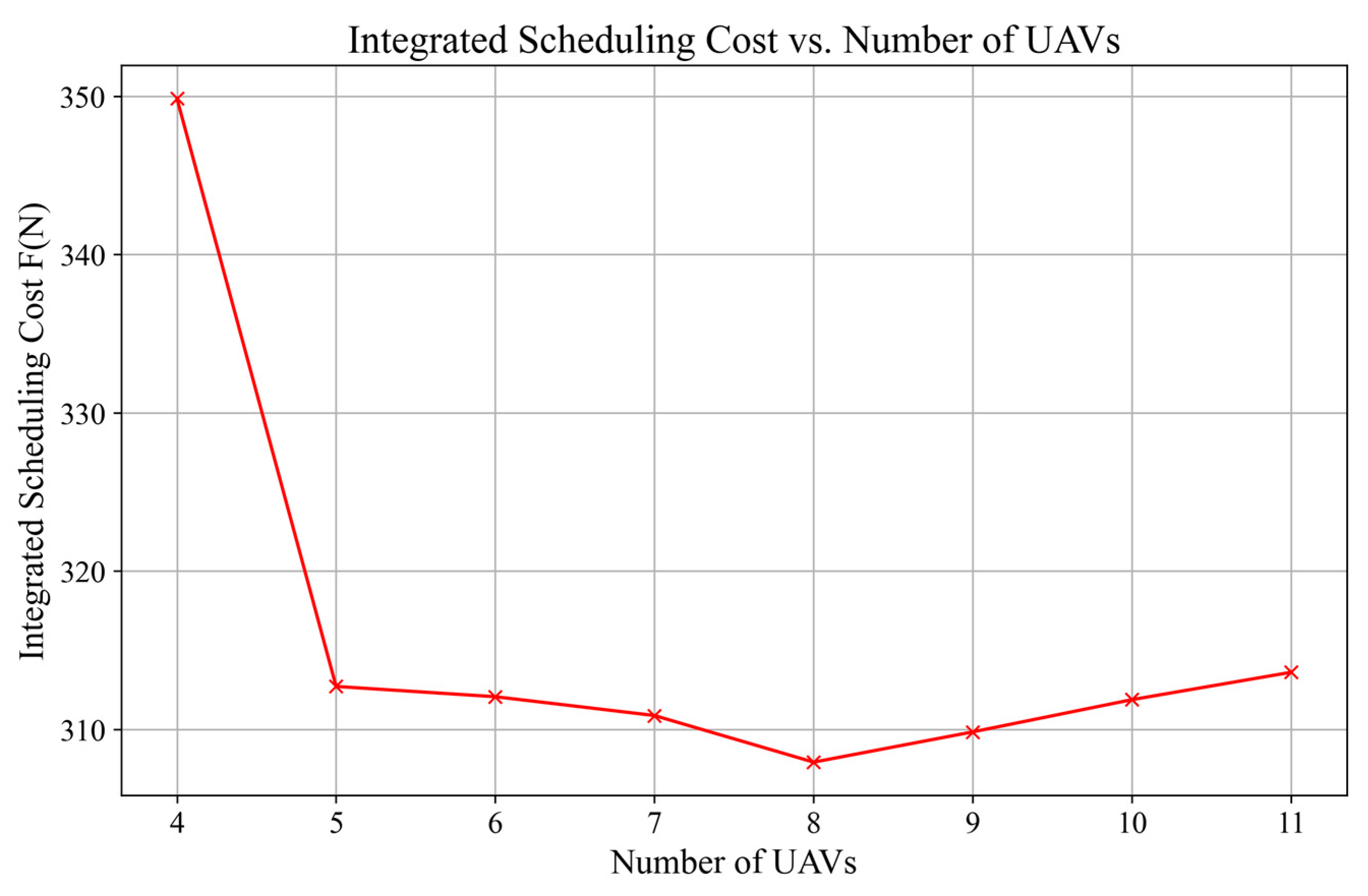
5.2. Stage 1: GWO-Based Fleet Sizing Analysis
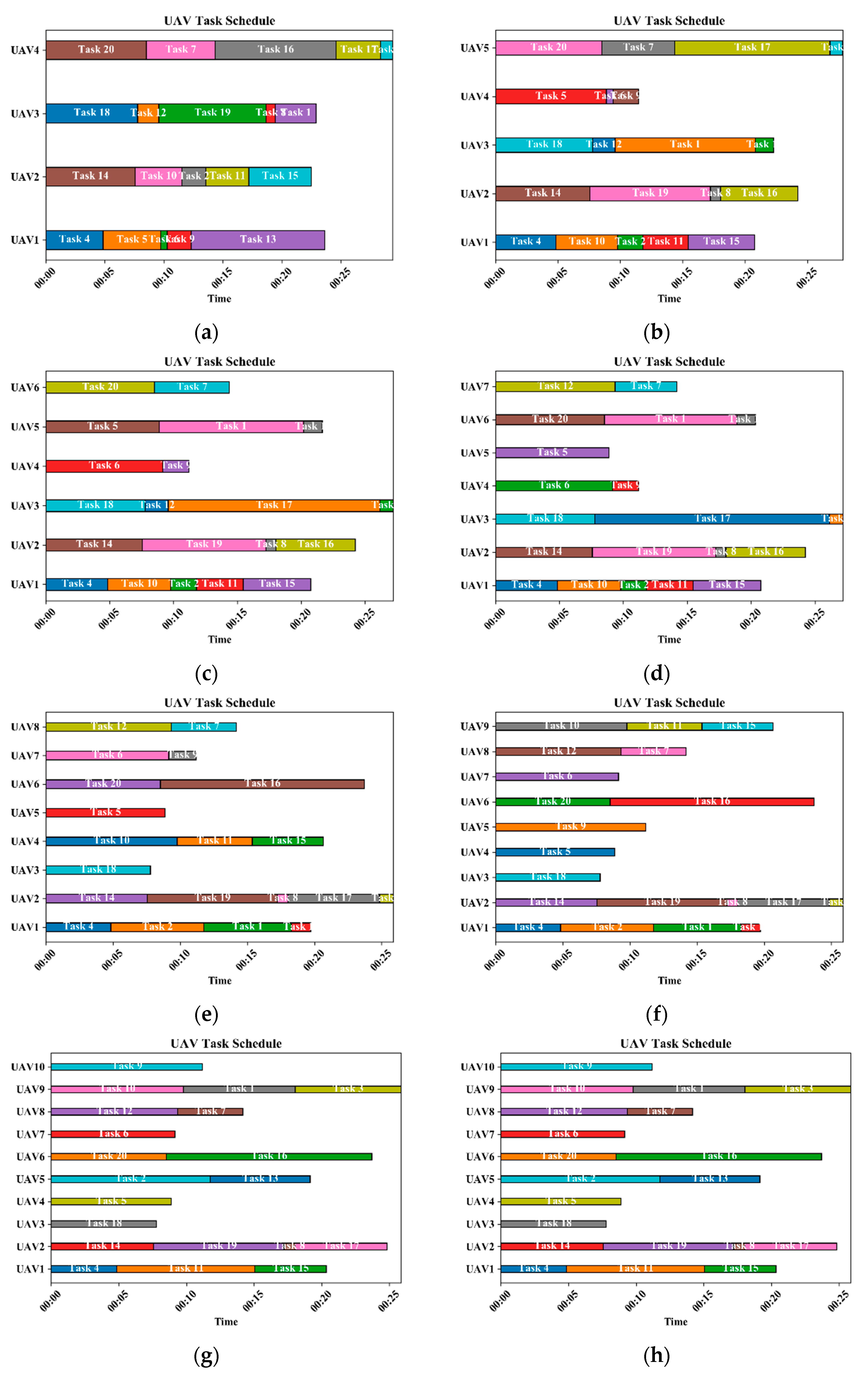
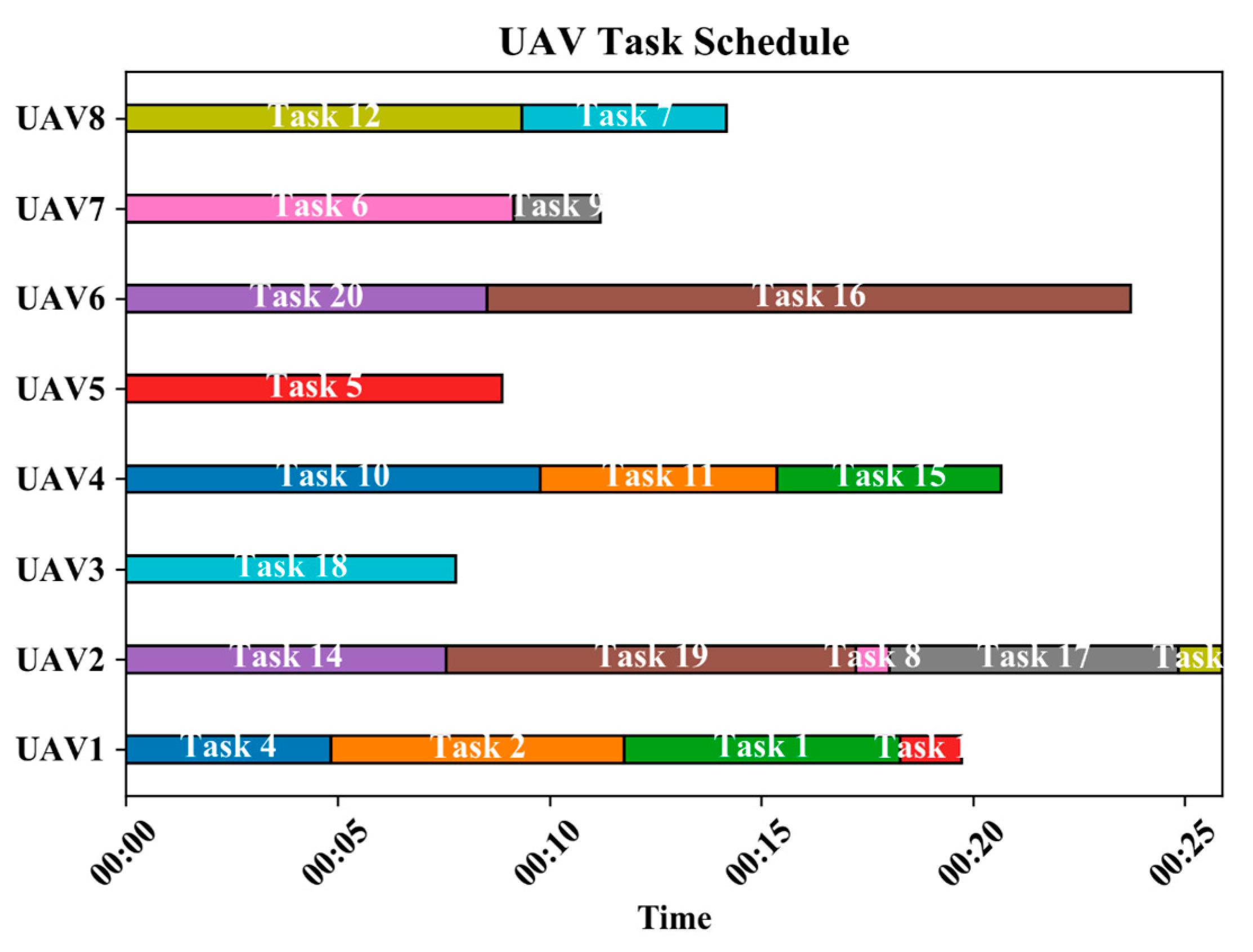
5.3. Stage 2: Task Allocation for the Optimal Fleet
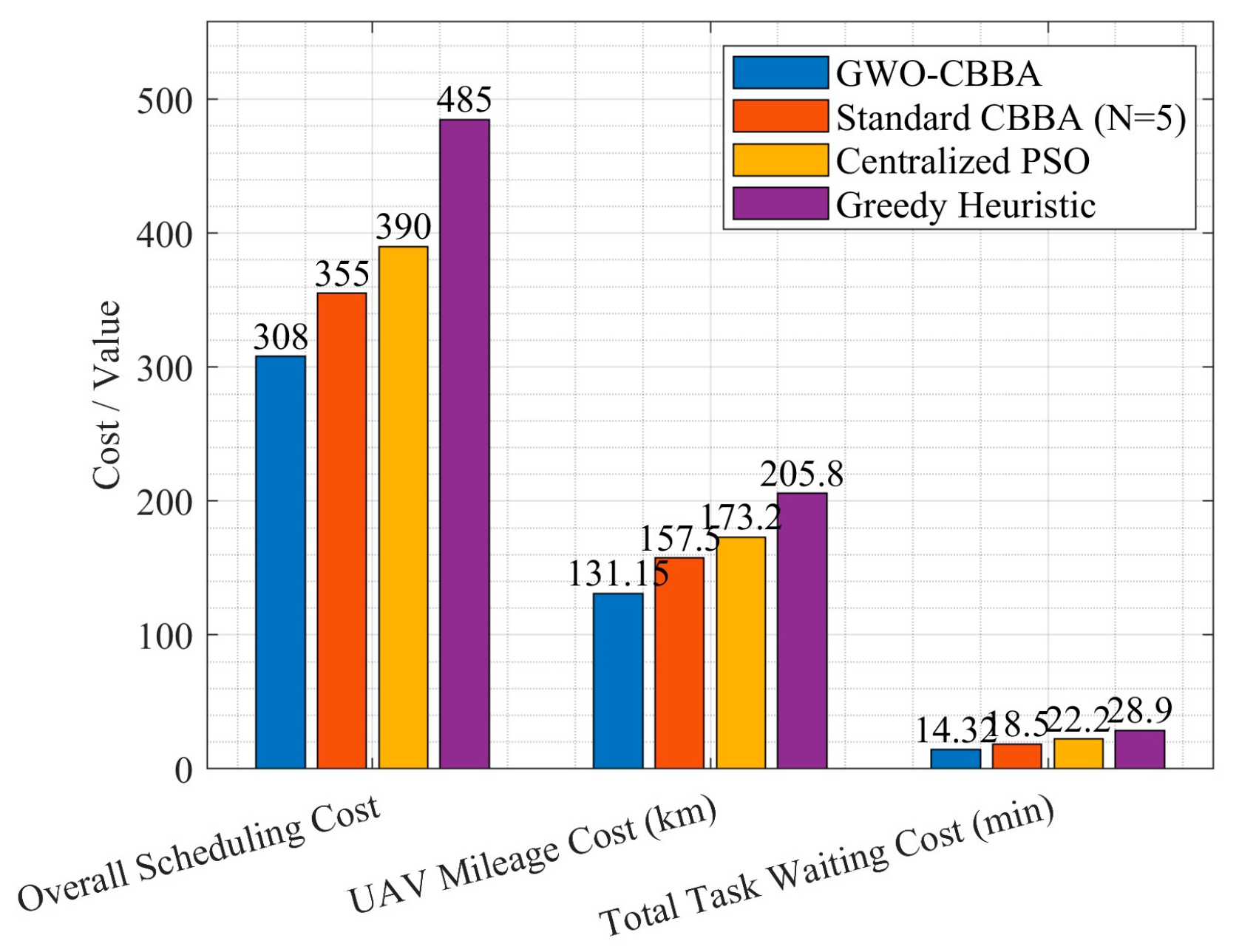
5.4. Comparative Analysis and Discussion
6. Conclusions
7. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Linker, C.; Mena-Arciniega, C.; Xing, S. military applications, and opportunities of unmanned aerial vehicles. Aviation 2024, 28, 115–127. [Google Scholar] [CrossRef]
- Alexan, W.; Aly, L.; Korayem, Y.; Gabr, M.; El-Damak, D.; Fathy, A.; Mansour, H.A.A. Secure communication of military reconnaissance images over UAV-assisted relay networks. IEEE Access 2024, 12, 78589–78610. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, J.; Wang, Z.; Liu, X.; Zhou, S.; Shi, G.; Shi, Z. Formation Cooperative Intelligent Tactical Decision Making Based on Bayesian Network Model. Drones 2024, 8, 427. [Google Scholar] [CrossRef]
- Fang, Z.; Savkin, A.V. Strategies for optimized uav surveillance in various tasks and scenarios: A review. Drones 2024, 8, 193. [Google Scholar] [CrossRef]
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A.; Guizani, M. State-of-the-art and future research challenges in uav swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Hawashin, D.; Nemer, M.; Gebreab, S.A.; Salah, K.; Jayaraman, R.; Khan, M.K.; Damiani, E. Blockchain applications in UAV industry: Review, opportunities, and challenges. J. Netw. Comput. Appl. 2024, 230, 103932. [Google Scholar] [CrossRef]
- Wang, X.; Yin, S.; Luo, L.; Qiao, X. Research on Multi-UAV Task Assignment Based on a Multi-Objective, Improved Brainstorming Optimization Algorithm. Appl. Sci. 2024, 14, 2365. [Google Scholar] [CrossRef]
- Ghaffar, M.A.; Peng, L.; Aslam, M.U.; Adeel, M.; Dassari, S. Vehicle-UAV Integrated Routing Optimization Problem for Emergency Delivery of Medical Supplies. Electronics 2024, 13, 3650. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Q.; Mao, P.; Bai, Q.; Li, F.; Pavlova, S. Design and control of an ultra-low-cost logistic delivery fixed-wing UAV. Appl. Sci. 2024, 14, 4358. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Q.; Mao, P.; Bai, Q.; Li, F.; Pavlova, S. Risk Assessment and Distribution Estimation for UAV Operations with Accurate Ground Feature Extraction Based on a Multi-Layer Method in Urban Areas. Drones 2024, 8, 399. [Google Scholar] [CrossRef]
- Meng, Z.; Yu, K.; Qiu, R. Location-routing optimization of UAV collaborative blood delivery vehicle distribution on complex roads. Complex Intell. Syst. 2024, 10, 8127–8141. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, J.; Han, Q.; Song, H.; Guo, H. Optimal decision-making of post-disaster emergency material scheduling based on helicopter–truck–drone collaboration. Omega 2024, 127, 103104. [Google Scholar] [CrossRef]
- Julio, J.S.; Silva, D.F.; Smith, A.E. Drone-enabled material handling in smart manufacturing. Int. Trans. Oper. Res. 2025, 32, 3296–3315. [Google Scholar]
- Li, N.; Shi, Z.; Jin, J.; Feng, J.; Zhang, A.; Xie, M.; Min, L.; Zhao, Y.; Lei, Y. Design of Intelligent Firefighting and Smart Escape Route Planning System Based on Improved Ant Colony Algorithm. Sensors 2024, 24, 6438. [Google Scholar] [CrossRef] [PubMed]
- Debnath, D.; Vanegas, F.; Sandino, J.; Hawary, A.F.; Gonzalez, F. A Review of UAV Path-Planning Algorithms and Obstacle Avoidance Methods for Remote Sensing Applications. Remote Sens. 2024, 16, 4019. [Google Scholar] [CrossRef]
- Zhang, J.-D.; Shi, Z.-Y.; Zhang, A.-L.; Yang, Q.-M.; Shi, G.-Q.; Wu, Y. UAV trajectory prediction based on flight state recognition. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2629–2641. [Google Scholar] [CrossRef]
- Luo, J.; Tian, Y.; Wang, Z. Research on unmanned aerial vehicle path planning. Drones 2024, 8, 51. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, J.; Shi, G.; Ji, L.; Wang, D.; Wu, Y. Design of a UAV Trajectory Prediction System Based on Multi-Flight Modes. Drones 2024, 8, 255. [Google Scholar] [CrossRef]
- Shi, Z.; Shi, G.; Zhang, J.; Wang, D.; Xu, T.; Ji, L.; Wu, Y. Design of UAV flight state recognition system for multisensor data fusion. IEEE Sens. J. 2024, 24, 21386–21394. [Google Scholar] [CrossRef]
- Guo, H.; Miao, Z.; Ji, J.; Pan, Q. An effective collaboration evolutionary algorithm for multi-robot task allocation and scheduling in a smart farm. Knowl.-Based Syst. 2024, 289, 111474. [Google Scholar] [CrossRef]
- Yasser, M.; Shalash, O.; Ismail, O. Optimized decentralized swarm communication algorithms for efficient task allocation and power consumption in swarm robotics. Robotics 2024, 13, 66. [Google Scholar] [CrossRef]
- Lu, Y.; Da, C. Global and local path planning of robots combining ACO and dynamic window algorithm. Sci. Rep. 2025, 15, 9452. [Google Scholar] [CrossRef] [PubMed]
- Daviran, M.; Maghsoudi, A.; Ghezelbash, R. Optimized AI-MPM: Application of PSO for tuning the hyperparameters of SVM and RF algorithms. Comput. Geosci. 2025, 195, 105785. [Google Scholar] [CrossRef]
- Ma, B.; Pan, Y.; Xu, Y.; Gao, Z.; Zhang, Z.; Chen, C.; Li, C. UAV-Assisted Computing Power Network Task Allocation and 3D Urban Trajectory Optimization. IEEE Internet Things J. 2025, 12, 19294–19307. [Google Scholar] [CrossRef]
- Yan, S.; Pan, F.; Shi, Y.; Xu, J.; Zhang, D. Research on Task Allocation of Heterogeneous UAVs Based on DLR-CBBA. In Proceedings of the 2024 4th International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 19–21 April 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Shi, Z.; Jia, Y.; Shi, G.; Zhang, K.; Ji, L.; Wang, D.; Wu, Y. Design of motor skill recognition and hierarchical evaluation system for table tennis players. IEEE Sens. J. 2024, 24, 5303–5315. [Google Scholar] [CrossRef]
- Liu, C.H.; Chen, Z.; Tang, J.; Xu, J.; Piao, C. Energy-efficient UAV control for effective and fair communication coverage: A deep reinforcement learning approach. IEEE J. Sel. Areas Commun. 2018, 36, 2059–2070. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, J.; Shi, G.; Zhu, M.; Ji, L.; Wu, Y. Autonomous UAV Safety Oriented Situation Monitoring and Evaluation System. Drones 2024, 8, 308. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, M.; Yang, Q.; Liu, J.; Wang, D.; Zhang, J. Autonomous security evaluation model for UAV based on airborne information. In Proceedings of the 2023 6th International Conference on Information Communication and Signal Processing (ICICSP), Xi’an, China, 23–25 September 2023; IEEE: New York, NY, USA, 2023; pp. 785–789. [Google Scholar]



| Consideration | Specific Factors |
|---|---|
| UAV resources | Performance parameters such as the number of drones, endurance, payload, etc. |
| Mission requirements | Location, priority, start and end time, and resource requirements of tasks |
| Restrictive condition | Includes drone range limitations, communication range limitations, and mission time windows |
| Optimization goals | Minimize task completion time, minimize total energy consumption, and maximize task completion rate |
| Notation | Definition |
|---|---|
| N | Number of UAVs dispatched |
| C(N) | Dispatch cost functions |
| T(N) | Task time function |
| E(N) | Total energy consumption function |
| R(N) | Reliability function |
| S(N) | Security functions |
| Serial Number | UAV | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Position/km | (0,0) | (5.5,7.1) | (2.9,5.1) | (8.9,9.0) | (1.3,2.1) | (0.5,4.4) | (0.3,4.6) |
| Serial number | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Position/km | (6.5,2.8) | (6.8,5.9) | (0.2,5.6) | (2.6,4.2) | (2.8,6.9) | (4.4,1.6) | (5.4,7.8) |
| Serial number | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Position/km | (3.1,2.2) | (3.9,9.4) | (9.8,6.7) | (9.0,8.5) | (3.8,0.9) | (6.5,5.6) | (3.6,2.3) |
| Parameter Name | Size |
|---|---|
| Flight speed | 30 km/h |
| Maximum number of missions | 5 |
| Drone dispatch cost | 10 |
| Drone energy cost | 0.1 /min |
| Maximum mission execution time of the drone | 120 min |
| Number of wolves | 100 |
| Maximum number of exploration steps | 100 |
| Serial Number | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|
| Time | 16.84 | 14.87 | 14.72 | 14.57 | 14.34 | 14.34 | 14.27 | 14.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, W.; Ye, H.; Shi, Z. A Two-Stage Optimization Framework for UAV Fleet Sizing and Task Allocation in Emergency Logistics Using the GWO and CBBA. Drones 2025, 9, 501. https://doi.org/10.3390/drones9070501
Zhang Y, Xu W, Ye H, Shi Z. A Two-Stage Optimization Framework for UAV Fleet Sizing and Task Allocation in Emergency Logistics Using the GWO and CBBA. Drones. 2025; 9(7):501. https://doi.org/10.3390/drones9070501
Chicago/Turabian StyleZhang, Yongchao, Wei Xu, Helin Ye, and Zhuoyong Shi. 2025. "A Two-Stage Optimization Framework for UAV Fleet Sizing and Task Allocation in Emergency Logistics Using the GWO and CBBA" Drones 9, no. 7: 501. https://doi.org/10.3390/drones9070501
APA StyleZhang, Y., Xu, W., Ye, H., & Shi, Z. (2025). A Two-Stage Optimization Framework for UAV Fleet Sizing and Task Allocation in Emergency Logistics Using the GWO and CBBA. Drones, 9(7), 501. https://doi.org/10.3390/drones9070501






