Towards Efficiency and Endurance: Energy–Aerodynamic Co-Optimization for Solar-Powered Micro Air Vehicles
Abstract
1. Introduction
- (1).
- We proposed a co-optimization framework that evaluates aerodynamic and energy performance in parallel, resolving their trade-offs via multi-objective optimization.
- (2).
- We designed and tested a tailless SMAV prototype with vectored thrust and solar integration. Wind tunnel tests and flight experiments demonstrated its feasibility.
2. Self-Sustainable Energy for SMAV
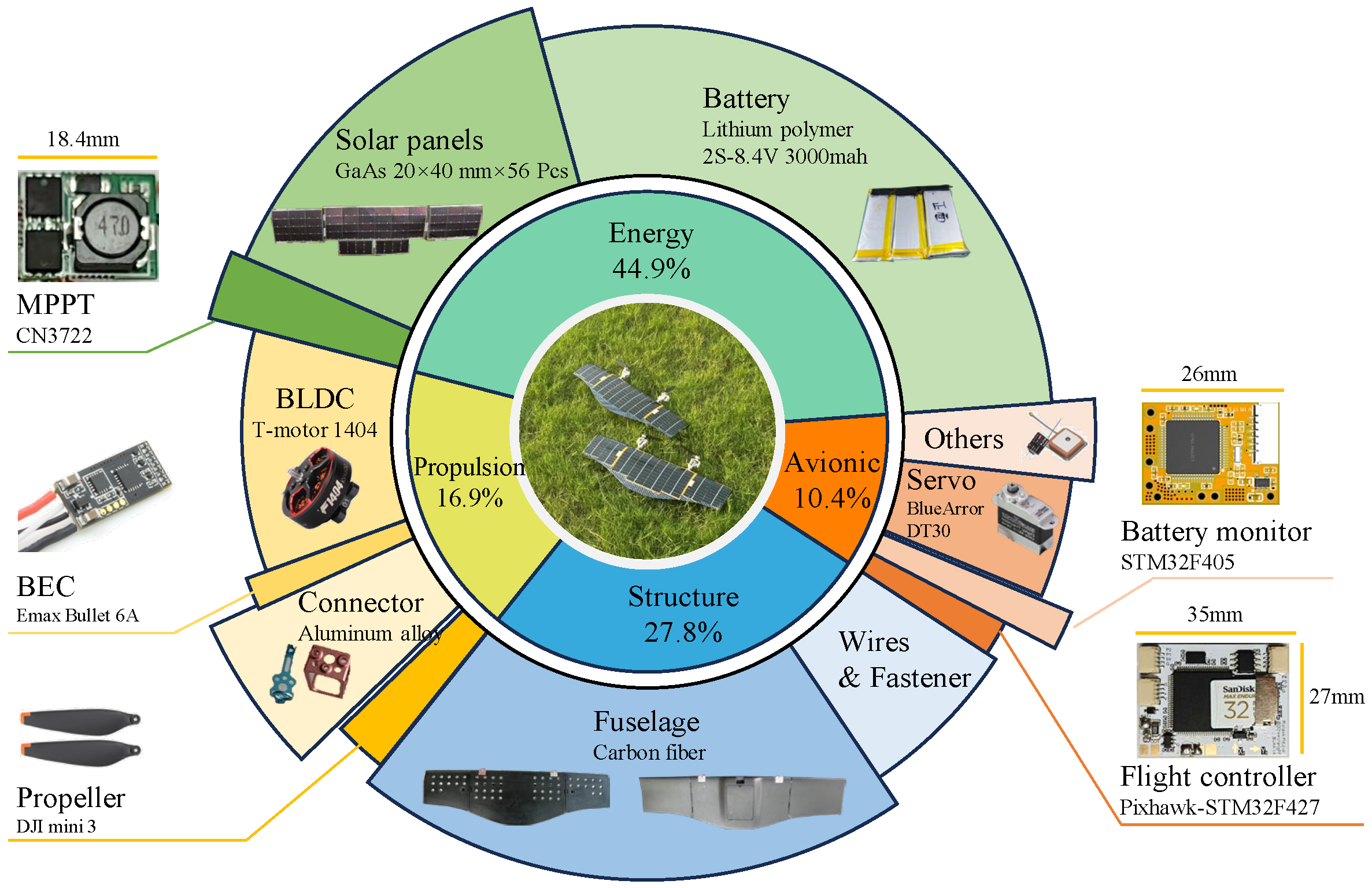
2.1. Energy System for SMAV
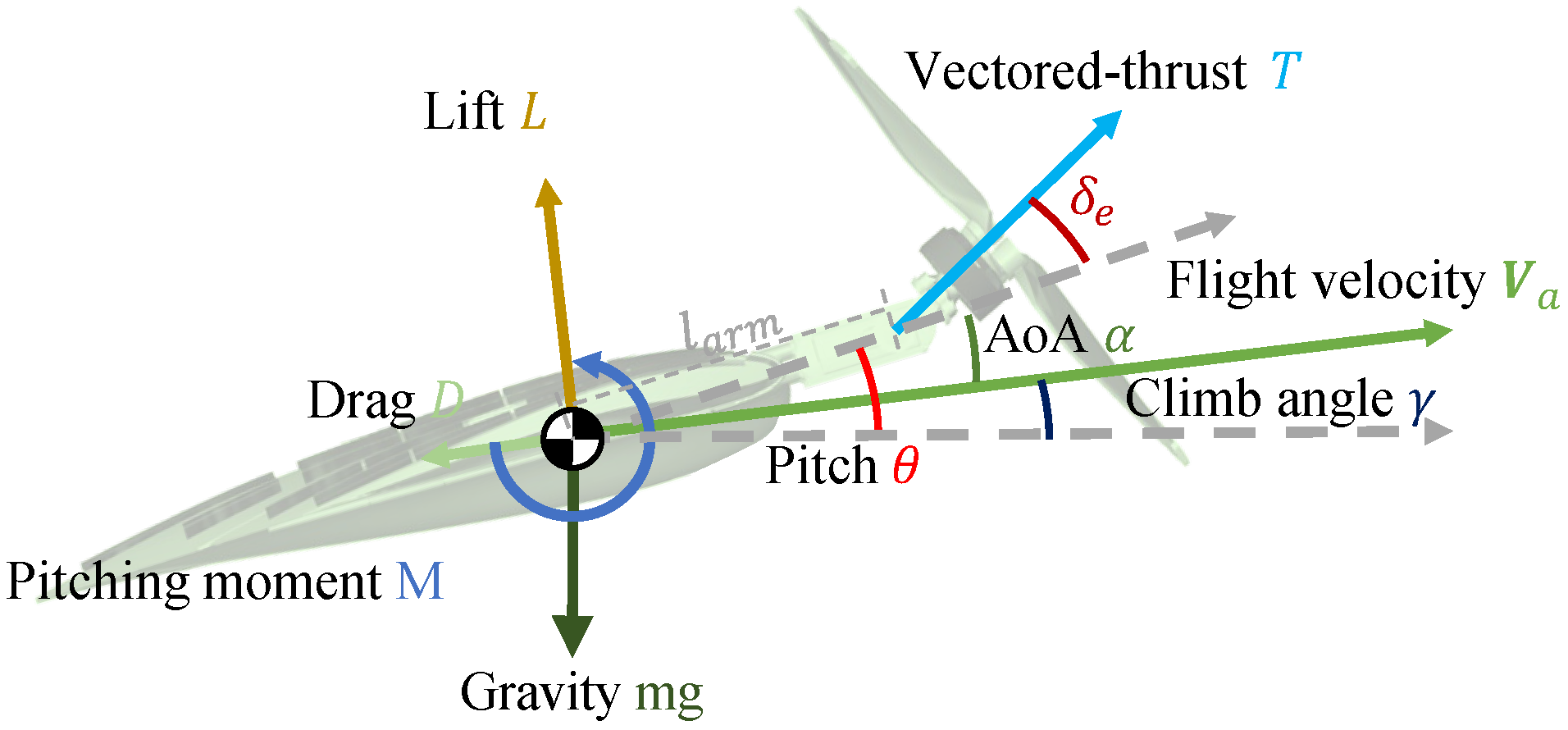
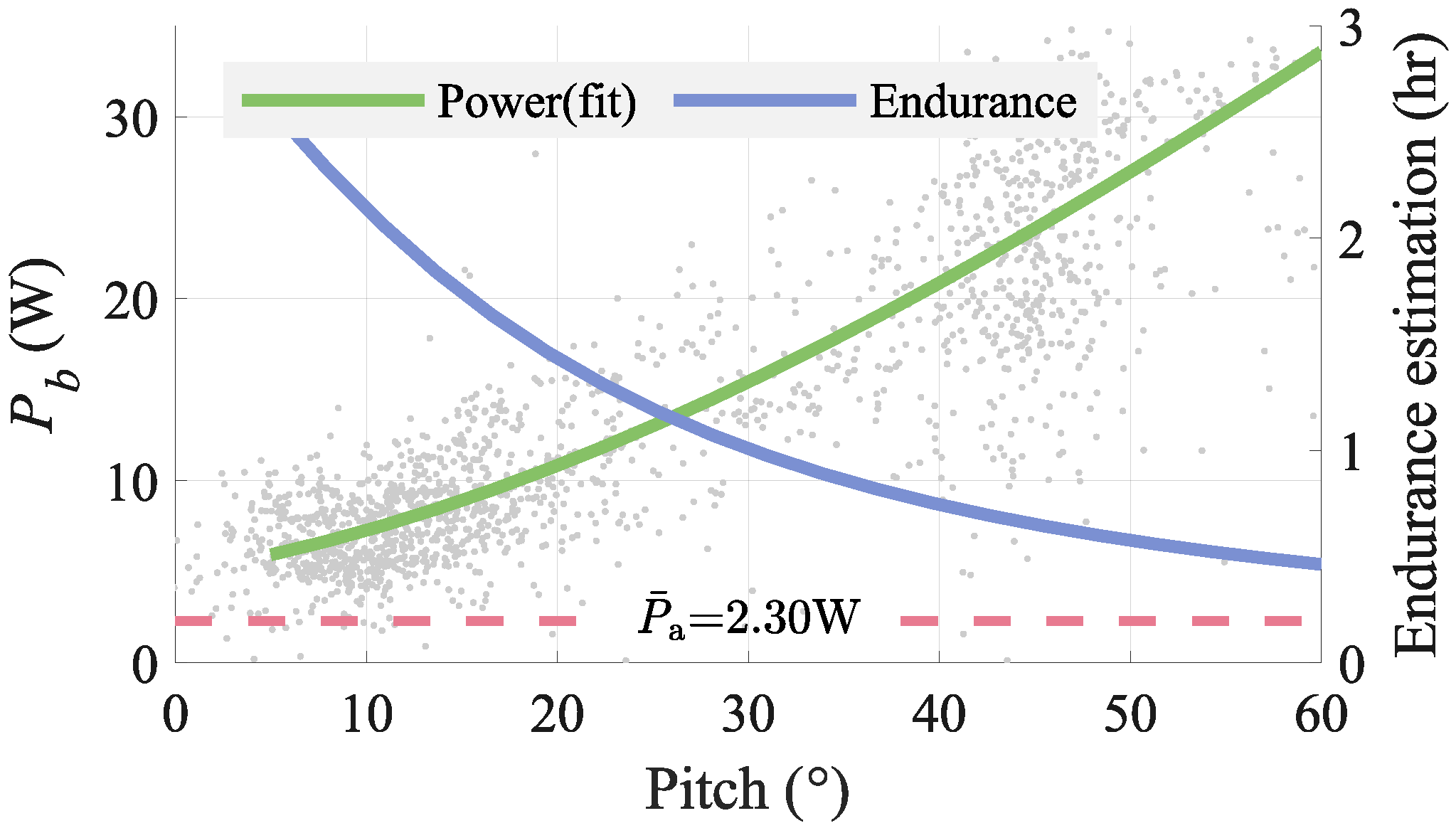
2.2. Goal: Evaluation of Flight Duration
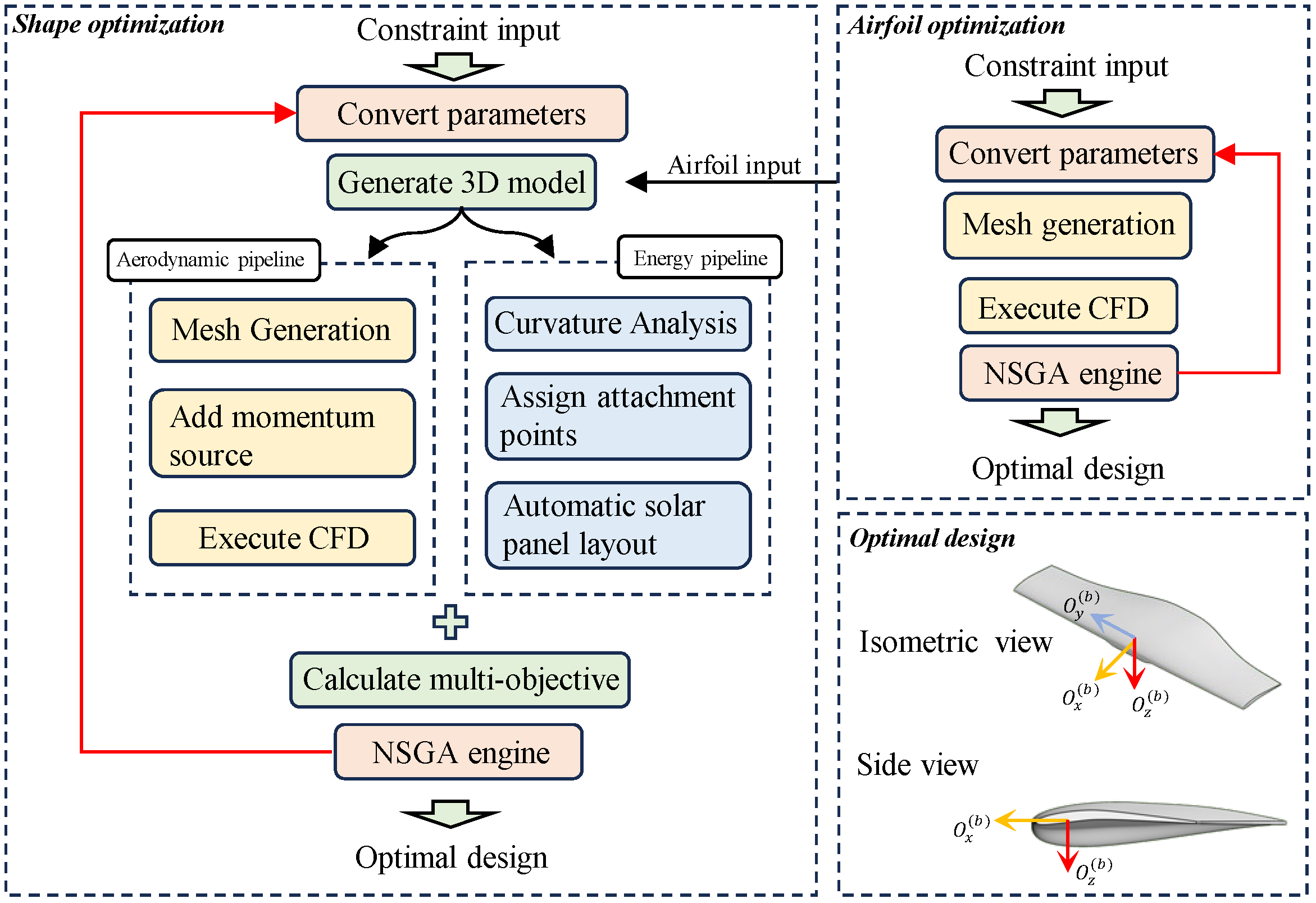
3. Shape Optimization Methodology
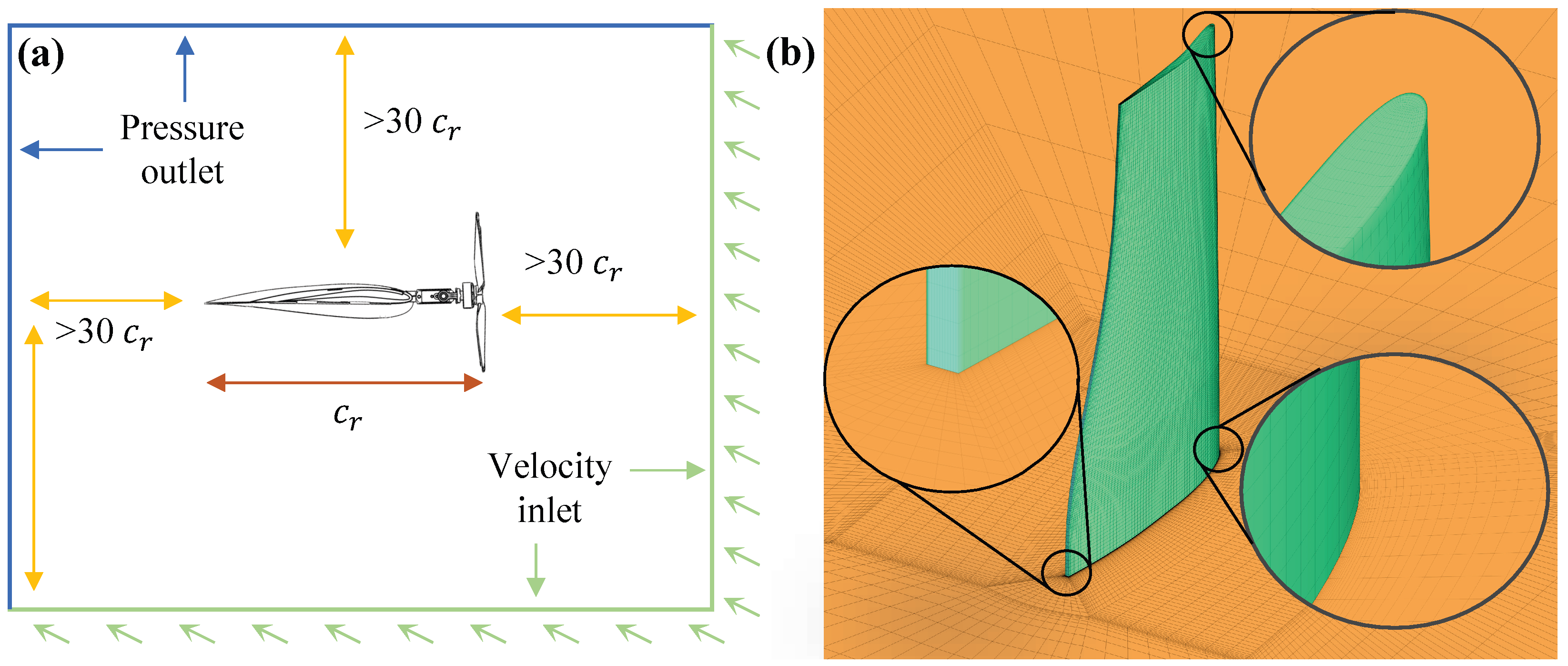
3.1. Turbulence Model and Meshes
3.2. MAV’s Geometry Control System
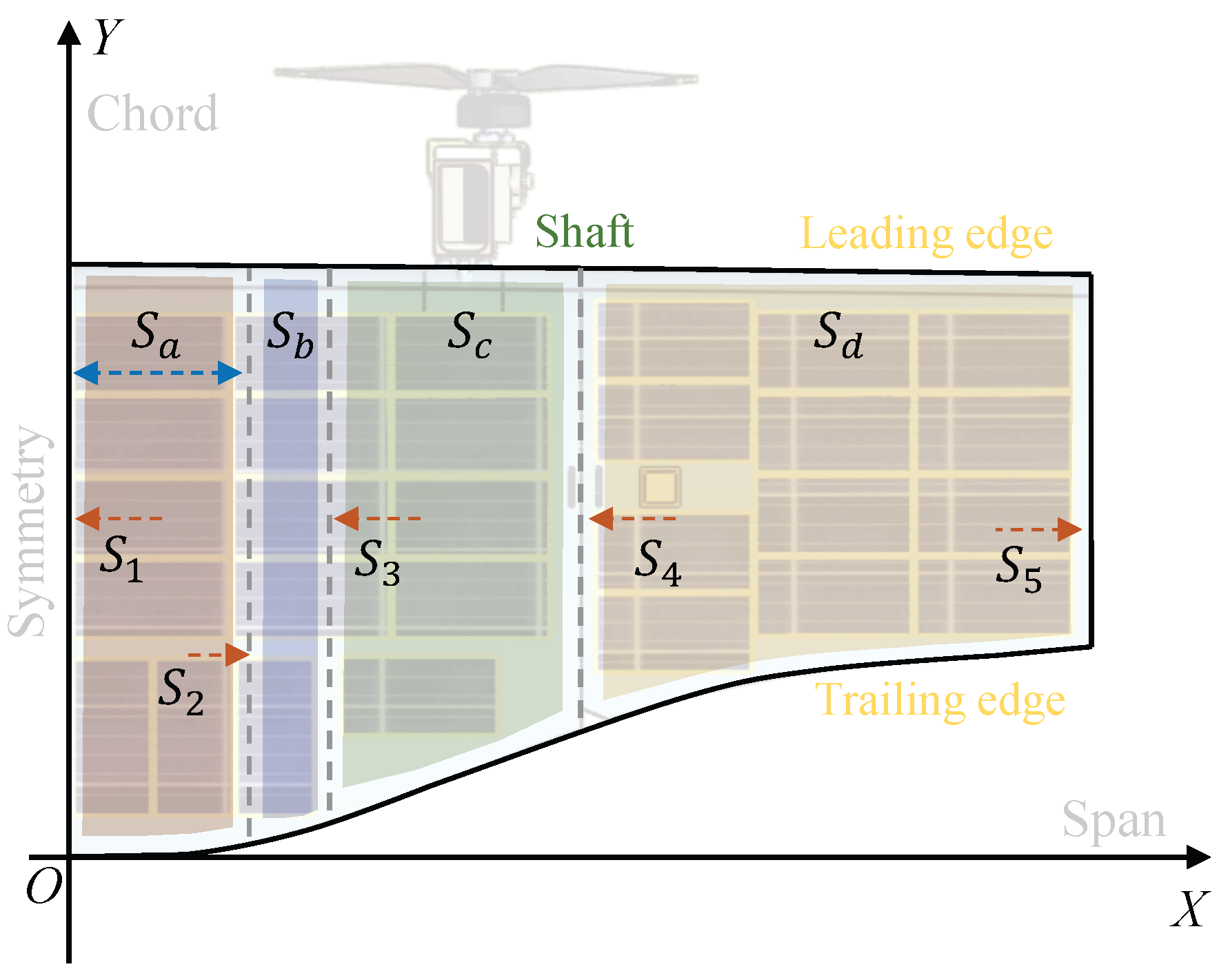
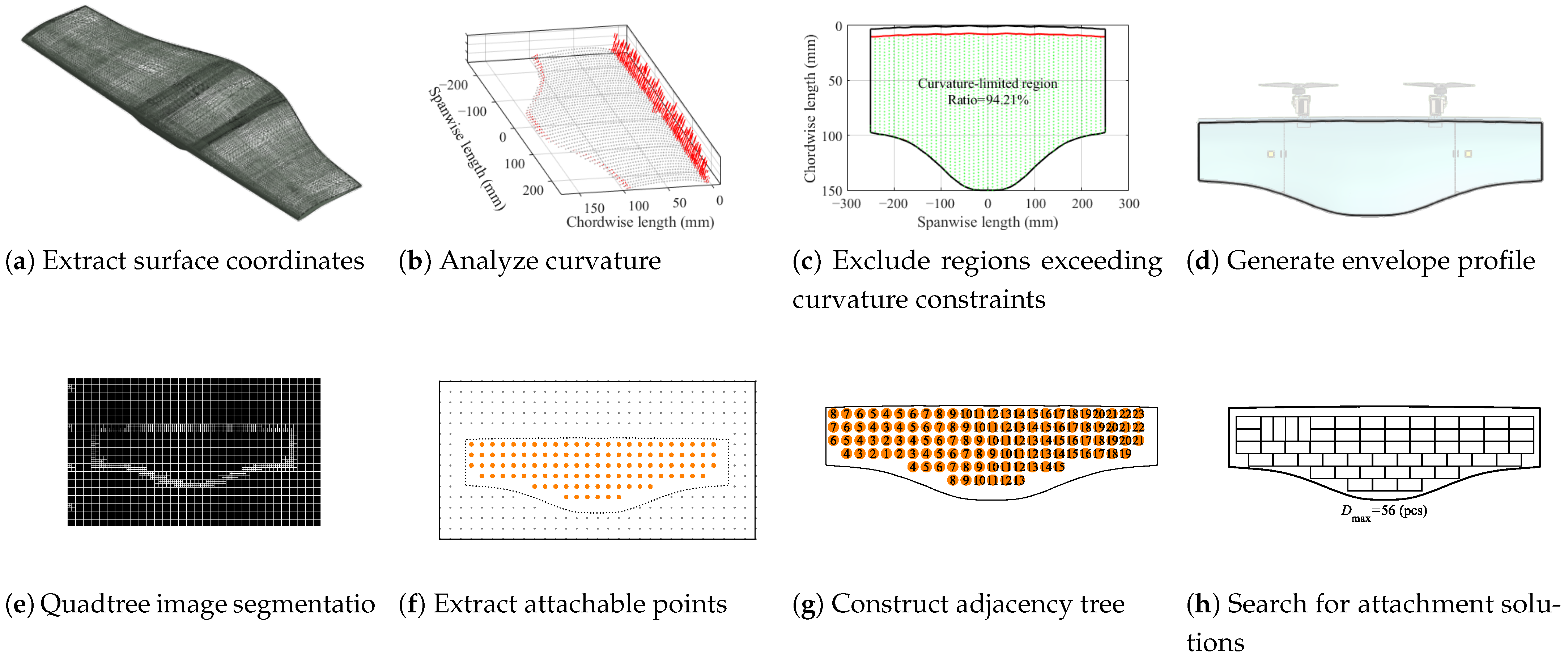
3.3. Adaptive Segmentation for Panel Deployment
3.3.1. Curvature Analysis
3.3.2. Assign Attachment Points
3.3.3. Panel Deployment
| Algorithm 1: Panel deployment |
 |
4. Advantage Validation
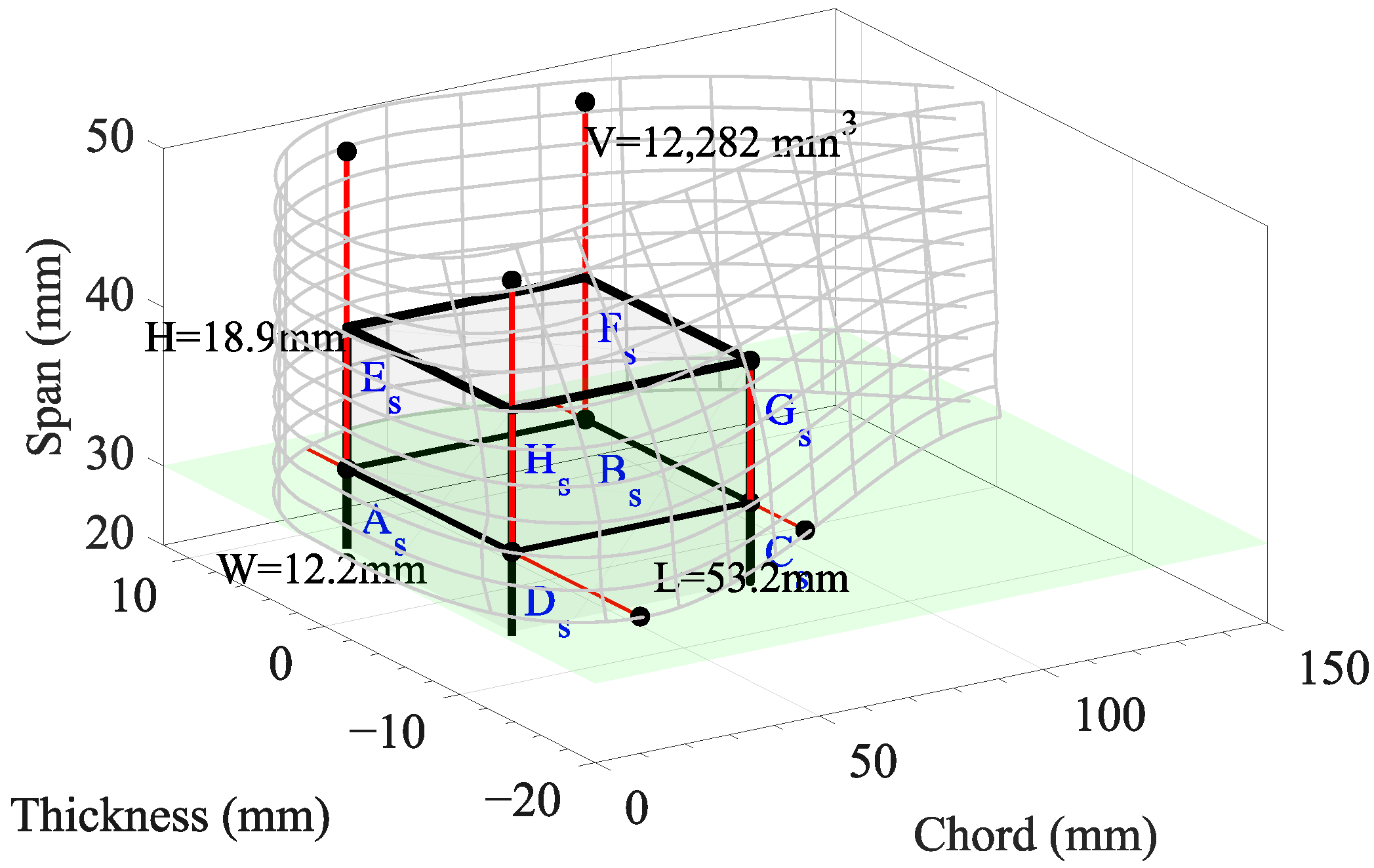
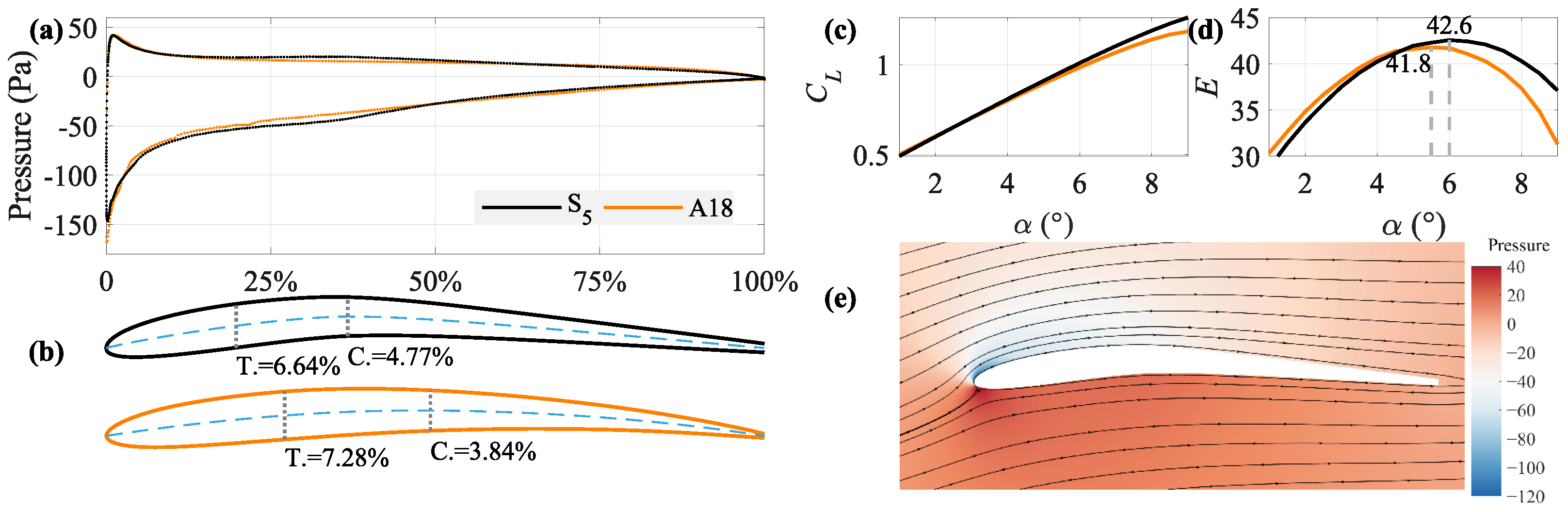
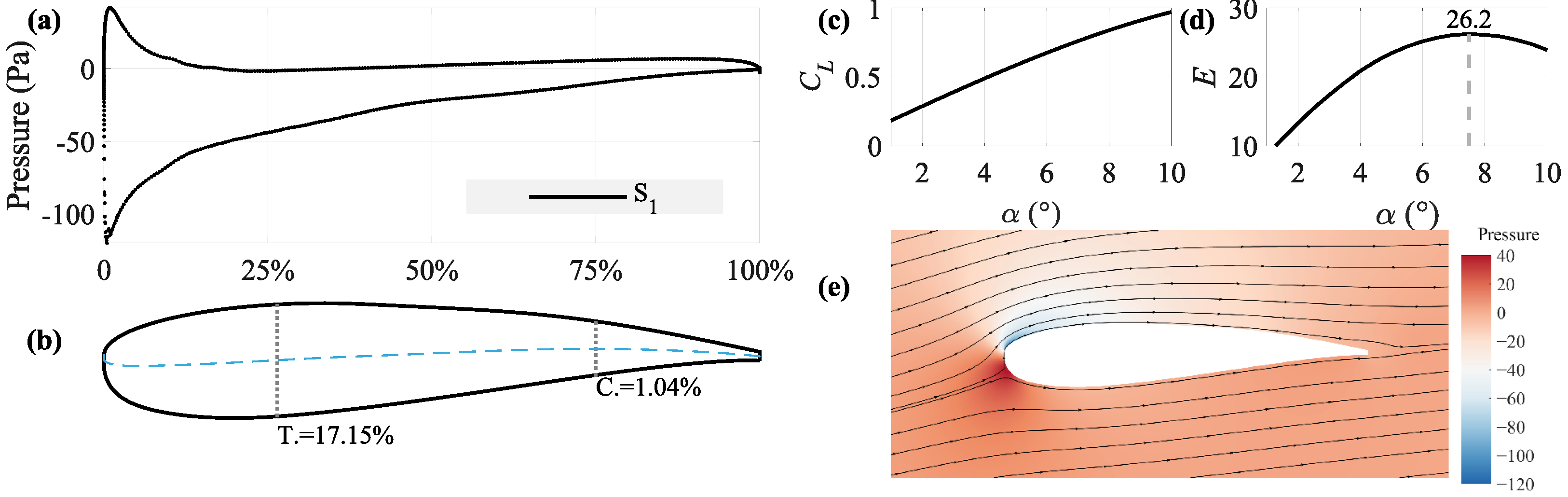
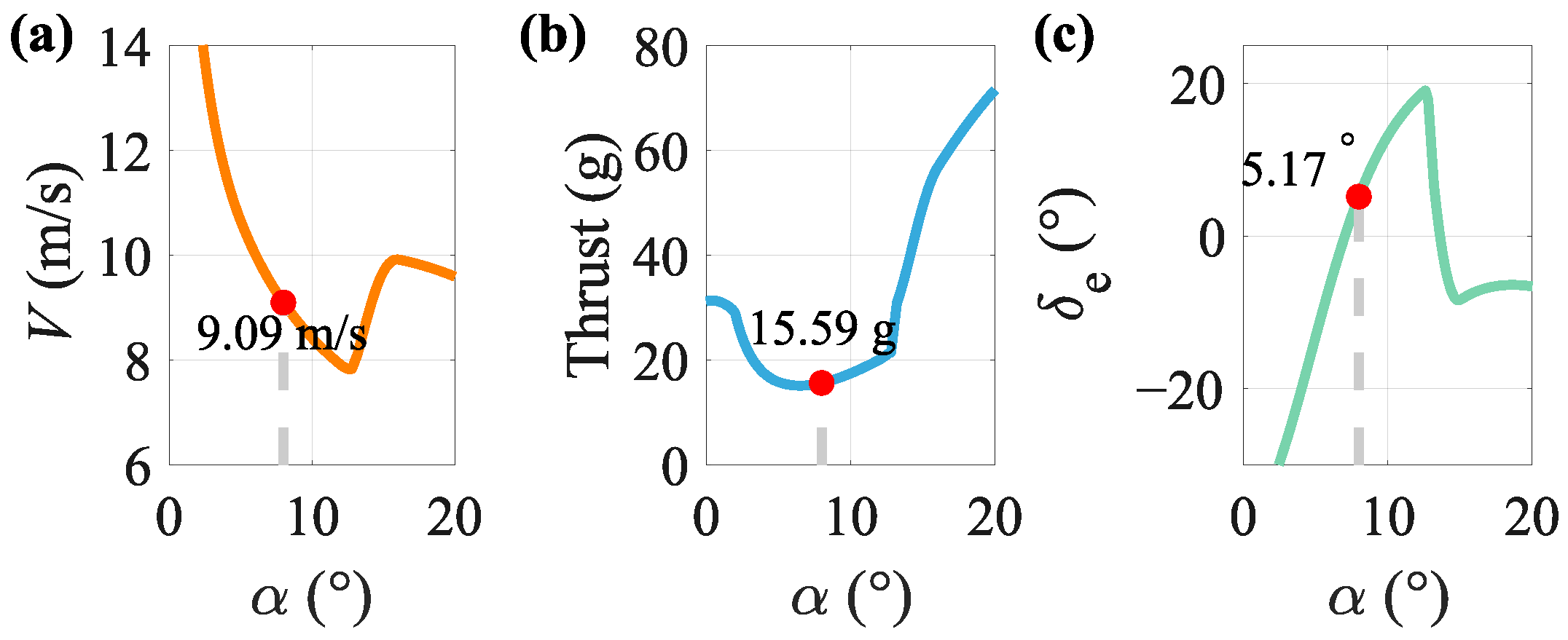
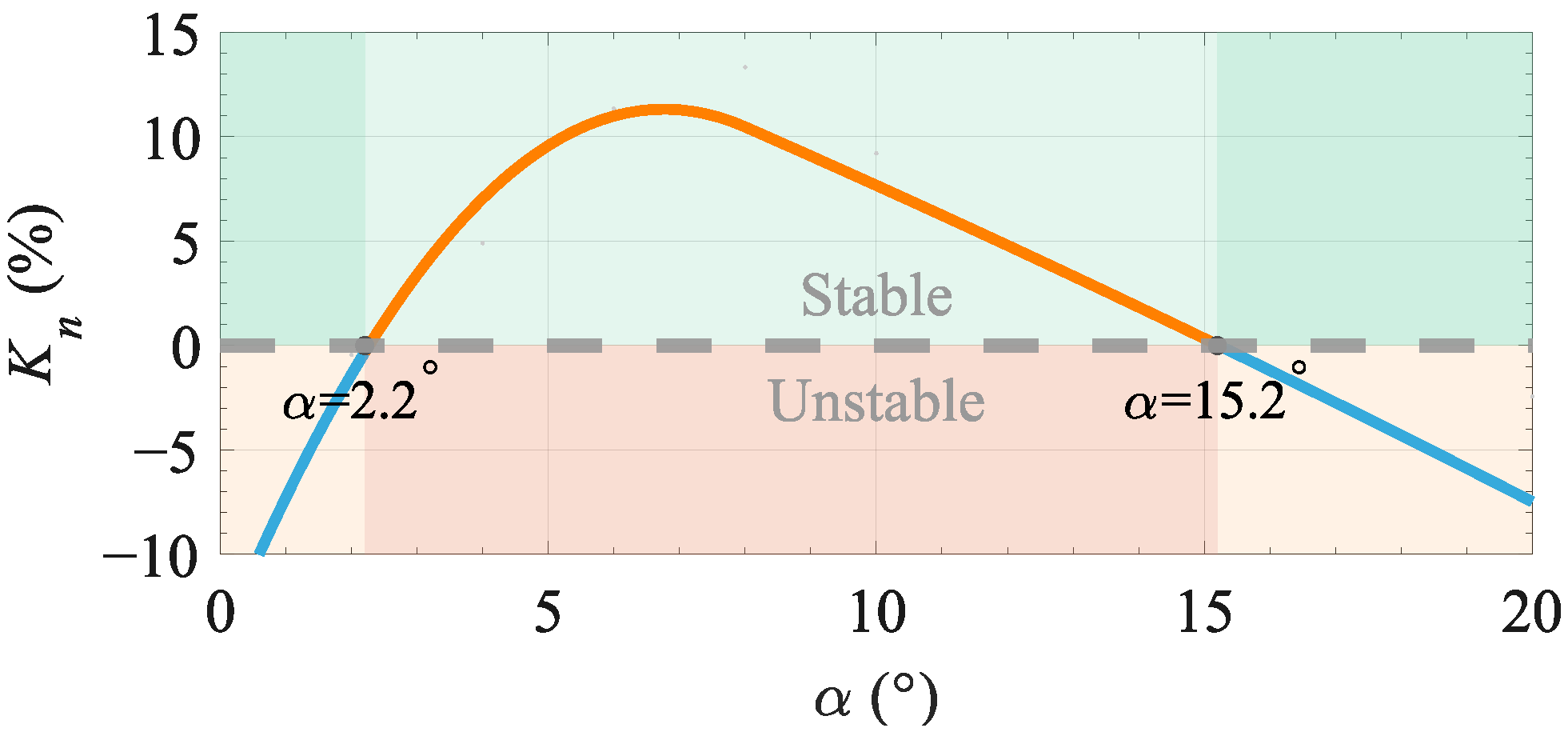
4.1. Optimization Results
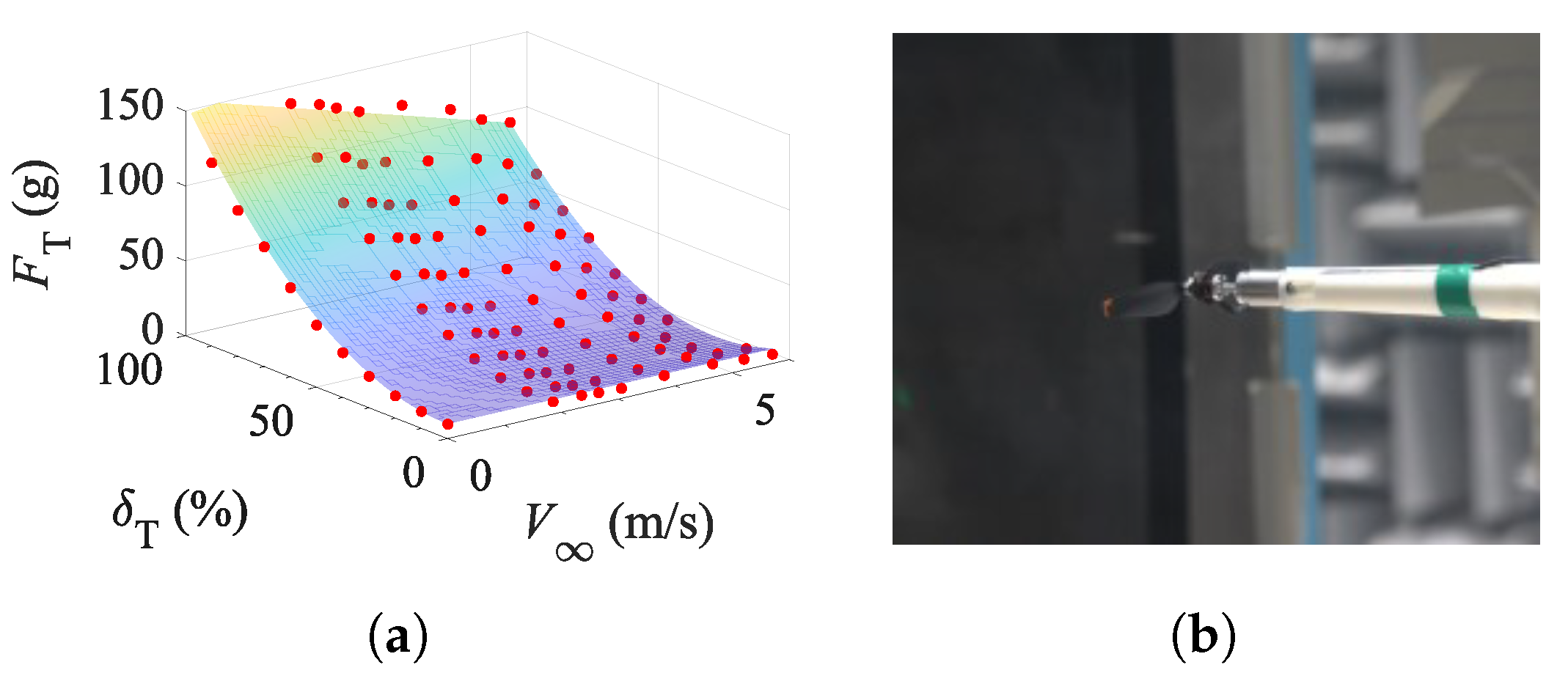
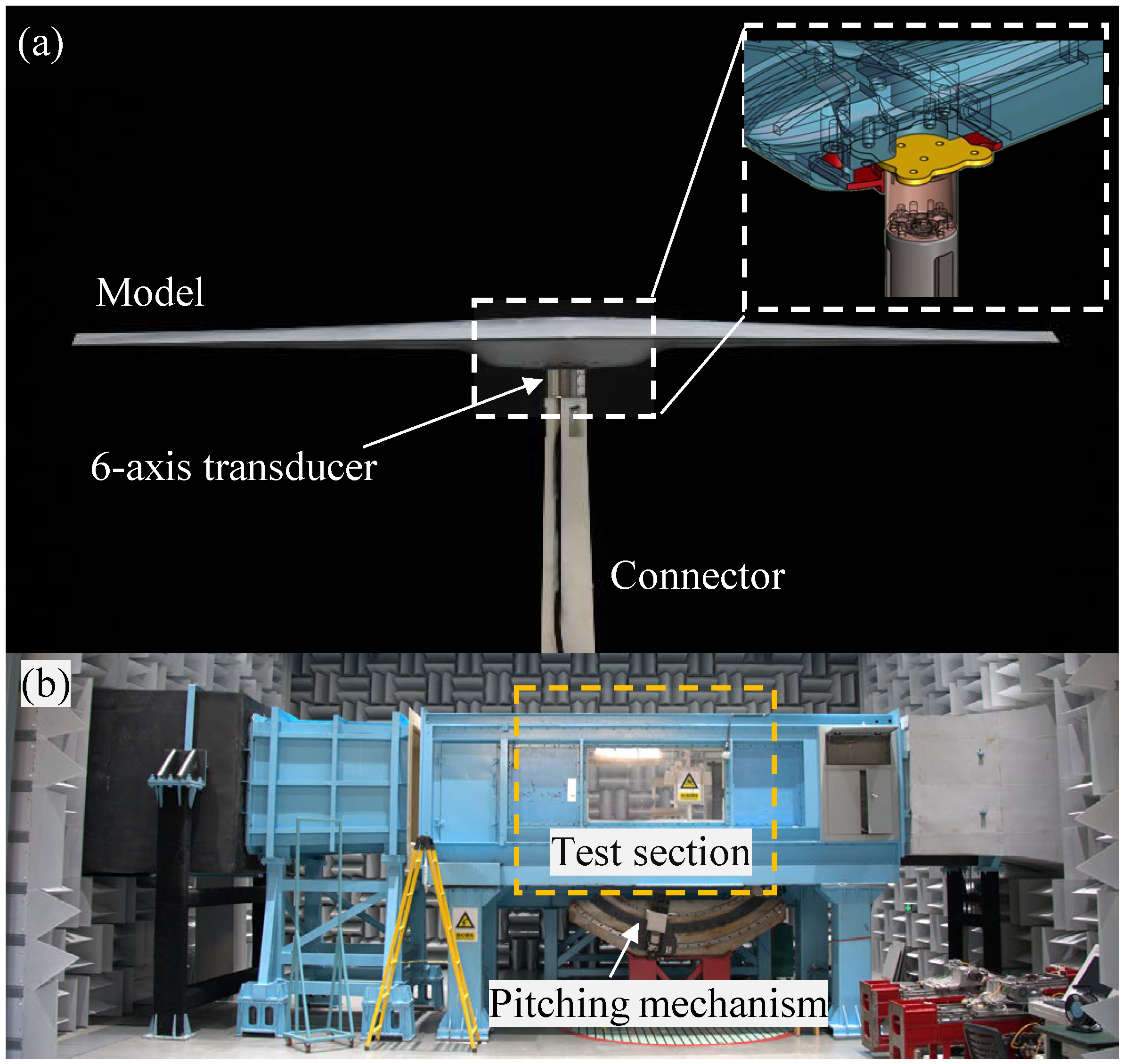
4.2. Wind Tunnel Experiment
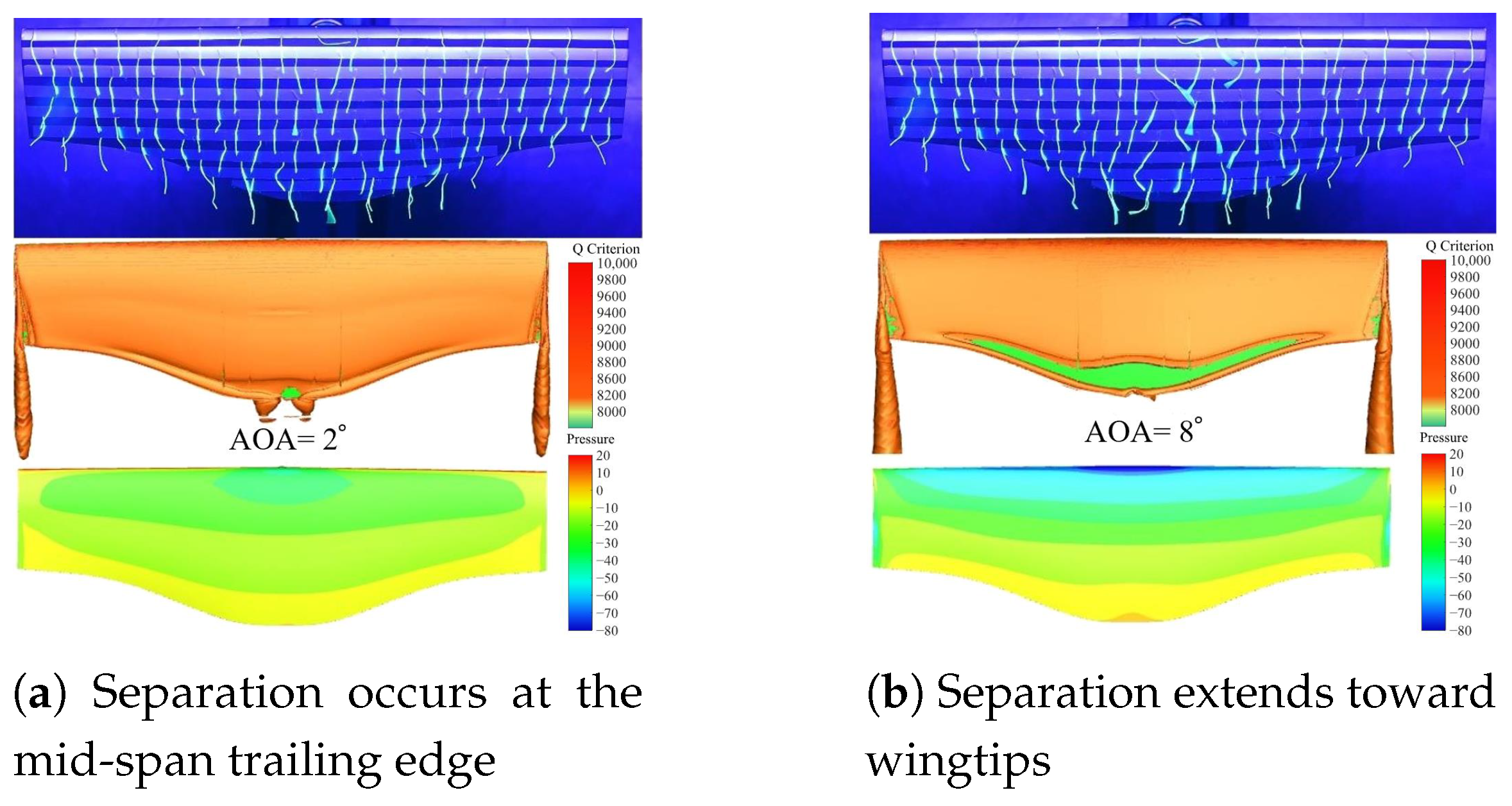
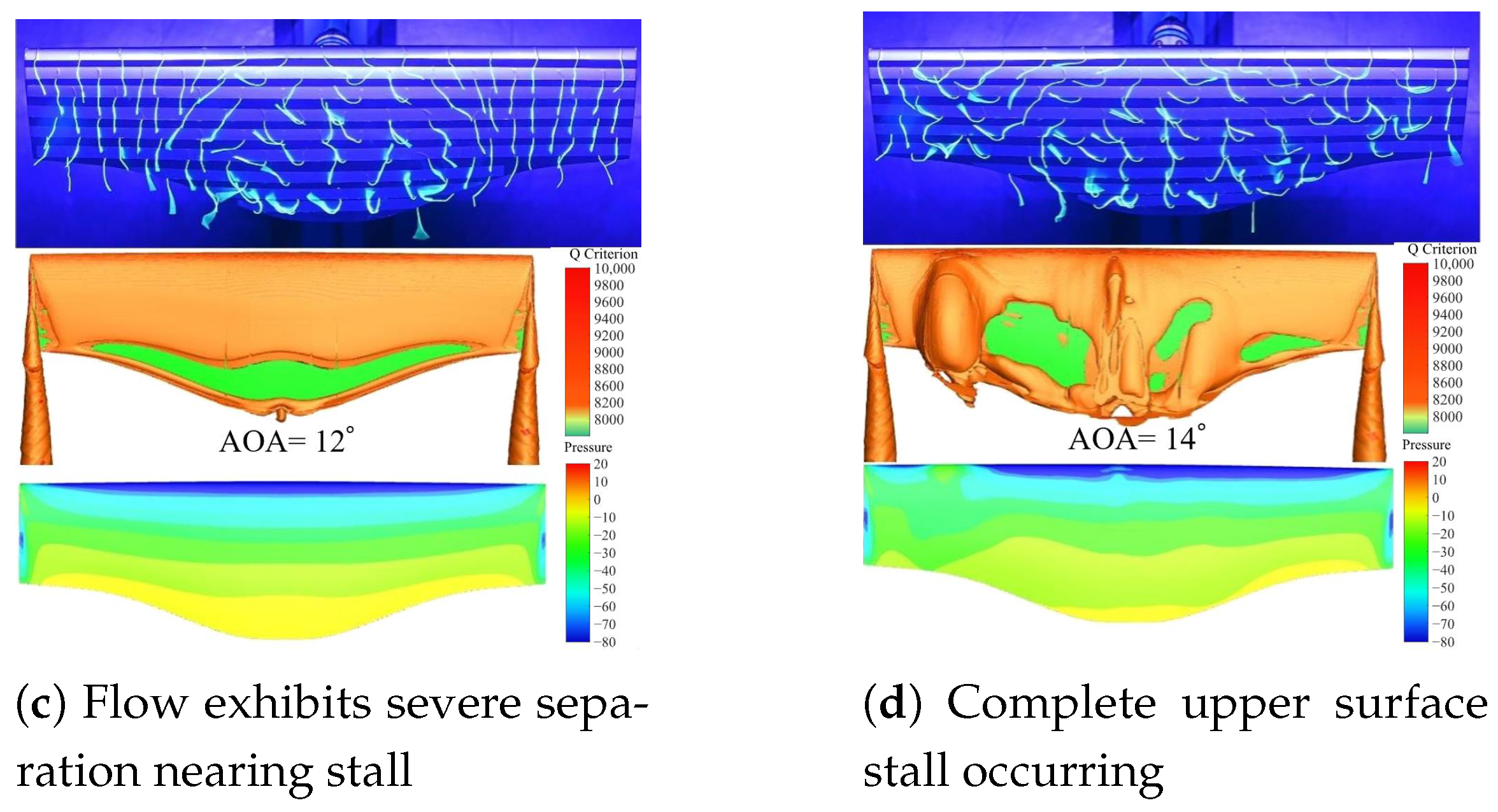
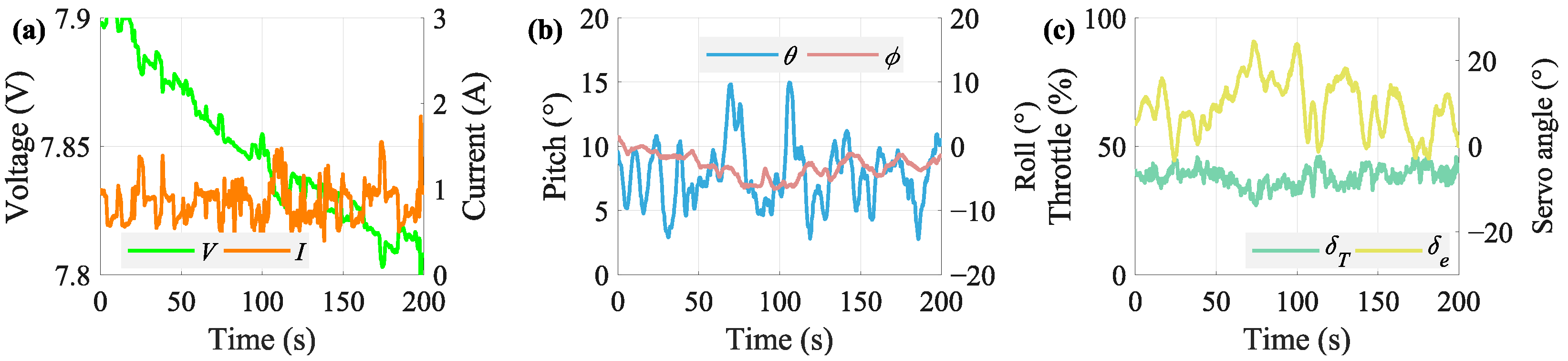
4.3. Flight in Reality
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Photovoltaic Energy Harvesting

Appendix B. Tiny MPPT Design for SMAV

Appendix C. Avionics Installation Space Analysis
Appendix D. Rechargeable Battery

Appendix E. Electric Propulsion
References
- Elbanhawi, M.; Mohamed, A.; Clothier, R.; Palmer, J.; Simic, M.; Watkins, S. Enabling technologies for autonomous MAV operations. Prog. Aerosp. Sci. 2017, 91, 27–52. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Khan, M.A.; Amjad, H.; Żywiołek, J. A Comprehensive Review of Micro UAV Charging Techniques. Micromachines 2022, 13, 977. [Google Scholar] [CrossRef] [PubMed]
- Airbus. Zephyr HAPS. 2025. Available online: https://www.airbus.com/en/products-services/defence/uas/zephyr (accessed on 6 July 2025).
- Lei, T.; Min, Z.; Gao, Q.; Song, L.; Zhang, X.; Zhang, X. The Architecture Optimization and Energy Management Technology of Aircraft Power Systems: A Review and Future Trends. Energies 2022, 15, 4109. [Google Scholar] [CrossRef]
- Brelje, B. Multidisciplinary Design Optimization of Electric Aircraft Considering Systems Modeling and Packaging. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2021. [Google Scholar]
- El-Salamony, M.E.; Aziz, M.A. Impact of N-Shaped Wing Morphing on Solar-Powered Aircraft. Unmanned Syst. 2020, 09, 309–320. [Google Scholar] [CrossRef]
- Siyu, L.; Kangwen, S.; Jian, G.; Haoquan, L. Receiving energy analysis and optimal design of crystalline silicon solar cell array on solar airship. Energy 2023, 282, 128988. [Google Scholar] [CrossRef]
- Wu, M.; Shi, Z.; Xiao, T.; Ang, H. Effect of wingtip connection on the energy and flight endurance performance of solar aircraft. Aerosp. Sci. Technol. 2021, 108, 106404. [Google Scholar] [CrossRef]
- El-Atab, N.; Mishra, R.B.; Alshanbari, R.; Hussain, M.M. Solar Powered Small Unmanned Aerial Vehicles: A Review. Energy Technol. 2021, 9, 2100587. [Google Scholar] [CrossRef]
- Sornek, K.; Augustyn-Nadzieja, J.; Rosikoń, I.; Łopusiewicz, R.; Łopusiewicz, M. Status and Development Prospects of Solar-Powered Unmanned Aerial Vehicles—A Literature Review. Energies 2025, 18, 1924. [Google Scholar] [CrossRef]
- Noth, A. Design of Solar Powered Airplanes for Continous Flight. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2008. [Google Scholar]
- Li, X.; Sun, K.; Li, F. General optimal design of solar-powered unmanned aerial vehicle for priority considering propulsion system. Chin. J. Aeronaut. 2020, 33, 2176–2188. [Google Scholar] [CrossRef]
- Yao, Z. Aerodynamic, Structures and Energy Coupled Multi-Objecitve Optimization for Solar Powered UAV’s Wing. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Peciak, M.; Skarka, W.; Mateja, K.; Gude, M. Impact Analysis of Solar Cells on Vertical Take-Off and Landing (VTOL) Fixed-Wing UAV. Aerospace 2023, 10, 247. [Google Scholar] [CrossRef]
- Carlson, S.J.; Papachristos, C. Solar Energy Harvesting for a Land-to-Recharge Tiltrotor Micro Aerial Vehicle. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Leutenegger, S.; Jabas, M.; Siegwart, R.Y. Solar Airplane Conceptual Design and Performance Estimation: What Size to Choose and What Endurance to Expect. J. Intell. Robot. Syst. 2010, 61, 545–561. [Google Scholar] [CrossRef]
- Turk, I.; Ozbek, E.; Ekici, S.; Karakoc, T.H. A conceptual design of a solar powered UAV and assessment for continental climate flight conditions. Int. J. Green Energy 2021, 19, 638–648. [Google Scholar] [CrossRef]
- Grasmeyer, J.; Keennon, M. Development of the Black Widow Micro Air Vehicle. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar] [CrossRef]
- Roberts, C.; Vaughan, M.; Bowman, W. Development of a solar powered micro air vehicle. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2002. [Google Scholar] [CrossRef][Green Version]
- Kellogg, J.; Bovais, C.; Foch, R.; McFarlane, H.; Sullivan, C.; Dahlburg, J.; Gardner, J.; Ramamurti, R.; Gordon-Spears, D.; Hartley, R.; et al. The NRL micro tactical expendable (MITE) air vehicle. Aeronaut. J. 2002, 106, 431–442. [Google Scholar] [CrossRef]
- Wu, H.; Sun, D.; Zhou, Z. Micro Air Vehicle: Configuration, Analysis, Fabrication, and Test. IEEE/ASME Trans. Mechatron. 2004, 9, 108–117. [Google Scholar] [CrossRef]
- Shyy, W.; Berg, M.; Ljungqvist, D. Flapping and flexible wings for biological and micro air vehicles. Prog. Aerosp. Sci. 1999, 35, 455–505. [Google Scholar] [CrossRef]
- Thipyopas, C.; Moschetta, J.M. A Fixed-Wing Biplane MAV for Low Speed Missions. Int. J. Micro Air Veh. 2009, 1, 13–33. [Google Scholar] [CrossRef]
- Keennon, M.; Klingebiel, K.; Won, H. Development of the Nano Hummingbird: A Tailless Flapping Wing Micro Air Vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar] [CrossRef]
- Leutenegger, S. Unmanned Solar Airplanes: Design and Algorithms for Efficient and Robust Autonomous Operation. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2014. [Google Scholar]
- Radmanesh, M.; Nematollahi, O.; Nili-Ahmadabadi, M.; Hassanalian, M. A novel strategy for designing and manufacturing a fixed wing MAV for the purpose of increasing maneuverability and stability in longitudinal axis. J. Appl. Fluid Mech. 2014, 7, 435–446. [Google Scholar] [CrossRef]
- ETH Zurich. Atlantiksolar. 2025. Available online: https://www.atlantiksolar.ethz.ch/ (accessed on 6 July 2025).
- Shaheed, M.H.; Abidali, A.; Ahmed, J.; Ahmed, S.; Burba, I.; Fani, P.J.; Kwofie, G.; Wojewoda, K.; Munjiza, A. Flying by the Sun only: The Solarcopter prototype. Aerosp. Sci. Technol. 2015, 45, 209–214. [Google Scholar] [CrossRef]
- Perez-Rosado, A.; Gehlhar, R.D.; Nolen, S.; Gupta, S.K.; Bruck, H.A. Design, fabrication, and characterization of multifunctional wings to harvest solar energy in flapping wing air vehicles. Smart Mater. Struct. 2015, 24, 065042. [Google Scholar] [CrossRef]
- D’Sa, R.; Jenson, D.; Papanikolopoulos, N. SUAV:Q—A hybrid approach to solar-powered flight. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3288–3294. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Design, manufacturing, and flight testing of a fixed wing micro air vehicle with Zimmerman planform. Meccanica 2016, 52, 1265–1282. [Google Scholar] [CrossRef]
- Wu, Y.; Du, X.; Duivenvoorden, R.; Kelly, J. The Phoenix Drone: An Open-Source Dual-Rotor Tail-Sitter Platform for Research and Education. In Proceedings of the IEEE 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar] [CrossRef][Green Version]
- Tetreault, E.; Rancourt, D.; Lussier Desbiens, A. Active Vertical Takeoff of an Aquatic UAV. IEEE Robot. Autom. Lett. 2020, 5, 4844–4851. [Google Scholar] [CrossRef]
- Aboelezz, A.; Hassanalian, M.; Desoki, A.; Elhadidi, B.; El-Bayoumi, G. Design, experimental investigation, and nonlinear flight dynamics with atmospheric disturbances of a fixed-wing micro air vehicle. Aerosp. Sci. Technol. 2020, 97, 105636. [Google Scholar] [CrossRef]
- Ionescu, O.N.; Cernica, I.; Manea, E.; Parvulescu, C.; Istrate, A.; Ionescu, G.; Suchea, M.P. Integration of Micro-Structured Photovoltaic Cells into the Ultra-Light Wing Structure for Extended Range Unmanned Aerial Vehicles. Appl. Sci. 2021, 11, 10890. [Google Scholar] [CrossRef]
- Elkunchwar, N.; Chandrasekaran, S.; Iyer, V.; Fuller, S.B. Toward battery-free flight: Duty cycled recharging of small drones. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 5234–5241. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, Z. An investigation on the aerodynamic performance of a hand-launched solar-powered UAV in flying wing configuration. Aerosp. Sci. Technol. 2022, 129, 107804. [Google Scholar] [CrossRef]
- Oliva, J. Design and Fabrication of a Solar Powered MAV. Ph.D. Thesis, Toronto Metropolitan University, Toronto, ON, USA, 2024. [Google Scholar] [CrossRef]
- Abidali, A.; Agha, S.A.; Munjiza, A.; Shaheed, M.H. Development of a solar powered multirotor micro aerial vehicle. Sci. Rep. 2024, 14, 5771. [Google Scholar] [CrossRef]
- Cao, X.; Liu, L. State-of-Charge Trajectory Planning for Low-Altitude Solar-Powered Convertible UAV by Driven Modes. Drones 2024, 8, 80. [Google Scholar] [CrossRef]
- Liller, J.; Goel, R.; Aziz, A.; Hester, J.; Nguyen, P. Development of a battery free, solar powered, and energy aware fixed wing unmanned aerial vehicle. Sci. Rep. 2025, 15, 6141. [Google Scholar] [CrossRef]
- Chu, Y.; Ho, C.; Lee, Y.; Li, B. Development of a Solar-Powered Unmanned Aerial Vehicle for Extended Flight Endurance. Drones 2021, 5, 44. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cipolla, V.; Dine, A.; Viti, A.; Binante, V. MDAO and Aeroelastic Analyses of Small Solar-Powered UAVs with Box-Wing and Tandem-Wing Architectures. Aerospace 2023, 10, 105. [Google Scholar] [CrossRef]
- Bakar, A.; Ke, L.; Liu, H.; Xu, Z.; Wen, D. Design of Low Altitude Long Endurance Solar-Powered UAV Using Genetic Algorithm. Aerospace 2021, 8, 228. [Google Scholar] [CrossRef]
- Manikandan, M.; Pant, R.S. Design optimization of a tri-lobed solar powered stratospheric airship. Aerosp. Sci. Technol. 2019, 91, 255–262. [Google Scholar] [CrossRef]
- Salunke, N.P.; Ahamad, R.A.J.; Channiwala, S. Airfoil Parameterization Techniques: A Review. Am. J. Mech. Eng. 2014, 2, 99–102. [Google Scholar] [CrossRef]
- Liu, H.; Di, W.; Wei, Z.; Li, D.; Xiang, J.; Tu, Z. Aerodynamic optimization design of low reynolds number aerofoils based on induced laminar separation. J. Phys. Conf. Ser. 2024, 2764, 012019. [Google Scholar] [CrossRef]
- García-Gascón, C.; Castelló-Pedrero, P.; García-Manrique, J.A. Minimal Surfaces as an Innovative Solution for the Design of an Additive Manufactured Solar-Powered Unmanned Aerial Vehicle (UAV). Drones 2022, 6, 285. [Google Scholar] [CrossRef]
- Liu, Y.; Du, H.; Xu, Z.; Sun, K.; Lv, M. Mission-based optimization of insulation layer for the solar array on the stratospheric airship. Renew. Energy 2022, 191, 318–329. [Google Scholar] [CrossRef]
- Rakshith, B.R.; Deshpande, S.M.; Narasimha, R.; Praveen, C. Optimal Low-Drag Wing Planforms for Tractor-Configuration Propeller-Driven Aircraft. J. Aircr. 2015, 52, 1791–1801. [Google Scholar] [CrossRef]
- Automation, A.I. F/T Sensor, Nano17 IP65/IP68. 2025. Available online: https://www.ati-ia.com/products/ft/ft_models.aspx?id=Nano17+IP65%2fIP68 (accessed on 6 July 2025).
- Pamadi, B.N. Performance, Stability, Dynamics, and Control of Airplanes, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar] [CrossRef]
- Pande, D.; Verstraete, D. Impact of solar cell characteristics and operating conditions on the sizing of a solar powered nonrigid airship. Aerosp. Sci. Technol. 2018, 72, 353–363. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, Y.; Li, J.; Zhang, L. Performance analysis of rotatable energy system of high-altitude airships in real wind field. Aerosp. Sci. Technol. 2020, 98, 105689. [Google Scholar] [CrossRef]
- Carlson, S.J.; Karakurt, T.; Arora, P.; Papachristos, C. Integrated Solar Power Harvesting and Hibernation for a Recurrent-Mission VTOL Micro Aerial Vehicle. In Proceedings of the IEEE 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 237–244. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, C.; Li, L.; Guo, Q. Parameter analysis of power system for solar-powered unmanned aerial vehicle. Appl. Energy 2021, 295, 117031. [Google Scholar] [CrossRef]




| Name | Year | Wing Span (cm) | Mass (g) | Duration (min) | Solar-Powered |
|---|---|---|---|---|---|
| Black widow [18] | 1999 | 15.0 | 56.0 | 22 | no |
| Sunbeam I [19] | 2002 | 38.1 | 71.0 | / | yes |
| MITE [20] | 2002 | 25.0 | 130.0 | / | no |
| TH380 [21] | 2004 | 38.0 | 154.0 | 5 | no |
| UFMAV [22] | 2004 | / | 55.0 | 15 | no |
| Sky-Sailor [11] | 2008 | 320.0 | 2440.0 | 1620 | yes |
| TYTO30 [23] | 2009 | 30.0 | 230.0 | / | no |
| Nano Hummingbird [24] | 2011 | 16.0 | 19.0 | 10 | no |
| SenseSoar [25] | 2014 | 310.0 | 5000.0 | / | yes |
| Radmanesh [26] | 2014 | / | 450.0 | 6 | no |
| AtlantikSolar [27] | 2014 | 565.0 | 6700.0 | / | yes |
| Solarcopter [28] | 2015 | / | 925.0 | / | yes |
| Robo Raven III [29] | 2015 | 116.8 | 346.0 | 5 | yes |
| SUAV:Q [30] | 2016 | / | 3664.0 | / | yes |
| Zimmerman MAV [31] | 2016 | 44.0 | 450.0 | 20 | no |
| Hummingbird [32] | 2018 | 42.0 | 650.0 | 20 | no |
| SUWAVE [33] | 2020 | 124.0 | 865.0 | / | yes |
| BlueBird MAV [34] | 2020 | 27.69 | 188.0 | 20 | no |
| Hirus (solar refit) [35] | 2021 | / | 875.0 | 210 | yes |
| Crazyflie (solar refit) [36] | 2021 | / | 40.7 | 4.7 | yes |
| MY-02 [37] | 2022 | 250.0 | 3000.0 | 720 | yes |
| MiniHawk-VTOL [15] | 2022 | 80.0 | 1000.0 | / | yes |
| Oliva [38] | 2024 | 55 | 248.0 | <70 | yes |
| Micro Solarcopter [39] | 2024 | / | 71.0 | 3.5 | yes |
| SCUAV [40] | 2024 | / | 4550.0 | 138 | yes |
| Variable | Value |
|---|---|
| Population size | 30 |
| Max iteration | 30 |
| Crossover probability | 0.3 |
| Mutation probability | 0.2 |
| Variable | Value |
|---|---|
| Weight | |
| Cruise speed | |
| Avionics power () | |
| Latitude | |
| Battery capacity | |
| Flight time | Aug. 2:00 p.m. |
| Wing area | |
| Mean chord length | |
| Solar panels () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, W.; Dong, X.; Wei, Z.; Liu, H.; Tu, Z.; Li, D.; Xiang, J. Towards Efficiency and Endurance: Energy–Aerodynamic Co-Optimization for Solar-Powered Micro Air Vehicles. Drones 2025, 9, 493. https://doi.org/10.3390/drones9070493
Di W, Dong X, Wei Z, Liu H, Tu Z, Li D, Xiang J. Towards Efficiency and Endurance: Energy–Aerodynamic Co-Optimization for Solar-Powered Micro Air Vehicles. Drones. 2025; 9(7):493. https://doi.org/10.3390/drones9070493
Chicago/Turabian StyleDi, Weicheng, Xin Dong, Zixing Wei, Haoji Liu, Zhan Tu, Daochun Li, and Jinwu Xiang. 2025. "Towards Efficiency and Endurance: Energy–Aerodynamic Co-Optimization for Solar-Powered Micro Air Vehicles" Drones 9, no. 7: 493. https://doi.org/10.3390/drones9070493
APA StyleDi, W., Dong, X., Wei, Z., Liu, H., Tu, Z., Li, D., & Xiang, J. (2025). Towards Efficiency and Endurance: Energy–Aerodynamic Co-Optimization for Solar-Powered Micro Air Vehicles. Drones, 9(7), 493. https://doi.org/10.3390/drones9070493








