Traj-Q-GPSR: A Trajectory-Informed and Q-Learning Enhanced GPSR Protocol for Mission-Oriented FANETs
Abstract
1. Introduction
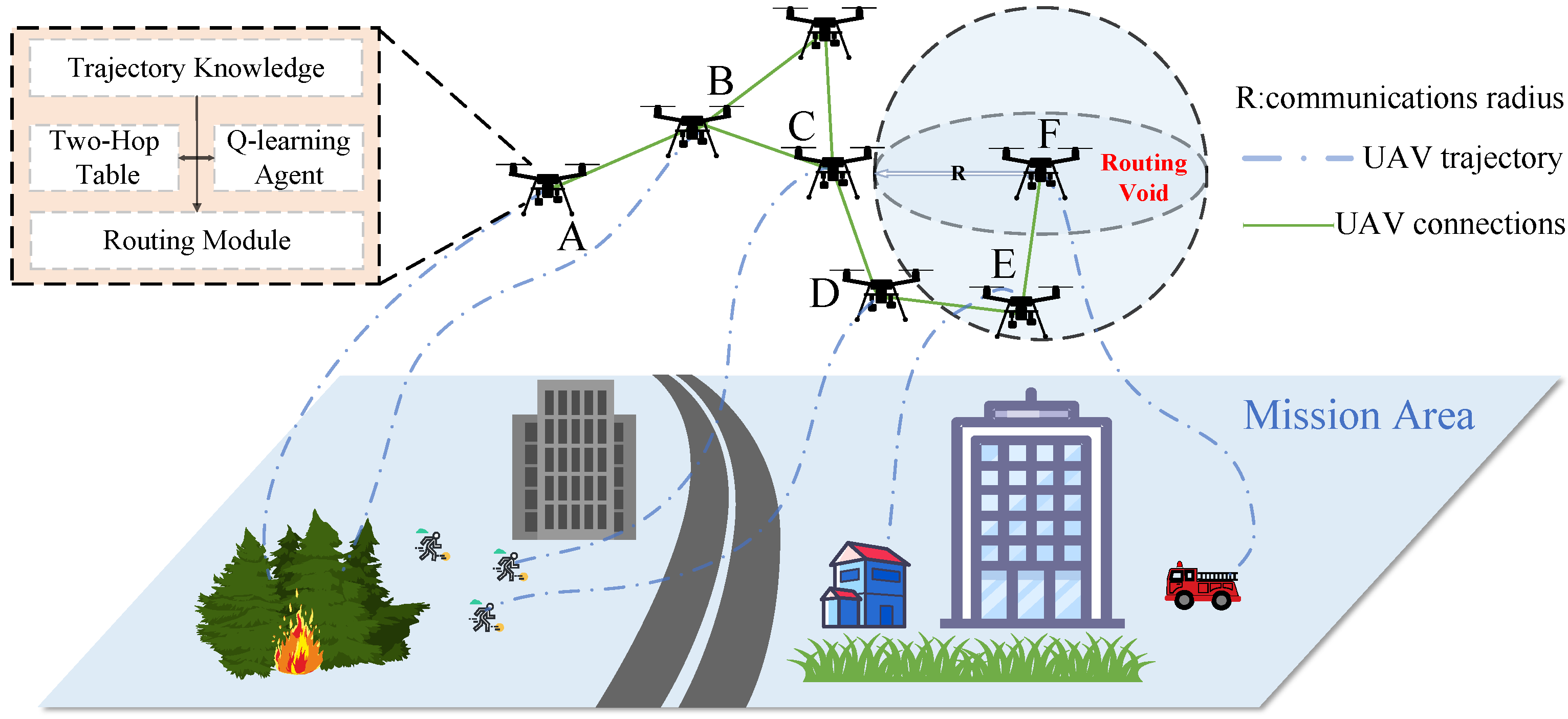
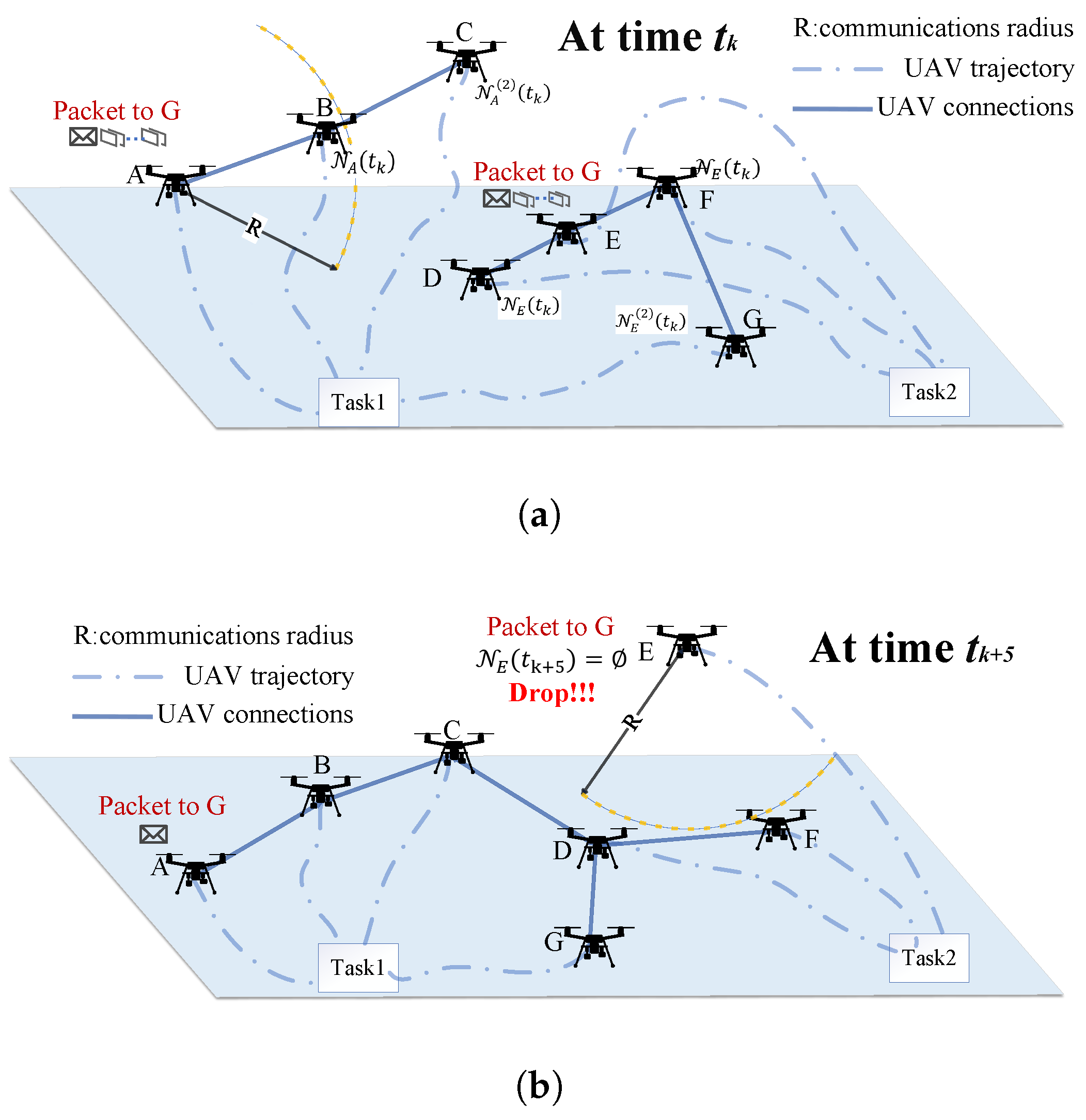
- Trajectory-Aware Neighbor Expansion: We propose a novel routing strategy for UAV swarms by leveraging mission-planner-derived trajectory knowledge. We develop a time-aware two-hop neighbor table that enables nodes to anticipate network dynamics, enhancing both local and global topological awareness. This proactive approach significantly reduces routing voids and fosters stable communication in dynamic environments;
- Q-Learning-Driven Routing Optimization: We introduce an adaptive routing framework for UAV networks, utilizing Q-learning to navigate their high dynamism. The framework incorporates a comprehensive state space, including two-hop distances, residual energy, queue lengths, and trajectory dynamics, and employs a multi-objective reward function with dynamically adaptive parameters. This design ensures balanced and efficient next-hop selection, promoting robust routing decisions under rapidly evolving network conditions;
- Latency-Focused Queue Scheduling: To improve real-time performance and load balance, we devise a composite delay model that leverages trajectory insights to refine packet transmission timing. This mechanism mitigates congestion, reduces end-to-end latency, and provides an effective queue management solution for high-load, multi-hop scenarios in UAV swarms;
- Comprehensive Simulation Validation: Through extensive ns-3 simulations, we assess Traj-Q-GPSR across diverse scenarios, varying node densities, UAV speeds, and CBR loads. Comparative evaluations reveal substantial enhancements in packet delivery ratio, end-to-end delay, routing efficiency, and throughput, demonstrating the robustness and effectiveness of our approach in dynamic UAV swarm settings.
2. Related Work
2.1. GPSR and Its Adaptations in Dynamic Networks
2.2. Trajectory-Aware Routing in FANETs Networks
2.3. Q-Learning-Based Routing Protocols
3. System Model
3.1. Network Model
3.2. Energy Model
3.3. Transmission Delay
4. The TRAJ-Q-GPSR Algorithm
4.1. Trajectory-Informed UAV Routing
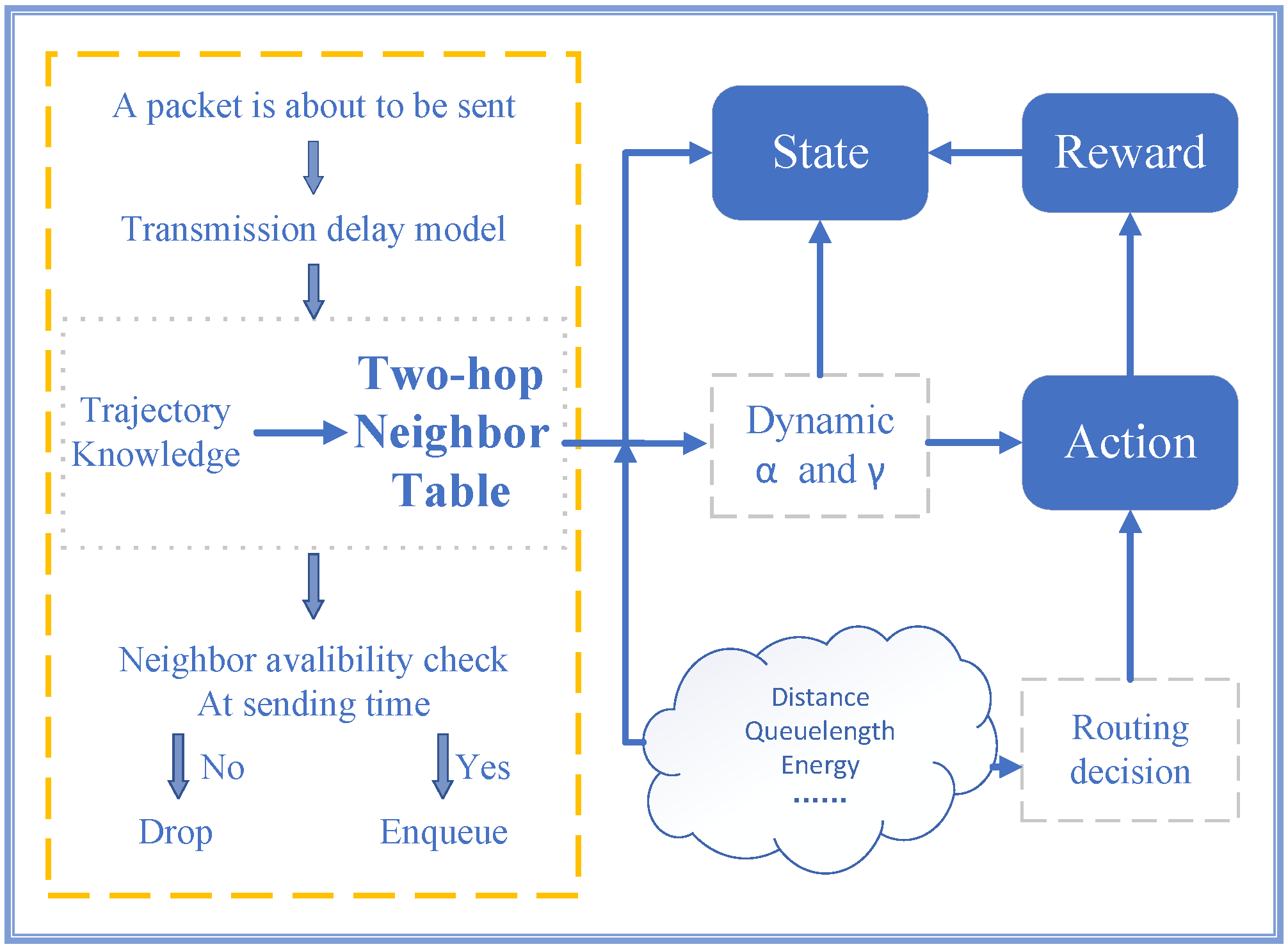
4.2. Q-Learning Framework and Theory
4.3. Traj-Q-GPSR Algorithm
4.3.1. Definition of State and Action Spaces
4.3.2. Design of the Reward Function
- Two-hop rewardThe two-hop reward is composed of single-hop rewards and their extension. The single-hop reward evaluates the immediate benefit of selecting a neighbor as the next hop when UAV node is in state s. It considers three key factors: distance, residual energy, and queue load, defined as
- Distance RewardPromotes selection of nodes closer to the destination, calculated as the proportion of distance reduced:Here, is the Euclidean distance from the current node to the destination , and is the distance from the neighbor to the destination. If , then , yielding a positive reward; otherwise, it is negative.
- Energy RewardThis prioritizes nodes with higher remaining energy to extend network lifetime:where is the remaining energy of , and is the maximum energy capacity.
- Queue Length RewardThis prefers nodes with lower loads to reduce transmission delay:
Expanding the single-hop reward to consider the influence of the next-hop neighbors, the two-hop reward is defined aswhere is the single-hop reward from to its neighbor , and is the degree of (number of neighbors). The normalization factor prevents reward inflation in highly connected regions. - Velocity Projection RewardIn UAV networks, node mobility affects link stability. The velocity projection reward leverages trajectory information to evaluate whether the selected next-hop UAV is moving toward the destination, improving adaptation to network dynamics.Given the velocity vector of UAV and the directional vector from to the destination , the reward is defined asA positive indicates movement toward the destination, yielding a positive reward; a negative value indicates movement away, resulting in a penalty. This encourages selecting UAVs whose motion trends enhance link availability.
- Routing Void PenaltyTo prevent routing voids—where no neighbor is closer to the destination than the current node—the penalty term refines void severity assessment. Void severity is defined aswhere is the number of neighbors closer to the destination than , and is the total number of neighbors. The penalty isIf , indicating a full routing void, the penalty is maximized.
4.3.3. Adaptive Q-Learning Parameters
4.4. Pseudo-Code
| Algorithm 1 Traj-Q-GPSR Algorithm |
|
5. Simulation Results and Discussions
5.1. Simulation Settings
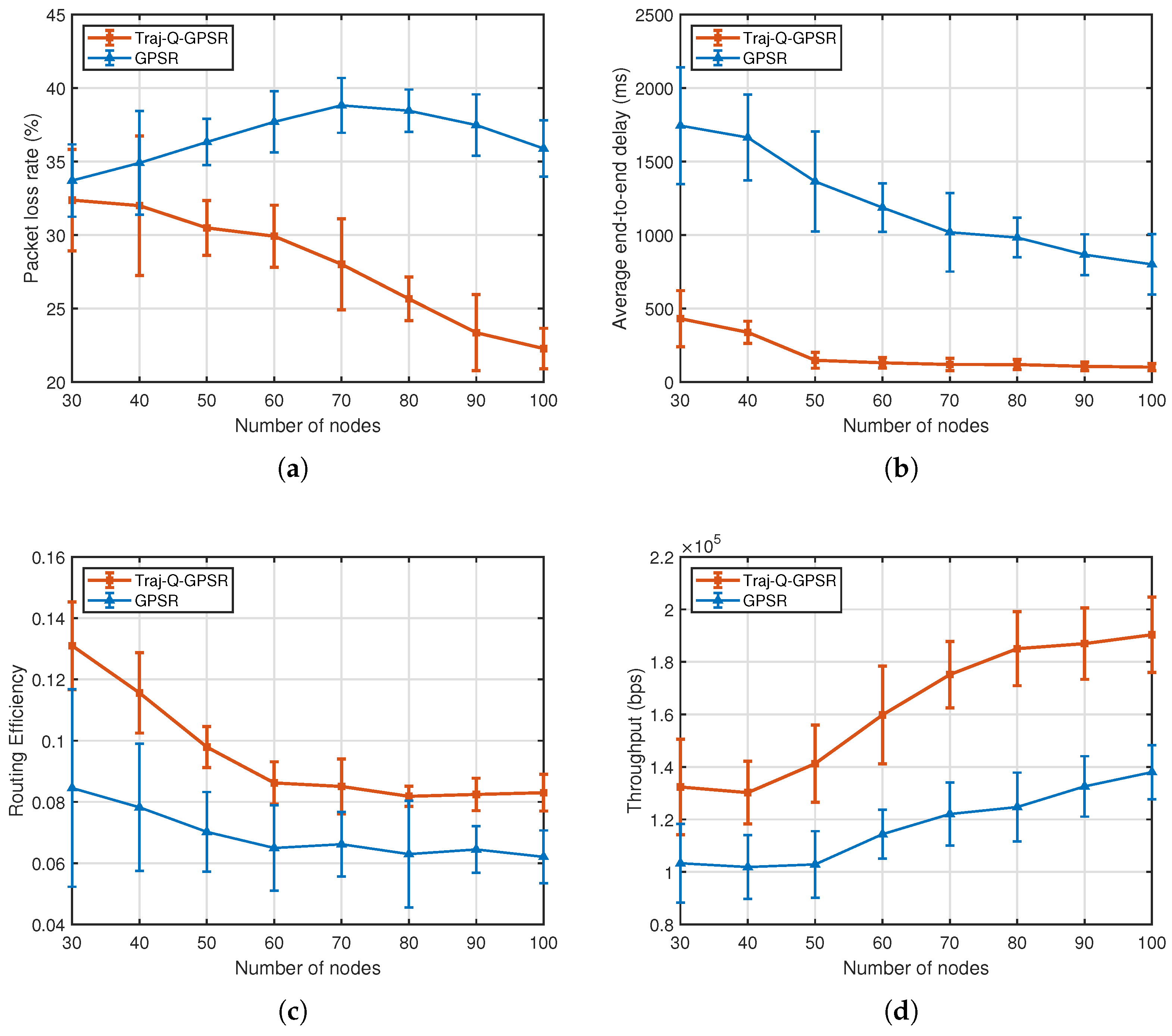
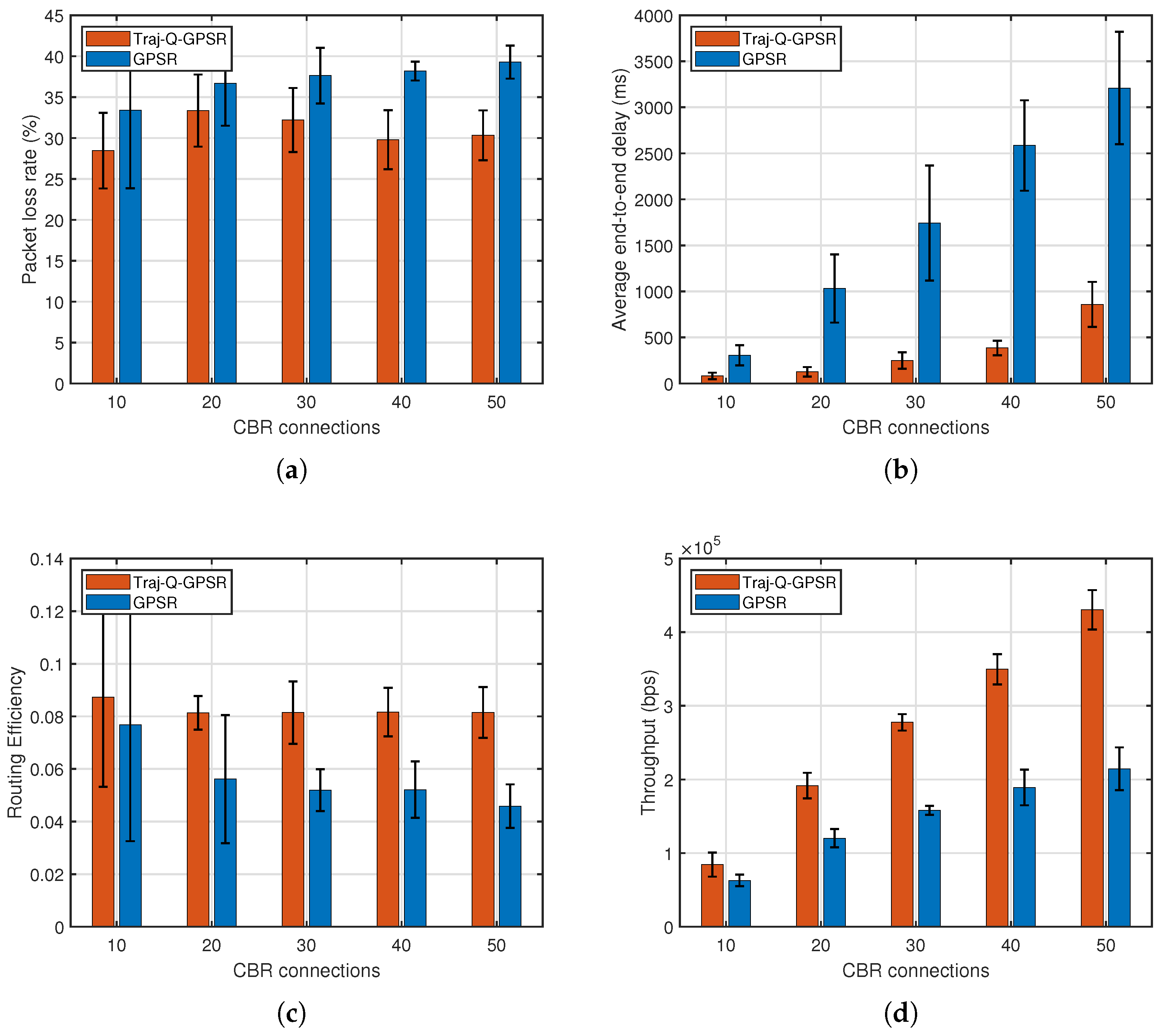
- Packet Loss Ratio (PLR):The PLR is defined as the ratio of lost packets to the total packets sent by the source, reflecting packet losses due to routing failures, congestion, or channel errors:A lower PLR indicates higher reliability and robustness in dynamic topologies and interference-prone environments.
- End-to-End Delay (E2ED): E2ED measures the total time a packet takes from transmission at the source to reception at the destination, capturing the timeliness of the protocol:where is the number of successfully received packets, and , are the send and receive timestamps of packet p.
- Routing Efficiency: To assess resource utilization in multi-hop scenarios, we define routing efficiency as the average ratio of successfully delivered packets per forwarding hop:This metric minimizes forwarding overhead while ensuring successful delivery. A higher value indicates better path optimization and resource efficiency.
- Throughput: Throughput quantifies the network’s capacity to successfully deliver payload data per unit time, in bits per second (bps):It directly reflects the protocol’s data delivery capability and bandwidth utilization under given network conditions.
5.2. Impact of Node Density
5.3. Impact of Node Mobility Speed
5.4. Impact of CBR Connections
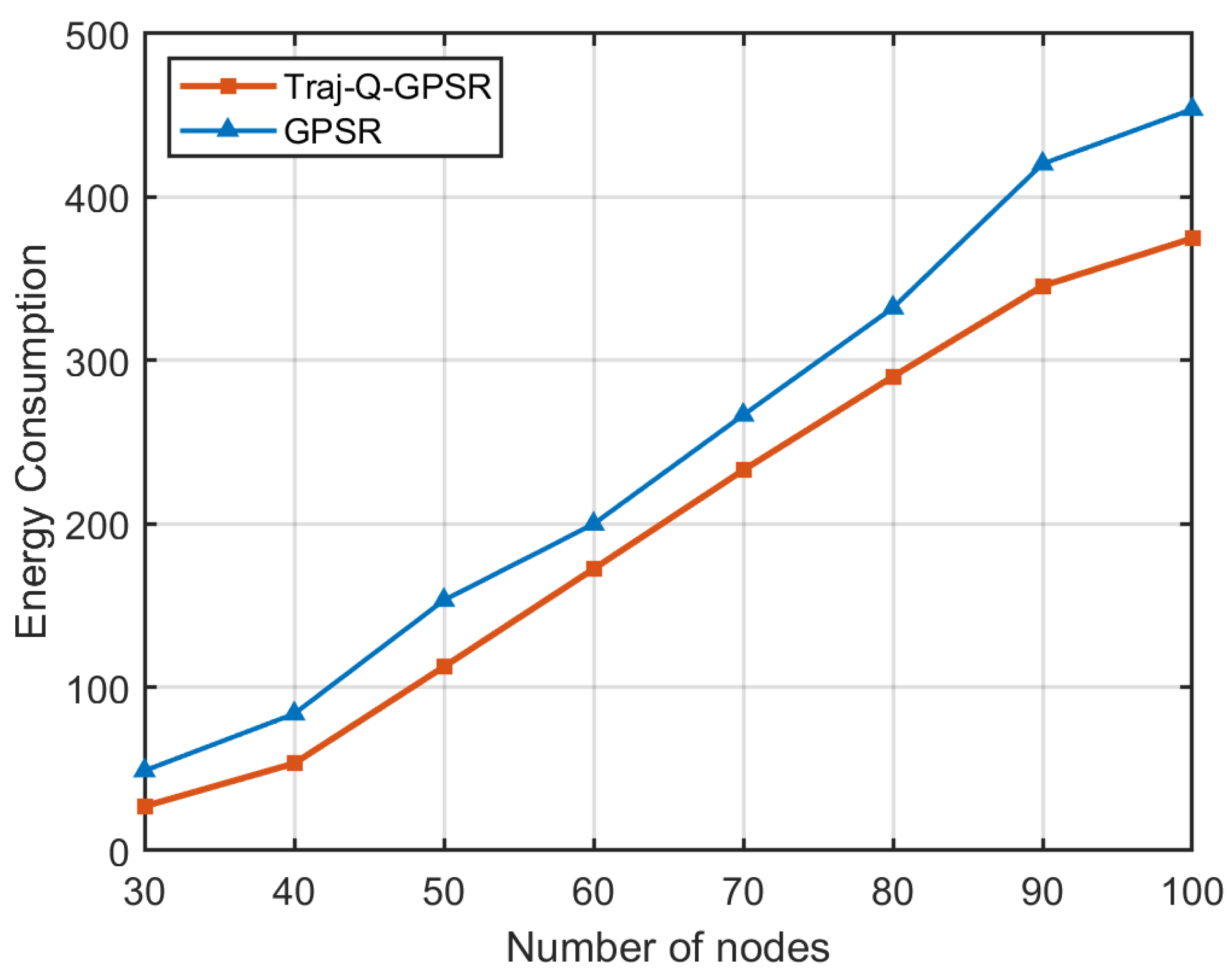
5.5. Energy Consumption
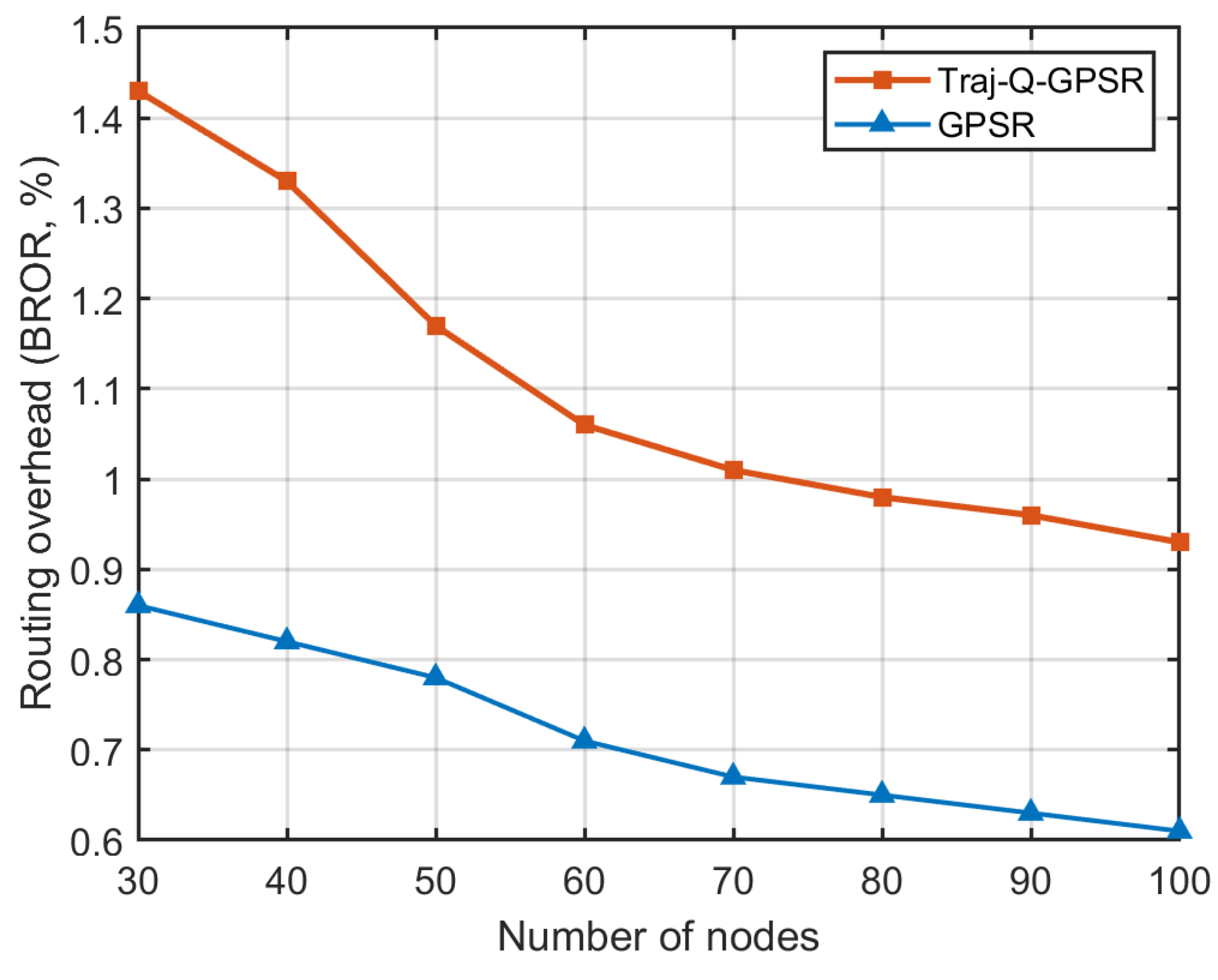
5.6. Routing Overhead
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| FANET | Flying Ad Hoc Network |
| VANET | Vehicular Ad Hoc Networks |
| GPSR | Greedy Perimeter Stateless Routing |
| Traj-Q-GPSR | Trajectory-Informed Q-learning-based GPSR |
| CBR | Constant Bit Rate |
| PLR | Packet Loss Ratio |
| MDP | Markov Decision Process |
| E2ED | End to End Delay |
| BROR | Byte-Level Routing Overhead Ratio |
References
- Sadaf, J.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A.; Guizani, M. State-of-the-Art and Future Research Challenges in UAV Swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Kaddour, M.; Oubbati, O.S.; Rachedi, A.; Lakas, A.; Bendouma, T.; Chaib, N. A Survey of UAV-Based Data Collection: Challenges, Solutions and Future Perspectives. J. Netw. Comput. Appl. 2023, 216, 103670. [Google Scholar] [CrossRef]
- Mehdi, H.; Ali, S.; Rahmani, A.M.; Lansky, J.; Nulicek, V.; Yousefpoor, M.S.; Yousefpoor, E.; Darwesh, A.; Lee, S.W. A Smart Filtering-Based Adaptive Optimized Link State Routing Protocol in Flying Ad Hoc Networks for Traffic Monitoring. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102034. [Google Scholar] [CrossRef]
- Ridha, G.; Mami, S.; Chokmani, K. Drones in Precision Agriculture: A Comprehensive Review of Applications, Technologies, and Challenges. Drones 2024, 8, 686. [Google Scholar] [CrossRef]
- Abbas, S.; Talib, M.A.; Ahmed, I.; Belal, O. Integration of UAVs and FANETs in Disaster Management: A Review on Applications, Challenges and Future Directions. Trans. Emerg. Telecommun. Technol. 2024, 35, E70023. [Google Scholar] [CrossRef]
- Mansoor, N.; Hossain, M.I.; Rozario, A.; Zareei, M.; Arreola, A.R. A Fresh Look at Routing Protocols in Unmanned Aerial Vehicular Networks: A Survey. IEEE Access 2023, 11, 66289–66308. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, B.; Pang, T.; Xu, H.; Gao, M.; Ding, Y.; Wang, X. Firefly Swarm Intelligence Based Cooperative Localization and Automatic Clustering for Indoor FANETs. PLoS ONE 2023, 18, E0282333. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, B.; Xu, H.; Pang, T.; Gao, M.; Liu, Z. A Task-Driven Scheme for Forming Clustering-Structure-Based Heterogeneous FANETs. Veh. Commun. 2025, 52, 100884. [Google Scholar] [CrossRef]
- Lakew, D.S.; Sa’ad, U.; Dao, N.-N.; Na, W.; Cho, S. Routing in Flying Ad Hoc Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2020, 22, 1071–1120. [Google Scholar] [CrossRef]
- Das, S.R.; Perkins, C.E.; Belding-Royer, E.M. Ad Hoc On-Demand Distance Vector (AODV) Routing; RFC 3561; Internet Engineering Task Force: Fremont, CA, USA, 2003. [Google Scholar] [CrossRef]
- Clausen, T.H.; Jacquet, P. Optimized Link State Routing Protocol (OLSR); RFC 3626; Internet Engineering Task Force: Fremont, CA, USA, 2003. [Google Scholar] [CrossRef]
- Karp, B.; Kung, H.T. GPSR: Greedy Perimeter Stateless Routing. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking (MobiCom ’00), Boston, MA, USA, 6–11 August 2000; ACM: New York, NY, USA, 2000; pp. 243–254. [Google Scholar] [CrossRef]
- Bengag, A.; Bengag, A.; Elboukhari, M. The GPSR Routing Protocol in VANETs: Improvements and Analysis. In Proceedings of the 3rd International Conference on Electronic Engineering and Renewable Energy Systems, Saidia, Morocco, 20–22 May 2022; Bekkay, H., Mellit, A., Gagliano, A., Rabhi, A., Koulali, M.A., Eds.; Lecture Notes in Electrical Engineering. Springer: Singapore, 2023; Volume 954, pp. 21–28. [Google Scholar] [CrossRef]
- Wang, C.-M.; Yang, S.; Dong, W.Y.; Zhao, W.; Lin, W. A Distributed Hybrid Proactive-Reactive Ant Colony Routing Protocol for Highly Dynamic FANETs with Link Quality Prediction. IEEE Trans. Veh. Technol. 2024, 74, 1817–1822. [Google Scholar] [CrossRef]
- Sharvari, N.P.; Das, D.; Bapat, J.; Das, D. Improved Q-Learning Based Multi-Hop Routing for UAV-Assisted Communication. IEEE Trans. Netw. Serv. Manag. 2024, 22, 1330–1344. [Google Scholar] [CrossRef]
- Sun, S.; Guo, X.; Liu, K. A Multi-Protocol Integrated Ad Hoc Networking Architecture. In Proceedings of the 2023 9th International Conference on Communication and Information Processing, Lingshui, China, 14–16 December 2023; ACM: New York, NY, USA, 2023; pp. 279–283. [Google Scholar] [CrossRef]
- Sang, Q.; Wu, H.; Xing, L.; Ma, H.; Xie, P. An Energy-Efficient Opportunistic Routing Protocol Based on Trajectory Prediction for FANETs. IEEE Access 2020, 8, 192009–192020. [Google Scholar] [CrossRef]
- Cui, J.; Ma, L.; Wang, R.; Liu, M. Research and Optimization of GPSR Routing Protocol for Vehicular Ad-Hoc Network. China Commun. 2022, 19, 194–206. [Google Scholar] [CrossRef]
- Alam, M.M.; Moh, S. Survey on Q-Learning-Based Position-Aware Routing Protocols in Flying Ad Hoc Networks. Electronics 2022, 11, 1099. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, M.; Dong, C.; Feng, Y.; Yuan, Y.; Feng, S.; Quek, T.Q.S. Routing Protocol for Heterogeneous FANETs with Mobility Prediction. China Commun. 2022, 19, 186–201. [Google Scholar] [CrossRef]
- Hu, D.; Yang, S.; Gong, M.; Feng, Z.; Zhu, X. A Cyber–Physical Routing Protocol Exploiting Trajectory Dynamics for Mission-Oriented Flying Ad Hoc Networks. Engineering 2022, 19, 217–227. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, L.; Song, X.; Shao, Z. Weight-Based PA-GPSR Protocol Improvement Method in VANET. Sensors 2023, 23, 5991. [Google Scholar] [CrossRef]
- Silva, A.; Reza, N.; Oliveira, A. Improvement and Performance Evaluation of GPSR-Based Routing Techniques for Vehicular Ad Hoc Networks. IEEE Access 2019, 7, 21722–21733. [Google Scholar] [CrossRef]
- Babu, S.; Rajkumar, P.A. Group Communication in Vehicular Ad-Hoc Networks: A Comprehensive Survey on Routing Perspectives. Wirel. Pers. Commun. 2024, 139, 2325–2377. [Google Scholar] [CrossRef]
- Alsalami, O.M.; Yousefpoor, E.; Hosseinzadeh, M.; Lansky, J. A Novel Optimized Link-State Routing Scheme with Greedy and Perimeter Forwarding Capability in Flying Ad Hoc Networks. Mathematics 2024, 12, 1016. [Google Scholar] [CrossRef]
- Rahmani, A.M.; Hussain, D.; Ismail, R.J.; Alanazi, F.; Belhaj, S.; Yousefpoor, M.S.; Yousefpoor, E.; Darwesh, A.; Hosseinzadeh, M. An Adaptive and Multi-Path Greedy Perimeter Stateless Routing Protocol in Flying Ad Hoc Networks. Veh. Commun. 2024, 50, 100838. [Google Scholar] [CrossRef]
- Zhou, Y.; Mi, Z.; Wang, H.; Lu, Y.; Tian, Y. SZLS-GPSR: UAV Geographic Location Routing Protocol Based on Link Stability of Communication Safe Zone. In Proceedings of the 2023 15th International Conference on Computer Research and Development (ICCRD), Hangzhou, China, 10–12 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 258–267. [Google Scholar] [CrossRef]
- Kumar, S.; Raw, R.S.; Bansal, A.; Singh, P. UF-GPSR: Modified Geographical Routing Protocol for Flying Ad-Hoc Networks. Trans. Emerg. Telecommun. Technol. 2023, 34, E4813. [Google Scholar] [CrossRef]
- Rahmani, A.M.; Haider, A.; Aurangzeb, K.; Altulyan, M.; Gemeay, E.; Yousefpoor, M.S.; Yousefpoor, E.; Khoshvaght, P.; Hosseinzadeh, M. A Novel Cylindrical Filtering-Based Greedy Perimeter Stateless Routing Scheme in Flying Ad Hoc Networks. Veh. Commun. 2025, 52, 100879. [Google Scholar] [CrossRef]
- Li, X.; Sun, H. Prediction-Based Reactive-Greedy Routing Protocol for Flying Ad Hoc Networks. Wirel. Netw. 2025, 31, 2893–2907. [Google Scholar] [CrossRef]
- Gupta, V.; Seth, D.; Yadav, D.K. An Energy-Efficient Trajectory Prediction for UAVs Using an Optimised 3D Improvised Protocol. Wirel. Pers. Commun. 2023, 132, 2963–2989. [Google Scholar] [CrossRef]
- Alam, M.M.; Moh, S. Joint Trajectory Control, Frequency Allocation, and Routing for UAV Swarm Networks: A Multi-Agent Deep Reinforcement Learning Approach. IEEE Trans. Mob. Comput. 2024, 23, 11989–11995. [Google Scholar] [CrossRef]
- Lin, N.; Huang, J.; Hawbani, A.; Zhao, L.; Tang, H.; Guan, Y.; Sun, Y. Joint Routing and Computation Offloading Based Deep Reinforcement Learning for Flying Ad Hoc Networks. Comput. Netw. 2024, 249, 110514. [Google Scholar] [CrossRef]
- Khoshvaght, P.; Tanveer, J.; Rahmani, A.M.; Altulyan, M.; Alkhrijah, Y.; Yousefpoor, M.S.; Yousefpoor, E.; Mohammadi, M.; Hosseinzadeh, M. Computational Intelligence-Based Routing Schemes in Flying Ad-Hoc Networks (FANETs): A Review. Veh. Commun. 2025, 53, 100913. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, J.; Yan, Z.; Wang, H.; Li, T. Can Routing Be Effectively Learned in Integrated Heterogeneous Networks? IEEE Netw. 2024, 38, 210–218. [Google Scholar] [CrossRef]
- Rovira-Sugranes, A.; Razi, A.; Afghah, F.; Chakareski, J. A Review of AI-Enabled Routing Protocols for UAV Networks: Trends, Challenges, and Future Outlook. Ad Hoc Netw. 2022, 130, 102790. [Google Scholar] [CrossRef]
- Huang, S.; Tang, J.; Zhou, Z.; Yang, G.; Davydov, M.V.; Wong, K.K. A Q-Learning and Fuzzy Logic Based Routing Protocol for UAV Networks. In Proceedings of the 2024 16th International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 24–26 October 2024; IEEE: Piscataway, NJ, USA, 2025; pp. 1090–1095. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. A Q-Learning-Based Topology-Aware Routing Protocol for Flying Ad Hoc Networks. IEEE Internet Things J. 2022, 9, 1985–2000. [Google Scholar] [CrossRef]
- Da Costa, L.A.L.F.; Kunst, R.; de Freitas, E.P. Q-FANET: Improved Q-Learning Based Routing Protocol for FANETs. Comput. Netw. 2021, 198, 108379. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.; He, C.; Jaffrès-Runser, K.; Xu, Y.; Li, Z.; Xu, Y. QMR: Q-Learning Based Multi-Objective Optimization Routing Protocol for Flying Ad Hoc Networks. Comput. Commun. 2020, 150, 304–316. [Google Scholar] [CrossRef]
- Pang, Y.; Dong, F.; Huang, R.; He, Q.; Shi, Z.; Chen, Z. A Resilient Packet Routing Approach Based on Deep Reinforcement Learning. In Proceedings of the 2024 IEEE 24th International Conference on Communication Technology (ICCT), Chengdu, China, 18–20 October 2024; IEEE: Piscataway, NJ, USA, 2025; pp. 741–747. [Google Scholar] [CrossRef]
- Bianchi, G. Performance Analysis of the IEEE 802.11 Distributed Coordination Function. IEEE J. Sel. Areas Commun. 2000, 18, 535–547. [Google Scholar] [CrossRef]
- BonnMotion—A Mobility Scenario Generation and Analysis Tool. Available online: https://sys.cs.uos.de/bonnmotion/ (accessed on 17 April 2025).
- Hosseinzadeh, M.; Ali, S.; Ionescu-Feleaga, L.; Ionescu, B.S.; Yousefpoor, M.S.; Yousefpoor, E.; Ahmed, O.H.; Rahmani, A.M.; Mehmood, A. A Novel Q-Learning-Based Routing Scheme Using an Intelligent Filtering Algorithm for Flying Ad Hoc Networks (FANETs). J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101817. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Yousefpoor, M.S.; Yousefpoor, E.; Lansky, J.; Min, H. A New Version of the Greedy Perimeter Stateless Routing Scheme in Flying Ad Hoc Networks. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102066. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Simulator | ns-3.31, MATLAB |
| Packet Size | 512 bytes |
| Simulation Time | 150 s |
| Simulation Area | |
| Speed Range | 10–30 m/s |
| Communication Range | 250 m |
| Bandwidth | 10 MHz |
| Number of Nodes | 30, 40, 50, 60, 70, 80, 90, 100 |
| Traffic Type | CBR |
| CBR Rate | 2 Mbps |
| Number of CBR Connections | 10, 20, 30, 40, 50 |
| HELLO interval | 1 s |
| Frequency of trajectory updates | 5 Hz |
| MAC Protocol | IEEE 802.11p |
| Transport Protocol | UDP |
| Initial Energy | 900–1000 J |
| Energy Threshold | 100 J |
| Propagation Model | Nakagami Model |
| Mobility Model | Gauss–Markov Mobility Model |
| Number of Nodes | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|
| Traj-Q-GPSR | 27.1 | 53.3 | 112.5 | 172.3 | 232.8 | 290.1 | 345.5 | 374.7 |
| GPSR | 48.9 | 83.7 | 153.2 | 199.8 | 266.6 | 332.1 | 420.3 | 453.7 |
| Field Name | Size (Bytes) |
|---|---|
| Packet Type | 1 |
| Number of Neighbors | 2 |
| Node ID | 2 |
| Current Coordinates () | 24 |
| Current Queue Length | 1 |
| Current Energy Level | 2 |
| Field Name | Size (Bytes) |
|---|---|
| Packet Type | 1 |
| Perimeter Mode Flag | 1 |
| Node ID | 2 |
| Destination Coordinates | 24 |
| Update Timestamp | 4 |
| Perimeter Entry Coordinates | 24 |
| Previous Hop Coordinates | 24 |
| Future Trajectory (5 × ) | 120 |
| Number of Nodes | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|
| Traj-Q-GPSR | 1.43% | 1.33% | 1.17% | 1.06% | 1.01% | 0.98% | 0.96% | 0.93% |
| GPSR | 0.86% | 0.82% | 0.78% | 0.71% | 0.67% | 0.65% | 0.63% | 0.61% |
| Number of Nodes | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|
| Traj-Q-GPSR | 4.08 | 6.65 | 9.81 | 13.57 | 17.93 | 22.87 | 28.42 | 34.56 |
| GPSR | 1.58 | 2.13 | 2.67 | 3.22 | 3.76 | 4.31 | 4.85 | 5.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Jiang, B.; Chen, S.; Xu, H.; Pang, T.; Gao, M.; Xia, F. Traj-Q-GPSR: A Trajectory-Informed and Q-Learning Enhanced GPSR Protocol for Mission-Oriented FANETs. Drones 2025, 9, 489. https://doi.org/10.3390/drones9070489
Wu M, Jiang B, Chen S, Xu H, Pang T, Gao M, Xia F. Traj-Q-GPSR: A Trajectory-Informed and Q-Learning Enhanced GPSR Protocol for Mission-Oriented FANETs. Drones. 2025; 9(7):489. https://doi.org/10.3390/drones9070489
Chicago/Turabian StyleWu, Mingwei, Bo Jiang, Siji Chen, Hong Xu, Tao Pang, Mingke Gao, and Fei Xia. 2025. "Traj-Q-GPSR: A Trajectory-Informed and Q-Learning Enhanced GPSR Protocol for Mission-Oriented FANETs" Drones 9, no. 7: 489. https://doi.org/10.3390/drones9070489
APA StyleWu, M., Jiang, B., Chen, S., Xu, H., Pang, T., Gao, M., & Xia, F. (2025). Traj-Q-GPSR: A Trajectory-Informed and Q-Learning Enhanced GPSR Protocol for Mission-Oriented FANETs. Drones, 9(7), 489. https://doi.org/10.3390/drones9070489






