A Novel Neural Network-Based Adaptive Formation Control for Cooperative Transportation of an Underwater Payload Using a Fleet of UUVs
Abstract
1. Introduction
- As far as we know, this study is the first to study cable-based collaborative underwater load transport. We fully consider the influence of ocean currents on collaborative transport and propose a formation controller based on adaptive control and neural networks. The results demonstrate that the control system is robust against uncertain system parameters, and the adaptive scheme can asymptotically obtain the ideal shape.
- Unlike the paper [34], where their controllers are designed using second-order nonlinear systems, a novel nonlinear adaptive controller is developed for Euler-Lagrange model based UUV systems. We will demonstrate that this controller significantly enhances the system’s ability to withstand external disturbances, thereby boosting its robustness.
- This paper proposes a reconfigurable formation motion planning mechanism for the cooperative transport of underwater payloads with multiple UUVs. The mechanism is efficient in trajectory planning, offering a smooth, continuous path that effectively sidestepping the common pitfall of getting trapped in local optima. It can manage diverse obstacle avoidance scenarios while ensuring the initial formation remains intact.
2. Preliminaries
2.1. Nomenclature
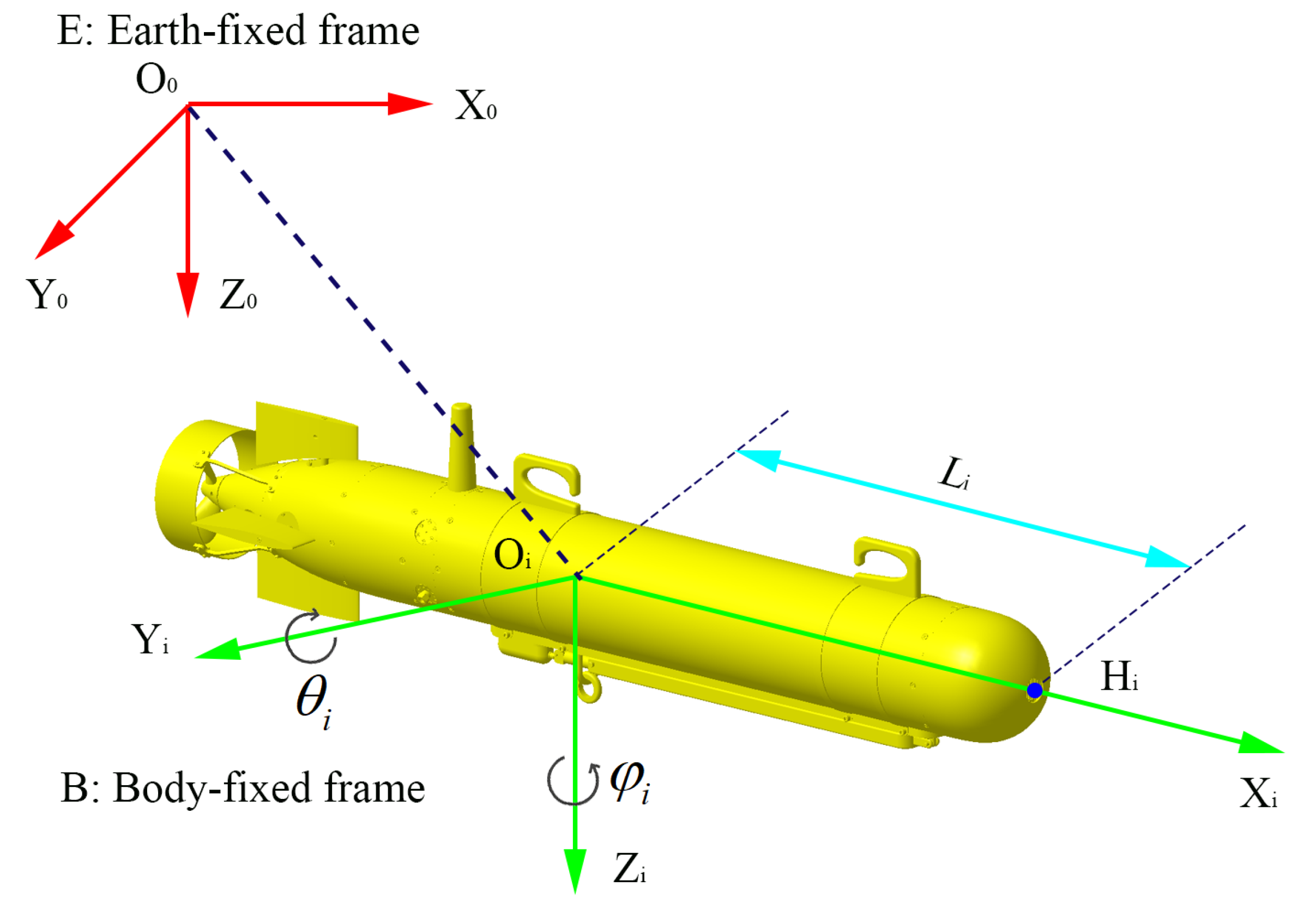
2.2. Modeling the UUV Kinematics
2.3. Graph Theory
2.4. Neural Network
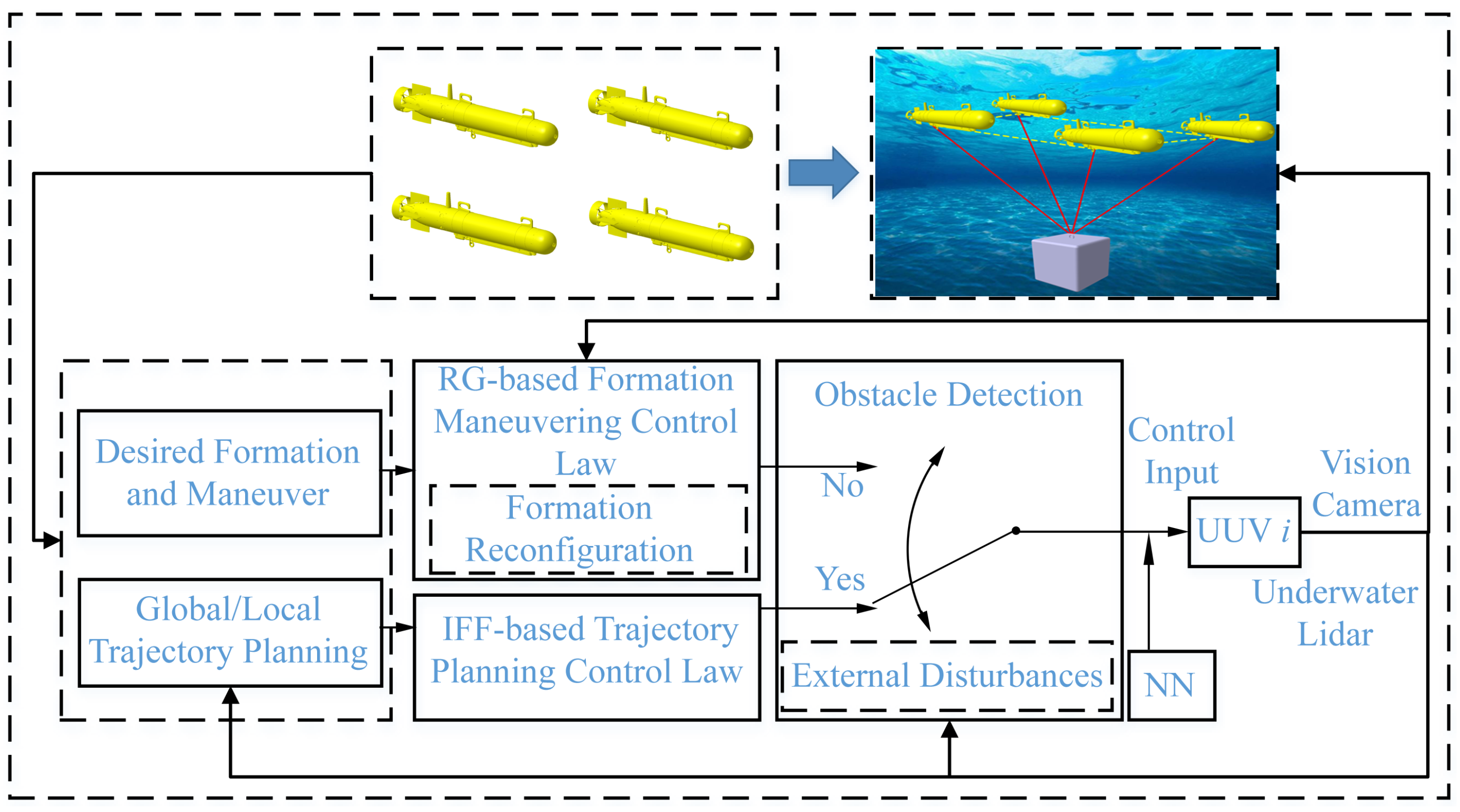
3. Motion Planning Design
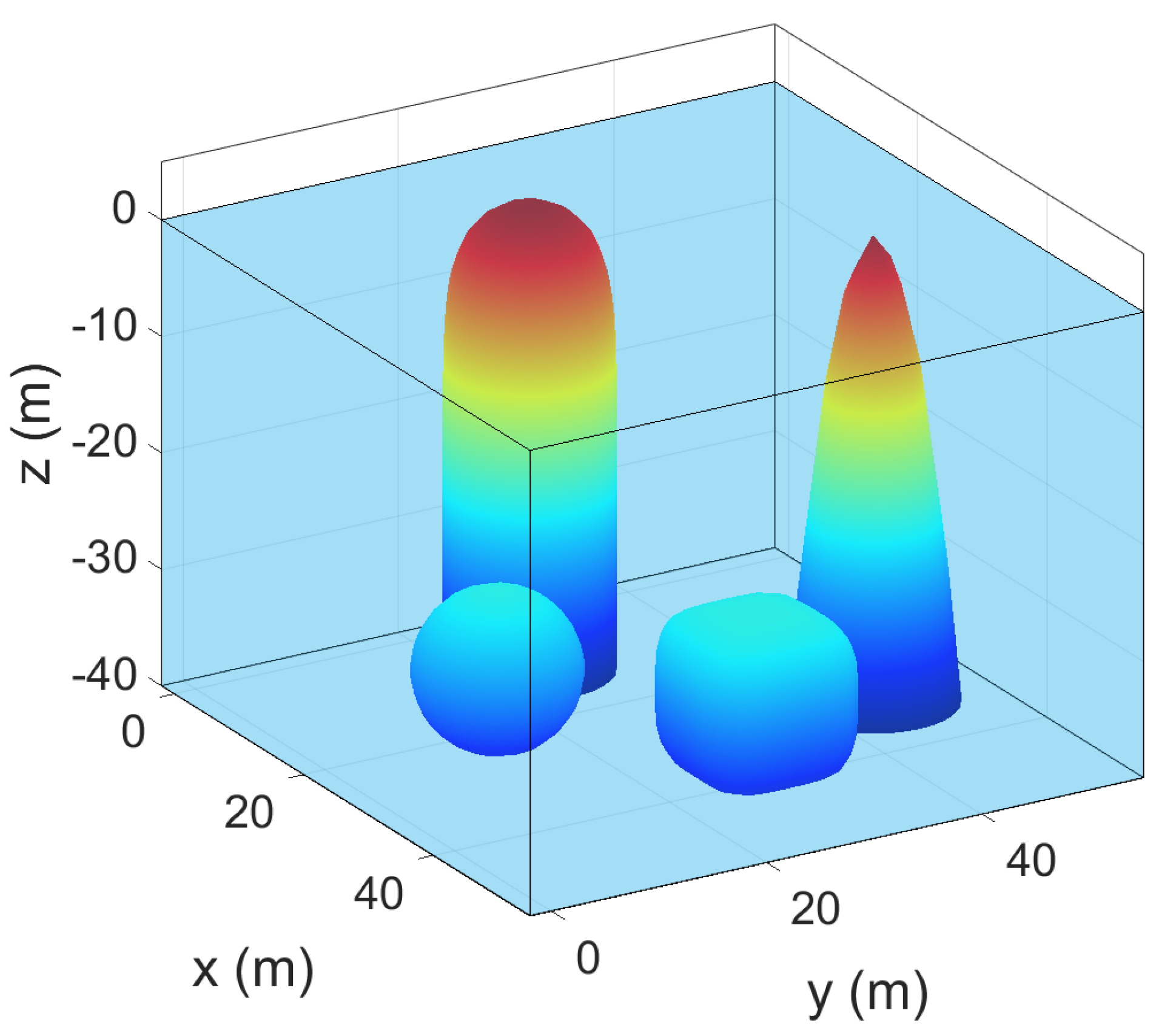
3.1. Modeling the Environment
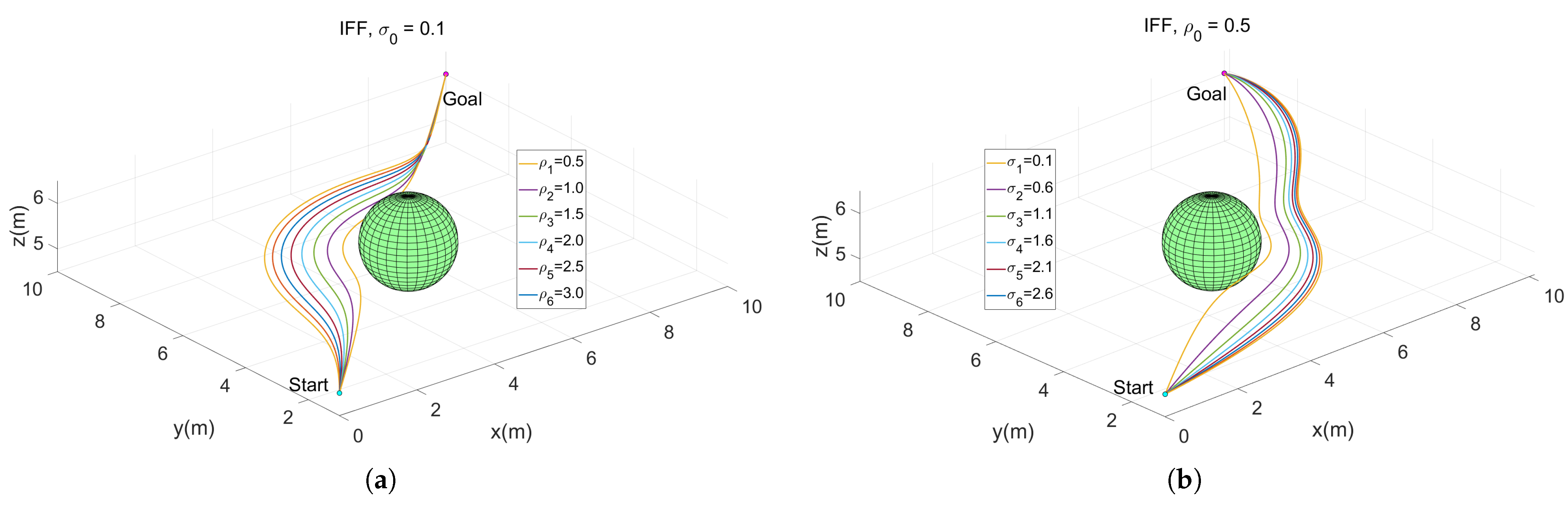
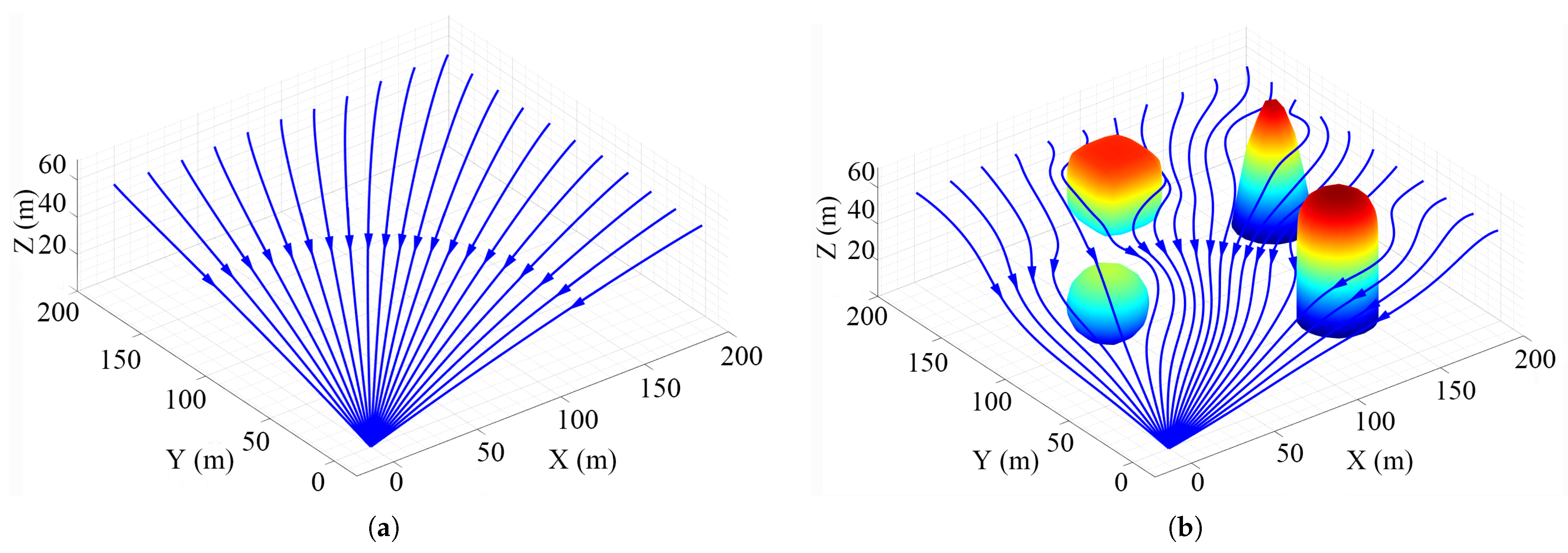
3.2. Formation Motion Planning
| Algorithm 1 Multi-AUU formation cooperative transportation motion planning based on IFF |
|
4. Formation Control Design
4.1. Formation Control Design
4.2. Stability Analysis
| Algorithm 2 Multi-UUV formation maintenance and formation maneuver using rigid graph based algorithm |
|
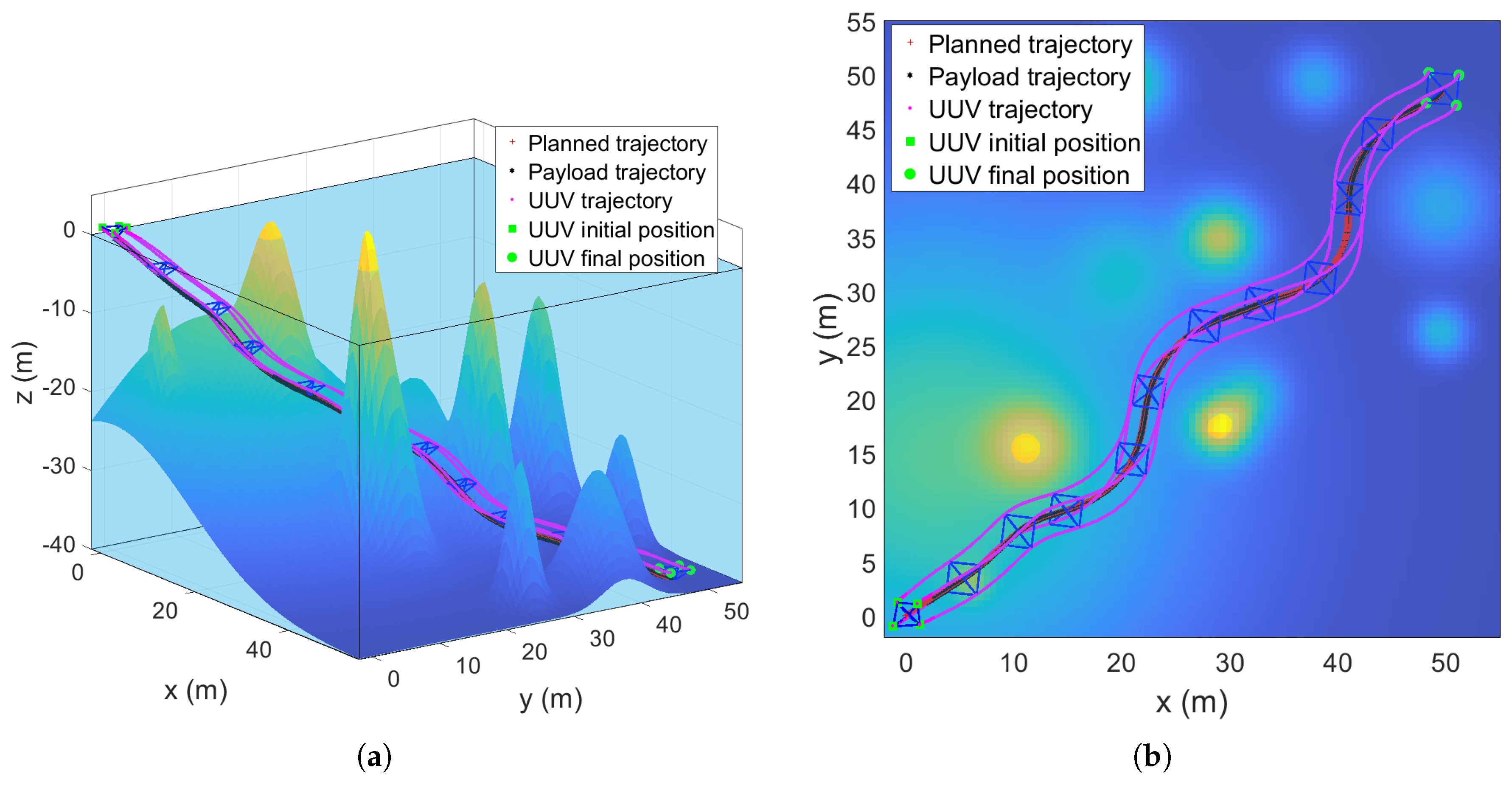
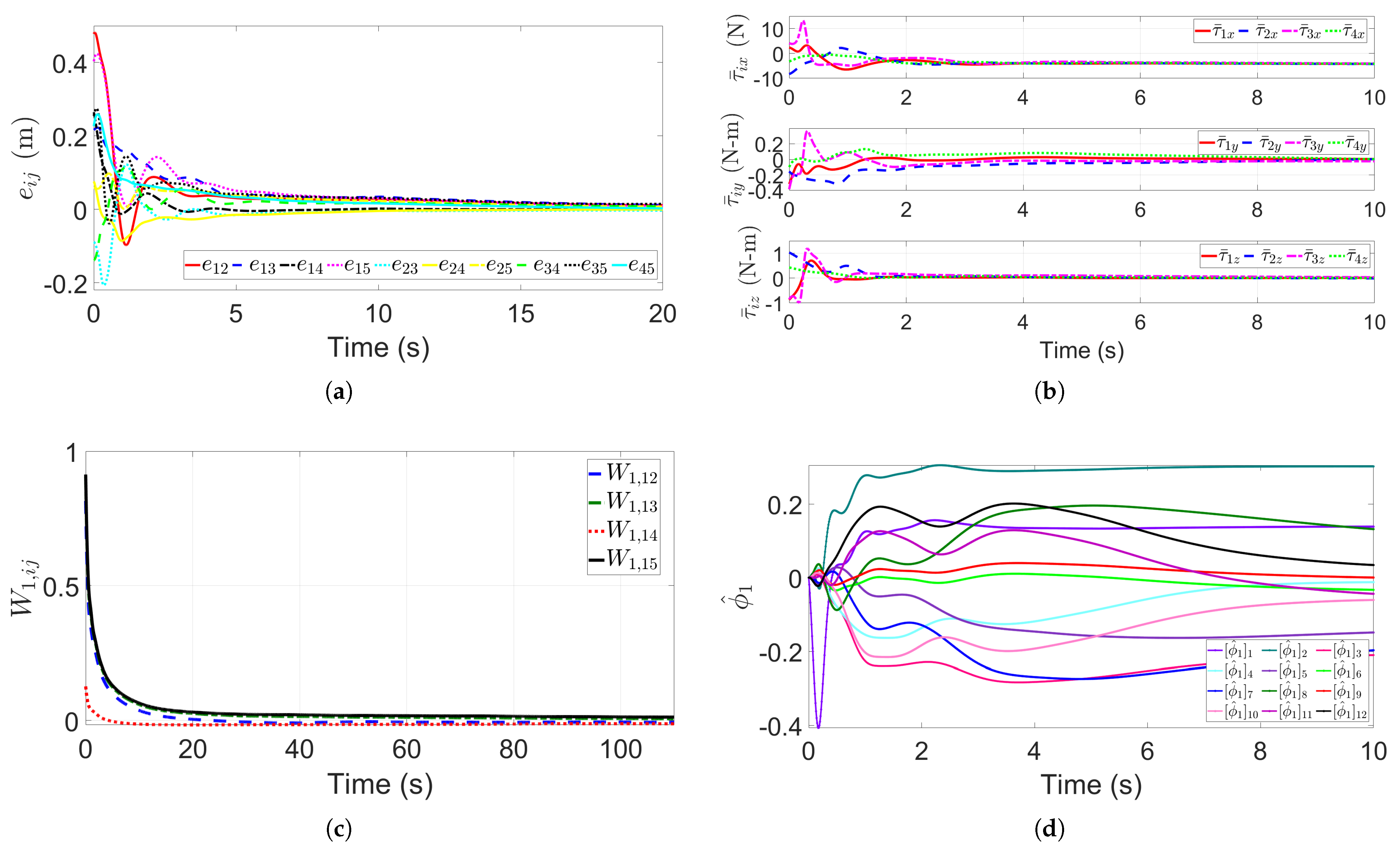
5. Simulation Results Analysis
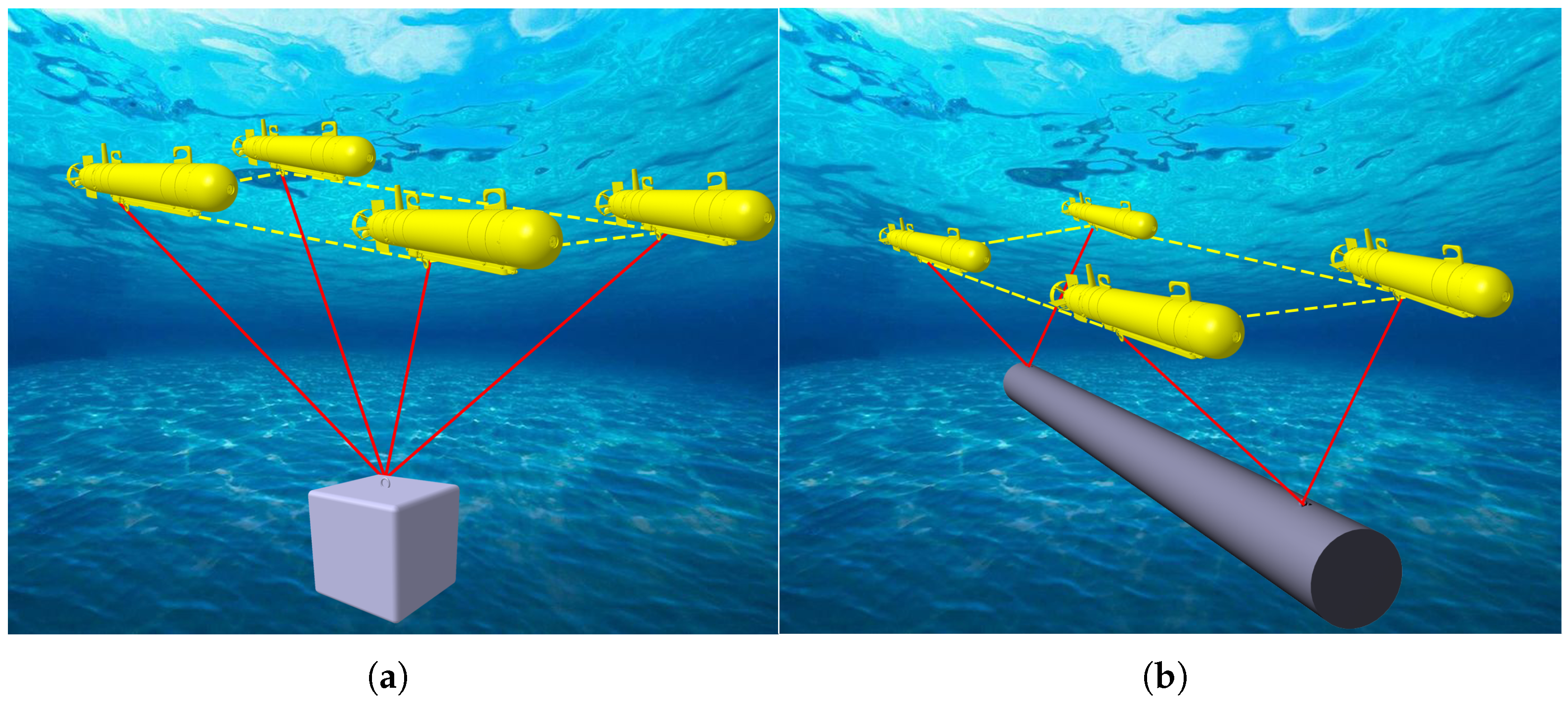
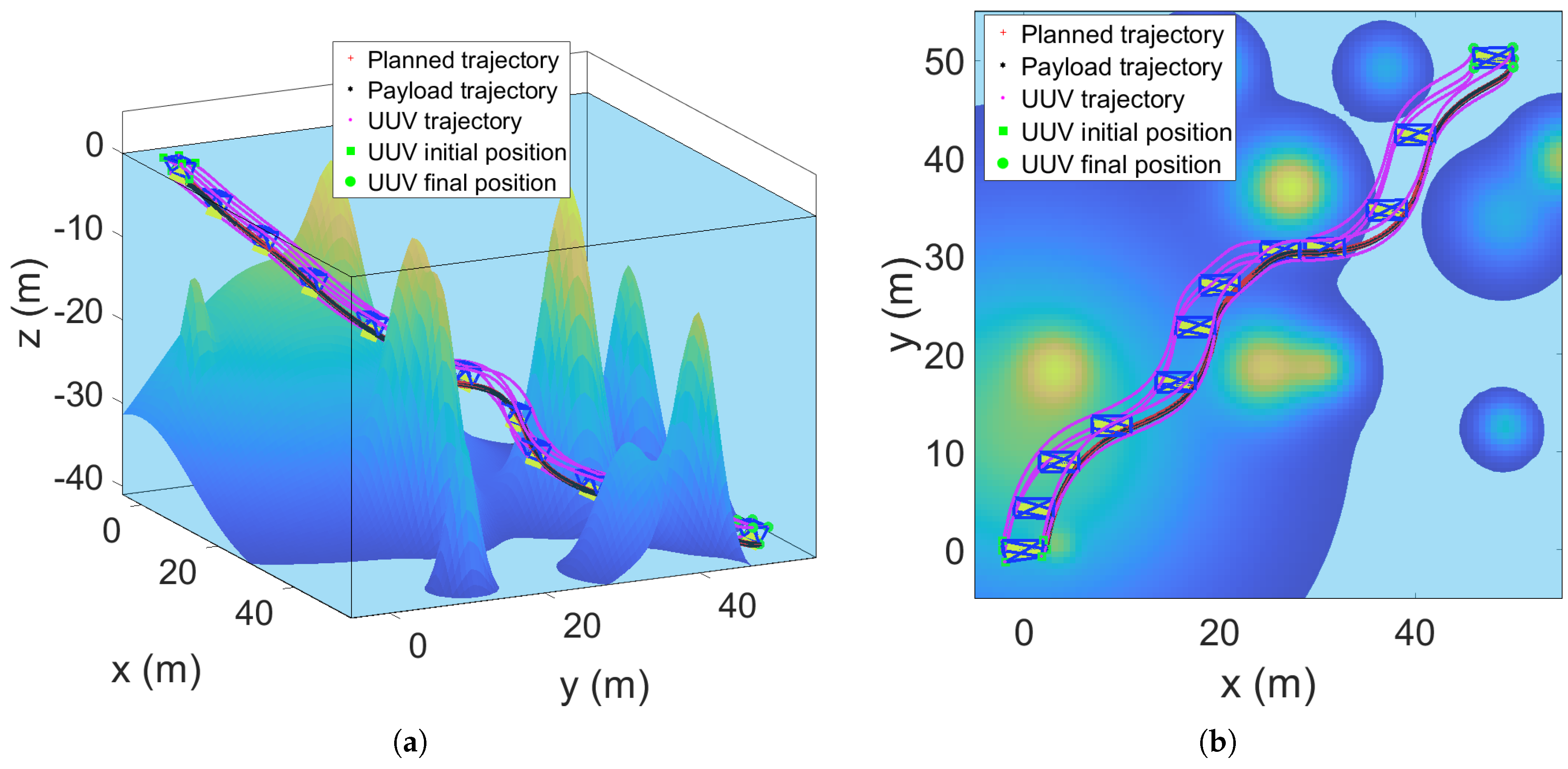
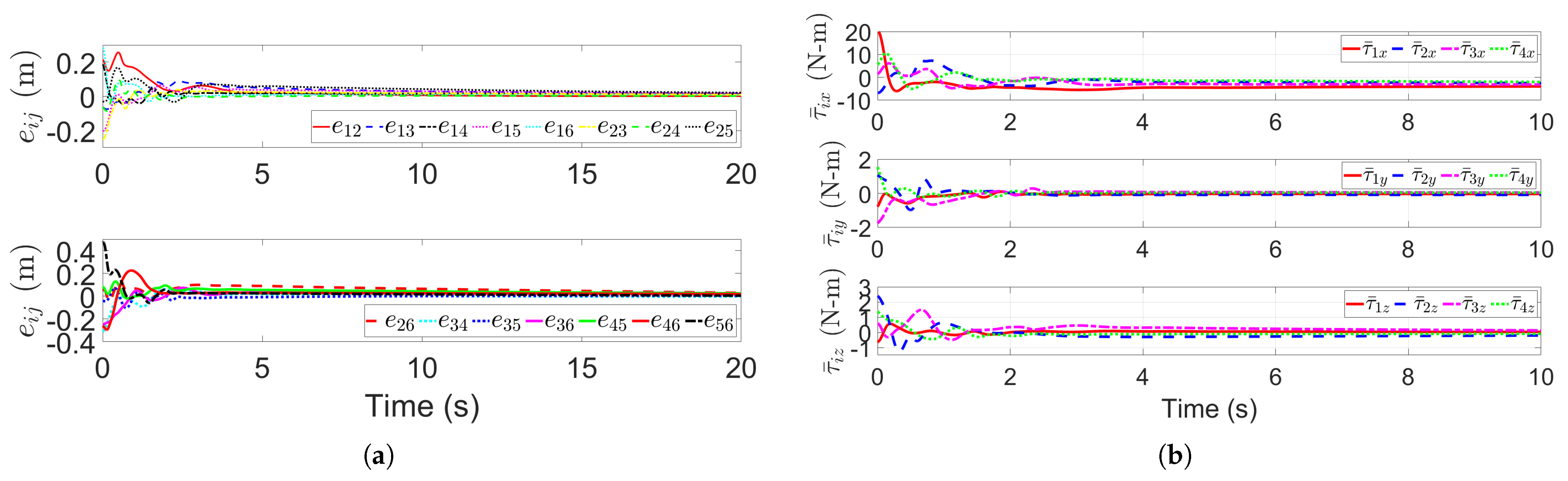
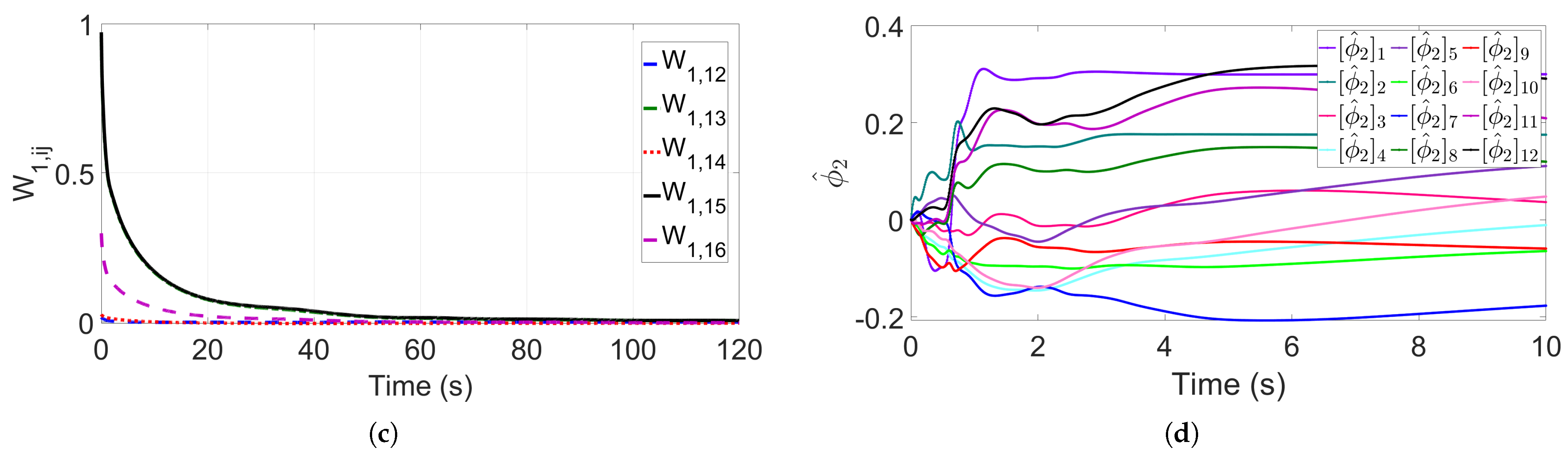
5.1. Multi-UUV Single Lifting Point Formation Transportation of a Payload
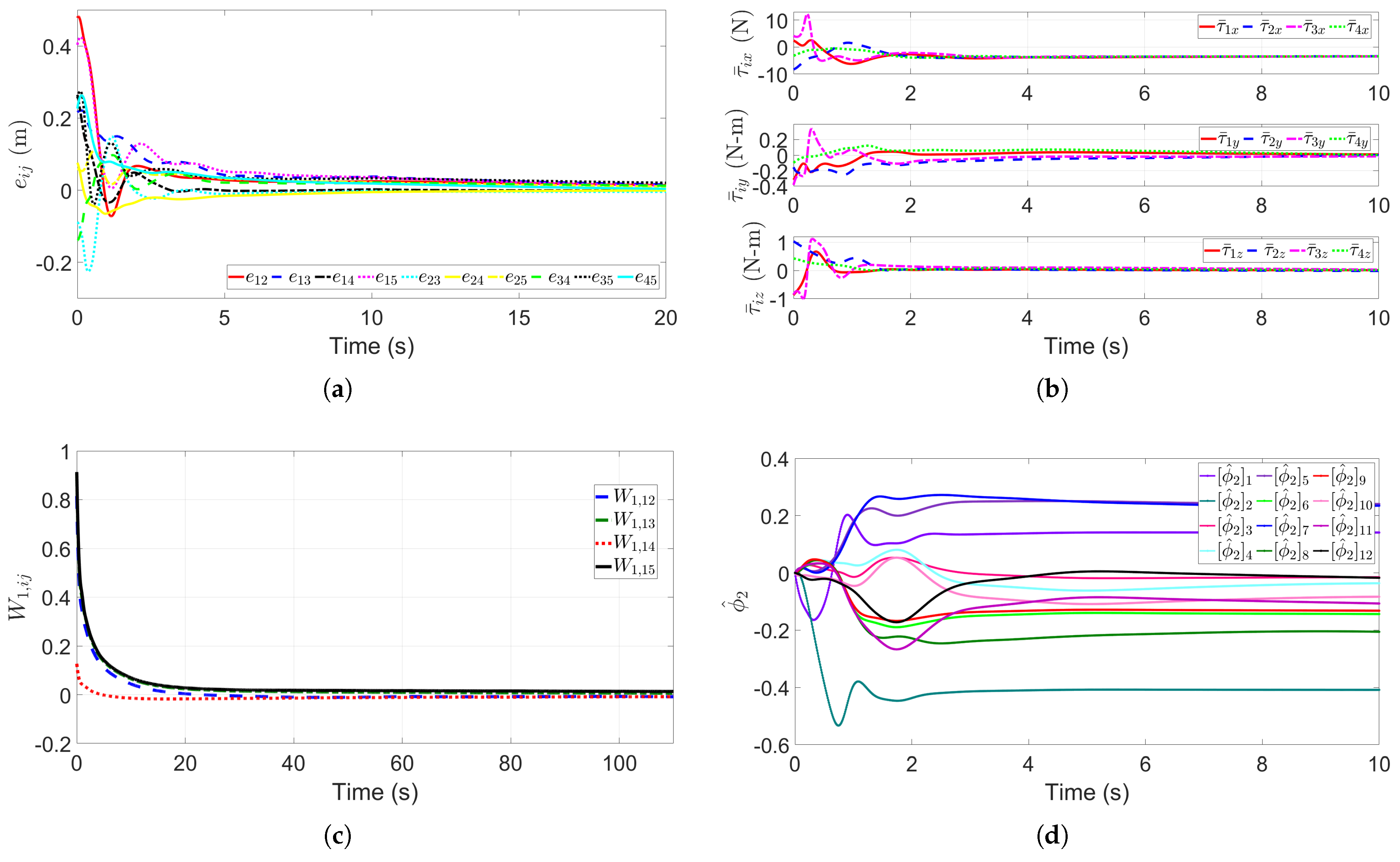
5.2. Multi-UUV Double Lifting Point Formation Transportation of a Payload
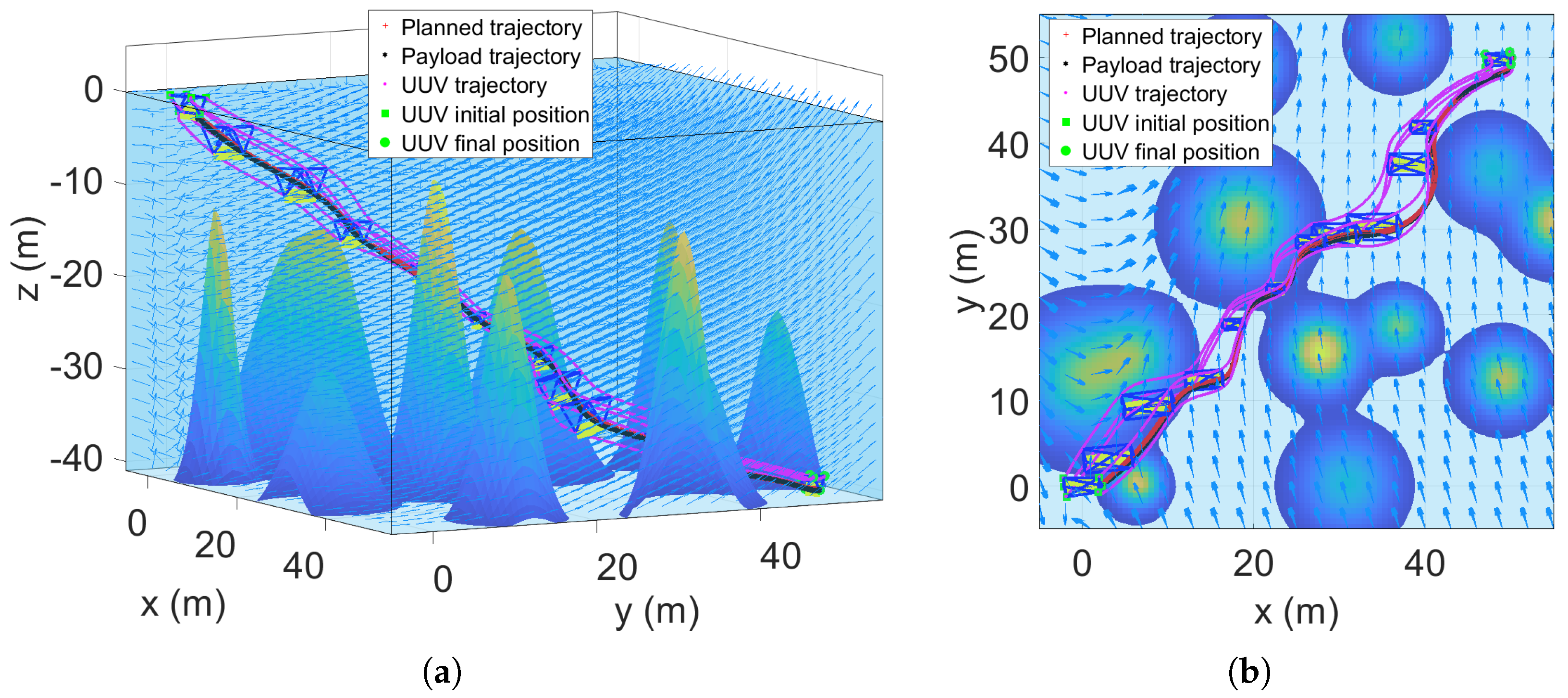
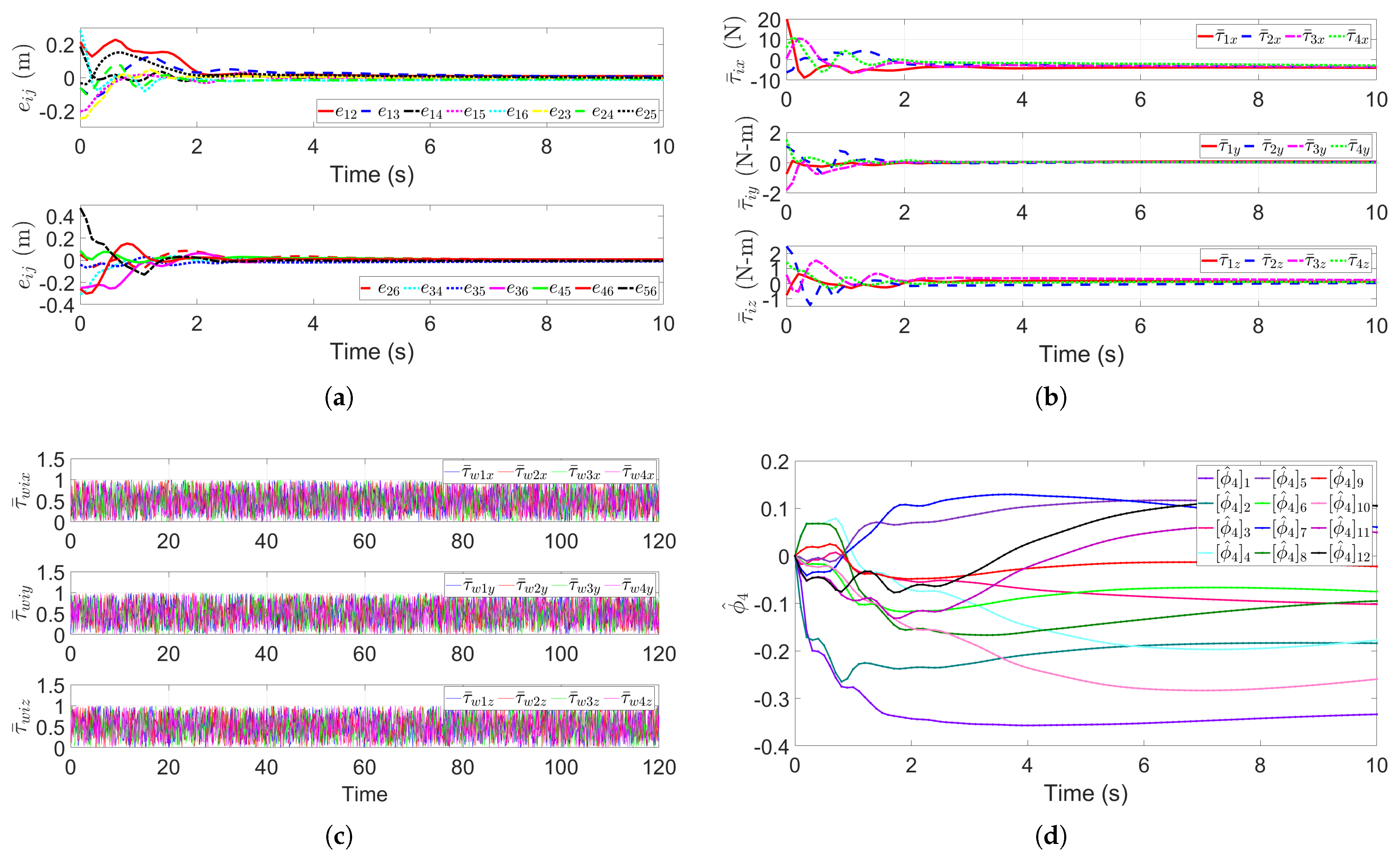
5.3. Multi-UUV Double Lifting Point Formation Transportation of a Payload in Dense Obstacle Environment Under External Disturbance
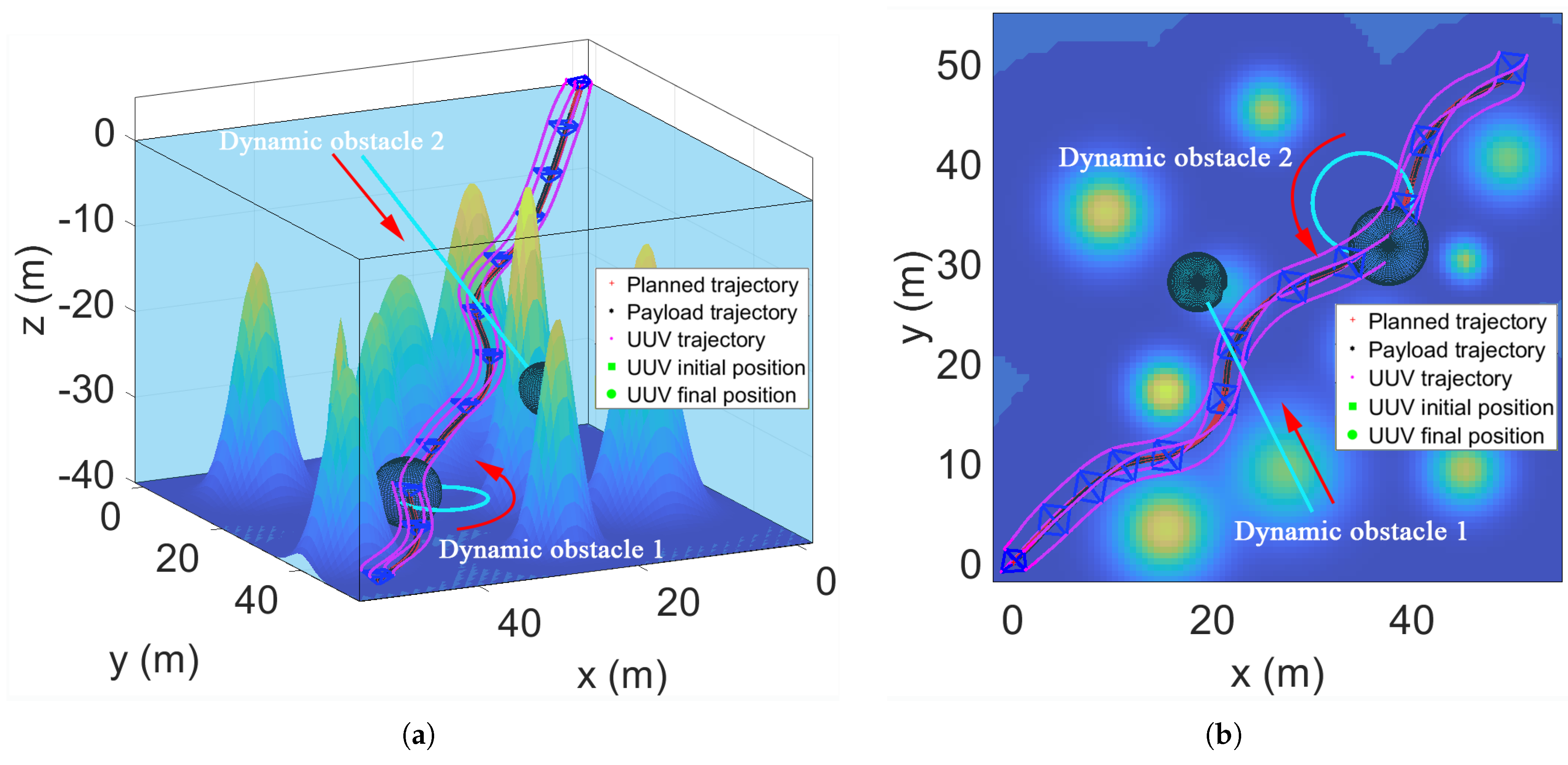
5.4. Multi-UUV Single Lifting Point Formation Transportation of a Payload in Dynamic Obstacle Environment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petillot, Y.R.; Antonelli, G.; Casalino, G.; Ferreira, F. Underwater Robots: From Remotely Operated Vehicles to Intervention-Autonomous Underwater Vehicles. IEEE Robot. Autom. Mag. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, D.; Pang, W.; Chen, Q. An Effective Strategy for Distributed Unmanned Underwater Vehicles to Encircle and Capture Intelligent Targets. IEEE Trans. Ind. Electron. 2024, 71, 12570–12580. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Lewis, F.L. Robust distributed formation controller design for a group of unmanned underwater vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1215–1223. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- He, L.; Xie, M.; Zhang, Y. A Review of Path Following, Trajectory Tracking, and Formation Control for Autonomous Underwater Vehicles. Drones 2025, 9, 286. [Google Scholar] [CrossRef]
- Wang, H.; Su, B. Event-triggered formation control of AUVs with fixed-time RBF disturbance observer. Appl. Ocean Res. 2021, 112, 102638. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, X.; Yang, X.; Chen, C.; Guan, X. Potential-Game-Driven Formation Control of AUVs: An Inverse-Reinforcement-Learning-Based Solution. IEEE J. Ocean. Eng. 2025, 50, 1165–1183. [Google Scholar] [CrossRef]
- Wang, M.; Pang, S.; Jin, K.; Liang, X.; Wang, H.; Yi, H. Construction and experimental verification research of a magnetic detection system for submarine pipelines based on a two-part towed platform. J. Ocean Eng. Sci. 2023, 8, 169–180. [Google Scholar] [CrossRef]
- Yu, H.; Ma, Y. A cooperative mission planning method considering environmental factors for UUV swarm to search multiple underwater targets. Ocean Eng. 2024, 308, 118228. [Google Scholar] [CrossRef]
- Li, J.; Bian, X.; Huang, H.; Jiang, T.; Liu, Y.; Wan, L. Hybrid visual servoing control for underwater vehicle manipulator systems with multiple cameras. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1742–1754. [Google Scholar] [CrossRef]
- Simetti, E.; Casalino, G. Manipulation and transportation with cooperative underwater vehicle manipulator systems. IEEE J. Ocean. Eng. 2017, 42, 782–799. [Google Scholar] [CrossRef]
- Jin, X.; Hu, Z. Adaptive cooperative load transportation by a team of quadrotors with multiple constraint requirements. IEEE Trans. Intell. Transp. Syst. 2023, 24, 801–814. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, F.; Huang, P. Formation planning for tethered multirotor UAV cooperative transportation with unknown payload and cable length. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3449–3460. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Bechlioulis, C.P.; Karras, G.C.; Kyriakopoulos, K.J. Cooperative impedance control for multiple underwater vehicle manipulator systems under lean communication. IEEE J. Ocean. Eng. 2021, 46, 447–465. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Karras, G.C.; Kyriakopoulos, K.J. A predictive control approach for cooperative transportation by multiple underwater vehicle manipulator systems. IEEE Trans. Control Syst. Technol. 2022, 30, 917–930. [Google Scholar] [CrossRef]
- De Oliveira, É.L.; Orsino, R.M.M.; Donha, D.C. Modular modeling and coordination control scheme for an underwater cooperative transportation performed by two I-AUVs. Control Eng. Pract. 2022, 125, 105198. [Google Scholar] [CrossRef]
- Conti, R.; Meli, E.; Ridolfi, A.; Allotta, B. An innovative decentralized strategy for I-AUVs cooperative manipulation tasks. Robot. Auton. Syst. 2015, 72, 261–276. [Google Scholar] [CrossRef]
- Pi, R.; Cieślak, P.; Ridao, P.; Sanz, P.J. Twinbot: Autonomous underwater cooperative transportation. IEEE Access 2021, 9, 37668–37684. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, L.; Yu, J.; Tan, M. Coordinated transport by multiple biomimetic robotic fish in underwater environment. IEEE Trans. Control Syst. Technol. 2007, 15, 658–671. [Google Scholar] [CrossRef]
- Shao, J.; Wang, L.; Yu, J. Development of an artificial fish-like robot and its application in cooperative transportation. Control Eng. Pract. 2008, 16, 569–584. [Google Scholar] [CrossRef]
- Bacelar, T.; Madeiras, J.; Melicio, R.; Cardeira, C.; Oliveira, P. On-board implementation and experimental validation of collaborative transportation of loads with multiple UAVs. Aerosp. Sci. Technol. 2020, 107, 106284. [Google Scholar] [CrossRef]
- Zhao, W.; Xia, Y.; Zhai, D.H.; Sun, Z.; Zhang, Y. Event-Triggered Formation Control of Unknown Autonomous Underwater Vehicles Subject to Arbitrarily Large Time-Varying Communication Delays. IEEE Trans. Veh. Technol. 2025, 74, 3901–3912. [Google Scholar] [CrossRef]
- Yao, M.; Yu, L.; Guo, K.; Lu, Y.; Zhang, W.; Qiao, L. Distributed Two-Layered Leader–Follower Affine Formation Control for Multiple AUVs in 3-D Space. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 85–95. [Google Scholar] [CrossRef]
- Yan, J.; Wu, C.; Yang, X.; Chen, C.; Guan, X. Minimum Time Formation Control of AUVs with Smooth Transition in Communication Topology. IEEE Robot. Autom. Lett. 2024, 9, 8698–8705. [Google Scholar] [CrossRef]
- Hadi, B.; Khosravi, A.; Sarhadi, P. Adaptive formation motion planning and control of autonomous underwater vehicles using deep reinforcement learning. IEEE J. Ocean. Eng. 2024, 49, 311–328. [Google Scholar] [CrossRef]
- Shojaei, K. Neural adaptive PID formation control of car-like mobile robots without velocity measurements. Adv. Robot. 2017, 31, 947–964. [Google Scholar] [CrossRef]
- Rani, M.; Kumar, N. A neural network based efficient leader–follower formation control approach for multiple autonomous underwater vehicles. Eng. Appl. Artif. Intell. 2023, 122, 106102. [Google Scholar] [CrossRef]
- Wang, H.; Lyu, W.; Yao, P.; Liang, X.; Liu, C. Three-dimensional path planning for unmanned aerial vehicle based on interfered fluid dynamical system. Chin. J. Aeronaut. 2015, 28, 229–239. [Google Scholar] [CrossRef]
- Celestini, D.; Primatesta, S.; Capello, E. Trajectory planning for UAVs based on interfered fluid dynamical system and Bézier curves. IEEE Robot. Autom. Lett. 2022, 7, 9620–9626. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N.; Su, Z. Formation obstacle avoidance: A fluid-based solution. IEEE Syst. J. 2019, 14, 1479–1490. [Google Scholar] [CrossRef]
- Niu, Y.; Yan, X.; Wang, Y.; Niu, Y. 3D real-time dynamic path planning for UAV based on improved interfered fluid dynamical system and artificial neural network. Adv. Eng. Inform. 2024, 59, 102306. [Google Scholar] [CrossRef]
- Tamanakijprasart, K.; Mondal, S.; Tsourdos, A. Dynamic path planning of UAV in three-dimensional complex environment based on interfered fluid dynamical system. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Chen, C. Adaptive formation control of networked robotic systems with bearing-only measurements. IEEE Trans. Cybern. 2021, 51, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Aryankia, K.; Selmic, R.R. Neural network-based formation control with target tracking for second-order nonlinear multiagent systems. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 328–341. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles: Design for Underactuated and Nonlinear Marine Systems; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Paliotta, C.; Lefeber, E.; Pettersen, K.Y.; Pinto, J.; Costa, M. Trajectory tracking and path following for underactuated marine vehicles. IEEE Trans. Control Syst. Technol. 2018, 27, 1423–1437. [Google Scholar] [CrossRef]
- Pang, W.; Zhu, D.; Chu, Z.; Chen, Q. Distributed adaptive formation reconfiguration control for multiple AUVs based on affine transformation in three-dimensional ocean environments. IEEE Trans. Veh. Technol. 2023, 72, 7338–7350. [Google Scholar] [CrossRef]
- Anderson, B.D.; Yu, C.; Fidan, B.; Hendrickx, J.M. Rigid graph control architectures for autonomous formations. IEEE Control Syst. Mag. 2008, 28, 48–63. [Google Scholar]
- Pang, W.; Zhu, D.; Sun, C. Multi-AUV Formation Reconfiguration Obstacle Avoidance Algorithm Based on Affine Transformation and Improved Artificial Potential Field Under Ocean Currents Disturbance. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1469–1487. [Google Scholar] [CrossRef]
- Lewis, F.L.; Jagannathan, S.; Yeşildirek, A. Neural network control of robot arms and nonlinear systems. In Neural Systems for Control; Academic Press: Cambridge, MA, USA, 1997; pp. 161–211. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]

| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| n-dimensional Euclidean space | Alternative error variable | ||
| real matrix space | , , | Lyapunov function | |
| n-dimensional identity matrix | Alternative error variable | ||
| 1-column vector | Introduced velocity variable | ||
| Undirected graph | Intended navigation speed of UUV | ||
| Set of vertices | Position of planned waypoint | ||
| Set of edges | Position of obstacle | ||
| The adjacency matrix | Position of goal | ||
| Formation framework | The maneuvering velocity of the flow | ||
| Neighbor set of the UUV i | Obstacle function | ||
| n | Number of UUVs | Initial navigation speed of | |
| Inertia matrix | Interfering modulation matrix of kth obstacle | ||
| Dentripetal/Coriolis terms matrix | Total interfering modulation matrix | ||
| Damping matrix | Weighting coefficient of kth obstacle | ||
| Position of UUV i | Radial normal vector of kth obstacle | ||
| , | Heading angle of UUV i | Tangent vector of kth obstacle | |
| Conversion matrix | Influence radius of the obstacle of kth obstacle | ||
| Linear velocity of UUV i | Tangential reaction coefficient of kth obstacle | ||
| Control input of UUV i | K | Number of obstacles | |
| Regression matrix | Total disturbance flow velocity | ||
| Model parameter | Velocity vector of kth dynamic obstacle | ||
| Parameter estimation of | , , | Parameters of formation controller | |
| Parameter estimation error | , | NN weights | |
| External disturbance | NN activation function | ||
| Rigidity matrix | L | Hidden neurons | |
| Desired distance between two UUV i and j | Diagonal matrix | ||
| Distance between two UUV i and j | Transposition of the matrix A | ||
| Distance error | ⊗ | Kronecker product | |
| Safe distance | 2-norm of a vector |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, W.; Zhu, D.; Chen, M.; Xu, W.; Wang, B. A Novel Neural Network-Based Adaptive Formation Control for Cooperative Transportation of an Underwater Payload Using a Fleet of UUVs. Drones 2025, 9, 465. https://doi.org/10.3390/drones9070465
Pang W, Zhu D, Chen M, Xu W, Wang B. A Novel Neural Network-Based Adaptive Formation Control for Cooperative Transportation of an Underwater Payload Using a Fleet of UUVs. Drones. 2025; 9(7):465. https://doi.org/10.3390/drones9070465
Chicago/Turabian StylePang, Wen, Daqi Zhu, Mingzhi Chen, Wentao Xu, and Bin Wang. 2025. "A Novel Neural Network-Based Adaptive Formation Control for Cooperative Transportation of an Underwater Payload Using a Fleet of UUVs" Drones 9, no. 7: 465. https://doi.org/10.3390/drones9070465
APA StylePang, W., Zhu, D., Chen, M., Xu, W., & Wang, B. (2025). A Novel Neural Network-Based Adaptive Formation Control for Cooperative Transportation of an Underwater Payload Using a Fleet of UUVs. Drones, 9(7), 465. https://doi.org/10.3390/drones9070465









