Cooperative Drone and Water Supply Truck Scheduling for Wildfire Fighting Using Deep Reinforcement Learning

Abstract

Wildfires often spread rapidly and cause significant casualties and economic losses. Firefighting drones carrying water capsules provide an efficient way for wildfire extinguishing, but their operational capabilities are limited by their payloads. This weakness can be compensated by using ground vehicles to provide mobile water supply. To this end, this paper presents an optimization problem of scheduling multiple drones and water supply trucks for wildfire fighting, which allocates burning subareas to drones, routes drones to perform fire-extinguishing operations in burning subareas and reload water between every two consecutive operations, and routes trucks to provide timely water supply for drones. To solve the problem within the limited emergency response time, we propose a deep reinforcement learning method, which consists of an encoder for embedding the input instance features and a decoder for generating a solution by iteratively predicting the subarea selection decision through attention. Computational results on test instances constructed upon real-world wilderness areas demonstrate the performance advantages of the proposed method over a collection of heuristic and metaheuristic optimization methods.

1. Introduction

Wildfires, such as forest fires and mountain fires, often spread rapidly and cause significant casualties and economic losses. Due to their high speed, flexibility, and accessibility, drones (unmanned aerial vehicles) have been increasingly used in firefighting operations in recent years [1,2,3]. Firefighting drones are typically high-payload drones, which can carry and disperse water or fire-extinguishing compounds to suppress fire in quite an efficient way. There are two common forms of firefighting drones. In the first form, a drone carries a hose that is connected to a ground facility, such that powerful water flow can be directly drawn from the ground water source for firefighting. However, the hose length and the water pressure strictly limit the operational range. In the second form, a drone carries a water capsule or fire-extinguishing bomb(s), which can be considerably more flexible than the first form. Nevertheless, the volume of water or fire-extinguishing compounds a drone can carry at a time is limited, and the drone often needs to fly back and forth between fire spots and water sources.

This study focuses on the second form, where firefighting drones carry water capsules to the fire site for fire-extinguishing. To compensate for its weakness, our approach considers using ground vehicles (water supply trucks) to provide mobile water supply for drones, such that the time consumed on water reloading can be significantly shortened and the efficiency of firefighting can be significantly improved. In this scenario, however, the cooperative scheduling of drones and water supply trucks, which needs to determine drone paths, truck paths, as well as docking locations where drones reload water from trucks, can be a challenging problem.

In this paper, we formulate an optimization problem of scheduling multiple drones and water supply trucks for firefighting in a wilderness area consisting of a subset of ignitable subareas and a subset of water resource subareas, where the fire dynamics is characterized using the wildfire spread model established in our previous work [4]. Each burning subarea will be allocated to a batch of drones for fire-extinguishing, and each drone will select either a truck or a water resource subarea to reload water between every two consecutive burning subareas in its operational sequence, as illustrated in Figure 1. The problem objective is to minimize the completion time of the operation, i.e., the time at which the fire is completely extinguished. To solve the problem within the limited emergency response time, we propose a deep reinforcement learning (DRL) network, which consists of an encoder for embedding the input instance features and a decoder for generating a solution by iteratively predicting the subarea selection decision through attention. We conduct extensive computational experiments on test instances constructed upon three wilderness areas in Zhejiang Province, China, and the results demonstrate the performance advantages of the proposed method over a collection of heuristic and metaheuristic optimization methods. The main contributions of this paper can be summarized as follows:

• We present an optimization problem of cooperatively scheduling drones and water supply trucks for wildfire fighting, which is increasingly popular but has been rarely studied in the literature.
• To meet the emergency response requirement, we propose a DRL method, which encodes a roadway network, airway network, environmental features, water supply information, and drone and truck features into high-level embeddings, which are then iteratively decoded to generate sequential decisions for the problem.
• We demonstrate the performance advantages of the proposed method compared to the state-of-the-art heuristic and metaheuristic optimization methods.

In the remainder of this paper, we review the related work in Section 2, formulate the cooperative drone–truck scheduling problem for wildfire fighting in Section 3, and propose the DRL method in Section 4; Section 5 presents the experimental results, and finally Section 6 concludes with discussions.

2. Related Work

Cooperative scheduling of drones and water supply trucks for firefighting, as to our knowledge, has not been reported in the literature. Here, we discuss related work in two aspects: (1) drone scheduling for firefighting; (2) cooperative drone–truck scheduling for other tasks (mainly delivery tasks).

2.1. Drone Scheduling for Firefighting

Early applications of drones in fire management mainly focused on sensing and monitoring tasks [1,5,6]. An early work of Kumar et al. [7] considered fire monitoring and fighting tasks performed by drones based on optimization of respective utility functions; however, they made an assumption that a drone can take unlimited fire suppressing fluid, which never holds in realistic situations. Only in recent years, with the increase in their payloads, drones have been directly used in fire extinguishing tasks. Ghamry et al. [8] developed a particle swarm optimization (PSO) algorithm for assigning drones to fire spots according to their relative distances and then planning each drone path to minimize the travel distance. However, the separation of two sub-problems might miss the optimal solution to the complete problem. Ausonio et al. [9] proposed a forest firefighting system that used a swarm of drones to generate a continuous flow of extinguishing liquid on the fire front, which was supported by battery replacement and extinguishing liquid refill. Yu et al. [10] used a scheduling algorithm to group drones for wildfire extinguishing, which was test on cases in New South Wales and East Victoria in Australia. Chen et al. [11] proposed a collaborative multi-drone scheduling framework for integrated sensing and operation in large-scale wildfires, which contained a spatio-temporal confidence-aware assessment model for pinpoint location and a priority graph-instructed scalable scheduler for drone coordination. Tan et al. [12] proposed a warm-up heuristic to schedule a limited number of drones to complete a number of firefighting tasks, but the heuristic cannot be extended to large-scale instances. Zhu et al. [13] proposed an adaptive multiple drone swarm collaborative firefighting strategy, which used a temperature change-driven adaptive step-length search strategy to detect fire spots and employed an emergency bidding algorithm to collaborate multiple drone swarms under limited resources. Also considering the scheduling of multi-swarm drones for forest firefighting, John et al. [14] proposed an information-driven search and divide and conquer mitigation control approach, where the local attraction among the swarm members helped the non-detector members reach the fire location faster, and the divide-and-conquer mitigation control ensured a non-overlapping fire sector allocation for all members quenching the fire. In [4], the authors presented a mathematical model for estimating wildfire spread and economic losses simultaneously, which can also help to determine the minimum number of firefighting drones in preparation for wildfire; based on the model, a metaheuristic optimization algorithm was used to schedule a limited number of drones in response to wildfire occurrence to minimize the total expected loss. Zheng et al. [15] studied a problem of cooperatively scheduling inspection drones and deicing drones for power grid deicing in icing disasters; the authors proposed a fully parallelizable evolutionary algorithm combining global search without individual interaction and adaptive local search that uses a fuzzy inference system to determine the operator to be applied on each solution. In [16], a hybrid memetic optimization and DRL method was proposed to cooperative schedule drones for railway catenary deicing to minimize the total negative effect caused by the freezing events on train operations, where DRL was used to adaptively select the most appropriate neighborhood search operators.

2.2. Cooperative Drone–Truck Scheduling

Drone–truck cooperation has been popularized in logistics to achieve complementary advantages [17]. To solve a collaborative truck–drone routing problem for contactless parcel delivery, Wu et al. [18] proposed an improved variable neighborhood descent that combines the Metropolis acceptance criterion of simulated annealing and tabu search, where the initial solution was generated based on K-means clustering and nearest neighbor. In [19], the authors proposed an encoder-decoder framework combined with reinforcement learning for truck-and-drone coordinated delivery routing, where all final deliveries are completed by drones while the truck acts as a movable charging station and a carrier. Weng et al. [20] considered cooperative truck–drone delivery in a restricted traffic zone, where the truck travels along the outer boundary of the zone to send and receive the drone for delivering the cargo to customers; the problem was solved by an adapted water wave optimization (WWO) algorithm. The truck–drone hybrid delivery model presented by Young Jeong and Lee [21] also used a truck to launch and collect multiple drones: the truck did not visit customers but moved between launch positions, looking for the best location to launch the drones. Liu et al. [22] proposed another truck–drone delivery model with multiple trucks, each equipped with a multi-visit drone; they designed a variable neighborhood search algorithm integrated with simulated annealing to solve the problem by constructing drone and truck routes synchronously. Recently, Lv et al. [23] presented a problem of collaborative human–drone–truck search-and-rescue task scheduling in earthquakes, where drones are used to quickly search for survivors who are expected to be ultimately rescued by human rescuers, while a truck serves as a mobile battery depot for drones, such that the survivors can be rescued as many as possible and as early as possible. To solve the problem, a memetic algorithm that combines the ecogeography-based optimization (EBO) for global exploration, adaptive local search for improving solution accuracy, and a modified simulated annealing for truck path planning.

The key difference between our study and existing studies on drone–truck cooperation for parcel (good) delivery is that the water taken by drones from supply trucks will be consumed in fire extinguishing, and the water should be released in the appropriate amount at the appropriate time in order to have effect on suppressing the fire. To the best of our knowledge, no existing studies have been conducted to solve this kind of problem.

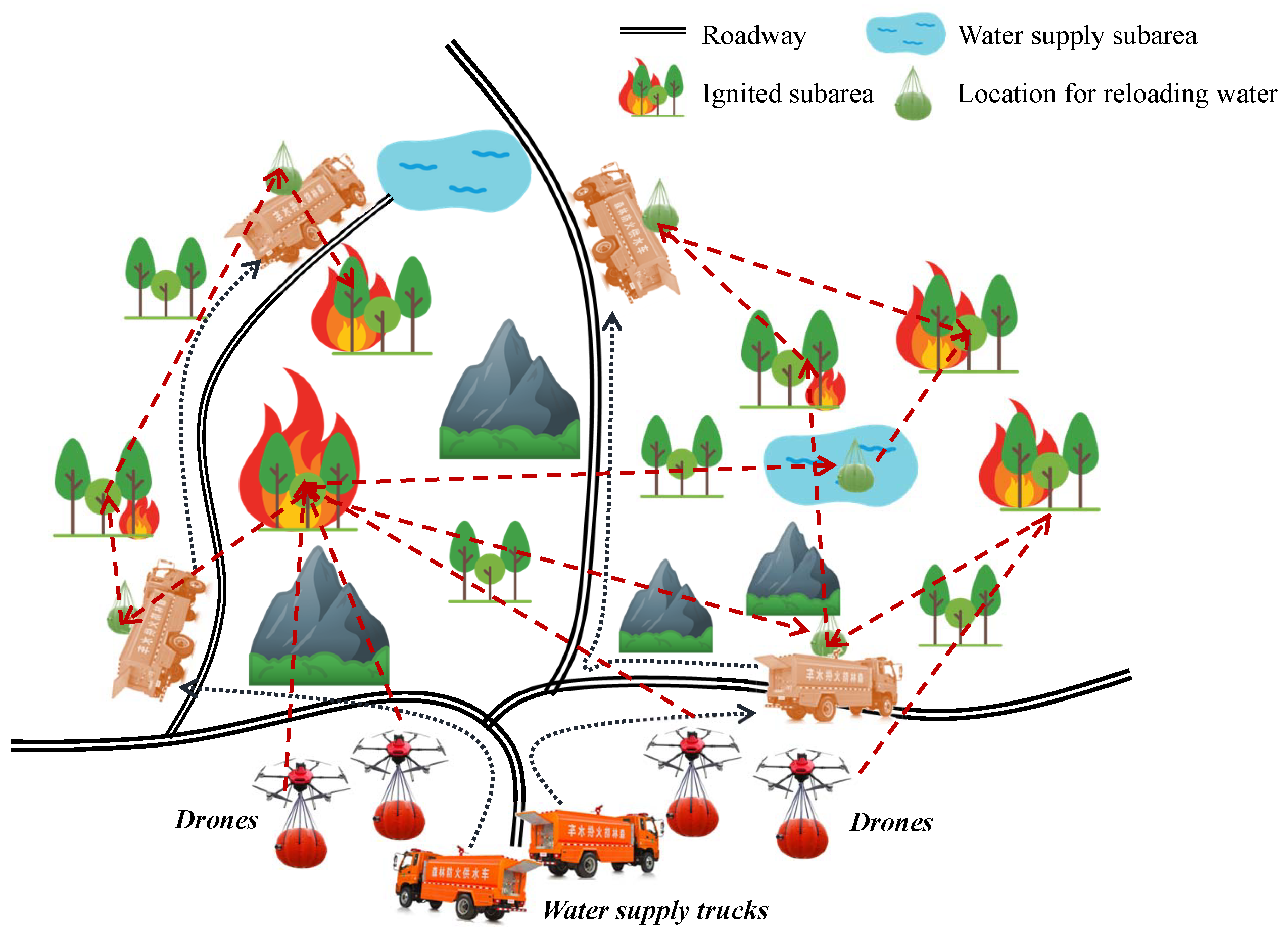
3. Problem Formulation

A wilderness area is divided into a set of subareas based on topographic features (e.g., one subarea of grassland and one subarea of shrubland) and boundaries (e.g., two subareas separated by a river). Among these subareas, two subsets are identified:

• The first subset of m ignitable subareas (e.g., woodlands, grasslands, and shrublands), denoted by $\mathbf{A}=\{{\mathrm{A}}_1,{\mathrm{A}}_2,\dots ,{\mathrm{A}}_m\}$.
• The second subset of $\tilde{m}$ water resource subareas (e.g., pools, lakes, and rivers), denoted by $\tilde{\mathbf{A}}=\{{\mathrm{A}}_{m+1},{\mathrm{A}}_{m+2},\dots ,{\mathrm{A}}_{m+\tilde{m}}\}$.

At the beginning time $t=0$, one or several fire (ignition) points are observed in $\mathbf{A}$. Our previous work [4] has established a wildfire spread model, which can be used to estimate

• For each ignitable subarea $A_i$ initially without fire, the expected time $t^{\mathrm{ig}}\left(i\right)$ that $A_i$ will be ignited;
• For each ignitable subarea $A_i$, the heat release rate $\theta (i,t)$ at any time $t\ge t^{\mathrm{ig}}\left(i\right)$.

The problem is to schedule a set $\mathbf{D}$ of $n^{\mathrm{D}}$ firefighting drones and a set $\mathbf{W}$ of $n^{\mathrm{W}}$ water supply trucks to extinguish the wildfire. The capacity (water volume) of a water capsule carried by a drone is q, the capacity of a water supply truck is Q, and the capacity of a water resource subarea $A_i$ is ${\mathcal{Q}}_i$. The volume of water needed for extinguishing the fire in each ignitable subarea $A_i$ at time t is proportional to its area $a_i$ and heat release rate $\theta (i,t)$. Nonetheless, a very accurate calculation of water volume for fire extinguishing is unnecessary; what we need to determine is the number of water capsules (i.e., number of drones) for extinguishing the fire in subarea $A_i$ at time t, which is estimated as

$$N(i,t)=\left\{\begin{array}{cc}⌈c_1{a}_i\theta (i,t)/q⌉,\hfill & \theta (i,t)<\widehat{\theta }\hfill \\ ⌈c_2{a}_i\theta (i,t)/q⌉,\hfill & \theta (i,t)\ge \widehat{\theta }\hfill \end{array}\right.$$

(1)

where $\lceil \rceil$ denotes rounding up to the closest integer, $c_1$ and $c_2$ are two constant coefficients, and $\widehat{\theta }$ is a threshold of heat release rate: when the heat release rate reaches the threshold, the fire development enters into the full combustion (flashover) stage [24] and the fire extinguishing becomes significantly more difficult. Therefore, $c_2$ is larger than $c_1$.

Without loss of generality, we use ${\mathrm{A}}_0$ to denote the fire station at which the drones and trucks are initially located (which can be easily extended to different initial locations of the drones and trucks). A drone can fly directly from a subarea to another, whereas a truck travels along the road. Therefore, we differentiate the following travel times between any two subareas $A_i$ and $A_{i^{\prime }}$ ($i,i^{\prime }\in \{0,1,\dots ,m+\tilde{m}\}$):

• $\mathrm{\Delta }{t}^{\mathrm{D}}(i,i^{\prime })$ consumed by a drone carrying a fully loaded water capsule from $A_i$ to $A_{i^{\prime }}$.
• $\mathrm{\Delta }{\overline{t}}^{\mathrm{D}}(i,i^{\prime })$ consumed by a drone carrying an empty water capsule from $A_i$ to $A_{i^{\prime }}$.
• $\mathrm{\Delta }{t}^{\mathrm{W}}(i,i^{\prime })$ consumed by a fully loaded water supply truck from $A_i$ to $A_{i^{\prime }}$.
• $\mathrm{\Delta }{\overline{t}}^{\mathrm{W}}(i,i^{\prime })$ consumed by an empty water supply truck from $A_i$ to $A_{i^{\prime }}$.

When the water volume carried by a water supply truck is $Q^{\prime }$, the corresponding travel time from $A_i$ to $A_{i^{\prime }}$ is estimated as

$$\mathrm{\Delta }{t}^{\mathrm{W}}(i,i^{\prime },Q^{\prime })=\mathrm{\Delta }{\overline{t}}^{\mathrm{W}}(i,i^{\prime })-\left(\mathrm{\Delta }{\overline{t}}^{\mathrm{W}}(i,i^{\prime })-\mathrm{\Delta }{t}^{\mathrm{W}}(i,i^{\prime })\right){\displaystyle \frac{Q^{\prime }}{Q}}$$

(2)

The first decision of the problem is a sequence $\mathbf{x}=\{x_1,x_2,\dots ,x_m\}$ of the m ignitable subareas, in order of which the firefighting operations are conducted. Let $\mathrm{\Delta }{t}^{\mathrm{F}}$ be the time duration for a drone to release water. For the first subarea $x_1$ in the sequence, the earliest arrival time $t\left(x_1\right)$ and the departure time $t^{†}\left(x_1\right)$ of a drone are as Equations (3) and (4), respectively:

$$\begin{array}{cc}\hfill t\left(x_1\right)& =\mathrm{\Delta }{t}^{\mathrm{D}}(0,x_1)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill t^{†}\left(x_1\right)& =t\left(x_1\right)+\mathrm{\Delta }{t}^{\mathrm{F}}\hfill \end{array}$$

(4)

The number of drones required for firefighting in $x_1$ is

$$N\left(x_1\right)=N(i,t\left(x_1\right))$$

(5)

Here, we use ${\mathbf{D}}_1\left(x_1\right)$ to denote the first batch of $N\left(x_1\right)$ drones for firefighting in $x_1$, and use ${\mathbf{D}}_0\left(x_1\right)=\mathbf{D}\setminus {\mathbf{D}}_1\left(x_1\right)$ to denote the set of remaining $n^{\mathrm{D}}-N\left(x_1\right)$ available drones in $A_0$. For the second batch ${\mathbf{D}}_2\left(x_2\right)$, if the number of drones in ${\mathbf{D}}_0\left(x_1\right)$ is sufficient, the drones are all selected from ${\mathbf{D}}_0\left(x_1\right)$; otherwise, some drones should be selected from ${\mathbf{D}}_1\left(x_1\right)$. Each of such drones, denoted by d, after completing its current task in $x_1$, should choose either a water resource subarea $A_i$ from $\tilde{\mathbf{A}}$ or a water supply truck w from the non-empty truck subset $\tilde{\mathbf{W}}\subseteq \mathbf{W}$ to reload water, such that it can arrive at the target $x_2$ at the earliest time denoted by $t(d,x_2)$:

$$\begin{array}{cc}\hfill t(d,x_2)=t^{†}\left(x_1\right)+min& (\underset{A_{\tilde{i}}\in \tilde{\mathbf{A}}}{min}(\mathrm{\Delta }{\overline{t}}^{\mathrm{D}}(1,\tilde{i})+\mathrm{\Delta }{t}^{\mathrm{D}}(\tilde{i},2)),\hfill \\ \hfill & \underset{w\in \tilde{\mathbf{W}}}{min}(\mathrm{\Delta }{\overline{t}}^{\mathrm{D}}(1,w_d)+\mathrm{\Delta }{t}^{\mathrm{D}}(w_d,2)))+\mathrm{\Delta }{t}^{\mathrm{L}}\hfill \end{array}$$

(6)

where $\mathrm{\Delta }{t}^{\mathrm{L}}$ denotes the time duration for reloading a water capsule.

After determining the second batch ${\mathbf{D}}_2\left(x_2\right)$, we update the sets of available drones in $A_0$ and $A_1$ as ${\mathbf{D}}_0\left(x_2\right)={\mathbf{D}}_0\left(x_1\right)\setminus {\mathbf{D}}_2\left(x_2\right)$ and ${\mathbf{D}}_1\left(x_2\right)={\mathbf{D}}_1\left(x_1\right)\setminus {\mathbf{D}}_2\left(x_2\right)$, respectively.

By analogy, for the i-th batch ${\mathbf{D}}_i\left(x_i\right)$, if the number of available drones in ${\mathbf{D}}_0\left(x_{i-1}\right)$ is insufficient (typically, there will be no drone left in $A_0$ after several batches, otherwise the problem is trivial), the drones should be selected from earlier batches ${\mathbf{D}}_{\mathbf{1}}\left(x_{i-1}\right),\dots ,{\mathbf{D}}_{\mathbf{i}-\mathbf{1}}\left(x_{i-1}\right)$; if a drone d is selected from the $i^{\prime }$-th batch ($i^{\prime }<i$), it should choose either a water resource subarea or a water supply truck to reload water, such that it can arrive at the target $x_i$ at the earliest time $t(d,x_i)$:

$$\begin{array}{cc}\hfill t(d,x_i)=t^{†}\left(x_{i^{\prime }}\right)+min& (\underset{A_{\tilde{i}}\in \tilde{\mathbf{A}}}{min}(\mathrm{\Delta }{\overline{t}}^{\mathrm{D}}(i^{\prime },\tilde{i})+\mathrm{\Delta }{t}^{\mathrm{D}}(\tilde{i},i)),\hfill \\ \hfill & \underset{w\in \tilde{\mathbf{W}}}{min}(\mathrm{\Delta }{\overline{t}}^{\mathrm{D}}(i^{\prime },w_d)+\mathrm{\Delta }{t}^{\mathrm{D}}(w_d,i)))+\mathrm{\Delta }{t}^{\mathrm{L}}\hfill \end{array}$$

(7)

For each i-th batch ${\mathbf{D}}_i\left(x_i\right)$, we iteratively select a drone $d^{\ast }$ with the earliest arrival time on $x_i$ among all candidate ones until the number of drones is sufficient:

$$d^{\ast }=\underset{d\in {\displaystyle \bigcup _{\iota =0}^{i-1}}{\mathbf{D}}_{\iota }\left(x_{\iota }\right)}{min}t(d,x_i)$$

(8)

The location of a water resource subarea is fixed, whereas the location of a water supply truck is movable. In Equations (6) and (7), $w_d$ is the docking location of the drone d and truck w for water reloading, which is determined by starting from truck location $w\left(t\right)$ at time $t=0$ if the truck has never been assigned or $t=t_w$ when the truck completes the last water supply task, searching along all road directions $\mathcal{RD}$ towards (closer to) either the current drone location $x_{i^{\prime }}$ or the target subarea $x_i$, such that $t(d,x_i)$ is minimized, as illustrated in Figure 2. Let $Q_w\left(t\right)$ be the water volume carried by the truck w at time t, the problem of docking location selection can be formulated as

$$w_d=\underset{\mathcal{R}\in \mathcal{RD}}{min}\underset{p\in \mathcal{R}}{min}\left(max\left(t^{†}\left(x_{i^{\prime }}\right)+{\overline{t}}^{\mathrm{D}}(i^{\prime },p),t_w+t^{\mathrm{W}}(w\left(t_w\right),p,Q_w\left(t_w\right))\right)+t^{\mathrm{D}}(p,x_i)\right)$$

(9)

which can be optimized efficiently using the Gaussian binary simulated annealing method proposed in [23]. Afterwards, for the selected truck w, its water volume will be reduced by q for each drone it supplied; whenever its water volume is smaller than q, the truck goes to the nearest water source subarea (including $A_0$) to reload water; in this case, w is removed from the non-empty truck set $\tilde{W}$ and, according to Equation (7), could not be chosen by drones until the truck has been reloaded.

After determining the i-th batch ${\mathbf{D}}_i\left(x_i\right)$, we update the sets of available drones in previous subareas as follows ($0\le \iota <i$):

$${\mathbf{D}}_{\iota }\left(x_i\right)={\mathbf{D}}_{\iota }\left(x_{i-1}\right)\setminus {\mathbf{D}}_i\left(x_i\right)$$

(10)

Thus, we obtain the earliest arrival time $t\left(x_i\right)$ and the departure time $t^{†}\left(x_i\right)$ of the i-th batch drones for subarea $x_i$ as Equations (11) and (12), which are exactly the beginning time and the end time of the firefighting operation in $x_i$, respectively:

$$\begin{array}{cc}\hfill t\left(x_i\right)& =\underset{d\in {\mathbf{D}}_i\left(x_i\right)}{min}t(d,x_i)\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill t^{†}\left(x_i\right)& =\underset{d\in {\mathbf{D}}_i\left(x_i\right)}{max}t(d,x_i)+\mathrm{\Delta }{t}^{\mathrm{F}}\hfill \end{array}$$

(12)

Note that a firefighting operation will change the fire spread. At each $t^{†}\left(x_i\right)$, we remove the fire in subarea $x_i$, and re-invoke the wildfire spread model [4] to estimate the fire spread after $t^{†}\left(x_i\right)$.

During the above iterative process, if the current subarea $x_i$ is not ignited, we swap $x_i$ and the next ignited subarea $x_{i^{\prime }}$ and thus continue the iterative calculations using Equations (7)–(12). If all remaining subareas $x_i,x_{i+1},\dots ,x_m$ are not ignited, the whole operation is completed, and their firefighting ending times $t^{†}(·)$ are simply set to 0.

The problem objective is to minimize the time at which the wildfire is completely extinguished:

$$\begin{array}{cc}\hfill min& f\left(\mathbf{x}\right)=min\left(\underset{1\le i\le m}{max}{t}^{†}\left(x_i\right)\right)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& t_{\mathbf{x}}^{\mathrm{ig}}\left(x_i\right)<t,\forall t>t^{†}\left(x_i\right),0<i\le m\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & \mathbf{x}\in {\mathcal{P}}_m\left(\{A_1,A_2,\dots ,A_m\}\right)\hfill \end{array}$$

(15)

where $t_{\mathbf{x}}^{\mathrm{ig}}\left(x_i\right)$ denotes the (last) ignition time in subarea $x_i$ under the fire extinguishing solution $\mathbf{x}$, and ${\mathcal{P}}_m$ denotes the set of all permutations of a given set. The constraint (14) indicates that after a fire extinguishing operation in $x_i$ at $t^{†}\left(x_i\right)$, the subarea should not be reignited. Given a solution $\mathbf{x}$, the flowchart for evaluating the objective function $f\left(\mathbf{x}\right)$ in Equation (13) is shown by Figure 3.

Note that our problem formulation does not explicitly consider battery consumption of drones. In practice, water supply trucks can also carry batteries (whose weight is significantly smaller than the weight of water): if the battery level of a drone is below a threshold, it can reload water and replace the battery simultaneously. Typically, during an operation, the frequency of battery replacement is significantly lower than that of the water reloading, and hence battery replacement will have a trivial effect on the whole schedule. In addition, trucks can serve as mobile base stations to enhance the communication between drones [25,26,27].

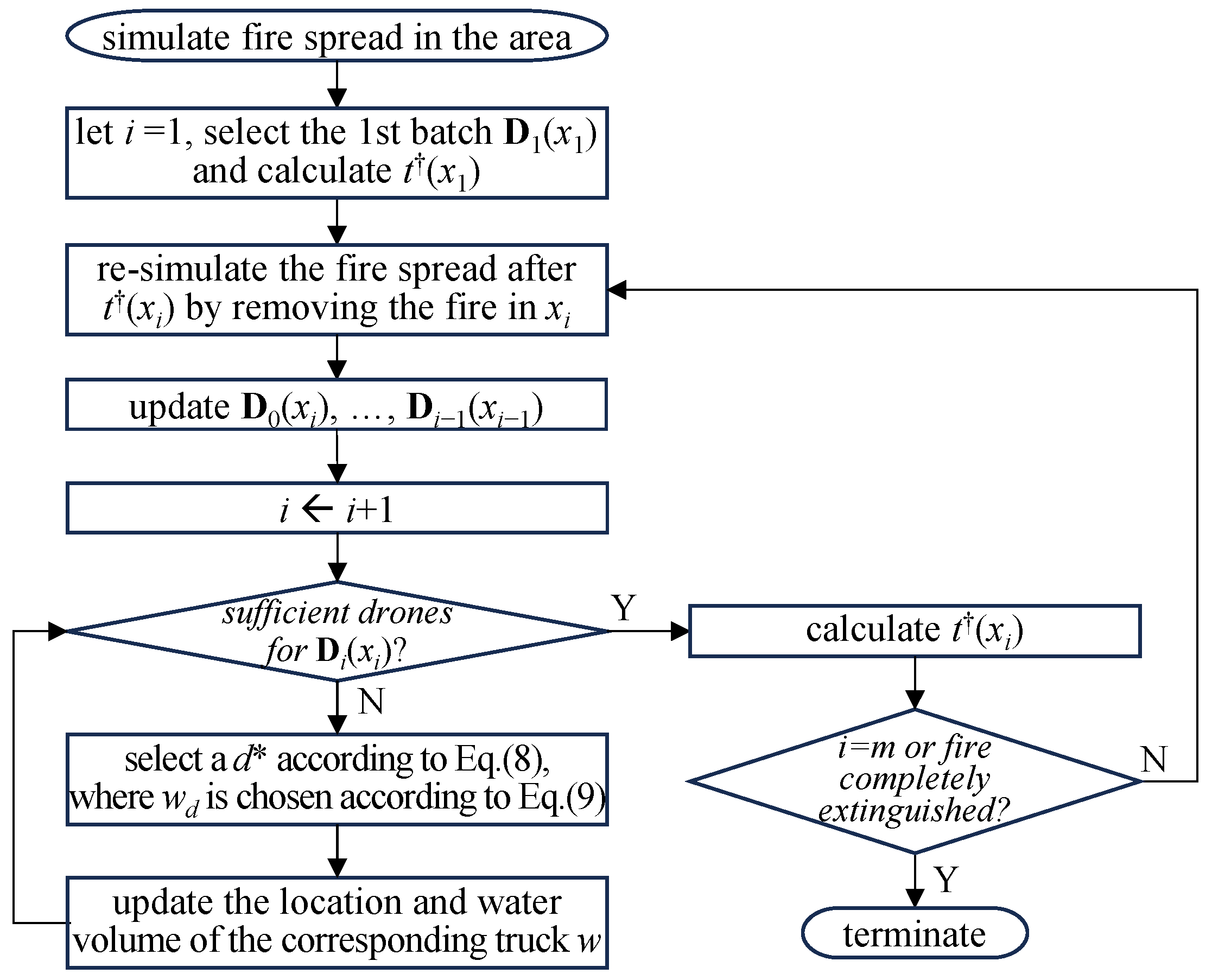
4. Deep Reinforcement Learning for the Problem

The proposed DRL network consists of an encoder and a decoder. The encoder takes a problem instance as the input and learns input features through embedding. The decoder generates a solution to the problem instance by iteratively predicting the subarea selection decision from the current state through attention. The architecture of the learning network is illustrated in Figure 4.

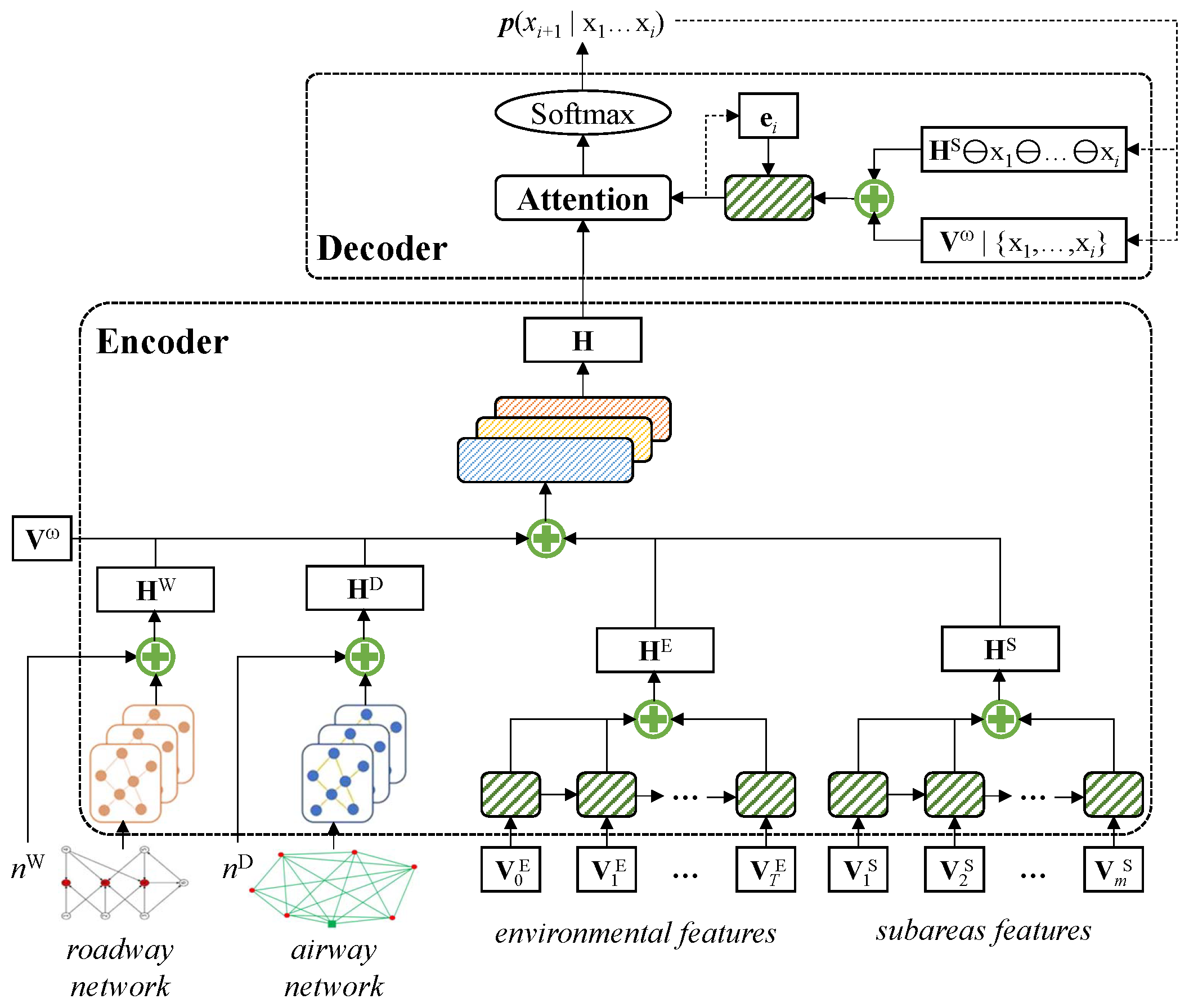
4.1. Encoder

The input to the encoder consists of the following parts:

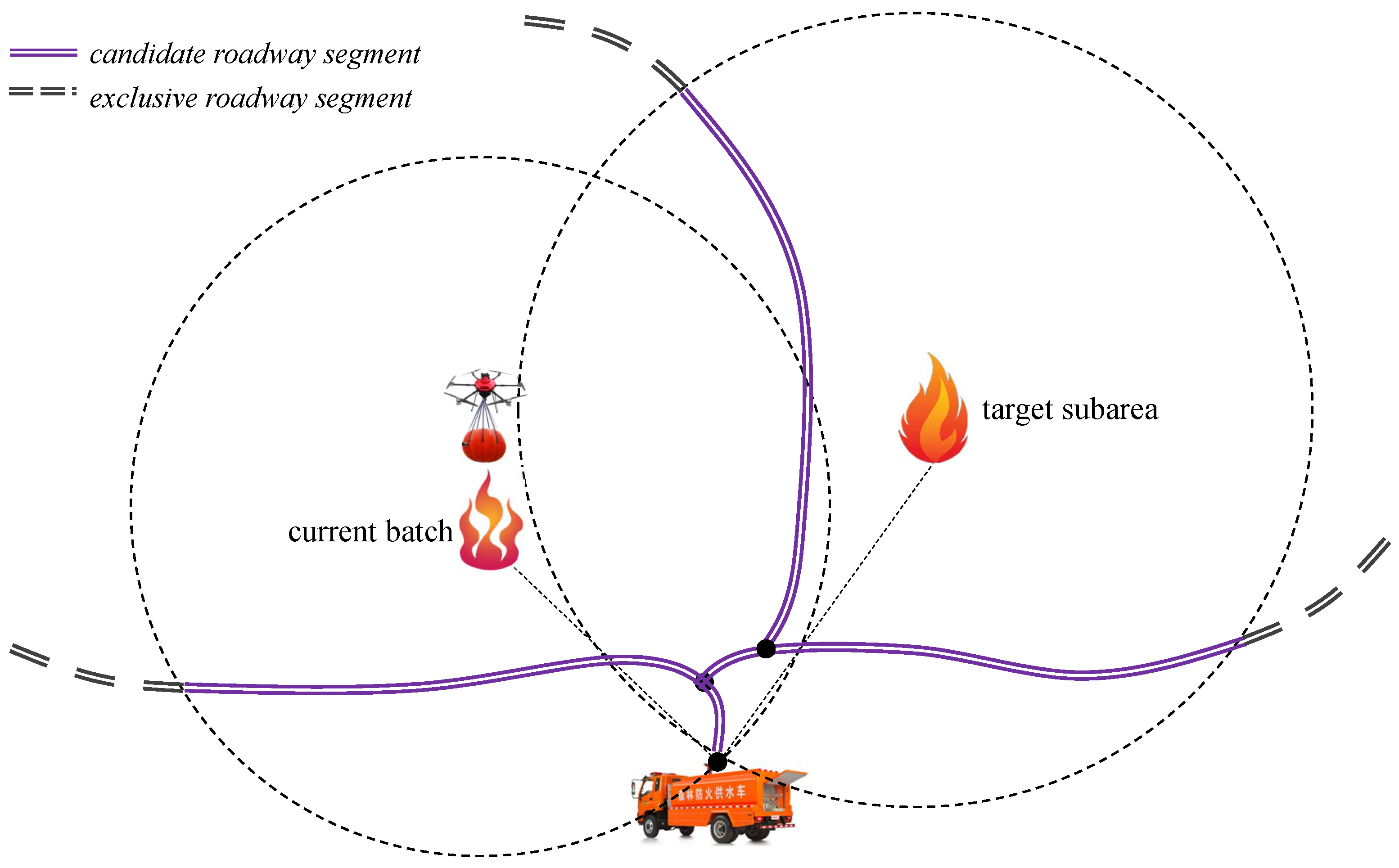
• A roadway network $G^{\mathrm{W}}$ used by water supply trucks, which is represented by a weighted adjacency matrix that saves the truck travel time on each edge (roadway segment).
• An airway network $G_D$ used by drones, also represented by a weighted adjacency matrix that saves the drone travel time on each edge (pair of vertices). The vertices of $G_D$ include not only the subareas, but also the vertices of $G_W$.
• T environmental feature vectors, each ${\mathbf{V}}_t^{\mathrm{E}}$ of which saving the temperature, humidity, wind force, and wind direction at time t during the decision period T ($t=0,1,\dots ,T-1$).
• m ignited subarea feature vectors, each ${\mathbf{V}}_i^{\mathrm{S}}$ saving the area, combustible vegetation density, total combustion heat, and initial ignition state (true or false) of an ignited subarea $A_i$ ($i=1,2,\dots ,m$).
• A water volume vector ${\mathbf{V}}^{\omega }$ that saves the water volume of each water supply subarea $A_{\tilde{i}}$ ($\tilde{i}=0,m+1,\dots ,m+\tilde{m}$).
• The number $n^{\mathrm{D}}$ of drones and number $n^{\mathrm{W}}$ of trucks.

$G^{\mathrm{W}}$ is processed by a graph neural networks (GNN) to generate the embedding, which is then concatenated with $n^{\mathrm{W}}$ to a hidden representation ${\mathbf{H}}^W$. Similarly, $G^{\mathrm{D}}$ is processed by another GNN to generate the embedding, which is concatenated with $n^{\mathrm{D}}$ to a hidden representation ${\mathbf{H}}^D$. The environmental feature vectors are iteratively processed by a recurrent neural network (RNN), where the t-th step takes both ${\mathbf{V}}_t^{\mathrm{E}}$ and the output of the $(t-1)$-th step as the input ($1\le t<T$); finally, the outputs of all steps are embedded into a hidden representation ${\mathbf{H}}^E$. The ignited subarea feature vectors are also iteratively processed by a RNN to generate a hidden representation ${\mathbf{H}}^S$. ${\mathbf{H}}^W$, ${\mathbf{H}}^D$, ${\mathbf{H}}^E$, ${\mathbf{H}}^S$, together with the water volume vector ${\mathbf{V}}^{\omega }$, are concatenated and fed into a convolution neural network, whose topmost representation $\mathbf{H}$ will be decoded by the decoder to construct the solution to the problem.

4.2. Decoder

The decoder performs m steps of decoding, each deciding the subarea $x_i$ to be added to the subarea sequence in the solution ($1\le i\le m$). At the first step, the subarea embedding ${\mathbf{H}}^S$ and the water volume vector ${\mathbf{V}}^{\omega }$ are concatenated and fed into a RNN; the RNN output together with the topmost representation $\mathbf{H}$ of the encoder are sent to an attention module, which produces the probability (normalized by a Softmax function) of each subarea of being selected, and the subarea with the maximum probability is selected as $x_1$. At each following $(i+1)$-th step, ${\mathbf{H}}^S$ is reconstructed by excluding the subarea $x_i$ selected at the previous step, and ${\mathbf{V}}^{\omega }$ is reconstructed by subtracting the water volume used by fire extinguishing in $x_i$; the concatenation of the updated ${\mathbf{H}}^S$ and ${\mathbf{V}}^{\omega }$, together with the RNN output at the previous step, are re-fed into the RNN, and then the attention module produces the probabilities $p(x_{i+1}=A_{\iota }|x_1,x_2,\dots ,x_i)$ ($1\le \iota \le m$) for selecting $x_{i+1}$. The procedure continues until the solution is complete.

4.3. Training Method

The training of the DRL network, parameterized by $\mathit{\theta }$, is to minimize the expected value of objective function (13) of the solution $\mathbf{x}$ generated according to the network policy $p_{\mathit{\theta }}$ for any problem instance (state) s:

$$\mathcal{L}\left(\mathit{\theta }\right|s)={\mathbb{E}}_{\mathbf{x}\sim p_{\mathit{\theta }}(\_|s)}f\left(\mathbf{x}\right|s)$$

(16)

Given a baseline $\mathit{base}\left(s\right)$, the gradient of the loss function is:

$${\nabla }_{\mathit{\theta }}\mathcal{L}\left(\mathit{\theta }\right|s)={\mathbb{E}}_{\mathbf{x}\sim p_{\mathit{\theta }}(\_|s)}\left((f\left(\mathbf{x}\right|s)-\mathit{base}\left(s\right)){\nabla }_{\mathit{\theta }}log{p}_{\mathit{\theta }}\left(\mathbf{x}\right|s)\right)$$

(17)

Using Monte Carlo sampling of B instances $\{s_1,s_2,\dots ,s_B\}$ from the problem distribution S, the gradient can be approximated as

$${\nabla }_{\mathit{\theta }}\mathcal{L}\left(\mathit{\theta }\right)=\sum _{j=1}^B\left((f\left({\mathbf{x}}_j\right|s_j)-\mathit{base}\left(s_j\right)){\nabla }_{\mathit{\theta }}log{p}_{\mathit{\theta }}\left({\mathbf{x}}_j\right|s_j)\right)$$

(18)

We employ the policy gradient with rollout baseline algorithm [28] to optimize the network parameters $\mathit{\theta }$ according to (18). The algorithm randomly initializes $\mathit{\theta }$ and uses the best network ${\mathit{\theta }}^{\ast }$ found so far as the baseline. At each epoch, the two networks are simultaneously tested on a batch of instances, and $\mathit{\theta }$ is improved using the Adam optimizer [29]; if ${\mathit{\theta }}^{\ast }$ performs significantly better than $\mathit{\theta }$ on the batch, $\mathit{\theta }$ is updated by ${\mathit{\theta }}^{\ast }$; otherwise, if $\mathit{\theta }$ is not updated for a consecutive number $\widehat{e}$ of epochs, $\mathit{\theta }$ is rolled back to ${\mathit{\theta }}^{\ast }$. The pseudo-code of the training method is presented in Algorithm 1. The time complexity of the algorithm is $O\left({\mathit{epoch}}_{max}{A}_{\mathrm{iter}}B\mathcal{D}\right)$, where $A_{\mathrm{iter}}$ is the number of iterations used by Adam in the inner loop, and $\mathcal{D}$ is the dimensionality of the data.

Algorithm 1: The policy gradient with rollout baseline algorithm for training the network.

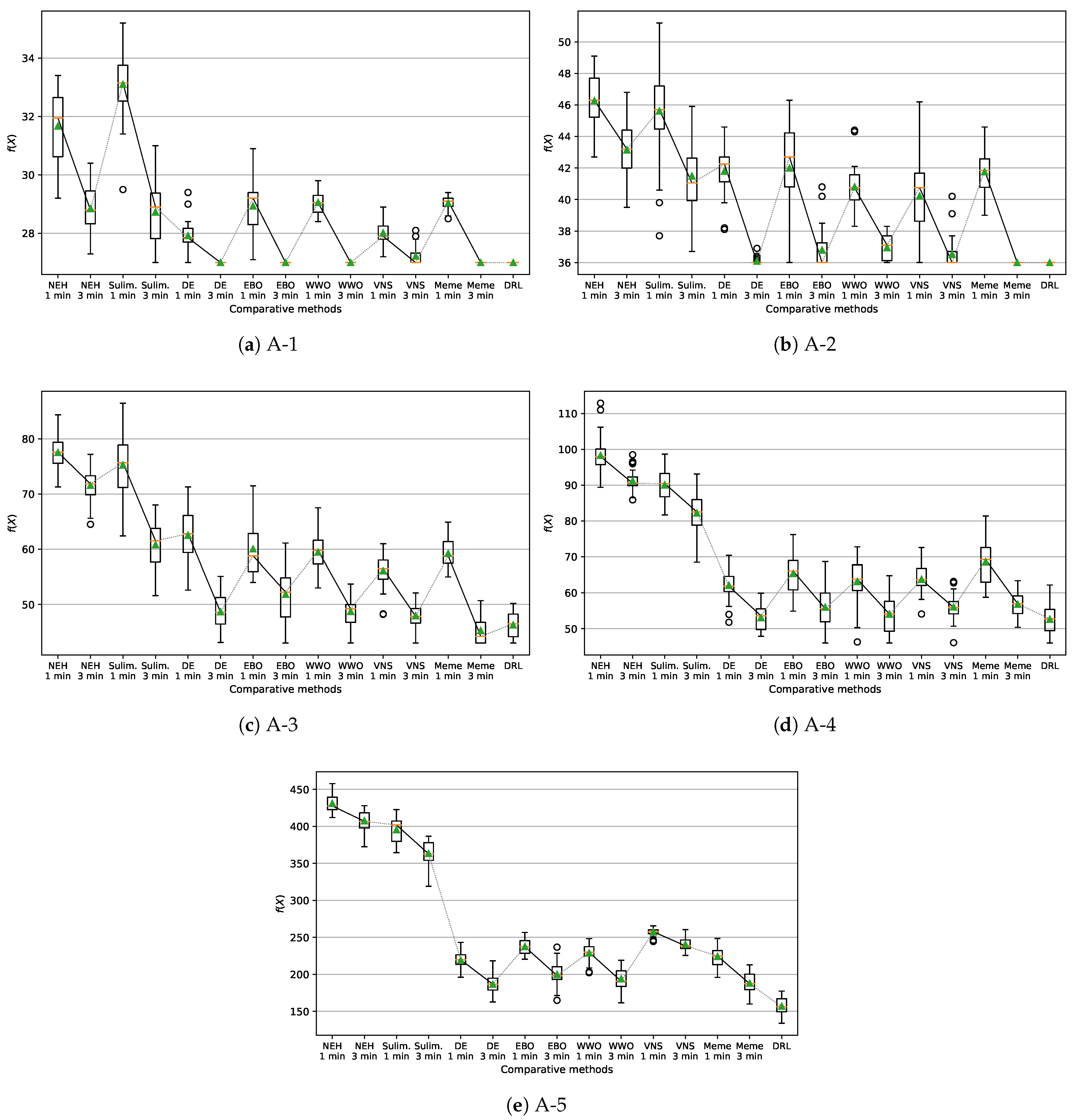
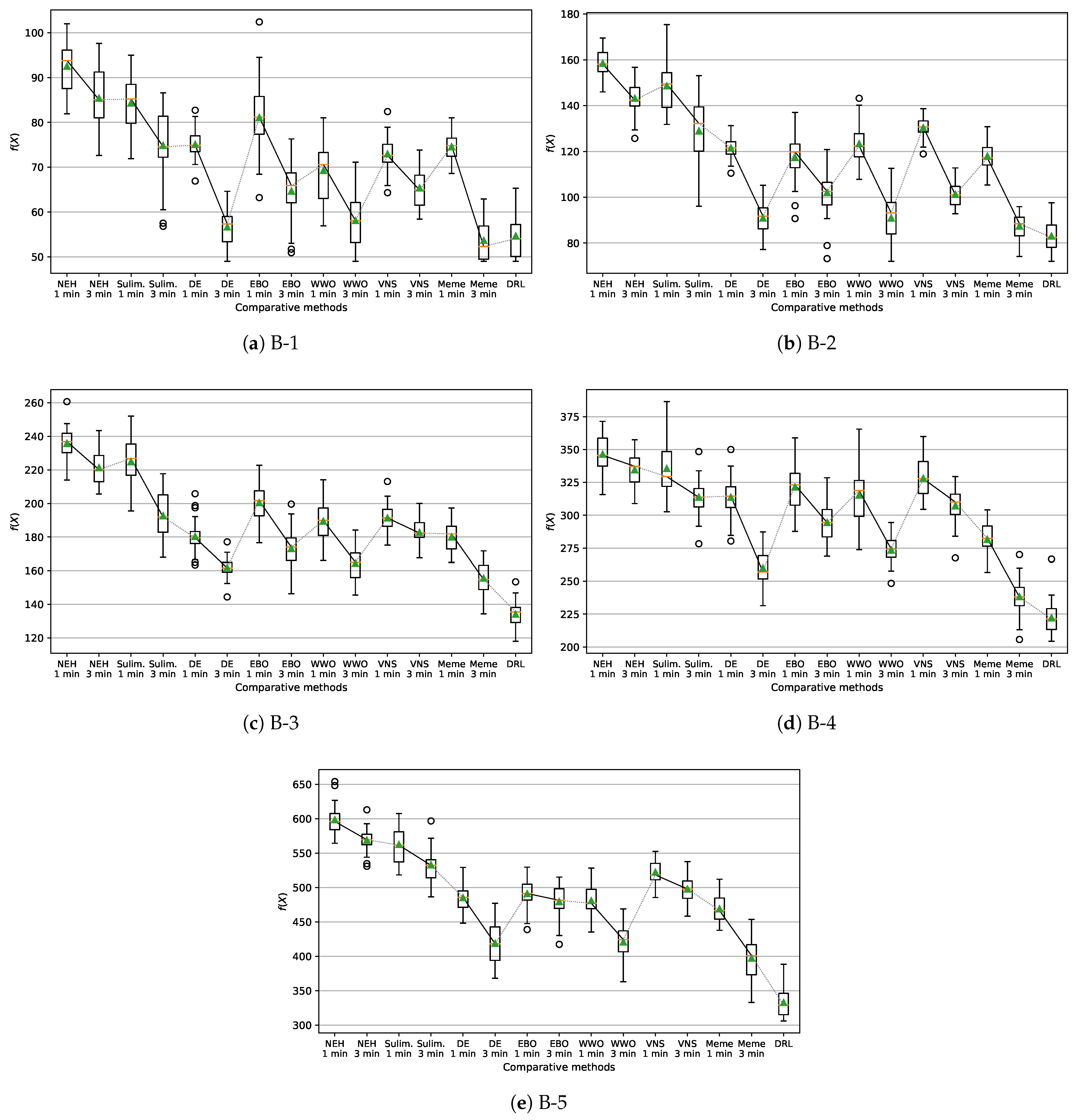
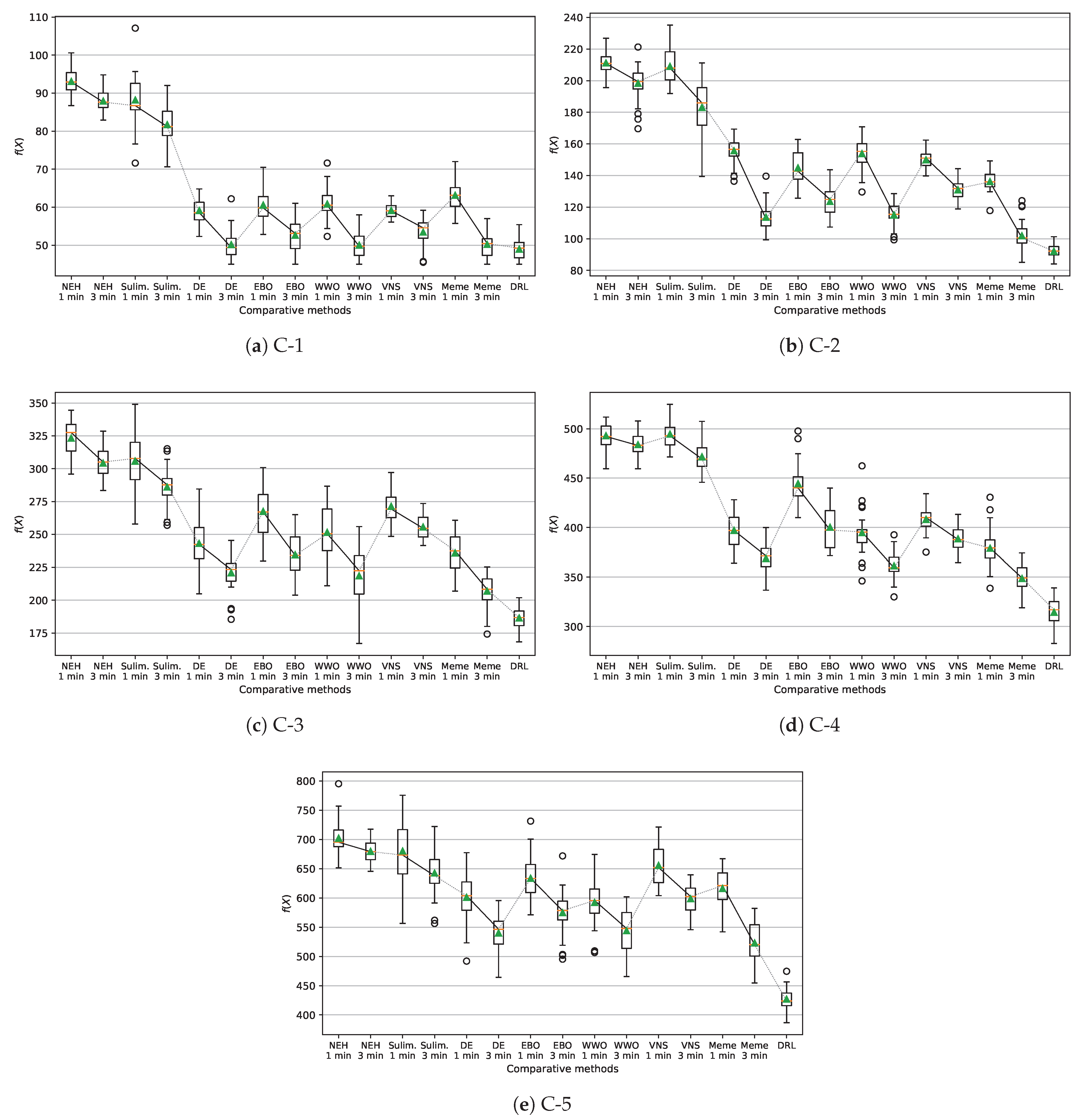
5. Computational Results

We select three wilderness areas, one belonging to the Hangzhou West Mountain Forest Park and two belonging to the Tianmu Mountain Nature Reserve, all in Zhejiang Province, China. Their subarea information is summarized in

Table 1. Main information of the three wilderness areas and the test instances used in the computational tests.

Wilderness Area	Num of Ignitable Subareas	Num of Water Supply Subareas	Test Instance	Num of Drones	Num of Trucks
			A-1	6	1
			A-2	8	1
A	127	16	A-3	10	2
			A-4	12	2
			A-5	15	2
			B-1	6	1
			B-2	8	1
B	189	12	B-3	10	2
			B-4	12	2
			B-5	15	2
			C-1	6	1
			C-2	10	2
C	265	19	C-3	15	2
			C-4	18	3
			C-5	21	3

. The function parameters of drones are set based on the specification of the Spider H200 UAV (https://spideruav.com/product/agricultural-drone/agri-drone-h200/, accessed on 15 April 2025). Currently, the first two areas are equipped with 10 drones and the last is equipped with 15 drones; we reasonably scale the range to test the performance under different numbers of drones. The number of trucks is set according to the guideline that one truck serves for around 8–10 drones. For each wilderness area, an instance of the proposed DRL network is established and trained by a wide set of problem instances generated by setting different initial ignition subareas, different wind and temperature conditions, and different numbers of drones and water supply trucks. The numbers of samples for training the three network instances are 200, 350, and 560, respectively.

For comparison, we implement the following heuristic/metaheuristic permutation optimization methods:

• Nawaz–Enscore–Ham (NEH) heuristic [30].
• Suliman heuristic [31] to solve each instance $\mathbf{x}$, and use the better one as the $\mathit{base}\left(\mathbf{x}\right)$.
• Discrete differential evolution (DE) metaheuristic [32].
• EBO metaheuristic [33].
• WWO metaheuristic [34] adapted for permutation optimization [35].
• Variable neighborhood search (VNS) algorithm [36].
• A memetic algorithm (denoted by Meme) for permutation optimization [37].

For each wilderness area, we choose five test instances with fire scales which increase from small to large, and the numbers of drones and trucks increase with the fire scale, as summarized in the last three columns in Table 1. For each of the seven heuristic/metaheuristic algorithms, we respectively record its results after one minute and three minutes of CPU running time on each instance: for an emergency firefighting operation, the solution time is expected to be within one minute and at most three minutes. The computational environment is a workstation with an Intel Core i9-13900 3.0 GHz CPU, one NVIDIA RTX 4090Ti 32 GB GDDR6X GPU, and 128 G DDR5 5600 MHz RAM. The operating system is Microsoft Windows 10. The algorithm is implemented with Python 3.8.5 and PyTorch 2.7.

Figure 5, Figure 6 and Figure 7 present the box plots of the results, which show the median (in yellow line), average (in green triangle), minimum, maximum, first quartile (Q1), and third quartile (Q3) of the objective function values obtained by each comparative method on each test instance over the 30 runs.

Table 2. CPU time (in seconds) consumed by DRL on the each test instance.

Instance	A-1	A-2	A-3	A-4	A-5	B-1	B-2	B-3	B-4	B-5	C-1	C-2	C-3	C-4	C-5
Time	12	12	14	14	15	15	15	18	19	21	17	21	23	29	32

presents the CPU time consumed by DRL on the each test instance. Given an instance to be solved, the trained DRL network can produce a solution very quickly, typically within 30 s, which is significantly shorter than the time consumed by those heuristic/metaheuristic algorithms.

On the small-size instances A-1 and A-2, DRL always obtains the optimal solutions. Among the seven heuristic/metaheuristic algorithms, on instance A-1, DE, EBO, WWO and Meme also obtain the optimal solution after three minutes, but their results after one minute are worse; on instance A-2, only Meme always obtains the optimal solution after three minutes, but its result after one minute is worse.

On the remaining instances, none of the methods can guarantee the optimal solutions. On instances A-3 and B-1, the results of Meme after three minutes are better than the results of DRL, while the the results of Meme after one minute as well as the results of the other six comparative algorithms are worse than the results of DRL. On all other instances, the results of DRL are significantly better than those of all seven comparative algorithms. On the largest-size instance C-5, in terms of median objective function values, the worst solution of NEH needs 695 min to extinguish the fire, the best solutions among the comparative algorithms except DRL need 621 and 520 min after running one and three minutes, respectively, and the solution of DRL needs only 424 min.

With increasing problem instance size, the solution space increases exponentially. NEH and Suliman heuristics start from a single solution and then iteratively try to improve the solution by heuristic operations such as reinsertion and permutation, which cannot explore the whole solution space effectively. Consequently, except for the smallest instance A-1, the performance of NEH and Suliman are unacceptable on all other instances. By using a population of solutions to simultaneously explore the solution space, the five metaheuristic algorithms are significantly more effectively than the two heuristics, and are expected to obtain good or relatively good results when the algorithms converge. Nevertheless, the metaheuristics typically need a considerable time to converge, whereas the solution time for emergency decisions such as firefighting scheduling is quite limited [38]. Using one or three minutes, the results obtained by these metaheuristics are still far from satisfactory on large-size instances. Among the five metaheuristics, the memetic algorithm combining global search and neighborhood search exhibits the best performance. VNS places most emphasis on neighborhood search, and hence exhibits relatively good performance on small-size instances, but its performance deteriorates quickly on large-size instances. EBO has a good global exploration ability in early search stages, but its solutions improve slowly due to the insufficient local search ability in late stages. DE also has a good global exploration ability, and it performs better than EBO because its crossover operator is more effective in escaping local optima. WWO balances global and local search using wavelength-based propagation and neighborhood-based breaking, and its overall performance is only worse than Meme and is better than the other three metaheuristics.

Unlike the heuristic/metaheuristic algorithms that explicitly use one or a population of individuals to search in the solution space, the proposed DRL learns the implicit mapping from input features of the problem instances to high-quality solutions, and uses this mapping to directly construct a solution for a given new instance. Thus, the solution time of DRL is mainly consumed in instance encoding and solution decoding, which is linearly or quasi-linearly (rather than exponentially) proportional to the instance size. For small-size instances, DRL learns the mapping from the state space to the solution space sufficiently and thus can produce the optimal or near-optimal solutions. For large-size instances, DRL can also produce acceptable solutions that are significantly better than the solutions of those heuristic/metaheuristic algorithms that can only explore a small portion of the larger solution space.

6. Conclusions

This paper studies a problem of cooperatively scheduling drones and trucks for extinguishing dynamic spreading wildfire, where the trucks provide a mobile water supply to support firefighting operations of the drones. The problem objective is to minimize the time in which the fire is completely extinguished. To efficiently solve this problem within the limited emergency response time, the proposed DRL method combines GNN and RNN to encode a roadway network, airway network, environmental features, water supply information, and drone and truck features into high-level embeddings, which are then iteratively decoded through RNN and attention to generate sequential decisions. Computational results demonstrate the significant performance advantages of DRL over the selected comparative heuristic and metaheuristic algorithms on the test instances constructed based upon real-world wilderness areas in Zhejiang Province, China.

This study focuses on the scenario where drones carrying water capsules for firefighting. Our ongoing work is extending the scenario to including drones carrying fire-extinguishing bombs and drones carrying water hoses, both of which can benefit from using trucks as mobile water resources. Our future work will also consider integrating firefighting operations with rescuing victims, which requires cooperative scheduling of drones, ground vehicles, and human rescuers [39,40,41].