UAV Spiral Maneuvering Trajectory Intelligent Generation Method Based on Virtual Trajectory
Abstract
1. Introduction
- 1.
- A virtual trajectory-based spiral maneuvering trajectory design method is proposed to realize efficient coordination between maneuver penetration and precision strike;
- 2.
- The Archimedes spiral is used in the design of the relative spiral, and the maneuvering amplitude and maneuvering frequency can be adjusted;
- 3.
- Combined with DRL to generate virtual trajectories, the hypersonic UAV can sense the target in real time during flight, effectively adjust the maneuvering trajectory, and achieve accurate strikes on moving targets.
2. Modeling of Spiral Maneuver Trajectory
2.1. Modeling of the UAV Motion
2.2. Kinematic Modeling with Virtual Center of Mass
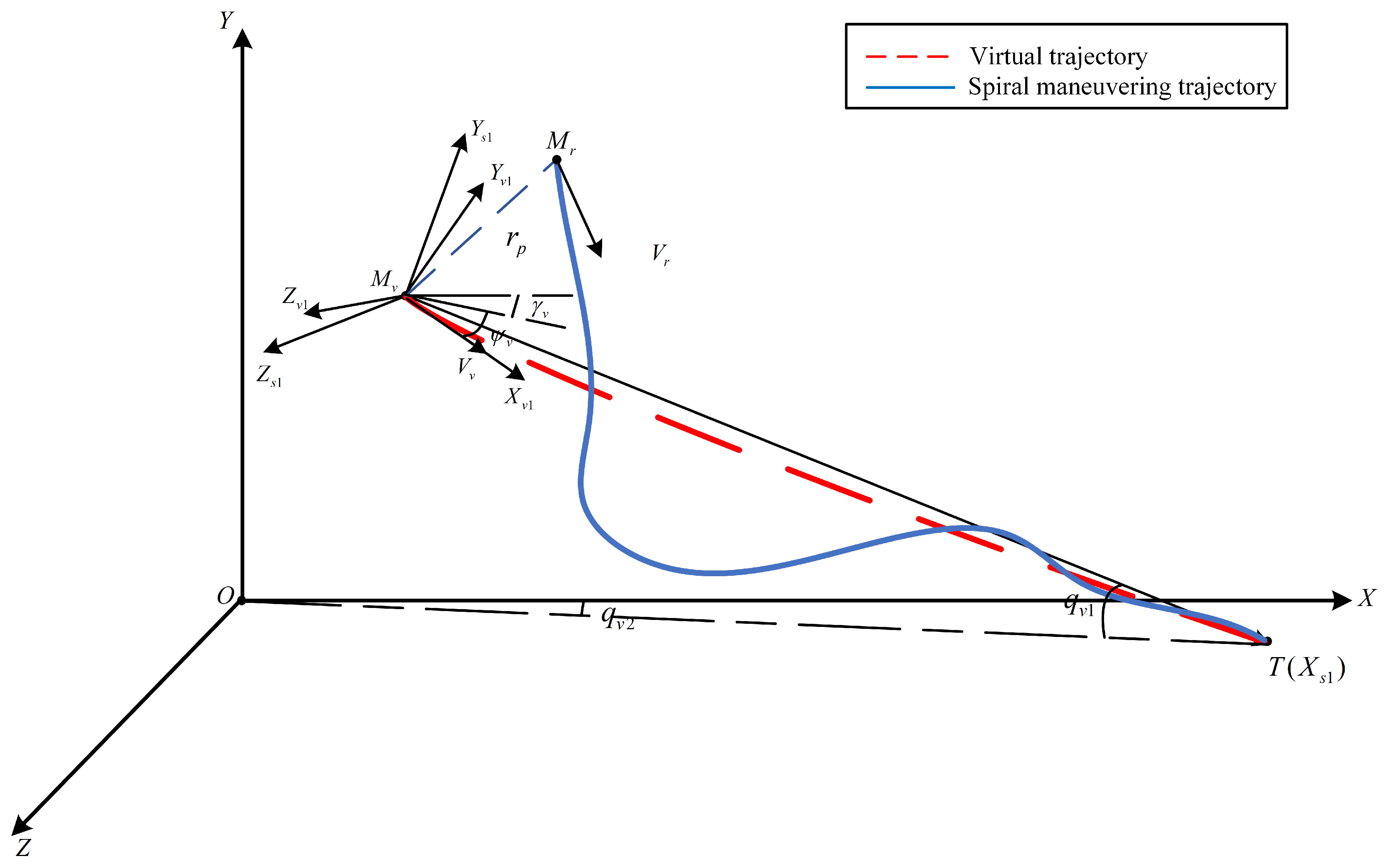
2.2.1. Definition and Transformation of Coordinate System
- 1.
- A virtual ballistic coordinate system, denoted as , is rigorously defined with its origin positioned at the VCM. The -axis is aligned with the velocity vector of the VCM, the -axis is orthogonally oriented upward within the vertical plane relative to and the -axis is determined via the right-hand rule to complete the orthonormal triad.
- 2.
- A virtual LOS coordinate system, denoted as , is rigorously defined with its origin positioned at the VCM. The -axis is aligned with the target vector, the -axis is orthogonally oriented upward within the vertical plane relative to and the -axis is determined via the right-hand rule to complete the orthonormal triad.
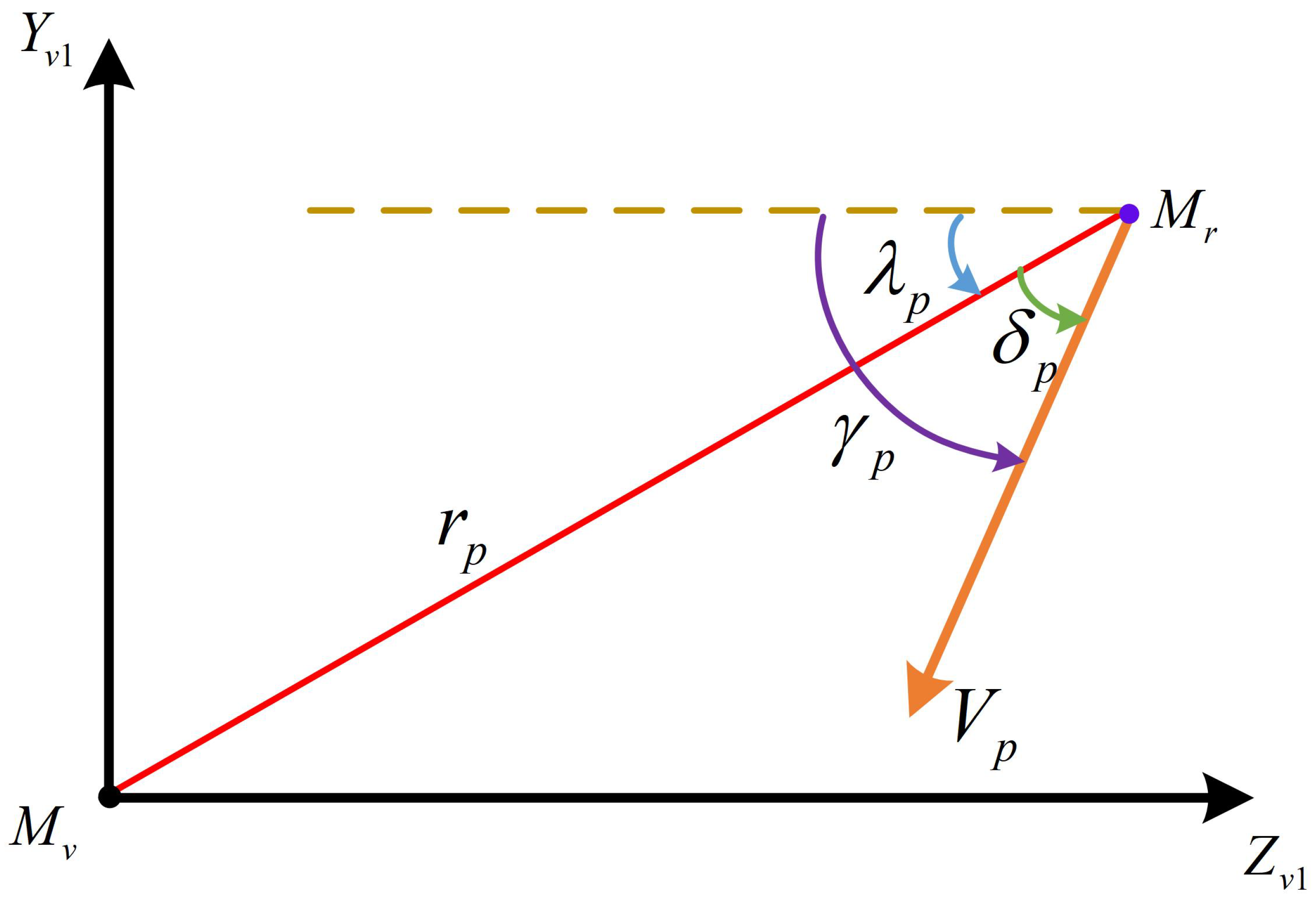
2.2.2. Relative Motion Model
3. Spiral Maneuvering Trajectory Design
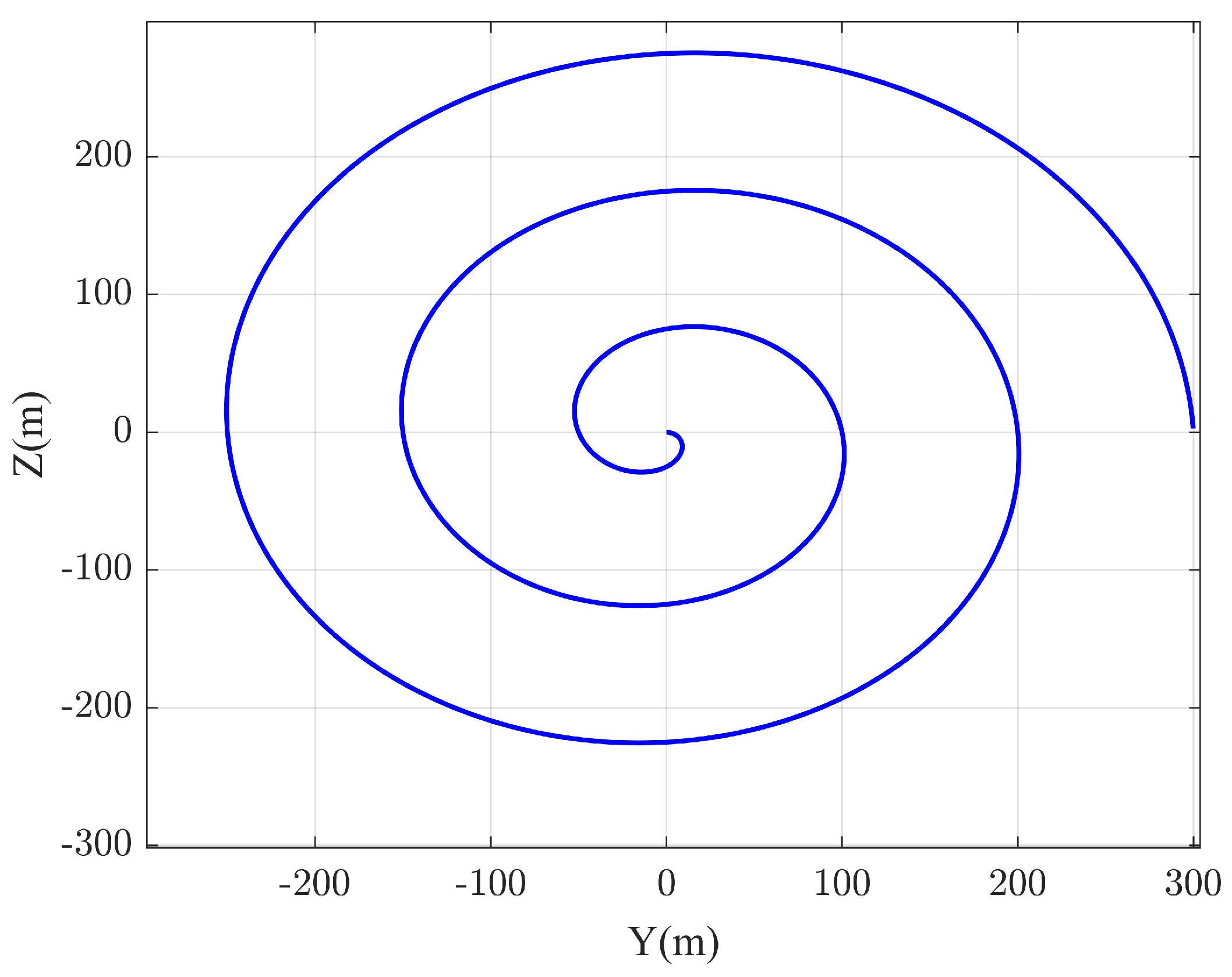
3.1. Plane Relative Spiral Motion Design Based on Archimedes Spiral
- 1.
- The initial LOS angle between the UAV and VCM is conventionally initialized to , enabling maneuver amplitude and frequency to be modulated by adjusting the number of spiral turns and the initial radial distance . Thus, the geometric configuration of the spiral is determined by the triad .
- 2.
- The total spiral maneuver duration often deviates from the UAV’s actual flight time. To reconcile this discrepancy, is numerically optimized via the Newton–Raphson iterative method to satisfy terminal guidance precision for stationary targets. For mobile targets, the adjusted maneuver time is adopted, advancing convergence to the virtual trajectory to mitigate kinematic discrepancies induced by target motion, thereby ensuring terminal guidance precision.
3.2. Virtual Trajectory Generation Based on DRL
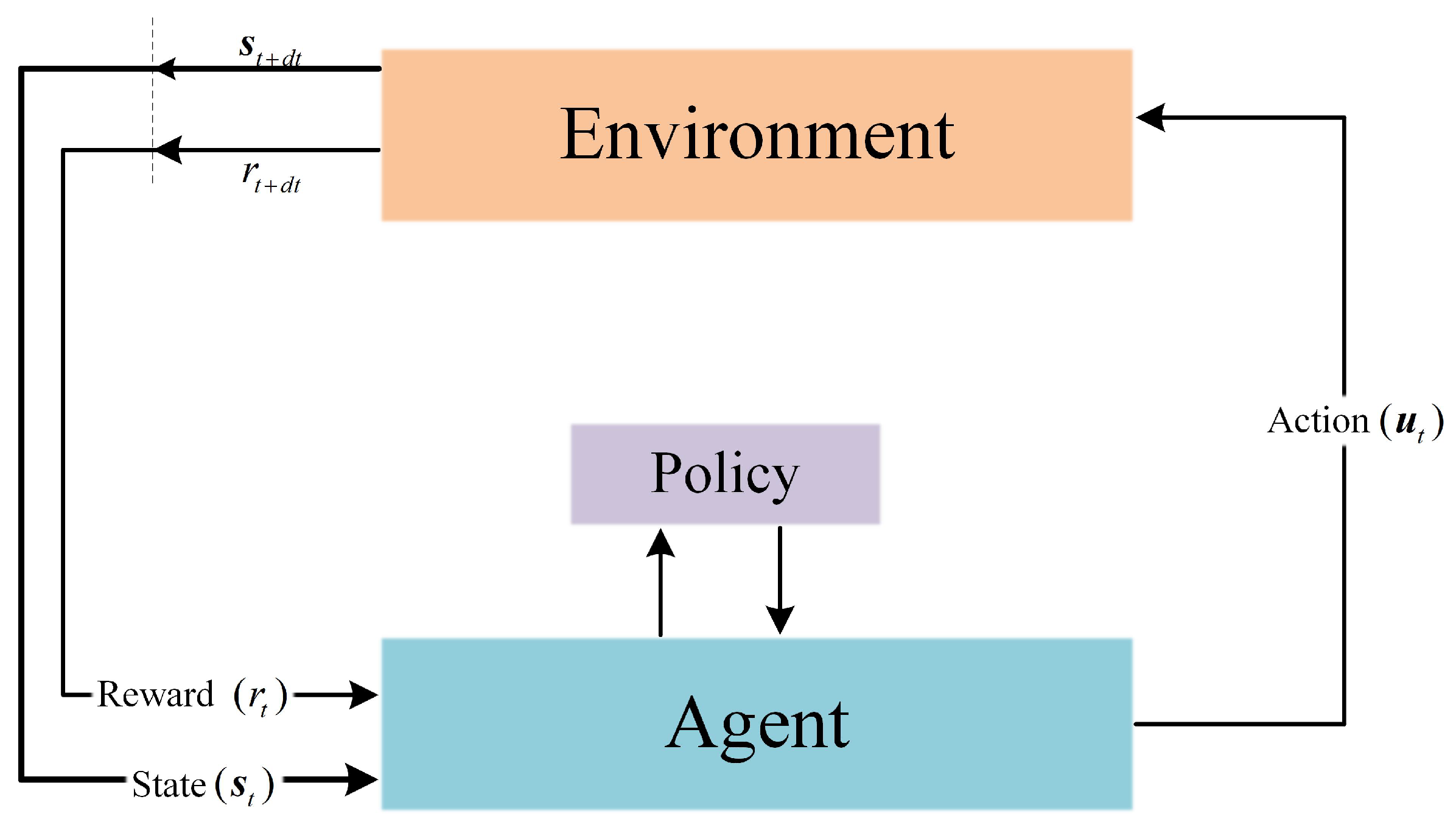
3.2.1. Reinforcement Learning Architecture
3.2.2. Interactive Scene
- (1)
- Target State Initialization
- (2)
- VCM State Initialization
- (3)
- VCM Velocity Compensation
3.2.3. MDP for Virtual Trajectory Generation
- (1)
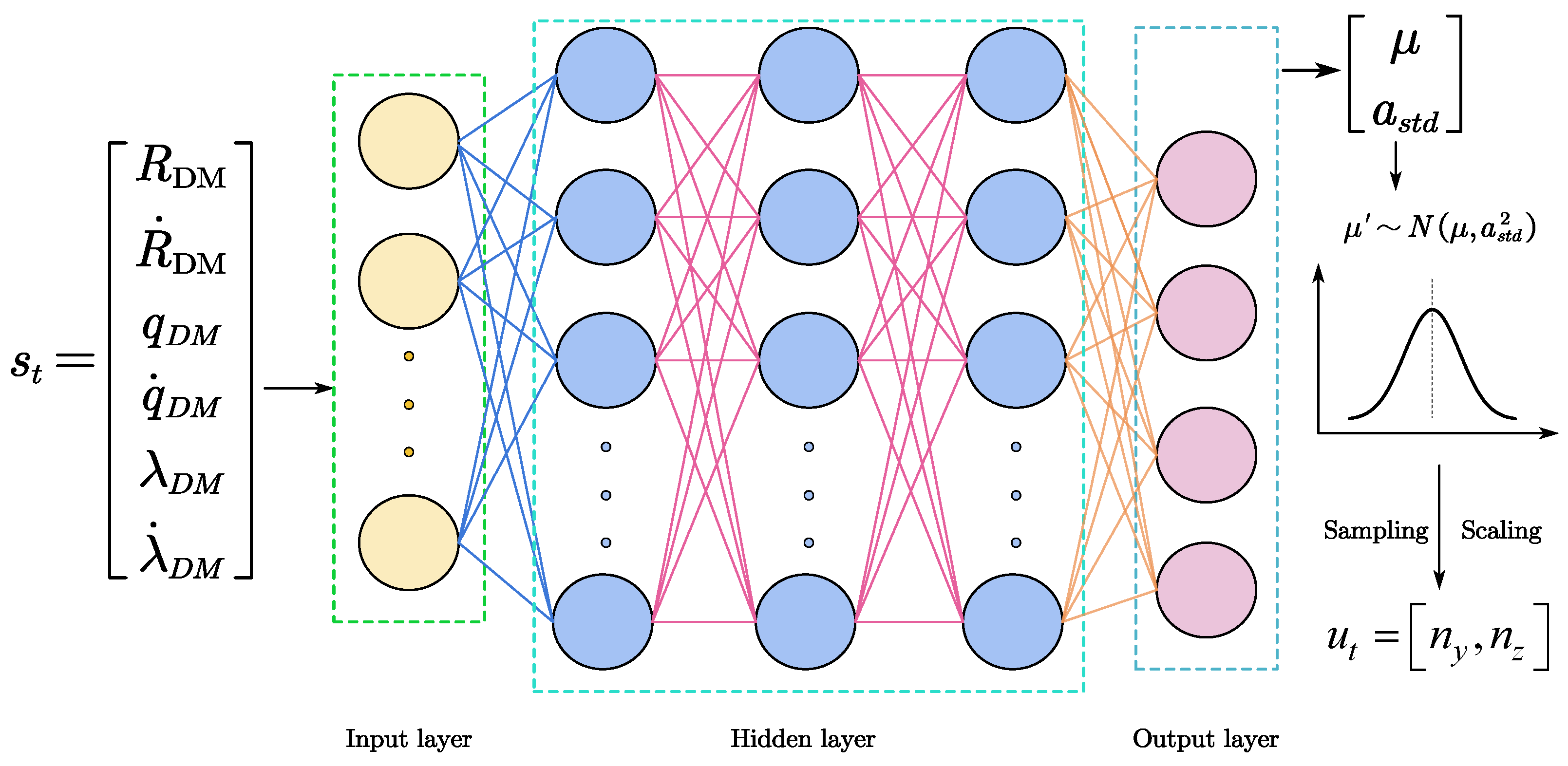
- State Space and Action Space Design
- (2)
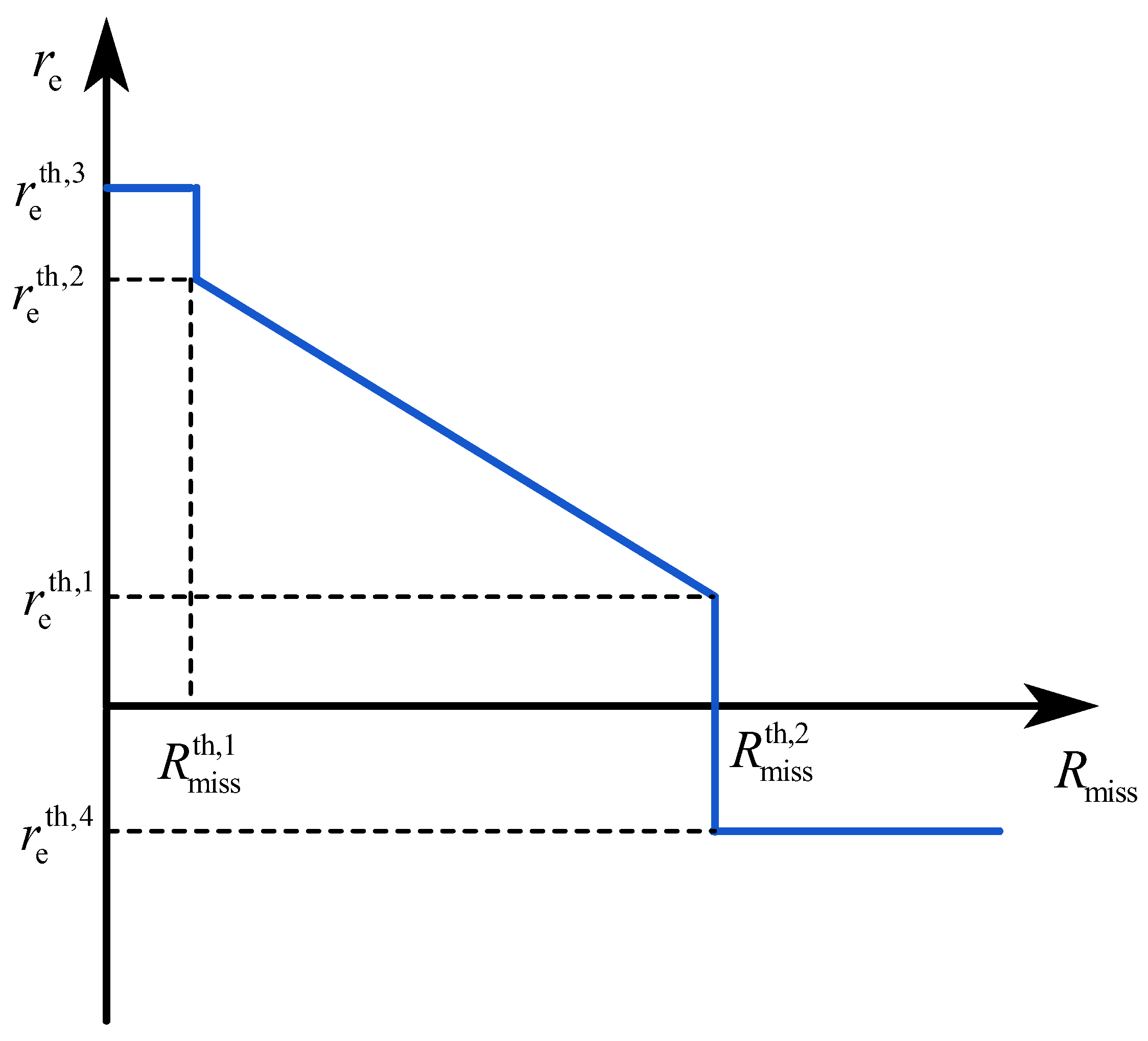
- Reward Function Architecture
3.2.4. Model Solving Based on PPO Algorithm
3.2.5. Network Structure Design
3.2.6. Learning Process
| Algorithm 1 Learning process |
|
3.3. Spiral Maneuvering Trajectory Generation
4. Simulation Analysis
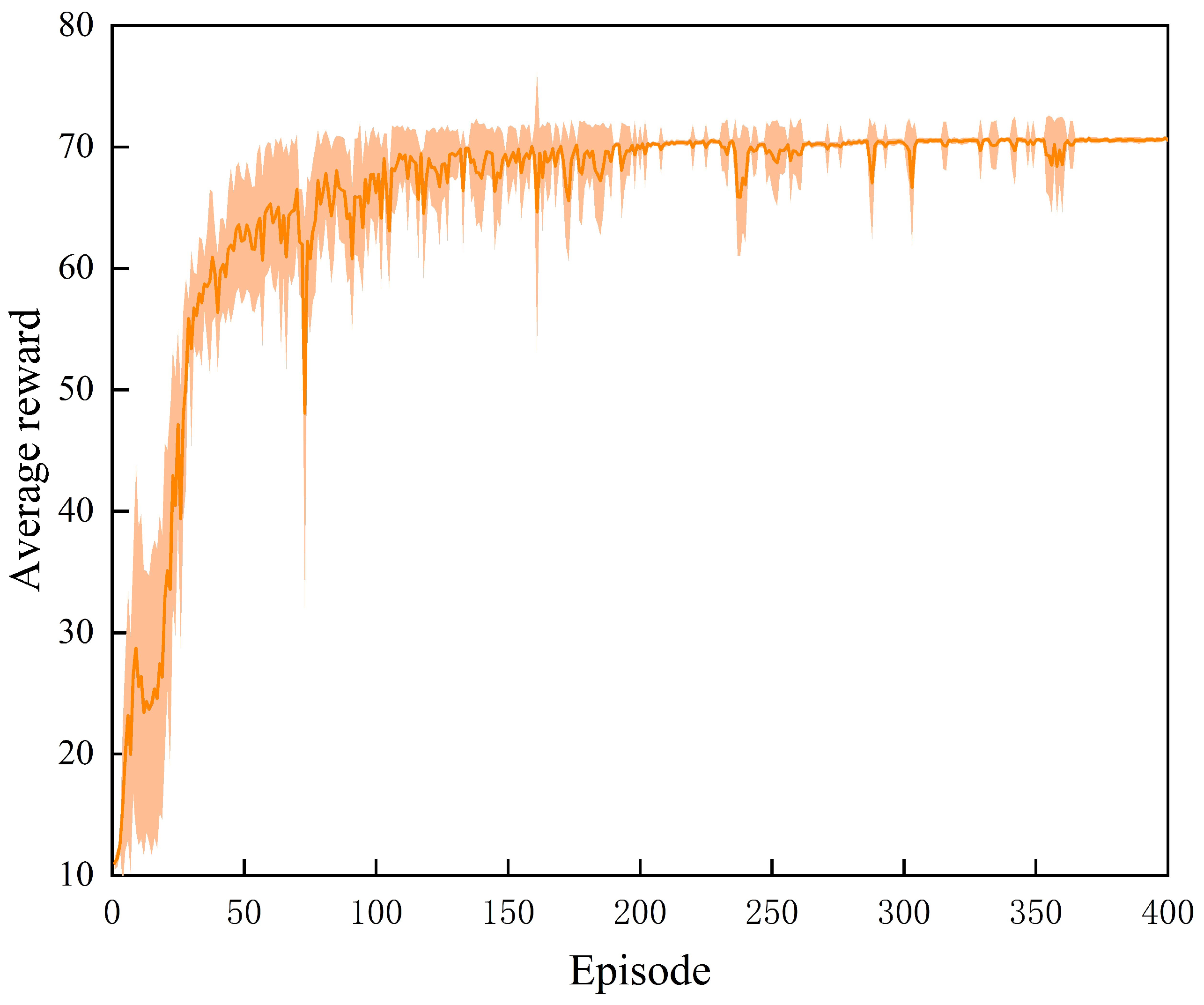
4.1. Training Process
4.2. Test Process
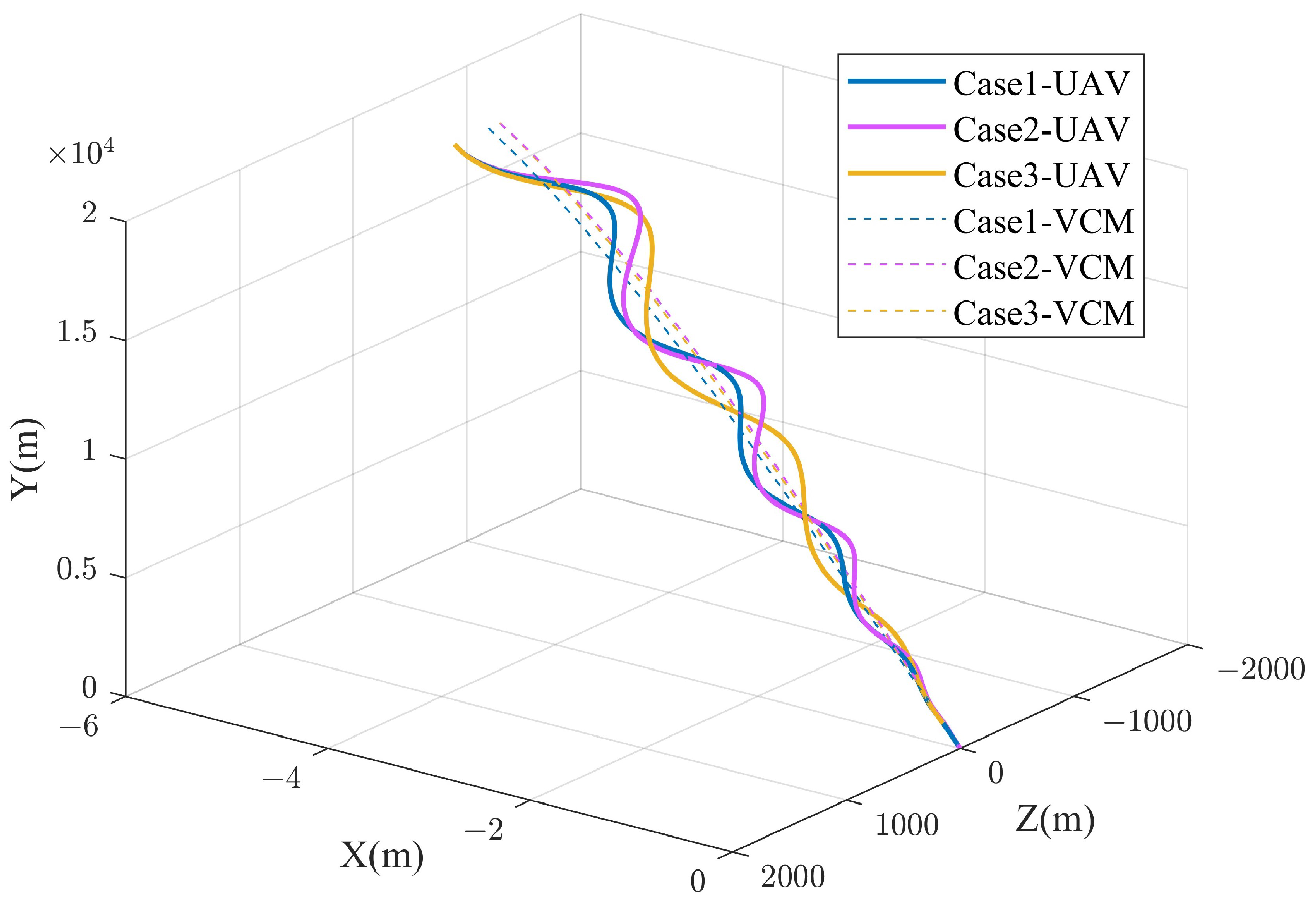
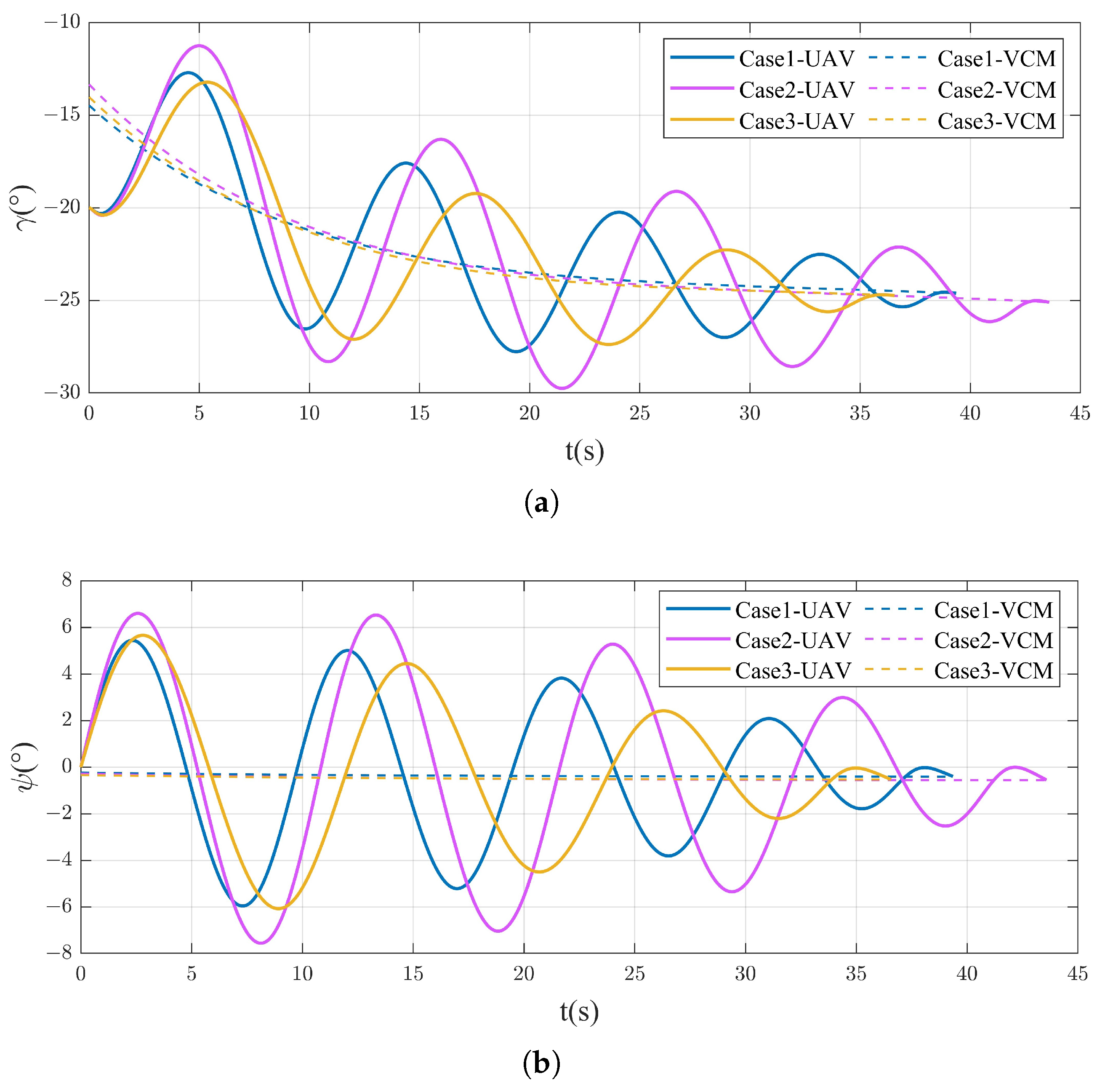
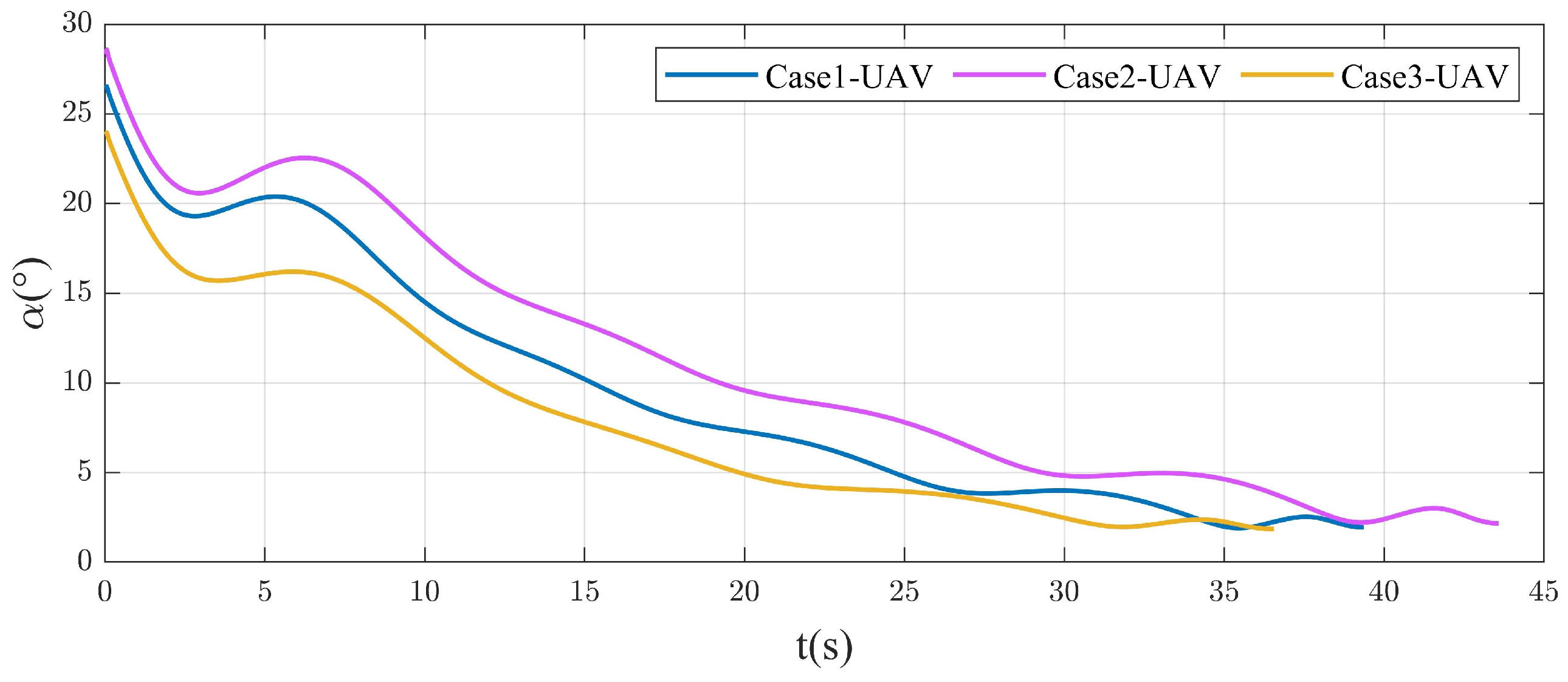
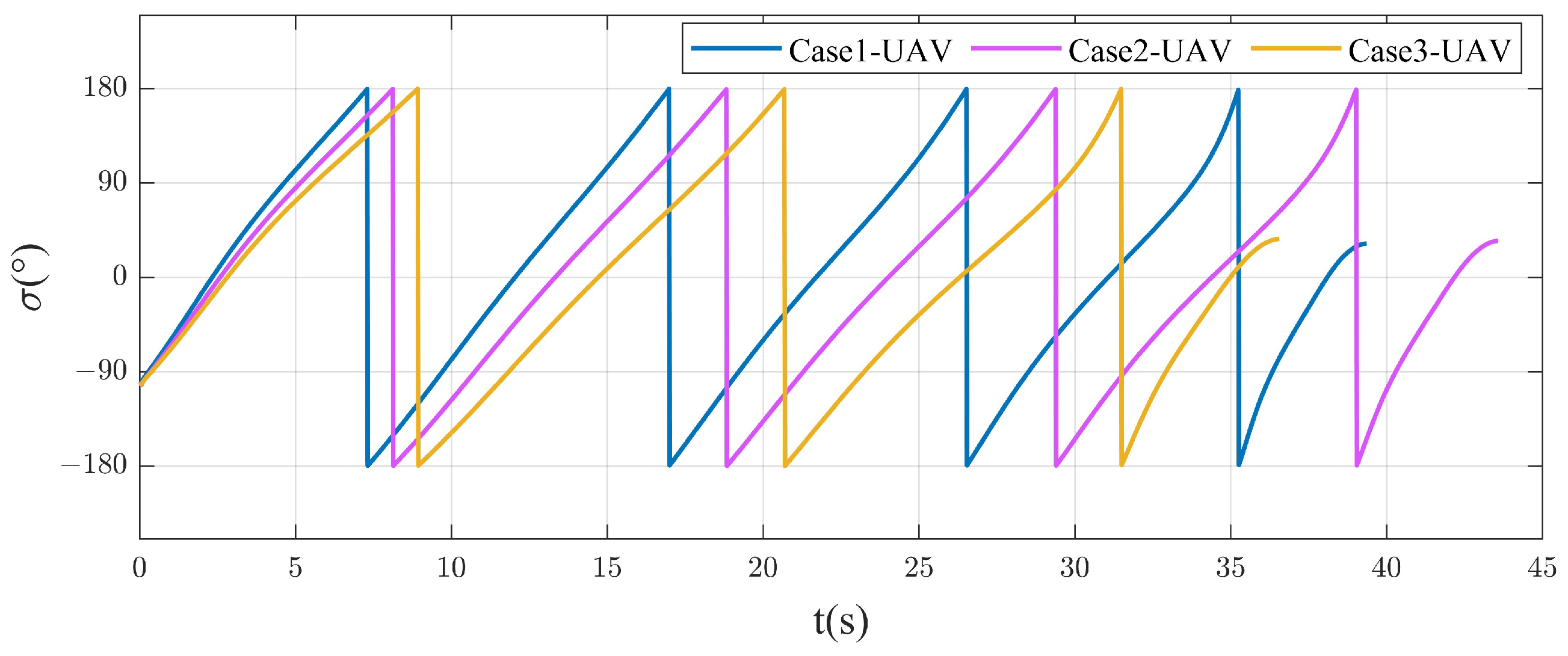
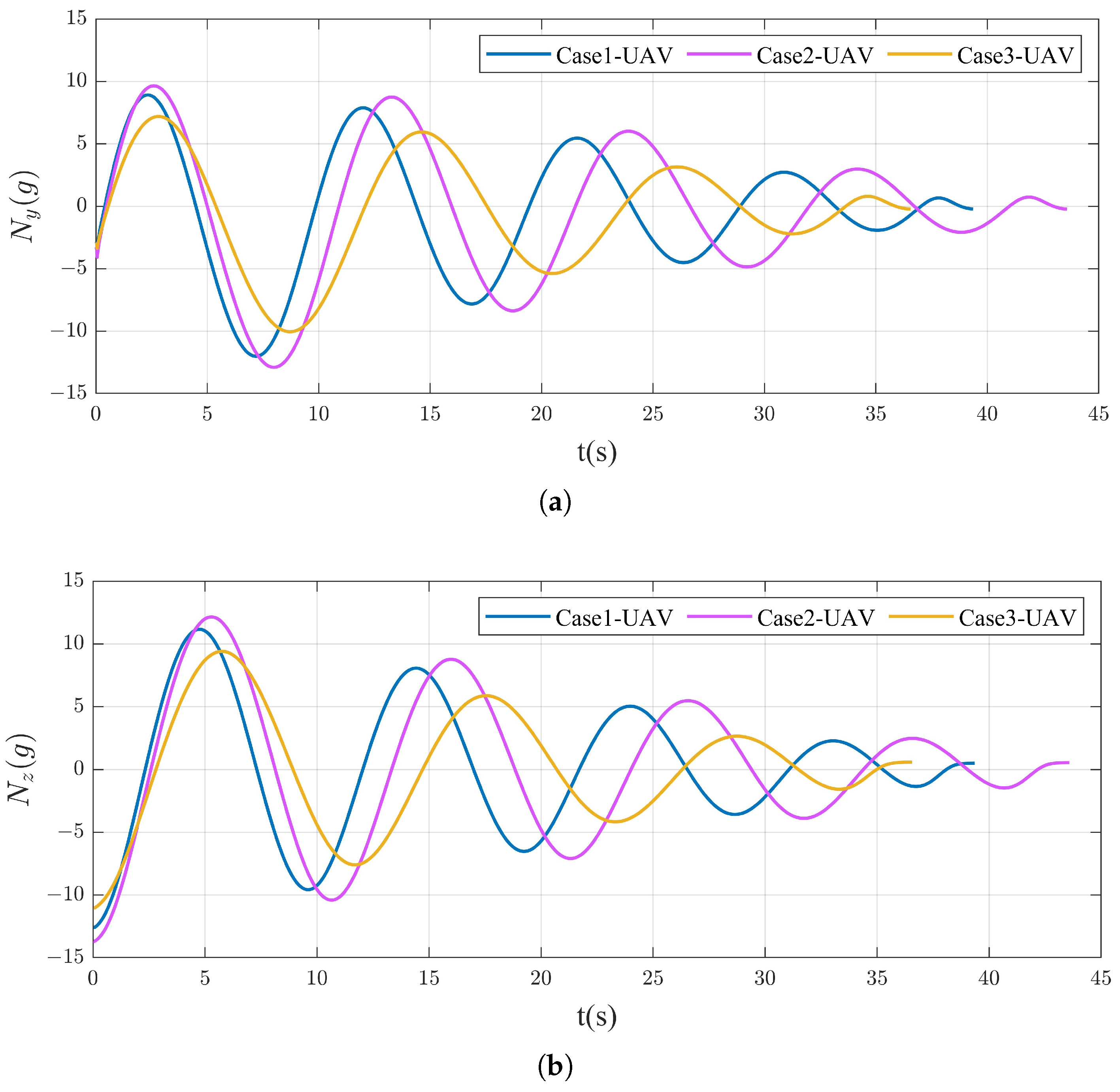
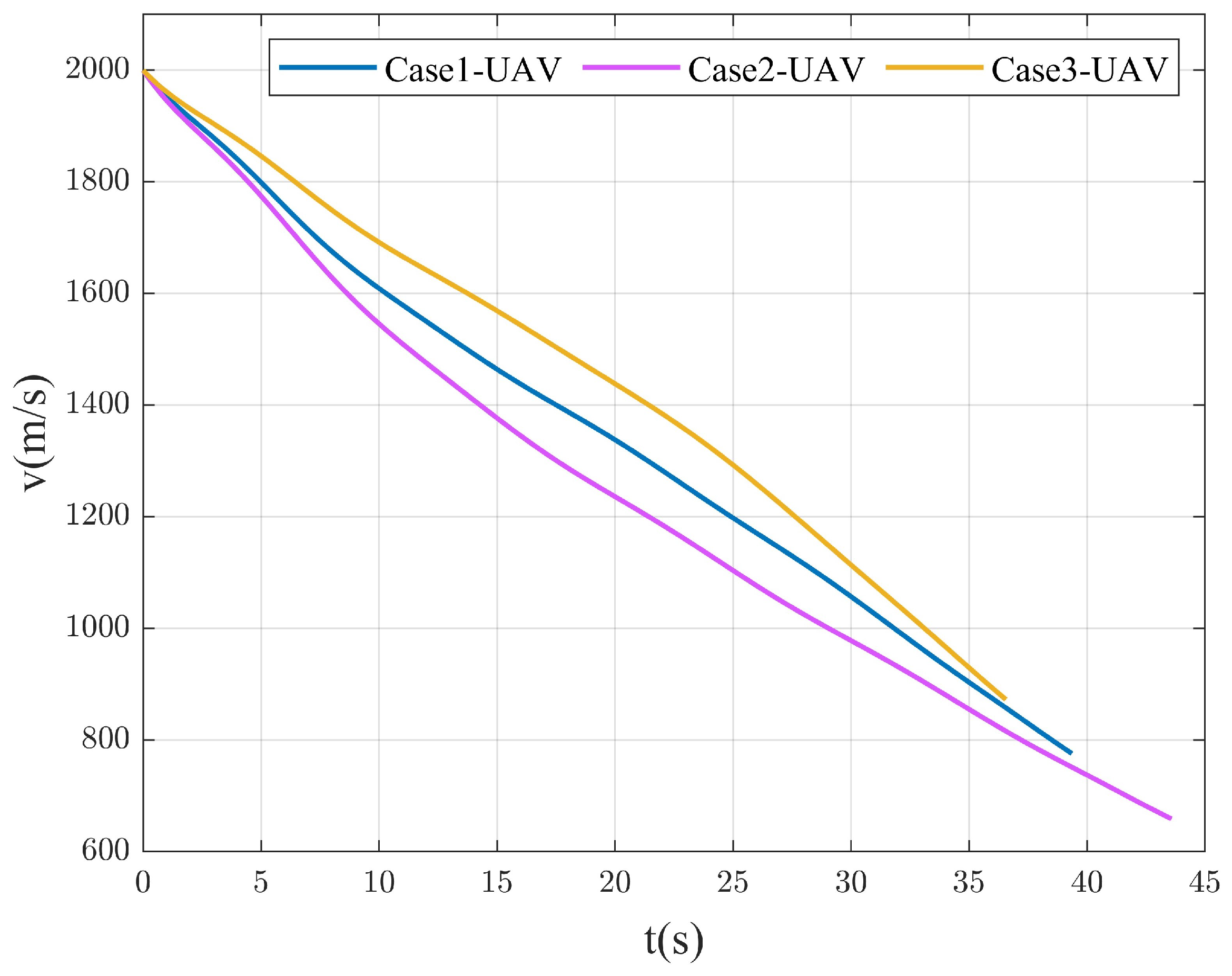
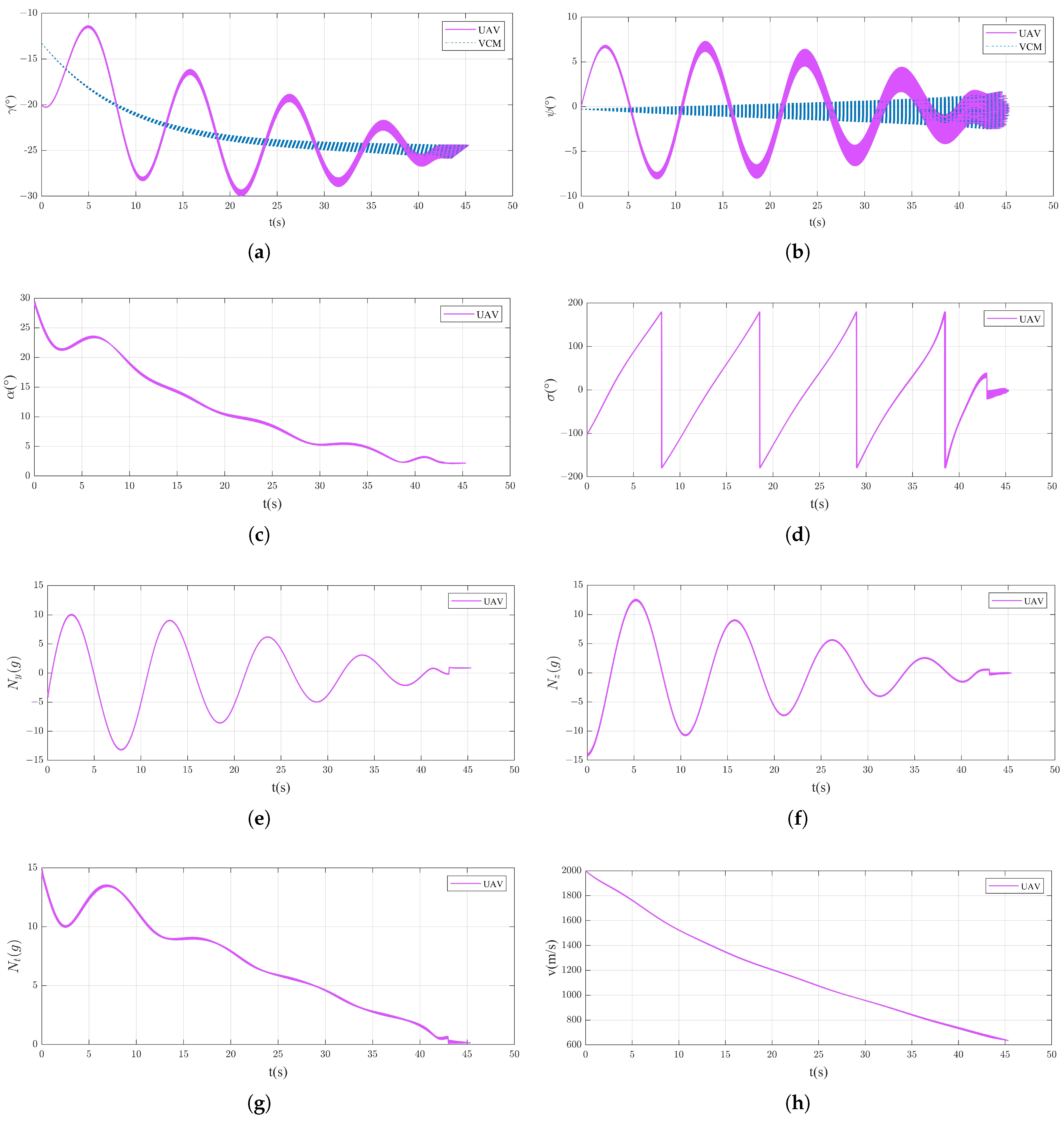
4.2.1. Different Spiral Parameters
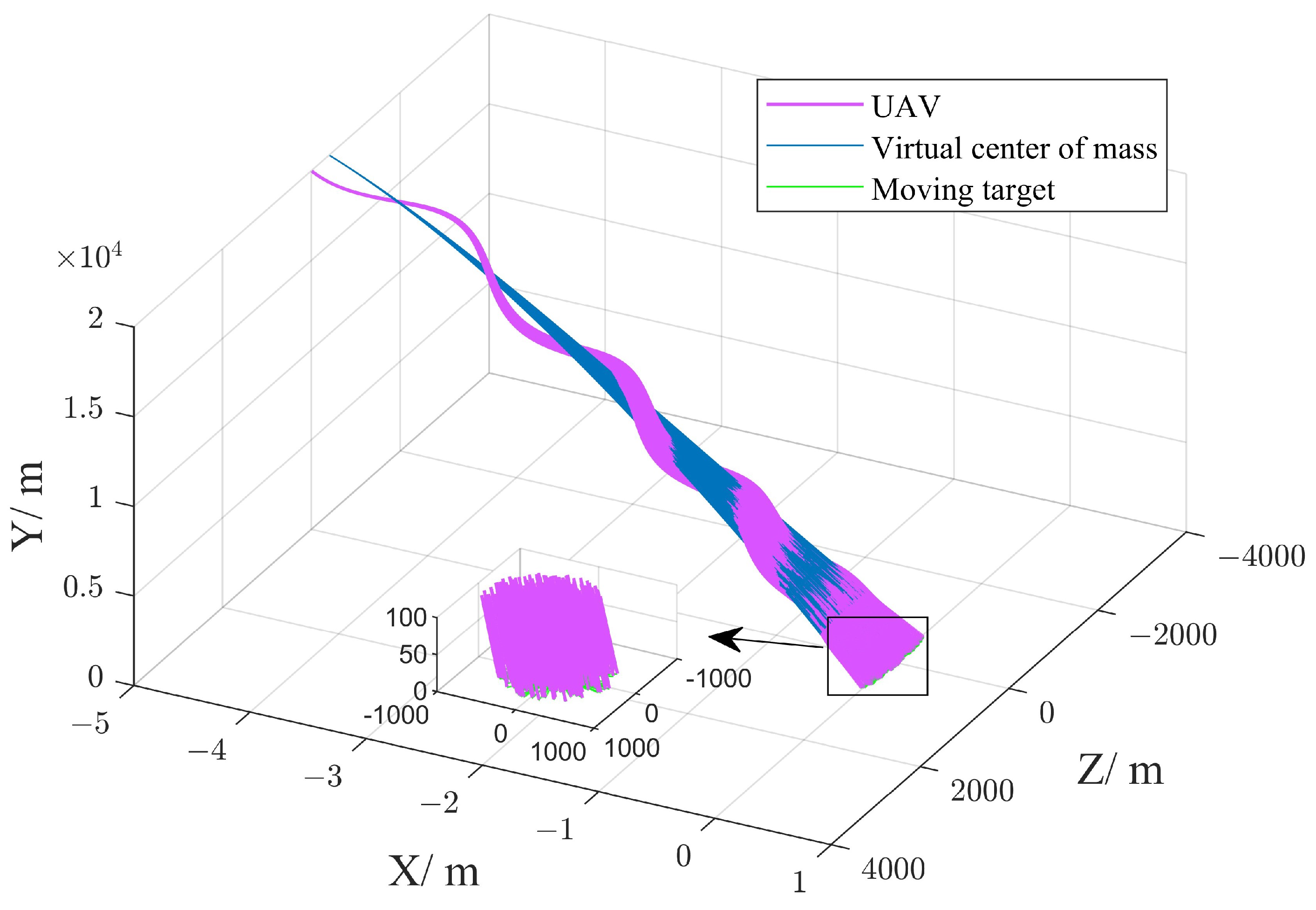
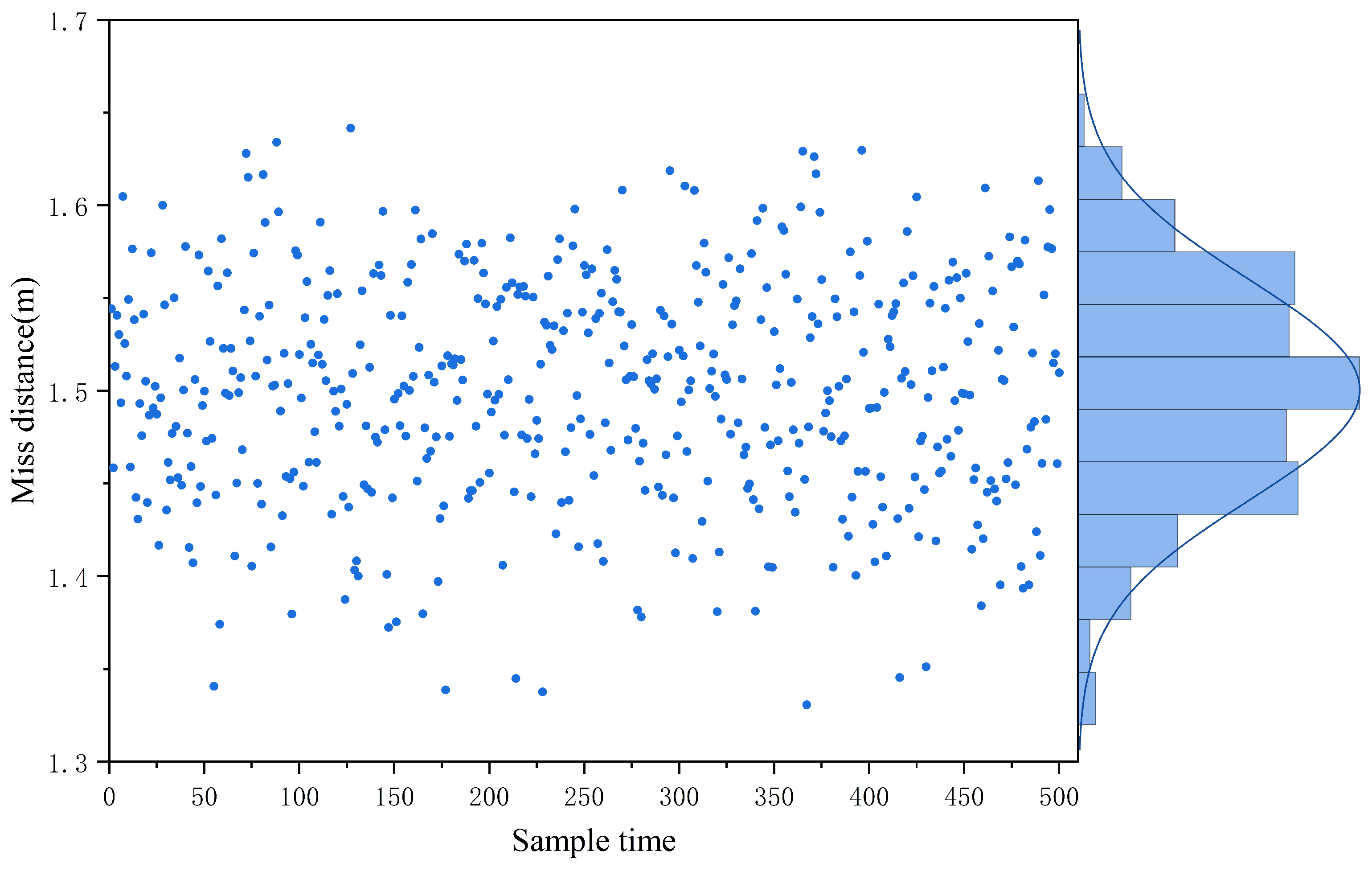
4.2.2. Attack Moving Target
4.3. Analysis of Computational Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| DRL | Deep reinforcement learning |
| MDP | Markov decision process |
| LOS | Line of sight |
| VCM | Virtual center of mass |
| RL | Reinforcement learning |
| GAE | Generalized advantage estimation |
| PPO | Proximal policy optimization |
References
- Guo, D.; Dong, X.; Li, D.; Ren, Z. Feasibility Analysis for Cooperative Interception of Hypersonic Maneuvering Target. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 4066–4071. [Google Scholar]
- Bużantowicz, W. Tuning of a Linear-Quadratic Stabilization System for an Anti-Aircraft Missile. Aerospace 2021, 8, 48. [Google Scholar] [CrossRef]
- Hu, Y.; Gao, C.; Li, J.; Jing, W. Maneuver mode analysis and parametric modeling for hypersonic glide vehicles. Aerosp. Sci. Technol. 2021, 119, 107166. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, J.; Bao, W.; Li, X.; Sun, H. A multi-constraint guidance and maneuvering penetration strategy via meta deep reinforcement learning. Drones 2023, 7, 626. [Google Scholar] [CrossRef]
- Luo, C.; Huang, C.; Ding, D.; Guo, H. Design of weaving penetration for hypersonic glide vehicle. Electron. Opt. Control 2013, 7, 67–72. [Google Scholar]
- Zhang, J.; Xiong, J.; Li, L.; Xi, Q.; Chen, X.; Li, F. Motion state recognition and trajectory prediction of hypersonic glide vehicle based on deep learning. IEEE Access 2022, 10, 21095–21108. [Google Scholar] [CrossRef]
- Zhu, J.; He, R.; Tang, G.; Bao, W. Pendulum maneuvering strategy for hypersonic glide vehicles. Aerosp. Sci. Technol. 2018, 78, 62–70. [Google Scholar] [CrossRef]
- Li, G.; Zhang, H.; Tang, G. Maneuver characteristics analysis for hypersonic glide vehicles. Aerosp. Sci. Technol. 2015, 43, 321–328. [Google Scholar] [CrossRef]
- Ohlmeyer, E.J. Root-mean-square miss distance of proportional navigation missile against sinusoidal target. J. Guid. Control. Dyn. 1996, 19, 563–568. [Google Scholar] [CrossRef]
- Kim, J.; Vaddi, S.; Menon, P.; Ohlmeyer, E. Comparison between three spiraling ballistic missile state estimators. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 7459. [Google Scholar]
- Yanushevsky, R. Analysis of optimal weaving frequency of maneuvering targets. J. Spacecr. Rocket. 2004, 41, 477–479. [Google Scholar] [CrossRef]
- Zhao, K.; Cao, D.; Huang, W. Maneuver control of the hypersonic gliding vehicle with a scissored pair of control moment gyros. Sci. China Technol. Sci. 2018, 61, 1150–1160. [Google Scholar] [CrossRef]
- Liang, Z.; Xiong, F. A Maneuvering Penetration Guidance Law Based on Variable Structure Control. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020; pp. 2067–2071. [Google Scholar]
- Bin, Z.; Tianze, L.; Tianyang, X.; Changshu, W. Cooperative guidance for maneuvering penetration with attack time consensus and bounded input. Int. J. Aeronaut. Space Sci. 2024, 25, 1395–1411. [Google Scholar] [CrossRef]
- Kim, Y.H.; Ryoo, C.K.; Tahk, M.J. Guidance synthesis for evasive maneuver of anti-ship missiles against close-in weapon systems. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1376–1388. [Google Scholar] [CrossRef]
- Yu, X.; Luo, S.; Liu, H. Integrated design of multi-constrained snake maneuver surge guidance control for hypersonic vehicles in the dive segment. Aerospace 2023, 10, 765. [Google Scholar] [CrossRef]
- He, L.; Yan, X. Adaptive terminal guidance law for spiral-diving maneuver based on virtual sliding targets. J. Guid. Control. Dyn. 2018, 41, 1591–1601. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, X.; Bai, Y.; Li, Y. Intelligent Online Multiconstrained Reentry Guidance Based on Hindsight Experience Replay. Int. J. Aerosp. Eng. 2023, 2023, 5883080. [Google Scholar] [CrossRef]
- Li, G.; Li, S.; Li, B.; Wu, Y. Deep Reinforcement Learning Guidance with Impact Time Control. J. Syst. Eng. Electron. 2024, 35, 1594–1603. [Google Scholar] [CrossRef]
- Wang, N.; Wang, X.; Cui, N.; Li, Y.; Liu, B. Deep reinforcement learning-based impact time control guidance law with constraints on the field-of-view. Aerosp. Sci. Technol. 2022, 128, 107765. [Google Scholar] [CrossRef]
- Fan, J.; Dou, D.; Ji, Y. Impact-angle constraint guidance and control strategies based on deep reinforcement learning. Aerospace 2023, 10, 954. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Kim, Y.; Han, Y.; Kwon, H.; Hong, D. Impact angle control guidance considering seeker’s field-of-view limit based on reinforcement learning. J. Guid. Control. Dyn. 2023, 46, 2168–2182. [Google Scholar] [CrossRef]
- Jiang, L.; Nan, Y.; Zhang, Y.; Li, Z. Anti-interception guidance for hypersonic glide vehicle: A deep reinforcement learning approach. Aerospace 2022, 9, 424. [Google Scholar] [CrossRef]
- Yan, T.; Liu, C.; Gao, M.; Jiang, Z.; Li, T. A Deep Reinforcement Learning-Based Intelligent Maneuvering Strategy for the High-Speed UAV Pursuit-Evasion Game. Drones 2024, 8, 309. [Google Scholar] [CrossRef]
- Tripathy, T.; Shima, T. Archimedean spiral-based intercept angle guidance. J. Guid. Control. Dyn. 2019, 42, 1105–1115. [Google Scholar] [CrossRef]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Engstrom, L.; Ilyas, A.; Santurkar, S.; Tsipras, D.; Janoos, F.; Rudolph, L.; Madry, A. Implementation matters in deep policy gradients: A case study on ppo and trpo. arXiv 2020, arXiv:2005.12729. [Google Scholar]
- Phillips, T.H. A Common Aero Vehicle (CAV) Model, Description, and Employment Guide; Schafer Corporation: Arlington, VA, USA, 2003. [Google Scholar]

| Serial Number | Euler Angle | Definition Description |
|---|---|---|
| 1 | The angular relationship between the and coordinate systems is defined by the velocity slope angle and velocity azimuth of the UAV. | |
| 2 | The angular relationship between the and coordinate systems is defined by the virtual velocity slope angle and virtual velocity azimuth of the VCM. | |
| 3 | The angular relationship between the and coordinate systems is defined by the LOS altitude angle and azimuth angle of the UAV. | |
| 4 | The angular relationship between the and coordinate systems is defined by the LOS altitude angle and azimuth angle of the VCM. |
| Network Level | Actor Network | Critic Network | ||
|---|---|---|---|---|
| Units | Activation Function | Units | Activation Function | |
| Input layer | 6 | None | 6 | None |
| Hidden layer 1 | 128 | Tanh | 128 | Tanh |
| Hidden layer 2 | 128 | Tanh | 128 | Tanh |
| Hidden layer 3 | 128 | Tanh | 128 | Tanh |
| Output layer | 4 | Tanh/Linear | 1 | Linear |
| Object | Physical Quantity | Value |
|---|---|---|
| UAV | −50 km, 20 km, 0 km | |
| 2000 m/s, −20°, 0° | ||
| Target | 0 m, 0 m, 0 m |
| Hyperparameter | Value | Hyperparameter | Value |
|---|---|---|---|
| 0.01 | 0.25 | ||
| 10.0 | 0.01 | ||
| 50.0 | 0.5 | ||
| 51.0 | 0.2 | ||
| 2.0 | 0.0001 | ||
| 100.0 | 0.0001 | ||
| 20,000 | 400 | ||
| 128 | 200 | ||
| 0.995 | 20 | ||
| 0.95 | 5.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Li, S.; Xian, Y.; Ren, L.; Liu, Z. UAV Spiral Maneuvering Trajectory Intelligent Generation Method Based on Virtual Trajectory. Drones 2025, 9, 446. https://doi.org/10.3390/drones9060446
Chen T, Li S, Xian Y, Ren L, Liu Z. UAV Spiral Maneuvering Trajectory Intelligent Generation Method Based on Virtual Trajectory. Drones. 2025; 9(6):446. https://doi.org/10.3390/drones9060446
Chicago/Turabian StyleChen, Tao, Shaopeng Li, Yong Xian, Leliang Ren, and Zhenyu Liu. 2025. "UAV Spiral Maneuvering Trajectory Intelligent Generation Method Based on Virtual Trajectory" Drones 9, no. 6: 446. https://doi.org/10.3390/drones9060446
APA StyleChen, T., Li, S., Xian, Y., Ren, L., & Liu, Z. (2025). UAV Spiral Maneuvering Trajectory Intelligent Generation Method Based on Virtual Trajectory. Drones, 9(6), 446. https://doi.org/10.3390/drones9060446






