Abstract
Unmanned aerial vehicles (UAVs) have emerged as a promising solution for collaborative search missions in complex environments. However, in the presence of interference, communication disruptions between UAVs and ground control stations can severely degrade coordination efficiency, leading to prolonged search times and reduced mission success rates. To address these challenges, this paper proposes a novel multi-agent deep reinforcement learning (MADRL) framework for joint spectrum and search collaboration in multi-UAV systems. The core problem is formulated as a combinatorial optimization task that simultaneously optimizes channel selection and heading angles to minimize the total search time under dynamic interference conditions. Due to the NP-hard nature of this problem, we decompose it into two interconnected Markov decision processes (MDPs): a spectrum collaboration subproblem solved using a received signal strength indicator (RSSI)-aware multi-agent proximal policy optimization (MAPPO) algorithm and a search collaboration subproblem addressed through a target probability map (TPM)-guided MAPPO approach with an innovative action-masking mechanism. Extensive simulations demonstrate superior performance compared to baseline methods (IPPO, QMIX, and IQL). Extensive experimental results demonstrate significant performance advantages, including 68.7% and 146.2% higher throughput compared to QMIX and IQL, respectively, along with 16.7–48.3% reduction in search completion steps versus baseline methods, while maintaining robust operations under dynamic interference conditions. The framework exhibits strong resilience to communication disruptions while maintaining stable search performance, validating its practical applicability in real-world interference scenarios.
1. Introduction
With characteristics such as low costs, good mobility, flexibility, and ease of deployment, unmanned aerial vehicles (UAVs) have found extensive applications in tasks such as communication coverage [1,2], reconnaissance [3,4], and search and rescue [5,6]. A notable advantage of multi-UAV missions over single-UAV operations is the enhancement of task efficiency and reliability, particularly in complex and large-scale task management scenarios [7]. This enhancement is achieved by leveraging the collaborative capabilities of multiple UAVs, which rely on real-time communication to ensure effective coordination and collaboration. The success of a multi-UAV collaborative mission is contingent upon the design of a coordination algorithm that ensures both efficient task execution among the UAVs and reliable communication between them.
Multi-UAV collaborative search is one of the typical application scenarios of multi-UAV systems. Such scenarios include post-disaster relief [8,9], coordinated targeting during operations [10,11], border patrol [12,13], and perimeter monitoring [14,15]. These tasks usually involve characteristics such as unknown target locations, wide-area coverage, and time sensitivity. Therefore, multi-UAV collaborative search algorithms often aim to maximize target detection rates, area coverage, and search efficiency. It is evident that a taxonomy of search methods exists and that these can be classified into two distinct categories: static search and dynamic search [16,17,18].
In static search, UAVs perform searches according to pre-planned routes, such as the Zamboni search [19] and spiral search [20], covering the entire task area to identify targets. In static environments or when there is no prior knowledge of the task area, static searches can yield good results due to their simplicity and ease of implementation, but they are often difficult to apply in dynamic environments.
In contrast, a dynamic search is more suitable for dynamic environments. Since the state information in a dynamic environment may change at any time, UAVs in dynamic searches make collaborative search decisions in each time slot based on their observations and communications with other UAVs, offering greater flexibility and applicability, thereby fostering extensive research in this area. Zheng et al. [21] proposed a distributed real-time-search path planning method based on the framework of distributed model predictive control. In order to address the issue of time-sensitive moving targets in uncertain dynamic environments, Yang et al. [22] provided an intelligent collaborative task planning scheme for UAV swarms based on hybrid artificial potential field and ant colony optimization. In [23], the authors investigated a multi-layer aerial computing network search scenario, and a multi-agent deep reinforcement learning method is proposed based on parameter sharing and action masking. To tackle the challenge of target searches by UAV swarms in unknown three-dimensional environments, paper [24] introduced a cooperative target search method based on the improved wolf pack algorithm, which enhances the efficiency of target search operations. In order to enhance the scalability and cooperation of UAV swarm search methods, the authors of [25] designed a distributed cooperative search method based on multi-agent reinforcement learning algorithms, which can operate efficiently in complex, large-scale environments. The author of [26] presented a weighted area model mapped by a Monte Carlo drift prediction model, and three reinforcement learning algorithms were employed to address the weighted area coverage issue during actual rescue processes. Paper [27] considered the issues of collaborative control and search area coverage in multi-UAV cooperative searches and used an enhanced binary logarithmic learning algorithm to address the problem.
Recent advances in multi-UAV cooperative systems have progressively addressed three critical aspects of collaborative operations: communication reliability, search efficiency, and interference resilience. While early studies primarily focused on optimizing search patterns and coverage strategies, the fundamental role of communication in enabling effective coordination has gained increasing recognition. Initial approaches to maintaining connectivity relied heavily on distance-based models, as demonstrated by local communication network architecture [28] and relay UAV deployment strategy [29]. Subsequent refinements incorporated more sophisticated connectivity maintenance techniques, including priority-based positioning systems [30] and deep Q-learning pheromone models [31], marking important steps toward robust multi-UAV operations.
The field has witnessed parallel developments in interference-resistant coordination, with notable contributions including robust trajectory planning using convex optimization by [32] and overlapped sensing schemes for improved transmission efficiency [33]. Decentralized architectures have emerged as a promising direction, exemplified by consensus-based ant colony optimization [34] and attention mechanism-enhanced planning for communication-restricted scenarios [35]. Bio-inspired techniques have shown particular promise, with bird flocking algorithms [36] and game-theoretic approaches [37] demonstrating effective coordination in complex environments. Recent learning-based methods have pushed the boundaries further, with deep reinforcement learning frameworks for joint computation offloading [38] and advantage dueling Q-learning algorithms setting new benchmarks for autonomous operations in unknown environments [39]. Various strategies have been proposed to handle communication disruptions, ranging from metacognitive decision-making [40] to information compensation methods [41], while dynamic adaptation techniques have been explored through multi-UAV deployment [29] and adaptive search strategies [34].
Despite these advancements, existing solutions exhibit three key limitations: (1) most distance-based connectivity models fail to account for external interference, (2) many learning approaches neglect real-time spectrum constraints, and (3) few frameworks successfully integrate communication and search optimization. While studies like [42,43] advanced search efficiency, they overlooked communication constraints, and approaches such as [44,45] addressed communication limitations without considering spectrum contentions. Even recent works like the human–UAV interaction system [46] and information fusion methods [47] retain centralized coordination elements, while the minimum time search algorithm [48] maintains dependence on ground station connectivity.
Our work bridges these gaps through three key innovations: first, by developing the first fully decentralized framework that jointly optimizes spectrum access and search efficiency; second, through a novel integration of RSSI-aware MAPPO for dynamic spectrum coordination; and third, via TPM-guided MAPPO with action masking for constrained search optimization. This comprehensive approach advances beyond current solutions by simultaneously addressing interference resilience and real-time adaptability while maintaining superior performance metrics, as clearly demonstrated in Table 1. The table highlights our unique position as the only solution that successfully integrates all four critical dimensions of multi-UAV cooperative systems under interference conditions.

Table 1.
Comparative analysis of related works.
In order to cope with the foregoing issues, we propose a collaborative search scheme for multi-UAVs under interference conditions based on a specifically designed multi-agent reinforcement learning algorithm. The significant contributions are as follows:
- A collaborative search model for multi-UAVs under interference conditions is established. Based on this model, an optimization problem is constructed with the goal of minimizing the total search time by jointly optimizing the channel selection and search heading angles of the UAVs. To reduce the complexity of solving the problem, the optimization is decomposed into two subproblems, corresponding to spectrum collaboration under interference conditions and undisturbed search collaboration.
- An MAPPO-based spectrum collaboration algorithm that only requires the RSSI of the channels is proposed to enhance the algorithm’s real-time responsiveness, allowing each UAV to complete the collaboration without needing to know the channel’s state information between other nodes.
- An MAPPO-based search collaboration algorithm that takes the TPM of the task area as a shared message is designed to optimize the heading of the UAVs. In addition, action masking based on the current state and the previous state is employed in the search collaboration to improve the convergence speed of the algorithm. The policy network is also delicately designed with two convolutional neural networks to match the two-dimensional TPM.
The rest of the study is organized as follows: Section 2 describes the UAV search model and the UAV communication model. The problem formulation is elaborated in Section 2.4. The MAPPO-based spectrum collaboration and search collaboration are detailed in Section 2.4. The numerical results are presented in Section 3. The paper concludes in Section 4.
2. System Model
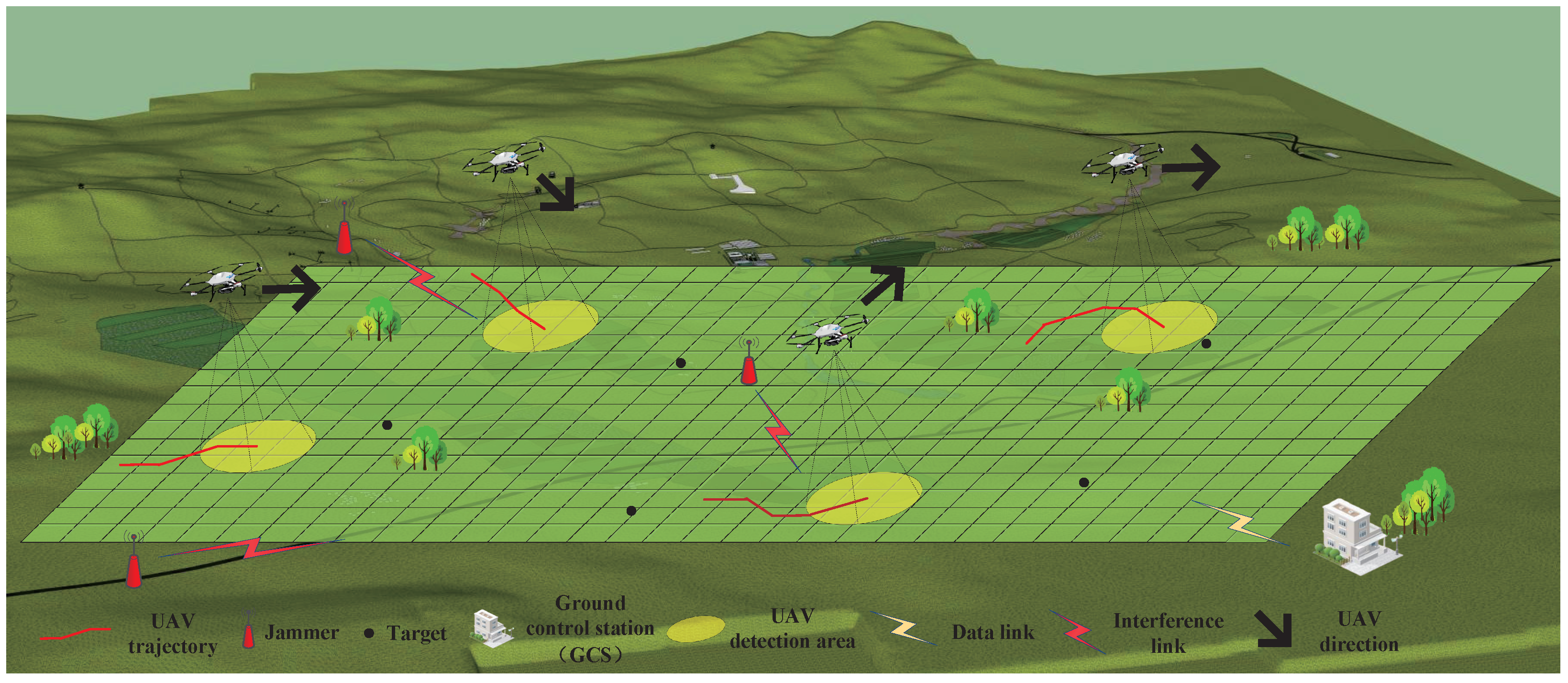
As shown in Figure 1, N reconnaissance UAVs collaboratively search an area containing M stationary targets at altitude H. For each reconnaissance UAV, the number of targets is unknown, and its perception of the environment is based on previous reconnaissance data or pertinent prior knowledge. Upon entering the task area, the reconnaissance UAVs employ onboard sensors to locate targets, collect reconnaissance data, and send this information to the ground control station in real time. The ground control station aggregates the detection data from all UAVs and subsequently broadcasts this information to each UAV, facilitating a collaborative search among multiple UAVs. Furthermore, there are several jammers in the task area that disrupt communication between the ground control station and the UAVs.
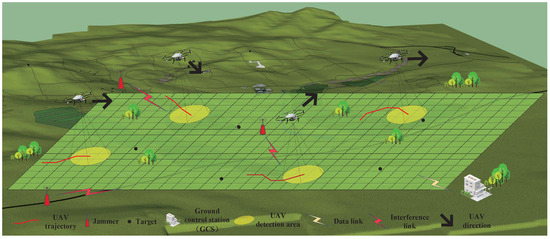
Figure 1.
System model.
2.1. UAV Search Model
To establish a multi-UAV collaborative search model, the task area is divided into discrete grids, with each grid being a square of side length L. Here, L represents the flight distance of the UAVs during one search decision cycle. Any grid within the task area can be represented by the coordinates of its center point , , .
To simplify the search space of the UAVs, we assume that each UAV can only move to one of the 8 neighboring grids, thus providing 8 feasible heading angles, denoted as , with the corresponding direction vectors represented as . Considering the turning angle constraints for the UAVs, we assume that the change in flight direction between two adjacent time slots cannot exceed 45°. Let the flight direction of the UAV i at time slot t be denoted as . Then, at time slot , the feasible flight direction set for the drone is . Since the distance traveled by the UAVs when flying diagonally () is times that of flying along the edge (), to ensure that the UAV is always centered in the grid when making a search decision, we assume that the corresponding flight speeds for the two types of flight directions are and v. Let represent the position of the drone at time t; then, the positional relationship of UAV i within two consecutive decision cycles can be expressed as
Assuming that the UAV conducts reconnaissance of the target using a downward-looking circular scanning method, as shown in Figure 1, the detection radius of the onboard sensors is , the detection probability is , and the false alarm probability is . Thus, the probability distribution for the UAVs detecting a target can be expressed as
where represents the probability of the UAV detecting the target at a distance l and . To reduce the complexity of probability calculations, we assume that there is at most one target in each grid of the task area.
2.2. Target Probability Map
To describe the probability distribution of the target in the task area at different time slots, we introduce the target probability map (TPM) [49]. The TPM for the task area at time slot t can be defined as
where represents the probability of a target at grid at time slot t. The TPM update formula derived from Bayes’ theorem is as follows:
where denotes the detection result of the UAV for the grid at time slot t. In general, , and it can be easily proven that for and for . For the grid in which UAVs bear no prior knowledge of the probability of the presence of a target, . As the search proceeds, . Let and be the thresholds for determining the absence and presence of a target, respectively. Once , it can be concluded that there is no target within the grid ; once , it can be determined that a target exists within grid .
To reduce the update complexity of (4) and shorten the decision time for the search task, a nonlinear transformation can be applied to , enabling the nonlinear update in (4) to be changed into a linear update. By setting as [50], Equation (4) can be rewritten as
Given that and , when , it follows that ; when , it follows that . Therefore, for , the decision thresholds can also be used to determine whether a target exists. For , it is considered that there is a target within the grid ; for , it is assumed that there is no target within the grid , where and .
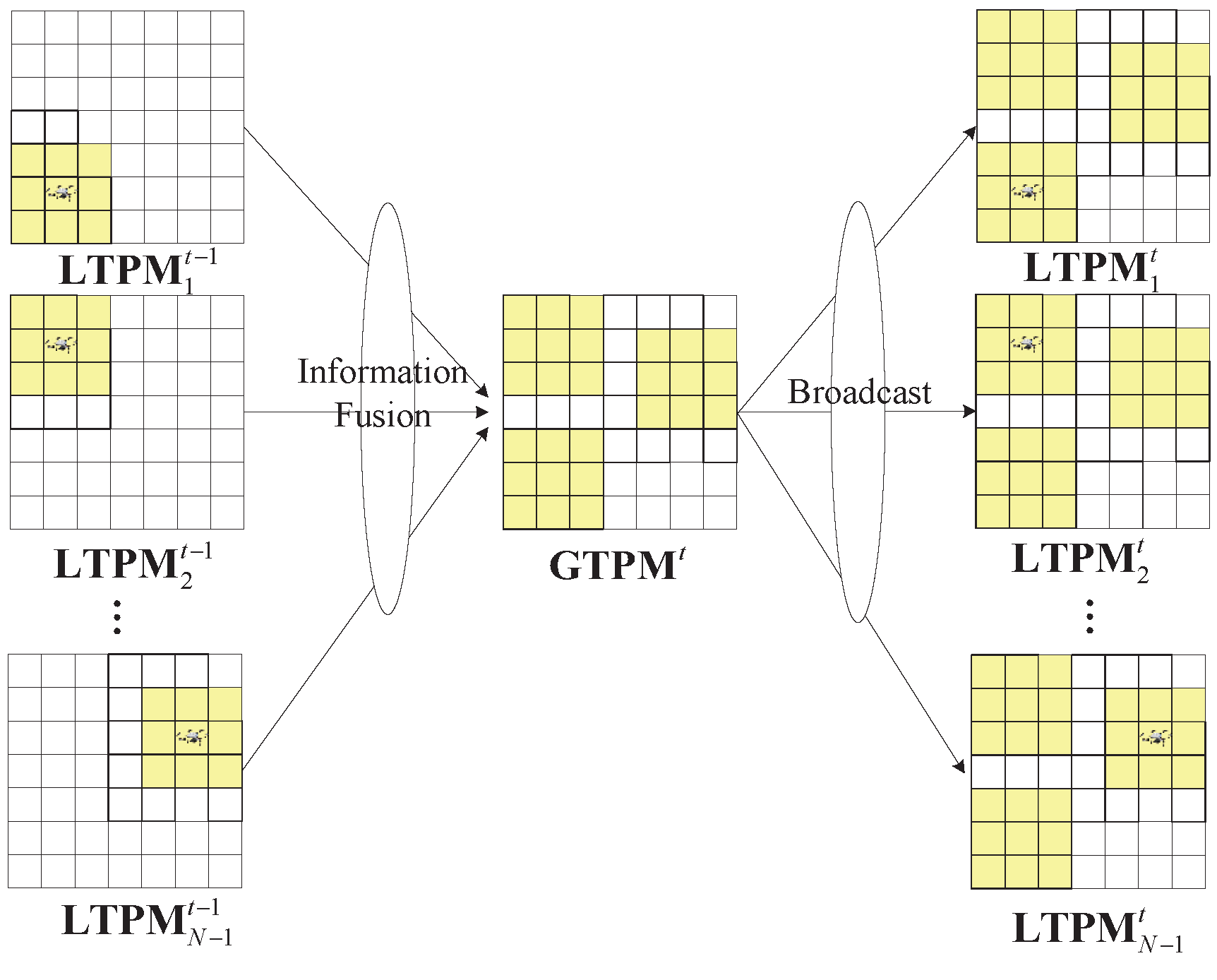
From the perspective of multi-UAV collaborative search, the TPM of the task area contains the probability distribution of targets within each grid of the task area, serving as an important basis for UAVs to make collaborative search decisions. Therefore, we assume that each UAV maintains its own TPM, referred to as LTPM (local TPM). As the search task progresses, each UAV updates its LTPM. Additionally, there is a global TPM, denoted as GTPM, maintained at the ground control station (GCS). The GTPM is updated based on the LTPM of each UAV, and in turn, the GTPM is used to update each UAV’s LTPM, as illustrated in Figure 2, where and represent the LTPM of UAV i and the GTPM of the GCS at time slot t, respectively. The yellow grid represents the UAV’s reconnaissance area (the updated portion of the LPTM). Such an updating process is essential for achieving collaborative search among multiple UAVs.
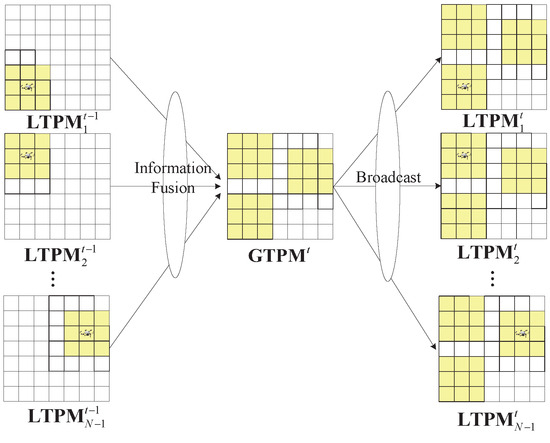
Figure 2.
Update of GTPM and LTPM.
Specifically, each decision cycle of a search task can be divided into four stages, as shown in Figure 3. In , each UAV performs the search task and updates its LTPM based on the search results. In , each UAV sends its updated LTPM to the GCS. During , the GCS fuses the LTPMs and updates the GTPM with the fused results. In , the GCS broadcasts the updated global TPM to each UAV. The UAVs use the received GTPM as their new LTPM and continue with the search task. Such a cycle is repeated until the search task is completed. Essentially, this is a centralized updating process of the TPM utilizing the GCS, which allows each UAV to receive updates from all other UAVs’ LTPMs, enabling collaborative search among all UAVs throughout each decision cycle.

Figure 3.
Decision cycle of a search task.
2.3. Channel Model
As mentioned above, to update the GTPM and LTPM, the UAVs and the ground control station must communicate during the second and fourth stages of each search decision cycle. In addition, there are jammers in the vicinity of the task area that randomly select channels to release interference. To quantitatively describe the TPM update process under interference conditions, this section will model the channels between the UAVs and the ground control station, the UAVs and the jammer, and the jammer and the ground control station.
The channels between the UAVs and the ground control station, as well as between the UAVs and the jammer, are all considered air-to-ground channels. For the sake of simplicity, the GCS denoted as G and the jammer denoted as J will hereinafter be collectively referred to as ground nodes denoted as X. Considering the impact of obstacles between the air and ground, such as trees and buildings, a mixed channel model of line-of-sight (LoS) and non-line-of-sight (NLoS) is employed to establish the air-to-ground channels between the UAVs and the ground nodes [51,52]. At each time slot, the channel between the UAVs and the ground nodes X can be expressed as
For the ground-to-ground channel between the jammer and the GCS, both large-scale fading and small-scale fading are considered [53]. Therefore, the channel between the two can be written as
where represents large-scale fading, which can be calculated using (7). On the other hand, signifies the small-scale fading that is frequency-dependent and assumed to follow an exponential distribution with a mean of 1 and a variance of 0.
2.4. UAV Communication Model
As previously mentioned, during the second stage of the search decision cycle , each UAV will transmit the updated LTPM back to the GCS. Due to the presence of interference, the available channels may be subject to random disruption, rendering it impossible to pre-assign a channel for each UAV to return the LTPM. Consequently, each UAV can only dynamically select a channel during . Ensuring the successful transmission of the LTPM necessitates the avoidance of interference channels by the UAVs, whilst also preventing the selection of the same channel as other UAVs. If all UAVs can successfully return information through appropriate channel selection, avoiding interference or mutual disturbance, this is referred to as achieving spectrum collaboration among the UAVs.
Assuming that M channels are available and each channel has a bandwidth of B, the received signal-to-noise ratio (SNR) at the GCS for UAV i on channel m during time slot of can be expressed as follows:
where denotes the transmission power of the UAVs. It is assumed that all UAVs possess identical transmission power. is defined as the set of all reconnaissance UAVs, and represents the channel selection of the UAV in time slot , which is defined as follows:
It is assumed that, within a designated time slot, each UAV is permitted to select only a single channel at most. Furthermore, it is posited that a channel can be selected by no more than one UAV. Consequently, the following conditions must be met by :
In (11), denotes the transmission power of the jammer, whilst serves as an indicator of whether channel m is subject to interference from the jammer at time slot , as defined below:
Furthermore, in (11), is employed to denote the set of all available channels, and is used to represent the power spectral density of Gaussian white noise.
In the context of the given parameters , the achievable rate of UAV i over channel m to the GCS at slot t can be expressed in accordance with Shannon’s formula as follows:
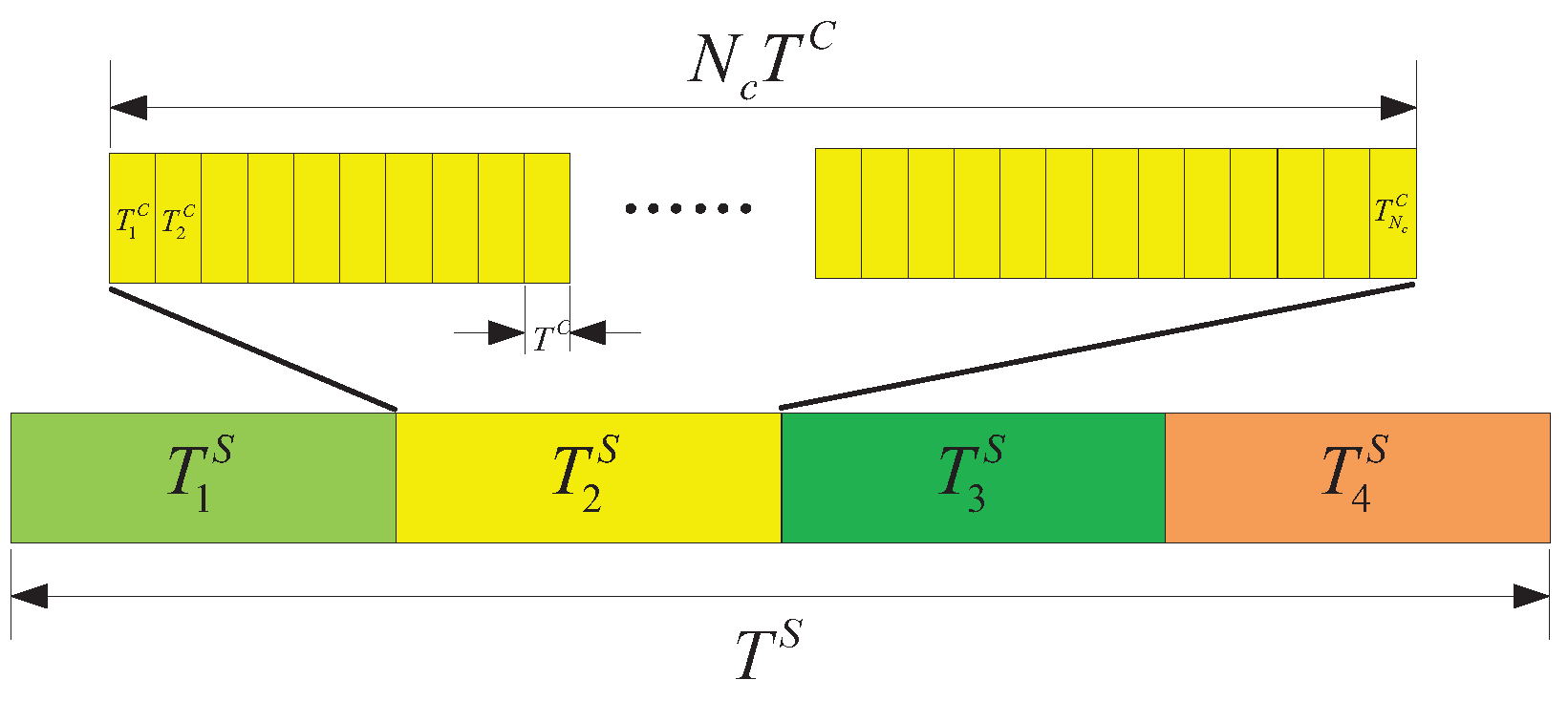
It is imperative to acknowledge the distinction between the search decision cycle and the spectrum decision cycle, which operate on disparate temporal scales. The search decision pertains to the direction in which the UAV flies and is typically measured in seconds, while the spectrum decision is related to alterations in channel status and is usually measured in milliseconds. Therefore, the utilization of t and is employed to differentiate between search decision time slots and spectrum decision time slots. Figure 4 illustrates the relationship between the search decision cycle and the spectrum decision cycle.
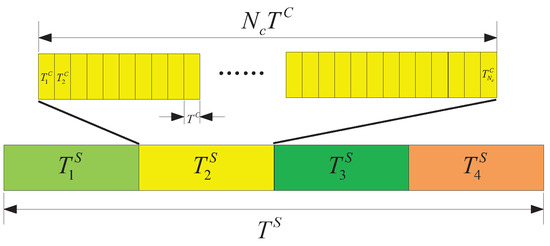
Figure 4.
Relationship between the search decision cycle and the spectrum decision cycle.
During the stage of the search decision cycle, there are spectrum decision cycles. Therefore, the total amount of data returned by UAV i in t-th search decision cycle is
In , the GCS disseminates the updated GTPM over all channels, while all UAVs listen on all channels. As this stage does not involve channel selection among multiple UAVs, we only consider spectrum collaboration during . Furthermore, we assume that the broadcast messages in can always be successfully received by each UAV.
Problem Formulation: The objective of multi-UAV collaborative search tasks is to enhance the efficiency of the search process within the designated task area while detecting the targets dispersed within that area. This paper delineates the completion of the search operation within the task area as follows: For any , it holds that or , where is the probability of the target’s presence in grid . Consequently, it can be concluded that under the specified threshold, a determination can be made regarding the presence or absence of targets in any grid within the task area.
For brevity, a factor is introduced to denote whether the grid has been previously searched at slot t. As outlined below,
We have discussed the updating process of the TPM in Section 2. During , following an independent search, UAV i updates its to at time slot t. It can be deduced from (2) and (5) that is related to , the position of UAV i during time slot t, the detection radius of the onboard sensor, the detection probability , and the false alarm probability . The relationship between and can thus be described by the following function:
During , the GCS updates using . In a similar manner, the relationship between the two can be expressed as a function given by
During , each UAV is responsible for receiving the broadcast message from the ground station and updating its own . The following has been established:
It is posited that at the beginning of the UAV’s task, the following equation holds:
With the above discussion, it is therefore possible to propose a joint optimization model that incorporates both spectrum collaboration and search collaboration, with the objective of minimizing the number of decision cycles given by (P1) as follows:
In (P1), denotes the search decision variable, which represents the heading angle of the UAV i during the t-th search decision, while signifies the spectrum decision variable, which indicates the channel selection during the -th spectrum decision within the t-th search decision cycle. T is the number of search decision cycles when the search task is completed. Constraint represents the nonlinear constraint on the heading angles of the UAV between two adjacent decision cycles, while constraint ensures that the UAV’s flight trajectory remains within the task area. Constraints and specify the value ranges for and , respectively. Furthermore, since the spectrum decision variable has been redefined as , the variable in Equations (13) and (14) is correspondingly changed to .
The optimization problem in (25) is nonlinear in nature and involves multiple integer variables, in addition to the inter-dependency of several variables. The search decision variable determines the distance between the UAV and the GCS, jammer, and other UAVs. This, in turn, affects the channel state and influences spectrum collaboration. The spectrum decision variable determines the amount of information sent back by each UAV during the of the search decision cycle, which in turn affects search collaboration. Additionally, problem (P1) incorporates real-time variables such as the small-scale fading factor of channel , random channel interference from the jammer, and the detection and false alarm probabilities of onboard sensors, which further introduce randomness into the search task. Convex optimization methods and heuristic algorithms are limited by their efficiency and their inability to adapt to complex time-varying environments. In the next section, the original joint optimization problem (P1) is to be transformed into two sub-optimization problems: spectrum collaboration and search collaboration. Subsequently, multi-agent reinforcement learning methods will be employed to achieve real-time collaboration among multiple UAVs in spectrum and search operations.
3. Proposed Algorithm
Multi-UAV spectrum collaboration is the foundation for achieving multi-UAV search collaboration. However, search decisions also impact spectrum decisions, as illustrated by (22), where the value of is related to both channel selection and the positions of the UAVs. This is due to the utilization of an absolute threshold. In order to decompose problem (P1) into two independent subproblems, the absolute threshold in Equation (22) is replaced with a relative threshold. That is, given the positions of the UAVs, spectrum decisions will only make maximum effort for collaboration, and Equation (22) can be rewritten as
In (26), denotes the maximum amount of information that each UAV is capable of transmitting to GCS during the t- search decision cycle, contingent on their respective positions. Meanwhile, signifies the threshold value. Consequently, this enables the formulation of the optimization problem (P2) solely concerning spectrum collaboration, which is written as follows:
In addition, the UAV’s heading angle is optimized based on the spectrum decisions, with the objective of minimizing the number of search decision cycles required to complete the search task. This results in the following optimization problem (P3):
At this point, the original optimization problem (P1) has been decomposed into two distinct subproblems: spectrum decision and search decision. Prior to implementing reinforcement learning as a solution to these two subproblems, a concise overview of multi-agent reinforcement learning and MAPPO will be provided. Subsequently, an MAPPO-based approach for both spectrum cooperation and search cooperation will be presented.
3.1. Structure of MARL
Multi-agent reinforcement learning is typically modeled as a Partially Observable Markov Decision Process (POMDP). POMDP is generally depicted as a six-tuple , where signifies the global state information, denotes the joint observation space of multiple agents, indicates the local observation space of agent i, denotes the joint action space of multiple agents, and represents the action space of agent i. At time step t, based on the local observation of the environment, agent i selects an action and receives a reward from the environment. Under the joint actions of multiple agents , the current global state transitions to the next state with some probability . At time step , agent i will obtain a local observation , which is a part of the new global state . The cumulative reward of agent i at time step t can be expressed as follows:
where is the discount factor that describes the influence of future rewards on the current cumulative return.
3.2. PPO-Based MARL
Proximal policy optimization (PPO) [54] is a policy optimization algorithm that has been employed in reinforcement learning since its inception by the OpenAI research team in 2017. It is currently regarded as one of the most prevalent and pragmatic algorithms within the domain of reinforcement learning.
In reinforcement learning, an agent engages with the environment to generate trajectories , with the objective of attaining enhanced cumulative rewards. The expected total reward can be expressed as follows:
where represents the parameters of the policy network, signifies the total reward accumulated by the agent throughout the trajectory, and denotes the reward received by the agent at time step t. signifies the probability of the trajectory occurring under the policy . To maximize the reward, the derivative of Equation (30) is taken, yielding the following form of the policy gradient
where denotes the advantage function, while and represent the action value function and the value function under the given policy , respectively. The advantage function describes the relative quality of actions given a particular state. During the policy improvement process, if , the probability is increased; otherwise, it is decreased. To enhance sample efficiency, an importance-sampling method is employed to collect samples, and Equation (31) can be rewritten as
The objective function corresponding to the gradient in the above equation is as follows:
where denotes the policy that interacts with the environment, and signifies the target policy. It is evident that the closer the two are, the more optimal the training outcomes. To this end, PPO-clip imposes constraints on the difference between them within a specified range through the implementation of a clipping function. The objective function associated with PPO-clip is as follows:
where . , which restricts x to the interval . Here, is a hyperparameter that represents the range for truncation.
In a multi-agent scenario, PPO is extended to multi-agent PPO (MAPPO) [55], where each agent possesses a policy network. The agent interacts with the environment based on its local observations in order to update its policy network. As a result, Equation (34) thus becomes
MAPPO is a reinforcement learning method that employs a combination of centralized training and decentralized execution (CTDE). During the centralized training process, the value network of agent i is configured to learn a centralized value function based on the global state , with the objective function being
where signifies the value network parameters of the agent i, and denotes the total return received by the agent i in global state . Following the acquisition of , the generalized advantage estimation (GAE) can be utilized to estimate , as demonstrated in the subsequent equation:
where denotes the temporal difference (TD) error, and is an additional hyperparameter that has been introduced in GAE.
3.3. MAPPO-Based Spectrum Collaboration
We define the POMDP elements corresponding to the spectrum collaboration optimization model (P2).
(1) Observation and state: In the - spectrum decision cycle, the local observation of UAV i comprises the received signal strength indication (RSSI) of all M channels: that is, . Here, represents the RSSI of the m- channel observed by UAV i, defined as
The first term of Equation (38) signifies the power received by UAV i from other UAVs through channel m. The subsequent term denotes the power received by UAV i from the jammer through channel m. The final term accounts for the power of the Gaussian white noise received by UAV i on channel m. Moreover, we merely concatenate the local observations of all agents to form global state information , which is given by
In order to differentiate between the same type of parameters for spectrum collaboration and search collaboration, superscripts “c”and “s” are utilized. For example, and denote local observations and global state information in spectrum collaboration, while and are employed to represent local observations and global state information in search collaboration. Other parameters are denoted in a similar fashion.
(2) Action: In the - spectrum decision cycle, UAV i randomly selects a channel m from the set of all channels to transmit back to the GC based on its local observation . Thus, .
(3) Reward: In order to optimize the objective function of the given optimization problem (P2) and thereby achieve spectrum collaboration among the UAVs, it is necessary to design a reward function that will encourage each agent to maximize its own achievable rate to GCS. Hence, the following reward function is therefore defined:
Furthermore, the multiplicative channel switching factor was intentionally incorporated with the objective of reducing the channel switching frequency of the UAVs and further cutting down on system overhead, which is defined as follows:
where is a hyperparameter. In the absence of channel switching between two consecutive spectrum decision cycles, the reward remains as it is. Conversely, when a channel switch occurs, the reward is reduced.
With regard to the network architecture, both the policy network and value network comprise multiple fully connected layers. It is important to acknowledge that during spectrum collaboration, UAVs located at the same position and under the same observation should select different channels. This implies that the strategies employed by different UAVs are distinct. Consequently, it is essential that each MAPPO agent incorporates a separate policy network and value network.
In conclusion, the proposed MAPPO-based spectrum collaboration algorithm under jamming conditions for (P2) is summarized in Algorithm 1.
| Algorithm 1: MAPPO-based spectrum collaboration under jamming conditions. |
 |
3.4. MAPPO-Based Search Collaboration
In a similar manner, the POMDP elements with regard to the search collaboration model (P3) are defined as follows.
(1) Observation and state: In the t- search decision cycle, the local observation of UAV i encompasses the it carries, the coordinates of the current grid it is located within, and its heading angle from the last search decision cycle, represented as . As for the global state information , this comprises three constituent elements: , obtained from the specified combination of from all UAVs, is written as
is the coordinates of the current grids occupied by all UAVs; is the heading angles of all UAVs in the previous time slot. Therefore, the following expression can be used to represent :
(2) Action: In the t- search decision cycle, the available actions for the UAVs are the eight given heading angles, denoted as , . However, to ensure that the actions of the UAVs satisfy constraints and in (P3) and also to accelerate the training speed, an action-masking mechanism is introduced. With regard to the boundary constraints in , action masking is primarily related to the current grid coordinates of the UAV, denoted as . The masked actions differ when the UAV is in different grids. As for the heading angle constraint in , action masking is contingent on the UAV’s heading angle from the preceding search decision, written as . Since both and can be obtained from the current observation , the final masked actions can be represented as follows:
In addition, to prevent all available actions from being masked, we introduce a hovering action into the action set. When all flight directions are masked, the UAV will hover, and in the next time slot after hovering, it can choose any of the eight flight directions.
(3) Reward: As the UAV conducts its search, the uncertainty of the task area undergoes a gradual decrease. Consequently, the variation in the uncertainty of the task area between two adjacent search decision cycles can be utilized to delineate the reward obtained from the UAV’s search. Firstly, it is necessary to define the uncertainty of the task area, and the uncertainty function of grid in the t- search decision cycle is defined as follows:
where is a constant greater than 0. When , the corresponding , indicating that the uncertainty of the grid is at its maximum. When or , the corresponding , which means that the presence of a target in grid can be fully determined, resulting in the lowest possible uncertainty for grid .
The joint reward for the UAV’s collaborative search during the t- search decision cycle can be expressed as follows:
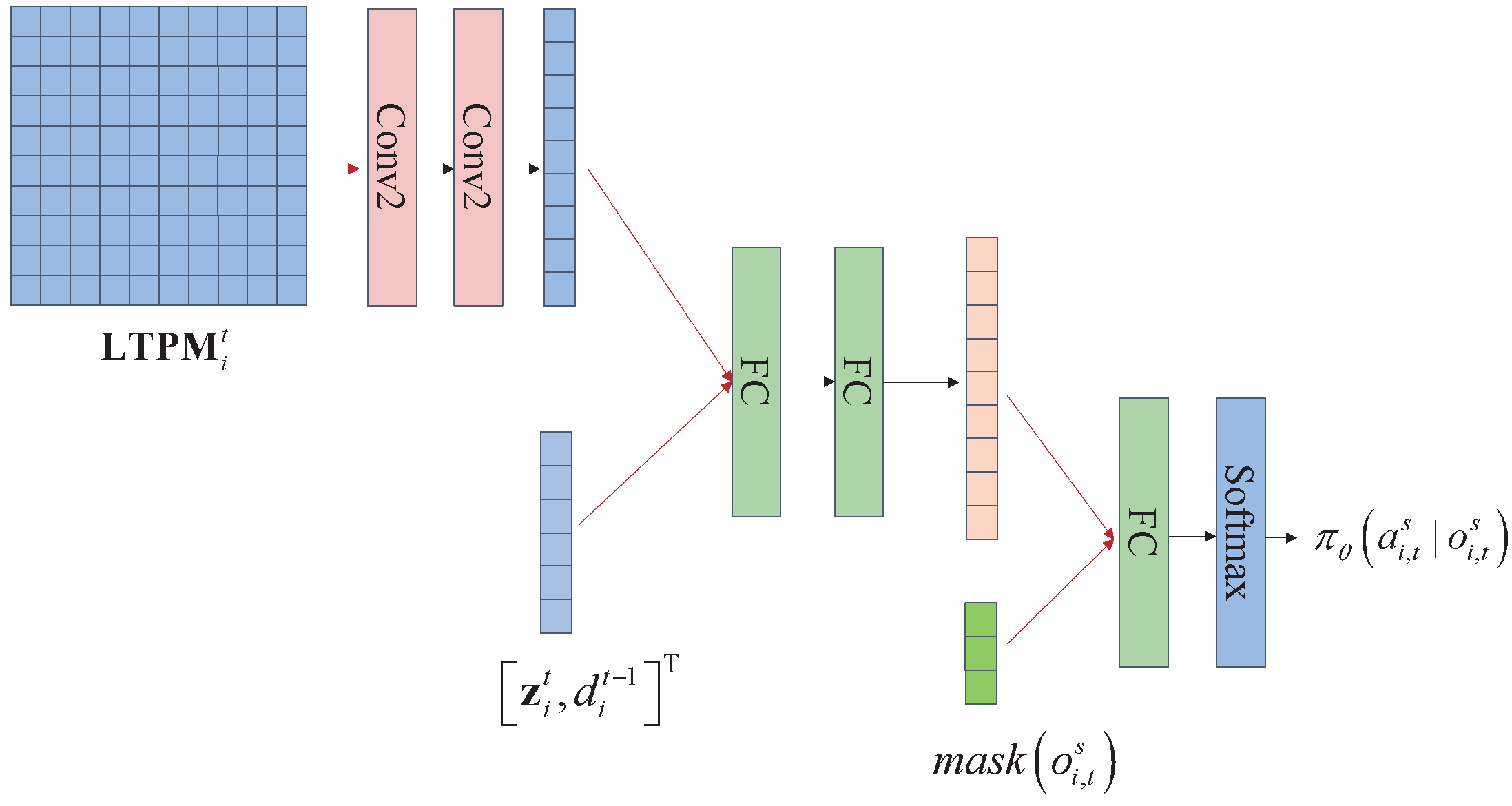
Finally, an explanation is provided of the network architecture. Given that the in the agent’s observations is two-dimensional data, a convolutional network is specifically used to extract features from it. Additionally, to avoid feature loss, pooling layers are not utilized. Subsequent to flattening the convolved data, it is concatenated with other data from the observations and fed into a fully connected multilayer network for further feature extraction. The masked action is then combined with the features and fed into a fully connected network, ultimately outputting action probabilities through a softmax layer. The value network also utilizes convolutional layers to process two-dimensional data in its input. Figure 5 illustrates the architecture of the policy network. Similarly to spectrum collaboration, each agent also employs a set of independent policy and value networks during search collaboration. The MAPPO-based search collaboration algorithm for (P3) is outlined in Algorithm 2.
| Algorithm 2: MAPPO-based search collaboration. |
 |
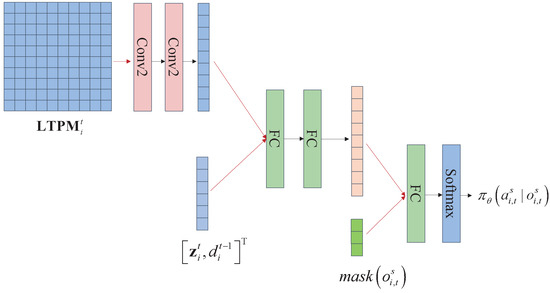
Figure 5.
The policy network architecture of the PPO-based search collaboration agent.
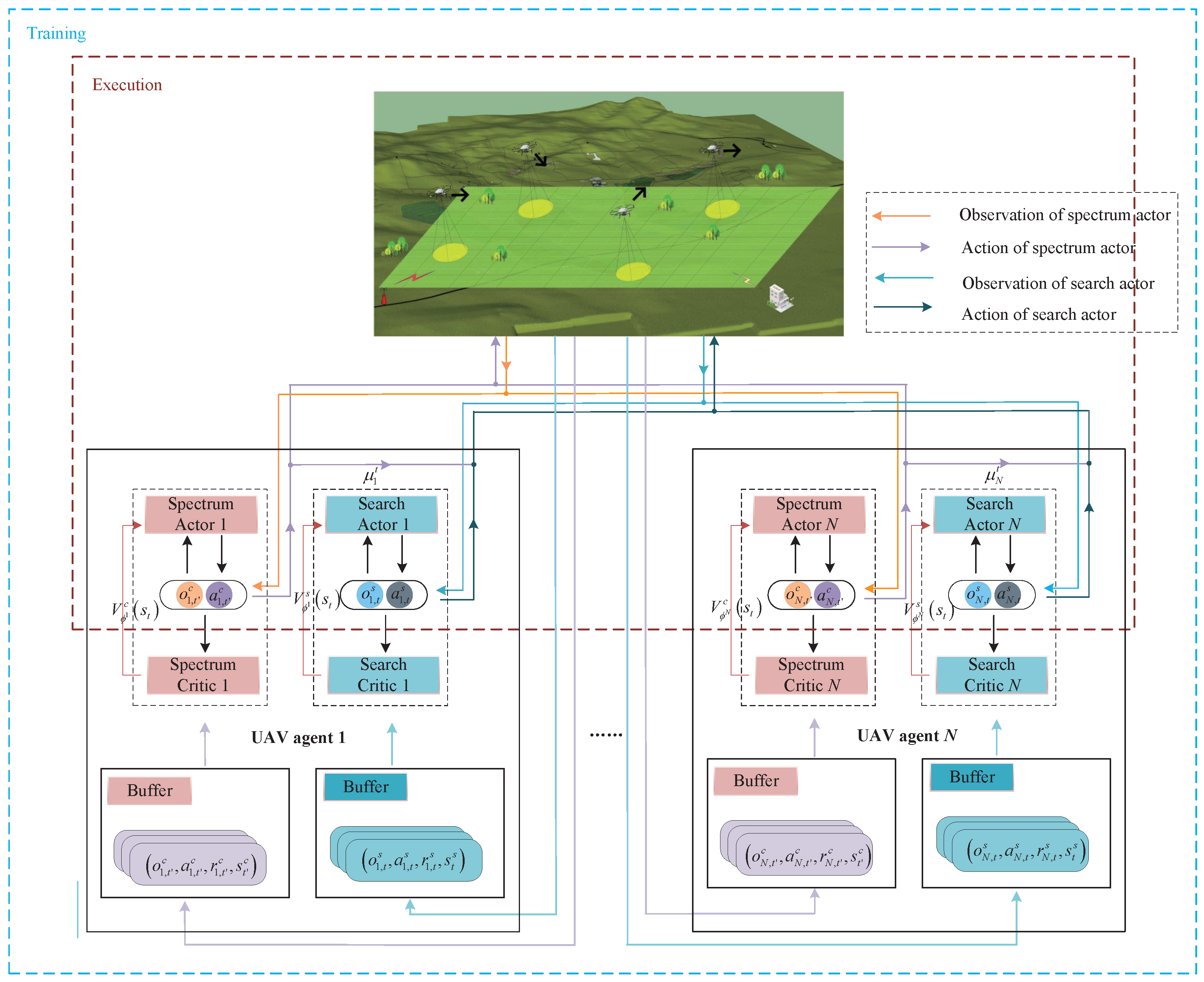
Once the N spectrum collaboration policy networks and N search collaboration policy networks are obtained from Algorithm 1 and Algorithm 2, respectively, and each UAV is loaded with one spectrum collaboration policy network and one search collaboration policy network, the N UAVs are then capable of performing joint search tasks under interference conditions, as illustrated in Figure 6.
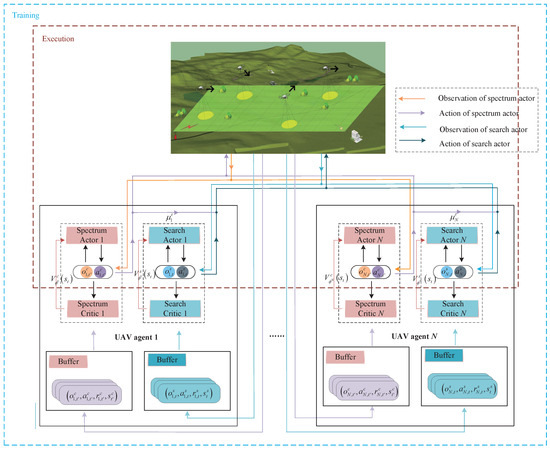
Figure 6.
The structure of proposed PPO-based algorithm.
3.5. Computational Complexity Analysis
The computational complexity of the proposed algorithm is fundamentally determined by three key factors: (1) the state-space dimensionality of the agents, (2) the action-space dimensionality, and (3) the architectural configuration of both the policy and value networks. For the search coordination agent, the policy network processes an TPM matrix through two convolutional layers followed by three fully connected layers, as shown in Figure 5, resulting in a complexity of , where represents the combined complexity factor of these operations. The corresponding value network shares a similar structure with slightly different fully connected layer dimensions, yielding a complexity of . In contrast, the spectrum coordination agent’s networks eliminate convolutional layers and operate on state variables proportional to the number of agents N, with complexities of for the policy network and for the value network. The total algorithm complexity combines these components as . Given that the grid resolution typically exceeds the number of UAVs, N, the overall complexity is dominated by the quadratic term , establishing a square relationship with the TPM matrix size. This analysis reveals that larger search areas or finer grid partitions will quadratically increase computation time, suggesting two practical optimization strategies: employing UAVs with greater coverage to reduce or strategically partitioning the mission area into subregions before algorithm application to maintain computational efficiency while preserving search effectiveness. The quadratic scaling behavior provides clear guidance for balancing algorithmic performance with operational requirements in real-world deployments.
4. Simulation and Results
In this section, we present the simulation scenario along with three baseline methods. The experimental results are then described and analyzed.
4.1. Parameter Setting
In the simulation, the mission area is assumed to be a rectangular region of 5 km × 5 km. The UAV search collaboration cycle and the spectrum collaboration cycle are set to 10 s and 100 ms, respectively, with 16 channels available. The flight speed v of the UAV is 20 m/s, and since the grid length is the distance that the UAV travels during a search–collaboration cycle, it is set to 200 m. Therefore, the entire mission area can be divided into a 25 × 25 grid. The UAV has a detection radius of 300 m, allowing it to simultaneously scan a 3 × 3 grid within its field of view. In addition, three jammers are strategically deployed to disrupt UAV communications. Each jammer employs a sweeping interference pattern characterized by deterministic channel switching through all M available channels, and the jammers share the same sweeping period but maintain random initial phase offsets. Further simulation parameters are given in Table 2.

Table 2.
Simulation parameters of the environment.
4.2. Performance Benchmark
To evaluate the performance of the proposed MAPPO-based method in both spectrum collaboration and search collaboration, three baseline methods are used for comparison.
(1) IPPO: IPPO-based spectrum collaboration method or search collaboration method. The network structure, observations, and rewards are identical to those in the MAPPO-based method. However, a key distinction is that, during the training phase, the critic network of IPPO solely utilizes the local observations of each agent as input, as opposed to the global state.
(2) QMIX: QMIX-based spectrum collaboration methods or search collaboration methods. The observations and rewards for the agents are exactly the same as those in the MAPPO-based method; the difference lies in the network structure utilized by each agent, which is QMIX-based, with a set of Q networks deployed for each agent. The architecture of these Q networks is identical to that of the corresponding MAPPO method, with all inputs as local observations. The outputs of all agents’ Q networks are then processed through a mixing Q network to obtain the global action value function, with the input to the mixing Q network as the global state.
(3) IQL: IQL-based spectrum collaboration methods or search collaboration methods. The observations and rewards for the agents are also the same as those in the MAPPO-based method. The distinguishing factor pertains to the deployment of a set of Q networks by each agent. The architecture of these Q networks is identical to that of the corresponding MAPPO method, with each agent’s Q network receiving local observations as input.
4.3. Performance Evaluation
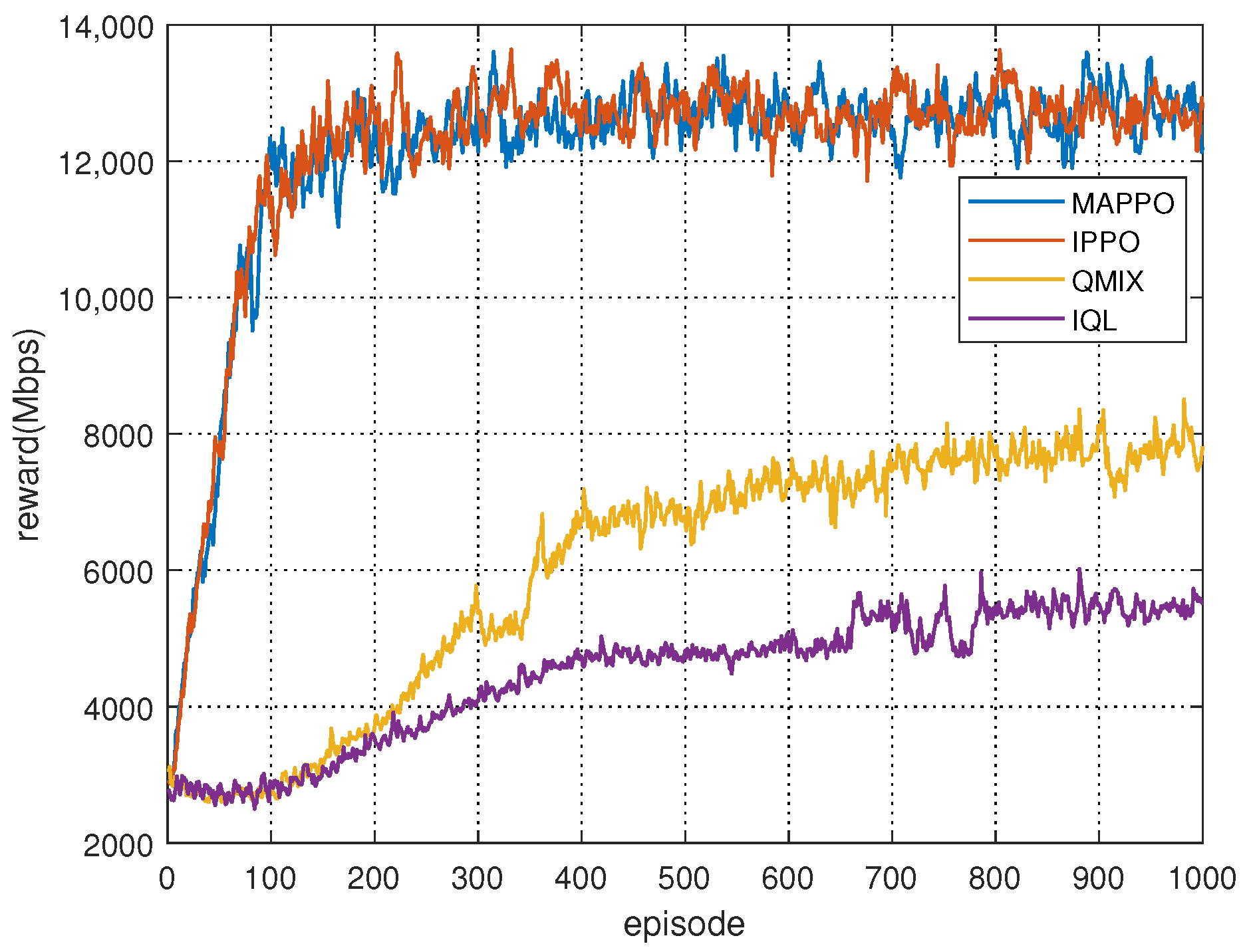
First, we conducted simulations to evaluate the convergence of the proposed Algorithm 1 and compare it with other baseline methods. The training process involved 1000 episodes, with each episode consisting of 1000 steps, and the reward of all agents for each episode was calculated. As illustrated in Figure 7, the MAPPO-based and IPPO-based spectrum collaboration methods demonstrate faster convergence and attain higher final convergence values. The proposed MAPPO-based spectrum collaboration achieves throughput improvements of 68.7% and 146.2% over QMIX and IQL, respectively. In contrast, QMIX exhibits slightly lower performance, while IQL demonstrates the poorest performance. In the context of spectrum collaboration, policy gradient-based reinforcement learning methods exhibit superior performance in comparison to those based on value functions. Despite the fact that MAPPO uses global states during training, the IPPO’s critic network, which only utilizes local observations, demonstrates performances very close to that of MAPPO. This is because the RSSI observed by different agents has a strong correlation, resulting in a high degree of similarity between local and global observations.
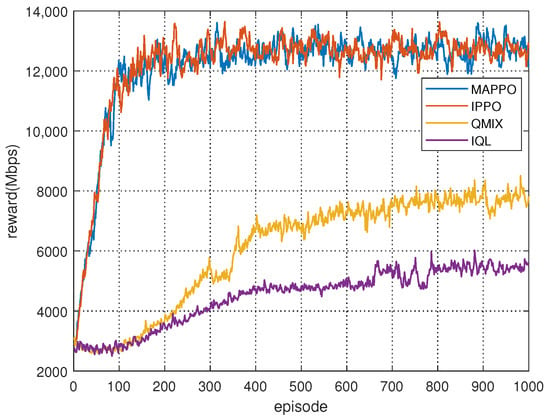
Figure 7.
Reward of MAPPO-based spectrum collaboration over training episodes.
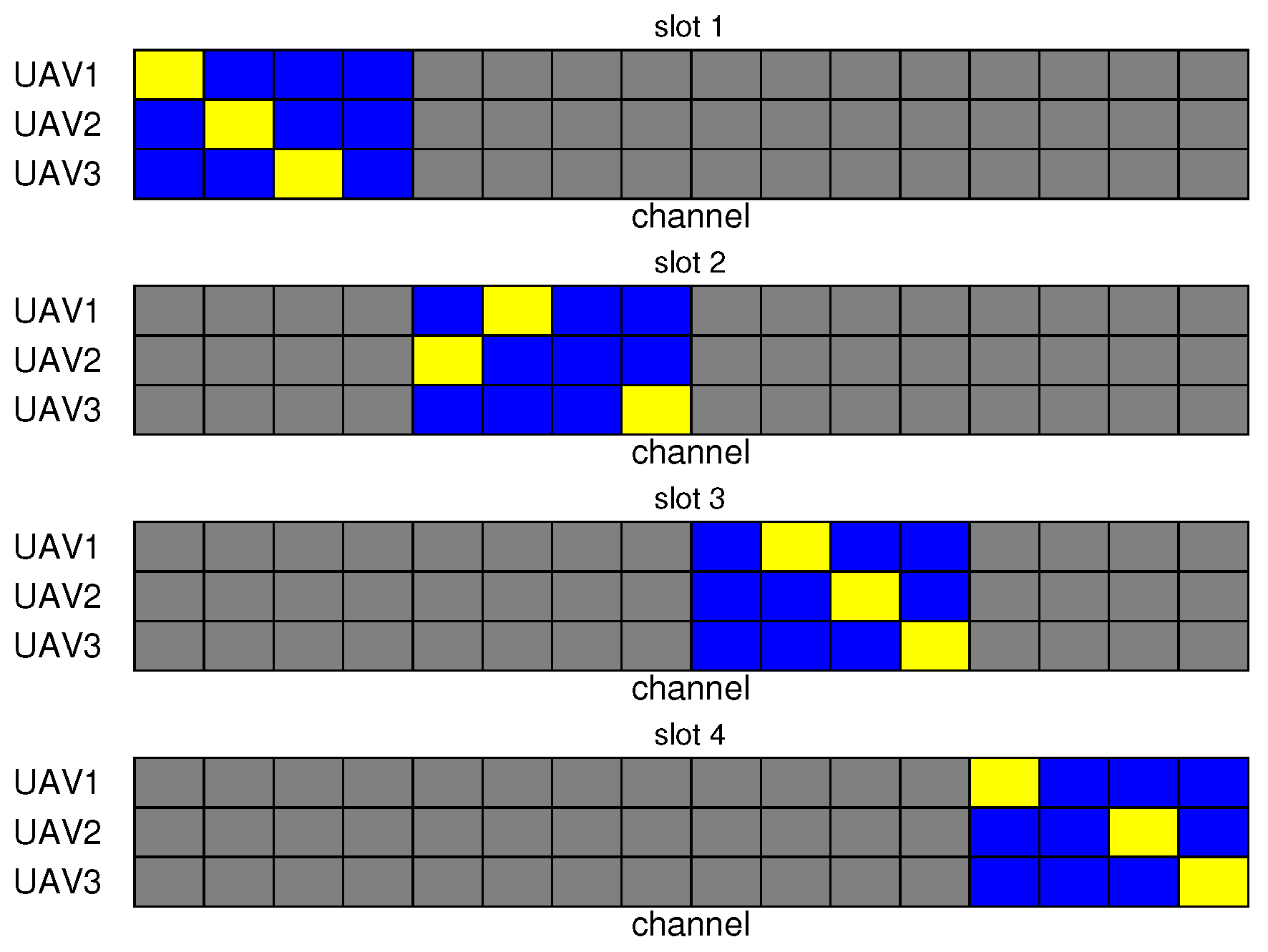
Following the convergence of the reward curve of the proposed MAPPO-based algorithm, a random selection of four consecutive steps from a single episode was conducted, where each step can be regarded as a spectrum decision cycle, to analyze the channel selection of the UAV during these four slots, as illustrated in Figure 8. The grey grids represent the interfered channels, the blue grids represent the available channels, and the yellow grids indicate the channels selected by the UAV. It is evident that in each decision cycle, the UAV not only avoids interfering channels but also avoids selecting the same channel as other UAVs. This outcome demonstrates the efficacy of the proposed algorithm in facilitating spectrum collaboration among UAVs in the presence of interference.
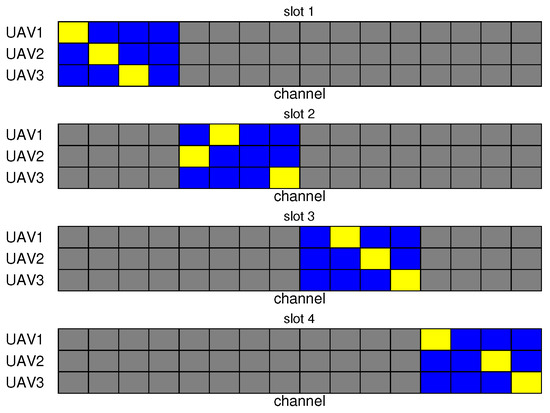
Figure 8.
UAV channel selection based on the proposed PPO-based spectrum collaboration algorithm.
A simulation was also conducted on the effect of the weighting factor in Equation (40) of the spectrum collaboration section. Under MAPPO-based spectrum collaboration, Figure 9a,b present the channel selections of the UAVs over 18 spectrum collaboration cycles for and , respectively. Distinct colors are employed to differentiate the various channels. It is evident from these figures that when , the UAVs can achieve spectrum utilization while reducing the number of channel switchings, thereby lowering the system overhead required for spectrum collaboration.

Figure 9.
The effect of the introduced weighting factor on channel switching. (a) . (b) .
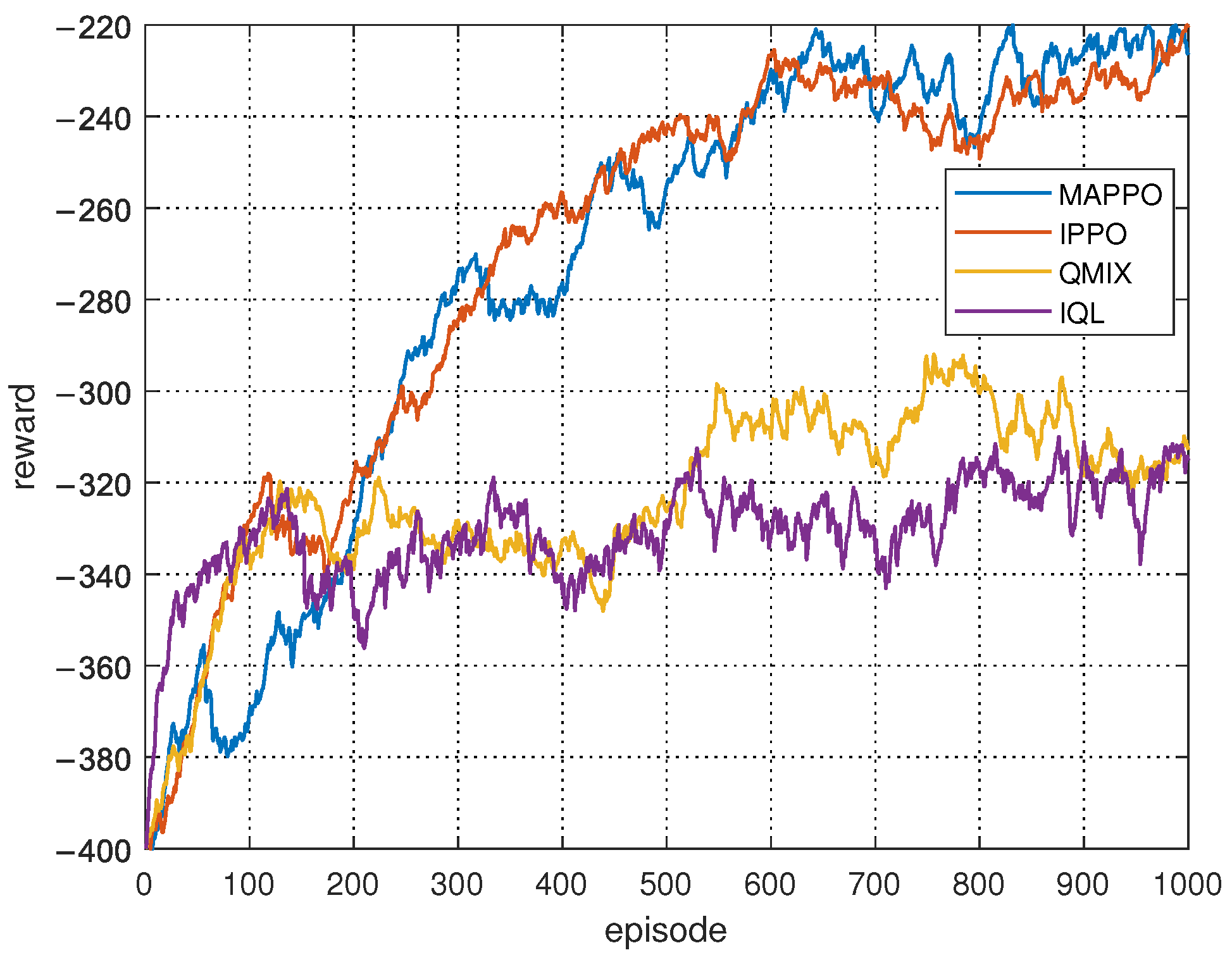
In Figure 10, a comparison of the convergence between the proposed MAPPO-based search collaboration algorithm and other baseline methods is presented. It is assumed that the agents achieve complete spectrum collaboration in each search decision cycle, i.e., in Equation (21). It is further assumed that all methods start with the same initial environment. During the training process, 1000 episodes were conducted, with each episode consisting of a maximum of 500 steps, thereby ensuring that the agents could complete the search task in each episode. As is evident in Figure 10, the proposed MAPPO-based algorithm and the IPPO-based algorithm demonstrate comparable performances, thus validating the efficacy of the proposed approach. This observation aligns with the findings of the convergence simulation of spectrum collaboration, wherein the performance of both algorithms is found to be similar. The underlying reason for this consistency in performance can be attributed to the assumption of complete spectrum collaboration, i.e., the condition where . This assumption results in the global states utilized by MAPPO becoming equivalent to the local states employed by IPPO during the training process. Furthermore, the performances of QMIX and IQL are relatively similar, as both are trapped in local optima, which also indicates that in collaborative search scenarios, policy gradient-based reinforcement learning algorithms still outperform value-function-based reinforcement learning algorithms.
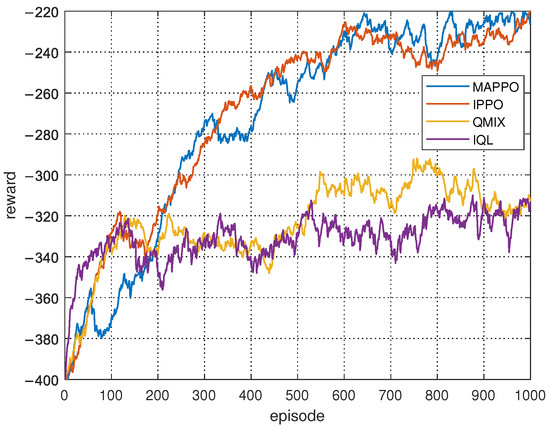
Figure 10.
Reward of MAPPO-based search collaboration over training episode.
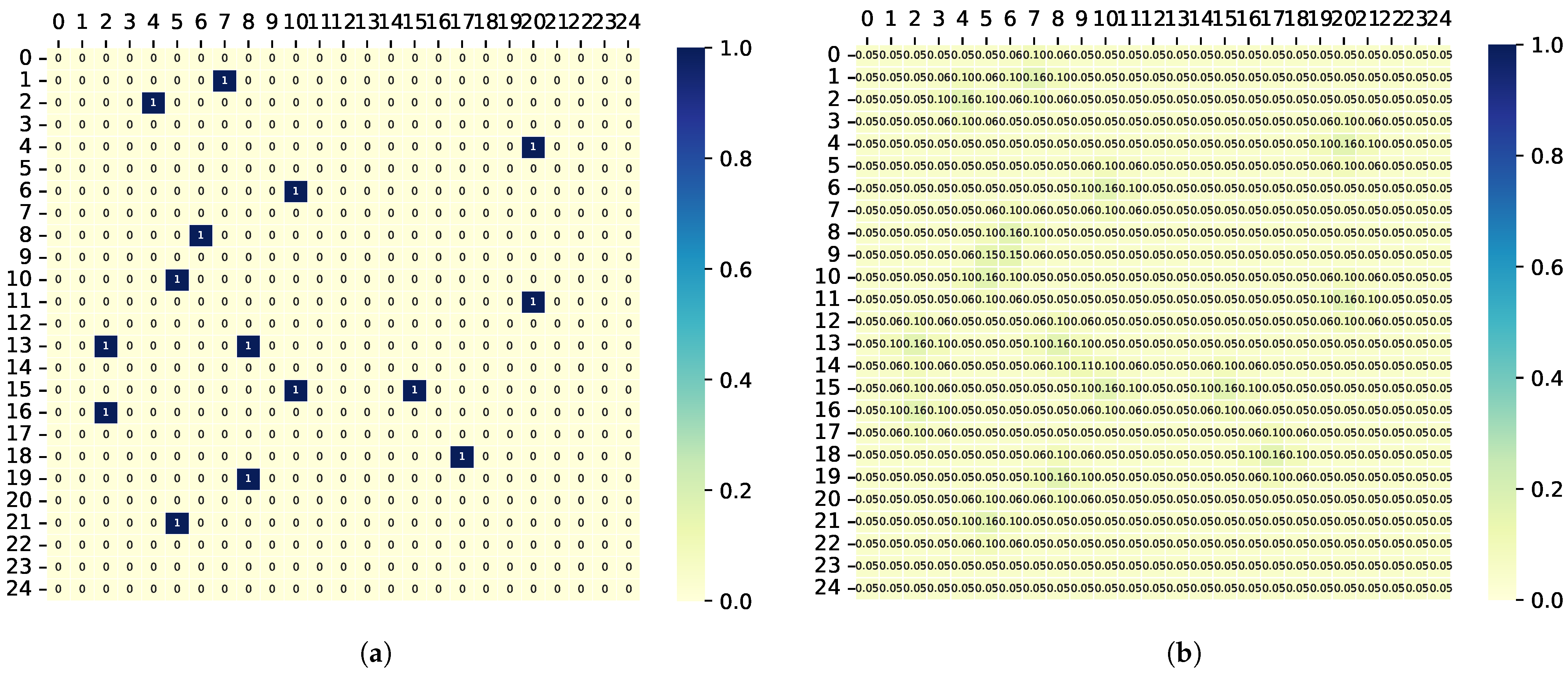
To validate the performance of the proposed MAPPO-based search collaboration algorithm, the search trajectories of the UAV were generated by both the proposed algorithm and baseline methods under the same initial conditions. The distribution of the targets within the task area is shown in Figure 11a. Based on the distribution of the targets, the corresponding initial TPM can be generated, as illustrated in Figure 11b. The methodology for generating the TPM entails the creation of a two-dimensional Gaussian probability distribution by Equation (47), centered at the location of each target in the sequence, which is then utilized to update the corresponding elements in the TPM. The remaining positions in the TPM are populated with , signifying the absence of targets.
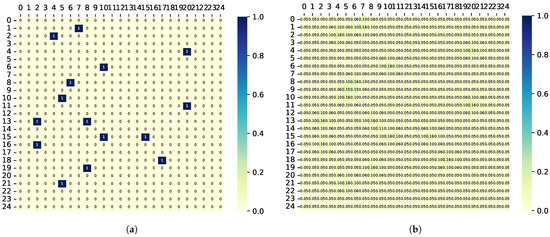
Figure 11.
Target distribution and the corresponding TPM. (a) Target distribution in the task area. (b) Corresponding original TPM of the task area.
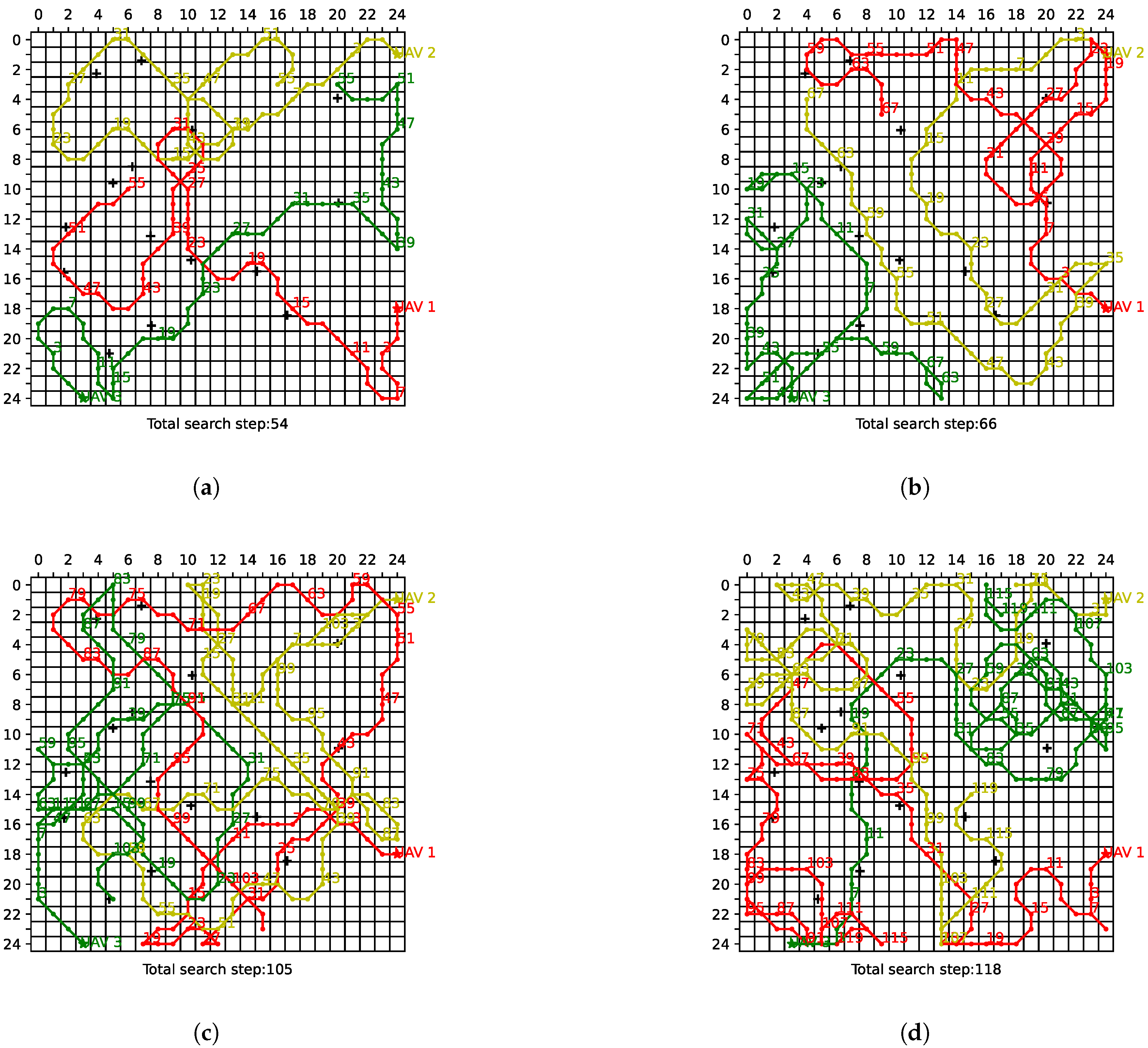
As illustrated in Figure 12, the search trajectories of the UAVs are depicted under various search collaboration methods, with complete spectrum collaboration. The red, yellow, and green poly-lines in the figure represent the motion trajectories of UAV 1, UAV 2, and UAV 3, respectively, with pentagrams indicating their starting points. To more clearly illustrate the UAVs’ movement paths, we label every 4th trajectory point with its corresponding step number. The crosses in the figure denote the targets. It is evident that, in comparison to alternative baseline methods, the MAPPO-based collaborative search algorithm requires a fewer number of steps to complete the search of the task area under identical initial conditions. It is discernible that the areas suspected of harboring targets are predominantly searched by a solitary UAV, which indicates that effective search collaboration is indeed attained among the diverse UAVs. Furthermore, the UAV flight trajectories satisfy the boundary constraint and turning constraint specified in (P3), thereby demonstrating the effectiveness of the action-masking mechanism. Due to the presence of the turning constraint, UAVs require more steps when executing turns of 90 degrees or more, resulting in circular trajectories, which better align with the actual flight characteristics of the UAVs. As demonstrated in Figure 12c,d, while the QMIX- and IQL-based methods attain a certain degree of spectrum collaboration, they exhibit substantial redundancy in their steps, signifying the presence of further optimization potential and the possibility of being trapped in local optima.
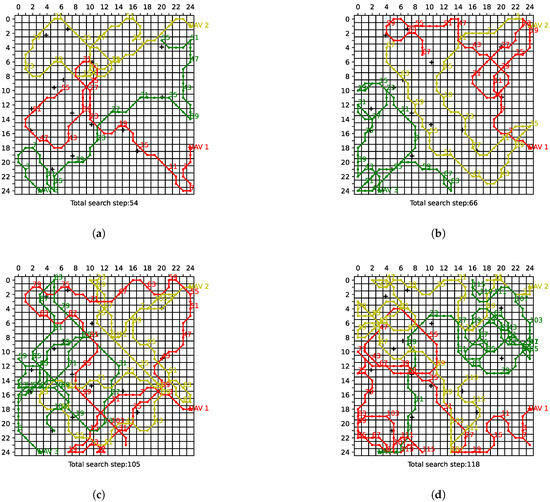
Figure 12.
The search trajectories of the UAVs under various search collaboration methods. (a) MAPPO. (b) IPPO. (c) QMIX. (d) IQL.
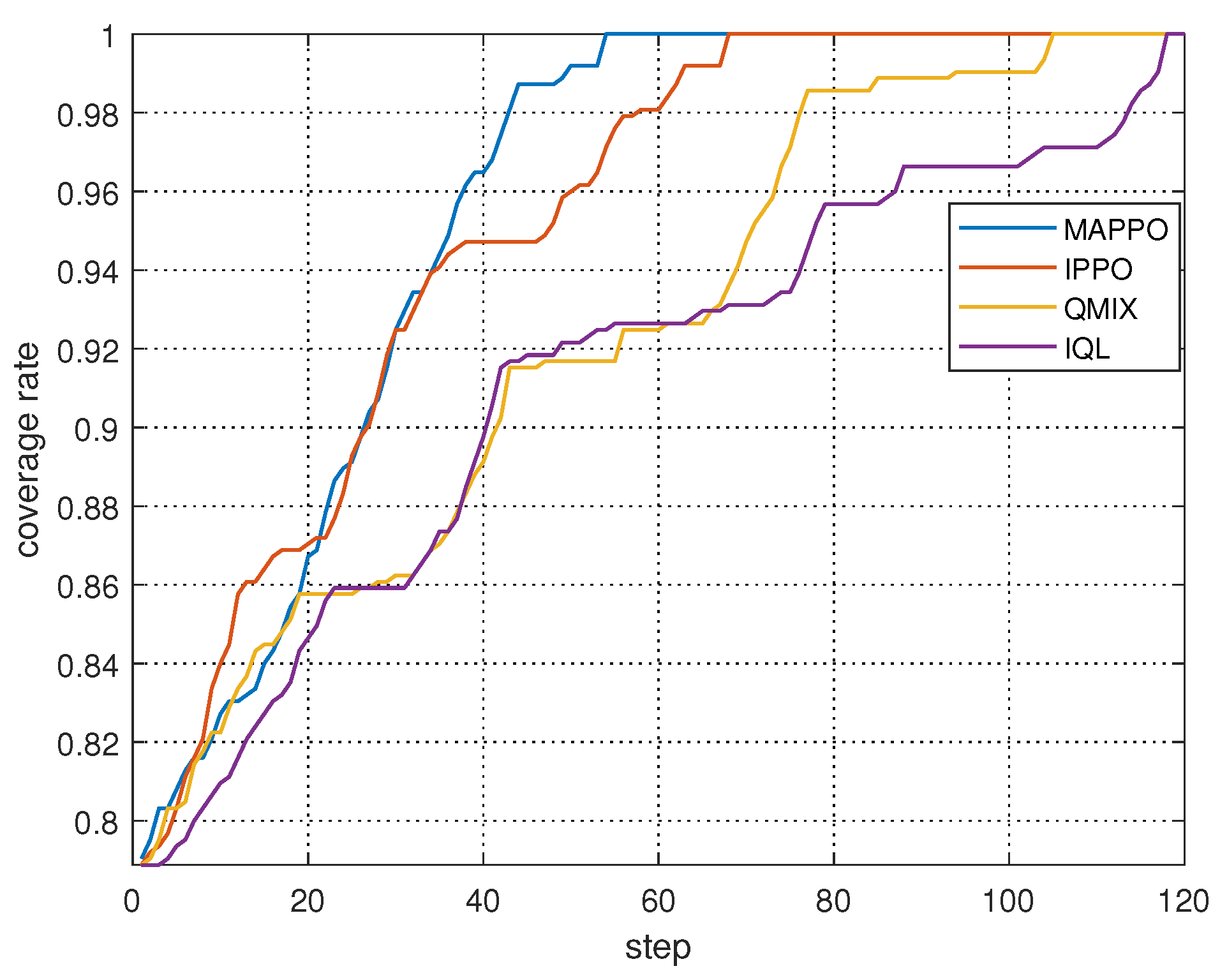
In Figure 13, a comparison is drawn between the coverage rates of the four algorithms under complete spectrum collaboration. Utilizing the TPM from Figure 11b as the initial TPM, the coverage rate commences at 78% due to the fact that 22% of the grid cells in this TPM continue to exhibit uncertainty. In comparison to the baseline algorithms, the proposed MAPPO-based algorithm requires the fewest steps, and for the majority of the search process, the coverage rate of the MAPPO-based algorithm exceeds that of the other algorithms, thereby indicating superior performance. However, between 10 and 20 steps, the IPPO- and QMIX-based methods demonstrate a higher coverage rate, suggesting that the proposed MAPPO-based algorithm provides a local optimum. This indicates that there is potential for enhancing the search efficiency.
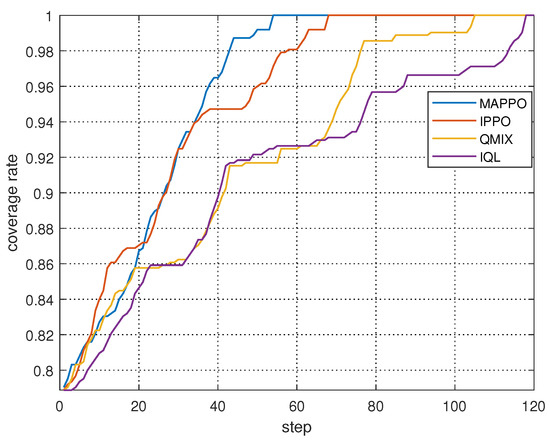
Figure 13.
Coverage rates of different collaborative search methods under complete spectrum collaboration.
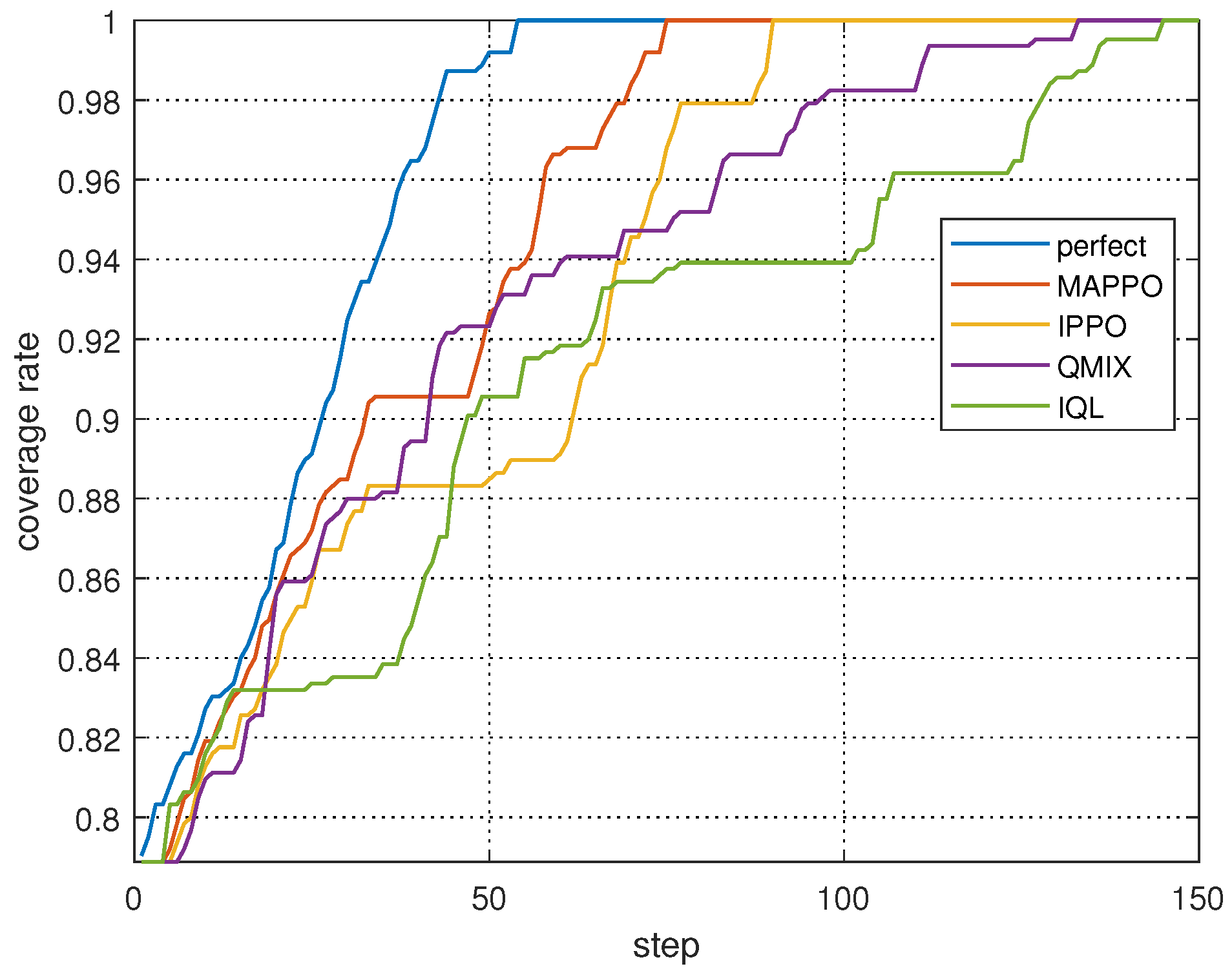
We also conducted a comparative analysis of the coverage rates of four distinct search collaboration methods under MAPPO-based spectrum collaboration. As depicted in Figure 14. Still utilizing the TPM from Figure 11b as the initial TPM, our analysis revealed that the “perfect” curve, representing an MAPPO-based collaborative search under complete spectrum collaboration, exhibited the optimal performance. Our experiments demonstrate that even with partial spectrum collaboration, the MAPPO-based search algorithm consistently outperforms baselines with 16.7–48.3% reductions in search completion steps. However, the coverage rate of the perfect collaboration is consistently greater than that of the MAPPO-based spectrum collaboration algorithm throughout the search process, as it achieves complete spectrum collaboration during the whole process. This simulation result reinforces the notion that spectrum collaboration is a significant factor impacting search collaboration. It is evident that the proposed spectrum collaboration algorithm is yet to attain full efficacy in achieving spectrum collaboration.
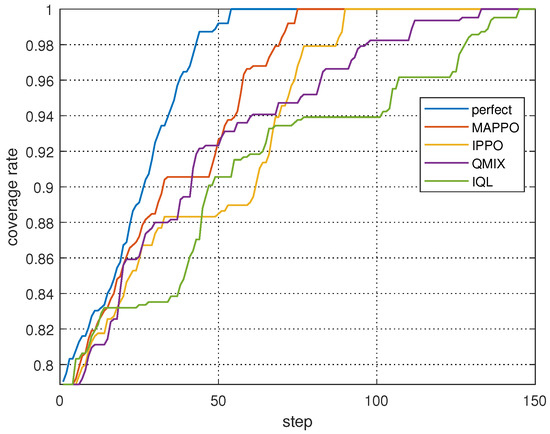
Figure 14.
Coverage rates of different collaborative search methods under MAPPO-based spectrum collaboration.
5. Conclusions
In this paper, we have developed a multi-UAV collaborative search scheme under interference conditions based on multi-agent reinforcement learning. An optimization problem was formulated to minimize the total search time by optimizing both the selection of channels and the search heading angles of the UAVs. The original problem was decomposed into two separate parts and solved by proposing RSSI-MAPPO and TPM-MAPPO. The simulation results indicated that our proposed scheme can ensure the collaborative search of UAVs under interference conditions, significantly reducing search times compared to other baseline algorithms. Our future work will focus on the following: (1) distributed LTPM exchange under interference and (2) game-theoretic meta-learning solutions for adaptive jammers, extending beyond the current fixed-pattern jamming scenario.
Author Contributions
Methodology, W.W., Y.D. and Y.C.; validation, W.W.; writing—original draft, W.W.; writing—review and editing, Y.C. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National University of Defense Technology Independent Innovation Science Fund under grant number 22-ZZCX-059.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hu, W.; Yu, Y.; Liu, S.; She, C.; Guo, L.; Vucetic, B.; Li, Y. Multi-UAV Coverage Path Planning: A Distributed Online Cooperation Method. IEEE Trans. Veh. Technol. 2023, 72, 11727–11740. [Google Scholar] [CrossRef]
- Lou, Z.; Wang, R.; Belmekki, B.E.Y.; Kishk, M.A.; Alouini, M.S. Terrain-Based UAV Deployment: Providing Coverage for Outdoor Users. IEEE Trans. Veh. Technol. 2024, 73, 8988–9002. [Google Scholar] [CrossRef]
- Li, X.; Lu, X.; Chen, W.; Ge, D.; Zhu, J. Research on UAVs Reconnaissance Task Allocation Method Based on Communication Preservation. IEEE Trans. Consum. Electron. 2024, 70, 684–695. [Google Scholar] [CrossRef]
- Zhang, B.; Lin, X.; Zhu, Y.; Tian, J.; Zhu, Z. Enhancing Multi-UAV Reconnaissance and Search Through Double Critic DDPG With Belief Probability Maps. IEEE Trans. Intell. Veh. 2024, 9, 3827–3842. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Y.; Li, D.; Shi, J.; Li, X.; Gao, L.; Yu, L.; Han, G.; Wu, J. An Adaptive Conversion Speed Q-Learning Algorithm for Search and Rescue UAV Path Planning in Unknown Environments. IEEE Trans. Veh. Technol. 2023, 72, 15391–15404. [Google Scholar] [CrossRef]
- Ribeiro, R.G.; Cota, L.P.; Euzébio, T.A.M.; Ramírez, J.A.; Guimarães, F.G. Unmanned-Aerial-Vehicle Routing Problem With Mobile Charging Stations for Assisting Search and Rescue Missions in Postdisaster Scenarios. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6682–6696. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, H.; Zhang, X.; Chang, Z.; Jäntti, R.; Yang, K. Toward Autonomous Multi-UAV Wireless Network: A Survey of Reinforcement Learning-Based Approaches. IEEE Commun. Surv. Tutor. 2023, 25, 3038–3067. [Google Scholar] [CrossRef]
- Sun, G.; He, L.; Sun, Z.; Wu, Q.; Liang, S.; Li, J.; Niyato, D.; Leung, V.C.M. Joint Task Offloading and Resource Allocation in Aerial-Terrestrial UAV Networks With Edge and Fog Computing for Post-Disaster Rescue. IEEE Trans. Mob. Comput. 2024, 23, 8582–8600. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Z.; Xu, Q.; Li, R.; Luan, T.H.; Wang, P. A Secure and Intelligent Data Sharing Scheme for UAV-Assisted Disaster Rescue. IEEE/ACM Trans. Netw. 2023, 31, 2422–2438. [Google Scholar] [CrossRef]
- Qian, M.; Chen, W.; Sun, R. A Maneuvering Target Tracking Algorithm Based on Cooperative Localization of Multi-UAVs with Bearing-Only Measurements. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Xu, K.; Song, C.; Xie, Y.; Pan, L.; Gan, X.; Huang, G. RMT-YOLOv9s: An Infrared Small Target Detection Method Based on UAV Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Lei, X.; Hu, X.; Wang, G.; Luo, H. A multi-UAV deployment method for border patrolling based on Stackelberg game. J. Syst. Eng. Electron. 2023, 34, 99–116. [Google Scholar] [CrossRef]
- Yang, D.; Wang, J.; Wu, F.; Xiao, L.; Xu, Y.; Zhang, T. Energy Efficient Transmission Strategy for Mobile Edge Computing Network in UAV-Based Patrol Inspection System. IEEE Trans. Mob. Comput. 2024, 23, 5984–5998. [Google Scholar] [CrossRef]
- Xu, W.; Wang, C.; Xie, H.; Liang, W.; Dai, H.; Xu, Z.; Wang, Z.; Guo, B.; Das, S.K. Reward Maximization for Disaster Zone Monitoring With Heterogeneous UAVs. IEEE/ACM Trans. Netw. 2024, 32, 890–903. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Huang, C. Decentralized Autonomous Navigation of a UAV Network for Road Traffic Monitoring. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2558–2564. [Google Scholar] [CrossRef]
- Lun, Y.; Wang, H.; Wu, J.; Liu, Y.; Wang, Y. Target Search in Dynamic Environments With Multiple Solar-Powered UAVs. IEEE Trans. Veh. Technol. 2022, 71, 9309–9321. [Google Scholar] [CrossRef]
- Shen, G.; Lei, L.; Zhang, X.; Li, Z.; Cai, S.; Zhang, L. Multi-UAV Cooperative Search Based on Reinforcement Learning With a Digital Twin Driven Training Framework. IEEE Trans. Veh. Technol. 2023, 72, 8354–8368. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, W.; Zuo, Y.; Gui, J.; Zhang, C. Multi-Objective Optimization of Dynamic Communication Network for Multi-UAVs System. IEEE Trans. Veh. Technol. 2024, 73, 4081–4094. [Google Scholar] [CrossRef]
- Peng, H.; Huo, M.l.; Liu, Z.z.; Xu, W. Simulation analysis of cooperative target search strategies for multiple UAVs. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 4855–4859. [Google Scholar]
- Zhang, Y.; Yuan, J.; Bao, H. Optimization algorithm and application of sand cat swarm based on sparrow warning mechanism and spiral search strategy. In Proceedings of the 2024 39th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Dalian, China, 7–9 June 2024; pp. 452–457. [Google Scholar]
- Zheng, J.; Ding, M.; Sun, L.; Liu, H. Distributed Stochastic Algorithm Based on Enhanced Genetic Algorithm for Path Planning of Multi-UAV Cooperative Area Search. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8290–8303. [Google Scholar] [CrossRef]
- Yang, F.; Ji, X.; Yang, C.; Li, J.; Li, B. Cooperative search of UAV swarm based on improved ant colony algorithm in uncertain environment. In Proceedings of the 2017 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 27–29 October 2017; pp. 231–236. [Google Scholar]
- Wu, J.; Luo, J.; Jiang, C.; Gao, L. Multi-UAV Cooperative Search in Multi-Layered Aerial Computing Networks: A Multi-Agent Deep Reinforcement Learning Approach. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 2791–2796. [Google Scholar]
- Ma, T.; Jiang, J.; Liu, X.; Liu, R.; Sun, H. Target Search of UAV Swarm Based on Improved Wolf Pack Algorithm. In Proceedings of the 2023 6th International Symposium on Autonomous Systems (ISAS), Nanjing, China, 23–25 June 2023; pp. 1–6. [Google Scholar]
- Hou, Y.; Zhao, J.; Zhang, R.; Cheng, X.; Yang, L. UAV Swarm Cooperative Target Search: A Multi-Agent Reinforcement Learning Approach. IEEE Trans. Intell. Veh. 2024, 9, 568–578. [Google Scholar] [CrossRef]
- Gao, Y.; Jin, G.; Guo, Y.; Zhu, G.; Yang, Q.; Yang, K. Weighted area coverage of maritime joint search and rescue based on multi-agent reinforcement learning. In Proceedings of the 2019 IEEE 3rd Advanced Information Management Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 11–13 October 2019; pp. 593–597. [Google Scholar]
- Ni, J.; Tang, G.; Mo, Z.; Cao, W.; Yang, S.X. An Improved Potential Game Theory Based Method for Multi-UAV Cooperative Search. IEEE Access 2020, 8, 47787–47796. [Google Scholar] [CrossRef]
- Fei, B.; Bao, W.; Zhu, X.; Liu, D.; Men, T.; Xiao, Z. Autonomous Cooperative Search Model for Multi-UAV With Limited Communication Network. IEEE Internet Things J. 2022, 9, 19346–19361. [Google Scholar] [CrossRef]
- Yanmaz, E.; Balanji, H.M.; Güven, Į. Dynamic Multi-UAV Path Planning for Multi-Target Search and Connectivity. IEEE Trans. Veh. Technol. 2024, 73, 10516–10528. [Google Scholar] [CrossRef]
- Balanji, H.M.; Yanmaz, E. Priority-Based Dynamic Multi-UAV Positioning for Multi-Target Search and Connectivity*. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]
- Devaraju, S.; Ihler, A.; Kumar, S. A Deep Q-Learning Connectivity-Aware Pheromone Mobility Model for Autonomous UAV Networks. In Proceedings of the 2023 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 20–22 February 2023; pp. 575–580. [Google Scholar]
- Wang, F.; Zhang, Z.; Zhou, L.; Shang, T.; Zhang, R. Robust Multi-UAV Cooperative Trajectory Planning and Power Control for Reliable Communication in the Presence of Uncertain Jammers. Drones 2024, 8, 558. [Google Scholar] [CrossRef]
- Meng, K.; He, X.; Wu, Q.; Li, D. Multi-UAV Collaborative Sensing and Communication: Joint Task Allocation and Power Optimization. IEEE Trans. Wirel. Commun. 2023, 22, 4232–4246. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, H.; Mersha, B.W.; Zhang, X.; Jin, Y. Distributed cooperative search method for multi-UAV with unstable communications. Appl. Soft Comput. 2023, 148, 110592. [Google Scholar] [CrossRef]
- Chai, S.; Yang, Z.; Huang, J.; Li, X.; Zhao, Y.; Zhou, D. Cooperative UAV search strategy based on DMPC-AACO algorithm in restricted communication scenarios. Def. Technol. 2024, 31, 295–311. [Google Scholar] [CrossRef]
- Shen, Y.; Wei, C.; Sun, Y.; Duan, H. Bird Flocking Inspired Methods for Multi-UAV Cooperative Target Search. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 702–706. [Google Scholar] [CrossRef]
- Yan, K.; Xiang, L.; Yang, K. Cooperative Target Search Algorithm for UAV Swarms With Limited Communication and Energy Capacity. IEEE Commun. Lett. 2024, 28, 1102–1106. [Google Scholar] [CrossRef]
- Luo, Q.; Luan, T.H.; Shi, W.; Fan, P. Deep Reinforcement Learning Based Computation Offloading and Trajectory Planning for Multi-UAV Cooperative Target Search. IEEE J. Sel. Areas Commun. 2023, 41, 504–520. [Google Scholar] [CrossRef]
- Kong, X.; Yang, J.; Chai, X.; Zhou, Y. An advantage duPLEX dueling multi-agent Q-learning algorithm for multi-UAV cooperative target search in unknown environments. Simul. Model. Pract. Theory 2025, 142, 103118. [Google Scholar] [CrossRef]
- Senthilnath, J.; Harikumar, K.; Sundaram, S. Metacognitive Decision-Making Framework for Multi-UAV Target Search Without Communication. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3195–3206. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X.; Yue, W.; Liu, Z. Cooperative search for dynamic targets by multiple UAVs with communication data losses. ISA Trans. 2021, 114, 230–241. [Google Scholar] [CrossRef] [PubMed]
- Day, R.; Salmon, J. Spatiotemporal Analysis of Multi-UAV Persistent Search and Retrieval with Stochastic Target Appearance. Drones 2025, 9, 152. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, X.; Fang, H.; Yang, Q. Distributed Formation Planning for Unmanned Aerial Vehicles. Drones 2025, 9, 306. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, Z.; Li, J.; Wang, L.; Zhang, X.; Gao, H. Communication-Constrained UAVs’ Coverage Search Method in Uncertain Scenarios. IEEE Sens. J. 2024, 24, 17092–17101. [Google Scholar] [CrossRef]
- Qian, Y.; Sheng, K.; Ma, C.; Li, J.; Ding, M.; Hassan, M. Path Planning for the Dynamic UAV-Aided Wireless Systems Using Monte Carlo Tree Search. IEEE Trans. Veh. Technol. 2022, 71, 6716–6721. [Google Scholar] [CrossRef]
- Sun, L.; Wang, J.; Wan, L.; Li, K.; Wang, X.; Lin, Y. Human-UAV Interaction Assisted Heterogeneous UAV Swarm Scheduling for Target Searching in Communication Denial Environment. IEEE Trans. Autom. Sci. Eng. 2025, 22, 4457–4472. [Google Scholar] [CrossRef]
- Yao, P.; Wei, X. Multi-UAV Information Fusion and Cooperative Trajectory Optimization in Target Search. IEEE Syst. J. 2022, 16, 4325–4333. [Google Scholar] [CrossRef]
- Pérez-Carabaza, S.; Scherer, J.; Rinner, B.; López-Orozco, J.A.; Besada-Portas, E. UAV trajectory optimization for Minimum Time Search with communication constraints and collision avoidance. Eng. Appl. Artif. Intell. 2019, 85, 357–371. [Google Scholar] [CrossRef]
- Khan, A.; Yanmaz, E.; Rinner, B. Information merging in multi-UAV cooperative search. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3122–3129. [Google Scholar]
- Hu, J.; Xie, L.; Lum, K.Y.; Xu, J. Multiagent Information Fusion and Cooperative Control in Target Search. IEEE Trans. Control Syst. Technol. 2013, 21, 1223–1235. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, Q.; Zhang, R. Accessing From the Sky: A Tutorial on UAV Communications for 5G and Beyond. Proc. IEEE 2019, 107, 2327–2375. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Liang, L.; Ye, H.; Li, G.Y. Spectrum Sharing in Vehicular Networks Based on Multi-Agent Reinforcement Learning. IEEE J. Sel. Areas Commun. 2019, 37, 2282–2292. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of PPO in Cooperative, Multi-Agent Games. arXiv 2022, arXiv:2103.01955. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).