Abstract
Unmanned aerial vehicle (UAV) swarms are widely applied in various fields, including military and civilian domains. However, due to the scarcity of spectrum resources, UAV swarm clustering technology has emerged as an effective method for achieving spectrum sharing among UAV swarms. This paper introduces a distributed heterogeneous multi-agent deep reinforcement learning algorithm, named HMDRL-UC, which is specifically designed to address the cluster-based spectrum sharing problem in heterogeneous UAV swarms. Heterogeneous UAV swarms consist of two types of UAVs: cluster head (CH) and cluster member (CM). Each UAV is equipped with an intelligent agent to execute the deep reinforcement learning (DRL) algorithm. Correspondingly, the HMDRL-UC consists of two parts: multi-agent proximal policy optimization for cluster head (MAPPO-H) and independent proximal policy optimization for cluster member (IPPO-M). The MAPPO-H enables the CHs to decide cluster selection and moving position, while CMs utilize IPPO-M to cluster autonomously under the condition of certain partial channel distribution information (CDI). Adequate experimental evidence has confirmed that the HMDRL-UC algorithm proposed in this paper is not only capable of managing dynamic drone swarm scenarios in the presence of partial CDI, but also has a clear advantage over the other existing three algorithms in terms of average throughput, intra-cluster communication delay, and minimum signal-to-noise ratio (SNR).
1. Introduction
As unmanned aerial vehicle (UAV) technology advances toward swarm intelligence and collaborative operations, UAV swarms have been increasingly applied in various fields, such as auxiliary communication, emergency response, target localization, reconnaissance exploration and internet of things (IoT) [1,2,3]. Recent studies demonstrate the versatility of UAVs in both fundamental tasks (e.g., autonomous parking occupancy detection [4]) and large-scale networked operations [5], highlighting the need for adaptive control in dynamic environments. Specially, flying ad hoc networks (FANETs), as a common organizational form of UAV swarms, can facilitate information interaction between UAVs and other devices based on the inter-UAV communication [6]. Furthermore, with the continuous development and upgrading of UAVs, various types of UAVs with different airborne capacities are included in the same group. Therefore, it becomes more practical to consider heterogeneous UAVs within FANETs [7].
However, as the number of UAVs within a network escalates, the conflict between the scarcity of spectrum resources and the necessity for reliable communication becomes increasingly acute. Spectrum sharing emerges as a potent strategy for resource utilization, aimed at facilitating dependable and secure communications within multi-UAV networks [8,9]. To achieve efficient spectrum sharing, the concept of coalition partitioning is introduced, which entails clustering the UAV swarm into distinct groups, particularly in scenarios involving multiple tasks [10]. In the context of a large-scale FANET, the adoption of clustering algorithms is imperative for effective networking and management [11]. Especially in heterogeneous scenarios, a single cluster consists of various types of UAVs, requiring efficient task completion while adhering to constraints related to latency, throughput, and other communication metrics.
In recent studies, clustering channels with similar interference characteristics have played a significant role in mitigating cross-channel interference and simplifying the demands of time synchronization, thereby lowering the overall system complexity [12,13]. In addition, clustering techniques have significantly enhanced the efficiency of spectrum utilization by partitioning spectrum resources into clusters [14,15]. Further, resource optimization within clusters has improved energy efficiency, allowing energy harvesting-supported device-to-device (EH-D2D) communication in multicast mode to utilize available energy more effectively, enhancing overall network performance [16]. And in [17], limited spectrum resources are effectively shared among a large number of users while simultaneously controlling interference and meeting quality of service (QoS) requirements. Moreover, clustering also achieves dynamic spectrum sharing. In [18], full-duplex user-centric ultra-dense networks adapt to changes in user numbers and locations through clustering schemes, dynamically adjusting the number and members of clusters to cope with dynamic network environments, maintaining the efficiency of spectrum sharing. It is evident that the application of clustering technology in complicated spectrum sharing networks is multifaceted. These effects will also collectively drive the development of UAV swarm communication networks toward greater efficiency and intelligence.
Many researchers have explored various clustering strategies for UAV swarms, with a focus on enhancing network performance, scalability, and adaptability [11,19,20,21,22,23,24]. A common clustering method is distance-based, such as K-means [19]. In contrast to the hard partitioning of K-means, an improved LB-FCM algorithm with a fuzzification parameter and a load balancing mechanism is proposed to enhance the algorithm’s flexibility and robustness in [20]. Further, UAVs are clustered according to an unsupervised scheme without pre-initializing the number in [21]. Swarm intelligence algorithm, like particle swarm optimization (PSO), is also adopted in [22], where a clustering routing protocol based on improved PSO algorithm determines the cluster head selection and clustering of FANETs in disaster response. To address the challenge of the mobility in UAV swarms, the UAV is clustered based on location prediction in [23], while the clustering problem is modeled as a graph cut problem in [24]. Moreover, in order to handle the multi-objective optimization in mobile edge computing (MEC), an iterative optimization algorithm based on penalty and block coordinate descent (BCD) is designed to tune the cluster head selection, positions, and transmit powers of UAVs in [11]. Recent studies further address critical challenges such as robustness in constrained environments [25] and energy-efficient control [26].
Nevertheless, the clustering approaches mentioned in the aforementioned articles mainly rely on a central control node, which limits the system’s ability to adapt to dynamic network conditions and recover from failures. To address this problem, distributed algorithms are proposed to enable autonomous clustering among UAVs. Coalition formation game (CFG) is used to jointly optimize task selection and spectrum allocation in UAV communication networks [27,28,29,30]. When the Global Navigation Satellite System (GNSS) is not functioning properly [29], CFG is also applied for clustering-based cooperative localization. Furthermore, a task scheduling-oriented clustering method for UAV swarms based on a dynamic super round has also been proposed in [31], which can effectively reduce the number of invalid clustering rounds. Moreover, recent decentralized frameworks, as exemplified in [32], have demonstrated progress in UAV swarm security enhancement through the systematic integration of machine learning methodologies. However, the above-mentioned distributed algorithm has high computational complexity, poor cooperation stability, lacks long-term planning capability, and has difficulty in adapting to dynamic environments.
Recently, reinforcement learning (RL) has been applied into the clustering of UAV swarms, significantly enhancing adaptive cooperative operation capability and task execution efficiency in complex environments [33,34,35]. Specially, due to the remarkable advantages of the multi-agent method, such as distributed decision-making, collaborative optimization, dynamic adaptation, and scalability, the authors in [33] researched the multi-agent RL algorithm, setting each UAV as an agent and determining the actions via an actor–critic network. However, the RL architecture suffers from insufficient heterogeneity and scalability. UAV swarms often contain heterogeneous individuals such as reconnaissance UAVs, transportation UAVs, and relay UAVs. There are significant differences in these heterogeneous individuals’ state and action spaces. Therefore, customized RL models are required, which exacerbates the computational and training complexity. Moreover, when the UAV swarm expands from a small scale (e.g., five UAVs) to a large scale (e.g., one hundred UAVs), the scale of RL parameters and the complexity of coordination increase superlinearly. To avoid the above drawback, the proximal policy optimization (PPO) algorithm [36], as an advanced RL method, offers significant advantages in addressing resource optimization problems for UAV swarms due to its stability, efficiency, and ease of implementation.
Motivated by the above, in this paper, we consider a heterogeneous UAV swarm, which needs to achieve spectrum sharing through reasonable clustering. Based on the multi-agent method and the PPO algorithm, a heterogeneous multi-agent deep reinforcement learning algorithm for UAV clustering (HMDRL-UC) is proposed to control the actions of UAVs in the presence of partial channel distribution information (CDI). The novel contributions of this paper can be summarized as follows:
- We consider a large-scale heterogeneous UAV swarm capable of meeting various mission requirements. The UAV swarm is divided into multiple small groups, and consists of two types of UAVs: cluster head (CH) and cluster member (CM). In particular, we study a practical setup, whereby the average communication delay for CMs and throughput for CHs are jointly optimized under the assumptions of knowing the partial CDI. Moreover, the link maintenance probability is discussed for CMs with the consideration of the mobility of CMs.
- We propose a novel distributed HMDRL-UC algorithm for heterogeneous UAV swarms, where each UAV acts as an intelligent agent. In detail, the HMDRL-UC is composed of two subalgorithms: the multi-agent PPO for CHs (MAPPO-H) and the independent PPO for CMs (IPPO-M). MAPPO-H is responsible for controlling the cluster selection and movement of CHs, while the IPPO-M is used to decide the cluster selection of CMs.
- A comprehensive performance analysis is carried out for the proposed HMDRL-UC algorithm, as well as a comparison with those of existing algorithms. The proposed HMDRL-UC algorithm demonstrates significant advantages in terms of average throughput, intra-cluster communication delay, and minimum signal-to-noise ratio (SNR). Moreover, it can optimize clustering for dynamic UAV swarm scenarios. Therefore, the HMDRL-UC algorithm is a highly promising clustering-based spectrum sharing candidate for multi-mission large-scale UAV swarm scenarios.
2. System Model and Problem Formulation
We consider a large UAV swarm to perform diversified reconnaissance missions, such as disaster monitoring, traffic management, environmental surveillance, etc. For example, the UAVs are equipped with a variety of sensing devices, including visible-light cameras, infrared cameras, or LiDAR, and they are supposed to conduct joint reconnaissance to obtain comprehensive reconnaissance results for a specific area. In order to improve the efficiency of mission completion, the UAVs are organized into small groups and maintain communication with each other for collaborative sensing and cooperative decision-making. Therefore, communication delay becomes one of the key factors in determining the operational efficiency of the system, especially in some mobile edge computing (MEC) networks [37,38]. However, due to the limitation of storage and processing capability onboard, some UAVs have to offload the collected data to the UAV with stronger ability. In this case, maximizing throughput can effectively improve the efficiency of data transmission. As shown in Figure 1, the UAV swarm consists of a control center, H cluster heads (CHs), and M cluster members (CMs). Among them, the control center has established stable communication links with CHs for swarm control and data transmission. CMs are divided into H clusters, where they collaborate to complete tasks and transmit data back to the corresponding CH. Nevertheless, given the rapid changes in tasks or environments, as well as the coordinated movement of the swarm, the relative positions of the CMs may undergo dynamic changes, which brings great challenges to the clustering of the UAV swarm. Consequently, the CMs are expected to cluster autonomously, while CHs adaptively select the service cluster and seek the optimal position.
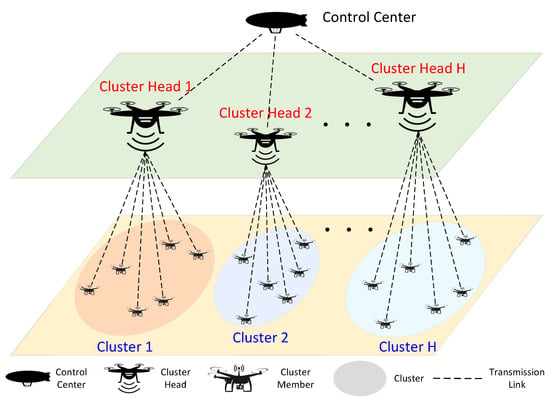
Figure 1.
Heterogeneous UAV swarm consisting of cluster heads and cluster members.
For the sake of simplicity, we define the clustering strategies for CMs, the cluster selection strategies for CHs and the three-dimensional (3D) location of CHs as , and , respectively. Note that both the radius of the cluster and the number of CMs within the cluster will influence the communication quality of the UAV swarm. An excessively large cluster radius may compromise the reliability of communication links between the CH and its service CMs. Furthermore, an excessive number of CMs within the cluster can result in significant communication delays. Therefore, we define the hth () cluster radius, number of CMs within the hth () cluster, maximum cluster radius, and maximum number of CMs within a cluster as , , , and , respectively.
2.1. Link Maintenance Probability Prediction of CMs
During the task execution, the relative movement between CMs can affect the clustering results. Hence, it is necessary to predict the communication link maintenance probability by predicting UAVs’ movements. We assume that the CMs transmit Hello packets periodically, and during the interval, the CMs maintain a constant velocity. As shown in Figure 2, is assumed to be stationary at time , while moves along the red line with a relative speed of . Both successfully receive each other’s Hello messages, which include timestamps, transmitted carrier frequency, and signal power to enable motion estimation. The predicted flight trajectory of and its relative speed are estimated using Doppler frequency shifts and received signal power variations across successive Hello packets, following the mobility prediction framework in [39]. Specifically, is derived from the Doppler shift as , where is the angle between the relative velocity and the LOS path, and is calculated using the path loss model to track distance changes over time. As suggested by [39], the link maintenance probability between and can be expressed as
where denotes the time threshold.
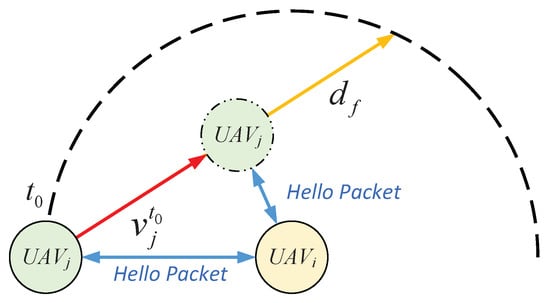
Figure 2.
The UAV’s mobility prediction model.
2.2. Channel Model
The air-to-air communication channel gains follow the Nakagami-m distributed fading model [40]. It is presumed that the channel gains are independent and identically distributed (i.i.d.), and remain constant during the transmission of each packet [41]. Hence, the probability density functions (PDFs) of the channel gains between and can be expressed as
where is the fading severity parameter, represents the Gamma function, is a random variable with mean value , and . The Nakagami-m fading parameter is constrained to , ensuring the Gamma function remains well defined. For , either attains a finite value (e.g., ) or represents a low-probability event (e.g., ), consistent with the physical interpretation of channel outages. Note that, in real-world UAV communication systems, corresponds to channel outages, which are inherently excluded during active communication phases.
In particular, because there are no obstacles in the sky, the path loss between and can be further described by the Friis free-space transmission formula. The standard Friis transmission equation defines the received power as
where is the transmit power; and are the antenna gains of the transmitter and receiver, respectively; is the wavelength; f denotes the center frequency of the carrier; is the distance between and ; and . In our system model, we assume isotropic antennas (omnidirectional radiation pattern), i.e., . The path loss is defined as the ratio of the transmitted power to the received power, which can be expressed as
Therefore, the SNR from to is shown as
where denotes the additive white Gaussian noise and represents the signal transmit power from to . Then, the successful packet transmission probability can be expressed by
where denotes the SNR threshold. In this way, the average transmission delay could be defined as
where and , respectively, denote the packet preparation delay and the packet transmission delay, and represents the average number of retransmissions, which can be defined as follows:
2.3. Problem Formulation
In this paper, our objective is to seek proper clustering strategies for CM, which minimizes the average intra-cluster communication delay and to identify optimal cluster selection strategy and locations for CHs to maximize overall cluster throughput, subject to the clustering constraints. The optimization problem can be described as follows:
subject to
where denotes the cluster number of the cluster set ; is one of ; represents the set of CMs; represents the set of CHs; and is the signal bandwidth from to . represents the communication probability of and , which can be described as
Similarly, the link status can be expressed as
The communication delay can be described as
where represents the shortest path between and .
The problem given by , and is a multi-objective nonlinear optimization problem. The commonly used method is to either decompose the joint optimization problem into smaller sub-problems for iterative optimization [11], resolve it through game theory [29], or utilize swarm intelligence methodologies [42]. However, the above methods may encounter high computational complexity and difficulties in handling high-dimensional, dynamically changing environments, etc. Therefore, in this paper, a distributed heterogeneous multi-agent deep reinforcement learning model called HMDRL-UC is proposed. Each UAV within the swarm is treated as an intelligent agent, autonomously making decisions through essential communications to address the highly dynamic and intricate scenarios of swarm movement. In particular, HMDRL-UC serves two types of UAVs: CHs and CMs, which are governed by MAPPO-H and IPPO-M, respectively. The tasks of CMs are to make decisions about clustering, while CHs are responsible for selecting the cluster to serve and for locating the optimal position.
3. Proposed Heterogeneous Multi-Agent Deep Reinforcement Learning Algorithm for UAV Clustering (HMDRL-UC)
In this section, we first introduce the framework of the HMDRL-UC, and its main parts. Then, the training procedure and complexity analysis are discussed for the HMDRL-UC.
3.1. The Framework of HMDRL-UC
As shown in Figure 3, the designed HMDRL-UC consists of two categories of agents: member agents and head agents, which server the CMs and the CHs, respectively. Both of them share the same environment. However, the HMDRL-UC allows member agents and head agents to have different observation spaces, actions spaces, and distinctive reward functions. The actions to be taken by agents are generated by an actor–critic structure. In detail, the actor network, called policy network, is responsible for action selection according to the current state, whereas the critic network predicts the future outcomes based on the action–state pairs to assesses the quality of the chosen actions. Furthermore, although the HMDRL-UC is a distributed framework, head agents employ a centralized training with a decentralized execution (CTDE) strategy, called the HAPPO-H algorithm, enabling them to share global information. Leveraging superior computational and communicative resources, head agents communicate with the control center during the centralized training phase, sharing their critic networks. This sharing of training data among head agents facilitates the identification of complex environments and globally optimal solutions. Specifically, after the model training is completed, a central control node is not required during the execution phase. In contrast, member agents, constrained by limited computational and communicative resources, adopt a fully decentralized independent training approach, called the IPPO-M algorithm, eliminating the need for communication with other agents during training. This approach enhances scalability and robustness. Each member agent can gain a precise understanding of the environment and enhance collaborative efficacy through the observation of others’ information. During the decentralized execution phase, member agents independently determine and select actions based on local observations.
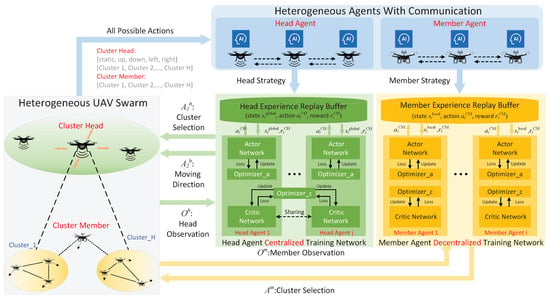
Figure 3.
The framework of the proposed HMDRL-UC algorithm.
3.2. The Design of IPPO-M
During the collective movement of UAV swarms, CMs must autonomously decide which cluster to join to facilitate collaborative communication. Considering the high scalability of a large number of CMs, yet their relatively weak on-board processing capabilities, we allow member agents to make decisions based on their individual local observations. Given that the actions mainly involve discrete choices, the IPPO algorithm framework is utilized to develop effective action strategies. Each CM is equipped with an IPPO-M subnetwork to obtain the optimal policy from the observation set to the action set with the help of the reward function .
3.2.1. Observation Set
As shown in Figure 2, the CMs periodically transmit Hello packets, which are utilized to estimate the velocity of neighboring UAVs and to forecast their movements. Further, by integrating the routing discovery protocol [43], the CM can acquire intra-cluster routing information and assess communication delays. To facilitate efficient clustering, the CM also broadcasts its cluster ID to neighboring areas. Consequently, the CM’s observation set encompasses both its own status and relevant information from neighboring agents. So, the observation set observed by a member agent consists of fourteen parts: its own position , its own velocity , its own cluster ID , its own communication delay , the position of the neighbor , the velocity of the neighbor , the cluster ID of the neighbor , the link maintenance probability between and , the path loss between and , estimated mean value , of the channel gain between and , the signal transmit power from to , the fading severity parameter , and the additive white Gaussian noise . Therefore, the observation set can be expressed as .
3.2.2. Action Set
Once the member agents obtain an observation of the environment, the actor network will generate a specific action for member agents according to the policy . In particular, the member agents are supposed to select an action from the discrete action set , where H is the number of clusters, and represents the member agent selected to join the hth cluster.
3.2.3. Reward
After taking the action , the member agent will receive a reward from the critic network. The critic network will evaluate the value of action on the basis of the influenced environment and inform the member agent whether this is a good action. In conclusion, we encourage member agents to establish stable connections with neighbors, so as to participate in cluster cooperation. Meanwhile, we punish the isolated points and the delay between the member agent and its neighbors. In this way, each member agent seeks to perform the action that maximizes its cumulative reward. Therefore, the reward function of the member agent is defined as
where and are the discount factors, represents the neighbor set of member agent , denotes the number of neighbors, and is the link maintenance probability between member agent and its neighbor at time t. indicates whether the member agent is an isolated node, which can be described as
3.3. The Design of MAPPO-H
Once CMs have formed stable clusters, the CHs first identify the cluster to be serviced, and then seek the most advantageous data transmit position to maximize the overall throughput of the UAV swarm. Therefore, the head agents have to determine two actions: the cluster to serve and the moving position. CHs generally possess more onboard processing capabilities and are less numerous; hence, we adopted the MAPPO algorithm to manage the actions of cluster head agents. Each CH is equipped with a MAPPO-H subnetwork to learn the optimal policy from the observation set to the action set with the help of reward function .
3.3.1. Observation Set
Because of the shared environment, the head agent is able to obtain the states of other head agents and also derives the states of member agents within the servicing cluster. Therefore, the head agent prioritizes information about its own position , its own cluster ID , the cluster ID of other head agents , and the position of its servicing member agents , where denotes the other head agents besides , and represents the member agents that the head agent serves. Meanwhile, the head agent can obtain the link maintenance probability between and , the path loss between and , estimated mean value of the channel gain between and , the signal transmit power from to , and the additive white Gaussian noise . Hence, the observation set of agent can be described as .
3.3.2. Action Set
In contrast to member agents, the action set for head agents is a two-dimensional discrete space , where represents the servicing cluster of the head agent , and denotes the moving position of the head agent .
3.3.3. Reward
Since the head agents can communicate and share training information with each other during the centralized training phase of the MAPPO algorithm, they have access to global information. To enhance training effectiveness, MAPPO-H incorporates a hybrid reward system. The rewards for head agents consist of both global and local components, motivating the head agents to maximize the overall throughput and maximize the minimum SNR with the member agents. The global and local reward functions can be expressed as
where represents the set of CHs, denotes the member agents that the head agent serves, and and are the signal bandwidth and SNR from to . In general, the global reward motivates the head agents to optimize the overall throughput. Only the head agent with the highest reward can serve the cluster, which avoids multiple head agents serving the same cluster simultaneously. Meanwhile, the local reward prompts the head agents to optimize the minimum SNR with the member agents, thereby minimizing the likelihood of communication disruptions. Therefore, the total reward for head agents can be defined as
where is used to make a trade-off between the global and local goals.
3.4. Training Procedure
The training procedure of the proposed HMDRL-UC algorithm is described in Algorithm 1. First, we initiate actor networks and critic networks for member agents with parameters and , while initiating actor networks and critic networks for head agents with parameters and . Then, the agents interact with the environment to obtain the trajectories of the member agent and the head agent at the time step t, where is the action taken by the member agent based on the observation set using the policy , i.e., . Similarly, . After executing the actions and , the rewards and and the next observation sets and are generated, respectively. Finally, the data and are, respectively, stored in the memory buffers for member agents and head agents, where and are the value estimates for critic networks of member agents and head agents, and and are the advantage functions of member agents and head agents. According to [40], and can be estimated via generalized advantage estimation (GAE) as follows:
where , , are the key hyperparameters for GAE that balance bias and variance in the advantage estimation, are the discount factors that control the weight of future rewards, and and are the target local critics of member agent and head agent , respectively.
In the practical implementation, the policy gradient for each actor network is calculated as
where is the sample average, and
In Equations (25) and (26), and denote the current policy with parameters , , , and ; and represent the updated policy with parameters , , , and ; and the clip function restricts the probability ratio and into the interval .
Meanwhile, the policy gradient for each critic network is calculated as
where , .
In the period of training, we iteratively update , , , and with the gradient in Equations (23), (24), (27) and (28), respectively. Then, , , , and are updated iteratively until the training process terminates.
| Algorithm 1 Network Training Stage of HMDRL-UC Algorithm |
|
3.5. Complexity Analysis
As suggested by [36,44], the complexity of the PPO algorithm is primarily determined by the forward and backward propagation of the neural network, and is related to the dimensions of the state space and action space, the number of layers and nodes per layer, as well as the number of samples per update. The proposed HMDRL-UC algorithm consists of IPPO-M algorithm and MAPPO-H algorithm. In the IPPO-M algorithm, the forward propagation of the actor network generates a trajectory , and back propagation calculates the policy gradient, with a computational complexity of , where I is the iteration number; B is the number of trajectories per iteration, i.e., the batch size; T is the length of each trajectory; is the number of layers in the actor network ; and is the number of hidden units per layer in the actor network . The advantage functions is calculated with a computational complexity of . The process of the critic network is similar to the actor network , with a computational complexity of , where is the number of layers in the critic network , and is the number of hidden units per layer in the critic network . Therefore, if there are M member agents in the heterogeneous UAV swarm, the computational complexity of the IPPO-M algorithm is . Different from the IPPO-M algorithm, all the head agents in the MAPPO-H algorithm share a single critic network. Hence, if there are H head agents, the computational complexity of the MAPPO-H algorithm is , where and are the number of layers and the number of hidden units per layer in the actor network ; and are the number of layers and the number of hidden units per layer in the critic network . In general, the ultimate computational complexity of the proposed HMDRL-UC algorithm is given by .
4. Simulation and Analysis
In this section, we evaluate the proposed HMDRL-UC algorithm from various simulation perspectives. Firstly, we conducted a performance comparison between the proposed HMDRL-UC algorithm and the existing algorithms. Then, we investigated the impact of different numbers of CMs on the performance of the proposed HMDRL-UC algorithm. Finally, we analyzed the influence of different speeds of CHs on the convergence speed of the HMDRL-UC algorithm.
4.1. Experiment Setting
We considered a heterogeneous UAV swarm uniformly distributed in the mission area. It is assumed that the UAVs in the swarm are divided into two types: CHs and CMs. The CHs were deployed at an altitude of , while the altitude of CMs ranged from to . The relative speed of CMs ranged from to , and the velocity of CHs was about . The transmit power of CMs was , and the SNR threshold of CHs was defined as . The central frequency of the carrier was set to be , while the bandwidth was . The background noise power was . The packet preparation delay and the packet transmission delay were set as and . The Hello interval was configured to last [27]. The maximum cooperative communication distance for CMs was set as [43]. The fading severity parameter was set to be 2 [40].
In the MAPPO-H algorithm, the initial learning rate was set to 0.007, the hidden layer dimension of the Multi-Layer Perceptron (MLP) was 128, the dimension of actor network was 256, and the dimension of critic network was 256. In the IPPO-M network, the learning rate was 0.0007, the hidden layer dimension of MLP was 64, the dimension of actor network was 128, and the dimension of critic network was 256. The batch size was set to 3200. Both actor network and critic network utilized the Adaptive Moment Estimation (Adam) optimizer, with the learning rate linearly decaying to 0.01 of its initial value. A total of 128 parallel environments were established for the simulation, which was conducted using Python 3.7 on a CPU (Intel Xeon Gold 6430, ARM Cortex-A72) and GPU (NVIDIA RTX A5000).
Figure 4 shows the clustering results under different numbers of clusters. We considered four scenarios: 2 CHs and 20 CMs in an area of , 4 CHs and 40 CMs in an area of , 6 CHs and 60 CMs in an area of , and 9 CHs and 90 CMs in an area of . We mainly compared the performance of the algorithms based on the following three metrics: average throughput, average intra-cluster delay, and average minimum SNR. Average throughput reflects the ability of CHs to collect information sent back from CMs, with higher values indicating better performance. Moreover, average intra-cluster delay reflects the performance of cooperative communication within clusters, where lower values indicate more efficient communication. Finally, the average minimum SNR reflects the ability of CHs to serve edge member agents, with higher values indicating better service quality.
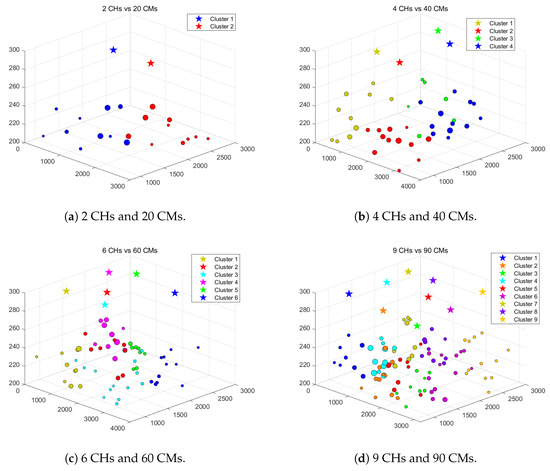
Figure 4.
The clustering results under different numbers of clusters.
4.2. Training Efficiency and Resource Consumption Analysis
Table 1 summarizes the training time, GPU/CPU resource consumption, and energy efficiency of the proposed HMDRL-UC algorithm under different UAV swarm scales. In general, we can observe that the training time and resource consumption of HMDRL-UC exhibit scalability across different UAV swarm scales. For the smallest scenario (2 CHs and 20 CMs), training completes in 2.1 h on CPU and 0.8 h on GPU, while the largest scenario (9 CHs and 90 CMs) requires 19.8 h (CPU) and 6.7 h (GPU), indicating a near-linear increase in computational demand with swarm size. GPU acceleration reduces training time by 60–66% compared to CPU, albeit with higher memory usage (8–17 GB). CPU utilization remains moderate (% with 64 threads), suggesting efficient parallelism. Energy consumption scales proportionally, reaching 3960 Wh (CPU) and 2010 Wh (GPU) for the largest configuration. In addition, the algorithm’s inference phase demonstrates hardware adaptability: on resource-constrained platforms like ARM Cortex-A72, IPPO-M requires only 0.12 Wh and 0.8 MFLOPs per inference, making it viable for embedded UAV systems with limited power budgets.

Table 1.
Training time and resource consumption of HMDRL-UC under different UAV swarm Sscales.
While HMDRL-UC requires substantial computational resources during centralized training, the trained models can be deployed on resource-constrained UAV hardware for decentralized execution. For instance, the IPPO-M actor network (128-dimensional hidden layer) occupies only 1.2 MB of memory and requires 0.3 ms per inference on an ARM Cortex-A72 embedded processor. By leveraging model quantization and pruning techniques, we further reduced the model size to 0.5 MB with negligible performance degradation. Additionally, the distributed nature of HMDRL-UC eliminates the need for real-time global coordination, making it feasible for UAVs with limited energy budgets (e.g., 10 W power consumption during inference).
4.3. Comparison
We provide numerical results to compare the performance of the proposed HMDRL-UC algorithm with the iterative coverage efficient clustering (CECA) algorithm [11], energy-efficient swarm intelligence-based clustering algorithm based on particle swarm optimization (SIC-PSO) [42], coalition formation game (CFG) algorithm [29], and deep deterministic policy gradient (DDPG) [45] under different numbers of UAV swarm clusters. It is worth to emphasize that, both the CECA algorithm and CFG algorithm focus on static scenarios of UAV swarms. While the SIC-PSO algorithm and the DDPG algorithm can handle clustering issues in dynamic UAV swarm scenarios, it requires prior Channel State Information (CSI). In contrast, the proposed HMDRL-UC algorithm not only addresses dynamic UAV swarm environments, but also requires only estimated channel gain distribution patterns, i.e., CDI.
Figure 5 compares the performance of the proposed HMDRL-UC algorithm with the other four algorithms in terms of average throughput, average intra-cluster delay, and average minimum SNR. It is clearly visible from the figure that as the number of UAV swarm clusters increases, both the average cluster throughput and the average minimum SNR slightly decrease, while the average intra-cluster delay gradually rises. This observation shows that as the number of clusters increases, the potential for clustering becomes more complex, leading to greater challenges in clustering. Hence, this can result in irregular cluster shapes, increased routing paths, and larger cluster areas. By contrast, in Figure 5a,c, the average throughput and average minimum SNR of the HMDRL-UC algorithm are obviously better than those achieved by the other four algorithms. Moreover, in Figure 5b, it can be clearly observed that the HMDRL-UC algorithm achieves the lowest average intra-cluster delay. From the above simulation results, the proposed HMDRL-UC algorithm achieved the best performances. This is because the HMDRL-UC algorithm utilizes a multi-agent deep reinforcement learning approach, where each agent observes the environment and extracts useful information through a deep neural network, learning their own action strategies. This enables a more effective handling of complex decision-making problems. Moreover, compared to the DDPG algorithm, HMDRL-UC employs a divide-and-conquer strategy by decoupling the optimization processes of MAPPO-H and IPPO-M, significantly reducing model complexity while achieving dynamic environment adaptation through partial CDI utilization instead of relying on complete CSI. Compared to the other algorithms, the proposed HMDRL-UC algorithm demonstrates greater robustness and scalability.
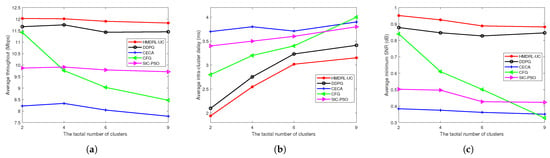
Figure 5.
Performance comparison under different numbers of clusters: (a) Average throughput comparison. (b) Average intra-cluster delay comparison. (c) Average minimum SNR comparison.
As quantitatively demonstrated in Table 2, the proposed HMDRL-UC algorithm delivers substantial performance enhancements across all critical metrics compared to baseline methods. In a representative scenario with 9 CHs and 90 CMs within a operational area, HMDRL-UC achieves remarkable throughput improvements of 3.5%, 52.6%, 40.0%, and 22.7% over DDPG, CECA, CFG, and SIC-PSO, respectively. The algorithm also demonstrates superior latency performance, reducing average intra-cluster delay by 5.9%, 17.9%, 20.0%, and 15.8% compared to the same baselines. Furthermore, HMDRL-UC maintains a 3.5%, 151.4%, 166.7%, and 109.5% advantage in minimum SNR preservation over DDPG, CECA, CFG, and SIC-PSO, respectively. Notably, HMDRL-UC pioneers dynamic adaptation capabilities in environments with partial CDI, addressing critical limitations of existing approaches: CECA and CFG are restricted to static operational modes, while SIC-PSO and DDPG depend on complete CSI. Moreover, the HMDRL-UC, through a heterogeneous design combining lightweight IPPO-M and the centralized training of MAPPO-H, achieves significantly enhanced performance, thereby validating its balanced advantage in managing the trade-off between complexity and performance. These systemic enhancements collectively confirm the effectiveness of our heterogeneous multi-agent framework in harmonizing network performance optimization, environmental adaptability, and practical deployment viability for large-scale UAV swarms.

Table 2.
Performance comparison of HMDRL-UC with baseline algorithms (9 CHs and 90 CMs).
4.4. Effects of Different Numbers of CMs
Figure 6 shows the cumulative reward values of member agents under different numbers of CMs. We conducted simulations in a scenario, with 20, 40, and 60 CMs grouped into 4 clusters. As can be observed from the figure, convergence occurs at 80 iterations for the 20 CMs case, at 260 iterations for the 40 CMs case, and at 700 iterations for the 60 CMs case. Moreover, the more cluster members there are, the slower the convergence speed becomes, the lower the cumulative reward value after convergence, and the greater the volatility. This is because as the number of CMs increases, each UAV has more potential communication partners, requiring the agent to process more environmental information to make decisions. This results in a larger state space, leading to slower convergence and greater instability. In addition, the increased complexity of UAV ad hoc networks inevitably leads to an increase in communication hops, which in turn causes a corresponding increase in latency. As a result, the cumulative reward value of member agents decreases.
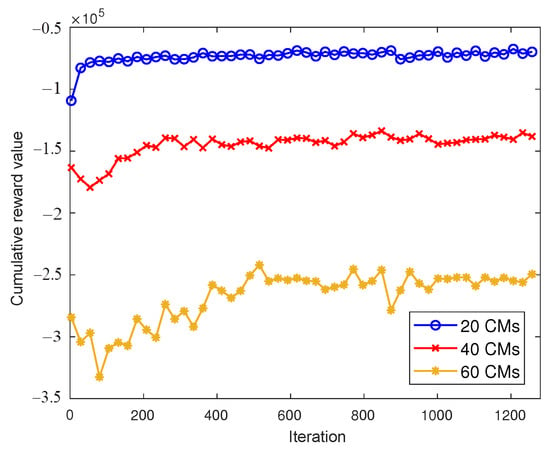
Figure 6.
Cumulative reward values of member agents under different numbers of CMs.
4.5. Effects of Different Speeds of CH
Figure 7 investigates the cumulative reward values of head agents under different speeds of CH. We conducted simulations with CH speeds of 100 m/s, 150 m/s, and 200 m/s, respectively. As shown in the figure, when the CH’s speed is 100 m/s, 150 m/s, and 200 m/s, the algorithm converges within 170, 150, and 131 iterations, respectively. It can also be observed that at the beginning stage, the CH’s cumulative reward is the highest when the speed is 150 m/s, followed by 200 m/s. However, at convergence, the cumulative reward values are similar when the speed is 100 m/s and 150 m/s, followed by 200 m/s.This is because as the CH’s speed increases, the CH will reach the optimal data transmission and reception position more quickly, and the algorithm will converge faster accordingly. However, since the action space of the CH is discrete, the step size for moving in space also increases with the speed. Therefore, at 200 m/s, the cluster head may be more likely to deviate from the optimal data transmission position.
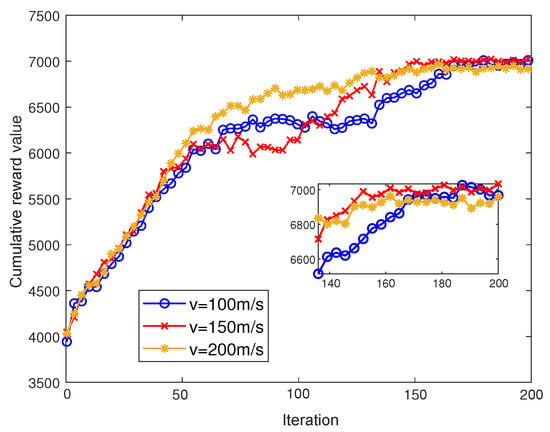
Figure 7.
Cumulative reward values of head agents under different speeds of the CH.
5. Conclusions
We propose a novel algorithm based on heterogeneous multi-agent deep reinforcement learning, named HMDRL-UC, for cluster-based spectrum sharing in large-scale heterogeneous UAV swarms. The HMDRL-UC algorithm consists of two parts: MAPPO-H and IPPO-M. The MAPPO-H algorithm equips CHs with decision-making capabilities for cluster selection and mobility planning, whereas CMs employ the IPPO-M algorithm to perform decentralized clustering operations based on CDI. Simulation results show that, compared to the other existing algorithms, our proposed HMDRL-UC algorithm can handle dynamic spectrum sharing scenarios under CDI conditions, achieving higher throughput and SNR while effectively reducing communication delay. While this work primarily focuses on role-based heterogeneity (CHs vs. CMs) and mobility dynamics, future research will extend HMDRL-UC to handle more complex heterogeneous scenarios, such as UAVs with varying computational capabilities, communication bandwidths, or energy constraints. Incorporating these factors could further enhance the algorithm’s practicality in real-world multi-mission UAV swarms. In general, the proposed HMDRL-UC algorithm is a promising clustering-based spectrum sharing algorithm for multi-mission UAV swarm scenarios.
Author Contributions
Conceptualization, X.L. and Y.W.; methodology, X.L. and Y.W.; software, Y.W. and Y.H.; validation, Y.W., Y.H. and C.L.; formal analysis, Y.W. and Y.H.; investigation, X.L., Y.W. and Y.L.; resources, X.L., Y.W., Y.L., C.L. and X.Z.; data curation, Y.W. and X.Z.; writing—original draft preparation, X.L. and Y.W.; writing—review and editing, X.L., Y.W., Y.L., C.L. and X.Z.; visualization, X.L. and Y.W.; supervision, Y.H. and C.L.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 62201582.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
We sincerely thank the editor and reviewers for their time and effort in reviewing our work.
Conflicts of Interest
There are no conflicts of interest or competing interests with regard to this study.
References
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A.; Guizani, M. State-of-the-Art and Future Research Challenges in UAV Swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, Y.; Wu, Y.; Wang, C.; Zang, D.; Abusorrah, A.; Zhou, M. PSO-Based Sparse Source Location in Large-Scale Environments with a UAV Swarm. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5249–5258. [Google Scholar] [CrossRef]
- Liu, C.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N. Cell-Free Satellite-UAV Networks for 6G Wide-Area Internet of Things. IEEE J. Sel. Areas Commun. 2021, 39, 1116–1131. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, B. Quadrotor-Enabled Autonomous Parking Occupancy Detection. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24–30 October 2020; pp. 8287–8292. [Google Scholar] [CrossRef]
- Fan, B.; Li, Y.; Zhang, R.; Fu, Q. Review on the Technological Development and Application of UAV Systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, H.; Mai, T.; Xiong, Z.; Wu, X.; Wu, D.; Guo, S. Learning to Routing in UAV Swarm Network: A Multi-Agent Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2023, 72, 6611–6624. [Google Scholar] [CrossRef]
- Li, S.; Li, J.; Xiang, C.; Xu, W.; Peng, J.; Wang, Z.; Liang, W.; Yao, X.; Jia, X.; Das, S.K. Maximizing Network Throughput in Heterogeneous UAV Networks. IEEE/ACM Trans. Netw. 2024, 32, 2128–2142. [Google Scholar] [CrossRef]
- Sun, Z.; Qi, F.; Liu, L.; Xing, Y.; Xie, W. Energy-Efficient Spectrum Sharing for 6G Ubiquitous IoT Networks Through Blockchain. IEEE Internet Things J. 2023, 10, 9342–9352. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Ding, G.; Xue, Z.; Zhang, L.; Xu, Y. Robust Spectrum Sharing in Air-Ground Integrated Networks: Opportunities and Challenges. IEEE Wirel. Commun. 2020, 27, 148–155. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Q.; Xu, Y.; Qi, N.; Fang, T.; Liu, D. Spectrum Allocation for Task-Driven UAV Communication Networks Exploiting Game Theory. IEEE Wirel. Commun. 2021, 28, 174–181. [Google Scholar] [CrossRef]
- You, W.; Dong, C.; Cheng, X.; Zhu, X.; Wu, Q.; Chen, G. Joint Optimization of Area Coverage and Mobile-Edge Computing with Clustering for FANETs. IEEE Internet Things J. 2021, 8, 695–707. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, W.; Wang, J.; Zhou, S.; Wang, C.X. Fine-Over-Coarse Spectrum Sharing with Shaped Virtual Cells for Hybrid Satellite-UAV-Terrestrial Maritime Networks. IEEE Trans. Wirel. Commun. 2024, 23, 17478–17492. [Google Scholar] [CrossRef]
- Wu, S.H.; Ko, C.H.; Chao, H.L. On-Demand Coordinated Spectrum and Resource Provisioning Under an Open C-RAN Architecture for Dense Small Cell Networks. IEEE Trans. Mob. Comput. 2024, 23, 673–688. [Google Scholar] [CrossRef]
- Bonati, L.; Polese, M.; D’Oro, S.; Basagni, S.; Melodia, T. NeutRAN: An Open RAN Neutral Host Architecture for Zero-Touch RAN and Spectrum Sharing. IEEE Trans. Mob. Comput. 2024, 23, 5786–5798. [Google Scholar] [CrossRef]
- Xie, N.; Ou-Yang, L.; Liu, A.X. Spectrum Sharing in mmWave Cellular Networks Using Clustering Algorithms. IEEE/ACM Trans. Netw. 2020, 28, 1378–1390. [Google Scholar] [CrossRef]
- Alhussien, N.; Gulliver, T.A. Joint Resource and Power Allocation for Clustered Cognitive M2M Communications Underlaying Cellular Networks. IEEE Trans. Veh. Technol. 2022, 71, 8548–8560. [Google Scholar] [CrossRef]
- Zeng, M.; Luo, Y.; Jiang, H.; Wang, Y. A Joint Cluster Formation Scheme with Multilayer Awareness for Energy-Harvesting Supported D2D Multicast Communication. IEEE Trans. Wirel. Commun. 2022, 21, 7595–7608. [Google Scholar] [CrossRef]
- Zhang, G.; Ke, F.; Zhang, H.; Cai, F.; Long, G.; Wang, Z. User Access and Resource Allocation in Full-Duplex User-Centric Ultra-Dense Networks. IEEE Trans. Veh. Technol. 2020, 69, 12015–12030. [Google Scholar] [CrossRef]
- Karmakar, R.; Kaddoum, G.; Akhrif, O. A Blockchain-Based Distributed and Intelligent Clustering-Enabled Authentication Protocol for UAV Swarms. IEEE Trans. Mob. Comput. 2024, 23, 6178–6195. [Google Scholar] [CrossRef]
- Dai, X.; Lu, Z.; Chen, X.; Xu, X.; Tang, F. Multiagent RL-Based Joint Trajectory Scheduling and Resource Allocation in NOMA-Assisted UAV Swarm Network. IEEE Internet Things J. 2024, 11, 14153–14167. [Google Scholar] [CrossRef]
- Asim, M.; ELAffendi, M.; El-Latif, A.A.A. Multi-IRS and Multi-UAV-Assisted MEC System for 5G/6G Networks: Efficient Joint Trajectory Optimization and Passive Beamforming Framework. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4553–4564. [Google Scholar] [CrossRef]
- Sun, G.; Qin, D.; Lan, T.; Ma, L. Research on Clustering Routing Protocol Based on Improved PSO in FANET. IEEE Sens. J. 2021, 21, 27168–27185. [Google Scholar] [CrossRef]
- Xu, W.; Ke, Y.; Lee, C.H.; Gao, H.; Feng, Z.; Zhang, P. Data-Driven Beam Management with Angular Domain Information for mmWave UAV Networks. IEEE Trans. Wirel. Commun. 2021, 20, 7040–7056. [Google Scholar] [CrossRef]
- Zhu, G.; Yao, H.; Mai, T.; Wang, Z.; Wu, D.; Guo, S. Fission Spectral Clustering Strategy for UAV Swarm Networks. IEEE Trans. Serv. Comput. 2024, 17, 537–548. [Google Scholar] [CrossRef]
- Petrlik, M.; Baca, T.; Hert, D.; Vrba, M.; Krajnik, T.; Saska, M. A Robust UAV System for Operations in a Constrained Environment. IEEE Robot. Autom. Lett. 2020, 5, 2169–2176. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Ren, B. Energy Saving Quadrotor Control for Field Inspections. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 52, 1768–1777. [Google Scholar] [CrossRef]
- Xing, N.; Zong, Q.; Dou, L.; Tian, B.; Wang, Q. A Game Theoretic Approach for Mobility Prediction Clustering in Unmanned Aerial Vehicle Networks. IEEE Trans. Veh. Technol. 2019, 68, 9963–9973. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Q.; Xu, Y.; Qi, N.; Guan, X.; Zhang, Y.; Xue, Z. Joint Task Assignment and Spectrum Allocation in Heterogeneous UAV Communication Networks: A Coalition Formation Game-Theoretic Approach. IEEE Trans. Wirel. Commun. 2021, 20, 440–452. [Google Scholar] [CrossRef]
- Ruan, L.; Li, G.; Dai, W.; Tian, S.; Fan, G.; Wang, J.; Dai, X. Cooperative Relative Localization for UAV Swarm in GNSS-Denied Environment: A Coalition Formation Game Approach. IEEE Internet Things J. 2022, 9, 11560–11577. [Google Scholar] [CrossRef]
- Huang, Y.; Qi, N.; Huang, Z.; Jia, L.; Wu, Q.; Yao, R.; Wang, W. Connectivity Guarantee Within UAV Cluster: A Graph Coalition Formation Game Approach. IEEE Open J. Commun. Soc. 2023, 4, 79–90. [Google Scholar] [CrossRef]
- Halder, S.; Ghosal, A.; Conti, M. Dynamic Super Round-Based Distributed Task Scheduling for UAV Networks. IEEE Trans. Wirel. Commun. 2023, 22, 1014–1028. [Google Scholar] [CrossRef]
- Halli Sudhakara, S.; Haghnegahdar, L. Security Enhancement in AAV Swarms: A Case Study Using Federated Learning and SHAP Analysis. IEEE Open J. Intell. Transp. Syst. 2025, 6, 335–345. [Google Scholar] [CrossRef]
- Hassan, M.Z.; Kaddoum, G.; Akhrif, O. Resource Allocation for Joint Interference Management and Security Enhancement in Cellular-Connected Internet-of-Drones Networks. IEEE Trans. Veh. Technol. 2022, 71, 12869–12884. [Google Scholar] [CrossRef]
- Guo, J.; Gao, H.; Liu, Z.; Huang, F.; Zhang, J.; Li, X.; Ma, J. ICRA: An Intelligent Clustering Routing Approach for UAV Ad Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2447–2460. [Google Scholar] [CrossRef]
- He, W.; Yao, H.; Mai, T.; Wang, F.; Guizani, M. Three-Stage Stackelberg Game Enabled Clustered Federated Learning in Heterogeneous UAV Swarms. IEEE Trans. Veh. Technol. 2023, 72, 9366–9380. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Bai, Z.; Lin, Y.; Cao, Y.; Wang, W. Delay-Aware Cooperative Task Offloading for Multi-UAV Enabled Edge-Cloud Computing. IEEE Trans. Mob. Comput. 2022, 23, 1034–1049. [Google Scholar] [CrossRef]
- Han, Z.; Zhou, T.; Xu, T.; Hu, H. Joint User Association and Deployment Optimization for Delay-Minimized UAV-Aided MEC Networks. IEEE Wirel. Commun. Lett. 2023, 12, 1791–1795. [Google Scholar] [CrossRef]
- Ni, M.; Zhong, Z.; Zhao, D. MPBC: A Mobility Prediction-Based Clustering Scheme for Ad Hoc Networks. IEEE Trans. Veh. Technol. 2011, 60, 4549–4559. [Google Scholar] [CrossRef]
- Vo, V.N.; Nguyen, L.M.D.; Tran, H.; Dang, V.H.; Niyato, D.; Cuong, D.N.; Luong, N.C.; So-In, C. Outage Probability Minimization in Secure NOMA Cognitive Radio Systems with UAV Relay: A Machine Learning Approach. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 435–451. [Google Scholar] [CrossRef]
- Vu, T.H.; Nguyen, T.V.; Kim, S. Wireless Powered Cognitive NOMA-Based IoT Relay Networks: Performance Analysis and Deep Learning Evaluation. IEEE Internet Things J. 2022, 9, 3913–3929. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. Localization and Clustering Based on Swarm Intelligence in UAV Networks for Emergency Communications. IEEE Internet Things J. 2019, 6, 8958–8976. [Google Scholar] [CrossRef]
- Hong, L.; Guo, H.; Liu, J.; Zhang, Y. Toward Swarm Coordination: Topology-Aware Inter-UAV Routing Optimization. IEEE Trans. Veh. Technol. 2020, 69, 10177–10187. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.; Zhao, X. Deep Reinforcement Learning Based Latency Minimization for Mobile Edge Computing with Virtualization in Maritime UAV Communication Network. IEEE Trans. Veh. Technol. 2022, 71, 4225–4236. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Zhou, D.; Xu, F.; Ma, J.; Ning, X. Deep Reinforcement Learning for Task Offloading and Resource Allocation in UAV Cluster-Assisted Mobile Edge Computing. IEEE J. Miniaturization Air Space Syst. 2024. early access. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).