Next Article in Journal
Energy Efficiency Optimization for UAV-RIS-Assisted Wireless Powered Communication Networks
Next Article in Special Issue
Optimization of Flight Planning for Orthomosaic Generation Using Digital Twins and SITL Simulation
Previous Article in Journal
Three-Dimensional Defect Measurement and Analysis of Wind Turbine Blades Using Unmanned Aerial Vehicles
Previous Article in Special Issue
Impact of UAV-Derived RTK/PPK Products on Geometric Correction of VHR Satellite Imagery
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Drones
Volume 9
Issue 5
10.3390/drones9050343
drones-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

The Synergistic Effects of GCPs and Camera Calibration Models on UAV-SfM Photogrammetry

by
Zixin Wang
1,2,
Leyan Shi
1,2,
Jinzhou Li
2,
Wen Dai
1,2,*,
Wangda Lu
2 and
Mengqi Li
3
1
Changwang School of Honors, Nanjing University of Information Science & Technology, Nanjing 210044, China
2
School of Geographical Sciences, Nanjing University of Information Science & Technology, Nanjing 210044, China
3
Department of Geography, University of Zurich, 8057 Zurich, Switzerland
*
Author to whom correspondence should be addressed.
Drones 2025, 9(5), 343; https://doi.org/10.3390/drones9050343
Submission received: 2 April 2025 / Revised: 27 April 2025 / Accepted: 28 April 2025 / Published: 1 May 2025
(This article belongs to the Special Issue Applications of UVs in Digital Photogrammetry and Image Processing)
Browse Figures
Versions Notes

Abstract

Previous studies have shown that the use of appropriate ground control points (GCPs) and camera calibration models can optimize photogrammetry. However, the synergistic effects of GCPs and camera calibration models on UAV-SfM photogrammetry are still unknown. This study used camera models with varying complexities under different GCP conditions (in terms of number and quality) for UAV-SfM photogrammetry. The correlation matrix and root mean squared error (RMSE) were used to analyze the synergistic effects of GCPs and camera models. The results show that (1) without GCPs, complex camera models reduce distortion parameter correlation and improve terrain modeling accuracy by about 70%, with Model C (with F, Cx, Cy, K1–K4, and P1–P4) being the most widely applicable. (2) Increasing the number of GCPs enhances the terrain modeling accuracy more effectively than increasing the camera model complexity, reducing the RMSE by 45–70%, while the model complexity does not affect the required GCP number. (3) A strong interaction exists between the GCP quality and camera models: High-quality GCPs enhance camera model performance, while complex camera models reduce the requirement of GCP quality. This study provides both theoretical insights and practical guidance for efficient and low-cost UAV-SfM photogrammetry in different scenarios.

1. Introduction

In recent years, consumer-grade unmanned aerial vehicles (UAVs) have been widely used across various fields of earth science, including terrain modeling [1,2,3], ecological environment monitoring [4,5,6], vegetation information extraction [7,8,9,10,11,12], and disaster response [13,14,15]. Particularly, consumer-grade UAVs combined with Structure-from-Motion (SfM) have gradually emerged as a key method for acquiring geographic data in terrain modeling due to their low cost, high spatial resolution, simple operation, and high degree of automation [16]. However, single-lens non-metric cameras on consumer-grade UAVs exhibit significant lens distortion, leading to large and spatially uneven terrain modeling errors compared with metric cameras. Consequently, camera calibration is critical for enhancing the accuracy and reliability of UAV-SfM photogrammetry [17].
Camera calibration is mainly categorized into two methods: pre-calibration and self-calibration [18,19,20]. Pre-calibration is often performed in-lab using convergent images and varying scene depths [19]. In contrast, self-calibration benefits from advancements in automatic feature recognition and matching technology. It has now been integrated into most commercial software, significantly simplifying the calibration process and currently making it the most widely adopted method [20]. From the imaging process, the radial, eccentric, and prismatic distortion model proposed by Brown has been extensively applied [18,21,22]. However, this model struggles to handle severe distortions effectively. To overcome this constraint, various modifications have been introduced, including the logarithmic calibration model [23], the fisheye camera field-of-view calibration model [24], the non-parametric radial distortion model [25], and an 18-parameter calibration model [26].
Photogrammetry communities have reached a consensus that the Brown model is suitable for camera calibration in most scenarios. Common photogrammetry software on the market (such as PIX4D mapper 4.4.12 and Agisoft Metashape Pro 1.5) primarily adopts the Brown model [27], which includes radial distortion, tangential distortion, and other parameters. However, previous studies have found that the correlation of the Brown model parameters and their ambiguous mathematical or physical significance can adversely affect camera calibration [28,29], leading to systematic errors such as ‘doming’ and ‘dishing’ effects [30,31,32]. Consequently, how to reduce parameter correlation and scientifically select an appropriate set of parameters has become particularly important. Xu et al. [33] suggested that a comprehensive combination of distortion parameters can significantly enhance aerial photogrammetric accuracy, with the radial distortion parameters K1 and K2 combination performing optimally under limited conditions. Dai et al. [34] found that higher camera angles can reduce parameter correlation and enhance camera calibration. Wang and Liu [35] also emphasized that the basic theory of over-parameterization and strong correlation are the focus of future research on camera calibration with the continuous proposal of the models.
The importance of the number of ground control points (GCPs) in improving UAV-SfM photogrammetry accuracy has been confirmed by many studies [36,37,38,39]. Previous studies have shown that appropriate GCPs and image collection strategies can optimize photogrammetry, and this optimization is closely related to camera model optimization [34]. However, existing studies primarily focused on the direct impact of GCPs on terrain modeling, with less attention given to the specific role of the GCP number and quality on camera calibration.
Apparently, the synergistic effects of GCPs and camera calibration models on UAV-SfM photogrammetry are still unknown. Specifically, it is unclear whether variations in the number and quality of GCPs influence camera model selection, how to determine the most suitable camera model to optimize calibration performance, and whether different camera models affect the required number and quality of GCPs when aiming for the same level of accuracy.
Therefore, this study aims to (1) conduct a comparative analysis of different camera models to explore their performance in UAV-SfM photogrammetry and propose a selection strategy for practical applications and (2) investigate the synergistic effects of GCPs (number and quality) and camera models, providing a theoretical basis for enhancing camera calibration and optimizing the accuracy of terrain modeling in UAV-SfM photogrammetry.

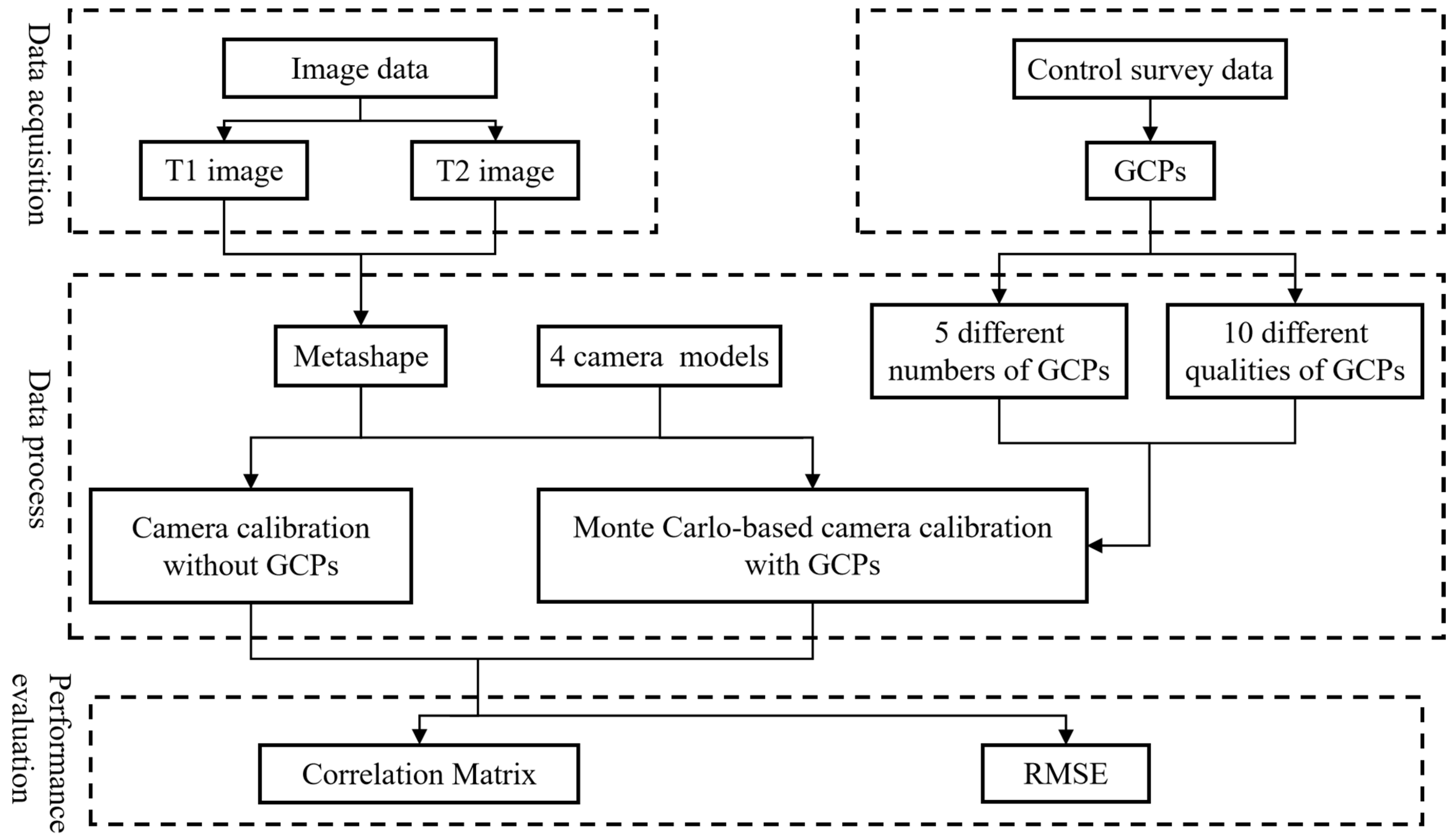
2. Methods

2.1. Basic Methods

This study first acquired image data and GCPs (detailed in Section 2.2) of two study areas (Figure 1). Next, we designed four camera models with different combinations of distortion parameters. We compared the effects of different camera models without GCPs (detailed in Section 2.3). In the condition with GCPs, different numbers and qualities of GCPs were configured for camera calibration (detailed in Section 2.4). Finally, we used correlation matrix and root mean squared error (RMSE) to evaluate camera model performance and terrain modeling accuracy (detailed in Section 2.5).

2.2. Study Areas and Data

2.2.1. Study Areas

We selected two small watersheds in Suide County, Yulin City, Shaanxi Province, as our study areas, T1 and T2. T1 is located in Liujiaping Village (110°17′3.2″ E, 37°33′48.8″ N), with an area of approximately 51,000 m2 and a maximum elevation difference of about 100 m. Its primary topographic features include gullies and incised channels. T2 is located in Wangmaozhuang Village (110°21′45.7″ E, 37°35′12.8″ N), with an area of approximately 36,000 m2 and a maximum elevation difference of about 80 m. Additionally, terraces have been constructed on the slopes, as shown in Figure 2. Both study areas have sparse vegetation and relatively rich microtopography, providing suitable geographical conditions for this study.

2.2.2. UAV Data Acquisition

  • Image Data
In this study, we acquired image data using a DJI Phantom 4 Pro (DJI, Shenzhen, China), a consumer-grade quadcopter UAV. It is equipped with a Sony Exmor R camera (Sony Group Corporation, Tokyo, Japan) featuring a 20-megapixel resolution, a 1-inch CMOS sensor, an 84° field of view, and a 35 mm equivalent focal length. The image data were collected in March 2021, when vegetation had not yet grown in the study areas, which facilitated UAV-SfM photogrammetry.
In the process of image data acquisition, parameters such as flight path, side and forward overlaps, camera angle, and flight altitude were preset by the ground-based radio remote control system to ensure the UAV could acquire image data stably and accurately. Given the single-lens nature of the consumer-grade UAV, the flight path of this study was designed in a grid-shaped pattern. Both side and forward overlaps were fixed at 80% to ensure comprehensive coverage of the study areas. To adapt to the undulating terrain, each takeoff point was selected midway up the hillside to enhance flight safety and ensure high-quality image data. When the camera angle was 0°, the flight altitudes of T1 and T2 were set to 100 m and 70 m, respectively, the corresponding ground sampling distances (GSDs) were 2.7 cm and 1.9 cm, and 167 and 118 images were acquired.
The image data were processed using Agisoft Metashape Pro 1.5, a 3D modeling software developed by Agisoft. The processing steps mainly include image quality checks, aerial triangulation, and dense point cloud matching. The primary purpose of image quality checks is to filter out photos affected by issues such as overexposure and blurring, which are unsuitable for subsequent processing. Aerial triangulation can determine the external orientation parameters of each image and the ground coordinates of tie points, which can be achieved in Metashape through the functions of aligning photos, placing markers, and optimizing cameras. Based on the exterior orientation parameters, the coordinates of homologous points can be calculated, ultimately generating the dense point cloud.
  • Control Survey Data
The field control survey in this study adopted GNSS-RTK technology, with a Topcon Hiper SR GNSS receiver (Topcon Corporation, Tokyo, Japan). The size of the GCP target is 1 m × 1 m, and its center can be identified within the flight altitude of 200 m. The horizontal and vertical accuracies of the GNSS-RTK survey were 0.010 m and 0.015 m, respectively, meeting the requirements for high-accuracy photogrammetry. To ensure that GCPs were evenly distributed in plane and elevation, we set up GCPs on the ridge lines, gully edges, and gully bottoms in each study area. A total of 33 and 31 GCPs were established in T1 and T2, respectively, providing a reliable reference for subsequent image processing and camera calibration.

2.3. Camera Models

Optical distortion in cameras arises from nonlinear geometric deformations during the imaging process, resulting from a combination of multiple distortion types. The distortion parameters typically include focal length (F), which defines the optical characteristics of the lens and directly affects image scaling; principal point (Cx and Cy) reflects the position of the imaging geometric center and is relevant to geometric alignment; radial distortion parameters (K1, K2, K3, and K4) are mainly used to describe the radial distortion caused by light passing through the lens, which will lead to straight lines curved in the image; tangential distortion parameters (P1, P2, P3, and P4) correct geometric deviations caused by improper lens assembly; and aspect ratio and skew (B1 and B2) address shape distortions of the image. Based on these distortion parameters, we designed four different camera models [40], where ‘✓’ indicates that the camera model includes and calibrates the corresponding parameters (as shown in Table 1). The camera model complexity increases progressively from Model A to Model D. In our study, we selected the camera distortion parameters for camera optimization by running a Python 3.12 script in Metashape Pro 1.5.
In the absence of GCPs, the overall accuracy of terrain modeling was evaluated by calculating the RMSE. Additionally, Moran’s I [41] was used to quantify the spatial correlation of errors to compare the performance of camera models.

2.4. The Synergistic Effects of GCPs and Camera Models

2.4.1. Interaction Between the Number of GCPs and Camera Models

To explore the interaction between the number of GCPs and camera models, we designed the following experiments. Firstly, we used Metashape to generate tie points, calibrate GCPs, and perform optimization. Once the accuracy requirement was met (total error within 1 pixel), we determined the camera model (Table 1) and the number of GCPs, followed by bundle adjustment. The number of GCPs was set as the only variable. For each camera model, we fixed the GCP quality at 1 mm and set five different GCP numbers, which were 2, 3, 5, 8, and 12. Then, the correlation matrices of the camera distortion parameters were calculated to assess whether the GCP number affects the camera calibration.
To avoid the bias caused by different spatial distributions under the same GCP number, this study adopted the Monte Carlo method to participate in the selection of GCPs and the optimization of bundle adjustment. The method was automated in Metashape through Python scripts, and the specific steps were as follows: First, during each bundle adjustment, GCPs were randomly selected based on the predefined number, while the rest served as checkpoints for performance evaluation. Next, the camera model was specified by defining the distortion parameters to be optimized. Then, with the number of randomly selected GCPs fixed, the above steps were repeated 50 times, and error information was recorded for each iteration. Finally, the entire procedure was repeated for different GCP numbers and camera models to evaluate their influence. Based on the error information obtained from the Monte Carlo method, the RMSEs of terrain modeling were calculated to investigate the interaction effects of the GCP number and camera models on terrain modeling accuracy.

2.4.2. Interaction Between the Quality of GCPs and Camera Models

This study explored the interaction between the quality of GCPs and camera models, which is essential for accurately estimating internal and external camera orientation parameters and correcting potential distortions. First, we investigated the effect of GCP quality on camera calibration by using correlation matrices, as described in Section 2.4.1. During the camera alignment and optimization steps, we set the quality of GCPs as the only variable. For each camera model, the number of GCPs was fixed at 10 (with the remaining GCPs used as checkpoints), and ten different GCP qualities were tested: 1, 2, 5, 10, 20, 50, 100, 200, 500, and 1000 mm. Specifically, in Metashape, marker accuracy represents the quality of GCPs, and adjusting the marker accuracy parameter can change the weights of GCPs in the bundle adjustment process [42].
Then, we investigated the interaction effects of GCP quality and camera models on terrain modeling accuracy. We also used the Monte Carlo method to randomly select GCPs for bundle adjustment (the specific process is similar to Section 2.4.1) to avoid the distribution issues of GCPs under different qualities.

2.5. Performance Evaluation

This study analyzed the correlation between distortion parameters to evaluate the performance of different camera models. We calculated the correlation coefficients between each distortion parameter [28] and plotted the correlation matrix. The calculation formula is shown in (1):
r i j = q i j q i i ∗ q j j
where q i j , q i i , and q j j represent the corresponding elements in the covariance matrix of distortion parameters.
In addition, to further analyze the synergistic effects of GCPs and camera calibration, we used the overall modeling results of UAV-SfM as the evaluation index of terrain modeling accuracy. Since we set a large number of GCPs in the study areas, the DEM generated by applying the UAV-SfM model with all GCPs corrected was used as the reference data. According to the reference DEM, the errors of different models were obtained by subtracting the reference DEM from the observational results derived from each model. Meanwhile, we used RMSE to quantify the overall accuracy of terrain modeling [43,44,45]. The calculation formula is shown in (2):
R M S E = ∑ i = 1 n ( X m o d e l , i − X o b s , i ) 2 n
where X m o d e l , i represents the predicted values, that is, the observation results under different camera models; X o b s , i represents the actual values from the reference DEM; and n is the total number of samples.

3. Results

3.1. Effects of Camera Models

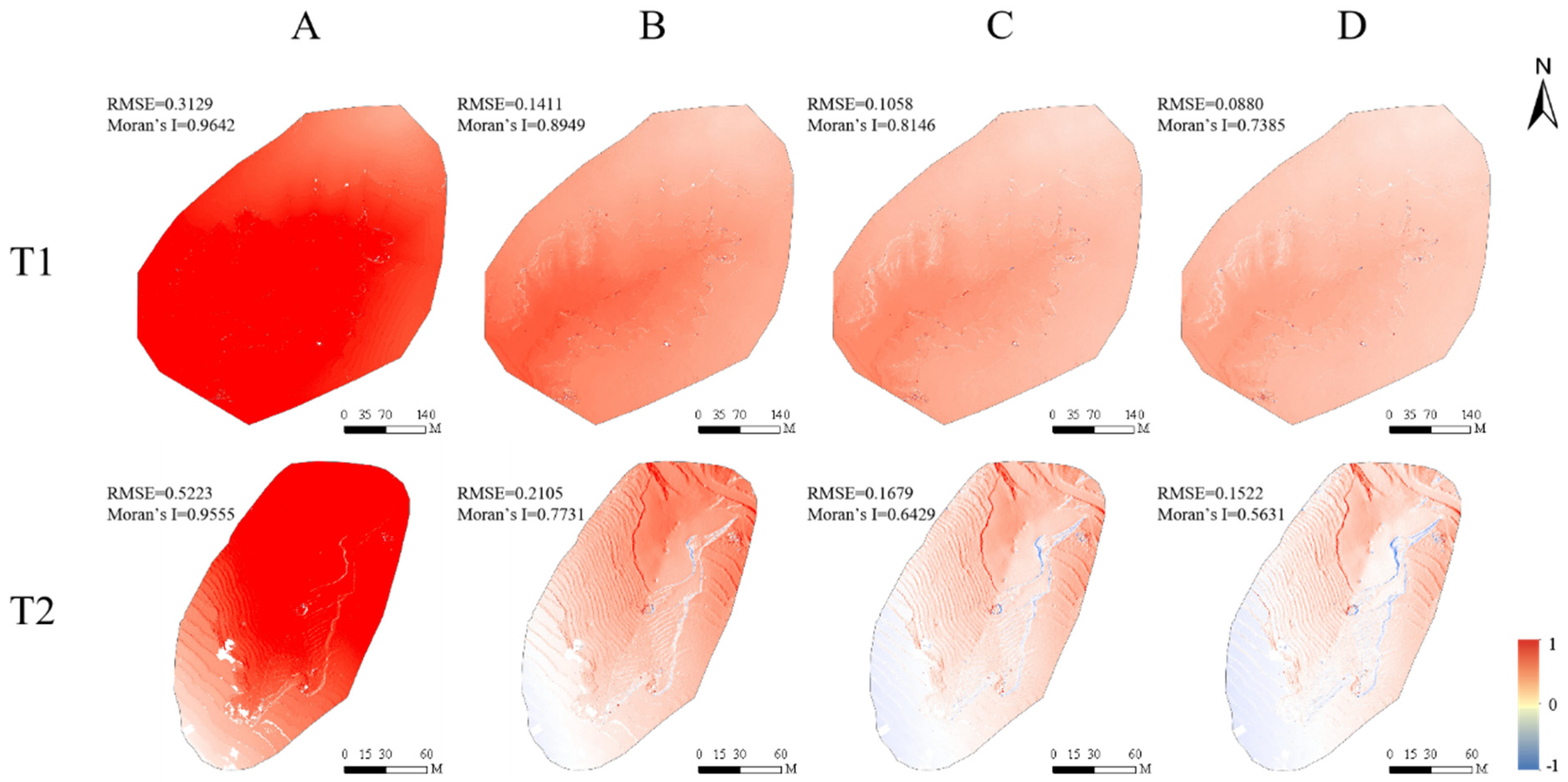
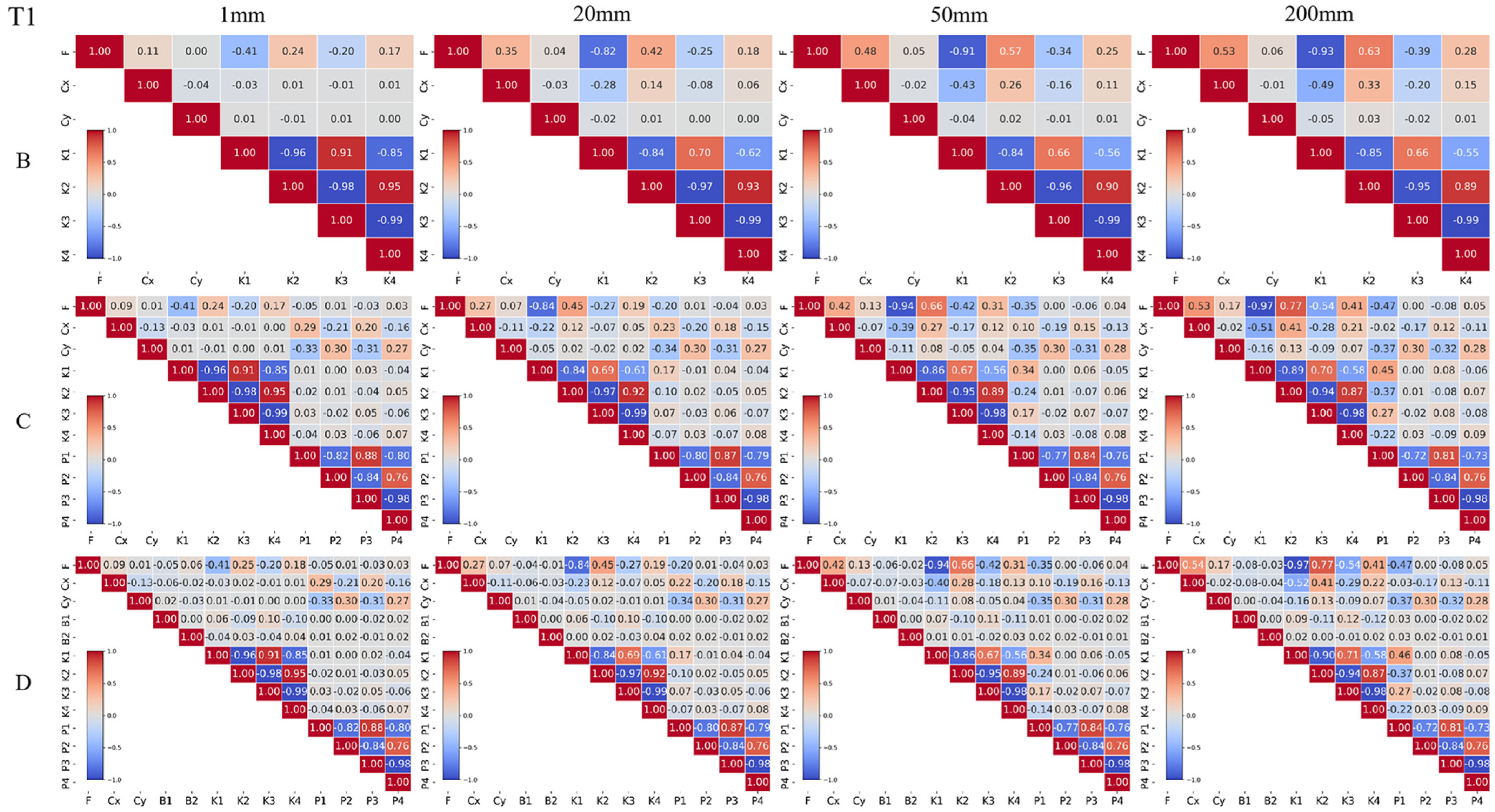
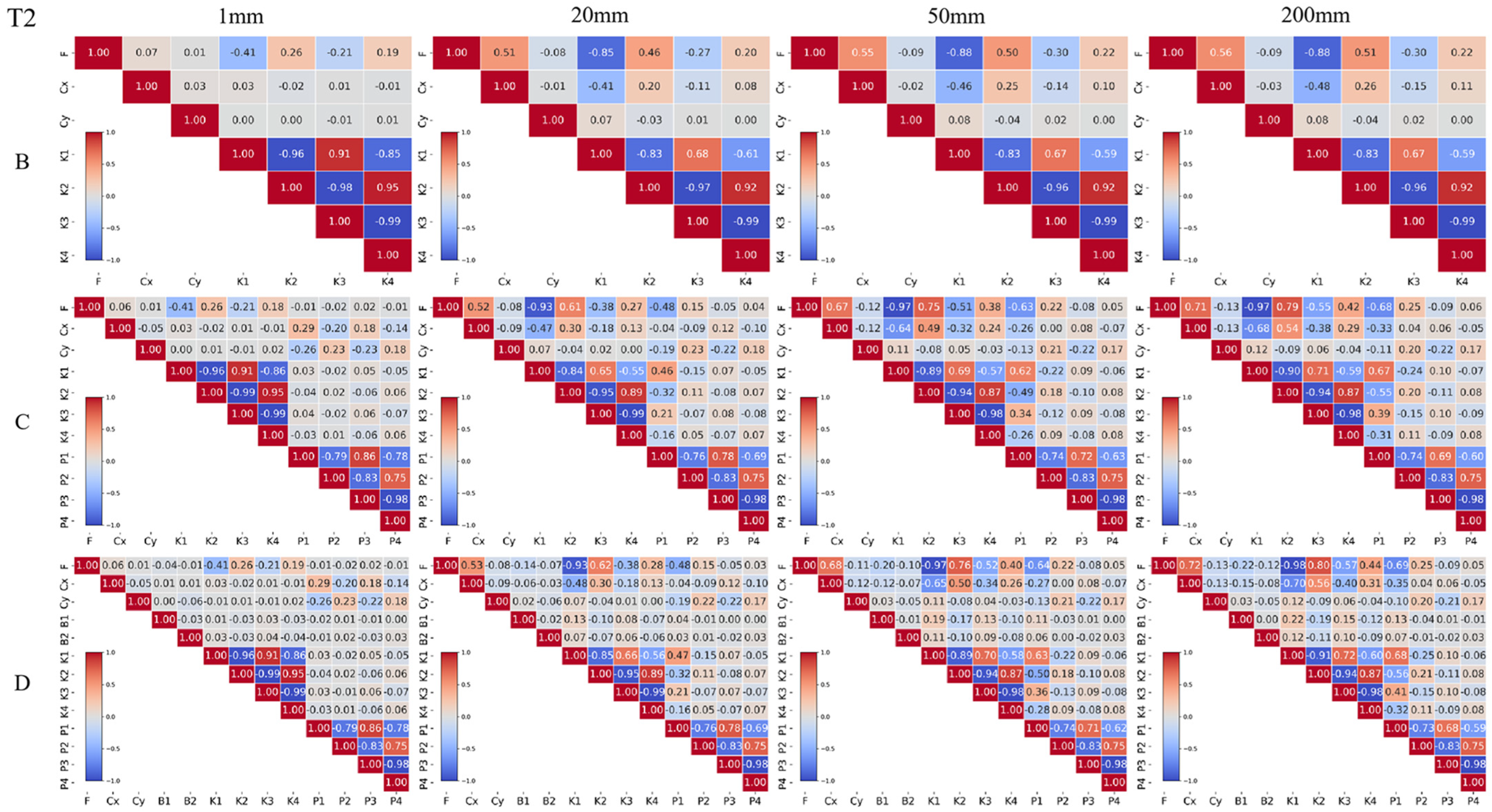
3.1.1. Camera Calibration Without GCPs

In the absence of GCPs, the correlation matrices between the distortion parameters of Models B, C, and D are presented in Figure 3. Overall, as camera model complexity increases, the correlation between distortion parameters tends to decrease. However, comparatively, after adding tangential distortion parameters (P1–P4) to Models C and D, the correlations between focal length (F) and radial distortion parameters (K1–K4), as well as between principal point (Cx and Cy) and radial distortion parameters (K1–K4), are slightly enhanced. This suggests that for the lack of GCPs, increasing model complexity helps to reduce the overall correlation between distortion parameters, yet it may also introduce the risk of overfitting.

3.1.2. Effects of Camera Models on Terrain Modeling Accuracy

Figure 4 shows the effects of different camera models on terrain modeling accuracy without GCPs. Both T1 and T2 exhibit similar trends, with Model A showing the highest RMSE and Models B, C, and D demonstrating a gradual decrease in RMSE values. From the RMSE values, Model D improves accuracy by approximately 70% compared with the simple model (especially Model A). This indicates that increasing the camera model complexity leads to a greater enhancement in accuracy. Regarding the spatial distribution of errors, Model A exhibits pronounced clustering characteristics in both study areas, and its Moran’s I is close to 1, indicating strong spatial correlation and substantial systematic errors. As the camera model complexity increases, the spatial distribution of errors is improved to some extent, showing a more randomized pattern. This suggests that although the complex models (Models C and D) may pose a risk of overfitting, they are nonetheless effective in improving accuracy and reducing the spatial correlation of errors in terrain modeling results.

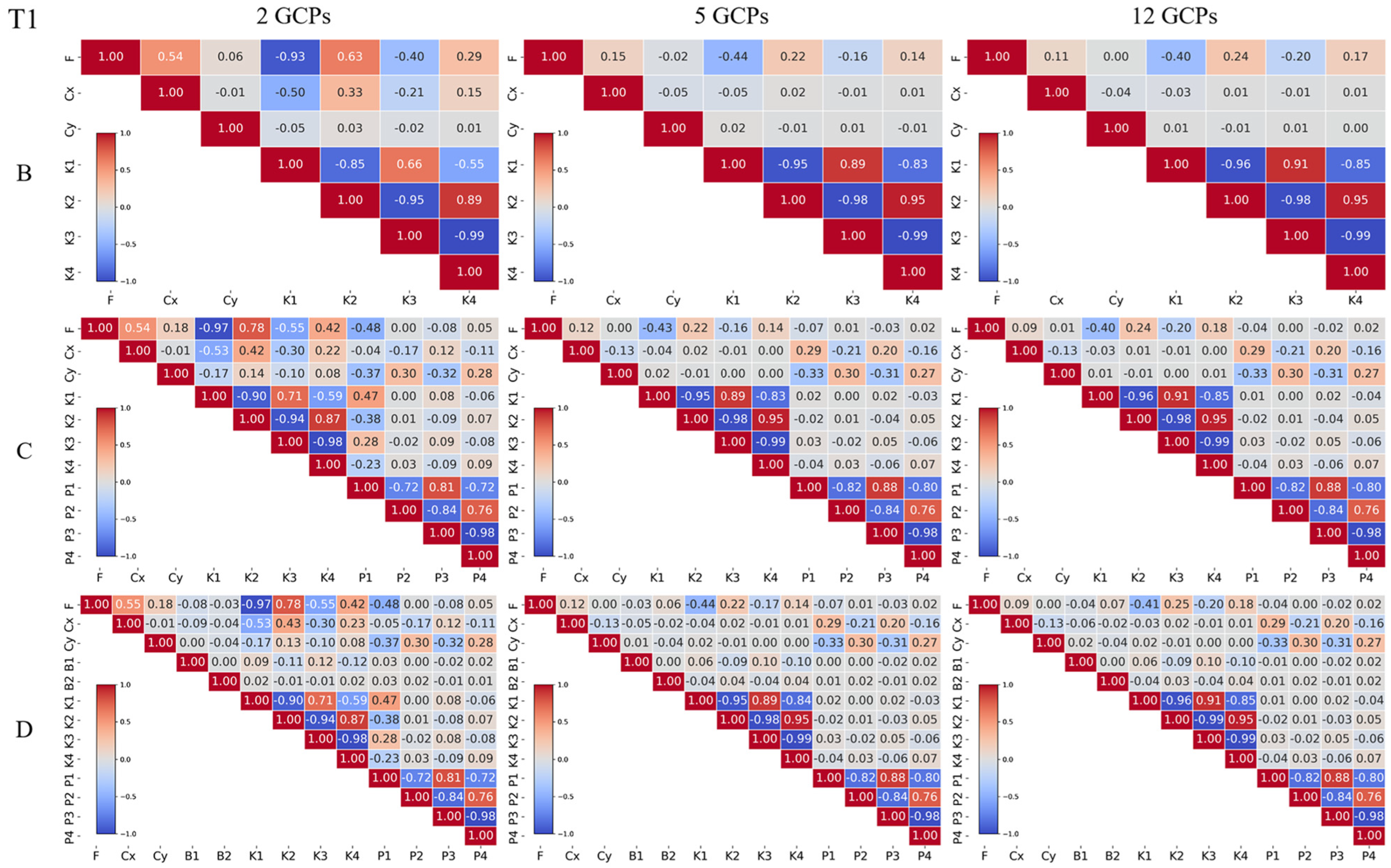
3.2. Interaction Between the Number of GCPs and Camera Models

3.2.1. Effects of GCP Number on Camera Calibration

Figure 5 and Figure 6 present the correlation matrices of distortion parameters of Models B, C, and D in T1 and T2 under different numbers of GCPs (2, 5, and 12). In Model B, increasing the number of GCPs reduces the correlation between the principal point (Cx and Cy) and radial distortion parameters (K1–K4); in Model C, the correlation between radial (K1–K4) and tangential distortion parameters (P1–P4) significantly decreases with the increase in the GCP number; the aspect ratio and skew (B1 and B2) are added to Model D, the correlation between them and other distortion parameters is weak, and the change is not obvious. These results show that, within the same camera model, an increase in the number of GCPs leads to a reduction in the correlation between distortion parameters, particularly between the principal point (Cx and Cy) and radial distortion parameters (K1–K4), as well as between radial (K1–K4) and tangential distortion parameters (P1–P4). However, radial distortion parameters (K1–K4) themselves have a strong correlation, as do the tangential distortion parameters (P1–P4). Furthermore, the correlation matrices for 12 GCPs closely resemble those for 5 GCPs, indicating that the performance of camera models cannot be further improved after more than 5 GCPs.
Although increasing the GCP number reduces parameter correlations within each camera model, the differences in correlations between the shared distortion parameters of Models B, C, and D remain low for the same GCP number. Given that parameter correlation affects calibration accuracy, we infer that the performance of Models B, C, and D is similar.

3.2.2. Interaction Effects on Terrain Modeling Accuracy

Figure 7 shows the interaction effects of the GCP number and camera models on terrain modeling accuracy. From the overall trend, as the number of GCPs increases, the RMSE decreases by 45% to 70%, indicating that increasing the GCP number can improve the terrain modeling accuracy. However, the rate of RMSE reduction declines substantially beyond five GCPs, corresponding to the results in Section 3.2.1 and further suggesting that the number of GCPs has a limited effect on camera models and terrain modeling accuracy.
For the same number of GCPs, the differences in RMSE under four camera models are very small and negligible, confirming comparable model performance and supporting the reasoning in Section 3.2.1. On the one hand, combined with the differences in performance of camera models under different GCP numbers, we can find that the effect of the camera model on terrain modeling accuracy is much smaller than the role of the GCP number. On the other hand, Figure 7 also shows that the camera model complexity exhibits no significant effect on the use of the GCP number. In other words, the complex and simple models show no significant difference in their requirement for the number of GCPs when achieving the same accuracy.

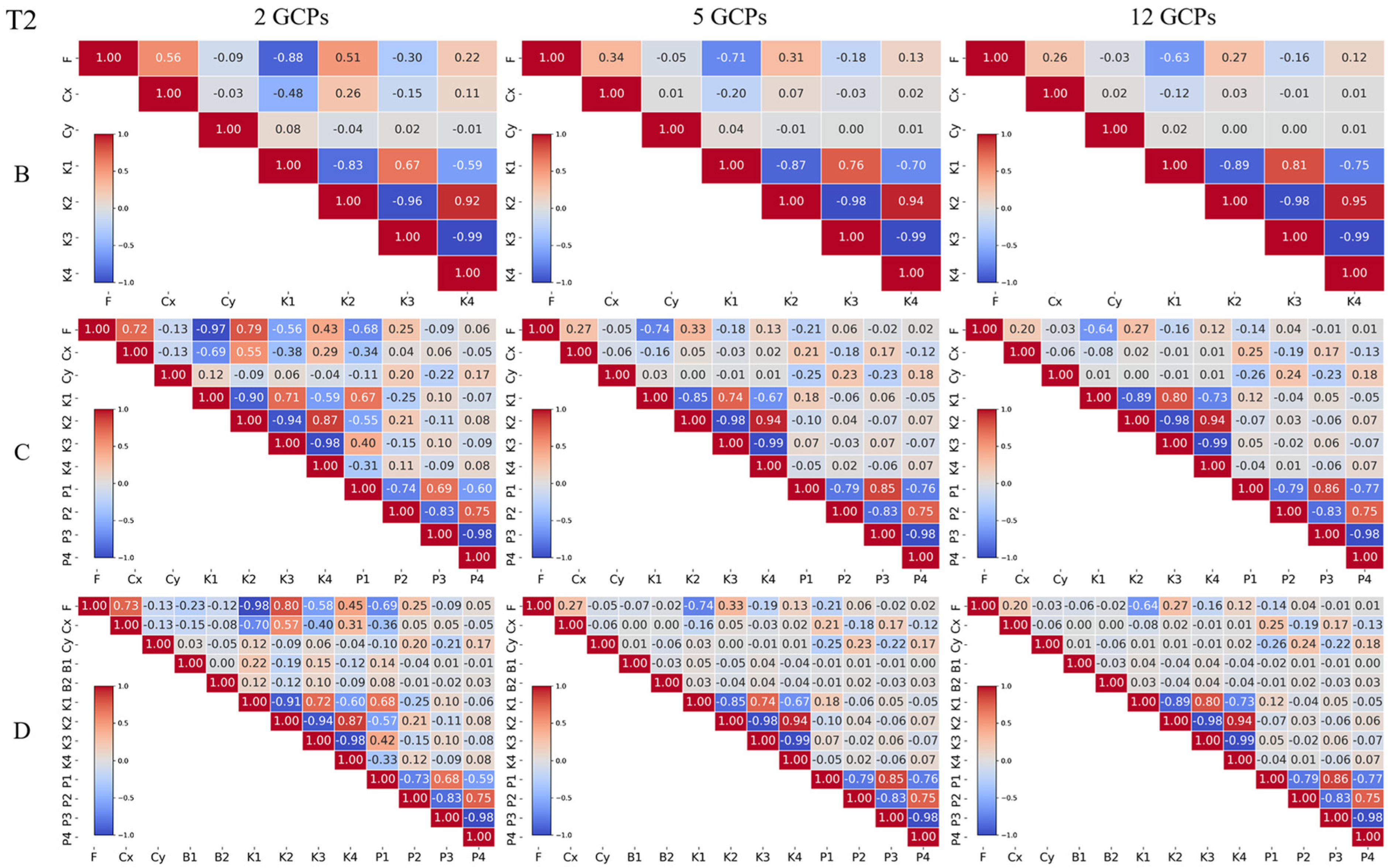
3.3. Interaction Between the Quality of GCPs and Camera Models

3.3.1. Effects of GCP Quality on Camera Calibration

Figure 8 and Figure 9 show the correlation matrices of distortion parameters of Models B, C, and D in T1 and T2 under different qualities of GCPs (1, 20, 50, and 200 mm). As the quality of GCPs improves from 200 mm to 1 mm, the correlation characteristics between the distortion parameters of each model are similar to those in Section 3.2.1, such as the correlations between principal points (Cx and Cy) and radial distortion parameters (K1–K4), as well as between the radial (K1–K4) and tangential distortion parameters (P1–P4) progressively decrease. This indicates that improving GCP quality significantly enhances the performance of camera models.
Under the same GCP quality, the shared distortion parameters in Model B generally exhibit a stronger correlation than those in Model C, particularly at lower qualities (50 mm and 200 mm). In contrast, the correlation differences between Models C and D are minimal across different GCP qualities. Therefore, we infer that Model B performs less effectively than Models C and D, with the latter two showing similar performance levels. Additionally, these findings further demonstrate the importance of high-quality GCPs for simpler models such as Model B, whereas more complex models can maintain stable calibration performance even with lower-quality GCPs.

3.3.2. Interaction Effects on Terrain Modeling Accuracy

Figure 10 shows the interaction effects of GCP quality and camera models on terrain modeling accuracy. Overall, Model A consistently exhibits significantly higher RMSE values than the other three models, especially in the case of high-quality GCPs. Within the range of GCP quality from 1 to 100 mm, the RMSE of Model A gradually increases and then remains relatively stable between 200 and 500 mm, followed by a sharp rise at 1000 mm. Models B, C, and D improve terrain modeling accuracy by approximately 45–65%, following a similar RMSE trend. However, the RMSE of Model B begins to increase at a higher GCP quality threshold. Specifically, in the range of 1 to 10 mm, the RMSE remains largely unchanged across the three models, indicating that their performance is relatively stable under high-quality GCPs; the RMSE of Model B starts to rise at 20 mm, while Models C and D show an upward trend at 50 mm, which indicates that the latter two models exhibit greater robustness to lower-quality GCPs; when the quality falls between 200 and 500 mm, the RMSE of the three models is almost the same. Additionally, we found that once the quality improves beyond 10 mm, Models B, C, and D show limited improvement in terrain modeling accuracy, which is particularly evident in T1.
Meanwhile, when the quality of GCPs is higher than 200 mm, the camera model complexity plays a more significant role in determining the required GCP quality. The simple models (especially Model A) often demand higher-quality GCPs to achieve the same terrain modeling accuracy as the complex models. For example, the terrain modeling accuracy of Model A with 2 mm GCPs is comparable to that of Model B with quality in the range of 50–100 mm. It should be noted that the effect of the camera models on GCP quality is related to the study area, with this effect being significantly more pronounced in T1 than in T2.

4. Discussion

4.1. Camera Model Selection Strategy

Due to the significant lens distortions commonly found in single-lens non-metric cameras on consumer-grade UAVs, these cameras are generally unsuitable for precise terrain modeling without calibration. Therefore, focusing on camera calibration models in UAV-SfM photogrammetry is necessary. This study compared four camera models without GCPs (Figure 3 and Figure 4). The results show that the complex models (especially Model C) have a lower correlation between distortion parameters, thereby enhancing the terrain modeling accuracy and mitigating the spatial correlation of errors, which is consistent with the existing studies [33]. At present, most research has focused on the imaging process and uses mathematical formulas to propose different camera models [18,21,22,23,24,25,46,47]. However, our study based on Metashape software aims to develop a practical strategy for camera model selection by exploring effective combinations of distortion parameters.
The results show that in addition to focusing on the radial distortion parameters (K1–K4) [33], incorporating tangential distortion parameters (P1–P4) is also essential for the camera calibration, even though Wang et al. [48] argued that these two types of distortion parameters are physically correlated by analyzing the manufacturing and assembly of the lenses. In this study, Model D exhibits the lowest RMSE and Moran’s I after adding aspect ratio and skew (B1 and B2), indicating superior terrain modeling accuracy, which is consistent with the conclusion [46]. However, the results of Models C and D are highly comparable. Theoretically, increasing the camera model complexity introduces additional distortion parameters, which can slow down computation. Therefore, considering practical applications, Model C provides a balanced solution, meeting calibration requirements without the risk of overfitting, which is in agreement with existing research [40].
Although this study provides valuable insights into camera calibration, it still has certain limitations. Factors such as the quality of experimental data, the diversity of acquisition environments, the choice of algorithms, and the performance of photogrammetric software may impact the reliability of the results. Moreover, the findings of this study have broader applicability, extending to other fields such as environmental monitoring and urban planning. Future research could further explore how different application scenarios influence the optimization of GCP configurations and camera models.

4.2. Interaction Between the Number of GCPs and Camera Models

This study demonstrates that the number of GCPs has a more significant effect on terrain modeling accuracy than the camera models (Figure 5 and Figure 6). Both GCPs and camera models contribute to accuracy improvements but function through distinct mechanisms. GCPs provide precise 3D coordinates, define the absolute orientation and scale of the external coordinate system, and constrain the bundle adjustment process [42], while camera models enhance measurement accuracy by correcting distortions in the camera’s optical system. However, an excessive number of GCPs is not necessary. We found that once the GCP number reaches five, additional GCPs provide diminishing returns in accuracy enhancement. This finding suggests that an optimal threshold for the GCP number exists in a given study area, which is consistent with the conclusions of Whitehead and Hugenholtz [37] and Mancini et al. [38].
While previous studies have demonstrated that camera calibration can be effectively enhanced by varying image acquisition strategies, such as using various camera angles [49], we focused on the role of GCPs in practical UAV-SfM workflows across complex terrains and also investigated the effect of camera models on the number of GCPs, extending the study of Dai et al. [34]. Our findings reveal that the camera model complexity does not significantly affect the selection of the GCP number. Specifically, all four camera models require nearly the same GCP number to achieve a comparable RMSE (Figure 7), suggesting that a more complex camera model does not necessarily reduce the requirement for the GCP number.
This study provides valuable insights into the selection of GCP numbers and camera models in practical applications. In accuracy-prioritized scenarios, increasing the number of GCPs (at least five) is a more effective strategy than simply adopting a more complex model. In cost-prioritized tasks, that is, when saving the cost of GCP acquisition (such as no GCPs), the complex Model D can be adopted. However, it is important to note that these conclusions may primarily apply to geomorphic conditions similar to those in this study. For other geomorphic areas, appropriate adjustments and optimizations should be made based on specific conditions. For instance, in larger or more topographically complex study areas, a higher number of GCPs may be required to achieve comparable calibration accuracy [50].

4.3. Interaction Between the Quality of GCPs and Camera Models

The results indicate that high-quality GCPs significantly enhance both camera calibration and terrain modeling accuracy. They enhance camera calibration by reducing unnecessary correlations between camera distortion parameters (Figure 8 and Figure 9), and Models B, C, and D improve the terrain modeling accuracy by about 45% to 65%. However, similar to the GCP number, GCP quality also appears to have a threshold, which is around 10 mm in this study. When the GCP quality is high (the marker accuracy is set to a low value), the coordinates of the GCPs are assigned greater weight in bundle adjustment, making them more influential in the optimization process. Conversely, low-quality GCPs contribute less to the bundle adjustment process. De Marco et al. [51] observed that setting marker accuracy to an overly low value may induce the ‘doming’ effect. Meanwhile, camera models also have an important effect on terrain modeling accuracy, especially at the medium quality (20 mm to 100 mm), where the complex models such as Models C and D exhibit significantly lower RMSEs than the simple models such as Models A and B (Figure 10).
Furthermore, we deeply explored the interaction between GCP quality and camera models. The results indicate that the camera model complexity has a significant impact on the required quality of GCPs. The complex models (Models C and D) require only lower-quality GCPs (Figure 10) to achieve the same terrain modeling accuracy. This provides an alternative solution for the scenarios where acquiring high-quality GCPs in field measurements is challenging. We suggest that the complex models with more distortion parameters such as Models C and D can more accurately capture the optical characteristics of the camera. Consequently, during camera optimization, even when the weight of GCPs is reduced, these models can partially compensate for GCP errors to ensure high-accuracy terrain modeling.
Unlike traditional studies that primarily focused on the effects of the GCP number and distribution [39,50,52] on terrain modeling accuracy, our study highlights the interaction between GCP quality and camera models, providing new insights into enhancing camera calibration in practical applications. However, the interaction may be influenced by regional terrain characteristics. For instance, in regions with larger areas and greater terrain relief, the effect of GCP quality on camera calibration may be more pronounced. In this study, terrain modeling accuracy variations in T1 are more noticeable than those in T2 (Figure 10).

5. Conclusions

This study compared four camera models and investigated the synergistic effects of GCPs and camera calibration in UAV-SfM photogrammetry. Based on experimental results and data analysis, the following conclusions were drawn:
  • Without GCPs, camera model selection is critical for improving camera calibration and terrain modeling accuracy. The use of complex camera models can reduce the overall correlation between distortion parameters. Compared with the simple model such as Model A (with only distortion parameter F), complex camera models can improve terrain modeling accuracy by approximately 70% and mitigate the spatial correlation. Model C (with F, Cx, Cy, K1–K4, and P1–P4) achieves a balance between camera model complexity and accuracy, making it a practical choice for most applications.
  • When GCPs are available, the number of GCPs has a more significant effect on the accuracy improvement than the camera models. Increasing the number of GCPs can reduce the correlation between distortion parameters and improve the performance of camera models, thus improving the terrain modeling accuracy by approximately 45% to 70%. At the same time, the camera model complexity does not influence the required number of GCPs.
  • When the GCP number is fixed, an interaction exists between the quality of GCPs and camera model selection. High-quality GCPs effectively mitigate the correlation between distortion parameters, leading to enhancing camera calibration and terrain modeling accuracy, with the RMSE of complex camera models decreasing by approximately 45% to 65%. Meanwhile, on the premise of ensuring effective calibration, complex camera models reduce the requirement for GCP quality. In other words, a more complex camera model should be chosen when the GCP quality is low.
The findings provide a valuable reference for the practical application of UAV-SfM photogrammetry, particularly in high-accuracy 3D modeling and topographic mapping. Future research could further explore the effects of camera calibration under various camera attitude combinations and develop optimization strategies for complex terrain scenarios. This will help to enhance the applicability and accuracy of UAV-SfM in diverse applications.

Author Contributions

Conceptualization, W.D.; Funding acquisition, W.D.; Methodology, Z.W. and L.S.; Software, L.S. and J.L.; Supervision, W.D.; Validation, L.S., J.L., and W.L.; Writing—original draft, Z.W.; Writing—review and editing, Z.W., W.D., J.L., and M.L. All authors have read and agreed to the published version of the manuscript.

Funding

We are grateful for the financial support provided by the National Natural Science Foundation of China (No. 42301478) and the China Postdoctoral Science Foundation (No. 2024M761474).

Data Availability Statement

The data that support the findings of this research are available from the author upon reasonable request.

Acknowledgments

Many thanks are given Ruibo Qiu for his helps in programming.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Pierzchała, M.; Talbot, B.; Astrup, R. Estimating Soil Displacement from Timber Extraction Trails in Steep Terrain: Application of an Unmanned Aircraft for 3D Modelling. Forests 2014, 5, 1212–1223. [Google Scholar] [CrossRef]
  2. Shahbazi, M.; Ménard, P.; Sohn, G.; Théau, J. Unmanned aerial image dataset: Ready for 3D reconstruction. Data Brief 2019, 25, 103962. [Google Scholar] [CrossRef] [PubMed]
  3. Chen, C.; Tian, B.; Wu, W.; Duan, Y.; Zhou, Y.; Zhang, C. UAV Photogrammetry in Intertidal Mudflats: Accuracy, Efficiency, and Potential for Integration with Satellite Imagery. Remote Sens. 2023, 15, 1814. [Google Scholar] [CrossRef]
  4. Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
  5. Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
  6. Jaud, M.; Bertin, S.; Beauverger, M.; Augereau, E.; Delacourt, C. RTK GNSS-Assisted Terrestrial SfM Photogrammetry without GCP: Application to Coastal Morphodynamics Monitoring. Remote Sens. 2020, 12, 1889. [Google Scholar] [CrossRef]
  7. Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and Digital Aerial Photogrammetry Point Clouds for Estimating Forest Structural Attributes in Subtropical Planted Forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
  8. Candiago, S.; Remondino, F.; De Giglio, M.; Dubbini, M.; Gattelli, M. Evaluating Multispectral Images and Vegetation Indices for Precision Farming Applications from UAV Images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef]
  9. Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
  10. Tu, Y.-H.; Phinn, S.; Johansen, K.; Robson, A.; Wu, D. Optimising drone flight planning for measuring horticultural tree crop structure. ISPRS J. Photogramm. Remote Sens. 2020, 160, 83–96. [Google Scholar] [CrossRef]
  11. Swayze, N.C.; Tinkham, W.T.; Vogeler, J.C.; Hudak, A.T. Influence of flight parameters on UAS-based monitoring of tree height, diameter, and density. Remote Sens. Environ. 2021, 263, 112540. [Google Scholar] [CrossRef]
  12. Kameyama, S.; Sugiura, K. Effects of Differences in Structure from Motion Software on Image Processing of Unmanned Aerial Vehicle Photography and Estimation of Crown Area and Tree Height in Forests. Remote Sens. 2021, 13, 626. [Google Scholar] [CrossRef]
  13. Zhao, N.; Lu, W.; Sheng, M.; Chen, Y.; Tang, J.; Yu, F.R.; Wong, K.K. UAV-Assisted Emergency Networks in Disasters. IEEE Wireless Commun. 2019, 26, 45–51. [Google Scholar] [CrossRef]
  14. Erdelj, M.; Natalizio, E.; Chowdhury, K.R.; Akyildiz, I.F. Help from the Sky: Leveraging UAVs for Disaster Management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
  15. Tuna, G.; Nefzi, B.; Conte, G. Unmanned aerial vehicle-aided communications system for disaster recovery. J. Netw. Comput. Appl. 2014, 41, 27–36. [Google Scholar] [CrossRef]
  16. Templin, T.; Popielarczyk, D.; Kosecki, R. Application of Low-Cost Fixed-Wing UAV for Inland Lakes Shoreline Investigation. Pure Appl. Geophys. 2018, 175, 3263–3283. [Google Scholar] [CrossRef]
  17. Luhmann, T.; Fraser, C.; Maas, H.-G. Sensor modelling and camera calibration for close-range photogrammetry. ISPRS J. Photogramm. Remote Sens. 2016, 115, 37–46. [Google Scholar] [CrossRef]
  18. Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
  19. Zhou, Y.; Rupnik, E.; Meynard, C.; Thom, C.; Pierrot-Deseilligny, M. Simulation and Analysis of Photogrammetric UAV Image Blocks—Influence of Camera Calibration Error. Remote Sens. 2020, 12, 22. [Google Scholar] [CrossRef]
  20. Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; Marcial-Pablo, M.d.J.; Enciso, J. Digital Terrain Models Generated with Low-Cost UAV Photogrammetry: Methodology and Accuracy. ISPRS Int. J. Geo-Inf. 2021, 10, 285. [Google Scholar] [CrossRef]
  21. Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
  22. Samper, D.; Santolaria, J.; Majarena, A.C.; Aguilar, J.J. Comprehensive simulation software for teaching camera calibration by a constructivist methodology. Measurement 2010, 43, 618–630. [Google Scholar] [CrossRef]
  23. Basu, A.; Licardie, S. Alternative models for fish-eye lenses. Pattern Recognit. Lett. 1995, 16, 433–441. [Google Scholar] [CrossRef]
  24. Devernay, F.; Faugeras, O. Straight lines have to be straight. Mach. Vision Appl. 2001, 13, 14–24. [Google Scholar] [CrossRef]
  25. Hartley, R.; Kang, S.B. Parameter-Free Radial Distortion Correction with Center of Distortion Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1309–1321. [Google Scholar] [CrossRef]
  26. Claus, D.; Fitzgibbon, A.W. A rational function lens distortion model for general cameras. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 213–219. [Google Scholar]
  27. Jaud, M.; Passot, S.; Allemand, P.; Le Dantec, N.; Grandjean, P.; Delacourt, C. Suggestions to Limit Geometric Distortions in the Reconstruction of Linear Coastal Landforms by SfM Photogrammetry with PhotoScan® and MicMac® for UAV Surveys with Restricted GCPs Pattern. Drones 2019, 3, 2. [Google Scholar] [CrossRef]
  28. Li, D. The Correlation Analysis of a Self-Calibrating Bundle Block Adjustment and the Test of Significance of Additional parameters. Geomat. Inf. Sci. Wuhan Univ. 1981, 6, 46–65. [Google Scholar] [CrossRef]
  29. Li, D. The Overcoming of the Overparametrization in Self-Calibrating Adjustment. Geomat. Inf. Sci. Wuhan Univ. 1986, 11, 95–104. [Google Scholar] [CrossRef]
  30. Obanawa, H.; Sakanoue, S. Conditions of Aerial Photography to Reduce Doming Effect. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6464–6466. [Google Scholar]
  31. Carbonneau, P.E.; Dietrich, J.T. Cost-effective non-metric photogrammetry from consumer-grade sUAS: Implications for direct georeferencing of structure from motion photogrammetry. Earth Surf. Process. Landf. 2017, 42, 473–486. [Google Scholar] [CrossRef]
  32. James, M.R.; Antoniazza, G.; Robson, S.; Lane, S.N. Mitigating systematic error in topographic models for geomorphic change detection: Accuracy, precision and considerations beyond off-nadir imagery. Earth Surf. Process. Landf. 2020, 45, 2251–2271. [Google Scholar] [CrossRef]
  33. Xu, X.; Xu, A.; Ma, L.; Jiao, H. The Influence of Lens Distortion Parameters on Measurement Accuracy of Image Points in Aerial Photogrammetry. Bull. Surv. Map. 2017, 0, 30–34. [Google Scholar] [CrossRef]
  34. Dai, W.; Zheng, G.; Antoniazza, G.; Zhao, F.; Chen, K.; Lu, W.; Lane, S.N. Improving UAV-SfM photogrammetry for modelling high-relief terrain: Image collection strategies and ground control quantity. Earth Surf. Process. Landf. 2023, 48, 2884–2899. [Google Scholar] [CrossRef]
  35. Wang, L.; Liu, G. Three Camera Lens Distortion Correction Models and Its Application. In Proceedings of the 2022 3rd International Conference on Geology, Mapping and Remote Sensing (ICGMRS), Zhoushan, China, 22–24 April 2022; pp. 462–467. [Google Scholar]
  36. Santos Santana, L.; Araújo E Silva Ferraz, G.; Bedin Marin, D.; Dienevam Souza Barbosa, B.; Mendes Dos Santos, L.; Ferreira Ponciano Ferraz, P.; Conti, L.; Camiciottoli, S.; Rossi, G. Influence of flight altitude and control points in the georeferencing of images obtained by unmanned aerial vehicle. Eur. J. Remote Sens. 2021, 54, 59–71. [Google Scholar] [CrossRef]
  37. Whitehead, K.; Hugenholtz, C.H. Applying ASPRS Accuracy Standards to Surveys from Small Unmanned Aircraft Systems (UAS). Photogramm. Eng. Remote Sens. 2015, 81, 787–793. [Google Scholar] [CrossRef]
  38. Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using Unmanned Aerial Vehicles (UAV) for High-Resolution Reconstruction of Topography: The Structure from Motion Approach on Coastal Environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef]
  39. Liu, X.; Lian, X.; Yang, W.; Wang, F.; Han, Y.; Zhang, Y. Accuracy Assessment of a UAV Direct Georeferencing Method and Impact of the Configuration of Ground Control Points. Drones 2022, 6, 30. [Google Scholar] [CrossRef]
  40. James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
  41. Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
  42. James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Processes Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
  43. Sadeq, H.A. Accuracy assessment using different UAV image overlaps. J. Unmanned Veh. Syst. 2019, 7, 175–193. [Google Scholar] [CrossRef]
  44. Torres-Sánchez, J.; López-Granados, F.; Borra-Serrano, I.; Peña, J.M. Assessing UAV-collected image overlap influence on computation time and digital surface model accuracy in olive orchards. Precis. Agric. 2018, 19, 115–133. [Google Scholar] [CrossRef]
  45. Domingo, D.; Ørka, H.O.; Næsset, E.; Kachamba, D.; Gobakken, T. Effects of UAV Image Resolution, Camera Type, and Image Overlap on Accuracy of Biomass Predictions in a Tropical Woodland. Remote Sens. 2019, 11, 948. [Google Scholar] [CrossRef]
  46. You, Z.; Luan, Z.; Wei, X. General lens distortion model expressed by image pixel coordinate. Opt. Tech. 2015, 41, 265–269. [Google Scholar] [CrossRef]
  47. Fitzgibbon, A.W. Simultaneous linear estimation of multiple view geometry and lens distortion. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 8–14 December 2001; p. I. [Google Scholar]
  48. Wang, J.; Shi, F.; Zhang, J.; Liu, Y. A new calibration model of camera lens distortion. Pattern Recognit. 2008, 41, 607–615. [Google Scholar] [CrossRef]
  49. Fraser, C.S. Automatic Camera Calibration in Close Range Photogrammetry. Photogramm. Eng. Remote Sens. 2013, 79, 381–388. [Google Scholar] [CrossRef]
  50. Dai, W.; Qiu, R.; Wang, B.; Lu, W.; Zheng, G.; Amankwah, S.O.Y.; Wang, G. Enhancing UAV-SfM Photogrammetry for Terrain Modeling from the Perspective of Spatial Structure of Errors. Remote Sens. 2023, 15, 4305. [Google Scholar] [CrossRef]
  51. De Marco, J.; Maset, E.; Cucchiaro, S.; Beinat, A.; Cazorzi, F. Remote SensingAssessing Repeatability and Reproducibility of Structure-from-Motion Photogrammetry for 3D Terrain Mapping of Riverbeds. Remote Sens. 2021, 13, 2572. [Google Scholar] [CrossRef]
  52. Atik, M.E.; Arkali, M. Comparative Assessment of the Effect of Positioning Techniques and Ground Control Point Distribution Models on the Accuracy of UAV-Based Photogrammetric Production. Drones 2025, 9, 15. [Google Scholar] [CrossRef]
Drones 09 00343 g001
Figure 1. Workflow of this study.
Figure 1. Workflow of this study.
Drones 09 00343 g001
Drones 09 00343 g002
Figure 2. Study areas and corresponding topographic maps.
Figure 2. Study areas and corresponding topographic maps.
Drones 09 00343 g002
Drones 09 00343 g003
Figure 3. Correlation matrices of distortion parameters under different camera models in T1 and T2. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Figure 3. Correlation matrices of distortion parameters under different camera models in T1 and T2. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Drones 09 00343 g003
Drones 09 00343 g004
Figure 4. RMSE, Moran’s I, and spatial distribution of errors under different camera models. The four columns A, B, C, and D represent the error analysis results under the conditions of camera models A, B, C, and D, respectively.
Figure 4. RMSE, Moran’s I, and spatial distribution of errors under different camera models. The four columns A, B, C, and D represent the error analysis results under the conditions of camera models A, B, C, and D, respectively.
Drones 09 00343 g004
Drones 09 00343 g005
Figure 5. Correlation matrices of distortion parameters under different numbers of GCPs in T1. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Figure 5. Correlation matrices of distortion parameters under different numbers of GCPs in T1. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Drones 09 00343 g005
Drones 09 00343 g006
Figure 6. Correlation matrices of distortion parameters under different numbers of GCPs in T2. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Figure 6. Correlation matrices of distortion parameters under different numbers of GCPs in T2. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Drones 09 00343 g006
Drones 09 00343 g007
Figure 7. RMSE of terrain modeling under different numbers of GCPs and camera models.
Figure 7. RMSE of terrain modeling under different numbers of GCPs and camera models.
Drones 09 00343 g007
Drones 09 00343 g008
Figure 8. Correlation matrices of distortion parameters under different qualities of GCPs in T1. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Figure 8. Correlation matrices of distortion parameters under different qualities of GCPs in T1. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Drones 09 00343 g008
Drones 09 00343 g009
Figure 9. Correlation matrices of distortion parameters under different qualities of GCPs in T2. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Figure 9. Correlation matrices of distortion parameters under different qualities of GCPs in T2. The heatmap shows correlation coefficients from −1 (blue) to 1 (red), with darker colors indicating stronger correlations.
Drones 09 00343 g009
Drones 09 00343 g010
Figure 10. RMSE of terrain modeling under different qualities of GCPs and camera models.
Figure 10. RMSE of terrain modeling under different qualities of GCPs and camera models.
Drones 09 00343 g010
Table 1. Design of camera models.
Table 1. Design of camera models.
Parameters
Focal Length
(F)		Principal Point
(Cx, Cy)		Radial Distortion
(K1, K2, K3, K4)		Tangential Distortion (P1, P2, P3, P4)Aspect Ratio and Skew
(B1, B2)
Camera
Model
A✓
B✓✓✓
C✓✓✓✓
D✓✓✓✓✓
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, Z.; Shi, L.; Li, J.; Dai, W.; Lu, W.; Li, M. The Synergistic Effects of GCPs and Camera Calibration Models on UAV-SfM Photogrammetry. Drones 2025, 9, 343. https://doi.org/10.3390/drones9050343

AMA Style

Wang Z, Shi L, Li J, Dai W, Lu W, Li M. The Synergistic Effects of GCPs and Camera Calibration Models on UAV-SfM Photogrammetry. Drones. 2025; 9(5):343. https://doi.org/10.3390/drones9050343

Chicago/Turabian Style

Wang, Zixin, Leyan Shi, Jinzhou Li, Wen Dai, Wangda Lu, and Mengqi Li. 2025. "The Synergistic Effects of GCPs and Camera Calibration Models on UAV-SfM Photogrammetry" Drones 9, no. 5: 343. https://doi.org/10.3390/drones9050343

APA Style

Wang, Z., Shi, L., Li, J., Dai, W., Lu, W., & Li, M. (2025). The Synergistic Effects of GCPs and Camera Calibration Models on UAV-SfM Photogrammetry. Drones, 9(5), 343. https://doi.org/10.3390/drones9050343

Article Metrics

Back to TopTop