Energy Efficiency Optimization for UAV-RIS-Assisted Wireless Powered Communication Networks

Abstract

In urban environments, unmanned aerial vehicles (UAVs) can significantly enhance the performance of wireless powered communication networks (WPCNs), enabling reliable communication and efficient energy transfer for urban Internet of Things (IoTs) nodes. However, the complex urban landscape characterized by dense building structures and node distributions severely hampers the efficiency of wireless power transmission. To address this challenge, this paper presents a novel framework for urban WPCN systems assisted by UAVs equipped with reconfigurable intelligent surfaces (UAV-RISs). The framework adopts time division multiple access (TDMA) technology to coordinate the transmission process of information and energy. Considering two TDMA methods, the paper jointly optimizes the flight trajectory of the UAV, the energy harvesting scheduling of ground nodes, and the phase shift matrix of the RIS with the goal of improving the energy efficiency of the system. Furthermore, deep reinforcement learning (DRL) is introduced to effectively solve the formulated optimization problem. Simulation results demonstrate that the proposed optimized scheme outperforms benchmark schemes in terms of average throughput and energy efficiency. Experimental data also reveal the applicability of different TDMA strategies: dynamic TDMA exhibits superior performance in achieving higher average throughput at ground nodes in urban scenarios, while traditional TDMA is more advantageous for total energy harvesting efficiency. These findings provide critical theoretical insights and practical guidelines for UAV trajectory design and communication network optimization in urban environments.

1. Introduction

With the rise of the Sixth Generation (6G) of wireless communication networks, achieving ultra-high spectral and energy efficiency while meeting high-density user connectivity demands has become a crucial research topic in both academia and industry, particularly highlighted in complex urban scenarios. However, as these demands increase, so does the energy consumption of wireless devices, and energy-constrained devices become a bottleneck restricting the quality of service in urban networks [1]. The question of how to sustainably and efficiently charge these energy-limited devices in densely populated urban environments has become a pressing issue. In order to solve this problem, Wireless Power Transfer (WPT) [2] technology came into being, and wireless powered communication networks (WPCNs) [3] were constructed. As a new framework for WPT, WPCN is considered a potential solution for 6G Green Internet of Things (IoTs) in the future [4].

WPCNs transmit energy to energy-constrained devices on the downlink through a hybrid access point (HAP), while wireless devices utilize the collected energy to transmit information on the uplink. This new framework provides a new way to achieve high energy efficiency and long-lasting communication. Liu et al. [5] investigated an unmanned aerial vehicle (UAV)-mounted intelligent reflecting surface -assisted simultaneous wireless information and power transfer system. By optimizing the UAV trajectory and employing a time-division multiple-access-based scheduling protocol, they maximized the minimum average achievable rate of multiple devices while meeting the energy-harvesting requirements of IoT devices. Zeng et al. [6] proposed a resource allocation algorithm for maximizing the energy efficiency of the system by considering constraints such as energy collection, transmission time, and user quality of service. Considering imperfect channel state information, Sun et al. [7] studied the robust resource allocation problem of sum-rate maximization. Although WPCNs have significant advantages in energy and information transmission, their network performance in urban environments is vulnerable to obstacle blocking in the above-mentioned network. This leads to a degradation in the quality of energy and information transmission between hybrid access points and nodes. Moreover, as the transmission distance increases, the transmission efficiency of a WPCN decreases due to signal attenuation. The efficiency of a WPCN can be improved by utilizing the high gain and transmit power resulting from deploying a large number of array antennas at transceiver nodes or relay nodes. However, multiple antennas and relays increase the processing complexity and hardware cost of transceiver nodes and relay nodes [8,9] while degrading the transmission performance of WPCNs. To overcome this problem, reconfigurable intelligent surfaces (RISs) have received extensive attention as an emerging technology with low power consumption and high energy efficiency.

RISs integrate large-scale passive reflection units that can independently adjust the phase shift and amplitude of the received signal, thus changing the transmission direction of the reflected signal [10]. Hua et al. [11] investigated the problem of a HAP propagating energy to the downlink in RIS-assisted WPCN systems with RISs optimizing the uplink transmission quality. The authors proposed three IRS beamforming configurations: full dynamic, partial dynamic, and static, utilizing a nonlinear energy-harvesting model aimed at reducing transmit energy consumption and meeting the minimum throughput requirements. Wang et al. [12] investigated the resource allocation problem in RIS-assisted WPCNs. The authors achieved the challenge of achieving the desired performance gain by co-designing active transmit and receive beamforming for hybrid base stations (HBSs), passive beamforming for IRSs, and transmit power for each radio-powered device and jammer node. Xie et al. [13] investigated time division multiple access protocols based on packet switching and user switching to evaluate the impact of energy recovery on system performance. Two different optimization problems were constructed by jointly optimizing the energy beamforming vectors, transmit power, and receive beamforming vectors, respectively, pointing out that protocols for IoT devices utilizing time division multiple access and energy recycling have a promising future for practical applications. Nevertheless, existing RIS technologies typically adopt fixed deployment modes, which have two significant limitations. First, static RIS deployment and reflection configurations fail to adapt dynamically to changes in urban user distributions. Second, RIS deployed at the ground level is prone to obstruction by buildings and obstacles, significantly increasing link interruption probabilities in complex urban environments.

To address these limitations, this paper proposes a model of a UAV equipped with a reconfigurable intelligent surface (UAV-RIS) and integrates it into an existing WPCN. This integration exploits the two-dimensional mobility of UAVs and the signal control capability of RISs, providing the possibility of dynamically optimizing the communication network. The UAV-RIS system can effectively improve the efficiency of information and energy transmission by changing its position in real time. Therefore, UAV-RIS-assisted power and information transmission has become a new research hotspot. Song et al. [14] proposed using an aerial RIS as a mobile relay to mitigate the impact of obstacles on communication quality by optimizing the RIS phase and UAV trajectory. In order to achieve fair communication, Yu et al. [15] took aerial RIS as a relay and maximized the minimum throughput among all MVs by jointly optimizing RIS passive beamforming, mobile vehicle (MV) scheduling, UAV trajectory, and power allocation. The subproblem was solved iteratively using Block Coodinate Descent (BCD) algorithm. Peng et al. [16] investigated SWIPT assisted by UAV-RIS by optimizing node associations, UAV trajectories, and power allocation ratios to maximize the minimum average transmission rate. To improve the durability of UAV-RIS, Truong et al. [17] developed a novel energy-harvesting scheme for SWIPT, utilizing resource allocation and the energy-harvesting of impacted radio frequency (RF) signals. A deep deterministic policy gradient (DDPG) scheme was designed to allocate the resources of the UAV-RIS successively in the time and spatial domains to maximize the total harvested energy. Zhou et al. [18] proposed a new Quality of Experience (QoE)-driven UAV-IRS-assisted WPCN framework. The architecture realizes the accurate quantification of QoE through a nonlinear satisfaction function, and an adaptive reflection unit configuration strategy to reduce resource consumption while satisfying QoE was designed.

For multivariate optimization problems, existing research typically fixes one variable and optimizes the others. However, this strategy is prone to falling into local optima and lacks comprehensive global information. With increasing demands in wireless networks, there is an urgent need for technologies that exhibit flexibility, adaptability, and the capability to satisfy practical constraints. Deep reinforcement learning (DRL), as an adaptive intelligent decision-making framework, integrates the advantages of deep learning and reinforcement learning, enabling automatic learning of optimal policies to adapt to dynamically changing wireless environments. Yang et al. [19] used RISs to help prevent secure communication from eavesdroppers. The DRL algorithm was used to optimize BS beamforming and RIS beamforming, which improved the secrecy rate and quality of service satisfaction. Nguyen et al. [20] designed a wireless power information transmission scheme, jointly optimizing UAV trajectories, power allocation, fixed IRS phasing, and node scheduling to maximize the transmission rate. The problem was reconstructed as a Markov decision process, and DRL was used to solve the optimization problem.

Inspired by the above discussion, this paper considers a UAV equipped with a reconfigurable intelligent surface (UAV-RIS)-assisted wireless powered communication network. It employs a ‘harvest then transmit’ protocol, in which an energy-constrained device first harvests energy wirelessly and uses all the collected energy for transmission in the remaining time. In addition, DRL is introduced to further optimize the performance of the WPCN to reduce energy consumption while increasing the data transmission rate. We used DRL to optimize the position, the phase configuration of the UAV-RIS, and the energy-harvesting scheduling of the ground nodes, aiming to solve energy efficiency in the UAV-RIS-assisted wireless powered communication network, with the following main contributions:

(1)

A UAV-RIS-assisted WPCN architecture is proposed to address the efficiency bottleneck of WPCNs under limited transmission distance and obstacle influence. To achieve the precise division of the time dimension, this paper adopts time division multiple access (TDMA) technology to achieve the parallel transmission of information and energy. On this basis, this article further introduces dynamic TDMA (DTDMA) technology to fully tap into the potential of time resources. It adopts a dual-layer time-division structure, which divides time at the macro level and allocates ground nodes at the micro level, achieving refined management and utilization of resources.

(2)

This paper proposes a system energy efficiency optimization problem for a UAV-RIS-assisted WPCN architecture based on TDMA and DTDMA. By establishing a joint optimization problem, the RIS phase shift matrix, time slot allocation ratio $\tau$ for energy-harvesting stages, and UAV trajectory optimization are comprehensively considered. We transformed the optimization problem into a DRL model to overcome the problems of high computational complexity and the complexity of traditional methods and employed a DDPG algorithm to solve it. By monitoring the rewards of environmental feedback, the DRL algorithm can iteratively adjust parameters, gradually optimize energy efficiency, and achieve the acquisition of optimal strategies.

(3)

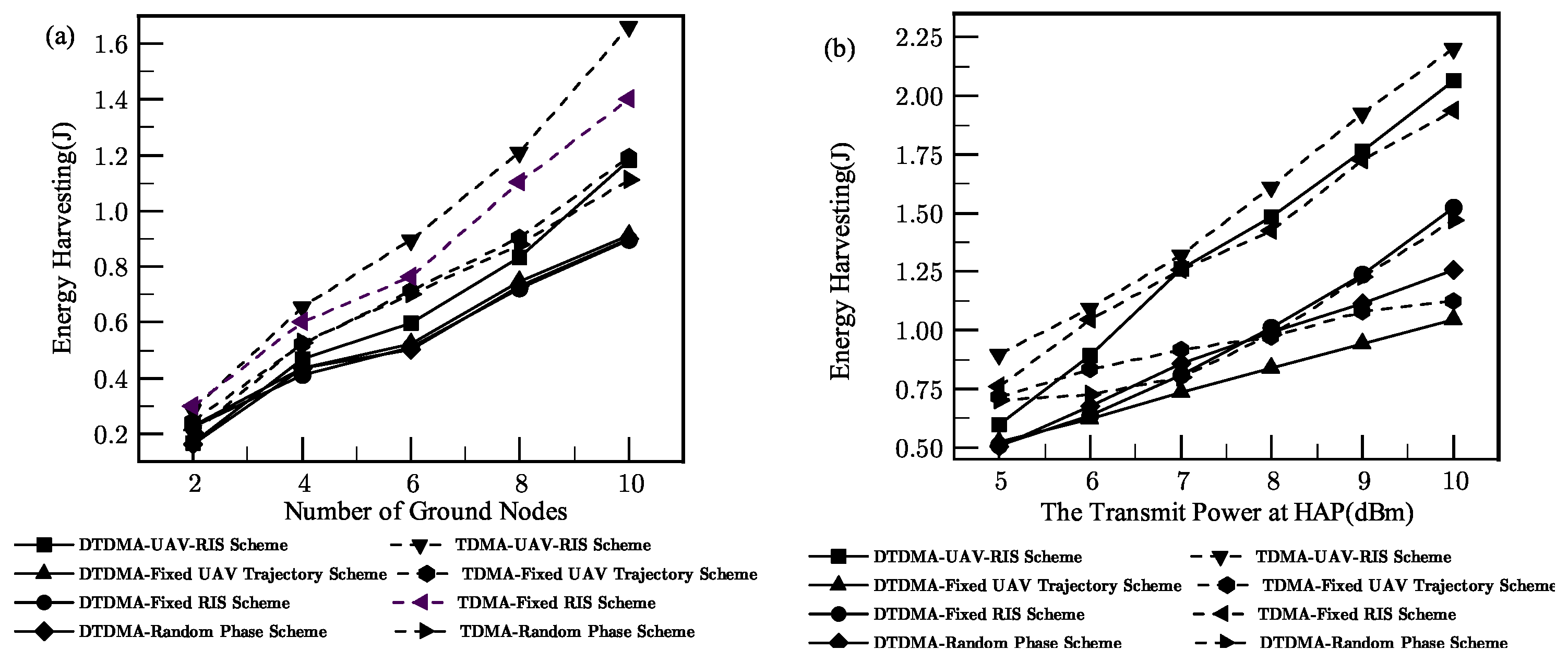
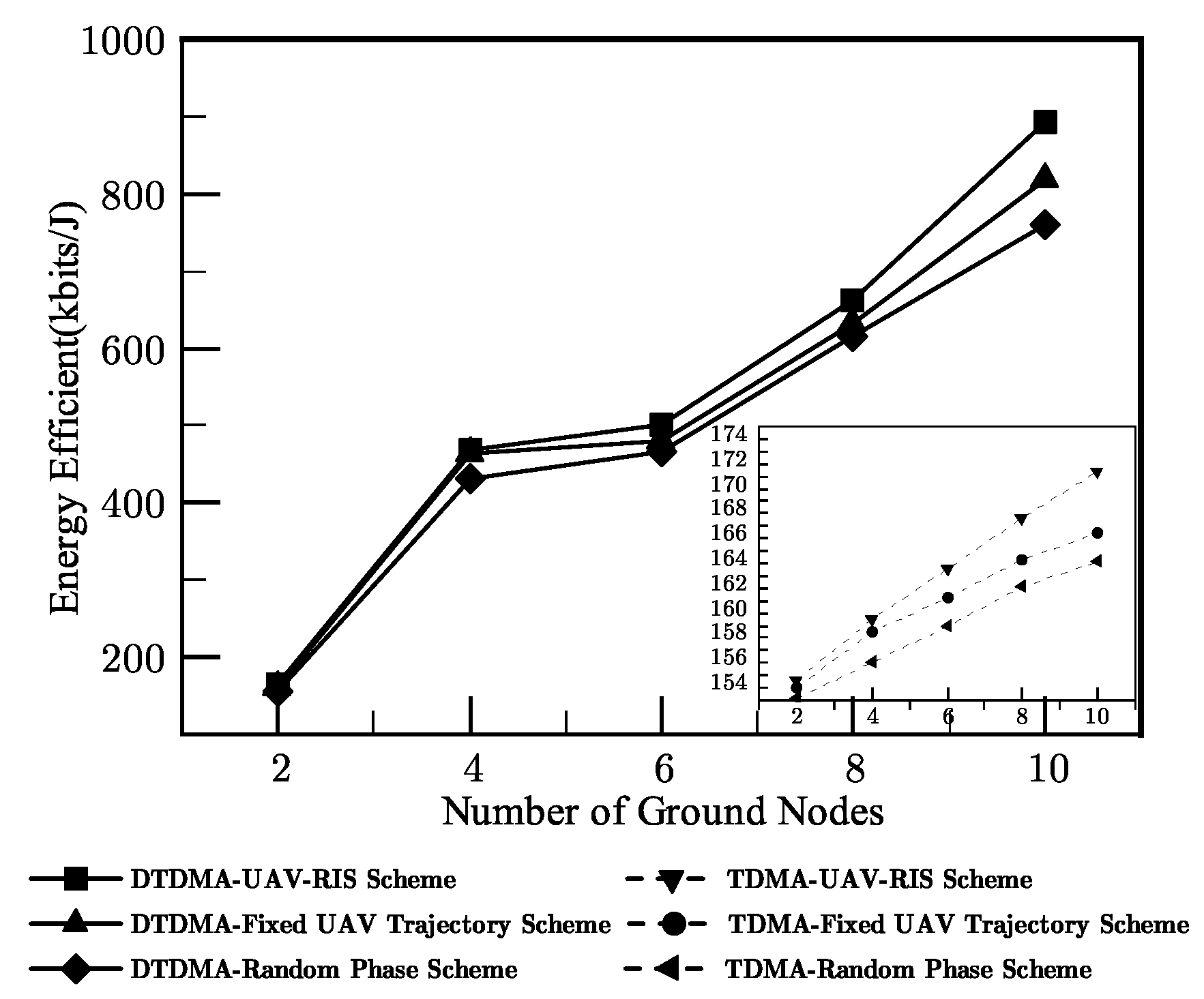
The simulation results have indicated that the proposed architecture significantly impacts WPCN performance, indicating a significant improvement in the effectiveness of this scheme compared to other methods, fully demonstrating its efficiency and superiority. In addition, this article reveals the advantages of different TDMA strategies, providing an important basis for selecting appropriate TDMA strategies in different application scenarios.

2. System Model and Problem Statement

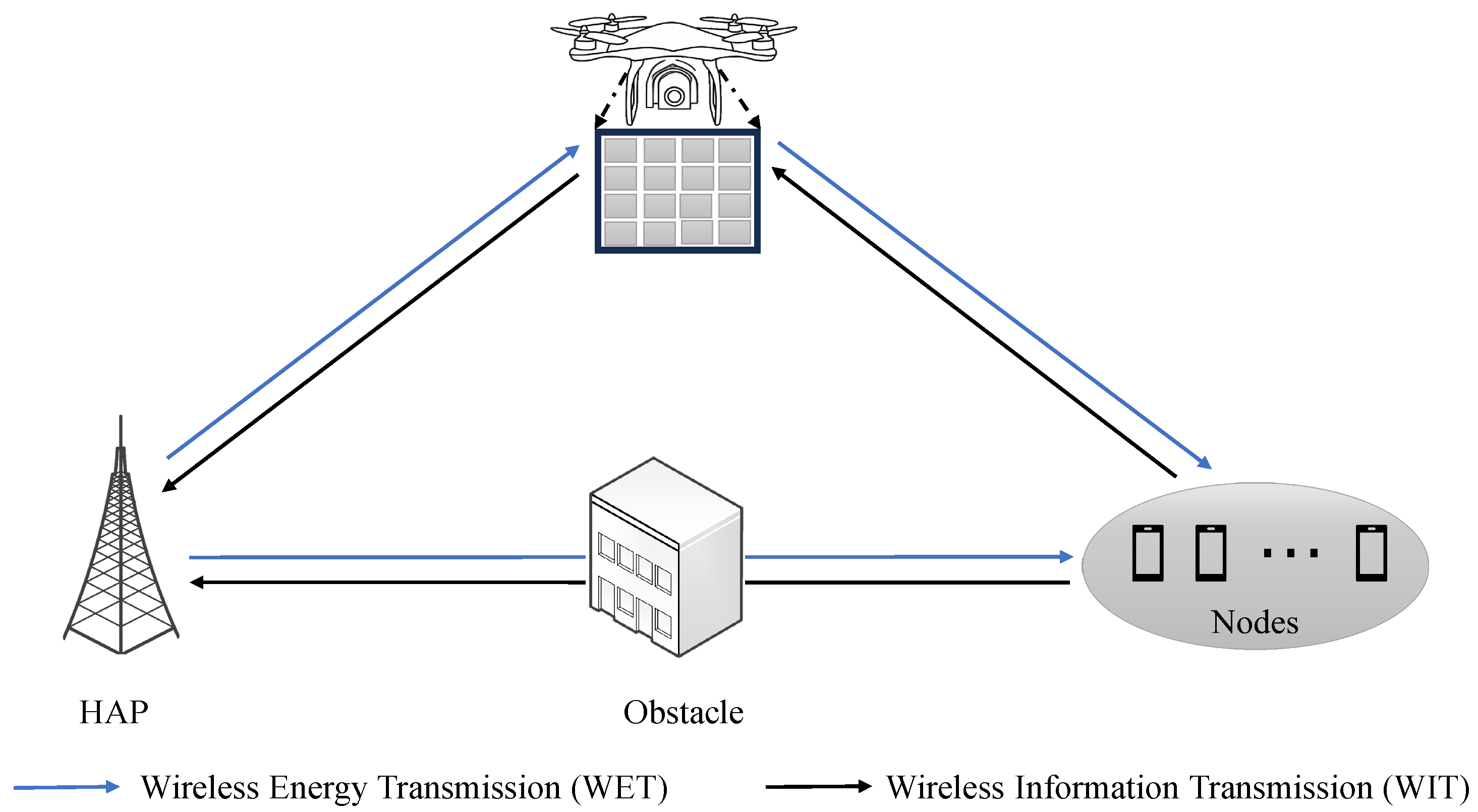
Given the challenges posed by obstacles in complex urban environments, which significantly impact channel quality between HAP and nodes, this paper introduces a framework leveraging UAV-RIS to bolster WPCN performance. As shown in Figure 1, the framework exploits the mobility of UAV-RIS to improve channel quality between hybrid access points and nodes. An RIS with M reflection units was deployed on a dynamic UAV to reconfigure the wireless channel conditions between HAPs and k single-antenna nodes by adjusting the phase shifts, and the set of nodes is defined as k = {1, 2, …, K}.

For the sake of generality, a two-dimensional Cartesian coordinate system is considered in this article. To mitigate the intricacy of the system, an assumption is made here that the takeoff and landing phases of UAV are not considered, and only the time-varying time of flight time T is considered. In time slot n, the coordinates of the UAV can be expressed as $q\left(n\right)=[x\left(n\right),y\left(n\right),h]\in {\mathbb{R}}^{3d},0\le n\le T$. It maintains a constant altitude h with an initial position of $q_0=[x\left(0\right),y\left(0\right),h]$.

2.1. Model of UAV-RIS-Assisted WPCN Based on TDMA

In order to provide services to different nodes at different times, this paper proposes a model based on TDMA for UAV-RIS-assisted WPCN.

In this model, UAV-RIS alters the state of a phase shifter in each time slot, enabling time-sharing services among nodes. Each time slot is segmented into two intervals, allocated according to the ratio $\tau$(n), where $\tau$(n) is used for energy transmission and 1−$\tau$(n) for information transmission. A Uniform Linear Array (ULA) of M cells is used within the RIS. For convenience of implementation, it is assumed that the amplitude of all elements is 1, and the reflection coefficient matrix can be expressed as Equation (1):

$$\mathrm{\Theta }\left[n\right]=\mathrm{diag}\left\{e^{j{\theta }_1\left[n\right]},e^{j{\theta }_2\left[n\right]},\dots ,e^{j{\theta }_M\left[n\right]}\right\}\in {\mathbb{C}}^{M\times M}$$

(1)

where $0\le {\theta }_m\left[n\right]\le 2\pi$ is the phase shift of the m$th$ element in the RIS at time slot n. Furthermore, channel state information can be obtained through existing methods (for example, minimum mean square error, maximum likelihood estimation, and deep learning prediction). Therefore, this chapter assumes that channel state information and node coordinates are perfectly known [21].

Since the direct communication link between HAPs and ground nodes is obscured by obstacles, resulting in the lack of a direct signal transmission path, UAV-RIS is introduced to address this issue. It can dynamically adjust the wireless propagation environment to establish an effective signal transmission channel between HAPs and nodes by means of reflection, thus overcoming the problem of unreachable direct paths. Thus, the reflection path in the system encompasses two links: the communication link between UAV-RIS and HAP, as well as the communication link between UAV-RIS and nodes. A distance based on a path loss model is used between HAP and UAV-RIS at time slot n, which takes into account distance and large-scale fading to ensure that the attenuation of the signal during transmission is accurately predicted and compensated. The signal during transmission is accurately predicted and compensated. The path loss $P{L}_m\left[n\right]$ [22] of the channel gain $g_{BU}\left[n\right]\in {\mathbb{C}}^{N\times M}$ of each reflective element from HAP to RIS is expressed as

$$P{L}_m\left[n\right]=\left(P_m\left(\mathrm{LoS}\right)\left[n\right]+\left(1-P_m\left(\mathrm{LoS}\right)\left[n\right]\ast \phi \right)\right)·{\left(d_{BU}\left[n\right]\right)}^{-\xi }$$

(2)

where $\xi$ denotes the path loss exponent, $\phi$ denotes the additional attenuation factor caused by NLoS connection, and $d_{BU}\left[n\right]=\sqrt{\parallel {\omega }_B{-q\left(n\right)\parallel }^2}$ denotes the distance separating HAP and the UAV-RIS. ${\omega }_B$ is the position of the HAP, and $P_m\left(LoS\right)\left[n\right]$ is the LoS probability between HAP and the RIS element, which can be calculated according to Equation (2):

$$P_m\left(LoS\right)\left[n\right]={\displaystyle \frac{1}{1+A·exp\left(-B\left({\theta }_m\left[n\right]-A\right)\right)}}$$

(3)

where constants A and B are determined by environmental factors [23]. The equation for calculating the elevation angle between HAP and the hyper-surface elements is as follows [16]:

$${\theta }_m\left[n\right]={\displaystyle \frac{180}{\pi }}{sin}^{-1}\left({\displaystyle \frac{h}{d_{BU}\left[n\right]}}\right)$$

(4)

The signal transmission between UAV-RIS and the nodes follows a small-scale Rician fading distribution, denoted as

$$g_{UK}\left[n\right]=\sqrt{{\beta }_0{\left(d_{UK}\left[n\right]\right)}^{-\epsilon }}·\left(\sqrt{{\displaystyle \frac{K_{\mathrm{rician}}}{1+K_{\mathrm{rician}}}}}{g}_{UK}^{LoS}+\sqrt{{\displaystyle \frac{1}{1+K_{\mathrm{rician}}}}}{g}_{UK}^{NLoS}\right)$$

(5)

where ${\beta }_0$ is the path loss at the reference distance $D_0$, $\epsilon$ is the path loss exponent, $d_{UK}\left[n\right]=\sqrt{\parallel q\left(n\right)-{\omega }_K{\parallel }^2}$ denotes the distance separating the UAV-RIS and nodes, ${\omega }_K$ denotes the location of the kth node, and $K_{\mathrm{rician}}$ denotes the Rician factor associated with small-scale fading. Additionally, the LoS path gain $g_{UK}^{LoS}$ consists of the array response of reflection units, while the NLoS path gain $g_{UK}^{NLoS}$ follows an independent and identically distributed complex Gaussian distribution with zero mean and unit variance.

Therefore, the reflected channel gain between HAP and node k is

$$g_k\left[n\right]=c_k\left[n\right]g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]$$

(6)

where $c_k\left[n\right]$ is a binary variable denoting that node k is connected to the HAP, and ${\sum }_{n=1}^N{c}_k\left[n\right]=1$ denotes that HAP is connected to only one node in a time slot. Thus, Equation (6) can be written as

$$g_k\left[n\right]=\left\{\begin{array}{cc}0,\hfill & c_k\left[n\right]=0\hfill \\ g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right],\hfill & c_k\left[n\right]=1\hfill \end{array}\right.$$

(7)

2.2. Model of UAV-RIS-Assisted WPCN Based on DTDMA

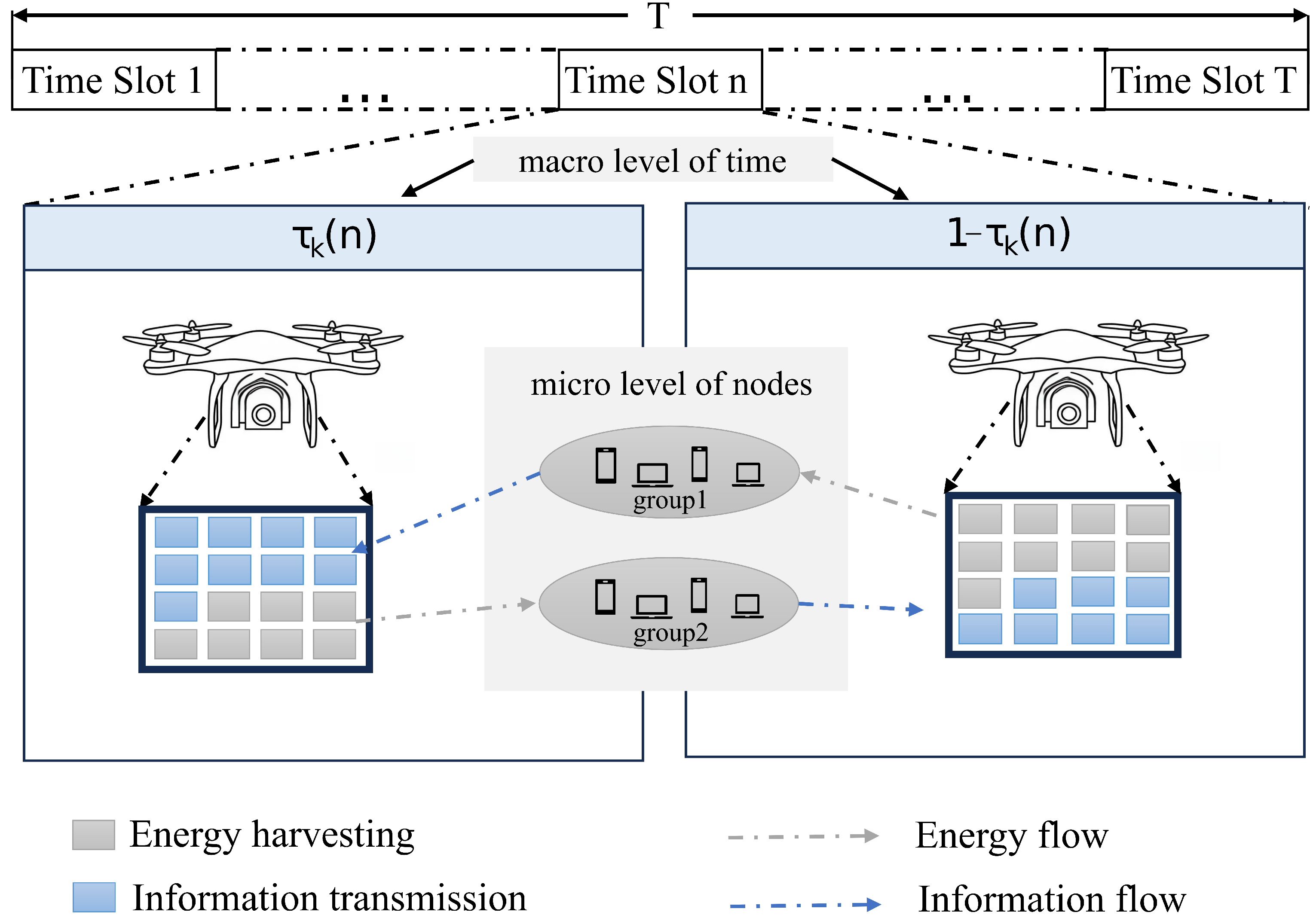
In order to maximize time resource utilization, this paper considers a DTDMA model, as per Figure 2. The model introduces a two-layer time division structure, which realizes a fine-grained allocation of resources at the macro and micro levels:

Macro level: Each time slot is divided into two complementary time windows, forming an efficient closed-loop system for resource utilization.

Micro level: The system divides the ground nodes into two functionally complementary subgroups based on their locations and performs uplink wireless information transmission (WIT) and downlink wireless energy transmission (WET) tasks in each time window.

In this two-layer time division structure, the system interchanges the functional roles of the two subgroups in two time windows of the same time slot, interleaving the WIT and WET tasks. At the same time, the ratio of the two time windows is dynamically adjusted according to real-time channel conditions and communication requirements. This role-switching mechanism achieves more accurate resource matching while maximizing the overall average throughput of the network.

A. Wireless energy transfer phase

In the WET phase, UAV-RIS reflects the energy signal from the HAP to the ground node. The kth ground node receives the signal as

$$y_E\left[n\right]=\left(g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]\right)\sqrt{P_B}X+{\sigma }^2$$

(8)

where ${\sigma }^2$ is the noise signal following a Gaussian distribution, and X and $P_B$ represent the symbol signal and transmit power of the HAP, respectively. Therefore, the power received by ground node k is

$$\begin{array}{cc}\hfill E_k\left[n\right]& =\eta \left((1-{\tau }_k\left[n\right])\underset{\mathrm{group}2}{\underbrace{P_B{\left|g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]\right|}^2}}\right.+\left.{\tau }_k\left[n\right]\underset{\mathrm{group}1}{\underbrace{P_B{\left|g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]\right|}^2}}\right)\hfill \end{array}$$

(9)

where $\eta$ is the EH efficiency.

B. Wireless information transfer phase

In the WIT phase, UAV-RIS can reflect the signals sent by the nodes to the HAP. Assuming the ground nodes rely solely on harvesting energy for WIT phase operation, the signal transmitted from them and received by the HAP is

$$y_I\left[n\right]=\left(g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]\right)\sqrt{P_k}{u}_n+{\sigma }^2$$

(10)

where $u_n$ is the symbol signal coming from the ground node to the HAP, and $P_k$ represents the transmit power of the kth user. Thus, the throughput of node k can be expressed by

$$\begin{array}{cc}\hfill R_k\left[n\right]& ={\tau }_k\left[n\right]\underset{\mathrm{group}1}{\underbrace{{log}_2\left(1+{\displaystyle \frac{P_k\left[n\right]{\left|g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]\right|}^2}{{\sigma }^2}}\right)}}\hfill \\ \hfill & +\left(1-{\tau }_k\left[n\right]\right)\underset{\mathrm{group}2}{\underbrace{{log}_2\left(1+{\displaystyle \frac{P_k\left[n\right]{\left|g_{UK}{\left[n\right]}^H\mathrm{\Theta }\left[n\right]g_{BU}\left[n\right]\right|}^2}{{\sigma }^2}}\right)}}\hfill \end{array}$$

(11)

2.3. Energy Consumption of the System

The propulsion energy consumption of the rotary-wing UAV [24] per time interval n is

$$\begin{array}{c}\hfill e_n^{UAV}=t_n^u\left(P_0\left(1+{\displaystyle \frac{3{\left(v_n\right)}^2}{U_{tip}^2}}\right)+{\displaystyle \frac{1}{2}}{d}_0\rho sG{\left(v_n\right)}^3\right.\left.+p_1{\left(\sqrt{1+{\displaystyle \frac{{\left(v_n\right)}^4}{4{\left(v_0\right)}^2}}}-{\displaystyle \frac{{\left(v_n\right)}^2}{2{\left(v_0\right)}^2}}\right)}^{{\displaystyle \frac{1}{2}}}\right)\end{array}$$

(12)

where $p_1$ and $p_0$ represent the drag power and induced power of the UAV during hovering; $U_{tip}$ represents the tip speed of the rotor blade; $v_0$ represents the induced velocity of the horizontal rotor within hover mode; $d_0$ and s denote the fuselage drag ratio and the stiffness of the wind turbine; $\rho$ and G represent the air density and the area swept by the rotation of the rotor, respectively.

The overall energy expenditure of this system can be formulated by

$$Q^{total}=E_B^C\left[n\right]+E_e^C\left[n\right]+E_k^C\left[n\right]+e_n^{UAV}-E_k\left[n\right]$$

(13)

where $E_k^C\left[n\right],E_B^C\left[n\right],$ and $E_e^C\left[n\right]$ are the energy consumption of the kth user, the HAP, and each reflection unit in time slot n, respectively. In practice, communication-related energy consumption is small and negligible.

2.4. Problem Statement

This paper aims to achieve maximum system energy efficiency via the integrated optimization of the RIS phase-shift reflection coefficient, UAV position, and the time allocation ratio $\tau$ of EH; it also aims to achieve synergistic management of communication quality and transmission energy consumption. Drawing from the foregoing analysis, the optimization problem is formulated as follows:

$$\begin{array}{cc}& P1:\underset{\theta ,q,\tau }{max}EE=\sum _{k=1}^K\sum _{n=1}^N{\displaystyle \frac{R_k\left[n\right]}{Q^{total}}}\hfill \\ & \mathrm{s}.\mathrm{t}.0<{\tau }_k\left[n\right]<1,\forall n\in N,\forall k\in K\hfill \\ & \phantom{\mathrm{s}.\mathrm{t}.}{X}_{UAV}\in Z\hfill \\ & \phantom{\mathrm{s}.\mathrm{t}.}v\le V_{max}\hfill \\ & \phantom{\mathrm{s}.\mathrm{t}.}0\le {\theta }_m\left[n\right]\le 2\pi ,m=1,2,\dots ,M\hfill \end{array}$$

(14)

We aim to enhance the energy efficiency of this system to its peak in all time slots. ${\tau }_k$(n) represents the proportion of transmission time during each slot; Z represents the horizontal flight area, ensuring the UAV’s movement remains within the defined limits; $V_{max}$ is the maximum speed of the rotary-wing UAV. It can be seen that Equation (14) is a non-convex Mixed Integer Nonlinear Programming problem. Solving P1 with traditional optimization methods partially will be computationally expensive, and once the solution is obtained, it is hard to readjust the optimization strategy quickly enough to be deployed online. DRL has been proven to be highly effective in decision-making and achieving optimal results in dynamic environments. Due to these reasons, we propose solutions based on DRL to address problem P1 and use these together to maximize energy efficiency and average throughput.

3. DRL-Based Design for Energy Efficiency Optimization

We established a DRL-based resource optimization framework that maximizes the total harvested energy and average throughput of UAV-RIS while ensuring minimum energy consumption for its flight and communication.

3.1. MDP Definition

This framework consists of two components: environment and agent. The environment–agent interaction follows a Markov decision process (MDP). The agent then evaluates the previous operation using the reward provided by the environment. The agent takes an action in the environment based on its current state and then uses the reward feedback from the environment to assess the quality of the previous action.

The MDP is characterized by a four-tuple $〈S,A,P,R〉$, where $S,A$ respectively denote state space and action space. P is the state transfer probability, indicating the likelihood of transitioning to the next state $s^{n+1}$ after taking an action $a^n$ at the current state $s^n$. R quantifies the reward that the agent receives for such a transition. Then, we construct a game in the equation to solve this problem.

Agent: Activate the central processor to operate as an autonomous agent. It discovers an optimal strategy that maximizes energy efficiency. After training, the action formulation is implemented on the UAV for forecasting and choosing parameters.

State space: The channel consists of reflection channels. Therefore, the state space is defined here as

$$\begin{array}{cc}\hfill s\left(n\right)=& \left\{g_1\left[n\right],g_2\left[n\right],\dots ,g_K\left[n\right]\right\}\in S\hfill \end{array}$$

(15)

Action space: The action space is characterized as $A=\{\tau ,v,\zeta ,\theta ,{\theta }_1,\dots ,{\theta }_M\}$. In state $s^n$, the UAV takes an action $a^n=\{{\tau }^n,v^n,{\zeta }^n,{\theta }^n,{\theta }_1^n,\dots ,{\theta }_m^n\}$ and moves to the next state $s^n=s^{n+1}$, where the position of the UAV in time slot n is denoted as

$$X_{UAV}^{n+1}=\left\{\begin{array}{c}{x}_{UAV}^{n+1}=x_{UAV}^n+v^{n}cos{\zeta }^n+\Delta x^{n+1}\hfill \\ y_{UAV}^{n+1}=y_{UAV}^n+v^{n}sin{\zeta }^n+\Delta y^{n+1}\hfill \\ H_{UAV}^{n+1}=H_{UAV}^n+\Delta H^{n+1}\hfill \end{array}\right.$$

(16)

where $\Delta x^{n+1}, \Delta y^{n+1}$ and $\Delta H^{n+1}$ represent the environmental noise affecting the flight at time step $(n+1)$. The flight angle of the UAV is set by constraining a parameter $\zeta$, and the speed of the UAV is set by constraining a parameter v during the flight of the UAV.

Reward: We devised a reward function to optimize system energy efficiency by minimizing both UAV power usage and additional communication power during transmission. Specifically, the function $r^n=r(s^n,a^n,s^{n+1})$ quantifies the immediate reward, guiding the UAV towards actions that maximize energy efficiency.

3.2. Agent Design and Algorithm Implementation

Our goal was to identify the best strategy for maximizing the expected reward. In a partially observable environment, the agent operates with limited knowledge and interacts to earn rewards. It adjusts its policy $\pi$ based on received rewards and performs new actions in updated states. Through iterative interaction, agents can find better strategies and better rewards. After each action, the drone updates its position and receives environmental feedback. The agent can select the appropriate speed and flight direction for the drone according to channel state information (CSI). Additionally, optimization is performed on the parameters $\tau$ and phase shift matrix to maximize network performance. This study employs a DRL algorithm to find the optimal strategy.

DDPG is a model-free, policy-free, and actor-critic-based DRL algorithm that can handle the task of continuous action space well. In DDPG, the actor network determines the best action of an agent in the current state s with a function $\pi \left(s\right|{\theta }^{\pi })$, while the critic network estimates the Q-value under the action pair in the current state with a function $Q(s,a|{\theta }^Q)$. DDPG consists of two actor-critic network pairs: the main network pair and the target network pair. The parameters of the critic network are updated based on the Temporal Difference (TD) error, and the parameters of the actor network are updated based on the output of the former. If a single network is used for both action selection and Q-value estimation, the update of the actor network’s parameter will directly affect the estimation results of the critic network, leading to instability during the training process. By introducing a target network, the interdependence between parameter updates can be reduced, and the stability of the algorithm can be improved.

In this paper, we build an experience replay pool D with capacity $N_B$. The phase shifts of all RIS elements are set randomly within the range of 0 to $2\pi$ at the beginning of training. Prior to each training iteration, all involved channels are first computed. Following this, the policy network processes the state $s^n$ as its input and then generates the corresponding action $a^n$ to be executed.

$$a^n=\pi \left(s^n|{\theta }_n^{\pi }\right)+N^n$$

(17)

where $N^n$ is the random noise. The current reward $r^n$ is calculated according to a corresponding action. Then, $s^{n+1}$ is obtained using Equation (15). Store $\{s^n,a^n,r^n,s^{(n+1)}\}$ as a transition to D; the value network then samples a small batch $\{s_j^n,a_i^n,r_j^n,s_j^{(n+1)}\}$ ($j=1,\dots ,N_B$) from it to calculate the target Q-value $y_j$.

$$y_j=\left\{\begin{array}{cc}{r}^{n+1},\hfill & j=N_B\hfill \\ r^{n+1}+\gamma Q\left(s^{n+1},{\displaystyle \frac{a^{n+1}}{{\theta }^{Q^{\prime }}}}\right),\hfill & j<N_B\hfill \end{array}\right.$$

(18)

The value network adjusts its parameters with the objective of reducing the loss function to an optimal level:

$$J\left({\theta }^Q\right)={\displaystyle \frac{1}{n}}\sum _{k=1}^n{\omega }_k{\left(y_i-Q\left(s^n,{\displaystyle \frac{\alpha t^n}{Q^{\prime }}}\right)\right)}^2$$

(19)

where $J\left({\theta }^o\right)$ is the value network loss function, $y_i$ is the target action value, n represents the sample count, and ${\omega }_k$ represents the sample weight. For each sample, the action $a^n$ taken at a given state $s^n$ is denoted by $Q(s^n,a^n/{\theta }^{Q^{\prime }})$, with the subsequent reward at the next time step represented by $r^{(n+1)}$. The discount factor $\gamma$ is also considered in this calculation.

Training employed the Adam optimizer for both the policy and value networks, with soft updates applied to the respective objective networks, as shown below:

$$\begin{array}{cc}\hfill {\theta }^{Q^{\prime }}& ={\psi }_a{\theta }^Q+(1-{\psi }_a){\theta }^{Q^{\prime }}\hfill \\ \hfill {\theta }^{{\pi }^{\prime }}& ={\psi }_c{\theta }^{\mu }+(1-{\psi }_c){\theta }^{{\pi }^{\prime }}\hfill \end{array}$$

(20)

where ${\psi }_a\ll 1,{\psi }_c\ll 1$ is the learning rate of the soft updates on the actor network and critic network, respectively.

The pseudo-code of the UAV-RIS-assisted WPCN communication strategy process based on DDPG is shown in Algorithm 1. During training, the agent engages with the environment to perceive the current state of the system $s^n$. At the start of each training round, a system state is initialized, and the initialized state is subsequently fed into the model. When the agent explores, the agent selects joint actions $a^n$ (time slot allocation, drone path, and phase shift design) guided by its current policy. Upon executing these actions, it observes a reward $r^n)$ and a new system $s^{n+1}$ state, which is deposited into the cache pool. Then, the state is updated by randomly drawing samples in this buffer to compute the target Q-value, followed by updating both the policy and value networks. The correlation parameters are iteratively refined until convergence, resulting in a trained model that incorporates optimized UAV routes and reflected beam formation matrix $\mathrm{\Phi }$ strategies based on the chosen actions.

In order to promote better exploration during the training process, this paper employs the Adaptive Ornstein–Uhlenbeck Action Noise function. This noise function has configurable noise intensity and was gradually reduced during the training process to help the agent explore more at the early stage of learning and gradually converge to the optimal policy, enhancing the agent’s ability to explore the environment better during the training process and eventually learn a high-performance policy.

Algorithm 1 UAV-RIS- assisted WPCN joint trajectory design; EH time and phase shift optimization design based on DDPG

Require:  Initial state of the system, discount factor $\gamma$, learning rate, experience replay size $N_D$, small batch size $N_B$ Ensure:  Best strategy 1: Initialization: 2:    Actor network $\pi (s\mid {\theta }^{\pi })$ and critic network $Q(s,a\mid {\theta }^Q)$, 3:    target actor network ${\pi }^{\prime }(s\mid {\theta }^{{\pi }^{\prime }})$ and target critic network $Q^{\prime }(s,a\mid {\theta }^{Q^{\prime }})$, 4:    ${\theta }^{{\pi }^{\prime }}={\theta }^{\pi }$, ${\theta }^{Q^{\prime }}={\theta }^Q$, 5:    experience replay buffer D, phase shift matrix $\mathrm{\Phi }$. 6: for episode = 1 to N do 7:    Accept the current environment and obtain the initial state $s\left(0\right)$; 8:    Initialize a random noise; 9:    for $n=1$ to N do 10:      Take state $s^n$ as input and get action $a^n$ from policy network; 11:      Execute the action to get the reward $r^n$ and state $s^{n+1}$; 12:      Store $(s^n,a^n,r^n,s^{n+1})$ in experience replay pool D; 13:      Draw a random batch of samples from D; 14:      Calculate the target Q-value $y_j$ according to (18); 15:      Minimize (19) to update the value network; 16:      Update the gradient of the strategy network using SGD; 17:      Update the policy network so that the actions of the policy network can better approximate the real actions; 18:      Softly update the target network parameters according to (20); 19:      Update the state $s^n=s^{n+1}$. 20:    end for 21: end for

3.3. Overall Algorithm Complexity Analysis

Traditional optimization algorithms often have high computational complexity, which limits their use in applications that require rapid response. Take the Successive Convex Approximation (SCA) algorithm as an example; its working principle is to iteratively approximate non-convex functions and solve the resulting convex subproblems at each step. Its complexity is $O\left(K_{\mathrm{it}}{\left(NK\right)}^{3.5}+MKN+N\right)$ [18], where the complexity of solving convex optimization problems using an interior-point method in CVX is $O\left(K_{\mathrm{it}}{\left(NK\right)}^{3.5}\right)$, with $K_{\mathrm{it}}$ being the number of SCA iterations [25]. $O\left(MKN\right)$ denotes the complexity of computing the optimal IRS phase, and $O\left(N\right)$ is the complexity of standard linear programming. As the problem size increases, this super-linear complexity growth makes solving large-scale problems extremely challenging. In contrast, DDPG optimizes the objective function through iterative updates of the policy network and Q network. The forward pass complexity of the policy network is $O\left(A^2+n_a^2+S^2\right)$ (where $A=M+N+3$ is the action space size, $S=MN$ is the state space size, and $n_a$ is the number of policy network parameters). The complexity of the Q network is $O\left(A^2+n_c^2+S^2\right)$ (where $n_c$ is the number of Q network parameters). The total complexity is $O\left[K\left((A^2+n_a^2+S^2)+(A^2+n_c^2+S^2)\right)\right]$, where K is the total number of training iterations. Unlike the super-linear growth of traditional methods, the quadratic complexity growth of DDPG makes it more advantageous in high-dimensional state spaces and real-time scenarios. Additionally, its ability to obtain feasible solutions with fewer iterations makes it more suitable for scenarios requiring rapid response and online deployment.

4. Simulation and Result Analysis

4.1. Experimental Setup

The purpose of this article is to use a DDPG-based scheme to generate the optimal time slot allocation ratio, RIS phase shift matrix, and drone trajectory for the system. Consider a 50 m × 50 m UAV flight area, where RIS deploys M = 16 reflector units to assist HAP in communicating with multiple ground nodes. Evaluate the performance of the UAV-RIS-assisted WPCN communication system through simulation analysis.

Refer to

Table 1. Parameter settings.

Simulation Parameters	Parameter Values	Simulation Parameters	Parameter Values
N	100	$U_{tip}$, $v_0$, $d_0$	120, 4.3, 0.6
Rician coefficient	5 dBm	s, rho, G	0.05, 1.225, 0.503
Bandwidth	1 MHz	$P_0$	${\displaystyle \frac{12\times {30}^3\times {0.4}^3}{8}}\times \rho sG$
EH efficiency	0.7	$P_1$	$(1.1 \times {20}^{3/2})$/$\sqrt{2\rho G}$
UAV height	10 m	Path loss at 1 m	−30 dB
HAP height	5 m	Noise power	−102 dBm
Discount factor	0.99	Experience replay buffer $N_D$	100,000
Learning rate	1 × ${10}^{-4}$	Number of reflection elements	16

for the remaining parameters.

4.2. Simulation Results Analysis

In this study, we used DDPG to jointly optimize the flight path of the drone, the time slot allocation ratio of EH, and the RIS phase shift configuration. Based on TDMA and DTDMA multiple-access technologies, we designed two optimization models and established the following two baseline algorithms as comparison criteria to evaluate the effectiveness of these models:

• Fixed drone trajectory baseline: In this baseline, assuming that the drone’s flight trajectory is preset and remains unchanged, we only optimize resource allocation for the UAV-RIS-assisted WPCN, including adjusting the EH time slot allocation ratio and RIS phase shift, and all operations are performed under the same constraints. This setting aims to evaluate the contribution of drone trajectory optimization to the improvement of system performance.
• Fixed RIS position baseline: In this baseline, we deploy RIS at a fixed location while keeping the components and parameters of other communication systems unchanged. Similarly, under the same constraint set, we optimize the resource allocation strategy, including the time slot allocation ratio of EH and RIS phase shift adjustment. This baseline is used to examine the influence of RIS positional flexibility on performance optimization.
• Random RIS phase shift baseline: In this baseline, the RIS phase shifts are randomly configured while keeping the components and parameters of other communication systems unchanged. Under the same set of constraints, we optimized the resource allocation strategy, including the time slot allocation ratio for energy harvesting and the UAV flight path. This baseline is used to evaluate the impact of RIS phase shift optimization on system performance.

Figure 3 compares the performance of three different reinforcement learning algorithms—DDPG, Twin Delayed deep deterministic policy gradient algorithm (TD3), and Proximal Policy Optimization (PPO)—in both the DTDMA-based and TDMA-based schemes. The figure shows that the cumulative rewards for all three algorithms increase with training steps in both environments. When the training steps reach 10k, all three algorithms tend to converge, though with differences in convergence levels and stability. In Figure 3a, the DDPG algorithm demonstrates the most excellent performance, not only rapidly increasing the cumulative reward to around −1.25 in the early stage but also showing relative stability throughout the subsequent training process with moderate fluctuations. The TD3 algorithm has a learning speed similar to DDPG but achieves a lower cumulative reward level and shows significantly greater volatility than the other two algorithms, which may be related to its dual critic network and delayed policy update mechanism. In comparison, although the PPO algorithm has a slower initial learning speed and slightly inferior performance to DDPG, its overall performance is more stable and predictable, demonstrating robustness in complex environments. In Figure 3b, the initial reward levels of the three algorithms are lower, and the learning curves are steeper. The performance of DDPG and PPO algorithms is relatively close, with the two alternately taking the lead at different stages, though the performance of PPO is more stable. The TD3 algorithm performs relatively poorly in this environment, with lower cumulative rewards and greater fluctuations. Considering the performance in both environments, the DDPG algorithm demonstrates the best overall performance, not only showing a clear advantage in cumulative rewards but also exhibiting good learning efficiency and stability. The PPO algorithm offers the best stability, making it suitable for long-term training scenarios. The TD3 algorithm, however, shows greater volatility. Based on the above analysis, this study selects the DDPG algorithm as the basic framework and introduces an adaptive OU action noise function, enabling it to explore more flexibly in continuous action spaces to adapt to the dynamic characteristics of complex communication systems.

Figure 4 depicts the fluctuating correlation between the average throughput of all ground nodes and the transmission power of the ground nodes under the proposed algorithm and baseline algorithm. From Figure 4a, the average throughput under all schemes shows an upward trend as the number of ground nodes escalates. Additionally, when there are two ground nodes, the performance gap between the TDMA-based and DTDMA-based approaches is minimal. However, as the node count grows, the scheme based on DTDMA shows a significant advantage, which is mainly due to the concurrent communication mode of DTDMA. It allows all ground nodes to participate in both WET and WIT at the same time within each time slot, which greatly improves the efficiency and throughput of data transfer and effectively reduces the total time of data transfer. On the contrary, TDMA-based schemes require nodes to transmit data and energy one by one, which limits the overall average throughput improvement. When the number of ground nodes is 10, the DTDMA-UAV-RIS scheme is 13.09% higher than the DTDMA-Fixed UAV trajectory scheme, and the TDMA-UAV-RIS scheme is 8.13% higher than the TDMA-Fixed UAV trajectory scheme. When there are six ground nodes, the average throughput increases in tandem with the rising transmission power of ground nodes and converges gradually, as shown in Figure 4b. The energy efficiency of the UAV-RIS schemes is higher than other benchmarks.

Figure 5 illustrates the relationship between the aggregate energy harvested by all ground nodes and two key factors: the count of ground nodes and the transmission power of the HAP. From Figure 5a, it can be seen that when there are two ground nodes, the energy collected by the two TDMA schemes is similar. As the quantity of ground nodes grows, the TDMA scheme demonstrates superior energy collection compared to the DTDMA scheme, primarily due to variations in WET principles. Due to only collecting energy during the $\tau$ time period, the former can utilize this time more intensively. However, in the DTDMA-based approach, one time slot is allocated to different node groups, which affects the overall energy collection efficiency of each group of nodes. When the number of ground nodes is 10, the energy collected by the UAV-RIS scheme is more than 10% higher than the other three schemes. Consider the impact of HAP transmission power on downlink energy transfer when the number of ground nodes is six, as shown in Figure 5b. As the transmission power of HAP is heightened, so is the transmission capacity, allowing for the transmission of more RF signals and thus increasing the total collected energy. The results show that the overall effect of energy collection based on TDMA outperforms that based on DTDMA, and the UAV-RIS scheme has a significantly better energy collection effect than the others. This occurs because the reflective pathway of the UAV-RIS takes into account both channel quality and distance, thereby significantly improving the performance of WPCN.

Figure 6 illustrates the correlation between energy efficiency and the number of ground nodes under the proposed algorithm versus the baseline algorithm. While the number of ground nodes increases, overall energy efficiency exhibits an upward trajectory. Comparing the use based on DTDMA and TDMA, the former has significantly higher energy efficiency, indicating that the dynamic time division multiple access mechanism can effectively improve energy utilization efficiency. When the ground node count is minimal, the energy efficiency difference between different schemes is relatively small. However, as the quantity of nodes escalates, the disparity progressively expands. The overall energy efficiency of the DTDMA-UAV-RIS scheme improved by 9.02% compared to the DTDMA-Fixed UAV Trajectory scheme and by 17.48% compared to the DTDMA-Random Phase scheme. At the same time, the TDMA-UAV-RIS scheme also achieved energy efficiency improvements compared to the TDMA-Fixed UAV Trajectory and the TDMA-Random Phase scheme, with increases of 2.94% and 4.38%, respectively.

Overall, these results validate that the trajectory optimization scheme for unmanned aerial vehicles based on dynamic time division multiple access can bring good energy utilization efficiency, especially when combined with UAV-RIS technology. It provides a valuable reference for drone energy management.

5. Conclusions

This study introduced the resource optimization problem of UAV-RIS-assisted WPCNs, considering the energy consumption generated by the system during transmission in urban environments. We propose a DRL algorithm, the joint optimization of the EH scheduling of ground nodes, RIS reflective beam formation, and the flight path of UAVs to maximize energy efficiency to its highest potential. This research can be broadly applicable to boost channel performance in intricate settings. In future research, we anticipate extending the complexity of the communication environment, expanding the flight area of the UAV, and considering various obstacle problems that may be encountered. This will help to evaluate more comprehensive performance in real application scenarios.