Inversion Model for Total Nitrogen in Rhizosphere Soil of Silage Corn Based on UAV Multispectral Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Experimental Design
2.3. Data Collection and Processing for the Experiment
2.3.1. UAV Multispectral Remote Sensing Imagery Acquisition and Processing
2.3.2. Soil Sampling and Total Nitrogen Determination
2.4. Construction and Selection of Vegetation Indices
2.5. Model Construction and Analysis
2.6. Model Accuracy Evaluation
3. Results and Analysis
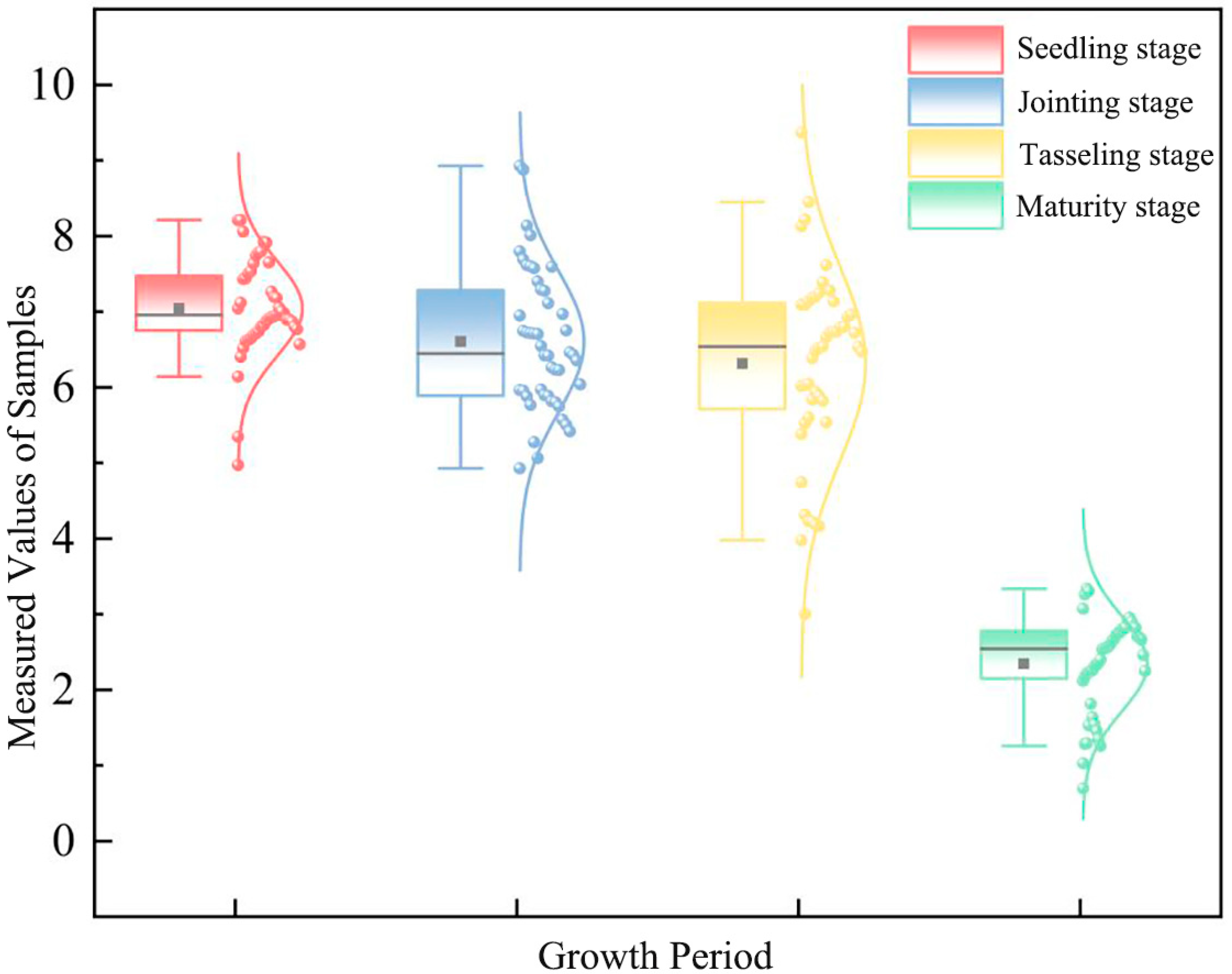
3.1. Statistical Analysis of Soil Total Nitrogen Content
3.2. Selection of Sensitive Variables
3.2.1. Comparative Analysis and Optimization Based on Multiple Spectral Index Selection Methods
3.2.2. Correlation Analysis of Spectral Indices
3.2.3. Post-Selection Model Inversion Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Davidson, E.A.; Mauzerall, D.L.; Searchinger, T.D.; Dumas, P.; Shen, Y. Managing nitrogen for sustainable development. Nature 2015, 528, 51. [Google Scholar]
- Spiertz, J.H.J. Nitrogen, sustainable agriculture and food security: A review. Agron. Sustain. Dev. 2010, 30, 43–55. [Google Scholar] [CrossRef]
- Rütting, T.; Aronsson, H.; Delin, S. Efficient use of nitrogen in agriculture. Nutr. Cycl. Agroecosystems 2018, 110, 1–5. [Google Scholar] [CrossRef]
- Pearcy, R.W.; Ehleringer, J.R.; Mooney, H.A.; Rundel, P.W.; Binkley, D.; Vitousek, P. Soil Nutrient Availability. Plant Physiol. Ecol. 1989. [Google Scholar] [CrossRef]
- Assefa, S.; Tadesse, S. The principal role of organic fertilizer on soil properties and agricultural productivity-a review. Agric. Res. Technol. Open Access J. 2019, 22, 1–5. [Google Scholar]
- Savci, S. Investigation of effect of chemical fertilizers on environment. Apcbee Procedia 2012, 1, 287–292. [Google Scholar]
- Liu, J.S.; Dai, J.; Liu, Y.; Guo, X.; Wang, Z.H. Effects of excessive nitrogen fertilization on soil organic carbon and nitrogen and nitrogen supply capacity in dryland. J. Plant Nutr. Fertil. 2015, 21, 112–120. [Google Scholar]
- Chen, G.; Yang, K.; Meng, Y.; Liu, D.; Jiang, Y.; Li, X. Screening and genetic characteristics of breeding materials of silage corn. Anim. Feed. Sci. Engl. Ed. 2011, 3, 4. [Google Scholar]
- Stone, M.L.; Solie, J.B.; Raun, W.R.; Whitney, R.W.; Taylor, S.L.; Ringer, J.D. Use of spectral radiance for correcting in-season fertilizer nitrogen deficiencies in winter wheat. Trans. ASAE 1996, 39, 1623–1631. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, L.; Zhao, L.; Liu, Z.; Lin, C.; Hu, Y.; Liu, L. Estimation of soil nutrient content using hyperspectral data. Agriculture 2021, 11, 1129. [Google Scholar] [CrossRef]
- Miao, Y.; Mulla, D.J.; Hernandez, J.A.; Wiebers, M.; Robert, P.C. Potential impact of precision nitrogen management on corn yield, protein content, and test weight. Soil Sci. Soc. Am. J. 2007, 71, 1490–1499. [Google Scholar]
- Cassman, K.G.; Dobermann, A.; Walters, D.T. Agroecosystems, nitrogen-use efficiency, and nitrogen management. AMBIO J. Hum. Environ. 2002, 31, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.L.; Biswas, D.K. Precision nitrogen management for sustainable corn production. Sustain. Agric. Rev. Cereals 2015, 33–62. [Google Scholar]
- Mu, H.B. Research on the Application of Near-Infrared Spectroscopy in the Evaluation of Nutritional Quality of Corn and Silage Quality. Doctoral Dissertation, Inner Mongolia Agricultural University, Hohhot, China, 2008. [Google Scholar]
- Li, Y.Q.; Yang, D.H.; Dao, J.; Wang, J.X. Inversion of main nutrient contents in red soil of mountain plain based on UAV multispectral remote sensing. J. Jiangxi Agric. Sci. 2021, 33, 63–67. [Google Scholar]
- Tao, P.F.; Wang, J.H.; Li, Z.Z.; Zhou, P.; Yang, J.J.; Gao, F.Q. Research on Inversion Models of Soil Nutrient Content Based on Hyperspectral Imaging. Geol. Resour. 2020, 29, 68–75+84. [Google Scholar]
- Thompson, L.J.; Puntel, L.A. Transforming unmanned aerial vehicle (UAV) and multispectral sensor into a practical decision support system for precision nitrogen management in corn. Remote Sens. 2020, 12, 1597. [Google Scholar] [CrossRef]
- Sáez-Plaza, P.; Michałowski, T.; Navas, M.J.; Asuero, A.G.; Wybraniec, S. An overview of the Kjeldahl method of nitrogen determination. Part I. Early history, chemistry of the procedure, and titrimetric finish. Crit. Rev. Anal. Chem. 2013, 43, 178–223. [Google Scholar]
- Maes, W.H.; Steppe, K. Perspectives for remote sensing with unmanned aerial vehicles in precision agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef]
- Jiachen, H.; Jing, H.; Gang, L.; Weile, L.; Zhe, L.; Zhi, L. Inversion analysis of soil nitrogen content using hyperspectral images with different preprocessing methods. Ecol. Inform. 2023, 78, 102381. [Google Scholar]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Support vector machines for classification and regression. Analyst 2010, 135, 230–267. [Google Scholar]
- Guo, J.; Wang, K.; Jin, S. Mapping of soil pH based on SVM-RFE feature selection algorithm. Agronomy 2022, 12, 2742. [Google Scholar] [CrossRef]
- Lyon, J.G.; Yuan, D.; Lunetta, R.S.; Elvidge, C.D. A change detection experiment using vegetation indices. Photogramm. Eng. Remote Sens. 1998, 64, 143–150. [Google Scholar]
- Dimkpa, C.; Bindraban, P.; McLean, J.E.; Gatere, L.; Singh, U.; Hellums, D. Methods for rapid testing of plant and soil nutrients. Sustain. Agric. Rev. 2017, 1–43. [Google Scholar]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote sensing algorithms for estimation of fractional vegetation cover using pure vegetation index values: A review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [PubMed]
- Wang, F.M.; Huang, J.F.; Tang, Y.L.; Wang, X.Z. New vegetation index and its application in estimating leaf area index of rice. Rice Sci. 2007, 14, 195. [Google Scholar]
- Zhao, W.; Ma, H.; Zhou, C.; Zhou, C.; Li, Z. Soil salinity inversion model based on BPNN optimization algorithm for UAV multispectral remote sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 6038–6047. [Google Scholar]
- Ju, C.; Chen, C.; Li, R.; Zhao, Y.; Zhong, X.; Sun, R.; Liu, T.; Sun, C. Remote sensing monitoring of wheat leaf rust based on UAV multispectral imagery and the BPNN method. Food Energy Secur. 2023, 12, e477. [Google Scholar]
- Manafifard, M. A new hyperparameter to random forest: Application of remote sensing in yield prediction. Earth Sci. Inform. 2024, 17, 63–73. [Google Scholar]
- Zhang, Z.; Liu, Z.; Guo, Y.; Han, J.; Li, Y. The application of partial least squares to Tibet's grassland biomass monitoring by remote sensing. Acta Agrestia Sin. 2009, 17, 735–739. [Google Scholar]
- Chen, L.; Huang, J.F.; Wang, F.M.; Tang, Y.L. Comparison between back propagation neural network and regression models for the estimation of pigment content in rice leaves and panicles using hyperspectral data. Int. J. Remote Sens. 2007, 28, 3457–3478. [Google Scholar]
- Wang, J.; Zhang, F.; Wang, Y.; Fu, Y.; Liang, Y. Identification of Salt Tolerance Genes in Rice from Microarray Data using SVM-RFE. In Proceedings of the 3rd International Conference on Bioinformatics and Computational Biology, New Orleans, LA, USA, 23–25 March 2011; pp. 30–35. [Google Scholar]
- Zhao, W.J.; Ma, F.F.; Ma, H.L. A Soil Salinity Inversion Model Based on UAV Multispectral Images. Trans. Chin. Soc. Agric. Eng. 2022, 38, 93–101. [Google Scholar]
- Guo, J.; Zhang, J.; Xiong, S.; Zhang, Z.; Wei, Q.; Zhang, W.; Feng, W.; Ma, X. Hyperspectral assessment of leaf nitrogen accumulation for winter wheat using different regression modeling. Precis. Agric. 2021, 22, 1634–1658. [Google Scholar]
- Li, W.; Zhu, X.; Yu, X.; Li, M.; Tang, X.; Zhang, J.; Xue, Y.; Zhang, C.; Jiang, Y. Inversion of nitrogen concentration in apple canopy based on UAV hyperspectral images. Sensors 2022, 22, 3503. [Google Scholar] [CrossRef]
- Wang, Q.L.; Li, S.; Lu, Y.L.; Peng, J.; Shi, Z.; Zhou, L.Q. Inversion of Nitrogen Content Based on a Large-Scale Soil Spectral Database. Acta Opt. Sin. 2014, 34, 308–314. [Google Scholar]
- Yang, F.; Li, R.; Feng, H.; Li, T.; Wang, G. Comparison of remote sensing inversion methods for winter wheat plant nitrogen content at different growth stages. J. Northeast. Agric. Sci. 2023, 48, 118–124. [Google Scholar]
- Laurin, G.V.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del Frate, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar]
- Liu, H.; Zhu, H.; Wang, P. Quantitative modelling for leaf nitrogen content of winter wheat using UAV-based hyperspectral data. Int. J. Remote Sens. 2017, 38, 2117–2134. [Google Scholar]





| Treatment | Before The Jointing Period | Jointing Period | Tasseling Period | Mature Stage | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Urea | Potassium Chloride | Urea Phosphate | Urea | Potassium Chloride | Urea Phosphate | Urea | Potassium Chloride | Urea Phosphate | Urea | Potassium Chloride | Urea Phosphate | |
| N1 | 21 | 9 | 14 | 105 | 94 | 40 | 172 | 43 | 53 | 13 | 0 | 0 |
| N2 | 20 | 95 | 158 | 7 | ||||||||
| N3 | 19 | 86 | 138 | 6 | ||||||||
| N4 | 17 | 75 | 122 | 4 | ||||||||
| Spectral Band | Center Wavelength/nm | Bandwidth/nm | Reflectance of Diffuse Reflector/% |
|---|---|---|---|
| Blue | 450 | 35 | 60 |
| Green | 555 | 25 | 60 |
| Red | 660 | 20 | 60 |
| Rededge1 | 720 | 10 | 60 |
| Rededge2 | 750 | 15 | 60 |
| Nir | 840 | 35 | 60 |
| Spectral Index | Formula | |
|---|---|---|
| Green Optimized Soil-Adjusted Vegetation Index | GOSAVI | GOSAVI = (NIR − G)/(NIR + G + 0.16) |
| Green Normalized Difference Vegetation Index | GNDVI | GNDVI = (NIR − G)/(NIR + G) |
| Greenness Difference Vegetation Index | GDVI | GDVI = NIR − G |
| Difference Vegetation Index | DVI | DVI = NIR − R |
| Chlorophyll Vegetation Index | CVI | CVI = (NIR × R)/G2 |
| Red Edge Chlorophyll Vegetation Index | CIRE | CIRE = (NIR/RE) − 1 |
| Green Soil-Adjusted Vegetation Index | GSAVI | GSAVI = 1.5[(NIR − G)/(NIR + G + 0.5)] |
| Modified Normalized Difference Index-Difference Vegetation Index | MNDI | MNDI = (NIR − RE)/(NIR − G) |
| Terrestrial Chlorophyll Index | MTCI | MTCI = (NIR − RE)/(RE − R) |
| Normalized Red Edge Index | NDRE | NDRE = (NIR − RE)/(NIR + RE) |
| Normalized Difference Vegetation Index | NDVI | NDVI = (NIR − R)/(NIR + R) |
| Normalized Near-Infrared Index | NNI | NNI = NIR/(NIR + RE + G) |
| Nitrogen Reflectance Index | NRI | NRI = (G − R)/(G + R) |
| Optimized Soil-Adjusted Vegetation Index | OSAVI | OSAVI = 1.16 × (NIR − R)/(NIR + R + 0.16) |
| Red Edge Normalized Difference Vegetation Index | RENDVI | RENDVI = (RE2 − RE1)(RE2 + RE1) |
| Soil-Adjusted Vegetation Index | SAVI | SAVI = 1.5(NIR − R)(NIR + R + 0.5) |
| Greening Rate Vegetation Index | GRVI | GRVI = NIR/G |
| Normalized Difference Red Edge | NREI | NREI = RE/(NIR + RE + G) |
| Plots | Period | Dataset | Sample | Max | Min | Mean | Standard Deviation | Variance | Coefficient of Variation |
|---|---|---|---|---|---|---|---|---|---|
| Silage corn | Seedling stage | Modeling set | 32 | 8.213 | 4.974 | 7.438 | 0.580 | 0.337 | 0.078 |
| Validation set | 16 | 8.060 | 5.346 | 7.138 | 0.397 | 0.630 | 0.088 | ||
| Total sample set | 48 | 8.213 | 4.975 | 7.292 | 0.629 | 0.393 | 0.126 | ||
| Jointing stage | Modeling set | 32 | 8.928 | 4.929 | 6.383 | 1.237 | 1.112 | 0.175 | |
| Validation set | 16 | 7.594 | 5.418 | 6.138 | 0.315 | 0.561 | 0.092 | ||
| Total sample set | 48 | 8.928 | 4.929 | 6.605 | 1.199 | 1.095 | 0.160 | ||
| Tasseling stage | Modeling set | 32 | 9.369 | 3.978 | 6.776 | 1.077 | 1.038 | 0.163 | |
| Validation set | 16 | 7.283 | 3.003 | 6.138 | 1.680 | 1.296 | 0.259 | ||
| Total sample set | 48 | 9.369 | 3.003 | 6.313 | 1.807 | 1.344 | 0.223 | ||
| Mature stage | Modeling set | 32 | 3.260 | 0.697 | 2.325 | 0.317 | 0.563 | 0.251 | |
| Validation set | 16 | 3.337 | 1.259 | 2.386 | 0.438 | 0.662 | 0.270 | ||
| Total sample set | 48 | 3.337 | 0.697 | 2.345 | 0.701 | 0.491 | 0.344 |
| Ranking | Seedling Stage | Jointing Stage | Tasseling Stage | Mature Stage |
|---|---|---|---|---|
| 1 | rededge2 | DVI | CVI | GDVI |
| 2 | SAVI | GDVI | GRVI | GOSAVI |
| 3 | NNI | green | rededge2 | GSAVI |
| 4 | OSAVI | GOSAVI | NREI | NDVI |
| 5 | GNDVI | OSAVI | NNI | DVI |
| 6 | nir | SAVI | blue | NRI |
| 7 | NDRE | GSAVI | NDRE | nir |
| 8 | GOSAVI | rededge2 | GNDVI | SAVI |
| 9 | DVI | CVI | nir | OSAVI |
| 10 | GSAVI | GRVI | CIRE | RENDVI |
| 11 | GDVI | NDRE | rededge1 | rededge2 |
| 12 | GRVI | NREI | red | GRVI |
| 13 | CIRE | NDVI | MNDI | CIRE |
| 14 | rededge1 | rededge1 | RENDVI | NREI |
| 15 | NREI | nir | green | NDRE |
| 16 | NRI | MTCI | MTCI | MTCI |
| 17 | CVI | NNI | NDVI | CIRE |
| 18 | MNDI | MNDI | GOSAVI | NNI |
| Variable Name | The VIP Fraction at the Seedling Stage | Whether the 1 Is Satisfied | VIP Scores in the Jointing Period | Whether the 1 Is Satisfied | VIP Fraction During Male Phase | Whether the 1 Is Satisfied | VIP Scores at the Maturation Stage | Whether the 1 Is Satisfied |
|---|---|---|---|---|---|---|---|---|
| GOSAVI | 1.032 | Yes | 1.242 | Yes | 1.250 | Yes | 1.036 | Yes |
| GNDVI | 1.143 | Yes | 1.083 | Yes | 1.208 | Yes | 1.179 | Yes |
| GDVI | 1.025 | Yes | 1.047 | Yes | 0.904 | No | 1.154 | Yes |
| DVI | 0.648 | No | 0.771 | No | 0.873 | No | 0.989 | No |
| CVI | 0.366 | No | 0.572 | No | 0.578 | No | 0.438 | No |
| CIRE | 1.135 | Yes | 0.889 | No | 1.284 | Yes | 0.876 | No |
| GSAVI | 1.130 | Yes | 1.025 | Yes | 1.085 | Yes | 1.274 | Yes |
| MNDI | 1.149 | Yes | 1.138 | Yes | 1.233 | Yes | 0.898 | No |
| MTCI | 1.120 | Yes | 1.180 | Yes | 0.695 | No | 1.311 | Yes |
| NDRE | 1.263 | Yes | 1.373 | Yes | 0.841 | Yes | 1.098 | Yes |
| NDVI | 1.212 | Yes | 1.352 | Yes | 1.226 | Yes | 1.426 | Yes |
| NNI | 0.594 | No | 0.457 | No | 0.086 | No | 0.768 | No |
| NRI | 0.641 | No | 0.598 | No | 0.748 | No | 0.725 | No |
| OSAVI | 1.038 | Yes | 0.943 | No | 1.039 | Yes | 0.784 | No |
| RENDVI | 0.639 | No | 0.675 | No | 0.590 | No | 0.681 | No |
| SAVI | 1.006 | Yes | 0.891 | No | 1.029 | Yes | 1.320 | Yes |
| GRVI | 0.734 | No | 0.877 | No | 0.871 | No | 0.544 | No |
| NREI | 1.185 | Yes | 0.915 | No | 0.720 | Yes | 0.694 | No |
| red | 0.665 | No | 0.463 | No | 0.674 | No | 0.496 | No |
| rededge1 | 1.109 | Yes | 1.288 | Yes | 1.285 | Yes | 1.242 | Yes |
| rededge2 | 1.128 | Yes | 0.894 | No | 1.138 | Yes | 0.785 | No |
| nir | 1.305 | Yes | 1.182 | Yes | 1.052 | Yes | 1.351 | yes |
| green | 0.876 | No | 1.066 | Yes | 1.007 | Yes | 0.849 | No |
| blue | 0.547 | No | 0.472 | No | 0.449 | No | 0.561 | No |
| Variable Name | Gray Seedling Association (GCD) | Whether GCD 0.8 Is Met | Pull Gray Correlation (Gcd) | Whether GCD 0.8 Is Met | Grey Grey Correlation (GCD) | Whether GCD 0.8 Is Met | MatMatcorrelation (GCD) | Whether GCD 0.8 Is Met |
|---|---|---|---|---|---|---|---|---|
| GOSAVI | 0.55 | No | 0.74 | No | 0.6 | No | 0.81 | Yes |
| GNDVI | 0.88 | Yes | 0.84 | Yes | 0.97 | Yes | 0.82 | Yes |
| GDVI | 0.82 | Yes | 0.87 | Yes | 0.84 | Yes | 0.72 | No |
| DVI | 0.68 | No | 0.71 | No | 0.71 | No | 0.78 | No |
| CVI | 0.46 | No | 0.52 | No | 0.48 | No | 0.49 | No |
| CIRE | 0.79 | No | 0.89 | Yes | 0.83 | Yes | 0.76 | No |
| GSAVI | 0.74 | No | 0.71 | No | 0.66 | No | 0.84 | Yes |
| MNDI | 0.51 | No | 0.70 | No | 0.73 | No | 0.68 | No |
| MTCI | 0.47 | No | 0.77 | No | 0.65 | No | 0.71 | No |
| NDRE | 0.9 | Yes | 0.85 | Yes | 0.88 | Yes | 0.83 | Yes |
| NDVI | 1.15 | Yes | 1.31 | Yes | 1.26 | Yes | 1.28 | Yes |
| NNI | 0.53 | No | 0.57 | No | 0.49 | No | 0.54 | No |
| NRI | 0.66 | No | 0.68 | No | 0.72 | No | 0.65 | No |
| OSAVI | 0.78 | No | 1.28 | Yes | 1.04 | Yes | 0.77 | No |
| RENDVI | 0.49 | No | 0.75 | No | 0.63 | No | 0.73 | No |
| SAVI | 0.45 | No | 0.75 | No | 0.68 | No | 0.63 | No |
| GRVI | 0.55 | No | 0.67 | No | 0.60 | No | 0.70 | No |
| NREI | 0.47 | No | 0.75 | No | 0.72 | No | 0.73 | No |
| red | 0.72 | No | 0.63 | No | 0.69 | No | 0.55 | No |
| rededge1 | 0.87 | Yes | 0.88 | Yes | 0.84 | Yes | 0.81 | Yes |
| rededge2 | 0.86 | Yes | 0.94 | Yes | 0.85 | Yes | 0.72 | No |
| nir | 0.89 | Yes | 0.82 | Yes | 0.8 | Yes | 0.82 | Yes |
| green | 0.31 | No | 0.66 | No | 0.81 | No | 0.69 | No |
| blue | 0.47 | No | 0.72 | No | 0.64 | No | 0.68 | No |
| Plots | Machine Learning Model | Growth Period | Validation Set | |||
|---|---|---|---|---|---|---|
| Before Screening | After Screening | |||||
| R2 | RMSE | R2 | RMSE | |||
| Silage corn | BPNN | Seedling stage | 0.362 | 1.280 | 0.465 | 1.231 |
| Jointing stage | 0.372 | 0.617 | 0.394 | 0.681 | ||
| Tasseling stage | 0.417 | 0.522 | 0.465 | 0.552 | ||
| Mature stage | 0.439 | 0.529 | 0.480 | 0.494 | ||
| RF | Seedling stage | 0.409 | 1.135 | 0.481 | 1.251 | |
| Jointing stage | 0.405 | 0.599 | 0.430 | 0.542 | ||
| Tasseling stage | 0.434 | 0.503 | 0.490 | 0.480 | ||
| Mature stage | 0.493 | 0.495 | 0.539 | 0.463 | ||
| PLSR | Seedling stage | 0.500 | 0.967 | 0.552 | 0.952 | |
| Jointing stage | 0.416 | 0.474 | 0.458 | 0.452 | ||
| Tasseling stage | 0.581 | 0.420 | 0.630 | 0.349 | ||
| Mature stage | 0.608 | 0.379 | 0.663 | 0.281 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yan, J.; Li, G.; Ma, W.; Yao, X.; Li, J.; Da, Q.; Li, X.; Cheng, K. Inversion Model for Total Nitrogen in Rhizosphere Soil of Silage Corn Based on UAV Multispectral Imagery. Drones 2025, 9, 270. https://doi.org/10.3390/drones9040270
Yang H, Yan J, Li G, Ma W, Yao X, Li J, Da Q, Li X, Cheng K. Inversion Model for Total Nitrogen in Rhizosphere Soil of Silage Corn Based on UAV Multispectral Imagery. Drones. 2025; 9(4):270. https://doi.org/10.3390/drones9040270
Chicago/Turabian StyleYang, Hongyan, Jixuan Yan, Guang Li, Weiwei Ma, Xiangdong Yao, Jie Li, Qihong Da, Xuchun Li, and Kejing Cheng. 2025. "Inversion Model for Total Nitrogen in Rhizosphere Soil of Silage Corn Based on UAV Multispectral Imagery" Drones 9, no. 4: 270. https://doi.org/10.3390/drones9040270
APA StyleYang, H., Yan, J., Li, G., Ma, W., Yao, X., Li, J., Da, Q., Li, X., & Cheng, K. (2025). Inversion Model for Total Nitrogen in Rhizosphere Soil of Silage Corn Based on UAV Multispectral Imagery. Drones, 9(4), 270. https://doi.org/10.3390/drones9040270





