Performance Analysis and Flow Mechanism of Close-Range Overlapping Rotor in Hover

Abstract

High payload capacity multi-rotor aerial vehicles are typically configured with multiple propellers to achieve the required aerodynamic lift. However, this design approach often results in an increased overall dimensional envelope, which introduces significant operational limitations in confined spatial environments such as urban airspace. By utilizing a limited overlap rotor configuration, the spatial utilization rate of an aircraft can be greatly improved, ensuring a sufficient thrust of rotor while simultaneously reducing the size of the aircraft. However, the slipstreams of two rotors overlap, which may create a significant aerodynamic interface. This paper utilizes numerical simulation based on the unsteady RANS (Reynolds-averaged Navier–Stokes) method to analyze the influence of parameters such as distance, blade distance, and rotation direction on the interference flow field of overlapping rotors. Research indicates that aerodynamic interference only affects the overlapping area between two rotors at the inner blade, leading to the offset of loading distribution on the blade, which can be explained by the slipstream effect, suction effect, and induced effects generated by two rotors. As the axis distance between two rotors decreases, the strengthening of the slipstream and suction effects leads to a rapid decrease in the aerodynamic efficiency of the two rotors. When the blade between the two rotors increases, the weakening of the suction effect and induced effects causes the load on the lower rotor to translate to the upper rotor. Moreover, the variation in the spatial distribution of the blade tip–vortex leads to blade–vortex interaction, which causes a change in the spanwise distribution of the load on the lower blade.

1. Introduction

As urban areas rapidly expand, the traditional transportation industry faces severe congestion problems. High-load multi-rotor aircraft with vertical takeoff and landing capabilities have great potential to improve the current urban transportation environments [1,2,3]. In order to maximize the payload capacity of multi-rotor aircraft, such aircraft are usually designed with an adequate quantity and dimension of rotors. Furthermore, multi-rotor aircraft design often considers the installation spacing between adjacent rotors, aiming to minimize their aerodynamic interactions. Although a relatively sufficient installation spacing can effectively control the aerodynamic interference between neighboring rotors, it significantly increases the aircraft’s dimensions, thereby causing problems such as larger flight site requirements and higher operational expenses. In recent years, multi-rotor aircraft with a limited overlapping rotor arrangement design have been proposed and developed to address the above problems. Due to this limited overlapping rotor arrangement design only requiring a limited height difference between adjacent rotors, space utilization efficiency is greatly improved. In addition, the partially overlapped rotor disks lead to an apparent decrease in the covering radius of the complete rotor array. However, aerodynamic interference occurs when the upper and lower rotor blades cross over, negatively impacting rotor performance [4,5]. Thus, it is crucial to investigate the flow field and unsteady air loads of overlapping rotors for the operational of safety multi-rotor aircraft.

As a critical design case of the overlapping rotor arrangement, the coaxial rotor layout has received much attention from researchers due to its excellent space utilization and torque self-balancing characteristics. Relevant rotor investigations primarily relied on experimental methods in the early stages. For instance, Harrington [6] quantified the fluctuations in the aerodynamic forces of different rotors arranged in a coaxial configuration, thereby generating significant empirical data. Lakshminarayan and Baeder [7] utilized a numerical simulation method based on a Reynolds-averaged Navier–Stokes (RANS) solver to simulate the Harington coaxial rotor model and summarize the coaxial rotors’ aerodynamic characteristics. Their findings indicated that the downwash from the upper rotor affected the lower blades, which caused a significant decrease in aerodynamic efficiency. Jeongwoo Ko [8] studied the wake vortex of coaxial rotors using high-resolution tracing methods. The study examined the interference mechanism between rotor blades and rotor tip vortices. In addition, the rotors’ wake instability with different rotor spacings was analyzed. Uehara [9] analyzed the aerodynamic performance differences between same-rotation and counterrotation coaxial rotor configurations. The study summarized the offset angles’ impact on the aerodynamic performance of each rotor and wake vortex in detail. Furthermore, some studies [10,11,12] reported that the interaction between the blade tip vortexes of the top rotor and the lower blade may cause extra structural vibrations and aerodynamic noise concerns.

The tandem helicopter design, similar to the coaxial rotor configuration design, also involves the aerodynamic interference problem between adjacent rotors. For instance, Pruyn and Alexander [13] conducted tests on an Army CH-47A helicopter to investigate the thrust characteristics of tandem rotors under different flying conditions. The study results revealed the effect of rotor tip vortexes on the nearby rotors’ local blade tip loads. Harris [14] designed wind tunnel experiments to quantify the hover aerodynamic characteristics of tandem rotors. Meanwhile, an engineering approximation method was proposed to quickly calculate the hover performances of tandem rotors with different overlap factors between the two rotors. Mantas Brazinskas [15] designed and built a small-scale experimental setup to examine how the overlap factor impacts small rotors’ thrust and power characteristics. Zhou [16] investigated the effect of lateral separation between a small, unmanned aircraft’s propellers in hover conditions. Shukla and Komerath [17] utilized the particle image velocimetry (PIV) technique to investigate the interacting wake of a side-by-side configuration between two rotors in hover conditions.

In addition to experimental methods, computational fluid dynamics (CFD) tools are also effective in studying aerodynamic interference problems between rotors. In recent years, many scholars have successively developed mid-fidelity aerodynamic solvers to design multi-rotor aircraft. Tan [18,19] employed a vortex-based approach to investigate the flow field characteristics and unsteady aerodynamic loads of tandem rotors. Alvarez [20,21,22] validated the accuracy of models used for evaluating the aerodynamic interactions between rotors in different configurations, such as side-by-side, quadrotor, and so on. Algarotti and Zanotti [23] analyzed the aerodynamic characteristics of a multi-rotor aircraft’s overlapping rotors by using PIV tests and the vortex panel method (VPM). Cao [24] developed a novel actuator disk load prediction model based on the blade element momentum theory and achieved a high-precision and efficient simulation of the slipstream of the rotors. Siddhant Desai [25] investigated the efficacy of the Virtual Blade Model (VBM) in predicting the aerodynamic performance characteristics of propellers in different conditions, which was validated through comparative analysis with experimental measurements. Chankyu Son [26] developed a novel actuator disk model (ADM) coupled with lifting-line theory, which overcame the limitations of conventional ADMs in accurately describing the tip loss correction of rotor tip vortices. However, most of these studies focused on the aerodynamic performance of rotors with a greater axis distance, and it is difficult for these approaches to accurately capture blade–vortex interactions when the rotors are close to each other.

Although a series of research papers have successively reported the aerodynamic interference mechanisms between rotors, the study objects of these papers mainly refer to side-by-side rotors and coaxial rotors. Additionally, most papers still utilize experimental methods to investigate the aerodynamic interference mechanisms between rotors. Namely, there is a lack of CFD modeling for investigating the aerodynamic interference problems (e.g., blade–vortex interactions and load offset on the blade) in overlapping rotor configurations, which are hard to solve by employing experimental methods. Therefore, the present paper utilized the sliding mesh methodology and unsteady RANS method to calculate rotors’ load distribution and the vortex structures between blades. The paper’s primary purpose was to investigate the flow field characteristics and interference mechanisms between the blades of overlapping rotors under different conditions, aiming to guide the design of multi-rotor aircraft with an overlapping rotor arrangement.

The remainder of this paper is organized as follows: Section 2 introduces the research object and defines the operating conditions. Section 3 presents numerical methods and verifies their reliability. Section 4 analyzes the flow field characteristics and aerodynamic load distributions of the overlapping rotors under different conditions in detail. Appendix A provides the definitions of parameter symbols employed in the present study.

2. Materials and Methods

2.1. Governing Equations

The three-dimensional RANS equations with conserved integral forms are solved in the inertial coordinate system to obtain the unsteady flow field characteristics near overlapping rotors. In one control volume, the RANS equations can be written as follows:

$$\frac{\partial }{\partial t}{\displaystyle \underset{V}{\iiint }}\mathit{W}dV+{\displaystyle \underset{S}{\iint }}\left({\mathit{F}}_{\mathit{C}}-{\mathit{F}}_v\right)\cdot \mathit{n}dS=0$$

(1)

$$\mathit{n}={\left[\begin{array}{lll}{\mathit{n}}_x\hfill & {\mathit{n}}_y\hfill & {\mathit{n}}_z\hfill \end{array}\right]}^T$$

(2)

$${\mathit{F}}_{\mathit{C}}=\left[\begin{array}{c}\rho {\mathit{V}}_r\\ \rho u{\mathit{V}}_r+{\mathit{n}}_{x}p\\ \rho v{\mathit{V}}_r+{\mathit{n}}_{y}p\\ \rho w{\mathit{V}}_r+{\mathit{n}}_{z}p\\ \rho H{\mathit{V}}_r+{\mathit{V}}_{t}p\end{array}\right]$$

(3)

where S and V represent the surface area and volume of the control volume, respectively. r and p denote the density and pressure of airflow, respectively. E is the total energy and H is the total enthalpy per unit mass. u, v, and w are the cartesian velocity components. ${\mathit{V}}_r$ is the relative velocity between the blade and the flow field, and ${\mathit{V}}_t$ is the relative velocity of a mesh unit. The elements of vector $\mathit{W}={\left[\rho ,\rho u,\rho v,\rho w,\rho H\right]}^T$ denote conservative variables. $\mathit{n}$ is the surface normal vector of the control element. The vectors ${\mathit{F}}_{\mathit{C}}$ and ${\mathit{F}}_{\mathit{v}}$ denote the inviscid and viscous fluxes, respectively.

To balance accuracy and computational cost, the Shear Stress Transport (SST) k-ω model is used for fully turbulent computations in this paper. The upwind spatial differencing technique is employed to solve both the convection and pressure factors. The central differencing strategy is used to solve the viscosity term. Precision of the second order is preserved in both the spatial and temporal dimensions. In order to achieve precise time accuracy in an unsteady flow field, the dual-time step method is utilized for temporal integration [27]. The sub-iteration of the pseudo time step is set to 10. Assuming that the physical time step is set to 360 in one resolution of the rotor, each time interval corresponds to an azimuth angle of 1 degree.

2.2. Boundary Condition and Mesh Generation

The sliding mesh method is employed to describe the complicated rotational movements of two overlapping rotors (Figure 1). The computational domain consists of stationary and rotational regions. The stationary regions include closed-field and far-field regions. The multi-block structured mesh method is employed in the rotational and far-field regions to enhance the mesh quality. In addition, unstructured tetrahedral meshes are generated adaptively between the two overlapping rotors in the closed-field region. The total number of volume meshes is approximately 48 million. The stationary and rotational regions correspond to 24 million and 14 million grid cells, respectively. Each rotor blade’s boundary layer comprises 25 mesh layers, with a first-layer height of 5×10c (c denotes the chord length at a position of 0.75R along the rotor blade). This design assures that most of the mesh points on the rotor surface have a y+ value less than 10. Furthermore, the meshes in the propellers’ slipstream regions and rotor blade tip areas are refined to capture the flow field information accurately (Figure 2).

2.3. Validation

This paper selected a standard single-rotor model with a rotating speed of 2100 revolutions per minute (RPM) as the validation model. The boundary condition setup, mesh generation method, and calculation method selection for the validation model follow the introduction in Section 3.1 and Section 3.2. Furthermore, three sets of the coarse, medium, and fine meshes were, respectively, generated, aiming to study the influence of mesh quantity on the single-rotor model’s thrust and torque (

Table 1. Mesh convergence validations for a standard single-rotor configuration.

Type	Number of Overall Grid (×106)	Thrust/N	Torque/N·m
Coarse	15.04	538.9	35.10
Medium	28.36	539.4	35.21
Fine	49.96	539.6	35.24

). The medium-mesh model was selected as the calculation mesh model for the standard single-rotor model. As shown in Table 1, an increase in the mesh quantity caused almost no significant changes in the computed thrust or torque values of the standard single-rotor model. Thus, it can be concluded that the selected mesh model can simultaneously satisfy accuracy requirements and calculation efficiency.

A validation experiment was carried out to measure the force characteristics of a coaxial rotor system with two blades, aiming to validate the boundary setup, mesh generation, and numerical method described in the preceding paragraphs [28].

Figure 3a illustrates the configuration of the experimental setup utilized in this study. A pair of coaxial rotors, each with a radius of 0.8 m, are mounted on a sliding base and connected to DC motors, with the spacing between the two rotors set at 0.35 m. Each rotor is independently controlled by electronic speed controllers, and their rotational speeds are monitored using optical tachometers. The aerodynamic loads acting on each rotor are measured through thrust and torque sensors. Figure 3b presents the specifications for blade geometry, including the twist distribution, chord distribution, and airfoil profiles of the rotor blades.

Figure 4 illustrates a comparison of the thrust and torque on each rotor at different rotational speeds, based on numerical calculations and experimental data. By conducting a comparison between the experimental data and the computational fluid dynamics (CFD) results, the thrust can be properly calculated, with maximum errors of 3% and 2% for the upper and lower rotors. The torque of each rotor computed through CFD has a maximum error of 3% for the upper rotor and 8% for the lower rotor. The relative error is a result of the deformation of blades during the experiment, which is not taken into account in the simulation. Essentially, the simulator employed in this study has the ability to accurately analyze the aerodynamic performance of a coaxial rotor system.

3. Results and Discussions

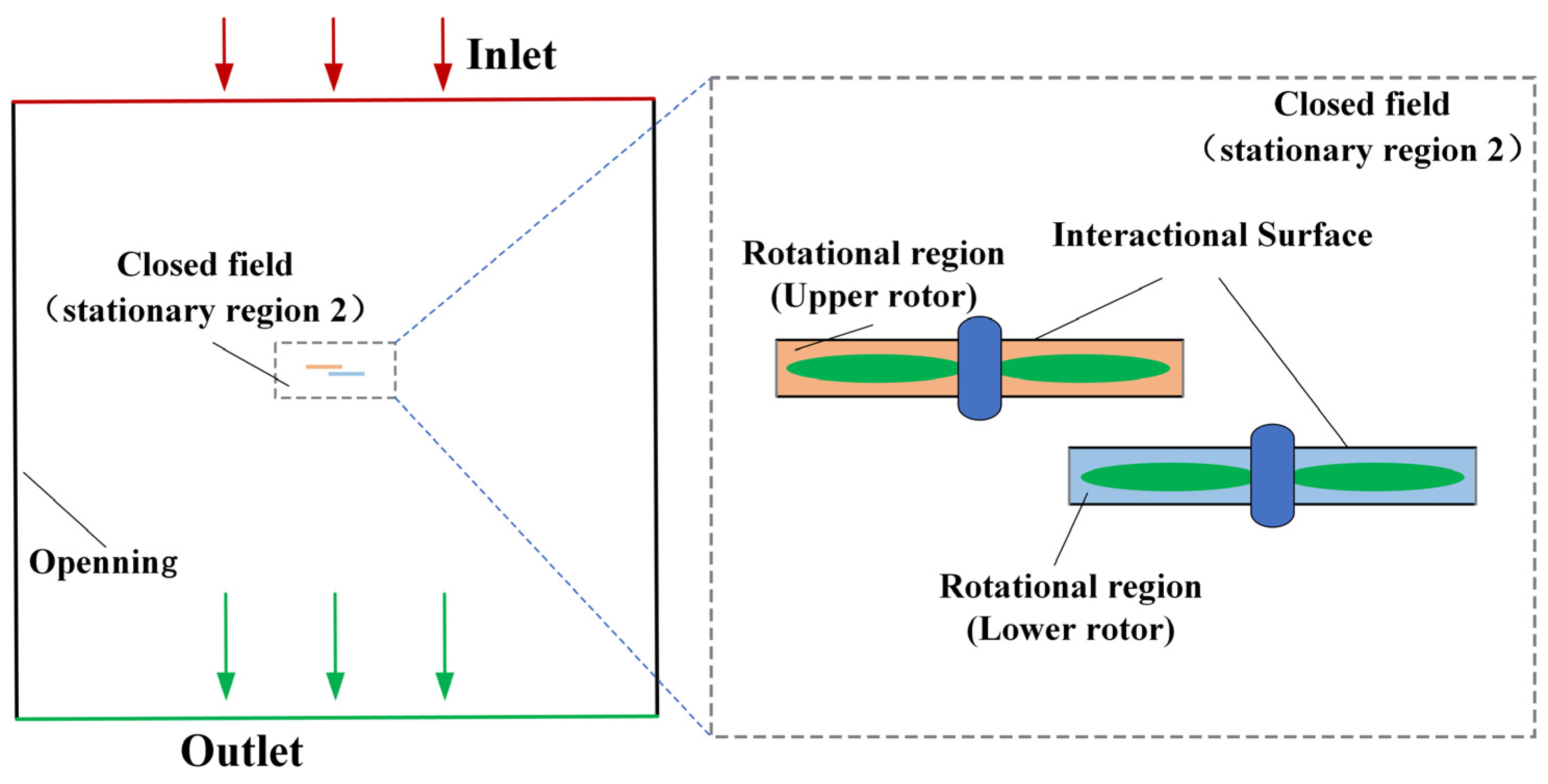
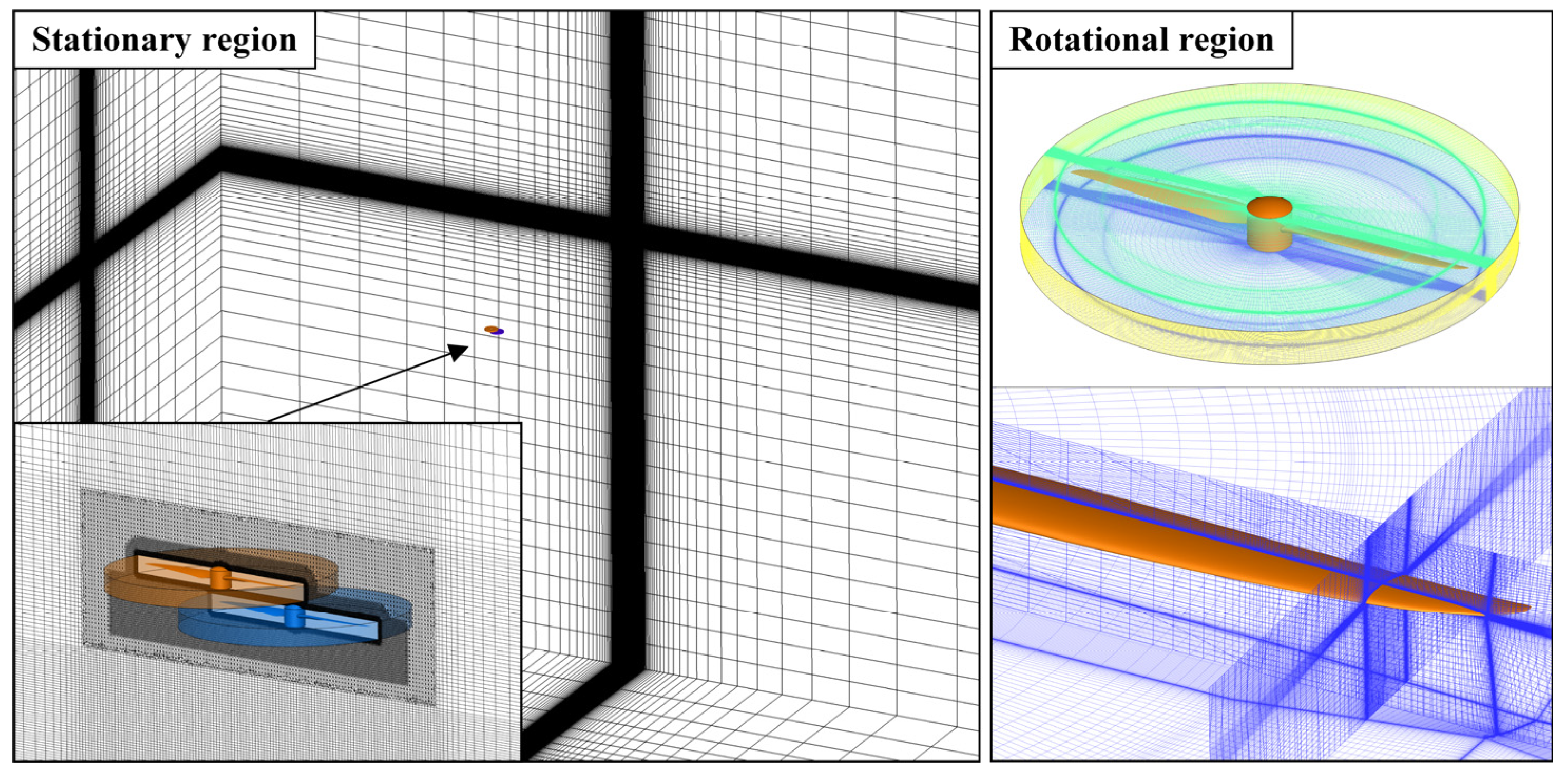
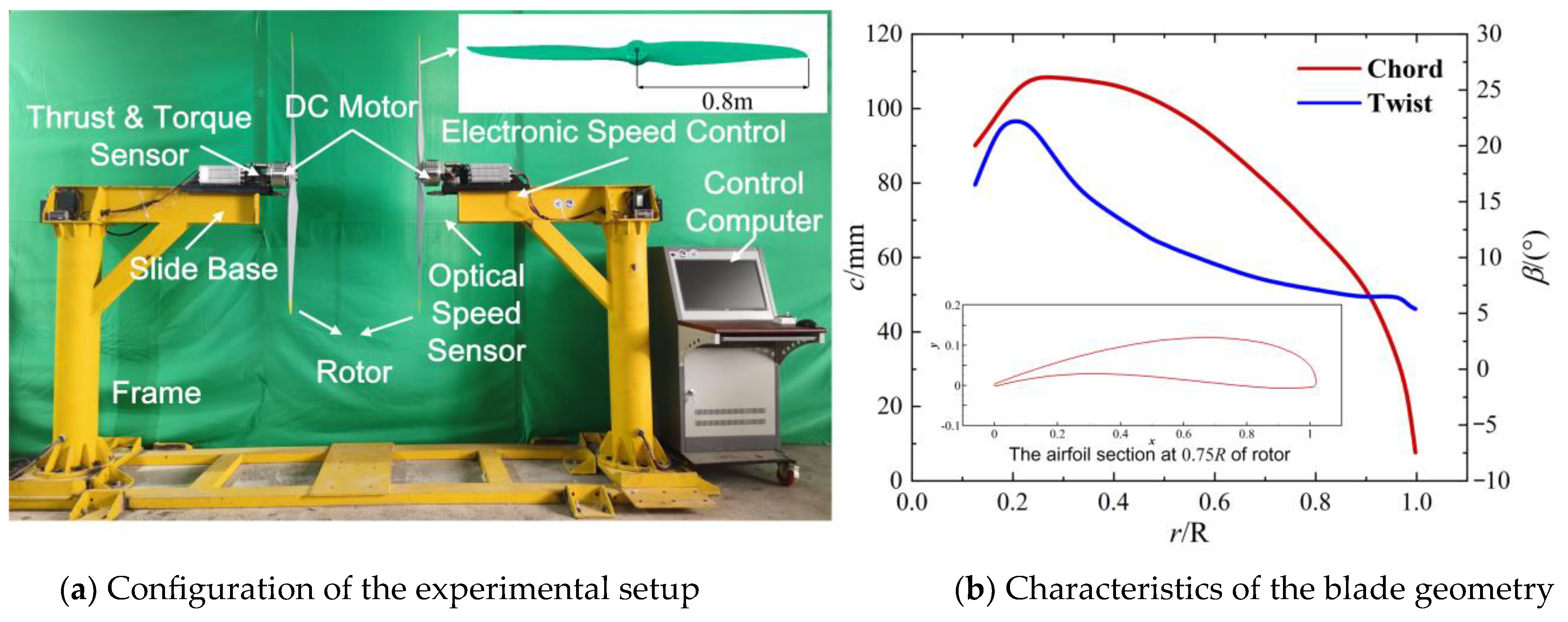
3.1. Aerodynamic Interaction of the Overlapping Rotor

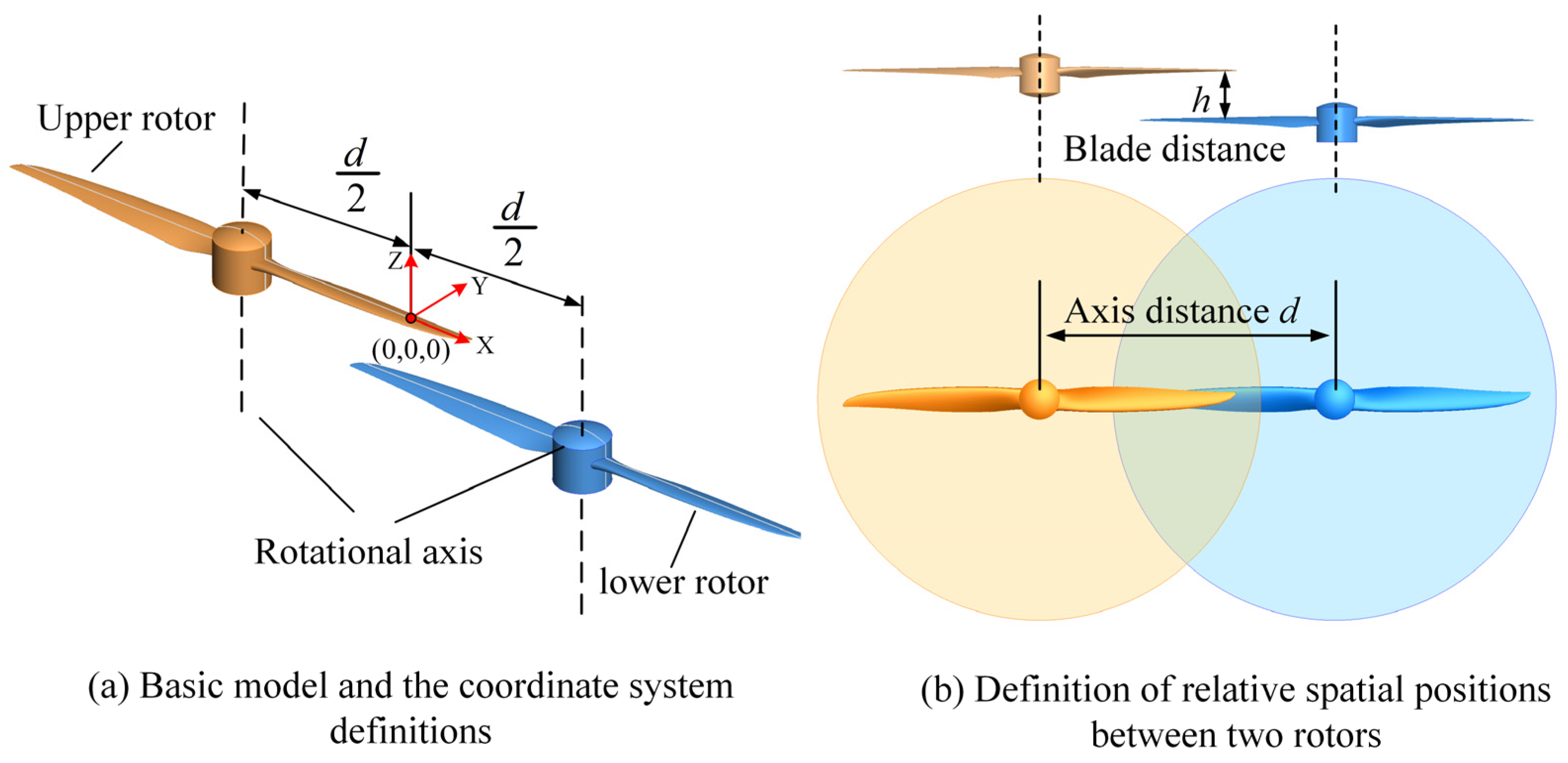
When viewed from above, the basic model of two rotors organized in an overlapping configuration is refined, as seen in Figure 5. In the coordinate system, the Z-axis is defined as the axis of rotation, while the X-axis is defined as the direction of the initial phase expansion of the rotor. Subsequently, in accordance with the right-hand rule, the direction of the Y-axis in the coordinate system can be defined. The origin of the coordinate system is defined to be situated along the horizontal plane of the upper rotor, precisely at the midway of the rotational axis between the two rotors. Figure 5b defines the blade distance, h, as the axial distance between two rotor blades, and the axis distance, d, as the spanwise distance between the rotating axis of two rotors. Divided by the diameter D of the rotor, the axis distance and blade distance can be expressed by the dimensionless parameters d/D and h/D.

The analysis of the aerodynamic interaction mechanism is conducted with the overlapping rotors in hover states. The axis distance d/D between the two rotors is set as 0.75 and each rotor has half a blade in the overlapping area (r/R is larger than 0.5, r is the distance from the location to the rotational axis, and R is the radius of the rotor). The blade distance h/D is set as 0.156 and the rotational velocity for the two rotor blades of the overlapping rotor configuration is set as 2100 RPM.

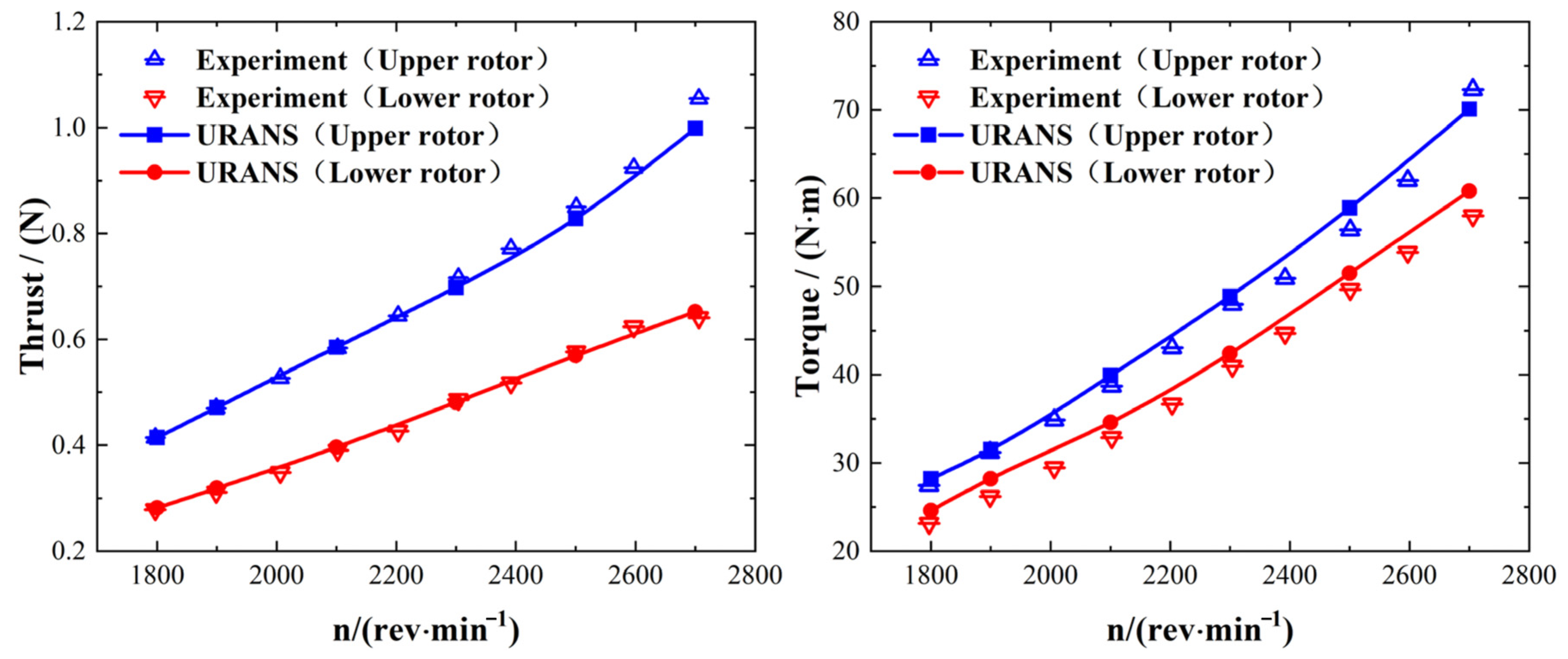
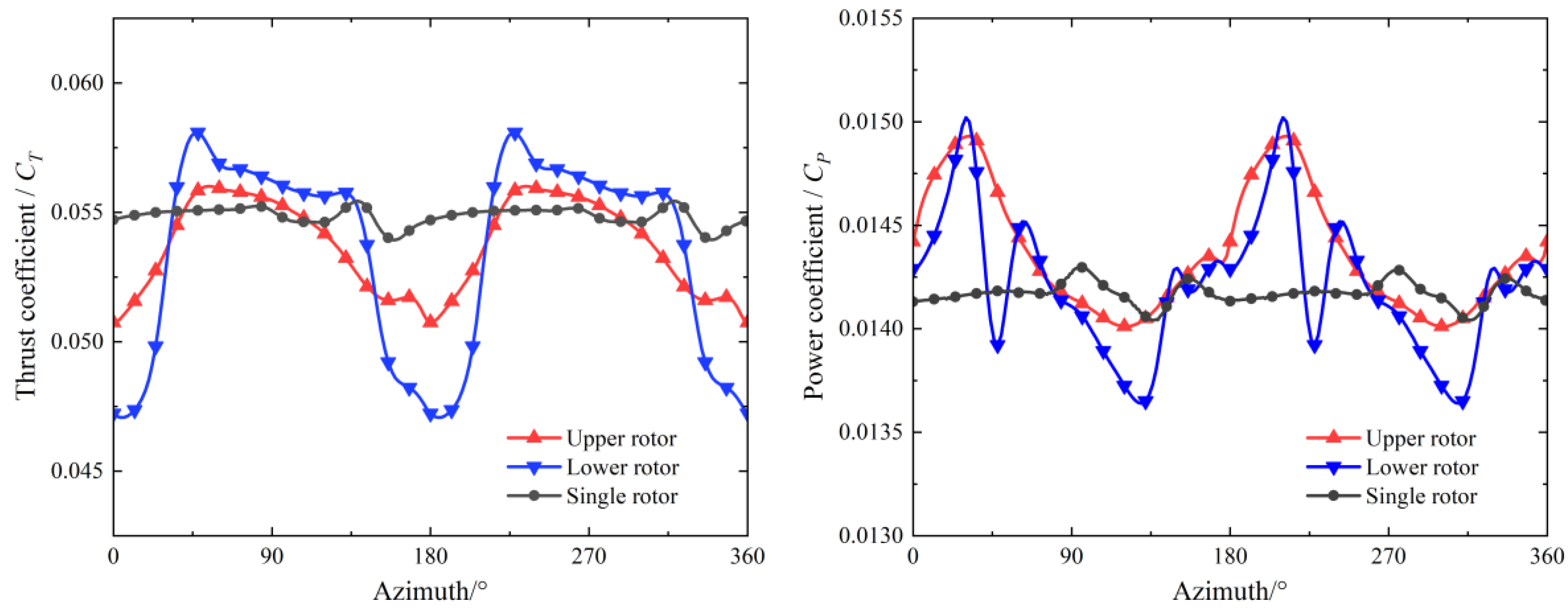
Figure 6 shows the temporal performances of the overlapping rotor and single-rotor configurations. The single-rotor configuration corresponds to the upper rotor without the lower rotor’s interference. From Figure 6, both the thrust coefficients (C_T) and power coefficients (C_P) for both the upper and lower rotors of the overlapping rotor configuration exhibit periodic fluctuations as the azimuth angle increases. In contrast, the C_T and C_p of the single-rotor configuration nearly maintain a flat trend, with an azimuth angle range of 0–360°.

Both C_T and C_P show periodic unsteady fluctuations, while the single rotor nearly stays stable. As seen in Figure 6, the C_T values of the upper and lower rotors rapidly decrease when the blade approaches and increase again. The fluctuation in the C_T of the lower rotor is much larger than that of the upper rotor. Moreover, another small fluctuation appears on the trough of the curve where the blades meet. This aerodynamic interference is because the slipstream and attached vortex of the blade influence the positive attack angle of the other rotor. The mechanism analysis of the overlapping rotor configuration primarily considers suction, slipstream, and induced effects, which can be explained as follows.

As Figure 7 shows, the meeting of the two rotors’ blades can be approximated by two airfoils moving in opposite directions. When the two rotor blades meet in the overlapping area, the suction and slipstream effects induce additional axial velocities in the upper and lower blades, decreasing their thrust by decreasing their actual attack angles. When the two rotor blades approach each other, the induced velocity produced by the attached vortex on each blade will alter the flow field around the neighboring rotor blade. Additionally, the relative position variation of the two rotor blades causes changes in the strengths of the induced effects. When two blades meet but do not coincide, the attached vortex on a blade induces upside flow and leads to an increase in thrust on the other blade. As the blade elements of the two counterrotating rotors transition from a state of crossing to moving apart, the induced flow reverses direction, thereby altering the aerodynamic interference effects and ultimately resulting in significant unsteady variations in the thrust and torque distributions across the upper and lower rotor blade elements.

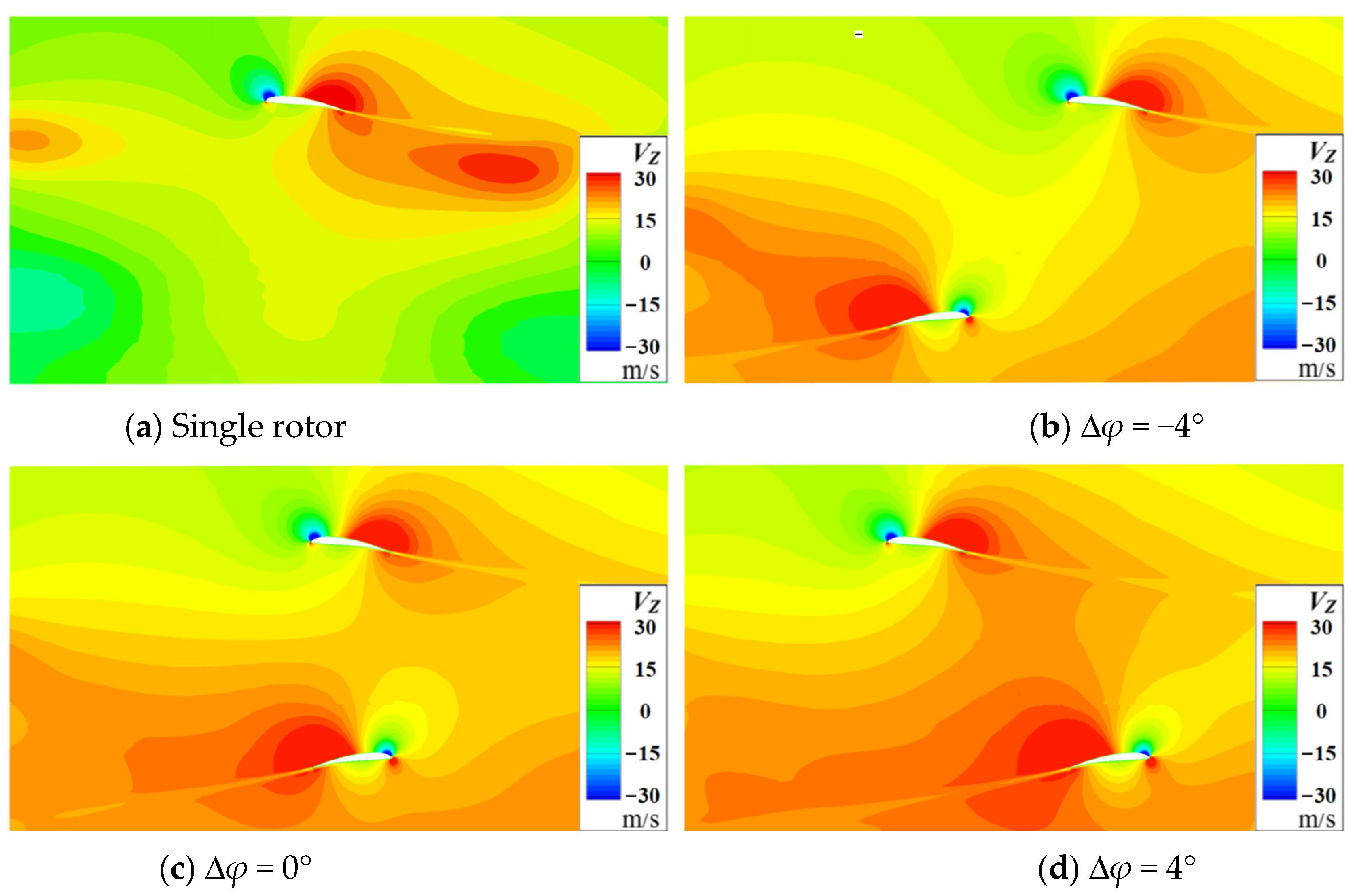
Figure 8 gives the Vz contours of 0.75R sections for the overlapping rotors and the single rotor. For the single rotor, the section is located at 0.75R of a blade, and for the overlapping system, this is the blade within the overlapping area. As shown in Figure 8a, an upwash flow is induced ahead of the leading edge of the single rotor and a strong downwash flow is induced behind the trailing edge. As shown in Figure 8b–d, when the two blades approach each other, the upwash of the upper and the lower blades meet together. Each blade is under the upwash of another blade, so the thrust of each rotor will increase. When the blades move away, each blade lies in the downwash of another blade, so the interaction between two blades changes to be the opposite. Moreover, the induced upwash flow around two blades only appears in a small region. This means the interaction between two rotors caused by induced effects is weak. However, the downwash flow is also influenced by the slipstream effect, resulting in a stronger Vz between the two blades. As the lower rotor is under the wake of the upper rotor, the downwash interaction on the lower rotor is stronger than that of the upper rotor.

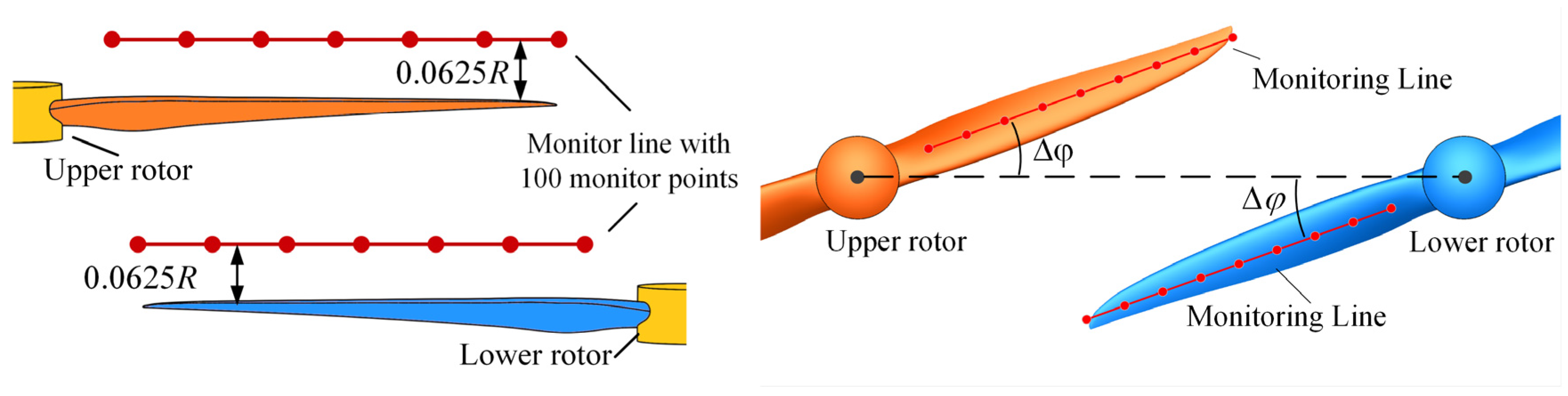
As Figure 9 shows, each monitor line is arranged above the upper and lower rotor blades with a distance of 0.0625R, and 100 monitor points are evenly distributed on each line. The gap angle between the monitor line and the line where the two blades of each rotor will meet is defined as the Dφ. When the two blades do not meet, the value of angle Dφ is negative. When the two blades move away from each other, the angle Dφ changes to be positive.

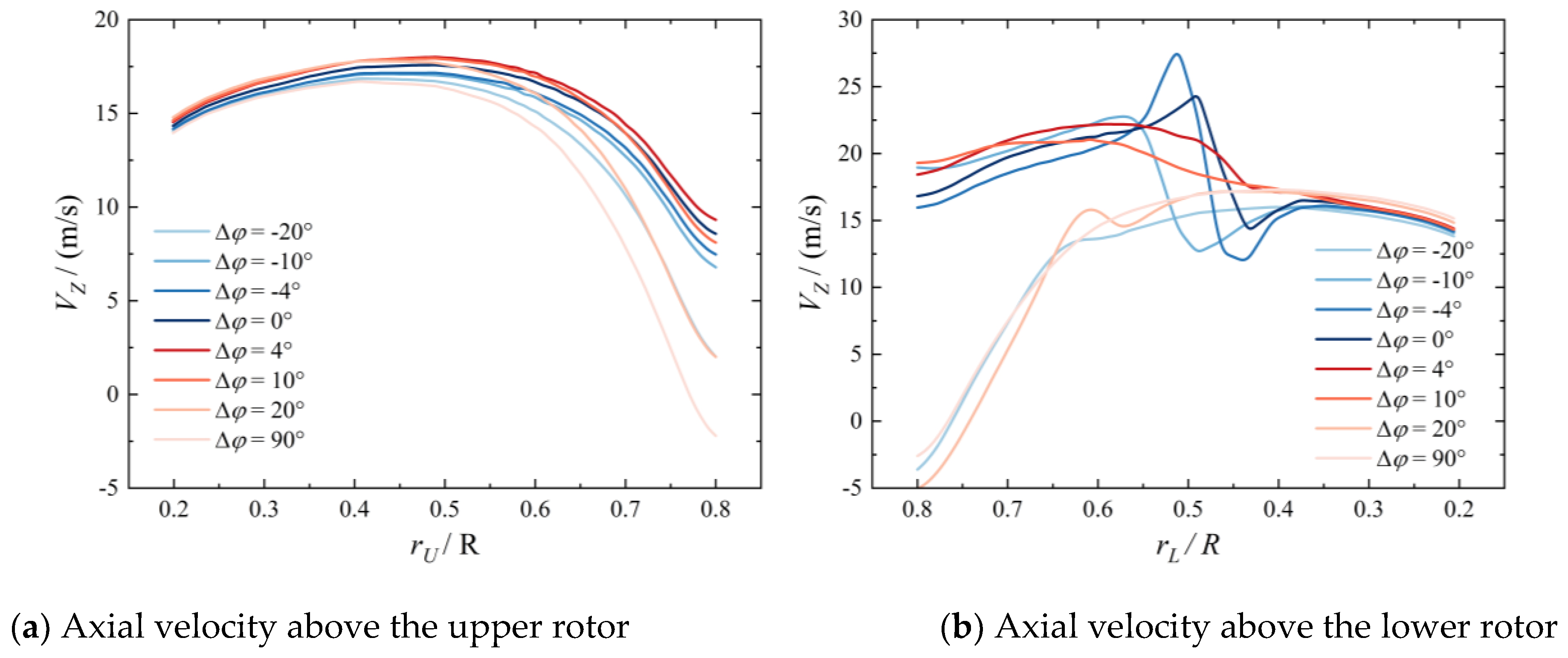
Figure 10 shows the distribution of axial velocity V_z on the monitor line during the meeting and separation of the two rotors with different Δφ angles. When the Δφ is ±20 deg and 90 deg, the blades of the two rotors move far from each other and the interaction on the flow field between the two rotors is slight, so the distributions of axial velocity Vz near the upper rotor and lower rotor are similar. In Figure 10a, when the Δφ increases, the Vz changes mildly in the range outside of the overlapping area between the two rotors, where the r/R is less than 0.5. In the overlapping area, the Vz of the upper rotor quickly increases until the two rotor grow close. With the blades of the two rotors meeting and passing by, the Vz above the upper rotor increases at first and then decreases, so the suction effect and induced effect are verified. In Figure 10b, when the two rotors meet each other, the induced effect on the curve of Vz distribution is also observed at the monitor line above the lower rotor. The slipstream effect is also verified because of the significant increase in Vz in the overlapping area. However, when the Δφ is less than -10 deg or larger than 10 deg, the Vz in the overlapping area drops quickly. This indicates that the slipstream is strong, but can only influence a limited range of the flow field. Additionally, an S-shape fluctuation appears on the curve of Vz in Figure 10b near the location r/R = 0.5. This is the influence of the upper rotor’s blade vortex.

3.2. Effect of the Axis Distance

To analyze the effect of the axis distance between two rotors on the overlapping rotor system, the blade distance h/D is set as 0.156 and the rotational velocity for the two rotors remains as 2100 RPM in this section.

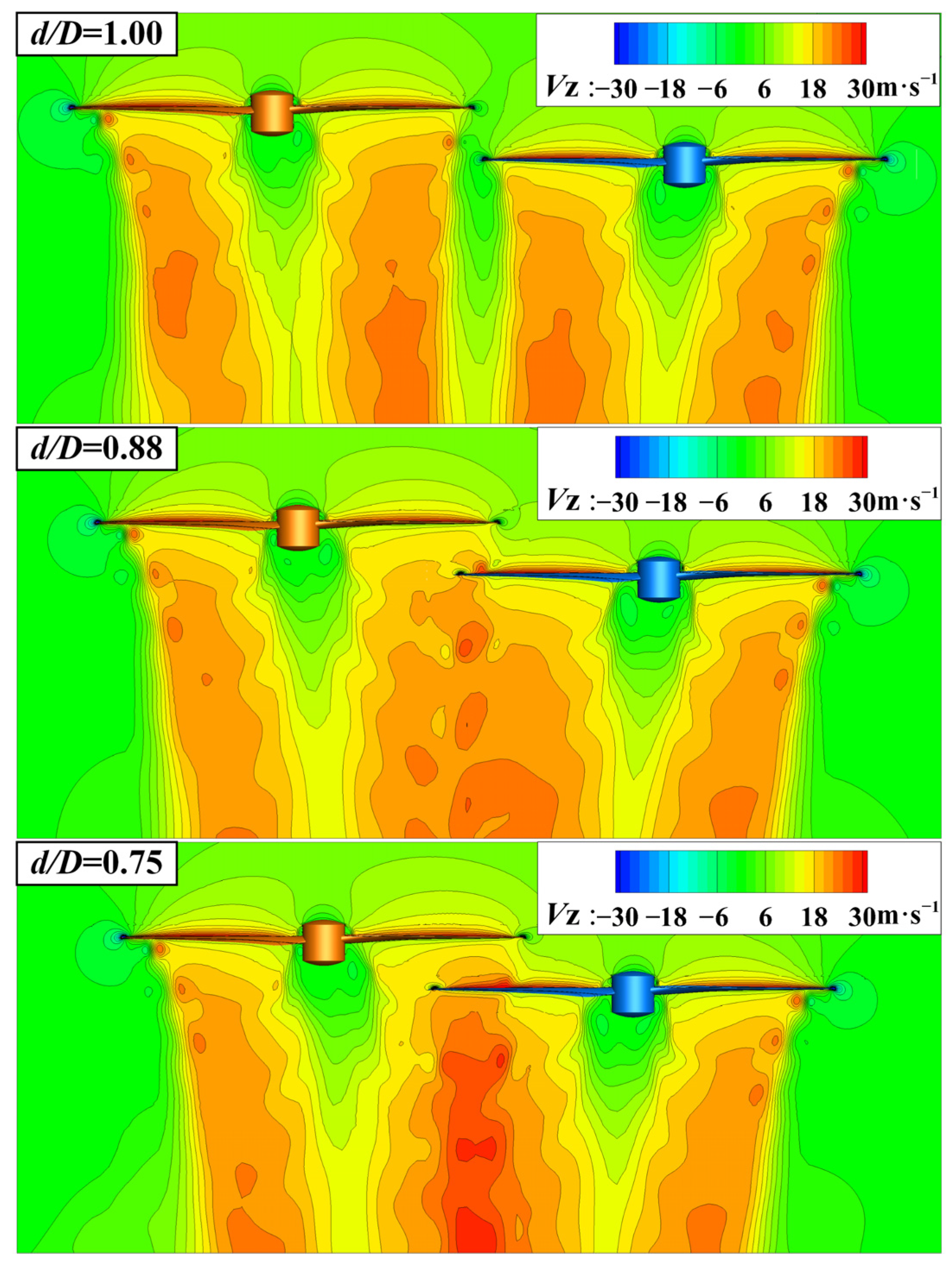
Figure 11 shows the axial velocity contour distributions for overlapping rotor configurations with different axial installation distances. When the two rotors start to overlap, there is no significant interaction among the slipstream regions of the upper and lower rotors. As the blade of the lower rotor comes into the wake of the upper rotor, the upper rotor is also within the suction flow of the lower rotor. A channel with high-speed flow is formed in the overlapping area. The velocity of the flow on the inlet of each rotor is higher, resulting in a decrease in the effective attack angle and thrust. As the axis distance decreases, the accelerating channel expands and the area of the blades affected by overlapping interference also increases. In addition, the slipstream regions of the two rotors exhibit an asymmetrical distribution relative to their corresponding rotor axes and the wakes of two rotors are attracted towards each other. This is because the high-speed flow is in the accelerating channel, resulting in the pressure difference between inside and outside of the overlapping area.

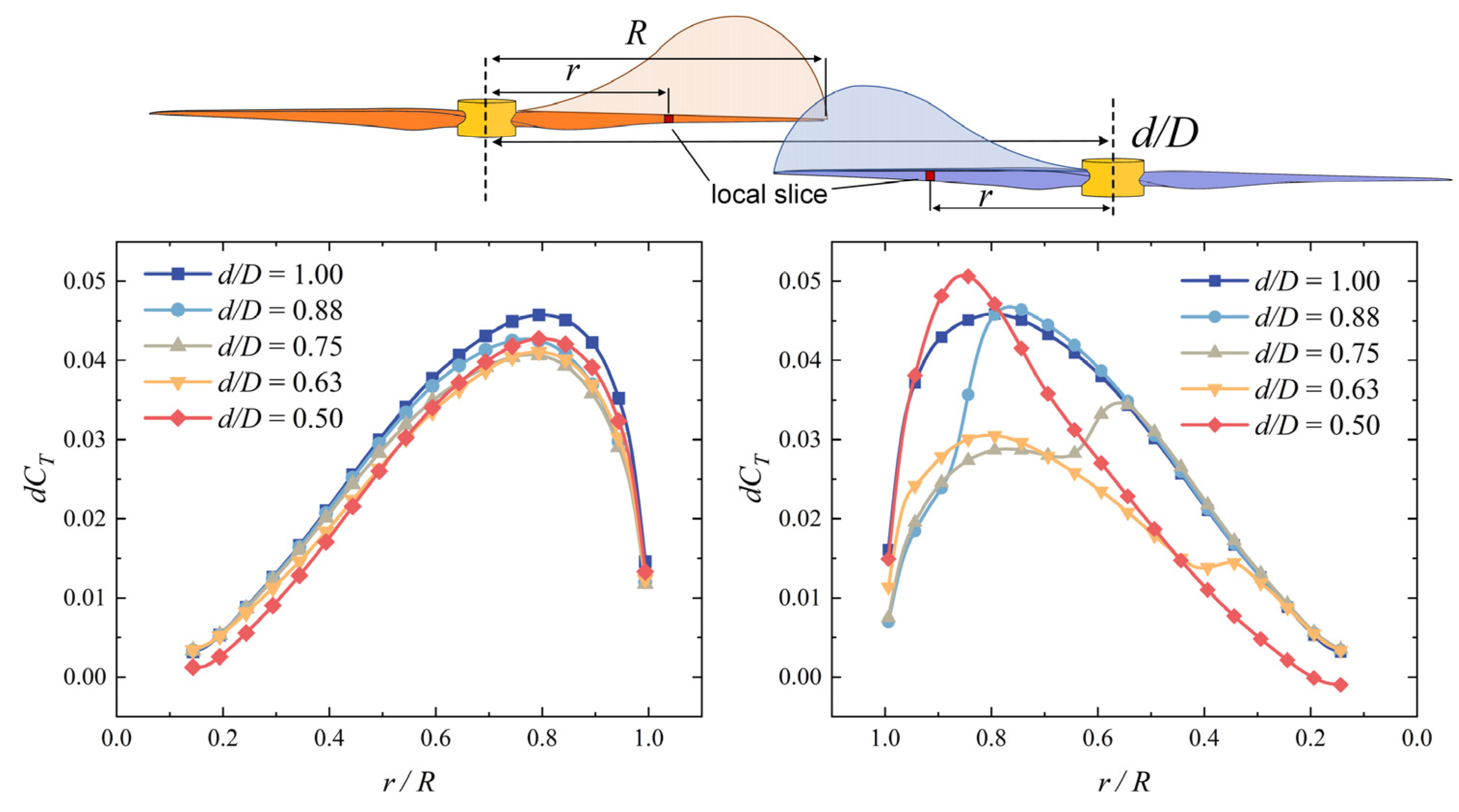
Figure 12 shows the spanwise load distributions on the blades of two rotors when they meet in the overlapping area at different axis distances. When the axis distance d/D is one, the two rotors have not overlapped. The curves of thrust distribution on the blades of two rotors are similar, without a strong interaction between each other. When the two rotors overlap, due to the interaction between the two rotors, the thrust distribution on the two rotors within the overlapping area decreases. Comparing the curve of thrust distribution in Figure 12, the variation in the curves of the lower rotor is much more significant than that for the upper rotor. This indicates that the slipstream effect is more powerful than the suction and induced effects. As the axis distance decreases, more of the area on the blades of the two rotors is affected by the interaction between the two rotors, resulting in a partial decrease in thrust distribution. As the axis distance d/D decreases to 0.5, the blade tip of the lower rotor is closed to the hub of the upper rotor, where the slipstream from the upper rotor is slow. With the weakening of the slipstream effect, the thrust on the tip of the lower rotor returns to a high level.

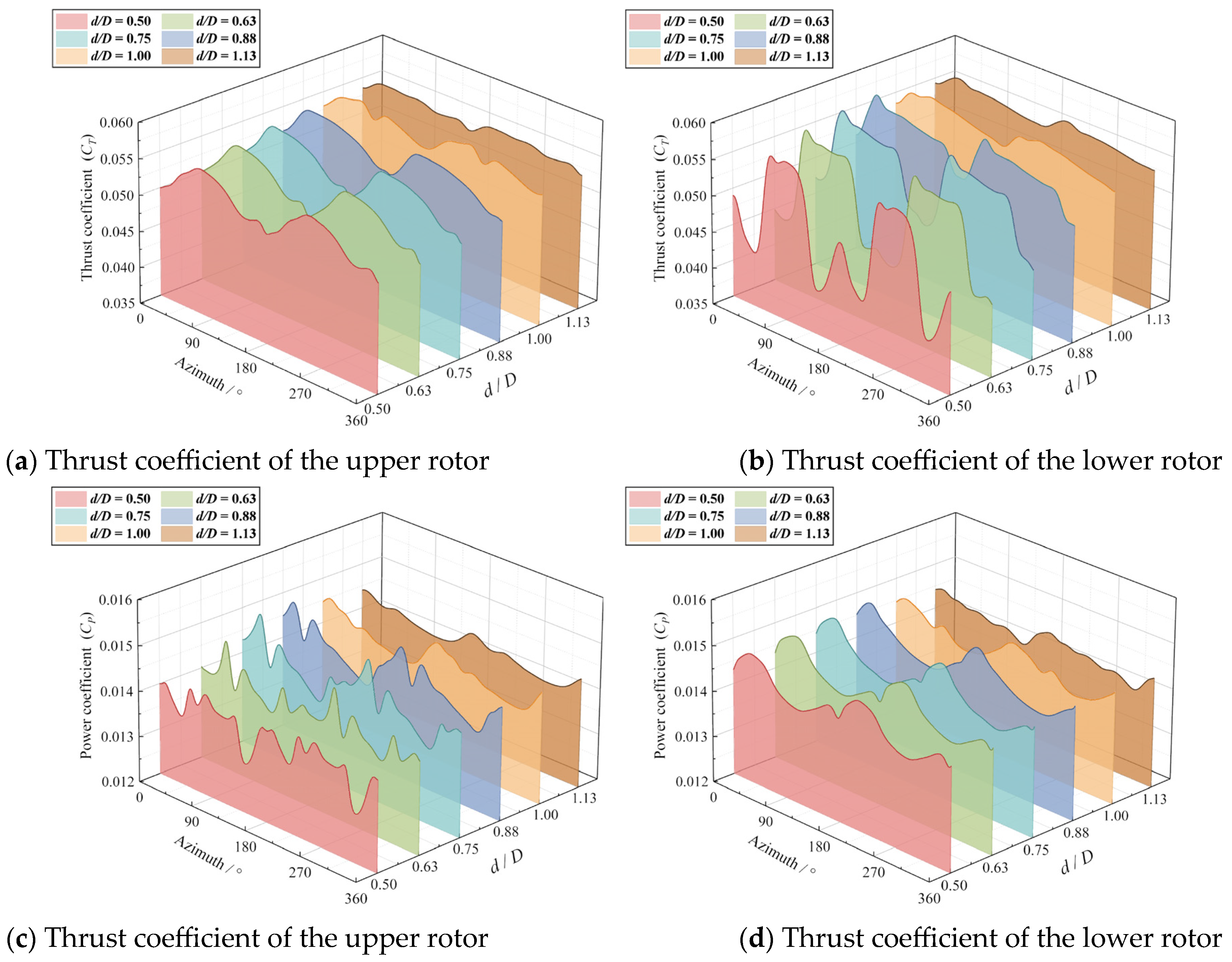
Figure 13 shows the variation characteristic curves of the thrust and power coefficients of the upper and lower rotor blades with azimuth angles at different axis distances. When the upper and lower rotor blades are not overlapping (i.e., d/D = 1.00 or 1.13), the lift and power coefficients of the two rotor blades fluctuate slightly within the azimuth angle range of 0–360°. In contrast, when the upper and lower rotor blades are partially overlapping (i.e., d/D < 1.00), the thrust coefficients of the two rotor blades experience unsteady periodic variations, due to the suction, slipstream, and induced effects. In addition, as the axis distance (d/D) decreases, the increased overlapping area between the two rotor blades results in apparent increases in both the range and magnitude of the two rotors’ thrust characteristic curves. As the distance between the axis of the two rotors decreases, the overlapping area increases quickly, which leads to increases in the range and magnitude of the unsteady fluctuations on the curve.

As shown in the Figure 13a,b, a small fluctuation appears on the thrust coefficient curves of the two rotors around the azimuth angle of 180° during a revolution because of the interaction between them. Because of the stronger slipstream effect, the fluctuation peak on the curve of the lower rotor is larger than that of the upper rotor. In Figure 13c,d, a fluctuation also appears on the power coefficient curves of the upper rotor and the fluctuation peak increases with a decreasing axis distance. The power coefficient of the lower rotor is very unsteady, and its curve changes from a single peak to multiple peaks as the axis distance decreases due to the influence of wake.

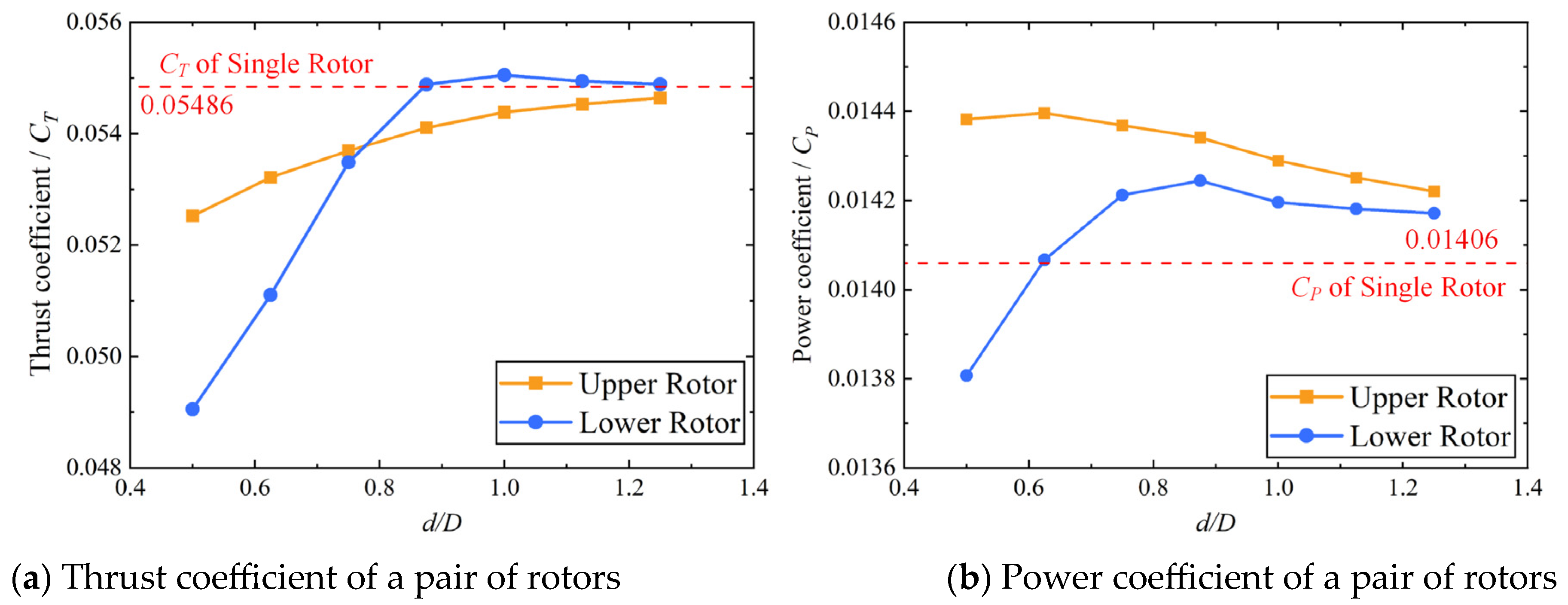
Figure 14 displays the average thrust and power coefficients in one revolution at different axis distances (d/D). When the two rotors are far from each other, the average thrust and power coefficients of each rotor blade are approximately the thrust and power coefficient of a single rotor. As the axis distance (d/D) decreases, the thrust coefficient of the upper rotor decreases and the power coefficient of the upper rotor increases uniformly. The thrust and power coefficients of the lower rotor increase slightly at first and then decrease rapidly when the lower rotor blade meets the upper rotor slipstream. In addition, the variation ranges of the thrust coefficient and power coefficient of the upper rotor are much lower than those of the lower rotor, which reconfirms that the intensity of the suction effect and induction effect is weaker than that of the slipstream effect. In general, when the overlapping area of the two rotors is small, the power coefficients of the two rotors are slightly increased, with the whole overlapping rotor system still maintaining a high thrust coefficient.

3.3. Effect of the Blade Distance

In this section, the axis distance d/D is set as 0.75 and the rotational velocity for the two rotors remains as 2100 RPM. To analyze the effect of the axis distance between two rotors to on overlapping rotor system, two monitor lines with 100 monitor points are arranged above the upper and lower rotor blades, as shown in Figure 9.

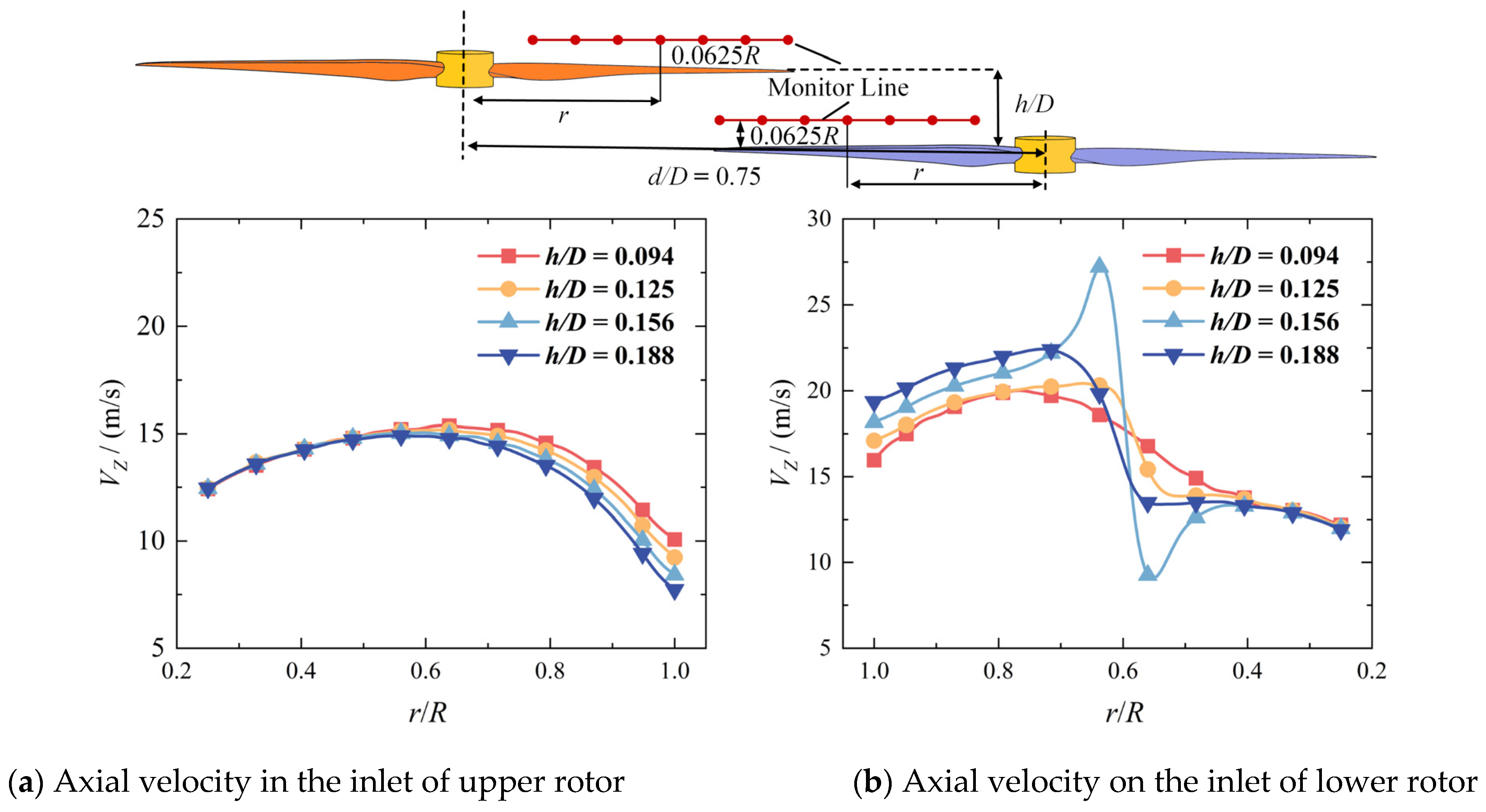
Figure 15 shows the distribution of axial velocity V_Z on the monitor line when two rotors meet. In Figure 15a, as the blade distance h/D increases, within the overlapping area, the V_Z in the inlet of the upper rotor increases because the suction effect and induced effect are enhanced at a short distance. In Figure 15b, the V_Z in the inlet of the lower rotor decreases with the h/D. This is because the compressed flow produced by the upper rotor does not have enough distance to accelerate, so the slipstream effect is weakened. In addition, there is an S-shaped fluctuation in the curve of V_Z around r/R = 0.6. This is caused by the tip leakage vortex, which induces a downward velocity on the left side and upward velocity on the other side. As the blade distance increases, the amplitude of the S-shaped fluctuation increases at first and then decreases.

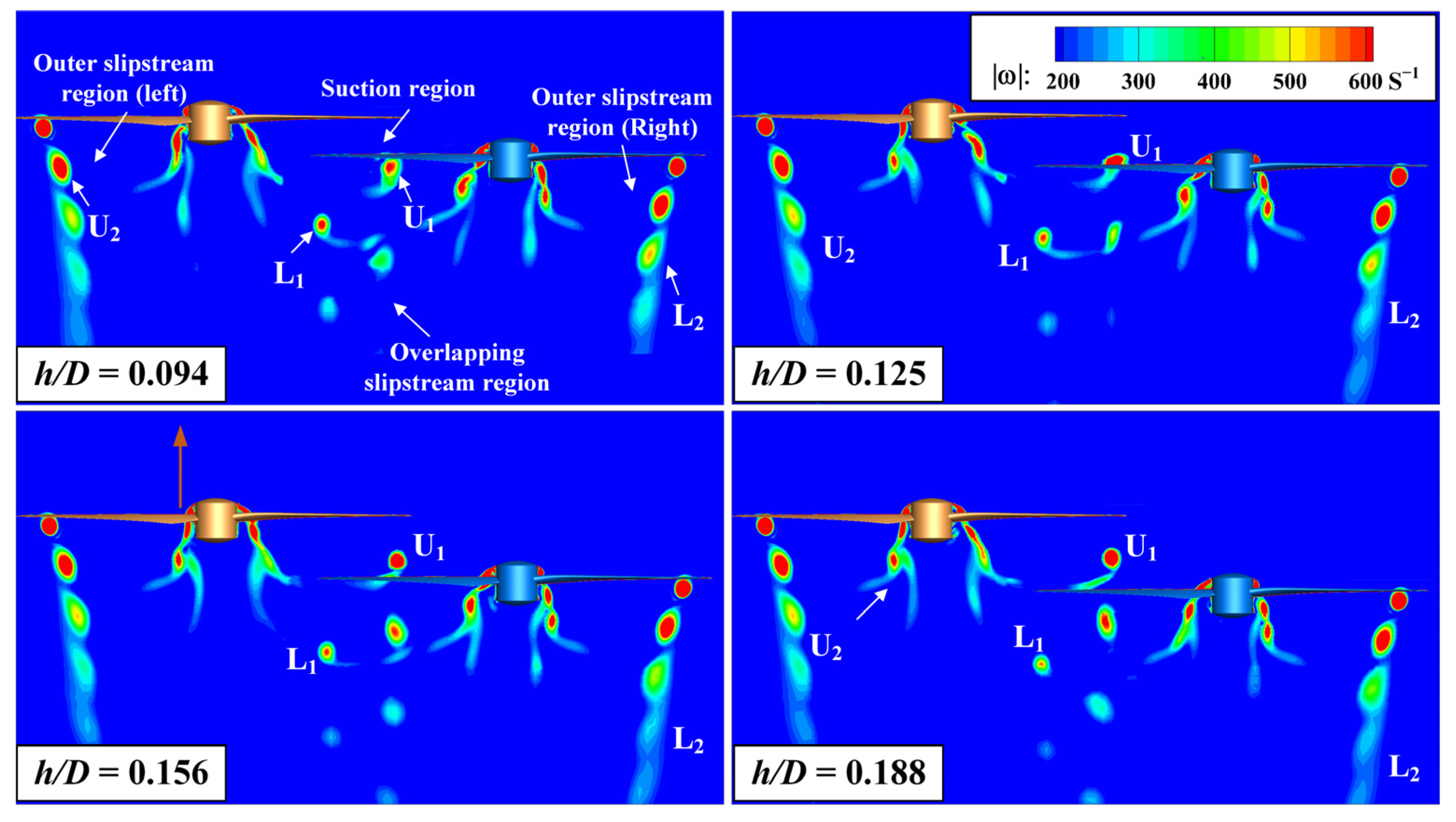
Figure 16 displays the vorticity magnitude contours at the vertical slice at different blade distances. Above all, the leakage vortex produced by the outer blade of the upper rotor is marked as U₁, whereas the vortex produced by the inner blade is marked as U₂. The flow field may be categorized into the following sections based on distinct spatial placements and disturbances: the overlapping slipstream region, the outer slipstream region, and the suction region. As the blade distance h/D is 0.094, the suction effect is stronger, leading to a high axial velocity flow in the suction area, so the vortex U₁ quickly passes through the suction region and meets the blade of the lower rotor in the overlapping slipstream area. With the blade distance h/D increases, the position of the vortex is variable. When the blade distance h/D is 0.125, the vortex U₁ directly impacts the lower blade, resulting in blade–vortex interaction (BVI). The partial attack angle on the lower rotor changes and the load distribution on the distribution shifts. Disturbed by the surface of the lower rotor, the vortex U₁ dissipates quickly. When the blade distance h/D continually increases to 0.188, the suction region is large and the vortex U₁ is far from the lower blade. The BVI phenomenon disappears and the structure of vortex U₁ recovers to being stable, which means that the fluctuations on the thrust distribution of the lower rotor will also disappear.

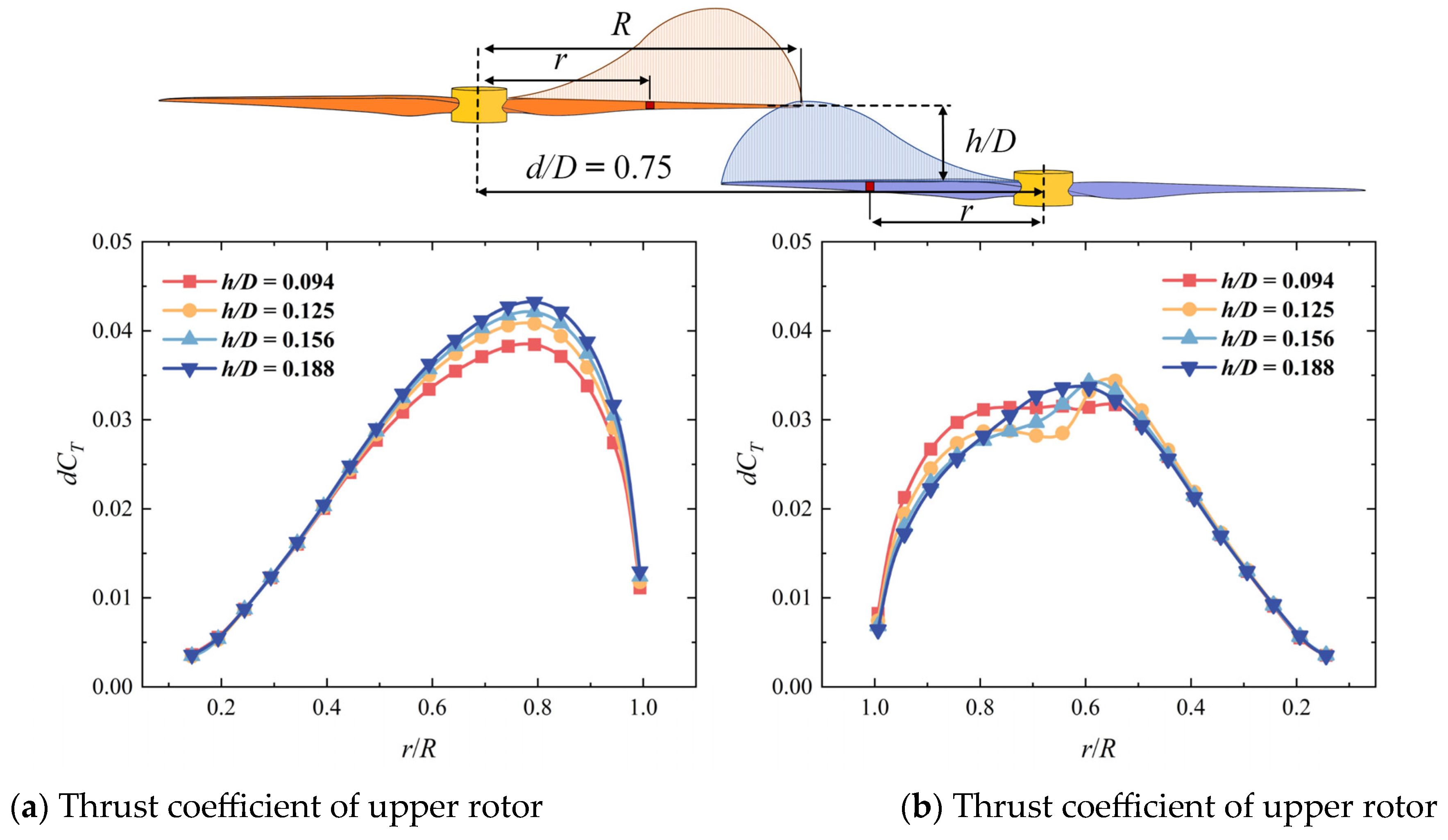
Figure 17 shows the spanwise load distributions on the blades of two rotors when they meet in the overlapping area at different blade distances. As the blade distance increases, because of the weakening of the interaction between two rotors, the thrust coefficient of the upper rotor increases and the thrust coefficient of the lower rotor decreases. However, the range of influence on the blades of the two rotors basically remains unchanged. In Figure 17 when the blade distance h/D is 0.125 and 0.156, an S-shaped fluctuation appears on the load distribution curve of the thrust coefficient at the position r/R = 0.6 because of the BVI effect between the tip leakage vortex of the upper rotor and the blade of the lower rotor. At the blade distance h/D is 0.188, the “S” shape fluctuation on the distribution curve disappears when the BVI effect disappears.

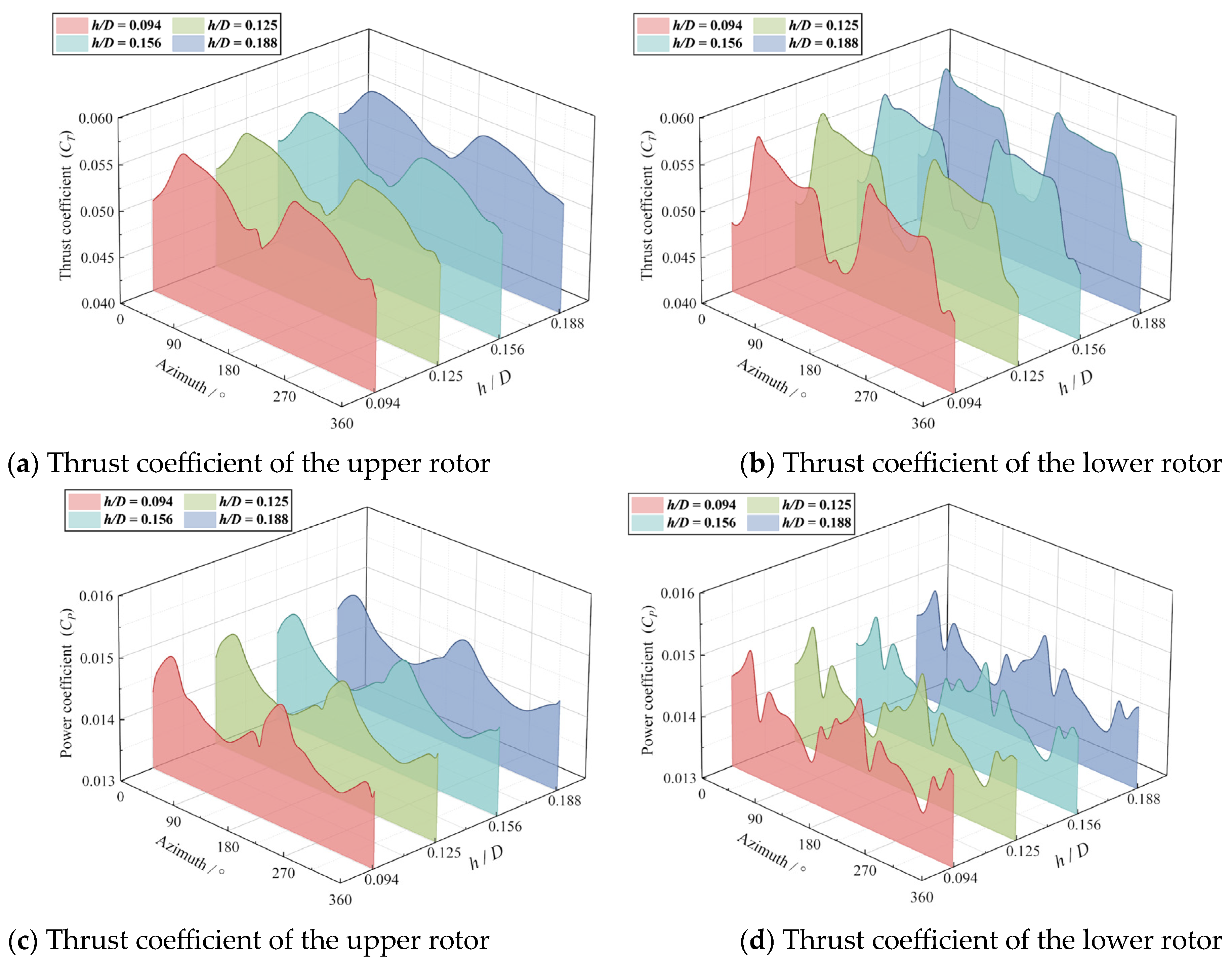
Figure 18 shows the variation characteristic curves of the thrust and power coefficients of the upper and lower rotor blades with azimuth angles at different blade distances. As shown in Figure 18a,b, at an azimuth angle when the two rotors do not meet, the thrust coefficients of each rotor are similar at different blade distances. When two rotors meet around the 180 deg azimuth angle, a significant fluctuation appears on the curve of coefficient and power coefficient. With the blade distance decreases, the amplitude of the fluctuation increases gradually because of the enhanced suction effect and induced effect. In addition, in Figure 18b, at an azimuth angle of around 150 deg, the thrust coefficient of the lower rotor decreases with a blade distance decrease. This may be caused by the variation in the circumferential velocity of the slipstream. In Figure 18c,d, as the blade distance decreases, the fluctuation also appears around an azimuth angle of 180 deg. However, the overall variation pattern of the power coefficient curve remains essentially unchanged.

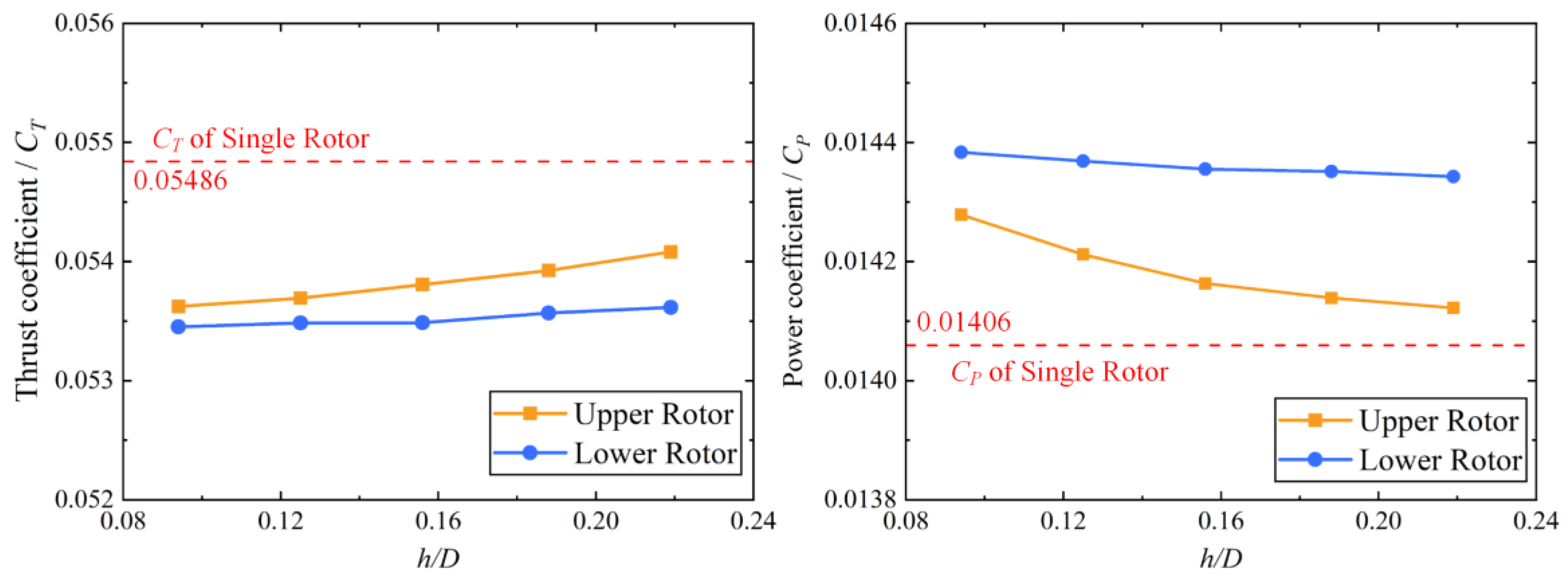
Figure 19 displays the average thrust and power coefficients in one revolution at different axis distances (d/D). As the blade distance increases, the suction effect and induced effect rapidly weaken. The thrust and power coefficient of the upper rotor progressively approach the characteristics of the single rotor. However, due to the fact that these effects constitute a weak interaction, the variation ranges of the thrust and power coefficients of the upper rotor are constrained. When the blade distance is close, the wake of the upper rotor has a slower velocity but a larger cover area. So, the average thrust and power coefficient of the lower rotor in one revolution change a little as the blade distance increases. In conclusion, reducing the blade distance between the two rotors will strengthen the interference between the two rotors and lead to a stronger fluctuation in load distribution when the two rotors are overlapping, but this has a limited influence on the aerodynamic performance of the whole overlapping rotor system. This may be beneficial for reducing the size of the rotor system to further improve space utilization for overlapping rotor configurations.

4. Conclusions

A CFD solver based on the RANS equations and hybrid sliding grid technology are established for unsteady aerodynamic simulations of overlapping rotors. The calculated results of the overlapping performance and flow field are analyzed. The following conclusions can be drawn:

As for the overlapping rotor system, when two blades do not meet, the aerodynamic characteristics of each rotor are similar to a single rotor with same configuration. When two blades overlap, an interaction appears between the two rotors, which can be explained by the coeffects of the slipstream effect, suction effect, and induction effect. The slipstream effect is caused by the wake of the upper rotor. The suction effect is caused by the suction of the lower rotor, which accelerates the flow above the blade. The induction effect is caused by the attached vortex on both rotor, which induces a different direction of velocity surrounding the blades. These effects affect the velocity distribution of the flow field around the two rotors and, thus, affect the actual angle of attack and load distribution on the blade of each rotor.

Axis distance is directly related to the overlapping area between the two rotors. When the axis distance between the two rotors is small, the interference of the slipstream effect is weak. The whole overlapping rotor system still maintains a high total thrust. When the axis distance is reduced to a certain value, the slipstream effect enhances rapidly, and the aerodynamic efficiency of the total overlapping system is greatly reduced.

Blade distance can significantly influence the suction and induced effects, which leads to a fluctuation in the load distribution of each rotor when they meet each other. At different blade distances, the spatial position relationship between the tip vortex of the upper rotor and the blade of the lower rotor will change, and the BVI phenomenon will appear when they meet. However, the slipstream effect is less affected by blade distance. The aerodynamic performance of the whole overlapping rotor system changes a little when the blade distance decreases.

In summary, overlapping rotor configurations retain potential for drone design. Under slight overlapping conditions, despite aerodynamic interactions among rotors, the time-averaged aerodynamic performance remains relatively high. Continually reducing the blade distance and axis distance can improve the spatial utilization efficiency of rotor arrays, but may induce a rapid escalation in aerodynamic interference. Achieving an optimal balance between spatial efficiency and aerodynamic stability will represent a critical research focus in the advancement of overlapping rotor configurations for UAV design in the future.