BiLSTM-Attention-PFTBD: Robust Long-Baseline Acoustic Localization for Autonomous Underwater Vehicles in Adversarial Environments
Abstract
1. Introduction
- Enhanced localization accuracy through the integration of direct signals and comprehensive feature extraction: The proposed method utilizes both raw measurements and derived features from particle filtering. The system integrates normalized likelihood computation and peak detection analysis to enhance system robustness in adverse conditions. For detailed explanations, see Section 5.1.
- Advanced temporal modeling with BiLSTM for the detection of abrupt maneuvers and signal losses: Conventional tracking systems often fail with complex temporal dynamics and dispersed information. Our BiLSTM architecture processes sequences bidirectionally, enabling the effective prediction of abrupt maneuvers and signal losses in adversarial environments.
- Capturing complex dependencies with multi-head attention mechanisms: Traditional models struggle with dispersed temporal dependencies and complex data interactions. Our multi-head attention mechanism examines multiple sequence positions simultaneously, enabling dynamic focus adjustment and effective pattern recognition in challenging environments.
2. Particle Filtering Localization
2.1. Particle Filtering for State Estimation
2.2. Particle Initialization
2.3. Prediction Step for State
2.4. Update Step for Particle Weight
2.5. Resampling Implementation
2.6. State Estimation
3. Limitations of Traditional Particle Filters in Adversarial Environments
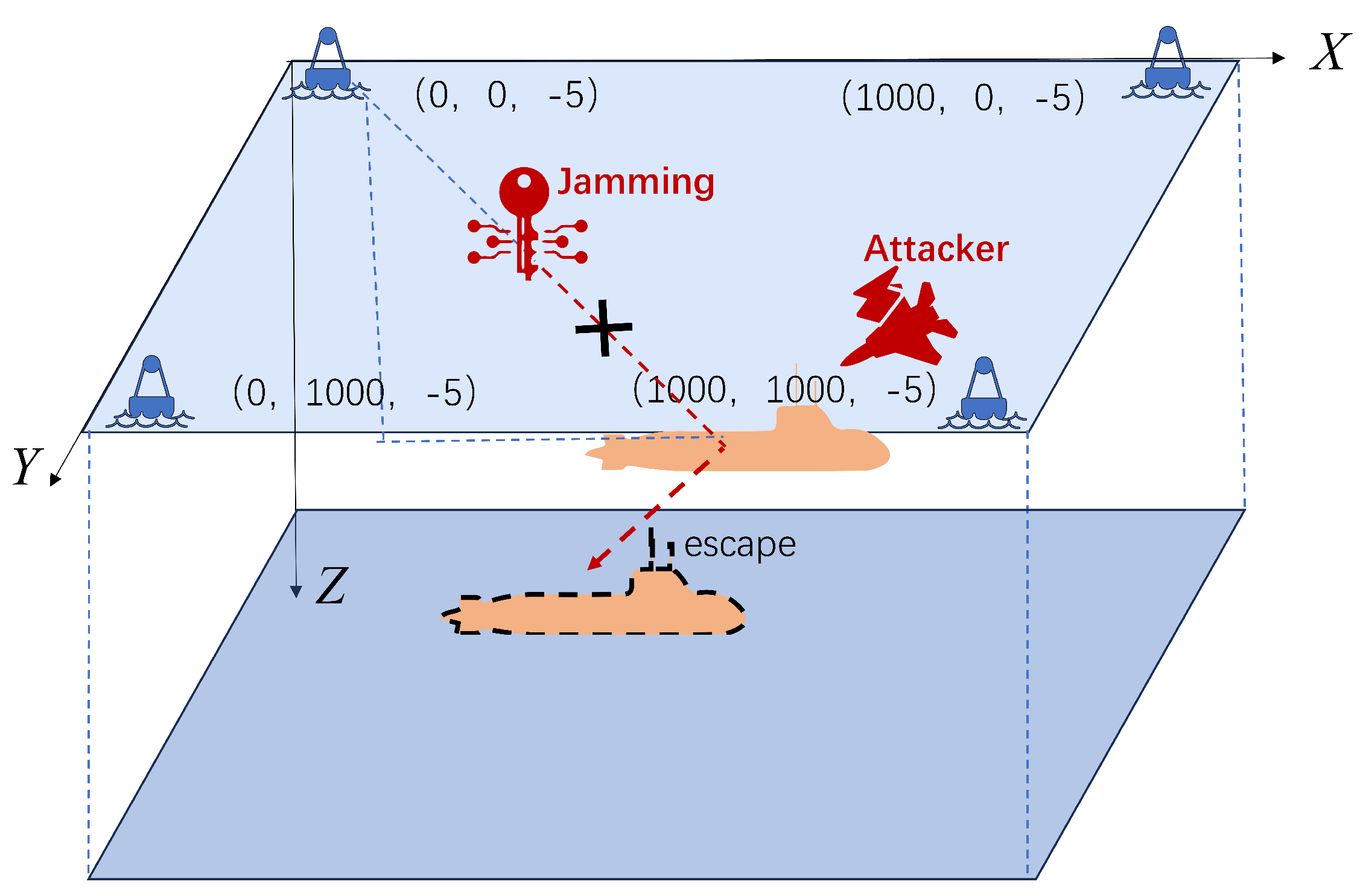
3.1. Mathematical Formulation of the Problem
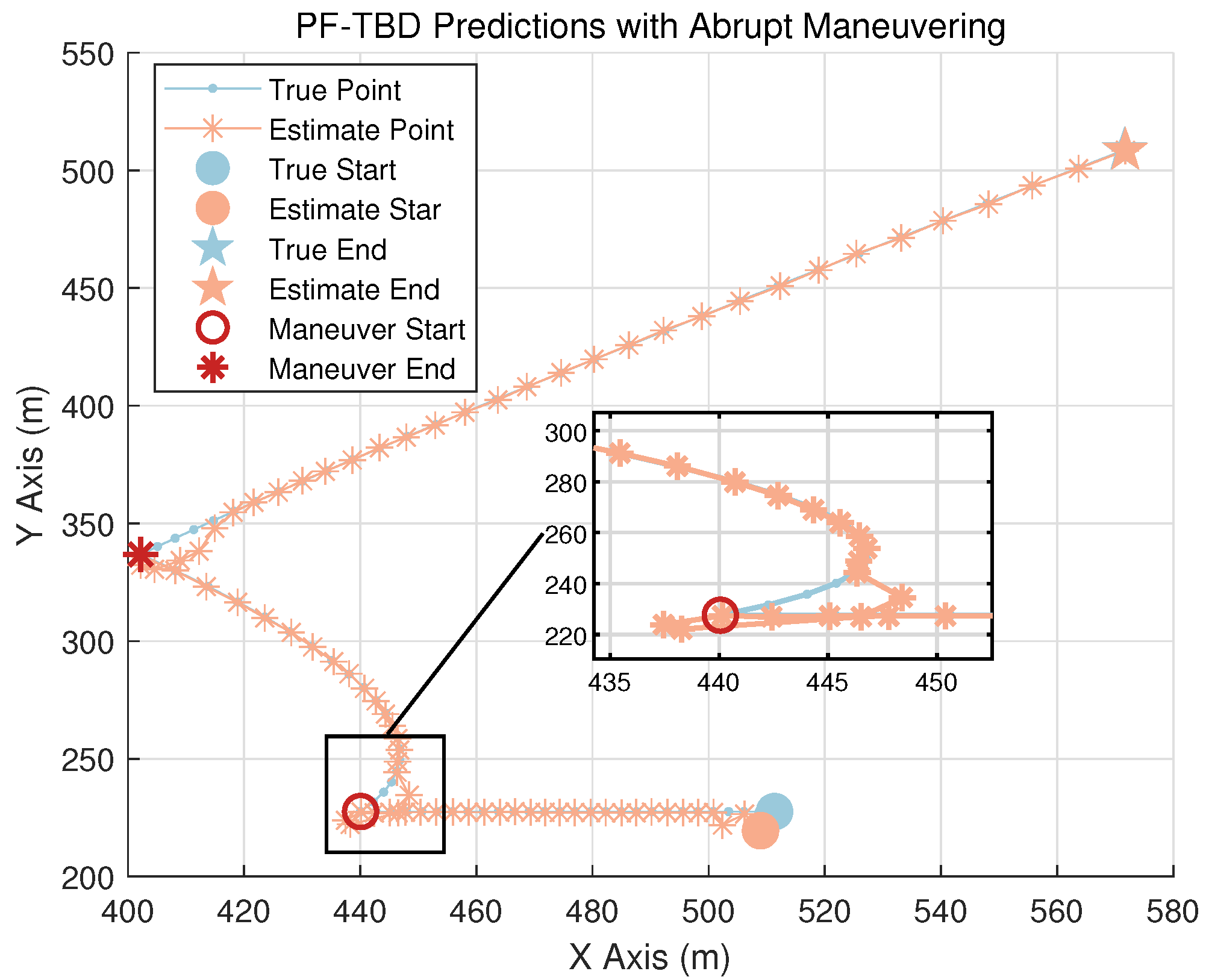
3.2. Impact of Abrupt Maneuvers
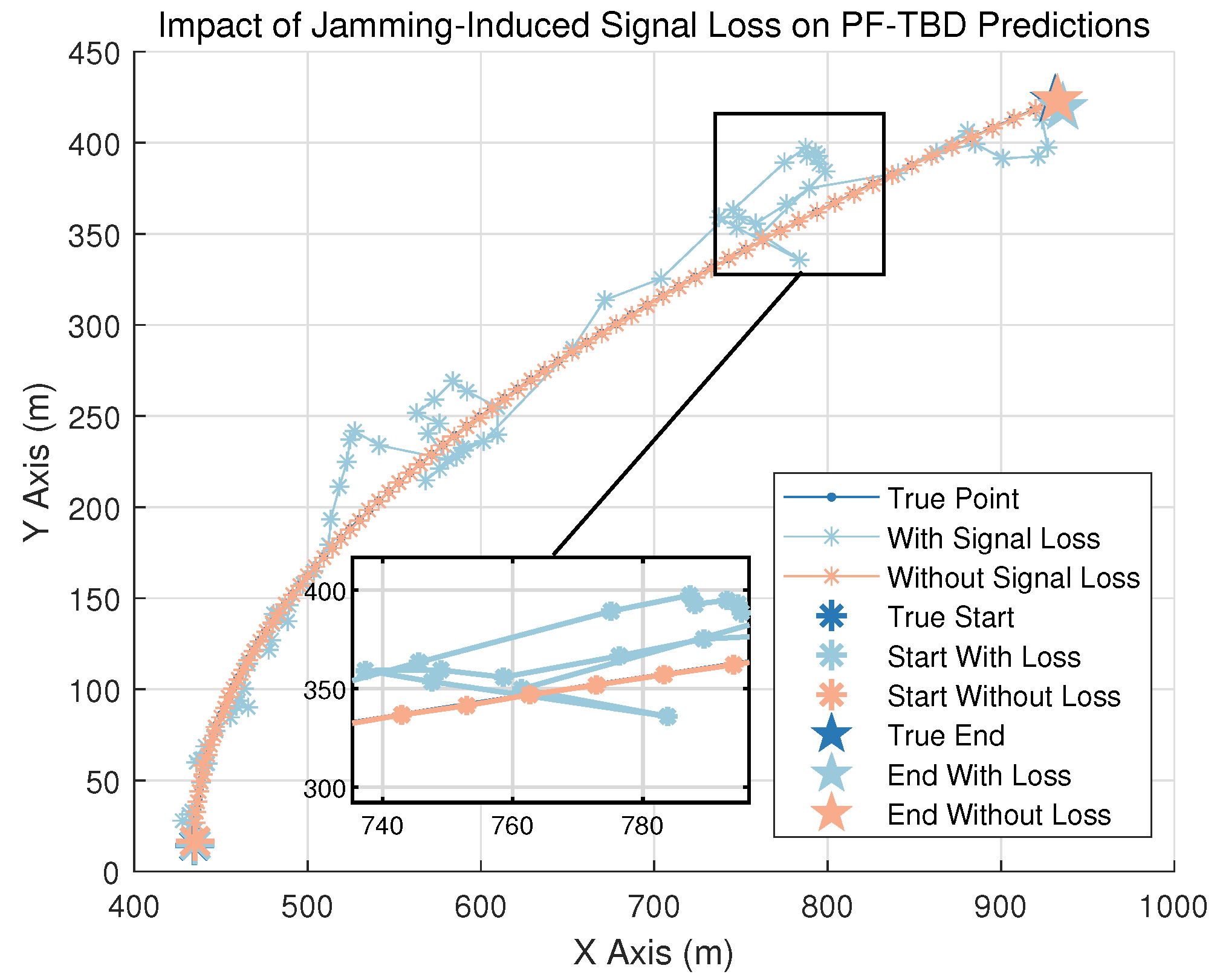
3.3. Effect of Signal Jamming
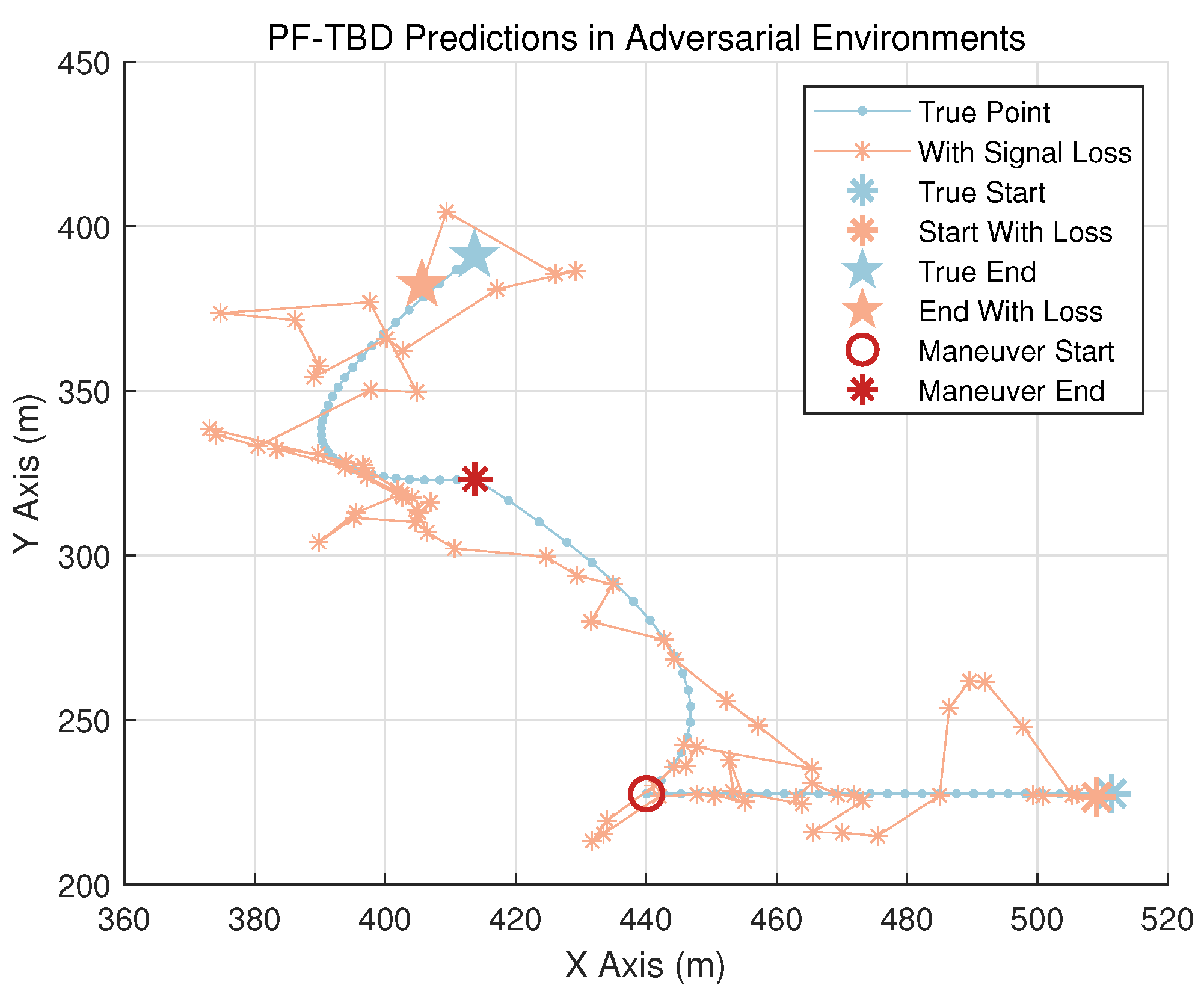
3.4. Severity of Adversarial Conditions
4. Deep Learning to Enhance Particle Filter Performance
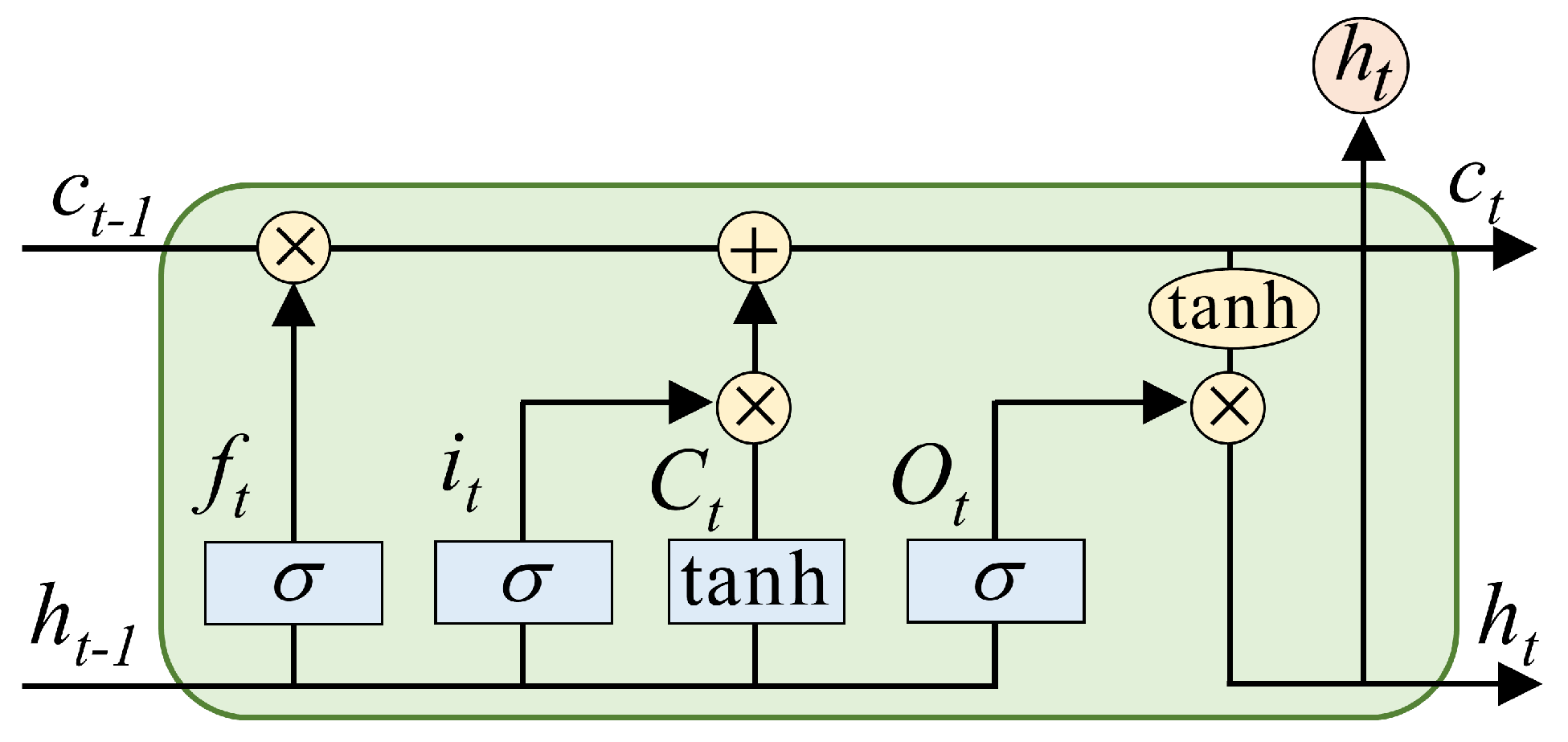
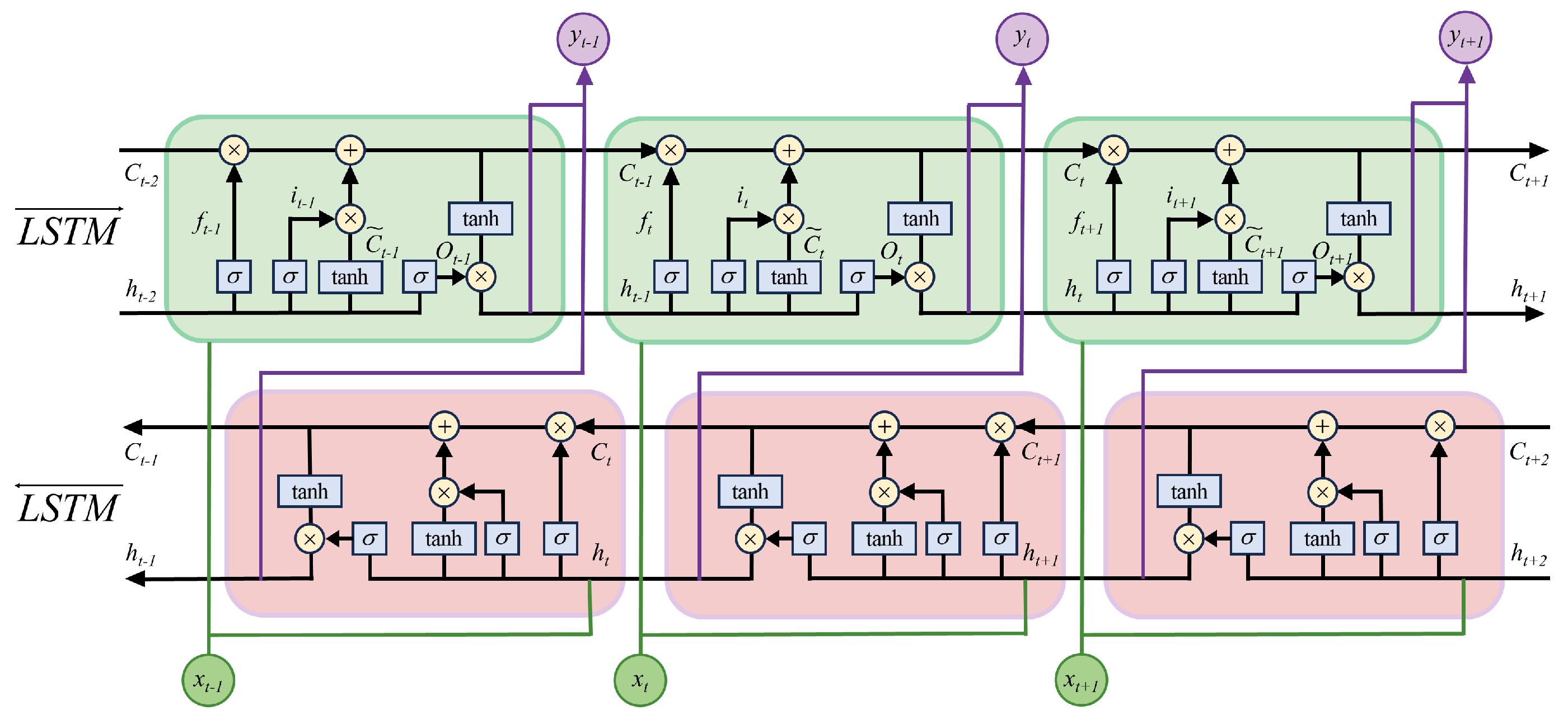
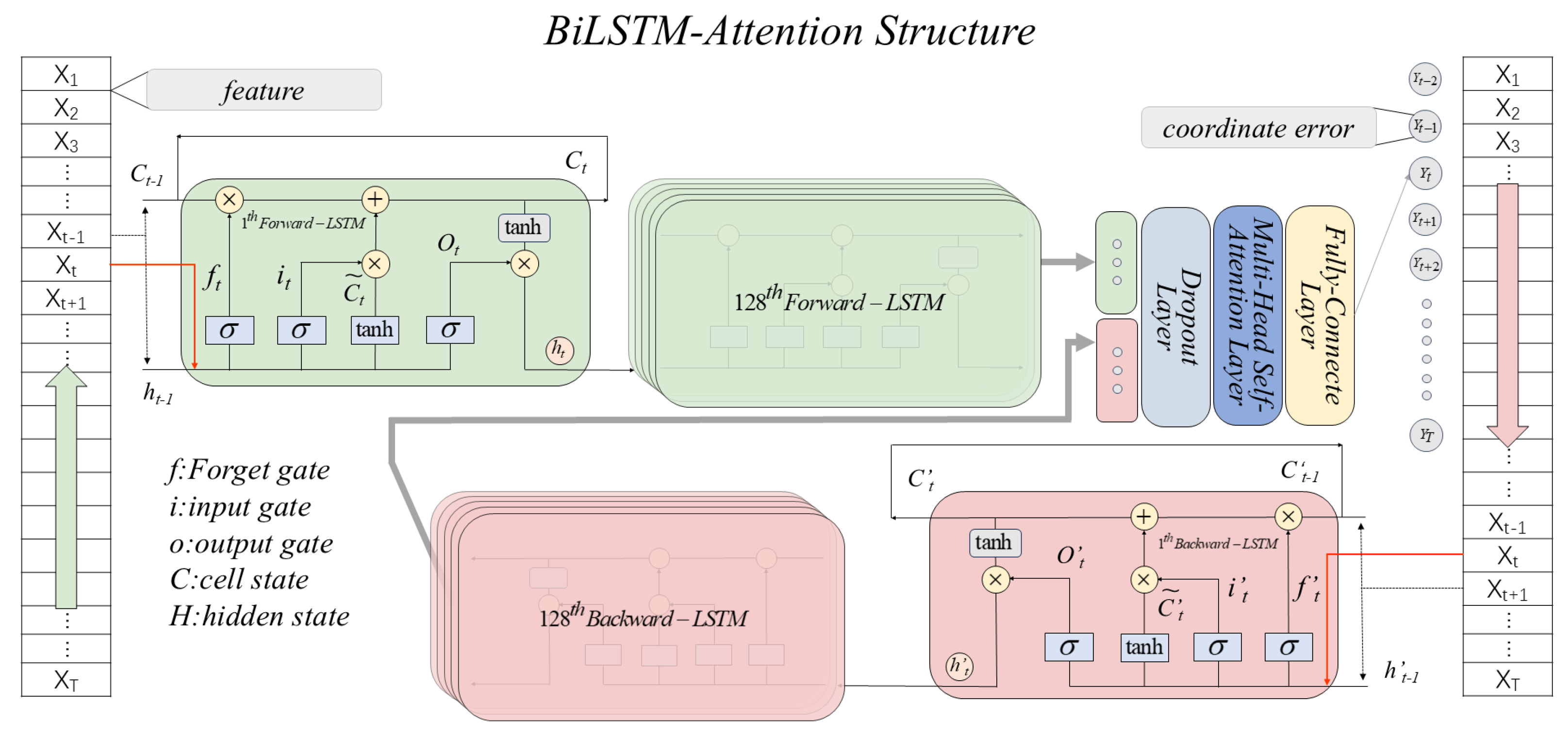
4.1. LSTM Cell Structure
4.2. BiLSTM Network Structure
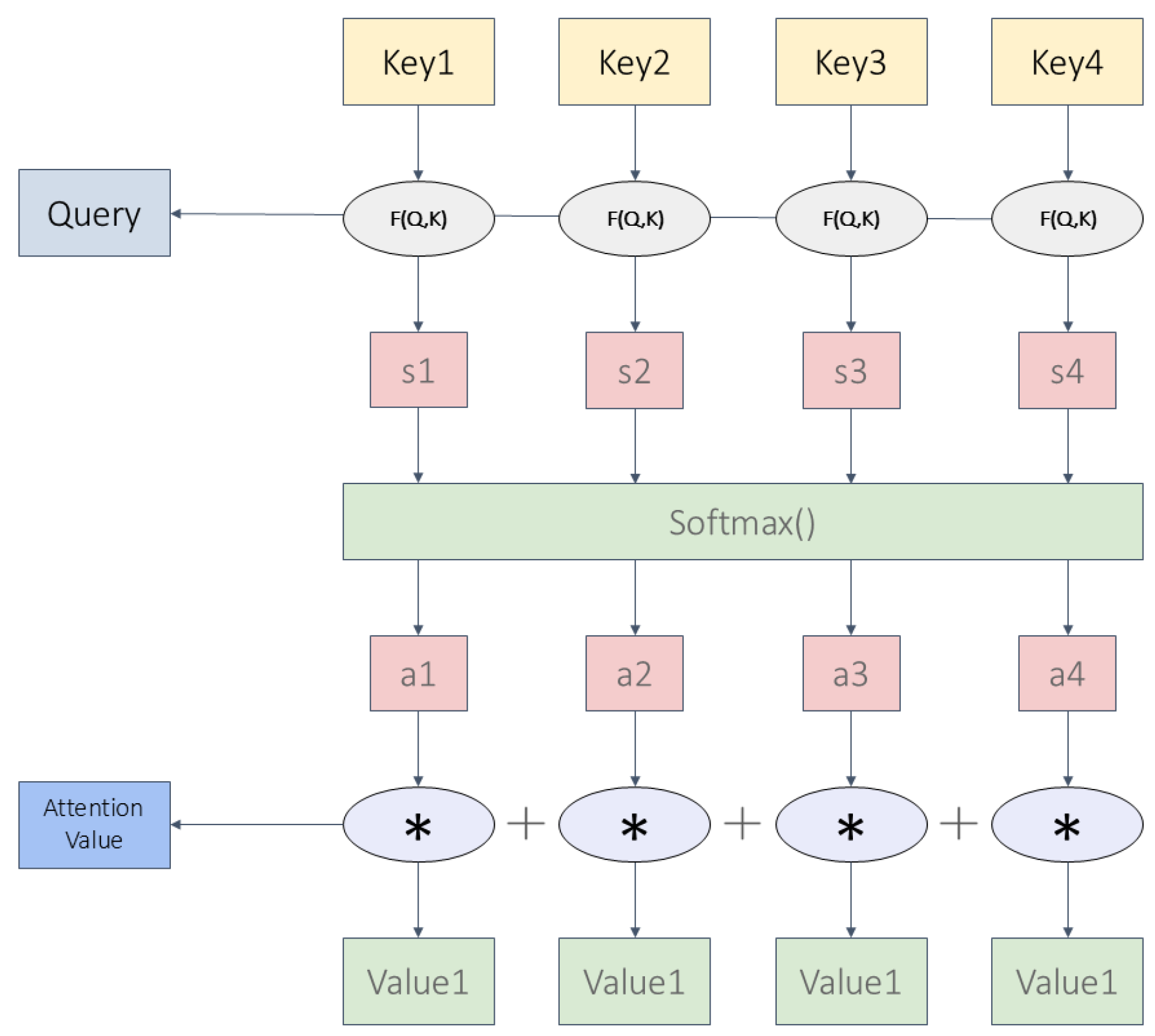
4.3. Attention Mechanism
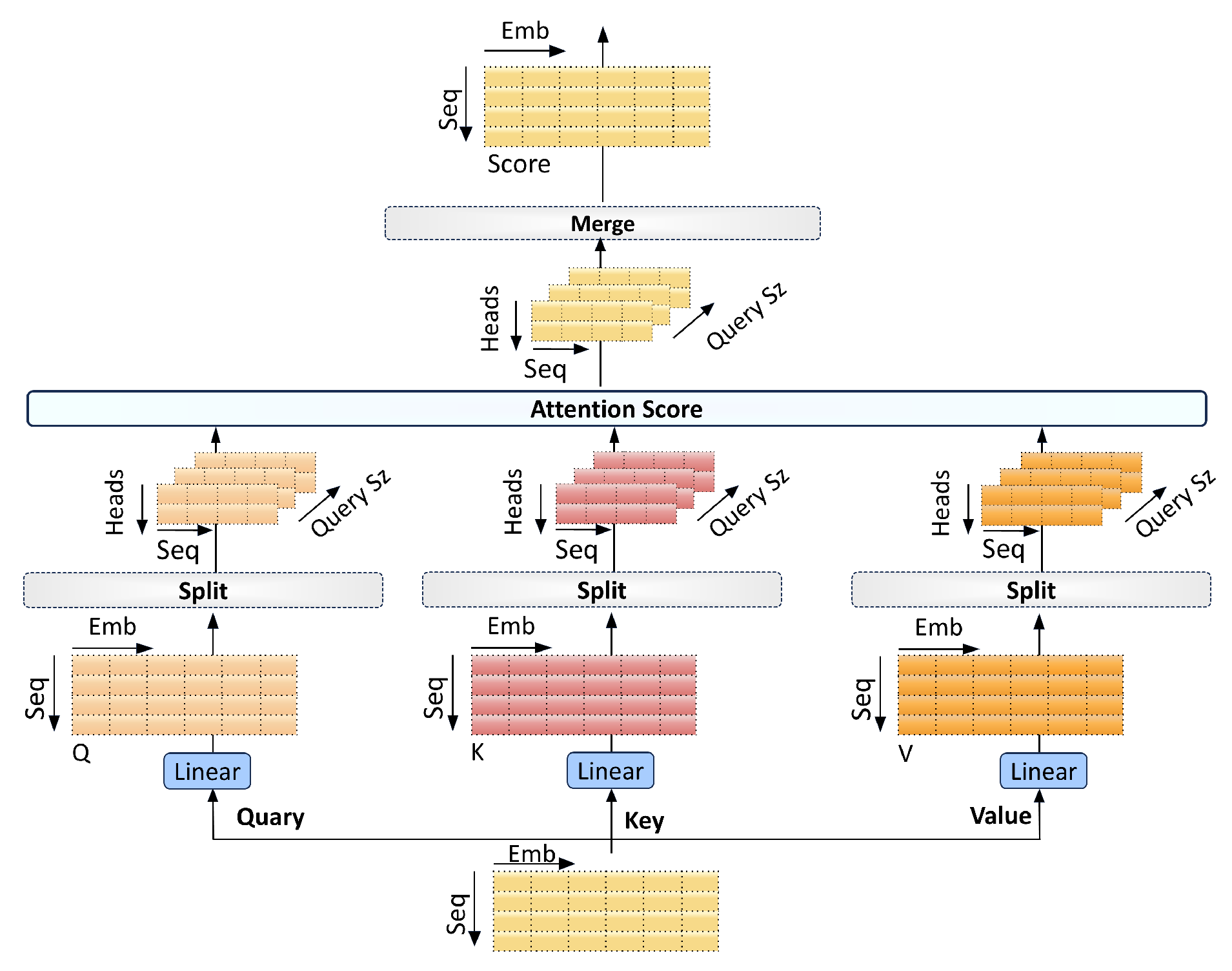
4.4. Multi-Head Attention Mechanism
5. Our Approach
5.1. Signal Features for Network Input
5.1.1. Estimated Position and Velocity
5.1.2. Position and Velocity Variance
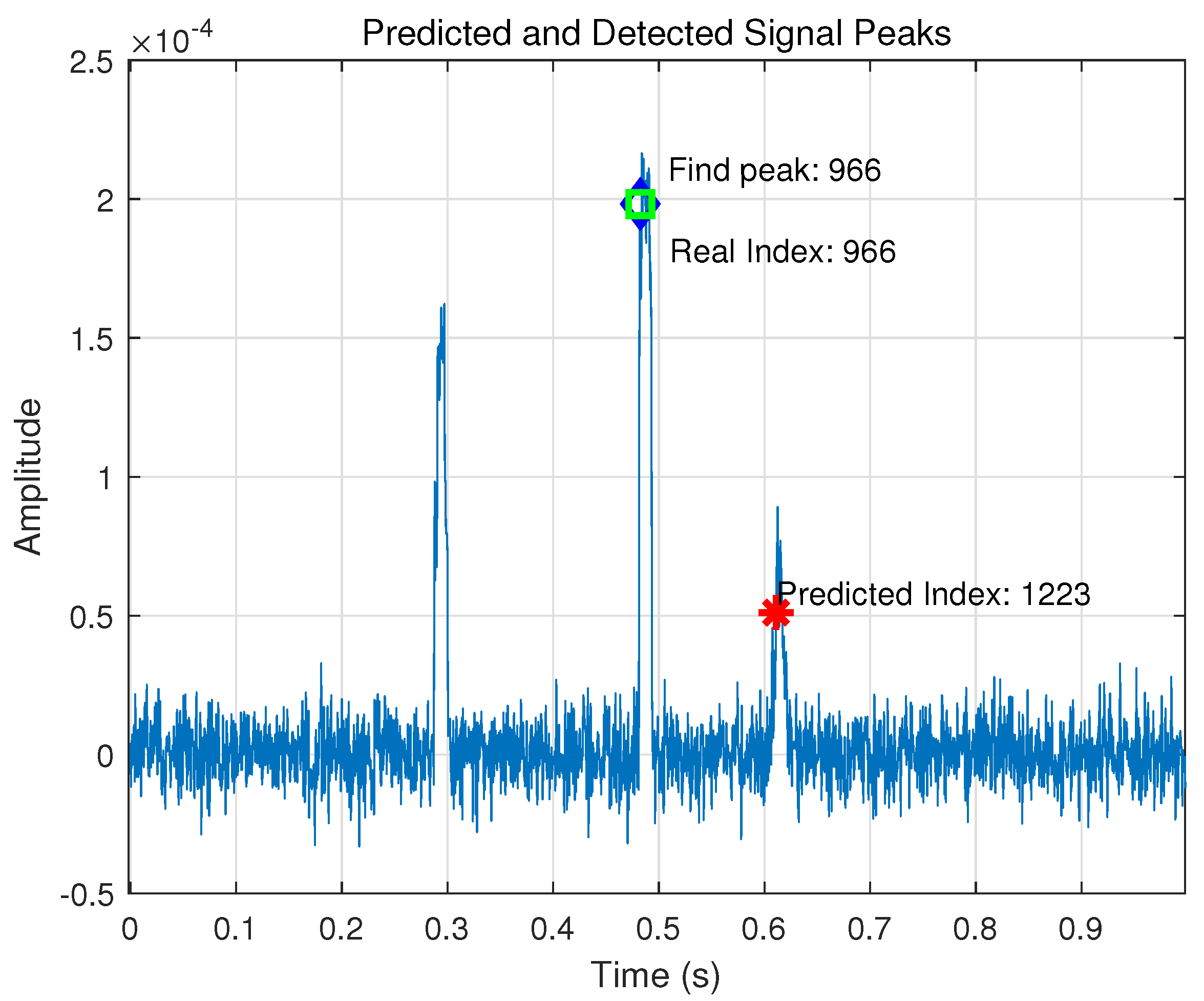
5.1.3. Signal Peak Information
5.1.4. Likelihood Value Feature Extraction for Each Hydrophone
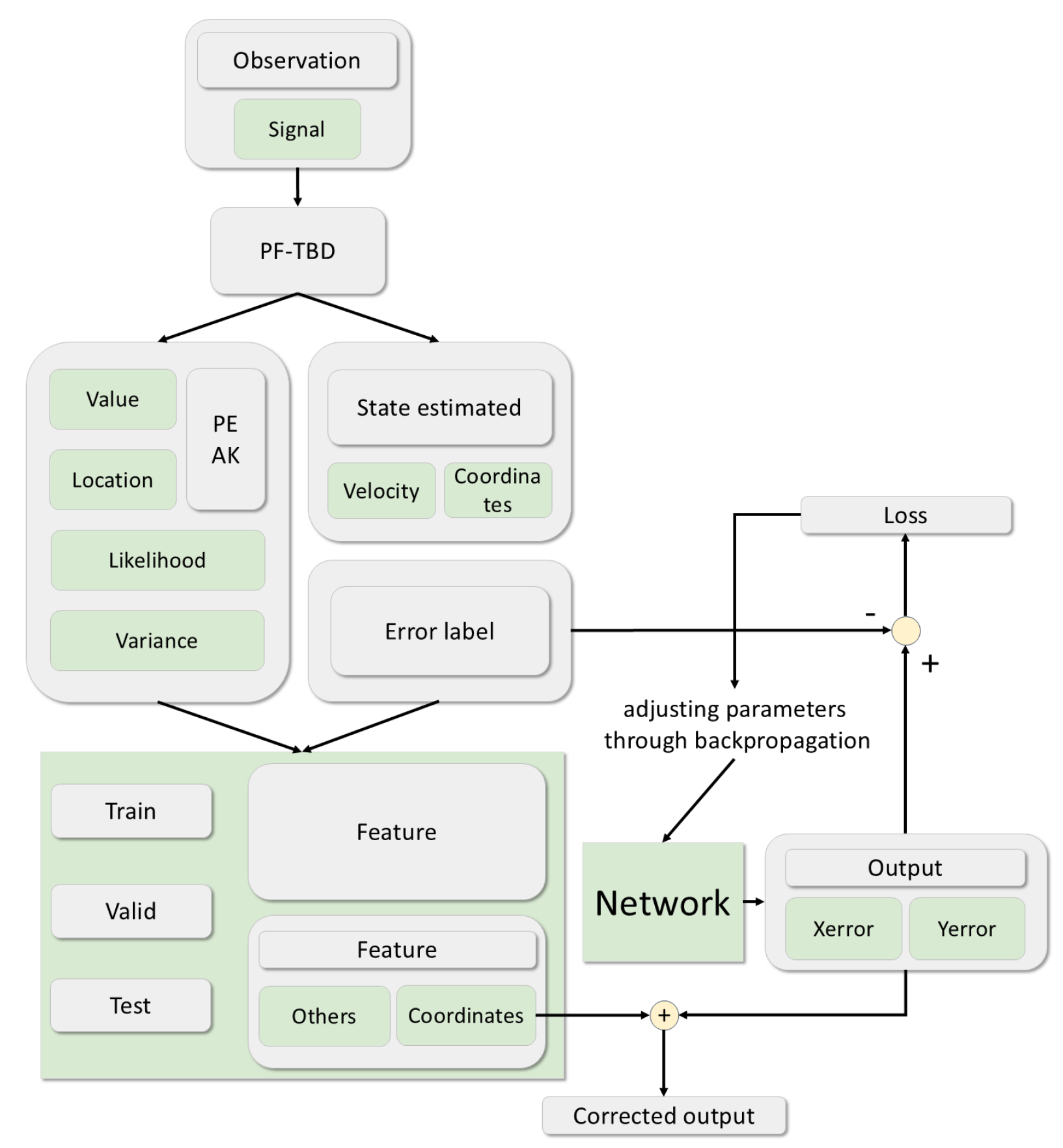
5.2. BiLSTM-Attention for Error Prediction
5.3. Error Correction with Network
6. Simulation and Results
6.1. Simulation and Experimental Setup
6.2. Dataset Construction
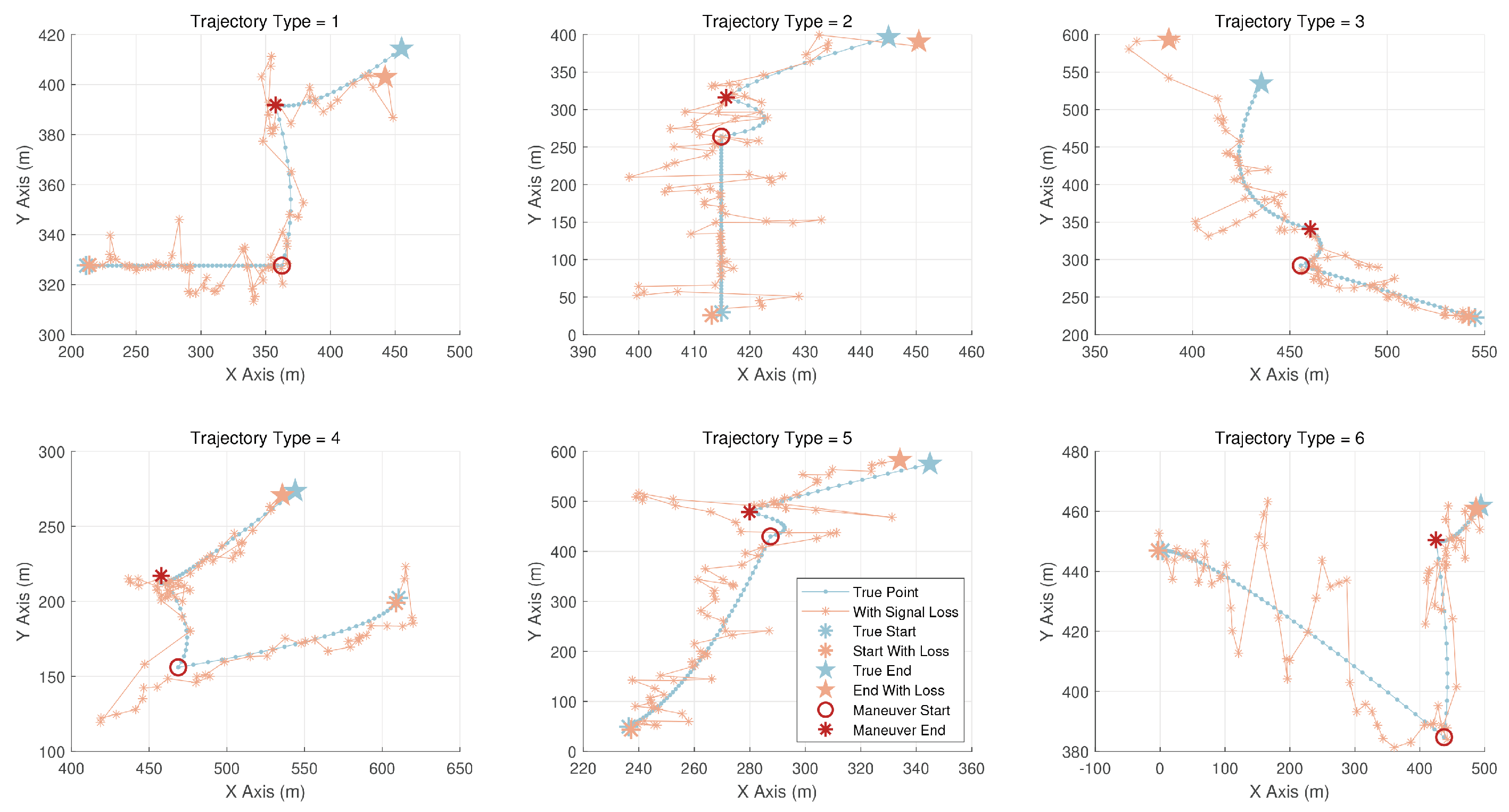
6.2.1. Trajectory Data
6.2.2. Feature Extraction at Each Time Step
6.2.3. Normalization and Dataset Preparation
- Input: A sequence of time steps, where each step contains a feature vector that includes information such as position, velocity, acceleration, and likelihood values.
- Output: The predicted error in the x and y coordinates at the corresponding time step allows the network to learn temporal dependencies and predict localization errors over time.
6.3. Experimental Evaluation Indicators
6.4. Result
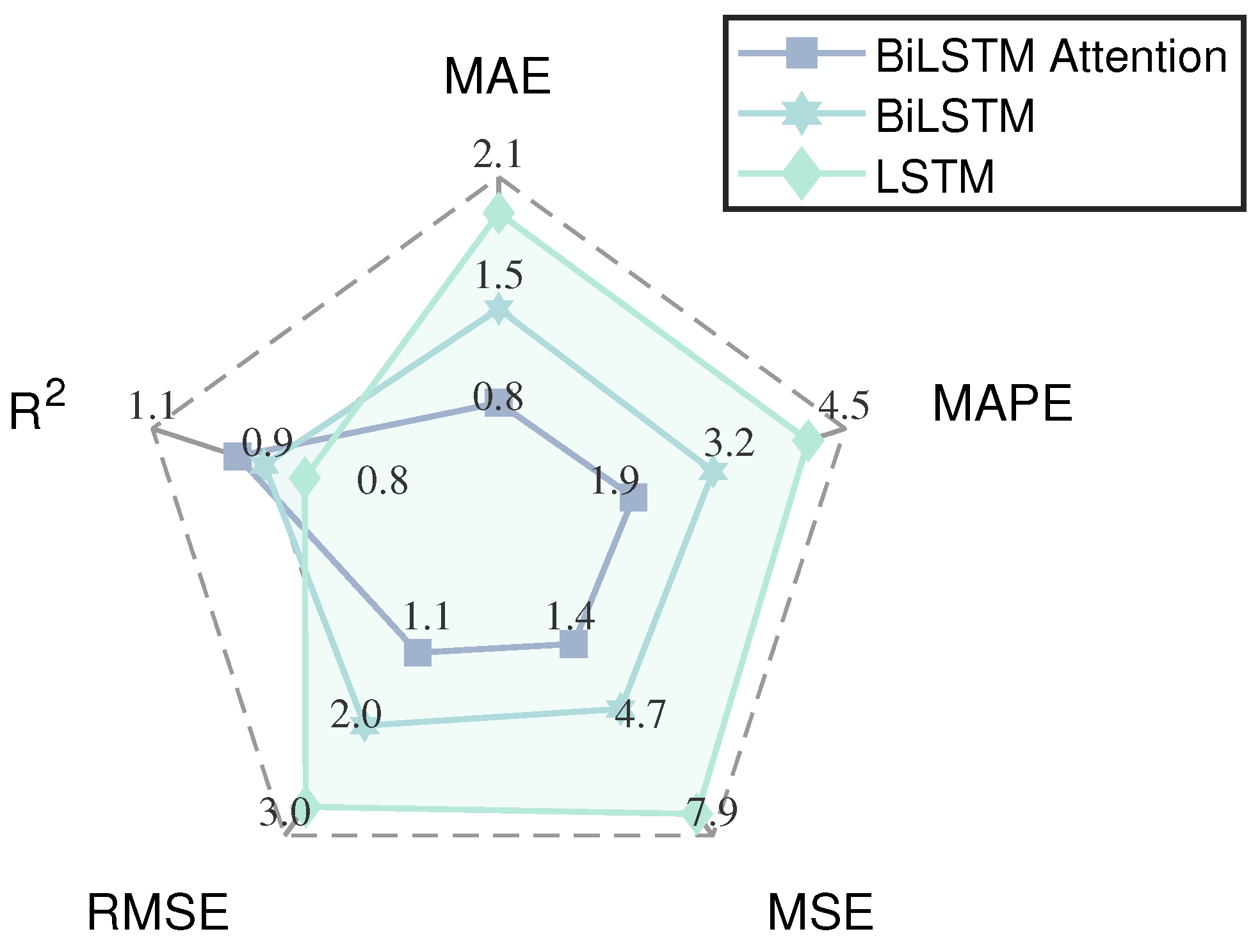
6.4.1. Performance Comparison
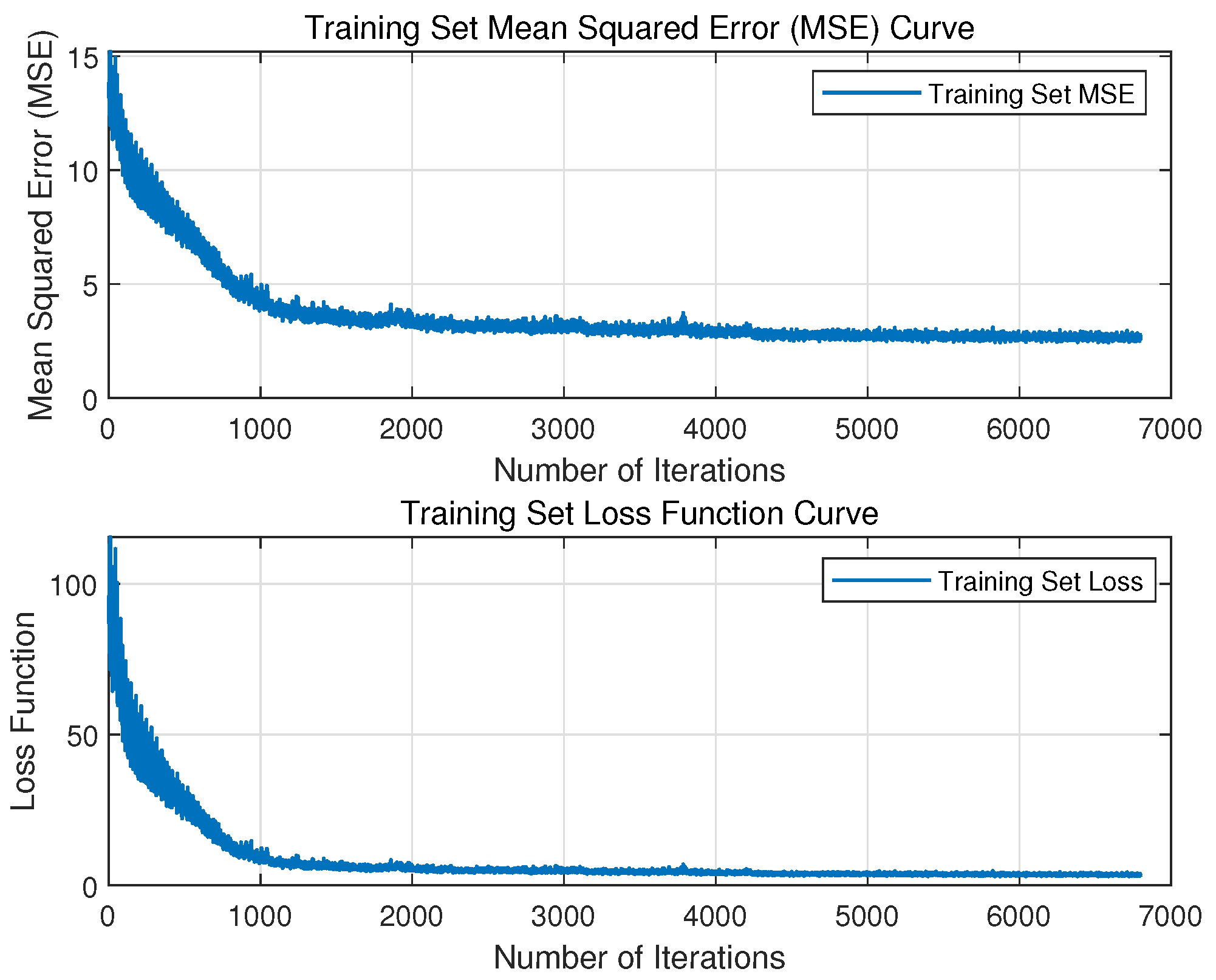
6.4.2. Training Loss and RMSE
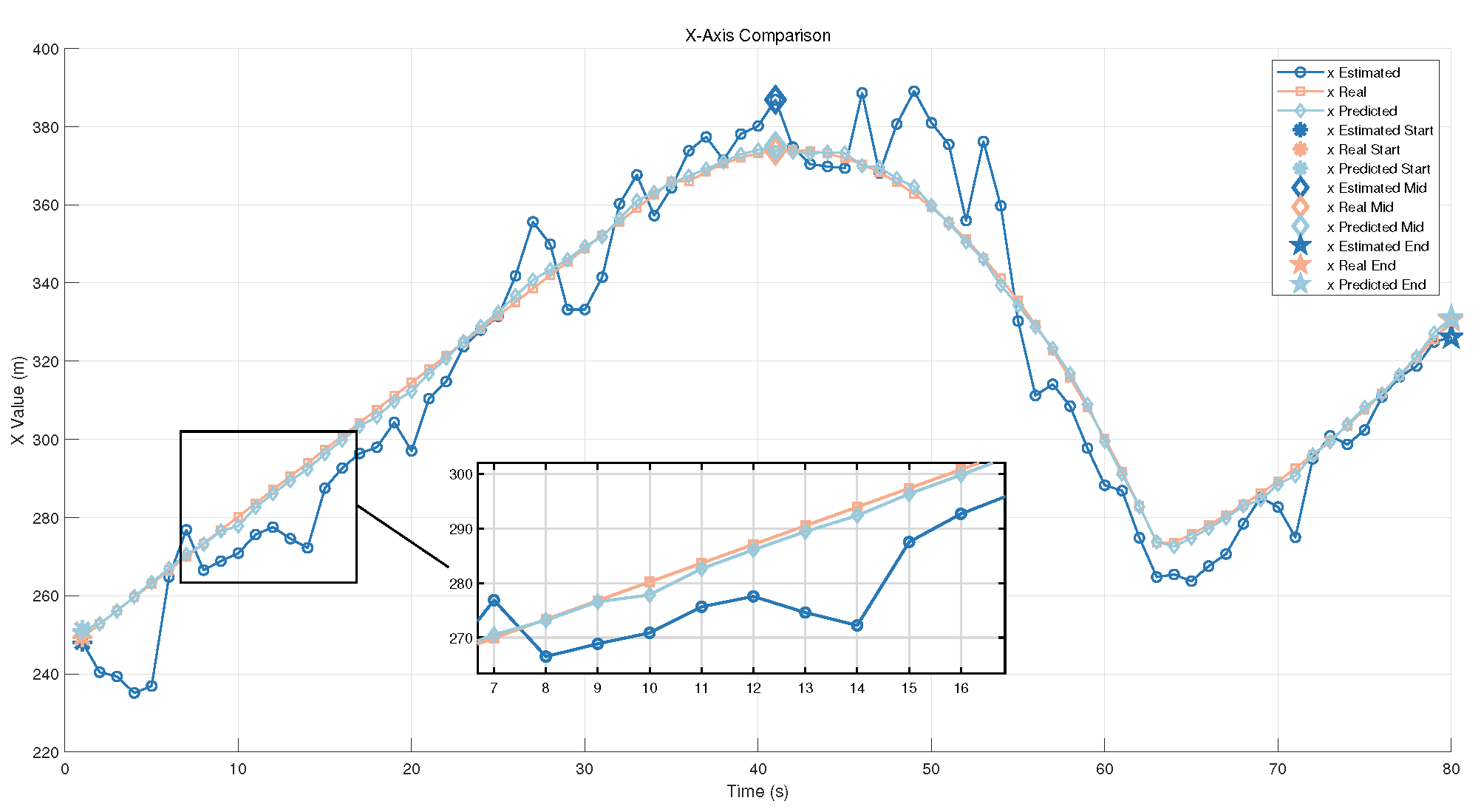
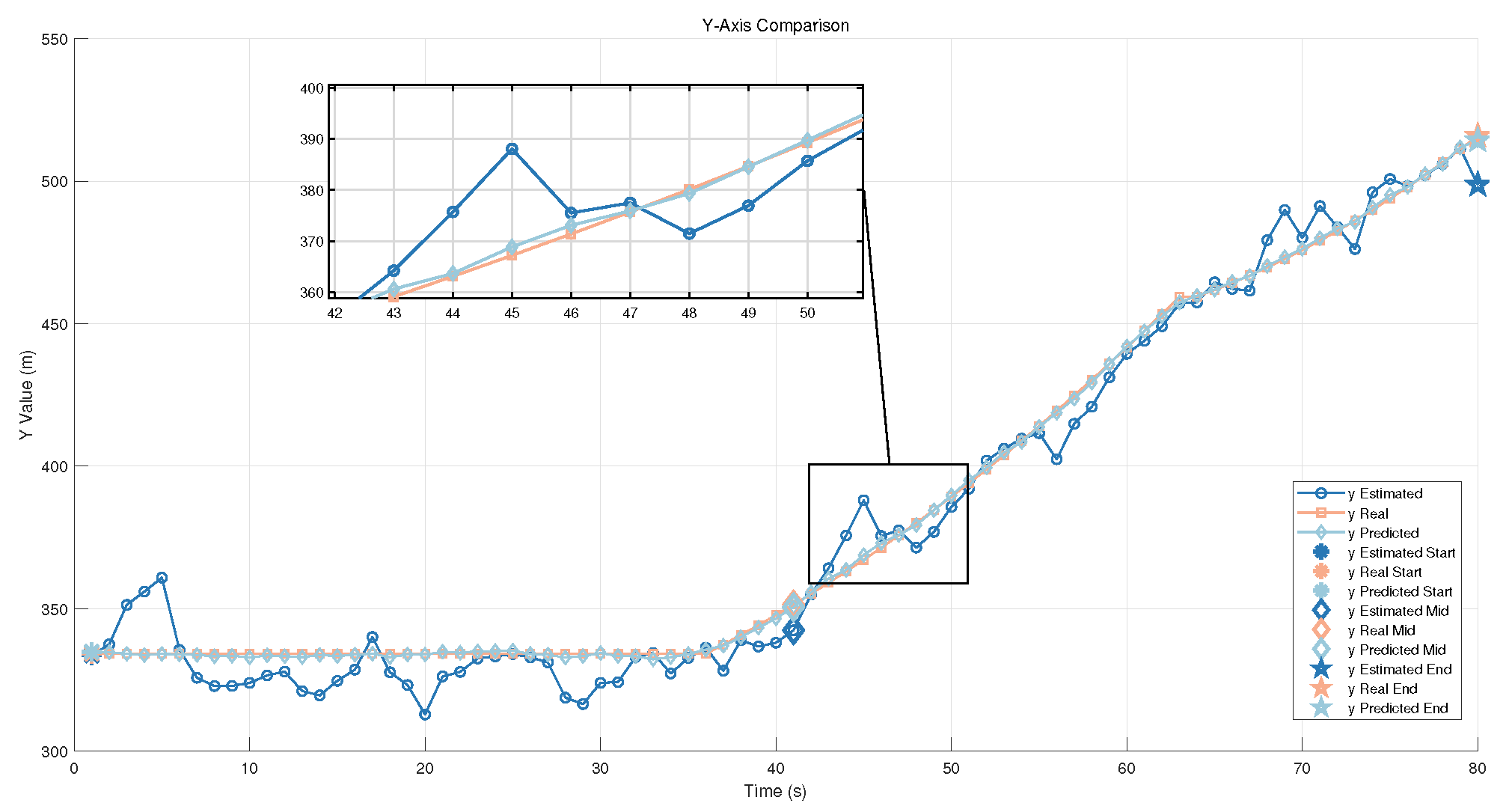
6.4.3. Position Estimation Error
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
DURC Statement
Conflicts of Interest
References
- Lv, P.-F.; Guo, J.; Lv, J.-Y.; He, B. Integrated Navigation of Autonomous Underwater Vehicle Based on HG-RNN and EKF. In Proceedings of the OCEANS 2024, Singapore, 15–18 April 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, S.; Liu, G.; Meng, W. Range-Only Single Beacon Based Multisensor Fusion Positioning for AUV. IEEE Sens. J. 2023, 23, 23399–23409. [Google Scholar] [CrossRef]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Li, J.; Wang, T. Underwater Localization Techniques. Underw. Acoust. J. 2023, 18, 88–97. [Google Scholar]
- Aditya, R.; Balasubramanian, S. Survey of underwater acoustic localization methods. Ocean Eng. 2018, 20, 105–117. [Google Scholar]
- Morelande, M.; Ristic, B. Signal-to-noise ratio threshold effect in track before detect. IET Radar Sonar Navig. 2009, 3, 601–608. [Google Scholar] [CrossRef]
- Fang, Q.; Wang, X. Non-cooperative MPSK modulation detection using machine learning techniques. In Proceedings of the 2021 IEEE International Conference on Communications, Montreal, QC, Canada, 14–18 June 2021; pp. 1–5. [Google Scholar]
- Wang, Y.; Yan, H.; Pan, C.; Liu, S. Measurement-Based Analysis of Characteristics of Fast Moving Underwater Acoustic Communication Channel. In Proceedings of the 2022 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 12–13 December 2022; pp. 47–52. [Google Scholar] [CrossRef]
- Wang, J.; Cai, P.; Yuan, D. An Underwater Acoustic Channel Simulator for UUV Communication Performance Testing. In Proceedings of the 2010 IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; pp. 2286–2290. [Google Scholar] [CrossRef]
- Coskun, A.; Kale, I. Blind Multidimensional Matched Filtering Techniques for Single Input Multiple Output Communications. IEEE Trans. Instrum. Meas. 2010, 59, 1056–1064. [Google Scholar] [CrossRef]
- Hamidi, E.; Weiner, A.M. Phase-Only Matched Filtering of Ultrawideband Arbitrary Microwave Waveforms via Optical Pulse Shaping. J. Light. Technol. 2008, 26, 2355–2363. [Google Scholar] [CrossRef]
- Daffalla, M.M. Adaptive multifunction filter for radar signal processing. In Proceedings of the 2013 International Conference on Computing, Electrical and Electronic Engineering (ICCEEE), Khartoum, Sudan, 26–28 August 2013; pp. 35–39. [Google Scholar] [CrossRef]
- Naus, K.; Piskur, P. Applying the Geodetic Adjustment Method for Positioning in Relation to the Swarm Leader of Underwater Vehicles Based on Course, Speed, and Distance Measurements. Energies 2022, 15, 8472. [Google Scholar] [CrossRef]
- Bi, X.; Du, J.; Zhang, Q.; Wang, W. Improved Multi-Target Radar TBD Algorithm. J. Syst. Eng. Electron. 2015, 26, 1229–1235. [Google Scholar] [CrossRef]
- Aharonovich, I.; Bray, K.; Shimoni, O. Florescent Nanodiamonds for Biomedical Applications. In Proceedings of the 2016 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 June 2016; p. 1. [Google Scholar]
- Li, H.; Zhang, Z. Long-baseline navigation with multi-model particle filters. In Proceedings of the IEEE Oceans Conference, Seattle, WA, USA, 27–31 October 2019; pp. 300–305. [Google Scholar]
- Pan, H.; Zhang, L. Impact of time synchronization attacks on underwater sensor networks. IEEE Trans. Sens. Netw. 2022, 21, 1213–1222. [Google Scholar]
- Smith, A.; Doe, J. Obstacle avoidance in autonomous underwater vehicles: A review. Electronics 2021, 11, 2301. [Google Scholar]
- Liu, C.; Lv, Z.; Xiao, L.; Su, W.; Ye, L.; Yang, H.; You, X.; Han, S. Efficient Beacon-Aided AUV Localization: A Reinforcement Learning Based Approach. IEEE Trans. Veh. Technol. 2024, 73, 7799–7811. [Google Scholar] [CrossRef]
- Stefanidou, A.; Politi, E.; Chronis, C.; Dimitrakopoulos, G.; Varlamis, I. A Deep Reinforcement Learning Approach for Navigation and Control of Autonomous Underwater Vehicles in Complex Environments. In Proceedings of the 2024 18th International Conference on Control, Automation, Robotics and Vision (ICARCV), Dubai, United Arab Emirates, 12–15 December 2024; pp. 750–755. [Google Scholar] [CrossRef]
- Yao, J.; Yang, J.; Zhang, C.; Zhang, J.; Zhang, T. Autonomous Underwater Vehicle Trajectory Prediction with the Nonlinear Kepler Optimization Algorithm–Bidirectional Long Short-Term Memory–Time-Variable Attention Model. J. Mar. Sci. Eng. 2024, 12, 1115. [Google Scholar] [CrossRef]
- Li, C.; Hu, Z.; Zhang, D.; Wang, X. System Identification and Navigation of an Underactuated Underwater Vehicle Based on LSTM. J. Mar. Sci. Eng. 2025, 13, 276. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Qi, B.; Hao, Y. Long Baseline Acoustic Localization Based on Track-Before-Detect in Complex Underwater Environments. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Fortmann, T. Target Tracking: A Bayesian Approach; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Maskell, S.; Gordon, N. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. Proc. IEEE 2002, 92, 401–422. [Google Scholar]
- Michaels, J.E.; Michaels, T.E. Detection of sudden target maneuvers in particle filters. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1075–1091. [Google Scholar]
- Ma, X.; Karkus, P.; Hsu, D.; Lee, W.S. Particle Filter Recurrent Neural Networks. arXiv 1905. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Li, Q.; Xiao, Y.; Ban, X. Passive Sonar Target Tracking Based on Deep Learning. J. Mar. Sci. Eng. 2022, 10, 181. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Simulation Area | 1000 m × 1000 m |
| Localization System | Long Baseline (LBL) |
| Buoy Positions | [(0, 0, −5), (1000, 0, −5), |
| (1000, 1000, −5), (0, 1000, −5)] | |
| Water Depth | 200 m |
| Sound Speed | 1520 m/s |
| Carrier Frequency | 37.5 kHz |
| Number of Particles | 2500 |
| Max Range () | 20 m |
| Max Velocity () | 20 m/s |
| Signal-to-Noise Ratio (SNR) | −12 dB |
| Pulse Repetition Frequency (PRF) | 1 Hz |
| Pulse Repetition Time (PRT) | 1 s |
| Pulse Width | 10 ms |
| Pulse Bandwidth | 100 Hz |
| Sampling Rate () | 2 kHz |
| Waveform | Rectangular Pulse |
| Bottom Loss | 10 dB |
| Number of Paths | 10 |
| Type | Description |
|---|---|
| 1 | Lateral movement |
| 2 | Vertical movement |
| 3 | Diagonal movement (combining lateral and vertical speeds) |
| 4 | Curved movement with lateral acceleration |
| 5 | Curved movement with vertical acceleration |
| 6 | Complex curved movement with both lateral and vertical acceleration |
| Metric | BiLSTM-Attention | BiLSTM | LSTM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Validation | Test | Training | Validation | Test | Training | Validation | Test | |
| MAE | 0.72368 | 0.88564 | 0.90614 | 1.0043 | 1.4121 | 1.4079 | 1.419 | 1.9544 | 1.919 |
| MAPE | 2.8529 | 4.2637 | 2.1524 | 3.8393 | 7.1145 | 3.0427 | 4.6777 | 8.5696 | 4.1049 |
| MSE | 0.90529 | 1.439 | 1.5599 | 1.7915 | 3.8673 | 3.7198 | 3.7154 | 7.6711 | 7.211 |
| RMSE | 0.95147 | 1.1996 | 1.249 | 1.3385 | 1.9666 | 1.9287 | 1.9275 | 2.7697 | 2.6853 |
| 0.98869 | 0.98145 | 0.98298 | 0.97657 | 0.94615 | 0.95219 | 0.9507 | 0.89159 | 0.90554 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Lou, Y.; Zhao, Y.; Sun, S.; Cheng, J. BiLSTM-Attention-PFTBD: Robust Long-Baseline Acoustic Localization for Autonomous Underwater Vehicles in Adversarial Environments. Drones 2025, 9, 204. https://doi.org/10.3390/drones9030204
Jia Y, Lou Y, Zhao Y, Sun S, Cheng J. BiLSTM-Attention-PFTBD: Robust Long-Baseline Acoustic Localization for Autonomous Underwater Vehicles in Adversarial Environments. Drones. 2025; 9(3):204. https://doi.org/10.3390/drones9030204
Chicago/Turabian StyleJia, Yizhuo, Yi Lou, Yunjiang Zhao, Sibo Sun, and Julian Cheng. 2025. "BiLSTM-Attention-PFTBD: Robust Long-Baseline Acoustic Localization for Autonomous Underwater Vehicles in Adversarial Environments" Drones 9, no. 3: 204. https://doi.org/10.3390/drones9030204
APA StyleJia, Y., Lou, Y., Zhao, Y., Sun, S., & Cheng, J. (2025). BiLSTM-Attention-PFTBD: Robust Long-Baseline Acoustic Localization for Autonomous Underwater Vehicles in Adversarial Environments. Drones, 9(3), 204. https://doi.org/10.3390/drones9030204







