Deep Reinforcement Learning-Enabled Trajectory and Bandwidth Allocation Optimization for UAV-Assisted Integrated Sensing and Covert Communication

Abstract

The growing interest in integrated sensing and communication (ISAC) has accelerated the development of unmanned aerial vehicles (UAVs) and drones for secure data transmission. In this study, the optimization of UAV trajectory and bandwidth allocation within the ISAC framework is investigated, with a focus on covert communication under energy constraints. We propose a novel deep reinforcement learning (DRL) algorithm, Soft Actor-Critic for Covert Communication and Charging (SAC-CC), to address this problem. The SAC-CC algorithm maximizes the CCTR by dynamically allocating bandwidth for sensing and communication tasks while adjusting the UAV’s trajectory to manage energy consumption. This approach ensures accurate tracking of the adversarial UAV to maintain effective covert communication. Experimental results show that SAC-CC significantly outperforms existing DRL algorithms in CCTR and improves UAV endurance. Also, its robustness under different adversarial trajectories, covert communication requirements, and charging conditions is validated. Furthermore, the UAV’s flight altitude, along with the number and distribution pattern of adversarial UAVs, directly affect covert communication performance. Finally, the study emphasizes the trade-offs among bandwidth allocation, sensing accuracy, and the balance between power spectral density and UAV energy capacity, providing key insights for the practical configuration of bandwidth and energy parameters in UAV-assisted ISAC systems.

1. Introduction

Unmanned aerial vehicles (UAVs)/drones have emerged as a pivotal technology within contemporary wireless networks, leveraging their distinctive aerial advantages and operational flexibility [1]. They play an increasingly prominent role in applications requiring real-time data acquisition and dissemination, such as environmental monitoring, traffic surveillance, and military reconnaissance [2,3,4,5]. These applications demand not only efficient data collection but also rapid response capabilities, rendering UAVs indispensable for covert and time-sensitive missions where operational secrecy is paramount. Consequently, the significance of UAVs in covert operations is evident. Their value in such missions is further amplified by their stealth capabilities and ability to access otherwise inaccessible areas.

With the advent of 6G technology, the increasing demand for high data rates, low latency, and enhanced connectivity has positioned integrated sensing and communication (ISAC) systems as a promising framework to address these challenges [6]. ISAC systems are broadly categorized into three fundamental types: time division multiplexing (TDM), frequency division multiplexing (FDM), and simultaneous same-frequency ISAC [2]. Each type employs distinct strategies to manage the separation or integration of sensing and communication functionalities at the physical layer, optimizing performance and resource utilization. TDM ISAC sequentially performs sensing and communication tasks, offering straightforward implementation and mitigating direct interference [7]. For instance, in [8], researchers utilized a millimeter-wave dual-mode radar in intelligent vehicle and highway systems to control vehicle distances effectively. The radar mode was employed to measure distance, while the communication mode facilitated the exchange of critical data, demonstrating the potential of time-division technology in enhancing road safety and communication efficiency. However, TDM physically segregates sensing and communication functions, which potentially compromises system efficiency or spectral utilization. Thus, simultaneous same-frequency ISAC, which executes sensing and communication tasks concurrently, has garnered significant attention for its ability to share antennas and RF chains, thereby significantly enhancing spectrum efficiency. For instance, a direct sequence ultra-wideband-based integrated radar and communication system employs distinct pseudo-noise codes for code division multiplexing, boosting overall system performance [9]. Simultaneous same-frequency ISAC often encounters significant design complexity due to mutual interference between sensing and communication signals [10]. To address this challenge, optimizing resource allocation becomes essential for balancing the trade-off between communication and sensing to enhance overall system performance [11]. Unlike simultaneous same-frequency ISAC, frequency division multiplexing (FDM) ISAC operates sensing and communication on distinct frequency bands, improving spectral resource utilization. For instance, an orthogonal frequency-division multiple (OFDM) ISAC system in [12] optimized OFDM signal structures, enhancing accuracy in angle, distance, and velocity estimation and significantly improving ISAC performance. Building on this, we propose a dynamic frequency division multiplexing (DFDM) ISAC scheme, which dynamically allocates bandwidth between sensing and communication tasks [13]. DFDM retains the flexibility of traditional FDM while offering enhanced adaptability through real-time adjustments based on operational requirements. Unlike TDM, DFDM eliminates inefficiencies caused by time-switching and reduces interference by assigning separate frequency bands for sensing and communication. These features make DFDM particularly advantageous in scenarios demanding efficient spectrum utilization and interference management, such as UAV-assisted covert communication systems.

Given these advantages, UAVs can serve as cost-effective airborne platforms to support ISAC services. The integration of UAVs with ISAC systems is critical for various applications, including traffic accident rescue operations, detection of unauthorized surveillance activities, and connectivity enhancement in areas with surging temporary service demands. Numerous studies have investigated UAV-assisted ISAC systems to further leverage UAVs’ mobility, covert communication capabilities, and cost-efficiency [14,15,16,17,18,19,20]. For example, in [18], the authors proposed a framework for beamforming design and trajectory optimization in a UAV-empowered adaptable ISAC system, enhancing system performance by jointly optimizing the UAV’s trajectory and beamforming strategies. An alternating optimization algorithm was employed to address the non-convex problem, maximizing average throughput while ensuring quality of service for both communication and sensing. Similarly, ref. [19] explored cooperative trajectory planning and resource allocation, formulating a joint problem to minimize Cramér-Rao lower bounds (CRLB) for target location estimation under communication QoS constraints. By decomposing the problem into sub-problems, efficient algorithms were proposed to achieve optimal solutions. Another study [20] focused on real-time trajectory design for secure UAV-ISAC communications, using an EKF-based method to track the legitimate user’s location and an iterative algorithm based on successive convex approximation (SCA) to solve the non-convex optimization problem.

Despite significant theoretical and methodological advancements, UAV trajectory design and resource allocation in ISAC and covert communication still face practical challenges. Many studies rely on convex optimization approaches, which struggle to handle the dynamic and complex nature of real-world scenarios. Approximation methods that transform non-convex problems into convex ones or use iterative solutions often fail to achieve global optima. Additionally, existing research always oversimplifies the motion of adversarial UAVs, assuming stationary or known trajectories, which is rarely realistic. Moreover, the issue of UAVs’ limited battery capacity is often ignored, which significantly impacts mission sustainability and performance, particularly in covert communication operations where energy constraints can be a major bottleneck. To address these challenges, deep reinforcement learning (DRL) provides a more adaptive and efficient solution. Algorithms like DQN [16] and TD3 [17] have been applied to UAV navigation and control, while the Soft Actor-Critic (SAC) algorithm has shown promise in balancing exploration and exploitation. SAC has been successfully used in mobile edge computing for secure data transfer [21], demonstrating its effectiveness in stochastic and dynamic environments, making it well suited for UAV applications. Hence, this study proposes a novel framework incorporating the SAC-CC algorithm into the UAV-assisted ISAC system, with a particular emphasis on energy constraints in covert communication scenarios. Specifically, our framework addresses an eavesdropping confrontation scenario involving friendly and adversarial UAVs. In this context, the friendly UAV, referred to as Alice (A-UAV), is tasked with conducting covert communication with the base station (BS). Meanwhile, the adversarial UAV, referred to as Willie (W-UAV), operates with an unknown trajectory and aims to eavesdrop on the communication between A-UAV and the BS. To counter this threat, the A-UAV needs to estimate the trajectory of the W-UAV using its sensing capabilities and then strategically plan its own flight path and dynamically allocate bandwidth resources to more effectively accomplish the covert communication mission. Thus, the primary objective of this study is to maximize the cumulative covert transmission rate (CCTR) by jointly optimizing the A-UAV’s trajectory and dynamic bandwidth allocation between sensing and communication under limited bandwidth.

This study aims to maximize the CCTR by jointly optimizing the A-UAV’s trajectory and dynamic bandwidth allocation under limited battery capacity. To achieve this, the A-UAV must design its flight path based on the W-UAV’s trajectory, which is unknown and must be estimated using its sensing capabilities. However, radar position estimation errors directly impact the A-UAV’s ability to predict the W-UAV’s movements, thereby affecting covert communication performance. Additionally, the A-UAV operates under strict battery energy constraints, as flying, sensing, and communication tasks all consume energy. When the remaining energy is not sufficient to support both the upcoming ISAC task and the flying to the nearest charging station after the task, the A-UAV must immediately charge to avoid depletion. Charging interrupts sensing and communication tasks, leading to increased radar estimation errors, disrupted W-UAV tracking, and degraded covert communication quality due to suboptimal trajectory planning. In summary, energy constraints and the charging mechanism serve as objective constraints, while radar estimation errors indirectly affect covert communication performance. Results of this study emphasize the trade-off between covert communication performance, radar accuracy, and energy efficiency, highlighting their joint impact on optimizing system performance under real-world scenarios. The key contributions of this work are as follows:

• This study introduces a dynamic bandwidth allocation framework for UAV-assisted ISAC, integrating energy management into A-UAV trajectory optimization. It dynamically tracks W-UAV trajectories to optimize covert communication and reconnaissance under energy and charging constraints. This design ensures efficient task execution in energy-constrained environments, facilitating real-world deployment.
• A specialized DRL algorithm, SAC-CC, is developed to address the high dynamics of the optimization problem. SAC-CC is tailored to adapt to stochastic rewards and real-time online adjustments, significantly improving A-UAV performance and adaptability in complex W-UAV scenarios compared to traditional methods.

2. System Model

As illustrated in Figure 1, we consider a scenario where the A-UAV assists ISAC in making covert communication with a BS while defending against an adversarial W-UAV. Each ISAC task lasts for a fixed duration of $\delta$, during which the A-UAV performs both sensing and communications. The A-UAV transmits routine information to the BS at a fixed height h, chosen to minimize path loss and facilitate accurate detection of the adversarial W-UAV’s position. Meanwhile, the W-UAV attempts to eavesdrop from a higher fixed height H to enhance its stealth and expand its reconnaissance range. Utilizing its radar functionality, the A-UAV detects the W-UAV and dynamically adjusts its trajectory to mitigate eavesdropping risks during communications. The BS is located at the origin, with K charging stations ($C{S}_1,C{S}_2,\dots ,C{S}_K$) positioned around it to provide energy replenishment. Depending on its remaining battery energy, the A-UAV decides whether to fly to the nearest CS for charging or proceed with the next ISAC task after completing the current one. No ISAC task is performed while the A-UAV is en route to charge or during the charging process, until it is fully charged. Thus, we define a time slot as the interval between the starting times of two consecutive ISAC tasks. The maximum duration of the A-UAV’s mission is denoted as T.

2.1. Radar Model

For the A-UAV, the transmit symbol $s\left[i\right]$ is concurrently utilized for both uplink communications with the BS and radar tracking of the W-UAV. To optimize the frequency spectrum efficiency of the power amplifier, a fixed, flat power spectral density (PSD) $P_0$ is employed. The communication bandwidth $B_{comm}\left[n\right]$ and radar bandwidth $B_{radar}\left[n\right]$ at the n-th time slot (with the notation ‘$\left[n\right]$’ maintaining consistent meaning throughout this paper) are subject to the constraint $B_{comm}\left[n\right]+B_{radar}\left[n\right]=B_{total}$, where $B_{total}$ is a constant. As a result, the radar’s transmit power can be expressed as $P_{radar}\left[n\right]=P_0{B}_{radar}\left[n\right]$. In practical environments, the uncertainty of signal propagation paths makes it impossible to definitively determine whether the propagation channel from the A-UAV to the W-UAV is in Line-of-Sight (LoS) or Non-Line-of-Sight (NLoS) conditions. Therefore, we employed a method that integrates the channel’s LoS conditions by considering the weighted probabilities of both LoS and NLoS scenarios. The probability of a LoS occurrence is given by:

$${\mathsf{\Gamma }}_{w,\text{LoS}}\left[n\right]={\displaystyle \frac{1}{{\lambda }_{1}exp\left(-{\lambda }_2\left[arcsin\left(\frac{H-h}{d_w\left[n\right]}\right)\right]-{\lambda }_1\right)+1}},$$

(1)

where $d_w\left[n\right]$ denotes the distance from the A-UAV to the W-UAV, and ${\lambda }_1$ and ${\lambda }_2$ are S-curve parameters that depend on the environment. Thus, the radar channel gain is given by

$${\overline{\mathsf{\Lambda }}}_w\left[n\right]={\mathsf{\Gamma }}_{w,\mathrm{LoS}}\left[n\right]{d_w\left[n\right]}^{-{\omega }_{\text{LoS}}}+(1-{\mathsf{\Gamma }}_{w,\text{LoS}}\left[n\right]){d_w\left[n\right]}^{-{\omega }_{\text{NLoS}}},$$

(2)

where ${\omega }_{\text{LoS}}$ and ${\omega }_{\text{NLoS}}$ are the path loss exponents for the LoS and NLoS scenarios, respectively. Thus, the received signal at the W-UAV is given by

$$y_w^i\left[n\right]=e^{j2\pi {\nu }_w\left[n\right]T}\sqrt{{\overline{\mathsf{\Lambda }}}_w\left[n\right]P_{\text{radar}}\left[n\right]}s\left[i\right]+n_w^i\left[n\right],$$

(3)

where i indexes the sequence of L complex-valued symbols transmitted from the A-UAV to the W-UAV, and $e^{j2\pi {\nu }_w\left[n\right]T}$ accounts for the phase shift induced by the Doppler effect, with ${\nu }_w\left[n\right]$ representing the Doppler frequency shift. Each transmitted symbol $s\left[i\right]$ has unit power. $n_w^i\left[n\right]$ is the AWGN at the W-UAV, which follows a complex normal distribution $\mathcal{CN}(0,{\sigma }_w^2)$, where ${\sigma }_w^2$ denotes the noise variance, in practical applications, and ${\sigma }_w$ depends on factors such as environmental interference and the sensitivity of the receiving device [22]. Following [13], the radar estimation rate $R_{\text{radar}}$ in the n-th time slot is given by

$$R_{\text{radar}}\left[n\right]={\displaystyle \frac{1}{2T_{\text{update}}}}{log}_2\left(1+\gamma ·B_{\text{radar}}{\left[n\right]}^3·{d_w\left[n\right]}^{-4}\right),$$

(4)

where $T_{\text{update}}$ is the radar status update interval, $B_{\text{radar}}\left[n\right]$ is the radar signal bandwidth, $d_w\left[n\right]$ represents the distance between the A-UAV and the W-UAV, and $\gamma$ is a constant related to the radar signal’s transmission power, antenna gain, target radar cross-section (RCS), and noise PSD.

The radar target parameters vector ${\mathbf{p}}_r\left[n\right]={[{\nu }_w\left[n\right],{\theta }_w\left[n\right],{\phi }_w\left[n\right]]}^T$ can be estimated by processing the echo signals from the W-UAV, resulting in the estimation ${\widehat{\mathbf{p}}}_r\left[n\right]={[{\widehat{\nu }}_w\left[n\right],{\widehat{\theta }}_w\left[n\right],{\widehat{\phi }}_w\left[n\right]]}^T$, where ${\theta }_w\left[n\right]$ and ${\phi }_w\left[n\right]$ represent the azimuth angle and elevation angle from the A-UAV to the W-UAV, respectively. Considering the relationship between these parameters and the states of the A-UAV and W-UAV, the following equations hold

$$\begin{array}{cc}\hfill {\nu }_w\left[n\right]& ={\displaystyle \frac{2{({\dot{\mathbf{L}}}_w\left[n\right]-{\dot{\mathbf{L}}}_a\left[n\right])}^T({\mathbf{L}}_w\left[n\right]-{\mathbf{L}}_a\left[n\right])f_c}{c{d}_w\left[n\right]}},\hfill \\ \hfill sin{\theta }_w\left[n\right]& ={\displaystyle \frac{x_w\left[n\right]-x_a\left[n\right]}{d_w\left[n\right]cos{\phi }_w\left[n\right]}},\hfill \\ \hfill sin{\phi }_w\left[n\right]& ={\displaystyle \frac{H-h}{d_w\left[n\right]}},\hfill \end{array}$$

(5)

where vector ${\mathbf{L}}_a\left[n\right]$ and ${\dot{\mathbf{L}}}_a\left[n\right]$ represent the position and speed of the A-UAV, respectively. Similarly, ${\mathbf{L}}_w\left[n\right]$ and ${\dot{\mathbf{L}}}_w\left[n\right]$ denote the position and speed of the W-UAV. Given the estimation vector $\widehat{\mathbf{w}}[n-1]={[{\widehat{\mathbf{L}}}_w{[n-1]}^T,{\widehat{\dot{\mathbf{L}}}}_w{[n-1]}^T]}^T$ at time slot $n-1$, the following coarse prediction is made for the next time slot:

$$\widehat{\mathbf{w}}\left[n\right|n-1]=\mathbf{A}\widehat{\mathbf{w}}[n-1],$$

(6)

where $\mathbf{A}=\left[\begin{array}{cc}{\mathbf{I}}_2& \delta {\mathbf{I}}_2\\ \mathbf{O}& {\mathbf{I}}_2\end{array}\right]$, and $\mathbf{O}$ is the 2-order zero matrix. Thus, according to the radar tracking algorithm in [23], the state estimation of the W-UAV at the next time slot is given by

$$\widehat{\mathbf{w}}\left[n\right]=\widehat{\mathbf{w}}\left[n\right|n-1]+{\mathbf{F}}_n\left({\widehat{\mathbf{p}}}_r\left[n\right]-{\overline{\mathbf{p}}}_r\left[n\right]\right),$$

(7)

where ${\overline{\mathbf{p}}}_r\left[n\right]$ is obtained by substituting the W-UAV state with $\widehat{\mathbf{w}}\left[n\right|n-1]$ in (5), and ${\mathbf{F}}_n$ is the Kalman gain matrix determined by the radar estimation rate. A larger $R_{\text{radar}}\left[n\right]$ results in more accurate state estimation of the W-UAV. The radar position estimation error at the n-th time slot is given by

$$e\left[n\right]={\displaystyle \frac{\parallel {\widehat{\mathbf{L}}}_w\left[n\right]-{\mathbf{L}}_w{\left[n\right]\parallel }_2}{\parallel {\mathbf{L}}_w{\left[n\right]\parallel }_2}}.$$

(8)

The $e\left[n\right]$ represents the performance of the sensing functionality, reflecting the inherent trade-off between communication and sensing performance. To maximize the CCTR, the A-UAV must design its flight trajectory based on the W-UAV’s trajectory. However, since the W-UAV’s trajectory is unknown, the A-UAV must estimate it using its sensing capabilities. The resulting position estimation error directly affects its ability to predict the W-UAV’s behavior, ultimately influencing the performance of covert communication.

2.2. Communications Model

For the uplink communications to the BS, the propagation channel can either be Line-of-Sight (LoS) or Non-Line-of-Sight (NLoS). Accordingly, the probability of a LoS occurrence is given by

$${\mathrm{\Gamma }}_{b,\text{LoS}}\left[n\right]={\displaystyle \frac{1}{{\lambda }_{1}exp\left(-{\lambda }_2\left[arcsin\left(\frac{h}{d_b\left[n\right]}\right)-{\lambda }_1\right]\right)+1}},$$

(9)

where $d_b\left[n\right]$ denotes the distance from the A-UAV to the BS. Therefore, the communication channel gain is expressed as

$${\overline{\mathsf{\Lambda }}}_b\left[n\right]={\mathrm{\Gamma }}_{b,\text{LoS}}\left[n\right]{d_b\left[n\right]}^{-{\omega }_{\text{LoS}}}+(1-{\mathrm{\Gamma }}_{b,\text{LoS}}\left[n\right]){d_b\left[n\right]}^{-{\omega }_{\text{NLoS}}}.$$

(10)

Denote the communication transmission power as $P_{\text{comm}}\left[n\right]=P_0{B}_{\text{comm}}\left[n\right]$, and the received signal at the BS is given by

$$y_b^i\left[n\right]=e^{j2\pi {\nu }_b\left[n\right]T}\sqrt{{\overline{\mathsf{\Lambda }}}_b\left[n\right]P_{\text{comm}}\left[n\right]}s\left[i\right]+n_b^i\left[n\right],$$

(11)

where ${\nu }_b\left[n\right]$ represents the Doppler frequency shift and $n_b^i\left[n\right]$ is the AWGN at the BS, which follows a complex normal distribution $\mathcal{CN}(0,{\sigma }_b^2)$, with ${\sigma }_b^2$ being the noise variance which is also influenced by environmental interference and the sensitivity of the receiving device. Thus, the covert transmission rate is

$$R_{\text{comm}}\left[n\right]=B_{\text{comm}}\left[n\right]{log}_2\left(1+{\displaystyle \frac{{\overline{\mathsf{\Lambda }}}_b\left[n\right]P_{\text{comm}}\left[n\right]}{{\sigma }_b^2}}\right).$$

(12)

Considering the potential eavesdropping by W-UAV during transmission, we aim to reduce the eavesdropping probability as much as possible by adopting the constraint from [17] (12a) as follows:

$$l\left[n\right]\le 2{ϵ}^2,$$

(13)

where

$$l\left[n\right]=L\left[ln({\beta }_w\left[n\right]+1)-{\displaystyle \frac{{\beta }_w\left[n\right]}{{\beta }_w\left[n\right]+1}}\right],$$

(14)

and $ϵ$ is a very small threshold determining the required level of covertness, with ${\beta }_w\left[n\right]={\displaystyle \frac{{\overline{\mathsf{\Lambda }}}_w\left[n\right]P_{\text{radar}}\left[n\right]}{{\sigma }_w^2}}$. This ensures the covert uplink communications from the A-UAV to the BS, making it difficult to detect even under scrutiny by the W-UAV.

2.3. Energy Model

Energy constraints and the charging mechanism are essential objective limitations that the A-UAV must consider during covert communication tasks. In our system, the total energy consumption of the A-UAV includes the propulsion power for flying and the ISAC (Integrated Sensing and Communication) power. Given its limited battery capacity, the A-UAV must operate within a finite energy budget. However, the charging process takes time, during which all tasks are halted, including tracking the W-UAV’s trajectory. This interruption increases position estimation errors, ultimately degrading covert communication quality due to suboptimal trajectory planning. Specifically, the flight velocity $V\left[n\right]$ varies within the interval $[V_{\text{min}},V_{\text{max}}]$, and the flying direction is determined by the azimuth angle $\theta \left[n\right]$. Thus, the position vector of the A-UAV at time slot n is updated as

$${\mathbf{L}}_a\left[n\right]={\mathbf{L}}_a[n-1]+V\left[n\right][cos\theta \left[n\right],sin\theta \left[n\right]]\delta ,$$

(15)

when no charging is performed. Specifically, when flying to the nearest CS, the A-UAV always operates at the maximum velocity $V_{\text{max}}$ to minimize delays in detecting the W-UAV caused by deactivating ISAC. During this process, only propulsion energy consumption is considered. Following [24], the propulsion power is given by

$$P_f\left[n\right]=p_1\left(1+{\displaystyle \frac{3v{\left[n\right]}^2}{{\Omega }^2{r}^2}}\right)+p_2{\left(\sqrt{1+{\displaystyle \frac{v{\left[n\right]}^4}{4{\varrho }^4}}}-{\displaystyle \frac{v{\left[n\right]}^2}{2{\varrho }^2}}\right)}^{1/2}+{\displaystyle \frac{1}{2}}q\psi \varkappa {\rm Y}v{\left[n\right]}^3,$$

(16)

where r, $\varkappa$, ${\rm Y}$, and $\psi$ are intrinsic parameters of the rotor used in the A-UAV, representing the rotor radius, rotor solidity, rotor disk area, and fuselage drag coefficient, respectively. Additionally, $\Omega$ and $\varrho$ represent the angular velocity of the rotor and the mean rotor induced velocity in forward flight, respectively. q denotes the air density during flight, $p_1$ is the rotor profile power during hover, and $p_2$ is the induced power during hover. The ISAC power is defined as $P_0{B}_{\text{total}}$, as detailed in Section 2.1, and remains constant throughout the mission. If, after completing a single ISAC task, the remaining battery level is insufficient to support both the next ISAC task and the energy required to fly to the nearest CS for charging after that task, the A-UAV must immediately proceed to charge. Therefore, if no charging occurs, the energy consumption in the n-th time slot is divided into energy for propulsion $P_f\left[n\right]\delta$ and energy for ISAC $P_0{B}_{\text{total}}\delta$. The remaining energy at the end of the n-th time slot is given by

$$\begin{array}{cc}\hfill E\left[n\right]& =E[n-1]-P_f\left[n\right]\delta -P_0{B}_{\text{total}}\delta ,\hfill \\ \hfill {\delta }_c\left[n\right]& =0,\hfill \end{array}$$

(17)

where ${\delta }_c\left[n\right]$ represents the time delay for the next ISAC task. Otherwise, if charging occurs, we have

$$\begin{array}{cc}\hfill E\left[n\right]& =E_{\text{max}},\hfill \\ \hfill {\delta }_c\left[n\right]& ={\displaystyle \frac{d_{cs}\left[n\right]}{V_{\text{max}}}}+{\displaystyle \frac{E_{\text{max}}-\left(E[n-1]-P_f\left[n\right]\delta -P_0{B}_{\text{total}}\delta -\frac{P_f\left[n\right]d_{cs}\left[n\right]}{V_{max}}\right)}{P_c}},\hfill \end{array}$$

(18)

where $d_{cs}\left[n\right]$ is the distance between ${\mathbf{L}}_a\left[n\right]$ and its nearest CS, ${\displaystyle \frac{P_f\left[n\right]d_{cs}\left[n\right]}{V_{max}}}$ represents the propulsion energy consumption required to fly for charging, $E_{max}$ is the maximum total energy, and $P_c$ is the fixed charging power.

2.4. Problem Formulation

Let $C\left[n\right]=1$ or 0 denote whether to fly for charging or not at the end of the n-th ISAC task, respectively. The covert communication rate refers to the communication rate between the A-UAV and the BS in one time slot under the constraint of anti-eavesdropping. Within the maximum mission time T, the CCTR is obtained by summing the covert communication rates of each time slot. To maximize the CCTR, we let $B_{\text{radar}}\left[n\right]=\rho \left[n\right]B_{\text{total}}$, and propose the following optimization model:

$$\begin{array}{cc}& \underset{\rho \left[n\right],V\left[n\right],\theta \left[n\right]}{max}\sum _{n=1}^N{R}_{\mathrm{comm}}\left[n\right]\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \rho \left[n\right]\in [0,1],\hfill \end{array}$$

(19b)

$$\begin{array}{cc}\hfill & V\left[n\right]\in [V_{\text{min}},V_{\text{max}}],\hfill \end{array}$$

(19c)

$$\begin{array}{cc}\hfill & l\left[n\right]\le 2{ϵ}^2,\hfill \end{array}$$

(19d)

$$\begin{array}{cc}\hfill & E[n-1]\ge P_f\left[n\right]\delta +q{d}_{\mathrm{cs}}\left[n\right]:C\left[n\right]=0,\hfill \end{array}$$

(19e)

$$\begin{array}{cc}\hfill & E[n-1]<P_f\left[n\right]\delta +q{d}_{\mathrm{cs}}\left[n\right]:C\left[n\right]=1,\hfill \end{array}$$

(19f)

where Constraint (19b) governs the bandwidth allocation between sensing and communications, (19c) ensures that the A-UAV operates within the regular velocity limits, (19d) prevents eavesdropping, and Constraints (19e) and (19f) determine whether the A-UAV should charge, depending on the remaining energy $E[n-1]$.

3. Deep Reinforcement Learning Solution

3.1. Markov Decision Process Formulation

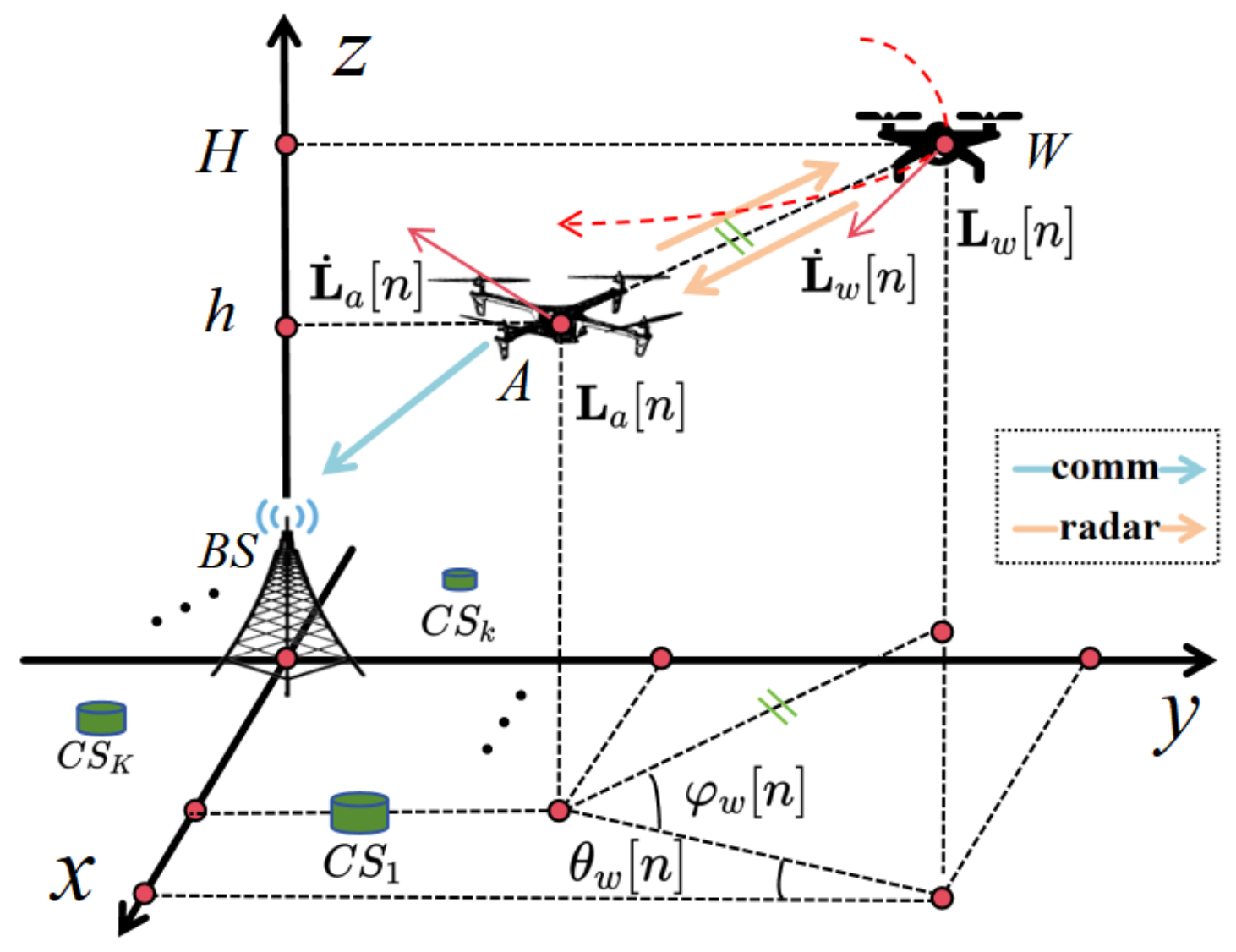
In this section, we reformulate Problem (19a) by optimizing A-UAV trajectory and bandwidth allocation between sensing and communications as a discrete-time Markov Decision Process (MDP). A DRL-based algorithm, SAC-CC, is developed as the solution to this MDP problem. The MDP is represented by the quadruple $<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R}>$, where $\mathcal{S}$ is the state space, $\mathcal{A}$ is the action space, $\mathcal{P}$ is the state transition probability, and $\mathcal{R}$ is the reward function. The state, action, reward, and state transition probability are defined as follows:

(1) The state at the n-th time slot is given by $s\left[n\right]=\{{\mathbf{L}}_a\left[n\right],{\widehat{\mathbf{L}}}_w\left[n\right],{\widehat{\dot{\mathbf{L}}}}_w\left[n\right],E\left[n\right]\}$, where ${\mathbf{L}}_a\left[n\right]=[x_a\left[n\right],y_a\left[n\right]]$ is the horizontal position of the A-UAV, ${\widehat{\mathbf{L}}}_w\left[n\right]=[{\widehat{x}}_w\left[n\right],{\widehat{y}}_w\left[n\right]]$ is the estimated position of the W-UAV, ${\widehat{\dot{\mathbf{L}}}}_w\left[n\right]=[{\widehat{\dot{x}}}_w\left[n\right],{\widehat{\dot{y}}}_w\left[n\right]]$ is the estimated speed of the W-UAV, and $E\left[n\right]$ represents the remaining energy.

(2) The action is defined as $a\left[n\right]=\left\{\rho \right[n],V[n],\theta [n\left]\right\}$.

(3) To facilitate better convergence and optimization, a reward shaping mechanism is introduced to address the requirements of the charging selection mechanism, communication rewards, radar position estimation error penalties, and anti-eavesdropping penalties. Specifically, when the A-UAV is charging, we set $R(s,a)=0$. When not charging, the radar position error and eavesdropping penalties are incorporated into the communication reward. The reward shaping is defined as

$$\begin{array}{c}\hfill R=\left\{\begin{array}{cc}{R}_{\text{comm}}\left[n\right]·(1-k)·(1-tanh\left(e\left[n\right]\right))\hfill & \text{if}l\left[n\right]>2{ϵ}^2\hfill \\ R_{\text{comm}}\left[n\right]·(1-tanh\left(e\left[n\right]\right))\hfill & \text{otherwise}\hfill \end{array}\right.,\end{array}$$

(20)

where $e\left[n\right]$ is the radar position estimation error at the n-th time slot, and

$$k=min(tanh\left({\displaystyle \frac{l\left[n\right]-2{ϵ}^2}{2{ϵ}^2}}\right),0.99),$$

(21)

is the eavesdropping penalty factor.

(4) The state transition probability is denoted as $Pr\left(s\right[n+1\left]\right|s\left[n\right],a\left[n\right])$, which represents the probability of transitioning from state $s\left[n\right]$ to $s[n+1]$ with action $a\left[n\right]$.

3.2. Proposed SAC-CC Algorithm

In this paper, we address environmental uncertainty by employing a policy-based, model-free DRL approach known as SAC. This off-policy actor-critic algorithm is particularly suitable for scenarios involving continuous action spaces [25]. We have tailored the SAC algorithm to handle charging scenarios and covert communication, referred to as SAC-CC. The goal is to optimize the A-UAV’s trajectory and bandwidth allocation between sensing and communications, while adhering to constraints such as covertness, energy limitations, and maximum propulsion power to maximize the CCTR.

As illustrated in Figure 2, to encourage exploration and avoid premature convergence, the SAC-CC incorporates an entropy regularization term. It consists of one actor network parameterized as $\varphi$, and two critic networks parameterized as ${\Theta }_1$ and ${\Theta }_2$ with their corresponding target networks parameterized as ${\Theta }_1^{\prime }$ and ${\Theta }_2^{\prime }$, respectively. The actor network generates a policy ${\pi }_{\varphi }\left(a\right|s)$, which defines the probability distribution of actions given a state s. The critic networks estimate the state-action value functions, $Q_{{\Theta }_1}(s,a)$ and $Q_{{\Theta }_2}(s,a)$. The SAC-CC updates the actor network to maximize the expected cumulative reward, which includes an entropy term, and updates the critic networks by minimizing the temporal difference errors between predicted and target values. For the actor network, the updates are given by the following formulas:

$${\nabla }_{\varphi }J\left(\varphi \right)={\mathbb{E}}_{s,a}\left[{\nabla }_{\varphi }log{\pi }_{\varphi }\left(a\right|s)\left(\underset{i=1,2}{min}{Q}_{{\Theta }_i}(s,a)-\alpha log{\pi }_{\varphi }\left(a\right|s)\right)\right].$$

(22)

Here, (22) is the gradient of the actor network’s loss function that takes into account the impact of the entropy regularization, with respect to its parameters $\varphi$. In the SAC-CC, $\alpha$ is the entropy regularization coefficient which adjusts the randomness of the policy to control the trade-off between exploration and exploitation. For the critic networks, one quantifies the mean squared error between the the estimated state-action value of the critic’s and the target’s as

$$L\left({\theta }_i\right)={\mathbb{E}}_{s,a,s^{\prime },\pi }\left[{\left(Q_{{\Theta }_i}(s,a)-\left(r+\gamma {\mathbb{E}}_{a^{\prime }\sim \pi }\left[\underset{j=1,2}{min}{Q}_{{\Theta }_j^{\prime }}(s^{\prime },a^{\prime })-\alpha log{\pi }_{\varphi }\left(a^{\prime }\right|s^{\prime })\right]\right)\right)}^2\right],i\in \{1,2\}.$$

(23)

Thus, the gradient of (23) can be derived in a similar form to that of (22) and subsequently applied in the training process. To stabilize the learning process, the SAC-CC algorithm employs a soft update rule for the target critic networks:

$${\Theta }_i^{\prime }\leftarrow \tau {\Theta }_i+(1-\tau ){\Theta }_i^{\prime },i\in \{1,2\}.$$

(24)

This soft update rule gradually aligns the target network’s parameters with those of the learned critic networks, where $\tau$ is the soft-update rate, facilitating a smoother learning curve.

The SAC-CC algorithm initializes the replay buffer B and the network weights. The reward function is designed to account for two key aspects: (1) a reduction in communication rewards due to potential eavesdropping by the W-UAV, and (2) penalties for radar position estimation errors. At each time slot n, the agent’s experience, consisting of the current state $s\left[n\right]$, the selected action $a\left[n\right]$, the received reward $r\left[n\right]$, and the subsequent state $s[n+1]$, is stored as a tuple $\left(s\right[n],a[n],r[n],s[n+1\left]\right)$ in the replay buffer B. Once $N_{\text{upd}}$ experiences have been accumulated in B, a mini-batch is sampled to update the network parameters. Each training episode begins with the A-UAV in its initial state $s\left[0\right]$ and continues until the maximum mission duration T is reached.

We now focus on SAC-CC’s core network structure—the actor network and two critic networks—to provide an in-depth analysis of its computational complexity. Assume each network contains M layers. In the actor network ${\pi }_{\varphi }$, the m-th layer consists of ${\iota }_{{\varphi }_m}$ nodes, while in the critic networks, $Q_{{\Theta }_1}$ and $Q_{{\Theta }_2}$, the m-th layers have ${\iota }_{{\Theta }_{1,m}}$ and ${\iota }_{{\Theta }_{2,m}}$ nodes, respectively. For this analysis, the computational cost associated with batch normalization and ReLU activation layers is excluded. During each training iteration, the batch size is B, influencing both forward and backward propagation. The computational complexity of the actor network for forward propagation through a single layer is $O({\iota }_{{\varphi }_m}·{\iota }_{{\varphi }_{m+1}})$. Similarly, the computational complexities for the critic networks $Q_{{\Theta }_1}$ and $Q_{{\Theta }_2}$ are $O({\iota }_{{\Theta }_{1,m}}·{\iota }_{{\Theta }_{1,m+1}})$ and $O({\iota }_{{\Theta }_{2,m}}·{\iota }_{{\Theta }_{2,m+1}})$, respectively. Considering both forward and backward propagation, the overall computational complexity of the SAC-CC algorithm is multiplied by a factor of 2 and can be expressed as

$$O\left(2B·\left(\sum _{m=0}^{M-1}{\iota }_{{\varphi }_m}·{\iota }_{{\varphi }_{m+1}}+\sum _{m=0}^{M-1}{\iota }_{{\Theta }_{1,m}}·{\iota }_{{\Theta }_{1,m+1}}+\sum _{m=0}^{M-1}{\iota }_{{\Theta }_{2,m}}·{\iota }_{{\Theta }_{2,m+1}}\right)\right).$$

(25)

This formula integrates the complexity of the actor network and the two critic networks, and takes into account the impact of the batch size on the overall complexity, as well as the double computation of forward and backward propagation. This analysis allows us to more accurately assess the computational resource requirements of the SAC-CC algorithm under different network configurations, ensuring that our assessment is both comprehensive and accurate.

4. Numerical Results

The numerical simulations are conducted based on the environmental parameters specified in

Table 1. Additional simulation parameters.

Parameter	Description	Value
$t_{\mathrm{up}}$	Radar pulse repetition time	0.001 s
$\delta$	Each single ISAC task lasts time length	5 s
$({\lambda }_1,{\lambda }_2)$	S-curve parameter for LoS probability	(0.5, 0.5)
${\omega }_{\mathrm{LoS}}$	Path loss exponent for Line of Sight	2
${\omega }_{\mathrm{NLoS}}$	Path loss exponent for Non-Line of Sight	3.5
$({\sigma }_w,{\sigma }_b)$	Noise standard deviation	(1, 0.1)
$(h,H)$	Altitude of A-UAV and W-UAV	(200 m, 500 m)
$P_0$	Power spectral density	10 W/MHz
$B_{total}$	Total bandwidth	1 MHz
v	flying velocity	5 m/s–15 m/s
$E_{\max }$	Maximum battery capacity	10,000 J
$P_c$	Charging power	50 W
$2{ϵ}^2$	Anti-eavesdropping threshold	0.01
q	Air density	1.225 kg/m³
$\Omega$	Rotor angular velocity	300 rad/s
$\varrho$	Mean rotor induced velocity in forward flight	4.03 m/s
r	Rotor radius	0.4 m
$\psi$	Fuselage drag coefficient	0.6
$\varkappa$	Rotor solidity	0.05
${\rm Y}$	Rotor disk area	0.503 m²
$p_1$	Rotor profile power during hover	80 W
$p_2$	Induced power during hover	88.6 W

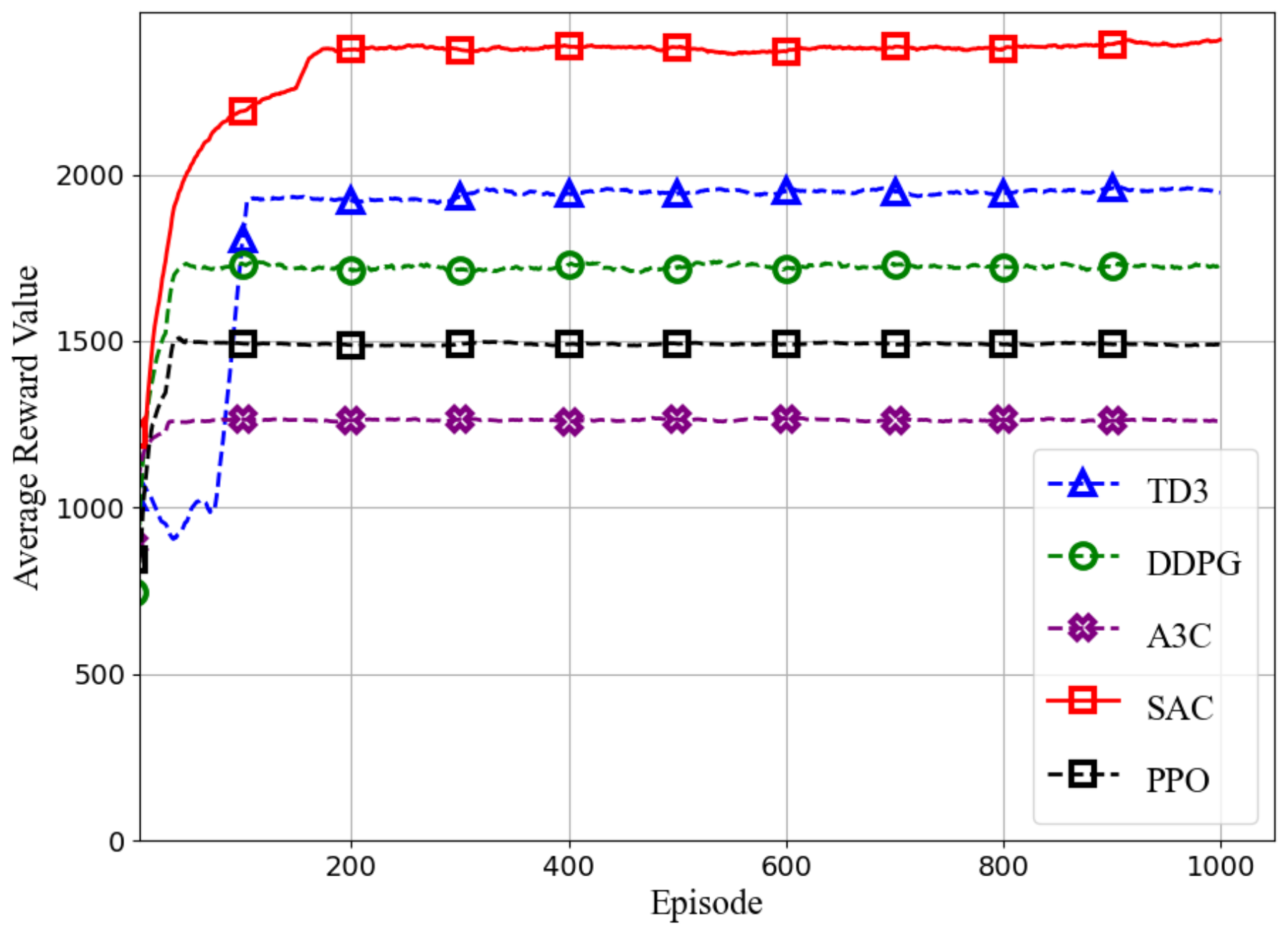
. We first compare our proposed SAC-CC with other policy gradient-based DRL algorithms—DDPG [26], TD3 [27], PPO [28], and A3C [29]—in terms of average reward over training episodes. The numerical simulations are based on the environmental parameters in Table 1. As shown in Figure 3, SAC-CC achieves rapid convergence and high stability, reaching an average reward of approximately 2398. This is due to its entropy-regularized exploration strategy, which effectively balances exploration and exploitation in complex environments. Minor reward fluctuations after convergence are attributed to environmental dynamics, entropy regularization, and the reward function’s variability. TD3, which uses delayed policy updates and dual critic networks to reduce overestimation, converges more slowly at around 1950, while improving stability, it limits exploration compared to SAC-CC. DDPG achieves an average reward of 1725, with delayed updates and noise reduction enhancing stability, but its deterministic policy limits exploration diversity relative to SAC-CC’s stochastic policy. PPO and A3C perform worse, with average rewards of 1488 and 1261, respectively. PPO’s conservative policy updates hinder aggressive exploration, while A3C’s asynchronous execution introduces high variance, leading to instability and suboptimal performance. These results demonstrate SAC-CC’s superiority in UAV-assisted ISAC tasks, excelling in balancing exploration, exploitation, stability, and convergence speed, which are essential for optimizing UAV trajectories and bandwidth allocation in dynamic and adversarial environments.

All experiments are conducted on an NVIDIA GeForce RTX 3060 Laptop GPU. The SAC-CC algorithm achieves an average decision-making time of 0.6 milliseconds per step. For comparison, other state-of-the-art DRL algorithms—A3C, DDPG, TD3, and PPO—have average decision-making times of 0.9 ms, 4.4 ms, 0.8 ms, and 0.6 ms per step, respectively. These results demonstrate that DRL methods, including SAC-CC, can meet the millisecond-level response demands of high-dynamic UAV tracking scenarios. Notably, SAC-CC outperforms other policy gradient DRL methods in real-time performance, underscoring its efficiency and effectiveness in addressing real-time challenges in UAV covert communication and tracking tasks.

In Figure 3, the performance of different DRL algorithms was analyzed from the perspective of training convergence, focusing on their ability to maximize the reward function defined in (20) and (21). Building on this, Figure 4 directly compares the CCTR, which represents the original optimization objective of our UAV-assisted ISAC problem in (19a), across various DRL algorithms. This analysis provides a comprehensive evaluation of DRL algorithms’ adaptability under varying levels of eavesdropping threshold $2{ϵ}^2$ defined in (13). The results in Figure 4 demonstrate that the SAC-CC algorithm achieves the CCTR within the range of 3215–4230 bps/Hz across all values of $2{ϵ}^2$, significantly surpassing the 1299–3198 bps/Hz range achieved by other DRL algorithms. The graph exhibits an upward trend in the average covert transmission rate for all algorithms as $2{ϵ}^2$ increases. This trend reflects the fact that a larger $2{ϵ}^2$ value allows for greater flexibility in the A-UAV’s covert communication, enabling higher transmission rates while maintaining covertness. Notably, the consistently steep trajectory of the SAC-CC algorithm underscores its advanced capability to balance the trade-off between transmission rate and covertness. Therefore, the conclusions derived from both figures collectively validate the optimality of our proposed algorithm over other DRL algorithms, and subsequent experimental results and analyses will focus on SAC-CC.

To explore the trade-off between radar position estimation error $e\left[n\right]$ and CCTR, the results are shown in Figure 5. When $e\left[n\right]$ is low, the improved accuracy of position estimation reduces tracking errors but consumes more bandwidth resources, which could otherwise be used for communication, leading to a decrease in CCTR. Conversely, a higher $e\left[n\right]$ saves radar bandwidth but may compromise position estimation accuracy, increasing tracking errors and similarly reducing CCTR. This highlights the existence of an optimal $e\left[n\right]$ that maximizes CCTR while maintaining covert communication quality. Additionally, Figure 5 demonstrates that the SAC-CC algorithm consistently achieves a higher CCTR compared to other DRL algorithms across different $e\left[n\right]$ values, further demonstrating its superior performance in optimizing UAV trajectory and bandwidth allocation in dynamic environments.

To thoroughly evaluate the effectiveness of the SAC-CC algorithm under various W-UAV flight trajectories, we present the A-UAV’s trajectory, along with the total rewards, the CCTR, and the average covertness indicator $\overline{l}$ derived from (14), as shown in Figure 6. In Scenario W1, the W-UAV stays in close proximity to the BS, requiring the A-UAV to increase its distance from the W-UAV to maintain covert communication, which also increases its distance from the BS. This constraint yields the lowest CCTR of 3436 bps/Hz and an average covertness indicator $\overline{l}$ of 0.0078, remaining below the eavesdropping threshold of 0.01 and highlighting the challenges of maintaining covert communication in such proximity to the BS. In Scenario W2, the W-UAV follows an expanded trajectory, increasing its distance from the BS and providing the A-UAV with greater flexibility in flight. This results in the highest CCTR of 3914 bps/Hz and an average $\overline{l}$ of 0.0082, still below the eavesdropping threshold of 0.01, demonstrating the A-UAV’s improved covert communication performance when the W-UAV is farther from the BS. In Scenario W3, the W-UAV maintains a stable flight pattern consistently on one side of the BS, enabling the A-UAV to operate in a fixed mission area on the opposite side. This configuration minimizes trajectory adjustments and optimizes the balance between covert communication and energy efficiency. The A-UAV achieves a CCTR of 3610 bps/Hz and an average $\overline{l}$ of 0.0019, which remains below the eavesdropping threshold of 0.01. These results underscore the SAC-CC algorithm’s capability to effectively balance covert communication, energy efficiency, and trajectory optimization, ensuring reliable performance across diverse scenarios.

Next, we analyze the effectiveness of the algorithm under varying CS quantities and spatial distributions, with the W-UAV’s trajectory fixed to W2 in Figure 7. In the CS1 distribution, the limited number of charging stations, which are only concentrated in the second quadrant, often places the A-UAV (our unmanned aerial vehicle) in close proximity to the W-UAV, thereby increasing the risk of eavesdropping. Under this setup, the A-UAV achieves a CCTR of 4089 bps/Hz, maintaining effective covertness despite the proximity to the W-UAV. The CS2 distribution, which is only in the first quadrant and far from the origin BS, poses greater challenges for the A-UAV in terms of both charging and communication. As a result, the A-UAV’s CCTR decreases to its lowest value of 3590 bps/Hz, with $\overline{l}$ reaching 0.0072, still below the eavesdropping threshold of 0.01, demonstrating the trade-off challenges between charging and communication in terms of the overall reward. In contrast, the CS3 distribution features a greater number of CSs distributed evenly across all four quadrants, providing the A-UAV with more options. This setup allows for a wider range of trajectories and dynamic adjustments to the distance from the W-UAV, resulting in the highest CCTR of 4271 bps/Hz, and $\overline{l}$ of 0.0059, still below the eavesdropping threshold of 0.01. These results highlight that a well-planned layout of CSs is essential for optimizing the A-UAV’s performance under covert communication and energy constraints.

To thoroughly evaluate the SAC-CC algorithm, we extend its functionality and compare its performance in different multi-adversary UAV scenarios. In Scenario 1, as shown in Figure 8, four W-UAVs with distinct trajectories are located in the first, second, third, and fourth quadrants, respectively. To maximize the CCTR, the A-UAV strategically flies near multiple charging stations (CS) close to the central BS. This setup enables the A-UAV to dynamically plan its trajectory with sufficient energy supply, effectively avoid eavesdropping by adversarial UAVs, and maintain a reliable communication link with the BS. The SAC-CC algorithm achieves high CCTR in this scenario by optimizing trajectory and bandwidth allocation while minimizing eavesdropping risks. In Scenario 2, two adversarial UAVs with broader trajectories span the first–third and third–fourth quadrants, respectively. Here, the A-UAV opts to stay near a charging station in the second quadrant, avoiding the charging stations near the BS due to the proximity of adversarial UAVs, which increases the risk of eavesdropping. This strategy balances the distance between the A-UAV, adversarial UAVs, and the BS, optimizing the trade-off between covert communication and link quality. A comparison of these scenarios highlights the SAC-CC algorithm’s adaptability and robustness in multi-adversary environments. It dynamically adjusts flight strategies based on adversarial UAV layouts and trajectories, ensuring optimal covert communication performance. These results highlight the SAC-CC algorithm’s effectiveness in handling complex adversarial threats, offering strong technical support for real-world multi-adversary UAV scenarios.

Moreover, the impact of algorithm settings and total bandwidth on the CCTR is assessed in Figure 9. We compare three SAC-CC variants: SAC-CC (full covert communication and charging), SAC-FP (fixed propulsion power with velocity at 10 m/s), and SAC-FB (fixed bandwidth allocation ratio of 0.5). The results verify that SAC-CC consistently performs the best under different bandwidths. Also, the CCTRs of all algorithms first increase and then decline after reaching their peaks as the total bandwidth increases from 1 MHz to 15 MHz. This reflects the fundamental trade-off between bandwidth resources and energy consumption, as a larger total bandwidth increases energy consumption, directly affecting the A-UAV’s trajectory and CCTR by necessitating more frequent charging. Furthermore, the SAC-FB model performs the worst, highlighting the importance of effective bandwidth allocation in improving the CCTR. These insights are crucial for adjusting system parameters based on the available bandwidth in practical applications.

Next, we conduct an in-depth analysis of the impact of PSD and A-UAV’s total energy (energy capacity) in Figure 10. The results follow a trend similar to Figure 9: as the A-UAV’s total energy increases, the CCTR initially improves but eventually declines. This occurs because higher total energy extends the A-UAV’s endurance; however, it also prolongs a single charging time, which may reduce the number of effective ISAC tasks. When the drawbacks of extended charging outweigh the benefits of increased endurance, the CCTR begins to decrease. Additionally, the optimal PSD is found to be 10 W/MHz. Moreover, although a higher PSD supports better ISAC performance, it also negatively affects the CCTR due to greater energy consumption and more frequent charging. These findings provide valuable insights and practical recommendations for efficient A-UAV mission planning in the future. For long-duration missions, excessive PSD should be avoided to prevent unnecessary energy consumption. Additionally, the total energy should be optimized rather than maximized, taking into account the trade-off between endurance and charging time.

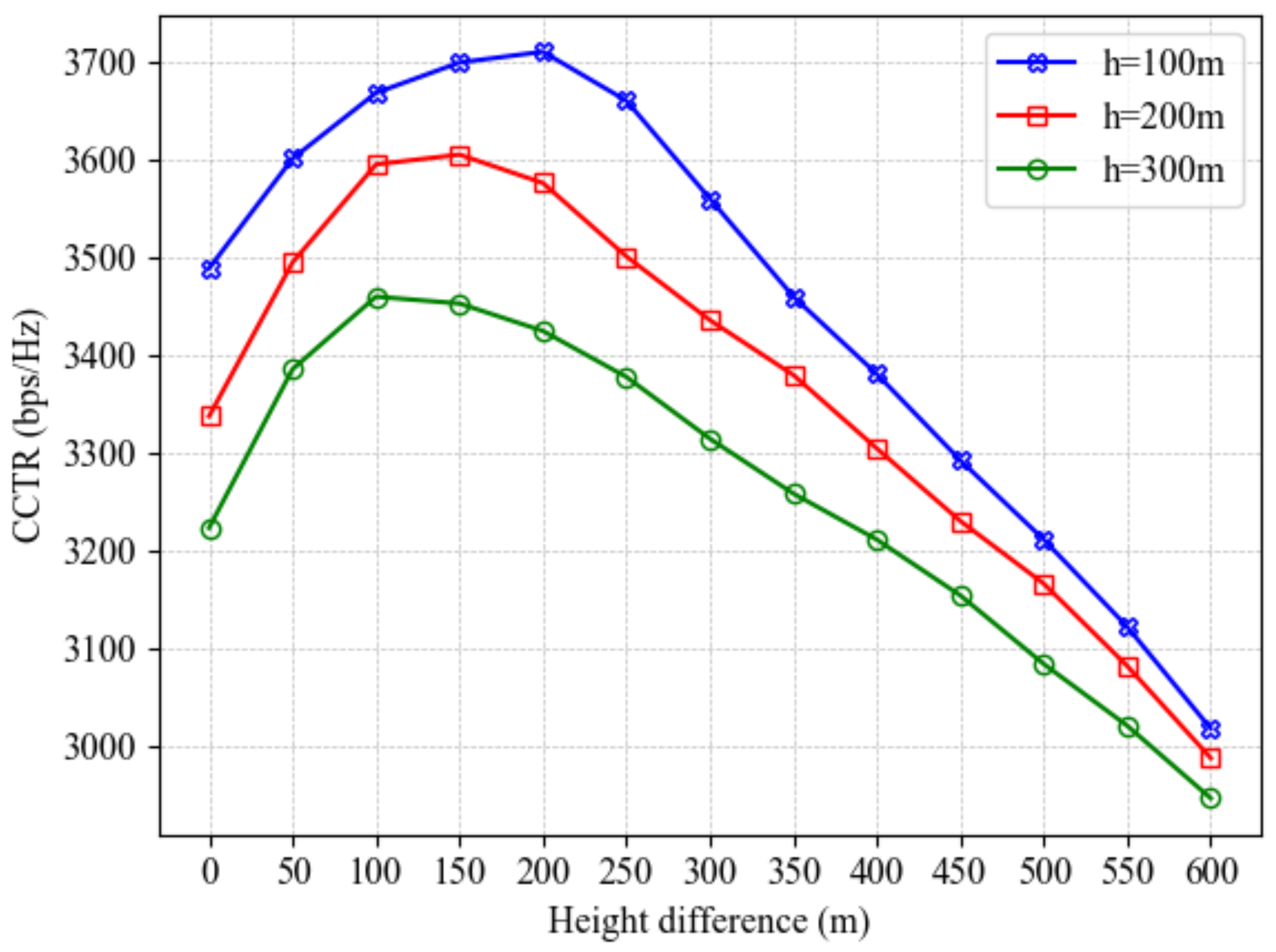
Figure 11 illustrates the impact of the height and height difference between the A-UAV and W-UAV on the CCTR under varying A-UAV altitudes (100 m, 200 m, and 300 m). The x-axis represents the height difference, defined as the W-UAV’s altitude minus the A-UAV’s altitude. Since the W-UAV typically operates at a higher altitude for enhanced stealth and reconnaissance range, the simulations set its flight altitude to be greater than or equal to that of the A-UAV. The results reveal that a lower A-UAV altitude, such as 100 m, achieves a higher CCTR peak and exhibits stronger adaptability. This is because lower altitudes minimize communication link loss between the A-UAV and the ground BS, ensuring a more reliable foundation for covert communication. Even with a small height difference, the A-UAV can maintain high communication quality, resulting in superior CCTR performance. Conversely, higher A-UAV altitudes increase communication link loss with the BS, leading to reduced overall CCTR performance. This highlights the significant influence of A-UAV altitude on covert communication, with lower altitudes being more favorable for maintaining high-quality communication links. For each curve, the CCTR initially increases and then decreases as the height difference grows. When the height difference is small, the W-UAV’s proximity to the A-UAV enhances its eavesdropping capability, limiting the CCTR. However, as the height difference increases, the W-UAV’s eavesdropping capability diminishes due to the greater separation, reducing the likelihood of signal interception and allowing the CCTR to rise. Beyond a certain point, further increases in the height difference significantly impair the A-UAV’s ability to estimate the W-UAV’s position accurately. Since the A-UAV relies on radar signals to track the W-UAV and plan its trajectory, increased estimation errors hinder its ability to maintain efficient covert communication. Ultimately, the negative impact of higher estimation errors outweighs the benefits of reduced eavesdropping capability, causing the CCTR to decline. This analysis suggests that there exists an optimal height difference where the A-UAV can effectively balance the W-UAV’s reduced eavesdropping capability and its own position estimation accuracy, thereby achieving the best covert communication performance.

5. Conclusions

This study proposes an innovative optimization framework for deploying ISAC systems on UAVs, designed to enhance long-term endurance and covert communication performance in dynamic environments. We present the SAC-CC algorithm, which jointly optimizes A-UAV trajectories and bandwidth allocation to maximize the CCTR. Numerical results validate the superiority of the SAC-CC algorithm over other DRL methods, highlighting its robustness and adaptability in complex adversarial scenarios. This study also explores the trade-offs among key parameters, including bandwidth, sensing accuracy, energy consumption, and power spectral density (PSD), offering practical insights for parameter configuration in real-world applications. The proposed SAC-CC algorithm framework demonstrates broad application potential thanks to its robust covert communication planning capabilities and adaptability in highly dynamic UAV confrontation scenarios. In military reconnaissance and patrol missions—characterized by extended durations, high dynamics, and environmental complexity—UAVs must navigate challenging and ever-changing conditions while operating in hostile environments. These scenarios demand long-term covert communication capabilities to minimize the detection risk. The SAC-CC algorithm addresses these challenges by optimizing UAV flight trajectories and communication spectrum allocation, dynamically adjusting paths and strategies to ensure efficient, reliable, and covert communication under such complex conditions. Additionally, the SAC-CC algorithm exhibits strong adaptability to varying distributions of charging stations, allowing it to perform effectively across scenarios with differing levels of charging support, such as in urban and suburban environments. This flexibility further underscores its suitability for diverse real-world applications.

Although this study primarily focuses on optimizing covert communication in one-on-one UAV confrontation scenarios, the proposed SAC-CC algorithm framework exhibits strong scalability, making it adaptable to more complex network environments. As discussed, the extended SAC-CC algorithm maintains robust covert communication capabilities even in scenarios involving multiple adversarial UAVs. Moreover, the algorithm holds promising potential for further extensions. For instance, in scenarios involving a network of multiple friendly UAVs, the SAC-CC algorithm can be adapted to the MASAC (Multi-Agent Soft Actor–Critic) algorithm by incorporating joint actions, shared rewards, updated policy and value function mechanisms, as well as communication and coordination strategies, effectively addressing interactions among multiple agents [30]. Furthermore, the algorithm is capable of adapting to more sophisticated energy management requirements by dynamically optimizing charging strategies and task prioritization. These scalability features open new avenues for future research on covert communication within large-scale UAV confrontation networks, further enhancing the algorithm’s applicability and versatility in complex and dynamic environments.