Increasing Automation on Mission Planning for Heterogeneous Multi-Rotor Drone Fleets in Emergency Response
Highlights
- In less than two minutes we generate efficient trajectories for drones in a heterogeneous fleet to obtain reliable maps with uniform precision.
- A balanced strategy showed benefits in extensive comparisons of decomposition algorithms for non-convex areas with no-fly zones. Consistent gain in trajectories is also observed relative to the state of the art.
- First responders will quickly understand the situation after a disaster and prioritize action thanks to the complete coverage and a precise mapping of large or complex areas.
Abstract
1. Introduction
2. Previous Works
3. Materials and Methods
- The comparison with EAMC in Section 4.3 was performed on a first hardware configuration: Intel(r) Core(tm) i7-1255U (Santa Clara, CA, USA), CPU @ 1700 MHz, 10-Core laptop with 16 GB of RAM, while the validation was executed with a second configuration: Intel(r) Core(tm) i5-7300HQ CPU @ 2.50 GHz 4-Core laptop with 8 GB of RAM. The EAMC written in C++ [38] was executed on the first configuration through Windows Subsystem for Linux (WSL).
- The experiments in Section 4.4 were executed by separating steps. For the partitioning (step 2), executions have been performed with a third hardware configuration: Intel i5-1135G7 (4 Cores) laptop with 16 GB of RAM, while path planning (including steps 1 and 3) was executed with the second hardware configuration.
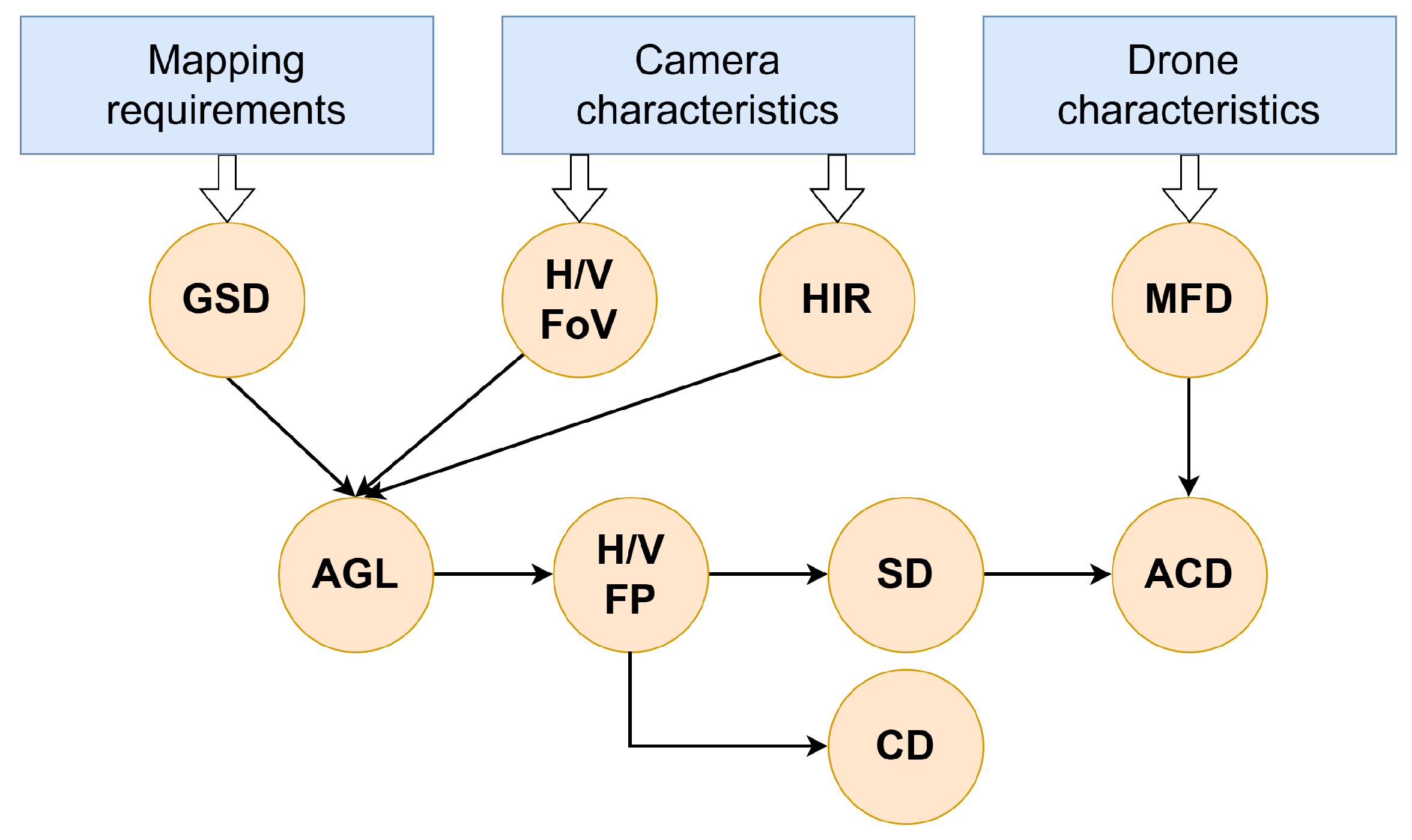
3.1. Fleet Analysis
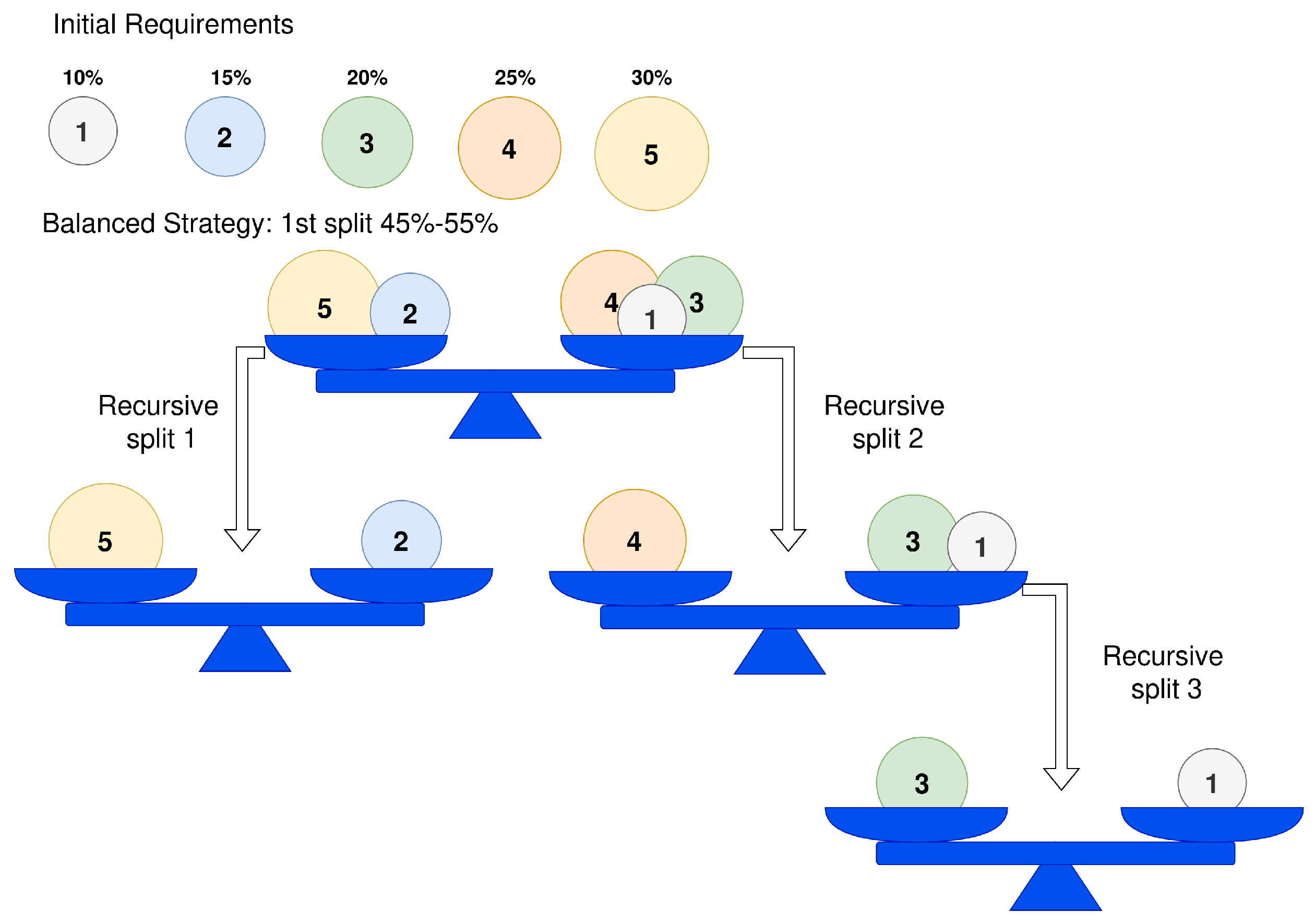
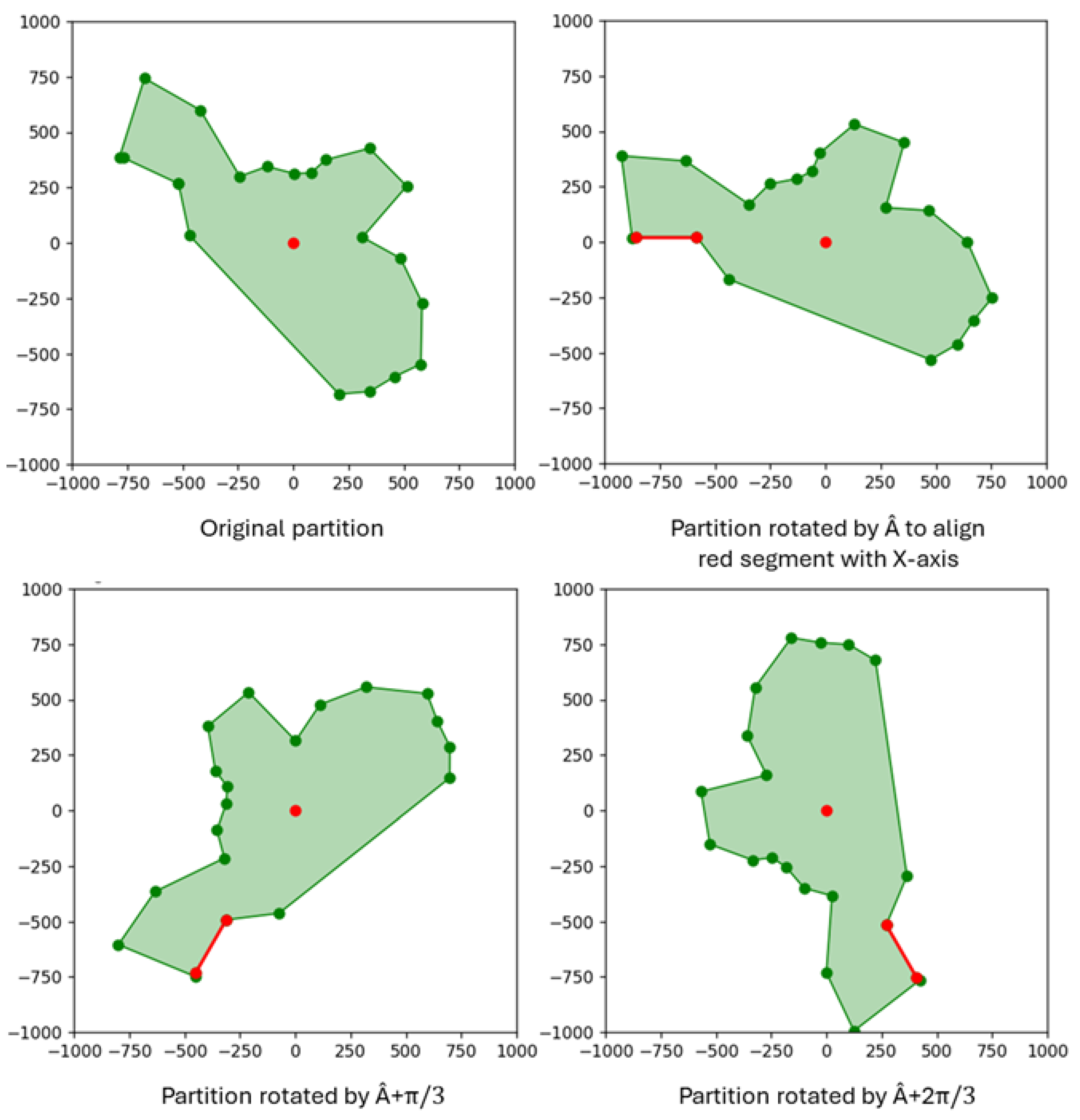
3.2. Area Decomposition
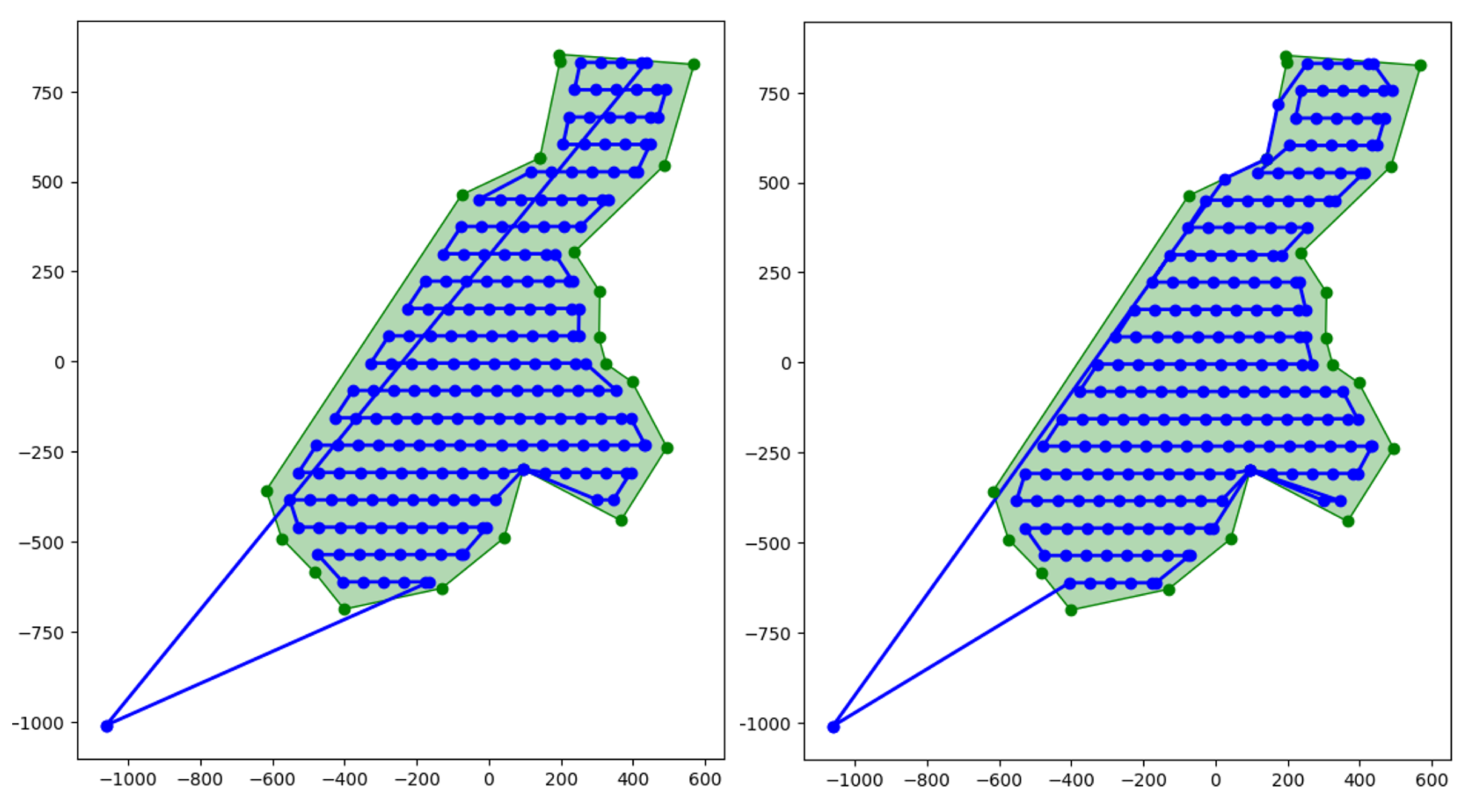
3.3. Path Planning
3.3.1. Grid and Graph Creation
3.3.2. Path Calculation
- Minimize the number of turns:
- If multiple trajectories have the same minimum number of turns, select the one with the shortest length:where is the set of candidate trajectories for a given partition, and is the selected optimal trajectory.
3.3.3. Trajectory Refinement: Avoidance of No-Fly Zones
3.3.4. Computational Considerations in Trajectory Generation
3.4. Metrics
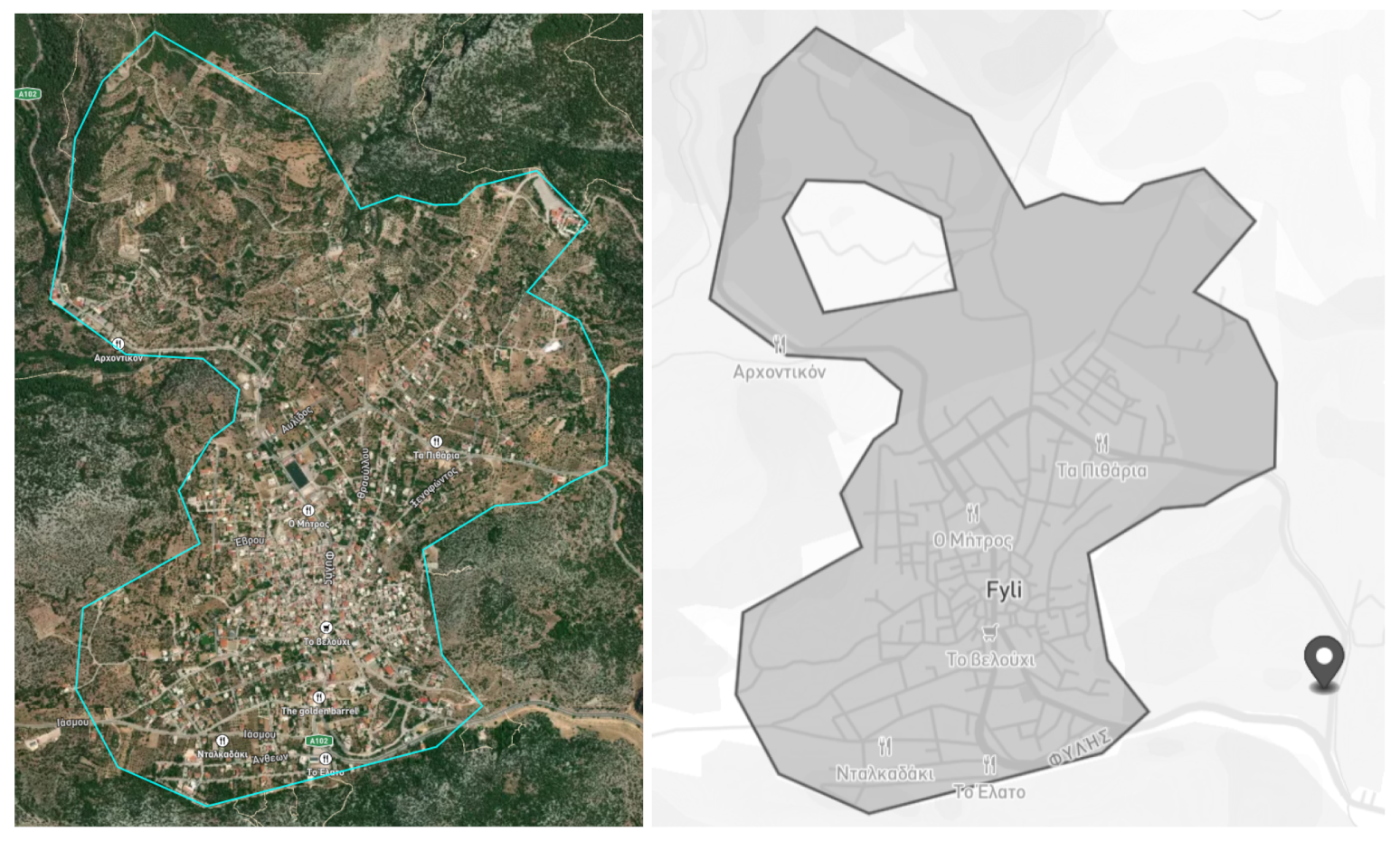
3.5. Example of Fyli Scenario
3.5.1. Area of Interest
3.5.2. Drones Fleet
3.5.3. Algorithm Steps
4. Experimentation and Results
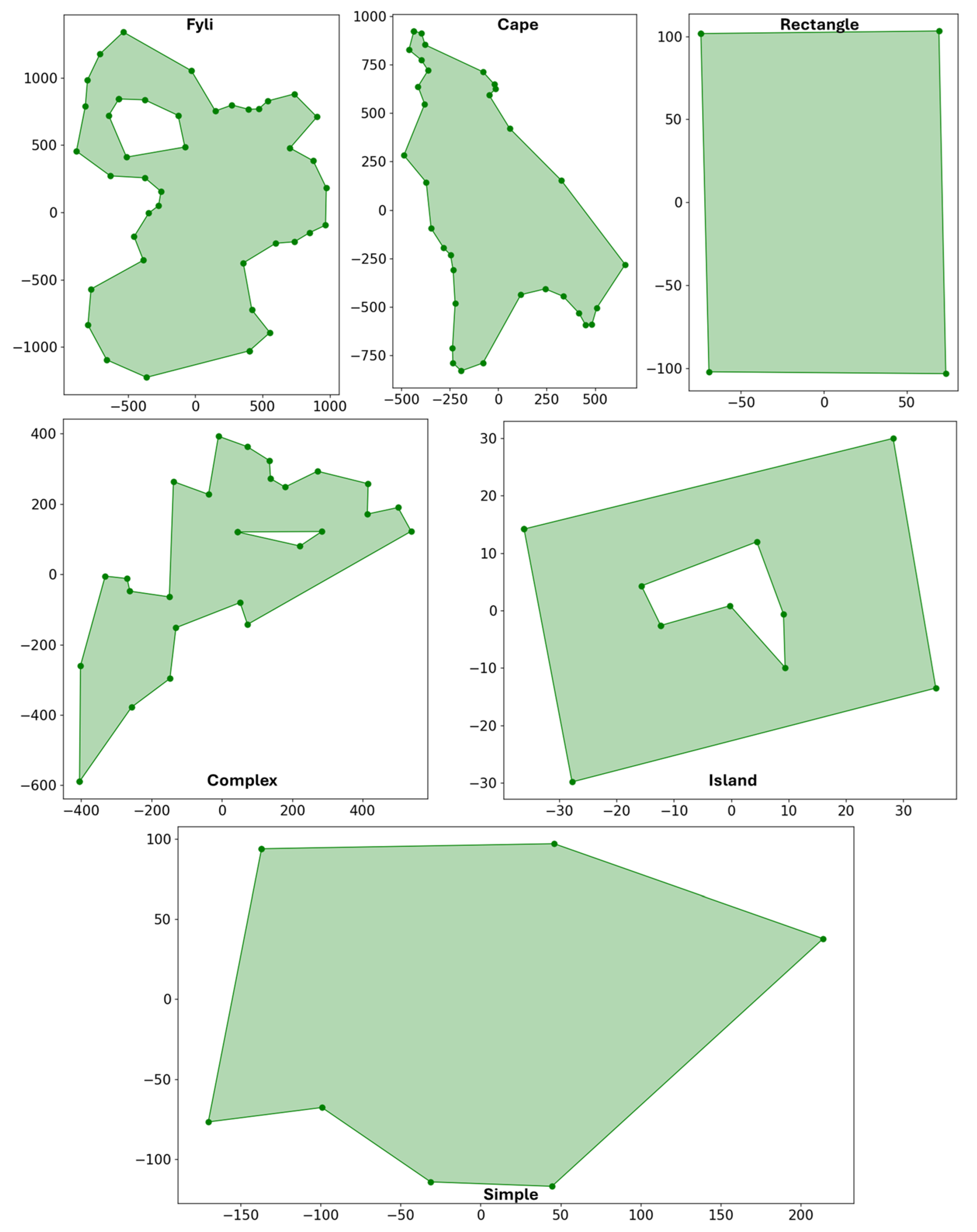
4.1. Scenarios
4.1.1. Fyli and EAMC Scenarios
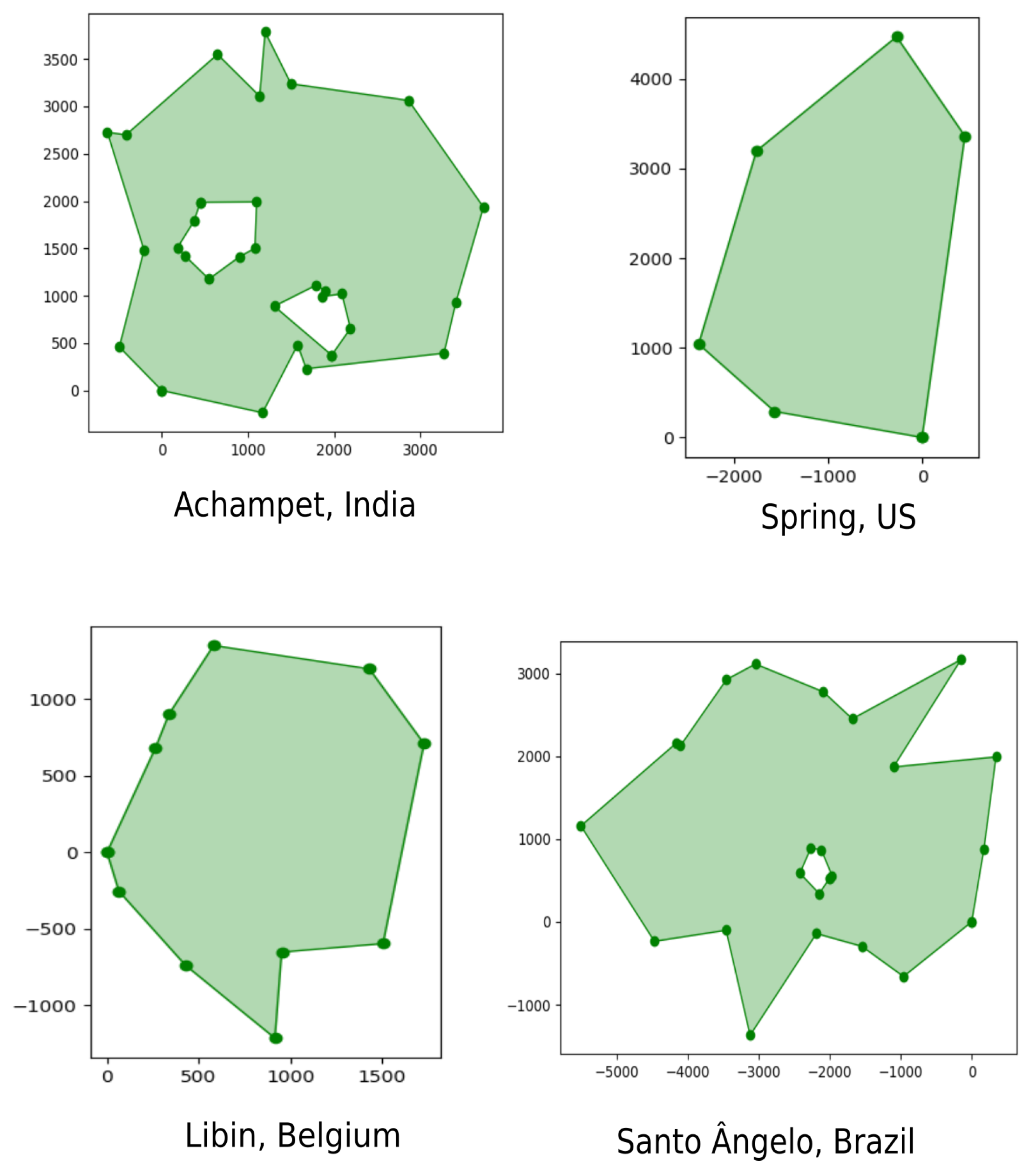
4.1.2. One Hundred Polygons Dataset
4.2. Evaluation Setup
4.3. Homogeneous Fleet Algorithm Validation and Comparison
4.3.1. Algorithm Comparison
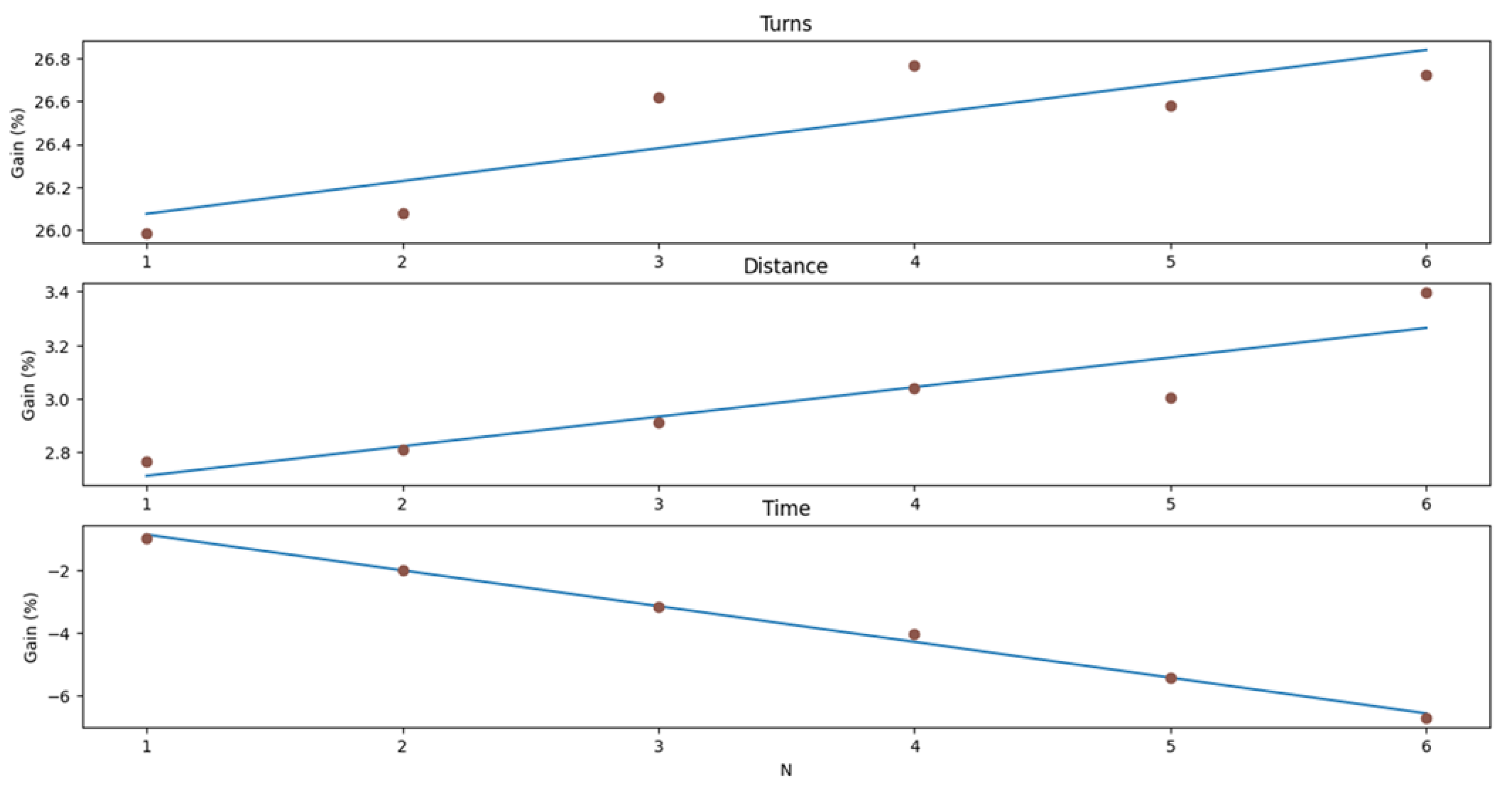
4.3.2. Distance Reduction Validation
4.4. Heterogeneous Fleet Performance Analysis
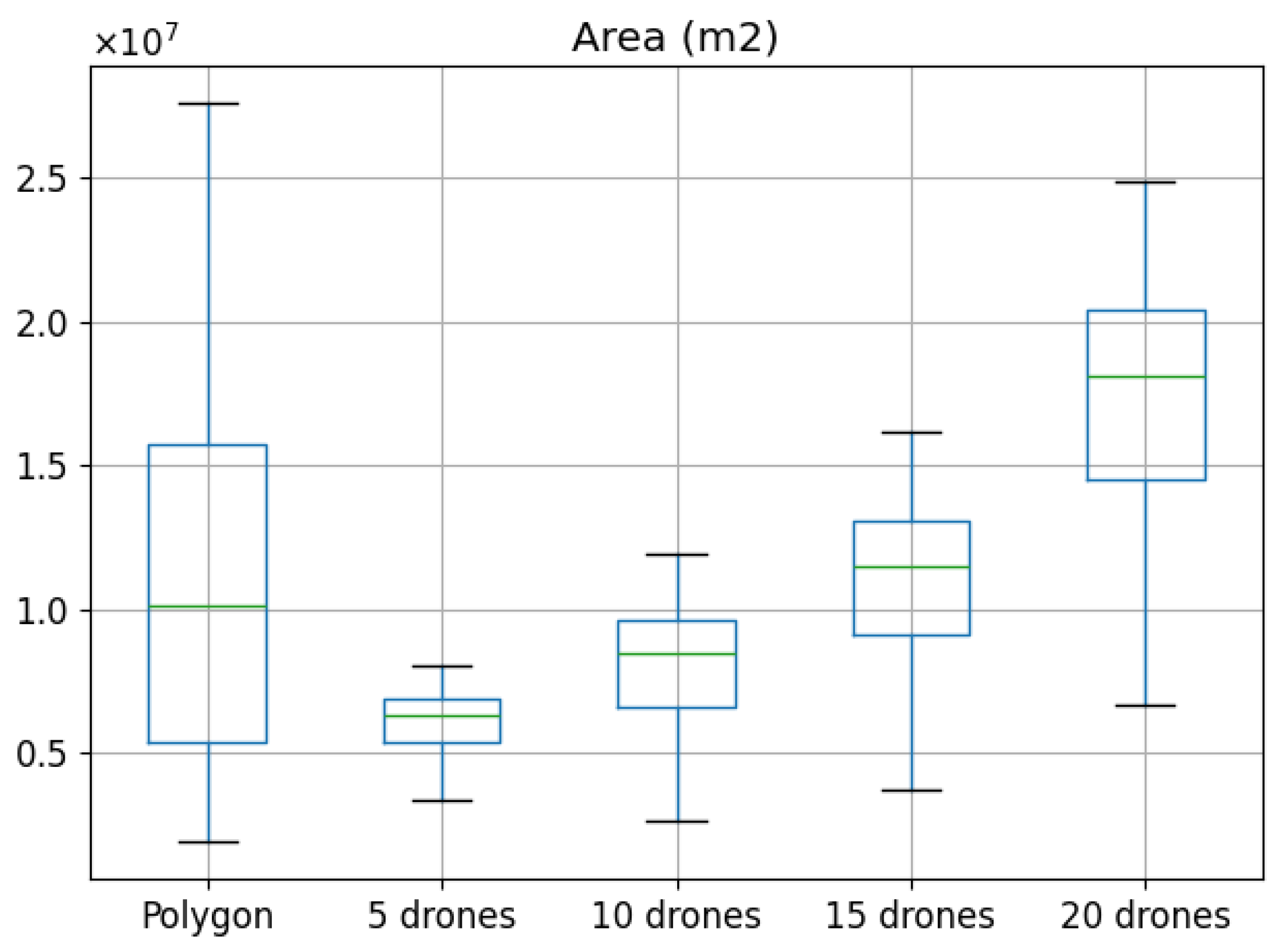
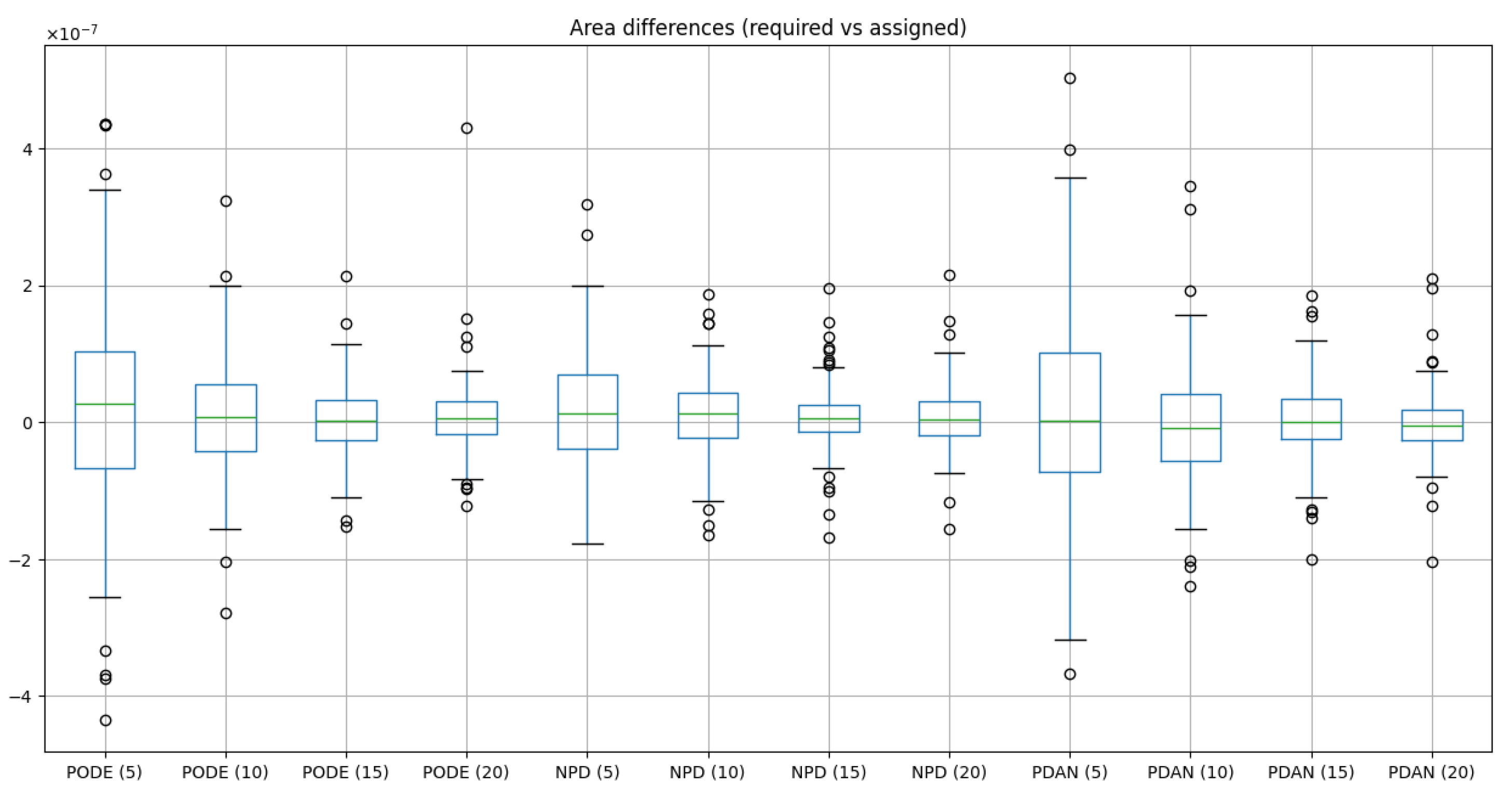
4.4.1. Area Requirements Calculation
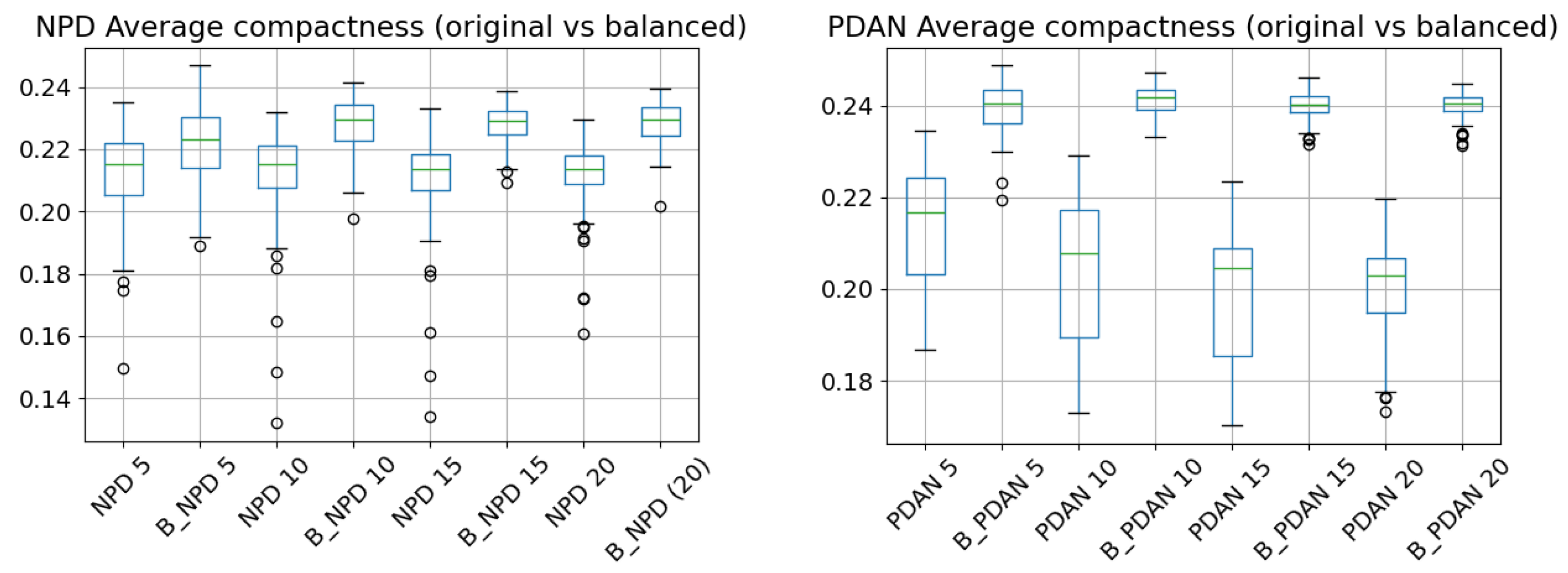
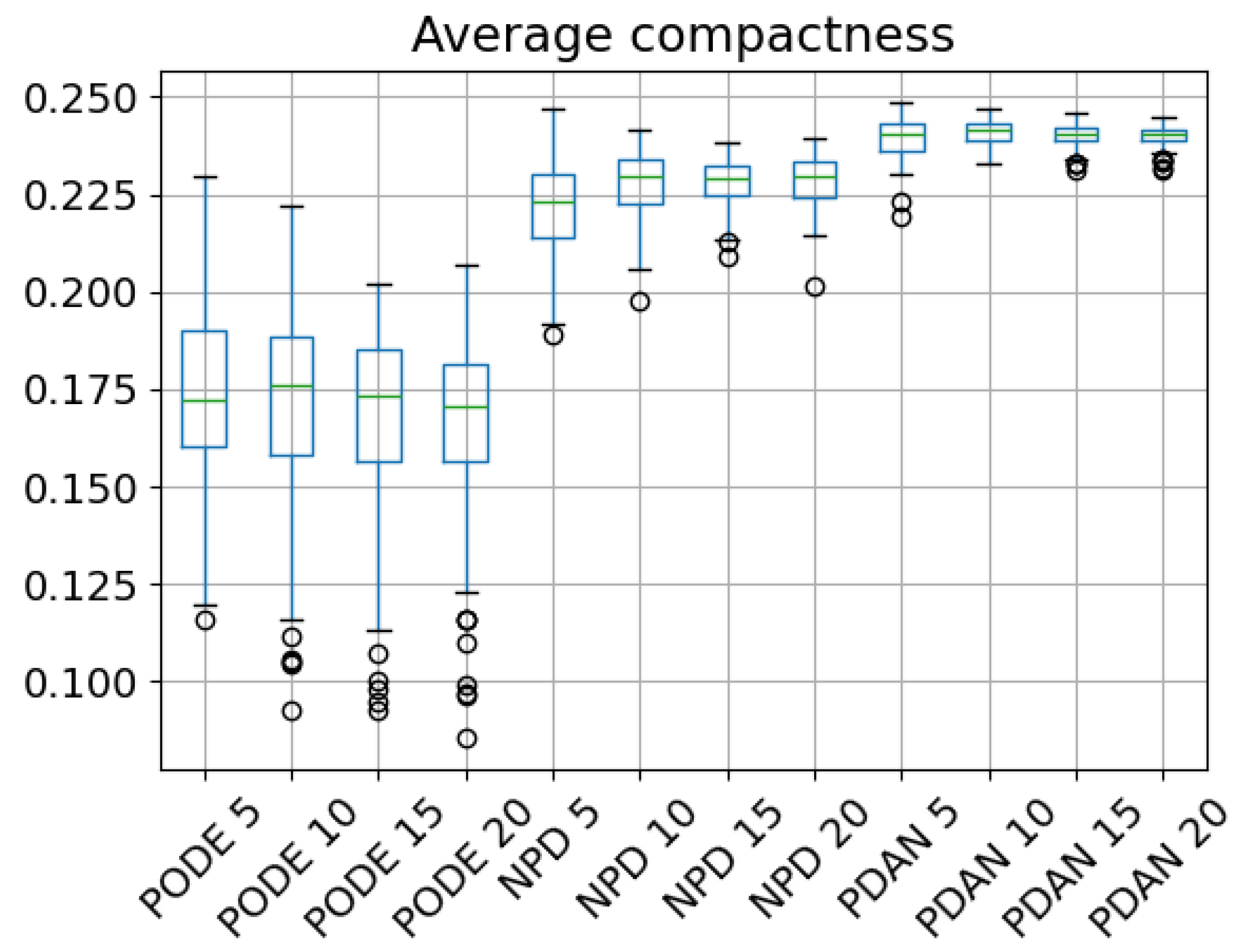
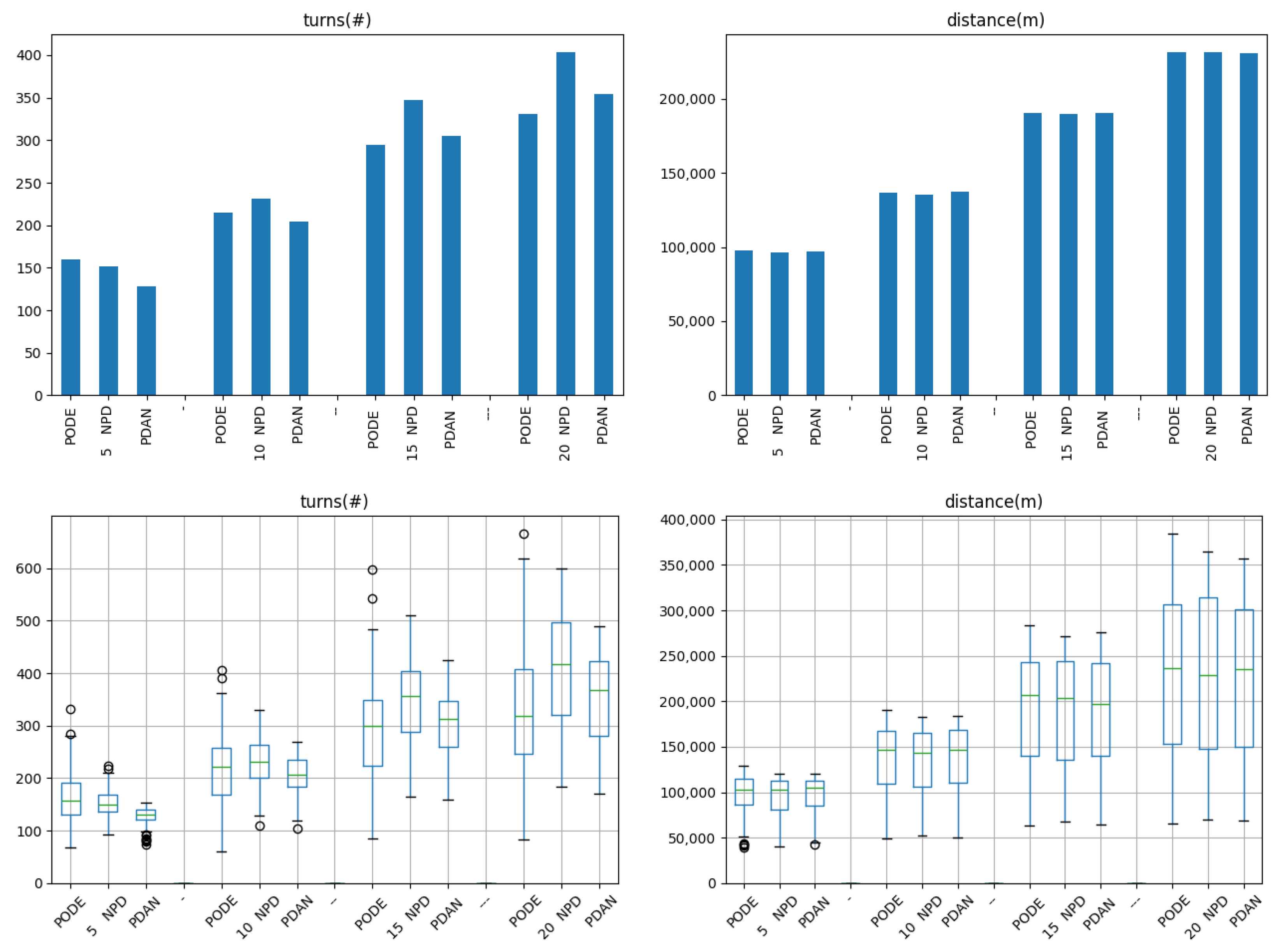
4.4.2. Partition Algorithm Comparison
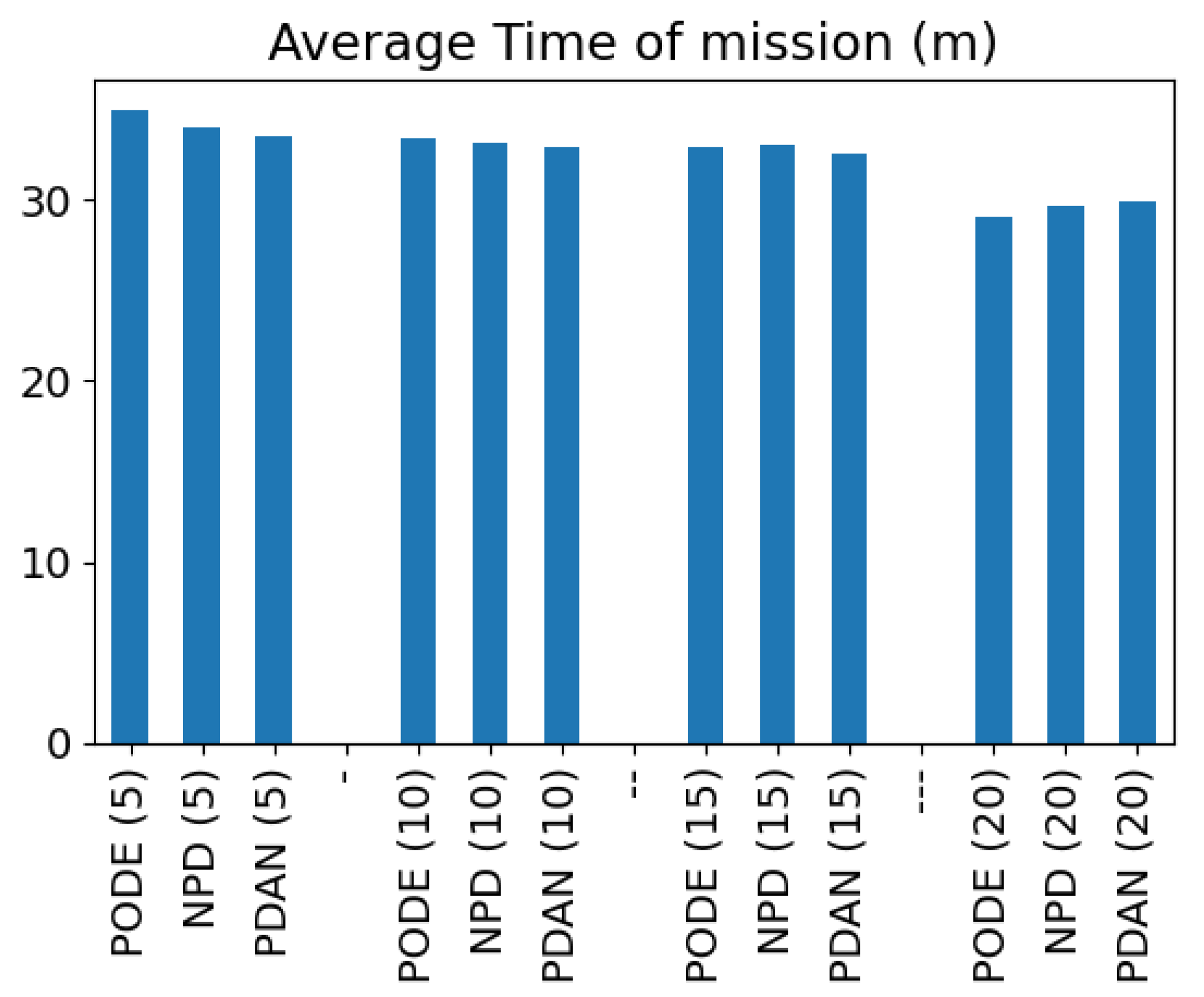
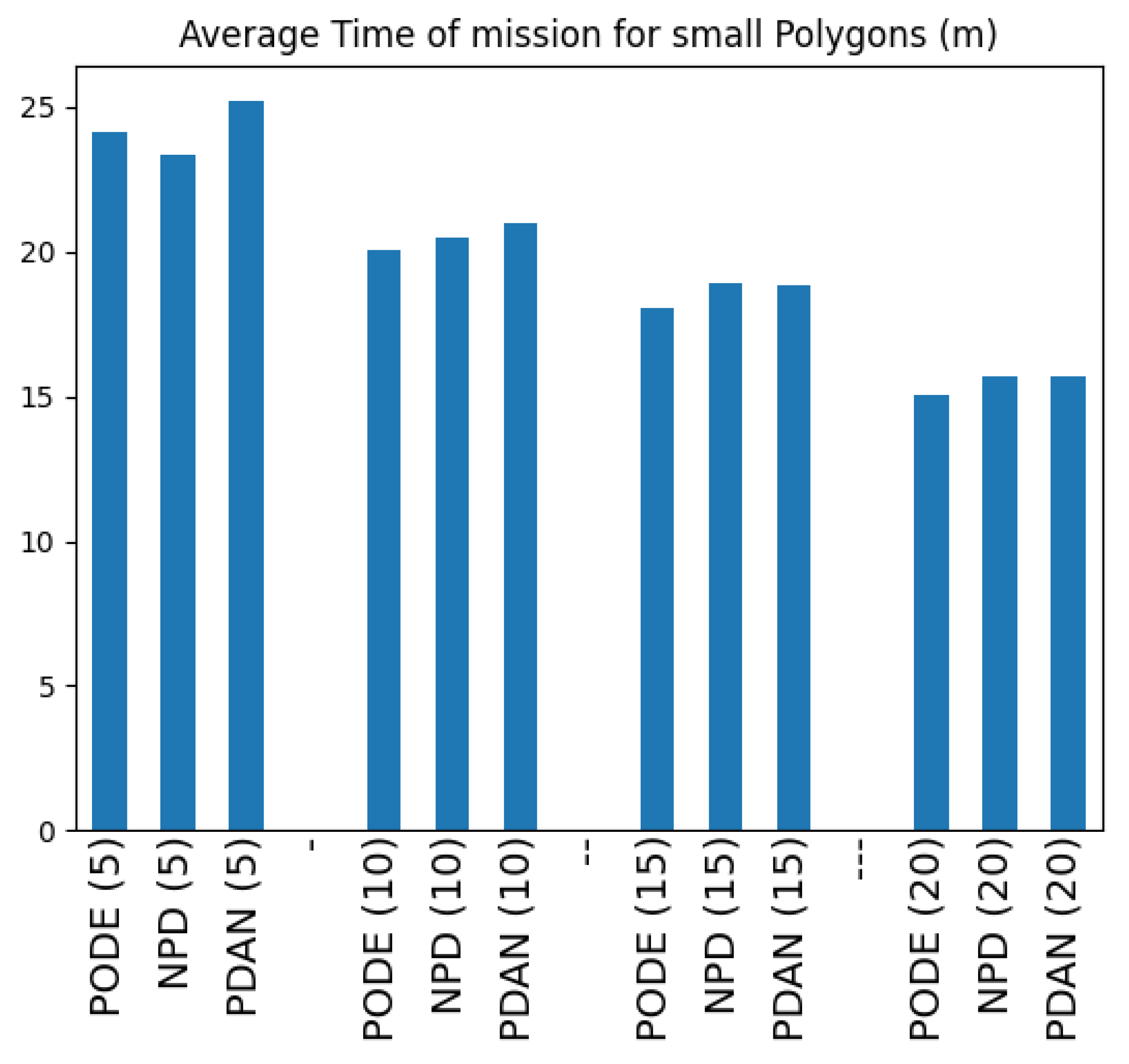
4.4.3. Trajectory Generation Metrics
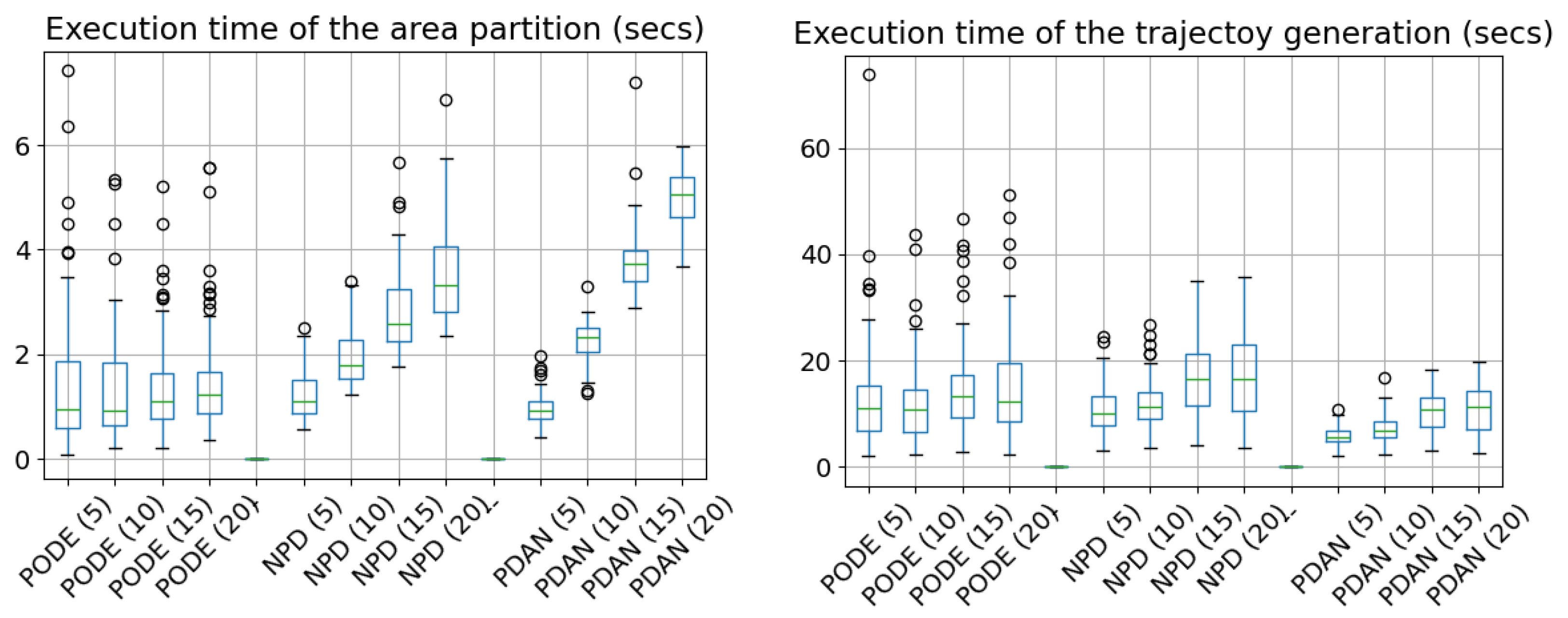
4.4.4. Computational Performance
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 4DT | Four-dimension trajectory |
| C2C | Command and Control left |
| CPP | Coverage Path Planning |
| DARP | Distributed Autonomous Robot Planning |
| DRR | Disaster Risk Reduction |
| EAMC | Energy-Aware Multi-UAV Coverage |
| GSD | Ground Sampling Distance |
| IoT | Internet of Things |
| NPD | Non-convex Polygon Decomposition |
| PDAN | Polygon Decomposition by Analytics |
| PODE | Polygon Decomposition |
| PPP | Polygon Partition Problem |
| UAV | Unmanned Aerial Vehicle |
| UN | United Nations |
| WSL | Windows Subsystem for Linux |
References
- Van Loenhout, J.; Below, R.; McClean, D. The Human Cost of Disasters: An Overview of the Last 20 Years (2000–2019); Technical Report; Centre for Research on the Epidemiology of Disasters (CRED): Brussels, Belgium; United Nations Office for Disaster Risk Reduction (UNDRR): Geneva, Switzerland, 2020. [Google Scholar]
- Center, A.D.R. Sendai Framework for Disaster Risk Reduction 2015–2030; Technical Report; United Nations Office for Disaster Risk Reduction: Geneva, Switzerland, 2015. [Google Scholar]
- Kucharczyk, M.; Hugenholtz, C.H. Remote sensing of natural hazard-related disasters with small drones: Global trends, biases, and research opportunities. Remote Sens. Environ. 2021, 264, 112577. [Google Scholar] [CrossRef]
- Román, A.; Tovar-Sánchez, A.; Roque-Atienza, D.; Huertas, I.; Caballero, I.; Fraile-Nuez, E.; Navarro, G. Unmanned aerial vehicles (UAVs) as a tool for hazard assessment: The 2021 eruption of Cumbre Vieja volcano, La Palma Island (Spain). Sci. Total Environ. 2022, 843, 157092. [Google Scholar] [CrossRef]
- Manzini, T.; Murphy, R.; Merrick, D. Quantitative Data Analysis: CRASAR Small Unmanned Aerial Systems at Hurricane Ian. In Proceedings of the 2023 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Naraha, Japan, 13–15 November 2023; pp. 7–12. [Google Scholar] [CrossRef]
- Ozturkcan, S. Technology and Disaster Relief: The Türkiye-Syria Earthquake Case Study. In Innovation; IntechOpen: Rijeka, Croatia, 2023; Chapter 13. [Google Scholar]
- IEDO. International Report on Best Practices in Robotics 2022; IEDO: Washington, DC, USA, 2022. [Google Scholar]
- Janik, P.; Zawistowski, M.; Fellner, R.; Zawistowski, G. Unmanned Aircraft Systems Risk Assessment Based on SORA for First Responders and Disaster Management. Appl. Sci. 2021, 11, 5364. [Google Scholar] [CrossRef]
- Vincent-Lambert, C.; Pretorius, A.; Van Tonder, B. Use of Unmanned Aerial Vehicles in Wilderness Search and Rescue Operations: A Scoping Review. Wilderness Environ. Med. 2023, 34, 580–588. [Google Scholar] [CrossRef]
- Grabmaier, I.; Bittner, S.; Kainz, S.; Barrado, C.; Bagiyan, V.; Bakunts, S.; Zamora, D. Enhancing community participation in Disaster Risk Management: Recommendations for an inclusive approach. Open Res. Europe 2025, 5, 50. [Google Scholar] [CrossRef]
- Maza, I.; Ollero, A. Multiple UAV cooperative searching operation using polygon area decomposition and efficient coverage algorithms. In Distributed Autonomous Robotic Systems 6; Springer: Berlin/Heidelberg, Germany, 2007; pp. 221–230. [Google Scholar]
- Xu, A.; Viriyasuthee, C.; Rekleitis, I. Optimal Complete Terrain Coverage Using an Unmanned Aerial Vehicle. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2513–2519. [Google Scholar] [CrossRef]
- Ghaddar, A.; Merei, A.; Natalizio, E. PPS: Energy-Aware Grid-Based Coverage Path Planning for UAVs Using Area Partitioning in the Presence of NFZs. Sensors 2020, 20, 3742. [Google Scholar] [CrossRef]
- Wu, Y.; Yin, H.; Chen, X.; Zhang, M. Multicircuit route planning for UAVs performing the terrain coverage task. IEEE Internet Things J. 2024, 11, 23765–23779. [Google Scholar] [CrossRef]
- Xiao, S.; Tan, X.; Wang, J. A Simulated Annealing Algorithm and Grid Map-Based UAV Coverage Path Planning Method for 3D Reconstruction. Electronics 2021, 10, 853. [Google Scholar] [CrossRef]
- Li, J.; Yang, X.; Yang, Y.; Liu, X. Cooperative Mapping Task Assignment of Heterogeneous Multi-UAV Using an Improved Genetic Algorithm. Knowl. Based Syst. 2024, 296, 111830. [Google Scholar] [CrossRef]
- Datsko, D.; Nekovar, F.; Penicka, R.; Saska, M. Energy-aware multi-uav coverage mission planning with optimal speed of flight. IEEE Robot. Autom. Lett. 2024, 9, 2893–2900. [Google Scholar] [CrossRef]
- Sanz-Martos, S.; Lopez-Franco, M.D.; Alvarez-Garcia, C.; Granero-Moya, N.; Lopez-Hens, J.M.; Camara-Anguita, S.; Pancorbo-Hidalgo, P.L.; Comino-Sanz, I.M. Drone applications for emergency and urgent care: A systematic review. Prehospital Disaster Med. 2022, 37, 502–508. [Google Scholar] [CrossRef]
- Daud, S.M.S.M.; Yusof, M.Y.P.M.; Heo, C.C.; Khoo, L.S.; Singh, M.K.C.; Mahmood, M.S.; Nawawi, H. Applications of drone in disaster management: A scoping review. Sci. Justice 2022, 62, 30–42. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, N. Region coverage-aware path planning for unmanned aerial vehicles: A systematic review. Phys. Commun. 2023, 59, 102073. [Google Scholar] [CrossRef]
- Yucesoy, E.; Balcik, B.; Coban, E. The role of drones in disaster response: A literature review of operations research applications. Int. Trans. Oper. Res. 2025, 32, 545–589. [Google Scholar] [CrossRef]
- Inès, J.; Annett, W.; Simone, D. Manual for CEMS-Rapid Mapping Products; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Alkhatib, A.A.; Jaber, K.M.; Al-Madi, M. A Proposed Automatic Forest Fire Extinguishing and Prevention System Using Drones. In Proceedings of the 2024 IEEE International Humanitarian Technologies Conference (IHTC), Bari, Italy, 25–27 November 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar]
- Cao, Z.L.; Huang, Y.; Hall, E.L. Region filling operations with random obstacle avoidance for mobile robots. J. Robot. Syst. 1988, 5, 87–102. [Google Scholar] [CrossRef]
- Apostolidis, S.D.; Kapoutsis, P.C.; Kapoutsis, A.C.; Kosmatopoulos, E.B. Cooperative multi-UAV coverage mission planning platform for remote sensing applications. Auton. Robot. 2022, 46, 373–400. [Google Scholar] [CrossRef]
- Iqbal, M.M.; Ali, Z.A.; Khan, R.; Shafiq, M. Motion Planning of UAV Swarm: Recent Challenges and Approaches. In Aeronautics; IntechOpen: Rijeka, Croatia, 2022; Chapter 3. [Google Scholar]
- Cheng, Q.; Zhang, Z.; Du, Y.; Li, Y. Research on Particle Swarm Optimization-Based UAV Path Planning Technology in Urban Airspace. Drones 2024, 8, 701. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, Y.; Wei, W. HSEPSO: A Hierarchical Self-Evolutionary PSO Approach for UAV Path Planning. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ’25), Málaga, Spain, 14–18 July 2025; pp. 1577–1584. [Google Scholar] [CrossRef]
- Lee, J.H.; Jeong, S.K.; Ji, D.H.; Park, H.Y.; Kim, D.Y.; Choo, K.B.; Jung, D.W.; Kim, M.J.; Oh, M.H.; Choi, H.S. Unmanned Surface Vehicle Using a Leader–Follower Swarm Control Algorithm. Appl. Sci. 2023, 13, 3120. [Google Scholar] [CrossRef]
- Adoni, W.Y.H.; Fareedh, J.S.; Lorenz, S.; Gloaguen, R.; Madriz, Y.; Singh, A.; Kühne, T.D. Intelligent Swarm: Concept, Design and Validation of Self-Organized UAVs Based on Leader–Followers Paradigm for Autonomous Mission Planning. Drones 2024, 8, 575. [Google Scholar] [CrossRef]
- Alaa, D.; Abdelmadjid, K.; Fadhila, L. Intelligent path planning algorithms for UAVs: Classification, complexity analysis, hybrid ablation insights, and future directions. Adv. Mech. Eng. 2025, 17, 16878132251355020. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E.; Pastor, E. Flight planning in multi-unmanned aerial vehicle systems: Nonconvex polygon area decomposition and trajectory assignment. Int. J. Adv. Robot. Syst. 2021, 18, 1729881421989551. [Google Scholar] [CrossRef]
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multi-Robot workspace division based on compact polygon decomposition. IEEE Access 2021, 9, 165795–165805. [Google Scholar] [CrossRef]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. DARP: Divide areas algorithm for optimal multi-robot coverage path planning. J. Intell. Robot. Syst. 2017, 86, 663–680. [Google Scholar] [CrossRef]
- Papakostas, L.; Geladaris, A.; Mastrogeorgiou, A.; Sharples, J.; Hattenberger, G.; Chatzakos, P.; Polygerinos, P. Optimized Area Coverage in Disaster Response Utilizing Autonomous UAV Swarm Formations. In Proceedings of the 2025 33rd Mediterranean Conference on Control and Automation (MED), Tangier, Morocco, 10–13 June 2025; pp. 630–635. [Google Scholar] [CrossRef]
- Miah, M.S.; Knoll, J. Area coverage optimization using heterogeneous robots: Algorithm and implementation. IEEE Trans. Instrum. Meas. 2018, 67, 1380–1388. [Google Scholar] [CrossRef]
- Sadrabadi, M.T.; Peiró, J.; Innocente, M.S.; Rein, G. Conceptual design of a wildfire emergency response system empowered by swarms of unmanned aerial vehicles. Int. J. Disaster Risk Reduct. 2025, 124, 105493. [Google Scholar] [CrossRef]
- Datsko, D.; Nekovar, F.; Penicka, R. GitHub-Ctu-Mrs/EnergyAwareMCPP: Energy-Aware Multi-UAV Coverage Mission Planning with Optimal Speed of Flight. Available online: https://github.com/ctu-mrs/EnergyAwareMCPP (accessed on 10 November 2025).
- Skorobogatov, G.; Calvo, T.; Barrado, C.; Salamí, E. Compact Workspace Decomposition Based on a Bottom-Up Approach. IEEE Access 2025, 13, 3917–3928. [Google Scholar] [CrossRef]
- Khiati, W.; Moumen, Y.; Zerrouk, I.; Berrich, J.; Bouchentouf, T. Air Surveillance Planning Approach for Large Areas. In Proceedings of the 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS), Marrakech, Morocco, 28–30 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Khiati, W.; Moumen, Y.; Habchi, A.E.; Zerrouk, I.; Berrich, J.; Bouchentouf, T. Grid Based approach (GBA): A new approach based on the grid-clustering algorithm to solve a CPP type problem for air surveillance using UAVs. In Proceedings of the 2020 Fourth International Conference on Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 21–23 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Bellingham, J.; Tillerson, M.; Richards, A.; How, J.P. Multi-Task Allocation and Path Planning for Cooperating UAVs. In Cooperative Control: Models, Applications and Algorithms; Butenko, S., Murphey, R., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2003; pp. 23–41. [Google Scholar] [CrossRef]
- Calvo, T.; Salamí, E.; Barrado, C.; Zerrouk, I. Dataset: Polygons for Testing Disaster Scenarios and UAS Swarms Usage. 2025. Available online: https://zenodo.org/records/15746579 (accessed on 10 November 2025).
- Bauersfeld, L.; Scaramuzza, D. Range, Endurance, and Optimal Speed Estimates for Multicopters. IEEE Robot. Autom. Lett. 2022, 7, 2953–2960. [Google Scholar] [CrossRef]








| Drone Type | Maximum Flight Distance | Speed | Field of View H, V | Image Resolution |
|---|---|---|---|---|
| (km) | (m/s) | (Deg) | (Pixels) | |
| Parrot Anafi AI | 22.5 | 14 | 64.6, 50.7 | 8000 × 6000 |
| DJI MINI 4 Pro | 18 | 11.3 | 69.7, 55.1 | 8064 × 6048 |
| DJI Phontom 4 Pro V2.0 | 18.63 | 10.35 | 71.5, 56.7 | 4864 × 3648 |
| DJI Air3 | 22.08 | 8 | 69.6, 55 | 8064 × 6048 |
| Skydio X2E Color | 20 | 8.3 | 67.7, 53.4 | 4056 × 3040 |
| Skydio X10 | 36 | 15 | 80.2, 64.6 | 8192 × 6144 |
| Yuneec H520E | 17.01 | 10.125 | 78.3, 62.8 | 4864 × 3648 |
| Drone Type | Maximum Surface (ha) | Area Requirement (ha) |
|---|---|---|
| Parrot Anafi AI | 136.5 | 44.8 |
| DJI MINI 4 Pro | 101.3 | 33.2 |
| DJI Phontom 4 Pro V2.0 | 64.2 | 21.0 |
| DJI Air3 | 134.2 | 44.0 |
| Skydio X2E Color | 59.1 | 19.4 |
| Skydio X10 | 250.3 | 82.0 |
| Yuneec H520E | 63.3 | 20.1 |
| Scenario Name | Cape | Complex | Fyli | Island | Rectangle | Simple |
|---|---|---|---|---|---|---|
| Area size (m2) | 903,979.52 | 302,285.38 | 2,666,993.92 | 2681.54 | 29,348.95 | 55,807.64 |
| Convex | False | False | False | False | True | False |
| Number of vertices | 34 | 24 | 36 | 5 | 5 | 8 |
| Number of holes | 0 | 1 | 1 | 1 | 0 | 0 |
| Drones’ distance from | ||||||
| the polygon centroid (m) | 1348.24 | 47.63 | 1390.77 | 31.50 | 58.05 | 47.84 |
| Type | N | %NonConv | Area [km2] | Compactness | Vertices | Holes |
|---|---|---|---|---|---|---|
| Original | 100 | 95.0 | 11.12 ± 6.59 | 0.19 ± 0.03 | 13.8 (5–21) | 1.61 (0–4) |
| Convex hull | 100 | 0.0 | 12.88 ± 7.68 | 0.26 ± 0.01 | 8.85 (5–14) | 0 (0–0) |
| Scenario Name | Cape | Complex | Fyli | Island | Rectangle | Simple |
|---|---|---|---|---|---|---|
| Number of drones | 3 | 3 | 3 | 1 | 3 | 3 |
| Sweep distance (m) | 35 | 10 | 55 | 5 | 8 | 6 |
| Lateral offset (m) | 17.5 | 5 | 27.5 | 2.5 | 4 | 3 |
| Algorithm | Parameter | Cape | Complex | Fyli | Island | Rectangle | Simple |
|---|---|---|---|---|---|---|---|
| EAMC [17] | Minimum subpolygons per UAV | 4 | 3 | 3 | 1 | 1 | 1 |
| Rotations per cell | 4 | 3 | 3 | 5 | 3 | 5 | |
| Our three-step method | Number of Steiner points | 70 | 45 | 35 | 35 | 70 | 35 |
| EAMC | Our 3-Step Method | |||||||
|---|---|---|---|---|---|---|---|---|
| Scenarios | Number of Turns | Flight Distance (m) | Flight Time (s) | Coverage (%) | Number of Turns | Flight Distance (m) | Flight Time (s) | Coverage (%) |
| cape | 162 | 35,633.6 | _ | _ | 97 | 35,254.87 | 871.42 | 100.0 |
| complex | 291 | 36,331.1 | _ | _ | 240 | 34,287.51 | 841.12 | 99.99 |
| fyli | 127 | 59,665.7 | _ | _ | 139 | 59,358.95 | 1466.05 | 100.0 |
| island | 38 | 615.489 | _ | _ | 35 | 694.91 | 49.63 | 100.0 |
| rectangle | 54 | 4373.02 | _ | _ | 54 | 4315.18 | 106.56 | 100.0 |
| simple | 103 | 10,580.8 | _ | _ | 138 | 9981.93 | 245.32 | 99.99 |
| Results | Fleet1 (5 UAVs) | Fleet2 (10 UAVs) | Fleet3 (15 UAVs) | Fleet4 (20 UAVs) |
|---|---|---|---|---|
| Number of polygons | 26 | 43 | 56 | 70 |
| Normal test | 0.78 | 3.80 | 5.77 | 5.81 |
| p-value (normality) | 0.67 | 0.14 | 0.055 | 0.054 |
| t-statistic | −3.76 | −8.60 | −6.21 | −3.67 |
| p-value (t-test) | 9.08 × 10−4 | 8.03 × 10−11 | 7.18 × 10−8 | 4.66 × 10−4 |
| Confidence interval | [−3632, −1062] | [−14,856, −9214] | [−23,156, −11,865] | [−18,466, −5471] |
| Mean distance gain | 3.19% | 9.31% | 6.17% | 0.37% |
| Fleet Size | Not Fully Covered |
|---|---|
| 5 | 71 |
| 10 | 60 |
| 15 | 43 |
| 20 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zerrouk, I.; Salamí, E.; Barrado, C.; Hattenberger, G.; Pastor, E. Increasing Automation on Mission Planning for Heterogeneous Multi-Rotor Drone Fleets in Emergency Response. Drones 2025, 9, 816. https://doi.org/10.3390/drones9120816
Zerrouk I, Salamí E, Barrado C, Hattenberger G, Pastor E. Increasing Automation on Mission Planning for Heterogeneous Multi-Rotor Drone Fleets in Emergency Response. Drones. 2025; 9(12):816. https://doi.org/10.3390/drones9120816
Chicago/Turabian StyleZerrouk, Ilham, Esther Salamí, Cristina Barrado, Gautier Hattenberger, and Enric Pastor. 2025. "Increasing Automation on Mission Planning for Heterogeneous Multi-Rotor Drone Fleets in Emergency Response" Drones 9, no. 12: 816. https://doi.org/10.3390/drones9120816
APA StyleZerrouk, I., Salamí, E., Barrado, C., Hattenberger, G., & Pastor, E. (2025). Increasing Automation on Mission Planning for Heterogeneous Multi-Rotor Drone Fleets in Emergency Response. Drones, 9(12), 816. https://doi.org/10.3390/drones9120816











