Energy-Efficient Uplink Communication in UAV-Enabled MEC Networks with Pinching Antennas
Highlights
- By jointly optimizing communication, computation, and mobility, a comprehensive solution for energy-efficient unmanned aerial vehicle (UAV) operations in next-generation wireless networks is proposed. A novel integration of a reconfigurable pinching antenna (PA) system, non-orthogonal multiple acces (NOMA)-based uplink transmission, and multi-access edge computing (MEC)-enabled task offloading tailored to the dynamic and energy-constrained nature of UAV networks is proposed, which ensures robust communication and efficient computation.
- A mixed-integer non-linear program is formulated to minimize total energy consumption, jointly optimizing UAV trajectories, offloading ratios, transmit powers, and PA positions while ensuring minimum data rates, collision avoidance, and coverage of all ground target points.
- The proposed approach is promising with respect to reliable data rates, collision avoidance, and complete coverage of ground target points, and it is suitable for real-time UAV network applications.
- The results demonstrate that the proposed framework can achieve 20–45% energy savings compared to baseline methods while maintaining data rates above the required minimum and near-perfect coverage satisfaction. These gains stem from the adaptive reconfiguration of the PA system, which enhances channel gains in dynamic aerial environments, and the synergistic integration of NOMA and MEC, which enables efficient spectrum utilization and computation offloading.
Abstract
1. Introduction
2. Related Works
- A novel integration of a reconfigurable PA system, NOMA-based uplink transmission, and MEC-enabled task offloading tailored to the dynamic and energy-constrained nature of UAV networks is proposed, which ensures robust communication and efficient computation.
- A mixed-integer non-linear program is formulated to minimize total energy consumption, jointly optimizing UAV trajectories, offloading ratios, transmit powers, and PA positions while ensuring minimum data rates, collision avoidance, and the coverage of all ground target points.
- A block coordinate descent (BCD) algorithm combined with successive convex approximation (SCA) and one-dimensional grid search is proposed, which provides a computationally efficient solution that converges to a locally optimal point. The proposed algorithm is suitable for real-time UAV network applications.
3. System Model
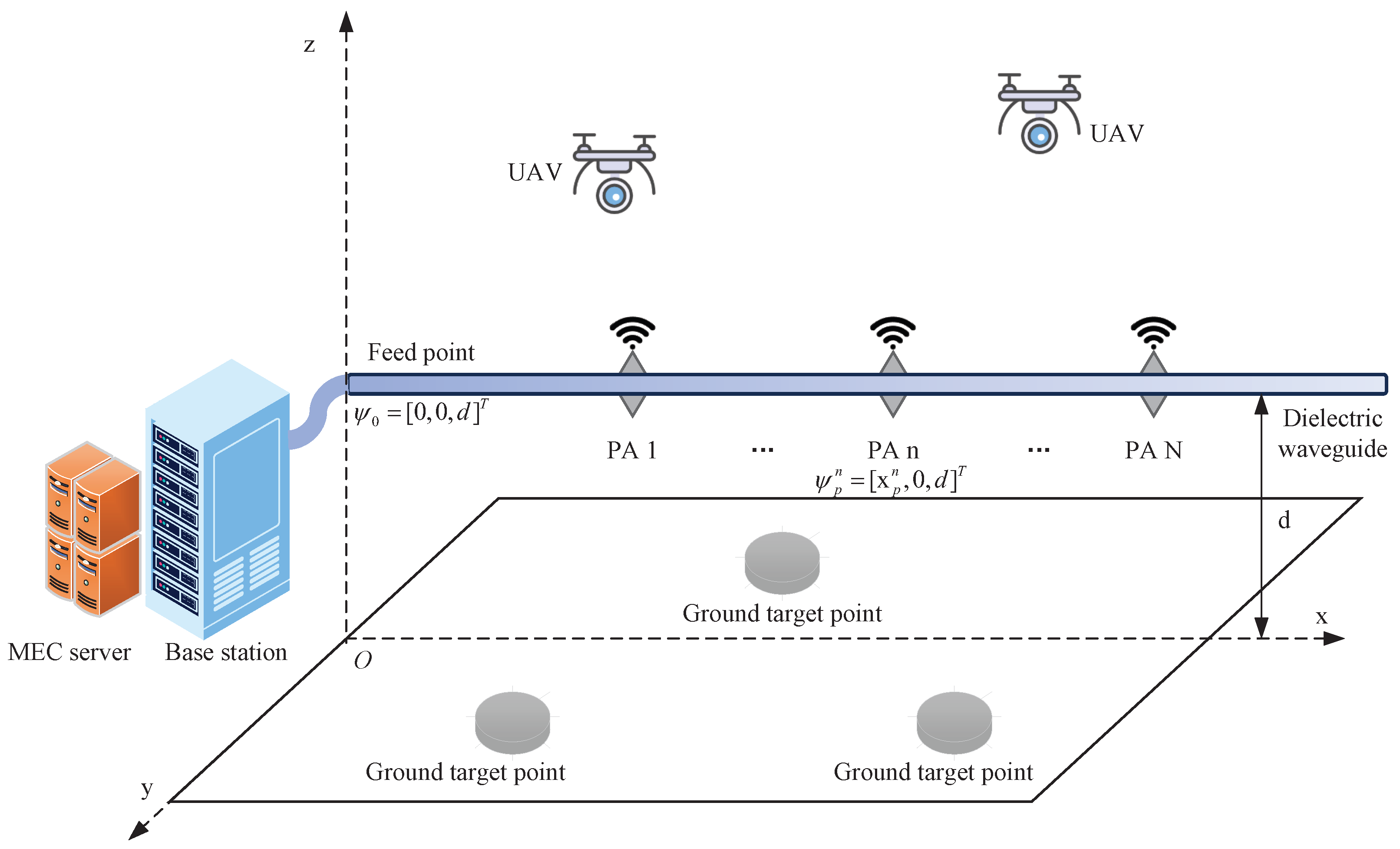
3.1. Access Network Model
3.2. Task Offloading Energy Consumption
3.3. Local Computation Energy Consumption
3.4. Propulsion Energy Consumption
3.5. Optimization Problem
4. Optimization Algorithm Design
4.1. BCD Framework
| Algorithm 1 Block coordinate Descent for Energy Minimization. |
|
4.2. Subproblem for Offloading Ratios
4.3. Subproblem for Transmit Powers
4.4. Subproblem for PA Positions
4.5. Subproblem for UAV Trajectories and Coverage Variables
4.6. Convergence and Complexity Analysis
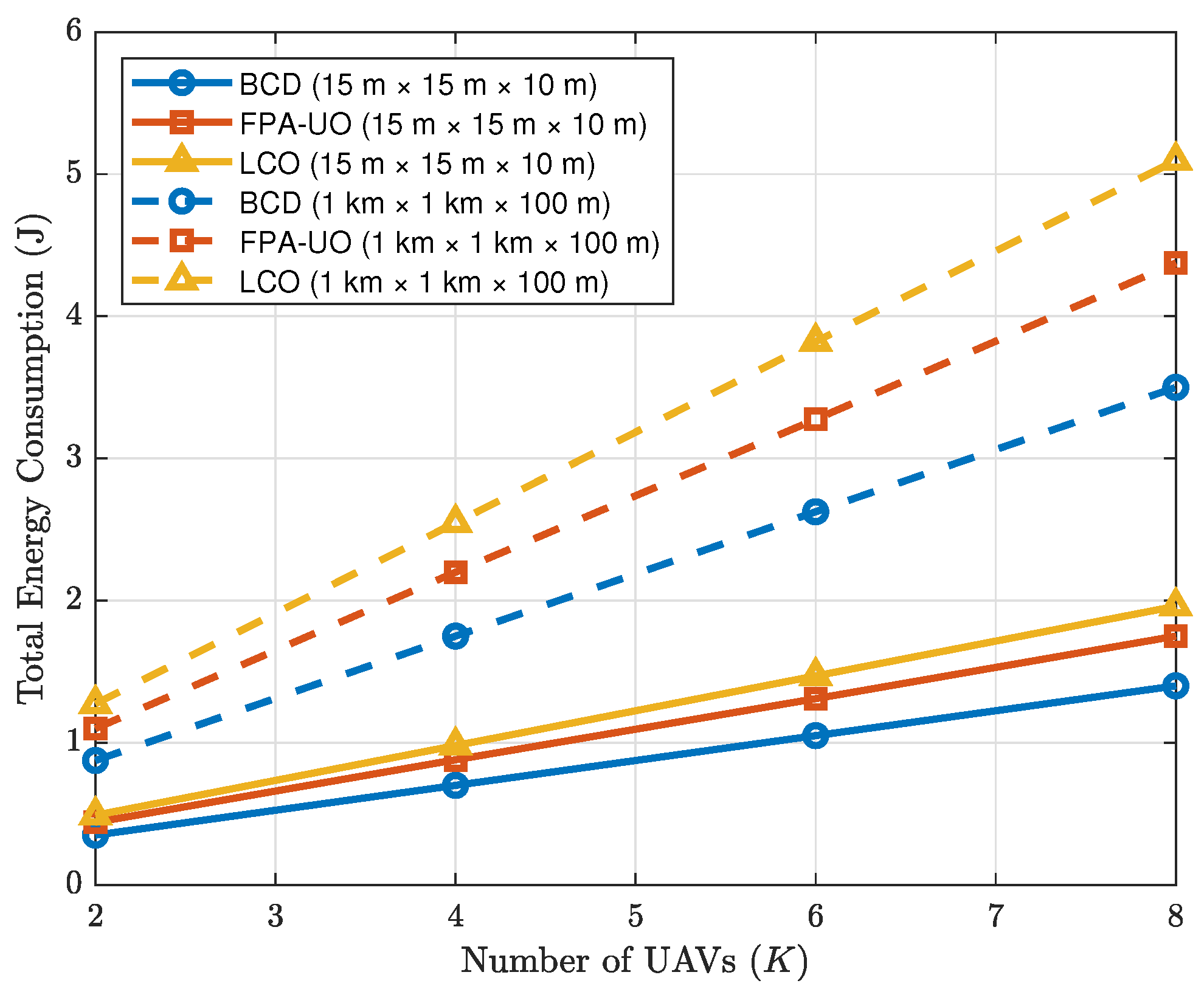
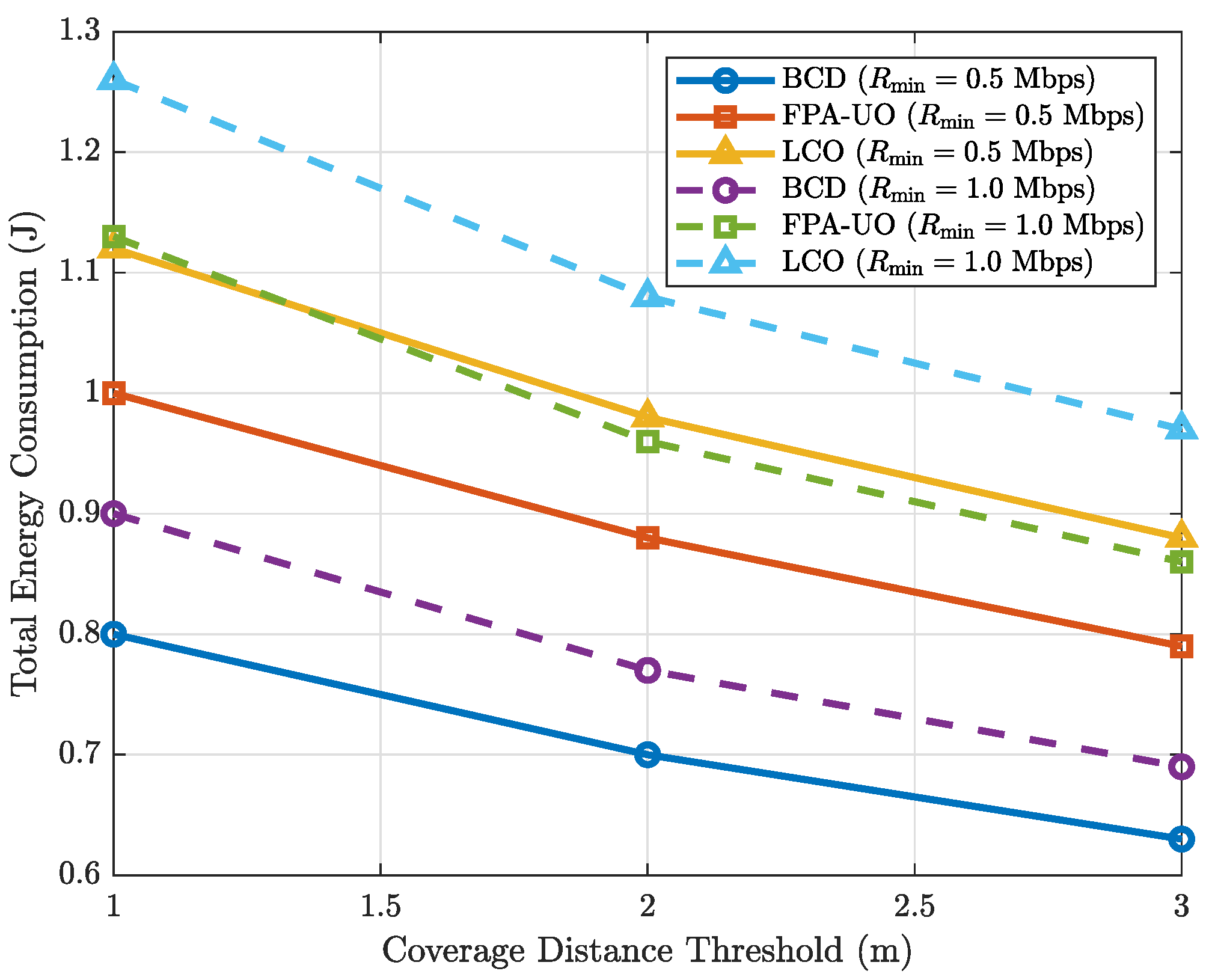
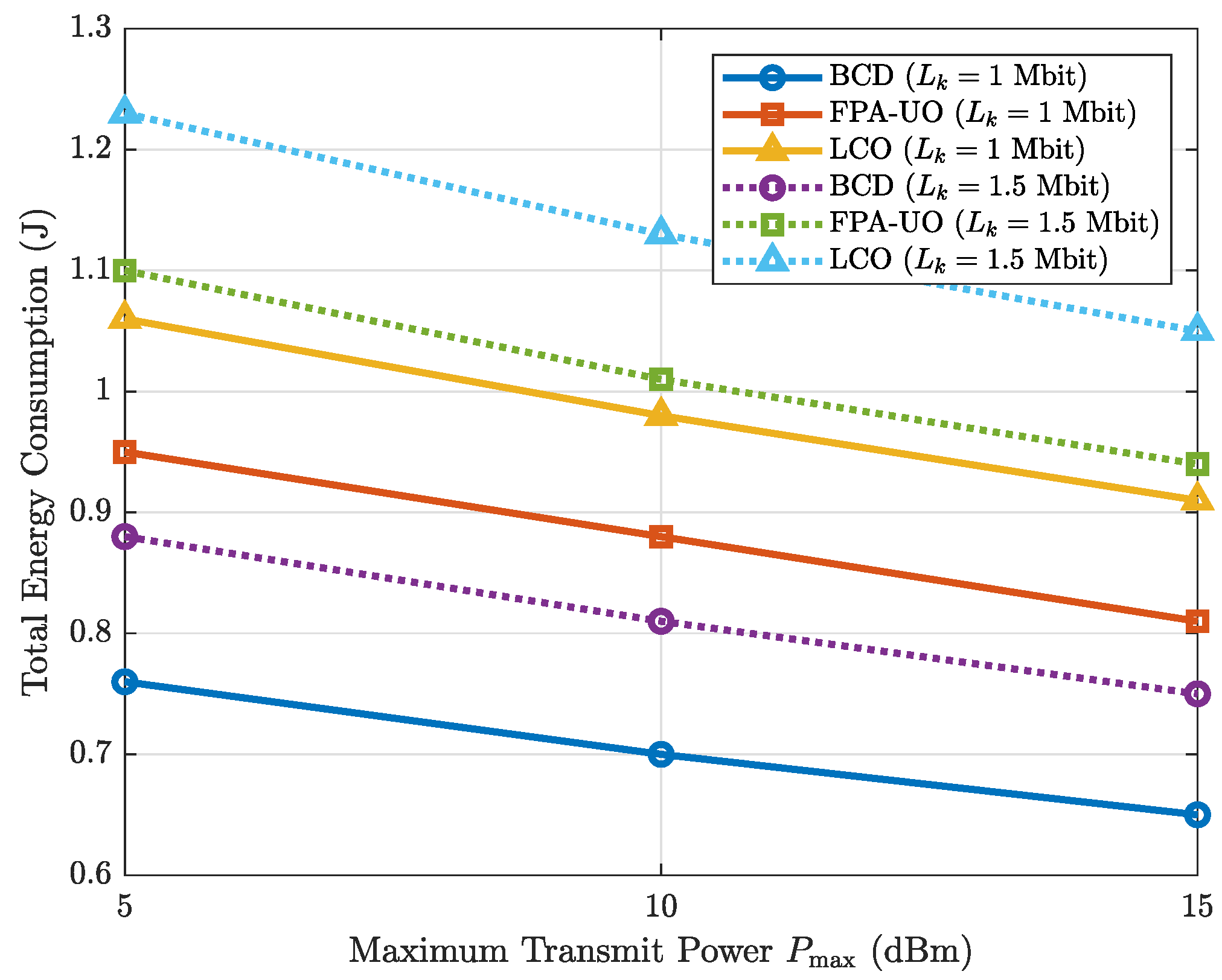
5. Simulation Results
5.1. Simulation Setup
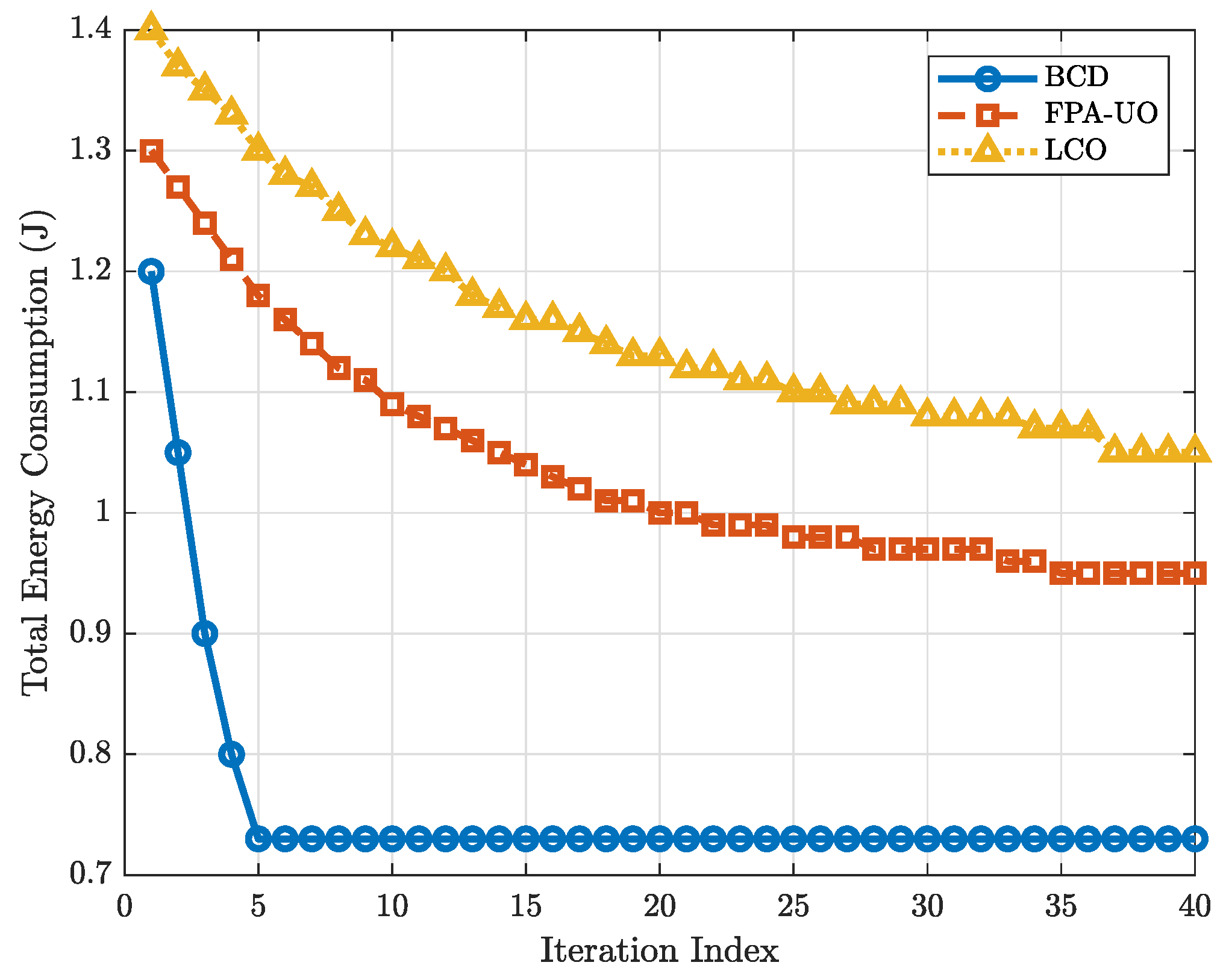
- Fixed PA and Uniform Offloading (FPA-UO): PA positions are fixed equally spaced along the waveguide, and offloading ratios are set to . Only UAV trajectories and transmit powers are optimized.
- Local Computation Only (LCO): UAVs perform all computations locally (), optimizing only trajectories and transmit powers, with PA positions equally spaced.
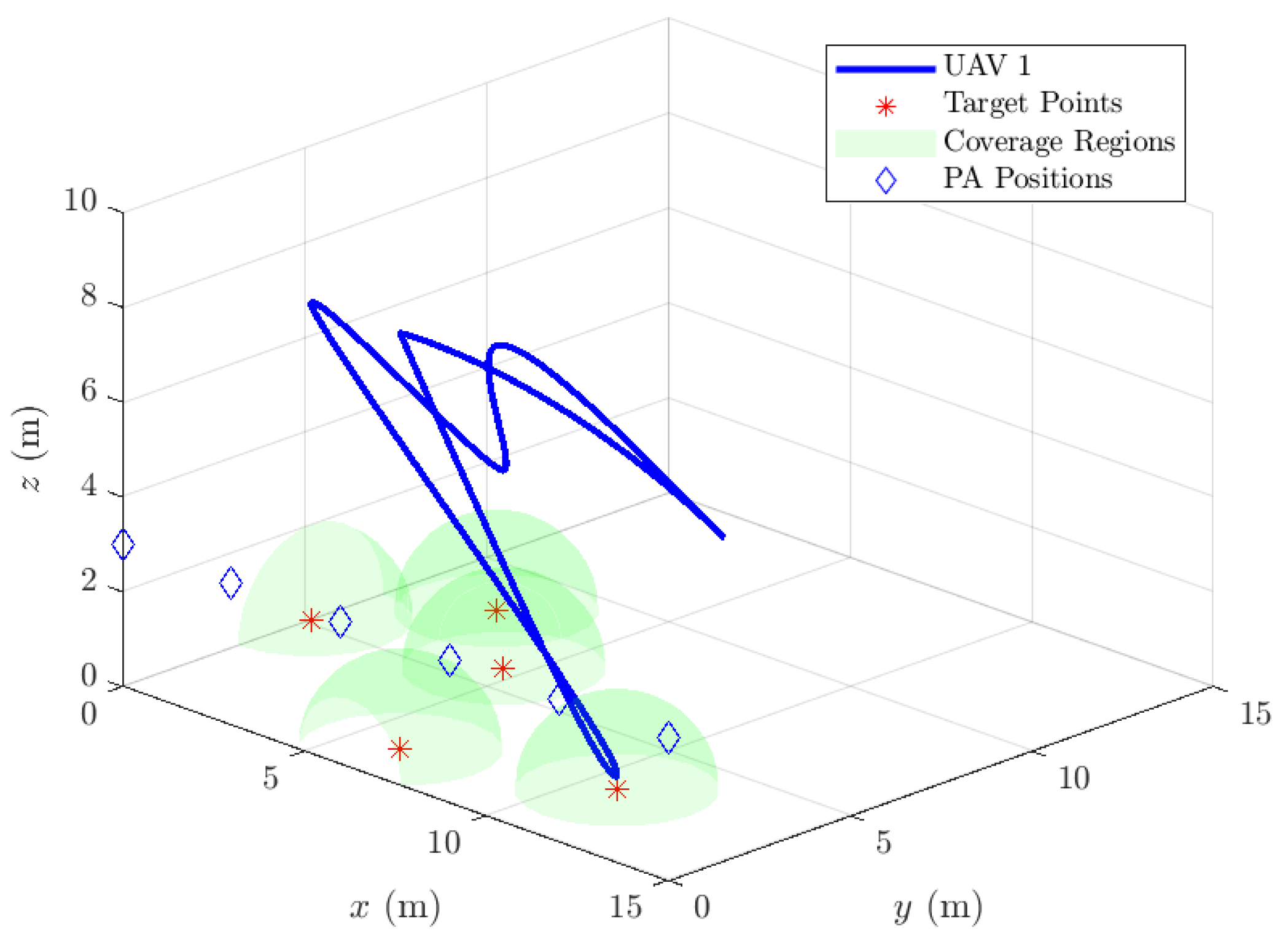
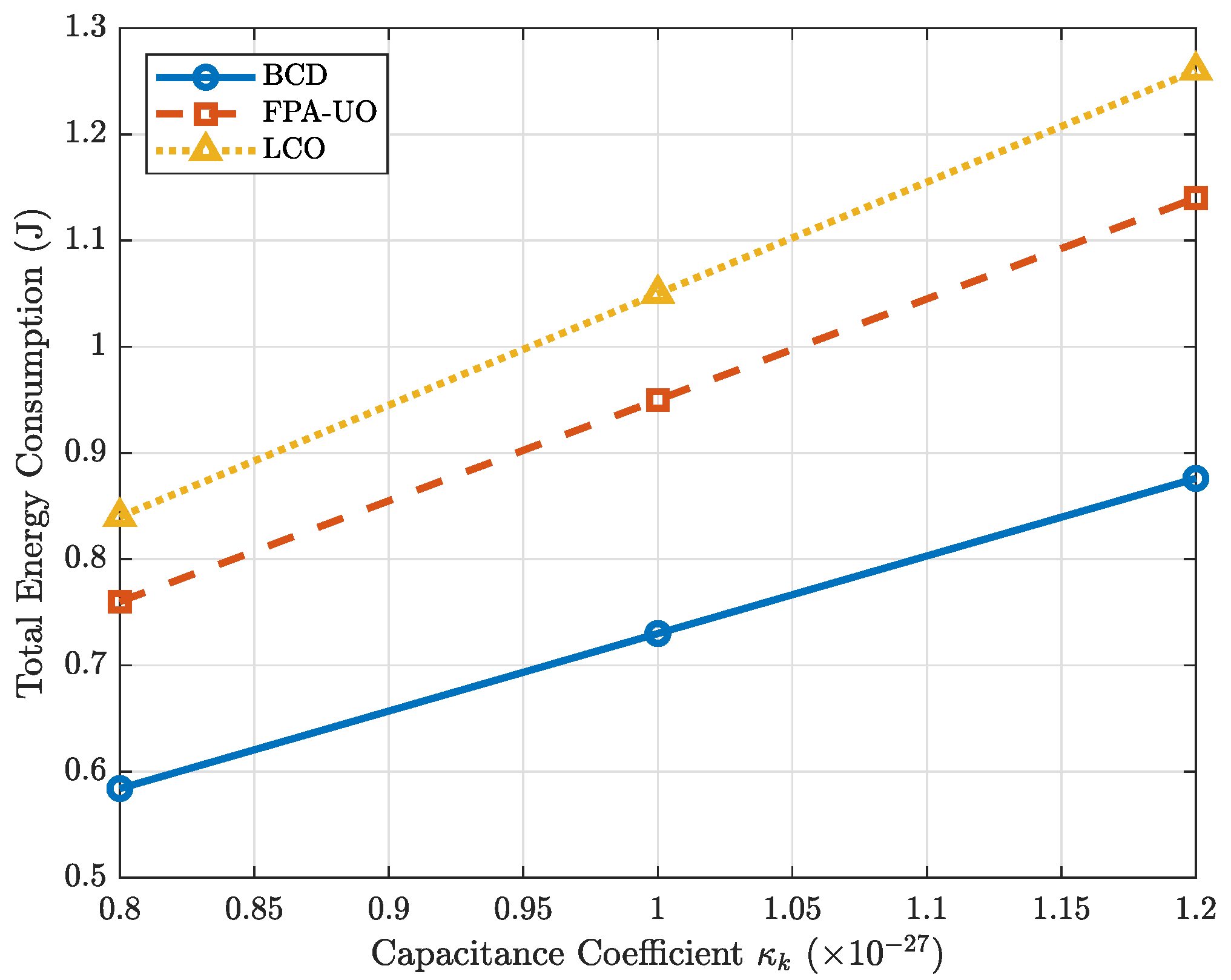
5.2. Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Jiang, C.; Han, Z.; Ren, Y.; Maunder, R.G.; Hanzo, L. Taking Drones to the Next Level: Cooperative Distributed Unmanned-Aerial-Vehicular Networks for Small and Mini Drones. IEEE Veh. Technol. Mag. 2017, 12, 73–82. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Du, G.; Chen, J.; Wang, J.; Li, Q. ISAC-Aided UAV Swarms: From Networked Perception to Capability Evolution. IEEE Commun. Mag. 2024, 62, 60–66. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y. Energy-efficient data uploading for cellular-connected UAV systems. IEEE Trans. Commun. 2020, 19, 7279–7292. [Google Scholar] [CrossRef]
- Shen, C.; Chang, T.H.; Gong, J.; Zeng, Y.; Zhang, R. Multi-UAV interference coordination via joint trajectory and power control. IEEE Trans. Signal Process. 2020, 68, 843–858. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Y.; Zhang, Z.; Lu, X. Energy consumption minimization for NOMA-based secure UAV-MEC network. China Commun. 2025, 22, 202–216. [Google Scholar] [CrossRef]
- Li, Q.; Wang, J.; Si, P.; Zhang, Y.; Chen, J.; Jiang, C. Energy-Efficient Communication and Computing Scheduling in UAV-Aided Industrial IoT. IEEE Internet Things J. 2024, 11, 30430–30441. [Google Scholar] [CrossRef]
- Wu, X.; Liang, L.; Wen, W.; Huang, Z.; Liu, X.; Jia, Y. DRL-based trajectory optimization and computation-aware resource allocation for UAV-assisted edge computing networks. IEEE Internet Things J. 2025, 12, 540–558. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X.; Rui, Y.; Dang, X.; Jia, G.; Guizani, M. Joint resource allocation and 3D-position optimization for UAV-assisted MEC network with noma. IEEE Trans. Netw. Sci. Eng. 2025, 12, 1440–1456. [Google Scholar] [CrossRef]
- Singh, S.K.; Agrawal, K.; Singh, K.; Li, C.-P.; Ding, Z. NOMA enhanced hybrid RIS-UAV-assisted full-duplex communication system with imperfect SIC and CSI. IEEE Trans. Commun. 2022, 70, 7609–7627. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Chen, H.; Han, C.; Li, L.; Do, D.-T.; Mumtaz, S.; Nallanathan, A. UAV-enabled multi-pair massive MIMO-NOMA relay systems with low-resolution ADCS/DACS. IEEE Trans. Veh. Technol. 2024, 73, 2171–2186. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, B.; Liu, C.; Lin, K. Intelligent power allocation optimization algorithm for enhanced CR-NOMA network via densenet-BILSTM. IEEE Trans. Cogn. Commun. Netw. 2025, 11, 2543–2553. [Google Scholar] [CrossRef]
- Vu, T.H.; Nguyen, T.-V.; Pham, Q.-V.; da Costa, D.B.; Kim, S. Short-packet communications for uav-based noma systems under imperfect CSI and SIC. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 463–478. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A survey on mobile edge computing: The communication perspective. IEEE Commun. Surveys Tuts. 2017, 19, 2322–2358. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-uav enabled wireless networks. IEEE Trans. Wireless Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. Flexible-Antenna Systems: A Pinching-Antenna Perspective. IEEE Trans. Commun. 2025, 73, 9236–9253. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Mu, X.; Ouyang, C.; Xu, X.; Ding, Z. Pinching-antenna systems: Architecture designs, opportunities, and outlook. IEEE Commun. Mag. [CrossRef]
- Zhuo, B.; Gu, J.; Duan, W.; Wen, M.; Peng, L.; Ho, P.H. P-NOMA for pinching-antenna systems (PASS). IEEE Wireless Commun. Lett. 2025; early access. [Google Scholar] [CrossRef]
- Ai, Y.; Mu, X.; Si, P.; Liu, Y. Delay Minimization in Pinching-Antenna-enabled NOMA-MEC Networks. arXiv 2025, arXiv:2510.16296. [Google Scholar]
- Tyrovolas, D.; Tegos, S.A.; Diamantoulakis, P.D.; Ioannidis, S.; Liaskos, C.K.; Karagiannidis, G.K. Performance Analysis of Pinching-Antenna Systems. IEEE Trans. Cogn. Commun. Netw. 2025; early access. [Google Scholar] [CrossRef]
- Ai, Y.; Liu, C.; Peng, M. Joint user association and resource allocation for cost-efficient NOMA-enabled F-RANs. Digital Commun. Netw. 2024, 10, 1686–1697. [Google Scholar] [CrossRef]
- Zhao, H.; Hao, Q.; Huang, H.; Gui, G.; Ohtsuki, T.; Sari, H.; Adachi, F. Online Trajectory Optimization for Energy-Efficient Cellular-Connected UAVs With Map Reconstruction. IEEE Trans. Veh. Technol. 2024, 73, 3445–3456. [Google Scholar] [CrossRef]
- Lu, W.; Ding, Y.; Gao, Y.; Chen, Y.; Zhao, N.; Ding, Z.; Nallanathan, A. Secure NOMA-Based UAV-MEC Network Towards a Flying Eavesdropper. IEEE Trans. Commun. 2022, 70, 3364–3376. [Google Scholar] [CrossRef]
- Tun, Y.K.; Dán, G.; Park, Y.M.; Hong, C.S. Joint UAV Deployment and Resource Allocation in THz-Assisted MEC-Enabled Integrated Space-Air-Ground Networks. IEEE Trans. Mob. Comput. 2025, 24, 3794–3808. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, L.; Dai, Y. MO-AVC: Deep-Reinforcement-Learning-Based Trajectory Control and Task Offloading in Multi-UAV-Enabled MEC Systems. IEEE Internet Things J. 2024, 11, 11395–11414. [Google Scholar] [CrossRef]
- Zhong, R.; Liu, X.; Liu, Y.; Chen, Y. Multi-Agent Reinforcement Learning in NOMA-Aided UAV Networks for Cellular Offloading. IEEE Trans. Wirel. Commun. 2022, 21, 1498–1512. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Chen, G.; Ding, Z. Sum-Rate Maximization for NOMA-Assisted Pinching-Antenna Systems. IEEE Wireless Commun. Lett. 2025, 14, 2728–2732. [Google Scholar] [CrossRef]
- Xu, Y.; Ding, Z.; Cai, D.; Wong, V.W.S. QoS-Aware NOMA Design for Downlink Pinching-Antenna Systems. IEEE Trans. Commun. 2025; early access. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, X.; Liu, A.; Liu, Y. Two-Timescale Joint Transmit and Pinching Beamforming for Pinching-Antenna Systems. IEEE Wireless Commun. Lett. 2025, 14, 2897–2901. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Renzo, M.D.; Tao, M.; Yuan, X. Robust Secure UAV Communications With the Aid of Reconfigurable Intelligent Surfaces. IEEE Trans. Wireless Commun. 2021, 20, 6402–6417. [Google Scholar] [CrossRef]
- 3GPP. Further Enhancements to LTE Time Division Duplex (TDD) for Downlink-Uplink Interference Management and Traffic Adaptation; 3rd Generation Partnership Project, Technical Report, 3GPP TR 36.828; 3GPP: Sophia Antipolis, France, 2012. [Google Scholar]
- Tegos, S.A.; Diamantoulakis, P.D.; Ding, Z.; Karagiannidis, G.K. Minimum Data Rate Maximization for Uplink Pinching-Antenna Systems. IEEE Wireless Commun. Lett. 2025, 14, 1516–1520. [Google Scholar] [CrossRef]
- Fang, F.; Xu, Y.; Ding, Z.; Shen, C.; Peng, M.; Karagiannidis, G.K. Optimal Resource Allocation for Delay Minimization in NOMA-MEC Networks. IEEE Trans. Commun. 2020, 68, 7867–7881. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Song, S.H.; Letaief, K.B. Stochastic joint radio and computational resource management for multi-user mobile-edge computing systems. IEEE Trans. Wireless Commun. 2017, 16, 5994–6009. [Google Scholar] [CrossRef]
- Dai, X.; Duo, B.; Yuan, X.; Tang, W. Energy-Efficient UAV Communications: A Generalized Propulsion Energy Consumption Model. IEEE Wireless Commun. Lett. 2022, 11, 2150–2154. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]


| Method | ||||
|---|---|---|---|---|
| Proposed BCD | 100 | 100 | 99.8 | 99.5 |
| FPA-UO | 98.5 | 97.2 | 95.8 | 94.0 |
| LCO | 97.0 | 95.5 | 93.2 | 91.8 |
| Metric | BCD (Small Scale) | BCD (Large Scale) |
|---|---|---|
| Total Energy (J) | 1.40 | 3.50 |
| Average Data Rate (Mbps) | 0.72 | 0.65 |
| Coverage Ratio (%) | 100 | 100 |
| Convergence Iterations | 12–18 | 15–20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, Y.; Liu, C.; Li, M. Energy-Efficient Uplink Communication in UAV-Enabled MEC Networks with Pinching Antennas. Drones 2025, 9, 796. https://doi.org/10.3390/drones9110796
Ai Y, Liu C, Li M. Energy-Efficient Uplink Communication in UAV-Enabled MEC Networks with Pinching Antennas. Drones. 2025; 9(11):796. https://doi.org/10.3390/drones9110796
Chicago/Turabian StyleAi, Yuan, Chang Liu, and Meng Li. 2025. "Energy-Efficient Uplink Communication in UAV-Enabled MEC Networks with Pinching Antennas" Drones 9, no. 11: 796. https://doi.org/10.3390/drones9110796
APA StyleAi, Y., Liu, C., & Li, M. (2025). Energy-Efficient Uplink Communication in UAV-Enabled MEC Networks with Pinching Antennas. Drones, 9(11), 796. https://doi.org/10.3390/drones9110796







