1. Introduction
UAVs and drones have rapidly proliferated in both the civilian and military domains due to their mobility, flexibility, and ability to operate as coordinated teams [
1]. Modern multi-UAV systems undertake missions ranging from urban surveillance and environmental monitoring to search and rescue and delivery logistics [
2]. By deploying multiple UAVs cooperatively, these systems can cover large areas and perform tasks in parallel, achieving far greater efficiency than any single UAV. For example, a fully autonomous swarm of palm-sized drones has been shown to navigate a dense forest, requiring real-time coordination to avoid obstacles and inter-drone collisions [
3]. This showcases the potential of multi-UAV teams to operate in complex, previously inaccessible environments, but also underscores the need for robust task allocation and coordination strategies to manage such missions.
From a broad perspective, the MATA problem addresses how to assign a set of tasks among multiple autonomous agents (robots or UAVs) to optimize the overall performance [
4]. In the specific context of multi-robot systems, MUTA refers to the coordinated process of assigning mission tasks to a team of drones. Effective task allocation becomes critical when no single UAV has the capability or capacity to accomplish all tasks alone—a common situation in complex missions such as wide-area surveillance or disaster response. In these scenarios, tasks must be intelligently divided among UAVs according to each drone’s capabilities (e.g., sensor payload, endurance) and the mission requirements. Recent work has emphasized that multi-UAV missions introduce unique challenges not seen in other multi-robot settings. For instance, persistent monitoring tasks with UAVs must contend with time-varying environmental states, limited flight endurance (propulsion energy capacity), and constrained communication ranges between aerial units [
2]. Failing to account for these factors can significantly degrade mission performance. This is highlighted in a distributed persistent monitoring approach, where dynamic task reallocation is continually needed to handle evolving information and keep data fresh [
2]. In general, as the number of drones and tasks grows, the task allocation problem quickly becomes combinatorially complex and intractable to solve optimally in real time (the assignment problem is NP-hard in many formulations). This has motivated a spectrum of approaches, from classical optimization to market-based auctions and machine learning, which yield sufficient solutions within practical time ranges for multi-UAV applications.
A fundamental design decision for MUTA is the coordination architecture, which can be roughly divided into centralized and distributed schemes. In a centralized architecture, a single control node (either an onboard designated UAV or a ground control station) is responsible for aggregating global state information, computing the optimal or near-optimal tasking assignment for the entire fleet, and issuing commands accordingly [
5]. The advantages of this approach are that it guarantees global optimality under certain assumptions, simplifies system-wide monitoring, and facilitates the integration of complex optimization algorithms [
6,
7]. However, centralized solutions have some key drawbacks, including single points of failure, large communication overheads (which scale poorly with increasing team sizes), reduced robustness in dynamic or competitive environments, and latency issues due to non-real-time data aggregation and decision computation [
8,
9].
Conversely, distributed architectures decentralize the decision-making process across individual UAVs or local clusters. Each agent independently computes task assignments based on locally available information and peer-to-peer communications, often using consensus algorithms or market-based negotiation mechanisms [
10,
11]. Distributed schemes inherently improve scalability, reduce the reliance on high-bandwidth communication links, and increase fault tolerance by eliminating central points of failure [
2,
12]. Nevertheless, decentralized approaches may yield suboptimal allocation due to incomplete global information, require complex coordination protocols to reach consensus, and can be susceptible to communication delays and inconsistent state knowledge among agents [
6,
7].
Centralized algorithms like the Hungarian assignment method can produce globally optimal allocations under complete information [
13]. However, this optimality comes at the cost of heavy communication and a single point of failure. Every UAV must continuously share its status (position, fuel, etc.) with the central controller, which can overload networks and create bottlenecks [
13]. Moreover, if the central node fails or loses connectivity, the entire mission could be jeopardized [
13]. By contrast, distributed (or decentralized) approaches avoid any one single leader; drones make decisions locally through peer-to-peer communication or consensus. This yields far greater robustness to failures and communication dropouts and tends to scale better as the team grows [
13]. The trade-off is that distributed methods may sacrifice some optimality and coordination precision. Without a global view, drones might make locally rational choices that are suboptimal globally—leading to conflicts (e.g., multiple UAVs choosing the same task) or idle resources [
13]. For example, market-based auction algorithms allow UAVs to bid for tasks and iteratively reach an assignment; these are highly scalable and flexible, but they typically find near-optimal rather than truly optimal allocations. Recent research has explored hybrid architectures (sometimes called hierarchical or hybrid coordination), where elements of centralized planning are combined with distributed execution to achieve the best of both worlds [
2]. Overall, the choice of a centralized vs. distributed strategy has profound implications for MUTA performance, especially in contested or communication-limited environments.
Another important consideration is the mode of cooperation among UAVs. In some missions, tasks are independent and can be simply divided among individual drones. In others, such as transporting a heavy payload or in a wide-area search, forming coalitions or sub-teams of UAVs for a task can be advantageous. Recent works have begun treating MUTA as a coalition formation problem, using game-theoretic frameworks [
1]. In such formulations, UAVs decide not only which tasks to take but also whether to team up with other drones to execute a task jointly. Compared to a single UAV operating alone, appropriately grouping UAVs into coalitions can dramatically enhance the task efficiency for complex objectives [
1]. These coalition-based approaches introduce additional layers of decision-making (e.g., how to split rewards among UAVs, how to ensure stable cooperation within a coalition), but they are highly relevant for missions like disaster response, where tasks might demand multiple drone capabilities simultaneously. In summary, the background of MUTA is rooted in classic multi-agent assignment problems but extended by the distinct constraints and possibilities of drone technology, which include high mobility, energy limits, wireless communication, and the ability to coordinate in swarms or formations. This paper is motivated by the need to systematically evaluate how different task allocation algorithms (centralized optimal, distributed heuristic, learning-based, etc.) perform in coordinating UAV teams, given the growing deployment of drone swarms in real-world applications.
1.1. Challenges in Task Allocation
Effectively allocating tasks among multiple UAVs is difficult due to several overlapping challenges that must be addressed simultaneously. We highlight some of the key challenges below, particularly focusing on those that are salient in multi-UAV contexts.
Computational Complexity and Scalability
Optimal MUTA is an inherently combinatorial problem that becomes intractable at scale. Even a simplified assignment scenario (where each drone performs one task at a time) can be mapped to an NP-hard assignment problem when extended with realistic constraints [
14]. The number of possible task-to-UAV allocations grows exponentially with the team size and task count, making a brute-force search impractical [
15,
16]. This is exacerbated in dynamic scenarios, where the assignment may need to be recomputed frequently as new tasks appear or conditions change. Thus, algorithms must be designed to scale gracefully. A related issue is communication scalability: a centralized allocator requires gathering cost/utility information from all UAVs, incurring an O(m·n) communication overhead for m drones and n tasks each cycle [
15,
16]. This can quickly tax wireless bandwidth and processing resources in a large drone swarm [
15,
16]. Decentralized approaches mitigate the single-channel bottleneck, but they still require agents to exchange messages to reach a consensus on assignments. Without careful management, the message complexity can explode as the fleet grows. In sum, ensuring that task allocation methods remain computationally and communicatively efficient for large multi-UAV teams is a primary concern [
15].
Optimality vs. Real-Time Responsiveness
There is an inherent trade-off between solution optimality and decision speed in task allocation. On one hand, centrally optimized algorithms (e.g., integer programming solvers or exhaustive search) can, in theory, find the assignment that minimizes the total cost or maximizes the reward for the mission [
17]. However, these methods often require significant time and complete, up-to-date information from all drones. In fast-changing environments, the “optimal” allocation may arrive too late to be useful. On the other hand, distributed or greedy heuristic methods can react very quickly to new tasks or events—sometimes in near-constant time by local computation—but they trade away guarantees of optimality [
15,
16]. A task allocation that is considered optimal at one moment may become suboptimal moments later as UAV positions and task states evolve. Many distributed schemes (e.g., auctions, consensus algorithms) prioritize adaptability and low communication, accepting a slight loss in solution quality. The challenge is to find a balanced approach that yields high-quality assignments within the tight timing constraints of UAV missions. For example, a multi-agent RL approach was used to coordinate heterogeneous UAVs, enabling on-the-fly task reallocation with minimal delays and maintaining the performance even as the team size scaled to dozens of drones [
18]. Such learning-based or anytime algorithms aim to continuously improve task allocations and approach optimality over time, without stalling the mission with lengthy computations.
Dynamic and Uncertain Environments
Multi-UAV operations are often conducted in dynamic environments with significant uncertainty. In real-world deployments like disaster response, military missions, or environmental surveillance, tasks can arrive unpredictably (e.g., a new fire outbreak to monitor, a new target spotted) and task requirements can change as scenarios unfold. A previously optimal task assignment can be invalidated by the appearance of a high-priority new task or the sudden inaccessibility of an area [
11,
19]. Therefore, task allocation algorithms must handle dynamic changes—they should recompute or adjust assignments efficiently as new tasks appear or old tasks evolve. This might involve techniques like continuous replanning, rolling horizon optimization, or agents making local decisions based on current observations. Uncertainty further complicates planning: UAVs may have imprecise information about task rewards or their own states (due to sensor noise or communication delays). Travel times or task completion times might be stochastic. Algorithms thus need to be robust to incomplete and noisy information, perhaps by anticipating changes or quickly correcting assignments when surprises occur. For example, some approaches incorporate safety margins or periodic reallocation triggers to cope with uncertainty [
11,
19]. Overall, the dynamic nature of UAV missions demands task allocation methods that are reactive and adaptive, rather than one-shot static plans.
Communication Constraints
Reliable communication is a persistent challenge for distributed UAV swarms. Drones often operate in environments with limited bandwidth, intermittent connectivity, or strict line-of-sight constraints (e.g., within buildings, underground, or over long distances). High communication demands can severely degrade a task allocation algorithm’s performance. For instance, auction-based methods where UAVs continuously broadcast bids for tasks may work well in a lab or simulation, but, in the field, these messages can be lost or delayed, leading to suboptimal or failed allocations [
20,
21]. Studies have shown that algorithms that perform well with perfect networking can break down when packet loss or latency is introduced. The challenge is to design communication-efficient task allocation algorithms that minimize the amount of information exchanged or that can tolerate delays and dropouts. Some recent advances leverage consensus protocols that require only neighbor-to-neighbor communication and can converge despite asynchronous updates or occasional message loss [
20,
21]. Another strategy keeps communication local by structuring the team into clusters or hierarchies, limiting how far messages must travel [
20,
21]. Ultimately, as UAVs often operate on wireless ad hoc networks, resilience to communication disruptions is a key requirement for any practical multi-UAV coordination strategy.
Robustness to Agent Failures
In critical missions (e.g., search and rescue, exploration of hazardous areas), it is realistic to expect that some UAVs might fail, lose power, or drop out due to collisions, propulsion energy depletion, or other hazards. A robust task allocation system must dynamically reassign the tasks of a failed drone to others so that the mission can continue with minimal degradation. Centralized systems are particularly vulnerable: if the central controller UAV goes down, it can cripple the whole team’s coordination [
22,
23]. Decentralized approaches inherently distribute decision-making, which improves fault tolerance—the failure of one drone (even if it is a leader for some tasks) can be detected and compensated for by others without a single point of collapse [
22]. For example, a recent framework called MAGNNET combined multi-agent deep learning with graph neural networks to enable fully decentralized task allocations; it demonstrated improved scalability and fault tolerance in simulations, continuing to perform well even as agents were removed or communications were intermittently lost [
13,
22,
23]. Another aspect of robustness is handling sudden surges in task load. If a large number of new tasks appears at once (e.g., multiple disaster sites in an earthquake), the allocation algorithm should gracefully redistribute the workload and avoid overloading any single UAV [
22,
23]. In summary, ensuring graceful degradation and quick recovery in the face of drone failures or other disruptions is crucial for MUTA. Techniques like redundant task assignments, peer monitoring (drones watching each other’s status), and on-the-fly replanning contribute to a robust allocation system.
Fairness and Load Balancing
While not always a major technical requirement, fairness in task distribution can impact the long-term effectiveness of a multi-UAV team. If one or two drones consistently handle the largest workloads or the most strenuous tasks, they may exhaust their batteries or even suffer faster wear and tear, while other UAVs remain underutilized. In human–robot or mixed-initiative teams, unfair task allocation can also affect human trust and team morale [
20,
24]. Therefore, some task allocation strategies incorporate load-balancing mechanisms. For instance, each UAV’s current workload or recent task history can be factored into new assignment decisions. There is often a tension between purely cost-optimal assignments (which might overburden the most capable UAV) and fair assignments that spread tasks more evenly. Metrics have been proposed to explicitly measure how balanced an allocation is across the fleet. In UAV networks, a balanced approach might extend the overall mission duration by preventing any single drone from draining its propulsion energy too quickly. The challenge for the algorithm is to achieve good performance while avoiding severe workload imbalances. In practice, modest fairness constraints (like avoiding assigning a new task to a UAV that is already at capacity if an alternative UAV is available) can significantly improve the team’s resilience and longevity [
20,
24].
In summary, the task allocation problem for multi-UAV systems lies at the intersection of combinatorial optimization, real-time systems, and networked robotics. An effective solution must navigate the complexities of scale, dynamic changes, limited communication, and the practical realities of drone operations (like failures and propulsion energy limits). The above challenges often conflict with each other—improving one aspect (say, making the solution more optimal) might worsen another (like the computation time or communication load). The goal for researchers is to design algorithms that balance these trade-offs, delivering reliable and efficient task assignments for drone swarms in real-world conditions.
1.2. Research Gaps and Objectives
Thanks to intensive research over the past decade, a wide range of algorithms now exist for MUTA [
11,
15]. However, important gaps remain in our understanding of how different approaches compare and which are best suited for certain scenarios. Early research in MUTA tended to develop bespoke algorithms for specific mission types, without providing a broader comparative perspective. For example, one study might propose a new allocation method tailored to a surveillance mission, while another study might design a centralized planner for a delivery drone network, but each is evaluated in isolation, under its own assumptions and environment [
25,
26]. This means that, until recently, we lacked “horizontal” comparisons across algorithm families [
9,
27]. Researchers seldom directly compare a centralized optimal method against a distributed heuristic under identical conditions, leaving practitioners unsure of how each would perform outside of their respective case studies [
12,
28,
29].
In the literature, most comparative studies have been narrow in scope. Some works focus only on one class of algorithms—for instance, comparing different distributed algorithms with each other (assuming a decentralized setting) while excluding centralized or learning-based approaches from the analysis [
30,
31]. Other works may compare a classic centralized algorithm against a few heuristics, but these often neglect realistic issues like communication delays or dynamic task arrivals in their evaluations [
9,
31]. In short, there has been a lack of unified benchmarking. As Alqefari and Menai (2025) point out in their recent survey, studies often evaluate task allocation methods under varying assumptions and metrics, making it difficult to draw general conclusions or best practices [
9]. For example, one paper might measure success purely by the total task completion time, while another prioritizes the communication overhead or success rate, complicating direct comparison [
12,
20]. No consensus has emerged on which algorithmic paradigm is “best” for multi-UAV coordination, partly because each has advantages under certain conditions (e.g., centralized for static environments vs. distributed for highly dynamic situations) [
15,
27].
Another gap is the relative scarcity of evaluations that combine multiple real-world challenges in one scenario. Many experiments simplify the problem to isolate one factor, e.g., testing algorithms in a static environment with no new tasks, assuming perfect communication, or having a moderate team size [
9,
9]. In reality, a multi-UAV mission may involve all these challenges at once—a large team in a dynamic environment with intermittent communication and potential UAV failures [
2,
30]. Few studies have stress-tested algorithms under such comprehensive conditions [
32]. Notably, most prior benchmarks either use static or mildly dynamic settings [
27]. There are few datasets or simulations that consider high-frequency task influx, large-scale surges in task load, and agent dropouts together across competing algorithms [
26]. As a consequence, we do not fully know how, for example, a market-based method holds up when both communication is lossy and tasks arise rapidly, compared to how a learning-based method or an optimization-based method would cope in the same stressful scenario [
11,
32].
The objective of our work is to fill these gaps by providing a unified evaluation of major task allocation algorithms for multi-UAV systems. We aim to rigorously compare a representative set of algorithms—spanning centralized, distributed, and learning-based approaches—under identical conditions and across a variety of scenarios. By doing so, we seek to answer the following questions: Which algorithms handle highly dynamic task streams best? How much optimality do distributed methods lose in exchange for scalability and robustness? At what team size or task load does a centralized method break down? Moreover, we incorporate practical factors (like communication limits and UAV failures) into the evaluation, to examine each method’s robustness beyond idealized assumptions. Ultimately, the goal is not to declare a single “winner” but to chart the trade-offs: identifying which algorithm is preferable under what circumstances. This type of comprehensive comparison can provide valuable guidance to practitioners in choosing a solution for a given multi-UAV application. It can also highlight the strengths of each approach and reveal areas where improvement or hybridization is needed (for example, if a learning-based method performs well generally but struggles with fairness or specific constraint handling, which points to future research directions).
In summary, while the toolkit of MUTA algorithms has grown, the lack of unified comparisons and integrated testing has left a gap in understanding when and why to choose one method over another. Our research addresses this by benchmarking diverse algorithms within a common framework, thereby providing insights into their relative performance, limitations, and suitability for various multi-UAV mission profiles. The findings are intended to both inform real-world deployments (by matching algorithms to use cases) and pinpoint where further research is needed (such as improving an algorithm’s scalability or adaptability).
1.3. Contributions of This Paper
This paper presents a systematic study of MATA with the following contributions.
Comprehensive Comparison Framework
We propose a unified framework for the comparison of centralized and distributed task allocation methods (e.g., Hungarian, auction, CBBA, and auction 2-opt refinement algorithms) in both static and dynamic scenarios. The implementation in this study is available on GitHub:
https://github.com/YunzeSong/Multi-UAVs-Task-Allocation-Algorithms.git (accessed on 18 April 2025).
Reproducible Simulation Environment
A simulation framework is developed in Python with standardized interfaces to evaluate algorithms across various scales (small, medium, large) and dynamic conditions.
Multi-Dimensional Evaluation Metrics
We establish evaluation metrics covering the total cost, computation time, convergence, communication overhead, robustness, and scalability, supported by clear visualizations.
Analysis of Centralized vs. Distributed Trade-Offs
This paper analyzes the trade-offs between global optimality and scalability/robustness, especially under dynamic task arrivals and agent failures.
4. Experiments
This section presents a comparative analysis of the four task allocation algorithms (Hungarian, auction, CBBA, auction 2-opt refinement algorithm) under three categories of experimental conditions (static tasks, dynamic tasks, and robustness tests under adverse conditions). Performance is evaluated using several metrics—total cost, completion rate, response delay, computational time, communication overhead, and fairness—with an emphasis on interpreting the numerical results to identify trends and trade-offs.
4.1. Experimental Settings
Our simulation framework, implemented in Python, provides a unified evaluation environment for various task allocation algorithms, including centralized optimization techniques such as the Hungarian algorithm and other custom plug-in modules. In this 2D simulator, agents and tasks are randomly distributed across a predefined area, with Euclidean distances used to compute travel costs, and tasks can appear either statically or dynamically. Each algorithm processes the current task and agent state information according to its unique strategy. Ultimately, the algorithms output agent–task assignments and record performance metrics such as the computation time and iteration count. This modular design not only standardizes the evaluation process across different algorithms but also facilitates direct and effective comparisons between them.
In detail, all experiments reported in this paper are conducted using Python (3.10). Numerical computations and data manipulations are performed using NumPy (1.24.2) and SciPy (1.10.1). Agent communications and network topologies are modeled using NetworkX (3.0). Reinforcement learning algorithms are implemented with Stable-Baselines3 (2.0.0), which relies on PyTorch (2.0.0) as the deep learning backend. Data visualization and plots are generated using Matplotlib (3.7.1). The experimental environment is set up on an Ubuntu 22.04 platform, equipped with a dual-socket configuration with Intel Xeon Gold 6338 processors.
4.2. Evaluation Metrics
Total Cost
The total cost is the primary optimization metric, measured by the total travel distance or task completion time across all agents. This metric directly reflects efficient resource utilization, including fuel and time.
Completion Rate
The completion rate represents the proportion of tasks that are successfully assigned and executed relative to the total generated. A high completion rate indicates that the algorithm can handle nearly all tasks, which is crucial in emergency scenarios or under task surges, preventing critical failures due to missed assignments.
Response Delay
The response delay measures the time between a task being posted and its assignment to an agent. A low delay means that urgent tasks are addressed promptly. Centralized approaches may incur higher delays due to replanning the entire assignment, while distributed or RL methods tend to assign tasks immediately.
Computational Time
The computational time quantifies the real time required to generate the assignment solution, typically measured in milliseconds or seconds. Shorter computational times support more frequent replanning and enhance system scalability, particularly as the problem size increases.
Communication Messages
Communication messages quantifies the number and volume of messages exchanged in distributed algorithms, including bidding and consensus messages. A reduced overhead conserves bandwidth and energy and reveals how well different methods scale in terms of the messaging burden.
Fairness
Fairness is defined based on the balance in task allocation among agents. Specifically, we quantify fairness by calculating the standard deviation of the number of tasks assigned to each agent. A smaller standard deviation indicates that tasks are more evenly distributed among agents, signifying higher fairness. Conversely, a larger standard deviation reflects greater disparities, meaning that some agents bear significantly heavier workloads than others. This metric provides a straightforward measure of how equitably tasks are shared within the multi-agent system and is commonly employed in similar task allocation research.
4.3. Static Task Allocation
The objective of this experiment is to comparatively evaluate the performance of four task allocation algorithms in a static task allocation setting. In this configuration, all tasks are available and published at the initial time step (t = 0), thus creating a one-shot assignment scenario where the complete set of tasks is known a priori. This setup facilitates an isolated analysis of each algorithm’s behavior and performance, eliminating the complications that arise from dynamic or time-varying environments.
The experimental scenarios are designed to encompass a range of problem complexities, ensuring that the conclusions drawn are robust and applicable across different scales of operation. Three distinct scenarios are implemented. The small-scale scenario involves 10 tasks to be assigned among 5 agents, a setting that serves as a baseline to reveal the fundamental operational differences among the algorithms. The medium-scale scenario increases the problem complexity by considering 50 tasks distributed over 15 agents, providing a more challenging environment that tests the scalability and efficiency of the proposed methods under moderately demanding conditions. The large-scale scenario presents an even more complex challenge, with 200 tasks allocated among 40 agents, thereby demonstrating the computational efficiency, convergence characteristics, and overall robustness of each algorithm.
To ensure statistical significance and account for any stochastic variability inherent in the allocation process, each scenario is independently repeated over 30 rounds. This repeated experimentation allows for a thorough assessment of the consistency and performance reliability across different task–agent configurations. All agents are assumed to have homogeneous communication and computation capabilities, and the experiments operate under the assumption of a static environment without any dynamic changes in task availability or agent functionality. This controlled experimental design is intended to provide clear insights into the relative merits and limitations of each algorithm in handling various scales of static task allocation problems.
4.4. Dynamic Task Allocation
Building on the insights gained from the static task allocation experiment, the next phase of our study introduces a more complex, dynamic environment in which tasks arrive over time. In this setting, the responsiveness and real-time processing capabilities of the allocation algorithms are tested as they contend with continuously emerging tasks. Rather than the one-shot scenario previously analyzed, this dynamic task flow scenario requires the system to continually update and reallocate tasks according to a predetermined schedule, thereby simulating realistic operational conditions.
The dynamic environment is designed around three distinct task publication frequencies to represent varying system loads and urgency levels. In the slow scenario, the system releases 2 tasks every 10 time units, creating relatively relaxed conditions that still capture the challenges of real-time processing. The medium scenario increases the complexity, with 5 tasks released every 5 time units, thus introducing a moderate level of temporal pressure and necessitating more efficient allocation processes. In the fast scenario, the highest system demand is simulated by releasing 10 tasks every 2 time units, placing significant strain on the algorithms to process and assign tasks rapidly and accurately.
The total simulation duration is set to 100 time units, ensuring that the dynamic flow of tasks is sustained over a sufficiently long period to reveal the operational nuances of each allocation strategy. To ensure that the results are statistically significant and robust, each dynamic scenario is repeated over 30 independent rounds. This comprehensive experimental setup enables a detailed assessment of how well the algorithms adapt to varying temporal complexities and provides deeper insights into their performance in environments where task arrivals are continuous and time-critical.
4.5. Robustness Testing
Following the analysis of both static and dynamic settings, we now extend our investigation to include robustness testing under abnormal conditions. This phase is specifically designed to challenge the resilience of the allocation algorithms when confronted with unexpected events, such as sudden task surges and agent failures, which are common in real-world scenarios.
In this experiment, the focus is on assessing how well the algorithms maintain their functionality and overall performance when facing disruptive events. The testing framework introduces three distinct abnormal conditions. First, in the surge scenario, a large number of tasks is suddenly released in the middle of the simulation, representing a scenario where the system experiences a sudden and significant increase in workload. Second, in the failure scenario, certain agents randomly experience failures during the operational period, rendering them temporarily unable to process or allocate tasks until they recover, thus simulating intermittent agent dysfunction. Lastly, the combined scenario simultaneously incorporates both the task surge and agent failures, thereby simulating a particularly challenging environment where multiple adverse events occur concurrently.
Each of these abnormal scenarios is simulated over a total time period of 100 time units, ensuring that the dynamic behavior of the system is thoroughly observed. To account for stochastic variations and to reinforce the statistical robustness of the findings, each scenario is independently repeated over 20 rounds. This rigorous experimental design provides a comprehensive evaluation of the algorithms’ robustness under conditions of unpredictability and stress, offering valuable insights into their practical resilience and reliability in the face of operational anomalies.
The robustness tests introduce unreliable communications and robot failures. Under message loss, distributed algorithms (auction, auction 2-opt refinement algorithm, CBBA) show degradation: CBBA is the most sensitive due to its multi-round consensus, leading to delayed or missed assignments; the auction and auction 2-opt refinement algorithms recover via timeout and rebidding mechanisms, albeit with suboptimal allocations. The centralized Hungarian method remains robust provided that robots can communicate with the center, but network partitions remove isolated robots from the pool.
In robot failure scenarios, all methods experience proportional declines in their completion rates. The auction and auction 2-opt refinement algorithms rebid the tasks of failed robots promptly, incurring higher costs and delays for reassignment. CBBA requires additional consensus iterations to redistribute tasks, introducing longer interruptions. The Hungarian controller recomputes optimal assignments upon failure, minimizing cost increases but pausing execution during replanning.
5. Results
The following subsections detail the results for each scenario type and explain the observed behavior of the algorithms with respect to each evaluation metric.
In all experiments, the total cost is measured in meters (m); the completion rate is expressed as a percentage (%); the response delay and computational time are both measured in seconds (s); communication messages is reported as a count of messages; and fairness is measured as a dimensionless number (standard deviation).
5.1. Static Task Allocation
Table 1,
Table 2 and
Table 3 present the comparative results of the four task allocation algorithms under three different static scenarios with increasing problem sizes. The following analysis and discussion are based on the data presented in these three tables, providing a systematic comparison of the algorithms’ effectiveness and efficiency as the problem size increases.
Under the conditions described above, the centralized Hungarian algorithm produced the lowest-total-cost solution among the four methods, as expected given its optimal assignment guarantee. The auction-based method and the consensus-based algorithms (CBBA and its distributed variant, the auction 2-opt refinement algorithm) achieved total costs that were only marginally higher than that of the Hungarian baseline (typically within a few percent of the minimum), reflecting their effectiveness in approximating the optimal allocation through iterative bidding and negotiation.
In our static assignment context, the completion rate is defined as the ratio of tasks assigned in a single, one-shot allocation to the total number of tasks. Since each agent can only execute one task at a time, when the number of tasks exceeds the number of agents (which is common in static benchmarks), only a subset of tasks can be matched and scheduled in this single-step assignment. Therefore, the completion rate in this context reflects the one-time matching efficiency of each algorithm and is typically less than 100% whenever the number of tasks exceeds the number of agents. In contrast, dynamic task assignment experiments allow agents to iteratively take on new tasks as they become available, eventually achieving full task completion over time.
The initial assignment response delay was minimal for most methods: the Hungarian method dispatched all tasks in a single batch after a brief computation (polynomial-time optimization completed in milliseconds for the tested problem sizes). The auction, CBBA, and auction 2-opt refinement algorithms incurred slightly longer assignment delays due to multiple bidding or negotiation rounds; however, these delays remained in the order of seconds and did not significantly hinder execution.
Regarding computational effort, the Hungarian algorithm was the most time-efficient in the static scenario. The Hungarian algorithm’s cubic complexity was manageable for the tested sizes. In contrast, the auction and auction 2-opt refinement algorithms required more computation time overall due to iterative bid evaluations, and CBBA added overhead from its two-phase bundle construction and conflict resolution process.
The communication overhead followed a similar pattern: the centralized Hungarian approach required only minimal messaging (gathering task information and broadcasting final assignments). The auction and auction 2-opt refinement algorithms exchanged multiple messages per task (bids, replies, and notifications), proportional to the number of bidding rounds, while CBBA incurred a high message count owing to its repeated consensus iterations. Fairness in task distribution was high and roughly equivalent across methods, as optimal or near-optimal assignments divided tasks nearly evenly among robots, resulting in a comparable workload balance.
5.2. Dynamic Task Allocation
Table 4,
Table 5 and
Table 6 summarize the performance of the four task allocation algorithms under dynamic task arrival scenarios of varying intensity. These tables provide the basis for the following comparative analysis, which examines how each algorithm responds to different levels of dynamism in task allocation and highlights their respective strengths and limitations under varying operational pressures.
In the dynamic task allocation scenario, tasks arrived over time, requiring continual assignment updates. The centralized Hungarian approach, rerun upon each task arrival, maintained a low total cost by recomputing near-optimal assignments for the evolving task set; however, this introduced noticeable delays for new tasks as the solver’s workload grew. In contrast, the auction and auction 2-opt refinement algorithms handled tasks incrementally in a distributed manner: robots immediately bid on arriving tasks, yielding prompt assignments and low response delays. Their cumulative total costs remained close to optimal, with a slight trade-off in optimality for responsiveness. CBBA adapted by integrating new tasks into each robot’s bundle followed by consensus rounds, producing timely allocations at costs marginally above those of the auction-based methods.
The completion rates remained very high for all methods. Fairness in the dynamic context decreased for all methods relative to the static case: cost-driven algorithms tended to overutilize a subset of robots, while CBBA and the auction 2-opt refinement algorithm sometimes mitigated imbalances through consensus. Quantitatively, the variance in tasks per robot increased, with consensus-based algorithms showing a marginally better load balance than greedy approaches.
The communication overhead showed a clear scale-dependent trend. For small problem sizes, CBBA incurred the highest message volume due to its intensive all-to-all consensus. As the scale increased, however, the auction and auction 2-opt algorithms required substantially more messages because their iterative bidding processes grow rapidly with more agents and tasks. Centralized approaches kept the message counts consistently low. This demonstrates that, while CBBA is communication-intensive for small teams, it scales more efficiently than auction-based methods as the system size increases.
5.3. Robustness Testing
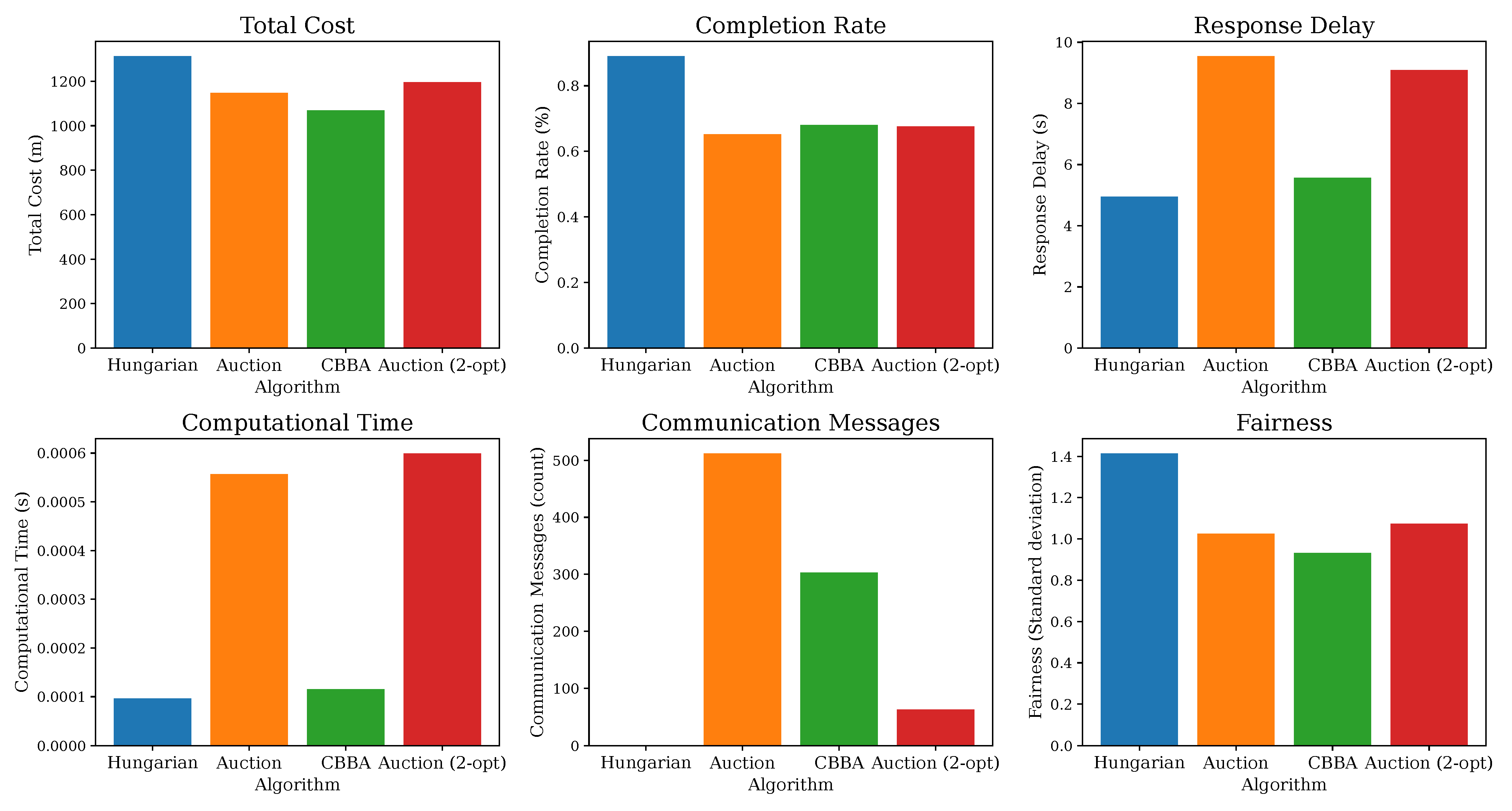
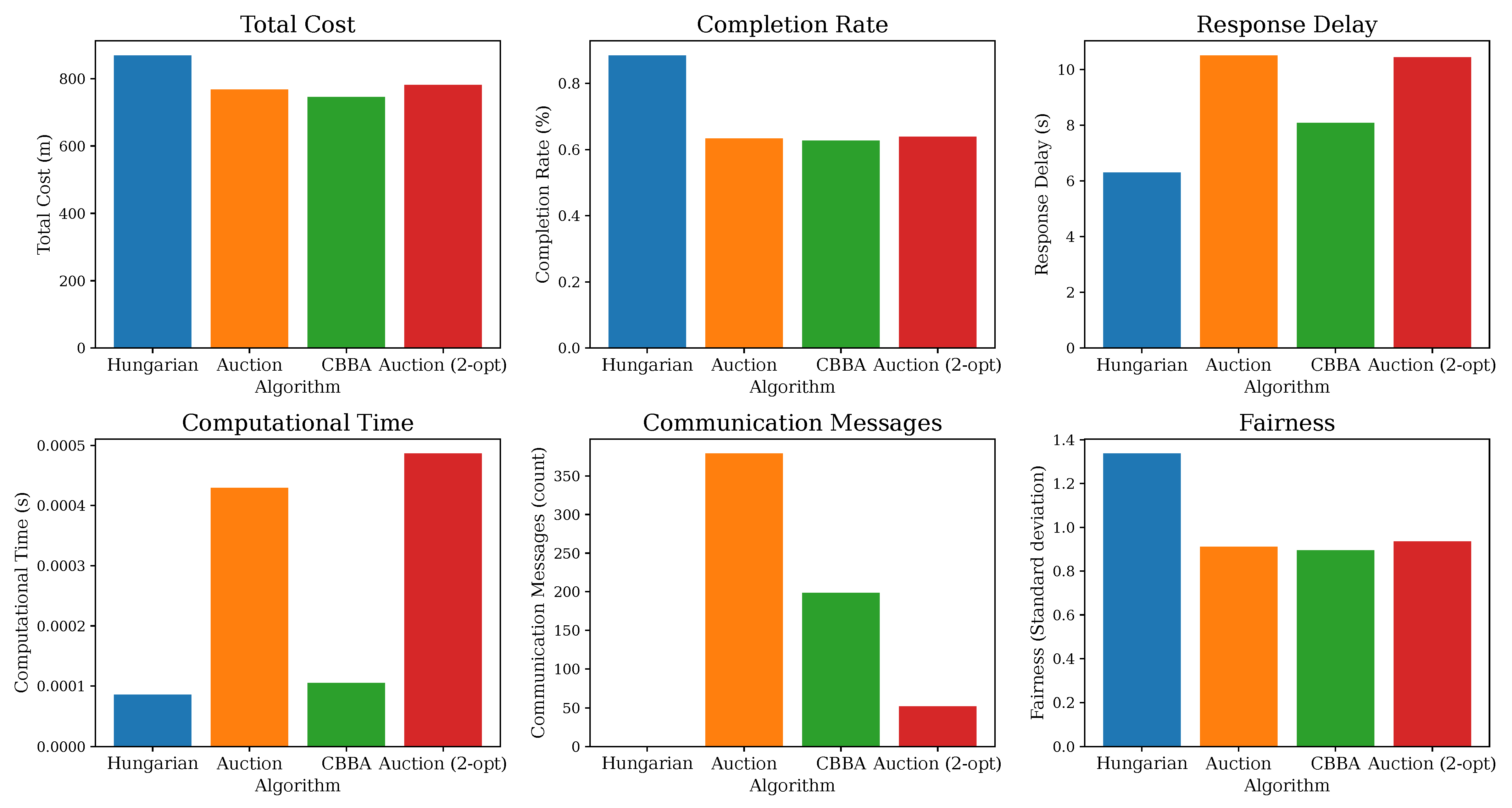
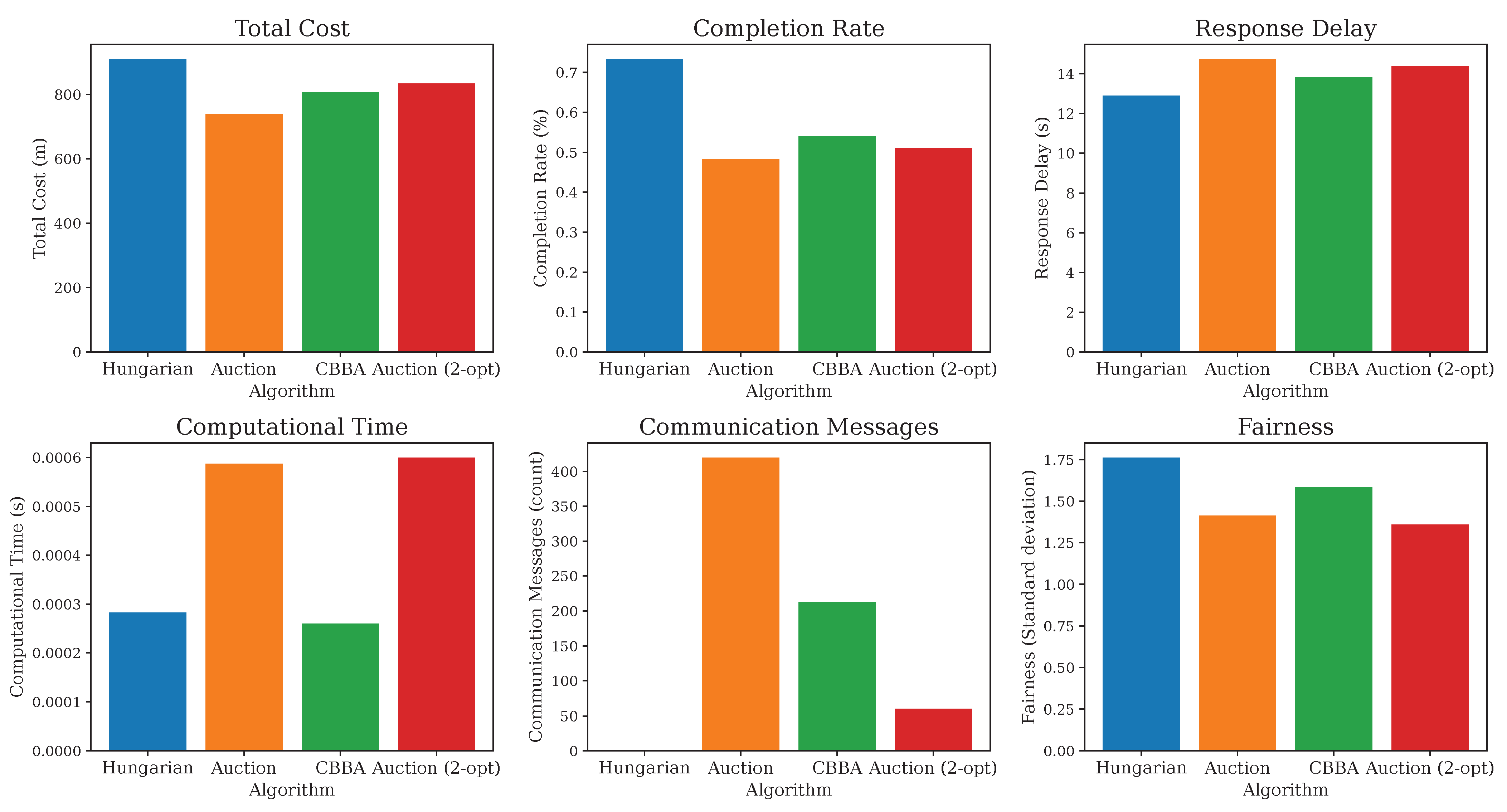
Figure 1,
Figure 2 and
Figure 3 provide a visual comparison of the four task allocation algorithms across three distinct robustness testing scenarios, and
Figure 4 illustrates the functionality and overall performance of the algorithms under a combined scenario involving multiple concurrent adverse events. These figures form the foundation for the following robustness analysis, enabling a nuanced assessment of each algorithm’s adaptability and reliability under both normal operation and adverse events.
Adverse conditions increased the total cost across all methods, with the Hungarian algorithm best containing cost growth in failure scenarios and distributed algorithms incurring moderate penalties. The completion rates fell under severe network losses and failures, with CBBA being most impacted by message drops and all methods losing in-progress tasks upon failure. Response delays worsened under disturbances—distributed methods faced extra iterations or rebidding, and the Hungarian method paused during replanning. The communication overhead spiked for the auction and auction 2-opt refinement algorithms and CBBA under unreliable networks, while the Hungarian approach showed little change. The fairness decreased as failures and partitions concentrated the workload on surviving or connected robots.
5.4. Limitations and Problems in the Experiments
In our experiments, there were several problems that existed. The Hungarian algorithm was originally designed to solve square (n × n) assignment problems. When the numbers of agents and tasks are not equal (n ≠ m), as in our experiments, the algorithm exhibits several limitations. To handle this, the cost matrix must be padded with dummy rows or columns to ensure that it is a square. However, this introduces artificial assignments that do not have real-world meaning. Thus, this algorithm can usually obtain the optimal solution when allocating tasks from n to n, but it may not be the best allocation scheme when allocating tasks from n to m.
Regarding the Bertsekas -auction algorithm, it can solve both the n-to-n assignment problem and the n-to-m problem. However, it can only yield an approximately optimal solution rather than a globally optimal one. The Bertsekas -auction algorithm is essentially a discrete optimization method based on price adjustments. Since task prices are updated in fixed increments of , the algorithm can only achieve an approximately optimal solution with an error bounded by . When the utility values are real numbers, this discrete update mechanism may obscure subtle differences between assignments, preventing the algorithm from precisely identifying the true optimum. Therefore, without employing -scaling, the Bertsekas -auction algorithm cannot guarantee global optimality. The auction 2-opt refinement algorithm, as a variant of the normal -auction algorithm, has the same limitation.
Regarding the CBBA algorithm, although it offers strong flexibility and distributed capabilities for n-to-m task allocation problems, it also exhibits several limitations under such asymmetric configurations. When the number of agents significantly exceeds the number of tasks, the algorithm tends to produce unbalanced assignments, where a few agents monopolize most tasks, while others remain idle. Conversely, in scenarios with a high task-to-agent ratio, the communication overhead increases substantially and frequent bundle reconstructions due to conflicts reduce the convergence efficiency. Furthermore, CBBA’s greedy local bundle construction lacks global path optimality and offers limited control over the number of tasks assigned per agent.
5.5. Experimental Summary
Overall, each algorithm upheld its core strengths and weaknesses under adversity: the Hungarian method retained cost-optimality but lacked agility; the auction, CBBA, and auction 2-opt refinement algorithms adapted flexibly at the expense of communication and costs under stress. No single approach is universally superior; the choice depends on which performance criteria—cost, responsiveness, fault tolerance, or communication efficiency—are most critical for the intended operational context.
6. Conclusions
This work has presented a unified evaluation framework for the comparison of four multi-UAV task allocation algorithms, namely the centralized Hungarian algorithm, the Bertsekas -auction algorithm, the consensus-based bundle algorithm, and the auction 2-opt refinement algorithm, under realistic drone mission constraints such as limited flight time, propulsion energy endurance, and intermittent communication. By embedding UAV-specific cost models (e.g., energy consumption per flight segment) and modeling communication topologies reflective of line-of-sight restrictions, our simulations captured the key operational challenges faced by drone swarms in applications like area surveillance, search and rescue, and cooperative inspection.
In static mission scenarios, where all tasks are known a priori, the centralized Hungarian method consistently achieves the lowest total travel distance and energy usage, making it the natural choice for small-scale aerial mapping or preplanned inspection paths. However, as the number of UAVs and tasks grows or when new waypoints emerge mid-flight, the need to replan globally introduces non-negligible delays and imposes heavy communication burdens on the ground station or lead drone.
Auction-based heuristics and the auction 2-opt refinement algorithm strike a balance between optimality and responsiveness by allowing each drone to bid locally for incoming tasks. These methods deliver near-optimal allocations with only moderate computational overheads, enabling drones to react quickly when, for example, a sudden hotspot appears in a wildfire monitoring mission. Their decentralized nature also reduces the reliance on a single point of control, albeit at the cost of extra message exchanges to maintain consistent task prices.
The CBBA approach further enhances mission robustness by employing a consensus mechanism: when a drone fails or its propulsion energy runs critically low, the remaining UAVs renegotiate task bundles through peer-to-peer communication, redistributing responsibilities without central intervention. This resilience comes with increased messaging, making CBBA most suitable for high-stakes operations like disaster response, where the need for reliability outweighs the need for bandwidth conservation.
No single algorithm universally outperforms the others across all UAV mission profiles. Instead, practitioners should select based on the mission’s tolerance for cost deviations, the permissible latency, the communication environment, and the failure risk. For tightly choreographed aerial inspections in urban canyons with reliable links, a centralized solver might suffice. In contrast, rapidly evolving search-and-rescue scenarios over rugged terrain require auction-based or consensus-driven methods.
Looking ahead, we plan to explore hybrid architectures that combine the precise cost minimization of centralized planners with the adaptivity of decentralized, learning-based policies. Embedding advanced fairness and load-balancing objectives will help to prevent individual drones from exhausting their batteries prematurely. We will also optimize consensus protocols for bandwidth-limited radio networks and validate our findings on physical UAV platforms, accounting for real-world energy profiles, heterogeneous payloads, and environmental disturbances such as wind gusts.
By strategically integrating the strengths of diverse coordination paradigms like global optimality, rapid replanning, and fault-tolerant consensus, we move closer to achieving autonomous drone swarms that can safely, efficiently, and reliably execute complex missions in the dynamic airspace of tomorrow.