Performance Analysis of Unmanned Aerial Vehicle-Assisted and Federated Learning-Based 6G Cellular Vehicle-to-Everything Communication Networks
Highlights
- The paper explores the variations in queuing and processing delays in a UAV-assisted C-V2X communications environment, with a focus on the international mobile telecommunication (IMT)-2030-based UAV-assisted 6G C-V2X communications.
- The queuing delay and processing delay are compared in a federated learning scenario and a gross data offloading scenario.
- For gross data offloading, we consider event-triggered cooperative perception messages (CPMs) and periodically transmitted basic safety messages (BSMs). The implication of the main finding is that the delay in FL scenario is less than that in the gross data offloading scenario.
- The queuing stability is ensured in the problem formulation.
Abstract
1. Introduction
- Different classes of packets such as control data, signaling data, or raw sensor information packets that are transmitted with different priorities, resulting in varying queuing and processing delays [12].
- Larger packets require more time for processing and transmission, which directly increases both and the waiting time in queues [20].
- The scheduling policy, window size, and channel access mechanisms that impact the duration for which a packet must wait in a queue before being transmitted, thus impacting .
- The underlying edge processing infrastructure at the vehicles, the processing server embedded in a UAV, the available bandwidth, queuing policies, and congestion significantly influence both queuing delay and processing delay [21].
- Queuing delay (): This is defined as the total time the packets spend in a queue at the UAV waiting to be transmitted to the PS plus the time packets spend waiting at the UAV buffer to be processed by the PS [3].
- Processing delay (): This represents the time taken to optimally partition a packet and process all the packets at the PS [22]. It includes the time taken at the UAV to compute the global model parameters under the gross data offloading scenario.
1.1. Contributions
- We investigate the balance between latency and utility when a UAV selects vehicles during each FedAvg iteration. This latency is benchmarked against the delay encountered in bulk data offloading scenarios.
- We analyze and investigate the interplay between latency and UAV energy consumption, examining how model convergence rate, delay variability, data sample size, and packet size interrelate. Additionally, we explore the failure rate in adhering to service time constraints relative to packet delay and UAV energy usage.
- We assess the frequency of constraint breaches as vehicle numbers rise within a realistic UAV-supported C-V2X communication framework. Consequently, we determine the optimal vehicle count that a UAV can accommodate without surpassing these constraints.
1.2. Organization
2. Related Work
3. System Model and Problem Formulation
3.1. UAV–Vehicle Queuing Model
- (i).
- Assuming gross data offloading from vehicles to the UAV.
- (ii).
- Considering FL where non-i.i.d. sensor data are processed at the in-vehicle ES, and subsequently, only the completed model parameter updates are communicated to the UAV.
3.2. Problem Formulation
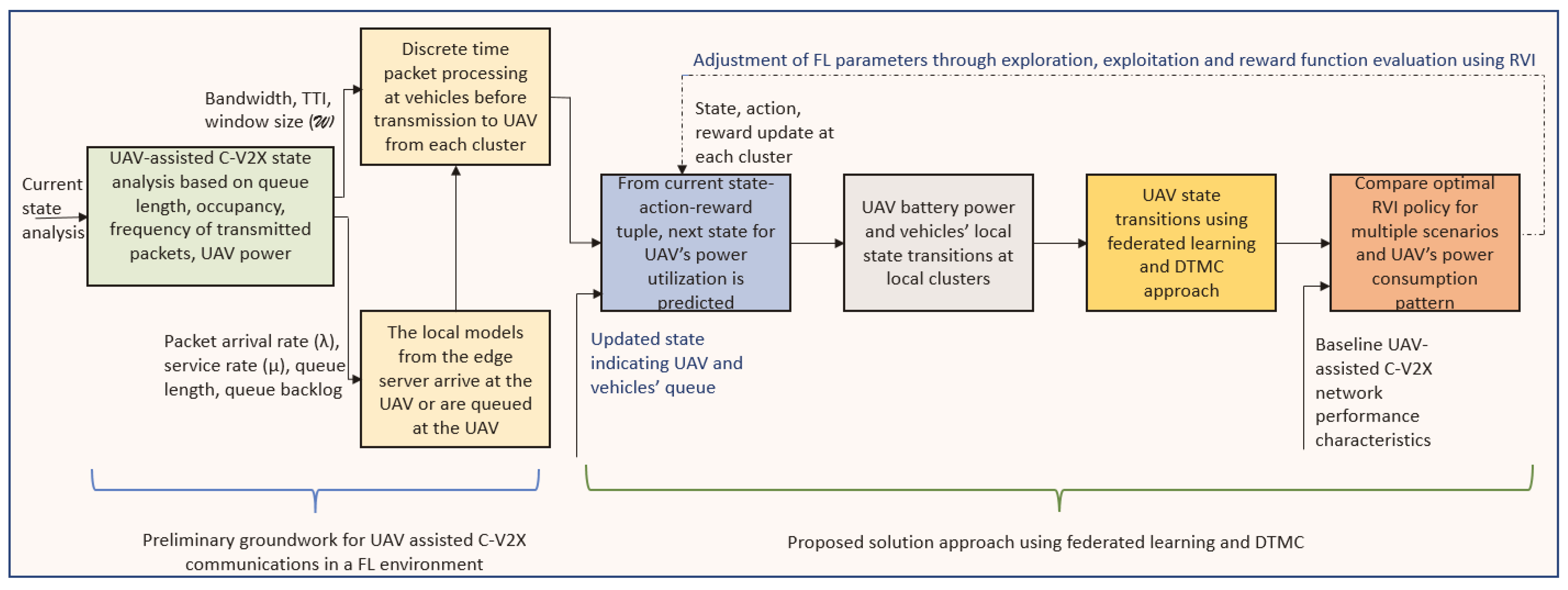
4. Proposed Solution
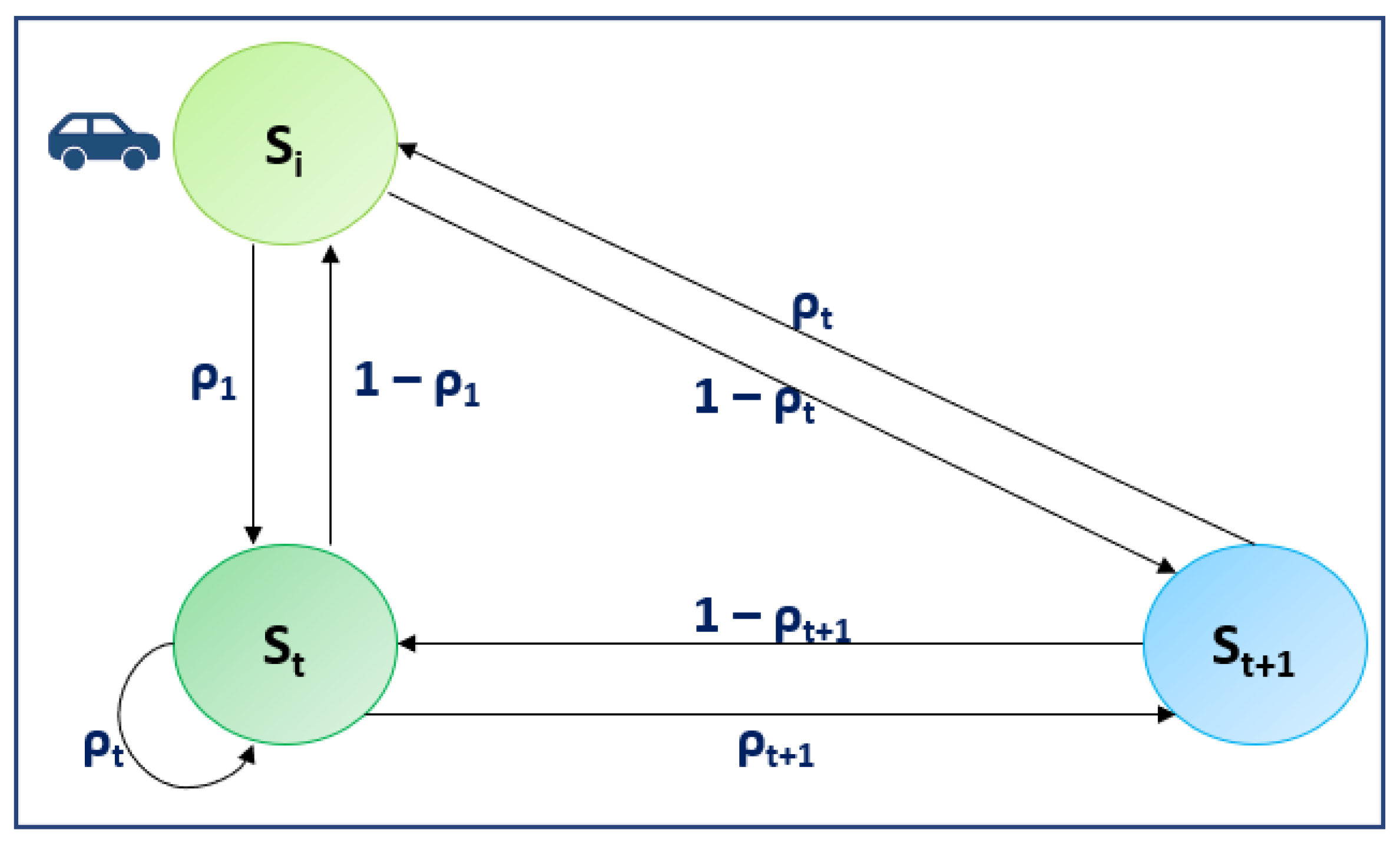
4.1. Intermittent States and State Transitions at the Vehicles
4.2. UAV Occupancy and State Transitions
- is the duration for which a packet remains in the queue before arriving at the UAV.
- is the UAV occupancy indicator, where indicates that a packet is in the UAV’s queue, and indicates otherwise.
- is the queue occupancy indicator, where indicates that a packet is waiting in the queue, and indicates an empty queue.
- represents the duration for which a packet remains at the UAV.
- is a stochastic process representing the number of packets transmitted;
- is a stochastic process denoting the number of transmission windows elapsed since the start.
4.3. Impact of UAV Occupancy on Packet Queue
- (i).
- : packet queuing time.
- (ii).
- : buffer queue’s occupancy indicator.
- (iii).
- : UAV occupancy indicator.
- (iv).
- : occupancy indicator of the transmission queue.
- (v).
- : UAV occupancy indicator for the transmission queue.
- (vi).
- : status update at the UAV.
- (vii).
- : duration for which a packet remains at the UAV.
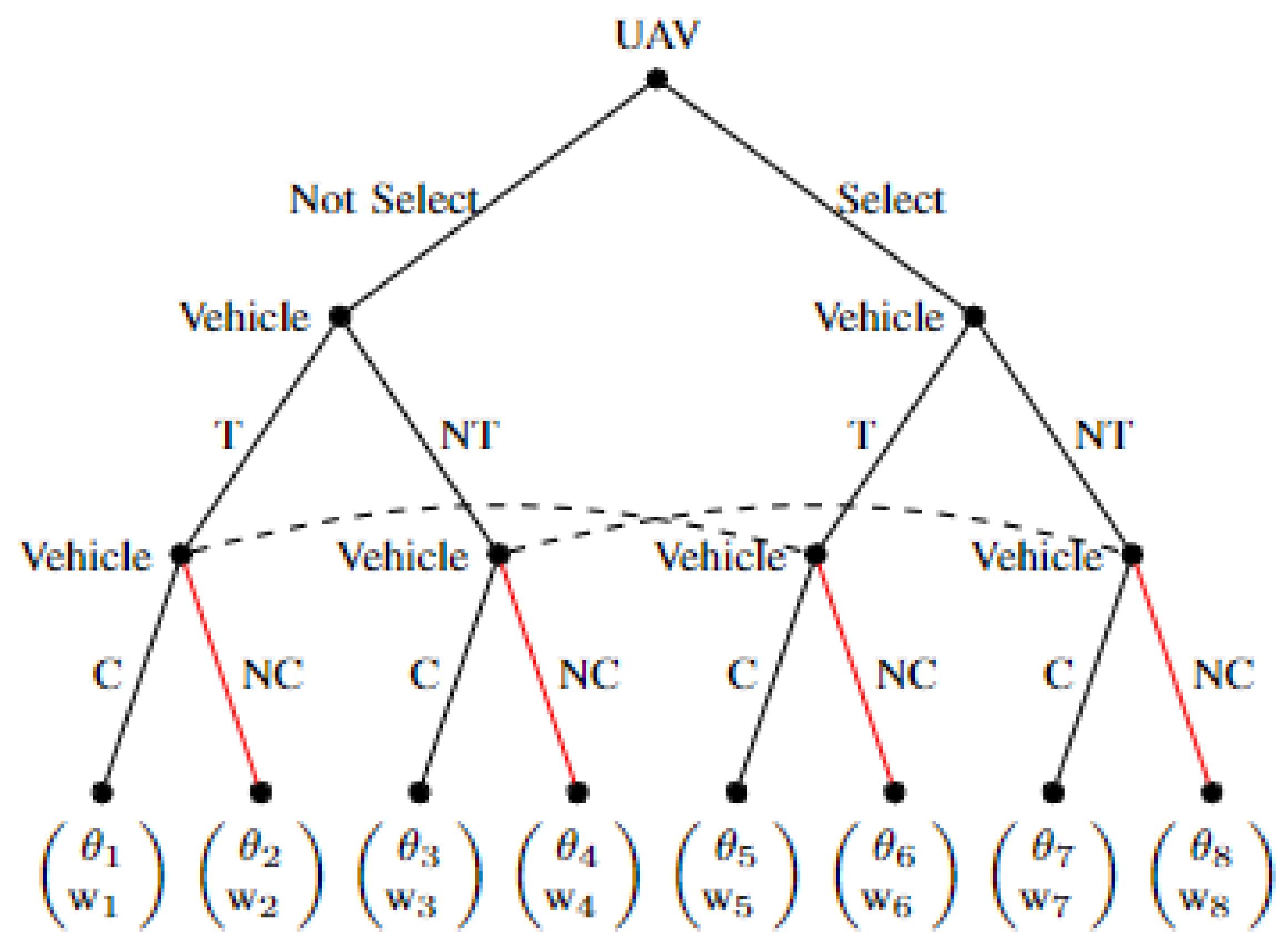
4.4. Federated Learning Based on Message Priority
5. Simulation Results and Discussion
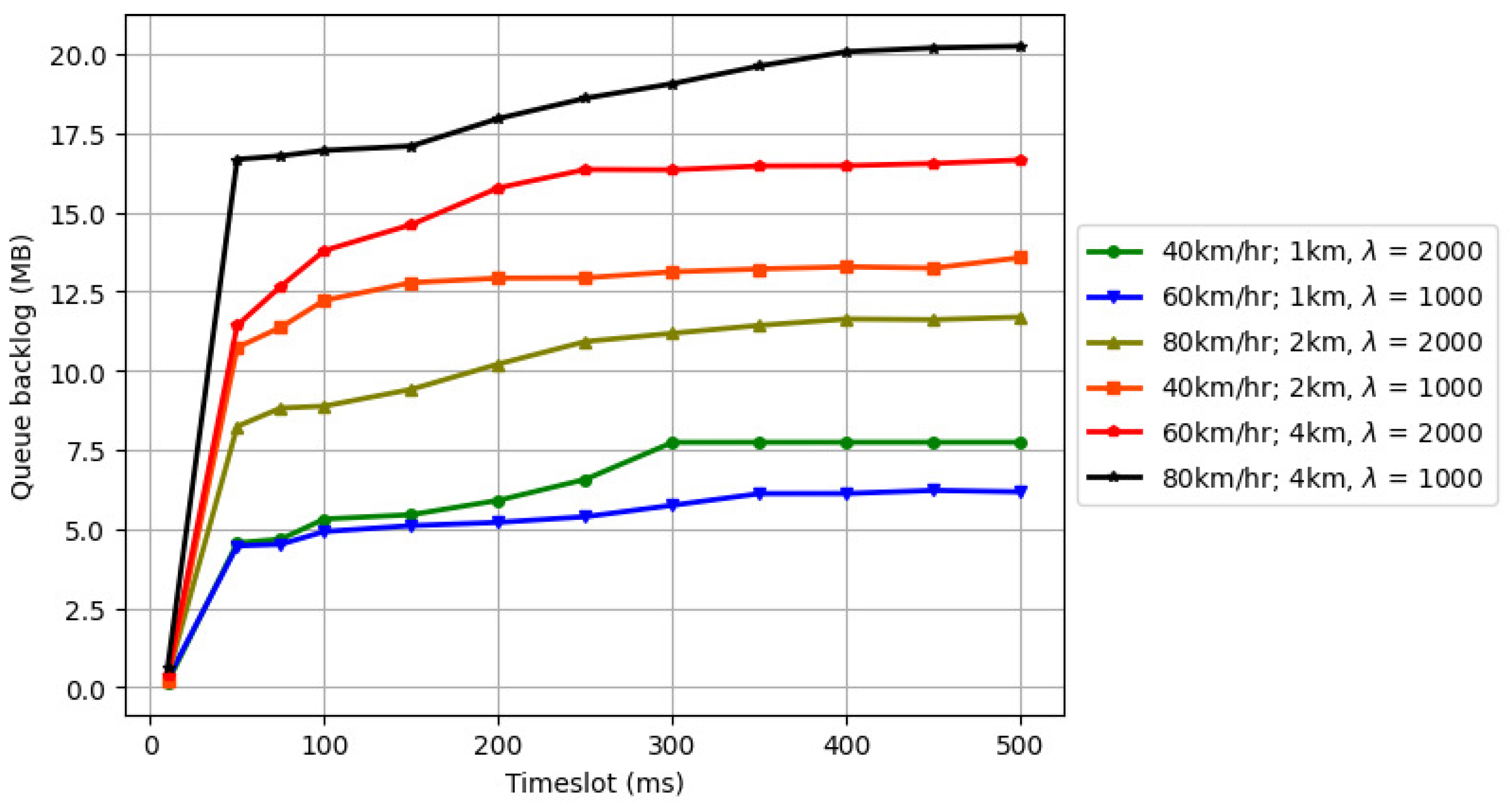
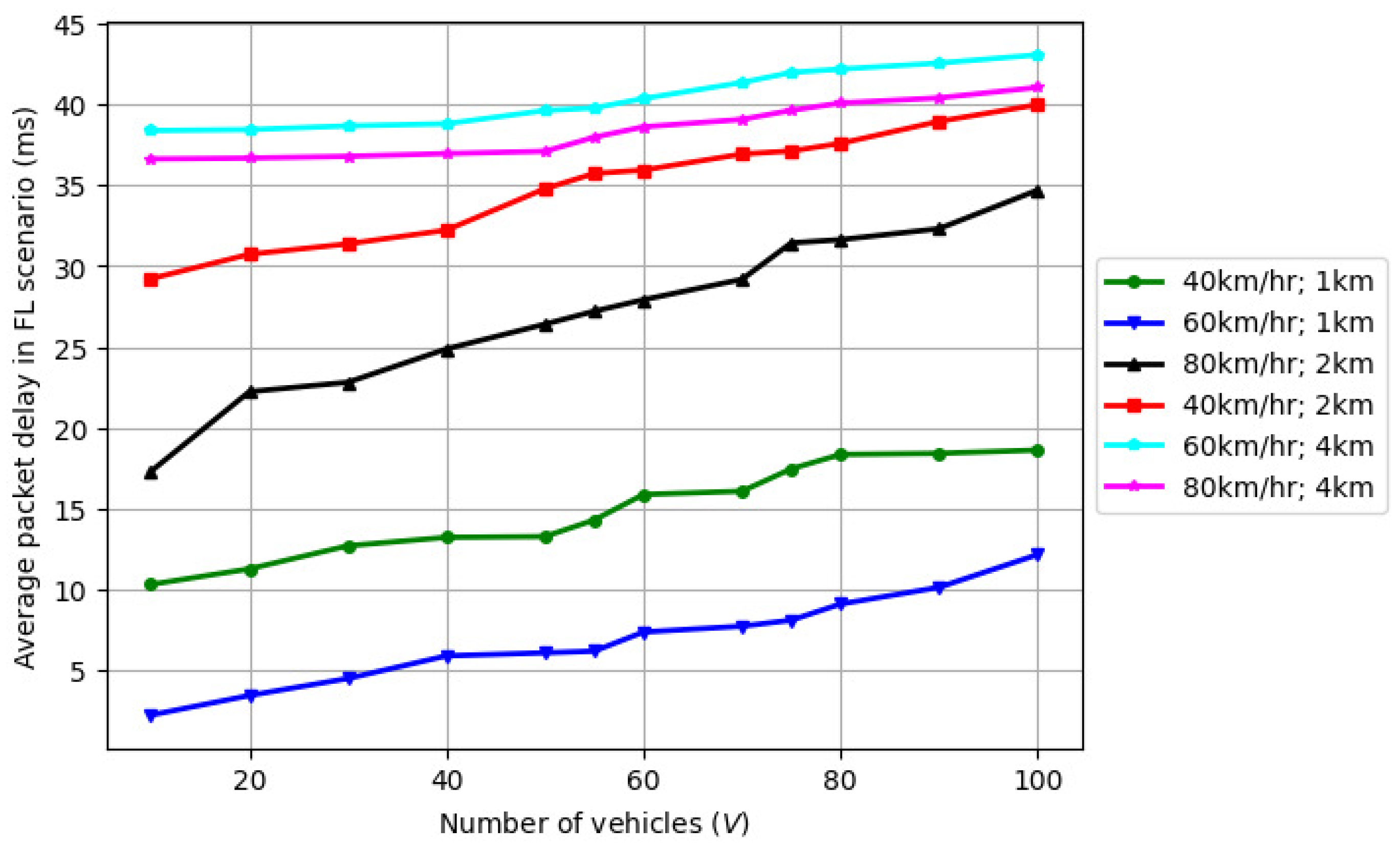
5.1. Variation in Transmission Window Length () and Queue Backlog with Varying Number of Vehicles (V)
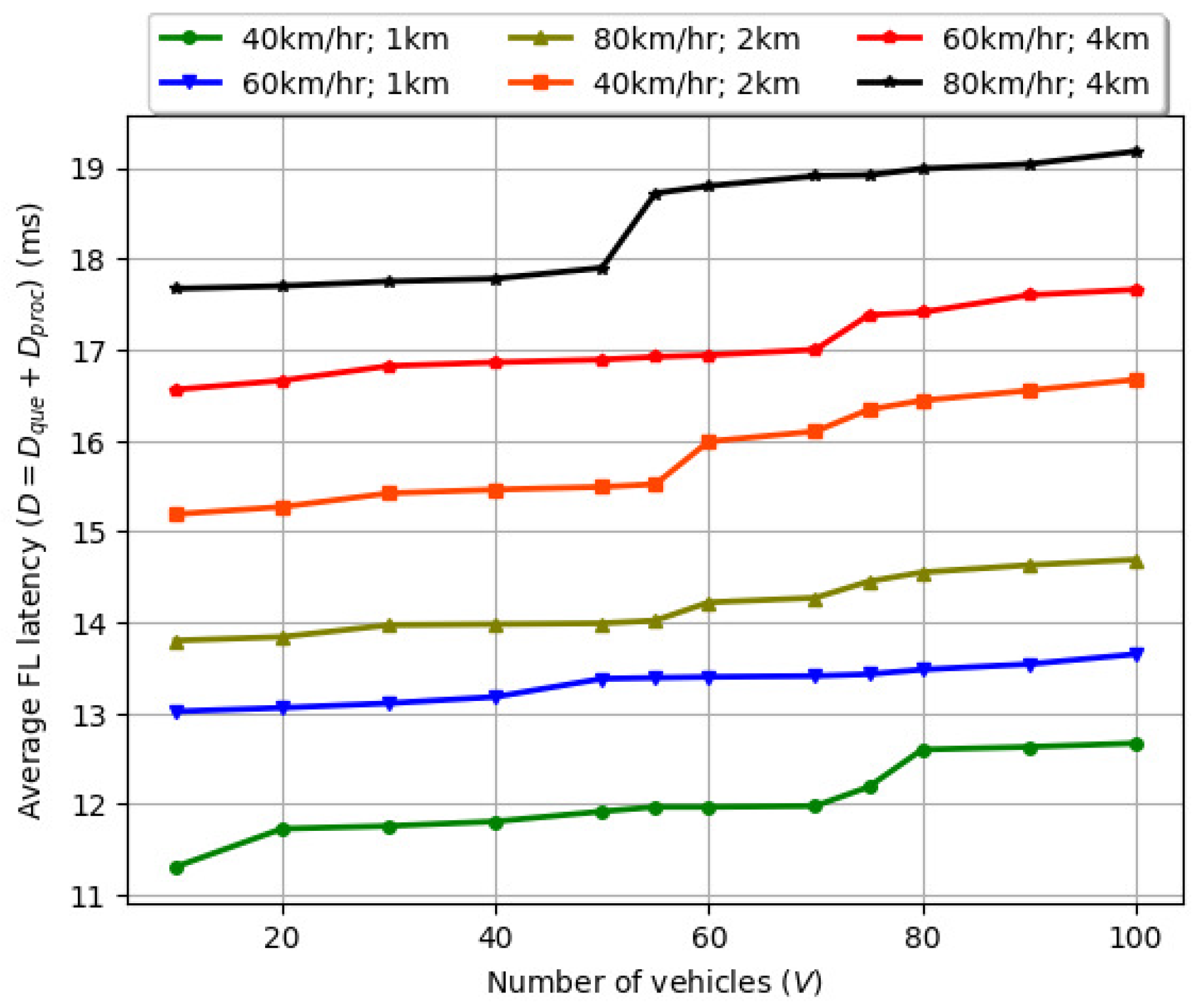
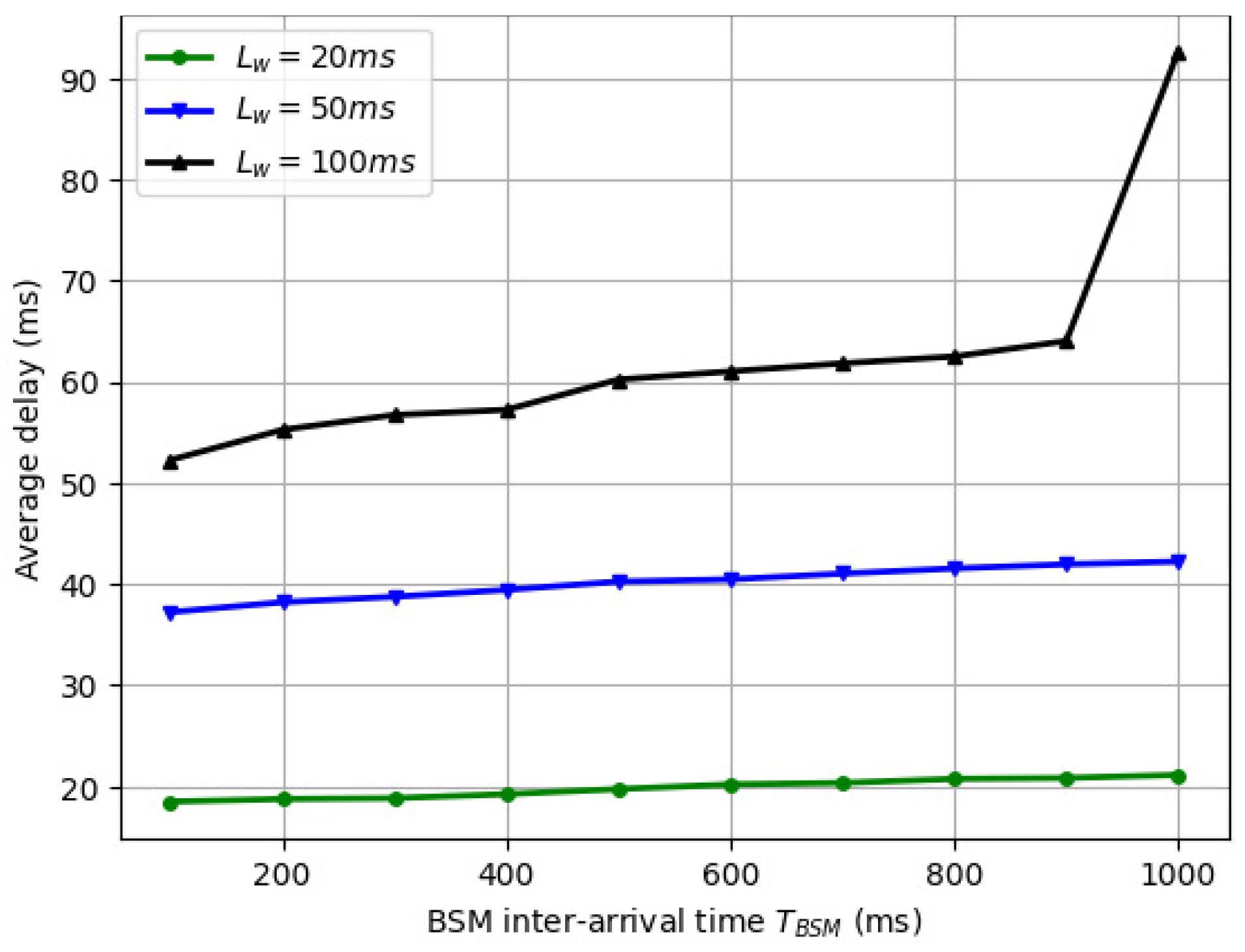
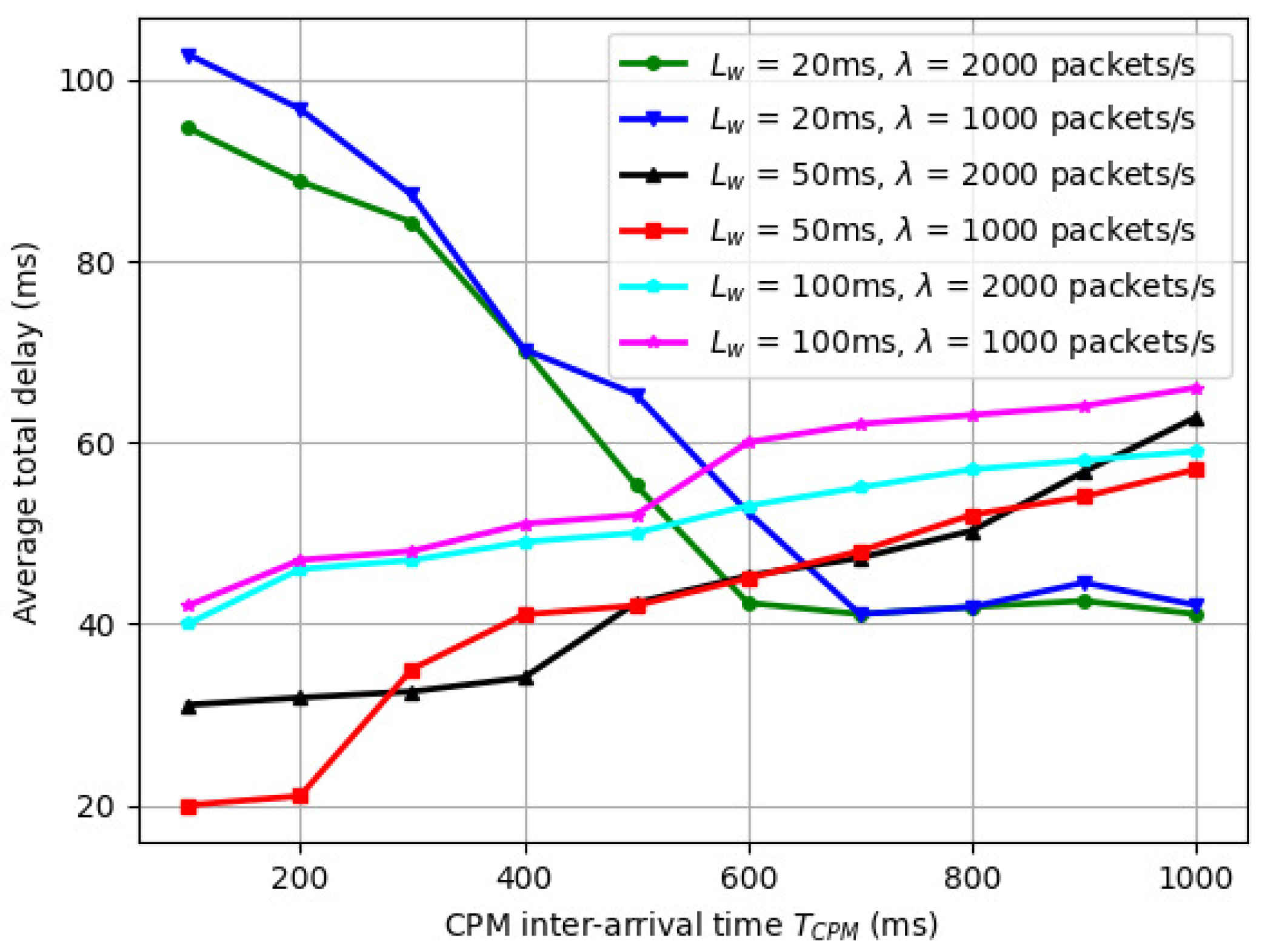
5.2. Variation in Average Delay with Inter-Arrival Time of BSM and CPM Packets with (V)
5.3. Variation in Average Energy Consumption (Joules/s) of UAV with Varying V
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3GPP | Third-generation partnership project |
| 6G | Sixth-generation (communication networks) |
| AR | Augmented reality |
| BCD | Block coordinate descent |
| BPP | Bin packing problem |
| BS | Base stations |
| BSM | Basic safety messages |
| CPM | Cooperative perception messages |
| CPU | Central processing unit |
| CSI | Channel state information |
| CSRs | Candidate single-subframe resources |
| C-V2X | Cellular vehicle-to-everything |
| DAVN | Drone-assisted vehicular network |
| DTMC | Discrete-time Markov chain |
| ES | Edge server |
| FedAvg | Federated averaging |
| FedSGD | Federated stochastic gradient descent |
| FL | Federated learning |
| FRL | Federated reinforcement learning |
| i.i.d. | Independent and identically distributed |
| IMT | International mobile telecommunications |
| ITS | Intelligent transportation systems |
| KL | Kullback–Leibler |
| LoS | Line-of-sight |
| MBS | Macro base station |
| MDP | Markov decision process |
| MINLP | Mixed-integer nonlinear programming |
| Non-i.i.d. | Non-independent and identically distributed |
| NLoS | Non-line-of-sight |
| PS | Parameter server |
| RL | Reinforcement learning |
| RSU | Roadside unit |
| RVI | Relative value iteration |
| SAE | Society of automotive engineers |
| SDP | Semi-definite programming |
| SGD | Stochastic gradient descent |
| SINR | Signal-to-interference noise ratio |
| SPS | Sensing-based semi persistent scheduling |
| TTI | Transmission time interval |
| UAV | Unmanned aerial vehicle |
| V2V | Vehicle-to-vehicle |
| V2I | Vehicle-to-infrastructure |
| VR | Virtual reality |
References
- Fu, F.; Wang, Y.; Li, S.; Yang, L.T.; Zhao, R.; Dai, Y.; Yang, Z.; Zhang, Z. Incentive Mechanism Against Bounded Rationality for Federated Learning-Enabled Internet of UAVs: A Prospect Theory-Based Approach. IEEE Internet Things J. 2024, 11, 20958–20969. [Google Scholar] [CrossRef]
- Amadeo, M.; Campolo, C.; Molinaro, A.; Harri, J.; Rothenberg, C.E.; Vinel, A. Enhancing the 3GPP V2X Architecture with Information-Centric Networking. Future Internet 2019, 11, 199. [Google Scholar] [CrossRef]
- Schiessl, S.; Al-Zubaidy, H.; Skoglund, M.; Gross, J. Delay Performance of Wireless Communications with Imperfect CSI and Finite-Length Coding. IEEE Trans. Commun. 2018, 66, 6527–6541. [Google Scholar] [CrossRef]
- Wang, H.; Lv, T.; Lin, Z.; Zeng, J. Energy-Delay Minimization of Task Migration Based on Game Theory in MEC-Assisted Vehicular Networks. IEEE Trans. Veh. Technol. 2022, 71, 8175–8188. [Google Scholar] [CrossRef]
- Gemici, O.F.; Hokelek, I.; Crpan, H.A. Modeling Queuing Delay of 5G NR with NOMA Under SINR Outage Constraint. IEEE Trans. Veh. Technol. 2021, 70, 2389–2403. [Google Scholar] [CrossRef]
- Syed Ammad Ali, S.; Xavier, F.; Rasha, K. A Survey on Artificial-Intelligence-Based Internet of Vehicles Utilizing Unmanned Aerial Vehicles. Drones 2024, 8, 353. [Google Scholar]
- Abadal, S.; Han, C.; Petrov, V.; Galluccio, L.; Akyildiz, I.F.; Jornet, J.M. Electromagnetic Nanonetworks Beyond 6G: From Wearable and Implantable Networks to On-Chip and Quantum Communication. IEEE J. Sel. Areas Commun. 2024, 42, 2122–2142. [Google Scholar] [CrossRef]
- Pennanen, H.; Hanninen, T.; Tervo, O.; Tolli, A.; Latva-Aho, M. 6G: The Intelligent Network of Everything. IEEE Access 2025, 13, 1319–1421. [Google Scholar] [CrossRef]
- Paul, A.; Singh, K.; Li, C.P.; Dobre, O.A.; Duong, T.Q. Digital Twin-Aided Vehicular Edge Network: A Large-Scale Model Optimization by Quantum-DRL. IEEE Trans. Veh. Technol. 2025, 74, 2156–2173. [Google Scholar] [CrossRef]
- Shi, W.; Zhou, H.; Li, J.; Xu, W.; Zhang, N.; Shen, X. Drone Assisted Vehicular Networks: Architecture, Challenges and Opportunities. IEEE Netw. 2018, 32, 130–137. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, G.; Zhong, Q.; Zheng, H.; Zhao, S. UAV-Aided Vehicular Communication Design With Vehicle Trajectory’s Prediction. IEEE Wirel. Commun. Lett. 2021, 10, 1212–1216. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Personalized Federated Learning based Joint Latency and Power Optimization for UAV-assisted C-V2X Communications. In Proceedings of the IEEE ICC Workshop on Cooperative Communications and Computations in Space-Air-Ground-Sea Integrated Networks, Montreal, QC, Canada, 8 June 2025; pp. 1507–1512. [Google Scholar]
- Ji, S.; Jiang, W.; Walid, A.; Li, X. Dynamic Sampling and Selective Masking for Communication-Efficient Federated Learning. IEEE Intell. Syst. 2022, 37, 27–34. [Google Scholar] [CrossRef]
- Gupta, V.; Luqman, A.; Chattopadhyay, N.; Chattopadhyay, A.; Niyato, D. TravellingFL: Communication Efficient Peer-to-Peer Federated Learning. IEEE Trans. Veh. Technol. 2024, 73, 5005–5019. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Zhang, Y.; Wan, S. Energy-Latency Tradeoff for Joint Optimization of Vehicle Selection and Resource Allocation in UAV-Assisted Vehicular Edge Computing. IEEE Trans. Green Commun. Netw. 2025, 9, 445–458. [Google Scholar] [CrossRef]
- Shaik, T.; Tao, X.; Li, L.; Xie, H.; Cai, T.; Zhu, X.; Li, Q. FRAMU: Attention-Based Machine Unlearning Using Federated Reinforcement Learning. IEEE Trans. Knowl. Data Eng. 2024, 36, 5153–5167. [Google Scholar] [CrossRef]
- Chen, S.; Jin, T.; Xia, Y.; Li, X. Metadata and Image Features Co-Aware Semi-Supervised Vertical Federated Learning With Attention Mechanism. IEEE Trans. Veh. Technol. 2024, 73, 2520–2532. [Google Scholar] [CrossRef]
- Sempere-García, D.; Sepulcre, M.; Gozalvez, J. LTE-V2X Mode 3 scheduling based on adaptive spatial reuse of radio resources. Ad Netw. 2021, 113, 102351. [Google Scholar] [CrossRef]
- Wijesiri N. B. A., G.P.; Samarasinghe, T.; Haapola, J. Performance Enhancement of C-V2X Mode 4 Utilizing Multiple Candidate Single-Subframe Resources. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15328–15333. [Google Scholar] [CrossRef]
- Zhu, C.; Shi, Y.; Zhao, H.; Chen, K.; Zhang, T.; Bao, C. A Fairness-Enhanced Federated Learning Scheduling Mechanism for UAV-Assisted Emergency Communication. Sensors 2024, 24, 1599. [Google Scholar] [CrossRef]
- Yang, B.; Shi, H.; Xia, X. Federated Imitation Learning for UAV Swarm Coordination in Urban Traffic Monitoring. IEEE Trans. Ind. Inform. 2023, 19, 6037–6046. [Google Scholar] [CrossRef]
- Abhishek, G.; Fernando, X. Latency Analysis of UAV-Assisted Vehicular Communications Using Personalized Federated Learning with Attention Mechanism. Drones 2025, 9, 497. [Google Scholar] [CrossRef]
- Ng, J.S.; Lim, W.Y.B.; Dai, H.N.; Xiong, Z.; Huang, J.; Niyato, D.; Hua, X.S.; Leung, C.; Miao, C. Joint Auction-Coalition Formation Framework for Communication-Efficient Federated Learning in UAV-Enabled Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2326–2344. [Google Scholar] [CrossRef]
- Zhan, Y.; Li, P.; Guo, S.; Qu, Z. Incentive Mechanism Design for Federated Learning: Challenges and Opportunities. IEEE Netw. 2021, 35, 310–317. [Google Scholar] [CrossRef]
- Moreira, I.; Pimentel, C.; Barros, F.P.; Chaves, D.P.B. Modeling Fading Channels With Binary Erasure Finite-State Markov Channels. IEEE Trans. Veh. Technol. 2017, 66, 4429–4434. [Google Scholar] [CrossRef]
- Wijesiri N.B.A., G.P.; Haapola, J.; Samarasinghe, T. A Discrete-Time Markov Chain Based Comparison of the MAC Layer Performance of C-V2X Mode 4 and IEEE 802.11p. IEEE Trans. Commun. 2021, 69, 2505–2517. [Google Scholar] [CrossRef]
- Wang, P.; Li, D.; Zhang, Y.; Chen, X. UAV-Assisted Vehicular Communication System Optimization With Aerial Base Station and Intelligent Reflecting Surface. IEEE Trans. Intell. Veh. 2024, 1–12. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, W.; Ni, Y.; Xia, W.; Gui, G.; Zhu, C. Deep Deterministic Policy Gradient-Based Rate Maximization for RIS-UAV-Assisted Vehicular Communication Networks. IEEE Trans. Intell. Transp. Syst. 2024, 25, 15732–15744. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, L.; Wu, X.; Tang, Y.; Liu, W.; Sun, D. Joint Resource Allocation for UAV-Assisted V2X Communication with Mean Field Multi-Agent Reinforcement Learning. IEEE Trans. Veh. Technol. 2025, 74, 1209–1223. [Google Scholar] [CrossRef]
- Hosseini, M.; Ghazizadeh, R. Stackelberg Game-Based Deployment Design and Radio Resource Allocation in Coordinated UAVs-Assisted Vehicular Communication Networks. IEEE Trans. Veh. Technol. 2023, 72, 1196–1210. [Google Scholar] [CrossRef]
- Hirai, T.; Murase, T. Performance Evaluation of NOMA for Sidelink Cellular-V2X Mode 4 in Driver Assistance System With Crash Warning. IEEE Access 2020, 8, 168321–168332. [Google Scholar] [CrossRef]
- Segawa, Y.; Tang, S.; Ueno, T.; Ogishi, T.; Obana, S. Improving Performance of C-V2X Sidelink by Interference Prediction and Multi Interval Extension. IEEE Access 2022, 10, 42518–42528. [Google Scholar] [CrossRef]
- Zhou, J.; Tian, D.; Sheng, Z.; Duan, X.; Qu, G.; Zhao, D.; Cao, D.; Shen, X. Robust Min-Max Model Predictive Vehicle Platooning with Causal Disturbance Feedback. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15878–15897. [Google Scholar] [CrossRef]
- Ali, Z.; Lagen, S.; Giupponi, L.; Rouil, R. 3GPP NR-V2X Mode 2: Overview, Models and System-Level Evaluation. IEEE Access 2021, 9, 89554–89579. [Google Scholar] [CrossRef]
- Li, X.; Cheng, L.; Sun, C.; Lam, K.Y.; Wang, X.; Li, F. Federated-Learning-Empowered Collaborative Data Sharing for Vehicular Edge Networks. IEEE Netw. 2021, 35, 116–124. [Google Scholar] [CrossRef]
- Kang, B.; Yang, J.; Paek, J.; Bahk, S. ATOMIC: Adaptive Transmission Power and Message Interval Control for C-V2X Mode 4. IEEE Access 2021, 9, 12309–12321. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Fernando, X.; Kashef, R. Joint Trajectory and Pilot Assignment Optimization for UAV Enabled Cell-Free Massive MIMO. In Proceedings of the IEEE ICC Workshop on Cooperative Communications and Computations in Space-Air-Ground-Sea Integrated Networks, Montreal, QC, Canada, 8 June 2025; pp. 1876–1881. [Google Scholar]
- He, J.; Yang, K.; Chen, H.H. 6G Cellular Networks and Connected Autonomous Vehicles. IEEE Netw. 2021, 35, 255–261. [Google Scholar] [CrossRef]
- Ali, R.; Zikria, Y.B.; Garg, S.; Bashir, A.K.; Obaidat, M.S.; Kim, H.S. A Federated Reinforcement Learning Framework for Incumbent Technologies in Beyond 5G Networks. IEEE Netw. 2021, 35, 152–159. [Google Scholar] [CrossRef]
- Huang, X.; Li, P.; Yu, R.; Wu, Y.; Xie, K.; Xie, S. FedParking: A Federated Learning Based Parking Space Estimation With Parked Vehicle Assisted Edge Computing. IEEE Trans. Veh. Technol. 2021, 70, 9355–9368. [Google Scholar] [CrossRef]
- Liao, Y.; Wu, Y.; Zhao, S.; Zhang, D. Unmanned Aerial Vehicle Obstacle Avoidance Based Custom Elliptic Domain. Drones 2024, 8, 397. [Google Scholar] [CrossRef]
- Xia, Y.; Shao, X.; Ding, T.; Liu, J. Prescribed intelligent elliptical pursuing by UAVs: A reinforcement learning policy. Expert Syst. Appl. 2024, 249, 123547. [Google Scholar] [CrossRef]
- Fu, J.; Yao, W.; Sun, G.; Tian, H.; Wu, L. An FTSA Trajectory Elliptical Homotopy for Unmanned Vehicles Path Planning with Multi-Objective Constraints. IEEE Trans. Intell. Veh. 2023, 8, 2415–2425. [Google Scholar] [CrossRef]
- Deng, D.; Wang, C.; Wang, W. Joint Air-to-Ground Scheduling in UAV-Aided Vehicular Communication: A DRL Approach With Partial Observations. IEEE Commun. Lett. 2022, 26, 1628–1632. [Google Scholar] [CrossRef]
- Bedewy, A.M.; Sun, Y.; Kompella, S.; Shroff, N.B. Optimal Sampling and Scheduling for Timely Status Updates in Multi-Source Networks. IEEE Trans. Inf. Theory 2021, 67, 4019–4034. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, X. Traffic Prediction-Enabled Energy-Efficient Dynamic Computing Resource Allocation in CRAN Based on Deep Learning. IEEE Open J. Commun. Soc. 2022, 3, 159–175. [Google Scholar] [CrossRef]
- Li, Y.; Ma, D.; An, Z.; Wang, Z.; Zhong, Y.; Chen, S.; Feng, C. V2X-Sim: Multi-Agent Collaborative Perception Dataset and Benchmark for Autonomous Driving. IEEE Robot. Autom. Lett. 2022, 7, 10914–10921. [Google Scholar] [CrossRef]
- Shinde, S.S.; Tarchi, D. Joint Air-Ground Distributed Federated Learning for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9996–10011. [Google Scholar] [CrossRef]
- Shinde, S.S.; Tarchi, D. A Markov Decision Process Solution for Energy-Saving Network Selection and Computation Offloading in Vehicular Networks. IEEE Trans. Veh. Technol. 2023, 72, 12031–12046. [Google Scholar] [CrossRef]
- Khazali, A.; Bozorgchenani, A.; Tarchi, D.; Shayesteh, M.G.; Kalbkhani, H. Joint Task Assignment, Power Allocation and Node Grouping for Cooperative Computing in NOMA-mmWave Mobile Edge Computing. IEEE Access 2023, 11, 93664–93678. [Google Scholar] [CrossRef]
- Fontanesi, G.; Zhu, A.; Arvaneh, M.; Ahmadi, H. A Transfer Learning Approach for UAV Path Design with Connectivity Outage Constraint. IEEE Internet Things J. 2023, 10, 4998–5012. [Google Scholar] [CrossRef]
- Chen, M.; Poor, H.V.; Saad, W.; Cui, S. Convergence Time Optimization for Federated Learning Over Wireless Networks. IEEE Trans. Wirel. Commun. 2021, 20, 2457–2471. [Google Scholar] [CrossRef]
- Samarakoon, S.; Bennis, M.; Saad, W.; Debbah, M. Distributed Federated Learning for Ultra-Reliable Low-Latency Vehicular Communications. IEEE Trans. Commun. 2020, 68, 1146–1159. [Google Scholar] [CrossRef]






| Reference | Key Problem Addressed | Methodology Used | Existing Gaps | Our Proposed Solution |
|---|---|---|---|---|
| [27,28,29,30] | UAVs are deployed as aerial base stations and wireless network relays for vehicular networks to achieve low-latency and reliable communication. | Use of UAVs to establish LoS links, edge computing, and traffic offloading in 6G-enabled vehicular networks and automotive applications. | High mobility of vehicles and UAVs leads to Doppler spreads, packet collisions, scheduling constraints, latency, and reliability issues. | Integrate UAV trajectory optimization with adaptive scheduling policies for latency reduction and reliable communication with vehicles in FL environment. |
| [9,31,32] | Minimizing packet collisions and transmission delays in UAV–vehicle communication networks. | State machine and queuing models with multiple DTMCs, hidden Markov models, and adaptive window-based transmission control. | The iterative solutions increase processing delay, random arrivals add to latency, optimization of adaptive window size is a constraint. | Propose FL-enabled dynamic packet scheduling combining DTMC with adaptive feedback. |
| [12,19,33] | Queue-length and queue-backlog optimization; sojourn time minimization in C-V2X networks. | Machine learning-based adaptive transmission window-size adjustment, convex optimization techniques such as interior-point, bisection search and golden-section search. | Centralized convex optimization approaches are not scalable to larger networks due to heterogeneous and non-i.i.d packets; limited application of time-bound scheduling approaches. | Design decentralized FL-based queue optimization integrated with UAV-assisted C-V2X communication; the proposed approach is verified for scalability. |
| [34,35] | Delay reduction in FL-enabled vehicular communications. | Decentralized FL with SGD and FedAvg aggregation; self-organizing learning for scalability. | FedAvg leads to bias from repeated updates, data heterogeneity is not considered which leads to sub-optimal global model. | Introduce weighted and fairness-aware aggregation with UAV-assisted scheduling to balance non-i.i.d and heterogeneous data distributions. |
| [27,32,36,37] | Task scheduling and resource allocation in UAV-vehicular communications using FL. | Time–frequency scheduling policies, model synchronization at a centralized server, UAV trajectory and power optimization. | Assumption of perfect channels; minimal retransmissions; UAV scheduling conflicts for vehicles with simultaneous transmissions. | Joint UAV trajectory, power allocation, and distributed scheduling using stochastic optimization approaches. |
| [25,38,39,40] | Correlation and heterogeneity in vehicular sensing data for FL convergence. | Spatio-temporal correlation models, DTMC-based topology-aware scheduling, MAC protocol with time-slotted hopping. | Vehicles with fewer sensors are excluded from participating in FL, unequal weight assignment in aggregation, optimal convergence not guaranteed. | Propose correlation-aware FL aggregation with UAV-assisted clustering to ensure fairness and improve FL model convergence. |
| Symbol | Definition |
|---|---|
| Total delay | |
| Queuing delay | |
| Processing delay | |
| FL model parameters; impact the communication delay and bandwidth usage | |
| Weight parameters: matrices that determine the behavior of the FL model | |
| Transmission window length: time duration allocated for data transmission | |
| Uplink time for vehicles | |
| Downlink time for vehicles to receive the updated global model from UAV | |
| UAV transmission power; impacts communication range and energy consumption | |
| Predefined queuing probability to analyze system behavior under different traffic loads | |
| Hyper-parameters from vehicle v: size and frequency of updates to the UAV | |
| Spatial and temporal data describing UAV trajectory coordinates: position and movement | |
| Status indicator of a TTI | |
| UAV’s server utilization; implies load balancing for QoS management and task scheduling | |
| Packet arrival rate; impacts queue stability and latency in UAV-assisted C-V2X links | |
| Number of edge servers that perform real-time data processing at vehicles to generate local models | |
| Packet departure rate; ensures data flow, low-latency, buffer management, congestion control | |
| Random variables for latency analysis; represent uncertainties and variations in delay | |
| Steady-state probability: long-term probability that an agent is in a particular state | |
| UAV occupancy: state transition parameters | |
| Optimal policy that defines the best set of actions for the vehicles and UAV | |
| RVI value function; implies the expected reward of being in a particular state | |
| Expectation with respect to an action | |
| Steady state probability that m ESs are occupied | |
| Mean sojourn time of each packet in state : average time packets spend in a state | |
| Queuing probability | |
| A randomly generated real number from 0-1 | |
| A function to analyze latency | |
| accumulated after | |
| Probability of UAV’s state transitions | |
| A negligible delay incurred while the UAV remains idle | |
| Markov chain describing stochastic model of initial states of ES | |
| Markov chain describing stochastic model of initial states of UAV | |
| Variance in data slice to train a client; implies data diversity spanning different scenarios | |
| Ratio of samples in adjacent data slices; implies data distribution across vehicles in proximity |
| Parameter | Value |
|---|---|
| Number of in UAV | 1 |
| Vehicle mobility | Manhattan mobility |
| Edge server location | In-vehicle |
| Number of vehicles (V) | 1–100 |
| UAV deployment altitude | 100 m–2 km |
| Distance between vehicles | 10–100 m |
| UAV transmission power | 20 dBm (100 mW) |
| Communication frequency | 5.9 GHz |
| Payload size for BSM, CPM | 1 byte–3 Megabytes |
| Vehicle transmission power | 25 dBm (316.2 mW) |
| Road length | 1–5 km |
| Vehicle speed | 0–100 km/h |
| Standard deviation in speed | 10 km/h |
| Dataset used | V2X-Sim |
| Payload size of FL models | 1 byte–10 Megabytes |
| 100, 200, 300, 500 ms | |
| UAV receiving threshold | −80 dBm |
| 100–1000 ms | |
| Buffer size () at UAV | 1 GB |
| 1000, 2000 packets/s | |
| Mean speed of vehicles | 50 km/h |
| Reference | Proposed Method | Objectives | Cost Function | Reported Results |
|---|---|---|---|---|
| [12,22] |
|
|
|
|
| [22,48] |
|
|
|
|
| [51] |
|
|
|
|
| [50] |
|
|
|
|
| [49] |
|
|
|
|
| Our Work |
|
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, A.; Fernando, X. Performance Analysis of Unmanned Aerial Vehicle-Assisted and Federated Learning-Based 6G Cellular Vehicle-to-Everything Communication Networks. Drones 2025, 9, 771. https://doi.org/10.3390/drones9110771
Gupta A, Fernando X. Performance Analysis of Unmanned Aerial Vehicle-Assisted and Federated Learning-Based 6G Cellular Vehicle-to-Everything Communication Networks. Drones. 2025; 9(11):771. https://doi.org/10.3390/drones9110771
Chicago/Turabian StyleGupta, Abhishek, and Xavier Fernando. 2025. "Performance Analysis of Unmanned Aerial Vehicle-Assisted and Federated Learning-Based 6G Cellular Vehicle-to-Everything Communication Networks" Drones 9, no. 11: 771. https://doi.org/10.3390/drones9110771
APA StyleGupta, A., & Fernando, X. (2025). Performance Analysis of Unmanned Aerial Vehicle-Assisted and Federated Learning-Based 6G Cellular Vehicle-to-Everything Communication Networks. Drones, 9(11), 771. https://doi.org/10.3390/drones9110771







