1. Introduction
The rapid development of unmanned aerial vehicle (UAV) technology has garnered widespread global attention. As a technology with immense potential, UAVs have demonstrated significant application prospects in military, civilian, and commercial domains [
1,
2,
3,
4]. With advancements in technology and reductions in cost, UAVs are gradually transitioning from single-platform applications to swarm-based applications [
5]. A UAV swarm system refers to a system where multiple UAVs work collaboratively, sharing information and distributing tasks to accomplish complex missions [
6]. This system offers numerous advantages, such as high task-execution efficiency, strong reliability, and high flexibility. However, a key challenge facing UAV swarm systems is the rational allocation of tasks to achieve optimal system performance. The task-allocation problem for UAV swarms involves multiple factors, including task priority, UAV capabilities, and constraints, making it complex and diverse. It is a typical NP-hard problem, and the main difficulties in addressing it are problem modeling and model solving [
7].
In terms of problem modeling, the research on multi-task multi-constraint task-allocation problems is relatively limited, and there has been insufficient attention paid to multi-objective optimization algorithms. One of the significant advantages of UAV swarms over individual UAVs is their ability to perform diverse and complex tasks. Therefore, multi-task types are a key focus in the study of UAV swarm task allocation, and the task sequence constraints brought by multi-task types must also be taken into account. Some studies on this subject did not consider multiple task types and temporal constraints of tasks, lacking rigor [
8,
9]. Due to the complexity and diversity of UAV swarm task allocation, evaluation criteria for task-allocation schemes should not be overly singular. Thus, traditional single-objective optimization strategies are not applicable, and a multi-objective optimization strategy is more appropriate. Other studies converted multi-objective optimization problems into single-objective optimization problems by weighting, which leads to the solution schemes being subjectively influenced by the weights. Therefore, it is not conducive to comprehensive decision-making [
10,
11].
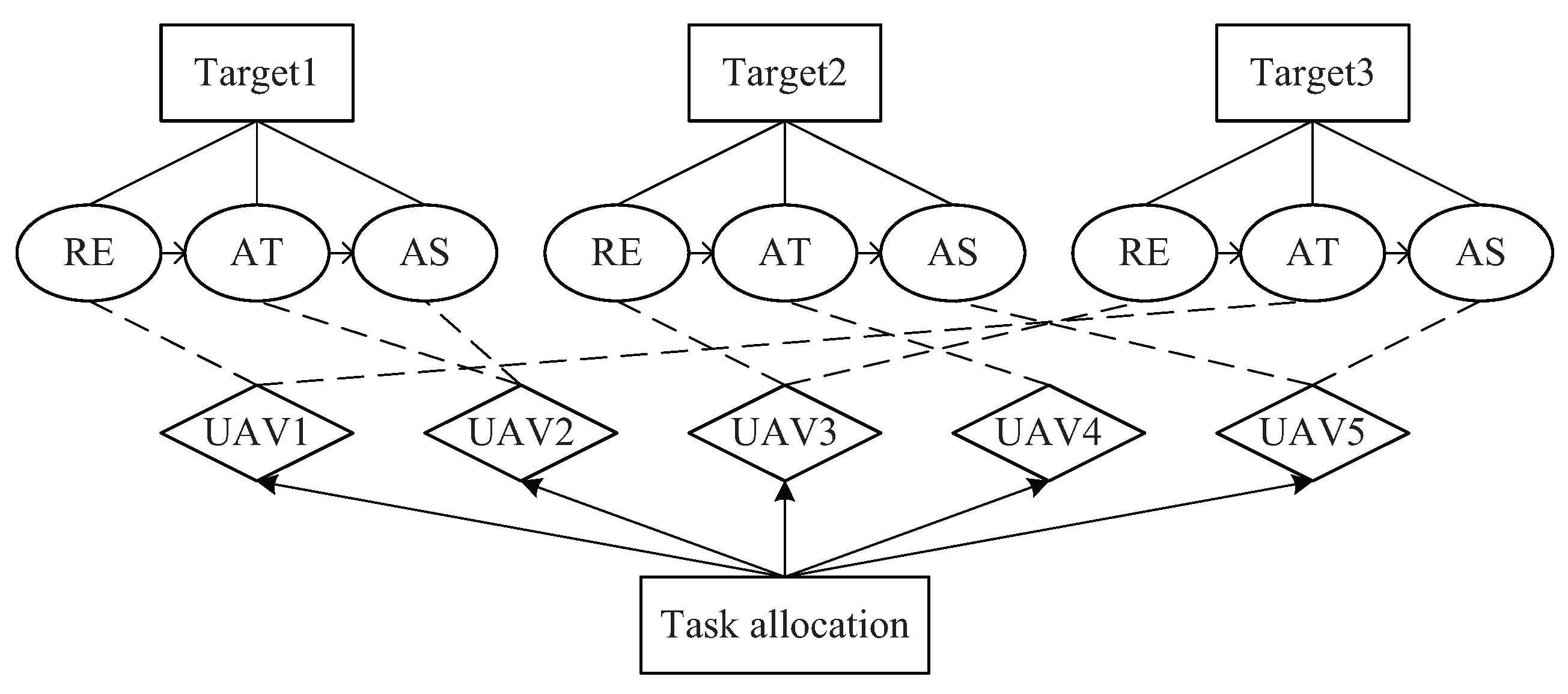
In response to the aforementioned issues, this paper describes the collaborative multi-task-allocation model as a multiple traveling salesman problem. The model considers multiple task types, temporal constraints, and multi-objective optimization. First, UAVs can perform reconnaissance, supplies delivery, and assessment tasks, and a UAV swarm is required to execute all three types of tasks for all targets. Second, the three tasks on each target must be strictly carried out in the order from reconnaissance, supplies delivery, to assessment, and some tasks have specific requirements for the time period of execution. Finally, three optimization objectives need to be considered: task reward, task execution cost, and task execution time.
Generally, solution approaches can be categorized into two main types: exact methods and approximate methods. Exact methods yield optimal solutions at the expense of higher computational time, whereas approximate methods obtain satisfactory solutions within limited time.
Exact methods, such as dynamic programming [
12] and branch-and-bound algorithms [
13], can provide accurate references for the analysis of task-allocation problems. Dynamic programming is a global optimization method for solving multi-step optimization problems. Task allocation, which involves optimizing the execution sequence of multiple tasks by UAVs, is well-suited for dynamic programming. To address the multi-area reconnaissance coverage problem, Xie et al. [
14] employed dynamic programming to recursively determine the optimal visiting sequence and entry–exit positions for multiple regions. In scenarios involving cooperative multi-UAV operations in adversarial environments, Alighanbari et al. [
15] applied a two-step look-ahead strategy to derive action plans for UAVs, achieving optimal solutions with reduced computation time. Branching methods, a class of tree search strategies, primarily include branch and bound, branch and price, and branch and cut. The branch-and-bound method prunes suboptimal branches during the solution of mixed-integer linear programming models, thereby avoiding extensive unnecessary searches. Casbeer et al. [
16] utilized a branch and price approach to solve temporally coupled problems. By leveraging the sparsity of constraint distributions, they decomposed the problem into smaller subproblems via column generation, progressively converging to the optimal solution while significantly reducing computational effort. Subramanyam et al. [
17] formulated a robust linear programming model for heterogeneous vehicle routing under worst-case scenarios and employed a branch and cut algorithm to dynamically introduce constraints, thereby approaching the optimal solution and obtaining a tight lower bound for the problem.
In contrast, approximate methods do not aim to obtain the optimal solution. Instead, they utilize heuristic information to guide the search process in order to achieve satisfactory solutions within polynomial time. In the field of task allocation for UAV swarms, evolutionary algorithms have emerged as popular and efficient approximate methods. Commonly used algorithms include particle swarm optimization (PSO) [
18], genetic algorithms (GA) [
19], and ant colony optimization (ACO) [
20]. Researchers have tailored these algorithms for specific problem environments through various improvements, such as strategy optimization [
21], algorithm hybridization [
22], and enhanced encoding schemes [
23]. These modifications have effectively advanced the development of UAV swarm task allocation. Based on the context of multi-UAV cooperative reconnaissance, Wang et al. [
21] further enhanced the population diversity and convergence capability of the algorithm by introducing a constraint-based particle initialization strategy, an experience-pool-based particle position reconstruction strategy, and a time-varying parameter adjustment strategy into the PSO. Liu et al. [
7] employed a greedy selection operator and introduced elite opposition-based learning, constructing opposition solutions from feasible solutions of the current problem to increase population diversity, thereby improving the convergence speed of the GA. He et al. [
24] first performed a preliminary search on the data using a simplified artificial fish swarm algorithm to generate an initial pheromone distribution, which was then transferred to an improved ACO for solution. This approach reduced the initial search blindness of the ACO and accelerated the algorithm’s convergence.
Ant lion optimizer (ALO) [
25] is a swarm intelligence algorithm proposed by Seyedali Mirjalili in 2015. It simulates the foraging behavior of antlions trapping ants. The main steps include random walking of ants, setting traps by antlions, ants falling into traps, antlions preying on ants, and antlions rebuilding traps. It has been widely applied in various fields, including computer science, engineering, energy, and operations management due to its ease of implementation, strong scalability, and high flexibility [
26].
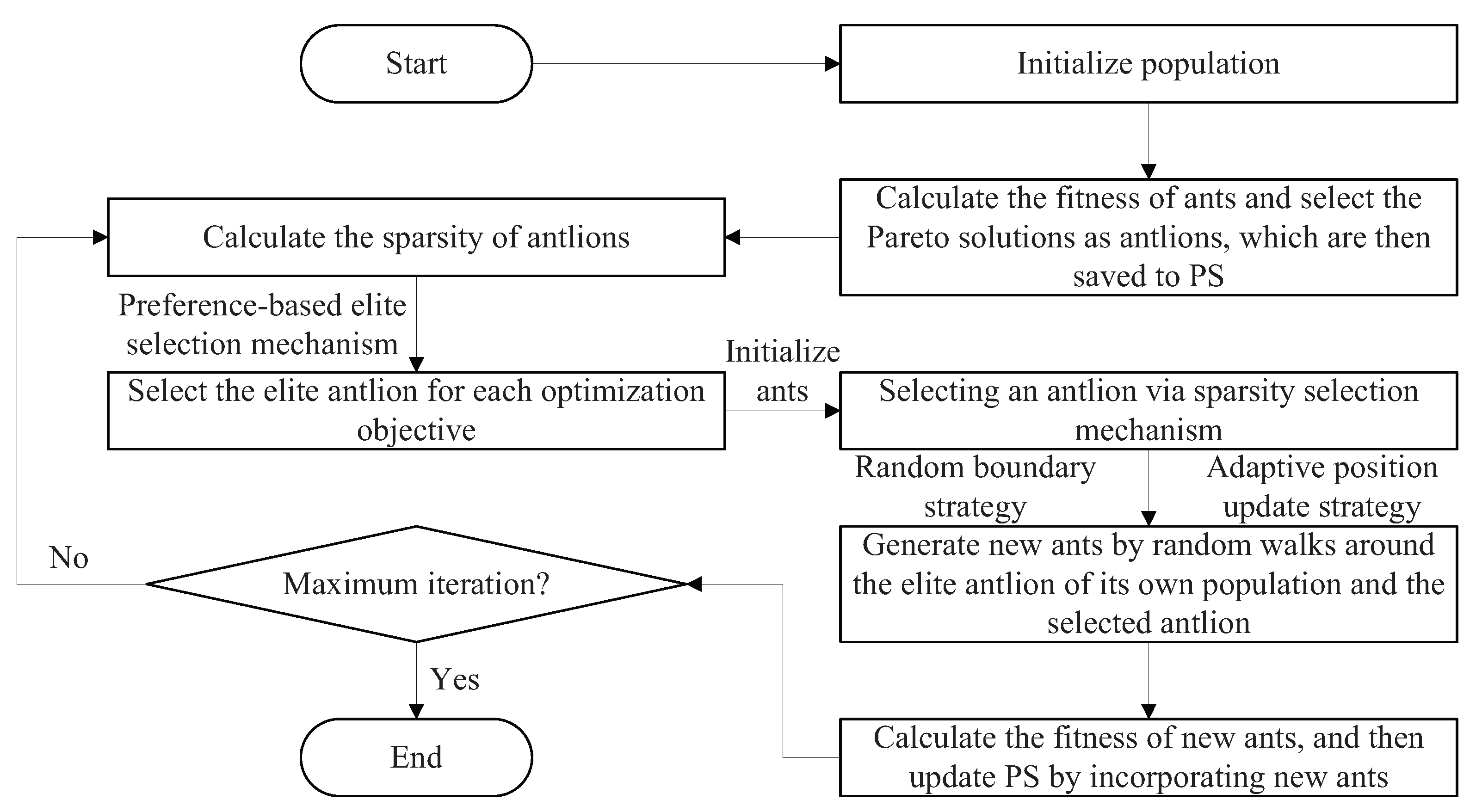
This paper proposes a multi-objective multi-population self-adaptive ant lion optimizer (MMSALO) to efficiently solve the model. To enhance global exploration, MMSALO replaces the roulette-wheel operator with a sparsity selection mechanism. A random boundary strategy redefines the margins of the random walk that each ant performs around an antlion, thereby increasing the population diversity. An adaptive position update schedule then biases early iterations toward sparsity-selected antlions to favor exploration, whereas later iterations pivot around the elite antlion to intensify exploitation. Finally, a preference-based elite selection scheme drives each ant to track the best individual discovered thus far along distinct objective dimensions, which strengthens the algorithm’s convergence behavior and improves the spread of the resulting Pareto front. This study implemented a comprehensive experiment comparing MMSALO with four representative algorithms on the DTLZ test function suite, multi-objective 0-1 knapsack problem (MOKP), and two task-allocation models. To address the complex, multiple constraints inherent in the task-allocation models, a dual-layer encoding scheme, and an adaptive penalty strategy are proposed. The results demonstrate the effectiveness and superiority of the proposed approach.
The remainder of this paper is organized as follows.
Section 2 formulates the task-allocation model for UAV swarms.
Section 3 presents the MMSALO algorithm in detail.
Section 4 describes the simulations and results. Finally, the conclusions of this study are presented in
Section 5.
4. Simulations and Results
Two experiments were designed to verify the effectiveness of the proposed MMSALO in solving the multi-task and multi-constraint task-allocation problem for UAV swarm. In experiment 1, the DTLZ test function suite and MOKP were employed to evaluate the distribution and convergence performance of MMSALO on both continuous and discrete problems, thereby validating its capability for solving multi-objective optimization problems. Experiment 2 employed a battlefield model to create a simulation environment and solved the multi-task and multi-constraint task-allocation model to verify the algorithm’s effectiveness. In the comparison, four algorithms were employed: MOALO, improved multi-objective particle swarm optimization (IMOPSO) [
29], improved non-dominated sorting genetic algorithm-II (INSGA-II) [
30], and improved non-dominated sorting genetic algorithm-III (INSGA-III) [
31]. These algorithms are specifically devised for the task-allocation problem of UAV swarms. IMOPSO balances diversity and convergence by adaptive angular region partitioning and a dedicated reuse rule for infeasible solutions, which effectively mitigates premature convergence. INSGA-II reshapes the non-dominated sorting criterion through a “constraint-tolerance” mechanism, significantly improving both convergence and feasibility under intricate constraints. INSGA-III introduces an enhanced reference-point association strategy to promote uniform solution distribution and employs a dynamic elite-selection scheme to balance exploration and exploitation, enabling rapid and evenly distributed convergence to optimal solutions in high-dimensional objective spaces with complex constraints. The detailed parameters of these algorithms are listed in
Table 3. Among these parameters,
and
denote the weighting coefficients for the ant’s random walk around the elite antlion and the roulette-wheel-selected antlion, respectively;
w denotes the weight vector;
and
represent the crossover probability and mutation probability, respectively. Both experiments were conducted on a computer equipped with an Intel i7-12650H CPU (2.30 GHz) and 16.0 GB of memory.
The performance of all algorithms was evaluated using hyper volume (HV) [
32]. The formulas for calculating HV is shown below:
where
P represents the set of non-dominated solutions within the target vector set calculated by the algorithm, while volume refers to the hypervolume calculated from the vector to the reference point.
4.1. Simulation on the Test Functions
In the experiment, the test functions were employed to evaluate the performance of MMSALO in solving multi-objective optimization problems. Given that the problem model in this study was a three-objective model, the number of objective functions, M, was set to 3.
The algorithms were assessed on DTLZ1 and DTLZ3, while
was set to 2 and 8. Because the dimensionality of the decision variables is
, the resulting problem dimensions are 4 and 10. The analytical expressions of the three-objective DTLZ1 and DTLZ3 are listed in
Table 4.
Given a set of
n items and a set of
m knapsacks, MOKP can be stated as Equation (
23):
where
is the profit of item
j in knapsack
i,
is the weight of item
j in knapsack
i, and
is the capacity of knapsack
i.
means that item
j is selected and put in all the knapsacks. Since this study addressed a three-objective optimization problem, the parameter
m was set to 3 to evaluate the performance of all algorithms when
n was set to 200 and 800, respectively.
Each algorithm-MMSALO, MOALO, IMOPSO, INSGA-II, and INSGA-III-was independently executed 20 times with a population size of 100 and a PS size of 100. For DTLZ1 and DTLZ3, the maximum number of iterations was set to 1000, and the reference point was defined as (5, 5, 5). For MOKP, the maximum number of iterations was set to 100, with a reference point at (1, 1, 1).
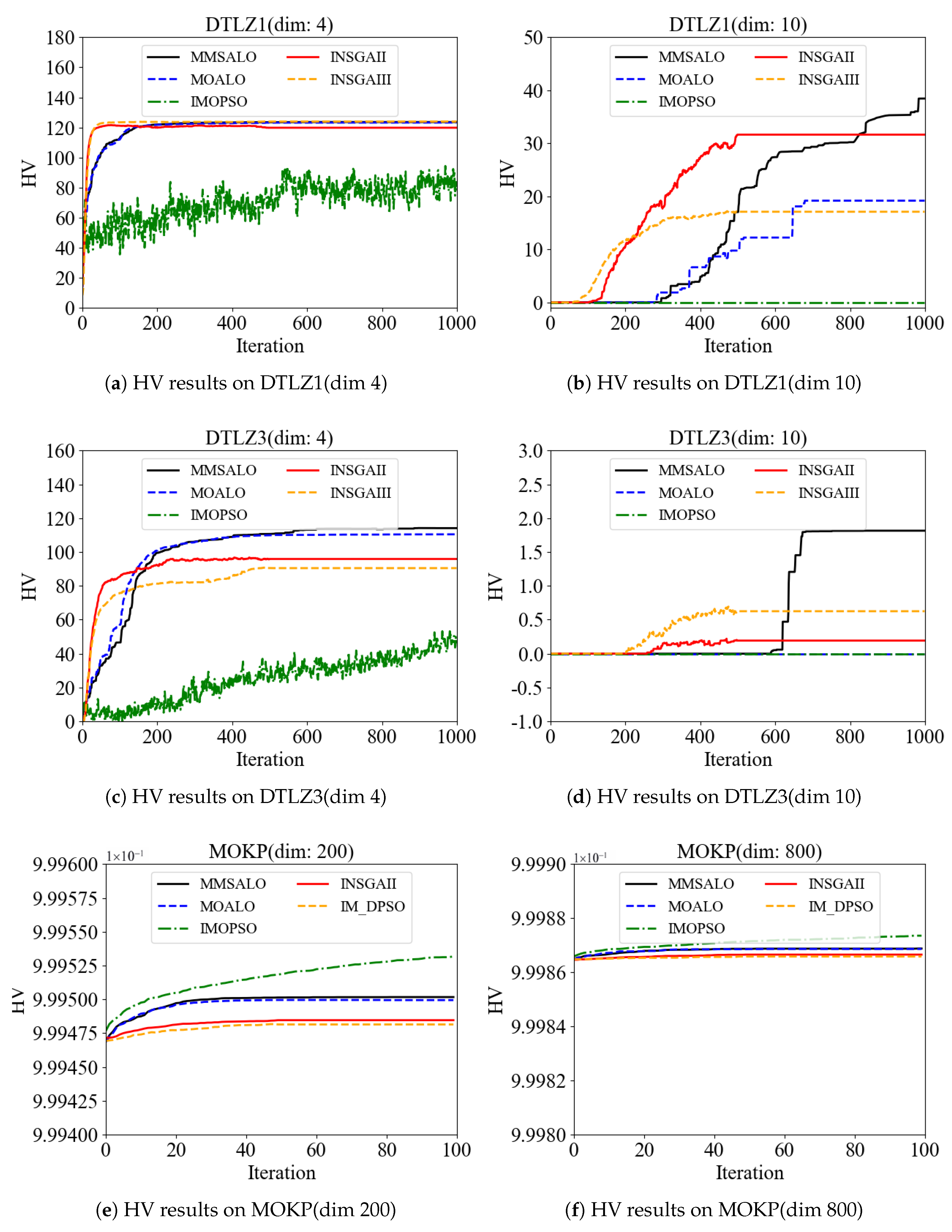
The comparison of HV results obtained by five algorithms on DTLZ1, DTLZ3, and MOKP is presented in
Table 5 and
Figure 4. In the comparison of the mean values of the HV results, it can be observed that among the six test functions, MMSALO outperforms the other four algorithms on DTLZ1 (
n = 10) and DTLZ3 and achieves the second-best performance on DTLZ1 (
n = 4) and MOKP. This demonstrates the overall superiority of MMSALO on these test functions. Compared to MOALO, MMSALO yields better results across all test functions, indicating that the proposed improvements enhance the algorithm’s exploitation capability and global search ability, thereby ensuring solution diversity. Furthermore, in the comparison of the standard deviations of the HV results, it can be seen that the standard deviations of MMSALO and MOALO are comparable, with each performing better on certain test functions. This confirms that the proposed modifications do not compromise the stability of the algorithm.
Table 6 reports the
p-values obtained from the Wilcoxon rank-sum test on HV. At
= 0.05, most
p-values for the two MMSALO-optimal and two MMSALO-second-best metrics were significantly lower than
, demonstrating the statistically significant superiority of MMSALO over the comparison algorithms.
Table 7 presents the average time required for all algorithms to run the test functions once. It can be observed that the computation times of MMSALO and MOALO are within the same order of magnitude. Compared to MOALO, MMSALO requires a longer computation time because its PS reaches the capacity limit more rapidly, owing to the sparsity selection mechanism, thus necessitating additional PS update operations. However, on the MOKP (
n = 200) instance, MMSALO exhibits a shorter runtime than does MOALO. This occurs because the test problem is relatively simple, leading both algorithms to approach the capacity limit almost simultaneously. Since MMSALO employs a direct sparsity selection mechanism while MOALO utilizes a sparsity-based roulette wheel selection, MMSALO achieves faster updates once the PS capacity is reached, resulting in a shorter overall computation time for MMSALO in this scenario.
Table 8 presents the HV and runtime results of the ablation studies conducted for MMSALO on the DTLZ test suite. In the table, “SS” denotes the sparsity selection mechanism component, “RB” represents the random boundary strategy component, “APU” indicates the adaptive position update strategy component, and “PBES” refers to the preference-based elite selection mechanism component. A comparative analysis between MMSALO and MOALO on MOKP is omitted here due to the negligible differences observed in their HV results. As can be observed, the performance contributions of the different components are relatively balanced, with each component demonstrating distinct advantages across different problems. Collectively, these components contribute to the enhanced overall performance of MMSALO.
4.2. Simulation on the Task Allocation Model
To address the intricate and multiple constraints introduced by the task-allocation model, we introduce a double-layer encoding scheme and an adaptive penalty strategy.
4.2.1. Double-Layer Encoding
The present study employs a real-number encoding method, representing individual positions as real-valued vectors. These vectors are then mapped to the discrete solution space of task allocation through a specific approach. This method allows individuals to search in the continuous domain space and converts the continuous encoding into practical task-allocation schemes through a particular decoding process.
The task-allocation scheme is represented by a task-allocation vector, which comprises two rows. The length of each row corresponds to the number of targets multiplied by the number of task types. Each element in the first row corresponds to a task assigned to a target and is encoded as a real number. The integer part of this value indicates the UAV assigned to execute the task, while the fractional part denotes the task’s priority, with a smaller value representing higher priority. The elements in the second row are also real numbers and are used to determine whether the corresponding task is reconnaissance, supplies delivery, or assessment. For tasks associated with the same target, they are classified as reconnaissance, supplies delivery, and assessment in ascending order of the values in the second row.
Figure 5 illustrates the mapping between the algorithm encoding and the task-allocation result in a scenario where two UAVs are assigned to two targets. Specifically, given the task-allocation result [[1.2837, 2.8449, 2.5364, 1.0482, 2.4619, 1.2984], [1.3283, 2.2581, 1.9564, 1.1012]], the following interpretation applies: tasks 1, 4, and 6 on target 2 are assigned to UAV 1, with task priorities of 0.2837, 0.0482, and 0.2984, respectively. The execution sequence is task 4, followed by task 1 and then task 6. Similarly, tasks assigned to UAV 2 can be derived accordingly. For target 1, the second-row values for tasks 1, 2, and 3 are 1.3283, 2.2581, and 1.9564, respectively. Sorting these values in ascending order yields the following task sequence: task 1 (reconnaissance), task 3 (supplies delivery), and task 2 (assessment). The same logic applies to target 2.
4.2.2. Adaptive Penalty Function
The introduction of appropriate constraint-handling methods can effectively enhance the search efficiency of algorithms for feasible solutions. These methods achieve a balance between convergence, diversity, and feasibility by weighting constraint violations and coordinating the exploration of feasible and infeasible regions. Common constraint-handling methods include penalty function methods, constraint dominance methods, and learning-based methods [
33]. Each of these methods has its own focus and can leverage its strengths in different aspects. Penalty function methods handle constraints by adding penalty terms for constraint violations to the objective function, ensuring that the solution set meets the constraints. Constraint dominance methods prioritize feasible solutions by comparing the feasibility of solutions with their dominance relationships. Learning-based methods utilize machine learning techniques to predict and improve the search process of the algorithm. In this study, an adaptive penalty function method was adopted, which dynamically adjusts the penalty value based on the degree of constraint conflicts during the search process. This approach avoids the need for parameter tuning and enhances the convergence speed of the algorithm.
The adaptive penalty function method converts the original constrained optimization problem into an unconstrained one by incorporating a penalty term into the objective function. This penalty term adjusts the optimization target value of the model based on the degree of constraint violation of the solution. In this study, an adaptive penalty function was designed to calculate the total number of constraint violations for a given solution. The total number of violations was then multiplied by a fixed value to serve as the penalty term. The modified objective function incorporating the penalty term is as follows:
where
F denotes the objective function,
represents the solution found by the algorithm during the optimization process,
indicates the feasible region,
r is the total number of constraint violations, and
N is an adaptive value set here to the number of tasks. This allows the algorithm to increase the penalty for infeasible solutions in more complex problems, thereby driving the algorithm to find feasible solutions more rapidly.
Algorithm 6 shows the pseudocode of adaptive penalty function for calculating the total number of violations, which considers the UAV range constraint, UAV supplies-delivery capability constraint, task temporal sequence constraint, and task time window constraint.
| Algorithm 6 Adaptive penalty function |
- Input:
Task allocation solution - Output:
The total number of constraint violations r
; for i in do Obtain the task list of UAV i through ; Calculate the flight distance d of UAV i using ; if then ; end if Obtain the number of supplies-delivery tasks l executed by UAV i through ; if then ; end if end for for j in do Obtain the task list on target j through ; if then ; end if if then ; end if for task k in do if then ; end if if then ; end if end for end for
|
4.2.3. Task-Allocation Model Configuration and Experimental Results
In the simulation, two scenarios were established. The first scenario simulated the process of six UAVs performing tasks at 18 targets, while the second scenario simulated the process of eight UAVs performing tasks at 24 targets. The positions of the targets and UAVs were simplified as points. The total coverage area of the operational zone was 90,000 km2, represented by the x-axis coordinates (0, 300) and y-axis coordinates (0, 300). To reflect realistic conditions, UAVs with lower flight speeds were assigned a greater maximum range. The task capability parameter of a UAV was positively correlated with its value, and the probability of task failure was positively correlated with its value. The reconnaissance task was required to be completed within the first 4000 s to ensure the UAV swarm’s grasp of global information. The supplies-delivery task was required to be completed within the first 8000 s to avoid the issue of reconnaissance information becoming obsolete due to excessive task intervals. Additionally, a minimum time interval of 300 s was required to be maintained between the assessment and supplies-delivery tasks to ensure that personnel at the target location have received the supplies. Reconnaissance and assessment tasks did not consume any onboard resources, whereas every supplies-delivery task consumed exactly one unit. The speed, task capability parameter, and UAV value varied among individuals. Limited by their range and onboard resources, the UAVs were restricted in the number of tasks they can perform.
Table 9 and
Table 10 list the detailed information of the UAVs, targets, and the tasks on these targets under Scenario 1.
Table 11 and
Table 12 list the detailed information of the UAVs, targets, and the tasks on these targets under Scenario 2.
The population size was 100, the maximum number of iterations was 100, and the PS archive capacity was 100. MMSALO, MOALO, IMOPSO, INSGA-II, and INSGA-III were executed independently 20 times. The reference point was set to (108, 108, 108) for Scenario 1 and (192, 192, 192) for Scenario 2. The resulting HV values for the five algorithms are compared in
Table 13. To facilitate HV computation, the objective values of task execution time were linearly scaled to [0, 108] in Scenario 1 and to [0, 192] in Scenario 2.
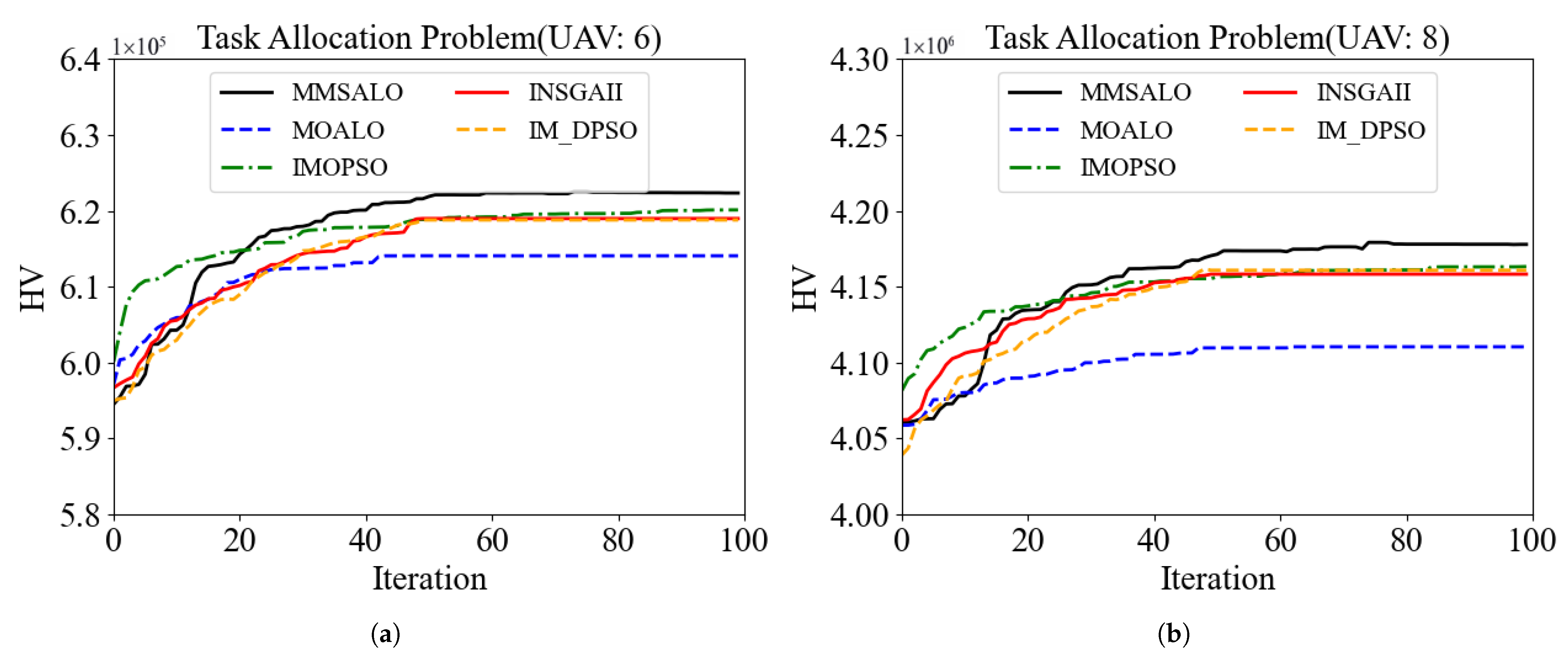
Table 13 and
Figure 6 show that MMSALO achieves the highest average HV across all scenarios, demonstrating its superior capability in tackling the multi-task, multi-constraint assignment problem for UAV swarms. Moreover, MMSALO exhibits a significantly smaller HV standard deviation than does ƒMOALO, indicating enhanced stability. Because operational environments preclude repeated algorithmic runs to cherry-pick favorable solutions, this increased robustness renders MMSALO more valuable in practice.
Table 14 presents the
p-values of the Wilcoxon rank-sum test. It can be observed that when
is set to 0.05, all
p-values are significantly lower than
. This indicates that the performance of MMSALO is statistically significantly better than that of the comparison algorithms.
Table 15 presents the average computation time required for each algorithm to solve the task-allocation problem in a single run. As can be observed, the computation times of MMSALO and MOALO remain within the same order of magnitude. Due to the significantly higher complexity of the task-allocation problem compared to the test functions, the computation times of IMOPSO, INSGA-II, and INSGA-III increase by one order of magnitude. In contrast, the computation times of MMSALO and MOALO show no significant change. This demonstrates the favorable scalability of MMSALO and its efficient performance in addressing complex problems.
Table 16 presents the HV and runtime results obtained from the ablation experiments conducted by MMSALO on the task-allocation problem. It can be observed that “SS” and “APU” contribute significantly when addressing complex problems.
Collectively, MMSALO attains the highest HV value and outperforms the competing algorithms by a statistically significant margin. These results demonstrate that the sparsity selection mechanism, random boundary strategy, adaptive position update rule, and preference-based elite selection mechanism collectively enhance algorithmic performance, enabling MMSALO to provide an effective reference for analyzing multi-task, multi-constraint task-allocation problems in UAV swarms.
5. Conclusions
The UAV swarm collaborative task-allocation problem considered in this study is a multi-objective, multi-constrained optimization problem. The main conclusions drawn are as follows:
A multi-task, multi-constraint task-allocation model for UAV swarms was established. To meet the demands of practical applications, more detailed constraints need to be considered. Three optimization objectives were introduced to effectively evaluate various allocation schemes. A double-layer encoding mechanism and an adaptive penalty function method were designed to handle the key constraints. Compared with traditional penalty methods, this approach can dynamically adjust the penalty values based on the degree of constraint violations during the search process, thereby avoiding the need for parameter tuning and accelerating the convergence speed of the algorithm.
The MMSALO algorithm is proposed to effectively solve the model. MMSALO integrates a sparsity selection mechanism that significantly improves global exploration. A random boundary strategy increases the stochasticity and diversity of the ant walks around antlions, thereby enhancing population diversity. An adaptive position update strategy balances exploration in the early phase and exploitation in the latter phase. A preference-based elitist selection mechanism further strengthens the search capability and ensures better solution distribution. Simulation results demonstrate the feasibility of the allocation model and confirm that the resulting schedules accurately capture the characteristics of both UAVs and tasks. Comparative experiments against state-of-the-art algorithms verify the superior performance of the proposed MMSALO.
This study was limited to the task allocation for stationary targets using a centralized strategy and did not account for potential collisions among UAVs. In future work, we plan to design larger-scale scenarios and account for uncertainties in real-world environments. A distributed task0allocation approach will be adopted and dynamic task-reallocation strategies developed. Corresponding models and algorithms will also be investigated.