1. Introduction
The hypersonic gliding vehicle (HGV) is now a key focus in global military research due to its deep penetration, precision strikes, and high maneuverability. As hypersonic technology competition grows, real-time HGV trajectory prediction is essential for aerospace defense and combat intent analysis [
1,
2].
Within the domain of trajectory prediction, present methodologies are primarily categorized based on the nature of the targets being predicted. The first category pertains to low-altitude, low-speed targets, including conventional aviation aircraft and unmanned aerial vehicles (UAVs) [
3,
4]. These entities exhibit moderate velocities, predictable flight paths, and are supported by an abundance of data conducive to analytical studies. The extant scholarly research has predominantly utilized techniques such as deep learning algorithms [
4,
5], machine learning models [
6], and database matching [
7] to discern and exploit the regularities within their flight paths. Conversely, the second category addresses high-altitude, high-velocity targets, which are exemplified by ballistic missiles. Despite their rapid pace, these targets adhere to more consistent motion dynamics [
8,
9]. Leveraging this predictability, researchers have applied a suite of analytical tools, including analytical solutions [
9,
10], numerical integration techniques [
11,
12], and regression analysis methods [
13], to precisely determine their trajectories.
However, HGV targets operate at significantly higher speeds than conventional aircraft, lacking predefined flight routes and mission-specific characteristics, along with limited historical trajectory data. Consequently, the majority of the existing algorithms for predicting trajectories are predicted on the offensive standpoint [
14,
15,
16], with a dearth of studies addressing the defensive perspective. The extant methodologies for trajectory prediction can be broadly classified into three distinct categories: based on standard control models, based on inference from combat intentions and grounded in parameter identification techniques.
The first method hinges on the assumption that HGVs execute maneuvers within the confines of established control models, thereby delineating their motion trajectories. Li et al. [
17] have delved into predicting HGV trajectories under such typical control laws, achieving commendable prediction accuracy. Nonetheless, this approach is decided on specific modes, limiting the generalization capabilities of the prediction model. A method that depends on intention inference is centered on discerning the adversary’s strategic objectives, aiming to forecast the trajectory by simulating the target’s strike path. Li et al. [
18] introduced a multimodel and multi-intention fusion approach based on Bayesian inference. This dual-layer fusion strategy amalgamates diverse maneuvering patterns and intentions, enhancing the precision and resilience of the trajectory forecasts. Although this method offers significant strategic insights, integrating attack intentions with dynamic battlefield conditions and quantifying the importance of various qualitative elements remain as challenges.
The last method based on parameter identification emphasizes the identification and representation of control parameter information for the HGV. According to learning the variation law of the lift-to-drag ratio, Wang et al. [
19] have employed curve fitting techniques to facilitate trajectory forecasting. While their approach adeptly integrates the lift-to-drag ratio with the target’s state for predictive purposes, its utility is confined to the longitudinal plane and does not extend to three-dimensional trajectories. Zhai et al. [
20] pioneered the definition of a novel suite of aerodynamic parameters, fitting them via the least squares method, thereby achieving 3D trajectory prediction. However, this methodology has limitations in conditions of nonlinear aerodynamic scenarios, such as abrupt alterations in the aircraft’s aerodynamic properties. Further advancing the field, Zhang et al. [
21] introduced an ensemble empirical mode and attention long short-term memory (LSTM) network, harnessing the ability of neural networks to model nonlinear aerodynamic accelerations. This innovative approach, while effective, necessitates extensive datasets for training to ensure robust performance.
It is evident that current research methodologies have several limitations:
Traditional linear fitting methods, such as the least squares method, often struggle to accurately represent parameters with nonlinear characteristics. Meanwhile, deep learning techniques, though predictive, often necessitate a vast amount of trajectory data, which is not feasible in practical scenarios;
Most methods are built upon the premise that control quantities or parameters adhere to specific patterns, thereby limiting their versatility and adaptability across diverse contexts.
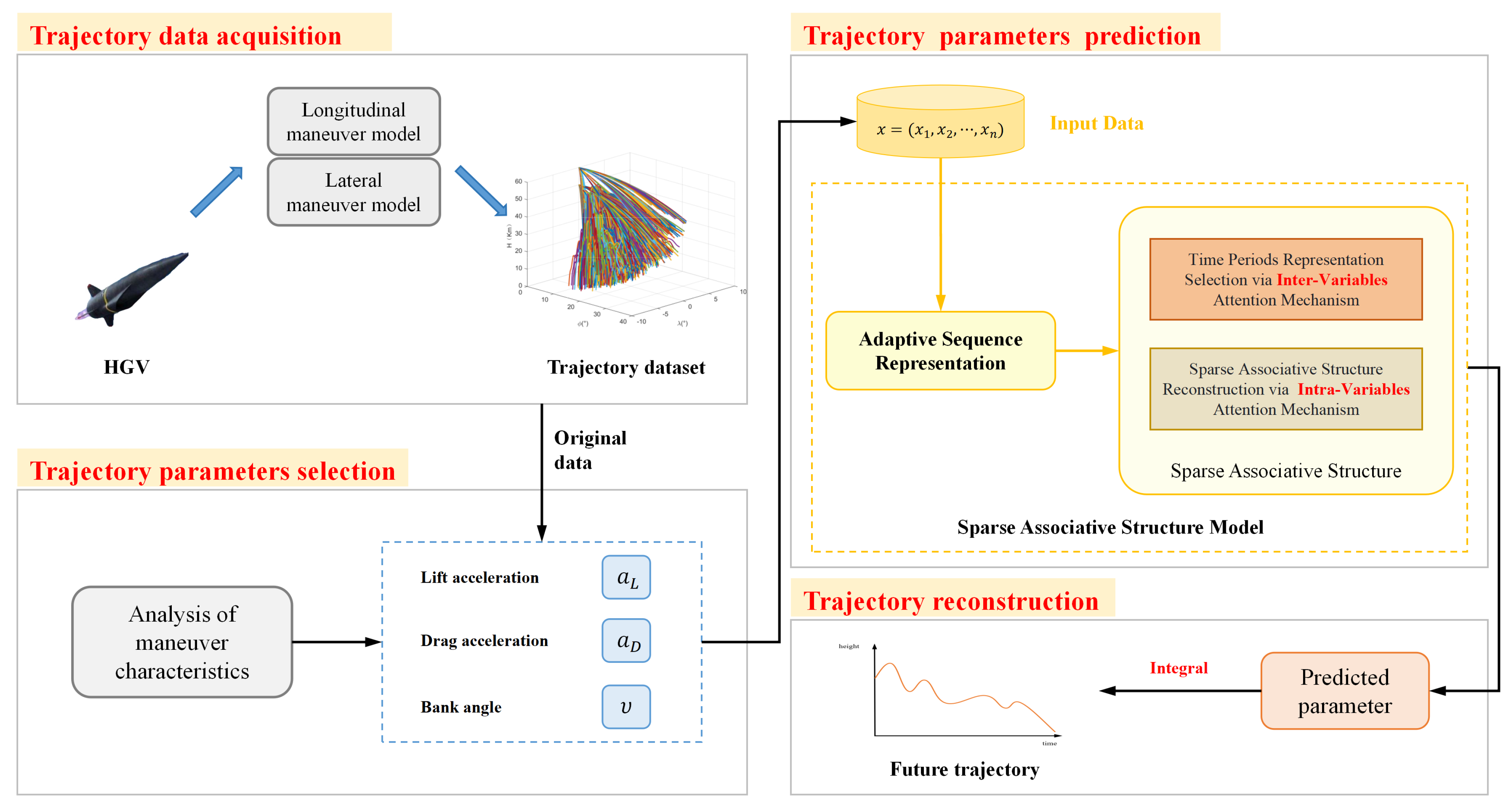
Given the inherent nature of HGV trajectory prediction as a time-series task, this study frames it as a transfer learning problem from historical to future trajectories. We propose addressing existing limitations by introducing methods from time-series domain adaptation.
The primary contributions of this paper are as follows:
- (1)
Based on the motion model of an HGV, we devise a rapid trajectory generation method tailored for various maneuvering patterns, thereby establishing a comprehensive trajectory dateset of the HGV.
- (2)
This paper introduces a trajectory parameter prediction method grounded in the Sparse Associative Structure Model (SASM) [
22]. We are the first to apply the SASM from the field of time domain adaptation to HGV trajectory prediction. Compared to traditional methods, the proposed method can harness the deep learning capability of the SASM, adeptly uncovering the intricate interplay between established state variables and the predictive variables that shape a trajectory. By distilling and transferring these associative relationships, the accuracy of our method is greatly improved compared to some mainstream algorithms. This innovation enhances the adaptability and predictive prowess of our model, offering a more efficient and effective solution for trajectory prediction.
The rest of the paper is organized as follows. A method to generate HGV trajectory quickly in various maneuvering patterns is designed in
Section 2.
Section 3 utilizes the dynamic equations of the HGV to dissect its maneuverability characteristics and strategically selects parameters that are crucial for trajectory prediction. In
Section 4, an SASM trajectory parameter prediction algorithm is devised, accompanied by a detailed explanation of its implementation ideas and measures.
Section 5 presents the simulation experiments conducted to evaluate the performance of the proposed algorithm, while
Section 6 offers a comprehensive conclusion of the paper.
5. Simulation
In this section, we carry out simulation experiments to verify the effectiveness of the algorithm.
5.1. Sample Settings and Parameter Settings
The simulation analysis in this paper is conducted in the Python environment, and we utilize the Pytorch framework to construct the network. The hardware is configured with an Interi7 processor and a gegforce 2060 graphics card.
- (2)
Trajectory Dataset Setting
During the training phase, we generate 15,000 HGV trajectories based on the trajectory generation method mentioned in
Section 2.3. The initial state parameters setting and control parameters setting of the HGV are shown in
Table 2 and
Table 3, respectively. The explanations of the state parameters and control parameters are shown in
Section 2.1 and
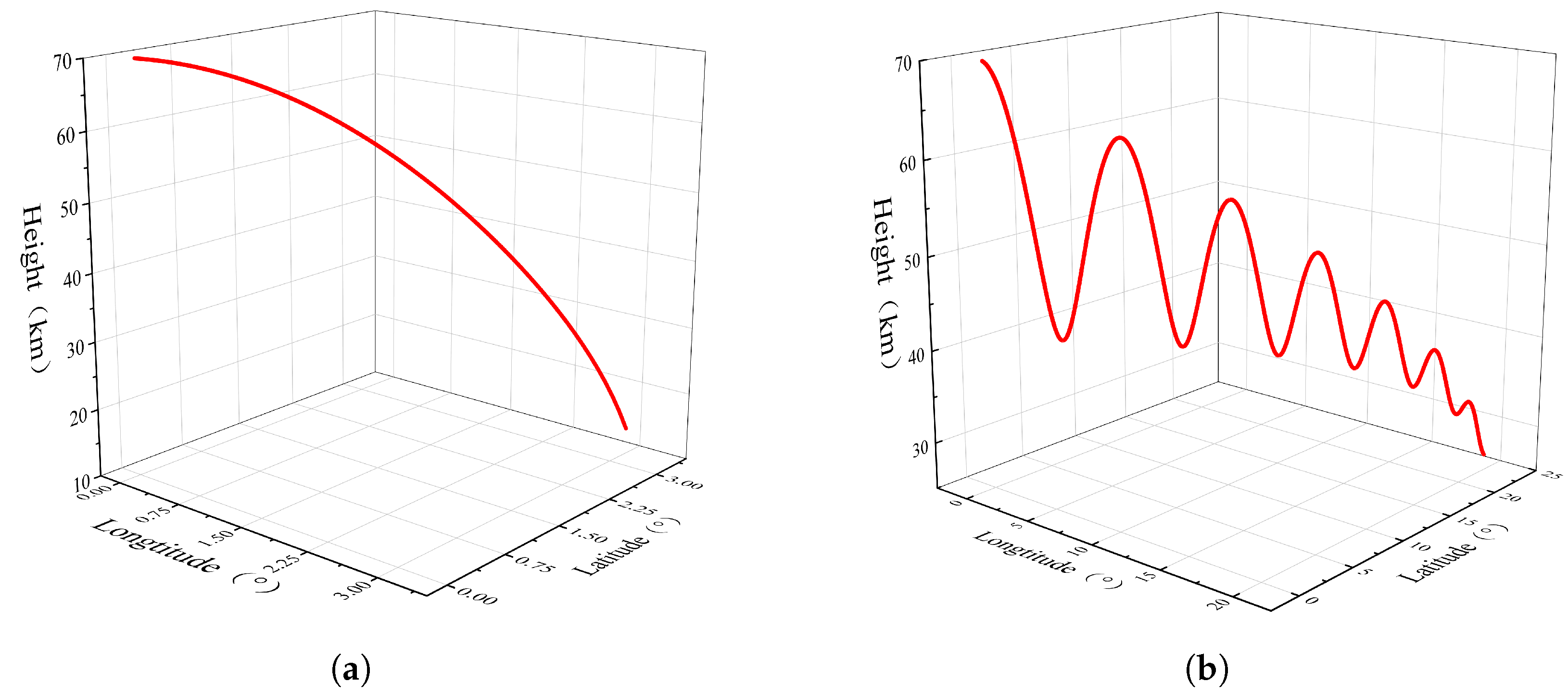
Section 2.2. Random flight trajectories of the HGV can be obtained by randomly selecting and combining the values of the initial state parameters and the related parameters of control variables. Therefore, each trajectory in the dataset is distinct. The trajectory dataset of the HGV is shown in
Figure 7.
During model training, we used the adaptive moment estimation (Adam) optimizer and L2 loss function. The parameters of the Adam optimizer and the SASM are shown in
Table 4.
During the training phase, 80% of the data were used for model training, 10% for validation data, and 10% for testing data.
Meanwhile, in order to objectively evaluate the performance of the proposed model in this paper, two indicators were adopted here to measure the prediction error, namely, the Mean Square Error (MSE) and the Mean Absolute Error (MAE), with the corresponding formulas as follows:
where
and
a are the parameters predicted by the SASM and the true value, respectively.
We also calculated the average error of spatial distance (AESD) of the trajectory prediction error with the following formula:
where
is the length of predicted time series, and
indicates the location of
ith test data and true data in the three dimensions of longitude, latitude, and height predicted at
k time, respectively.
What is more, we compared the model’s transfer ability from known data to unknown data in order to validate the model’s generalization ability. We used different sources of data for the training model and the final test model, namely, the sources of data came from different types of HGVs. The inherent parameters (mass, cross section, etc.) of different kinds of vehicles are different, leading to their different flight paths, even under the same initial conditions. Specifically, we conducted verification experiments on three sets of trajectories generated for three types of HGVs. The number of test sets for each of the three types was 250.
5.2. Presentation and Comparison of Experimental Results
To comprehensively evaluate the performance of our proposed SASM model, we engaged in a comparative analysis that contrasted the predictive results of our SASM model with those produced by a singular LSTM model, a GRU model, and a sophisticated CNN-LSTM model [
27]. This comparative analysis delved into three crucial dimensions: the architecture and parameters of the models, the prediction errors of the parameters, and the comparison of trajectory prediction curves.
5.2.1. Architecture and Parameters of Models
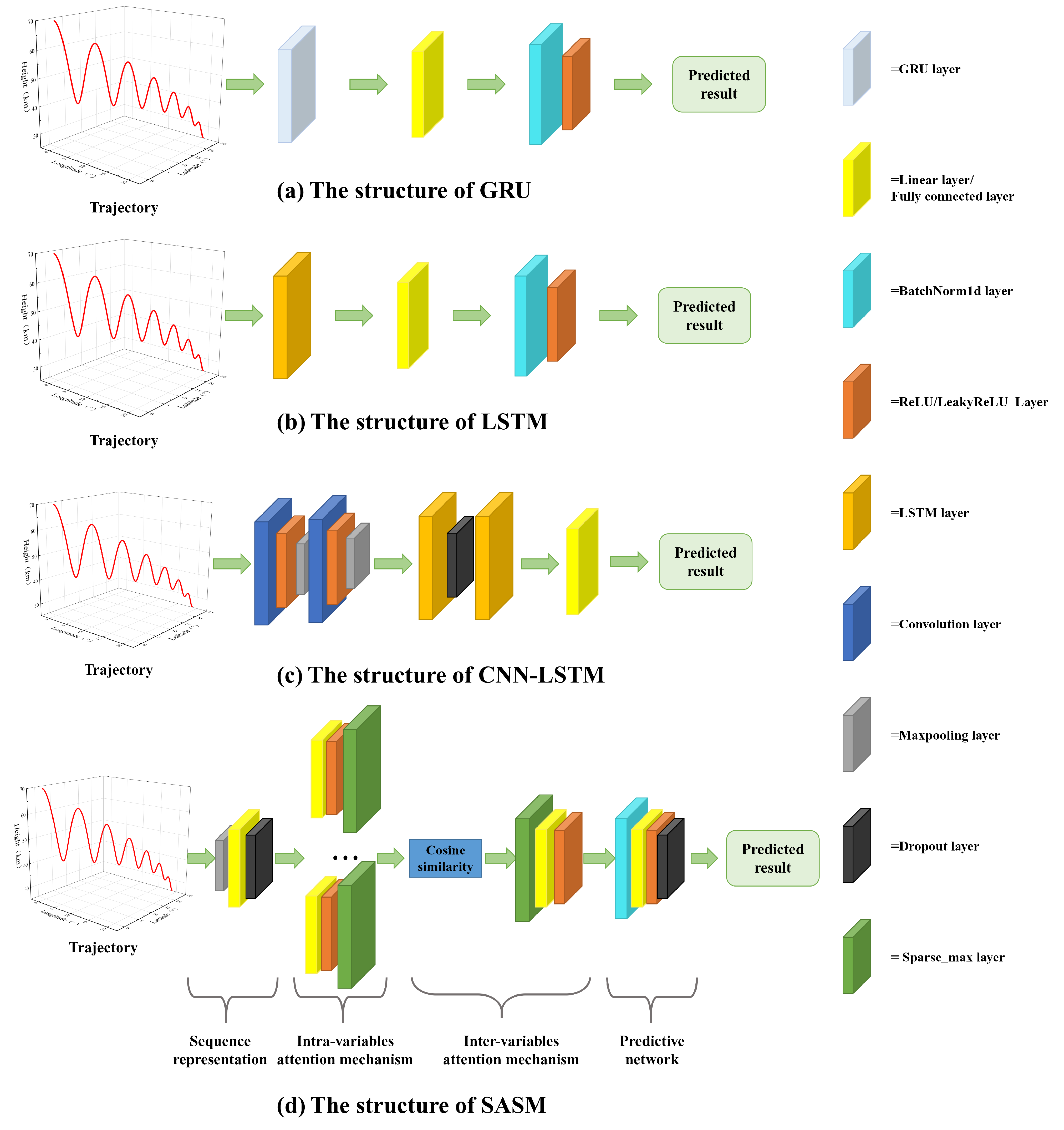
The different architectures of the above three models are depicted in
Figure 8. The number of input features was 6 for each model.
The LSTM model includes a LSTM hidden layer, a linear layer, a 1D batch normalization layer, a ReLU activation layer, and a fully connected layer. The size of the hidden layer of the LSTM was set to 50. The number of kernels was set to 1 in the fully connected layer.
Compared to the LSTM, the GRU model simplifies the structure of the LSTM. There are only two gates in the GRU, namely, a reset gate and an update gate. The structure and parameters settings are consistent with the LSTM, except that the first layer is replaced with a GRU layer.
The CNN-LSTM model comprises two sections: a convolution part and an LSTM part. The convolution portion consists of two identical structures, with each featuring a convolution layer, a ReLU activation layer, and a max pooling layer. The LSTM section, on the other hand, includes two LSTM layers and a dropout layer. The two convolution layers contain 32 individual 1 × 3 convolution kernels each. The dropout rate of two dropout layers is 0.2. Its two LSTM layers both have 50 hidden nodes. The size of kernel is 1 in the final fully connected layer.
The SASM model, as devised in this paper, is structured into four components. Initially, the trajectory data are fed into the sequence representation module, which comprises an adaptive max pooling layer, an LSTM hidden layer, and a dropout layer. The adaptive length of the adaptive max pooling layer is 900. The LSTM has 10 hidden nodes, and the dropout rate is 0.2. Following separate processing through intravariable and intervariable attention mechanisms, the associative structural representation was obtained. The input and output feature dimensions of the attention network were both 10. Finally, this representation was input into the predictive network, from which future parameters were predicted. The predictive network was constructed with a 1D batch normalization layer, a linear layer, a ReLU activation layer, and a dropout layer. The size of the linear layer was set to 50.
5.2.2. Prediction Errors of Parameters
We examined three different types of HGVs (described as I, II, and III in
Table 5) as the test data, where the prediction errors of parameters are illustrated in
Table 5.
Based on
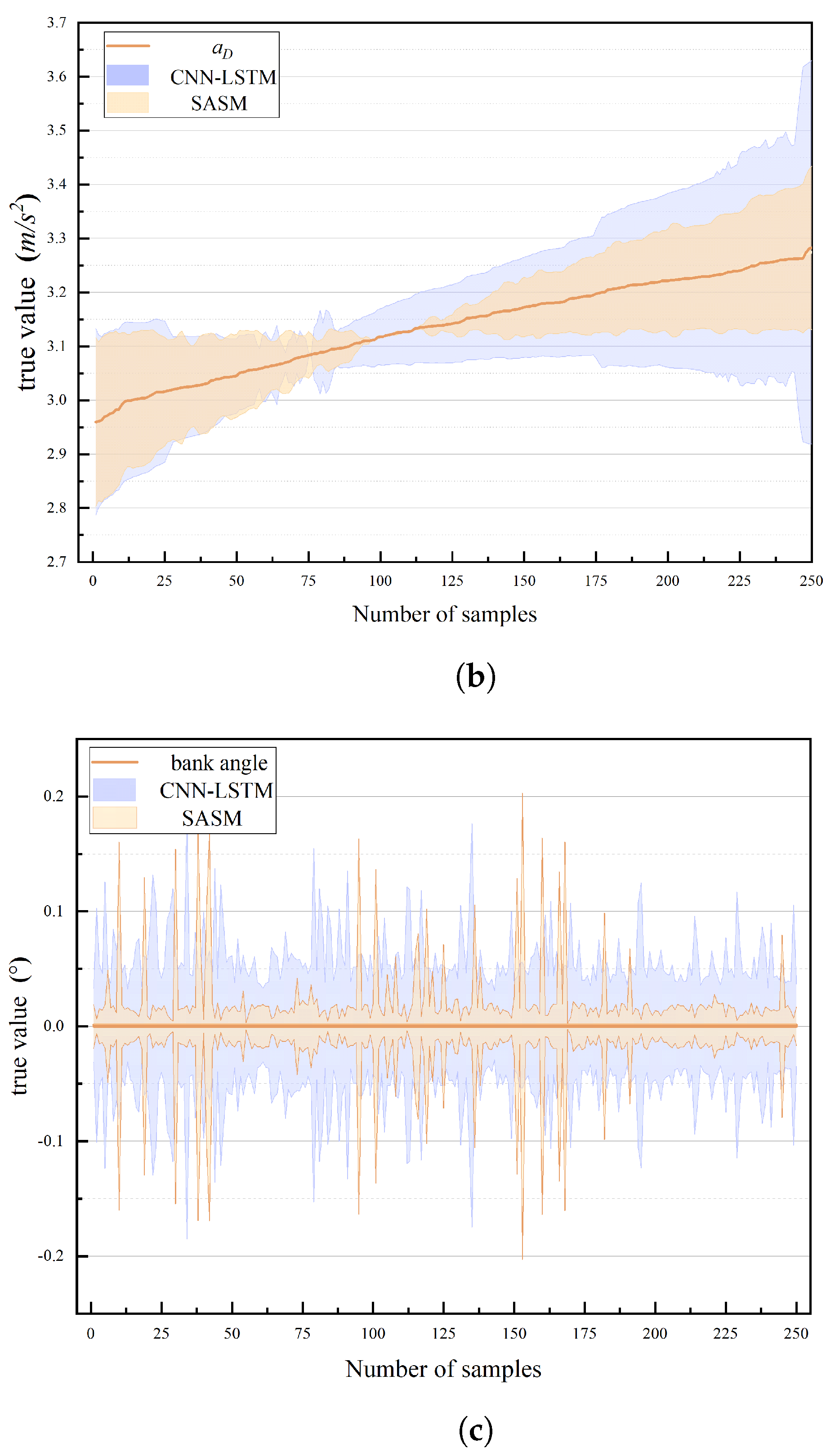
Table 5, it is clear that the two evaluation metrics (MSE and MAE) of the SASM outperformed the LSTM, GRU and CNN-LSTM in predicting the parameters for each category of the HGV. Specifically, in the prediction of aerodynamic lift acceleration, the SASM method demonstrated a notable improvement, with the maximum MSE reduction rate reaching 22.56% and the maximum MAE reduction rate reaching 19.39%, both when contrasted with the LSTM method. The performance enhancement was further accentuated in the prediction of drag acceleration, where the reduction rates for the MSE and MAE were at their zenith, peaking at 35.31% and 31.28%, respectively, across the three types of test data. Most notably, the SASM model exhibited a significant leap in the precision of bank angle prediction. The maximum reduction rates for the MSE and MAE are strikingly high, at 93.86% and 73.29%, respectively. The SASM’s MSE values are a mere one-third of those produced by the CNN-LSTM and a tenth of those from the LSTM, underscoring the model’s exceptional predictive accuracy in this parameter.
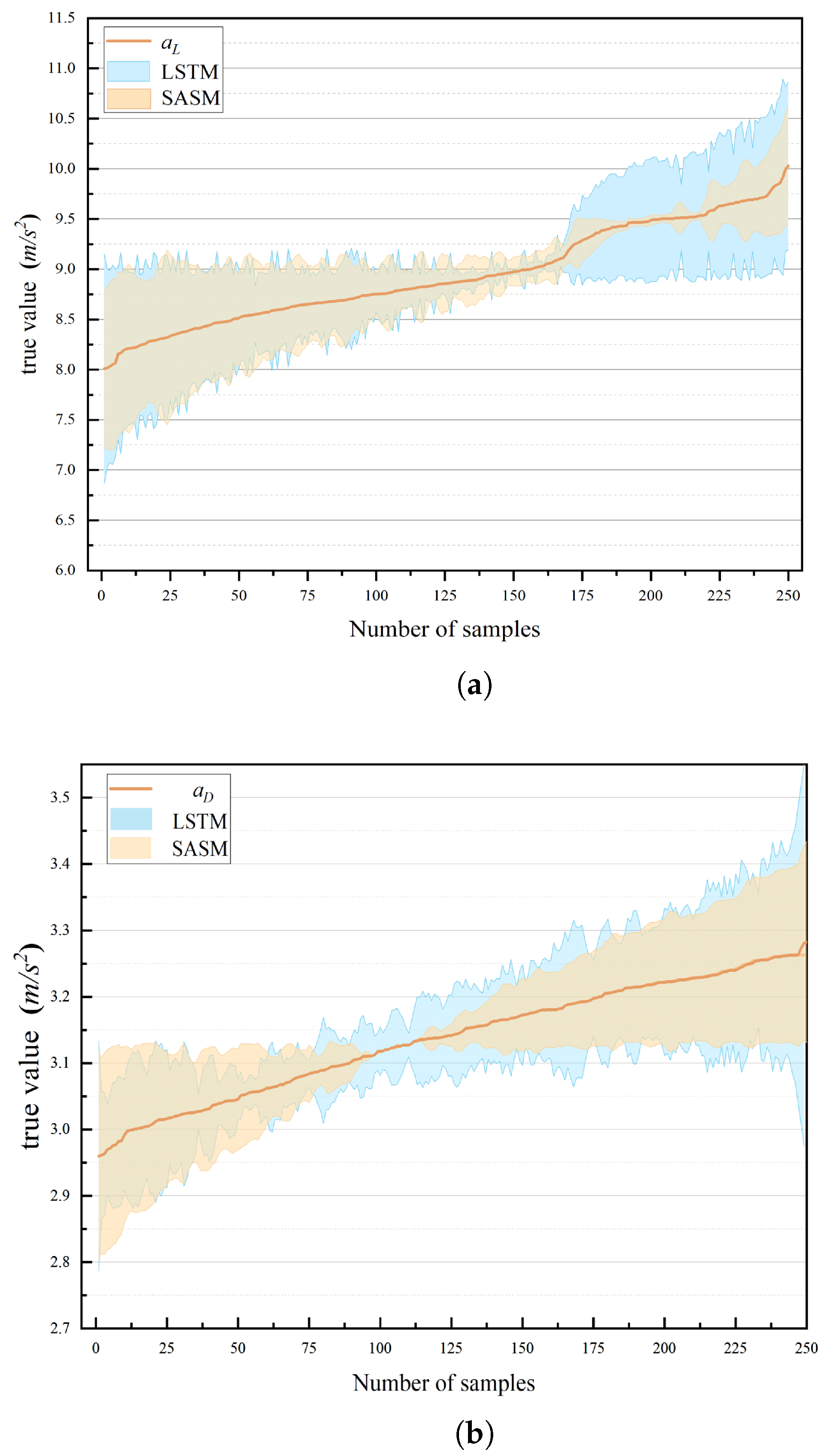
Furthermore, taking test data I as an example, we conducted a comparative analysis of the predictive performance between our proposed model and the LSTM model across various numerical ranges of parameters, as depicted in
Figure 9.
Figure 9a–c illustrate the error curve when predicting the aerodynamic lift acceleration
, drag acceleration
, and bank angle
for the SASM and LSTM models, respectively. Initially, as shown in
Figure 9a, the error bands of the two models are quite similar. However, as
increased, the predictive error for both models decreased, reaching a nadir for the LSTM when
equaled 9.25
. At this point, the LSTM’s error margin expanded noticeably, whereas the error for the SASM (represented by the orange area) is considerably smaller than that of the LSTM (the blue area). Furthermore, when
reached 9.5
, the error for the SASM escalated at a more gradual pace compared to the LSTM.
Figure 9b exhibits a pattern akin to that in
Figure 9a, with the SASM model demonstrating superior predictive performance for the drag acceleration
within the range of [3.1, 3.2]
.
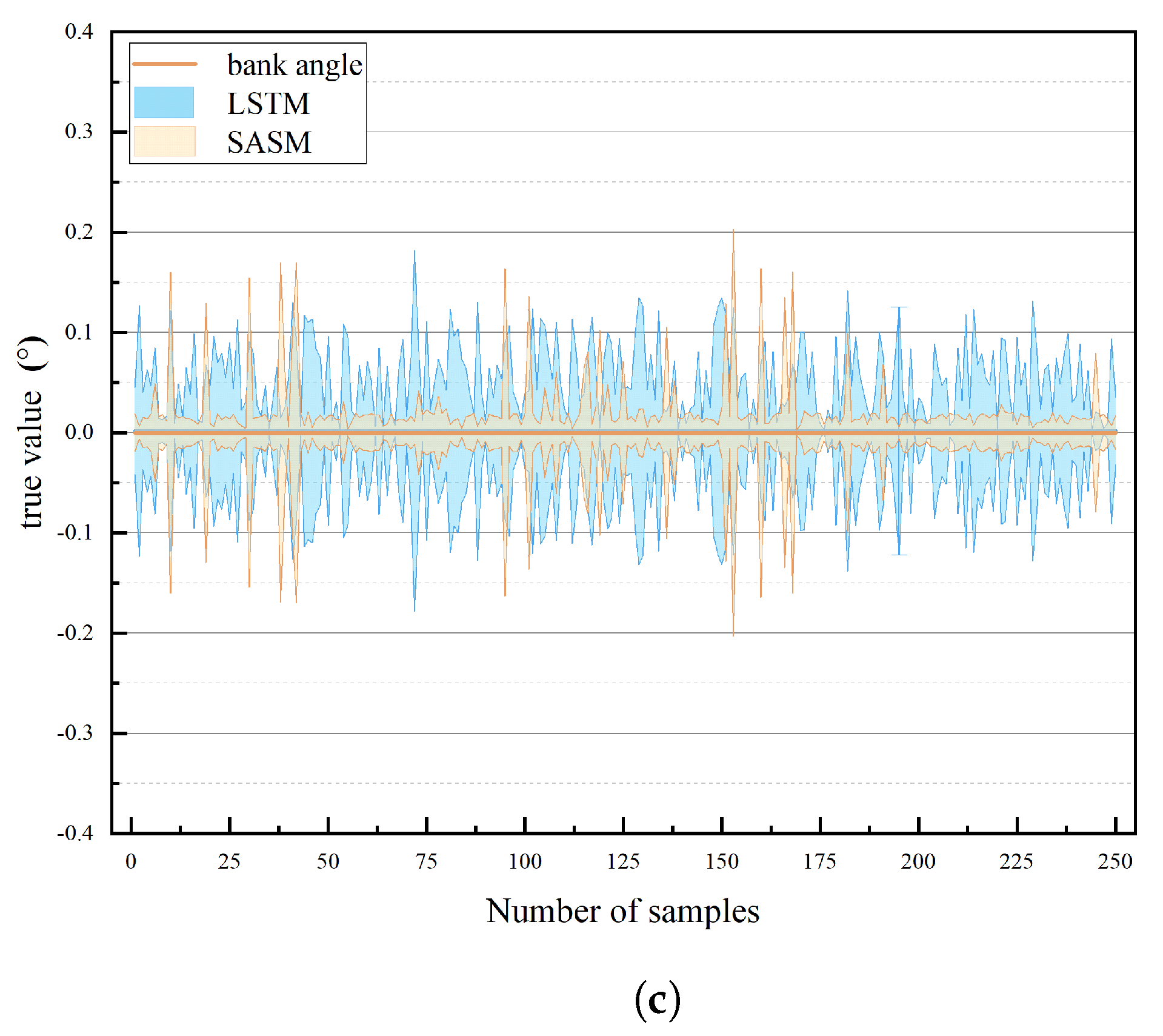
Figure 9c demonstrates a notably smaller error band for the SASM model, compared to LSTM. While it is true that the LSTM model exhibited superior performance at certain, albeit rare, data points, the overall trend highlights the SASM model’s advantage in terms of consistency and precision in predictions.
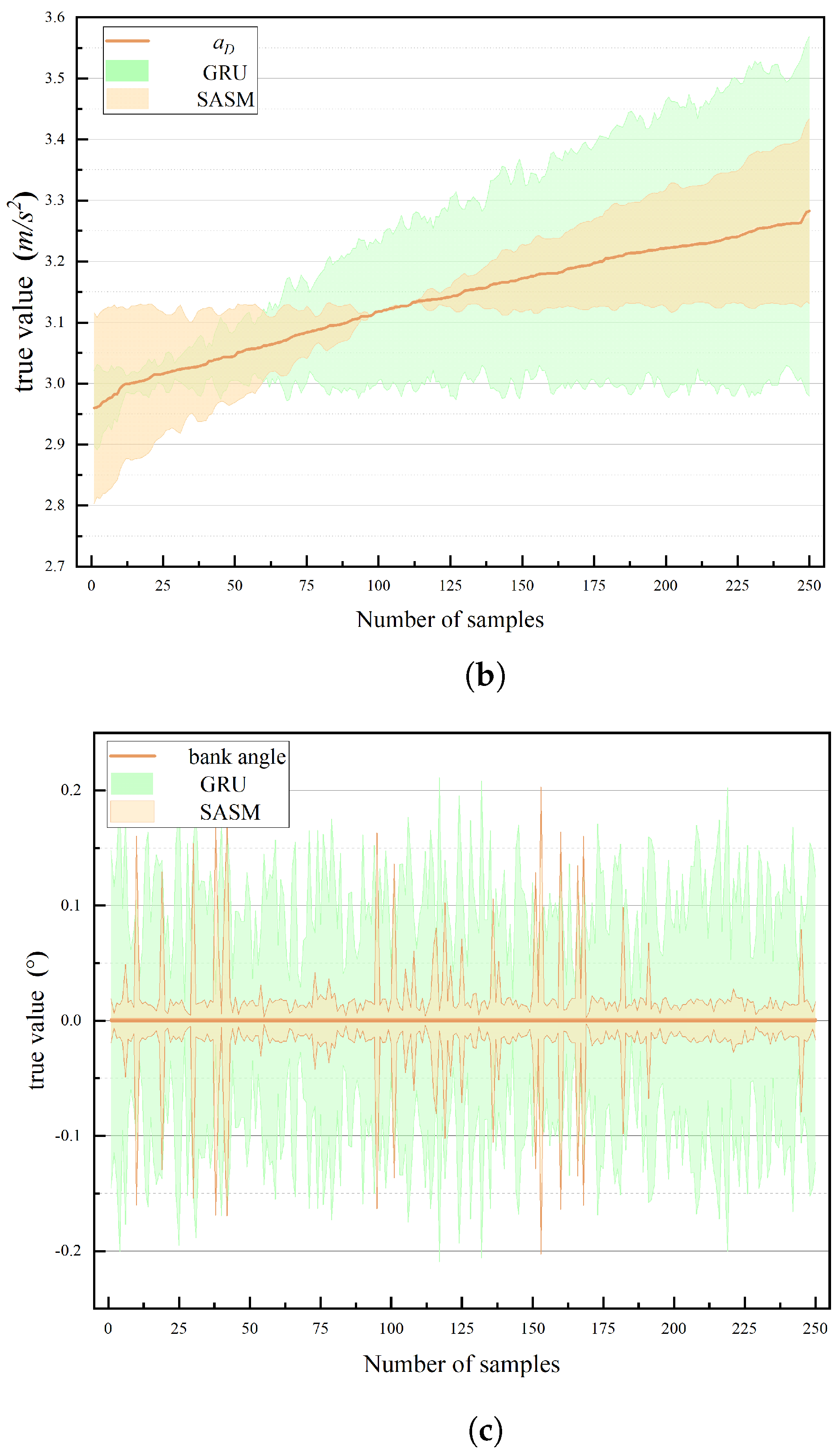
Additionally,
Figure 10 presents a comparative analysis of the error between the SASM and CNN-LSTM models. In
Figure 10a, prior to reaching 9.25
, the prediction errors for the aerodynamic lift acceleration
were decreasing for both the SASM and GRU model. And their error bands are quite similar. Subsequently, the error bands expanded, with the GRU model exhibiting a more rapid and pronounced increase compared to the SASM model. Similarly, the trends observed in
Figure 10b,c, mirror those seen in
Figure 10a.
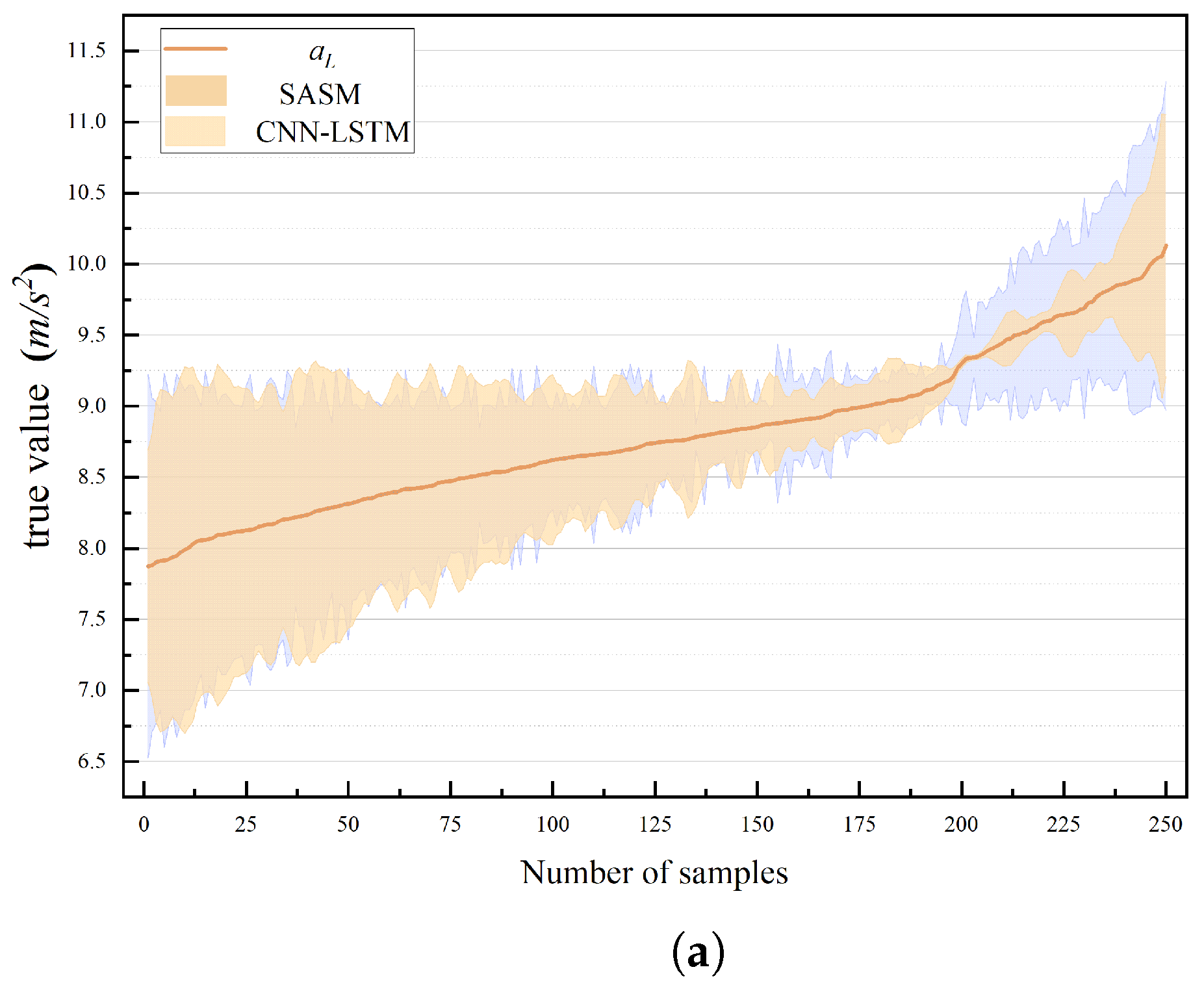
and
error curves of CNN-LSTM model in
Figure 11a are similar to the curves of GRU model, except that entire errors of GRU are smaller than CNN-LSTM. For error curve of
, GRU model does not perform as well as CNN-LSTM model, as shown in
Figure 11. In summary, the ranking of models based on prediction error is SASM < CNN-LSTM < GRU < LSTM, while the ranking based on prediction accuracy is the inverse: SASM > GRU > CNN-LSTM > LSTM.
5.3. Comparison of Trajectory Prediction Curves
The reconstructed trajectory of the HGV was generated utilizing the parameters forecasted by the SASM method and subsequently compared against the predictions of the LSTM, GRU, and CNN-LSTM method. The 100-step future trajectories of the HGV for each model are illustrated in
Figure 12.
Figure 12a presents a three-dimensional visualization of both the predicted and actual trajectories.
Figure 12b depicts the two-dimensional plot of the predicted and actual trajectories in terms of latitude and height.
As can be seen from
Figure 12a, the 3D predicted trajectories of all four models generally maintained the trend of the actual trajectory. Notably, the SASM method demonstrated the smallest error and superior predictive performance compared to other models. The projected values of the three methodologies onto the latitude and longitude coordinate axes demonstrated minimal deviation from the actual values, with the primary disparity manifesting in the height prediction, as
Figure 12b shows. It is evident that the prediction based on the SASM was closest to the true trajectory and had the smallest error. The GRU followed closely, with the CNN-LSTM slightly behind the GRU, while the LSTM exhibited a more pronounced deviation from the actual trajectory compared to the other two models. Overall, the models’ predictive accuracy values are ranked as follows: SASM > GRU> CNN-LSTM > LSTM.
The AESD and average processing time of three models are detailed in
Table 6. Notably, the SASM method exhibited the lowest AESD among the three, with a value of 0.049518. This represents a substantial 90.21% reduction in the AESD compared to the LSTM method. Furthermore, the average processing time of the SASM was also the shortest, clocking in at 7.790 (assuming the unit is appropriate for the context), which is approximately 49.7% faster than the LSTM method. These results underscore the efficiency and accuracy advantages of the SASM method over the LSTM method for the given application.
6. Results
This paper introduces a groundbreaking trajectory forecasting approach that integrates the Sparse Associative Structure Model (SASM) with deep learning and dynamic equations, addressing the longstanding challenges of accuracy and generalization in traditional methods. We applied the research of time domain adaptation to the field of theHGV, which has provided a new way to solve the field of the HGV.
Firstly, we constructed a comprehensive trajectory database that encompasses diverse maneuvering modes, laying a robust foundation for our predictive model. Subsequently, we identified three crucial trajectory parameters as prediction targets and devised a prediction model based on the SASM. Ultimately, this trained model was leveraged to anticipate the trajectory parameters of the HGV, enabling the reconstruction of their future trajectories for real-time prediction. In the simulation experiment, we compared the generalization performance of the models by comparing their prediction accuracy on different data sets. In particular, the test data sets and training data sets were derived from different types of aircraft. The simulation results show that the prediction accuracy of the SASM was superior to the LSTM, GRU, and CNN-LSTM models. Notably, the SASM reduced the trajectory prediction error by an impressive 50.35% and shortened the average processing time by 48.7% compared to the LSTM model. This proposed methodology has demonstrated remarkable proficiency in forecasting trajectories for three distinct types of HGVs, boasting both high prediction accuracy and excellent generalization capabilities.
However, the method proposed in this paper also has the following limitations: (1) The model is currently capable of short-term trajectory prediction for HGVs, with long-term predictions remaining a challenge. (2) Complex maneuver trajectories pose difficulties for accurate prediction. As such, future research endeavors should focus on advancing these aspects of trajectory prediction to further enhance their applicability and accuracy.