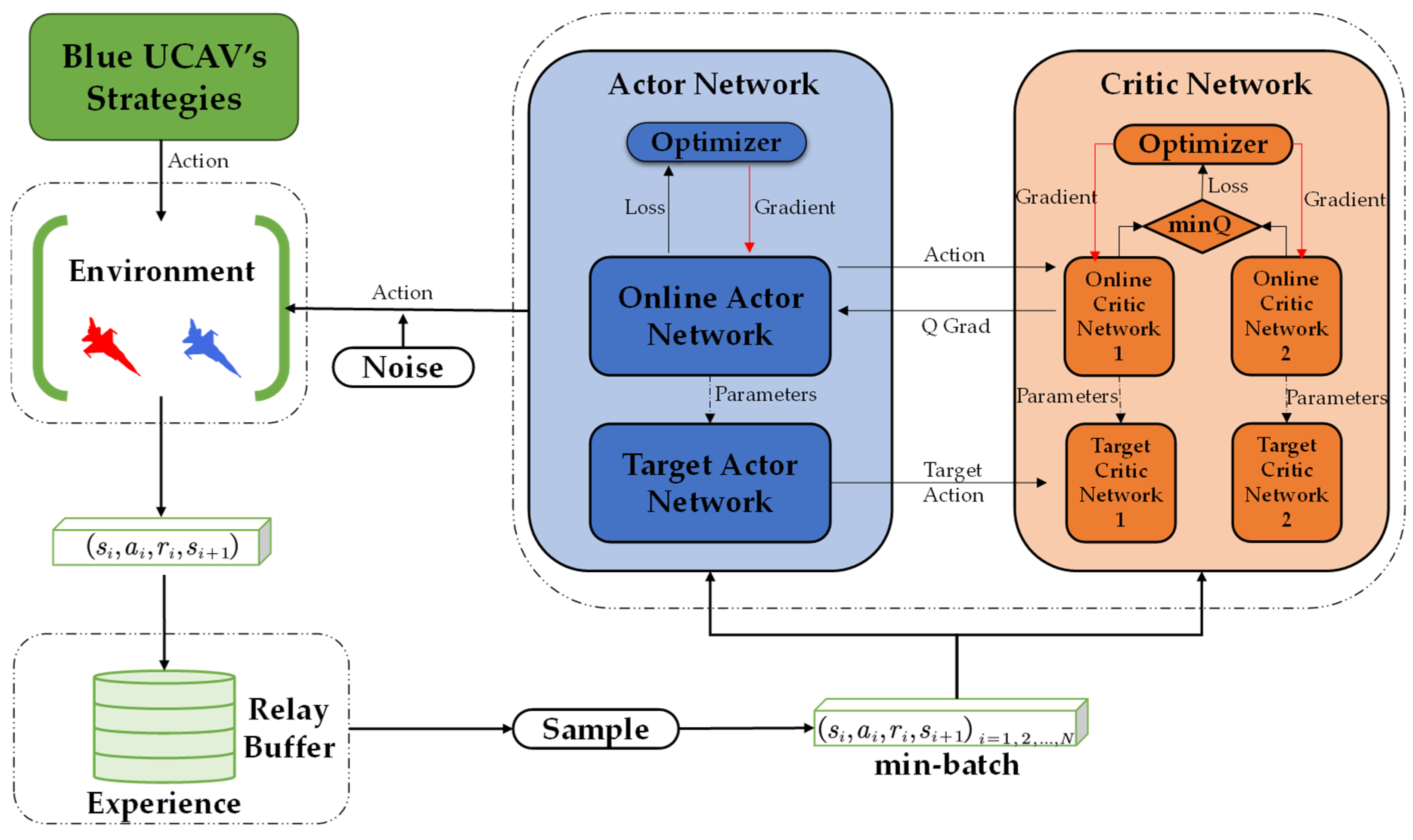
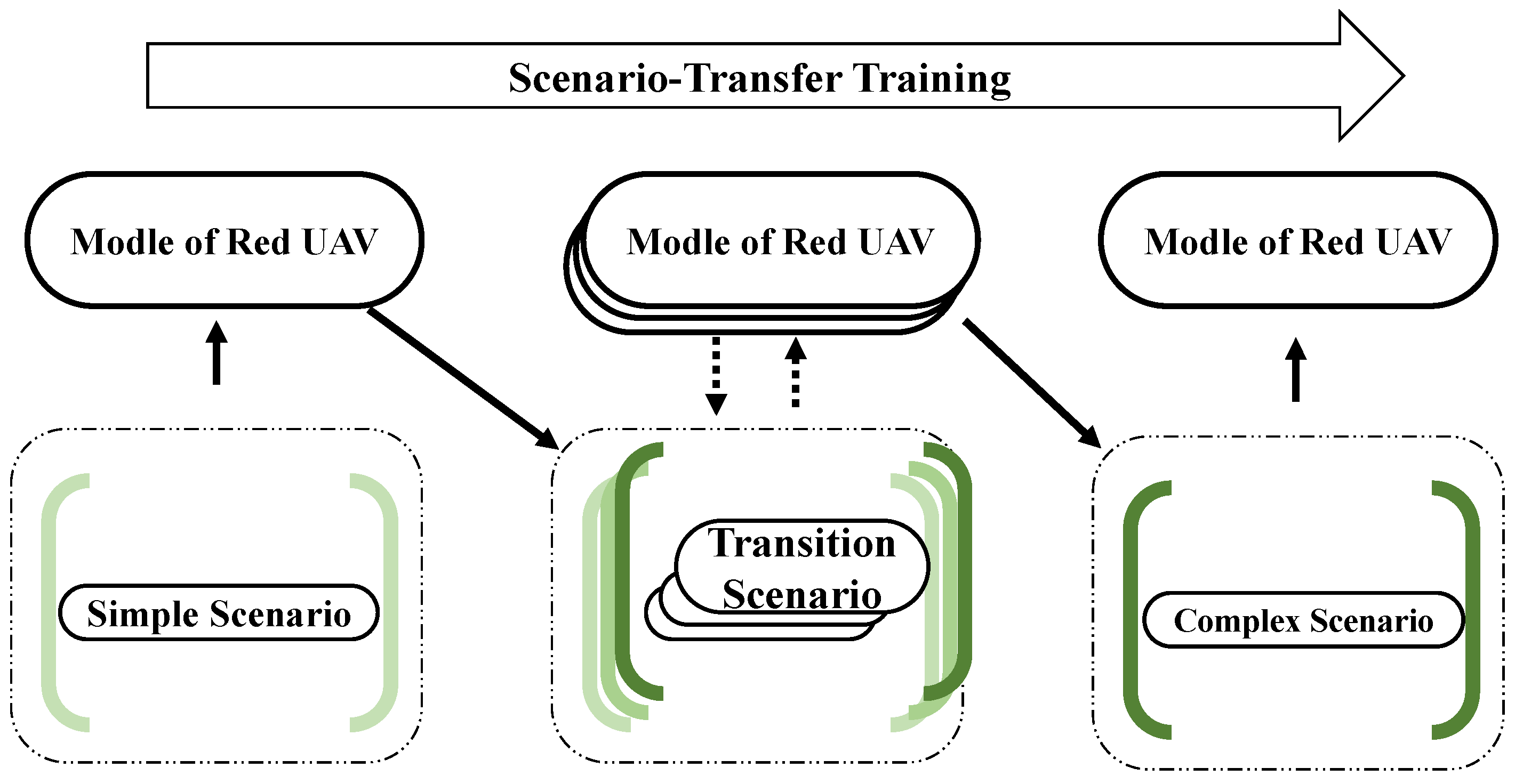
1. Introduction
In recent years, the rapid advancement of unmanned aerial vehicle (UAV) technologies has led to the development of UAV swarms that exhibit superior coordination, intelligence, and autonomy compared to traditional multi-UAV systems [
1]. As evidenced by global conflicts, the use of UAV swarms for saturation attacks is becoming a predominant trend in UAV operations, posing a significant threat to air defense [
2].
To counter these attacks, many researchers have proposed the use of defensive unmanned combat aerial vehicle (UCAV) swarms. The results suggest that UCAV swarms offer a potential solution to the threats posed by UAV swarms [
3]. While a UCAV is typically defined as an UAV used for intelligence, surveillance, target acquisition, reconnaissance, and drone strikes, this paper specifically refers to an innovative UAV that combines the advantages of multi-rotor aircraft, such as vertical take-off and landing (VTOL), with fixed-wing aircraft like long endurance and high speed cruise [
4].
Currently, UCAVs are predominantly controlled either through pre-programmed codes or in real-time by operators at a ground station. The former method, however, lacks flexibility due to the incomplete nature of battlefield information and the difficulty of achieving desired outcomes under conditions of uncertain information. The latter method requires the consideration of communication stability and delay, both of which significantly impact air combat [
5]. Furthermore, as the number of UCAVs increases, so does the cost of organization, coordination, and operator cooperation. Consequently, these current methods are incapable of controlling large-scale swarms of UCAVs. Therefore, autonomous maneuvering decision-making based on real-time situations has become a critical issue for UCAV swarms. This is currently one of the most important research topics in the field of UAV intelligence [
6].
Achieving autonomous air combat for UCAV hinges on the successful integration of detection, decision-making, and implementation processes. Since the 1950s, numerous methods have been proposed to develop algorithms capable of autonomously conducting air combat [
7]. These methods can be broadly categorized into two types: rule-based and optimization-based. The former employs expert knowledge accumulated through pilot experiences or dynamic programming approaches to formulate maneuver strategies based on varying positional contexts [
8,
9]. The latter transforms the air-to-air scenario into an optimization problem [
10,
11] that can be solved using numerical computation techniques such as particle swarm optimization (PSO) [
12], minimum time search (MTS) [
13], and pigeon-inspired optimization (PIO) [
14], among others. However, the decision-making system designed based on expert knowledge exhibits strong subjectivity in situation assessment, target allocation, and air combat maneuver decision-making processes. Consequently, the rule-based method lacks sufficient flexibility to handle complex, dynamic, and uncertain air combat situations. Given that the dynamic model of UCAVs is intricate and typically expressed as a nonlinear differential equation, it requires significant computing resources and time for numerical computation. Furthermore, the optimization-based method faces a dimension disaster when the number of UCAVs on both sides increases significantly [
15]. Additionally, accurately predicting an enemy’s intentions, tactics, equipment performance, and other information during combat is generally unattainable. These factors collectively limit the applicability of the aforementioned methods.
More recently, deep reinforcement learning methods have recently been extensively applied to air combat decision-making problems, encompassing both visual range and beyond visual range decisions [
16]. On 27 June 2016, the artificial intelligence system, Alpha-Dogfight, triumphed over an experienced American air combat expert who piloted a four-generation aircraft in a simulated combat environment. This victory marked a significant milestone in the application of artificial intelligence to air combat maneuver decision-making. Subsequently, the Defense Advanced Research Projects Agency (DARPA) initiated the Air Combat Evolution (ACE) program, aimed at advancing and fostering trust in air-to-air combat autonomy. The ultimate objective of the ACE program is to conduct a live flight exercise involving full-scale aircraft [
7].
Currently, numerous researchers have explored the application of deep reinforcement learning in UCAV air combat maneuver decision-making. For instance, Piao H. et al. introduced a purely end-to-end reinforcement learning approach and proposed a key air combat event reward shaping mechanism. The experimental results demonstrated that multiple valuable air combat tactical behaviors emerged progressively [
17]. Kong W. et al. took into account the error of aircraft sensors and proposed a novel autonomous aerial combat maneuver strategy generation algorithm based on the state-adversarial deep deterministic policy gradient algorithm. Additionally, they proposed a reward shaping method based on the maximum entropy inverse reinforcement learning algorithm to enhance the efficiency of the aerial combat strategy generation algorithm [
18]. Hu D. et al. proposed a novel dynamic quality replay method based on deep reinforcement learning to guide UCAVs in air combat to learn tactical policies from historical data efficiently, thereby reducing dependence on traditional expert knowledge [
16]. Puente-Castro A. et al. developed a reinforcement learning-based system capable of calculating the optimal flight path for a swarm of UCAVs to achieve full coverage of an overflight area for tasks without establishing targets or any prior knowledge other than the given map [
19]. This work provides a valuable reference for a swarm of UCAVs to carry out autonomous air combat.
However, previous research on autonomous air combat maneuver decision-making often encounters limitations due to the complexity of the combat environment, simplified assumptions, overreliance on expert knowledge, and low learning efficiency from large-scale exploration spaces. For instance, due to the intricacy of the three-dimensional space dynamic model, most researchers have assumed that UCAVs move in a two-dimensional plane [
20,
21,
22] or in a highly simplified three-dimensional model [
16]. This simplification results in the loss of significant details regarding air combat maneuvers. Research on sequential decision-making problems has also revealed that conventional deep learning methods are heavily dependent on expert knowledge and exhibit low learning efficiency when obtaining effective knowledge from large-scale exploration spaces due to the complexity of the air combat environment. Moreover, since the maneuvering of UCAVs is influenced by the search space, the discretion of actions significantly impacts the results. In refs. [
23,
24], the action space was discretized into seven actions on the horizontal plane, while in ref. [
25], the action space was expanded to include thirty-six actions. Finally, in refs. [
7,
18], a model of continuous action space was established. Currently, selecting an appropriate method for deep reinforcement learning in continuous action space is a hot topic in academic research.
This study advances the field with the following contributions:
A three-dimensional UCAV dynamics model was developed for deep reinforcement learning in continuous action space, with continuous actions of tangential overload, normal overload, and roll angle as maneuver inputs, aligning UCAV maneuvers with real-world conditions.
An improved twin delayed deep deterministic (TD3) training method was proposed, integrating “scenario-transfer training” to enhance training efficiency by 60%, facilitating faster convergence of the deep reinforcement learning algorithm.
The method’s effectiveness was validated through a comparative analysis with the experienced fighter pilots’ strategies across four scenarios, marking the first literature comparison of deep reinforcement learning maneuver decisions against expert pilot maneuvers.
The remainder of this paper is organized as follows. In
Section 2, the problems concerned in this work and system modeling based on the Markov decision process (MDP) are stated.
Section 3 introduces the training environment for UCAV aerial combat. In
Section 4, the improved TD3 algorithm based on the idea of “scenario-transfer training” is depicted in detail. Then, the simulation results regarding the maneuver of “nose-to-nose turn” are presented and discussed in
Section 5. Finally,
Section 6 summarizes this work and provides some suggestions and proposals for further research.
2. System Modeling Based on Markov Decision Process
2.1. The Dynamic Model of UCAVs
The dynamic model of UCAVs is modeled in the inertial coordinate system, in which the X-axis is pointed to the east, the Y-axis is pointed to the north, and the Z-axis is pointed to the sky, as shown in
Figure 1 Since this paper focused on the maneuver decision algorithm of UCAVs, the torque imbalance in state transition was ignored, and our main attention was given to the relative position and velocity between two UCAVs. Therefore, the six-degree-of -freedom (6-DoF) dynamic model of UCAVs was selected to analyze the force characteristics.
During the level flight, the main forces acting on the UCAV are the propulsion, gravity, and aerodynamics, so a body coordinate system should be built. The original point of the body coordinate system is in the mass center of the UCAV, the
xb-axis is pointed to the head of UCAV, which is paralleled with the propulsion and velocity, the
yb-axis is pointed to the down of the UCAV, and the
zb-axis points to the wing of the UCAV according to the right hand rule. Transforming the inertial coordinate system
O-XYZ into the body coordinate system
O-xbybzb, the simplified dynamic equation [
26] of the UCAV can be obtained, as shown in Equation (1):
In Equation (1), g represents the acceleration of gravity, v represents the velocity of UCAV, and the constraints of should be satisfied. The direction of velocity can be represented by two angles: the pitch angle , which indicates the angle between the velocity v and the plane of OXY, the other is the yaw angle , which indicates the angle between the projection of velocity in the plane of OXY and the X-axis. nt and nf are the tangential overload and normal overload, respectively, and μ is the roll angle of the UCAV.
The kinematics equation of the UCAV in the
OXYZ coordinate system can be described as follows:
Through the integral calculation of Equation (2), the flight path of the UCAV represented by x, y, and z in the inertial coordinate system OXYZ can be obtained. Then, the 6-DoF model of the red UCAV can be built by the combination of Equations (1) and (2). It should be noted that the dynamic equations of the blue UCAV are also defined by Equations (1) and (2), and factors such as the aerodynamic forces, moments, and stall characteristics of the aircraft during deceleration are considered.
2.2. State Definition of UCAV Based on MDP
The process of reinforcement learning is always modeled by MDP, which can be represented by a quadruple
, in which
S is the state space,
A is the action space,
R is the reward, and
γD is the discount. The state
S of the UCAV in the MDP framework is defined by the dynamic equation constrained by Equations (1) and (2) in
Section 2.1. According to the viewpoint of the MDP, the air combat between UCAVs can be treated as follows: the red UCAV (an agent with ability of environmental perception) takes some maneuver actions based on one of policy
π under the condition of known current state
S, and obtains some kinds of reward from the environment. Supposing the instant reward function that feedbacks from the environment to UCAV is
, then the cumulative rewards of the UCAV in the current state can be defined as
, and
is the discount factor. The greater the discount factor, the more the current reward is impacted by the pass reward. The ultimate goal of reinforcement learning framework based on the Markov decision process model is to allow the UCAV to learn the optimal policy
π, then the UCAV can decide on the optimal action according to optional policy
π to obtain the maximum reward, as shown in
Figure 2.
In the aerial combat depicted in
Figure 2, the red and blue aircraft are named as the red UCAV and blue UCAV, respectively. The state can be fully described by the current motion parameters, that is, the position, velocity, and attitude angle, as shown in Equation (3).
However, compared with the state described by the UCAVs, the state described by the relative position, velocity, and attitude of the blue UCAV to red UCAV is more intuitive to understand the situation in aerial combat, as shown in
Figure 3.
ρ is a vector, which represents the direction of line of sight from the red UCAV to blue UCAV, and the amplitude of
ρ is
D (i.e.,
).
α is the angle between the projection of
ρ on the plane of the
OXY and
Y-axis, and
β is the angle between
ρ and the plane of
OXY.
p,
e are the angles between the vector of
vr,
vb and vector line of sight
ρ, respectively, which can be calculated as follows:
Thus, the state in Equation (3) can be rewritten as follows:
It can be seen from the above equation that the rewritten state not only describes the situation in air combat more intuitively, but also reduces the dimension of the state space.
In order to improve the convergence performance of deep neural networks, the state parameters in Equation (3) should be preprocessed, as shown in
Table 1.
2.3. Action Definition and Reward Function
In this paper, three continuous actions were used to control the maneuver of the UCAV:
where
Ac is the action set, and
ntc,
nfc, Δ
μc are the commanders of
nt,
nf, and Δ
μc, respectively. The relationship between them can be expressed as follows:
As shown in
Figure 2,
nt and
nf are the tangential overload and normal overload, respectively, and Δ
μc is the command of the differential roll angle of the UCAV. By selecting different combinations of actions, the UCAV can maneuver to the desired state, and each set of action values in Equation (6) corresponds to an action in the maneuver library of the UCAV.
The reward given by environment is based on the agent’s position with respect to its adversary, and its goal is to position the adversary with its weapons engagement zone (WEZ) [
7], and most weapons systems provide the UCAV controller with an indication of the radar line of sight (LOS) when they are locked on a target [
27]. Thus, as shown in
Figure 3, if the distance between the red UCAV and blue UCAV is smaller than the effective shooting distance, and the LOS meets the locking requirements of the red UCAV to blue UCAV, the red UCAV will obtain the reward 1, on the contrary, if the LOS meets the locking requirements of the blue UCAV to red UCAV, the red UCAV will obtain the reward −1. Therefore, the reward function can be designed as follows:
where
D* is the maximum distance to achieve the locking requirements and is proportional to the maximum attack distance of the weapon system on the UCAV platform.
p* is the maximum angle when the locking requirements are achieved between the velocity direction of the red UCAV and LOS angle, and
e* is the blue one. These two angles are related to the maximum attack angle of the weapon system on the UCAV platform; in this paper,
D* = 200 m,
.
However, it is obvious that the rewards are sparse, as defined in Equation (8), since both UCAVs need to take many actions to obtain one reward. Rewards are sparse in the real world, and most of today’s reinforcement learning algorithms struggle with such sparsity. One solution to this problem is to allow the agent to create rewards for itself, thus making rewards dense and more suitable for learning [
28]. In order to solve this problem, we added the so called “process rewards” to guide the process of reinforce learning for the UCAV. The “process rewards” included four parts: the angle reward
r1, distance reward
r2, height reward
r3, and velocity reward
r4. The calculation equation regarding these four rewards is defined in Equation (9).
where Δ
h is the height difference between the red UCAV and blue UCAV, and
vmax and
vmin are the maximum and minimum velocity that the UCAVs can achieve in the flight, respectively.
In summary, we obtain the comprehensive reward as shown in the following equation:
where
k1,
k2,
k3,and
k4 are the weight of the rewards, these values ranging between 0 and 1, and their sum is 1. Currently, the reward weight
ki is determined by the method of trial-and-error, so adaptive reward techniques will be adopted in future research.
During the simulation round in reinforcement learning, the UCAV selects the action according to certain policy π, and obtains the reward R from the environment, where the aim of reinforcement learning is to obtain the maximum rewards. The round ends when the number of steps per round reaches the maximum value, or when one UCAV locks the other to obtain the preset rewards continuously.
4. The Improved TD3 Algorithm Based on Scenario-Transfer Training
One of the key ideas about reinforcement learning is to accumulate experience through continuous trial and error. However, it is often not effective to directly try to solve particularly complex problems by the reinforcement learning method without a certain technique [
32,
33,
34]. As shown in
Figure 6 in
Section 3, the reward value needs to be trained to steady after about 20,000 steps, and the convergence speed of the algorithm is very slow. Through the analysis of the training process, it was found that the reason why it was difficult to find the optimal strategy for the red UCAV was that the strategy of the blue UCAV controlled by the min–max strategy was too strong at the beginning of the training. Therefore, it was unable to effectively accumulate rewards for the red UCAV, and a lot of ineffective explorations were conducted with little sense such as away from the battlefield, landing, flying away, and so on. In other words, it is hard to obtain effective rewards when learning from scratch in a complex scenario. Inadequate reward accumulation leads to the slow convergence of learning and poor results.
In order to solve this problem, we proposed a scenario-transfer training (STT) method to train the strategy of the red UCAV based on the TD3 algorithm. STT was first proposed to solve the problem in that it is hard to train a good model directly [
21,
22]. The principle of STT is shown in
Figure 8. The training for a task can be achieved by training in several simple but similar transition scenarios, in which the first one is called the source scenario and the last is called the target scenario. A reinforcement learning model can first be trained in the source scenario, then in several transition scenarios, and finally in the target scenario. The experience trained in each scenario is memorized in the model, which is used as the base model for subsequent training.
In order to validate the effectiveness of the improved algorithm based on the STT method, referring to the work of Zhang et al. [
21], we conducted comprehensive experiments to illustrate the effectiveness of STT with the TD3 algorithm as the baseline in this paper.
Three training scenarios corresponding to three kinds of maneuvering strategies of the blue UCAV were designed from simple to complex, respectively. In the first case, the initial state of the blue UCAV was chosen randomly, and then kept to conduct the linear motion; this was called the simple scenario. In the second case, the initial state of the blue UCAV was also chosen randomly, but its action was randomly selected from the maneuver action library at each decision moment; this case was named the transitional scenario. In the third case, although the initial state of the blue UCAV was also chosen randomly, its action was controlled by the min–max strategy at each decision moment; this case was named the complex scenario. The step numbers that decide the scenario transfer were defined as
Ns,
Nt, and
Nc, respectively. The training process of the TD3 algorithm improved by STT is described in Algorithm 1. Suppose that there are N red UCAVs and M blue UCAVs in the combat task. We first initialized the parameters of all models randomly, and then the parameters of the models were updated through the training.
| Algorithm 1. The process of the training method for air combat based on the TD3 algorithm improved by STT. |
| Step 1: | Initializing parameters of online actor network and two online critic networks |
| Step 2: | Initializing parameters of target actor network and two target critic networks |
| Step 3: | Initializing the experience pool |
| Step 4: | for episode = i:
if i < maximum episode:
if i < Ns episode:
● The action ai is chosen from the simple scenario
elif i < Nt and i > Ns:
● The action ai is chosen from the transitional scenario
elif i < Nc and i > Nt:
● The action ai is chosen from the complex scenario
endif
● Getting the reward ri and si+1 by putting si and ai into Equations (6) and (10)
● The quadruple is stored into the experience pool
● Selecting N samples from experience pool randomly
● Computing expected reward of action ai by evaluating the next output value of critic network, and calculating yi by Equation (13)
● Updating the parameters of online critic network by Equation (12)
● Updating the parameters of online actor network by Equation (14)
● Updating the parameters of target actor and critic networks by that of online actor and critic networks after a delay time
end if
end for |
| Step 5: | End |
The comparative analysis regarding the simulation was carried out in Python (the source code will be uploaded in GitHub when the paper is published), and the total number of training steps was set as 30,000. The method of the TD3 algorithm in
Section 3.1 was used for the baseline, and the red UCAV was trained by this method from beginning to end. The method of the improved TD3 algorithm in Algorithm 1 was used as the comparison, and the red UCAV was trained in the simple, transition, and complex scenarios, and the values of
Ns,
Nt,
Nc were set as 10,000, 20,000, and 30,000, respectively. The comparison of the average reward in different training scenarios is shown in
Figure 9.
It can be seen from
Figure 9 that the average reward of the designed training method in Algorithm 1 based on the STT method was higher than that of the direct training based on the TD3 algorithm. The designed training method in Algorithm 1 started to converge rapidly after 20,000 steps, and the final average reward was higher than that of the direct training. At the same time, it could be intuitively observed that the red UCAV did not learn the experience from zero after the scenario transfer. The experience in the previous scenario was inherited, as indicated in the arrow in
Figure 9, and the average reward in each scenario improved rapidly compared with the method of the TD3 algorithm in
Section 3.1.
In addition, since the complexity of the algorithm is strongly related to the iteration as well as the storage space and computational time, the faster the algorithm converges, the less computational time is required. The consumed times for the training of the two methods were also compared. The results showed that the training time of the method improved by STT was less, about 60% than that of the traditional TD3 algorithm, as shown in
Figure 10. The main reason for this phenomenon is that the min–max strategy of the blue UCAV consumed too much computing resources, while the training scenarios such as the simple scenario and transition scenario consumed little computing resources and could provide good training results.
As shown in the arrows in
Figure 9, the training scene transition was accompanied by a sharp change in the reward values. The average reward decreased sharply during the transition. Although the reward value recovered quickly after the transition, this discontinuity may have affected the stability of training.
To mitigate this problem, we proposed a ‘soft-update’ scenario optimization technique in this paper. In this method, the strategy of the blue UCAV in each scenario is probabilistically selected from a predefined strategy library instead of following the fixed strategy shown in Algorithm 1. In this way, the probability distribution for selecting the strategy is not constant; it changes during the training process and gradually becomes more inclined to complex scenarios as the training proceeds.
In the training phase including the first
Ns steps, the probabilities of choosing the first and second strategies in simple scenes are represented as
Pa and 1 −
Pa, respectively. In the transition phase, spanning from
Ns to
Nt steps, the probabilities of selecting the second and third strategies are denoted as
Pb and 1 −
Pb, respectively. Following the
Nt step, in the complex scene phase, the third strategy is consistently chosen until the
Nc step. The probability model for strategy selection in each scenario is articulated as follows:
where
s is the training step.
The algorithm’s efficacy can be enhanced in accordance with the definition delineated in Equation (15).
Figure 11 juxtaposes the training outcomes of various methodologies.
While the convergence criterion of the reward system may be altered by this strategy, employing distinct convergence rules at various stages of the learning process can facilitate a seamless transition and meet the convergence criteria. The training method, enhanced by scenario-transfer training and the soft update defined in Equation (15), outperformed other methods in terms of both the training speed and average reward. Furthermore, it is evident from
Table 5 that the convergence speed of the improved method surpassed that of the other methods. These results validate the effectiveness of the training method proposed in this paper.
5. Analysis of Optimal Maneuvering Strategy
The art of aerial combat is a delicate dance of strategy and execution, where basic fighter maneuvers (BFMs) form the bedrock of tactical mastery [
27]. This concept extends to the domain of UCAVs, where BFMs are categorized into two types: primary maneuvers, which are executed independently of an adversary such as accelerations and climbs; and relative maneuvers, which are performed with respect to an opposing aircraft. This academic endeavor is dedicated to unraveling the optimal strategy for maneuver decision-making within the context of relative maneuvers.
The core objective of this research was to delve into the subtleties of relative maneuvers, with a particular emphasis on studying the “red” UCAV’s optimal strategies for engaging with the “blue” UCAV across various UCAV air combat scenarios. We were particularly intrigued by the quantification of the changes in reward, state, and control quantities for both the red and blue UCAVs under optimal maneuvering conditions.
A hallmark of air combat maneuvers is the finite number of possible initial conditions, with the nose-to-nose turn serving as a quintessential tactical maneuver. The pivotal question that arises is one that even seasoned fighter pilots grapple with: “In a nose-to-nose turn, should one execute a dive loop or a climbing loop to ensure the most advantageous firing angle?” This study sought to unravel this enigma by analyzing the state of nose-to-nose turns during aerial engagements.
Subsequent content will delve into four critical scenarios (equal advantage, height advantage, height disadvantage, and lateral difference) to analyze the optimal maneuvers determined by machine learning algorithms for two UCAVs with identical flight performance meeting head-on. These four scenarios will serve as foundational blocks for more complex scenarios, enabling a comprehensive understanding of the decision-making process of the algorithm from multiple perspectives.
Following this, we will juxtapose these maneuvers with those recommended by fighter pilots, assessing the similarity of flight trajectories and the reasonableness of the machine learning-derived maneuvers. The ultimate goal is to evaluate their practical applicability in real-world scenarios. This paper introduces a novel methodology for studying UCAV air combat theory, which holds the potential to underpin the rapid generation of air combat decision-making.
5.1. Introduction to “Nose-to-Nose Turn”
The most classic tactical maneuver in one-versus-one maneuvering is the nose-to-nose turn, in which the red and blue UCAVs are roughly evenly matched, with the same energy status and opposite speed directions approaching each other. For such a state, the experience of a manned fighter pilot is to make a descending turn after spotting the opposing fighter and before entering the weapon firing range, converting altitude to angular advantage rather than wasting extra speed.
Figure 12 depicts how this tactic is used. At time “T
1”, the two fighters meet head-on at nearly the same altitude and speed. During the battle, the fighter’s energy is always valuable and challenging to obtain, so both pilots should try to gain as much energy as possible at this moment. The red UCAV should climb at the maximum rate of energy gain and run the engines at full power to gain energy as soon as possible. As the red UCAV pulls up to corner point speed, it changes to level flight and makes a sharp turn to the right at time “T
2” to gain additional flight-path separation in the lateral direction. As the target approaches, the red fighter reverses its direction and begins an offensive lead turn facing the opponent, forcing the opponent to fly past the attacker at time “T
3” to eliminate the flight-path separation and achieve a defense against this attack. Accordingly, the red UCAV changes turn direction at time “T
3” and cuts to the inside of the target aircraft that is making a horizontal turn. At time “T
4”, it changes turn direction and leads the turn, converting the resulting flight-path separation into an angular advantage. This tactic by the red UCAV will prompt the opponent to respond with a downturn so that the fighter can continue to turn low without an excessive loss of altitude relative to the target.
5.2. Initial Conditions with Equal Advantages
Based on the introduction in
Section 5.1, we first simulated the nose-to-nose turn under ideal equilibrium (i.e., assuming that the UCAVs are of the same height and fly along a straight line relative to each other) and observed the coping strategy based on the method proposed in this paper. The initial states of the red and blue UCAVs are shown in
Table 5.
Figure 13 shows the optimal maneuvering strategy of the nose-to-nose turn obtained by the red UCAV based on the TD3 algorithm in the case of
Table 5, where
Figure 13a is the optimal maneuver trajectory diagram of the nose-to-nose turn based on the TD3 algorithm,
Figure 13b is the corresponding reward curve of the red and blue UCAVs,
Figure 13c is the speed change curve,
Figure 13d is the attitude angle change curve, and
Figure 13e is the corresponding control command value curve.
The confrontation between the red and blue UCAVs commenced at “T
1”, as depicted in
Figure 13a, with both UCAVs approaching head-on. As the distance between them diminished, the reward values for both parties decreased continuously, indicative of a shift from a non-threatening to a critical state, as modeled in
Figure 13b. As illustrated in
Figure 13c, each UCAV adopted a distinct strategy in response to the emerging threat. The red UCAV opted for deceleration, while the blue UCAV accelerated. Subsequently, at “T
2” and “T
3”, the blue UCAV increased its speed to execute a left turn, aiming to evade the red UCAV via velocity. Conversely, the red UCAV initiated a left turn to establish a posture conducive to executing a horizontal turn before turning right. This maneuvering created an appropriate arc along the trajectory, thereby increasing the lateral separation from the blue UCAV. By “T
3”, the red UCAV had accomplished its posture realignment, at which point a discrepancy in the reward functions of the red and blue UCAVs became apparent. During “T
3–T
5”, the red UCAV commenced acceleration to assume a pursuit stance, thereby narrowing the gap with the blue UCAV. As observed in
Figure 13b, the cumulative reward values of the red and blue UCAVs exhibited a diverging trend. By “T
5–T
6”, the red UCAV had achieved a stable angular superiority over the blue UCAV. As the distance closed, the red UCAV secured a stable firing range and angle after regulating its speed. The discrepancy in reward values began to show a directional shift, indicating the red UCAV’s dominant position. Post “T
6”, the red UCAV was in the phase of selecting the optimal moment to initiate an attack on the blue UCAV. The differing strategies of the red and blue UCAVs were further elucidated by the variations in the attitude angle and control command depicted in
Figure 13d,e. At “T
1”, the red UCAV initiated a roll angle command to adjust its attitude first, while the blue UCAV triggered a tangential acceleration command to surge toward the red UCAV before attempting an evasive left turn.
A comparison between
Figure 12 and
Figure 13a revealed a high degree of similarity between the optimal maneuver of a nose-to-nose turn derived from the enhanced TD3 algorithm and the optimal maneuver mode informed by combat experience. Both approaches advocated for the blue UCAV to enter an accelerated left turn state in the initial phase, while the red UCAV should initially adjust its attitude, execute a horizontal turn with a small turning radius, extend the lateral distance to gain an angular advantage, and subsequently reduce the distance to the blue UCAV via acceleration. This sequence could continuously augment the angular advantage against the blue UCAV, culminating in a stable firing advantage. This comparison also underscores that the established UCAV chase model adeptly reflected the “dogfight” dynamics in aerial combat and yielded the optimal maneuver for the red UCAV against the blue UCAV. The analysis presented herein addresses the query posed at the outset of this section: “In a head-on turn, should one execute a dive loop or a climbing loop to secure the most advantageous firing angle?” The results provided by the improved TD3 algorithm suggest that, under optimal equilibrium, the optimal maneuver is neither a dive loop nor a climbing loop, but rather a “horizontal loop.” In this scenario, the red UCAV can achieve attitude adjustment with minimal energy expenditure and secure an angular advantage.
5.3. Initial Conditions with Vertical Differences
Assuming that the red and blue UCAVs have different heights and fly along a straight line, we observed the red UCAV’s coping strategy based on the improved TD3 algorithm. We divided the cases with longitudinal differences into two types. The first as that the red side was higher than the blue side, so it had an energy advantage, which was defined as case 1. The other is that the red side was lower than the blue side. In this case, the blue side had an energy advantage, which was defined as case 2. The initial states of the red and blue UCAVs are shown in
Table 6.
5.3.1. Initial Conditions with Vertical Advantages
Figure 14 shows the optimal coping maneuver strategy of the nose-to-nose turn obtained by the red UCAV based on the improved TD3 algorithm under case 1 in
Table 6, where
Figure 14a is the optimal maneuver trajectory diagram of the nose-to-nose turn,
Figure 14b is the corresponding reward curve of the red and blue UCAVs,
Figure 14c is the speed change curve,
Figure 14d is the attitude angle change curve, and
Figure 14e is the corresponding control command value change curve.
It can be seen from
Figure 14a that the red and blue UCAVs began to fly nose-to-nose at time “T
1”. As the distance became closer, the reward values of both sides decreased, as shown in
Figure 14b. This trend was highly similar to that in
Figure 13b.
Figure 14c shows the speed change trend where the red UCAV decelerated first while the blue UCAV accelerated. Unlike the situation in
Figure 13, at times “T
2” and “T
4”, the blue UCAV accelerated to turn right and climbed upward. In contrast, the red UCAV first dived to shorten the distance with the blue UCAV and then adjusted the relative posture with the blue UCAV through the dive loop. At time “T
5”, the red side completed its posture adjustment, and the gap between the reward values of the red and blue sides expanded. At time “T
5–T
6”, the red side formed a stable angle advantage over the blue side. As the distance approached, the red side formed a stable shooting distance and angle against the blue side after adjusting its speed, thus the red side has occupied a dominant advantage. After “T
6”, the red side will choose the opportunity to fire and shoot the blue side. Comparing
Figure 12,
Figure 13a, and
Figure 14a, it can also be seen that when the red side has a height advantage, the optimal maneuver is a dive loop.
5.3.2. Initial Conditions with Vertical Disadvantage
Figure 15 shows the optimal coping maneuver strategy of a nose-to-nose turn obtained by the red UCAV based on the improved TD3 algorithm under case 2 in
Table 6, where
Figure 15a is the optimal maneuver trajectory diagram of the nose-to-nose turn,
Figure 15b is the corresponding reward curve of the red and blue UCAVs,
Figure 15c is the speed change curve,
Figure 15d is the attitude angle change curve, and
Figure 15e is the corresponding control command value change curve.
As illustrated in
Figure 15a, the blue UCAV initially possessed a substantial altitude advantage. This advantage granted it more flexibility to transition between potential and kinetic energy, thereby increasing its likelihood of achieving higher reward values at the outset. However, our algorithm inhibited the blue UCAV from fully capitalizing on this advantage. As the distance between the two aircraft diminished, the blue UCAV opted to accelerate into a rightward turn, while the red UCAV executed a subtle climbing cycle by turning right to modify its posture. Concurrently, as depicted in
Figure 15b, it is important to note that the reward value for both UCAV consistently decreased. This trend markedly deviated from the patterns observed in
Figure 13b and
Figure 14b. Following the initial engagement, the reward value of the blue drone surpassed that of the red drone, primarily due to its altitude advantage. After the red drone completed its posture adjustment, the reward value of the blue UCAV experienced a rapid decline, and at time “T
4”, the reward values of the two aircraft began to invert. As shown in
Figure 15c, during the period “T
4–T
6”, the red drone persistently accelerated from
Vmin to
Vmax. This action narrowed the gap with the blue drone while maintaining an advantage in pursuit. By the time “T
7”, the red drone had successfully intercepted the blue drone and established a stable advantage.
Upon comparing
Figure 12, and
Figure 13a,
Figure 14a and
Figure 15a, it becomes evident that when the red side is at a height disadvantage, the most effective maneuvering strategies are climbing and looping. Despite the cumulative reward value of the red side not being high throughout the process, the initial height advantage held by the blue side was successfully negated through optimal maneuvering.
5.4. Initial Conditions with Lateral Differences
Finally, we analyzed the nose-to-nose turn with a lateral difference. Assuming that the red and blue UCAVs had the same height, flew along a relatively straight line, and had a distance difference in the lateral direction, we observed the red UCAV’s coping strategy based on the machine learning algorithm. Because the lateral difference was symmetrical, we assumed that the Y coordinate of the red side was positive and that of the blue side was negative. The lateral distance difference between the two sides was 400 m. The initial states of the red and blue UCAVs are shown in
Table 7.
Figure 16 shows the optimal coping maneuver strategy of a nose-to-nose turn obtained by the red UCAV based on the TD3 algorithm in the case of
Table 7, where
Figure 16a is the optimal maneuver trajectory diagram of nose-to-nose turn based on the improved TD3 algorithm,
Figure 16b is the corresponding reward curve of the red and blue UCAVs,
Figure 16c is the speed change curve,
Figure 16d is the attitude angle change curve, and
Figure 16e is the corresponding control command value change curve.
Figure 16a illustrates a scenario involving a lateral difference, where the red and blue UCAVs commenced a head-on approach at “T
1”. As the distance between them continued to close, the blue UCAV opted to execute a right turn for a climb, and concurrently, the red UCAV adjusted its flight attitude by also turning right to climb, mirroring the situation depicted in
Figure 13a. Between “T
4” and “T
5”, following the completion of attitude adjustment by the red UCAV, a stable angular advantage was established, and the discrepancy in reward values between the red and blue sides started to widen. Due to the lateral separation under the initial conditions, the relative distance between the red UCAV and the blue UCAV became relatively close after the right turn. Consequently, the red UCAV could maintain an appropriate firing distance from the blue UCAV while sustaining an angular advantage without the need for excessive acceleration. As depicted in
Figure 16c, in contrast to
Figure 13c,
Figure 14c and
Figure 15c, this is the first instance where the red UCAV initiated deceleration and speed adjustment without reaching
Vmax. This strategic maneuver allowed the red UCAV to lock onto the blue UCAV as early as “T
5” and establish a stable advantage.
Furthermore,
Figure 16a demonstrates that when the red side encountered a lateral difference, the optimal tactic was to follow the trajectory of the blue side, complete the posture adjustment with a subtle right climbing loop, and subsequently secure a lock on the blue UCAV by regulating its speed.
5.5. Summary
The present study systematically analyzed the optimal strategies for the red UCAV to respond to the blue UCAV in various tactical scenarios during a nose-to-nose turn. By comparing the results from
Figure 12,
Figure 13a,
Figure 14a,
Figure 15a, and
Figure 16a, we determined that the blue UCAV’s coping strategies were consistent with the classic nose-to-nose turn tactics, which involved accelerating the turn to evade the opponent. This consistency served as a crucial starting point for our further analysis.
Our research has also provided a sound answer to the pivotal question raised in
Section 5: “Should we perform a dive loop or a climbing loop to secure the most favorable firing angle during the nose-to-nose turn?” This question, which has historically been challenging for professional fighter pilots to resolve quickly, has now been addressed through the analysis of the strategies derived from our enhanced TD3 algorithm.
The strategies employed by the red UCAV were found to be closely related to the initial conditions of the engagement. The performance of our method varied across different scenarios, as evidenced by the distinct flight trajectories and reward value curves. The method’s sensitivity to changes in these conditions underscores its capability to accurately identify various tactical situations. Additionally, the trained agent’s proficiency in quickly recognizing and addressing its limitations through effective maneuvers was demonstrated.
In
Section 5.2, the experimental results indicate that when the red and blue sides were in an ideal balance, the optimal coping strategy for the red UCAV was a horizontal loop. This is a strategic choice that is not typically considered in ideal scenarios by pilots. In
Section 5.3, when the red side held a height advantage, the best strategy was to execute a dive loop, leveraging the height advantage to quickly adjust the posture as the opponent approached. Conversely, when the red side was at a height disadvantage, as outlined in
Section 5.3, the best strategy was to follow the blue UCAV with a climbing loop. In
Section 5.4, when there was a lateral difference between the red and blue sides, the red side had extra space to adjust the angle compared to the balanced state. Therefore, a significant turning radius climbing loop was used to modify its attitude.
When examining these scenarios collectively (
Figure 13c,
Figure 14c,
Figure 15c, and
Figure 16c), it became evident that the coping strategies of the red UCAV, as trained by our improved TD3 algorithm, maintained a consistent decision-making logic across different scenarios: first, adopting deceleration to adjust the attitude, and then, after obtaining the angular advantage, adjusting the distance with the blue UCAV through acceleration. This approach aligns with the experience of fighter pilots that “it is easier to change the angle than the speed”, which is a fundamental principle in the fighter community. This principle can be applied as a strategic framework for air combat and offers a valuable reference for the pilots’ air combat training.
6. Conclusions
This study has made significant advancements in the field of UCAV maneuver decision-making by leveraging deep reinforcement learning. The key contributions of this paper are as follows:
Firstly, we addressed the issue of slow convergence in the TD3 algorithm by introducing a novel “scenario-transfer training” approach. This method successfully accelerated the training process, reducing the convergence time by approximately 60%. This enhancement is crucial for practical applications where time efficiency is paramount.
Secondly, we conducted an in-depth analysis of the improved TD3 algorithm in the context of 1v1 air combat scenarios. Our analysis extended to the strategic decision-making process during the “nose-to-nose turn”, a critical maneuver in aerial combat. We also evaluated the optimal strategies for executing dive loops or climb loops to achieve the most advantageous firing angle. The strategies derived from the improved TD3 algorithm indicate a strong correlation with the initial state of the red UCAV. Importantly, the machine learning-generated optimal maneuvers aligned closely with the reference actions taken by experienced fighter pilots, affirming the reasonableness and practicality of the maneuvers produced by our algorithm.
Overall, this research not only provides a novel theoretical framework for UCAV air combat, but also offers substantial technical support for the rapid and effective generation of UCAV air combat decisions.
Future Work
While the current study has made substantial progress, it is not without its limitations, which also point to directions for future research.
Limitations:
The current model is primarily focused on 1v1 air combat scenarios. The complexity of multi-UCAV engagements and the decision-making under dynamic and uncertain environments have not been fully addressed.
The generalizability of the trained model may be limited by the scope of the training data and the diversity of the simulated combat scenarios.
The model overlooks some interference factors that may arise in real-world situations such as the duration of weapon effects and disturbances from external factors like electromagnetic interference.
Future Work:
To broaden the application of our method, future research should extend to multi-UCAV cooperative combat, considering the intricacies of decision-making and coordination among multiple UCAVs.
Enhancing the model’s generalizability through transfer learning and domain adaptation techniques could enable it to handle a wider range of combat scenarios.
Efforts to optimize the computational efficiency of the algorithm are necessary to ensure its viability for real-time combat decision-making.
Investigating the integration of the deep reinforcement learning approach with other decision-making techniques, such as rule-based and optimization-based methods, could lead to a more robust and adaptable UCAV maneuver decision-making system.
Addressing the challenges of hardware deployment is crucial. This includes advancing the integration of the algorithm into physical systems, refining experimental models, and establishing robust test environments, with the aim of validating the algorithm’s performance in real-world settings.
In conclusion, this study has laid the groundwork for further advancements in UCAV air combat theory and decision-making. The proposed method holds promise for transforming the way UCAVs engage in aerial combat, and continued research in this area will be essential for the development of future UCAV technologies and air combat strategies.