Autonomous Vehicles Traversability Mapping Fusing Semantic–Geometric in Off-Road Navigation
Abstract
1. Introduction
2. Related Work
2.1. Traversability Assessment
2.2. Off-Road Autonomous Navigation
3. Method and Implementation
3.1. Traversability Semantic Mapping
3.2. Traversability Geometric Assessment
3.3. Traversability Mapping
3.4. Motion Planning
3.5. Path Following
4. Experimental Setup
4.1. Terrain Traversability Evaluation
4.2. Outdoor Navigation
- Success Rate: The proportion of trials in which the autonomous vehicle successfully traveled to its target without failing or colliding with obstacles.
- Trajectory Roughness: The total of all vertical motion gradients encountered by the autonomous vehicle through its trajectory.
- Normalized Trajectory Length: The ratio of the length of the navigation trajectory to the linear distance between the autonomous vehicle and the target point for all successful experiments.
- Trajectories Selection: The ratio of the distance traveled by the autonomous vehicle on the most efficiently traversable surface to the total planned trajectory length.
- Mean Velocity: The autonomous vehicle’s mean velocity while traversing various surfaces along the planned path.
4.3. Comparision and Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An Efficient Probabilistic 3D Mapping Framework Based on Octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Fankhauser, P.; Bloesch, M.; Gehring, C.; Hutter, M.; Siegwart, R. Robot-centric Elevation Mapping with Uncertainty Estimates. In Mobile Service Robotics; World Scientific: Poznań, Poland, 2014; pp. 433–440. [Google Scholar] [CrossRef]
- Ahtiainen, J.; Stoyanov, T.; Saarinen, J. Normal Distributions Transform Traversability Maps: LIDAR-Only Approach for Traversability Mapping in Outdoor Environments. J. Field Robot. 2017, 34, 600–621. [Google Scholar] [CrossRef]
- Zhang, B.; Li, G.; Zheng, Q.; Bai, X.; Ding, Y.; Khan, A. Path Planning for Wheeled Mobile Robot in Partially Known Uneven Terrain. Sensors 2022, 22, 5217. [Google Scholar] [CrossRef] [PubMed]
- Angelova, A.; Matthies, L.; Helmick, D.; Perona, P. Fast Terrain Classification Using Variable-Length Representation for Autonomous Navigation. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Los Alamitos, CA, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef]
- Filitchkin, P.; Byl, K. Feature-based Terrain Classification for LittleDog. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 1387–1392. [Google Scholar] [CrossRef]
- Saucedo, M.A.; Patel, A.; Kanellakis, C.; Nikolakopoulos, G. Memory Enabled Segmentation of Terrain for Traversability Based Reactive Navigation. In Proceedings of the 2023 IEEE International Conference on Robotics and Biomimetics (ROBIO), Koh Samui, Thailand, 4–9 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, B.; Zhao, X.; Zhao, H. An Active and Contrastive Learning Framework for Fine-Grained Off-Road Semantic Segmentation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 564–579. [Google Scholar] [CrossRef]
- Schilling, F.; Chen, X.; Folkesson, J.; Jensfelt, P. Geometric and Visual Terrain Classification for Autonomous Mobile Navigation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 2678–2684. [Google Scholar] [CrossRef]
- Weerakoon, K.M.K.; Sathyamoorthy, A.J.; Patel, U.; Manocha, D. TERP: Reliable Planning in Uneven Outdoor Environments Using Deep Reinforcement Learning. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 9447–9453. [Google Scholar] [CrossRef]
- Ewen, P.; Li, A.; Chen, Y.; Hong, S.; Vasudevan, R. These Maps are Made for Walking: Real-Time Terrain Property Estimation for Mobile Robots. IEEE Robot. Autom. Lett. 2022, 7, 7083–7090. [Google Scholar] [CrossRef]
- Ewen, P.; Chen, H.; Chen, Y.; Li, A.; Bagali, A.; Gunjal, G.; Vasudevan, R. You’ve Got to Feel It to Believe It: Multi-Modal Bayesian Inference for Semantic and Property Prediction. arXiv 2024, arXiv:2402.05872. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, November 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Alshawi, R.; Hoque, T.; Flanagin, M.C. A Depth-Wise Separable U-Net Architecture with Multiscale Filters to Detect Sinkholes. Remote Sens. 2023, 15, 1384. [Google Scholar] [CrossRef]
- Wellhausen, L.; Dosovitskiy, A.; Ranftl, R.; Walas, K.; Cadena, C.; Hutter, M. Where Should I Walk? Predicting Terrain Properties from Images via Self-supervised Learning. IEEE Robot. Autom. Lett. 2019, 4, 1509–1516. [Google Scholar] [CrossRef]
- Sathyamoorthy, A.J.; Weerakoon, K.M.K.; Guan, T.; Liang, J.; Manocha, D. TerraPN: Unstructured Terrain Navigation using Online Self-Supervised Learning. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 7197–7204. [Google Scholar] [CrossRef]
- Wermelinger, M.; Fankhauser, P.; Diethelm, R.; Krüsi, P.; Siegwart, R.Y.; Hutter, M. Navigation Planning for Legged Robots in Challenging Terrain. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1184–1189. [Google Scholar] [CrossRef]
- Krusi, P.; Furgale, P.; Bosse, M.; Siegwart, R. Driving on Point Clouds: Motion Planning, Trajectory Optimization, and Terrain Assessment in Generic Nonplanar Environments. J. Field Robot. 2017, 34, 940–984. [Google Scholar] [CrossRef]
- Dixit, A.; Fan, D.D.; Otsu, K.; Dey, S.; Agha-Mohammadi, A.A.; Burdick, J.W. STEP: Stochastic Traversability Evaluation and Planning for Risk-Aware off-road Navigation; Results from the DARPA Subterranean Challenge. arXiv 2023, arXiv:2303.01614. [Google Scholar] [CrossRef]
- Chavez-Garcia, R.O.; Guzzi, J.; Gambardella, L.M.; Giusti, A. Learning Ground Traversability from Simulations. IEEE Robot. Autom. Lett. 2018, 3, 1695–1702. [Google Scholar] [CrossRef]
- Wellhausen, L.; Hutter, M. ArtPlanner: Robust Legged Robot Navigation in the Field. Field Robot. 2023, 3, 413–434. [Google Scholar] [CrossRef]
- Bozkurt, S.; Atik, M.E.; Duran, Z. Improving Aerial Targeting Precision: A Study on Point Cloud Semantic Segmentation with Advanced Deep Learning Algorithms. Drones 2024, 8, 376. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on point sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar] [CrossRef]
- Guan, T.; He, Z.; Song, R.; Manocha, D.; Zhang, L. TNS: Terrain Traversability Mapping and Navigation System for Autonomous Excavators. In Proceedings of the Robotics: Science and Systems XVIII, New York, NY, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Siva, S.; Wigness, M.B.; Rogers, J.G. Robot Adaptation to Unstructured Terrains by Joint Representation and Apprenticeship Learning. In Proceedings of the Robotics: Science and Systems XV, Freiburg im Breisgau, Germany, 22–26 June 2019. [Google Scholar] [CrossRef]
- Kahn, G.; Abbeel, P.; Levine, S. LaND: Learning to Navigate from Disengagements. IEEE Robot. Autom. Lett. 2021, 6, 1872–1879. [Google Scholar] [CrossRef]
- Gregory, K.; Pieter, A.; Sergey, L. Badgr: An autonomous Self-supervised Learning-Based Navigation System. IEEE Robot. Autom. Lett. 2021, 6, 1312–1319. [Google Scholar] [CrossRef]
- Shan, T.; Wang, J.; Englot, B.; Doherty, K.A.J. Bayesian Generalized Kernel Inference for Terrain Traversability Mapping. In Proceedings of the Conference on Robot Learning, PMLR, Zürich, Switzerland, 29–31 October 2018; pp. 829–838. [Google Scholar]
- Vega-Brown, W.; Doniec, M.; Roy, N. Nonparametric Bayesian Inference on Multivariate Exponential Families. Adv. Neural Inf. Process. Syst. 2014, 27, 2546–2554. [Google Scholar] [CrossRef]
- Bellone, M.; Messina, A.; Reina, G. A New Approach for Terrain Analysis in Mobile Robot Applications. In Proceedings of the 2013 IEEE International Conference on Mechatronics (ICM), Vicenza, Italy, 27 February–1 March 2013; pp. 225–230. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal Sampling-based Path Planning Focused via Direct Sampling of an Admissible Ellipsoidal Heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar] [CrossRef]
- Scout-2.0. Available online: https://iqr-robot.com/product/agilex-scout-2-0/ (accessed on 17 August 2024).
- Wei, X.; Yixi, C.; Dongjiao, H.; Jiarong, L.; Fu, Z. Fast-lio2: Fast Direct Lidar-inertial Odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Guan, T.; Kothandaraman, D.; Chandra, R.; Sathyamoorthy, A.J.; Weerakoon, K.; Manocha, D. GA-Nav: Efficient Terrain Segmentation for Robot Navigation in Unstructured Outdoor Environments. IEEE Robot. Autom. Lett. 2022, 7, 8138–8145. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The Dynamic Window Approach to Collision Avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Jian, Z.; Lu, Z.R.; Zhou, X.; Lan, B.; Xiao, A.; Wang, X.; Liang, B. PUTN: A Plane-fitting Based Uneven Terrain Navigation Framework. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Shanghai, China, 23–27 October 2022; pp. 7160–7166. [Google Scholar] [CrossRef]
- Chen, D.; Zhuang, M.; Zhong, X.; Wu, W.; Liu, Q. RSPMP: Real-time Semantic Perception and Motion Planning for Autonomous Navigation of Unmanned Ground vehicle in off-road environments. Appl. Intell. 2023, 53, 4979–4995. [Google Scholar] [CrossRef]



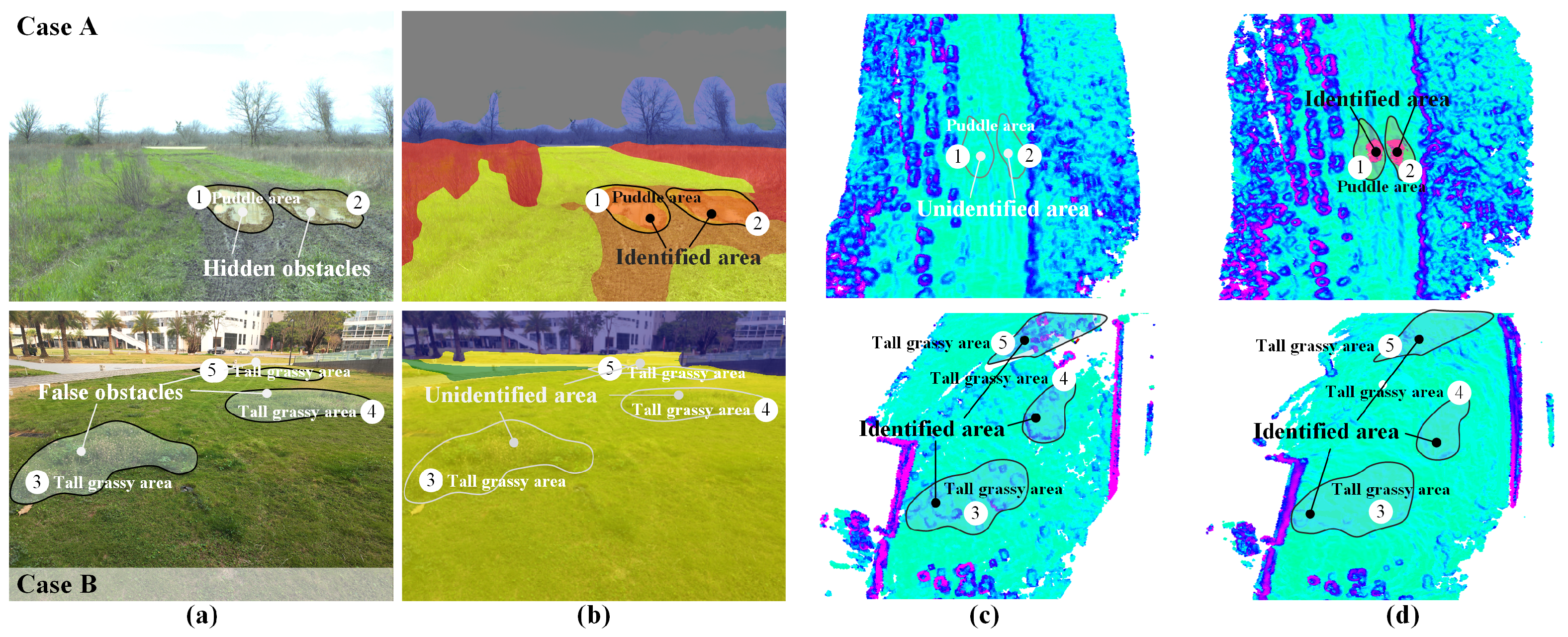
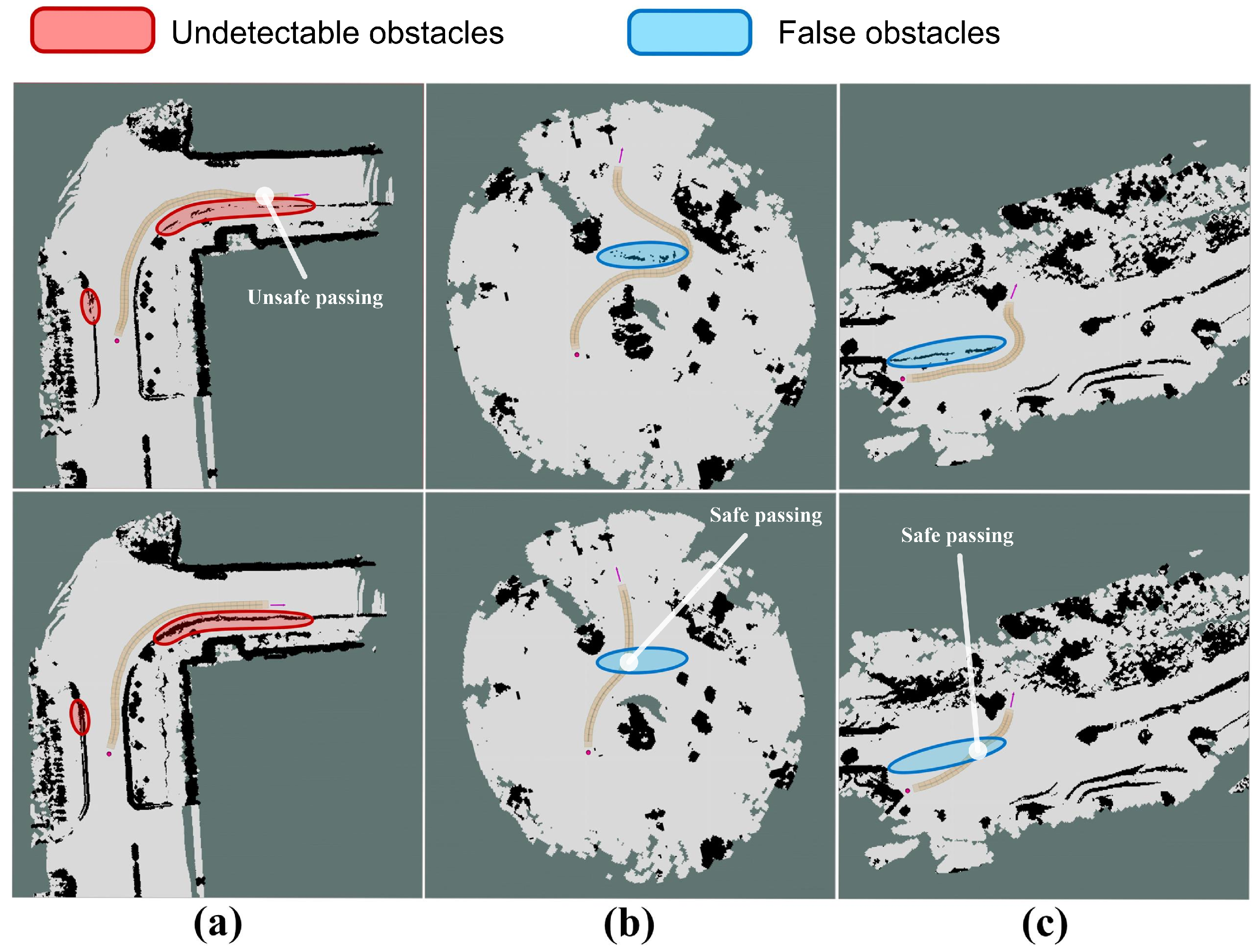

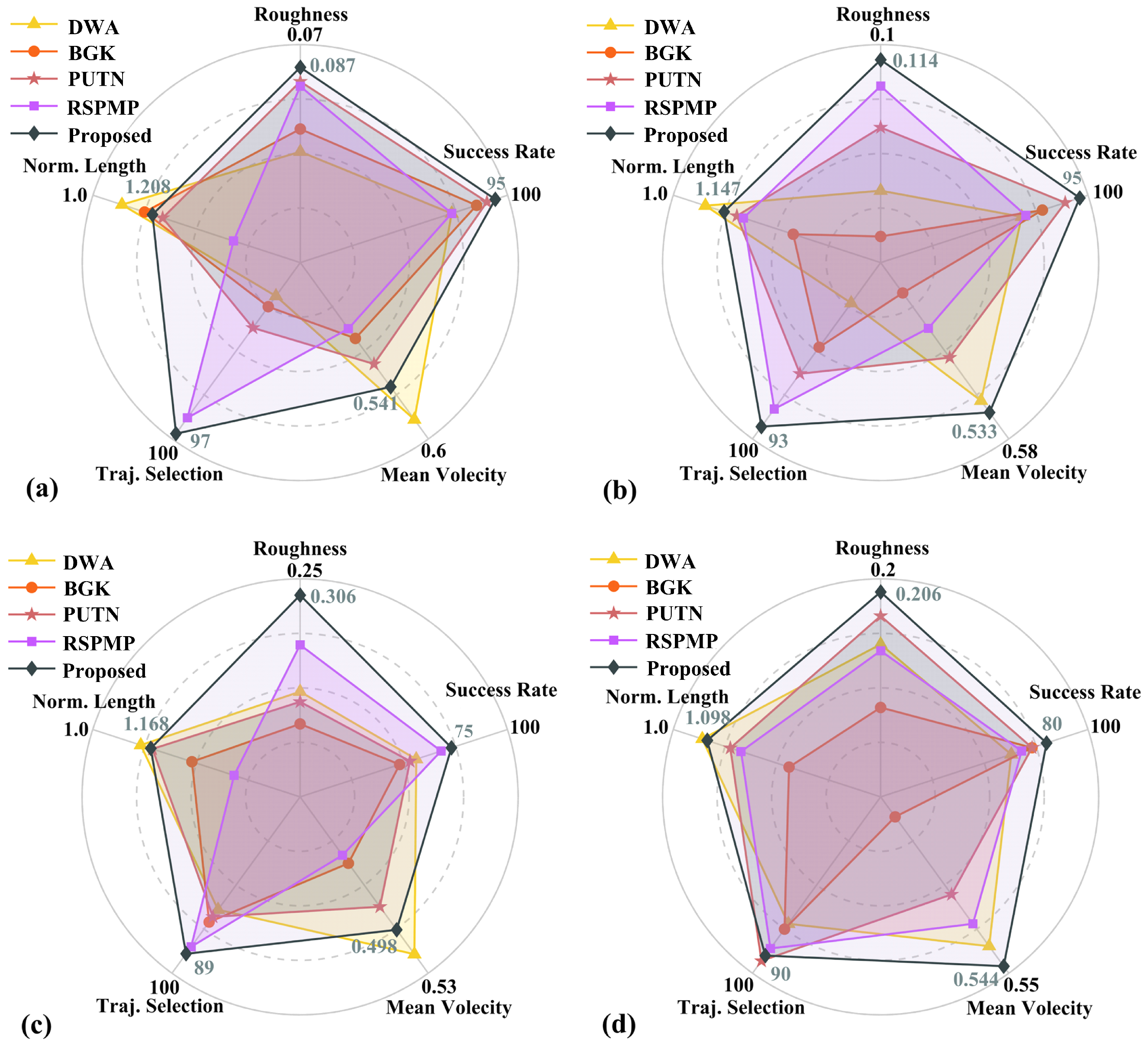
| Metrics | Method | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|---|
| Success Rate (%) | DWA | 75 | 70 | 55 | 65 |
| BGK | 85 | 80 | 50 | 75 | |
| PUTN | 90 | 90 | 55 | 75 | |
| RSPMP | 75 | 70 | 70 | 70 | |
| Proposed | 95 | 95 | 75 | 80 | |
| Traj. Roughness | DWA | 0.183 | 0.234 | 0.638 | 0.230 |
| BGK | 0.159 | 0.276 | 0.749 | 0.259 | |
| PUTN | 0.139 | 0.176 | 0.673 | 0.217 | |
| RSPMP | 0.114 | 0.138 | 0.477 | 0.233 | |
| Proposed | 0.087 | 0.114 | 0.306 | 0.206 | |
| Norm. Traj. Length | DWA | 1.127 | 1.093 | 1.139 | 1.084 |
| BGK | 1.187 | 1.347 | 1.287 | 1.335 | |
| PUTN | 1.235 | 1.184 | 1.173 | 1.165 | |
| RSPMP | 1.423 | 1.203 | 1.409 | 1.196 | |
| Proposed | 1.208 | 1.147 | 1.168 | 1.098 | |
| Traj. Selection (%) | DWA | 19 | 23 | 64 | 72 |
| BGK | 25 | 48 | 71 | 75 | |
| PUTN | 37 | 63 | 68 | 93 | |
| RSPMP | 88 | 83 | 85 | 86 | |
| Proposed | 97 | 93 | 89 | 90 | |
| Mean Velocity | DWA | 0.578 | 0.541 | 0.516 | 0.527 |
| BGK | 0.486 | 0.431 | 0.449 | 0.417 | |
| PUTN | 0.515 | 0.497 | 0.481 | 0.483 | |
| RSPMP | 0.475 | 0.467 | 0.443 | 0.508 | |
| Proposed | 0.541 | 0.553 | 0.498 | 0.544 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Chen, W.; Xu, C.; Qiu, J.; Chen, S. Autonomous Vehicles Traversability Mapping Fusing Semantic–Geometric in Off-Road Navigation. Drones 2024, 8, 496. https://doi.org/10.3390/drones8090496
Zhang B, Chen W, Xu C, Qiu J, Chen S. Autonomous Vehicles Traversability Mapping Fusing Semantic–Geometric in Off-Road Navigation. Drones. 2024; 8(9):496. https://doi.org/10.3390/drones8090496
Chicago/Turabian StyleZhang, Bo, Weili Chen, Chaoming Xu, Jinshi Qiu, and Shiyu Chen. 2024. "Autonomous Vehicles Traversability Mapping Fusing Semantic–Geometric in Off-Road Navigation" Drones 8, no. 9: 496. https://doi.org/10.3390/drones8090496
APA StyleZhang, B., Chen, W., Xu, C., Qiu, J., & Chen, S. (2024). Autonomous Vehicles Traversability Mapping Fusing Semantic–Geometric in Off-Road Navigation. Drones, 8(9), 496. https://doi.org/10.3390/drones8090496







