Risk Assessment and Motion Planning for MAVs in Dynamic Uncertain Environments
Abstract
1. Introduction
- A rational and efficient risk definition. Our approach accounts for MAV dynamics, leading to the creation of a rational risk assessment potential field. This field is finely tuned to align with the MAV’s preferred motion magnitude and direction, ensuring that the risk assessment is sensitive to the vehicle’s operational characteristics and navigational intent.
- A dynamic risk-aware MAV motion planning method in dynamic uncertain environments. In this paper, we propose an approach to motion planning for MAVs that considers a comprehensive set of risk factors. Our method focuses on increasing the safety of MAV flights by generating collision-free paths and reducing flight distances, while also incorporating risk assessment into the planning phase to account for varying levels of risk.
2. Related Work
2.1. Risk Assessment
2.2. Risk-Aware Motion Planning
3. Preliminaries
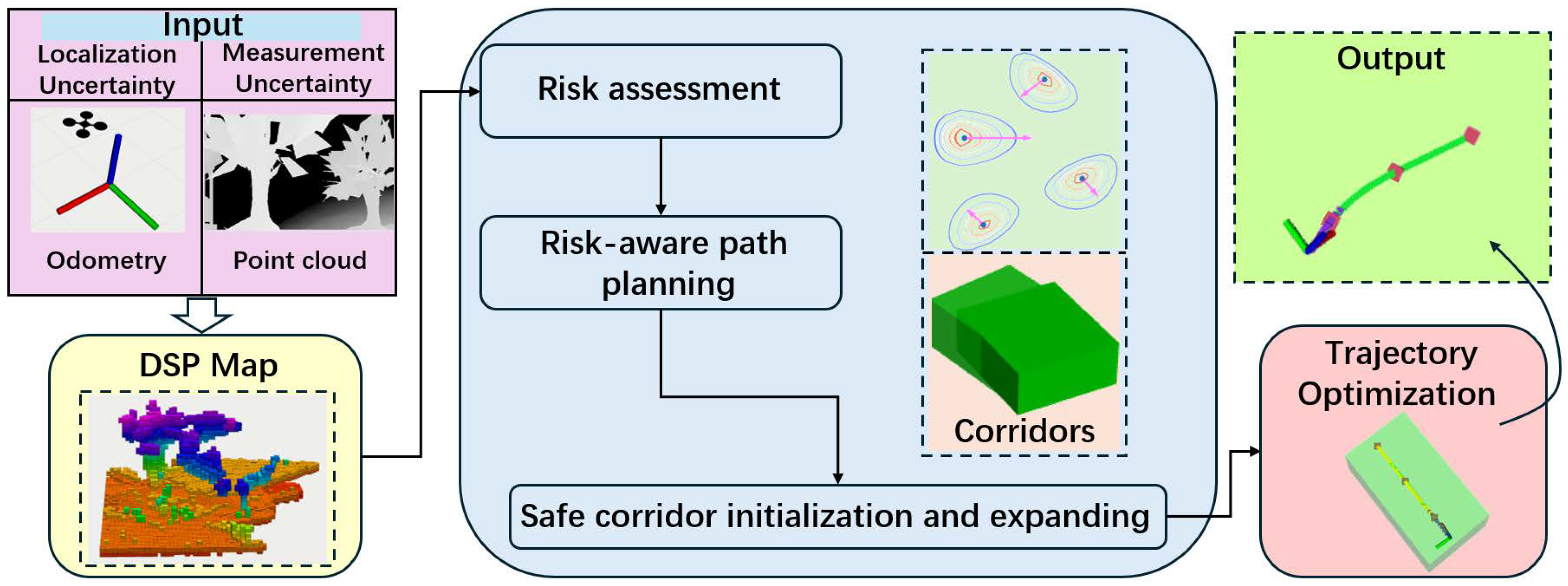
4. Methodology
4.1. System Overview
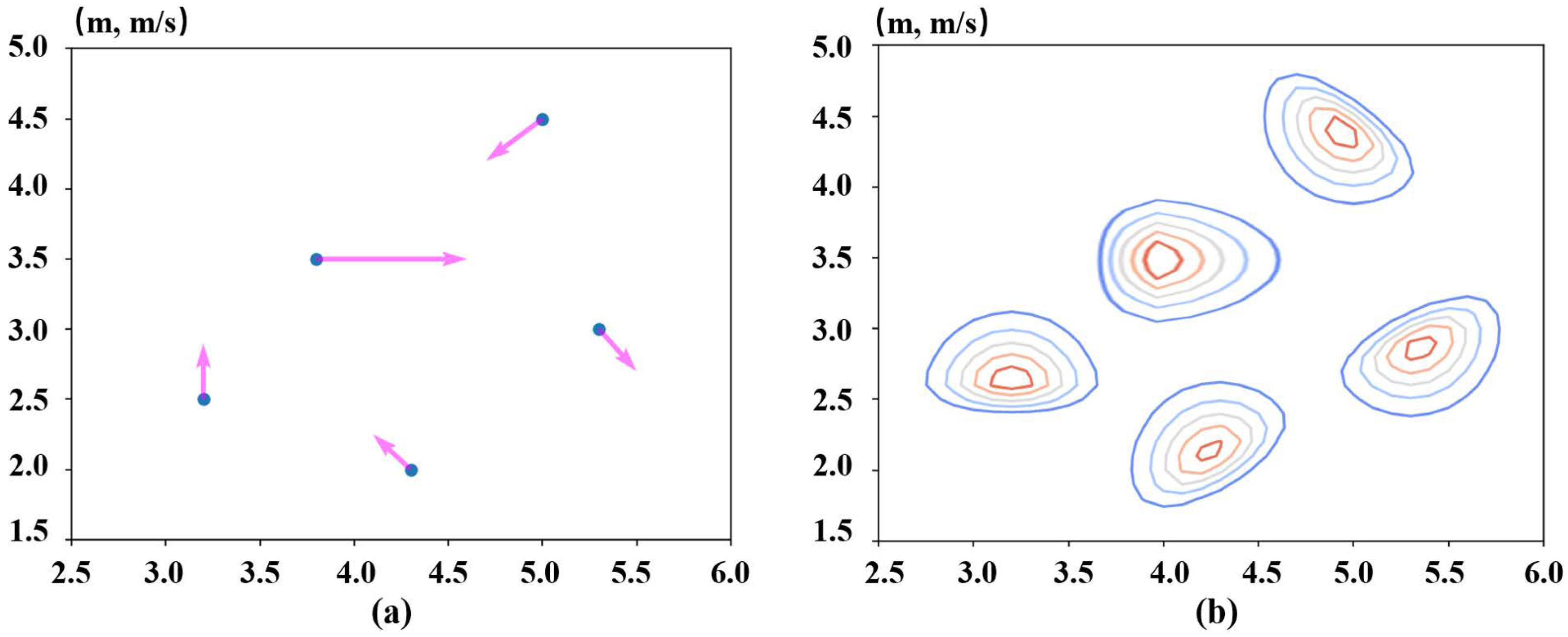
4.2. Occupancy Risk Cost
4.3. Risk Definition
4.4. Risk-Aware Path Planning
4.5. Safety Corridor Generation and Trajectory Optimization
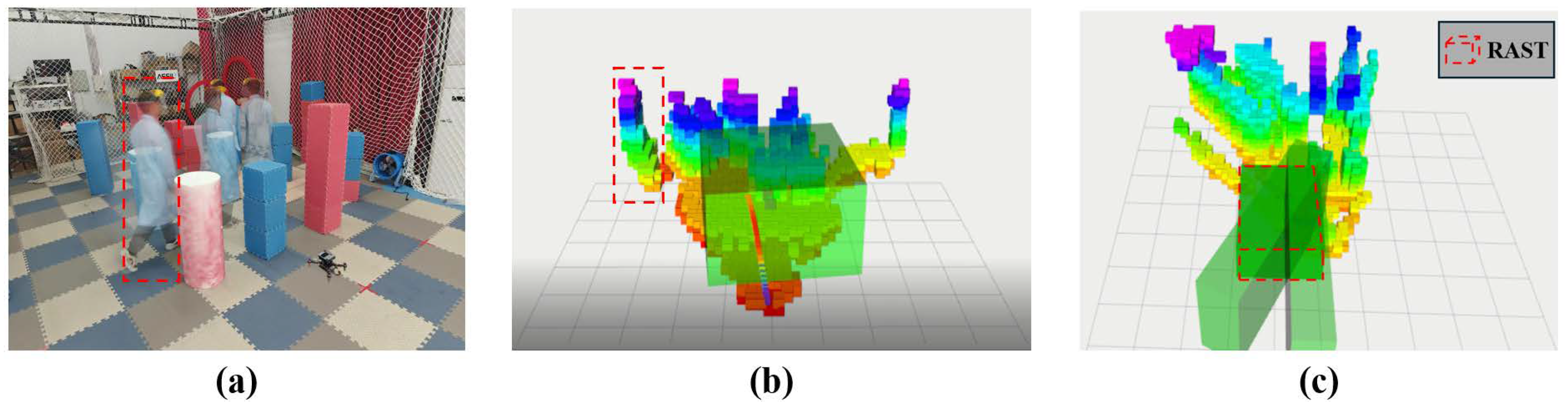
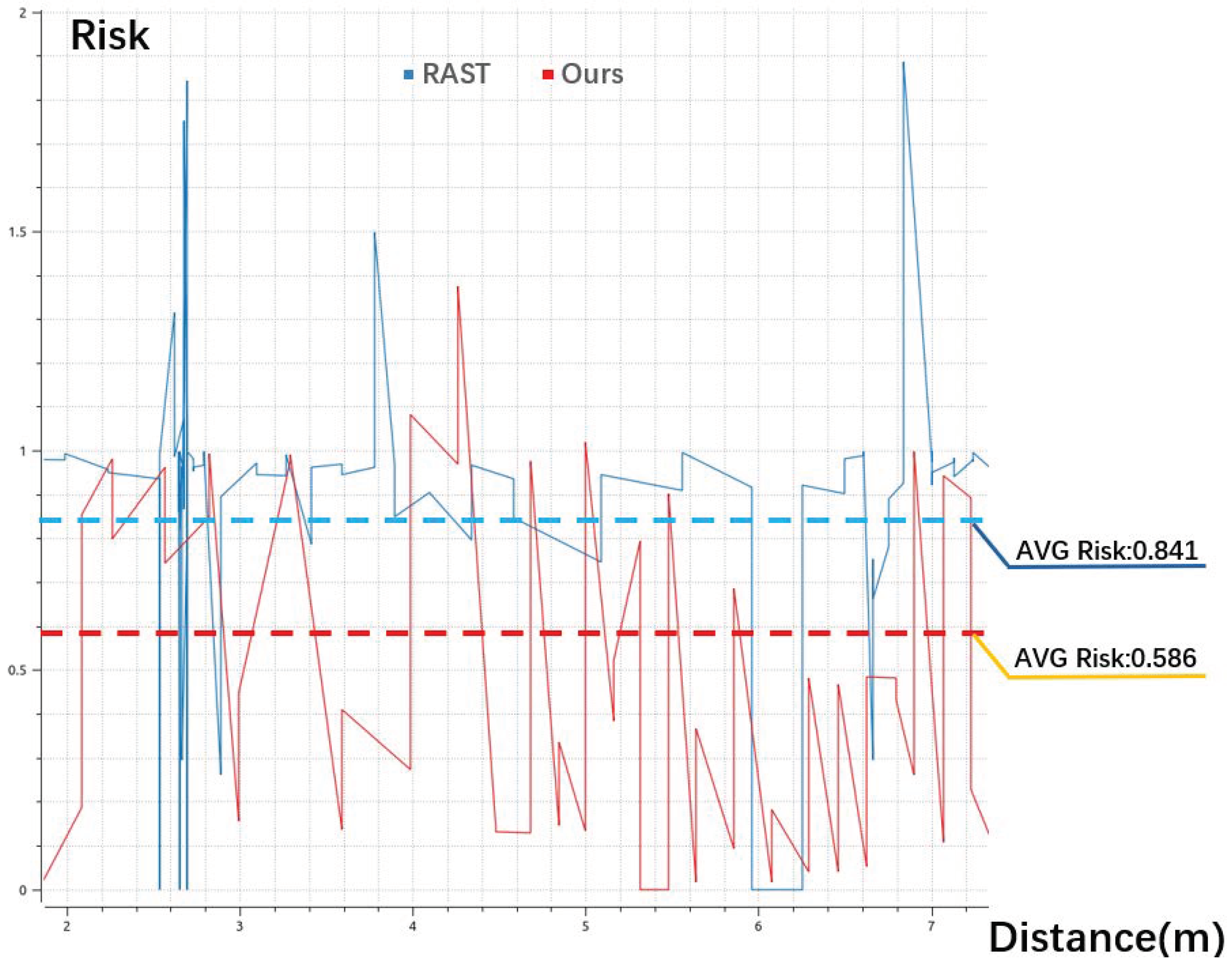
5. Results
5.1. Simulation Tests
5.2. Real-World Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oleynikova, H.; Lanegger, C.; Taylor, Z.; Pantic, M.; Millane, A.; Siegwart, R.; Nieto, J. An open-source system for vision-based micro-aerial vehicle mapping, planning, and flight in cluttered environments. J. Field Robot. 2020, 37, 642–666. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, H.; Alonso-Mora, J. Robust Vision-based Obstacle Avoidance for Micro Aerial Vehicles in Dynamic Environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2682–2688. [Google Scholar] [CrossRef]
- Tordesillas, J.; How, J.P. MADER: Trajectory Planner in Multiagent and Dynamic Environments. IEEE Trans. Robot. 2022, 38, 463–476. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Pumarola, A.; Vakhitov, A.; Agudo, A.; Sanfeliu, A.; Moreno-Noguer, F. PL-SLAM: Real-time monocular visual SLAM with points and lines. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4503–4508. [Google Scholar] [CrossRef]
- Jiang, R.; Yang, S.; Ge, S.S.; Wang, H.; Lee, T.H. Geometric Map-Assisted Localization for Mobile Robots Based on Uniform-Gaussian Distribution. IEEE Robot. Autom. Lett. 2017, 2, 789–795. [Google Scholar] [CrossRef]
- Konolige, K.; Marder-Eppstein, E.; Marthi, B. Navigation in hybrid metric-topological maps. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3041–3047. [Google Scholar] [CrossRef]
- Gunathillake, A.; Huang, H.; Savkin, A.V. Sensor-Network-Based Navigation of a Mobile Robot for Extremum Seeking Using a Topology Map. IEEE Trans. Ind. Inform. 2019, 15, 3962–3972. [Google Scholar] [CrossRef]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Fraichard, T. A Short Paper about Motion Safety. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1140–1145. [Google Scholar] [CrossRef]
- Tsiotras, P.; Bakolas, E. A hierarchical on-line path planning scheme using wavelets. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 2806–2812. [Google Scholar] [CrossRef]
- Dhawale, A.; Yang, X.; Michael, N. Reactive Collision Avoidance Using Real-Time Local Gaussian Mixture Model Maps. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3545–3550. [Google Scholar] [CrossRef]
- Bena, R.M.; Zhao, C.; Nguyen, Q. Safety-Aware Perception for Autonomous Collision Avoidance in Dynamic Environments. IEEE Robot. Autom. Lett. 2023, 8, 7962–7969. [Google Scholar] [CrossRef]
- Richter, C.; Vega-Brown, W.; Roy, N. Bayesian Learning for Safe High-Speed Navigation in Unknown Environments. In Robotics Research: Volume 2; Bicchi, A., Burgard, W., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 325–341. [Google Scholar] [CrossRef]
- Tordesillas, J.; How, J.P. Deep-PANTHER: Learning-Based Perception-Aware Trajectory Planner in Dynamic Environments. IEEE Robot. Autom. Lett. 2023, 8, 1399–1406. [Google Scholar] [CrossRef]
- Chen, G.; Dong, W.; Peng, P.; Alonso-Mora, J.; Zhu, X. Continuous Occupancy Mapping in Dynamic Environments Using Particles. IEEE Trans. Robot. 2024, 40, 64–84. [Google Scholar] [CrossRef]
- Majumdar, A.; Pavone, M. How Should a Robot Assess Risk? Towards an Axiomatic Theory of Risk in Robotics. In Proceedings of the Robotics Research; Amato, N.M., Hager, G., Thomas, S., Torres-Torriti, M., Eds.; Springer: Cham, Switzerland, 2020; pp. 75–84. [Google Scholar]
- Şenbaşlar, B.; Sukhatme, G.S. Probabilistic Trajectory Planning for Static and Interaction-aware Dynamic Obstacle Avoidance. arXiv 2023, arXiv:2302.12873. [Google Scholar]
- Liu, T.; Zhang, F.; Gao, F.; Pan, J. Tight Collision Probability for UAV Motion Planning in Uncertain Environment. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 1055–1062. [Google Scholar] [CrossRef]
- Chen, G.; Wu, S.; Shi, M.; Dong, W.; Zhu, H.; Alonso-Mora, J. RAST: Risk-Aware Spatio-Temporal Safety Corridors for MAV Navigation in Dynamic Uncertain Environments. IEEE Robot. Autom. Lett. 2023, 8, 808–815. [Google Scholar] [CrossRef]
- Tordesillas, J.; Lopez, B.T.; Everett, M.; How, J.P. FASTER: Fast and Safe Trajectory Planner for Navigation in Unknown Environments. IEEE Trans. Robot. 2022, 38, 922–938. [Google Scholar] [CrossRef]
- Foehn, P.; Kaufmann, E.; Romero, A.; Penicka, R.; Sun, S.; Bauersfeld, L.; Laengle, T.; Cioffi, G.; Song, Y.; Loquercio, A.; et al. Agilicious: Open-source and open-hardware agile quadrotor for vision-based flight. Sci. Robot. 2022, 7, eabl6259. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, D.; Pinto, L.; Gupta, A. Learning to fly by crashing. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3948–3955. [Google Scholar] [CrossRef]
- Xie, Z.; Dames, P. DRL-VO: Learning to Navigate Through Crowded Dynamic Scenes Using Velocity Obstacles. IEEE Trans. Robot. 2023, 39, 2700–2719. [Google Scholar] [CrossRef]
- Yang, H.; Yao, C.; Liu, C.; Chen, Q. RMRL: Robot Navigation in Crowd Environments With Risk Map-Based Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2023, 8, 7930–7937. [Google Scholar] [CrossRef]
- Dharmadhikari, M.; Dang, T.; Solanka, L.; Loje, J.; Nguyen, H.; Khedekar, N.; Alexis, K. Motion Primitives-based Path Planning for Fast and Agile Exploration using Aerial Robots. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 179–185. [Google Scholar] [CrossRef]
- Lopez, B.T.; How, J.P. Aggressive 3-D collision avoidance for high-speed navigation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5759–5765. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. A computationally efficient algorithm for state-to-state quadrocopter trajectory generation and feasibility verification. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3480–3486. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar] [CrossRef]
- Primatesta, S.; Guglieri, G.; Rizzo, A. A Risk-Aware Path Planning Strategy for UAVs in Urban Environments. J. Intell. Robot. Syst. 2018, 95, 629–643. [Google Scholar] [CrossRef]
- Mahler, R.P.S. Statistical Multisource-Multitarget Information Fusion; Artech House, Inc.: London, UK, 2007. [Google Scholar]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multitarget filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar] [CrossRef]
- Pierson, A.; Schwarting, W.; Karaman, S.; Rus, D. Navigating Congested Environments with Risk Level Sets. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5712–5719. [Google Scholar] [CrossRef]
- Chen, J.; Liu, T.; Shen, S. Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1476–1483. [Google Scholar] [CrossRef]
- Helbing, D.; Molnár, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282–4286. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Wang, Z.; Ye, H.; Xu, C.; Gao, F. EGO-Planner: An ESDF-Free Gradient-Based Local Planner for Quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 478–485. [Google Scholar] [CrossRef]



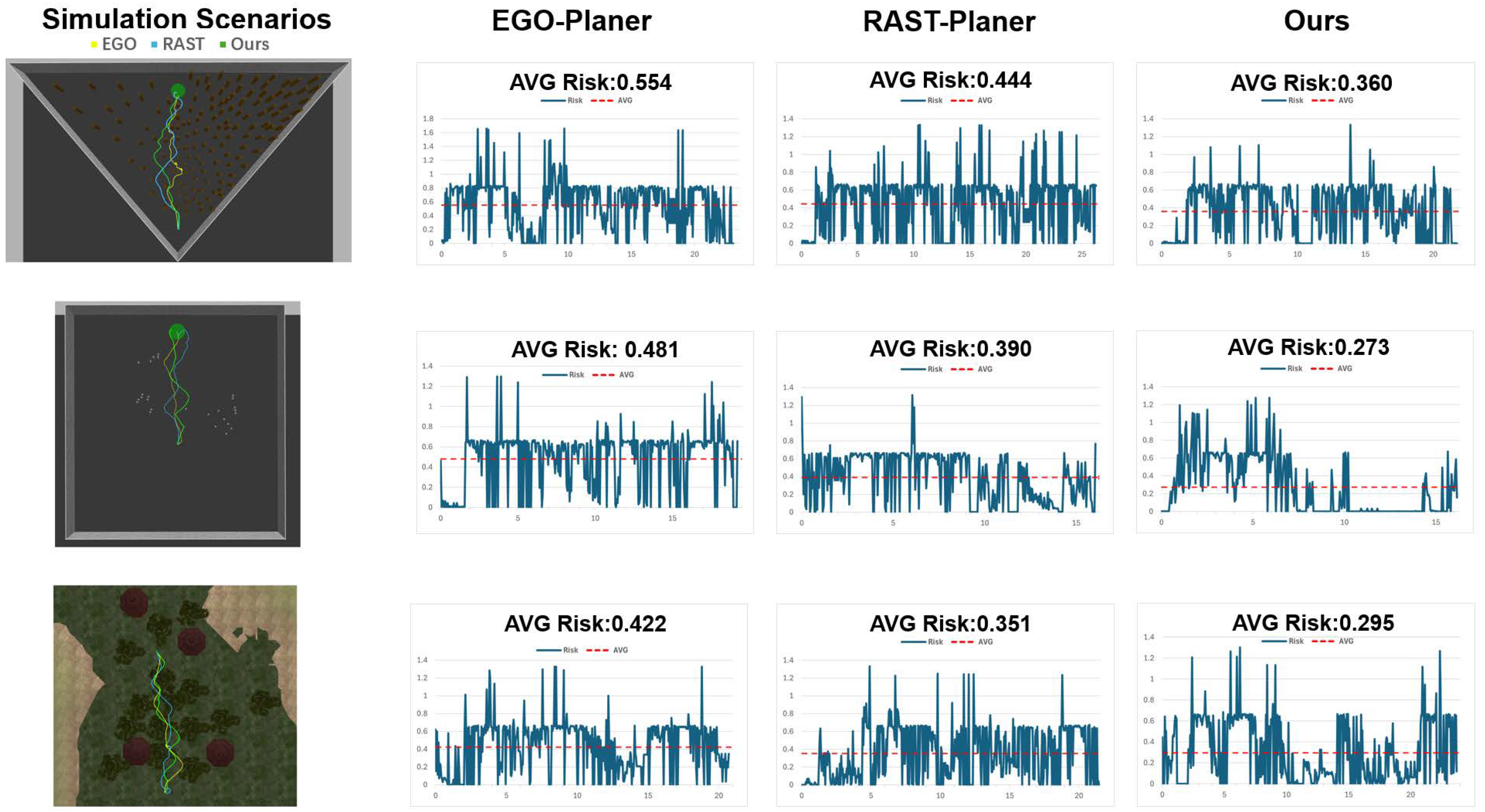

| Envir. | Method | Suss. Rate (%) | Travel Time (s) | Traj. Length (m) | AVG Risk |
|---|---|---|---|---|---|
| Static | EGO | 60.0 | 23.48 | 44.73 | 0.56 |
| RAST | 62.5 | 26.23 | 46.80 | 0.45 | |
| Ours | 75.0 | 21.74 | 49.12 | 0.35 | |
| Dynamic | EGO | 47.5 | 31.49 | 47.42 | 0.52 |
| RAST | 55.0 | 28.37 | 45.81 | 0.41 | |
| Ours | 62.5 | 29.50 | 48.23 | 0.27 | |
| Sim-world | EGO | 57.5 | 20.71 | 44.79 | 0.43 |
| RAST | 72.5 | 21.48 | 43.17 | 0.36 | |
| Ours | 80.0 | 23.70 | 46.26 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, X.; Zhu, H.; Zhu, X.; Yao, W. Risk Assessment and Motion Planning for MAVs in Dynamic Uncertain Environments. Drones 2024, 8, 497. https://doi.org/10.3390/drones8090497
Xia X, Zhu H, Zhu X, Yao W. Risk Assessment and Motion Planning for MAVs in Dynamic Uncertain Environments. Drones. 2024; 8(9):497. https://doi.org/10.3390/drones8090497
Chicago/Turabian StyleXia, Xingyu, Hai Zhu, Xiaozhou Zhu, and Wen Yao. 2024. "Risk Assessment and Motion Planning for MAVs in Dynamic Uncertain Environments" Drones 8, no. 9: 497. https://doi.org/10.3390/drones8090497
APA StyleXia, X., Zhu, H., Zhu, X., & Yao, W. (2024). Risk Assessment and Motion Planning for MAVs in Dynamic Uncertain Environments. Drones, 8(9), 497. https://doi.org/10.3390/drones8090497






