Cross-Correlation Characteristic Measurements and Analysis for Multi-Link A2G Channels Based on a Multi-UAV System
Abstract
1. Introduction
- A multi-link A2G channel model under urban scenarios is proposed. The channel impulse response (CIR) of each UAV-to-ground link is modeled as spatially variant. A cross-correlation function is adopted to represent the multi-link channel similarity between different spatial positions. And, expressions for the multi-link channel cross-correlation are derived.
- A multi-UAV cooperative channel measurement system is developed. In this system, an orthogonal channel measurement signal which can avoid cross-interference between multiple UAVs is specially designed. Some hardware processing algorithms are implemented in a field-programmable gate array (FPGA), which can benefit the accuracy of measurement and reduce the stress of data storage.
- Based on the measurement system, a multi-UAV cooperative channel measurement campaign was conducted on a campus at the 3.6 GHz frequency band, and a large number of measurement data were obtained. Based on the measurement data, we analyze the large-scale channel characteristics and the cross-correlation characteristics of channel parameters. The analysis will provide a reference for the design of multi-UAV cooperative communication systems.
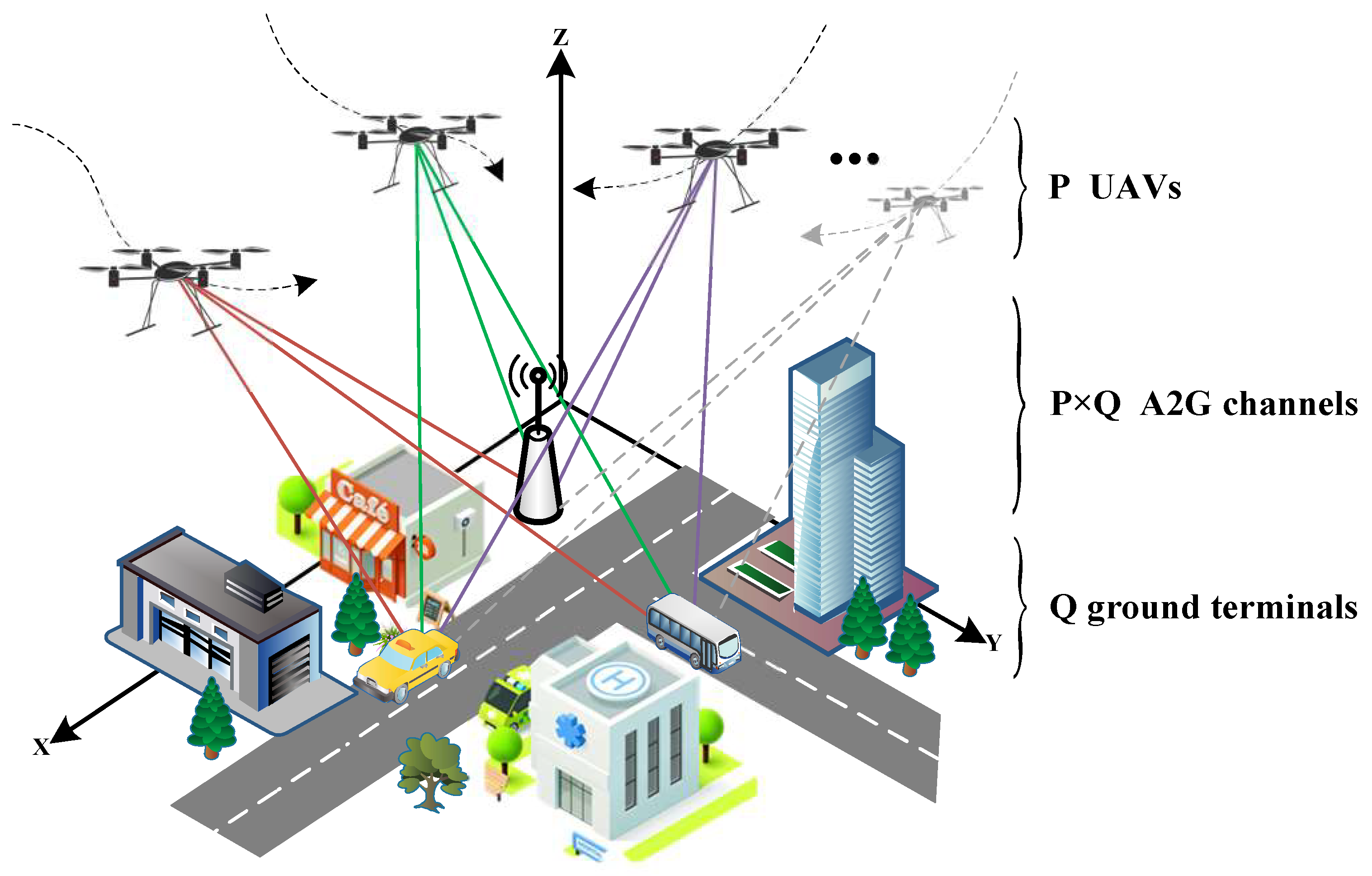
2. Multi-Link A2G Channels
3. Multi-UAV Based A2G Channel Measurement System
3.1. Multi-UAV Based Channel Measurement Scheme
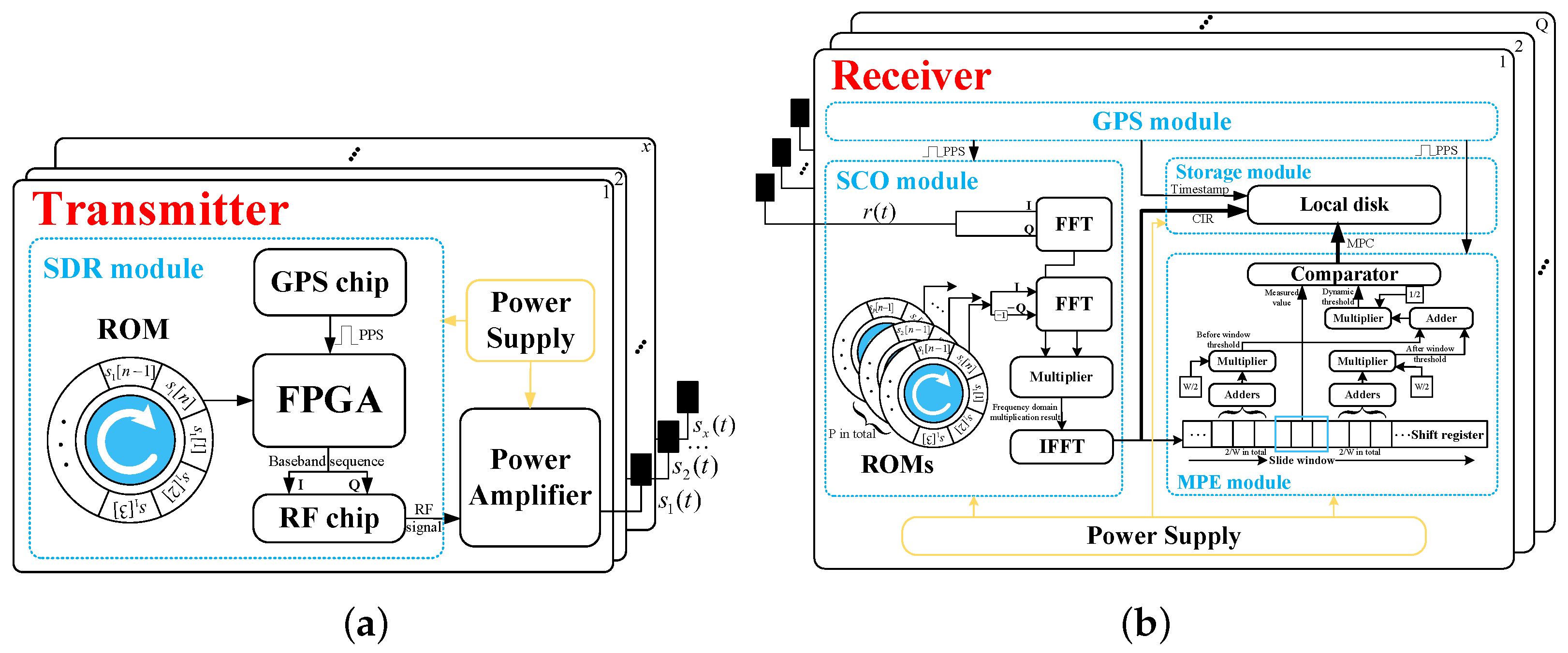
3.2. Implementation of Measurement System
3.3. Channel Characteristics Acquisition
4. Measurement Results and Analysis
4.1. System Setup
4.2. Measurement Campaigns
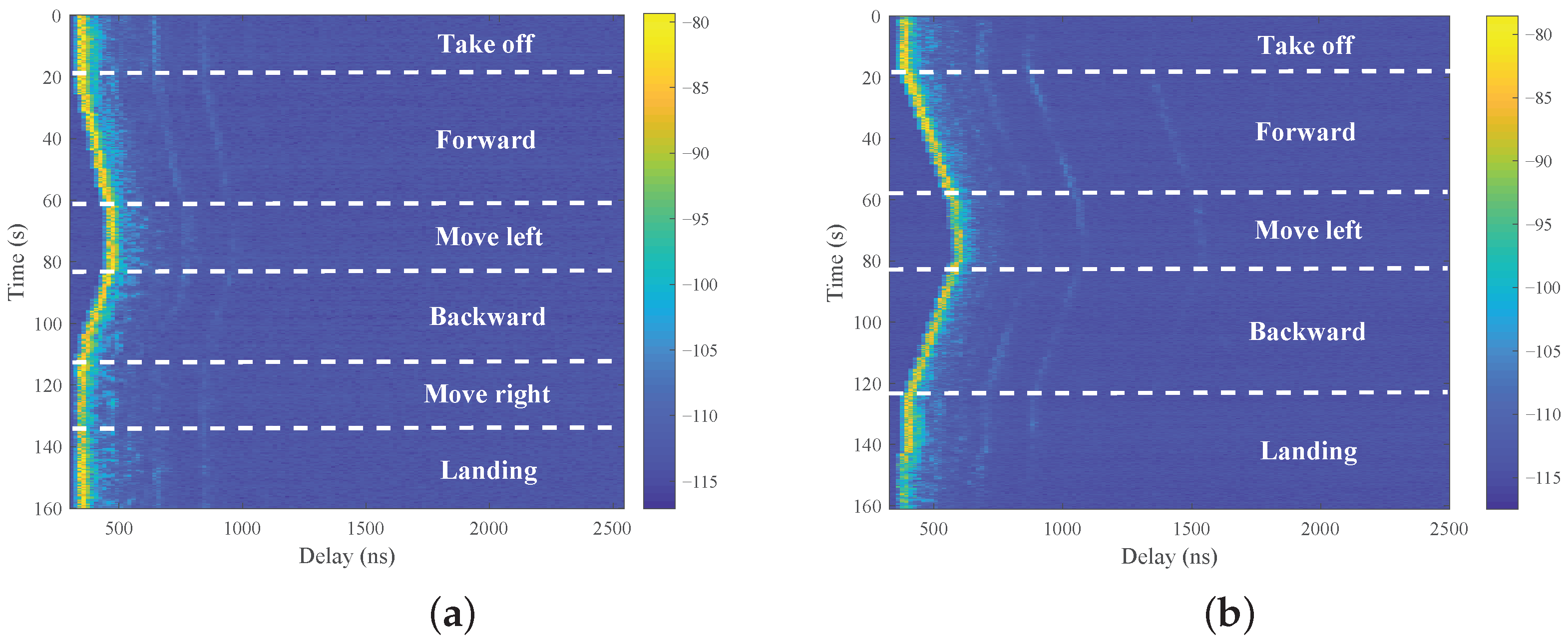
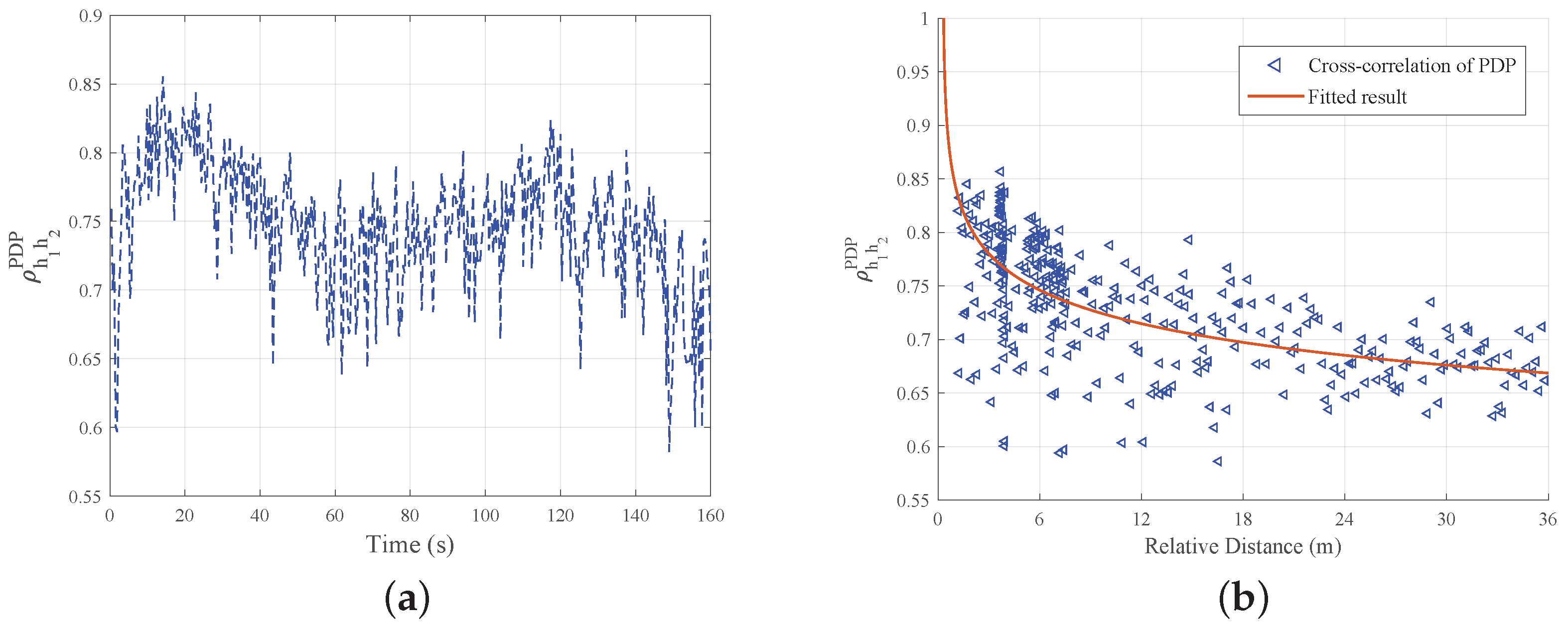
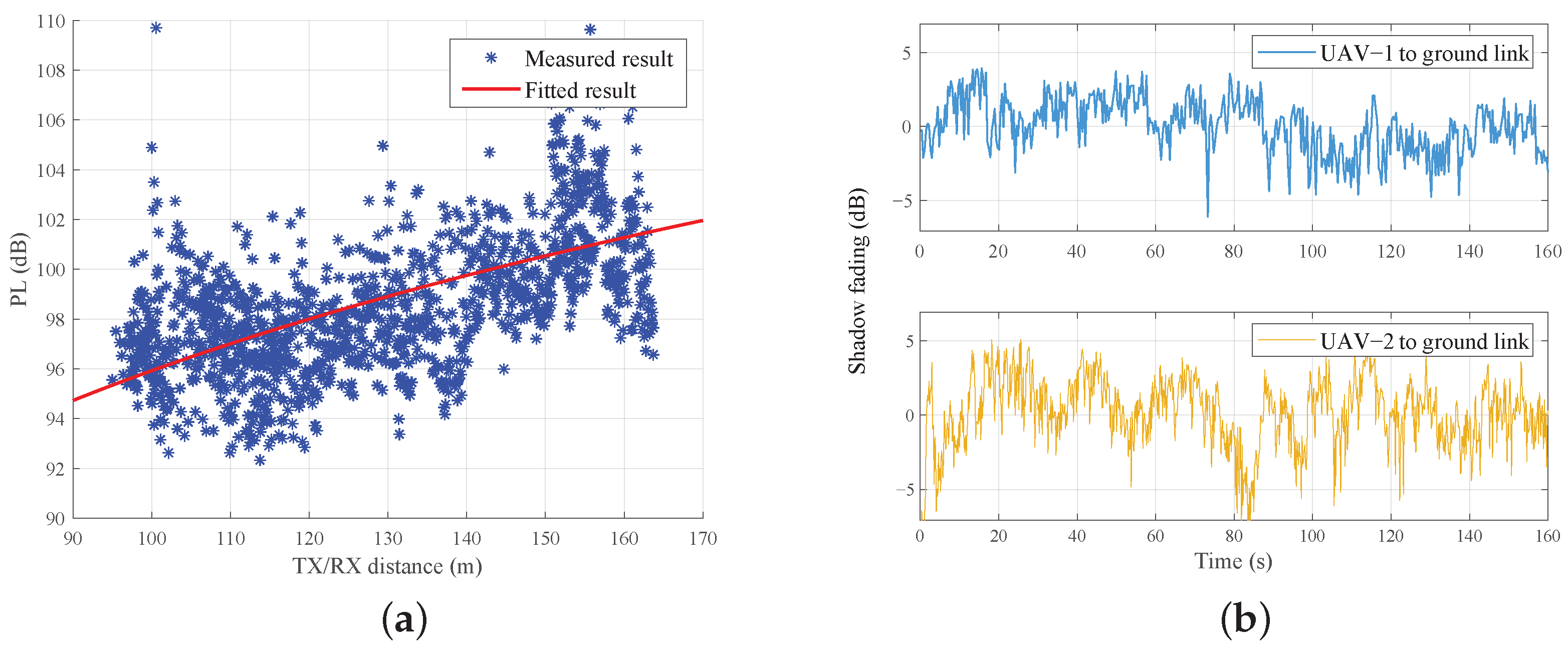
4.3. Channel Cross-Correlation Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayat, S.; Yanmaz, E.; Muzaffar, R. Survey on Unmanned Aerial Vehicle Networks for Civil Applications: A Communications Viewpoint. IEEE Commun. Surv. Tutor. 2016, 18, 2624–2661. [Google Scholar] [CrossRef]
- Silvagni, M.; Tonoli, A.; Zenerino, E.; Chiaberge, M. Multipurpose UAV for Search and Rescue Operations in Mountain Avalanche Events. Geomat. Nat. Hazards Risk 2016, 8, 18–333. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Pan, J.; Ye, N.; Yu, H.; Hong, T.; AI-Rubaye, S.; Mumtaz, S.; AI-Dulaimi, A.; Chih-Lin, I. AI-Driven Blind Signature Classification for IoT Connectivity: A Deep Learning Approach. IEEE Trans. Wirel. Commun. 2022, 21, 6033–6047. [Google Scholar] [CrossRef]
- You, X.; Wang, C.X.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Huang, Y.; Zhang, C.; Jiang, Y.; Wang, J.; et al. Towards 6G Wireless Communication Networks: Vision, Enabling Technologies, and New Paradigm Shifts. Sci. China Inf. Sci. 2021, 64, 1–74. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Z.; Wang, C.-X.; Zhang, J.; Dang, J.; Wu, L.; Zhang, H. A Novel 3D UAV Channel Model for A2G Communication Environments Using AoD and AoA Estimation Algorithms. IEEE Trans. Commun. 2020, 68, 7232–7246. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Song, M.; Li, H.; Ning, B.; Pedersen, G.F.; Fan, W. Machine Learning-based 3D Channel Modeling for U2V mmWave Communications. IEEE Int. Things J. 2022, 9, 17592–17607. [Google Scholar] [CrossRef]
- Hua, B.; Zhou, T.; Zhu, Q.; Mao, K.; Bao, J.; Zhong, W. A Realistic 3D Non-stationary Channel Model for UAV-to-vehicle Communications Incorporating Fuselage Posture. China Commun. 2023, 20, 277–290. [Google Scholar] [CrossRef]
- Zeng, L.; Liao, X.; Xie, W.; Ma, Z.; Xiong, B.; Jiang, H. UAV-to-Ground Channel Modeling: (Quasi-)Closed-Form Channel Statistics and Manual Parameter Estimation. China Commun. 2024. early access. [Google Scholar] [CrossRef]
- Ni, H.; Zhu, Q.; Hua, B.; Mao, K.; Pan, Y.; Ali, F.; Zhong, W.; Chen, X. Path Loss and Shadowing for UAV-to-Ground UWB Channels Incorporating the Effects of Built-Up Areas and Airframe. IEEE Intell. Transp. Syst. 2024. early access. [Google Scholar] [CrossRef]
- Jiang, H.; Zeng, Z.; Wu, L.; Dang, J. Three-Dimensional Geometry-Based UAV-MIMO Channel Modeling for A2G Communication Environments. IEEE Commun. Lett. 2018, 22, 1438–1441. [Google Scholar] [CrossRef]
- Na, Z.; Liu, Y.; Shi, J.; Liu, C.; Gao, Z. UAV-Supported Clustered NOMA for 6G-Enabled Internet of Things: Trajectory Planning and Resource Allocation. IEEE Int. Things J. 2021, 8, 15041–15048. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Mi, H.; Yang, M.; Wang, N.; Zhong, Z.; Fan, W. Modeling and Analysis of MIMO Multipath Channels with Aerial Intelligent Reflecting Surface. J. Select. Areas Commun. 2022, 40, 3027–3040. [Google Scholar] [CrossRef]
- Shi, M.; Yang, K.; Niyato, D.; Yuan, H.; Zhou, H.; Xu, Z. The Meta Distribution of SINR in UAV-Assisted Cellular Networks. IEEE Trans. Commun. 2023, 71, 1193–1206. [Google Scholar] [CrossRef]
- Jiang, H.; Xiong, B.; Zhang, H.; Basar, E. Physics-based 3D End-to-End Modeling for Double-RISs Assisted Non-stationary UAV-to-ground Communication Channels. IEEE Trans. Commun. 2023, 71, 4247–4261. [Google Scholar] [CrossRef]
- Hua, B.; Ni, H.; Zhu, Q.; Wang, C.-X.; Zhou, T.; Mao, K.; Bao, J.; Zhang, X. Channel Modeling for UAV-to-Ground Communications with Posture Variation and Fuselage Scattering Effect. IEEE Trans. Commun. 2023, 71, 3103–3116. [Google Scholar] [CrossRef]
- Lian, Z.; Wang, Y.; Su, Y.; Ji, P.; Ling, L.; Zhang, Z.; Jin, B.; Luo, H. A Novel Beam Channel Model and Capacity Analysis for UAV-enabled Millimeter-Wave Communication Systems. IEEE Wirel. Commun. 2024, 23, 3617–3632. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Wang, C.-X.; Ye, X.; Ponce, J.G.; Cai, X.; Miao, Y.; Cui, Z.; Wu, Q.; Fan, W. A Survey on Channel Sounding Technologies and Measurements for UAV-Assisted Communications. IEEE Trans. Instrum. Meas. 2024. early access. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air–ground Channel Characterization for Unmanned Aircraft Systems—Part III: The Suburban and Near-urban Environments. IEEE Trans. Veh. Technol. 2017, 66, 6607–6618. [Google Scholar] [CrossRef]
- Khawaja, W.; Ozdemir, O.; Erden, F.; Guvenc, I.; Matolak, D.W. Ultra-wideband Air-to-ground Propagation Channel Characterization in an Open Area. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4533–4555. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Liu, Y.; Chang, H.; Zhang, J.; Zhang, M.; Poechmueller, P.; Wang, C.X. AG Channel Measurements and Characteristics Analysis in Hilly Scenarios for 6G UAV Communications. China. Commun. 2022, 19, 32–46. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Lin, Z.; Wu, Q.; Huang, Y.; Cai, X.; Zhong, W.; Zhao, Y. Sparse Bayesian Learning-Based 3D Radio Environment Map Construction—Sampling Optimization, Scenario-Dependent Dictionary Construction and Sparse Recovery. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 80–93. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Lin, Z.; Chen, J.; Ding, G.; Wu, Q.; Gu, G.; Gao, Q. Sparse Bayesian Learning-Based Hierarchical Construction for 3D Radio Environment Maps Incorporating Channel Shadowing. IEEE Wirel. Commun. 2024. early access. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, W.; Zuo, Y.; Gui, J.; Zhang, C. Multi-Objective Optimization of Dynamic Communication Network for Multi-UAVs System. IEEE Trans. Veh. Technol. 2024, 73, 4081–4094. [Google Scholar] [CrossRef]
- Wang, X.; Fei, Z.; Zhang, J.A.; Huang, J.; Yuan, J. Constrained Utility Maximization in Dual-Functional Radar-Communication Multi-UAV Networks. IEEE Trans. Commun. 2021, 69, 2660–2672. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Guo, S.; Yuan, D. Deployment and Association of Multiple UAVs in UAV-Assisted Cellular Networks With the Knowledge of Statistical User Position. IEEE Wirel. Commun. 2022, 21, 6553–6567. [Google Scholar] [CrossRef]
- Bai, L.; Huang, Z.; Feng, T.; Cheng, X. A Non-Stationary Channel Model for 6G Multi-UAV Cooperative Communication. IEEE Wirel. Commun. 2024, 23, 949–961. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Rashdan, I. Measurement-based Fading Characteristics Analysis and Modeling of UAV to Vehicles Channel. Veh. Commun. 2023, 45, 100707. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Sun, Y.; Yue, H.; Chai, J. Low-Altitude UAV Air-to-Ground Multilink Channel Modeling and Analysis at 2.4 and 5.9 GHz. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 2135–2139. [Google Scholar] [CrossRef]
- Hoellinger, J.; Makhoul, G.; D’Errico, R.; Marsault, T. Channel Correlation and Stationarity in mm-wave V2V Channels. In Proceedings of the 2023 European Conference on Antennas and Propagation (EuCAP), Florence, Italy, 26–31 March 2023; pp. 1–5. [Google Scholar] [CrossRef]
- He, R.; Renaudin, O.; Kolmonen, V.; Haneda, K.; Zhong, Z.; Ai, B.; Oestges, C. Characterization of Quasi-Stationarity Regions for Vehicle-to-Vehicle Radio Channels. IEEE Trans. Antennas Propag. 2015, 63, 2237–2251. [Google Scholar] [CrossRef]
- Zhou, T.; Tao, C.; Liu, L.; Liu, K. Investigation of Cross-correlation Characteristics for Multi-link Channels in High-speed Railway Scenarios. China Commun. 2018, 15, 108–117. [Google Scholar] [CrossRef]
- Zhang, X.; He, R.; Yang, M.; Ai, B.; Wang, S.; Li, W.; Sun, W.; Li, L.; Huang, P.; Xue, Y. Measurements and Modeling of Large-Scale Channel Characteristics in Subway Tunnels at 1.8 and 5.8 GHz. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 561–565. [Google Scholar] [CrossRef]
- Zhang, D.; Ai, B.; Fei, D.; Chen, Z. Comparison of Different Sounding Waveforms for a Wideband Correlation Channel Sounder. In Proceedings of the 2021 International Conference on Electronic Information Technology and Radio Technology (EITRT), Qingdao, China, 22–24 October 2021; pp. 119–126. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Qiu, Y.; Liu, X.; Song, M.; Fan, W.; Kokkeler, A.; Miao, Y. A UAV-Aided Real-Time Channel Sounder for Highly Dynamic Nonstationary A2G Scenarios. IEEE Trans. Instrum. Meas. 2023, 72, 6504515. [Google Scholar] [CrossRef]
- Ding, X.; Zhou, K.; Li, G.; Yang, K.; Gao, X.; Yuan, J.; An, J. Customized Joint Blind Frame Synchronization and Decoding Methods for Analog LDPC Decoder. IEEE Trans. Commun. 2024, 72, 756–770. [Google Scholar] [CrossRef]
- Ovchinnikov, V.V.; Ryabova, N.V.; Elsukov, A.A. Adaptive HF Signal Detection Algorithm CFAR and Its Verification By Means of SDR Based Digital Ionosonde with USRP Platform. In Proceedings of the 2018 International Conference on Synchronization and Information Processing (SYNCHROINFO), Minsk, Belarus, 4–5 July 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Qiu, Z.; Chu, X.; Calvo-Ramirez, C.; Briso, C.; Yin, X. Low Altitude UAV Air-to-Ground Channel Measurement and Modeling in Semiurban Environments. Wirel. Commun. Mob. Comput. 2017, 2017, 1587412. [Google Scholar] [CrossRef]

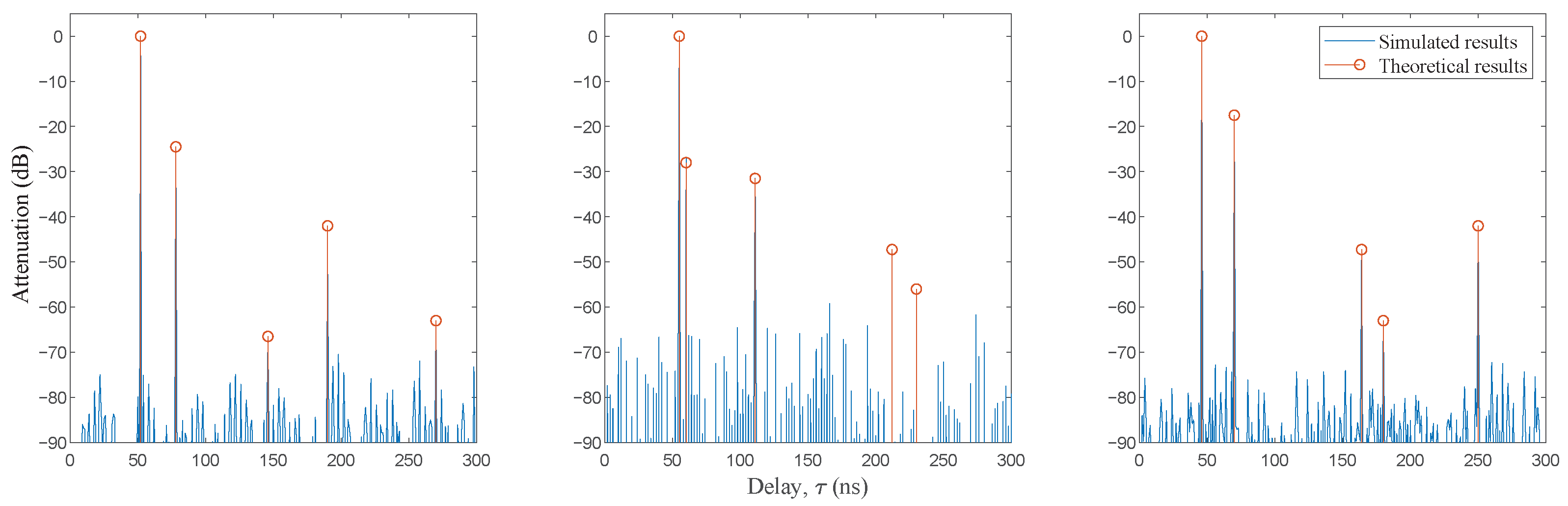




| Channel Parameters | Tap 1 | Tap 2 | Tap 3 | Tap 4 | Tap 5 | |
|---|---|---|---|---|---|---|
| Channel-1 | Delay (ns) | 52 | 78 | 146 | 190 | 270 |
| Attenuation (dB) | 0 | −24.5 | −66.5 | −42 | −63 | |
| Channel-2 | Delay (ns) | 55 | 60 | 111 | 212 | 230 |
| Attenuation (dB) | 0 | −28 | −31.5 | −47.26 | −56 | |
| Channel-3 | Delay (ns) | 46 | 70 | 164 | 180 | 250 |
| Attenuation (dB) | 0 | −17.55 | −47.23 | −63 | −42 | |
| Simulation sample rate: 100 MHz ZC sequence length: 1024 | ||||||
| System Components | Features | ||
|---|---|---|---|
| Aerial TX | Hexacoper UAV | Maximum payload: 5 kg | |
| SDR module | Frequency range: 75–6000 MHz Bandwidth: 61.44 MHz Accuracy of GPS PPS: 20 ns | ||
| Power amplifier | Frequency range: 600–6000 MHz Gain: 42 dB | ||
| Power supply | Battery Capacity: 44,800 mAh Output voltage: DC 24/12/5 V | ||
| Omnidirectional antenna | Frequency range: 3200–3900 MHz Gain: 3 dBi | ||
| Ground RX | SDR platform | Data process module | Data processing rate: 6.6 GB/s |
| RF Module | Frequency range: 200–4400 MHz Bandwidth: 100 MHz | ||
| GPS module | Accuracy of GPS 1PPS: 15 ns | ||
| Omnidirectional antenna | Frequency range: 3200–3900 MHz Gain: 3 dBi | ||
| High-rate disk array | Disk capacity: 24 TB Data transferring rate: 3.6 GB/s | ||
| Power supply | Battery Capacity: 23.2 Ah Output voltage: AC 220 V | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Zhu, Q.; Li, H.; Mao, K.; Li, H.; Chen, X.; Hua, B.; Zhong, W. Cross-Correlation Characteristic Measurements and Analysis for Multi-Link A2G Channels Based on a Multi-UAV System. Drones 2024, 8, 416. https://doi.org/10.3390/drones8080416
Ye X, Zhu Q, Li H, Mao K, Li H, Chen X, Hua B, Zhong W. Cross-Correlation Characteristic Measurements and Analysis for Multi-Link A2G Channels Based on a Multi-UAV System. Drones. 2024; 8(8):416. https://doi.org/10.3390/drones8080416
Chicago/Turabian StyleYe, Xuchao, Qiuming Zhu, Hangang Li, Kai Mao, Hanpeng Li, Xiaomin Chen, Boyu Hua, and Weizhi Zhong. 2024. "Cross-Correlation Characteristic Measurements and Analysis for Multi-Link A2G Channels Based on a Multi-UAV System" Drones 8, no. 8: 416. https://doi.org/10.3390/drones8080416
APA StyleYe, X., Zhu, Q., Li, H., Mao, K., Li, H., Chen, X., Hua, B., & Zhong, W. (2024). Cross-Correlation Characteristic Measurements and Analysis for Multi-Link A2G Channels Based on a Multi-UAV System. Drones, 8(8), 416. https://doi.org/10.3390/drones8080416










