Aerial Map-Based Navigation by Ground Object Pattern Matching
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions
1.3. Outline
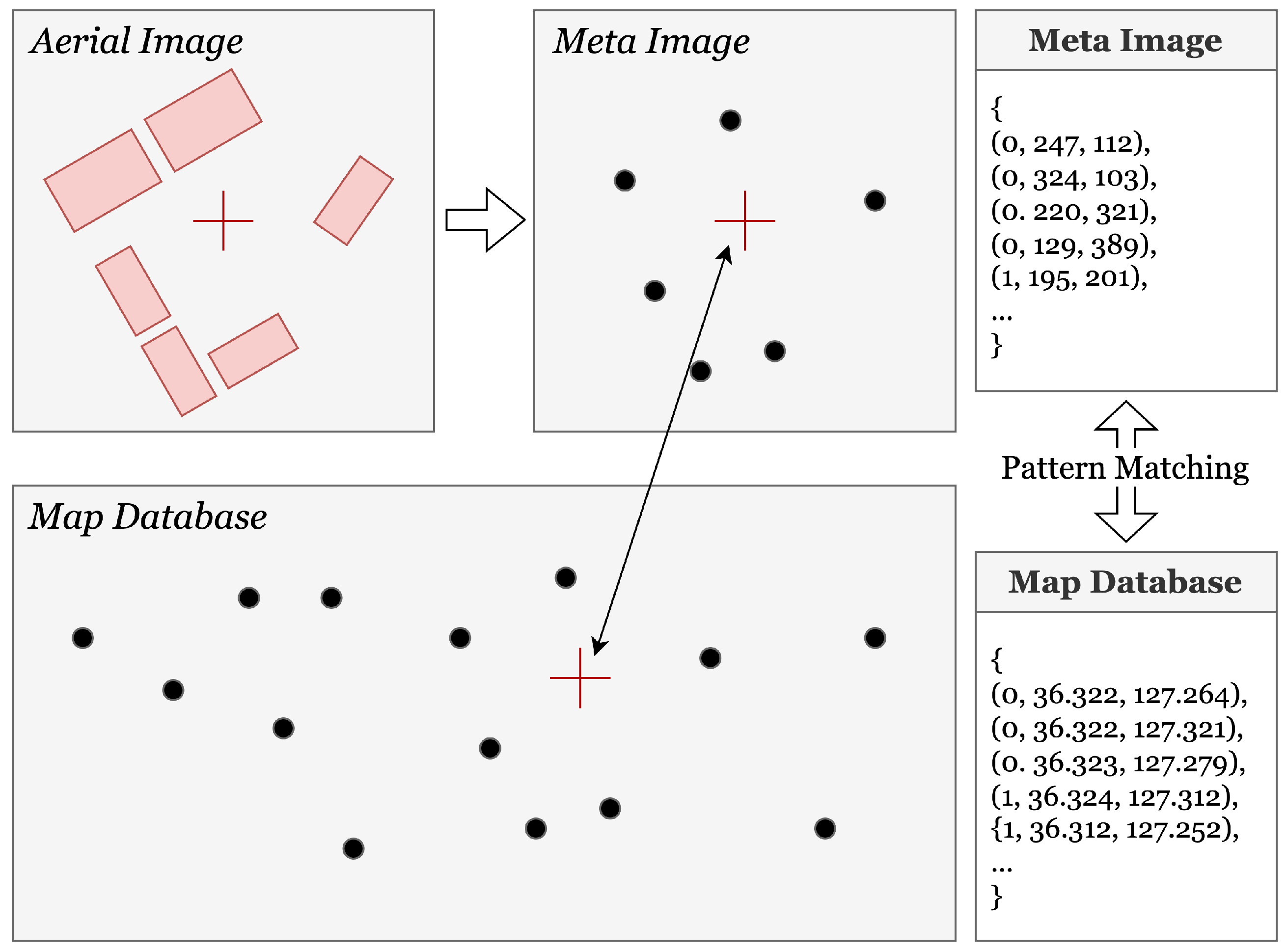
2. Proposed Map-Based Navigation System
2.1. Image Processing
2.1.1. Dataset
2.1.2. Training and Validation
2.2. Localization by Map Matching
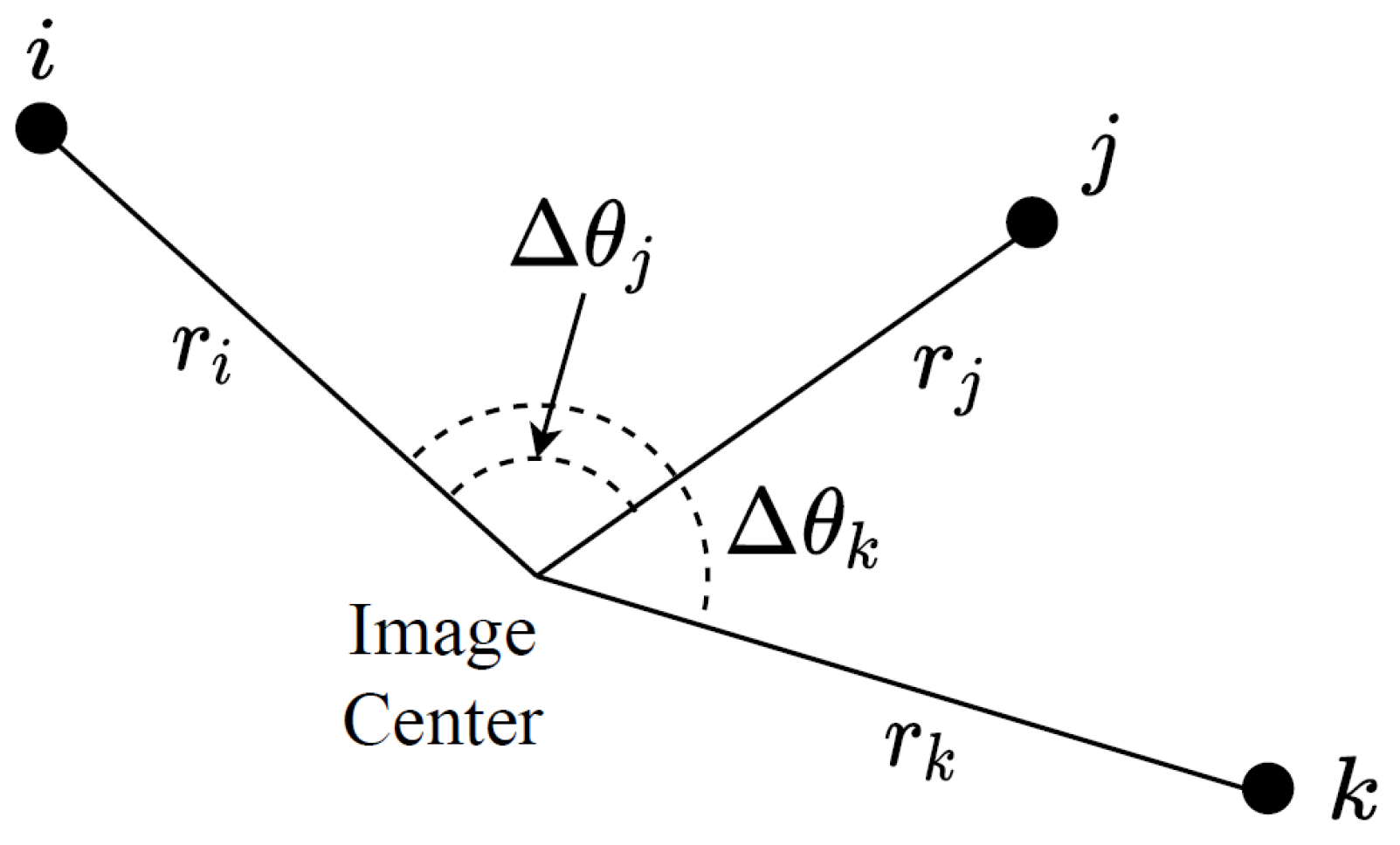
2.2.1. Pattern-Matching Algorithm
| Algorithm 1 Proposed pattern-matching algorithm |
|
2.2.2. Iterating over Object Pairs
| Algorithm 2 Finding position candidates by circle intersection |
|
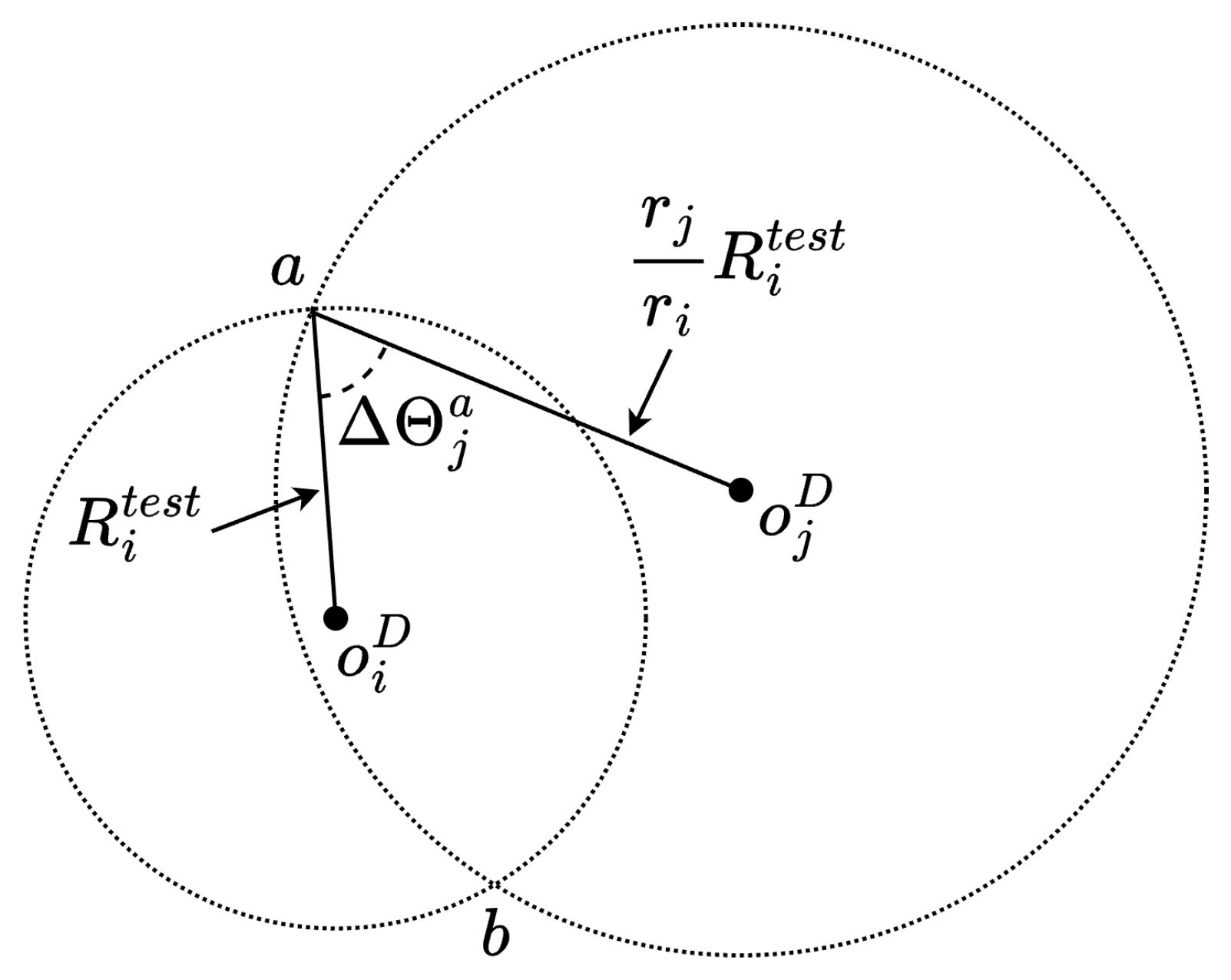
2.2.3. Finding Position Candidate by Circle Intersection
2.3. Data Fusion with Inertial Measurements
3. Flight Experiments
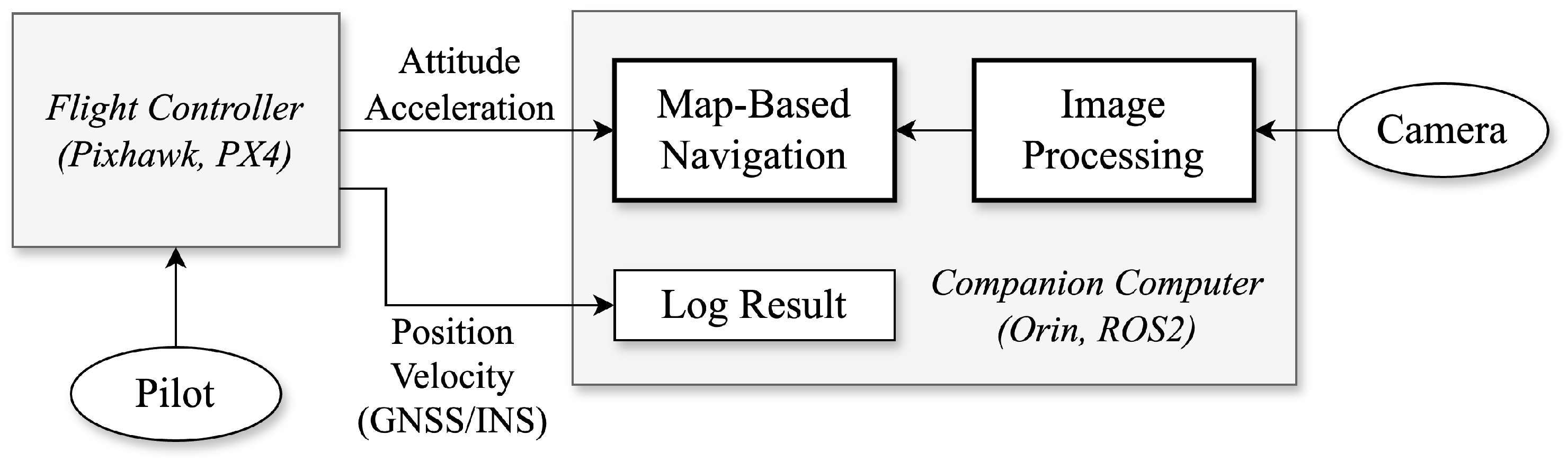
3.1. Unmanned Aircraft System
3.2. Database Generation
3.3. Test Area and Scenario
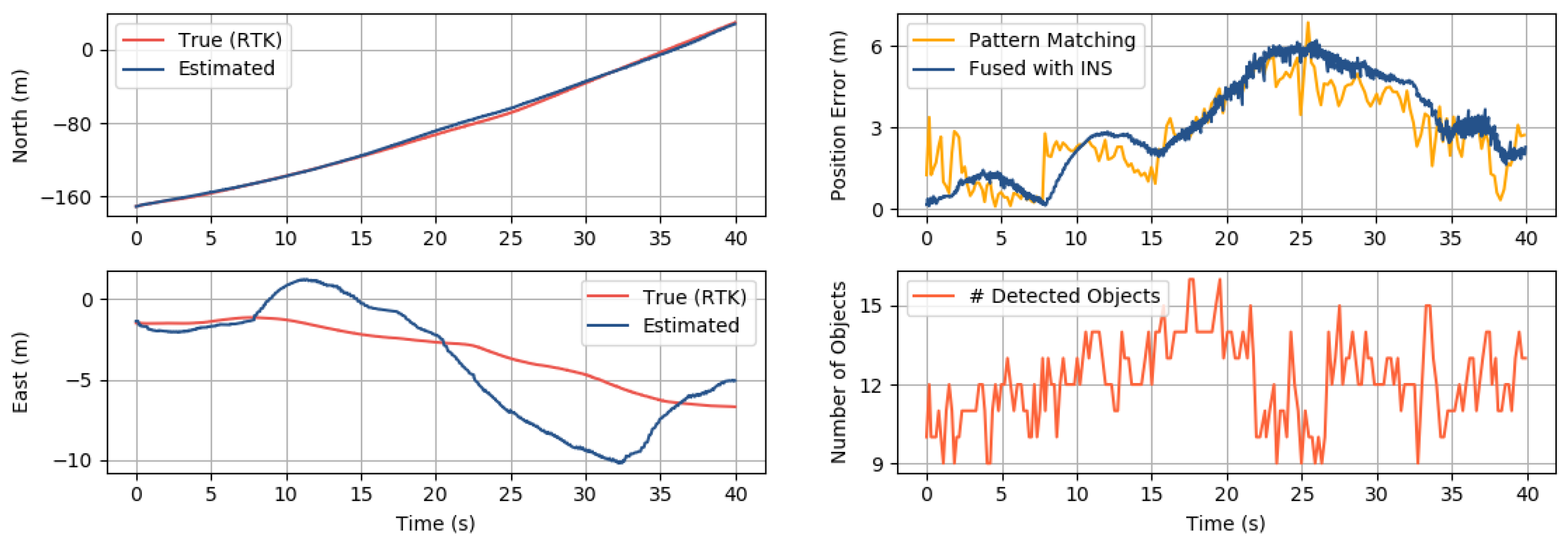
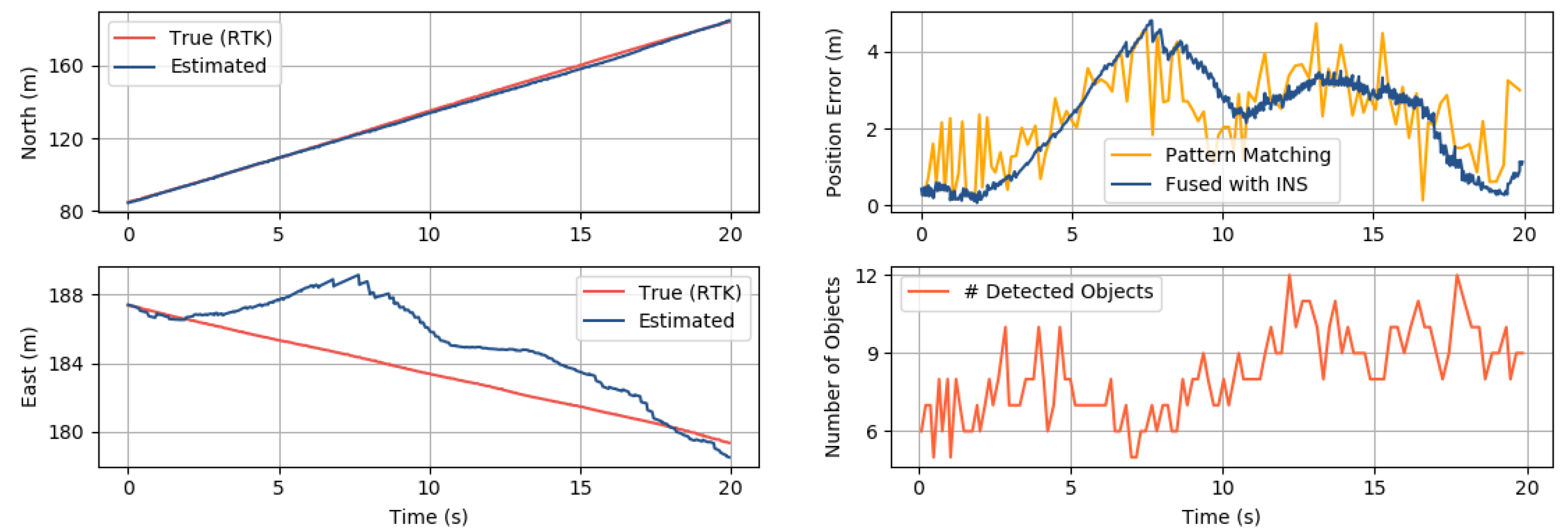
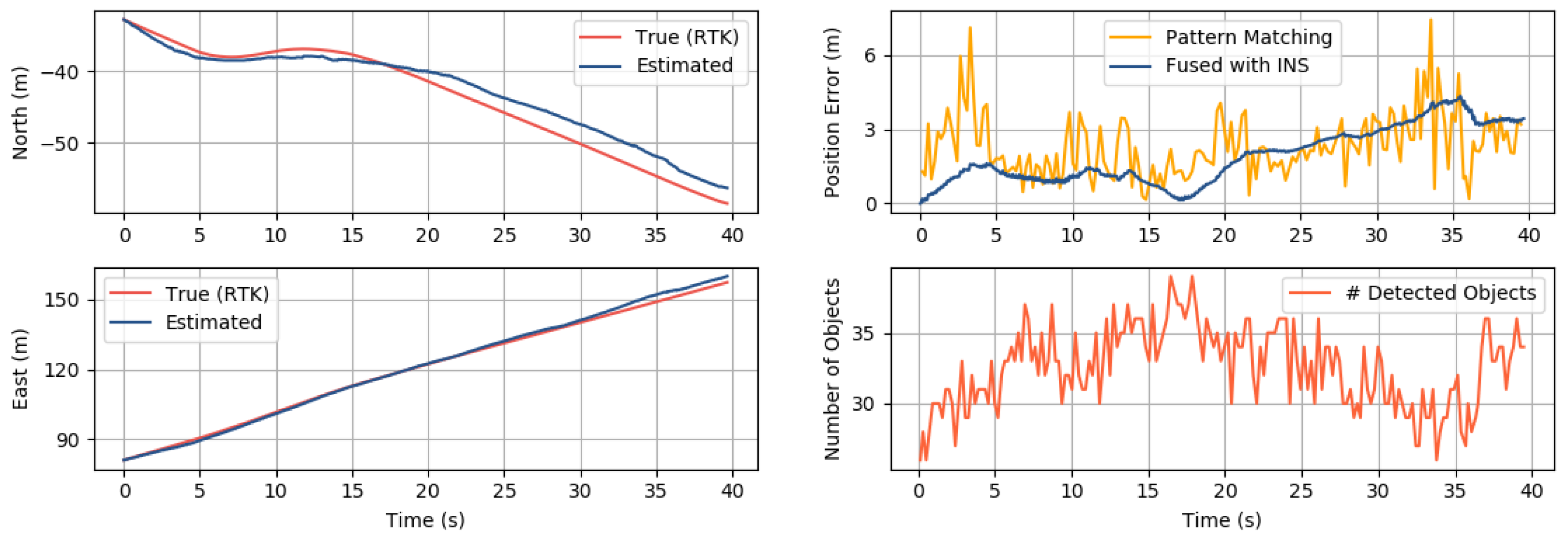
3.4. Results and Discussion
3.4.1. Position Accuracy
3.4.2. Computation Time
3.4.3. Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Kalman Filter
Appendix A.1. Process Model
Appendix A.2. Measurement Model
References
- Kim, Y.; Hong, K.; Bang, H. Utilizing out-of-sequence measurement for ambiguous update in particle filtering. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 493–501. [Google Scholar] [CrossRef]
- Spiegel, P.; Dambeck, J.; Holzapfel, F. Slant range analysis and inflight compensation of radar altimeter flight test data. Navig. J. Inst. Navig. 2016, 63, 491–507. [Google Scholar] [CrossRef]
- Sim, D.G.; Park, R.H.; Kim, R.C.; Lee, S.U.; Kim, I.C. Integrated position estimation using aerial image sequences. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1–18. [Google Scholar]
- Rodriguez, J.J.; Aggarwal, J. Matching aerial images to 3-D terrain maps. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 1138–1149. [Google Scholar] [CrossRef]
- Kim, Y.; Bang, H. Vision-based navigation for unmanned aircraft using ground feature points and terrain elevation data. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2018, 232, 1334–1346. [Google Scholar] [CrossRef]
- El Garouani, A.; Alobeid, A.; El Garouani, S. Digital surface model based on aerial image stereo pairs for 3D building. Int. J. Sustain. Built Environ. 2014, 3, 119–126. [Google Scholar] [CrossRef]
- Shan, M.; Wang, F.; Lin, F.; Gao, Z.; Tang, Y.Z.; Chen, B.M. Google map aided visual navigation for UAVs in GPS-denied environment. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 114–119. [Google Scholar]
- Zhuo, X.; Koch, T.; Kurz, F.; Fraundorfer, F.; Reinartz, P. Automatic UAV image geo-registration by matching UAV images to georeferenced image data. Remote. Sens. 2017, 9, 376. [Google Scholar] [CrossRef]
- Bay, B.; Andreas, E.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Bublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Hong, K.; Kim, S.; Bang, H. Particle filter approach to vision-based navigation with aerial image segmentation. Aerosp. Inf. Syst. 2021, 18, 964–972. [Google Scholar] [CrossRef]
- Wang, T.; Celik, K.; Somani, A.K. Characterization of mountain drainage patterns for GPS-denied UAS navigation augmentation. Mach. Vis. Appl. 2016, 27, 87–101. [Google Scholar] [CrossRef]
- Volkova, A.; Gibbens, P.W. More robust features for adaptive visual navigation of UAVs in mixed environments. J. Intell. Robot. Syst. 2018, 90, 171–187. [Google Scholar] [CrossRef]
- Kim, Y. Aerial map-based navigation using semantic segmentation and pattern matching. arXiv 2021, arXiv:2107.00689. [Google Scholar]
- Park, J.; Kim, S.; Hong, K.; Bang, H. Visual semantic context and efficient map-based rotation-invariant estimation of position and heading. Navig. J. Inst. Navig. 2024, 71, 634. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision—ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. Springer: Cham, Switzwerland, 2016; pp. 21–37. [Google Scholar]
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Aihub Dataset. Available online: https://www.aihub.or.kr/ (accessed on 14 April 2024).
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Intersection of two circles. Available online: https://paulbourke.net/geometry/circlesphere/ (accessed on 20 March 2024).
- Kim, Y.; Bang, H. Introduction to Kalman filter and its applications. In Introduction and Implementations of the Kalman Filter; Govaers, F., Ed.; IntechOpen: London, UK, 2018. [Google Scholar]










| Meters per Pixel | Resolution | The Number of Images |
|---|---|---|
| 0.25 m/pixel | 50,000 | |
| 0.25 m/pixel | 5000 | |
| 0.12 m/pixel | 1000 |
| Class | Precision | Recall | mAP0.5 | mAP0.5:0.95 |
|---|---|---|---|---|
| All | 0.857 | 0.768 | 0.614 | 0.845 |
| Building | 0.886 | 0.745 | 0.618 | 0.857 |
| Greenhouse | 0.828 | 0.791 | 0.611 | 0.833 |
| Name | Height | Speed | # Objects | RMSE |
|---|---|---|---|---|
| Area 1 | 92 m | 2–7 m/s | 9–15 | 3.33 m |
| Area 2 | 132 m | 4–6 m/s | 5–12 | 2.60 m |
| Area 3 | 127 m | 2–4 m/s | 25–39 | 2.22 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Back, S.; Song, D.; Lee, B.-Y. Aerial Map-Based Navigation by Ground Object Pattern Matching. Drones 2024, 8, 375. https://doi.org/10.3390/drones8080375
Kim Y, Back S, Song D, Lee B-Y. Aerial Map-Based Navigation by Ground Object Pattern Matching. Drones. 2024; 8(8):375. https://doi.org/10.3390/drones8080375
Chicago/Turabian StyleKim, Youngjoo, Seungho Back, Dongchan Song, and Byung-Yoon Lee. 2024. "Aerial Map-Based Navigation by Ground Object Pattern Matching" Drones 8, no. 8: 375. https://doi.org/10.3390/drones8080375
APA StyleKim, Y., Back, S., Song, D., & Lee, B.-Y. (2024). Aerial Map-Based Navigation by Ground Object Pattern Matching. Drones, 8(8), 375. https://doi.org/10.3390/drones8080375






