SLAKA-IoD: A Secure and Lightweight Authentication and Key Agreement Protocol for Internet of Drones

Abstract

The existing authentication and key agreement (AKA) schemes for the internet of drones (IoD) still suffer from various security attacks and fail to ensure required security properties. Moreover, drones generally have limited memory and computation capability. Motivated by these issues, a secure and lightweight AKA protocol for IoD (SLAKA-IoD) is proposed based on physical unclonable function (PUF), “exclusive or” (XOR) operation and hash function, which are simple cryptographic operations and functions that can provide better performance. In the SLAKA-IoD protocol, a drone and the ground station (GS) perform mutual authentication and establish a secure session key between them, and any two drones can also perform mutual authentication and establish a secure session key between them. Via informal security analysis, formal security analysis using the strand space model, and security verification based on the Scyther tool, the SLAKA-IoD protocol is proven to resist various security attacks and ensure required security properties. Further comparative analysis shows that the SLAKA-IoD protocol can provide more security features, and is generally lightweight as compared with these related AKA protocols for IoD, so it is suitable for IoD.

1. Introduction

A drone or unmanned aerial vehicle (UAV) is a versatile platform for communication. It can provide flexibility in altitude, line-of-lighting, mobility, etc. Due to its advantages, drones are no longer only used in military applications, but they are also being adopted in various government and civilian applications, including traffic management, goods delivery, inventory tracking, disaster management, surveillance and monitoring, wireless communication, etc. [1,2,3,4,5]. In these applications, drones are generally integrated into the internet of things (IoT), which results in the internet of drones (IoD) [6,7].

In the IoD, drones are deployed in an open environment and communicate wirelessly with nature; they are prone to various security threats, including impersonation attack, man-in-the-middle attack, replay attack, drone physical capture attack, and so on [8,9,10,11]. One feasible security solution is to deploy authentication and key agreement (AKA) schemes for the IoD, which prevent any sensitive information sharing via an insecure wireless channel [12,13]. These schemes aim to verify the legitimate identity of communication entities and establish secure channels between communication entities. In other words, communication entities in the IoD should have the capability to mutually authenticate each other and establish a secure session key for subsequent communications.

In the last few years, many researchers have proposed various AKA schemes for IoD [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. However, these AKA schemes for IoD still suffer from potential security attacks and fail to ensure required security properties, such as replay attack, drone physical capture attack, desynchronization attack, anonymity and untraceability. Moreover, drones have limited memory and computation capability generally. Hence, storing secret keys and executing standard cryptography algorithms are also a challenge [6]. Motivated by these issues, we propose a secure and lightweight AKA protocol for IoD (hereafter referred to as SLAKA-IoD protocol), and analyze and measure its security and performance. Our major contributions are briefly summarized in the following:

• We propose the SLAKA-IoD protocol based on physical unclonable function (PUF), “exclusive or” (XOR) operation and hash function, which are simple cryptographic operations and functions that can provide better performance. Moreover, the introduction of PUF can bring better security. This protocol can achieve mutual authentication and establish a secure session key between communication entities in the IoD.
• We present an informal security analysis to show that the SLAKA-IoD protocol is secure against various security attacks and ensures required security properties. In addition, we provide a formal security analysis of the protocol using the strand space model [43,44,45], and perform a security verification of the protocol based on the Scyther tool [46,47]. Finally, a comparison of the SLAKA-IoD protocol with other related AKA protocols for IoD in terms of security features is given.
• We perform a performance analysis of the SLAKA-IoD protocol in terms of computation, communication and storage cost. Then, a comparison of the SLAKA-IoD protocol with other related AKA protocols for IoD in terms of computation, communication and storage cost is also provided.

The rest of this paper is organized as follows. Section 2 discusses the related works of the AKA for IoD. In Section 3, the system model for IoD is introduced. Section 4 describes our proposed SLAKA-IoD protocol. Section 5 provides a security analysis of the protocol. In Section 6, a performance analysis of the protocol is also presented. Finally, we conclude the paper in Section 7.

2. Related Works

In the last few years, numerous AKA schemes have been presented to ensure security and privacy in the IoD. Chaudhry et al. [14] designed a certificate-based generic access control scheme for IoD. However, it cannot resist impersonation attack and does not provide anonymity [15]. Won et al. [16] proposed an elliptical curve cryptography (ECC)-based certificateless AKA scheme for IoD. However, this scheme fails to provide user anonymity [17]. Cheon et al. [18] presented an AKA scheme based on homomorphic encryption to provide useful services in IoD environments. Unfortunately, it suffers from insider and session key disclosure attacks.

Ever [19] proposed a secure and efficient AKA framework for mobile sinks utilized in IoD environments, which is based on bilinear pairing. However, it is pointed out that the scheme cannot resist impersonation and drone physical capture attacks, and also does not provide perfect forward secrecy [20]. To overcome these attacks, Nikooghadam et al. [20] presented an ECC-based secure and lightweight AKA scheme for IoD. However, Ali et al. [21] pointed out that the scheme still suffers from potential security attacks, including insider, replay and impersonation attacks. Moreover, the scheme does not provide secure mutual authentication between communication entities.

Likewise, Rodrigues et al. [22] presented an ECC-based authentication method for UAV communication. Dogan et al. [23] proposed an ECC-based authentication protocol to provide mutual authentication between UAV and base station devices. However, they cannot resist drone physical capture attack. Tanveer et al. [24] devised an AKA scheme for IoD, which employs hash function and authenticated encryption with associative data (AEAD). However, the scheme cannot provide an anonymity feature, which was pointed out in [14]. Tanveer et al. [25] proposed an AKA scheme based on both AEAD and ECC to enable indecipherable communication for the IoD networks. However, the proposed security scheme does not guarantee dynamic privacy preservation.

The above AKA schemes are not suitable for resource-constrained IoD because they require high computation and communication overheads. In order to meet the resource-constrained requirement of drones, many lightweight AKA schemes for IoD have been proposed. In [26], Wazid et al. introduced several security challenges along with necessary security requirements for IoD environments, and designed a user AKA scheme for IoD. However, this scheme is unable to resist impersonation attack and does not guarantee perfect backward secrecy [27].

After that, Alladi et al. [27] presented an enhanced AKA scheme, which is a two-stage AKA scheme for software-defined networking (SDN)-based UAV networks and is lightweight. However, Beebak et al. [28] pointed out that this scheme cannot resist offline password guessing, replay, man-in-the-middle (MITM), and session key disclosure attacks. In addition, the scheme does not provide data confidentiality and perfect forward secrecy.

Further, Srinivas et al. [29] proposed a temporal credential-based anonymous lightweight user AKA scheme in IoD environments, named TCALAS. However, the scheme cannot resist impersonation attacks and also does not provide user traceability [30]. To overcome the security weaknesses of this scheme, Ali et al. [30] presented an enhanced AKA scheme for IoD. Unfortunately, the scheme is still prone to MITM, replay, session key disclosure, and impersonation attacks.

However, none of the above AKA schemes are secure against drone tampering and physical attacks. Because secret information required for authentication is stored in the drone’s physical memory, an adversary can easily extract this critical information and perform various attacks. To overcome this shortcoming, PUFs have been used in the AKA schemes for IoD to resist drone physical capture attack recently. These PUFs utilize the inherent randomness that is introduced during the manufacturing process of a silicon device. This makes it very difficult to clone or reproduce them [31,32].

Alladi at al. [33] proposed a PUF-based AKA scheme, which achieves mutual authentication between UAV and the ground station (GS) and establishes a session key between them. However, the scheme suffers from replay and desynchronization attacks and does not provide PUF challenge–response pair protection. Bansal et al. [34] designed a similar scheme, so it also has the same security issues. Alladi et al. [35] proposed a lightweight mutual authentication scheme for UAV-GS authentication based on PUF, then extended this scheme to support UAV-UAV authentication. Nevertheless, this scheme still cannot resist replay and desynchronization attacks and does not provide PUF challenge–response pair protection.

Further, Pu et al. [36] presented a lightweight authentication protocol for unmanned aerial vehicles using PUF and chaotic system to protect the communication between drone and GS. However, it cannot resist drone physical capture attack because the PUF challenge–response pair of each drone is stored in the drone’s storage. Moreover, this protocol also cannot resist replay and desynchronization attacks, and does not provide PUF challenge–response pair protection. After that, they proposed another lightweight and privacy-preserving mutual AKA protocol for IoD environments [37]. This protocol also uses PUF and a chaotic system to perform mutual authentication and establish a secure session key between communication entities in the IoD. Unfortunately, the same security issues as those in the scheme in [36] still exist in the scheme. Karmakar et al. [38] designed a PUF and fuzzy extractor-based UAV-GS authentication mechanism, considering the noise reduction that occurs in PUFs. In addition, some blockchain-based UAV authentication mechanisms were proposed [39,40,41,42]. They mainly facilitate the cooperation of UAVs from different domains. Some important related works are summarized in

Table 1. The summary of the related AKA schemes for IoD.

Scheme	Year	Cryptographic Techniques	Advantages	Limitations
Won et al. [16]	2017	Utilize ECC	Provides a certificateless AKA scheme	Does not provide user anonymity [17]
Cheon et al. [18]	2018	Utilize homomorphic encryption	Provides useful services in IoD environments	Does not resist session key disclosure and insider attacks
Rodrigues et al. [22]	2019	Utilize ECC	Provides mutual authentication for UAV communication	Does not resist drone physical capture and ESL attacks
Wazid et al. [26]	2019	Utilize one-way hash function and fuzzy extractor	Provides three-factor security	Does not resist impersonation attack and does not guarantee perfect backward secrecy [27]
Srinivas et al. [29]	2019	Utilize one-way hash function and fuzzy extractor	Provides three-factor security	Does not resist impersonation attacks and does not provide user traceability [30]
Ever [19]	2020	Utilize ECC, bilinear pairing and one-way hash function	Provides a secure and efficient AKA framework for mobile-sinks utilized in IoD environments	Does not resist drone physical capture and impersonation attacks, and does not provide perfect forward secrecy [20]
Tanveer et al. [24]	2020	Utilize one-way hash function and AEAD	Provides UAV-GS mutual authentication	Does not provide an anonymity feature [14]
Alladi et al. [27]	2020	Utilize PUF	Provides a mutual authentication mechanism for 5G-aided UAV networks	Does not prevent MITM, replay, offline password guessing, and session key disclosure attacks, and does not ensure data confidentiality or perfect forward secrecy [28]
Ali et al. [30]	2020	Utilize one-way hash function, symmetric encryption and fuzzy extractor	Provides a mutual authentication protocol for IoD-based city environments	Does not prevent MITM, replay, session key disclosure, and impersonation attacks
Alladi et al. [35]	2020	Utilize one-way hash function, PUF and symmetric encryption	Provides UAV-GS authentication and UAV-UAV authentication	Does not resist replay and desynchronization attacks
Pu et al. [36]	2020	Utilize one-way hash function, PUF and chaotic system	Protects the communication between drone and GS	Does not resist drone physical capture, replay, and desynchronization attacks
Chaudhry et al. [14]	2021	Utilize certificate	Provides generic access control scheme for IoD	Does not resist impersonation attack and does not provide anonymity [15]
Nikooghadam et al. [20]	2021	Utilize ECC and one-way hash function	Provides user anonymity and untraceability	Does not resist replay, insider, and impersonation attacks, and does not ensure mutual authentication [21]
Alladi at al. [33]	2021	Utilize PUF and one-way hash function	Provides lightweight mutual authentication between UAV and GS	Does not resist replay and desynchronization attacks
Bansal et al. [34]	2021	Utilize PUF and one-way hash function	Provides lightweight mutual authentication between UAV and GS	Does not resist replay and desynchronization attacks
Tanveer et al. [25]	2022	Utilize ECC and AEAD	Provides indecipherable communication in IoD networks	Does not guarantee dynamic privacy preservation
Pu et al. [37]	2022	Utilize one-way hash function, PUF and chaotic system	Provides UAV-GS authentication and UAV-UAV authentication	Does not resist drone physical capture, replay and desynchronization attacks
Dogan et al. [23]	2023	Utilize ECC	Provides mutual authentication between UAV and base station devices	Does not resist drone physical capture attack
Karmakar et al. [38]	2024	Utilize one-way hash function, PUF and fuzzy extractor	Considers the noise reduction that occurs in PUFs	Does not provide PUF challenge–response pair protection

.

Therefore, we design a new, secure and lightweight AKA protocol for IoD based on PUF, XOR operation, and hash function, aiming to resolve security and efficiency shortcomings of the existing AKA schemes for IoD.

3. System Model

3.1. Network Model

The network model considered in this paper is illustrated in Figure 1, which consists of legitimate drones and a GS.

In Figure 1, compared to the GS, drones have limited memory and computation capability, and connect to the GS over an insecure wireless channel. Without loss of generality, the following two scenarios are considered for AKA in this paper:

• A drone wants to establish a secure communication session with the GS by performing AKA between the two entities, which is called drone-GS AKA;
• A drone wants to establish a secure communication session with another drone by performing AKA between the two entities, which is called drone–drone AKA.

In addition, each drone is equipped with a PUF, which is regarded as an integrated circuit. It takes an input and produces an output according to its unique physical characteristics [35]. PUF can be denoted as $R=PUF(C)$, where $PUF()$ denotes PUF function, $C$ denotes the input challenge and, $R$ denotes the output response. For a PUF, the same challenge will lead to the same response. However, if the same challenge is provided to different PUFs, then totally different responses will be generated [36,37]. In other words, the PUF is designed to produce an output for any input, which is like a fingerprint based on the physical microstructure of the device. The ideal PUF offers the properties of uniqueness, reliability, unpredictability, and unclonability [17].

3.2. Threat Model

In the network model shown in Figure 1, the network entities exchange information through a public wireless communication channel, which is exposed to various security risks. By taking advantage of the public nature of the wireless communication channel, $MA$ can compromise the information exchanged between the network entities, where $MA$ denotes a malicious attacker (MA). Consequently, we present the widely accepted Dolev and Yao (DY) threat model [48] to evaluate the security of SLAKA-IoD. Under the DY threat model, $MA$ can capture and eavesdrop on all the communicated information or messages of the network’s nodes. $MA$ can also alter, forge, delete, and implant bogus information while communicating with the network entities.

We also apply the Canetti and Krawczyk (CK) threat model [49] on the SLAKA-IoD. The CK threat model is more powerful than the DY threat model. According to the CK threat model, through session-hijacking attacks, $MA$ can compromise secret information and session states. Therefore, based on the CK threat model, $MA$ may attempt ephemeral secret leakage (ESL) attacks on the SLAKA-IoD protocol. Moreover, $MA$ can physically capture the drones of SLAKA-IoD because they may move to an unattended hostile area accidentally. As a result, by performing power analysis attacks [50] on these captured drones, $MA$ can extract the secret parameters stored in their memory.

4. Proposed SLAKA-IoD Protocol

The proposed scheme is organized into three phases, namely the drone registration phase, the drone-GS authentication and key agreement phase, and the drone–drone authentication and key agreement phase. Usually, the drone-GS authentication and key agreement phase is mandatory, while the drone–drone authentication and key agreement phase is performed on demand.

Table 2. The notations used in this scheme.

Notation	Description
$D_i$$, D_j$$, GS$	$i\mathrm{t}\mathrm{h}$ drone, $j\mathrm{t}\mathrm{h}$ drone, and ground station
${ID}_i$$, {ID}_j$$, {ID}_s$	Identities of $D_i$$, D_j$, and $GS$, respectively
${PID}_i$$, {PID}_j$	Pseudo-identities of $D_i$$\mathrm{and} D_j$, respectively
$N_i$$, N_j$$, N_s$	Random numbers of $D_i$$, D_j$$\mathrm{and} GS$, respectively
$T_i$$, T_s$	Timestamps of $D_i$$\mathrm{and} GS$, respectively
$T_i^{*}$$, T_s^{*}$	Message reception time of $T_i$$\mathrm{and} T_s$, respectively
$(C_{i,1},R_{i,1})$$, (C_{i,2},R_{i,2})$	Two PUF challenge–response pairs of $D_i$
$(C_{j,1},R_{j,1})$$, (C_{j,2},R_{j,2})$	Two PUF challenge–response pairs of $D_j$
$C_i^n$$, C_j^n$	New PUF challenges of $D_i$$\mathrm{and} D_j$, respectively
${PID}_i^n$$, {PID}_j^n$	New pseudo-identities of $D_i$$\mathrm{and} D_j$, respectively
${PUF}_i()$$,{PUF}_j()$	PUFs of $D_i$$\mathrm{and} D_j$, respectively
${MK}_{ij}$	Master key between $D_i$$\mathrm{and} D_j$
${SK}_{is}$	Session key between $D_i$$\mathrm{and} GS$
${SK}_{ij}$	Session key between $D_i$$\mathrm{and} D_j$
${SKID}_{is}$$, {SKID}_{ij}$	Key indexes of ${SK}_{is}$$\mathrm{and} {SK}_{ij}$, respectively
$∆T$	Maximum transmission time delay
$h()$	Hash function
$\left|\right|$$, ⨁$	Concatenation operation and XOR operation

presents the notations used in this scheme.

4.1. Drone Registration Phase

In this phase, the ground station, $GS$, registers each drone, $D_i$, in an offline mode or a close-range cable mode before deployment in the IoD field. The phase is illustrated in Figure 2.

The detailed description of the drone registration phase is as follows:

• For each drone, $D_i$, the ground station, $GS$, assigns an identity, ${ID}_i$, generates two challenges, $C_{i,1}$ and $C_{i,2}$, and computes a pseudo-identity, ${PID}_i=h({ID}_i|\left|C_{i,1}\right||C_{i,2})$, where $h()$ denotes a hash function and $\left|\right|$ denotes a concatenation operation. Then, $GS$ sends $\{{PID}_i,{ID}_s,C_{i,1},C_{i,2}\}$ to $D_i$ via a secure channel (i.e., an offline mode or a close-range cable mode), where ${ID}_s$ denotes the identity of $GS$.
• Upon receiving the messages, the drone, $D_i$, computes $R_{i,1}={PUF}_i(C_{i,1})$ and ${HR}_{i,1}=h(C_{i,1}||R_{i,1})$, where ${PUF}_i()$ denotes the PUF of $D_i$. This means that $(C_{i,1},R_{i,1})$ is a challenge–response pair from the PUF of $D_i$, where $C_{i,1}$ denotes the input challenge and $R_{i,1}$ denotes the output response. Then, $D_i$ sends $\left\{{HR}_{i,1}\right\}$ to $GS$ via a secure channel (i.e., an offline mode or a close-range cable mode). Finally, $D_i$ stores $\{{PID}_i,{ID}_s,C_{i,1},C_{i,2}\}$ in its storage.
• After obtaining $\left\{{HR}_{i,1}\right\}$ from $D_i$, $GS$ stores $\{{ID}_i,{{PID}_i, ID}_s,{HR}_{i,1}\}$ in its database.
  Once the drone, $D_i$, is registered in $GS$, the registration interface of $D_i$ is closed.

4.2. Drone-GS Authentication and Key Agreement Phase

In this phase, $D_i$ and $GS$ authenticate each other, and establish a session key between them. The phase is illustrated in Figure 3.

The detailed description of the drone-GS authentication and key agreement phase is as follows:

• $D_i$ generates a random number, $N_i$, and a timestamp, $T_i$, respectively. Then, $D_i$ computes $R_{i,1}={PUF}_i(C_{i,1})$ and ${HR}_{i,1}=h(C_{i,1}||R_{i,1})$, and computes $R_{i,2}={PUF}_i(C_{i,2})$ and ${HR}_{i,2}=h(C_{i,2}||R_{i,2})$. Similarly, $(C_{i,2},R_{i,2})$ is also a challenge–response pair from the PUF of $D_i$, where $C_{i,2}$ denotes the input challenge and $R_{i,2}$ denotes the output response. Finally, $D_i$ computes ${R_i=HR}_{i,2}⨁h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right||{HR}_{i,1})$ and $M_i=h({PID}_i|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})$, and then sends $\{{PID}_i,N_i,R_i,T_i,M_i\}$ to $GS$, where $⨁$ denotes an XOR operation.
• Upon receiving the messages, $GS$ verifies the freshness of $\left|T_i^{\mathrm{*}}-T_i\right|\le ∆T$, where $T_i^{\mathrm{*}}$ and $∆T$ are the message reception time and maximum transmission time delay, respectively. If $T_i$ is valid, the $GS$ retrieves ${HR}_{i,1}$ based on ${PID}_i$ and computes $M_i^{\mathrm{*}}=h({PID}_i|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})$. Then, the $GS$ checks whether $M_i^{\mathrm{*}}$ is equal to $M_i$. If the condition is not valid, the $GS$ terminates the current authentication. Otherwise, the $GS$ computes ${HR}_{i,2}=R_i⨁h\left({PID}_i\left|\left|{ID}_s\right|\right|N_i\left|\left|T_i\right|\right|{HR}_{i,1}\right)$. Then, the $GS$ generates a random number, $N_s$, and a new challenge, $C_i^n$, for $D_i$, respectively. Moreover, the $GS$ computes ${PID}_i^n=h({ID}_i||C_i^n)$,$X_s=C_i^n⨁h\left({PID}_i\left|\left|{ID}_s\right|\right|N_i\left|\left|N_s\right|\right|{HR}_{i,1}\right)$, $Y_s={PID}_i^n⨁h({PID}_i|\left|{ID}_s\right|\left|T_i\right||N_s$ $\left|\right|{HR}_{i,1})$, ${SK}_{is}=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$, ${SKID}_{is}=h({PID}_i||{ID}_s)$, and $M_s=h(N_s|\left|X_s\right|\left|Y_s\right||{SK}_{is})$, where ${PID}_i^n$ denotes a new pseudo-identity for $D_i$, ${SK}_{is}$ denotes a session key between $D_i$ and $GS$, and ${SKID}_{is}$ is the key index of ${SK}_{is}$. Finally, $GS$ sends $\{N_s,X_s,Y_s,M_s\}$ to $D_i$, then stores ${PID}_i^n$ and ${HR}_{i,2}$.
• After obtaining the messages, $D_i$ computes ${SK}_{is}=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$, ${SKID}_{is}=h({PID}_i||{ID}_s)$, and $M_s^{\mathrm{*}}=h(N_s|\left|X_s\right|\left|Y_s\right||{SK}_{is})$. Then, $D_i$ checks whether $M_s^{\mathrm{*}}$ is equal to $M_s$. If the condition is not valid, $D_i$ terminates the current authentication. Otherwise, $D_i$ computes $C_i^n=X_s⨁h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right||{HR}_{i,1})$ and ${PID}_i^n=Y_s⨁h({PID}_i|\left|{ID}_s\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$. Finally, $D_i$ updates ${PID}_i={PID}_i^n$, $C_{i,1}=C_{i,2}$, and $C_{i,2}=C_i^n$.

After the drone-GS authentication and key agreement phase, $D_i$ and the $GS$ communicate using the session key, ${SK}_{is}$, which can be updated through a next round of this phase.

It should be noted that the $GS$ not only stores old values $\{{PID}_i,{HR}_{i,1}\}$, but also new values $\{{PID}_i^n,{HR}_{i,2}\}$, with the goal of resisting desynchronization attacks. In the next round of this phase or the next drone–drone authentication and key agreement phase, when the new values $\{{PID}_i^n,{HR}_{i,2}\}$ are used successfully, the $GS$ updates ${PID}_i={PID}_i^n$ and ${HR}_{i,1}$=${HR}_{i,2}$.

4.3. Drone–Drone Authentication and Key Agreement Phase

In this phase, $D_i$ and $D_j$ authenticate each other with the help of $GS$, and establish a session key between them. The phase is illustrated in Figure 4.

The detailed description of the drone–drone authentication and key agreement phase is as follows:

• $D_i$ generates a random number, $N_i$, and a timestamp, $T_i$, respectively. Then, $D_i$ computes $R_{i,1}={PUF}_i\left(C_{i,1}\right)$ and ${HR}_{i,1}=h(C_{i,1}||R_{i,1})$, and computes $R_{i,2}={PUF}_i\left(C_{i,2}\right)$ and ${HR}_{i,2}=h(C_{i,2}||R_{i,2})$. Finally, $D_i$ computes ${R_i=HR}_{i,2}⨁h({PID}_i||{PID}_j$ $\left|\right|{ID}_s\left|\right|N_i\left|\right|T_i\left|\right|{HR}_{i,1})$ and $M_i=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})$, and then sends $\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\}$ to the $GS$. ${PID}_j$ denotes a pseudo-identity for $D_j$, and can be obtained from the $GS$ or $D_j$ before the drone–drone authentication and key agreement phase.
• Upon receiving the messages, the $GS$ verifies the freshness of $\left|T_i^{\mathrm{*}}-T_i\right|\le ∆T$. If $T_i$ is valid, the $GS$ retrieves ${HR}_{i,1}$ based on ${PID}_i$ and computes $M_i^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})$. Then, the $GS$ checks whether $M_i^{\mathrm{*}}$ is equal to $M_i$. If the condition is not valid, the $GS$ terminates the current authentication. Otherwise, the $GS$ computes ${HR}_{i,2}=R_i⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right||{HR}_{i,1})$. Then, the $GS$ generates a random number, $N_s$, a timestamp, $T_s$, a master key, ${MK}_{ij}$, between $D_i$ and $D_j$, and a new challenge, $C_j^n$, for $D_j$. Moreover, the $GS$ retrieves ${HR}_{j,1}$ based on ${PID}_j$ and computes ${PID}_j^n=h({ID}_j||C_j^n)$, $X_{s,1}=C_j^n⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right||{HR}_{j,1})$, $Y_{s,1}={PID}_j^{0n}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|T_s\right|\left|N_s\right||{HR}_{j,1})$, $K_{s,1}={MK}_{ij}⨁{HR}_{i,1}⨁h({PID}_i|\left|{PID}_j\right||{ID}_s$ $\left|\right|N_i\left|\right|T_s\left|\right|N_s\left|\right|{HR}_{j,1})$ and $M_{s,1}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|X_{s,1}\right|\left|Y_{s,1}\right|\left|K_{s,1}\right|\left|T_s\right||{HR}_{j,1})$, where ${PID}_j^n$ denotes a new pseudo-identity for $D_j$. Finally, the $GS$ sends $\{{PID}_i,{PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\}$ to $D_j$.
• After obtaining the messages, $D_j$ verifies the freshness of $\left|T_s^{\mathrm{*}}-T_s\right|\le ∆T$, where $T_s^{\mathrm{*}}$ and $∆T$ are the message reception time and maximum transmission time delay, respectively. If $T_s$ is valid, $D_j$ computes $R_{j,1}={PUF}_j(C_{j,1})$ and ${HR}_{j,1}=h(C_{j,1}||R_{j,1})$, where ${PUF}_j()$ denotes the PUF of $D_j$. This means that $(C_{j,1},R_{j,1})$ is a challenge–response pair from the PUF of $D_j$, where $C_{j,1}$ denotes the input challenge and $R_{j,1}$ denotes the output response. Then, $D_j$ computes $M_{s,1}^{*}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|X_{s,1}\right|\left|Y_{s,1}\right|\left|K_{s,1}\right|\left|T_s\right||{HR}_{j,1})$ and checks whether $M_{s,1}^{*}$ is equal to $M_{s,1}$. If the condition is not valid, $D_j$ terminates the current authentication. Otherwise, $D_j$ computes $C_j^n=X_{s,1}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right||{HR}_{j,1})$, ${PID}_j^n=Y_{s,1}⨁ h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|T_s\right|\left|N_s\right||{HR}_{j,1})$ and ${MK}_{ij}⨁{HR}_{i,1}=K_{s,1}⨁ h({PID}_i|\left|{PID}_j\right||{ID}_s$ $\left|\right|N_i\left|\right|T_s\left|\right|N_s\left|\right|{HR}_{j,1})$. Then, $D_j$ generates a random number, $N_j$, and computes $R_{j,2}={PUF}_j\left(C_{j,2}\right)$ and ${HR}_{j,2}=h(C_{j,2}||R_{j,2})$. Similarly, $(C_{j,2},R_{j,2})$ is also a challenge–response pair from the PUF of $D_j$, where $C_{j,2}$ denotes the input challenge and $R_{j,2}$ denotes the output response. Moreover, $D_j$ computes ${SK}_{ij}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_j\right||{(MK}_{ij}⨁{HR}_{i,1}⨁{HR}_{j,1}))$, ${SKID}_{ij}=h({PID}_i||{PID}_j)$, ${R_j=HR}_{j,2}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|T_s\right|\left|N_s\right|\left|N_j\right||{HR}_{j,1})$, $M_{j,1}=h(N_i|\left|N_j\right||{SK}_{ij})$ and $M_{j,2}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right|\left|T_s\right|\left|N_j\right|\left|M_{j,1}\right|\left|R_j\right||{HR}_{j,1})$, where ${SK}_{ij}$ denotes a session key between $D_i$ and $D_j$, and ${SKID}_{ij}$ is the key index of ${SK}_{ij}$. Finally, $D_j$ sends $\{N_j,M_{j,1},R_j,M_{j,2}\}$ to the $GS$, then stores ${PID}_j^n$ and $C_j^n$.
• Upon receiving the messages, the $GS$ computes $M_{j,2}^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right||T_s$ $\left|\right|N_j\left|\right|M_{j,1}\left|\right|R_j\left|\right|{HR}_{j,1})$. Then, the $GS$ checks whether $M_{j,2}^{\mathrm{*}}$ is equal to $M_{j,2}$. If the condition is not valid, the $GS$ terminates the current authentication. Otherwise, the $GS$ generates a new challenge $C_i^n$ for $D_i$, and computes ${PID}_i^n=h({ID}_i||C_i^n)$ and ${HR}_{j,2}=R_j⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|T_s\right|\left|N_s\right|\left|N_j\right||{HR}_{j,1})$. Then, the $GS$ computes $X_{s,2}=C_i^n⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right|\left|N_j\right|\left|N_i\right||{HR}_{i,1})$, $Y_{s,2}={PID}_i^n⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right||N_j$ $\left|\right|T_i\left|\right|{HR}_{i,1})$, $K_{s,2}={MK}_{ij}⨁{HR}_{j,1}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right|\left|N_j\right|\left|T_i\right|\left|N_i\right||{HR}_{i,1})$ and $M_{s,2}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right|\left|N_j\right|\left|M_{j,1}\right|\left|X_{s,2}\right|\left|Y_{s,2}\right|\left|K_{s,2}\right||{HR}_{i,1})$. Finally, the $GS$ sends $\{N_s,N_j,M_{j,1},X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\}$ to $D_i$, then stores ${PID}_j^n$, ${HR}_{j,2}$, ${PID}_i^n$ and ${HR}_{i,2}$.
• After obtaining the messages, $D_i$ computes $M_{s,2}^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right||T_i$ $\left|\right|N_s\left|\right|N_j\left|\right|M_{j,1}\left|\right|X_{s,2}\left|\right|Y_{s,2}\left|\right|K_{s,2}\left|\right|{HR}_{i,1})$ and checks whether $M_{s,2}^{\mathrm{*}}$ is equal to $M_{s,2}$. If the condition is not valid, $D_i$ terminates the current authentication. Otherwise, $D_i$ computes $C_i^n=X_{s,2}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right|\left|N_j\right|\left|N_i\right||{HR}_{i,1})$, ${PID}_i^n=Y_{s,2}⨁h({PID}_i$ $\left|\right|{PID}_j\left|\right|{ID}_s\left|\right|N_s\left|\right|N_j\left|\right|T_i\left|\right|{HR}_{i,1})$ and ${MK}_{ij}⨁{HR}_{j,1}=K_{s,2}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right|\left|N_j\right||T_i$ $\left|\right|N_i\left|\right|{HR}_{i,1})$. Moreover, $D_i$ computes ${SK}_{ij}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_j\right||({MK}_{ij}⨁{HR}_{j,1}$ $⨁{HR}_{i,1}))$, ${SKID}_{ij}=h({PID}_i||{PID}_j)$ and $M_{j,1}^{\mathrm{*}}=h(N_i|\left|N_j\right||{SK}_{ij})$, and checks whether $M_{j,1}^{\mathrm{*}}$ is equal to $M_{j,1}$. If the condition is not valid, $D_i$ terminates the current authentication. Otherwise, $D_i$ updates ${PID}_i={PID}_i^n$, $C_{i,1}=C_{i,2}$ and $C_{i,2}=C_i^n$.

After the drone–drone authentication and key agreement phase, $D_i$ and $D_j$ communicate using the session key, ${SK}_{ij}$, which can be updated through a next round of this phase.

It should be noted that the $GS$ not only stores old values $\{{PID}_i,{HR}_{i,1}\}$, but also new values $\{{PID}_i^n,{HR}_{i,2}\}$, with the goal of resisting desynchronization attacks. In the next round of this phase or the next drone-GS authentication and key agreement phase, when the new values $\{{PID}_i^n,{HR}_{i,2}\}$ are used successfully, the $GS$ updates ${PID}_i={PID}_i^n$ and ${HR}_{i,1}$ = ${HR}_{i,2}$.

Similarly, the $GS$ not only stores old values $\{{PID}_j,{HR}_{j,1}\}$, but also new values $\{{PID}_j^n,{HR}_{j,2}\}$, with the goal of resisting desynchronization attacks. In the next round of this phase or the next drone-GS authentication and key agreement phase, when the new values $\{{PID}_j^n,{HR}_{j,2}\}$ are used successfully, the $GS$ updates ${PID}_j={PID}_j^n$ and ${HR}_{j,1}$=${HR}_{j,2}$.

In addition, $D_j$ not only stores old values $\{{PID}_j,C_{j,1},C_{j,2}\}$, but also new values $\{{PID}_j^n,C_j^n\}$, with the goal of resisting desynchronization attacks. In the next round of this phase or the next drone-GS authentication and key agreement phase, when the new values $\{{PID}_j^n,C_j^n\}$ are used successfully, $D_j$ updates ${PID}_j={PID}_j^n$, $C_{j,1}=C_{j,2}$ and $C_{j,2}=C_j^n$.

5. Security Analysis

In this section, we first perform informal security analysis of SLAKA-IoD. Then, we provide a formal security analysis of SLAKS-IoD based on the strand space model. Third, we also provide security verification through the Scyther tool (v1.1.3) to prove the security of SLAKA-IoD. Finally, we compare the security features of SLAKA-IoD with other related schemes.

5.1. Informal Security Analysis

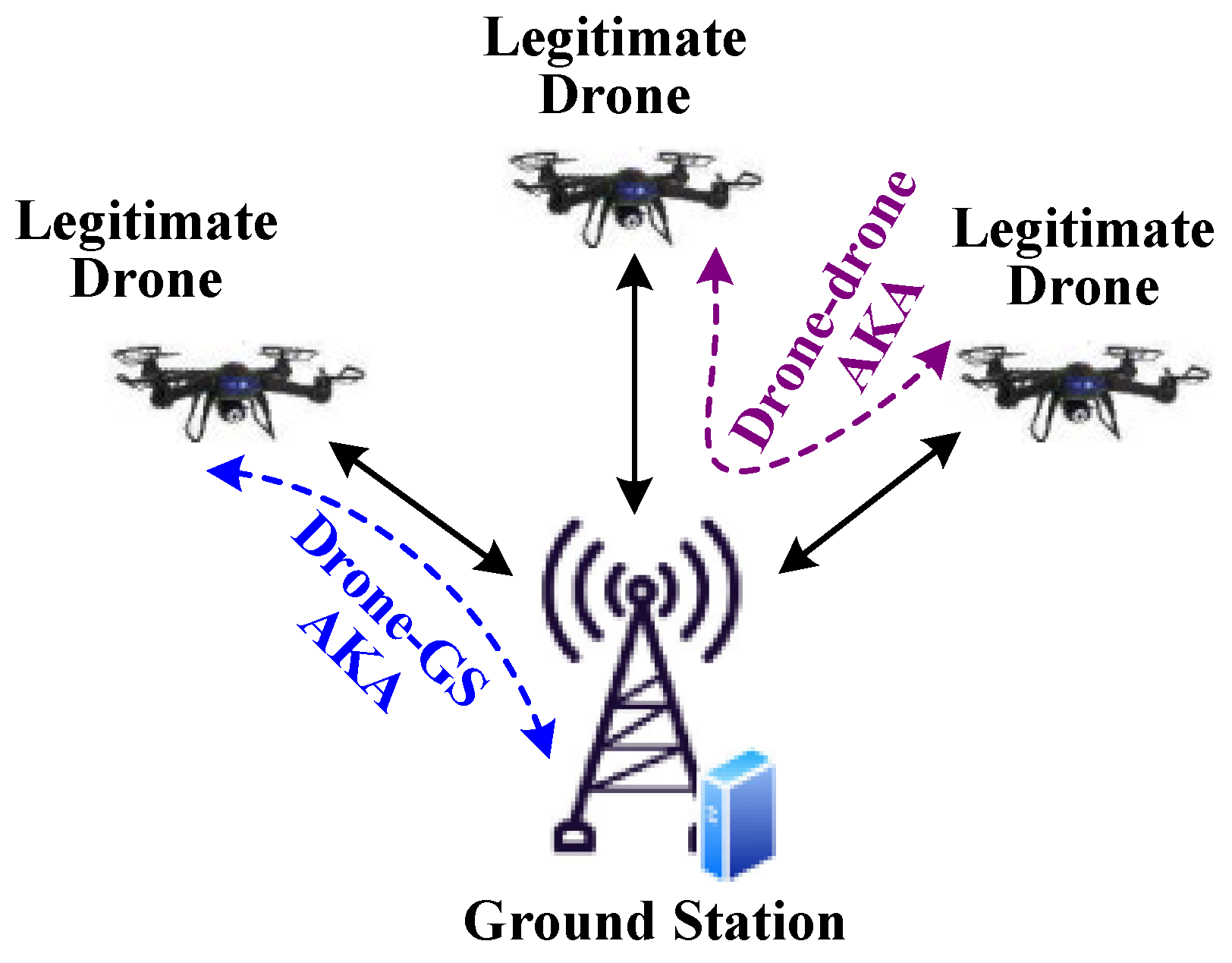
This section evaluates the security of SLAKA-IoD based on informal security analysis. We prove that SLAKA-IoD can resist various potential security attacks and provide mutual authentication, session key agreement, anonymity and untraceability.

(1)

Impersonation Attack

In the drone-GS authentication and key agreement phase of SLAKA-IoD, if $MA$ wants to impersonate $D_i$, then it needs to construct $\{{PID}_i,N_i,R_i,T_i,M_i\}$. However, it is impossible to calculate $R_i$ and $M_i$ because $MA$ does not know ${HR}_{i,1}$. Similarly, if $MA$ wants to impersonate the $GS$, then it needs to construct $\{N_s,X_s,Y_s,M_s\}$, but it cannot calculate $X_s$, $Y_s$ and $M_s$ because $MA$ does not know ${HR}_{i,1}$.

In the drone–drone authentication and key agreement phase of SLAKA-IoD, if $MA$ wants to impersonate $D_i$, then it needs to construct $\{{PID}_i, {PID}_j,N_i,R_i,T_i,M_i\}$, but it cannot calculate $R_i$ and $M_i$ because $MA$ does not know ${HR}_{i,1}$. If $MA$ wants to impersonate $D_j$, then it needs to construct $\{N_j,M_{j,1},R_j,M_{j,2}\}$, but it cannot calculate $R_j$, $M_{j,1}$ and $M_{j,2}$ because $MA$ does not know ${HR}_{j,1}$. Similarly, if $MA$ wants to impersonate $GS$, then it needs to construct $\{{PID}_i, {PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\}$ or $\{N_s,N_j, M_{j,1}, X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\}$, but it cannot calculate $X_{s,1}$, $Y_{s,1}$, $K_{s,1}$, $M_{s,1}$, $X_{s,2}$, $Y_{s,2}$, $K_{s,2}$ and $M_{s,2}$ because $MA$ does not know ${HR}_{i,1}$ and ${HR}_{j,1}$.

Consequently, SLAKA-IoD can resist impersonation attacks.

(2)

Replay Attack

In the drone-GS authentication and key agreement phase of SLAKA-IoD, $\{{PID}_i,N_i,R_i,T_i,M_i\}$ is protected with ${HR}_{i,1}$ and includes $T_i$, where ${HR}_{i,1}$ is unknown to $MA$ and $T_i$ is the current timestamp of $D_i$. Hence, $\{{PID}_i,N_i,R_i,T_i,M_i\}$ cannot be replayed. $\{N_s,X_s,Y_s,M_s\}$ is protected with ${SK}_{is}$ and includes $N_i$, where ${SK}_{is}$ is extended from ${HR}_{i,1}$ and $N_i$ is the random number of $D_i$. Thus, $\{N_s,X_s,Y_s,M_s\}$ cannot be replayed.

In the drone–drone authentication and key agreement phase of SLAKA-IoD, $\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\}$ is protected with ${HR}_{i,1}$ and includes $T_i$. Similarly, $\{{PID}_i,{PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\}$ is protected with ${HR}_{j,1}$ and includes $T_s$, where ${HR}_{j,1}$ is unknown to $MA$ and $T_s$ is the current timestamp of the$GS$. Hence, $\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\}$ and $\{{PID}_i,{PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\}$ cannot be replayed. $\{N_j,M_{j,1},R_j,M_{j,2}\}$ is protected with ${HR}_{j,1}$ and includes $N_s$, where $N_s$ is the random number of the $GS$. Similarly, $\{N_s,N_j,M_{j,1},X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\}$ is protected with ${HR}_{i,1}$ and includes $N_i$. Hence, $\{N_j,M_{j,1},R_j,M_{j,2}\}$ and $\{N_s,N_j,M_{j,1},X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\}$ cannot be replayed.

Therefore, SLAKA-IoD can resist replay attacks.

(3)

Denial of Service (DoS) Attack

If $MA$ wants to perform DoS attacks on the SLAKA-IoD protocol, then it must be able to replay some messages of the protocol, or forge some legitimate messages of the protocol. As just described, $\{{PID}_i,N_i,R_i,T_i,M_i\}$, $\{N_s,X_s,Y_s,M_s\}$, $\{{PID}_i, {PID}_j,N_i,R_i,T_i,M_i\}$, $\{{PID}_i, {PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\}$, $\{N_j,M_{j,1},R_j,M_{j,2}\}$ and $\{N_s,N_j, M_{j,1}, X_{s,2},Y_{s,2},$ $K_{s,2},M_{s,2}\}$ cannot be replayed. In addition, these messages are protected with ${HR}_{i,1}$ or ${HR}_{j,1}$, which are unknown to $MA$. As a result, $MA$ cannot forge them. Hence, SLAKA-IoD can resist DoS attacks.

(4)

MITM Attack

If $MA$ wants to perform MITM attacks on the SLAKA-IoD protocol, then it must intercept and tamper with the messages in the protocol. According to the above description, $\{{PID}_i,N_i,R_i,T_i,M_i\}$, $\{N_s,X_s,Y_s,M_s\}$, $\{{PID}_i, {PID}_j,N_i,R_i,T_i,M_i\}$, $\{{PID}_i, {PID}_j,N_i,N_s,X_{s,1},$ $Y_{s,1},K_{s,1},T_s,M_{s,1}\}$, $\{N_j,M_{j,1},R_j,M_{j,2}\}$ and $\{N_s,N_j, M_{j,1}, X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\}$ are protected with ${HR}_{i,1}$ or ${HR}_{j,1}$, which are unknown to $MA$. As a result, $MA$ can intercept these messages, but it cannot tamper with them. Hence, SLAKA-IoD can prevent MITM attacks.

(5)

Drone Physical Capture Attack

Assume that $MA$ has physically captured $D_i$ or $D_j$. Then, by performing power analysis attacks on them, $MA$ can obtain the stored information of $D_i$ or $D_j$, including ${ID}_s$, ${PID}_i$, ${PID}_j$, $C_{i,1}$, $C_{i,2}$, $C_{j,1}$, $C_{j,2}$, ${PID}_j^n$ and $C_j^n$. Although $MA$ can obtain this information, it cannot try to probe or alter the integrated circuits of captured drones to retrieve the output responses of their PUFs, because this attempt will irreversibly modify the slight physical variations in the integrated circuits and in turn destroy these PUFs. That is to say, $MA$ cannot obtain $R_{i,1}$, $R_{i,2}$, $R_{j,1}$ and $R_{j,2}$ based on $C_{i,1}$, $C_{i,2}$, $C_{j,1}$, $C_{j,2}$ and $C_j^n$, respectively, resulting in $MA$ not being able to obtain ${HR}_{i,1}$, ${HR}_{i,2}$, ${HR}_{j,1}$ and ${HR}_{j,2}$ to compute any session key in SLAKA-IoD. Thus, SLAKA-IoD can prevent drone physical capture attacks.

(6)

Desynchronization Attack

For the drone-GS authentication and key agreement phase of SLAKA-IoD, $D_i$ stores old values $\{{PID}_i,C_{i,1},C_{i,2}\}$ before receiving the second message of the phase, and updates ${PID}_i={PID}_i^n$, $C_{i,1}=C_{i,2}$ and $C_{i,2}=C_i^n$ after receiving the second message of the phase. In addition, $GS$ not only stores old values $\{{PID}_i,{HR}_{i,1}\}$, but also new values $\{{PID}_i^n,{HR}_{i,2}\}$. Thus, whether or not $MA$ blocks the second message of the phase to perform desynchronization attacks, there is always a set of pseudo-identity and key material values used for this phase between $D_i$ and $GS$.

For the drone–drone authentication and key agreement phase of SLAKA-IoD, $D_i$ stores old values $\{{PID}_i,C_{i,1},C_{i,2}\}$ before receiving the fourth message of the phase, and updates ${PID}_i={PID}_i^n$,$C_{i,1}=C_{i,2}$ and $C_{i,2}=C_i^n$ after receiving the fourth message of the phase. In addition, $GS$ not only stores old values, $\{{PID}_i,{HR}_{i,1}\}$ and $\{{PID}_j,{HR}_{j,1}\}$, but also new values, $\{{PID}_i^n,{HR}_{i,2}\}$ and $\{{PID}_j^n,{HR}_{j,2}\}$. $D_j$ not only stores old values, $\{{PID}_j,C_{j,1},C_{j,2}\}$, but also new values, $\{{PID}_j^n,C_j^n\}$, which will be used to update ${PID}_j={PID}_j^n$, $C_{j,1}=C_{j,2}$ and $C_{j,2}=C_j^n$. Thus, whether or not $MA$ blocks the third or fourth message of the phase to perform desynchronization attacks, there is always a set of pseudo-identity and key material values used for this phase among $D_i$, $D_j$ and the $GS$.

Hence, SLAKA-IoD can prevent desynchronization attacks.

(7)

Session Key Disclosure Attack

In the drone-GS authentication and key agreement phase of SLAKA-IoD, ${SK}_{is}=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$. However, $MA$ cannot compute the session key, ${SK}_{is}$, because it does not know ${ID}_s$ and ${HR}_{i,1}$.

In the drone–drone authentication and key agreement phase of SLAKA-IoD, ${SK}_{ij}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_j\right||{(MK}_{ij}⨁{HR}_{i,1}⨁{HR}_{j,1}))$. However, $MA$ cannot compute the session key, ${SK}_{ij}$, because it does not know ${MK}_{ij}$, ${HR}_{i,1}$ and ${HR}_{j,1}$.

Thus, SLAKA-IoD is resilient to session key disclosure attacks.

(8)

ESL Attack

Based on the CK threat model, $MA$ can compromise the session state and secret credentials apart from all the activities permitted under the DY threat model. In the drone-GS authentication and key agreement phase of SLAKA-IoD, even if $MA$ can obtain the long-term secret $\left\{{ID}_s\right\}$, it cannot compute the session key, ${SK}_{is}$, because it does not know ${HR}_{i,1}$, which is computed by running the PUF of $D_i$.

In the drone–drone authentication and key agreement phase of SLAKA-IoD, even if $MA$ can obtain the short-term secret $\left\{{MK}_{ij}\right\}$, it cannot compute the session key, ${SK}_{ij}$, because it does not know ${HR}_{i,1}$ and ${HR}_{j,1}$, which are computed by running PUFs of $D_i$ and $D_j$, respectively.

Consequently, SLAKA-IoD is resilient to ESL attacks.

(9)

Anonymity and Untraceability

For the drone-GS authentication and key agreement phase of SLAKA-IoD, ${PID}_i$ is used instead of ${ID}_i$, and ${PID}_i$ is different in each round of the phase. In addition, ${PID}_i^n$ is secret, which prevents $MA$ from associating ${PID}_i$ and ${PID}_i^n$.

For the drone–drone authentication and key agreement phase of SLAKA-IoD, ${PID}_i$ and ${PID}_j$ are used instead of ${ID}_i$ and ${ID}_j$, respectively, and ${PID}_i$ are ${PID}_j$ are different in each round of the phase, respectively. In addition, ${PID}_i^n$ and ${PID}_j^n$ are secret, which prevents $MA$ from associating ${PID}_i$ with ${PID}_i^n$, and associating ${PID}_j$ with ${PID}_j^n$.

Note that $MA$ can obtain both ${PID}_j$ and ${PID}_j^n$ by physically capturing $D_j$ for the drone–drone authentication and key agreement phase of SLAKA-IoD. However, it is no longer meaningful for $MA$ to track its physically captured $D_j$. Therefore, SLAKA-IoD provides anonymity and untraceability.

(10)

Mutual Authentication

In the drone-GS authentication and key agreement phase of SLAKA-IoD, after receiving $\{{PID}_i,N_i,R_i,T_i,M_i\}$, the $GS$ computes $M_i^{*}=h({PID}_i|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})$ and checks whether $M_i^{*}$ is equal to $M_i$. If the condition is valid, $GS$ successfully authenticates $D_i$ because only $D_i$ and $GS$ know ${HR}_{i,1}$. Similarly, upon receiving $\{N_s,X_s,Y_s,M_s\}$, $D_i$ computes ${SK}_{is}=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$ and $M_s^{*}=h(N_s|\left|X_s\right|\left|Y_s\right||{SK}_{is})$, and then checks whether $M_s^{*}$ is equal to $M_s$. If the condition is valid, $D_i$ successfully authenticates the $GS$ because only $D_i$ and $GS$ know ${HR}_{i,1}$.

In the drone–drone authentication and key agreement phase of SLAKA-IoD, after receiving $\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\}$, the $GS$ computes $M_i^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})$ and checks whether $M_i^{\mathrm{*}}$ is equal to $M_i$. If the condition is valid, $GS$ successfully authenticates $D_i$ because only $D_i$ and $GS$ know ${HR}_{i,1}$. Similarly, upon receiving $\{{PID}_i,{PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\}$,$D_j$ computes $M_{s,1}^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|X_{s,1}\right||Y_{s,1}$ $\left|\right|K_{s,1}\left|\right|T_s\left|\right|{HR}_{j,1})$ and checks whether $M_{s,1}^{\mathrm{*}}$ is equal to $M_{s,1}$. If the condition is valid, $D_j$ successfully authenticates both $D_i$ and $GS$. This is because only $D_j$ and $GS$ know ${HR}_{j,1}$, and ${PID}_i$ is included in $h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|X_{s,1}\right|\left|Y_{s,1}\right|\left|K_{s,1}\right|\left|T_s\right||{HR}_{j,1})$. After obtaining $\{N_j,M_{j,1},R_j,M_{j,2}\}$, the $GS$ computes $M_{j,2}^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right|\left|T_s\right|\left|N_j\right|\left|M_{j,1}\right||R_j$ $\left|\right|{HR}_{j,1})$ and checks whether $M_{j,2}^{\mathrm{*}}$ is equal to $M_{j,2}$. If the condition is valid, the $GS$ successfully authenticates $D_j$ because only $D_j$ and the $GS$ know ${HR}_{j,1}$. Further, upon receiving $\{N_s,N_j,M_{j,1},X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\}$, $D_i$ computes $M_{s,2}^{\mathrm{*}}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right|\left|N_j\right||M_{j,1}$ $\left|\right|X_{s,2}\left|\right|Y_{s,2}\left|\right|K_{s,2}\left|\right|{HR}_{i,1})$ and checks whether $M_{s,2}^{\mathrm{*}}$ is equal to $M_{s,2}$, computes ${SK}_{ij}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_j\right||{(MK}_{ij}⨁{HR}_{i,1}⨁{HR}_{j,1}))$,$M_{j,1}^{\mathrm{*}}=h(N_i|\left|N_j\right||{SK}_{ij})$ and checks whether $M_{j,1}^{\mathrm{*}}$ is equal to $M_{j,1}$. If these conditions are valid, $D_i$ successfully authenticates both $D_j$ and the $GS$. This is because only $D_i$ and the $GS$ know ${HR}_{i,1}$, and only $D_i$ and $D_j$ can compute ${SK}_{ij}$.

Hence, SLAKA-IoD provides mutual authentication.

(11)

Forward and Backward Secrecy

For the drone-GS authentication and key agreement phase of SLAKA-IoD, even if $MA$ can obtain the current session key, ${SK}_{is}$, it cannot compromise the session key of any past session or any future session. This is because ${HR}_{i,1}$ is different in each round of the phase and cannot be obtained by $MA$, where ${HR}_{i,1}$ is used to compute ${SK}_{is}=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$.

For the drone–drone authentication and key agreement phase of SLAKA-IoD, even if $MA$ can obtain the current session key, ${SK}_{ij}$, it cannot compromise the session key of any past session or any future session. This is because ${MK}_{ij}$, ${HR}_{i,1}$ and ${HR}_{j,1}$ are different in each round of the phase and cannot be obtained by $MA$, where ${MK}_{ij}$, ${HR}_{i,1}$ and ${HR}_{j,1}$ are used to compute ${SK}_{ij}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_j\right||{(MK}_{ij}⨁{HR}_{i,1}⨁{HR}_{j,1}))$.

Hence, SLAKA-IoD provides forward and backward secrecy.

(12)

PUF Challenge–Response Pair Protection

In the above SLAKA-IoD, ${HR}_{i,1}$ and ${HR}_{i,2}$ instead of $R_{i,1}$ and $R_{i,2}$ are securely transmitted to the $GS$ and are stored in the $GS$. Similarly, ${HR}_{j,1}$ and ${HR}_{j,2}$ instead of $R_{j,1}$ and $R_{j,2}$ are securely transmitted to the $GS$ and are stored in the $GS$. As a result, it is difficult for $MA$ to obtain $R_{i,1}$, $R_{i,2}$, $R_{j,1}$ and $R_{j,2}$. Even if $MA$ can obtain ${HR}_{i,1}$ and ${HR}_{i,2}$, it cannot guess $R_{i,1}$ and $R_{i,2}$ in reverse based on them, as they are generated by hashing $R_{i,1}$ and $R_{i,2}$, respectively. Similarly, even if $MA$ can obtain ${HR}_{j,1}$ and ${HR}_{j,2}$, it cannot guess $R_{j,1}$ and $R_{j,2}$ in reverse based on them, as they are generated by hashing $R_{j,1}$ and $R_{j,2}$, respectively.

Additionally, $C_{i,1}$ and $C_{i,2}$ are stored in $D_i$ instead of the $GS$. Similarly, $C_{j,1}$ and $C_{j,2}$ are stored in $D_j$ instead of $GS$. Therefore, in order to obtain the PUF challenge–response pairs of $D_i$, it is also necessary for $MA$ to capture $D_i$ to obtain $C_{i,1}$ and $C_{i,2}$. Similarly, in order to obtain the PUF challenge–response pairs of $D_j$, it is also necessary for $MA$ to capture $D_j$ to obtain $C_{j,1}$ and $C_{j,2}$.

Hence, SLAKA-IoD provides PUF challenge–response pair protection.

5.2. Formal Security Analysis Based on the Strand Space Model

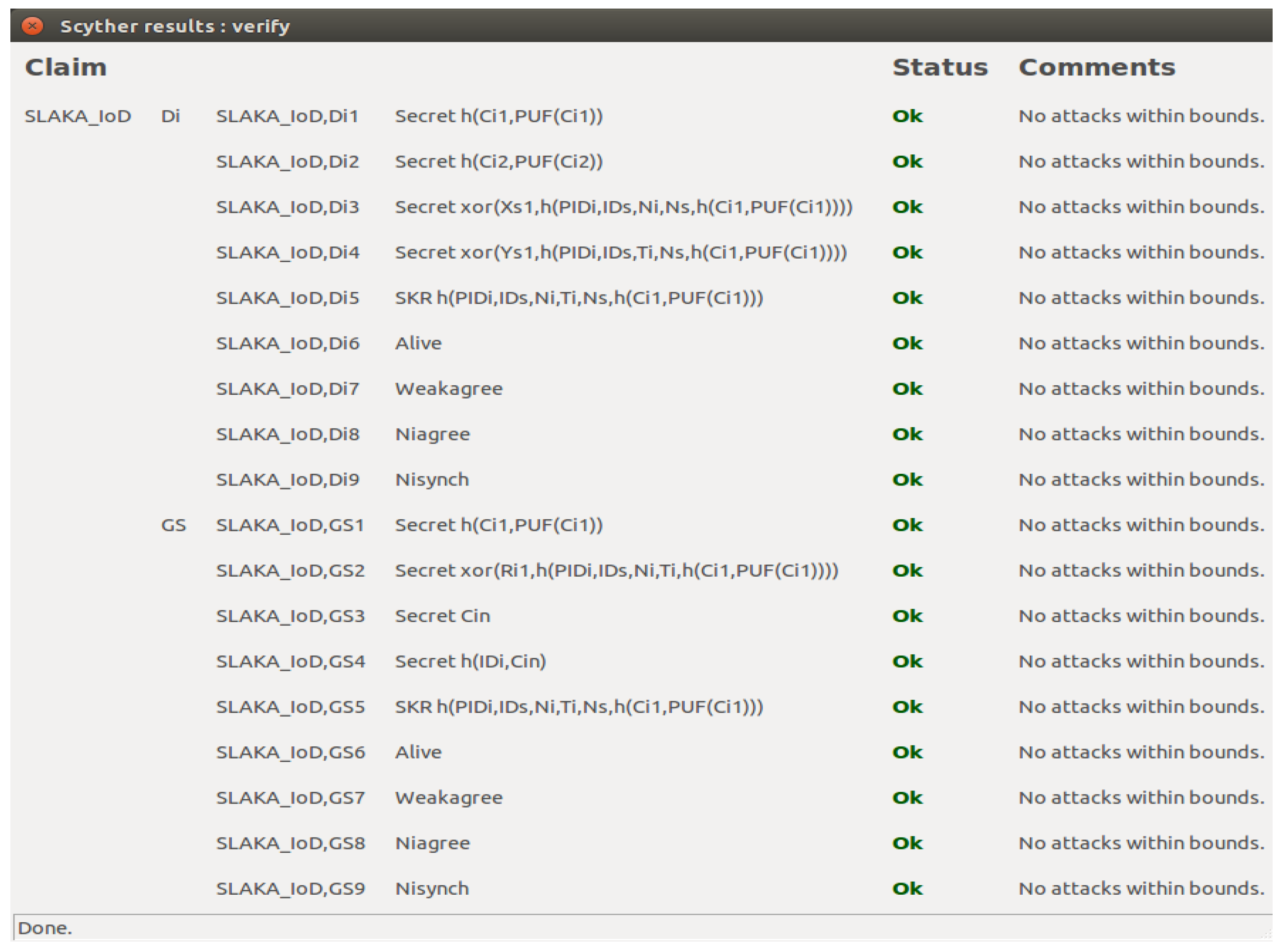
Because the strand space model [43,44] is a well-studied formal analysis method for security protocols, we use the strand space model to analyze the security of our proposed SLAKA-IoD protocol as follows.

Definition 1. 

An infiltrated strand space, $\Sigma ,\mathcal{P}$, is a space for the drone-GS authentication and key agreement phase of SLAKA-IoD if it is the union of three kinds of strands: (1) Initiator strands, $s\in Init[D_i, GS, {PID}_i, {ID}_s, N_i, N_s, T_i, C_i^n, {PID}_i^n, {HR}_{i,2}]$ with trace: $<+\left\{{PID}_i,N_i,R_i,T_i,M_i\right\},-\{N_s,X_s,Y_s,M_s\}>$. The principal associated with this strand is $D_i$ (2) Responder strands, $r\in Resp[D_i, GS, {PID}_i, {ID}_s, N_i, N_s, T_i, C_i^n, {PID}_i^n, {HR}_{i,2}]$ with trace: $<-\left\{{PID}_i,N_i,R_i,T_i,M_i\right\},+\{N_s,X_s,Y_s,M_s\}>$. The principal associated with this strand is $GS$. (3) Penetrator strands, $p\in \mathcal{P}$ [43,44].

Theorem 1. 

Suppose (1) $\Sigma$ is a space for the drone-GS authentication and key agreement phase of SLAKA-IoD, and $\mathcal{C}$ is a bundle containing an initiator strand, $s\in Init[D_i, GS, {PID}_i, {ID}_s, N_i, N_s, T_i, C_i^n, {PID}_i^n, {HR}_{i,2}]$; (2) ${HR}_{i,1}\notin K_p$; (3) $N_i$ and $N_s$ are uniquely originating in $\Sigma$. Then, $\mathcal{C}$ contains a unique responder strand, $r\in Resp[D_i, GS, {PID}_i, {ID}_s, N_i, N_s, T_i, C_i^n, {PID}_i^n, {HR}_{i,2}]$.

Proof of Theorem 1. 

According to assumption (2), ${HR}_{i,1}\notin K_p$. Since ${SK}_{is}=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right||{HR}_{i,1})$, ${SK}_{is}\notin K_p$. By assumption (3), $N_s$ is uniquely originating in $\mathsf{\Sigma }$ by assumption (3), so $M_s=h(N_s|\left|X_s\right|\left|Y_s\right||{SK}_{is})\subset term(<s,2>)$ must uniquely originate on a responder strand $r\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}[D_i,GS,{PID}_i,{ID}_s,N_i,N_{\mathrm{s}},{\mathrm{T}}_i,C_i^n,{PID}_i^n,{{(HR}_{i,2})}^{\prime }]$. By assumptions (2) and (3), ${HR}_{i,1}\notin K_p$ and $N_i$ is uniquely originating in $\mathsf{\Sigma }$, so ${(M_i)}^{\prime }=h({PID}_i|\left|N_i\right|\left|{{(R}_i)}^{\prime }\right|\left|T_i\right||{HR}_{i,1})\subset term(<r,1>)$ must uniquely originate on $s$ according to assumption (1), where ${(R_i)}^{\prime }={({HR}_{i,2})}^{\prime }⨁h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right||{HR}_{i,1})$. According to $\mathrm{s}$ and Definition 1, ${{(HR}_{i,2})}^{\prime }={HR}_{i,2}$ and ${{(R}_i)}^{\prime }=R_i$. Hence, $r\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}[D_i,GS,{PID}_i,{ID}_s,N_i,N_{\mathrm{s}},{\mathrm{T}}_i,C_i^n,{PID}_i^n,{HR}_{i,2}]$. □

According to Theorem 1, $D_i$ successfully authenticates $GS$, and can establish an injection agreement [43,44] with them.

Theorem 2. 

Suppose: (1) $\Sigma$ is a space for the drone-GS authentication and key agreement phase of SLAKA-IoD, and $\mathcal{C}$ is a bundle containing a responder strand $r\in Resp[D_i, GS, {PID}_i, {ID}_s, N_i, N_s, T_i, C_i^n, {PID}_i^n, {HR}_{i,2}]$; (2) ${HR}_{i,1}\notin K_p$; (3) $N_i$ is uniquely originating in $\Sigma$, and $T_i$ is a fresh timestamp to prevent replay. Then, $\mathcal{C}$ contains a unique initiator strand $s\in Init[D_i, GS, {PID}_i, {ID}_s, N_i, N_s, T_i, C_i^n, {PID}_i^n, {HR}_{i,2}]$.

Proof of Theorem 2. 

According to assumptions (2) and (3), ${HR}_{i,1}\notin K_p$ and $N_i$ is uniquely originating in $\mathsf{\Sigma }$, so $M_i=h({PID}_i|\left|N_i\right|\left|{R_i\left|\right|T}_i\right||{HR}_{i,1})\subset term(<r,1>)$ must uniquely originate on an initiator strand $s\in \mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}[D_i,GS,{PID}_i,{ID}_s,N_i,{{(N}_{\mathrm{s}})}^{\prime },T_i,{{(C}_i^n)}^{\prime },{{(PID}_i^n)}^{\prime },{HR}_{i,2}]$. Since ${HR}_{i,1}\notin K_p$, ${{(M}_s)}^{\prime }=h({{(N}_s)}^{\prime }|\left|{(X_s)}^{\prime }\right|\left|{(Y_s)}^{\prime }\right||{({SK}_{is})}^{\prime })\subset term(<s,2>)$ must originate on a responder strand $r^{\prime }\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}[D_i,GS,{PID}_i,{ID}_s,N_i,{{(N}_{\mathrm{s}})}^{\prime },T_i,{{(C}_i^n)}^{\prime },{{(PID}_i^n)}^{\prime },{HR}_{i,2}]$ according to assumption (1), where $(X_s)={{(C}_i^n)}^{\prime }⨁h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|{(N_s)}^{\prime }\right||{HR}_{i,1})$, ${{(Y}_s)}^{\prime }={({PID}_i^n)}^{\prime }⨁ h({PID}_i|\left|{ID}_s\right|\left|T_i\right|\left|{(N_s)}^{\prime }\right||{HR}_{i,1})$ and ${({SK}_{is})}^{\prime }=h({PID}_i|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|{{(N}_s)}^{\prime }\right||{HR}_{i,1})$. As a result, $term\left(<r,1>\right)=term\left(<r^{\prime },1>\right)=\{{PID}_i,N_i,R_i,T_i,M_i\}$, i.e., $\{{PID}_i,N_i,R_i,T_i,M_i\}$ is replayed, which contradicts with assumption (3). Hence, $r^{\prime }=r$, so ${{(N}_s)}^{\prime }=N_s$, ${{(C}_i^n)}^{\prime }=C_i^n$ and ${{(PID}_i^n)}^{\prime }={PID}_i^n$. That is to say, $s\in \mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}[D_i,GS,{PID}_i,{ID}_s,N_i,N_s,T_i,C_i^n,{PID}_i^n,{HR}_{i,2}]$. □

According to Theorem 2, $GS$ successfully authenticates $D_i$, and can establish an injection agreement [43,44] with them.

From Theorems 1 and 2, mutual authentication between $D_i$ and $GS$ is established. Additionally, injection agreement between $D_i$ and $GS$ is established, so replay and MitM attacks between $D_i$ and $GS$ are overcome according to the definition of the injection agreement [43,44].

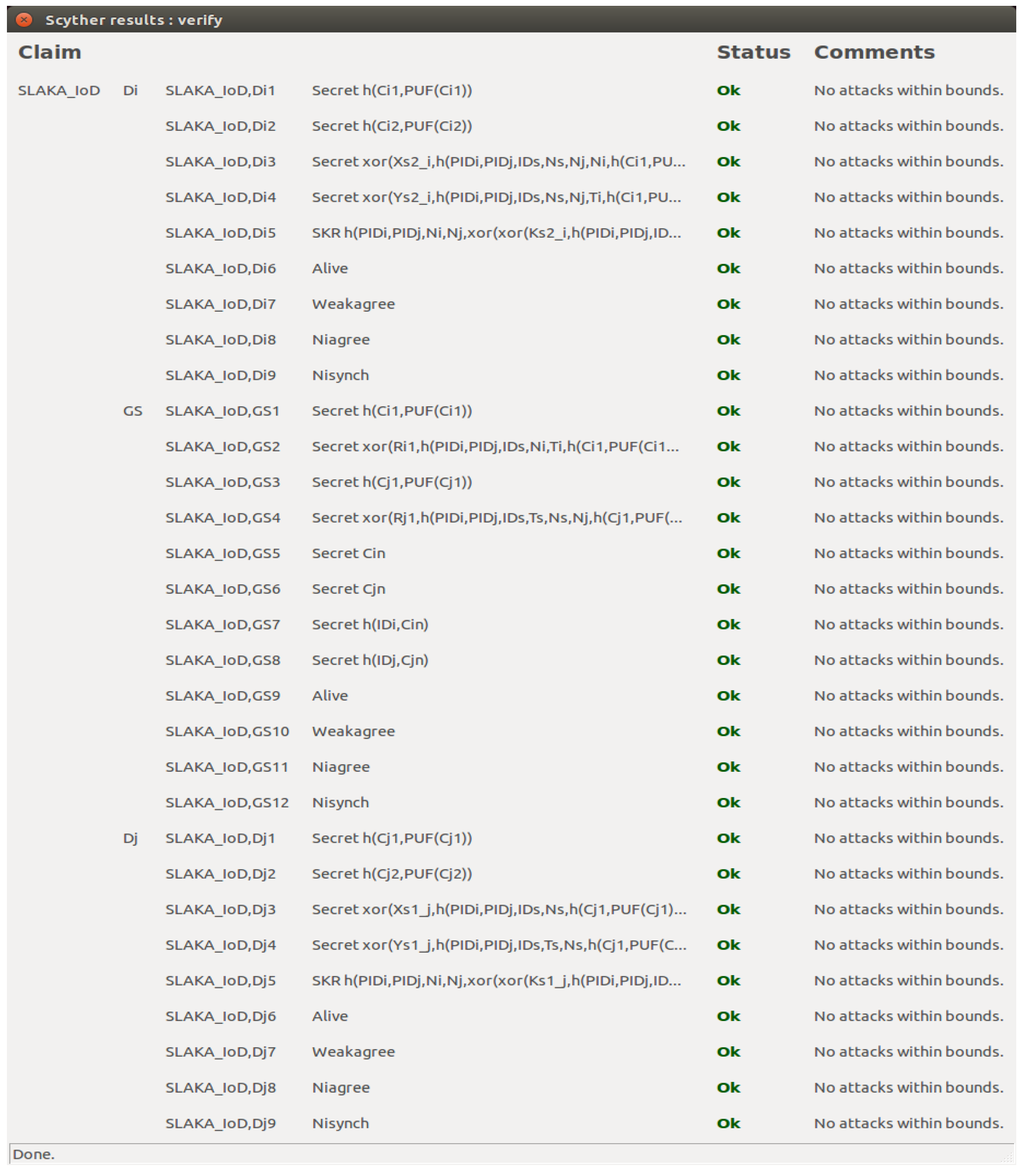
Definition 2. 

An infiltrated strand space $\Sigma ,\mathcal{P}$ is a space for the drone–drone authentication and key agreement phase of SLAKA-IoD if it is the union of four kinds of strands: (1) Initiator strands $s\in Init\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i, {MK}_{ij},C_i^n, {PID}_i^n, {HR}_{i,2}\right]$ with trace: $<+\left\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\right\},-\left\{N_s,N_j, M_{j,1}, X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\right\}>$. The principal associated with this strand is $D_i$; (2) Responder strands $r\in Resp\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j, N_s, T_s, {MK}_{ij},C_j^n, {PID}_j^n,{HR}_{j,2}\right]$ with trace:$<-\left\{{PID}_i, {PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\right\},+\left\{N_j,M_{j,1},R_j,M_{j,2}\right\}>$. The principal associated with this strand is $D_j$; (3) Server strands $t\in Serv\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i,T_s, {MK}_{ij},C_i^n,C_j^n, {PID}_i^n, {PID}_j^n,{HR}_{i,2},{HR}_{j,2}\right]$ with trace: $<-\left\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\right\},+\left\{{PID}_i, {PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\right\},$ $-\left\{N_j,M_{j,1},R_j,M_{j,2}\right\},+\left\{N_s,N_j, M_{j,1}, X_{s,2},Y_{s,2},K_{s,2},M_{s,2}\right\}>.$ The principal associated with this strand is $GS$; (4) Penetrator strands $p\in \mathcal{P}$ [43,44].

Theorem 3. 

Suppose: (1) $\Sigma$ is a space for the drone–drone authentication and key agreement phase of SLAKA-IoD, and $\mathcal{C}$ is a bundle containing an initiator strand $s\in Init\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i, {MK}_{ij},C_i^n, {PID}_i^n,{HR}_{i,2}\right]$; (2) ${HR}_{i,1}, {HR}_{j,1}\notin K_p$; (3) $N_i$, $N_j$ and $N_s$ are uniquely originating in $\Sigma$. Then, $\mathcal{C}$ contains a unique responder strand $r\in Resp\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, {(T_s)}^{\prime }, {MK}_{ij},{(C_j^n)}^{\prime }, {{(PID}_j^n)}^{\prime },{{(HR}_{j,2})}^{\prime }\right]$ and a unique server strand $t\in Serv[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i,{(T_s)}^{\prime }, {MK}_{ij},C_i^n,{(C_j^n)}^{\prime }, {PID}_i^n, {{(PID}_j^n)}^{\prime },$ ${HR}_{i,2},{{(HR}_{j,2})}^{\prime }]$.

Proof of Theorem 3. 

According to assumptions (2) and (3), ${HR}_{i,1}\notin K_p$ and $N_s$ is uniquely originating in $\mathsf{\Sigma }$. Since $M_{s,2}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|N_s\right|\left|N_j\right|\left|M_{j,1}\right|\left|X_{s,2}\right|\left|Y_{s,2}\right|\left|K_{s,2}\right||{HR}_{i,1})$, $M_{s,2}\subset term(<s,2>)$ must uniquely originate on a server strand $t\in \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,T_i,{(T_s)}^{\prime },{MK}_{ij},C_i^n,{{(C}_j^n)}^{\prime },{PID}_i^n,{{(PID}_j^n)}^{\prime },{{(HR}_{i,2})}^{\prime },{{(HR}_{j,2})}^{\prime }]$. By assumption (3), $N_i$ is uniquely originating in $\mathsf{\Sigma }$. Since ${HR}_{i,1}\notin K_p$, ${(M_i)}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{{(R}_i)}^{\prime }\right|\left|T_i\right||{HR}_{i,1})\subset term(<t,1>)$ must uniquely originate on $s$ according to assumption (1), where ${(R_i)}^{\prime }={{(HR}_{i,2})}^{\prime }⨁h({PID}_i|\left|{{PID}_j\left|\right|ID}_s\right|\left|N_i\right|\left|T_i\right||{HR}_{i,1})$. According to $s$ and Definition 2, ${{(HR}_{i,2})}^{\prime }={HR}_{i,2}$ and ${{(R}_i)}^{\prime }=R_i$. Hence, $t\in \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,T_i,{(T_s)}^{\prime },{MK}_{ij},C_i^n,{(C_j^n)}^{\prime },{PID}_i^n,{{(PID}_j^n)}^{\prime },{HR}_{i,2},{{(HR}_{j,2})}^{\prime }]$. By assumptions (2) and (3), ${HR}_{j,1}\notin K_p$ and $N_j$ is uniquely originating in $\mathsf{\Sigma }$, so ${(M_{j,2})}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right|\left|{(T_s)}^{\prime }\right|\left|N_j\right|\left|M_{j,1}\right|\left|{{(R}_j)}^{\prime }\right||{HR}_{j,1})\subset term(<t,3>)$ must uniquely originate on a responder strand $r\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,{(T_s)}^{\prime },{MK}_{ij},{{(C}_j^n)}^{″},{({PID}_j^n)}^{″},{{(HR}_{j,2})}^{\prime }\right]$, where ${{(R}_j)}^{\prime }={{(HR}_{j,2})}^{\prime }⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{(T_s)}^{\prime }\right|\left|N_s\right|\left|N_j\right||{HR}_{j,1})$. Since ${HR}_{j,1}\notin K_p$ and $N_s$ is uniquely originating in $\mathsf{\Sigma }$, ${{(M}_{s,1})}^{″}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|{{(X}_{s,1})}^{″}\right|\left|{{(Y}_{s,1})}^{″}\right|\left|{{(K}_{s,1})}^{\prime }\right|\left|{{(T}_s)}^{\prime }\right||{HR}_{j,1})\subset term(<r,1>)$ must uniquely originate on $t$, where ${(X_{s,1})}^{″}={(C_j^n)}^{″}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right||{HR}_{j,1})$,${{(Y}_{s,1})}^{″}={{(PID}_j^n)}^{″}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{(T_s)}^{\prime }\right|\left|N_s\right||{HR}_{j,1})$ and ${(K_{s,1})}^{\prime }={MK}_{ij}⨁{HR}_{i,1}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|{(T_s)}^{\prime }\right|\left|N_s\right||{HR}_{j,1})$. According to Definition 2, ${{(C}_j^n)}^{″}={{(C}_j^n)}^{\prime }$ and ${\left({PID}_j^n\right)}^{″}={({PID}_j^n)}^{\prime }$. Hence, $r\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,{(T_s)}^{\prime },{MK}_{ij},{(C_j^n)}^{\prime },{({PID}_j^n)}^{\prime },{{(HR}_{j,2})}^{\prime }\right]$. □

According to Theorem 3, $D_i$ successfully authenticates $GS$ and $D_j$, and can establish an injection agreement [43,44] with each of them. Note that ${(T_s)}^{\prime }$, ${(C_j^n)}^{\prime }$, ${({PID}_j^n)}^{\prime }$ and ${{(HR}_{j,2})}^{\prime }$ are not known to $D_i$ because they are only used between $GS$ and $D_j$.

Theorem 4. 

Suppose: (1) $\Sigma$ is a space for the drone–drone authentication and key agreement phase of SLAKA-IoD, and $\mathcal{C}$ is a bundle containing a responder strand $r\in Resp\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_s, {MK}_{ij},C_j^n, {PID}_j^n,{HR}_{j,2}\right]$; (2)${HR}_{i,1}, {HR}_{j,1}\notin K_p$; (3) $N_i$ and $N_s$ are uniquely originating in $\Sigma$, and $T_s$ is a fresh timestamp to prevent replay. Then, $\mathcal{C}$ contains a unique initiator strand $s\in Init\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j, N_s, {{(T}_i)}^{\prime }, {MK}_{ij},{{(C}_i^n)}^{\prime }, {{(PID}_i^n)}^{\prime }, {{(HR}_{i,2})}^{\prime }\right]$ and a unique server strand $t\in Serv[D_i, D_j,GS, {PID}_i, {PID}_j, {ID}_s, N_i, N_j,N_s, {{(T}_i)}^{\prime },T_s, {MK}_{ij},{{(C}_i^n)}^{\prime },C_j^n, {{(PID}_i^n)}^{\prime }, {PID}_j^n,$ ${{(HR}_{i,2})}^{\prime },{HR}_{j,2}]$.

Proof of Theorem 4. 

According to assumptions (2) and (3), ${HR}_{j,1}\notin K_p$ and $N_s$ is uniquely originating in $\mathsf{\Sigma }$. Since $M_{s,1}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|X_{s,1}\right|\left|Y_{s,1}\right|\left|K_{s,1}\right|\left|T_s\right||{HR}_{j,1})$, $M_{s,1}\subset term\left(<r,1>\right)$ must uniquely originate on a server strand $t\in \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,{{(N}_j)}^{\prime },N_s,{{(T}_i)}^{\prime },T_s,{MK}_{ij},{{(C}_i^n)}^{\prime },C_j^n,{{(PID}_i^n)}^{\prime },{PID}_j^n,$ ${{(HR}_{i,2})}^{\prime },{{(HR}_{j,2})}^{\prime }]$. Since ${HR}_{j,1}\notin K_p$, ${(M_{j,2})}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right|\left|T_s\right|\left|{(N_j)}^{\prime }\right|\left|{{(M}_{j,1})}^{\prime }\right|\left|{{(R}_j)}^{\prime }\right||{HR}_{j,1})\subset term(<t,3>)$ must originate on a responder strand $r^{\prime }\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,{(N_j)}^{\prime },N_s,T_s,{MK}_{ij},C_j^n,{PID}_j^n,{{(HR}_{j,2})}^{\prime }\right]$, where ${{(SK}_{ij})}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{{(N}_j)}^{\prime }\right||({MK}_{ij}⨁{HR}_{i,1}⨁{HR}_{j,1}))$, ${{(R}_j)}^{\prime }={{(HR}_{j,2})}^{\prime }⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|T_s\right|\left|N_s\right|\left|{(N_j)}^{\prime }\right||{HR}_{j,1})$ and ${(M_{j,1})}^{\prime }=h(N_i|\left|{{(N}_j)}^{\prime }\right||{{(SK}_{ij})}^{\prime })$. As a result, $term\left(<r,1>\right)=term\left(<r^{\prime },1>\right)=\left\{{PID}_i,{PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\right\}$, i.e., $\left\{{PID}_i,{PID}_j,N_i,N_s,X_{s,1},Y_{s,1},K_{s,1},T_s,M_{s,1}\right\}$ is replayed, which contradicts with assumption (3). Hence, $r^{\prime }=r$, so ${{(N}_j)}^{\prime }=N_j$ and ${{(HR}_{j,2})}^{\prime }={HR}_{j,2}$. That is to say, $t\in \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,{{(T}_i)}^{\prime },T_s,{MK}_{ij},{{(C}_i^n)}^{\prime },C_j^n,{{(PID}_i^n)}^{\prime },{PID}_j^n,{{(HR}_{i,2})}^{\prime },{HR}_{j,2}]$. By assumptions (2) and (3), ${HR}_{i,1}\notin K_p$ and $N_i$ is uniquely originating in $\mathsf{\Sigma }$, so ${\left(M_i\right)}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|{\left|{(R}_i\right)}^{\prime }\left|\right|{{(T}_i)}^{\prime }\left|\right|{HR}_{i,1})\subset term\left(<t,1>\right)$ must uniquely originate on an initiator strand $s\in \mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,{{(N}_j)}^{″},{{(N}_s)}^{″},{{(T}_i)}^{\prime },{{(MK}_{ij})}^{″},{(C_i^n)}^{″},{{(PID}_i^n)}^{″},{{(HR}_{i,2})}^{\prime }\right]$, where ${(R_i)}^{\prime }={({HR}_{i,2})}^{\prime }⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|{{(T}_i)}^{\prime }\right||{HR}_{i,1})$. Since ${HR}_{i,1}\notin K_p$, ${(M_{s,2})}^{″}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|{(T_i)}^{\prime }\right|\left|{{(N}_s)}^{″}\right|\left|{(N_j)}^{″}\right|\left|{{(M}_{j,1})}^{″}\right|\left|{(X_{s,2})}^{″}\right|\left|{(Y_{s,2})}^{″}\right|\left|{{(K}_{s,2})}^{″}\right||{HR}_{i,1})\subset term(<s,2>)$ must originate on a server strand $t^{\prime }\in \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,{{(N}_j)}^{″},{{(N}_s)}^{″},{{(T}_i)}^{\prime },{{{(T}_s)}^{″}}^{\prime },{{(MK}_{ij})}^{″},{{(C}_i^n)}^{″},{{(C}_j^n)}^{″\prime },{{(PID}_i^n)}^{″},{{(PID}_j^n)}^{″\prime },{({HR}_{i,2})}^{\prime },{{(HR}_{j,2})}^{″\prime }]$, where ${(X_{s,2})}^{″}={(C_i^n)}^{″}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{{(N}_s)}^{″}\right|\left|{(N_j)}^{″}\right|\left|N_i\right||{HR}_{i,1})$,${(Y_{s,2})}^{″}={{(PID}_i^n)}^{″}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{{(N}_s)}^{″}\right|\left|{{(N}_j)}^{″}\right|\left|{(T_i)}^{\prime }\right||{HR}_{i,1})$, ${(K_{s,2})}^{″}={{(MK}_{ij})}^{″}⨁{HR}_{j,1}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{{(N}_s)}^{″}\right|\left|{(N_j)}^{″}\right|\left|{(T_i)}^{\prime }\right|\left|N_i\right||{HR}_{i,1})$,${({SK}_{ij})}^{″}=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{{(N}_j)}^{″}\right||{(({MK}_{ij})}^{″}⨁{HR}_{j,1}⨁{HR}_{i,1}))$ and ${(M_{j,1})}^{″}=h(N_i|\left|{{(N}_j)}^{″}\right||{{(SK}_{ij})}^{″})$. As a result, $term\left(<t,1>\right)=term\left(<t^{\prime },1>\right)=\left\{{PID}_i,{PID}_j,N_i,{{(R}_i)}^{\prime },{{(T}_i)}^{\prime },{\left(M_i\right)}^{\prime }\right\}$, i.e., $\{{PID}_i,{PID}_j,N_i,{(R_i)}^{\prime },{(T_i)}^{\prime },{(M_i)}^{\prime }\}$ is replayed, which contradicts with assumption (3). Hence, $t^{\prime }=t$, so ${{(N}_j)}^{″}=N_j$, ${{(N}_s)}^{″}=N_s$, ${{(MK}_{ij})}^{″}={MK}_{ij}$, ${{(C}_i^n)}^{″}={{(C}_i^n)}^{\prime }$ and ${{(PID}_i^n)}^{″}={{(PID}_i^n)}^{\prime }$. That is to say, $s\in \mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,{{(T}_i)}^{\prime },{MK}_{ij},{{(C}_i^n)}^{\prime },{{(PID}_i^n)}^{\prime },{{(HR}_{i,2})}^{\prime }\right]$. □

According to Theorem 4, $D_j$ successfully authenticates $GS$ and $D_i$, and can establish an injection agreement [43,44] with each of them. Note that ${(T_i)}^{\prime }$, ${{(C}_i^n)}^{\prime }$, ${{(PID}_i^n)}^{\prime }$ and ${{(HR}_{i,2})}^{\prime }$ are not known to $D_j$ because they are only used between $GS$ and $D_i$.

Theorem 5. 

Suppose: (1) $\Sigma$ is a space for the drone–drone authentication and key agreement phase of SLAKA-IoD, and $\mathcal{C}$ is a bundle containing a server strand, $t\in Serv[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i,T_s, {MK}_{ij},C_i^n,C_j^n, {PID}_i^n, {PID}_j^n,{HR}_{i,2},{HR}_{j,2}]$; (2) ${HR}_{i,1}, {HR}_{j,1}\notin K_p$; (3) $N_i$, $N_j$ and $N_s$ are uniquely originating in $\Sigma$, and $T_i$ is a fresh timestamp to prevent replay. Then, $\mathcal{C}$ contains a unique initiator strand $s\in Init\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i, {MK}_{ij},C_i^n, {PID}_i^n,{HR}_{i,2}\right]$ and a responder strand $r\in Resp\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_s, {MK}_{ij},C_j^n, {PID}_j^n,{HR}_{j,2}\right]$.

Proof of Theorem 5. 

By assumptions (2) and (3), ${HR}_{i,1}\notin K_p$ and $N_i$ is uniquely originating in $\mathsf{\Sigma }$, so $M_i=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|R_i\right|\left|T_i\right||{HR}_{i,1})\subset term\left(<t,1>\right)$ must uniquely originate on an initiator strand $s\in \mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, {{(N}_j)}^{\prime },{{(N}_s)}^{\prime }, T_i, {{(MK}_{ij})}^{\prime }, {(C_i^n)}^{\prime }, {{(PID}_i^n)}^{\prime },{HR}_{i,2}\right]$. Since ${HR}_{i,1}\notin K_p$, ${(M_{s,2})}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|T_i\right|\left|{{(N}_s)}^{\prime }\right|\left|{(N_j)}^{\prime }\right|\left|{{(M}_{j,1})}^{\prime }\right|\left|{(X_{s,2})}^{\prime }\right|\left|{(Y_{s,2})}^{\prime }\right|\left|{{(K}_{s,2})}^{\prime }\right||{HR}_{i,1})\subset term(<s,2>)$ must originate on a server strand $t^{\prime }\in \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}[D_i, D_j,GS, {PID}_i, {PID}_j, {ID}_s, N_i, {{(N}_j)}^{\prime },{{(N}_s)}^{\prime }, T_i,{{(T}_s)}^{″}, {{(MK}_{ij})}^{\prime },{{(C}_i^n)}^{\prime },{(C_j^n)}^{″}, {{(PID}_i^n)}^{\prime }, {{(PID}_j^n)}^{″},{HR}_{i,2},{{(HR}_{j,2})}^{″}]$, where ${(X_{s,2})}^{\prime }={(C_i^n)}^{\prime }⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{{(N}_s)}^{\prime }\right|\left|{(N_j)}^{\prime }\right|\left|N_i\right||{HR}_{i,1})$,${(Y_{s,2})}^{\prime }={{(PID}_i^n)}^{\prime }⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{{(N}_s)}^{\prime }\right|\left|{{(N}_j)}^{\prime }\right|\left|T_i\right||{HR}_{i,1})$, ${(K_{s,2})}^{\prime }={{(MK}_{ij})}^{\prime }⨁{HR}_{j,1}⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|{{(N}_s)}^{\prime }\right|\left|{(N_j)}^{\prime }\right|\left|T_i\right|\left|N_i\right||{HR}_{i,1})$,${({SK}_{ij})}^{\prime }=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|{{(N}_j)}^{\prime }\right||({({MK}_{ij})}^{\prime }⨁{HR}_{j,1}⨁{HR}_{i,1}))$ and ${(M_{j,1})}^{\prime }=h(N_i|\left|{{(N}_j)}^{\prime }\right||{{(SK}_{ij})}^{\prime })$. As a result, $term\left(<t,1>\right)=term\left(<t^{\prime },1>\right)=\left\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\right\}$, i.e., $\left\{{PID}_i,{PID}_j,N_i,R_i,T_i,M_i\right\}$ is replayed, which contradicts with assumption (3). Hence, $t^{\prime }=t$, so ${{(N}_j)}^{\prime }=N_j$, ${{(N}_s)}^{\prime }=N_s$, ${{(MK}_{ij})}^{\prime }={MK}_{ij}$, ${{(C}_i^n)}^{\prime }=C_i^n$ and ${{(PID}_i^n)}^{\prime }={PID}_i^n$. That is to say, $s\in \mathrm{I}\mathrm{n}\mathrm{i}\mathrm{t}\left[D_i, D_j,GS, {PID}_i, {PID}_j,{ID}_s, N_i, N_j,N_s, T_i, {MK}_{ij},C_i^n, {PID}_i^n, {HR}_{i,2}\right]$. By assumptions (2) and (3), ${HR}_{j,1}\notin K_p$ and $N_j$ is uniquely originating in $\mathsf{\Sigma }$, so $M_{j,2}=h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_i\right|\left|N_s\right|\left|T_s\right|\left|N_j\right|\left|M_{j,1}\right|\left|R_j\right||{HR}_{j,1}) \subset term(<t,3>)$ must uniquely originate on a responder strand $r\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,T_s,{MK}_{ij},{{(C}_j^n)}^{″\prime },{({PID}_j^n)}^{″\prime },{HR}_{j,2}\right]$. Since ${HR}_{j,1}\notin K_p$ and $N_s$ is uniquely originating in $\mathsf{\Sigma }$, ${{(M}_{s,1})}^{″\prime }=h({PID}_i|\left|{PID}_j\right|\left|N_i\right|\left|N_s\right|\left|{{(X}_{s,1})}^{″\prime }\right|\left|{{(Y}_{s,1})}^{″\prime }\right|\left|K_{s,1}\right|\left|T_s\right||{HR}_{j,1})\subset term(<r,1>)$ must uniquely originate on $t$, where ${{(X}_{s,1})}^{″\prime }={(C_j^n)}^{″\prime }⨁h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|N_s\right||{HR}_{j,1})$ and ${{(Y}_{s,1})}^{″\prime }={{(PID}_j^n)}^{″\prime }⨁ h({PID}_i|\left|{PID}_j\right|\left|{ID}_s\right|\left|T_s\right|\left|N_s\right||{HR}_{j,1})$. According to Definition 2, ${{(C}_j^n)}^{″\prime }=C_j^n$ and ${{(PID}_j^n)}^{″\prime }={PID}_j^n$. Hence, $r\in \mathrm{R}\mathrm{e}\mathrm{s}\mathrm{p}\left[D_i,D_j,GS,{PID}_i,{PID}_j,{ID}_s,N_i,N_j,N_s,T_s,{MK}_{ij},C_j^n,{PID}_j^n,{HR}_{j,2}\right]$. □

According to Theorem 5, $GS$ successfully authenticates $D_i$ and $D_j$, and can establish an injection agreement [43,44] with each of them.

From Theorems 3–5, mutual authentication among $D_i$, $D_j$ and $GS$ is established. Additionally, injection agreement among $D_i$, $D_j$ and $GS$ is established. Hence, according to the definition of the injection agreement [43,44], replay and MitM attacks among $D_i$, $D_j$ and $GS$ are overcome.

5.3. Security Verification Based on the Scyther Tool

The Scyther tool [46,47] is a security protocol formal analysis tool. It can provide explicit termination for infinite state aggregation protocols and unlimited sessions. In addition, it can support multi-protocol parallel analysis. The Scyther tool uses the security protocol description language (SPDL) to describe and analyze security protocols. It provides a set of claims to test various security goals, such as authentication and secrecy. In the Scyther tool, two secret claims are applied to state confidentiality, including Secret (i.e., secret) and SKR (i.e., session key reveal). The Scyther tool provides different degrees of authentication strength. In the Scyther tool, several forms of authentication claims including Alive (i.e., aliveness), Weakagree (i.e., weak agreement), Niagree (i.e., non-injection agreement), and Nisynch (i.e., non-injection synchronization) are used to detect replay, MitM attacks, reflection, etc. The detailed description of formal definitions for all Scyther claims can be found in [47].

We model our proposed SLAKA-IoD protocol in SPDL, and then specify the security properties of the SLAKA-IoD protocol according to a series of claims of the Scyther tool. The security verification result of the drone-GS authentication and key agreement phase of SLAKA-IoD is shown in Figure 5.

From Figure 5, the drone-GS authentication and key agreement phase of SLAKA-IoD successfully make certain all Scyther claims. Additionally, there are no attacks found in the testing of the Scyther tool. According to Figure 5, ${HR}_{i,1}$, ${HR}_{i,2}$, $C_i^n$, ${PID}_i^n$ and ${SK}_{is}$ are secret. Moreover, weak agreement, aliveness, non-injection agreement and non-injection synchronization between $D_i$ and $GS$ are established. As a result, replay and MitM attacks between $D_i$ and $GS$ are overcome [47].

The security verification result of the drone–drone authentication and key agreement phase of SLAKA-IoD is shown in Figure 6.

From Figure 6, the drone–drone authentication and key agreement phase of SLAKA-IoD successfully makes certain all Scyther claims. Additionally, there are no attacks found in the testing of the Scyther tool. According to Figure 6, ${HR}_{i,1}$, ${HR}_{i,2}$, $C_i^n$, ${PID}_i^n$, ${HR}_{j,1}$, ${HR}_{j,2}$, $C_j^n$, ${PID}_j^n$ and ${SK}_{ij}$ are secret. Moreover, weak agreement, aliveness, non-injection agreement and non-injection synchronization among $D_i$, $D_j$ and $GS$ are established. As a result, replay and MitM attacks among $D_i$, $D_j$ and $GS$ are overcome [47].

According to the above security verification result of the SLAKA-IoD protocol using the Scyther tool, the SLAKA-IoD protocol is secure.

5.4. Security Comparison

In

Table 3. Comparison of the security features of the drone-GS authentication and key agreement phase.

Features	[33]	[34]	[35]	[36]	[37]	SLAKA-IoD
${SF}_1$	✓	✓	✓	✓	✓	✓
${SF}_2$	✗	✗	✗	✗	✗	✓
${SF}_3$	✗	✗	✓	✗	✓	✓
${SF}_4$	✓	✓	✓	✓	✓	✓
${SF}_5$	✓	✓	✓	✓	✗	✓
${SF}_6$	✗	✗	✗	✓	✗	✓
${SF}_7$	✓	✓	✓	✓	✓	✓
${SF}_8$	✓	✓	✓	✗	✗	✓
${SF}_9$	✓	✓	✓	✗	✓	✓
${SF}_{10}$	✓	✓	✓	✓	✓	✓
${SF}_{11}$	✓	✓	✓	✓	✓	✓
${SF}_{12}$	✗	✗	✗	✗	✗	✓

${SF}_1$: “Resistance of impersonation attack”; ${SF}_2$: “Resistance of replay attack”; ${SF}_3$: “Resistance of DoS attack”; ${SF}_4$: “Resistance of MITM attack”; ${SF}_5$: “Resistance of drone physical capture attack”; ${SF}_6$: “Resistance of desynchronization attack”; ${SF}_7$: “Resistance of session key disclosure attack”; ${SF}_8$: “Resistance of ESL attack”; ${SF}_9$: “Provision of anonymity and untraceability”; ${SF}_{10}$: “Provision of mutual authentication”; ${SF}_{11}$: “Provision of forward and backward secrecy”; ${SF}_{12}$: “Provision of PUF challenge-response pair protection”; ✓: “Support the security feature”; ✗: “Does not support the security feature”.

and

Table 4. Comparison of the security features of the drone–drone authentication and key agreement phase.

Features	[22]	[35]	[37]	SLAKA-IoD
${SF}_1$	✓	✓	✓	✓
${SF}_2$	✓	✗	✗	✓
${SF}_3$	✓	✗	✓	✓
${SF}_4$	✓	✓	✓	✓
${SF}_5$	✗	✓	✗	✓
${SF}_6$	✓	✗	✗	✓
${SF}_7$	✓	✓	✓	✓
${SF}_8$	✗	✗	✗	✓
${SF}_9$	✓	✓	✓	✓
${SF}_{10}$	✓	✓	✓	✓
${SF}_{11}$	✓	✓	✓	✓
${SF}_{12}$	✗	✗	✗	✓

, we compare the security features of the SLAKA-IoD protocol with other related AKA protocols for IoD [22,33,34,35,36,37].

From Table 3, the drone-GS authentication and key agreement phase in [33] cannot resist replay, DoS, and desynchronization attacks and does not provide PUF challenge–response pair protection. The drone-GS authentication and key agreement phase in [34] has the same security features as the drone-GS authentication and key agreement phase in [33]. The drone-GS authentication and key agreement phase in [35] cannot resist replay and desynchronization attacks and does not provide PUF challenge-response pair protection. The drone-GS authentication and key agreement phase in [36] cannot resist replay, DoS and ESL attacks, and does not provide anonymity, untraceability and PUF challenge–response pair protection. The drone-GS authentication and key agreement phase in [37] cannot resist replay, drone physical capture, desynchronization and ESL attacks and does not provide PUF challenge–response pair protection. In contrast, the drone-GS authentication and key agreement phase of SLAKA-IoD supports all of the security features in Table 3.

From Table 4, the drone–drone authentication and key agreement phase in [22] cannot resist drone physical capture and ESL attacks and does not provide PUF challenge–response pair protection. The drone–drone authentication and key agreement phase in [35] cannot resist replay, DoS, desynchronization and ESL attacks, and does not provide PUF challenge–response pair protection. The drone–drone authentication and key agreement phase in [37] cannot resist replay, drone physical capture, desynchronization and ESL attacks, and does not provide PUF challenge–response pair protection. In contrast, the drone–drone authentication and key agreement phase of SLAKA-IoD supports all of the security features in Table 4.

Hence, the SLAKA-IoD protocol offers more security features as compared with these related AKA protocols for IoD [22,33,34,35,36,37].

6. Performance Analysis

This section presents a detailed performance analysis of the SLAKA-IoD protocol in terms of computation, communication, and storage cost. Meanwhile, we compare the SLAKA-IoD protocol with other related AKA protocols for IoD in these respects.

6.1. Computation Cost

Based on the existing experimental results reported from [15], we consider $T_{ecm}$ (time to execute ECC point multiplication) ≈ 2.92 ms, $T_h$ (time to execute hash function) ≈ 0.311 ms, and $T_{sed}$ (time required for symmetric encryption/decryption ≈ 0.425 ms for the drone. We also consider $T_{ecm}$ (time to execute ECC point multiplication) ≈ 0.605 ms, $T_h$ (time to execute hash function) ≈ 0.029 ms, and $T_{sed}$ (time required for symmetric encryption/decryption ≈ 0.036 ms for the GS. According to [22,33,34,35,36,37], key extension function, message authentication code function, Duffing map function and Henon map function require the same amount of computation as the hash function. In addition, the time required for XOR, message cascading, PUF, or random number generation is relatively small and can be ignored.

During the drone-GS authentication and key agreement phase, the computation cost at the GS side in our proposed SLAKA-IoD is 8$T_h$ ≈ 0.232 ms, while the AKA schemes of [33,34,35], refs. [36,37] require 8$T_h$ ≈ 0.232 ms, 7$T_h$ ≈ 0.203 ms, 5$T_h$ ≈ 0.145 ms, 4$T_h$ ≈ 0.116 ms, and 11$T_h$ ≈ 0.319 ms. The computation cost at drone side in our proposed SLAKA-IoD is 9$T_h$ ≈ 2.799 ms, while the schemes of [33,34,35,36,37] require 8$T_h$ ≈ 2.488 ms, 7$T_h$ ≈ 2.177 ms, 5$T_h$ ≈ 1.555 ms, 4$T_h$ ≈ 1.244 ms, and 11$T_h$ ≈ 3.421 ms. In

Table 5. Comparison of the computation cost of the drone-GS authentication and key agreement phase.

Schemes	Drone(${\mathit{D}}_{\mathit{i}}$)	GS	Total Cost
[33]	2.488 ms	0.232 ms	2.720 ms
[34]	2.177 ms	0.203 ms	2.380 ms
[35]	1.555 ms	0.145 ms	1.700 ms
[36]	1.244 ms	0.116 ms	1.360 ms
[37]	3.421 ms	0.319 ms	3.740 ms
SLAKA-IoD	2.799 ms	0.232 ms	3.031 ms

, we compare the computation cost of SLAKA-IoD with other related AKA schemes [33,34,35,36,37] during the drone-GS authentication and key agreement phase.

From Table 5, the computation cost of SLAKA-IoD is slightly higher than that of the AKA schemes in [33,34,35,36], and slightly lower than that of the AKA scheme in [37] during the drone-GS authentication and key agreement phase. However, SLAKA-IoD can resist more security attacks and provide more security properties as compared to other related AKA schemes [33,34,35,36,37] during this phase.

During the drone–drone authentication and key agreement phase, the computation cost at GS side in our proposed SLAKA-IoD is 14$T_h$ ≈ 0.406 ms, while the AKA schemes of [22,35], and [37] require 2$T_{ecm}$ + 9$T_h$ ≈ 1.471 ms, 3$T_{sed}$ + 11$T_h$ ≈ 0.427 ms, and 21$T_h$ ≈ 0.609 ms. The computation cost at the drone $D_i$ side in our proposed SLAKA-IoD is 11$T_h$ ≈ 3.421 ms, while the schemes of [22,35], and [37] require 3$T_{ecm}$ + 5$T_h$ ≈ 10.315 ms, 2$T_{sed}$+ 5$T_h$ ≈ 2.405 ms, and 15$T_h$ ≈ 4.665 ms. The computation cost at the drone $D_j$ side in our proposed SLAKA-IoD is 11$T_h$ ≈ 3.421 ms, while the schemes of [22,35], and [37] require 3$T_{ecm}$ + 4$T_h$ ≈ 10.004 ms, $T_{sed}$ + 6$T_h$ ≈ 2.291 ms, and 11$T_h$ ≈ 3.421 ms. In

Table 6. Comparison of the computation cost of the drone–drone authentication and key agreement phase.

Schemes	Drone (${\mathit{D}}_{\mathit{i}}$)	GS	Drone (${\mathit{D}}_{\mathit{j}}$)	Total Cost
[22]	10.315 ms	1.471 ms	10.004 ms	21.790 ms
[35]	2.405 ms	0.427 ms	2.291 ms	5.123 ms
[37]	4.665 ms	0.609 ms	3.421 ms	8.695 ms
SLAKA-IoD	3.421 ms	0.406 ms	3.421 ms	7.248 ms

, we compare the computation cost of SLAKA-IoD with other related AKA schemes [22,35,37] during the drone–drone authentication and key agreement phase.

From Table 6, the computation cost of SLAKA-IoD is slightly higher than that of the AKA scheme in [35], slightly lower than that of the AKA scheme in [37], and significantly lower than that of the AKA scheme in [22] during the drone–drone authentication and key agreement phase. However, SLAKA-IoD can resist more security attacks and provide more security properties as compared to other related AKA schemes [22,35,37] during this phase.

For SLAKA-IoD, if the number of drones in an IoD is $n$, then the computation cost of the drone-GS authentication and key agreement phase is $3.031n$ ms. Theoretically, the computation cost of the drone–drone authentication and key agreement phase will reach $(7.248\times n!)/(\left(n-2\right)!\times 2)$ ms. However, in reality, this phase is performed on demand, so it will not lead to a sudden increase in computation cost. Hence, the SLAKA-IoD protocol is suitable for IoD in terms of computation cost.

6.2. Communication Cost

To evaluate communication cost and storage cost, we consider that the sizes of the request flag, timestamp, identity, master key, random number, hash value, message authentication code, Duffing map value, Henon map value, PUF challenge, PUF response and ECC point are 16 bits, 32 bits, 160 bits, 128 bits, 128 bits, 160 bits, 160 bits, 256 bits, 256 bits, 32 bits, 320 bits, 320 bits, respectively [22,33,34,35,36,37].

During the drone-GS authentication and key agreement phase, the communication cost in our proposed SLAKA-IoD is {160 + 128 + 160 + 32 + 160} + {128 + 160 + 160 + 160} = 640 + 608 = 1248 bits, while the AKA schemes of [32,33,34,35,36] require {128 + 160} + {32 + 256 + 128 + 160} + {128 + 320 + 128 + 160} = 288 + 576 + 736 = 1600 bits, {128 + 160} + {32 + 256 + 128 + 160} + {128 + 320 + 128 + 160} = 288 + 576 + 736 = 1600 bits, {160 + 128 + 160} + {256 + 160} + {320+128+160} = 448 + 416 + 608 = 1472 bits, {128 + 160} + {32 + 256 + 160} + {256 + 160} = 288 + 448 + 416 =1152 bits, and {256 + 160} + {256 + 160} + {256 + 256 + 160} = 416 + 416 + 672 =1506 bits. In

Table 7. Comparison of the communication cost of the drone-GS authentication and key agreement phase.

Schemes	No. of Messages	Communication Cost
[33]	3	1600 bits
[34]	3	1600 bits
[35]	3	1472 bits
[36]	3	1152 bits
[37]	3	1506 bits
SLAKA-IoD	2	1248 bits

, we compare the communication cost of SLAKA-IoD with other related AKA schemes [33,34,35,36,37] during the drone-GS authentication and key agreement phase.

From Table 7, the communication cost of SLAKA-IoD is slightly higher than that of the AKA scheme in [36], and significantly lower than that of the AKA schemes in [33,34,35,37] during the drone-GS authentication and key agreement phase. However, SLAKA-IoD can resist more security attacks and provide more security properties as compared to other related AKA schemes [33,34,35,36,37] during this phase. Moreover, the number of messages in SLAKA-IoD is less than the number of messages in the AKA schemes of [33,34,35,36,37] during the drone-GS authentication and key agreement phase.

During the drone–drone authentication and key agreement phase, the communication cost in our proposed SLAKA-IoD is {160 + 160 + 128 + 160 + 32 + 160} + {160 + 160 + 128 + 128 + 160 + 160 + 160 + 32 + 160} + {128 + 160 + 160 + 160} + {128 + 128 + 160 + 160 + 160 + 160 + 160} = 800 + 1248 + 608 + 1056 = 3712 bits, while the AKA schemes of [22,34], and [36] require {160 + 320 + 160 + 32 + 160} + {32 + 160 + 160 + 160 + 320} + {320 + 32 + 160} + {320 + 32 + 160} = 832 + 832 + 512 + 512 = 2688 bits, {16 + 160} + {16 + 160} + {256} + {256} + {1472} + {1472} = 800 + 1248 + 608 + 1056 + 1472 + 1472 = 3808 bits, and {256 + 256 + 160} + {256 + 160} + {256 + 256 + 160} + {256 + 256 + 256 + 160} + {256 + 256 + 160} + {256 + 160} = 672 + 416 + 672 + 928 + 672 + 416 = 3776 bits. In

Table 8. Comparison of the communication cost of the drone–drone authentication and key agreement phase.

Schemes	No. of Messages	Communication Cost
[22]	4	2688 bits
[35]	6	3808 bits
[37]	6	3776 bits
SLAKA-IoD	4	3712 bits

, we compare the communication cost of SLAKA-IoD with that of other related AKA schemes [22,35,37] during the drone–drone authentication and key agreement phase.

From Table 8, the communication cost of SLAKA-IoD is slightly higher than that of the AKA scheme in [22], and significantly lower than that of the AKA schemes in [35,37] during the drone–drone authentication and key agreement phase. However, SLAKA-IoD can resist more security attacks and provide more security properties as compared to other related AKA schemes [22,35,37] during this phase. Moreover, the number of messages in SLAKA-IoD is less than the number of messages in the AKA schemes of [35,37] during the drone–drone authentication and key agreement phase.

For SLAKA-IoD, if the number of drones in an IoD is $n$, then the communication cost of the drone-GS authentication and key agreement phase is $1248n$ bits. Theoretically, the communication cost of the drone–drone authentication and key agreement phase will reach $(3712\times n!)/(\left(n-2\right)!\times 2)$ bits. However, in reality, this phase is performed on demand, so it will not lead to a sudden increase in communication cost. Hence, the SLAKA-IoD protocol is suitable for IoD in terms of communication cost.

6.3. Storage Cost

During the drone-GS authentication and key agreement phase, the storage cost at GS side in our proposed SLAKA-IoD is 160 + 160 + 160 + 160 + 160 + 160 = 960 bits, while the AKA schemes of [33,34,35,36,37] require 160 + 160 + 32 + 320 = 672 bits, 160 + 160 + 32 + 320 = 672 bits, 160 + 160 + 32 + 320 = 672 bits, 160 + 160 + 32 + 320 = 672 bits, and 160 + 160 + 160 + 32 + 320 = 832 bits. The storage cost at drone side in our proposed SLAKA-IoD is 160 + 160 + 32 + 32 = 384 bits, while the schemes of [33,34,35,36,37] require 160 + 160 = 320 bits, 160 + 160 = 320 bits, 160 + 160+32 = 352 bits, 160 = 160 bits, and 160 + 160 + 32 + 320 = 672 bits. In

Table 9. Comparison of the storage cost of the drone-GS authentication and key agreement phase.

Schemes	Drone (${\mathit{D}}_{\mathit{i}}$)	GS	Total Cost
[33]	320 bits	672 bits	992 bits
[34]	320 bits	672 bits	992 bits
[35]	352 bits	672 bits	1024 bits
[36]	160 bits	672 bits	832 bits
[37]	672 bits	832 bits	1504 bits
SLAKA-IoD	384 bits	960 bits	1344 bits

, we compare the storage cost of SLAKA-IoD with other related AKA schemes [33,34,35,36,37] during the drone-GS authentication and key agreement phase.

From Table 9, the storage cost of SLAKA-IoD is higher than that of the AKA schemes in [33,34,35,36], and lower than that of the AKA scheme in [37] during the drone-GS authentication and key agreement phase. However, SLAKA-IoD can resist more security attacks and provide more security properties as compared to other related AKA schemes [33,34,35,36,37] during this phase.

During the drone–drone authentication and key agreement phase, the storage cost at GS side in our proposed SLAKA-IoD is 160 + [160 + 160 + 160] × 2 + [160 + 160] × 2 = 1760 bits, while the AKA schemes of [22,35], and [37] require 128 + 128 = 256 bits, 160 + [160 + 32 + 320] × 2 = 1184 bits, and 160 + [160 + 160 + 32 + 320] × 2 = 1504 bits. The storage cost at the drone $D_i$ side in our proposed SLAKA-IoD is 160 + 160 + 32 + 32 = 384 bits, while the schemes of [22,35], and [37] require 160 + 128 + 320 + 320 = 928 bits, 160 + 160 + 32 = 352 bits, and 160 + 160 + 160 + 32 + 320 = 832 bits. The storage cost at the drone $D_j$ side in our proposed SLAKA-IoD is 160 + 160 + 32 + 32 + 160 + 160 = 704 bits, while the schemes of [22,35] and [37] require 160 + 128 + 320 + 320 = 928 bits, 160 + 160 + 32 = 352 bits, and 160 + 160 + 160 + 32 + 320 = 832 bits. In

Table 10. Comparison of the storage cost of the drone–drone authentication and key agreement phase.

Schemes	Drone (${\mathit{D}}_{\mathit{i}}$)	GS	Drone (${\mathit{D}}_{\mathit{j}}$)	Total Cost
[22]	928 bits	256 bits	928 bits	2112 bits
[35]	352 bits	1184 bits	352 bits	1888 bits
[37]	832 bits	1504 bits	832 bits	3168 bits
SLAKA-IoD	384 bits	1760 bits	704 bits	2848 bits

, we compare the storage cost of SLAKA-IoD with other related AKA schemes [22,35,37] during the drone–drone authentication and key agreement phase.

From Table 10, the storage cost of SLAKA-IoD is higher than that of the AKA scheme in [22,35], and lower than that of the AKA scheme in [37] during the drone–drone authentication and key agreement phase. However, SLAKA-IoD can resist more security attacks and provide more security properties as compared to other related AKA schemes [22,35,37] during this phase.

In summary, the storage of the SLAKA-IoD protocol is higher than that of the AKA schemes in [22,33,34,35,36]. This is mainly because the SLAKA-IoD protocol increases some necessary storage to prevent desynchronization attacks. Moreover, the increase in storage mainly occurs on the GS, which is usually a device with better performance. For SLAKA-IoD, if the number of drones in an IoD is $n$, then the minimum storage cost of the SLAKA-IoD is $(384n+160+800n$) bits and the maximum storage cost of the SLAKA-IoD is $(704n+160+800n$) bits. This is because the information stored on the drone and GS is shared by both the drone-GS authentication and key agreement phase and the drone–drone authentication and key agreement phase. Thus, it will not lead to a sudden increase in storage cost. Therefore, the SLAKA-IoD protocol is still suitable for IoD in terms of storage cost.

7. Conclusions

In this paper, we propose a secure and lightweight AKA protocol for IoD (i.e., SLAKA-IoD protocol) based on PUF, XOR operation and hash function. This SLAKA-IoD protocol can achieve mutual authentication and establish a secure session key between communication entities in the IoD. The SLAKA-IoD protocol includes the drone registration phase, the drone-GS authentication and key agreement phase, and the drone–drone authentication and key agreement phase. During the drone-GS authentication and key agreement phase, the drone and GS mutually authenticate each other, and establish a secure session key between them. During the drone–drone authentication and key agreement phase, any two drones can mutually authenticate each other, and establish a secure session key between them.

Then, we perform an informal security analysis of the SLAKA-IoD protocol, a formal security analysis of the protocol using the strand space model, and security verification of the protocol based on the Scyther tool. As a result, the SLAKA-IoD protocol is secure against various security attacks and ensures required security properties. In addition, we give a comparison of the SLAKA-IoD protocol with other related AKA protocols for IoD in terms of security features. The comparison result shows that the SLAKA-IoD protocol can provide more security features as compared with these related AKA protocols for IoD.

Finally, we present a performance analysis of the SLAKA-IoD protocol in terms of computation, communication, and storage cost, and then provide a comparison of the SLAKA-IoD protocol with other related AKA protocols for IoD in terms of them. The comparison result shows that the SLAKA-IoD protocol is generally lightweight as compared with these related AKA protocols for IoD, so it is suitable for IoD.

In the SLAKA-IoD protocol, the ideal PUF is applied. However, the noise in PUFs remains an issue. Therefore, we will further design new, secure, and lightweight AKA protocols for IoD, which consider non-ideal PUFs.