Abstract
UAV mission planning is one of the core problems in the field of UAV applications. Currently, mission planning needs to simultaneously optimize multiple conflicting objectives and take into account multiple mutually coupled constraints, and traditional optimization algorithms struggle to effectively address these difficulties. Constrained multi-objective evolutionary algorithms have been proven to be effective methods for solving complex constrained multi-objective optimization problems and have been gradually applied to UAV mission planning. However, recent advances in this area have not been summarized. Therefore, this paper provides a comprehensive overview of this topic, first introducing the basic classification of UAV mission planning and its applications in different fields, proposing a new classification method based on the priorities of objectives and constraints, and describing the constraints of UAV mission planning from the perspectives of mathematical models and planning algorithms. Then, the importance of constraint handling techniques in UAV mission planning and their advantages and disadvantages are analyzed in detail, and the methods for determining individual settings in multiple populations and improvement strategies in constraint evolution algorithms are discussed. Finally, the method from the related literature is presented to compare in detail the application weights of constrained multi-objective evolutionary algorithms in UAV mission planning and provide directions and references for future research.
1. Introduction
With the rapid development of Unmanned Aerial Vehicle (UAV) technology, UAV mission planning (UMP) has become an important research area that has attracted much attention. UMP has been increasingly used in a variety of fields, such as agriculture, logistics, rescue, and environmental monitoring [1,2], which has placed higher demands on UAVs in complex and changing environments and created higher requirements for UAVs to fulfil their tasks efficiently and safely. The core goals of UMP include mission assignment, trajectory planning, and obstacle avoidance. Through accurate mathematical models and advanced planning algorithms, it aims to enable a planning system to quickly respond to changes in the environment and adjust and optimize a planning scheme in real time. Therefore, UMP needs to be applicable not only in static environments but also in dynamic and uncertain environments, ensuring that UAVs can safely perform their missions in a variety of environments.
Traditional optimization methods often face a number of challenges when dealing with UMP problems [3]. First, UMP usually involves multiple conflicting optimization objectives, such as the conflict between the shortest trajectory and the lowest energy consumption. In practice, UAVs need to select the shortest trajectory to shorten their flight times, and at the same time, they need to reduce energy consumption to improve their efficiency when performing their missions. However, UAVs usually need to detour or adjust their flight altitudes in order to effectively avoid obstacles or unfavorable weather conditions, which increases their energy consumption. Second, UMP also needs to satisfy various coupled constraints, such as flight time, flight altitude limits, and environmental changes, which constrain each other and increase the complexity of UMP. Traditional optimization methods usually struggle to deal with multiple conflicting objectives at the same time [4,5] and perform poorly when faced with complex constraints, making it difficult to find an effective UMP solution.
The proposal of constrained multi-objective evolutionary algorithms (CMOEAs) has provided an effective approach to address these challenges. CMOEAs transform a problem into a multi-dimensional space by introducing the theory of multi-objective optimization to solve the Pareto optimal solution set, which determines the optimal balance of various optimization objectives. Secondly, CMOEAs incorporate constraint handling techniques, using methods such as adaptive functions, penalty functions, and repair strategies to deal with constraints and ensure that the UMP solutions generated during the search process satisfy the constraints. This approach provides a large set of candidate solutions so that the decision maker can choose the most appropriate solution according to their specific needs. It can also effectively deal with complex environmental changes and constraints. Therefore, CMOEAs improve the efficiency and flexibility of UAV mission planning and enhance the adaptability and reliability of UAVs in uncertain environments [6,7,8].
This paper provides a comprehensive review of CMOEAs in UMP. A detailed review of the mathematical models, classification of constraint handling techniques, and improvement strategies for UMP is presented from a new perspective, aiming to provide valuable references for scholars in the field of UMP research. To the best of our knowledge, no study has systematically summarized this topic. The main contributions of this paper can be summarized as follows:
- Firstly, UMP is classified in detail according to the execution links and operation modes of the planning system, and a new classification method is proposed according to the constraint processing techniques of UAV goal priority and constraint priority. Then, the key factors constraining the performance of UMP are discussed from the perspectives of both the mathematical model of UMP and the planning algorithm.
- By elaborating the UMP execution process based on a differential evolutionary algorithm, we clarify the embedded modules based on the constraint handling techniques in CMOEAs and outline the advantages and disadvantages of each current constraint handling technique. In addition, we introduce the CMOEA framework for solving optimization problems.
- According to the UMP execution process based on CMOEAs, we highlight individual setup methods for different populations and improvement strategies to help researchers and scholars quickly find suitable setup methods for different planning scenarios. At the same time, we propose for the first time to evaluate UMP performance from the perspective of UAV performance metrics and algorithm performance metrics together.
The rest of this paper is organized as follows: Section 2 describes the classification of UMP, its applications in different domains, and its constraints. Section 3 discusses the mathematical models of UMP and classical algorithm-based planning methods. Section 4 describes the constraint handling techniques in CMOEA-based UMP and the related literature. Section 5 details methods for determining individual settings in different populations, improvement strategies, and performance evaluation metrics. Section 6 describes the methodology for searching the literature on CMOEA-based UMP. The last section provides a summary and identifies future research directions.
2. Preliminary Information
This section first introduces the basic classification of UMP problems and the application areas involved. Then, the key role of UMP in 3D map reconstruction is described. Finally, the challenges and constraints faced by UMP are discussed from the perspectives of both mathematical modeling and planning algorithms for UAVs.
2.1. Basic Classification of UMP
UMP can be divided into mission assignment, trajectory planning, and trajectory replanning according to the execution aspects [9]. The mission assignment stage focuses on the reasonable assignment of different missions to multiple UAVs, with the goal of optimizing the efficiency of mission execution and resource utilization. A UAV can dynamically adjust a UAV mission assignment scheme through intelligent algorithms and data analysis according to the nature of the mission, the degree of urgency, and the demand for resources. Trajectory planning plans optimal trajectories for UAVs to ensure the successful completion of a mission. Obstacles and dangerous areas must be avoided during the planning process, the core of which lies in the use of a Geographic Information System (GIS), sensor data, and advanced trajectory optimization algorithms to solve safe and efficient flight trajectories. Trajectory replanning is a key technology used to cope with unexpected situations during UMP execution, ensuring mission flexibility and safety by adjusting a UAV’s flight trajectory in real time. This process involves rapid responses and the analysis of real-time environmental data, such as weather changes, the appearance of obstacles, or adjustments to mission requirements. This class division method not only helps to systematically study the various execution aspects of UMP but also promotes the development and application of related technologies. By continuously improving mission assignment, trajectory planning, and trajectory replanning technologies, UMP systems can meet the needs of different application scenarios and enable UAVs to have higher autonomy and reliability when facing various complex environments [10,11].
UMP can be classified as offline or online based on its mode of operation [12]. Offline planning is usually performed prior to mission execution with pre-collected environmental data, identified mission requirements, and comprehensive mission assignment and trajectory planning using optimization algorithms and simulation techniques, which can provide detailed mission scenarios and trajectory coordinates to ensure optimal UMP performance in known environments [13]. However, offline planning is less flexible and is not able to cope with sudden environmental changes or dynamic constraints during mission execution. An online planning system, on the other hand, obtains real-time environmental sensing and mission status data during mission execution and adjusts a UAV’s mission assignment and flight trajectory in real time through dynamic planning and real-time optimization algorithms, such as online learning, local search, and reinforcement learning. The advantage of online planning systems is that they can flexibly respond to dynamically changing environments and unexpected situations to ensure the reliability and safety of task execution. This classification method is applicable to different mission requirements and operating environments, providing different solutions for UMP. At the same time, it is also possible to design a hybrid planning system by integrating the advantages of offline and online planning systems. This type of system performs comprehensive offline planning before mission execution and makes real-time adjustments using online planning during execution, providing the optimal UMP solution [14].
UMP can be categorized as objective-first or constraint-first. Objective-first UMP focuses on prioritizing the optimization of a UAV’s objectives with the aim of improving the efficiency of mission planning, reducing energy consumption, minimizing flight time, maximizing the mission completion rate, etc. These optimization techniques usually use advanced planning algorithms such as genetic algorithms, particle swarm optimization, and ant colony algorithms to solve for the optimal solutions. Constraint prioritization focuses on constraint handling techniques for UAVs, concentrating on complex constraints in mission planning such as flight altitude limits, obstacle avoidance requirements, communication coverage, and energy constraints. Commonly used constraint handling techniques include the penalty function method, the constraint dominance relation, and the feasibility-first method [15,16,17]. The penalty function method deals with constraint violation by adding penalty terms to the objective function, the constraint dominance relation compares the advantages and disadvantages of different solutions based on the satisfaction of constraints, and the feasibility-first method gives preference to solutions satisfying hard constraints and optimizes the soft constraints on this basis. Through this class division method, UMP research can be targeted to solve different practical problems and provide strong support for the efficient execution of complex missions, which not only promotes progress related to constrained multi-objective optimization problems but also facilitates the wide application of UAV technology in various fields.
2.2. UMP Applications in Different Fields
UMP involves knowledge from several disciplines, such as computer science, control theory, communication technology, and artificial intelligence [18,19,20], and with the rapid development of UAV technology and the continuous expansion of application scenarios, the application of UMP in various fields has become increasingly widespread. This section first introduces the different stages and execution processes of UMP, then explores the application of UMP in various areas.
Figure 1 illustrates the different execution stages of UMP, the execution process, and its specific applications in various fields. UMP can be divided into four main phases: preparation, planning, execution, and post-processing. The preparation stage mainly involves the definition of mission requirements, initialization, and self-testing of the UAV; these steps ensure that the mission requirements are clear and that the UMP system is able to function properly. The planning stage focuses on environmental awareness, cooperative communication, mission analysis, and optimization theory and uses advanced algorithms and optimization techniques to develop efficient and safe mission scenarios that meet specific optimization objectives and constraints. The execution phase involves mission implementation, real-time monitoring, and dynamic adjustment, which ensure that the UAV performs the mission as planned and can adjust the planning scheme in real time. The reprocessing stage involves data processing, result analysis, and report generation, which provide optimization recommendations for the UMP system through in-depth analysis of data from the execution process. Currently, UMP is used in a variety of fields: in the field of agriculture, UMP is used for precision agriculture and crop monitoring [21]; in the field of environmental monitoring, UMP is used to collect and analyze data in real time to evaluate environmental changes [22]; and in the field of logistics and distribution, UMP ensures that parcels are delivered to their destinations efficiently and accurately [23]. In addition, UMP plays a crucial role in areas such as search and rescue and infrastructure inspection [24,25]. The efficient execution process of UMP not only improves the efficiency and safety of the application field but also enhances the accuracy and resource utilization of the executed missions. In this section, the execution process of UMP is elaborated in detail, using the 3D map reconstruction technique in UMP as an example, as shown in Figure 2.
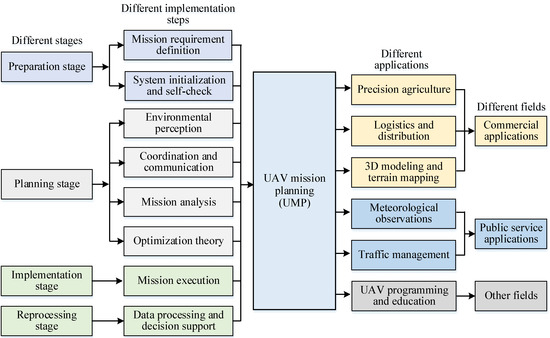
Figure 1.
UMP applications in different fields.
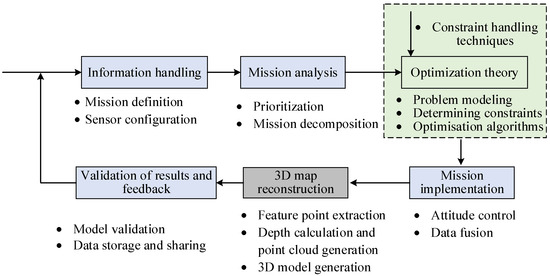
Figure 2.
Three-dimensional map reconstruction technique in UMP.
Figure 2 demonstrates the 3D map reconstruction technique in UMP. Urban reconstruction after a natural disaster such as a flood is carried out as follows:
- The preparation stage begins with a comprehensive assessment of the scope and severity of the impact of the disaster, including the collection of geographic information and data on the damage to buildings, roads, and infrastructure in the disaster area. Based on this information, specific missions for UAVs are defined, such as panoramic photography of the disaster area, detailed surveys of damaged buildings, assessments of road access conditions, inspections of critical infrastructure, and search and rescue missions. In addition, the type, number, and configuration of UAVs need to be determined to ensure that the various mission requirements can be met.
- In the planning stage, a UAV uses high-resolution cameras and sensors to sense the environment and collect a large amount of image information, which is transmitted to a ground control center or the cloud for processing through wireless communication technology. Then, image stitching and matching algorithms are used to preprocess the collected image data and build a 3D model of the disaster area. Next, a UAV mission assignment plan and a flight trajectory are developed to ensure that all critical areas are covered while avoiding obstacles and dangerous areas. The mission analysis includes the prioritization of missions, resource allocation, and time scheduling to optimize the UAV’s mission execution strategy.
- In the execution stage, the UAV carries out the actual operation in accordance with the planned mission assignment and flight trajectory, and real-time monitoring and adjustment of the UAV’s flight status and mission execution are carried out through the ground control station to ensure the smooth progression of the mission. At the same time, the real-time data transmission and processing system provides instant feedback on the situation, making it possible to respond quickly to emergencies and dynamically adjust the mission.
- In the reprocessing stage, the data collected by the UAV are processed and analyzed, which includes data collation, screening, cleaning, and storage, and high-precision maps of the disaster area are generated using image processing technology. Data analysis tools provide detailed assessments of the damage, reconstruction needs, and resource allocation in the disaster area, providing an accurate and reliable basis for decision makers.
The UMP implementation process stage can assist urban planners in redesigning urban layouts, road networks, and infrastructure layouts to improve the resilience of cities.
2.3. Limitations of UMP
UMP faces many limitations, including the complexity of heterogeneous UAV maneuvering performance, the diversity of multi-objective optimization requirements, the impacts of dynamic changes in real-time environments, and the stringent limitations of complex mission constraints [26,27]. These limitations make it extremely difficult to construct accurate mathematical models and design efficient optimization algorithms.
2.3.1. Complexity of Mathematical Models
The complexity of a mathematical model lies in the fact that UAV maneuvering performance and the planning environment place high demands on the mathematical model; for example, the maneuvering performances of UAVs make their flight dynamics highly nonlinear, and this nonlinear behavior is difficult to accurately describe using simple mathematical models, although it can reflect the flight characteristics and responses of UAVs in real time [28]. UAVs are affected by dynamic factors such as meteorological conditions and wind speed and direction during flight, and uncertainties in the planning environment sensing data (e.g., sensor errors and data delays) and the system’s own uncertainties (e.g., navigational errors and control noise) lead to the need for real-time adjustments and optimization of the UMP program, which increases the modeling difficulty [29]. Second, the motion of the UAV is controlled by multiple variables, such as attitude, velocity, position, and acceleration. There is a high degree of coupling between these variables, meaning that changing one variable affects multiple other variables, increasing the complexity of the modeling [30]. Finally, UAVs need to adjust their flight trajectories and attitudes in real time during flight, which puts high demands on the computational speed and accuracy of the mathematical model, which must be able to compute the optimal solution quickly to ensure a safe and efficient flight for the UAV.
2.3.2. Limitations of Planning Algorithms
The limitation of the UMP algorithm is that high-dimensional and multi-constraint optimization problems usually have complex search spaces, and the UAV planning system needs to deal with a large number of candidate solutions during the planning process, which leads to a drastic increase in the computation and memory requirements [31]. Meanwhile, when facing dynamically changing environments (e.g., sudden obstacles and real-time mission changes), the state-space and action-space data of UAVs are very large and continuous. Although UMP algorithms based on deep reinforcement learning perform well in handling continuous and high-dimensional data with high adaptability and real-time performance, their training process may require a large amount of computational resources and time [32]. Secondly, in practical applications, UAVs have limited computing power and energy, and complex algorithms struggle to perform efficient planning and real-time optimization when running on UAVs. Finally, the planning algorithms are highly dependent on high-quality environmental data and accurate UAV model data, and possible errors in the data in the real environment will affect the accuracy and reliability of the planning results. These limitations indicate that the existing UMP algorithms still need to be further improved in practical applications to enhance their efficiency, flexibility, and robustness to better meet complex mission requirements.
3. Description of UMP
This section first introduces the mathematical model of UMP and its main considerations, details the classification of UAV constraints, and classifies UAV constraints into deterministic constraints and uncertainty constraints. Then, the current classical algorithms used in UMP are summarized, classified, and briefly described.
3.1. Mathematical Modeling of UMP
UMP defines and optimizes UAV mission execution strategies and flight trajectories through precise mathematical descriptions [33]. These models typically include objective functions and constraints to meet specific mission requirements and environmental constraints. The objective function may involve minimizing flight time, reducing energy consumption, or maximizing mission coverage. Constraints incorporate aspects such as flight altitude limitations, obstacle avoidance, communication coverage, energy consumption, etc. Commonly used mathematical modeling methods include linear programming [34], nonlinear programming [35], integer programming [36], and dynamic programming [37]. Accurate optimization models can be built using these methods to ensure efficient and safe operation of UAVs in complex environments. Figure 3 shows the factors affecting the accurate mathematical modeling of UMP.
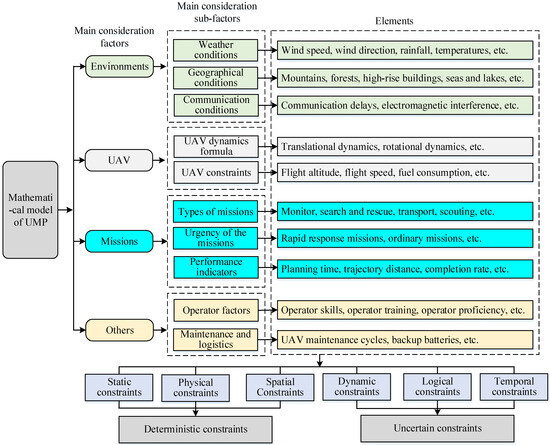
Figure 3.
Mathematical model of UMP.
Environmental perception is crucial for UMP [38]. Weather constraints, geographic constraints, and communication constraints directly affect UAV flight safety and mission execution efficiency. Bad weather such as strong winds and precipitation may lead to unstable flight, and UAVs will not take off for mission execution if the weather conditions are not conducive to flight. At the same time, complex terrain and obstacles increase flight difficulty, and insufficient communication signal coverage and interference affect communication and data transmission with the ground control center. Therefore, when planning UAV missions, the impact of environmental perception on UMP needs to be considered comprehensively to ensure smooth mission execution.
UAV dynamics and performance constraints directly affect the UMP program and its execution. A UAV’s dynamics include its flight performance, maneuverability, and flight stability [39]. These characteristics determine parameters such as a UAV’s speed, flight altitude, and fastest flight time when it is performing its mission. In addition, the performance constraints of a UAV, such as its load capacity, battery life, and sensor performance, also have significant impacts on UMP. Decision makers need to take these factors into account to determine the optimal flight trajectory, flight altitude, and flight speed to maximize the efficiency and success of mission execution.
The determination of the mission type, mission urgency, and planning time also has a significant impact on UMP [40]. Different types of missions (e.g., monitoring, search and rescue, delivery, etc.) have different models and execution modes for UAVs and thus require corresponding mission plans for different planning scenarios. The urgency of a mission directly affects its priority and execution schedule; urgent missions may require immediate deployment of UAVs, while non-urgent missions can be scheduled over a longer timeframe. In addition, sufficient planning time allows decision makers to more fully consider the various factors of a mission and develop a more reasonable and effective mission plan, whereas tight planning times may lead to imperfect and insufficient mission plans, increasing the risk and uncertainty of mission execution [41,42].
In general, the mathematical model of UMP is usually regarded as an optimal control problem, and the mathematical expression of an optimal control problem usually involves an objective function (performance index) and constraints (including dynamics constraints and control constraints). Together, these elements define a control system that needs to be optimized. The following is a general mathematical expression for the objective function of an optimal control problem [43,44,45], which is usually an integral form representing some performance metric that needs to be minimized or maximized:
where denotes the performance metric or objective function to be minimized (or maximized). and denote the initial and termination times, respectively. and denote the vector of state variables and the vector of control variables, respectively. is a Lagrangian function representing the operating cost of the system at time t for and . denotes the state cost at the termination time .
Dynamic constraints are usually represented by a set of differential equations that describe the evolution of the system state over time t:
where is the derivative of the state with respect to time t; is the dynamical equation of the system; and is the initial condition, which denotes the state of the system at the initial moment .
Control constraints limit the range of values of the control variable :
where and are the upper and lower bounds of the control variables, which may be constants or functions of time.
3.2. UMP Based on Traditional Optimization Algorithms
UMP based on traditional optimization algorithms uses different strategies and methods to find optimal or near-optimal planning solutions in a search space [46,47,48,49]. UMP based on traditional optimization algorithms is not only able to effectively cope with some types of mission requirements and environmental constraints but also ensures that UAVs are efficient and reliable during execution. We illustrate the application scope of UMP based on traditional optimization algorithms through the classification of UAV mission assignment, UAV trajectory planning, and UAV trajectory replanning, as shown in Figure 4.
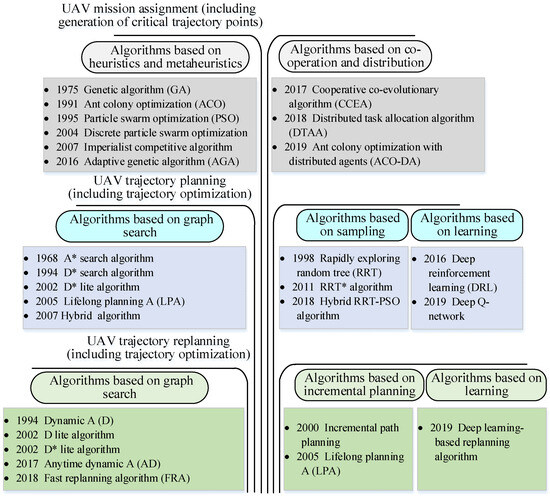
Figure 4.
UMP based on traditional optimization algorithms.
The UAV mission assignment problem aims to address whether it is reasonable to optimize the mission and UAV resources [50]. Task assignment is characterized by the need to efficiently assign missions among multiple UAVs in order to minimize the total mission time or maximize the mission benefit, taking into account resource constraints and mission priorities. The generation of critical trajectory points is crucial in this process. These trajectory points need to take into account environment modeling, obstacle avoidance requirements and optimization of UAV trajectories to ensure that the UAVs are able to complete their respective missions safely and efficiently. This not only improves the success rate of mission execution, but also makes effective use of UAV resources for the purpose of overall optimization.
UAV mission planning algorithms can be classified into two categories: heuristic and meta-heuristic based algorithms as follows: Genetic algorithm (GA) [51], Ant colony optimization (ACO) [52], Particle swarm optimization (PSO) [53] Discrete particle swarm optimization [54], Imperialist competitive algorithm [55], Adaptive genetic algorithm (AGA) [56]. Another class of algorithms is based on co-operation and distribution as follows: Cooperative co-evolutionary algorithm (CCEA) [57], Distributed task allocation algorithm (DTAA) [58], Ant colony optimization with distributed agents (ACO-DA) [59].
The UAV trajectory planning problem aims to plan the optimal trajectory of a UAV from the start point to the end point. Trajectory planning is characterized by the need to avoid obstacles and meet flight performance constraints while ensuring the shortest or safest path. Trajectory optimization performs an important role in this process by fine-tuning the initially planned trajectory through optimization algorithms in order to further improve the efficiency and safety of the trajectory. However, the methods of trajectory optimization in this category usually show excellent performance in solving UAV trajectory planning in static environments.
UAV trajectory planning algorithms include three categories, one is based on graph search algorithms, specifically: A* search algorithm [60,61], D* search algorithm [62,63], D* lite algorithm [64,65], Lifelong planning A (LPA) [66], Hybrid algorithm [67]. A class of sampling-based algorithms, specifically include: Rapidly exploring random tree (RRT) [68], RRT* algorithm [69,70], Hybrid RRT-PSO algorithm [71]. Another category is learning-based algorithms, specifically: Deep reinforcement learning (DRL) [72], Deep Q-network [73].
The UAV trajectory replanning problem aims to adjust the flight trajectory of a UAV in real time in a dynamic environment. Trajectory replanning is characterized by the need to respond in real time to changes in the environment or changes in the mission to ensure that the UAV is able to update its trajectory in real time during flight to avoid new obstacles or respond to new mission commands with a high degree of flexibility and real-time performance. In dynamic environments, trajectory optimization is still very important to ensure that the UAV is able to respond to unexpected situations and environmental changes with the best trajectory by continuously fine-tuning the local trajectory. This type of trajectory optimization not only provides refined adjustments to the initial trajectory, but also continuously optimizes it during the replanning process, enabling the UAV to perform efficient and safe flights in the face of complex dynamic environments.
UAV trajectory replanning algorithms mainly include three categories: one is based on graph search algorithms, specifically: Dynamic A (D) [74,75], D lite algorithm [76,77], D* lite algorithm [78], Anytime dynamic A (AD) [79], Fast replanning algorithm (FRA) [80]. One class of algorithms is based on incremental planning, specifically, Incremental path planning [81,82], Lifelong planning A (LPA) [83]. Another category is learning-based algorithms, specifically: Deep learning-based replanning algorithm [84].
Traditional optimization algorithms have many advantages, such as fast convergence, ease of implementation, and fewer parameters and implementation steps, and a large number of well-established tools and libraries (e.g., MATLAB, SciPy, Gurobi, etc.) are already available to be directly invoked. However, UMP (UAV mission planning) currently involves multiple conflicting optimization objectives. Conventional optimization algorithms usually deal with this by weighting multiple optimization objectives in a composite objective function, which may result in the absence of some important objective information. In addition, if UMP involves multiple nonlinear constraints or multiple coupled constraints that result in a feasible domain space with a complex shape, the convergence of traditional optimization algorithms is slower and the algorithms are less robust. When dealing with complex and multi-peaked optimization problems, traditional optimization algorithms usually focus on only one solution in a single search process, and they do not have a diversity mechanism. Therefore, they are prone to fall into a local optimum.
4. UMP Based on CMOEAs
This section first introduces a UMP flowchart, lists the classic CMOEA literature, and describes the core ideas of these algorithms. Next, the commonly used constraint handling techniques in CMOEAs are described in detail. Finally, a framework for CMOEAs based on constraint handling techniques is explored.
4.1. Flowchart of UMP
Figure 5 is based on the differential evolution (DE) algorithm [85], and the evolutionary process is divided into four modules: the initiation module, the main loop module of the algorithm, the termination module, and the output module. In the initiation module, first environmental information is obtained to determine the UAV start point and the mission. Next, the objective function and constraints are constructed, and the estimated voyage cost matrix is calculated. Then, the population (Pop) is initialized; the iteration number (Gen), variation rate (Rm), and crossover rate (Rc) are determined; and the fitness value is calculated for each individual. The main loop module of the algorithm generates the sub-generation population using the variation operator, crossover operator, and selection operator and re-evaluates the fitness value of each individual in the population after each iteration. The termination module determines whether a predefined termination condition (e.g., reaching the maximum number of iterations or converging to some optimal solution) has been reached. If the termination condition is reached, the output module is entered. Otherwise, the main loop module continues. The output module outputs the UMP solution that satisfies the conditions. However, using only differential evolutionary algorithms may lead to the following problems: (1) a lack of feasible solutions, as the algorithm may generate a large number of solutions that do not satisfy the actual constraints; (2) low-quality solutions, as the generated solutions may not be able to balance multiple optimization objectives; and (3) convergence, as the algorithm may have difficulty efficiently converging to the optimal solution in the presence of a large number of constraints.
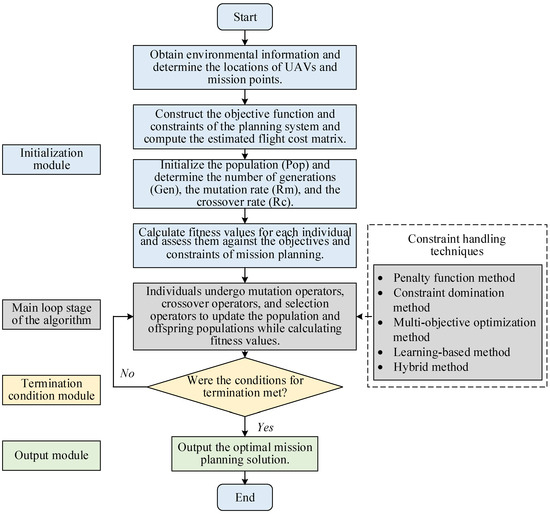
Figure 5.
Flowchart of UMP.
In order to overcome the above mentioned problems, constraint handling techniques are introduced in the main loop stage of the algorithm which include penalty function method [86], constraint domination method [87], multi-objective optimization method [88], learning-based method [89] and hybrid method [90,91]. In optimization algorithms, a series of methods and strategies are used to ensure that the generated solutions satisfy specific constraints (e.g., physical, environmental, and performance limitations, etc.) [92,93,94], and constraint processing techniques guide the algorithms in generating feasible and high-quality solutions by introducing constraints during the optimization process and eliminating or correcting solutions that do not satisfy the constraints. The advantages of multi-objective evolutionary algorithms based on constraint handling techniques are as follows:
- Guaranteed solution feasibility: In multi-objective optimization, constraint handling techniques ensure that each solution is optimized while satisfying all constraints. This means that all generated solutions are within the feasible domain, thus avoiding the generation of solutions that do not satisfy the constraints.
- Enhanced solution quality and diversity: multi-objective optimization requires finding a balance between different objectives, and constraint handling techniques help to generate a collection of solutions with a high degree of diversity, allowing the final solution to balance multiple optimization objectives.
- Accelerated convergence: constraint handling techniques allow algorithms to focus on the feasible domain faster by eliminating infeasible solutions, greatly reducing invalid searches and accelerating convergence.
- Enhanced robustness and adaptability of algorithms: In dynamically changing environments, UMP needs to adapt to different mission requirements and constraint changes. Constraint handling techniques increase the robustness and adaptability of an algorithm. Even when faced with new task insertions or changes in the environment, the constraint handling technique ensures that the solution set is able to adjust and satisfy the new constraints in a timely manner.
Table 1 describes the classical CMOEAs and some of the commonly used CMOEAs and details the core ideas of these algorithms.

Table 1.
CMOEAs.
4.2. Constraint Handling Techniques
Currently, common approaches to constraint handling include penalty function methods, constraint domination methods, multi-objective optimization methods, learning-based methods, and hybrid methods [103,104,105], which play different roles. Penalty function methods deal with constraints by adding a penalty term to the objective function for violating the constraints to ensure that the solution set satisfies the constraints [106]; constraint domination methods improve the efficiency of the algorithms by comparing the feasibility of the solutions with the dominance relationship and prioritizing feasible solutions [107]; multi-objective optimization methods aim to optimize multiple conflicting objectives at the same time by balancing more than one optimization objective [108]; learning-based methods use machine learning techniques to predict and improve the planning process, which improves the robustness of the algorithm [109]; and hybrid methods combine multiple optimization techniques [110], which integrates the advantages of different constraint handling techniques to improve the overall performance and solving efficiency of the algorithm. The specific advantages and disadvantages of different constraint handling techniques are shown in Table 2.

Table 2.
Constraint handling techniques.
4.3. A Framework for CMOEAs Based on Constraint Handling Techniques
In addition to the common constraint handling techniques described in Section 4.2, a CMOEA framework based on dual populations, dual stages, multiple populations, and multiple stages has also shown better performance when dealing with constrained multi-objective optimization problems in recent years [128,129,130]. Unlike constraint handling techniques, dual-population, dual-stage, multi-population, and multi-stage techniques improve global search capability and local optimization accuracy through the parallel computation of populations and the stage processing strategy, and their specific advantages and disadvantages are shown in Table 3.

Table 3.
Framework of CMOEAs based on constraint handling techniques.
5. Modifications to CMOEAs for UMP
In this section, we first classify the information contained in the individuals of the population. Before planning, we need to set the information for the individuals in the population, which contains key information such as the sequence of the UAVs, the sequence of the mission points, the cost of the voyage, the constraints, etc. The advantages and disadvantages of the individual setups will directly affect the degree of coverage of the CMOEAs in the search space and the efficiency of the execution [139]. Then, the improvement strategy in the UMP algorithm can improve the flexibility and adaptability of the algorithm. A reasonable improvement strategy is one of the key factors to ensure the stability of the algorithm. Finally, after UMP is completed, it is crucial to evaluate the effectiveness of the execution scheme, which can be carried out based on the performance indices of the UAV and the algorithm. After the comprehensive evaluation, the effectiveness of the information contained in different individuals and the improvement operators can be verified, and the individual information and optimization of the improvement operators can be updated.
5.1. Individual Expressions of Populations for UMP Based on CMOEAs
In CMOEA-based UMP, the form of representation of individuals in a population is crucial, and each solution is usually represented via encoding, which can be in the form of real-number encoding, binary encoding, or trajectory encoding, depending on the characteristics of the problem and the optimization objectives [140,141]. For example, in trajectory planning, an individual can be represented as an ordered sequence of nodes, where each node corresponds to a key point on the UAV flight trajectory. Each individual contains trajectory information as well as relevant parameters such as the order of task execution, flight altitude, and speed.
Figure 6 presents the individual expressions of UMP populations based on CMOEAs. Currently, the individual expressions of a population are usually classified into the following categories: UAV and mission sequences, trajectory points and flight information, environmental information, and constraint processing information.
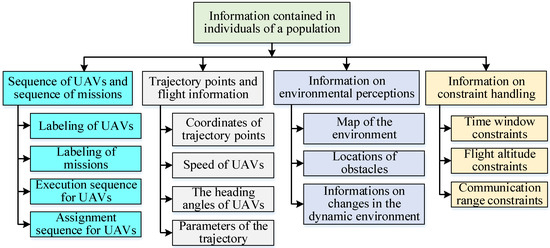
Figure 6.
Forms of individual expression of UMP populations based on CMOEAs.
- UAV and mission sequences constitute individual information, which can directly affect the assignment and scheduling of missions. This method can effectively balance the mission load of a UAV, reduce the conflict and waiting time between missions, and improve the efficiency of mission execution. However, this representation is relatively simple, and the UMP scheme is prone to violating constraints when faced with complex missions.
- Based on individual information contained in trajectory points and flight information, this method pays more attention to the performance metrics of UAVs, which can improve the accuracy of UMP and ensure safety and reliability when executing a mission. However, this method requires real-time monitoring and updating of the UAV status, which increases the complexity of the UMP system.
- Based on individual information obtained via environmental sensing, this method can help a UAV make more accurate decisions based on real-time data and help identify and avoid potential risks, thereby improving flight safety. However, the acquisition and processing of environmental information is complex and requires a large number of sensors and algorithms to analyze the data in real time, leading to increased demand for computational resources.
- Based on individual information obtained via constraint processing, this method is able to cope with different types of constraints and enhance the feasibility of the solution, thus generating a more reliable mission planning solution. However, conflicts may arise between different constraints, and trade-offs and adjustments are required when dealing with these conflicts, which increases the complexity of the algorithm in space and time.
5.2. Classification of UMP Improvement Strategies Based on CMOEAs
In addition to changing the forms of individual populations, some researchers and scholars have proposed different improvement strategies for the UMP algorithm [142,143]. The population collaboration modes can be divided into the adaptive population size strategy, the multiple independent populations parallel optimization strategy, and the multiple-population co-evolution strategy. The detailed improvement strategies are shown in Table 4:

Table 4.
Classification of UMP improvement strategies based on CMOEAs.
- The adaptive population size strategy improves the performance of the algorithm by dynamically adjusting the size of the population during the optimization process. With the current number of iterations, the population size is automatically increased or decreased to balance explorability and convergence. The solution space is extensively explored by larger populations in the early stage and quickly converged by smaller populations in the later stage. This method improves the search efficiency and solution quality of the algorithm.
- The multiple independent populations parallel optimization strategy optimizes multiple independent populations in parallel, each of which searches independently in a different region of the solution space. This method increases the diversity of the solutions and prevents the algorithm from falling into local optimal solutions, and parallel computation can significantly improve computational efficiency. Meanwhile, multiple independent populations can explore different regions of the solution space, which improves the probability of finding a globally optimal solution.
- The multiple-population co-evolution strategy improves the performance of the algorithm through information interaction and collaboration between different populations during the optimization process. Optimal individuals or some individuals can be exchanged between populations to promote diversity of understanding and information sharing. Through collaboration between populations, the global search ability of the algorithm is enhanced, overcoming the fact that a single population can easily fall into a local optimum and improving the global optimization effect.
The improvement operator strategies of the algorithm can be divided into the adaptive crossover and mutation strategy and the hybrid algorithm strategy as follows:
- The adaptive crossover and mutation strategy adapts to different stages by dynamically adjusting the probabilities of the crossover and mutation operators during the optimization process. The mutation probability is increased in the exploration phase and the crossover probability is increased in the exploitation phase to improve the search efficiency of the algorithm, while the convergence speed and global search capability of the algorithm are improved by balancing the exploration and exploitation processes using an adaptive adjustment strategy.
- By fusing the advantages of different optimization algorithms, the hybrid algorithm strategy enhances the robustness and global search ability of the algorithm and adapts to more complex multi-objective optimization problems.
The constraint processing techniques can be divided into the dynamic constraint processing strategy and the hybrid constraint processing strategy as follows:
- In the dynamic constraint processing strategy, the constraint processing method is dynamically adjusted during the optimization process according to the characteristics of the current solution and the changes in the constraints. By dynamically adjusting the constraint processing strategy, the flexibility and adaptability of the algorithm in dealing with complex constraints are enhanced and the feasibility of the algorithm is improved.
- The hybrid constraint processing strategy selects or combines different constraint processing techniques according to the actual situation during the optimization process in order to improve the effectiveness of constraint processing. By combining multiple constraint processing techniques, the algorithm’s ability to deal with complex constraints is improved to ensure the feasibility and optimality of the solution.
5.3. Performance Evaluation Metrics for CMOEA-Based UMP
A comprehensive evaluation of a solution is needed after UMP has been carried out, and this section focuses on the importance of algorithm performance for UMP from the perspectives of both UAV and algorithm performance metrics. Through these performance evaluation metrics, researchers and scholars are able to comprehensively understand and compare the performances of different algorithms in order to optimize the algorithms of UMP.
Figure 7 presents the performance evaluation metrics of CMOEA-based UMP. The performance metrics of the UAVs and algorithms can be used together to evaluate the effectiveness of UMP. The performance metrics of the UAVs include the shortest range, shortest flight time, lowest energy consumption, mission execution success rate, response time, and feasibility of the planning system [154,155]. The performance metrics of the algorithms include the diversity of solution sets, convergence, constraint handling efficiency, and algorithm scalability [156,157]. The diversity of the solution set measures the degree of diversity among the solutions in the set of Pareto optimal solutions, and a higher diversity indicates that the algorithm is able to find more non-dominated solutions, thus covering more solution space [158,159]. The convergence of the solution set measures the degree of approximation of the solution set to the true Pareto frontier. The higher the convergence, the closer the obtained solution is to the optimal solution, reflecting the algorithm’s ability to approximate the optimal solution during the solution process. Constraint handling efficiency refers to the ability of the algorithm to effectively handle constraints when solving multi-objective optimization problems. Efficient constraint handling not only improves the search efficiency and optimization effect of the algorithm but also ensures that high-quality feasible solutions can be generated in a complex mission environment. The constraint handling efficiency can be expressed by calculating the proportion of feasible solutions. The scalability of the algorithm refers to whether the algorithm is able to replace different algorithmic components through modular design to significantly improve the performance and efficiency of the UMP system when dealing with UMP problems of a larger scale. Therefore, the performance metrics of the UAVs and algorithms can comprehensively reflect the UMP performance.
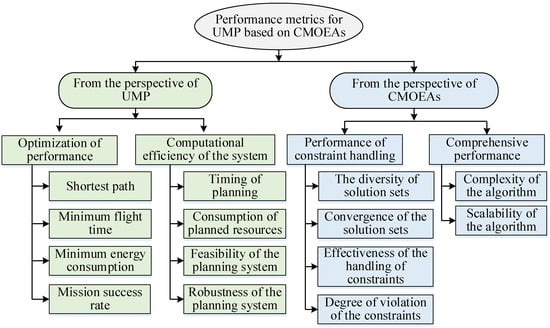
Figure 7.
Performance evaluation metrics of CMOEA-based UMP.
6. Discussion
In this section, we first introduce the method of searching for CMOEA-based UMP research, which was obtained by entering keywords into a data platform and filtering the relevant literature based on the year of publication and the type of publication. Then, we counted the number of studies on CMOEAs and the number of UMP studies based on CMOEAs in the last 20 years. Next, we counted the percentages of classical algorithms and CMOEAs in UMP research. Finally, we present the specific constraints and the proportions of optimization objectives in CMOEA-based UMP.
6.1. Collection of Statistical Data from the Literature
Figure 8 presents the scheme of this review for searching for UMP-related research based on CMOEAs. First, relevant keywords and key information (e.g., UAV mission planning, UAV scheduling, constraint handling techniques, etc.) were entered into digital libraries or academic databases (e.g., IEEE Xplore, SpringerLink, ScienceDirect, etc.). Then, the UMP literature based on CMOEAs was further filtered by setting restrictions on the timeframe and the publication categories (e.g., journals, conference papers, reviews, etc.). Using this method, we could usually retrieve the literature related to UMP cooperative mission planning, UMP path planning, UMP replanning, and so on. Ultimately, we needed to precisely find research that was relevant and representative of UMP and CMOEAs to ensure the comprehensiveness and accuracy of this study.
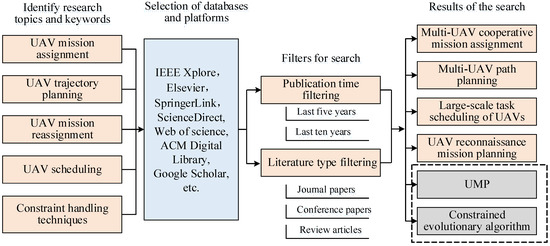
Figure 8.
Method of searching the literature.
6.2. Research Published on CMOEAs and CMOEA-Based UMP
In recent years, research on CMOEAs and CMOEA-based UMP has involved various aspects such as the theoretical improvement of algorithms, practical applications, and performance evaluation. Researchers have proposed various improved CMOEAs to enhance the effectiveness of UMP under complex constraints and verified their effectiveness in UMP through a large number of experiments. Figure 9 presents the numbers of CMOEA publications and CMOEA-based UMP publications in the literature from 2004 to 2024.
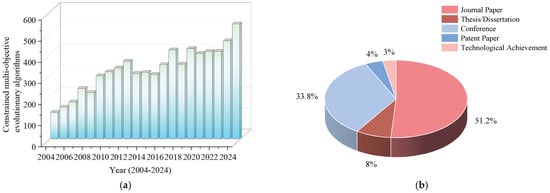
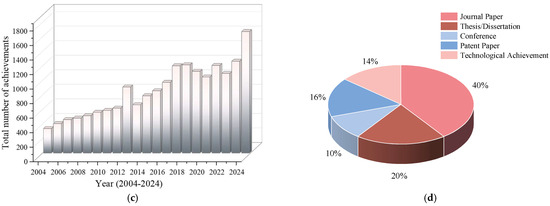
Figure 9.
Proportions of CMOEAs and numbers of CMOEA-based UMP publications in journals (2004–2024). (a) Total numbers of journal articles, conferences, patents, etc., published on CMOEAs (2004–2024); (b) proportions of journal articles, conferences, patents, etc., published on CMOEAs (2004–2024); (c) total numbers of CMOEA-based UMP journal papers, conferences, patents, etc., published (2004–2024); and (d) proportions of CMOEA-based UMP journal articles, conferences, patents, etc., published (2004–2024).
Figure 9 summarizes the proportions of CMOEAs and the numbers of CMOEA-based UMP publications in journals, etc., from 2004 to 2024. In Figure 9a, the variation in the total number of journal papers, conferences, and patents published on CMOEAs over the last 20 years is shown. It can be observed that the number of published CMOEAs has been growing steadily. In Figure 9b, it can be seen that journal papers have had the largest share, while patents and scientific and technological achievements have had the smallest number of publications. Figure 9c demonstrates the total numbers of UMP journal papers, conference papers, and patents involving CMOEA-based UMP over the last 20 years, which reflect the specific application of CMOEAs in UMP, and it can be seen that CMOEA-based UMP research results have been increasing in recent years. Figure 9d shows the proportions of CMOEA-based UMP literature in the total literature over the last 20 years, from which it can be seen that journal papers still have the largest proportion. Patents and scientific and technological achievements also account for large proportions. Therefore, the results of UMP based on CMOEAs are significant and tend to be converted into practical patents and scientific and technological achievements.
6.3. Proportions of Traditional Optimization Algorithms and CMOEAs in UMP
Due to the rapid development of machine learning and multiple intelligent algorithms, static UMP is rapidly undergoing a shift to dynamic UMP. In order to clearly show the change in the share of each algorithm, we describe the years 2004–2024 based on the first 10 years (2004–2013) and the last 10 years (2014–2024).
Figure 10a presents the proportions of each UMP algorithm from 2004 to 2013. Due to the high number of static path planning and UMP scenarios with fixed constraints studied in this time period, UMP based on the mathematical planning method was dominant. This method is suitable for solving exact optimization problems, and performs especially well on the trajectory planning problem. Comparatively speaking, UMP based on the graph theory method has obvious advantages in trajectory planning and obstacle avoidance, especially when topology and trajectory optimization need to be taken into account, and this method is able to effectively deal with the influence of moving obstacles on UAV trajectory planning. Secondly, UMP based on the sampling method and graph theory method accounted for comparable proportions. This was mainly due to the good performance of the sampling method in continuous space. Subsequently, there has been rapid development of UMP based on machine learning and reinforcement learning techniques, which are able to learn from data and optimize the mission planning process and perform especially well when facing complex and dynamic UMP environments. Finally, due to the limitations of computer arithmetic and the immaturity of CMOEAs, UMP based on CMOEAs accounted for a relatively small proportion of UMP during this period.
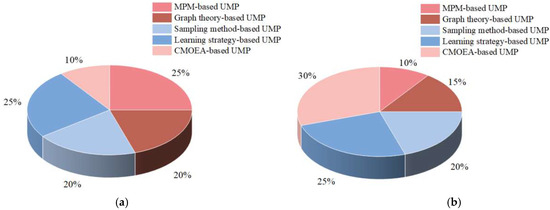
Figure 10.
Proportions of traditional optimization algorithms and CMOEAs in UMP over the last 20 years. (a) Proportions of each UMP algorithm (2004–2013); (b) proportions of each UMP algorithm (2014–2024).
Figure 10b presents the proportions of each UMP algorithm from 2014 to 2024. Firstly, the emergence of UMP for dynamic scenarios has led to a decrease in the share of mathematical planning methods. However, mathematical planning still maintains a certain proportion in some specific fields, such as air traffic control and logistics and distribution, which indicates that mathematical planning methods still play an important role in solving precise optimization problems. Secondly, graph theory-based UMP has gradually evolved from traditional mission assignment and trajectory planning towards more complex application fields, including UAV networks, communication switching, and securing UAV communications. Subsequently, optimization problems in continuous space have gradually occupied a major position compared to discrete space, so graph theory-based UMP still occupies a large proportion. With the rapid development of artificial intelligence and machine learning technologies, the application of learning strategy-based methods, such as reinforcement learning and deep learning, in UMP has gradually increased. Finally, with the significant increase in computer arithmetic power and the emergence of more mature CMOEAs, CMOEAs have become an effective solution for complex UMP problems, and thus the proportion of UMP based on CMOEAs has increased significantly.
These trends suggest that research and applications in the field of UMP are no longer limited to exact optimization problems and are moving towards more diverse, intelligent, and adaptable optimization problems.
6.4. Constraints and Optimization Objectives of UMP Based on CMOEAs
Figure 11 illustrates the weighting of constraints and optimization objectives for the mathematical model of UMP for the period from 2004 to 2024. As can be seen in Figure 11a, the constraints considered in the UMP literature included terrain constraints, UAV dynamics constraints, communication and control constraints, UAV performance constraints, and obstacle constraints. Terrain constraints ensure that a UAV flight trajectory avoids terrain obstacles. UAV dynamics constraints consider the flight dynamics of a UAV to ensure that it remains stable during flight. Communication and control constraints ensure that the communication and control signals between a UAV and the ground control station or other UAVs are smooth. UAV performance constraints focus on the flight capability of the UAV itself. Obstacle constraints consider obstacles in the planning environment to ensure safe UAV flight. These constraints accounted for almost equal proportions of the literature, indicating that all types of constraints were valued in UMP.
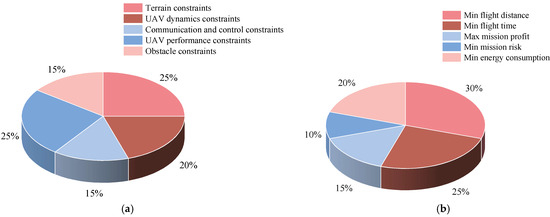
Figure 11.
The weighting of constraints and optimization objectives in the mathematical model of UMP over the last 20 years. (a) The proportions of constraints in the mathematical model of UMP (2004–2024); (b) the proportions of optimization objectives in the mathematical model of UMP (2004–2024).
As can be seen in Figure 11b, the optimization objectives considered for UMP included the minimum flight distance, minimum flight time, maximum mission benefit, minimum mission risk, and minimum energy consumption. The minimum flight distance not only reduces energy consumption but also improves the efficiency of mission accomplishment; the minimum flight time ensures that the mission can be accomplished in the shortest possible time; the maximum mission benefit focuses on the economic benefits and outcomes of the mission; the minimum mission risk considers potential risks and threats during mission execution; and the minimum energy consumption aims to prolong the endurance of the UAV and the time of mission execution. Among them, the shortest flight distance is the focus of current research, as it means that a UAV can reach a designated location in the shortest time and even return to load in time for the next mission, thus improving the overall mission effectiveness.
In summary, both the constraints and optimization objectives in UMP have been widely studied and applied in the literature, and both have important implications.
7. Future Research Directions and Conclusions
7.1. Future Research Directions
7.1.1. Integration with MCDA
The integration of CMOEA-based UMP with Multi-Criteria Decision Analysis (MCDA) methods remains one of the frontiers of current research. ELECTRE (Elimination et choix traduisant la realité) [160] and PROMETHEE (Preference ranking organization method for enrichment evaluations) [161] are two important MCDA methods that provide systematic and scientific decision support in the face of complex, multi-objective mission planning. For example, in UMP, the ELECTRE method helps decision makers to eliminate undesirable choices among multiple alternatives and find the optimal one by constructing transcendental relationships and evaluation matrices. And the PROMETHEE method provides a detailed basis for ranking and selection by comparing the strength of preferences between options, considering factors such as flight time, fuel consumption, mission priority and risk. By introducing these MCDA methods, UMP research can better cope with complex environments with multiple objectives and constraints, thus improving the efficiency and safety of mission execution. The integration of these methods will help develop a more intelligent and optimized UMP system, enhance UAV capabilities in mission assignment, trajectory optimization and risk assessment, and lay the foundation for the efficient deployment of future UAVs in various complex application scenarios. This not only promotes the development of UAV technology, but also provides new ideas and tools for the solution of CMOEAs.
7.1.2. Integration with 6G Networks
The integration of CMOEA-based UMP with sixth-generation mobile communication networks (6G) is a cutting-edge technology currently being researched. By combining CMOEAs and 6G networks, the efficiency and performance of UMP can be significantly improved. However, this integration faces a number of technical difficulties, including long communication delays, unstable data rates, and strict communication constraints. The details are as follows: First, when UAVs perform real-time missions, their high maneuverability and 6G network topology dynamics lead to UAV communication delays, which are due to the frequent switching of base station connections during the high-speed movements of the UAVs, thus increasing the network load and delay. Second, high-resolution, real-time video transmission requires a large amount of bandwidth and high data rates, and continuous data transmission may trigger network congestion. Finally, edge computing performs data processing through on-board devices, which reduces the need for continuous communication with a central server and thus shortens the response time. Therefore, UMP must consider communication constraints.
7.1.3. Integration with Area Blockchain Technology
The integration of CMOEA-based UMP with blockchain technology is also a current research hotspot. By combining CMOEAs and blockchain technology, the data security and integrity of airborne UAVs can be ensured, and this integration can help to enhance supply chain cooperation. However, it also faces many challenges, including data security, privacy protection, and scalability. The details are as follows: First, blockchain technology needs to handle a large amount of data in UMP, including information such as flight trajectories, mission execution statuses, and environmental monitoring, which require a high degree of security, and although blockchain technology can provide a certain degree of security, it also increases the complexity of data management. To ensure the security and reliability of UMP data, the constraints of data transmission and storage must be considered in the design. Secondly, UMP itself is a complex multi-constraint, multi-objective optimization problem, and the addition of blockchain technology requires additional consideration of issues such as data synchronization, which increases the complexity of the system design significantly. The constraints must be considered to balance these issues in multi-objective optimization while ensuring the proper functioning of the UMP system. Finally, the sizes of UAVs are likely to keep increasing, and UMP system design needs to be optimized under scalability constraints to ensure that it can handle increases in the amount of data and the number of nodes.
7.1.4. Integration with Quantum Computing
The integration of CMOEA-based UMP with quantum computing is also a current research frontier. By combining the powerful computational capability of quantum computing, the optimization of UMP can be significantly improved. The details are as follows: Firstly, the powerful computational ability of quantum computing can significantly improve the efficiency of CMOEAs, but quantum algorithms need to adapt to the constraint processing mechanisms of classical evolutionary algorithms. Deep modifications of the quantum computing framework are required to adapt to these constraint processing techniques. Second, quantum computing requires efficient encoding and quantum state representation of UMP constraints when processing UMP, which not only increases the complexity of algorithm design but also increases the demand for computational resources due to the ultra-high dimensionality of quantum states. This makes it difficult to perform accurate constraint evaluation among quantum states. In addition, the non-determinism of quantum computation and quantum error correction pose serious challenges to the real-time performance of UMP. A UMP system needs to respond to environmental changes in real time, and the results of quantum computation have a probabilistic nature to a certain degree. Therefore, when designing quantum evolutionary algorithms, it is necessary to consider how to deal with constraints stably and efficiently under the uncertainty of quantum computation. Finally, the integration of quantum computing and CMOEAs also faces challenges in data transmission and processing, as UAVs need to exchange and process data frequently during their missions. Determining how to efficiently achieve data synchronization and constraint processing under the framework of quantum computing is a major technical challenge.
7.2. Conclusions
This paper has provided a detailed summary of UMP based on CMOEAs. First, this paper described the traditional UMP classification method and proposed a new classification method from the new perspective of whether UAVs prioritize objectives or constraints. Then, according to the execution flow of CMOEAs, the embedded modules of constraint handling techniques were clarified, the classification of constraint handling techniques was elaborated in detail, and the algorithmic framework for solving multi-objective optimization problems was described. Then, we quickly found suitable planning scenarios based on the method for determining the individual settings in a population and the improvement strategy in CMOEAs. At the same time, we proposed UAV performance metrics and algorithmic metrics to evaluate the algorithm’s performance. Finally, we provided a detailed summary of the publication of CMOEAs, the publication of research on UMP based on CMOEAs, and the weights of the constraints and optimization objectives used in the mathematical model of UMP for the period from 2004 to 2024.
Author Contributions
Conceptualization, G.H. and M.H.; methodology, G.H. and X.W.; project administration, M.H.; supervision, M.H., F.H., X.Y. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 61403416.
Data Availability Statement
Not applicable.
Acknowledgments
Thanks to Min Hu for his important technical help and for providing experimental equipment and related materials.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, X.; Zheng, J.; Su, T.; Ding, M.; Liu, H. An Effective Dynamic Constrained Two-Archive Evolutionary Algorithm for Cooperative Search-Track Mission Planning by UAV Swarms in Air Intelligent Transportation. IEEE Trans. Intell. Transp. Syst. 2024, 25, 944–958. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Wu, Y.; Guo, Y. Multi-Conflict-Based Optimal Algorithm for Multi-UAV Cooperative Path Planning. Drones 2023, 7, 217. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, T.; Huang, S.; Li, K. A Hybrid Optimization Framework for UAV Reconnaissance Mission Planning. Comput. Ind. Eng. 2022, 173, 108653. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, T.; Gou, J.; Tao, C.; Wang, H. Heterogeneous Mission Planning for Multiple UAV Formations via Metaheuristic Algorithms. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3924–3940. [Google Scholar] [CrossRef]
- Ramirez Atencia, C.; Del Ser, J.; Camacho, D. Weighted Strategies to Guide a Multi-Objective Evolutionary Algorithm for Multi-UAV Mission Planning. Swarm Evol. Comput. 2019, 44, 480–495. [Google Scholar] [CrossRef]
- Causa, F.; Fasano, G.; Grassi, M. Multi-UAV Path Planning for Autonomous Missions in Mixed GNSS Coverage Scenarios. Sensors 2018, 18, 4188. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Qiu, S. A Decomposition-Based Constrained Multi-Objective Evolutionary Algorithm with a Local Infeasibility Utilization Mechanism for UAV Path Planning. Appl. Soft Comput. 2022, 118, 108495. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, C.; Yuan, Y.; Cui, J.; Qi, L. A Novel Multi-Objective Evolutionary Algorithm with a Two-Fold Constraint-Handling Mechanism for Multiple UAV Path Planning. Expert Syst. Appl. 2024, 238, 121862. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, Y.; Shan, M.; He, L.; Wang, D. Formation Reconstruction and Trajectory Replanning for Multi-UAV Patrol. IEEE/ASME Trans. Mechatron. 2021, 26, 719–729. [Google Scholar] [CrossRef]
- Tan, Y.; Yi, W.; Chen, P.; Zou, Y. An Adaptive Crack Inspection Method for Building Surface Based on BIM, UAV and Edge Computing. Autom. Constr. 2024, 157, 105161. [Google Scholar] [CrossRef]
- Zhen, Z.; Xing, D.; Gao, C. Cooperative Search-Attack Mission Planning for Multi-UAV Based on Intelligent Self-Organized Algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Zhang, X.; Dou, L.; Tian, B. Game of Drones: Multi-UAV Pursuit-Evasion Game with Online Motion Planning by Deep Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7900–7909. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Savkin, A.V.; Ni, W. Online UAV Trajectory Planning for Covert Video Surveillance of Mobile Targets. IEEE Trans. Autom. Sci. Eng. 2022, 19, 735–746. [Google Scholar] [CrossRef]
- Yin, C.; Xiao, Z.; Cao, X.; Xi, X.; Yang, P.; Wu, D. Offline and Online Search: UAV Multiobjective Path Planning under Dynamic Urban Environment. IEEE Internet Things J. 2018, 5, 546–558. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Y.; Hou, Z.; Zou, J.; Zheng, J. A Novel Multi-Population Evolutionary Algorithm Based on Hybrid Collaboration for Constrained Multi-Objective Optimization. Swarm Evol. Comput. 2024, 87, 101581. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, Q.; Li, X.; Li, X. A Surrogate-Assisted Multi-Objective Particle Swarm Optimization of Expensive Constrained Combinatorial Optimization Problems. Knowl.-Based Syst. 2021, 223, 107049. [Google Scholar] [CrossRef]
- Uribe, L.; Lara, A.; Deb, K.; Schütze, O. A New Gradient Free Local Search Mechanism for Constrained Multi-Objective Optimization Problems. Swarm Evol. Comput. 2021, 67, 100938. [Google Scholar] [CrossRef]
- Zhen, Z.; Zhu, P.; Xue, Y.; Ji, Y. Distributed Intelligent Self-Organized Mission Planning of Multi-UAV for Dynamic Targets Cooperative Search-Attack. Chin. J. Aeronaut. 2019, 32, 2706–2716. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Zarzour, H.; Kechida, A.; Taberkit, A.M. Deep Learning Techniques to Classify Agricultural Crops through UAV Imagery: A Review. Neural Comput. 2022, 34, 9511–9536. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Yen, G.G.; Wu, J.; Ren, H.; An, H.; Yang, J. Mission Planning for Energy-Efficient Passive UAV Radar Imaging System Based on Substage Division Collaborative Search. IEEE Trans. Cybern. 2023, 53, 275–288. [Google Scholar] [CrossRef]
- Nakshmi, J.V.N.; Hemanth, K.S.; Bharath, J. Optimizing Quality and Outputs by Improving Variable Rate Prescriptions in Agriculture Using UAVs. Procedia Comput. Sci. 2020, 167, 1981–1990. [Google Scholar] [CrossRef]
- Ibrahim, A.; Golparvar-Fard, M.; El-Rayes, K. Multiobjective Optimization of Reality Capture Plans for Computer Vision–Driven Construction Monitoring with Camera-Equipped UAVs. J. Comput. Civ. Eng. 2022, 36, 1981–1990. [Google Scholar] [CrossRef]
- Du, P.; He, X.; Cao, H.; Garg, S.; Kaddoum, G.; Hassan, M.M. AI-Based Energy-Efficient Path Planning of Multiple Logistics UAVs in Intelligent Transportation Systems. Comput. Commun. 2023, 207, 46–55. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Zhang, T.; Ju, C.; Suzuki, S.; Namiki, A. UAV High-Voltage Power Transmission Line Autonomous Correction Inspection System Based on Object Detection. IEEE Sens. J. 2023, 23, 10215–10230. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, W.; Liu, J.; Sun, C. Cooperative USV–UAV Marine Search and Rescue with Visual Navigation and Reinforcement Learning-Based Control. ISA Trans. 2023, 137, 222–235. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Xu, K.; Wang, Z.; Feng, T.; Tian, F. An Adaptive Population Size Based Differential Evolution by Mining Historical Population Similarity for Path Planning of Unmanned Aerial Vehicles. Inf. Sci. 2024, 666, 120432. [Google Scholar] [CrossRef]
- Jones, M.; Djahel, S.; Welsh, K. Path-Planning for Unmanned Aerial Vehicles with Environment Complexity Considerations: A Survey. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Ángeles-Rojas, D.; Santos-Sánchez, O.-J.; Salazar, S.; Lozano, R. Finite Horizon Nonlinear Suboptimal Control for an Autonomous Soaring UAV. Math. Probl. Eng. 2022, 2022, 2214217. [Google Scholar] [CrossRef]
- Jung, H.; Kim, J. Drone Scheduling Model for Delivering Small Parcels to Remote Islands Considering Wind Direction and Speed. Comput. Ind. Eng. 2022, 163, 107784. [Google Scholar] [CrossRef]
- Xu, J.; Ota, K.; Dong, M. Aerial Edge Computing: Flying Attitude-Aware Collaboration for Multi-UAV. IEEE Trans. Mob. Comput. 2023, 22, 5706–5718. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; Laganière, R.; Zhang, H.; Ding, L. A UAV to UAV Tracking Benchmark. Knowl.-Based Syst. 2023, 261, 110197. [Google Scholar] [CrossRef]
- Yue, L.; Yang, R.; Zuo, J.; Yan, M.; Zhao, X.; Lv, M. Factored Multi-Agent Soft Actor-Critic for Cooperative Multi-Target Tracking of UAV Swarms. Drones. 2023, 7, 150. [Google Scholar] [CrossRef]
- Ladosz, P.; Oh, H.; Zheng, G.; Chen, W.-H. A Hybrid Approach of Learning and Model-Based Channel Prediction for Communication Relay UAVs in Dynamic Urban Environments. IEEE Robot. Autom. Lett. 2019, 4, 2370–2377. [Google Scholar] [CrossRef]
- Luo, S.; Zhou, T.; Xiao, Y.; Lin, R.; Yan, Y. Predicting Spectrum Status Duration Using Non-Linear Homotopy Estimation Based HMM for UAV Communications. Signal Process. 2023, 212, 109131. [Google Scholar] [CrossRef]
- Bruni, M.E.; Khodaparasti, S.; Perboli, G. Energy Efficient UAV-Based Last-Mile Delivery: A Tactical-Operational Model With Shared Depots and Non-Linear Energy Consumption. IEEE Access 2023, 11, 18560–18570. [Google Scholar] [CrossRef]
- Chen, J.; Du, C.; Zhang, Y.; Han, P.; Wei, W. A Clustering-Based Coverage Path Planning Method for Autonomous Heterogeneous UAVs. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25546–25556. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Chen, J.; Han, Y. A Bionic Dynamic Path Planning Algorithm of the Micro UAV Based on the Fusion of Deep Neural Network Optimization/Filtering and Hawk-Eye Vision. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 3728–3740. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Xue, J.; Zeng, T.; Zhao, X. Location and Tracking of Environmental Pollution Sources under Multi-UAV Vision Based on Target Motion Model. Soft Comput. 2023, 27, 15337–15351. [Google Scholar] [CrossRef]
- Zhou, J.; Luo, M.; Song, L.; Hu, J. A Dynamic Group Key Agreement Scheme for UAV Networks Based on Blockchain. Pervasive Mob. Comput. 2023, 95, 101844. [Google Scholar] [CrossRef]
- Yang, L.; Ye, J.; Zhang, Y.; Wang, L.; Qiu, C. A Semantic SLAM-Based Method for Navigation and Landing of UAVs in Indoor Environments. Knowl.-Based Syst. 2024, 293, 111693. [Google Scholar] [CrossRef]
- Bordón-Ruiz, J.; Besada-Portas, E.; López-Orozco, J.A. Cloud DEVS-Based Computation of UAVs Trajectories for Search and Rescue Missions. J. Simul. 2022, 16, 572–588. [Google Scholar] [CrossRef]
- Wang, N.; Liang, X.; Li, Z.; Hou, Y.; Yang, A. PSE-D Model-Based Cooperative Path Planning for UAV&USV Systems in Anti-Submarine Search Missions. IEEE Trans. Aerosp. Electron. Syst. 2024, 16, 1–16. [Google Scholar] [CrossRef]
- Zhang, J.; Yue, X.; Zhang, H.; Xiao, T. Optimal Unmanned Ground Vehicle—Unmanned Aerial Vehicle Formation-Maintenance Control for Air-Ground Cooperation. Appl. Sci. 2022, 12, 3598. [Google Scholar] [CrossRef]
- Sufiyan, D.; Win, L.S.T.; Win, S.K.H.; Soh, G.S.; Foong, S. Joint Mechanical Design and Flight Control Optimization of a Nature-Inspired Unmanned Aerial Vehicle via Collaborative Co-Evolution. IEEE Robot. Autom. Lett. 2021, 6, 2044–2051. [Google Scholar] [CrossRef]
- Nejabat, E.; Nikoofard, A. Switching tube model predictive based controller design for multi-agent unmanned aerial vehicle system with hybrid topology. Int. J. Robust Nonlinear Control 2023, 33, 10468–10492. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, W.; Wang, H.; Han, J. UAV-to-UAV Target Re-Searching Using a Bayes-Based Spatial Probability Distribution Algorithm. Comput. Electr. Eng. 2024, 114, 109091. [Google Scholar] [CrossRef]
- Bai, X.; Wang, L.; Hu, Y.; Li, P.; Zu, Y. Optimal Path Planning Method for IMU System-Level Calibration Based on Improved Dijkstra’s Algorithm. IEEE Access 2023, 11, 11364–11376. [Google Scholar] [CrossRef]
- Zheng, J.; Ding, M.; Sun, L.; Liu, H. Distributed Stochastic Algorithm Based on Enhanced Genetic Algorithm for Path Planning of Multi-UAV Cooperative Area Search. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8290–8303. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-Enhanced UAV Path Planning with Spherical Vector-Based Particle Swarm Optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Bouras, A.; Bouzid, Y.; Guiatni, M. Multi-UAV Coverage Path Planning for Gas Distribution Map Applications. Unmanned Syst. 2022, 10, 289–306. [Google Scholar] [CrossRef]
- Cao, Y.; Wei, W.; Bai, Y.; Qiao, H. Multi-Base Multi-UAV Cooperative Reconnaissance Path Planning with Genetic Algorithm. Clust. Comput. 2019, 22, 5175–5184. [Google Scholar] [CrossRef]
- Mousa, M.H.; Hussein, M.K. Efficient UAV-Based Mobile Edge Computing Using Differential Evolution and Ant Colony Optimization. PeerJ Comput. Sci. 2022, 8, e870. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, H.; Wang, L. Three Dimensional Path Planning of UAV Based on Adaptive Particle Swarm Optimization Algorithm. J. Phys. Conf. Ser. 2021, 1846, 012007. [Google Scholar] [CrossRef]
- Phung, M.D.; Quach, C.H.; Dinh, T.H.; Ha, Q. Enhanced Discrete Particle Swarm Optimization Path Planning for UAV Vision-Based Surface Inspection. Autom. Constr. 2017, 81, 25–33. [Google Scholar] [CrossRef]
- Golalipour, K. A Novel Permutation-Diffusion Technique for Image Encryption Based on the Imperialist Competitive Algorithm. Multimed. Tools Appl. 2023, 82, 725–746. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, X.; Hu, S.; Zhou, D.; Cheng, N.; Lu, N. QoE-Driven Adaptive Deployment Strategy of Multi-UAV Networks Based on Hybrid Deep Reinforcement Learning. IEEE Internet Things J. 2022, 9, 5868–5881. [Google Scholar] [CrossRef]
- Meng, K.; Chen, C.; Wu, T.; Xin, B.; Liang, M.; Deng, F. Evolutionary State Estimation-Based Multi-Strategy Jellyfish Search Algorithm for Multi-UAV Cooperative Path Planning. IEEE Trans. Intell. Veh. 2024, 9, 1–19. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, X.; Wang, H.; Hu, Y.; Zhao, K.; Fan, J. Distributed Matching Theory-Based Task Re-Allocating for Heterogeneous Multi-UAV Edge Computing. China Commun. 2024, 21, 260–2781. [Google Scholar] [CrossRef]
- Dhanasekaran, S.; Ramalingam, S.; Vivek Karthick, P.; Silambarasan, D. An Improved Pilot Pattern Design-Based Channel Estimation in Wireless Communication Using Distribution Ant Colony Optimization. Simul. Model. Pract. Theory 2023, 129, 102820. [Google Scholar] [CrossRef]
- Tan, L.; Huang, X.; Lv, X.; Jiang, X.; Liu, H. Strong Interference UAV Motion Target Tracking Based on Target Consistency Algorithm. Electronics 2023, 12, 1773. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Q. Optimization Algorithm for AoI-Based UAV-Assisted Data Collection. Int. J. Distrib. Sens. Netw. 2024, 2024, 6691579. [Google Scholar] [CrossRef]
- Wang, X.; He, N.; Hong, C.; Wang, Q.; Chen, M. Improved YOLOX-X Based UAV Aerial Photography Object Detection Algorithm. Image Vis. Comput. 2023, 135, 104697. [Google Scholar] [CrossRef]
- Zu, L.; Wang, Z.; Liu, C.; Ge, S.S. Research on UAV Path Planning Method Based on Improved HPO Algorithm in Multitask Environment. IEEE Sens. J. 2023, 23, 19881–19893. [Google Scholar] [CrossRef]
- Zhang, J.; Wolek, A.; Willis, A.R. UAV-Borne Mapping Algorithms for Low-Altitude and High-Speed Drone Applications. Sensors 2024, 24, 2204. [Google Scholar] [CrossRef]
- Zagradjanin, N.; Pamucar, D.; Jovanovic, K.; Knezevic, N.; Pavkovic, B. Autonomous Exploration Based on Multi-Criteria Decision-Making and Using D* Lite Algorithm. Intell. Autom. Soft Comput. 2022, 32, 1369–1386. [Google Scholar] [CrossRef]
- Chen, X. UAV Patrol Path Planning Based on Machine Vision and Multi-Sensor Fusion. Open Comput. Sci. 2023, 13, 20220276. [Google Scholar] [CrossRef]
- Wang, R.-B.; Wang, W.-F.; Geng, F.-D.; Pan, J.-S.; Chu, S.-C.; Xu, L. UAV Path Planning in Mountain Areas Based on a Hybrid Parallel Compact Arithmetic Optimization Algorithm. Neural Comput. Appl. 2023, 13, 108473. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Umari, H.; Koirala, K. Multi-Robot Map Exploration Based on Multiple Rapidly-Exploring Randomized Trees. SN Comput. Sci. 2023, 5, 31. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X.; Jia, Q.; Liu, X.; Zhang, W. HPO-RRT*: A Sampling-Based Algorithm for UAV Real-Time Path Planning in a Dynamic Environment. Complex Intell. Syst. 2023, 9, 7133–7153. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Feng, J.; Zhao, H. An Improved RRT * UAV Formation Path Planning Algorithm Based on Goal Bias and Node Rejection Strategy. Unmanned Syst. 2023, 11, 317–326. [Google Scholar] [CrossRef]
- Xuefeng Chen, X.C.; Xuefeng Chen, W.T.; Wan Tang, X.Y.; Ximin Yang, L.Z.; Lingyun Zhou, L.L. PSO-VFA: A Hybrid Intelligent Algorithm for Coverage Optimization of UAV-Mounted Base Stations. J. Internet Technol. 2022, 23, 487–495. [Google Scholar] [CrossRef]
- He, H.; Yuan, W.; Chen, S.; Jiang, X.; Yang, F.; Yang, J. Deep Reinforcement Learning Based Distributed 3D UAV Trajectory Design. IEEE Trans. Commun. 2024, 23, 3736–3751. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Xu, F.; Cheng, S.; Su, W.; Wang, S. Dynamic Deployment Method Based on Double Deep Q-Network in UAV-Assisted MEC Systems. J. Cloud Comput. 2023, 12, 130. [Google Scholar] [CrossRef]
- Qiao, Z.; Wang, D.; Xu, J.; Pei, X.; Su, W.; Wang, D.; Bai, Y. A Comprehensive Design and Experiment of a Biplane Quadrotor Tail-Sitter UAV. Drones 2023, 7, 292. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Y.; Wang, B.; Qian, S.; Tian, Z.; Wang, X. Learning-Based Dynamic Connectivity Maintenance for UAV-Assisted D2D Multicast Communication. China Commun. 2023, 20, 305–322. [Google Scholar] [CrossRef]
- Lee, M.-T.; Chuang, M.-L.; Kuo, S.-T.; Chen, Y.-R. UAV Swarm Real-Time Rerouting by Edge Computing D* Lite Algorithm. Appl. Sci. 2022, 12, 1056. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, Y.; Zhou, Z.; Jin, M.; Yang, X.; Hu, F. Conflict-Based Search with D* Lite Algorithm for Robot Path Planning in Unknown Dynamic Environments. Comput. Electr. Eng. 2023, 105, 108473. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, X.; Li, M.; Yu, K.; Chen, Z.; Ni, C.; Teng, Y. Path Planning Method Based on D* Lite Algorithm for Unmanned Surface Vehicles in Complex Environments. China Ocean Eng. 2021, 35, 372–383. [Google Scholar] [CrossRef]
- Maw, A.A.; Tyan, M.; Nguyen, T.A.; Lee, J.-W. IADA*-RL: Anytime Graph-Based Path Planning with Deep Reinforcement Learning for an Autonomous UAV. Appl. Sci. 2021, 11, 3948. [Google Scholar] [CrossRef]
- Hasanzade, M.; Koyuncu, E. A Dynamically Feasible Fast Replanning Strategy with Deep Reinforcement Learning. J. Intell. Robot. Syst. 2021, 101, 13. [Google Scholar] [CrossRef]
- He, A.; Wang, C.; Liu, S.; Meehan, P.A. Path Planning Algorithm Based on Adaptive Model Predictive Control and Learning-Based Parameter Identification Approach for Incremental Forming Processes for Product Precision Improvements. Int. J. Adv. Manuf. Technol. 2023, 125, 4513–4528. [Google Scholar] [CrossRef]
- Bârsan, A.; Popp, M.O.; Rusu, G.P.; Maroșan, A.I. Robot-Based Incremental Sheet Forming—The Tool Path Planning. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1009, 012004. [Google Scholar]
- Yoon, S.; Shim, D.H. SLPA: Shape-Aware Lifelong Planning A* for Differential Wheeled Vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 16, 730–740. [Google Scholar] [CrossRef]
- Chen, X.; Ma, C.; Zhao, C.; Luo, Y. UAV Classification Based on Deep Learning Fusion of Multidimensional UAV Micro-Doppler Image Features. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3503205. [Google Scholar] [CrossRef]
- Wang, K.; Gao, S.; Zhou, M.; Zhan, Z.-H.; Cheng, J. Fractional Order Differential Evolution. IEEE Trans. Evol. Comput. 2024, 21, 1. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Q.; Huang, T. Resilient Penalty Function Method for Distributed Constrained Optimization under Byzantine Attack. Inf. Sci. 2022, 596, 362–379. [Google Scholar] [CrossRef]
- De Winter, R.; Milatz, B.; Blank, J.; van Stein, N.; Bäck, T.; Deb, K. Parallel Multi-Objective Optimization for Expensive and Inexpensive Objectives and Constraints. Swarm Evol. Comput. 2024, 86, 101508. [Google Scholar] [CrossRef]
- Cai, T.; Wang, H. A General Convergence Analysis Method for Evolutionary Multi-Objective Optimization Algorithm. Inf. Sci. 2024, 663, 120267. [Google Scholar] [CrossRef]
- Manogaran, G.; Ngangmeni, J.; Stewart, J.; Rawat, D.B.; Nguyen, T.N. Deep-Learning-Based Concurrent Resource Allocation Method for Improving the Service Response of 6G Network-in-Box Users in UAV. IEEE Internet Things J. 2023, 10, 3130–3137. [Google Scholar] [CrossRef]
- Tagawa, K.; Orito, Y. A Mapping-Based Constraint-Handling Technique for Evolutionary Algorithms with Its Applications to Portfolio Optimization Problems. SICE J. Control. Meas. Syst. Integr. 2022, 15, 62–76. [Google Scholar] [CrossRef]
- Peng, H.; Xu, Z.; Qian, J.; Dong, X.; Li, W.; Wu, Z. Evolutionary Constrained Optimization with Hybrid Constraint-Handling Technique. Expert Syst. Appl. 2023, 211, 118660. [Google Scholar] [CrossRef]
- Li, Y.; Gong, W.; Hu, Z.; Li, S. A Competitive and Cooperative Evolutionary Framework for Ensemble of Constraint Handling Techniques. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 2440–2451. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Z.; Qiu, J.; Zhang, L. Adaptive Constraint Handling Technique Selection for Constrained Multi-Objective Optimization. Swarm Evol. Comput. 2024, 86, 101488. [Google Scholar] [CrossRef]
- Yuan, Y.; Gao, W.; Huang, L.; Li, H.; Xie, J. A Two-Phase Constraint-Handling Technique for Constrained Optimization. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 6194–6203. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; Tibaduiza, D.A., Ed.; IEEE: New York, NY, USA, 2014; Volume 18, pp. 69–73. [Google Scholar]
- Tai, H.K.; Lin, H.; Siu, S.W.I. Improving the Efficiency of PSOVina for Protein-Ligand Docking by Two-Stage Local Search. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; Tibaduiza, D.A., Ed.; IEEE: New York, NY, USA, 2016; Volume 18, pp. 770–777. [Google Scholar]
- Montes de Oca, M.A.; Stutzle, T.; Birattari, M.; Dorigo, M. Frankenstein’s PSO: A Composite Particle Swarm Optimization Algorithm. IEEE Trans. Evol. Comput. 2009, 13, 1120–1132. [Google Scholar] [CrossRef]
- Hobbie, J.G.; Gandomi, A.H.; Rahimi, I. A Comparison of Constraint Handling Techniques on NSGA-II. Arch. Comput. Methods Eng. 2021, 28, 3475–3490. [Google Scholar] [CrossRef]
- Wu, H.; Nie, C.; Petke, J.; Jia, Y.; Harman, M. Comparative Analysis of Constraint Handling Techniques for Constrained Combinatorial Testing. IEEE Trans. Softw. Eng. 2021, 47, 2549–2562. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Q.; Luo, K. Differential Evolution Improvement by Adaptive Ranking-Based Constraint Handling Technique. Soft Comput. 2023, 27, 11485–11504. [Google Scholar] [CrossRef]
- Cantú, V.H.; Azzaro-Pantel, C.; Ponsich, A. Constraint-Handling Techniques within Differential Evolution for Solving Process Engineering Problems. Appl. Soft Comput. 2021, 108, 107442. [Google Scholar] [CrossRef]
- Han, D.; Du, W.; Jin, Y.; Du, W.; Yu, G. A Fuzzy Constraint Handling Technique for Decomposition-Based Constrained Multi- and Many-Objective Optimization. Inf. Sci. 2022, 597, 318–340. [Google Scholar] [CrossRef]
- Sathya, A.S.; Pipeleers, G.; Decre, W.; Swevers, J. A Weighted Method for Fast Resolution of Strictly Hierarchical Robot Task Specifications Using Exact Penalty Functions. IEEE Robot. Autom. Lett. 2021, 6, 3057–3064. [Google Scholar] [CrossRef]
- Antkiewicz, M.; Myszkowski, P.B. Balancing Pareto Front Exploration of Non-Dominated Tournament Genetic Algorithm (B-NTGA) in Solving Multi-Objective NP-Hard Problems with Constraints. Inf. Sci. 2024, 667, 120400. [Google Scholar] [CrossRef]
- Mahmud, S.; Abbasi, A.; Chakrabortty, R.K.; Ryan, M.J. A Self-Adaptive Hyper-Heuristic Based Multi-Objective Optimisation Approach for Integrated Supply Chain Scheduling Problems. Knowl.-Based Syst. 2022, 251, 109190. [Google Scholar] [CrossRef]
- Luo, Y.; Fu, G. UAV Based Device to Device Communication for 5G/6G Networks Using Optimized Deep Learning Models. Wirel. Netw. 2023, 251, 109190. [Google Scholar] [CrossRef]
- Duarte, G.R.; de Lima, B.S.L.P.; de Castro Lemonge, A.C. A Stigmergy-Based Island Model for Dynamic Evaluation of Constraint-Handling Techniques and Differential Evolution Algorithms. IEEE Trans. Evol. Comput. 2023, 27, 701–715. [Google Scholar] [CrossRef]
- Deb, K.; Datta, R. A Bi-Objective Constrained Optimization Algorithm Using a Hybrid Evolutionary and Penalty Function Approach. Eng. Optim. 2013, 45, 503–527. [Google Scholar] [CrossRef]
- Datta, R.; Deb, K. A Bi-Objective Based Hybrid Evolutionary-Classical Algorithm for Handling Equality Constraints. In Engineering Optimization; Tibaduiza, D.A., Ed.; IEEE: New York, NY, USA, 2011; Volume 45, pp. 313–327. ISBN 978-1-5090-0623-6. [Google Scholar]
- Kawachi, T.; Kushida, J.-i.; Hara, A.; Takahama, T. Efficient Parameter-Free Adaptive Penalty Method with Balancing the Objective Function Value and the Constraint Violation. Int. J. Comput. Intell. Stud. 2021, 10, 127. [Google Scholar] [CrossRef]
- Wang, B.-C.; Li, H.-X.; Feng, Y.; Shen, W.-J. An Adaptive Fuzzy Penalty Method for Constrained Evolutionary Optimization. Inf. Sci. 2021, 571, 358–374. [Google Scholar] [CrossRef]
- Shirmarz, A.; Ghaffari, A. A Novel Flow Routing Algorithm Based on Non-Dominated Ranking and Crowd Distance Sorting to Improve the Performance in SDN. Photonic Netw. Commun. 2021, 42, 167–183. [Google Scholar] [CrossRef]
- Li, L.; Li, G.; Chang, L. A Many-Objective Particle Swarm Optimization with Grid Dominance Ranking and Clustering. Appl. Soft Comput. 2020, 96, 106661. [Google Scholar] [CrossRef]
- Almojel, N.A.; Ahmed, A.E.S. Tasks and Resources Allocation Approach with Priority Constraints in Cloud Computing. Int. J. Grid High Perform. Comput. 2022, 14, 1–17. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, S.; Yang, B.; He, Y.; Pang, Z.; Gao, Y. A Coupling Optimization Method of Production Scheduling and Logistics Planning for Product Processing-Assembly Workshops with Multi-Level Job Priority Constraints. Comput. Ind. Eng. 2024, 190, 110014. [Google Scholar] [CrossRef]
- Beresnev, V.; Melnikov, A. ε-Constraint method for bi-objective competitive facility location problem with uncertain demand scenario. EURO J. Comput. Optim. 2020, 8, 33–59. [Google Scholar] [CrossRef]
- Mousavi, S.; Sajadi, S.M.; AlemTabriz, A.; Najafi, S.E. Location and Hierarchical Allocation Disaster with Combined ε-Constraint and Simulation-Based Optimization Approach. Simulation 2022, 98, 407–432. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, P.-Q.; Kong, X.; Zhao, J. A Constrained Multi-Objective Evolutionary Algorithm Assisted by an Additional Objective Function. Appl. Soft Comput. 2023, 132, 109904. [Google Scholar] [CrossRef]
- Cao, J.; Yan, Z.; Chen, Z.; Zhang, J. A Pareto Front Estimation-Based Constrained Multi-Objective Evolutionary Algorithm. Appl. Intell. 2023, 53, 10380–10416. [Google Scholar] [CrossRef]
- Liaw, R.-T. A Cooperative Coevolution Framework for Evolutionary Learning and Instance Selection. Swarm Evol. Comput. 2021, 62, 100840. [Google Scholar] [CrossRef]
- Zhu, H.; Jin, Y. Multi-Objective Evolutionary Federated Learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1310–1322. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Gao, W.; Huang, L.; Xie, J.; Gong, M. An Effective Knowledge Transfer Method Based on Semi-Supervised Learning for Evolutionary Optimization. Inf. Sci. 2022, 612, 1127–1144. [Google Scholar] [CrossRef]
- Wei, C.; Tang, Y.; Chuang Niu, C.N.; Hu, H.; Wang, Y.; Liang, J. Self-Supervised Representation Learning for Evolutionary Neural Architecture Search. IEEE Comput. Intell. Mag. 2021, 16, 33–49. [Google Scholar] [CrossRef]
- Sachdeva, K.; Gosain, A. Materialized View Selection Applying Differential Evolution Algorithm Combined with Ensembled Constraint Handling Techniques. Multimed. Tools Appl. 2021, 80, 31619–31645. [Google Scholar] [CrossRef]
- Xie, S.; Li, K.; Wang, W.; Wang, H.; Peng, C.; Jalil, H. A Tractive Population Assisted Dual-Population and Two-Phase Evolutionary Algorithm for Constrained Multi-Objective Optimization. IEEE Trans. Evol. Comput. 2023, 27, 1. [Google Scholar] [CrossRef]
- Xie, Y.; Li, J.; Li, Y.; Zhu, W.; Dai, C. Two-Stage Evolutionary Algorithm with Fuzzy Preference Indicator for Multimodal Multi-Objective Optimization. Swarm Evol. Comput. 2024, 85, 101480. [Google Scholar] [CrossRef]
- Lin, Q.; Li, J.; Liu, S.; Ma, L.; Li, J.; Chen, J. An Adaptive Two-Stage Evolutionary Algorithm for Large-Scale Continuous Multi-Objective Optimization. Swarm Evol. Comput. 2023, 77, 101235. [Google Scholar] [CrossRef]
- Zhong, X.; Yao, X.; Gong, D.; Qiao, K.; Gan, X.; Li, Z. A Dual-Population-Based Evolutionary Algorithm for Multi-Objective Optimization Problems with Irregular Pareto Fronts. Swarm Evol. Comput. 2024, 87, 101566. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.; Tian, Y.; Zhang, X.; Xiao, J. A Dual-Population Based Evolutionary Algorithm for Multi-Objective Location Problem under Uncertainty of Facilities. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7692–7707. [Google Scholar] [CrossRef]
- Xia, M.; Chong, Q.; Dong, M. A Constrained Multi-Objective Evolutionary Algorithm with Two-Stage Resources Allocation. Swarm Evol. Comput. 2023, 79, 101313. [Google Scholar] [CrossRef]
- Sun, X.; Guo, S.; Guo, J.; Du, B. A Two-Stage Interactive Evolutionary Algorithm for Multi-Objective Asynchronous Parallel Selective Disassembly Sequence Planning Problem. Comput. Ind. Eng. 2023, 175, 108855. [Google Scholar] [CrossRef]
- Zou, J.; Luo, J.; Liu, Y.; Yang, S.; Zheng, J. A Flexible Two-Stage Constrained Multi-Objective Evolutionary Algorithm Based on Automatic Regulation. Inf. Sci. 2023, 634, 227–243. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Z.; Jin, X.; Xu, Z.; Wang, Z.; Shen, P. A Novel Three-Stage Multi-Population Evolutionary Algorithm for Constrained Multi-Objective Optimization Problems. Complex Intell. Syst. 2024, 10, 655–675. [Google Scholar] [CrossRef]
- Qin, C.; Ming, F.; Gong, W.; Gu, Q. Constrained Multi-Objective Optimization via Two Archives Assisted Push–Pull Evolutionary Algorithm. Swarm Evol. Comput. 2022, 75, 101178. [Google Scholar] [CrossRef]
- Raju, M.S.S.; Dutta, S.; Mallipeddi, R.; Das, K.N. A Dual-Population and Multi-Stage Based Constrained Multi-Objective Evolutionary. Inf. Sci. 2022, 615, 557–577. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Wang, L.; Lu, C. A Tri-Population Based Co-Evolutionary Framework for Constrained Multi-Objective Optimization Problems. Swarm Evol. Comput. 2022, 70, 101055. [Google Scholar] [CrossRef]
- Agrawal, A.; Ghune, N.; Prakash, S.; Ramteke, M. Evolutionary Algorithm Hybridized with Local Search and Intelligent Seeding for Solving Multi-Objective Euclidian TSP. Expert Syst. Appl. 2021, 181, 115192. [Google Scholar] [CrossRef]
- Chandrasekaran, K.; Simon, S.P. Multi-Objective Scheduling Problem: Hybrid Approach Using Fuzzy Assisted Cuckoo Search Algorithm. Swarm Evol. Comput. 2012, 5, 1–16. [Google Scholar] [CrossRef]
- Bai, H.; Fan, T.; Niu, Y.; Cui, Z. Multi-UAV Cooperative Trajectory Planning Based on Many-Objective Evolutionary Algorithm. Complex Syst. Model. Simul. 2022, 2, 130–141. [Google Scholar] [CrossRef]
- Dasdemir, E.; Köksalan, M.; Tezcaner Öztürk, D. A Flexible Reference Point-Based Multi-Objective Evolutionary Algorithm: An Application to the UAV Route Planning Problem. Comput. Oper. Res. 2020, 114, 104811. [Google Scholar] [CrossRef]
- Wang, P.; Deng, Z. A Multi-Objective Quantum-Inspired Seagull Optimization Algorithm Based on Decomposition for Unmanned Aerial Vehicle Path Planning. IEEE Access 2022, 10, 110497–110511. [Google Scholar] [CrossRef]
- Issad, H.A.; Aoudjit, R.; Belkadi, M.; Rodrigues, J.J.P.C. Many-Objective Optimisation-Based Optimal Drone Deployment for Agricultural Zone. Int. J. Commun. Netw. Distrib. Syst. 2021, 26, 76. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Tan, S.; Liu, Y. A Multi-Objective Differential Evolution Algorithm Based on Domination and Constraint-Handling Switching. Inf. Sci. 2021, 579, 796–813. [Google Scholar] [CrossRef]
- Sabino, S.; Horta, N.; Grilo, A. Centralized Unmanned Aerial Vehicle Mesh Network Placement Scheme: A Multi-Objective Evolutionary Algorithm Approach. Sensors 2018, 18, 4387. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zhu, Y.; Kang, H.; Sun, X.; Chen, Q.; Wang, D. UAV Path Planning Based on Multi-Stage Constraint Optimization. Drones 2021, 5, 144. [Google Scholar] [CrossRef]
- Wu, Y.; Nie, M.; Ma, X.; Guo, Y.; Liu, X. Co-Evolutionary Algorithm-Based Multi-Unmanned Aerial Vehicle Cooperative Path Planning. Drones 2023, 7, 606. [Google Scholar] [CrossRef]
- Tang, M.; Hu, M.; Zhang, H.; Zhou, L. Research on Multi Unmanned Aerial Vehicles Emergency Task Planning Method Based on Discrete Multi-Objective TLBO Algorithm. Sustainability 2022, 14, 2555. [Google Scholar] [CrossRef]
- Liu, X.; Ma, J.; Chen, D.; Zhang, L.-Y. Real-Time Unmanned Aerial Vehicle Cruise Route Optimization for Road Segment Surveillance Using Decomposition Algorithm. Robotica 2021, 39, 1007–1022. [Google Scholar] [CrossRef]
- Bai, Z.; Zhou, H.; Shi, J.; Xing, L.; Wang, J. A Hybrid Multi-Objective Evolutionary Algorithm with High Solving Efficiency for UAV Defense Programming. Swarm Evol. Comput. 2024, 87, 101572. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, T.; He, W.; Zhang, Z. YOLOv7-UAV: An Unmanned Aerial Vehicle Image Object Detection Algorithm Based on Improved YOLOv7. Electronics 2023, 12, 3141. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, H.-L.; He, Z. A Constrained Multi-Objective Evolutionary Algorithm Using Valuable Infeasible Solutions. Swarm Evol. Comput. 2022, 68, 101020. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Tian, Y.; Li, C.; Yue, D. Cooperative Constrained Multi-Objective Dual-Population Evolutionary Algorithm for Optimal Dispatching of Wind-Power Integrated Power System. Swarm Evol. Comput. 2024, 87, 101525. [Google Scholar] [CrossRef]
- Li, W.; Gong, W.; Ming, F.; Wang, L. Constrained Multi-Objective Evolutionary Algorithm with an Improved Two-Archive Strategy. Knowl.-Based Syst. 2022, 246, 108732. [Google Scholar] [CrossRef]
- Peng, C.; Liu, H.-L.; Gu, F. An Evolutionary Algorithm with Directed Weights for Constrained Multi-Objective Optimization. Appl. Soft Comput. 2017, 60, 613–622. [Google Scholar] [CrossRef]
- Gu, Q.; Wang, Q.; Xiong, N.N.; Jiang, S.; Chen, L. Surrogate-Assisted Evolutionary Algorithm for Expensive Constrained Multi-Objective Discrete Optimization Problems. Complex Intell. Syst. 2022, 8, 2699–2718. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, B.; Kong, X.; Zhao, J. A Double Auxiliary Optimization Constrained Multi-Objective Evolutionary Algorithm. Math. Comput. Simul. 2024, 220, 567–579. [Google Scholar] [CrossRef]
- Roy, B. The Outranking Approach and the Foundations of Electre Methods. Theory Decis. 1991, 31, 49–73. [Google Scholar] [CrossRef]
- Brans, J.-P.; Mareschal, B. The PROMCALC & GAIA Decision Support System for Multicriteria Decision Aid. Decis. Support Syst. 1994, 12, 297–3105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).