1. Introduction
Unmanned Aerial Vehicles (UAVs) have achieved significant popularity in recent years, enabling autonomous flight without the need for human pilots. The versatility of UAVs is evident in their autonomous navigation and task execution, including a wide range of applications in both civilian and military domains. These applications span surveillance, reconnaissance, package delivery, and exploration [
1]. However, as the roles of UAVs evolve, navigating complex environments with agility becomes crucial. While path-planning algorithms ensure collision-free paths, their execution by the actual system may not be feasible. This is especially evident in agile vehicles, where additional limitations from dynamics or nonholonomic constraints must be considered. Kinodynamic motion planning addresses this issue, considering vehicle dynamics, input constraints, and state constraints.
Frazzoli et al. [
2,
3] provided some of the pioneering work on real-time kinodynamic motion planning. The proposed technique involves mapping the dynamics of the vehicle onto a finite-dimensional space, restricting the vehicle’s potential states to two categories: either a trim state or a maneuver state. Since then, the field has seen significant progress, yielding numerous trajectory-generation algorithms. Many researchers have adopted a two-step approach, separating geometric and temporal planning. Initially, an optimal collision-free geometric path is generated by linking a series of waypoints by straight lines. Subsequently, the path is smoothed and parameterized in time to ensure compliance with the vehicle dynamics. This smoothing step can be performed in various ways. For instance, one approach involves selecting the optimal sequence of trims and maneuvers from a precomputed library of motion primitives [
4]. Alternatively, a sequence of polynomial segments can be jointly optimized to connect waypoints into a smooth trajectory from start to goal [
5]. These two-step strategies significantly simplify the planning problem. However, the initial geometric path does not consider the dynamics of the vehicle, restricting the resulting trajectory to a specific homology class. This limitation may exclude the possibility of achieving a globally optimal (or even feasible) trajectory. Moreover, the final smoothed trajectory is not guaranteed to be obstacle-free.
Several studies have adopted a direct trajectory-generation approach that integrates the vehicle dynamics from the beginning, bypassing the two-step process. Many of these works leverage the inherent differential flatness property of quadrotor dynamics to represent trajectories using time-parameterized polynomials [
6,
7,
8,
9]. This transforms the trajectory-generation problem into the task of determining polynomial coefficients that meet specific constraints. While this approach has been extensively studied and applied in the context of quadrotors [
6,
7,
8,
9,
10], its applicability is limited to systems with similar dynamics. Extending this methodology to more complex systems such as Vertical Take-Off and Landing (VTOL) and fixed-wing aircraft presents significant challenges.
Other stream of research use methods based on direct trajectory optimization, such as [
11,
12,
13,
14], to design trajectories that account for the full system dynamics. However, converting the planning problem into a non-convex optimization problem and using local optimization techniques can fail to find a collision-free trajectory in cluttered environments. Additionally, most trajectory optimization methods are prone to becoming stuck in local minima. Consequently, there is growing interest in constructing global solutions for motion planning problems. Early attempts to address this challenge formulated the problem as a single optimization problem using a mixed-integer optimization approach [
15,
16]. However, this method is tractable only for a limited number of obstacles. More recent approaches, such as those exploiting convex decomposition of the environment [
17], allow for efficient computation but struggle with nonlinear dynamics, as this would result in a mixed-integer nonlinear problem, which is computationally intractable.
Motion primitives offer a promising alternative by combining the strengths of optimal control, which can handle arbitrary dynamics, with the effectiveness of graph-based algorithms that perform global searches in non-convex configuration spaces. This paper investigates motion primitives-based methods for addressing quadrotor kinodynamic motion planning, focusing on two main approaches. One approach [
8] generates motion primitives online through control input discretization and forward propagation of the dynamic equations of a simplified model, serving as a benchmark for comparison. Additionally, the approach presented in [
18] is revised and customized for quadrotor kinodynamic motion planning. Specifically, the differential flatness property of quadrotors is exploited to construct a library of precomputed trajectories during an offline phase. This library is then used online to concatenate the motion primitives using a search-based framework to obtain a complete trajectory. Moreover, to make the method computationally tractable, continuity between consecutive motion primitives is enforced only on a subset of the state variables (position, velocity, and acceleration). The methods are compared through both numerical simulations and real-world experiments to highlight the strengths and weaknesses of each approach.
The remainder of this paper is organized as follows:
Section 2 provides an overview of the quadrotor model and its differential flatness property.
Section 3 formulates the kinodynamic motion planning problem.
Section 4 introduces the methodology presented in [
18], aimed at generating an offline library of motion primitives tailored for systems with arbitrary dynamics. This method is then adapted to suit the quadrotor system within a search-based framework. Additionally, continuity between consecutive motion primitives is enforced on a subset of state variables to enhance computational tractability.
Section 5 introduces the state-of-the-art approach proposed in [
8], serving as a benchmark for comparison. Here, motion primitives for quadrotors are generated online through input discretization and forward propagation, employing a simplified model of vehicle dynamics.
Section 6 presents the numerical results.
Section 7 details the experimental outcomes. Finally,
Section 8 offers a comparative analysis of the two methods, while
Section 9 draws conclusions and delineates potential directions for future research.
Notation: denotes the set of (positive, nonnegative) real numbers, denotes the n-dimensional real coordinate space and the set of real matrices. Given , , denote .
The i-th vector of the canonical basis in is denoted and the identity matrix in is . Given vectors , the standard inner product is defined as . The Euclidean norm of a vector is .
The n-dimensional unit sphere is denoted as . The set is the 3D Special Orthogonal group. The map is defined such that given one has .
3. Kinodynamic Motion Planning: Problem Statement
Kinodynamic motion planning aims to find the optimal trajectory for a vehicle navigating from an initial state to a final state while considering both its kinematics and dynamics.
The kinodynamic motion planning problem can be formulated as an optimization problem, with the aim of finding the input functions
, the corresponding state trajectories
, and the total duration
T that minimize the cost function
J, all while adhering to specified constraints. The formulation is as follows:
Equation (3a) defines the cost function, which aims to strike a balance between minimizing the total time
T and minimizing the control effort required for the trajectory. This balance is governed by the weight parameter
. Equation (3b) enforces the system’s dynamics outlined in Equation (
1). Equation (3c) describes the state constraints, which consist of obstacle avoidance (non-convex) and limits on velocity and acceleration. Equation (3d) represents the control input constraints. The initial and final states in Equation (3e) and Equation (3f) correspond to the boundary conditions.
Explicitly solving Problem (3) is hard due to states and input constraints, as well as the non-convex nature of obstacle avoidance. An effective strategy to alleviate the computational load associated with motion planning involves transforming the problem into a graph-search problem. This method involves choosing a finite set of candidate solutions known as motion primitives. Motion primitives represent a collection of precomputed motions tailored for specific dynamic systems. These precalculated solutions address sub-problems, which can be concatenated to form a complete trajectory that effectively resolves the motion planning problem.
A motion primitive can be generated through various methodologies, including solving a Two-Point-Boundary-Value Problem (TPBVP) (see
Section 4) or forward integration of the state equations (see
Section 5). Additionally, motion primitives can be generated offline and stored in a database when dealing with complex systems (see
Section 4) or generated online when a simplified model accurately represents the dynamics of the system (see
Section 5).
4. Search-Based Kinodynamic Planning with Motion Primitives Library for Differentially Flat Quadrotors
This section builds upon the work presented in [
18], which addresses motion planning for systems with arbitrary dynamics through a two-phase approach: offline and online. During the offline phase, the state space is discretized to obtain a suitable number of initial and final condition pairs. Motion primitives are then computed as solutions to a TPBVP, using these initial and final conditions as boundary conditions. Finally, these motion primitives are stored in a library. This process shifts the computational demands of trajectory generation to the offline phase, significantly reducing the computational load during online motion planning. In the online phase, the task of the planner is to select suitable motion primitives from the library to generate a complete trajectory. This two-phase approach enables efficient online motion planning for various systems, including complete quadrotor models as well as more complex systems like fixed-wing and VTOL aircraft.
In this section, this methodology is modified by tailoring it specifically to the quadrotor system, leveraging its inherent differential flatness property. Moreover, to make the method computationally tractable, continuity between consecutive motion primitives is enforced only on a subset of the state variables. Finally, the original approach is modified by utilizing a search-based planner rather than a sampling-based one.
4.1. Motion Primitives Library
Given an initial and a final condition, a motion primitive is the solution to the following TPBVP:
Unlike the TPBVP presented in Problem (3), this formulation focuses solely on generating a short-duration motion primitive rather than solving the overall motion planning problem. Consequently, the total trajectory duration
T is replaced with the primitive duration
, and the final state
is no longer the goal; instead, it is determined by the desired state space discretization.
In traditional TPBVPs, enforcing system dynamics as constraints can be complex and computationally demanding. However, for flat quadrotor systems, since all state variables
x and control inputs
u can be expressed in terms of flat outputs
and their derivatives, Problem (
4) can be reformulated in the space of flat outputs where the system dynamics in Equation (
1) are inherently satisfied (see
Appendix A for further details). Moreover, when the goal is to generate a smooth trajectory, the yaw angle
is typically negligible, and therefore it is omitted here.
For flat quadrotors, the position along each axis can be represented as a k-th order polynomial
The corresponding velocity
, acceleration
and jerk
can be obtained by taking the derivatives of Equation (
5). Then, Problem (
4) can be reformulated as follows:
where
is the
qth derivative of the position. Additional constraints, such as initial and final conditions on jerk and snap, can also be considered.
The motion primitives database is generated through an offline process where Problem (
6) is solved for a suitable number of initial and final condition pairs obtained via discretization of the state space. Subsequently, the resulting optimal trajectories and optimal costs are stored in a Look-Up Table (LUT). Note that thanks to the differential flatness property, the library can be efficiently stored, as each primitive is defined by a set of coefficients
and a duration
.
Obstacle avoidance is not addressed at this stage of motion library generation. Once the library is computed, the planner will concatenate the motion primitives online to construct a complete trajectory while considering obstacles. To concatenate the primitives, the initial conditions of a candidate primitive must coincide with the final conditions of the previous one. Ideally, one would grid the entire state space and construct the motion primitives accordingly. However, this would result in a prohibitively large library. Therefore, in practice, these final and initial conditions are enforced only on a subset of the state variables. This ensures the continuity of the planned trajectory for this specific subset. The remaining state variables will be continuous along each motion primitive and will experience discontinuity only at the points where primitives are concatenated.
It is worth noting that in cases where a vehicle model is not available, trajectories can be obtained directly from experimental flight data [
2]. Therefore, it can be safely assumed that primitives are inherently compatible with vehicle dynamics.
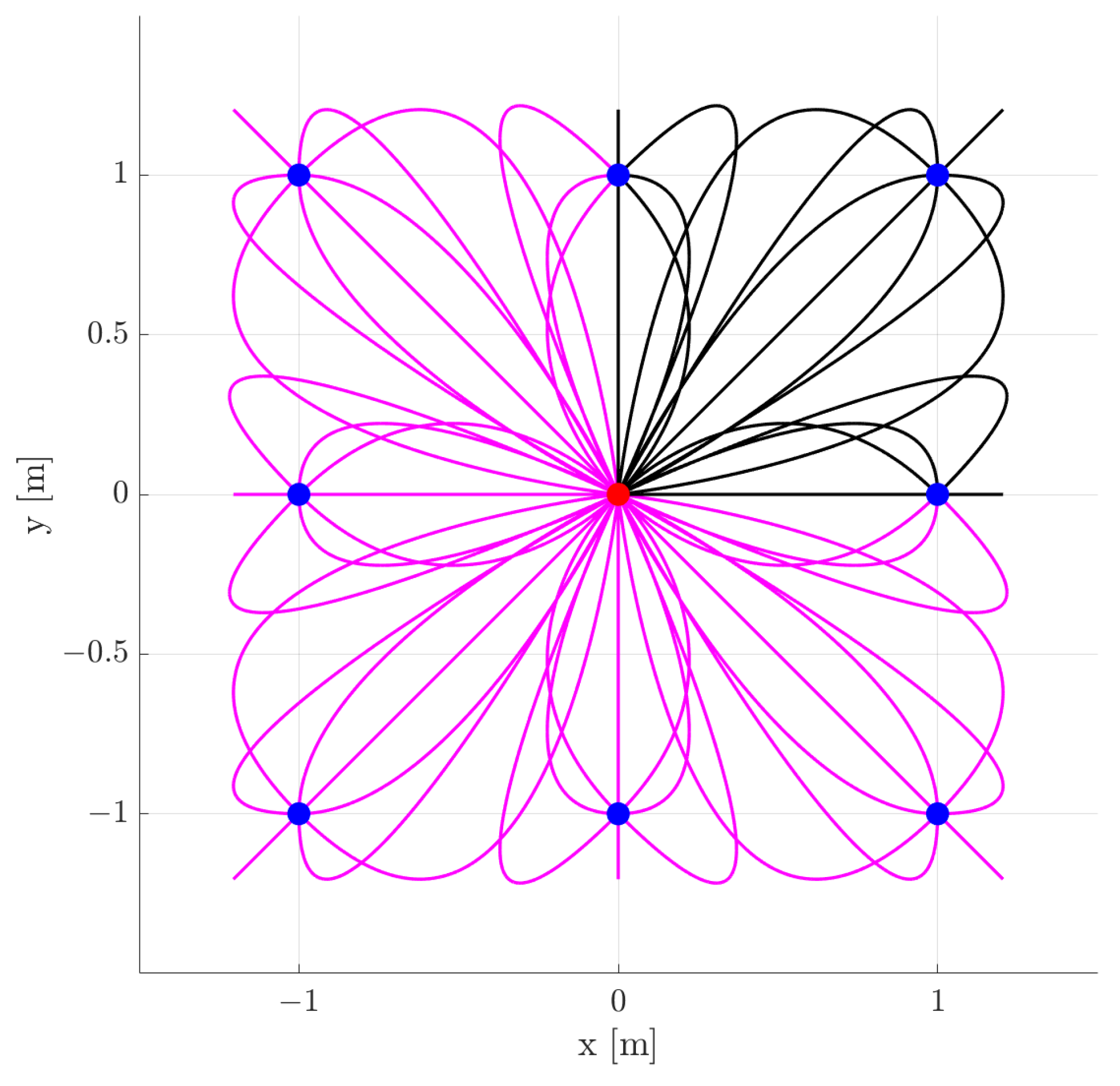
Figure 1 shows a subset of the motion primitives database for a quadrotor originating from the steady state
.
Invariance Properties
The motion primitive library can grow to include many primitives, requiring a considerable amount of memory for database storage. However, several invariance properties, extensively explored in previous works [
3,
22], can be leveraged to minimize this requirement.
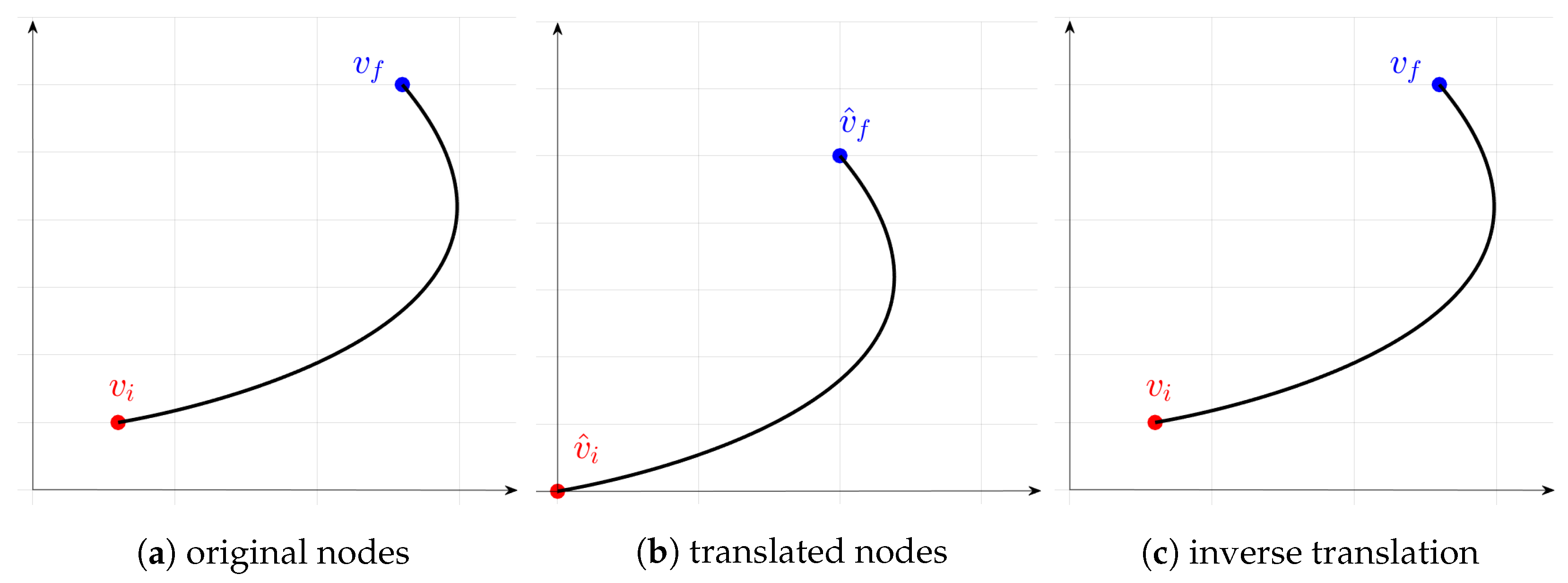
Dynamic systems, characterized by translation invariance, demonstrate consistent behavior under coordinate translations. This means that all trajectories can be rigidly translated to start from any arbitrary point. This property allows for the maintenance of a small database while covering the entire vehicle operating space. In practice, for the two-dimensional case, the initial position can be set to
during the database construction phase. Subsequently, the motion primitives can be easily translated to match any other initial position
, as shown in
Figure 2.
In particular, a first translation is performed on the pair of initial and final states
(
Figure 2a). This translation aims to relocate the initial state
to the origin of the library (
Figure 2b), resulting in a new pair of states
. Subsequently, a database query is executed to find the trajectory connecting these two states. Finally, an inverse translation is applied to restore the trajectory connecting the original pair of boundary states
(
Figure 2c).
Additionally, specific systems, like quadrotors, possess additional invariance properties, being invariant to horizontal plane translations and rotations about the vertical axis. Observing
Figure 1 it becomes evident that the motion primitives for the quadrotor are symmetric with respect to both the x- and y-axes. As a result, only trajectories within the first quadrant (depicted by black curves) need to be stored in the database. Trajectories in other quadrants (depicted by pink curves) can be generated through mirroring.
4.2. Library-Based Kinodynamic Motion Planning
The motion primitives library establishes a finite lattice discretization within the state space, enabling the construction of a graph representation
. Here,
represents the set of states, and
represents the set of edges. The states in
are the initial and final conditions obtained through the state space discretization. The edges in
are defined by selecting a subset of the motion primitives library, ensuring continuity of the desired state variables with those of the previous motion primitive. Through this graph representation, the motion planning problem can be rewritten as a graph-search problem. This search problem can be solved using either search-based [
8,
9], or sampling-based [
2,
3,
18,
23] algorithms, which differ mainly in the optimality of the solution and computational time.
Sampling-based methods avoid the explicit construction of the configuration space by randomly or systematically sampling the space to build a graph representation of the environment. Search-based methods, on the other hand, employ traditional search algorithms to navigate a predefined representation of the configuration space. The primary distinction between these two methods lies in their approach to motion planning. Search-based methods aim to find optimal solutions, prioritizing optimality, while sampling-based methods focus on finding feasible solutions, emphasizing practicality and efficiency. Therefore, sampling-based algorithms are fast and particularly useful for complex and high-dimensional spaces. However, sampling-based methods employ a randomized approach, which could represent an obstacle when fast online replanning is required. Specifically, paths generated by sampling-based methods during successive replanning phases may exhibit significant variations, making them less suitable for applications where path consistency is crucial [
9].
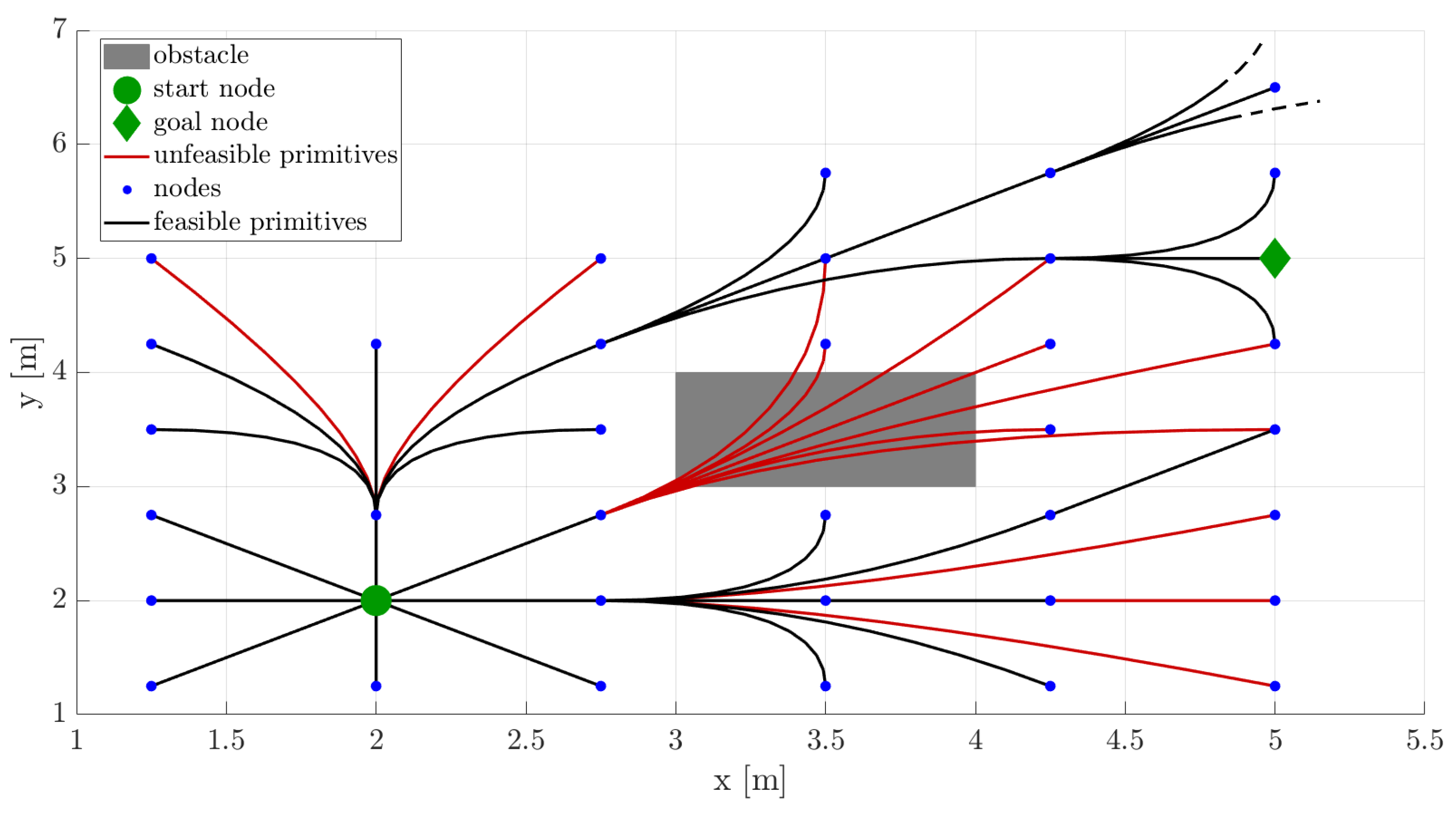
Based on these considerations, the A* algorithm [
24] is employed to efficiently solve this graph-search problem. A* employs the GetSuccessorsLibrary procedure described in Algorithm 1 to explore the state space and build the graph. When provided with the current node under expansion
v, this procedure is employed to query the database of motion primitives. This process involves a sequence of continuity checks and translations. Specifically, line 5 performs the continuity check, selecting primitives whose initial state
matches the current node
v. Line 6 executes the primitive translation, as illustrated in
Figure 2b,c. In line 7, a collision check is performed on the translated primitive
. If it passes the check, its final state
is added to the successors list along with its associated cost.
| Algorithm 1 Given the current node under expansion v and the motion primitive library , including initial states , final states , connecting primitives , and their associated effort costs c, find the set of successors Succ(v) and their cost SuccCost(v) |
- 1:
function GetSuccessorsLibrary(v, ) - 2:
Succ(v) ; - 3:
SuccCost(v) ; - 4:
for all do - 5:
if
then - 6:
TranslatePrimitive(); - 7:
if isCollisionFree() then - 8:
; - 9:
Succ(v) ← Succ(v) ; - 10:
SuccCost(v) ← SuccCost(v) ; - 11:
end if - 12:
end if - 12:
end for - 14:
return Succ(v), SuccCost(v); - 15:
end function
|
6. Numerical Simulations
This section presents the numerical simulations performed to demonstrate the effectiveness of the two methods. Specifically, a quadrotor is tasked with navigating from an initial state located at m to a final state positioned at m within a 2D 45 m × 15 m virtual environment. At both the initial and final states, velocity and eventually accelerations are set to zero.
Motion primitives library: To guarantee the automatic satisfaction of the system dynamics described in Equation (
1), the position
p must be at least four times differentiable. Therefore, a fifth-order polynomial representation of the 2D position is considered. This ensures continuity in terms of position, velocity, acceleration, jerk, snap, and the derivative of snap along each primitive. However, to prevent the library from becoming prohibitively large, the initial and final conditions for database generation are enforced only on position, velocity, and acceleration. As a result, the planned trajectory will be continuous in position, velocity, and acceleration. The remaining state variables will be continuous along each motion primitive and will experience discontinuity at the concatenation points.
The motion primitives library is generated by solving a particular instance of Problem (
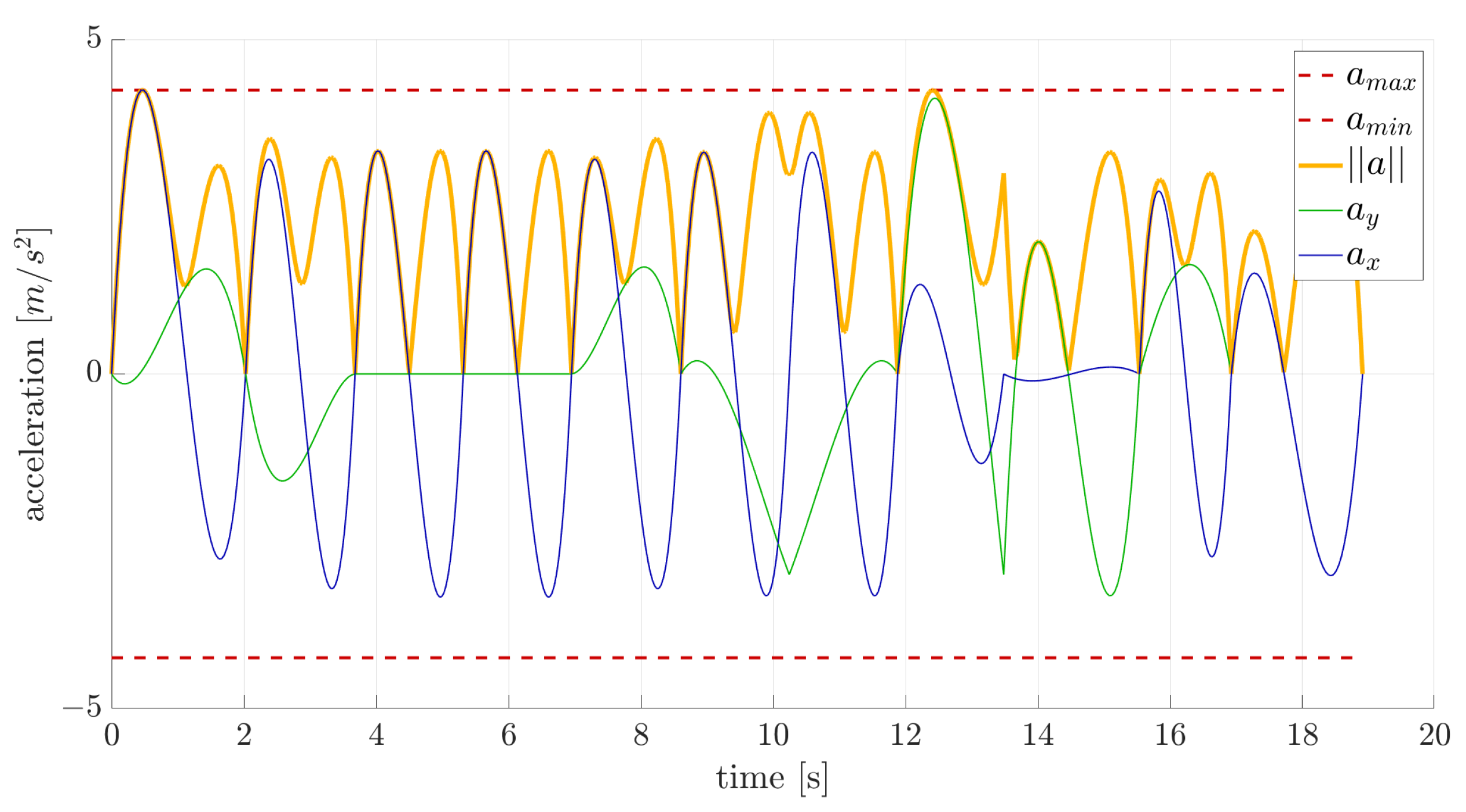
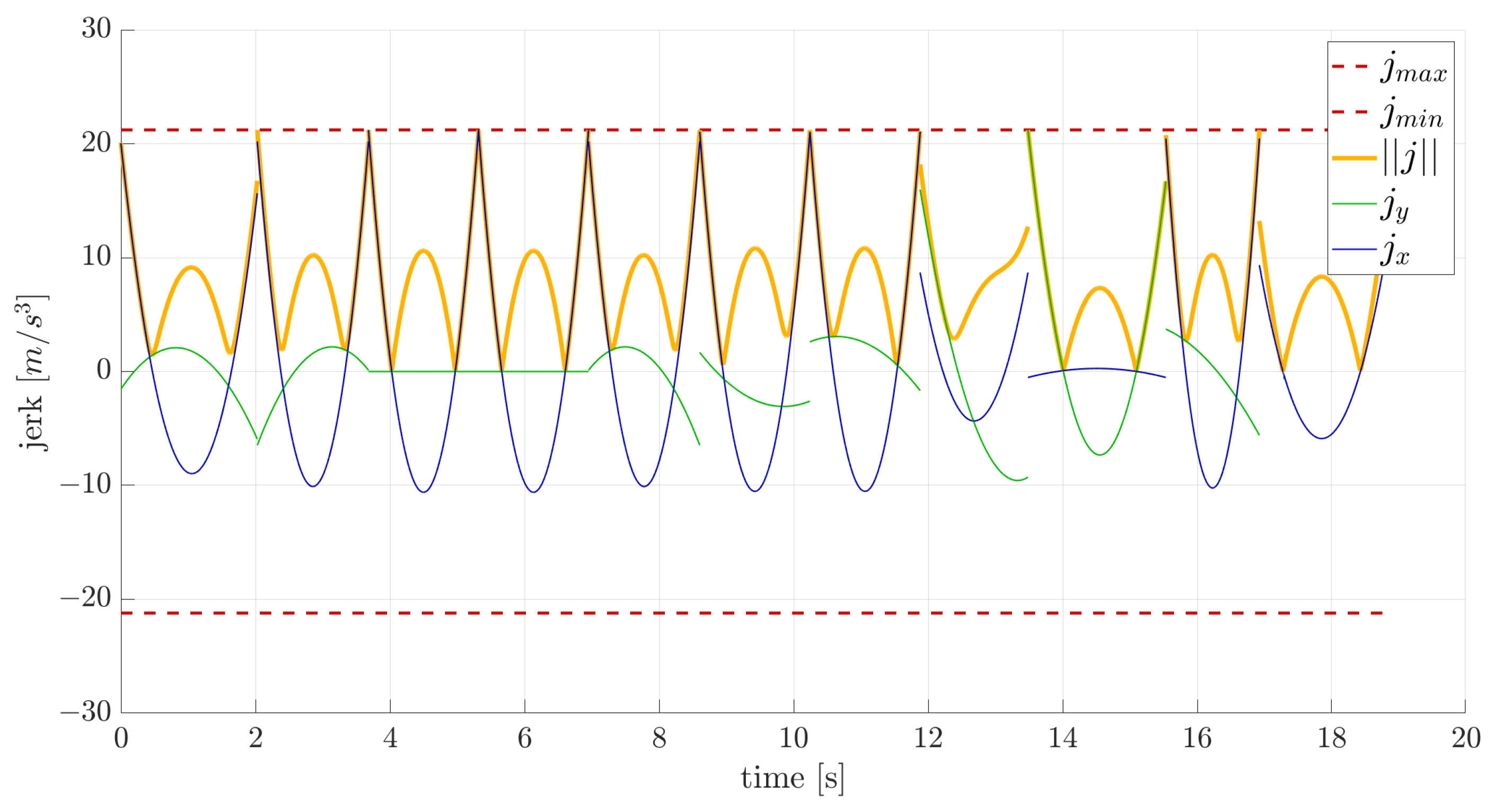
6) for every combination of initial and final states, employing MATLAB’s R2024a fmincon function. Specifically, a trade-off between the integral of the jerk squared and primitive duration is minimized. Constraints are imposed on total acceleration and total jerk, set, respectively, at
ms
−2 and
ms
−3. Note that by leveraging the differential flatness property, the imposition of constraints on acceleration and jerk effectively restricts the commanded thrust and commanded angular rates to ensure adherence to the actuation constraints. This ensures that the motion primitives remain feasible and executable within the physical constraints of the platform. Additional information can be found in
Appendix A.
Online motion primitives: To achieve a dynamically feasible trajectory, a fourth-order polynomial representation of position should be employed, with the snap serving as control input. However, planning in higher-dimensional spaces requires more time. Additionally, discretizing the snap is not intuitive due to its lack of direct physical meaning. Furthermore, an online feasibility check, as described in
Section 5.1, must be conducted for velocity, acceleration, and jerk. This process is computationally intensive when performed online, making it inefficient. In practice, it is more effective to sample over acceleration and employ second-order polynomials for position, as done in [
8]. This approach restricts the feasibility check to velocity alone, significantly reducing the online computational load. Additionally, discretizing acceleration is straightforward due to the well-understood impact of acceleration on the behavior of the system. Therefore, in this example, second-order polynomials are used to represent position. The 2D quadrotor state is defined as
and acceleration
is used as control input. Total velocity
is constrained to be lower than
ms
−1. Maximum acceleration along each axis is set to 3 ms
−2.
6.1. Parameters Selection and State Space Discretization
This section explains how the discretization of the state space, as well as input discretization and the primitive duration , influence planning performance. Furthermore, it elaborates on their selection process tailored to the specific application at hand.
State space discretization for library computation: The discretization of the state space significantly affects planning performance, including computation time and solution optimality. The grid resolution determines the density of the graph and the computation time. A fine-resolution grid results in a denser graph, allowing for a more complete search and smoother trajectories. However, a denser graph requires more exploration to reach the goal, thus increasing computation time due to the higher number of nearby nodes to be checked. Conversely, a coarse resolution grid limits the set of candidate solutions, which can potentially result in search failures. Specifically, if the state space discretization is not fine enough, the resulting problem could become infeasible. However, for computational reasons, a coarse grid is preferable as it reduces the number of neighbor connections to be evaluated, therefore speeding up the search process.
Determining the optimal state space discretization depends on the specific application. For this specific application, the following state space discretization has been found suitable. The database is assembled starting from an initial position at . It is based on a uniform square grid, where the final state position coordinates and each square cell spans one meter. These values have been selected based on the simulation environment. Given that the environment is large and filled with obstacles, it is beneficial to include both long (e.g., 4 m) and short (e.g., 1 m) motion primitives in the library. This approach allows the system to use shorter motion primitives for navigating through obstacle-dense regions to avoid collisions and longer primitives for traversing obstacle-free areas, ensuring smoother motion. Initial and final velocities () and initial and final accelerations () are each selected from a set of three values to prevent the library from becoming prohibitively large. Specifically, initial and final velocities are selected from ms−1, and initial and final accelerations are chosen from ms−2.
Control input discretization and motion primitive duration for online motion primitives computation: The motion primitives duration and the control input discretization have a significant effect on the planning performance, including computation time and optimality of the solution. The primitives duration determines the density of the graph and computation time. A small results in a denser graph, requiring more exploration to reach the goal, therefore increasing computation time. Conversely, large reduces the space of candidate solutions, potentially leading to search failures. Specifically, if the discretization of the control input is not fine enough, the resulting problem could become infeasible (i.e., the set of candidate solutions could be empty). Moreover, since the goal is to optimize the duration of the overall trajectory, the duration of the primitives imposes a lower bound on the optimality of the solution. As the duration of the motion primitives decreases, so does the cost of the optimal trajectory. However, for computational reasons, a longer duration is preferable. The control space discretization also influences the density of the graph and computation time: finer discretization yields a slower but more complete search and smoother trajectories, while coarser discretization produces the opposite effect. Moreover, finer control space discretization significantly increases computation time, making the approach impractical in practice.
The optimal combination of control input discretization and primitive duration depends on the specific application. For this specific application, the following values have proven to be suitable. To ensure a balance between search completeness and computational efficiency, the set of control inputs is discretized into nine options within the allowable range of ms−2 and the primitive duration is set at s.
6.2. Simulations Results
This section presents the results of the numerical simulations.
Planning with motion primitives library:
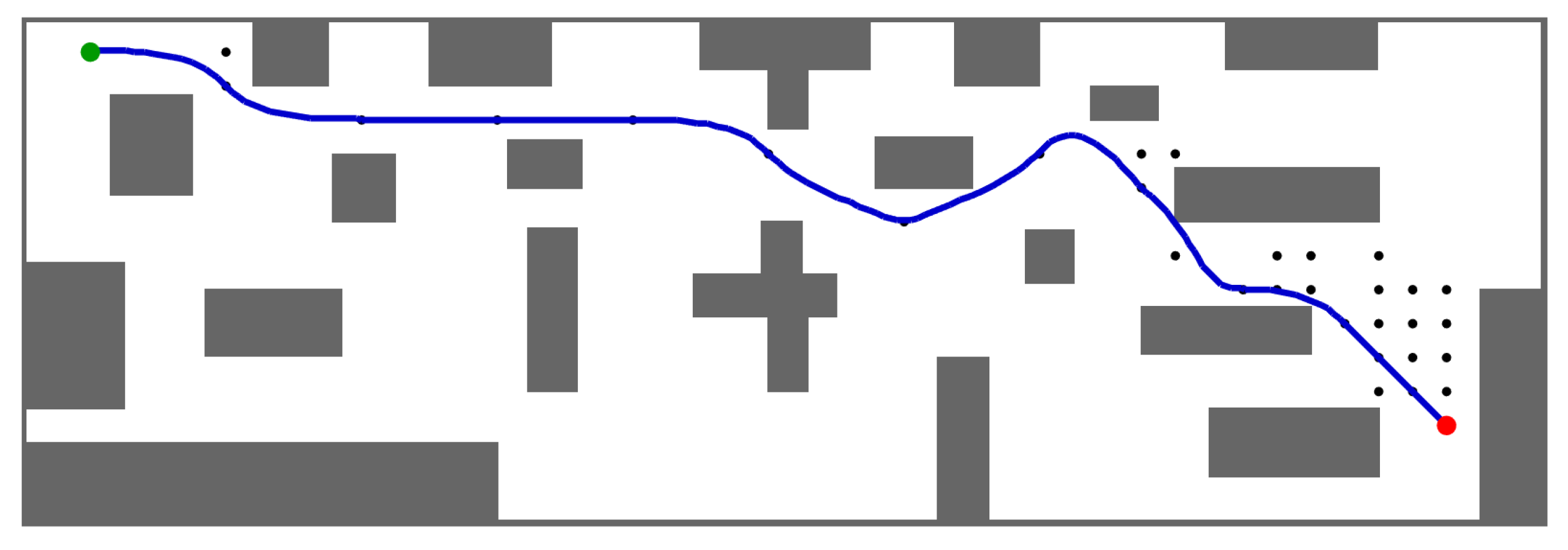
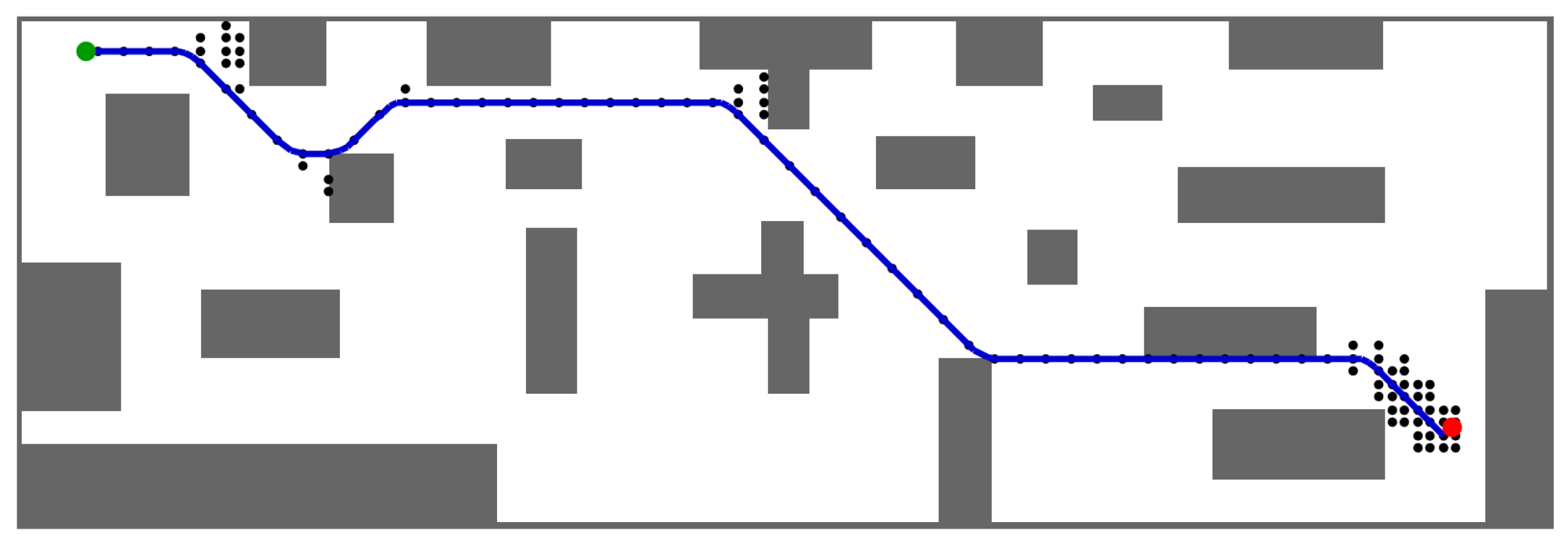
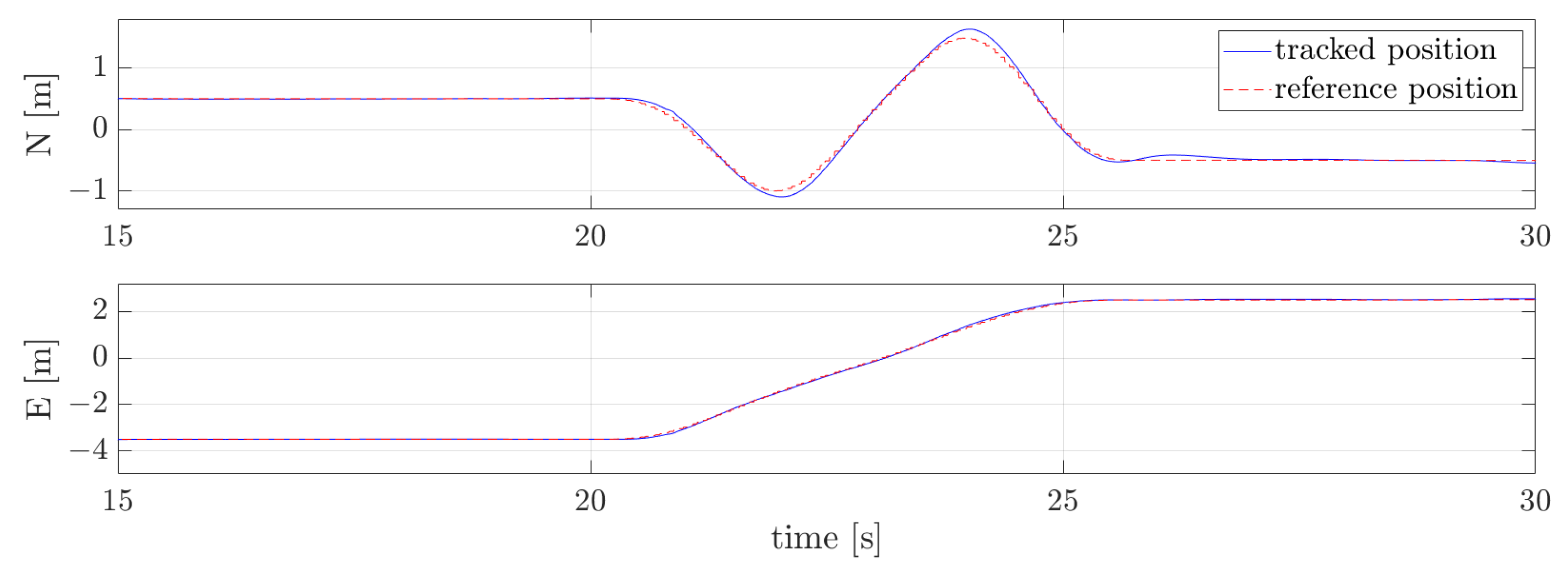
Figure 5 shows the optimal collision-free trajectory guiding the vehicle from the initial state (green dot) to the goal state (red dot).
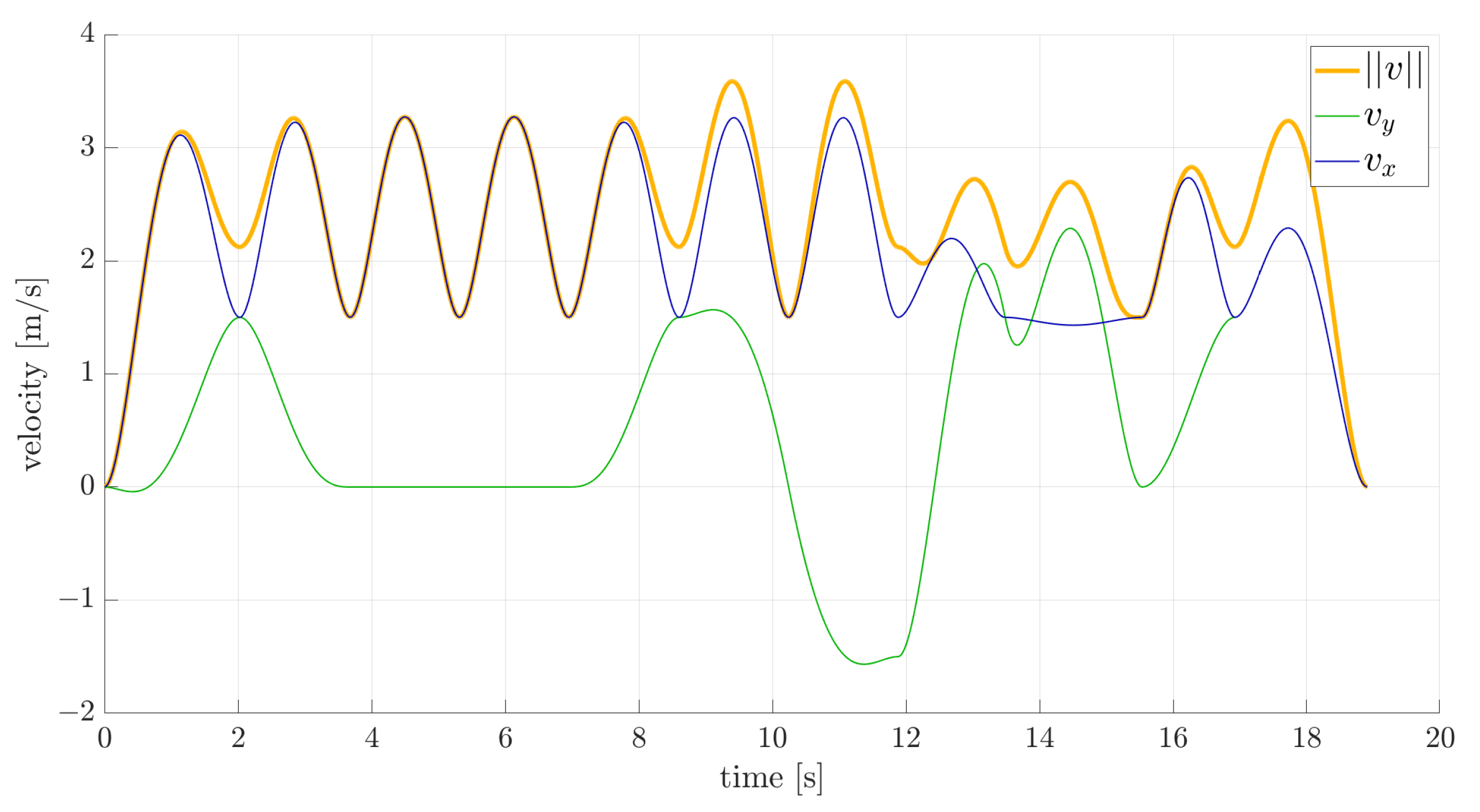
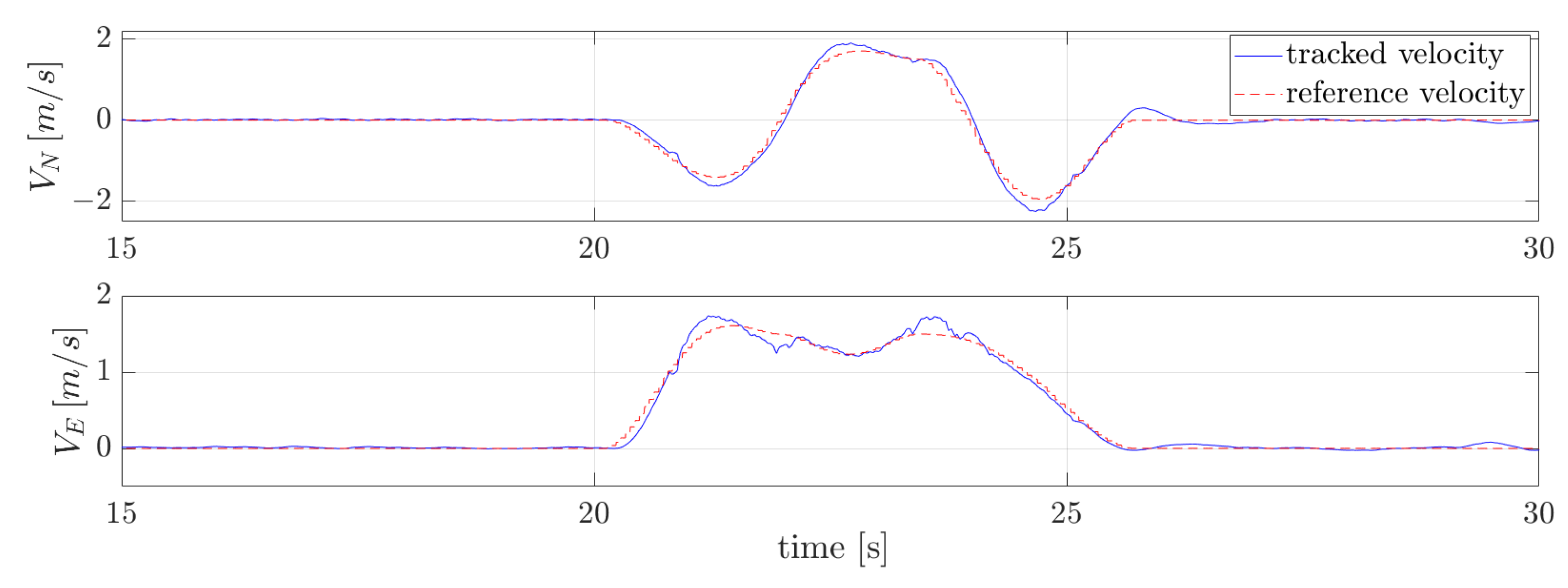
Figure 6,
Figure 7 and
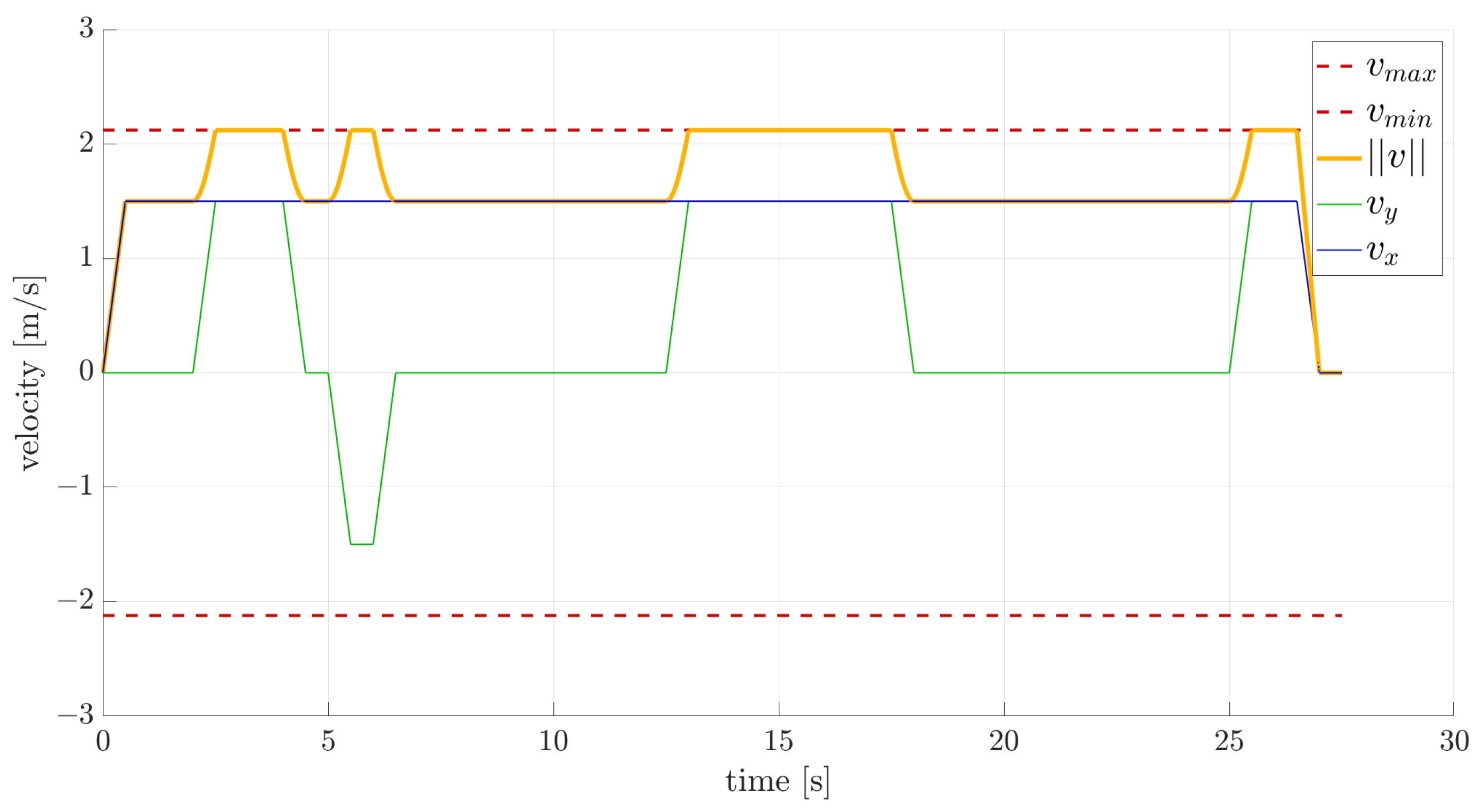
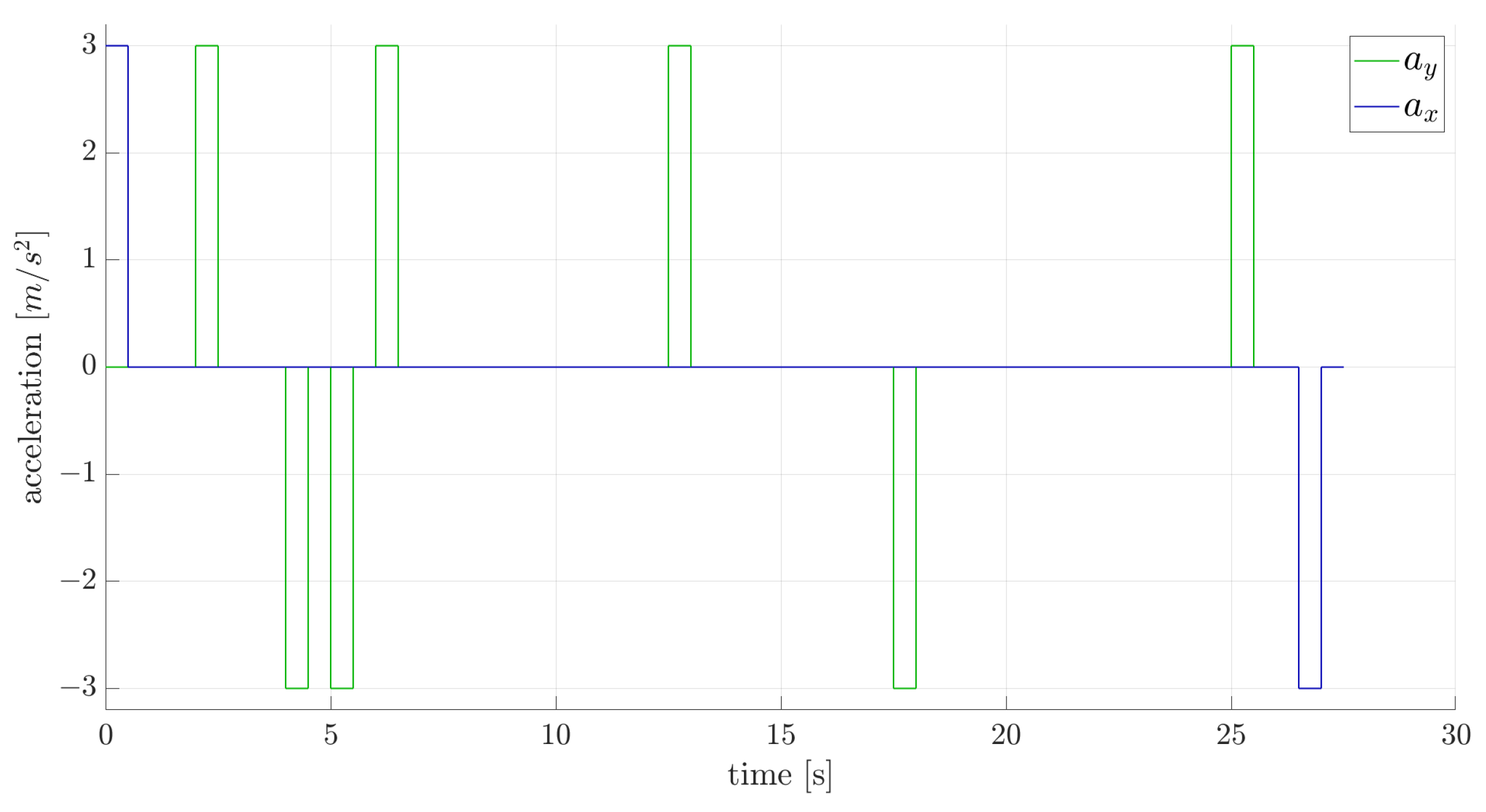
Figure 8 depict the velocity, acceleration, and actuation profiles. These figures demonstrate the efficacy of this approach in generating collision-free and dynamically feasible trajectories. Observing the velocity profile in
Figure 6, it is evident that rather than experiencing a gradual and continuous increase in velocity, sudden changes in acceleration occur. This issue arises from constraining velocity and acceleration at each node to match one of the values in the database precisely. To obtain a smoother trajectory, a finer state space discretization is required.
Planning with online motion primitives:
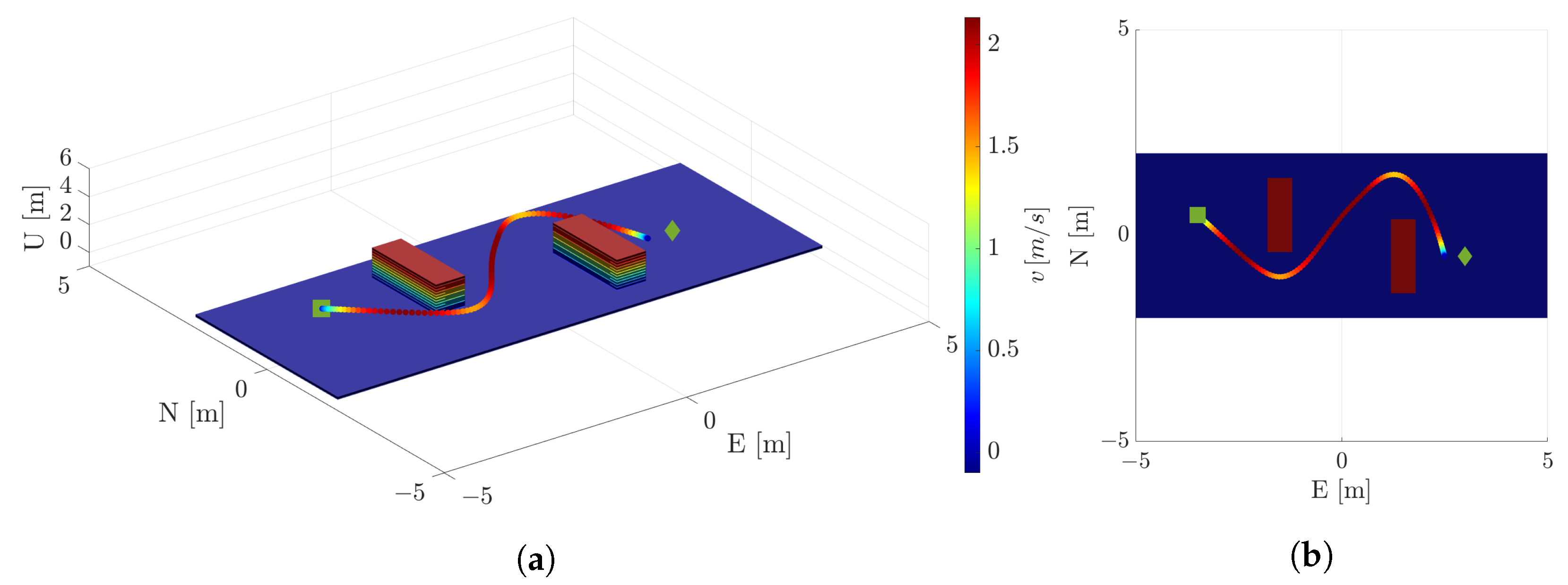
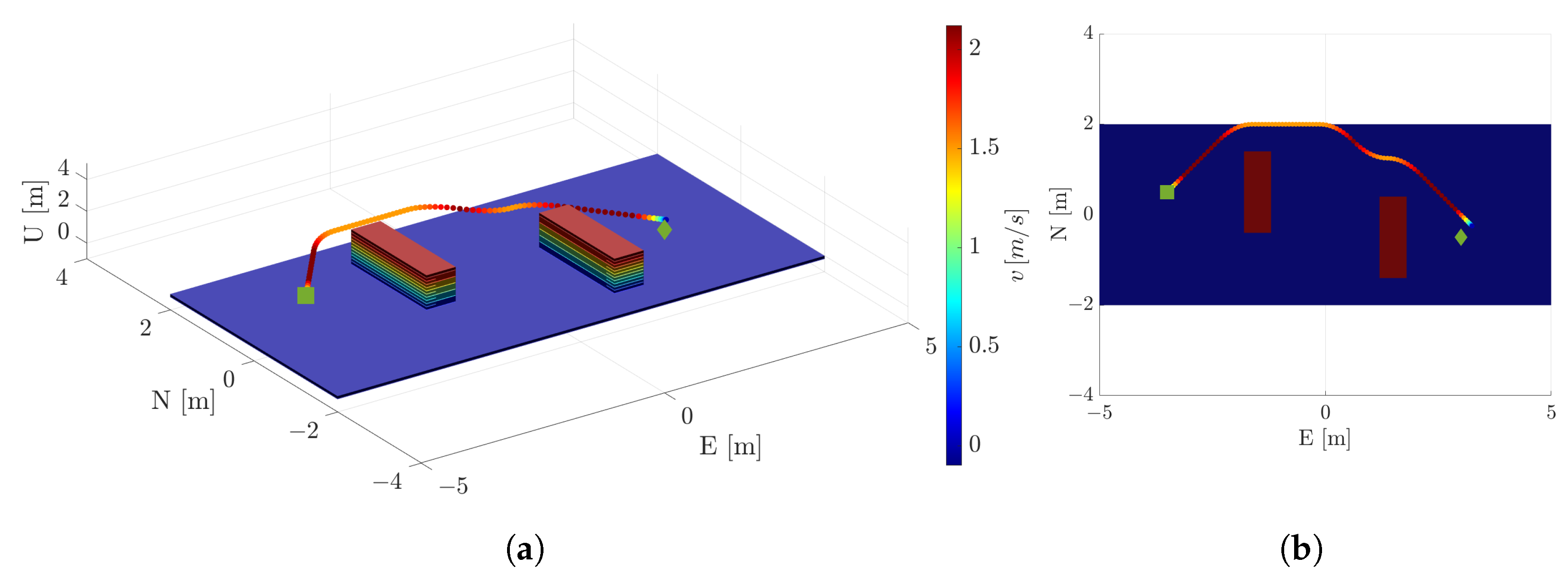
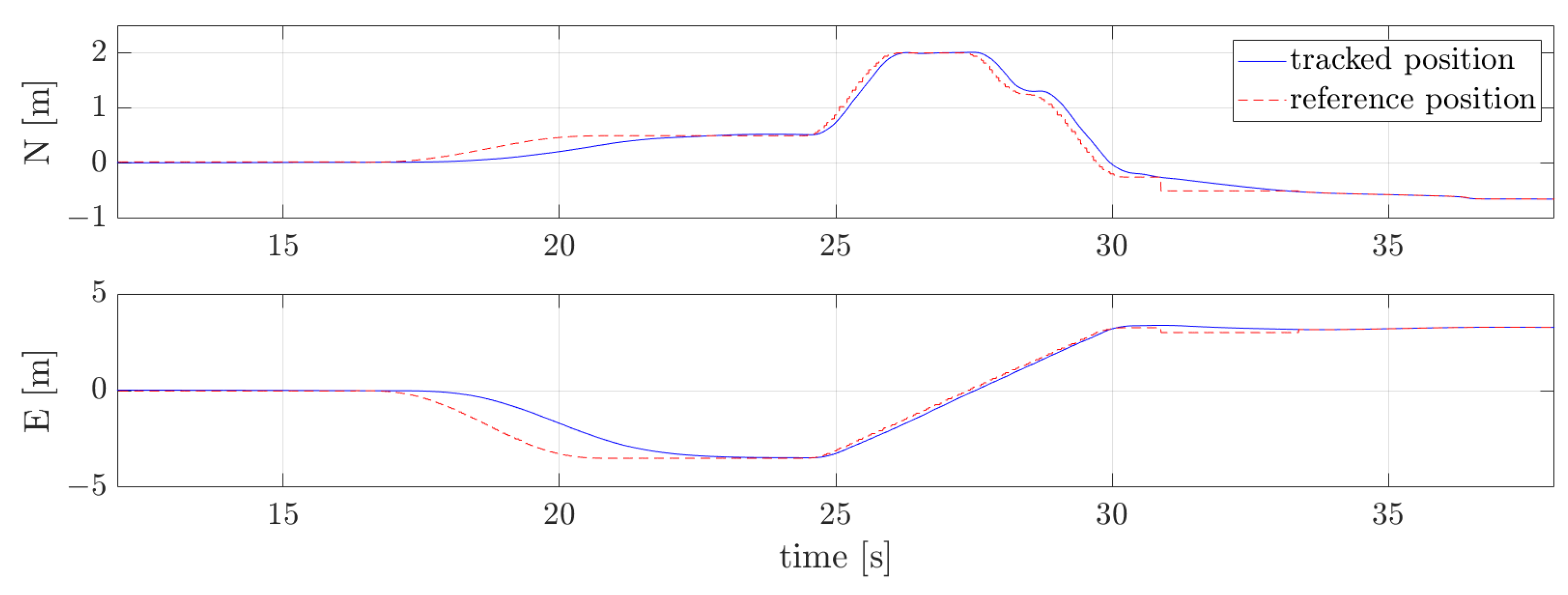
Figure 9 shows the optimal collision-free trajectory guiding the vehicle from the start state (green dot) to the target state (red dot).
Figure 10 and
Figure 11 show the velocity profile and the actuation (acceleration) profile for the optimal trajectory, demonstrating adherence to velocity constraints.
8. Discussion
This section delves into a comparative analysis of the two approaches, each offering distinct advantages. The selection of the appropriate method depends on the specific characteristics of the system at hand and its performance requirements. For a concise overview, the key features of both methods are summarized in
Table 1 and discussed in the following sections.
8.1. Adaptability to Complex Systems
The planning with online motion primitives method is advantageous when a simplified representation of the system accurately captures its dynamics. This approach is particularly useful in scenarios where moderate performance and tracking are acceptable, making a simplified model adequate to satisfy these requirements. However, its applicability to more complex systems is limited. On the other hand, the planning with motion primitives library method is the preferred choice when a simplified representation of the system fails to meet performance requirements, necessitating a more complex model. In fact, this method extends its applicability beyond differentially flat quadrotor systems to encompass a wide range of complex systems, including VTOL and fixed-wing aircraft. Its versatility is attributed to its capacity to shift the computational demands of trajectory generation to an offline phase, therefore ensuring precise solutions without compromising efficiency. Furthermore, this method is advantageous in scenarios requiring aggressive and agile maneuvers, where precise tracking and the full utilization of the system’s capabilities are essential.
8.2. Motion Primitives Duration
In the planning with online motion primitives method, all the motion primitives have the same duration, denoted as , which is usually set sufficiently large for computational reasons. However, this hinders the overall objective of achieving a minimum-time trajectory. In contrast, the planning with motion primitives library method employs minimum-time primitives generated by solving a TPBVP, aligning more closely with the objective of achieving a minimum-time trajectory.
8.3. Motion Primitives Feasibility Check
The planning with online motion primitives method generates motion primitives through control input discretization and forward propagation of the dynamic equations of a simplified model. Consequently, the resulting primitives are feasible with respect to control inputs (e.g., acceleration) but do not inherently incorporate velocity constraints, necessitating a subsequent feasibility check. This additional step involves further computations and significantly slows down the online trajectory computation. In contrast, the planning with motion primitives library method directly incorporates velocity, acceleration, and other constraints into its library, eliminating the need for a subsequent feasibility check and accelerating online trajectory computation.
8.4. Further Considerations
In a known environment, geometric considerations on the environment itself (e.g., environment dimensions, characteristics distances between obstacles) easily translate into grid selection. On the contrary, the tuning process for the control input set and the duration of primitives is more challenging, especially for complex systems.
9. Conclusions
This work addresses trajectory planning for UAVs in the presence of obstacles by introducing a library of motion primitives tailored for quadrotors. The versatility of this approach lies in its ability to shift the computational demands of trajectory generation to the offline phase of database construction. To further enhance computational tractability, continuity between consecutive motion primitives is enforced only on a subset of state variables (position, velocity, and acceleration). This method has proven effective in maintaining computational efficiency while ensuring accurate trajectory planning and proves promising for applications to more complex systems, including VTOL and fixed-wing aircraft.
The proposed method is compared with a state-of-the-art quadrotor-tailored search-based planner, which generates motion primitives online by discretizing control inputs and propagating the dynamic equations of a simplified model forward. However, this state-of-the-art approach is computationally efficient only for simple systems, such as single or double integrators. Conversely, the proposed library-based method enables efficient motion planning for arbitrary systems.
Notably, both methodologies demonstrate the ability to generate resolution-complete, collision-free, resolution-optimal, and dynamically feasible trajectories, as demonstrated by numerical and experimental results. Furthermore, a comparison of the two approaches highlights their respective strengths and weaknesses.
Future research will focus on addressing motion planning in unknown and dynamic environments. This involves vision-based dynamic replanning using real-time data to navigate and avoid newly detected obstacles. Furthermore, upcoming studies will concentrate on developing motion primitive libraries for the identified model of the quadrotor. Additionally, efforts will be directed toward mitigating the discontinuity of the state variables at the nodes. Although enforcing continuity during the library construction phase presents memory challenges, a potential solution involves generating a trajectory that guarantees only position and velocity continuity at the nodes. This trajectory will serve as a high-quality initial guess for an online trajectory-generation algorithm, with continuity in other states achieved in a receding horizon fashion.