A Supervised Reinforcement Learning Algorithm for Controlling Drone Hovering

Abstract

The application of drones carrying different devices for aerial hovering operations is becoming increasingly widespread, but currently there is very little research relying on reinforcement learning methods for hovering control, and it has not been implemented on physical machines. Drone’s behavior space regarding hover control is continuous and large-scale, making it difficult for basic algorithms and value-based reinforcement learning (RL) algorithms to have good results. In response to this issue, this article applies a watcher-actor-critic (WAC) algorithm to the drone’s hover control, which can quickly lock the exploration direction and achieve high robustness of the drone’s hover control while improving learning efficiency and reducing learning costs. This article first utilizes the actor-critic algorithm based on behavioral value Q (QAC) and the deep deterministic policy gradient algorithm (DDPG) for drone hover control learning. Subsequently, an actor-critic algorithm with an added watcher is proposed, in which the watcher uses a PID controller with parameters provided by a neural network as the dynamic monitor, transforming the learning process into supervised learning. Finally, this article uses a classic reinforcement learning environment library, Gym, and a current mainstream reinforcement learning framework, PARL, for simulation, and deploys the algorithm to a practical environment. A multi-sensor fusion strategy-based autonomous localization method for unmanned aerial vehicles is used for practical exercises. The simulation and experimental results show that the training episodes of WAC are reduced by 20% compared to the DDPG and 55% compared to the QAC, and the proposed algorithm has a higher learning efficiency, faster convergence speed, and smoother hovering effect compared to the QAC and DDPG.

1. Introduction

With the continuous development of drone control technology, the application mode of “drone+” is becoming increasingly widespread [1]. Aerial robots can become flight carriers for various aerial operations in different industries by carrying various devices and targeted configurations that meet application requirements. Many aerial drones are used as operational tasks for flight platforms, such as inspection, monitoring, obstacle removal, and cargo handling [2,3,4,5,6,7], which require drones to be able to hover for long periods of time. In addition to high requirements for the platform’s translational stability, the large inertia of the pitch and yaw channels caused by the operational tools loaded on the platform, as well as the impact of contact forces during operation, also require the platform to have strong anti-interference abilities. The use of flight control strategies with disturbance resistance and higher efficiency has also received attention. At present, the flight control methods for drones mainly include linear control methods [8,9,10], nonlinear control methods [11,12,13], and intelligent control methods [14,15,16,17]. The learning-based robot control method has received widespread attention in the field of automatic control [18,19,20], as it ignores the dynamic model of the robot and learns control methods through a large amount of motion data. In the latest Nature journal, Elia Kaufmann et al. [21], from the Robotics and Perception Group at the University of Zurich, studied the unmanned aerial vehicle autonomous system, Swift, which used deep reinforcement learning (DRL) algorithms to successfully defeat human champions in racing competitions, setting new competition records. It can be seen that reinforcement learning frameworks have become a promising algorithmic tool for improving the autonomous behavior of aerial robots [22,23,24,25]. Deep reinforcement learning, as a currently popular unsupervised learning framework, utilizes the perception ability of deep learning and the decision-making ability of reinforcement learning to achieve end-to-end control from input to output. It can be effectively applied to high-level decision-making systems and is becoming a commonly used framework for scholars from all walks of life to study aerial robot control algorithms [26].

At present, many researchers are trying to combine reinforcement learning with unmanned aerial vehicle systems to solve the autonomous control problem of flight robot systems [27,28,29,30]. Most reinforcement learning algorithms applied to unmanned aerial vehicle systems cannot be applied to real scenarios due to simple simulation scenario settings, and overly complex simulation scenarios can reduce learning efficiency. In response to this issue, Lee Myoung Hoon et al. [31] proposed a soft actor-critic (SAC) algorithm with post experience replay (HER), called SACHER, which is a type of deep reinforcement learning (DRL) algorithm. Their proposed SACHER can improve the learning performance of SAC and adopt SACHER in the path planning and collision avoidance control of drones. In addition, the paper also demonstrates the effectiveness of SACHER in terms of success rate, learning speed, and collision avoidance performance in drone operation. Zhongxing Li et al. [32] proposed using the reinforcement learning method to control the motor speed of quadcopter drones for hover control in order to improve the intelligent control level of quadcopter drones. Jia Zhenyu et al. [33] proposed introducing traditional control models to improve the training speed of reinforcement learning algorithms. By optimizing the proximal strategy in deep reinforcement learning, the control learning task of attitude stability was achieved, and it was verified that the algorithm can effectively control the stability of quadcopters in any attitude and is more versatile and converges faster than general reinforcement learning methods. The above references provide ideas for the innovative algorithm in this article.

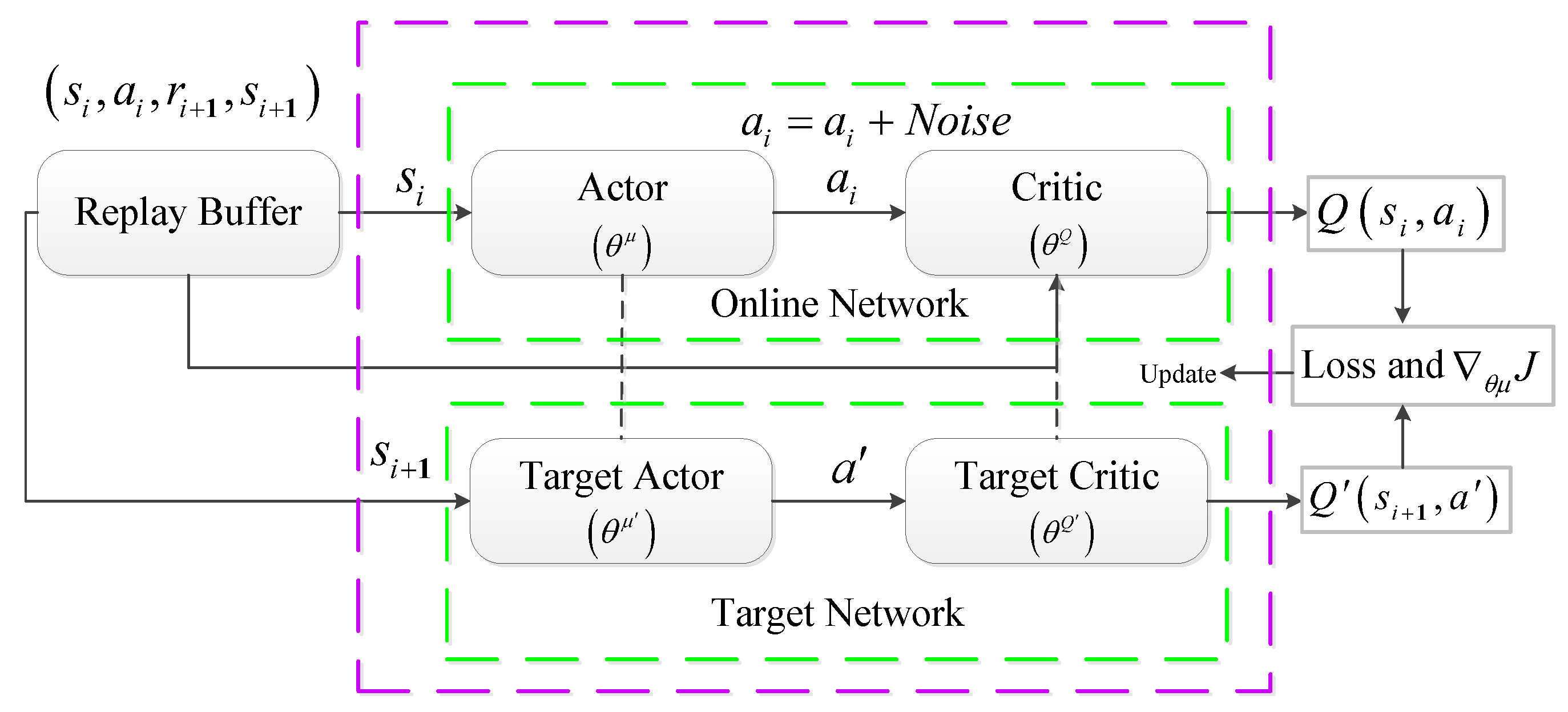
In this article, we will apply a new reinforcement learning algorithm, the WAC (watcher-actor-critic), to drone hover control, which can achieve high robustness of drone hover control while improving learning efficiency and reducing learning costs, preventing human manipulation from being affected by uncontrollable factors. The hover control of drones is part of low-level flight control with continuous and large-scale behavior space. Basic algorithms such as Monte Carlo reinforcement learning based on complete sampling and temporal differential reinforcement learning based on incomplete sampling will have low efficiency and may even fail to achieve good solutions. Even the deep Q-network algorithm (DQN) finds it difficult to learn a good result. The policy gradient algorithm based on Monte Carlo learning is not widely used in practical applications, mainly because it requires a complete state sequence to calculate the harvest. At the same time, using harvest instead of behavioral value also has high variability, which may lead to many parameter updates in a direction that is not the true direction of the policy gradient. The DQN proposed by Mnih V. et al. [22] is value-based reinforcement learning. Although it can solve many problems excellently, it still appears inadequate when facing learning problems with continuous behavior space, limited observation, and random strategies. To address this issue, Lillicrap, T.P. et al. [34] proposed a joint algorithm, the DDPG, based on value function and policy function, known as the actor-critic algorithm. It combines DQN on the basis of the PG algorithm proposed by Peters, J. et al. [35] and the DPG proposed by Silver, D. et al. [36]. In this context, this article will directly learn the strategy, which is viewed as a policy function with parameters for the drone state and propeller power output. By establishing an appropriate objective function and utilizing the rewards generated by drone interaction with the environment, the parameters of the policy function can be learned.

This article first uses the actor-critic algorithm based on behavioral value (QAC) and the deep deterministic policy gradient algorithm (DDPG) for drone hover control learning. By establishing approximate functions and policy functions for drone state value, on the one hand, policy evaluation and optimization can be based on the value function, and on the other hand, the optimized policy function will make the value function more accurately reflect the value of the state. The two mutually promote and ultimately obtain the optimal hovering strategy for drones. However, due to the unsupervised nature of this algorithm in reinforcement learning, the consequence of doing so is that the initial learning stage begins with a random exploration strategy, not to mention correct off-field guidance. The update of the strategy is also arbitrary or even explores in the opposite direction, resulting in a lower initial iteration speed and ultimately reducing the convergence speed of the objective function. In response to the above issues, this article proposes a deep deterministic policy gradient algorithm that adds a supervised network. Considering that most aircrafts currently use PID as the control algorithm in practical combat and the control effect is quite good and the excessive supervision can also affect the flexibility of the learning process, a PID controller with parameters provided by a three-layer neural network is used as the monitor in this article. The monitor will perform dynamic supervision during the strategy learning stage—that is, it will change the supervision intensity as the strategy learning progress changes. At the beginning of each learning episode, the supervision intensity is the highest, and by the end of the episode, the supervision is mostly removed. After the learning process reaches a certain stage, the supervision task is withdrawn, achieving unsupervised online learning. Finally, this article uses a classic reinforcement learning environment library, Python, and a current mainstream reinforcement learning framework, PARL, for simulation and deploys the algorithm to actual environments. A lightweight, drift-free multi-sensor fusion strategy for unmanned aerial vehicles as an autonomous localization method is used for practical exercises. The simulation and experimental results show that the reinforcement learning algorithm designed in this paper has a higher learning efficiency, faster convergence speed, and smoother hovering effect compared to the QAC and DDPG. This article takes improving the learning efficiency of drone hovering tasks as the starting point and adopts a PID controller combined with neural networks for supervised learning with reinforcement learning as the main approach and supervised control as the auxiliary to achieve the effect of rapid learning and smooth hovering of drones. From the above description, it can be seen that the advantages of the algorithm in this article are fast convergence speed and high training efficiency. 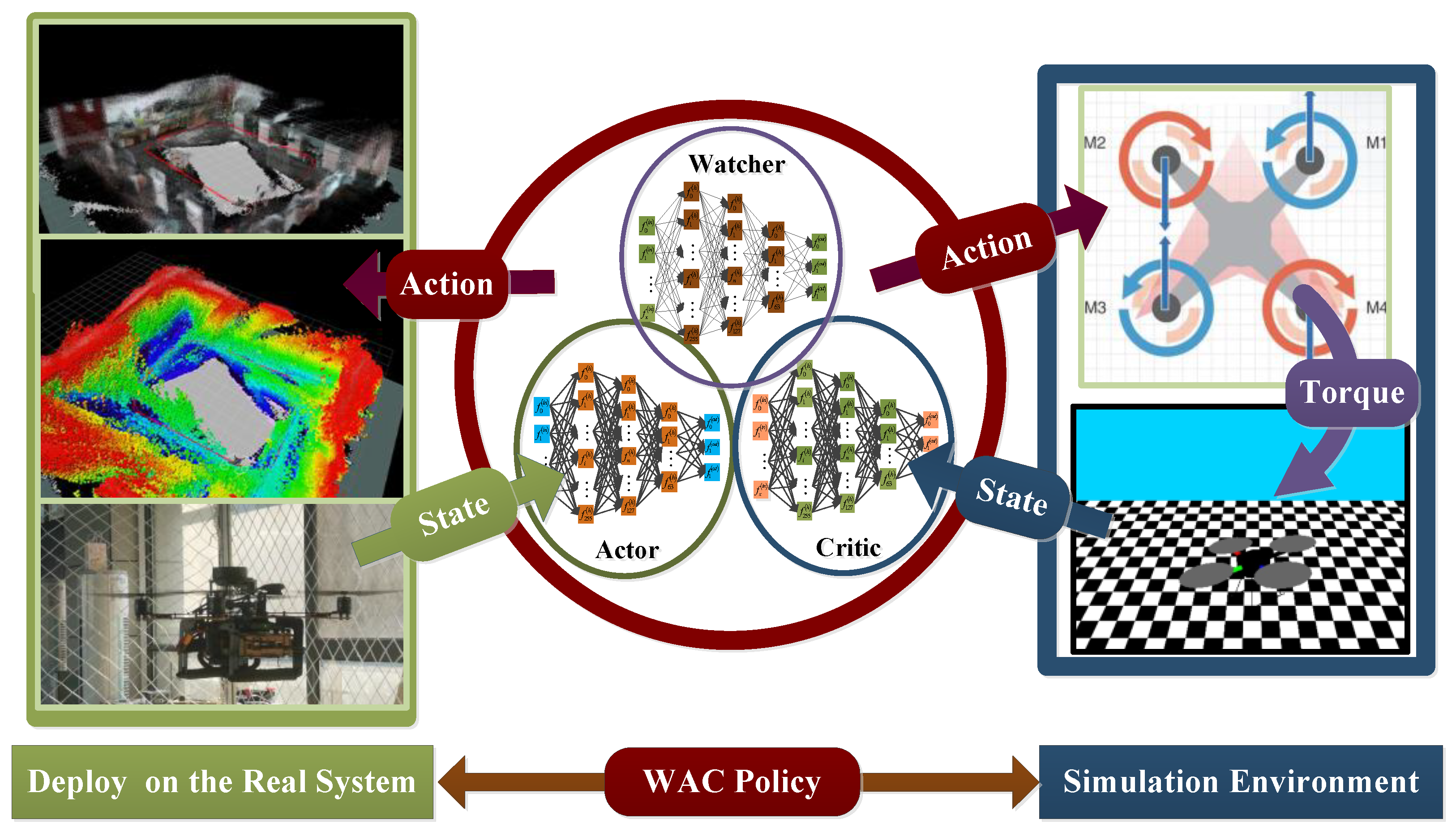Figure 1 illustrates the control strategy of this article. The right section describes how the algorithm guides the drone in simulation by providing the predicted actions for the drone propeller. This process is presented in the visualization window through the render() function in Gym. The left part is to deploy the trained strategy in the experimental environment.

The rest of this article is organized as follows. Section 2 introduces the proposed control method. The performance of this method is verified through simulation results in Section 3. Section 4 deploys this method to real drone systems. Section 5 focuses on concluding remarks.

2. Models and Methods

Section 2.1 describes the problem formulation of policy search in the reinforcement learning (RL) framework based on policy gradients. Section 2.2 describes the QAC and DDPG algorithms and introduces the proposed WAC method. In this article, the strategy is the controller learned by RL, which is formulated by combining the RL framework with a supervised controller.

2.1. Problem Formulation

Let the flight system of the drone be a continuous dynamic system with state feature, $s_t\in {ℝ}^s$, and system input, $a\in {ℝ}^a$, set as follows:

$$s_{t+1}=g\left(s_t,a\right)+{\mathrm{N}}_t$$

(1)

Among them, $s_{t+1}$ is the prediction of the next state based on the current state feature, $s_t$, after taking action, $a$, where $g\left(\cdot \right)$ is an unknown function and ${\mathrm{N}}_t$ is a random noise function that explores a small range around the control variable, while $t$ represents the time steps recorded in all the previous steps during the training process.

Assuming that each temporal process during the drone flight has a Markov property, the Markov decision process tuple, $〈S,A,P,R,\gamma 〉$, for the drone is established as follows:

$$\left\{\begin{array}{l}{s}_t={[p_{bx},p_{by},p_{bz},{\dot{p}}_{bx},{\dot{p}}_{by},{\dot{p}}_{bz},{\ddot{p}}_{bx},{\ddot{p}}_{by},{\ddot{p}}_{bz},{\omega }_{bx},{\omega }_{by},{\omega }_{bz},\theta ,\varphi ,\phi ,h]}^{\mathrm{T}},s_t\in S\\ a=\left[f_{p1},f_{p2},f_{p3},f_{p4}\right],a\in A\\ P_{s_t{s}_{t+1}}^a=\mathrm{E}\left[R_{t+1}|S_t=s_t,A_t=a\right]\\ R_{s_t}^a=\mathrm{E}\left[R_{t+1}|S_t=s_t,A_t=a\right]\\ \gamma \in \left[0,1\right]\end{array}\right.$$

(2)

where $S$ in tuple $〈S,A,P,R,\gamma 〉$ is a finite state set, and $s_t$ is a set of state representations in $S$. $p_{bx}$, $p_{by}$, and $p_{bz}$ are the position coordinates of the drone in the three coordinate axes of the body coordinate system. ${\dot{p}}_{bx}$, ${\dot{p}}_{by}$, and ${\dot{p}}_{bz}$ are the velocities of the drone in the three coordinate axes of the body coordinate system, and ${\ddot{p}}_{bx}$, ${\ddot{p}}_{by}$, and ${\ddot{p}}_{bz}$ are the accelerations of drone in the three coordinate axes of the body coordinate system. $h$ represents the flight altitude of the drone relative to the ground, while $s_t={[p_{bx},p_{by},p_{bz},{\dot{p}}_{bx},{\dot{p}}_{by},{\dot{p}}_{bz},{\ddot{p}}_{bx},{\ddot{p}}_{by},{\ddot{p}}_{bz},{\omega }_{bx},{\omega }_{by},{\omega }_{bz},\theta ,\varphi ,\phi ,h]}^{{\rm T}}$ describes the flight status of the drone in the aircraft coordinate system, which is composed of the drone’s current position $\left(p_{bx},p_{by},p_{bz}\right)$, velocity $\left({\dot{p}}_{bx},{\dot{p}}_{by},{\dot{p}}_{bz}\right)$, acceleration $\left({\ddot{p}}_{bx},{\ddot{p}}_{by},{\ddot{p}}_{bz}\right)$, angular velocity $\left({\omega }_{bx},{\omega }_{by},{\omega }_{bz}\right)$, Euler angle $\left(\theta ,\varphi ,\phi \right)$, and flight altitude, $h$. The $A$ in tuple $〈S,A,P,R,\gamma 〉$ is a finite set of control variables, where $a$ represents a set of control variables in $A$, where $f_{p1}$, $f_{p2}$, $f_{p3}$, and $f_{p4}$ represent the lift provided by the four propellers of the drone, and $a=\left[f_{p1},f_{p2},f_{p3},f_{p4}\right]$ describes the control variables executed in the four propeller axis directions under system control. The $P$ in tuple $〈S,A,P,R,\gamma 〉$ is a state transition probability matrix based on the control variable: $P_{s_t{s}_{t+1}}^a$ represents a set of transition probabilities in $P$; $P_{s_t{s}_{t+1}}^a$ represents the transition probability from the current state, $s_t$, to the next state, $s_{t+1}$, through $a$. The reward obtained during this process is $R_{t+1}$, and the subscripts, $t$ and $t+1$, in the upper variable represent the current time step and the next time step, respectively. The $R$ in tuple $〈S,A,P,R,\gamma 〉$ is a reward function based on the state and control variables; $R_{s_t}^a$ represents a set of reward values in the reward function, $R$, which is the reward obtained from $s_t$ after passing through $a$. The $\gamma$ in tuple $〈S,A,P,R,\gamma 〉$ is the decay factor, $S_t$ is the finite state set of the current time step, $t$, and $A_t$ is the finite control variable set of the current time step, $t$.

The reason for setting it this way is so that the actual drone can obtain the above state values from sensors, such as airborne gyroscopes and accelerometers, which facilitates further algorithm deployment work. The motion state update equation for drone hovering flight is established as follows:

$$\left\{\begin{array}{l}{s}_{t+1}=g\left(S_t=s_t,A_t=a|{\pi }_{\theta }\left(s_t,a\right)\right)+{\mathrm{N}}_t\\ {\pi }_{\theta }\left(s_t,a\right)=P\left[A_t=a|S_t=s_t,\theta \right]\end{array}\right.$$

(3)

where ${\pi }_{\theta }\left(s_t,a\right)$ is the hover flight control strategy, $\theta$ is the strategy parameter, $P\left[A_t=a|S_t=s_t,\theta \right]$ is the probability distribution matrix for executing the control variable, $a$, under given states, $s_t$ and $\theta$, $g\left(S_t=s_t,A_t=a|{\pi }_{\theta }\left(s_t,a\right)\right)$ is the dynamic equation obtained by continuously updating $\left\{\left(s_t,a\right),s_{t+1}\right\}$ for the strategy, and ${\mathrm{N}}_t$ is the noise function.

2.2. Propose Strategies

2.2.1. Actor-Critic Algorithm

The actor-critic algorithm relies on policy gradients. During this process, the use of a time difference (DT) algorithm to estimate the value of behavior is called QAC, which follows an approximate strategy gradient for learning. Firstly, the objective function, $J\left(\theta \right)$, is designed based on the policy, ${\pi }_{\theta }$, and then optimized accordingly [35]:

$$\left\{\begin{array}{l}{\theta }_{t+1}={\theta }_t+\gamma {\nabla }_{\theta }J\left({\theta }_t\right)\\ \nabla J\left({\theta }_t\right)\approx {\mathrm{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }\left(S,A|{\theta }_t\right)Q_{{\pi }_{\theta }}\left(S,A\right)\right]\end{array}\right.$$

(4)

The objective function gradient is transformed through sampling as follows:

$${\theta }_{t+1}={\theta }_t+\gamma {\nabla }_{\theta }\log {\pi }_{\theta }\left(s_t,a_t|{\theta }_t\right)Q_{\omega }\left(s_t,a_t\right)$$

(5)

where $\theta$ is the policy parameter, $\nabla$ is the gradient sign, $\gamma$ is the learning rate, ${\nabla }_{\theta }\log {\pi }_{\theta }\left(S,A|{\theta }_t\right)$ is the score function, $Q_{\omega }\left(S,A\right)$ is an approximate value function based on the policy, ${\pi }_{\theta }$, of the critic: $Q_{\omega }\left(S,A\right)\approx Q_{{\pi }_{\theta }}\left(S,A\right)$ with $\omega$ as its parameter.

The QAC algorithm utilizes both value-based and policy-based approaches, including a policy function and a behavioral value function. The actor interacts with the environment as a policy function to generate behavior, while the critic evaluates the policy as a value function. The QAC method learns increasingly accurate critics from its interaction with the environment, enabling single-step updates. Compared to simple policy gradients, the QAC can more fully utilize data. However, the critic in the QAC algorithm is still an approximate value function, which may introduce bias to deviate the predicted direction from the direction of the policy gradient. The DDPG also combines value function approximation (critic) and policy function approximation (actor). The use of target network and online network makes the learning process more stable and convergence more guaranteed. Therefore, it is based on actor-critic algorithm [35], but it is different from it (Figure 2).

2.2.2. WAC Algorithm

Supervised learning generates corresponding outputs for a given input based on a predictive model. For example, in reference [33], the authors introduced traditional control as an aid, which belongs in supervised learning. This article proposes that the supervisor in the algorithm plays this role. So, the proposed WAC algorithm is a supervised reinforcement learning algorithm and also belongs to the category of actor-critic algorithms. The specific control strategy is as follows:

$${\pi }_{\mathrm{WAC}}\left(s_t,a\right)=P\left[A_t=a^{\mu }\oplus a^W|S_t=s_t,{\theta }^{\mu },{\theta }^W\right]$$

(6)

where ${\theta }^{\mu }$ is the policy network parameter, and ${\theta }^W$ is the supervised network parameter. The WAC strategy advocates that the predicted behavior is the dynamic weighted behavior value, $A_t=a^{\mu }\oplus a^W$, given by the actor and the output behavior of the watcher network. The dynamic weights play a role in dynamic supervision, while the critic network estimates the behavior value based on the dynamic weighted behavior from the actor and watcher, calculates the gradient and critic loss of the objective function, and updates the parameters of each network.

Assuming the actor network function is $\mu \left({\theta }^{\mu }\right)$, the critic network function is $Q\left({\theta }^Q\right)$, the watcher network function is $W\left({\theta }^W\right)$, the target actor network function is ${\mu }^{\prime }\left({\theta }^{{\mu }^{\prime }}\right)$, and the target critic network function is $Q^{\prime }\left({\theta }^{Q^{\prime }}\right)$, the specific control process of the WAC strategy is shown in Figure 3: in the randomly selected state-action pairs $\left(s_i,a_i,r_{i+1},s_{i+1}\right)$ from the experience pool, state $s_i$ generates a specific behavior, $a^{\mu }$, through the actor network as one of the action input values of the critic network; the next state $s_{i+1}$ generates a predicted behavior, $a^{\prime }$, through the target actor network as the action input value of the target critic network for calculating the estimated value; the watcher network inputs the pre- and post-state values and error values from historical data into the PID supervisor, generating a specific behavior, $a^W$, as another action input value for the critic network; the behavior value $Q\left(s_i,a_i\right)$ corresponds to the critical network’s calculation state, $s_i$, and weighted behavior, $a_i$; the target critical network generates the behavioral value, $Q^{\prime }\left(s_{i+1},a^{\prime }\right)$, to calculate the target value, $Q_{T\arg et}$, based on the subsequent states, $s_{i+1}$ and $a^{\prime }$.

In the above process, if the reward obtained by interacting with the environment under the strategy ${\pi }_{\theta }$ is $R_{s,a}$, then the objective function is designed as follows:

$$J\left(\theta \right)={\mathrm{{\rm E}}}_{{\pi }_{\theta }}\left[R_{s,a}\right]$$

(7)

The task of the actor and watcher is to find the optimal behavior, $a_i=\alpha a^{\mu }+\beta a^W$, (where $\alpha$ and $\beta$ are dynamic weights) to maximize the value of the output behavior. The reward obtained by executing $a_i$ is $r_{i+1}$, and this conversion process is stored as $\left(s_i,a_i,r_{i+1},s_{i+1}\right)$. After the system stores enough of the conversion process, N random samples are taken to calculate the target value, $Q_{T\arg et}$, and the loss, $L$, of the critical network [35]:

$$Q_{T\arg et}=r_{i+1}+\chi Q^{\prime }\left(s_i,{\mu }^{\prime }\left(s_i|{\theta }^{{\mu }^{\prime }}\right)|{\theta }^{Q^{\prime }}\right)$$

(8)

$$L=\frac{1}{N}{\displaystyle \sum _i{\left(Q_{T\arg et}-Q\left(s_i,a_i|{\theta }^Q\right)\right)}^2}$$

(9)

The update method of the actor network adopts the gradient ascent method.

$${\nabla }_{{\theta }^A}J\approx \frac{1}{X}{\displaystyle \sum {\nabla }_a}Q\left(s,a|{\theta }^Q\right){|}_{s=s_i,a=\mu \left(s_i\right)\oplus W\left(s_i\right)}{\nabla }_{{\theta }^{\mu }}\mu \left(s|{\theta }^{\mu }\right){|}_{s_i}$$

(10)

The weighted behavior executed by the system is as follows:

$$a_t=\alpha \mu \left(s_t|{\theta }^{\mu }\right)+\beta W\left(s_t|{\theta }^W\right)+N_t$$

(11)

$\alpha$ and $\beta$ are constantly changing according to their learning progress, meeting the following requirements:

$$\alpha +\beta =1$$

(12)

The target network update is as follows:

$$\varsigma {\theta }^Q+\left(1-\varsigma \right){\theta }^{Q^{\prime }}\to {\theta }^{Q^{\prime }}$$

(13)

$$\varsigma {\theta }^{\mu }+\left(1-\varsigma \right){\theta }^{{\mu }^{\prime }}\to {\theta }^{{\mu }^{\prime }}$$

(14)

where $N_t$ is the noise function, and $\chi$ and $\varsigma$ are weights. ${\theta }^Q$, ${\theta }^{\mu }$, and ${\theta }^W$ are the weights of the critic network, $Q\left(s,a|{\theta }^Q\right)$, actor network, $\mu \left(s|{\theta }^{\mu }\right)$, and supervision network, $W\left(s|{\theta }^W\right)$, respectively. ${\theta }^{Q^{\prime }}$ and ${\theta }^{{\mu }^{\prime }}$ are the weights of the target critic network, $Q^{\prime }\left(s,a|{\theta }^{Q^{\prime }}\right)$, and target actor network, ${\mu }^{\prime }\left(s|{\theta }^{{\mu }^{\prime }}\right)$.

The PID controller corresponding to the watcher network is defined as follows:

$$\left\{\begin{array}{l}W(s_i)=K_{PID}e\left(k\right)\\ e\left(k\right)=s_i-s_d\end{array}\right.$$

(15)

where

$$K_{PID}=\left[\begin{array}{cccccccccc}{K}_P& K_I& K_D& 0& 0& 0& \cdots & 0& 0& 0\\ 0& 0& 0& K_P& K_I& K_D& \cdots & 0& 0& 0\\ & & & & ⋮& & & & & \\ 0& 0& 0& 0& 0& 0& \cdots & K_P& K_I& K_D\end{array}\right]\in {ℝ}^{a\times s}$$

(16)

$K_P$, $K_I$, and $K_D$ are the adjustment parameters corresponding to the state error, cumulative state error, and derivative of state error. $e\left(k\right)$ is the state error, and $s_i$ and $s_d$ are the sampled state and its reference values, respectively. The supervised neural network trains three parameters and passes them to the PID controller to calculate the specific behavior values and output them to the critical network. The training process for the supervised network applies a kinematic and dynamic analysis in traditional flight control, which will not be repeated in this article.

Algorithm 1 provides an overview of the proposed algorithm.

Algorithm 1: WAC Algorithm

Input: $\chi ,\varsigma ,\gamma ,{\theta }^Q,{\theta }^{\mu },{\theta }^W$ Output:optimized ${\theta }^Q,{\theta }^{\mu },{\theta }^W$ initialize $W\left(s|{\theta }^W\right)$ with weights ${\theta }^W$ Initial training to complete PID controller parameters via Watcher net by Equations (15) and (16) randomly initialize $Q\left(s,a|{\theta }^Q\right)$, $\mu \left(s|{\theta }^{\mu }\right)$, with weights ${\theta }^Q$, ${\theta }^{\mu }$ initialize target network $Q^{\prime }\left(s,a|{\theta }^{Q^{\prime }}\right)$, ${\mu }^{\prime }\left(s|{\theta }^{{\mu }^{\prime }}\right)$with weights ${\theta }^{Q^{\prime }}\leftarrow {\theta }^Q$, ${\theta }^{A^{\prime }}\leftarrow {\theta }^A$ initialize the experience cache space $\mathrm{M}$ for episode from 1 to Limit do   Initialize a noise function and receive the initial state   for t = 1 to $\mathrm{T}$ do Perform action $a_t$ via Equation (11), get reward $r_{t+1}$, next state $s_{t+1}$, store transition $\left(s_{t,}{a}_t,r_{t+1},s_{t+1}\right)$ in $\mathrm{M}$ sample a batch of random N transition $\left(s_{i,}{a}_i,r_{i+1},s_{i+1}\right)$ in $\mathrm{M}$, where $i=0,1,2,\cdots N$   set target value function via Equation (7)     update critic by minimizing the loss via Equations (8) and (9)   update actor policy by policy gradient via Equation (10)     update networks via Equations (13) and (14)   end for end for

We compared the performance of using the QAC algorithm, DDPG algorithm, and WAC algorithm in Section 3.

3. Simulations and Results Discussion

The open-source toolkit OpenAI Gym for reinforcement learning algorithms and the current mainstream reinforcement learning framework PARL are our simulation tools. PARL is a reinforcement learning framework based on PaddlePaddle, characterized by the following: (1) high flexibility and support for most reinforcement learning algorithms; (2) an open-source algorithm library for reinforcement learning with large-scale distributed capabilities; (3) the algorithm library has strong usability for industrial-level scenarios. The render function in the Gym library can be used to render the simulation environment and visually display the simulation effect. The drone in the PARL framework is a quadcopter aircraft equipped with an inertial module, which obtains its real-time position $\left(p_{bx},p_{by},p_{bz}\right)$, velocity $\left({\dot{p}}_{bx},{\dot{p}}_{by},{\dot{p}}_{bz}\right)$, acceleration $\left({\ddot{p}}_{bx},{\ddot{p}}_{by},{\ddot{p}}_{bz}\right)$, angular velocity $\left({\omega }_{bx},{\omega }_{by},{\omega }_{bz}\right)$, Euler angle $\left(\theta ,\varphi ,\phi \right)$, and flight altitude, $h$, in the body coordinate system by simulating sensors such as accelerometers and gyroscopes. This makes it easy to obtain the current drone’s flight status and transmit it to the input of the WAC algorithm. Output behavior, $a=\left[f_{p1},f_{p2},f_{p3},f_{p4}\right]$, describes the control variables executed in the four propeller axis directions under system control, and its learning process is the repetitive strategy function solving process. During drone hovering, the inertial module provides the current state data at each time step and determines the reward value: the greater the hovering error, the lower the reward value. The simulated computer configuration is an Intel(R) Core(TM) i5-7300HQ, and the simulation environment is Python 3.7.

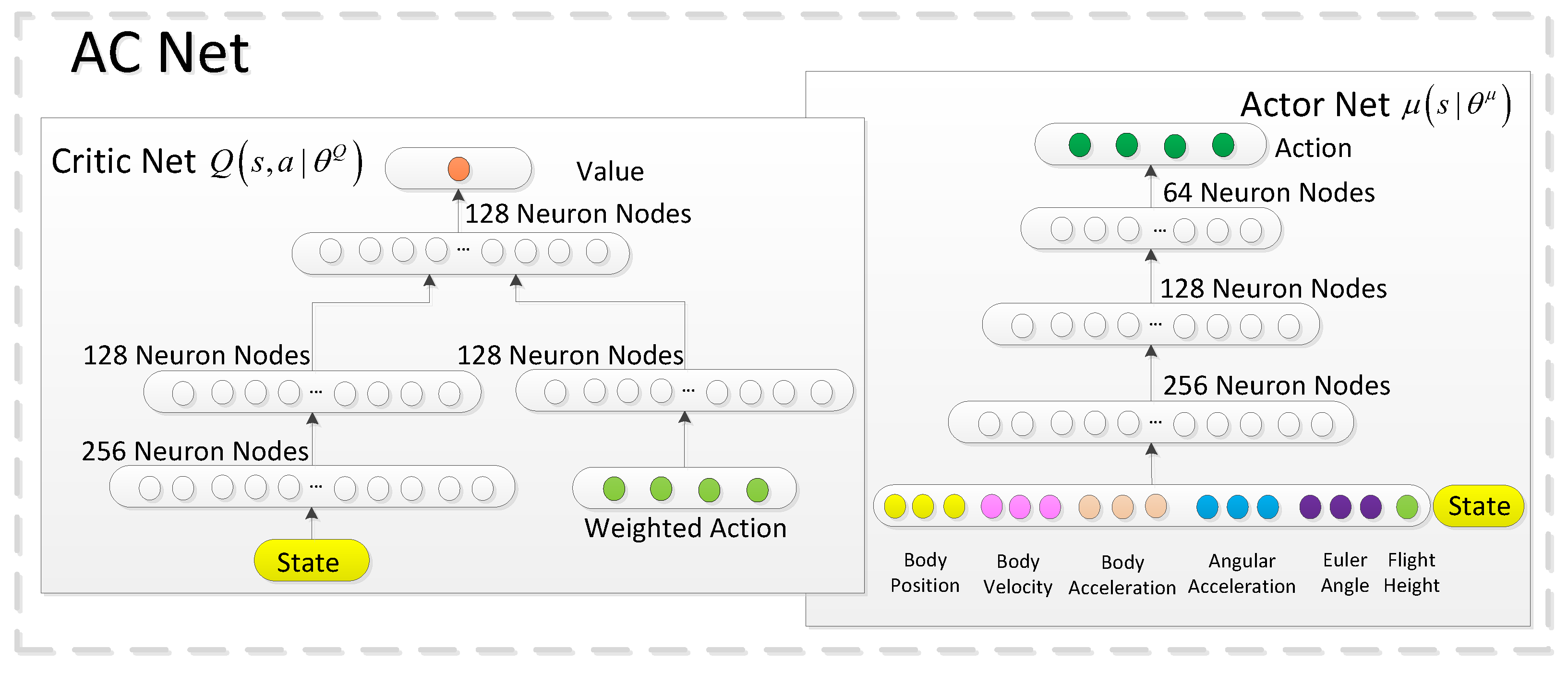
In the WAC, the actor and critic network structures are the same as the target actor and target critic network structures, respectively. The architecture of the actor-critic network (AC Net) is shown in Figure 4. Considering the need for the drone to extract features from observed states, we designed a total of three hidden layers for the critic. The hidden layers for the processing states and behaviors are first separated for operation, and the final hidden layer is fully connected together to output the value of state and behavior. The input received by the actor network is the number of features observed by the drone, and the specific value of each behavioral feature is the output. The actor network is designed with three hidden layers and fully connected layers. In order to achieve exploration, the algorithm uses the Ornstein–Uhlenbeck process as the noise model and adds a random noise to the generated behavior to achieve a certain range of exploration around the exact behavior. The neural network in the watcher is designed with three hidden layers and fully connected layers. The architecture is shown in Figure 5.

In the simulation, the reward rule set is that the closer the drone hovering height, $h$, is to the set hovering height (5 m), the greater the reward obtained. The target range is set to 0.5 m. If the hovering height is within 0.5 m of the target height, a reward value of 10 is obtained. If it exceeds the target range, a penalty value of −20 is obtained. If the height difference exceeds 20 m, a negative distance difference is chosen as the reward. The time step limit for one episode is $\mathrm{T}=1000$. If the time step exceeds the limit or the drone crashes ($h\le 0$), the current episode is stopped and reset to the next episode. The original intention was to adopt a dynamically supervised intervention behavior strategy, where the weights of watcher behavior and actor behavior gradually change with the training progress. Since our goal is to train high-quality actor networks, we place more emphasis on actor behavior in simulations. At the beginning of the initial training setting, both behaviors accounted for 50% each. Over time, the actor behavior gradually becomes dominant with increasing weights. At the same time, the watcher behavior weight gradually decreases and eventually tends to zero. The simulation time step is set to $t$ and the total number of simulation training steps to $\mathrm{\Gamma }$ with $\mathrm{\Gamma }=1 \times {10}^6$. The learning rate setting is as follows: $\chi =0.001$ and $\varsigma =0.002$, assuming ${\alpha }_0=0.5$ and ${\beta }_0=1-{\alpha }_0$. The weight in formula 12 is set as follows:

$$\left\{\begin{array}{l}\alpha ={\alpha }_0+{\beta }_0\cdot t/\mathrm{T}\\ \beta ={\beta }_0-{\beta }_0\cdot t/\mathrm{T}\end{array}\right.$$

(17)

Due to the fact that during the simulation process, the more time steps (iterations) spent on each episode (reaching the time step setting for hovering or crashing), the better the hovering effect, in episodes that reach the specified time step, the drone is always in the hovering state. If a crash occurs, it means that the next episode starts with less than 1000 steps per episode. Therefore, under the same total training steps, the more the crashes, the more the episodes, and the fewer time steps you take each time, the fewer the rewards you will receive. Figure 6 shows the reward values trained using the three algorithms with the horizontal axis representing the number of episodes. When the total time steps are the same, the fewer the episodes, the longer the duration of the hover state during each training process, and the more times the limited time steps are reached. 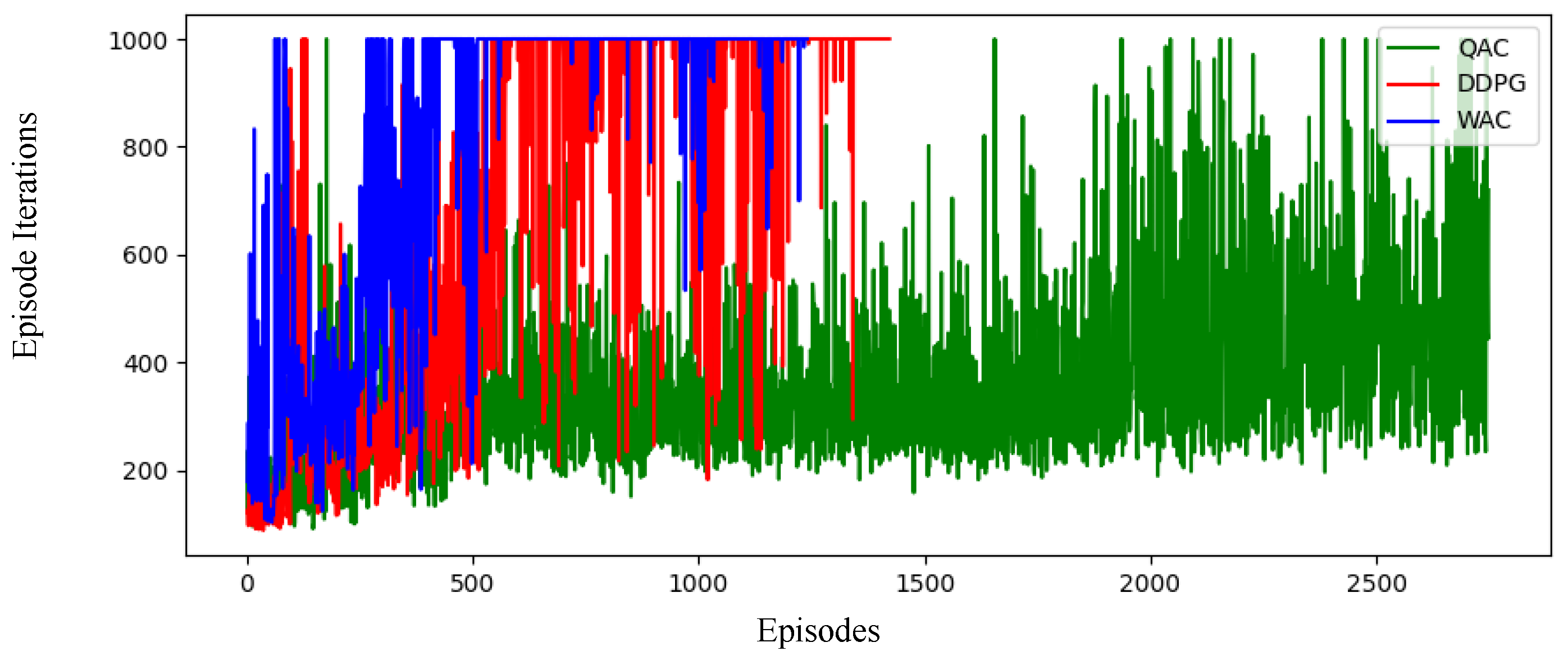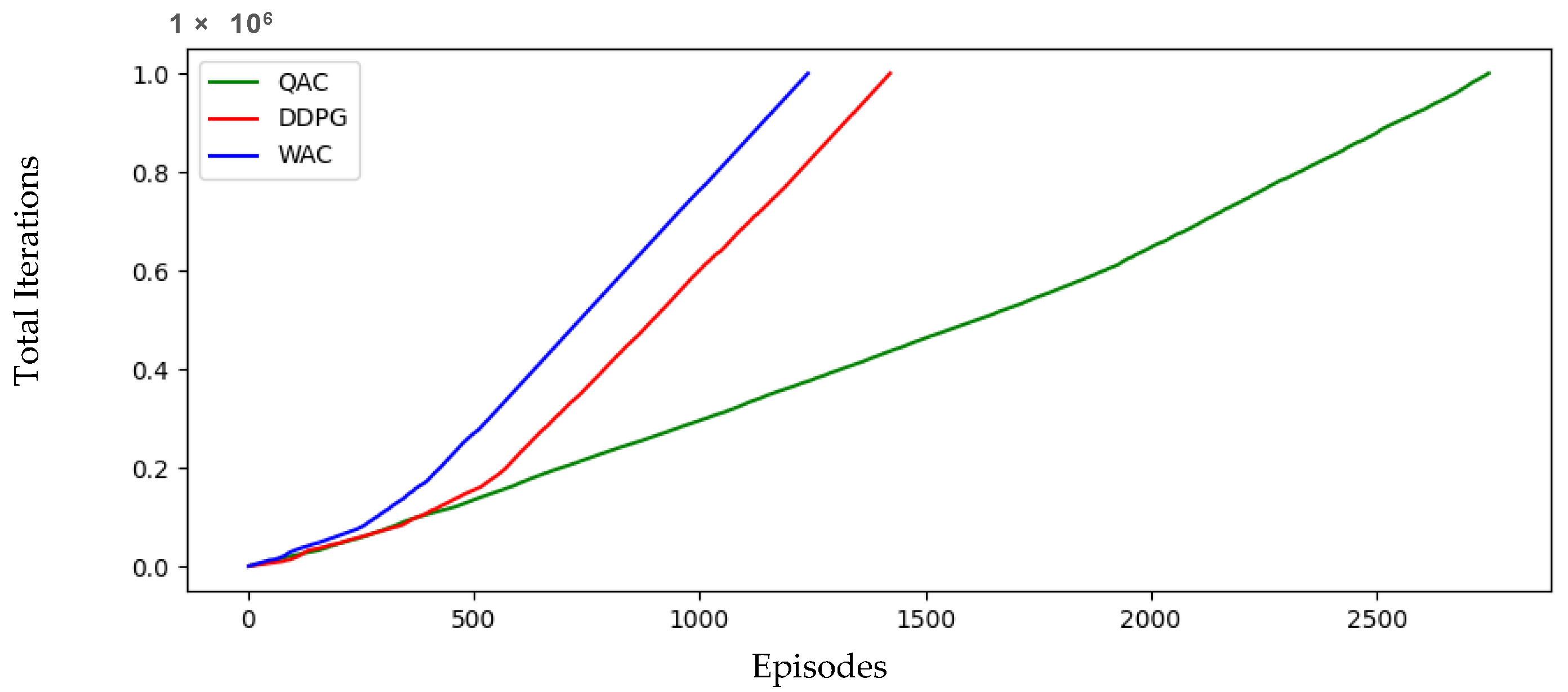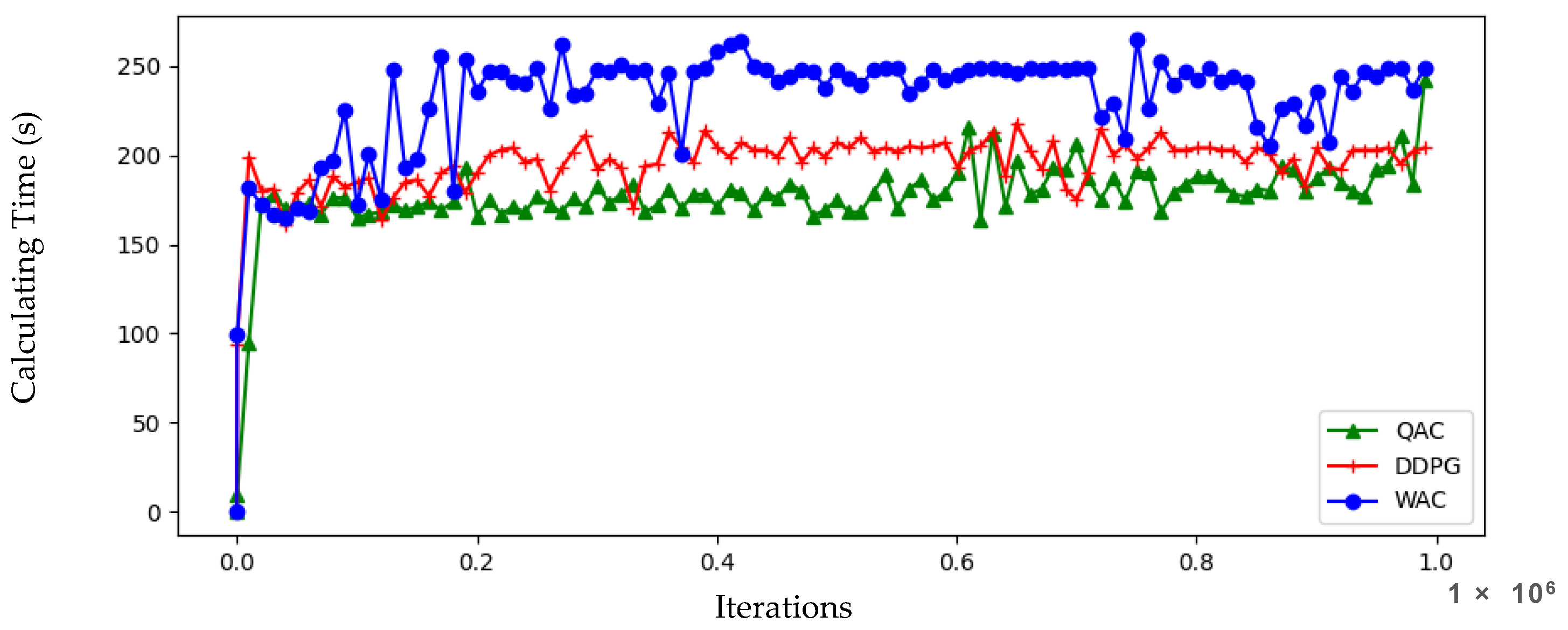Figure 7 shows the number of iterations taken per episode, while Figure 8 shows the total number of iterations. The training episodes of the WAC are reduced by 20% compared to the DDPG and 55% compared to the QAC. It is evident that the WAC algorithm has the lowest number of episodes, the highest reward value, and the most time steps in each episode, followed by the DDPG and QAC, which confirms the above statement. This indicates that our algorithm has significantly fewer crashes during training compared to the other two, and the chance of crashes during the learning process directly reduces training efficiency and effectiveness, indirectly indicating that the WAC has the highest training efficiency and effectiveness.

After simulation training, the network models of the three algorithms are separately loaded and flight data collected from the drone hovering state for 1000 iterations for analysis. Related simulation videos can be found in the Supplementary Materials section at the end of the article.

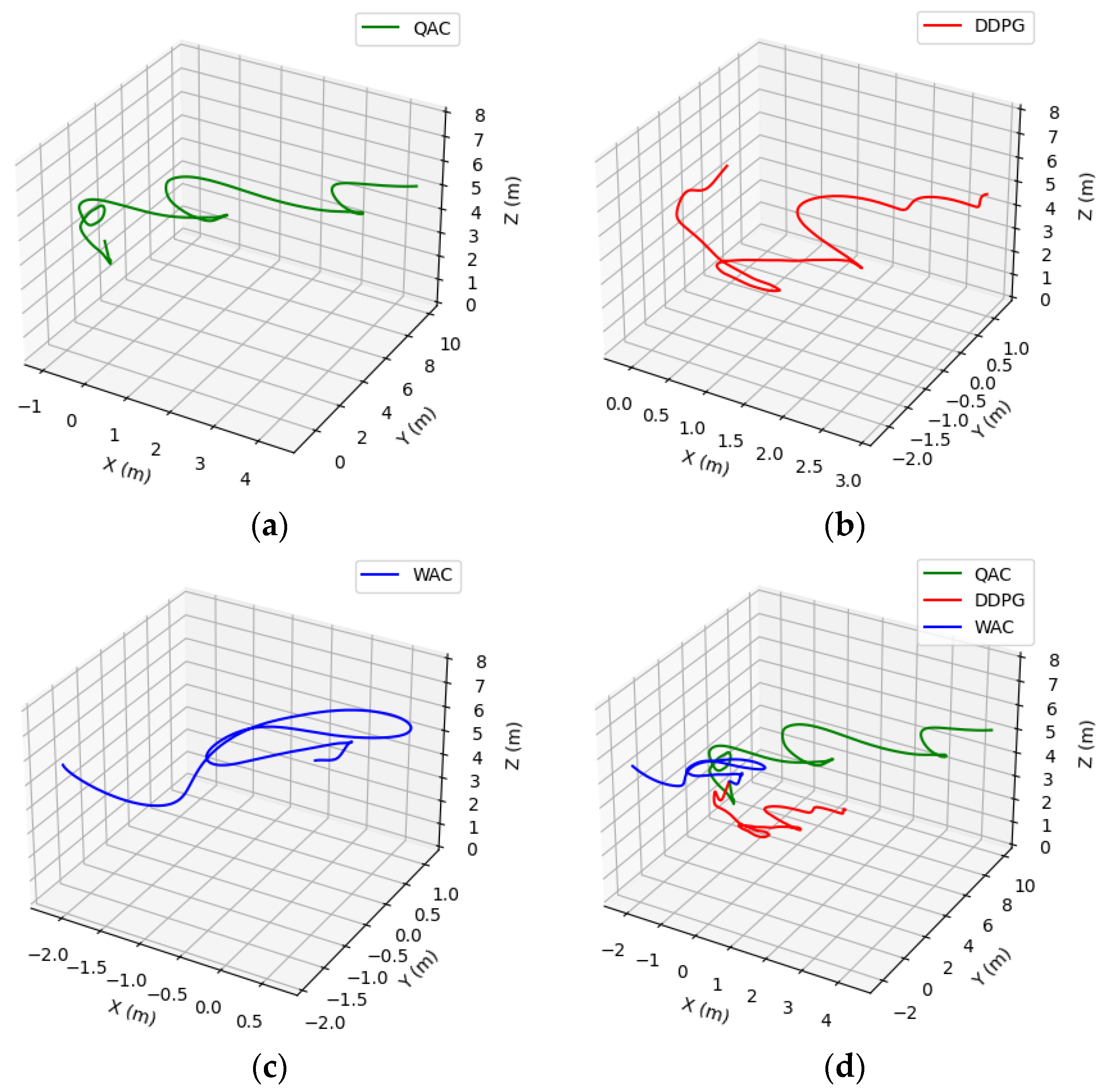
Figure 9a–c show the hovering trajectories of the drone after loading the three network models, respectively. It can be seen that none of the three algorithms have experienced a crash, while the hovering trajectory using the QAC algorithm has significant drift. From the trajectory integrated display in Figure 9d, it can also be seen that the drone under the WAC algorithm framework has the smallest hovering range, the best effect, and the lowest degree of drift. The following is a detailed introduction to the simulation results.

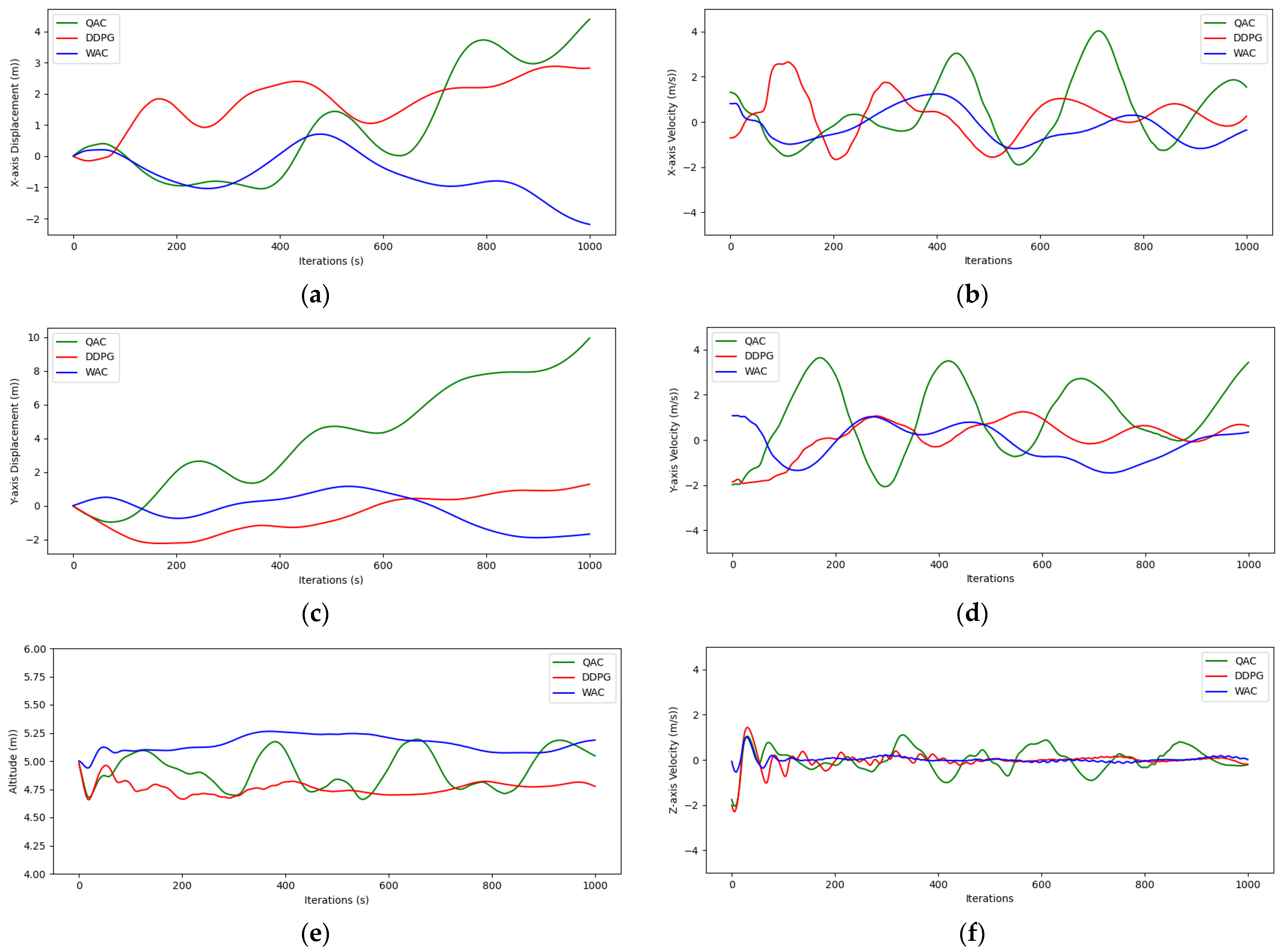
Figure 10a,c,e depict the displacement of the three algorithms on various coordinate axes. From the graph, it can be analyzed that the QAC has an increasing displacement deviation in the X and Y directions (the X-axis direction exceeds 4 m, and the Y-axis direction exceeds 10 m), while the other two algorithms are significantly more stable and hover near the specified point. 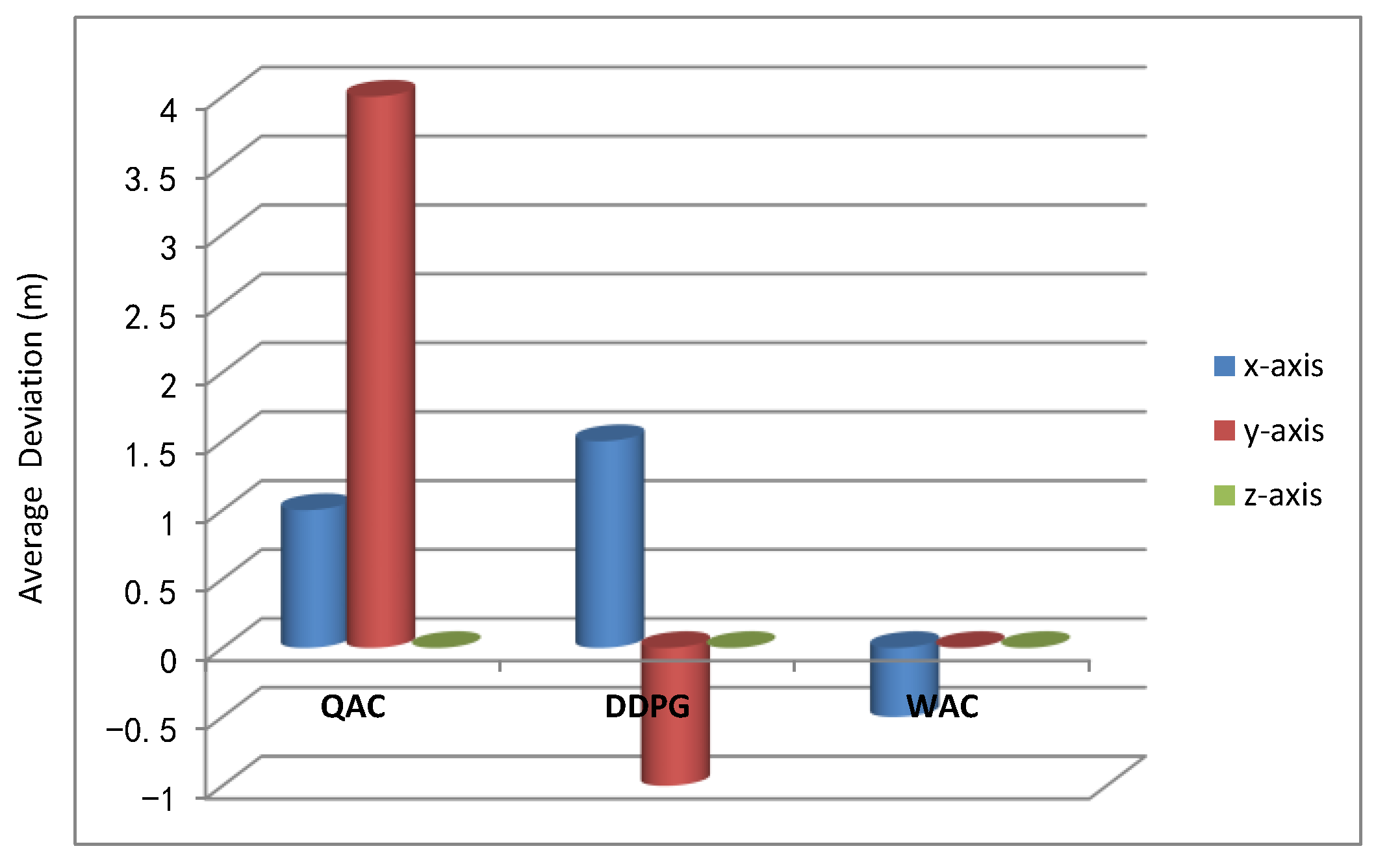The hovering altitude in Figure 10e indicate that the DDPG and WAC have better stability than the QAC in hovering altitude, and compared to the DDPG, the average hovering altitude of the WAC is closer to the target altitude. In order to more clearly demonstrate these deviations, we plotted a bar chart comparing the average deviations of each axis under the three algorithms in Figure 11. It is not difficult to see from the figure that the WAC exhibits good hovering characteristics followed by the DDPG, while the QAC is the most unstable. During drone hovering, the comparison of velocities in various axis directions under different algorithm frameworks in the geodetic coordinate system (Cartesian coordinate system) is shown in Figure 10b,d,f. From the figure, it can be concluded that the WAC and DDPG are equally stable in hovering flight speed and significantly superior to the QAC. And regarding the height aspect that we are most concerned about, the speed of the three algorithms is better than the other two coordinate axes, and the Z-axis speed of the WAC is basically stable at zero.

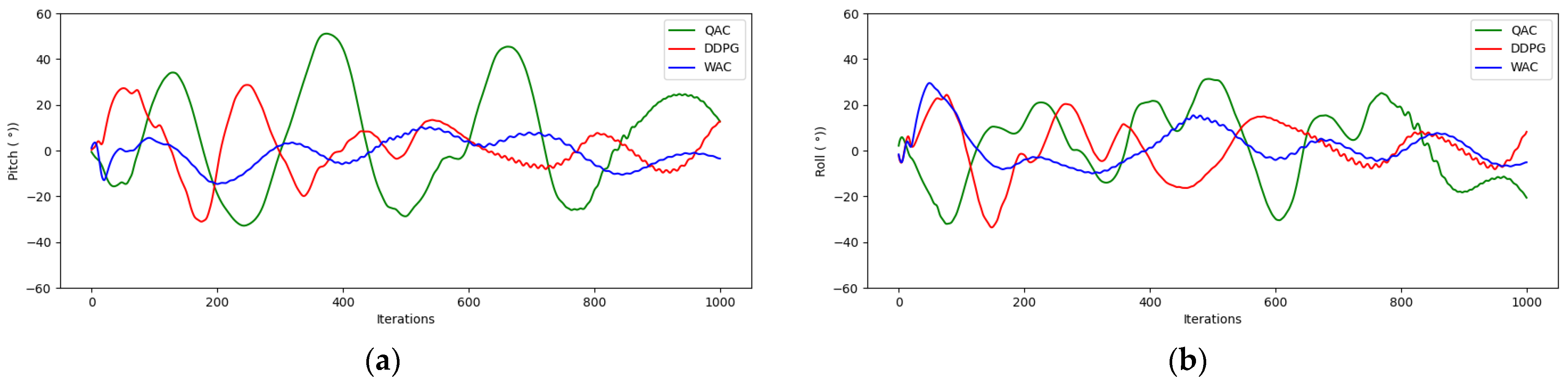
Since our research focuses on the hovering effect of drones, and the variation of drone yaw angle has little effect on hovering stability, we assume it to be always zero. Figure 12a,b show a comparison of pitch angle and roll angle changes during hovering using the three algorithms. The changes in pitch angle and roll angle represent the stationarity of the drone hovering flight. It can be seen that the amplitude of the WAC change is the smallest, and it is superior in the stationarity of hovering flight. The above simulation results all indicate that the WAC algorithm applied to drone hover control is more stable, and the hovering effect has been greatly improved compared to the DDPG and QAC. Next, we studied the training time cost of the three algorithms.

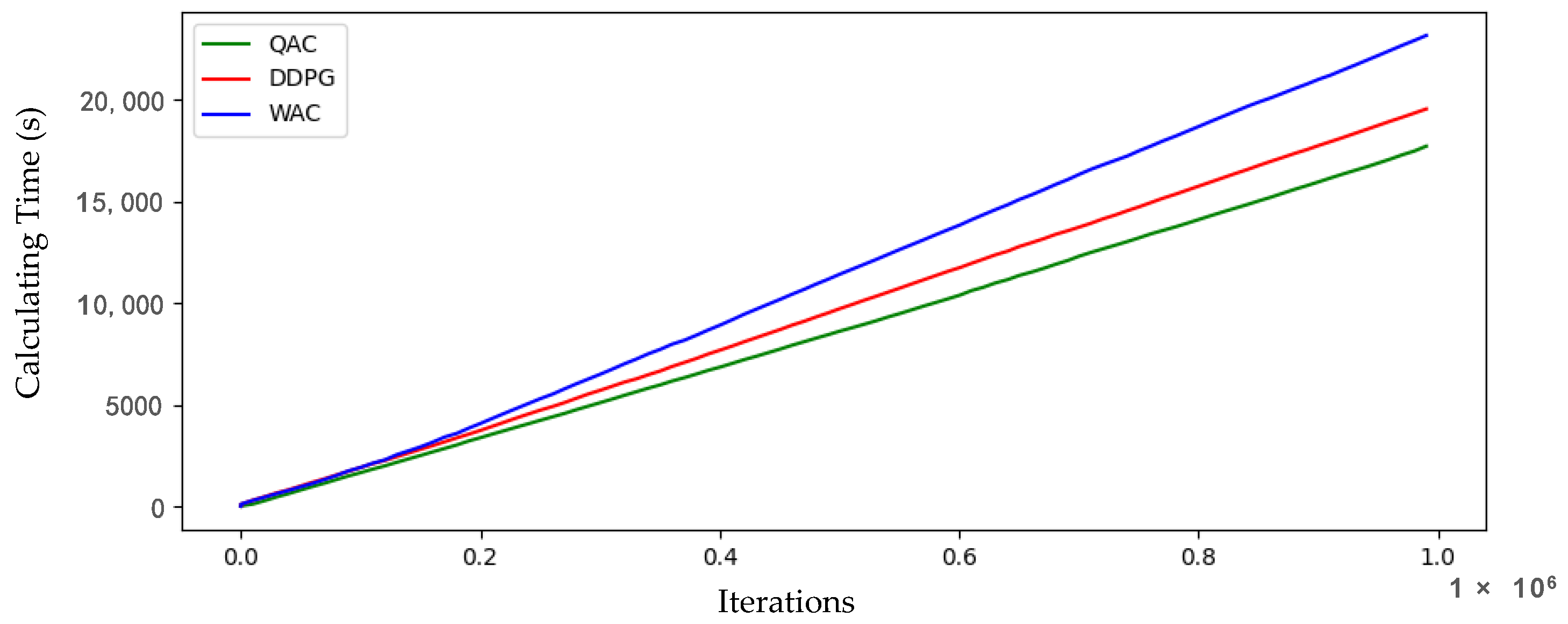
Figure 13 shows the cumulative training time curves of the various algorithms implemented by the computer. The WAC algorithm has a slightly longer training time than the other two algorithms due to the addition of the target network and supervised network. Compared to the QAC, DDPG also increases computational costs due to the addition of two backup networks. In order to quantitatively analyze the computational time cost of each algorithm, in the comparison of the computational cost per 10,000 iterations in Figure 14, the training time cost of the three algorithms is basically in an arithmetic sequence, and the elongation of this computational cost is within an acceptable range. From the simulation results in the previous text, it can be seen that the learning efficiency and hovering effect of using the WAC algorithm are significantly better than the other algorithms. However, our algorithm did not excessively increase the time cost due to the increase in supervised networks, and it is worth investing a small amount of computational cost to obtain larger learning results. With the increase of training frequency in the later stage and relying on high-quality models in the early stage, the training effects of the three algorithms will become better and better, but the WAC is undoubtedly the first model that meets the requirements. The three training models are loaded separately and the optimization time for each step is analyzed, as shown in Figure 15. The single step optimization time of the three algorithms shown in the figure remains below 1 millisecond with no significant difference, indicating that the proposed algorithm did not lag behind in optimization time.

We will deploy the WAC algorithm on a real drone in Section 4 and demonstrate its practical performance.

4. Algorithm Deployment

In order to verify the effect of our algorithm, we deployed the WAC algorithm on a self-developed quadcopter. The computing platform on the drone uses NVIDIA Jetson Xavier NX, and the flight control firmware is Pixhawk4, which uses Ethernet communication. Due to the tendency of IMU integration to cause deviation in the attitude, which affects the experimental results, and in order to more accurately describe the position and attitude of the drone, we added a visual system in the experiment. IMU can provide visual positioning during rapid motion, and visual positioning information can be used to correct IMU drift. The two are actually complementary. We adopted a lightweight and drift-free fusion strategy for drone autonomy and safe navigation [37]. The drone is equipped with a front facing camera, which can create visual geometric constraints and generate 3D environmental maps. The GNSS receiver is used to continuously provide pseudorange, Doppler frequency shift, and UTC time pulse signals to the drone navigation system. The Kanade–Lucas algorithm is used to track multiple visual features in each input image. Then, the position and attitude of the drone itself is monitored through multiple sensors installed on the body. The specific algorithm deployment process is shown in Figure 16. Our deployment environment is a laboratory of length × width × height of 10 m × 10 m × 4 m. With the help of SLAM mapping already completed by the drone, drone hovering experiments are carried out in this environment. The desired state is obtained as the state input of the WAC strategy through the combination of inertial module, visual module, and GNSS module, forming a cyclic iteration of state-decision-action, and hover flight verification is completed. The detailed configuration of the deployed drone is shown in

Table 1. Deployed drone configuration.

Module	Sensor	Type
Visual	Depth Camera	Intel D435i
Inertia	IMU	MPU-9250
GNSS	Antenna Receiver	BenTian-3070 u-blox ZED-F9P

. Related experimental videos can be found in the Supplementary Materials section at the end of the article.

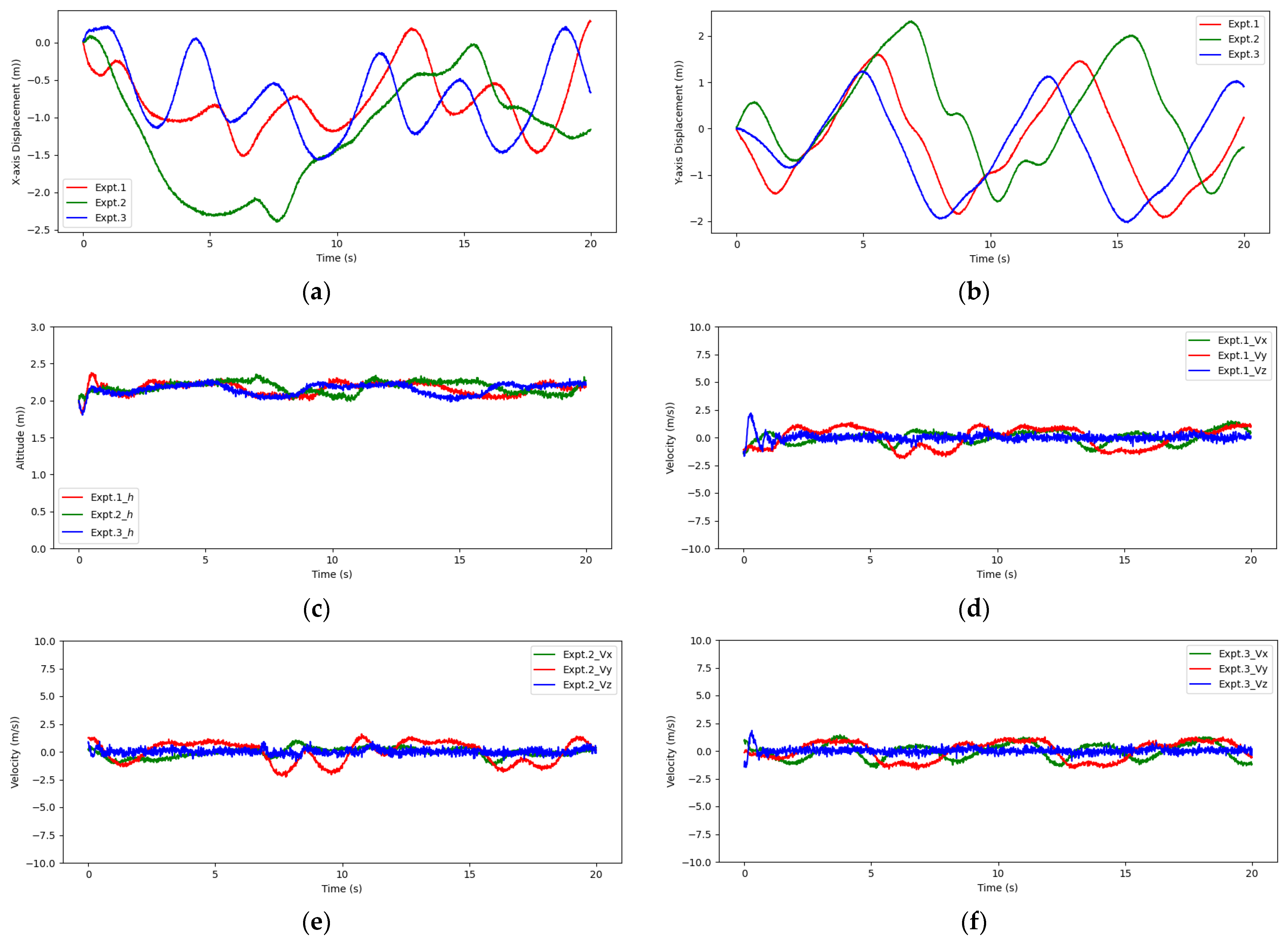
To verify the stability of the proposed algorithm, we loaded the trained network model into the quadcopter system and conducted three hovering experiments. Due to the height limitation of the experimental environment, the hovering altitude was set to 2 m, and the first 20 s of hovering flight data were selected for analysis. Figure 17a–c show the three hovering flight trajectories, while Figure 17d depicts the hovering trajectory in the same space for macroscopic observation. It can be seen that the three hovering flights of the drone revolve around the hovering target point, and the operation is good without any crashes. The hovering altitude curves of the three experiments (Figure 18c) also indicate that the hovering flight is very stable with a hovering altitude maintained around 2 m and a small fluctuation amplitude, which is basically consistent with the simulation experiment results.

Figure 18d–f illustrate the velocity changes along the three coordinated axes of three sets of experiments in the world coordinated system. The variation patterns of the three sets of flight data are fundamentally consistent with significant velocity changes on the X and Y axes, but they soon adjust to a slightly stable state. The Z-axis velocity that we are concerned about remained largely unchanged, which also provides stability to the drone’s hovering and achieves our expected hovering effect. Figure 19a,b show the performance of the pitch angles and roll angles of the drone in three sets of experiments, respectively. The translation range of the two Euler angles (±20°) is within our tolerance range. From the above curve, it can be seen that our algorithm has been deployed to real drones and performs well in all aspects, which is fundamentally consistent with the simulation results.

5. Conclusions

In this article, a new reinforcement learning algorithm (watcher-actor-critic, WAC) is applied to the hover control of drones. After using the actor-critic algorithm-based behavior value (QAC) and deep deterministic policy gradient algorithm (DDPG) for drone hover control learning, we proposed a deep deterministic supervised policy gradient algorithm that can quickly lock the exploration direction. Using a PID controller with parameters provided by a neural network as a dynamic monitor, the supervision intensity could be changed as the policy learning progress changes, ensuring that the exploration function of the policy network could be maximally maintained. Finally, a simulation was conducted using a classic reinforcement learning environment library, Python, and a current mainstream reinforcement learning framework, PARL. The training results show that the training episodes of the WAC are reduced by 20% compared to the DDPG and 55% compared to the QAC, after which the algorithm was deployed to a practical environment. A multi-sensor fusion strategy-based autonomous localization method for unmanned aerial vehicles was used for practical exercises. The simulation and experimental results show that the reinforcement learning algorithm designed in this paper has a higher learning efficiency, faster convergence speed, and smoother hovering effect compared to the QAC and DDPG without consuming too much computational cost and optimization time.

While proposing a better algorithm in this article, there are inevitably some aspects that need improvement or can make the proposed algorithm better, such as the following: (1) the significant drift phenomenon during hovering needs improvement; (2) the fluctuation of the Euler angle indicates that the drone flight was not smooth enough and needs to be strengthened; (3) the PID controller in the watcher can be replaced by other superior traditional controllers to achieve better hovering performance. We will focus on addressing these areas in future research.