Abstract
In contrast from traditional unmanned aerial vehicle communication via unlicensed spectrum, connecting unmanned aerial vehicles with cellular networks can extend their communication coverage and improve the quality of their service. In addition, the emerging dual-functional radar communication paradigm in cellular systems can better meet the requirements of location-sensitive tasks such as reconnaissance and cargo delivery. Based on the above considerations, in this paper, we study the simultaneous communication and target sensing issue in cellular-connected unmanned aerial vehicle systems. Specifically, we consider a two-cell coordinated system with two base stations, cellular unmanned aerial vehicles, and potential aerial targets. In such systems, the communication security issue of cellular unmanned aerial vehicles regarding eavesdropping on their target is inevitable since the main beam of the transmit waveform needs to point to the direction of the target for achieving a sufficient detection performance. Aiming at protecting the privacy of cellular transmission as well as performing target sensing, we exploit the physical layer security technique with the aid of constructive interference-based precoding. A transmit power minimization problem is formulated with constraints on secure and reliable cellular transmission and a sufficient radar signal-to-interference-plus-noise ratio. By specially designing the transmit beamforming vectors at the base stations, the received signals at the cellular users are located in the decision regions of the transmitted symbols while the targets can only receive wrong symbols. We also compare the performance of the proposed scheme with that of the traditional one without constructive interference. The simulation results show that the proposed constructive interference-based strategy can meet the requirements of simultaneous target sensing and secure communication, and also save transmit power compared with the traditional scheme.
1. Introduction
In recent years, unmanned aerial vehicles (UAVs) have shown great potential in military, civilian, and commercial applications due to their mobility and flexible deployment capabilities. Some typical instances include reconnaissance, panoramic shooting, cargo delivery, traffic control, image transmission, and the inspection of farmland. With such a wide range of application scenarios, the traditional UAV communication technique depending on unlicensed spectrum can no longer provide a satisfactory performance in tasks such as beyond line-of-sight or high-capacity communications. To fully explore the capabilities of UAVs, the 3rd Generation Partnership Project has released a study [1] that analyzes the possibility of UAVs serving as aerial user equipment in cellular networks, which are known as cellular-connected UAVs [2,3,4,5,6]. As discussed in [2,3,4,5,6], integrating UAVs in cellular networks will expand the communication coverage area and thus make it much easier to control UAVs. Additionally, the cellular communication protocol with licensed spectrum is specially designed, and can provide a stable and high-quality wireless communication service. For achieving these expectations, the interference caused by neighboring non-associated base stations (BSs) needs to be carefully managed through beamforming, power allocation, trajectory optimization, and access control.
Apart from its use in communication services, the cellular network has been recently explored to provide radar service, which is called a dual-functional radar communication (DFRC) system. In a DFRC cellular system, both the cellular spectrum and hardware platform of BSs are shared to detect, target, and transmit messages simultaneously. Due to the newly introduced target sensing capability, UAVs connected to cellular networks can better meet the requirements of location-sensitive tasks such as cargo delivery and emergency rescue. There have been considerable studies on signal waveform and transmission protocol design to achieve a trade-off between radar and communication performances. Among these techniques, multiple-input multiple-output (MIMO) stands out and has been shown to be promising for implementing DFRC functions. By designing the beamforming vector or precoding the matrix at the BS, a desired beam pattern for radar can be achieved, while satisfying the quality of service (QoS) requirement for each communication user. Based on this concept, the authors in [7,8,9] investigated the joint design of transmit waveform and receive filter for achieving DFRC. The difference is that the work in [7] optimized the waveform to approximate a given radar beam pattern while the work in [8] focused on the received signal-to-interference-plus-noise ratio (SINR). Compared with [7,8], the work in [9] also considered the per-antenna power constraint and peak-to-average-power ratio (PAPR) constraint. In practice, the target direction and channel state information (CSI) may be imperfect, which leads to performance losses for radar and communication functions. Thus, robust DFRC waveforms were studied in [10,11] with both imperfect CSI and hardware impairment taken into consideration. In contrast to the above works, where transmit and receive antennas are mounted at the same BS, the authors in [12] focused on bistatic DFRC MIMO systems.
Although introducing DFRC in cellular-connected UAV systems can help extend the monitoring range of UAVs, there are some security risks relating to privacy [13,14,15]. To achieve a given detection performance for radar, the main beam of the transmit waveform needs to point to the direction of the target or the direction to be detected. Since communication and radar share the same transmit signal, the information-bearing symbols used for cellular communications are inevitably leaked to unintended receivers, which threatens the privacy of cellular users. For solving this privacy issue, the physical layer security (PLS) [16,17,18,19,20] technique has been exploited, and especially the PLS approach with security-aware beamforming or precoding. To be more specific, by adjusting the weighting coefficient of each transmit antenna, the SINR of the information-bearing symbols is maximized at the intended receiver while being minimized in unintended directions. Multi-user interference and artificial noise (AN) are two common resources beneficial for decreasing the SINR at unintended receivers [21,22,23], where AN is also utilized as a baseline scheme in this paper. In [21], the authors exploited the multi-user interference as friendly jamming signals to degrade the signal quality for eavesdroppers. Similarly, the work in [22] proposed a multi-destination node as well as a friendly interference selection strategy, while the work in [23] introduced an energy harvesting signal as friendly interference. Artificial noise is often combined with multi-user interference to further improve the transmission security [24,25,26,27]. Inspired by the concept of PLS, there have been a series of studies focusing on secure DFRC in cellular-connected UAV systems [28,29,30].
Compared with AN, which needs additional transmit power, multi-user interference is more energy-saving since it is inherent in communication systems. With the appropriate utilization of multi-user interference, both security and the energy efficiency can be improved. Constructive interference [31,32] is a technique that exploits multi-user interference as a beneficial resource for saving transmit power. Through symbol-level precoding with knowledge of both data and CSI, the transmit power can be significantly reduced compared with the traditional interference suppression method. Specifically, the authors in [33] designed a precoding algorithm which transformed the interference from the stronger user into constructive resources for the weaker user. The benefit of constructive interference (CI) is also demonstrated in [34]. The authors in [35,36] studied CI in DFRC systems where both the communications and target detection performances were optimized. The work in [37] implemented CI with the aid of deep learning. Due to the energy-saving capability of CI, there has been research using CI for addressing the physical-layer secure transmission issue [38,39,40]. The work in [38] studied secure symbol-level precoding by utilizing multi-user interference as an anti-eavesdropping resource. A smarter eavesdropper with an optimal maximum likelihood detector was also studied in [39]. Furthermore, the secrecy performance with the CI-based method was analyzed in [40]. One can see that the CI technique has shown great potential in different kinds of communication systems.
Based on the above considerations, in this paper, we focus on the physical-layer secure transmission problem in DFRC UAV communications by means of constructive interference. In contrast to previous research [41,42], we consider a cellular-connected UAV system with two coordinated DFRC BSs. Each BS transmits message data to several cellular UAVs while at the same time using echo signals to detect targets. The targets are regarded as potential eavesdroppers. By designing the precoding vector at each BS, the high-quality reception of data at the intended UAVs, a sufficient output SINR of the radar echo waveform, and anti-eavesdropping against the targets can be achieved simultaneously. The major contributions of this paper are listed below.
(1) The secure UAV communication problem in a two-cell DFRC system is studied. For this system, the secure transmission from each BS to UAVs and target detection are simultaneously considered. Both the precoding strategies with and without CI technique are investigated.
(2) For the precoding with CI, the precoding vectors at the two BSs are obtained by solving a transmit power minimization problem with three sets of constraints. The first ones limit the phase of the received signals at the intended UAVs, which ensures that the intended UAVs can correctly detect the transmitted symbols. The second ones guarantee the minimum output SINR of the echo waveform for target detection. The remaining set of constraints push the received signals at the targets towards the destructive region for degrading the symbol detection performance at the targets.
(3) For the precoding without CI, AN is introduced to increase the output SINR of the radar echo waveform as well as cause interference to symbol detection at the targets. A transmit power minimization problem is formulated with constraints on the SINRs for symbol detection at the intended UAVs and targets, and also on the output SINR for radar echo waveform.
(4) Both the precoding schemes with and without CI are derived through an alternative optimization (AO) method. The numerical results demonstrate that the CI technique can significantly save transmit power while satisfying both the secure transmission and target detection requirements.
The remaining parts of this paper are organized as below. Section 2 describes the two-cell cellular-connected UAV system including a communication model, radar model, and problem formulation. The precoding algorithm with CI is provided in Section 3. The traditional precoding algorithm without CI is provided in Section 4. Section 5 presents the simulation results for comparing the performances of the above precoding algorithms. Finally, the paper is concluded in Section 6. The definitions of the acronyms are given in Table 1.

Table 1.
Definitions of acronyms.
Notations: In this paper, we use upper-case and lower-case bold letters to represent matrices and vectors, respectively. represents the set of complex matrices. For the vector , , , and denote the transpose, Hermitian transpose, and norm of the vector, respectively. For a scalar z, and denote the real and imaginary parts of z, respectively. Finally, represents the complex circular Gaussian distribution with the mean zero and covariance distribution.
2. System Model
In this section, we first describe the considered system including two coordinated BSs and the connected UAVs. Then, we clarify the two major models of a DFRC system, i.e., communication model and radar model. Finally, an optimization problem is formulated to minimize the transmit power of the BSs while meeting the communication and radar performance requirements.
2.1. System Description
As illustrated in Figure 1, we consider cellular-connected UAV communications in a coordinated two-cell DFRC system. There is a central unit connecting the two coordinated BSs to perform the joint design of transmit and receive beamforming with global CSI [43]. Each BS is assumed to be equipped with N transmit and receive antennas. Both the transmit and receive antenna arrays are uniform linear arrays with the element spacing being a half-wavelength. For the ith () BS, there are K UAVs acting as cellular users (CUs). The kth () UAV connected to the ith BS is denoted as . In addition to cellular communications, the ith BS also performs target detection with a single radar beam. The target of each BS is regarded as a potential eavesdropper which might wiretap the confidential messages sent from the BS to the CUs. The target of the ith BS is called target i. All the CUs and targets are assumed to be equipped with a single antenna.
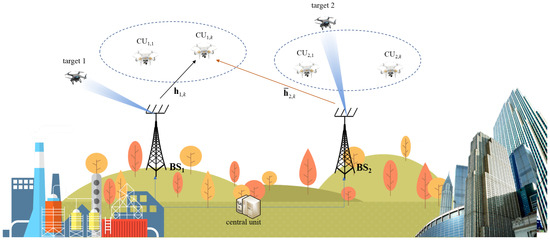
Figure 1.
System model: a two-cell DFRC system where UAVs are cellular users and targets are potential eavesdroppers.
For both radar and communication functions, the transmitted signal vector from the BS is the same. We use to represent the transmitted signal vector from the ith BS. The channels from the ith BS to and target i are denoted as and , respectively. Meanwhile, the signal transmitted from the other BS is actually the interference. We use () and to denote the channels from the th BS to and target i, respectively. Based on the above system description, the communication and radar signal models are discussed below.
2.2. Communication Model
Given the transmitted signal , the received signal at can be modeled as
In (1), the first term is the desired signal; the second term is the interference from the neighboring cell, with being the transmitted signal vector from the neighboring BS; the last term is the additive white Gaussian noise. The wireless channels are specified as and , where and are the path-loss coefficients, and and are the steering vectors for the transmit antenna array with respect to and , respectively.
Similarly, the received signal at target i is given by
where the first and the second terms are the desired signal from BS i and the interference from BS , respectively; and are the wireless channels with complex path-loss coefficients , , and steering vectors and with and being the angles with respect to the transmit antenna array; is the additive white Gaussian noise. Note that the signals in (2) actually reflect the wiretap capabilities, since target i is regarded as the potential eavesdropper of the ith cell.
Based on the received signals in (1) and (2), the UAVs and the targets try to recover the transmitted data from the corresponding BS. Since the CI-based precoding and the traditional precoding work differently, the detailed discussions on the communication signal models are given in Section 3 and Section 4.
2.3. Radar Model
For the ith BS, target detection is achieved by using the echo of the transmitted signal . Considering that there might be some environmental sources which can also reflect signals, the received signal at the ith BS can be expressed as
where the first term is the desired echo signal from target i; the second term is the signal-dependent unexpected echo from interfering sources; the third term is the interfering signal from neighboring BS; the last term is the additive white Gaussian noise. In (3), and are the steering vectors with respect to and , respectively; and denote the complex coefficients including both path-loss and reflection parameters for target i and the pth interfering source, respectively. is the interference channel from the th BS to the ith BS, where is the path-loss coefficient, and are the steering vectors with respect to and , respectively.
With the echo signal in (3), the ith BS uses a receive beamforming vector to enhance the SINR of target detection for the intended direction. The output of the filter can be expressed as
2.4. Optimization Problem Formulation
In this paper, we consider a transmit power minimization problem under constraints on both the communication and radar performances. To be more specific, the following three requirements need to be guaranteed: (1) individual reliable reception at each CU; (2) secure transmission against targets; and (3) a sufficient output SINR for the radar beam. Note that the first requirement depends on while the second requirement is related to . Since the detailed expressions for reliable and secure communications have not been given here, we introduce the functions and to represent these two expressions, respectively. Furthermore, the reliable and secure requirements are modeled as and , respectively, where and are the feasible sets satisfying the reliable and secure requirements.
With the above descriptions, the transmit power minimization problem in the two-cell DFRC system can be formulated as
where represents the minimum required SINR for target detection. One can see that the optimization in (6) involves a joint design of the transmit vector and the receive filter at each BS. Detailed optimization algorithms are given in the following sections.
3. Proposed CI-Based Secure Precoding
In this section, we first clarify the concept of CI and reformulate the optimization problem in (6). Then, the specific problem-solving algorithm is provided.
3.1. Problem Reformulation Based on CI
As discussed in [31], CI can transform the harmful multi-user interference into useful resources for pushing the received signal far away from the decision boundaries of quadrature amplitude modulation (QAM) or phase-shift keying (PSK) modulation. With enough spacing from the decision boundaries, the symbol detection is robust to noise and interference disturbance. This paper focuses on PSK modulation. For further clarifying the idea of CI, an illustration is given in Figure 2.
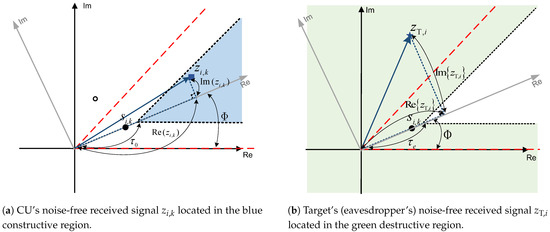
Figure 2.
The concept of CI-based secure precoding for 8PSK modulation, where is the symbol of interest and the two dashed red lines represent the decision boundaries of .
We take the reliable and secure transmission for as an example. The transmission for other users is similar. The data symbol intended to transmit to is denoted as , which is one point of the 8PSK constellation. As shown in Figure 2a, the blue sector with angle and infinite radius is the so-called constructive region [31]. When the noise-free received signal falls into this region, there is enough distance between the signal and the decision boundaries, which implies that the received signal is capable of resisting additive noise or interference. Based on (1), the noise-free received signal for can be given by
Note that, as illustrated in Figure 2a, how far the constructive region is from the decision boundary is determined by , which is actually the square root of the minimum required SINR. With the increase in , the constructive region is further from the decision boundaries, and thus the received signal is more robust to noise and interference disturbance.
The complementary set of the constructive region is defined as the destructive region, as shown by the green area in Figure 2b. The destructive region includes two parts: one is inside the decision region but very close to the decision boundaries; the other is outside the decision region. If the noise-free received signal falls into the destructive region, the symbol error rate (SER) will be quite high. Therefore, to prevent the target from wiretapping the messages for CUs, the noise-free received signal of target i (), which is given by
should be located in the destructive region, where has been given in (2). Moreover, as illustrated in Figure 2b, the SER decreases with the increase in , since the intersection of the destructive region and the decision region increases. Thus, the value of should be small enough to achieve secure transmission against target i. Note that actually represents the square root of the maximum allowed SINR for the targets (eavesdroppers).
Now we give the mathematical expressions for the above concerns. The constructive regions for different points of the PSK constellation have different expressions in the complex plane. To unify the expressions, we consider rotating the original coordinate system by the phase of . The new coordinate system is shown in gray in Figure 2. In the rotated new coordinate system, the requirement that is located in the constructive region can be mathematically expressed as
where and are the real and the imaginary parts of , respectively, which are given by
and
where and .
As for the destructive region of , it can be expressed as
where the real and the imaginary parts of can be derived as
and
respectively, where and . Without the loss of generality, in this paper, we focus on secure transmission for in each cell. Thus, when considering the secure transmission issue for the ith cell, the equivalent channels in the rotated coordinate system can be further clarified as and . However, the constraint in (12) is not convex. From Figure 2b, one can see that the destructive region can also be expressed as the union of the following three constraints:
Based on the above discussion, the optimization problem in (6) when using CI can be reformulated as
where constraint (16c) corresponds to the reliable communication requirement and constraint (16d) is related to the secure transmission requirement. It is worth noting that constraint (16d) actually includes three constraints, which implies that problem (16) is composed of three subproblems.
3.2. Problem-Solving Algorithm
From (5), one can see that constraint (16b) couples the optimization variables and , which requires the AO [41,43] method to optimize and alternately. Specifically, we optimize with a given and update ; then, we optimize with the updated . This iteration process continues until convergence.
(1) Solving with a given : For a given , the optimization problem (16) can be transformed into a feasibility problem by finding a satisfying constraint (16b). We reformulate (5) as
which is in the form of a Rayleigh quotient. For trying to satisfy constraint (16b), the value of should be maximized, which is achieved when
where denotes the largest generalized eigenvalue corresponding to the matrix pair . With , if constraint (16b) still cannot be satisfied, the iteration process terminates.
(2) Solving with given : with a known , the optimization problem (16) can be simplified as
However, the above optimization problem is still not convex due to constraints (19b) and (19d). For addressing this issue, we linearize the function by using the first-order Taylor expansion at the current point . The Taylor expansion function is denoted as , which can be derived as
With , the original optimization problem (19) is approximated as
Now, problem (21) can be regarded as three separate subproblems with (15a), (15b), or (15c) being the constraint on transmission security. Each subproblem is convex and thus can be efficiently solved using CVX [44]. From the three obtained solutions, the one with the minimum transmit power is selected as the final .
The above iteration process is summarized in Algorithm 1. As for the initial point , we adopt the iterative feasibility search algorithm (IFSA) [45] to find a feasible result. The main goal of the IFSA is the introduction of a positive slack variable s to enlarge the original feasible region. With the slack variable s, the constraints (15a), (15b), and (15c) are modified as
| Algorithm 1 The AO method for solving problem (16). |
|
By minimizing the slack variable, a feasible initial point of the original problem can be finally obtained. The detailed process of the IFSA method is summarized in Algorithm 2, where the newly introduced optimization problem for the IFSA is given by problem (23), shown below.
Note that the final result of Algorithm 2 is set as the initial point for Algorithm 1.
| Algorithm 2 IFSA method for finding an initial point of problem (16). |
|
4. Traditional Secure Precoding
In this section, we present the traditional secure precoding scheme as a baseline. We first provide an AN-aided secure transmission strategy and reformulate the optimization problem in (6). Then, the detailed problem-solving algorithm is discussed.
4.1. Problem Reformulation for Traditional Scheme
For the traditional scheme, the transmit precoding only depends on CSI. Similar to [46], the transmitted signal includes message data for the CUs and AN, which can be written as
where is the beamforming vector for ; is the AN transmitted from the ith BS with . Thus, the covariance of can be derived as
Similarly, by plugging (24) into (1) and (2), the received signals at and target i can be expressed as
and
respectively. Note that, in (28), the signal for is the one that target i interested in, which is consistent with the assumption in Section 3.
Now, we can reformulate the optimization problem in (6) as
where the expression for has been given in (26).
4.2. Problem-Solving Algorithm
Due to constraint (33b), the optimization problem in (33) is not convex. We also take an iterative problem-solving method. Before performing the iterations, we first introduce the auxiliary variable with . Now, problem (33) can be equivalently rewritten as
Now, we optimize and alternately. A detailed discussion is given below.
(1) Solving with a given : For a given , the optimization problem (34) can be transformed into a feasibility problem by finding a satisfying constraint (34b). According to (18), we can obtain the optimized given by
With , if constraint (34b) still cannot be satisfied, the iteration process terminates.
(2) Solving with a given : With a known , the optimization problem (34) is still not convex due to constraint (34i). For addressing this issue, we take the semidefinite relaxation approach [47], which omits the rank one constraint. The relaxed optimization problem can be derived as
Problem (36) is convex and thus can be solved via CVX. It is worth noting that due to the ignorance of the rank one constraint, the feasible range of problem (36) is larger than that of problem (33) with a given . Thus, by solving problem (36), we actually find a lower bound for the transmit power of the traditional secure precoding scheme.
The above iteration process is summarized in Algorithm 3. As for the initial point , we still adopt the IFSA to find a feasible result.
| Algorithm 3 The AO method for solving problem (33). |
|
5. Simulation Results
This section provides several typical simulation results to evaluate the performances of the proposed CI-based precoding scheme and the traditional precoding scheme. For the CI-based scheme, we consider quadrature phase shift keying (QPSK) modulation. In the following simulations, we set , , , , , , . As for the complex path-loss coefficients , , , , and , , they are assumed to follow complex Gaussian distribution with mean zero and variance −50 dB. For and , they are assumed to follow a complex Gaussian distribution with mean zero and variance −100 dB. The SINR requirements are set as dB, dB, and dB, unless otherwise specified. The simulation results below are obtained by averaging over different additive noise and transmit symbols.
Figure 3 depicts the convergence procedure of the proposed CI-based precoding scheme. As discussed in Section 3, the optimization problem for CI-based precoding actually includes three subproblems. For each subproblem, we adopt an iterative method to obtain the optimized result. The horizontal axis of the graph represents the number of iterations. Note that since the power of the additive noise is assumed to be one, the vertical axis actually represents the transmit signal-to-noise ratio (SNR). As illustrated in Figure 3, for all three subproblems, with the increase in the iteration number, the obtained transmit SNR first decreases and then tends to a constant, which verifies the convergence of Algorithm 1.
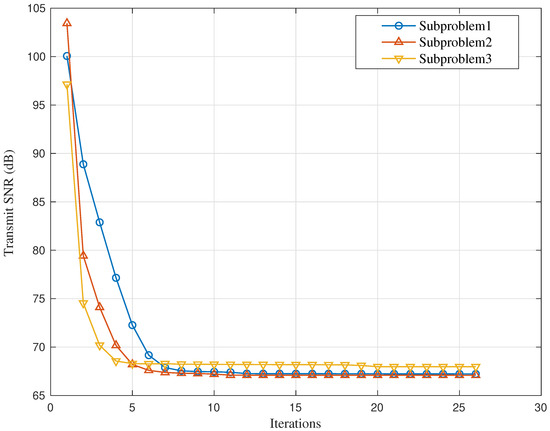
Figure 3.
Convergence of the proposed CI-based precoding scheme for different numbers of transmit antennas.
In Figure 4, we compare the received signals at the intended receiver and the eavesdropper with the aid of the proposed CI-based secure precoding. Specifically, we take and target 1 as an example, assuming that the transmitted symbol for is fixed as the one located in the first quadrant of the QPSK constellation. Here, is the intended receiver while target 1 is the eavesdropper. As shown in Figure 4, the received signals at are located within the first quadrant, which implies a reliable symbol reception at the intended receiver. In contrast, the received signals at target 1 are mostly out of the first quadrant, which implies a high SER at the eavesdropper. Note that, although we only plot the received signals at and target 1, the results for other CUs and targets are similar. Furthermore, Figure 5 compares the SER at and target 1. In accordance with the result in Figure 4, the SER at the CU decreases with the increase in the minimum required SINR , since the noise-free received signal is pushed deeper into the decision region as increases. As for the target, since its received signal is pushed far away from the decision region, the SER at the eavesdropper is high and independent of .
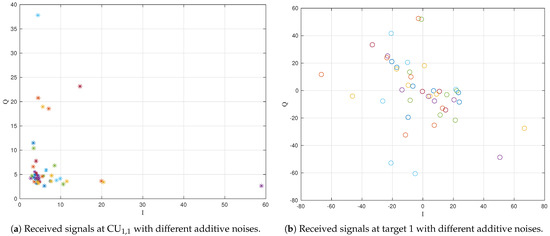
Figure 4.
Received signals at and target 1, assuming that the transmitted symbol for is fixed as the one located in the first quadrant of the QPSK constellation.
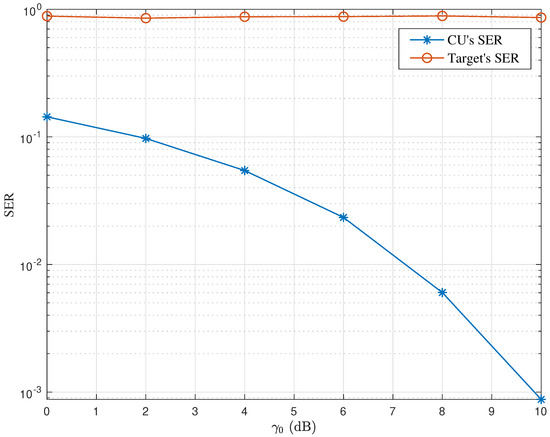
Figure 5.
SER comparison between the CU and the target.
Figure 6 depicts the normalized radar beam patterns generated by the proposed CI-based precoding for BS 1 and BS 2 with different target directions. In Figure 6a, the desired target detection direction for both BSs is assumed to be , while in Figure 6b, we have and . From Figure 6a, one can see that for the beam pattern curve of each BS, there is a significant peak at . Meanwhile, the values in the other directions are quite small, which meets the low-sidelobe requirement for the tradar beam pattern. Thus, the CI-based precoding strategy can focus energy in the intended target detection direction, which is beneficial for achieving a sufficient target detection performance. The beam pattern curves in Figure 6b also have significant peaks at and , which verifies the effectiveness of the CI-based precoding in terms of the radar SINR.
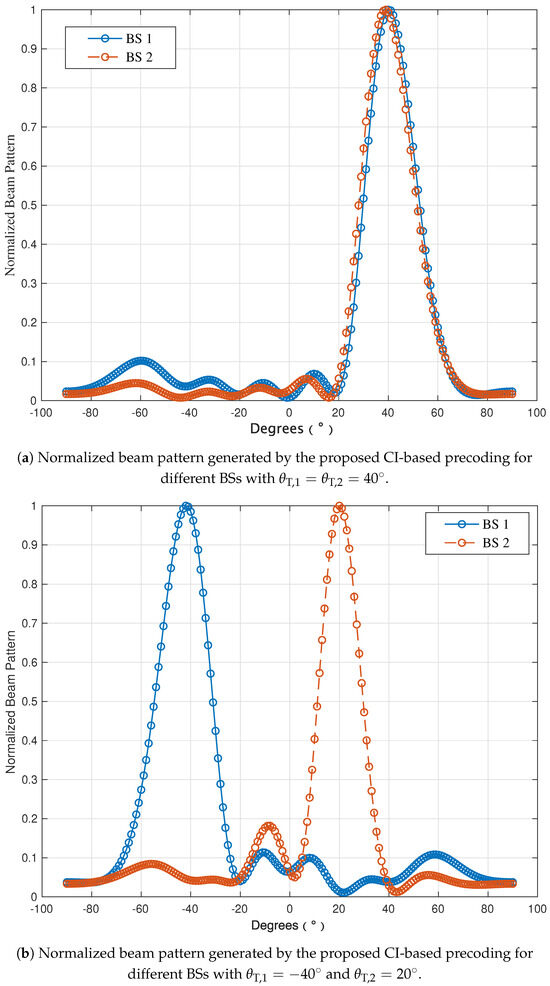
Figure 6.
Normalized beam patterns generated by the proposed CI-based precoding.
The above simulation results show that our proposed CI-based precoding scheme can achieve target detection and secure transmission simultaneously. Now, we compare the performance of the CI-based precoding scheme and the traditional precoding scheme from the perspective of energy saving. Figure 7 plots the transmit SNR versus the minimum required SINR for different radar SINR thresholds . First, it can be observed that with the same and requirement, the CI-based precoding can save transmit power compared with the traditional precoding scheme, which is the most significant advantage of the CI technique. Then, as can be seen from Figure 7, with the increase in either or , the required transmit SNR increases. This is because a larger indicates that the noise-free received signal needs to be pushed farther away from the decision boundary, which requires more transmit power. Similarly, a larger implies a higher radar SINR at the desired direction, which also requires more transmit power.
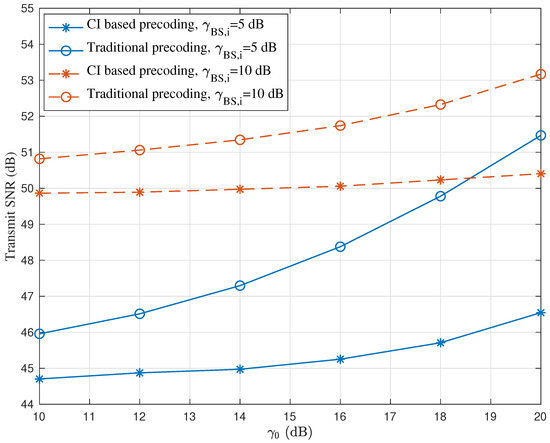
Figure 7.
Transmit SNR comparison between the CI-based precoding and the traditional precoding schemes.
Finally, we compare the transmit SNR between the CI-based precoding and the traditional precoding schemes for different PSK modulation orders, as shown in Figure 8. The QPSK, 8PSK, and 16PSK are taken as an example. First of all, similar to the results in Figure 7, the required transmit SNR of the traditional scheme is larger than that of the CI-based precoding scheme. Second, as increases, the required transmit SNR for both the schemes increases. Additionally, the required transmit SNR of the CI-based scheme increases slightly as the modulation order increases. This is because a higher modulation order leads to a smaller constructive region or feasible region of optimization problem (16). As for the traditional scheme, the transmit SNR is independent of the modulation order since the traditional precoding scheme is independent of the specific transmitted symbols.
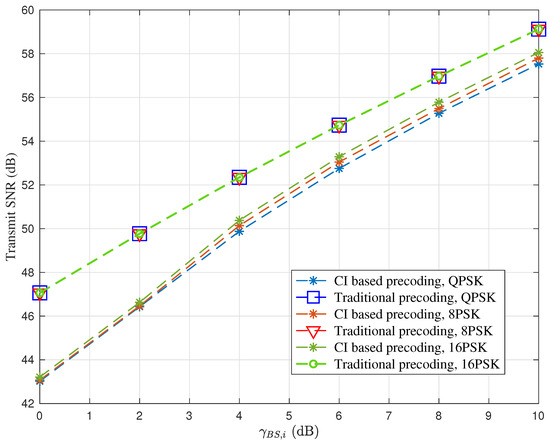
Figure 8.
Transmit SNR comparison between the CI-based precoding and the traditional precoding schemes for different PSK modulation orders.
6. Conclusions
In this paper, we studied the physical layer secure transmission problem in a two-cell coordinated DFRC UAV system. Similar to previous research, UAV targets were regarded as potential eavesdroppers. We considered secure transmission to cellular UAVs against UAV targets under constraints on a sufficient radar SINR. Aiming at achieving this secure DFRC purpose, the concept of CI was exploited to guarantee reliable symbol reception at intended cellular UAVs and symbol distortion at UAV targets. With the aid of CI, a transmit power minimization problem was formulated to design the beamforming vectors at the coordinated BSs. An iterative method was proposed to solve the formulated optimization problem. The simulation results were provided to verify the effectiveness of the proposed CI-based precoding scheme from the perspective of energy saving, e.g., up to , as shown in Figure 7, compared with the traditional scheme without CI. The above energy-saving benefit comes with the price of computational complexity, since the precoding matrix needs to be updated on a symbol level, which is an inevitable issue for CI-based precoding and all other symbol-level precoding techniques. Fortunately, the CI-based precoding is performed at base stations with high computational capabilities. Meanwhile, the complexity at the receiver side will be significantly reduced with only a simple decision stage for PSK modulation, which makes the CI technique particularly suitable for the downlink communication network in this paper. In future work, we will investigate the effect of imperfect channel state information on the system performance as well as low-complexity solvers for CI precoding.
Author Contributions
Conceptualization, methodology, software, validation, and writing—original draft preparation, Q.X.; methodology, software, validation, and writing—original draft preparation, J.Y.; methodology, validation, resources, writing—review and editing, X.W.; methodology, validation, writing—review and editing, project administration, M.-b.N.; conceptualization, validation, resources, writing—review and editing, M.S.M.; conceptualization, supervision, writing—review and editing, funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Natural Science Foundation of China under Grant No. 62201462.
Data Availability Statement
The original contributions presented in the study are included in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- 3GPP. Technical Specification Group Radio Access Network: Study on Enhanced LTE Support for Aerial Vehicles (Release 15); Report 36.777; 3GPP: Sophia Antipolis, France, 2017. [Google Scholar]
- Mei, W.; Zhang, R. Cooperative Downlink Interference Transmission and Cancellation for Cellular-Connected UAV: A Divide-and-Conquer Approach. IEEE Trans. Commun. 2020, 68, 1297–1311. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y. Energy Minimization for Cellular-Connected UAV: From Optimization to Deep Reinforcement Learning. IEEE Trans. Wirel. Commun. 2022, 21, 5541–5555. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, J. Performance Analysis of Location-Based Base Station Cooperation for Cellular-Connected UAV Networks. IEEE Trans. Veh. Technol. 2023, 72, 14787–14800. [Google Scholar] [CrossRef]
- Liu, X.; Zhong, W.; Wang, X.; Duan, H.; Fan, Z.; Jin, H.; Huang, Y.; Lin, Z. Deep Reinforcement Learning-Based 3D Trajectory Planning for Cellular Connected UAV. Drones 2024, 8, 199. [Google Scholar] [CrossRef]
- Challita, U.; Ferdowsi, A.; Chen, M.; Saad, W. Machine Learning for Wireless Connectivity and Security of Cellular-Connected UAVs. IEEE Wirel. Commun. 2019, 26, 28–35. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Z.; Tong, F.; Sun, P.; Feng, X.; Zhao, Z. Joint Design of Transmitting Waveform and Receiving Filter via Novel Riemannian Idea for DFRC System. Remote Sens. 2023, 15, 3548. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Arora, A.; Chatzinotas, S.; Ottersten, B. Joint Transmit Waveform and Receive Filter Design for Dual-Function Radar-Communication Systems. IEEE J. Sel. Top. Signal Process. 2021, 15, 1378–1392. [Google Scholar] [CrossRef]
- Wen, C.; Huang, Y.; Davidson, T.N. Efficient Transceiver Design for MIMO Dual-Function Radar-Communication Systems. IEEE Trans. Signal Process. 2023, 71, 1786–1801. [Google Scholar] [CrossRef]
- Liao, B.; Xiong, X.; Quan, Z. Robust Beamforming Design for Dual-Function Radar-Communication System. IEEE Trans. Veh. Technol. 2023, 72, 7508–7516. [Google Scholar] [CrossRef]
- Guo, B.; Liang, J.; Wang, T.; So, H.C.; Xu, J. Transmit Hardware Impairment Aware Waveform Design for MIMO DFRC. IEEE Trans. Signal Process. 2024, 72, 2858–2873. [Google Scholar] [CrossRef]
- Guo, B.; Liang, J.; Wang, G.; Tang, B.; So, H.C. Bistatic MIMO DFRC System Waveform Design via Fractional Programming. IEEE Trans. Signal Process. 2023, 71, 1952–1967. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; Wei, Z.; Yu, K.; Min, L.; Mumtaz, S. Uplink Secrecy Performance of RIS-Based RF/FSO Three-Dimension Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2024, 23, 1798–1809. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Yu, K.; Wei, Z.; Zhao, H.; Al-Dhahir, N.; Guizani, M.; Leung, V.C.M. Active Aerial Reconfigurable Intelligent Surface Assisted Secure Communications: Integrating Sensing and Positioning. IEEE J. Sel. Commun. 2024, 42, 2769–2785. [Google Scholar] [CrossRef]
- Yaacoub, E.; Abualsaud, K.; Mahmoud, M. Hybrid Encryption for Securing and Tracking Goods Delivery by Multipurpose Unmanned Aerial Vehicles in Rural Areas Using Cipher Block Chaining and Physical Layer Security. Drones 2024, 8, 111. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; He, Y.; Pang, L.; Xu, Q.; Zhang, R. An HAP and UAVs Collaboration Framework for Uplink Secure Rate Maximization in NOMA-Enabled IoT Networks. Remote Sens. 2022, 14, 4501. [Google Scholar] [CrossRef]
- Yerrapragada, A.K.; Eisman, T.; Kelley, B. Physical Layer Security for Beyond 5G: Ultra Secure Low Latency Communications. IEEE Open J. Comm. Soc. 2021, 2, 2232–2242. [Google Scholar] [CrossRef]
- Mitev, M.; Chorti, A.; Poor, H.V.; Fettweis, G.P. What Physical Layer Security Can Do for 6G Security. IEEE Open J. Veh. Technol. 2023, 4, 375–388. [Google Scholar] [CrossRef]
- Chorti, A.; Barreto, A.N.; Köpsell, S.; Zoli, M.; Chafii, M.; Sehier, P.; Fettweis, G.; Poor, H.V. Context-Aware Security for 6G Wireless: The Role of Physical Layer Security. IEEE Comm. Stand. Mag. 2022, 6, 102–108. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; Chakraborty, C.; Min, L.; He, Y.; Guduri, M. Covert Communications in Air-ground Integrated Urban Sensing Networks Enhanced by Federated Learning. IEEE Sens. J. 2024, 24, 5636–5643. [Google Scholar] [CrossRef]
- Li, M.; Ti, G.; Liu, Q. Secure Beamformer Designs in MU-MIMO Systems With Multiuser Interference Exploitation. IEEE Trans. Veh. Technol. 2018, 67, 8288–8301. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Huang, H.; Yin, Z.; Zhang, N.; Zhang, D. Securing Multidestination Transmissions With Relay and Friendly Interference Collaboration. IEEE Internet Things J. 2024, 11, 18782–18795. [Google Scholar] [CrossRef]
- Li, B.; Yang, Z.; Zou, Y.; Zhu, J.; Cao, W.; Shi, C. Securing Multiuser Communications via an Energy Harvesting Node: Jammer or Relay? IEEE Trans. Veh. Technol. 2023, 72, 8755–8769. [Google Scholar] [CrossRef]
- Lin, Y.; Shu, F.; Zheng, Y.; Liu, J.; Dong, R.; Chen, X.; Wu, Y.; Yan, S.; Wang, J. Two Low-Complexity Efficient Beamformers for an IRS- and UAV-Aided Directional Modulation Network. Drones 2023, 7, 489. [Google Scholar] [CrossRef]
- Min, L.; Li, J.; He, Y.; Si, Q. LAP and IRS Enhanced Secure Transmissions for 6G-Oriented Vehicular IoT Services. Drones 2023, 7, 414. [Google Scholar] [CrossRef]
- Tang, Z.; Sun, L.; Tian, X.; Niyato, D.; Zhang, Y. Artificial-Noise-Aided Coordinated Secure Transmission Design in Multi-Cell Multi-Antenna Networks With Limited Feedback. IEEE Trans. Veh. Technol. 2022, 71, 1750–1765. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Long, K. Joint Resource, Trajectory, and Artificial Noise Optimization in Secure Driven 3-D UAVs With NOMA and Imperfect CSI. IEEE J. Sel. Commun. 2021, 39, 3363–3377. [Google Scholar] [CrossRef]
- Salem, A.A.; Ismail, M.H.; Ibrahim, A.S. Active Reconfigurable Intelligent Surface-Assisted MISO Integrated Sensing and Communication Systems for Secure Operation. IEEE Trans. Veh. Technol. 2023, 72, 4919–4931. [Google Scholar] [CrossRef]
- Yu, X.; Xu, J.; Zhao, N.; Wang, X.; Niyato, D. Security Enhancement of ISAC via IRS-UAV. IEEE Trans. Wirel. Commun. 2024, 23, 15601–15612. [Google Scholar] [CrossRef]
- Xu, J.; Yu, X.; Xu, L.; Xing, C.; Zhao, N.; Wang, X.; Niyato, D. IRS-UAV Assisted Secure Integrated Sensing and Communication. IEEE Wirel. Commun. 2024, 31, 61–67. [Google Scholar] [CrossRef]
- Masouros, C.; Zheng, G. Exploiting Known Interference as Green Signal Power for Downlink Beamforming Optimization. IEEE Trans. Signal Process. 2015, 63, 3628–3640. [Google Scholar] [CrossRef]
- Li, A.; Spano, D.; Krivochiza, J.; Domouchtsidis, S.; Tsinos, C.G. A Tutorial on Interference Exploitation via Symbol-Level Precoding: Overview, State-of-the-Art and Future Directions. IEEE Commun. Surv. Tuts. 2020, 22, 796–839. [Google Scholar] [CrossRef]
- Wang, W.; Duan, L.; Liu, X.; Zhao, N. Enhancing MISO-NOMA Networks via Constructive Interference Precoding. IEEE Trans. Commun. 2024, 72, 510–523. [Google Scholar] [CrossRef]
- Gu, B.; Li, D.; Liu, Y.; Xu, Y. Exploiting Constructive Interference for Backscatter Communication Systems. IEEE Trans. Commun. 2023, 71, 4344–4359. [Google Scholar] [CrossRef]
- Pu, Z.; Wang, W.; Dong, F. Beamforming and Waveform Designing for Spectrum Coexistence System Based on Constructive Interference. IEEE Commun. Lett. 2022, 26, 2695–2699. [Google Scholar] [CrossRef]
- Pu, Z.; Wang, W.; Yan, Y.; Shao, X. Multi-User Interference Exploiting and Waveform Designing With PAPR Constraint for Radar and Communication Coexistence System. IEEE Commun. Lett. 2023, 27, 3048–3052. [Google Scholar] [CrossRef]
- Lei, Z.; Liao, X.; Gao, Z.; Li, A. CI-NN: A Model-Driven Deep Learning-Based Constructive Interference Precoding Scheme. IEEE Commun. Lett. 2021, 25, 1896–1900. [Google Scholar] [CrossRef]
- Liu, R.; Li, M.; Liu, Q.; Swindlehurst, A.L. Secure Symbol-Level Precoding in MU-MISO Wiretap Systems. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3359–3373. [Google Scholar] [CrossRef]
- Xu, Q.; Ren, P.; Swindlehurst, A.L. Rethinking Secure Precoding via Interference Exploitation: A Smart Eavesdropper Perspective. IEEE Trans. Inf. Forensics Secur. 2021, 16, 585–600. [Google Scholar] [CrossRef]
- Salem, A.; Masouros, C.; Wong, K.-K. On the Secrecy Performance of Interference Exploitation With PSK: A Non-Gaussian Signaling Analysis. IEEE Trans. Wirel. Commun. 2021, 20, 7100–7117. [Google Scholar] [CrossRef]
- Su, N.; Liu, F.; Wei, Z.; Liu, Y.-F.; Masouros, C. Secure Dual-Functional Radar-Communication Transmission: Exploiting Interference for Resilience Against Target Eavesdropping. IEEE Trans. Wirel. Commun. 2022, 21, 7238–7252. [Google Scholar] [CrossRef]
- Wang, B.; Wu, L.; Cheng, Z.; He, Z. Exploiting Constructive Interference in Symbol Level Hybrid Beamforming for Dual-Function Radar-Communication System. IEEE Wireless Commun. Lett. 2022, 11, 2071–2075. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, M. Joint Transmit Beamforming and Receive Filters Design for Coordinated Two-Cell Interfering Dual-Functional Radar-Communication Networks. IEEE Trans. Veh. Technol. 2022, 71, 12362–12367. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: MATLAB Software for Disciplined Convex Programming, Version 2.1. Available online: http://cvxr.com/cvx (accessed on 9 October 2024).
- Cheng, Y.; Pesavento, M. Joint Optimization of Source Power Allocation and Distributed Relay Beamforming in Multiuser Peer-to-Peer Relay Networks. IEEE Trans. Signal Process. 2012, 60, 2962–2973. [Google Scholar] [CrossRef]
- Khandaker, M.R.A.; Masouros, C.; Wong, K.-K. Constructive Interference Based Secure Precoding: A New Dimension in Physical Layer Security. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2256–2268. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, Q. Secure Beamforming Design for UAV-Empowered Integrated Sensing and Communication. Appl. Sci. 2024, 14, 7196. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).