Abstract
This article presents methods of planning unmanned aerial vehicle (UAV) missions in which individual platforms work together during the reconnaissance of objects located within a terrain. The planning problem concerns determining the flight routes of a swarm, where each UAV has the ability to recognize an object using a specific type of sensor. The experiments described in this article were carried out for drone formation; one drone works as a swarm information hub and exchanges information with the ground control station (GCS). Numerical models for mission planning are presented, which take into account the important constraints, simplifying the description of the mission without too much risk of losing the platforms. Several types of objective functions were used to optimize swarm flight paths. The mission models are presented in the form of mixed integer linear programming problems (MILPs). The experiments were carried out on a terrain model built on the basis of graph and network theory. The method of building a network on which the route plan of a drone swarm is determined is precisely presented. Particular attention was paid to the description of ways to minimize the size of the network on which the swarm mission is planned. The presented methods for building a terrain model allow for solving the optimization problem using integer programming tasks.
1. Introduction
A part of the drone swarm mission planning process is determining the flight routes of the swarm’s UAVs. The way in which the payload is used to identify targets must also be carefully planned. This is particularly important in a mission management situation in which several co-operating unmanned platforms are used.
In this article, the concept of a swarm means a group of UAVs that carry out a common mission. In such a mission, each of the UAVs is assigned to a task to be performed. Some UAVs identify targets at close range with EO/IR (electro-optical/infra-red) devices. Other drones use, for example, synthetic aperture radars (SARs) to recognize the targets from a distance of several kilometers. This work is a continuation of the previous work [1], which presents the method of mission planning for a swarm that performs reconnaissance tasks. In this swarm, there was no UAV with the task of co-ordinating the swarm’s activities (which is referred to in this article as an information hub).
The method of planning the flight paths of a swarm of drones presented in this article is often used in the military or emergency services. In this method of planning the swarm’s routes, the principle applies that individual platforms cannot communicate on a peer-to-peer basis, which is often referred to as a “mesh” network. Since drones can move away from the ground control station (GCS) to a considerable distance and lose radio range, to prevent this, one of the drones acts as an information hub, sometimes called an information retranslator. Such a drone is equipped with additional radio stations that enable communication with the GCS and any drones. However, at any given time, the retranslator always controls a maximum of one of the drones and collects data from this drone from object recognition. The retranslator, on the other hand, can collect telemetry data from each of them simultaneously. The retranslator is usually equipped with directional antennas, which makes it difficult to locate it and protects against signal jamming. Another model of drone operation is flight using a mesh network that allows each drone to communicate with another. However, such a network is easy to locate and jam.
Swarms of unmanned platforms are often categorized in the literature according to the way the swarm flight template is and the rules of communication among UAVs. A precise description of one of the categorization methods, as proposed by Wang, can be found in [2]. Wang’s approach to categorizing drone swarms is partially used in this article.
The authors of [2] present a categorization of swarms. Based on this categorization, it can be concluded that the basic operating model of a drone swarm is presented, using EO/IR to recognize objects from a given distance. Drones exchange information with each other. One of the drones is additionally equipped with a higher-power radio link, which allows for communication with the GCS. This drone allows for indirect data exchange with the GCS through any of the drones. Additionally, it transmits UAV statuses and reconnaissance data to the GCS. This model of operation is called communication retranslation, and it is very widely used in drones that operate for the purposes of military reconnaissance.
This article presents a method of building a robust linear optimization model that takes into account the possibility of temporary disturbances in communication between drones and the information hub. The swarm route plan determined by the mixed integer linear programming (MILP) model must meet many constraints described in detail in Section 3. First of all, the number of recognized objects in the mission is taken into account, with the basic assumption that during the flight, each drone can exchange data with the GCS using a drone acting as a retranslator. This means that at any moment of the flight, each drone has a radio range enabling contact with the GCS.
The robust component of the optimization model is based on the Soyster technique [3]. It concerns, in particular, the constraints related to ensuring communication among the drones performing their tasks. It should be remembered that the introduction of robust techniques to the optimization model allows for a larger number of solutions that may not necessarily be correct from the planner’s point of view. Therefore, the presented technique was used only for constraints on maintaining communication among UAVs. The study of the robustness of a swarm of drones to factors that may disrupt the course of the mission is present in the literature to an increasing extent. Hu et al. [4] proposed a method for assessing swarm robustness based on network theory, where the dynamic evolution of UAV swarms and the correlation of the information exchanged between the UAVs are taken into account.
In order to enhance the realism of the model, it was assumed that the UAV information hub is equipped with a synthetic aperture radar (SAR) and may conduct additional reconnaissance of the area. The model can be modified to include a drone swarm consisting of multiple retranslators, each managing its own group of drones. This configuration is not commonly found in the existing literature on swarm missions. The optimization problem proposed in this article represents a significant research achievement.
There is currently no uniform approach to planning a drone swarm mission due to the serious risk of jamming communication between them. Depending on the type of tasks, communication in a mesh network or the use of connections with a retranslator can be used. In military operations, the model based on the use of a retranslator currently dominates. In models used in the civilian market, mesh networks are preferred. However, it seems that the chosen direction of development will depend primarily on the possibility of securing the swarm from communication jamming.
This article is organized as follows. The Related Works section presents the current state of modeling the operation of drone swarms, along with the important works on which the model is based. The Methodology section introduces the optimization models used for planning a swarm mission, including the model of a transportation network representing the terrain and the optimization problems. It also presents groups of constraints, such as constraints for drone missions that do not have to co-operate, network flow preservation constraints in directed networks, and constraints for the optimization task in which one UAV co-ordinates the work of the others. Additionally, it presents different variants of the objective function. The Results section presents the important results of the experiments conducted. It also outlines the limitations of the drone swarm model and suggests possible directions for further research.
2. Related Works
It is crucial to determine the drone flight route and the payload assignment for object recognition tasks when managing a swarm mission comprising several collaborating unmanned platforms. In this type of mission, each UAV is assigned specific tasks. Some drones are tasked with recognizing objects in close proximity using EO/IR devices, whereas others utilize SAR for target recognition from distances of several kilometers.
As mentioned earlier, drone swarms are often divided into categories based on various types of criteria. The method of using the payload during reconnaissance missions is often taken into account. Based on the classification presented in the work [5], the problem of describing a UAV swarm can be divided into several layers: decision-making regarding the mission, planning, control, communication, and application.
In the decision-making layer of the swarm, plans are specified based on the tasks assigned to be performed. Tasks are usually assigned priorities, although this is not mandatory. The next planning layer defines mission details, such as the flight trajectories of individual drones. The control layer is responsible for controlling the correct implementation of the planned mission. The supervised tasks include obstacle avoidance tasks. In the communication layer, communication between drones is supervised. The scope of exchanged information is also taken into account, reconnaissance data fusion is carried out, etc. The description of the classification of swarm mission management algorithms can be checked in [6]. The article presents drone swarm route planning algorithms that fall within the conceptual scope of the planning layer. The mechanism for ensuring communication between drones using an information hub located in the communication layer is also described.
One approach to modeling the flight paths of a swarm of drones is to formulate the model as an MILP problem. These models are based on vehicle route planning with time windows (VRPTWs) and incorporate constraints for drones visiting specific waypoints within specified time intervals. Developing the model effectively can lead to obtaining the optimal solution if one exists. However, finding a solution often takes a long time, so heuristic algorithms are used to address this challenge. An example of such an algorithm is the flight planning algorithm of drones carrying parcels described in [7]. The algorithm takes into account such restrictions as limited flight time, capacity of UAV, etc. The authors solve the MILP problem and compare it with the proposed receding horizon task assignment (RHTA) heuristic, which gives lower-quality solutions but the solutions are found much faster. The interested reader should read [8], which has prepared an overview of the algorithms used to solve the task of planning drone missions, which are sent to carry out tasks from transport trucks. The article describes possible optimization approaches applicable to stand-alone drone operations and operations combined with vehicles.
The heuristic algorithms include ant colony optimization (ACO) [9] and particle swarm optimization (PSO) [10]. The bee colony algorithm [11], multi-swarm fruit fly optimization algorithm [12], and firefly algorithm [13] can also be used in swarm co-operative control. Research that considers travels through the arcs of a network is classified into arc routing problems. For example, ref. [14] discussed a capacitated routing problem that minimizes travel costs. The authors of [15] studied a drone routing problem, which allows for multiple visits on route segments. The authors of [16] describe the classic VRPTW problem for many vehicles, which is solved using the tabu search (TS) heuristic. An example of the use of the tabu search method is the work of Lu et al. [17], which presents a method of using drones in the e-commerce market. In one stage of the presented algorithm, an improved tabu search algorithm is used for route optimization based on specifying the number of drone calls.
Lu et al. [18] described a route planning method that takes into account the uncertainty of transportation time and cost due to seasonality and human factors. The developed algorithm called hybrid beetle swarm optimization (HBSO) was compared with popular methods such as genetic algorithms (GAs) and particle swarm optimization (PSO). The interested reader can find a large review of the literature for the described area in Lu’s work.
Amine Masmoudi et al. [19] described the drone vehicle routing problem, which involves designing combined routes and schedules for trucks and drones to serve customers with specific requirements. The problem involves time windows. An adaptive multi-start simulated annealing algorithm was proposed to solve the presented problems.
The algorithm presented in [1] describes the flight planning of a group of drones moving around a terrain model described in the form of a graph. Two or more drones are not allowed to fly over one route segment. In this article, the model has been extended to allow for the planning of complex missions that communicate with the GCS using an information hub drone.
The details of many of the works forming the foundation of movement planning algorithms on a directed network are beyond the scope of this article. For a comprehensive understanding of these algorithms, readers are recommended to refer to the excellent overview provided by Zhou [6].
3. Methodology
The models used to plan swarm missions in directed networks consist of several parts. The first group consists of constraints on flow behavior in directed networks. The next group consists of constraints specific to the unmanned aircraft performing reconnaissance. The last group consists of constraints related to planning the work of the swarm in which UAVs exchange data with each other. This section presents a version of the UAV flight path planning model. The model is based on the model presented in [1]. The model extensions presented in this section allow analysts to plan a swarm mission for which one of the UAVs will be the information center.
Let us assume that a vector describes a UAV with index u, where . is the maximum flight time of the UAV. is the set of the sensor indices of the UAV. s is an index of the sensor used. q indicates the type of UAV. The presented model describes the planning of swarm missions of two types of drone. The first group includes drones equipped with sensors used to recognize objects from a short distance. The second group includes UAVs equipped with sensors that allow for recognition from a longer distance. The UAVs from the second group also play the role of an element transmitting orders from GCSs to other drones (the information hubs).
3.1. Mission Network
The terrain model used for planning drone swarm missions depends on the method chosen to model the swarm optimization task. When using MILP models, the terrain is typically represented as a directed network.
The notation for the network used in an optimization problem is represented as . V is the set of vertices. Variable , , is a vector that describes each vertex of S, where the following applies: describes waypoint, , position, is the earliest date when the task can start, is the due date (latest date when a task should be completed), is the priority, and is the recognition time needed to complete the task by the UAV. Each arc of the network S described by the ordered pairs of vertices can have its priority, which is denoted below as ( are the indices of the vertices). Set V includes route points (waypoints) and the placements of the swarm’s take-off and landing.
Figure 1 shows a directed network, S, on which the swarm’s flight routes are determined. For the sake of the simplification of the presented model, means the waypoint with the three co-ordinates . The network model is an extension of the model presented in [20]. The model shown in this article takes into account the different heights of the points modeled by the network vertices. However, the differences in height are not significant. In practice, drones rarely change flight altitudes during missions, so such assumptions do not detract from the generality of the model.
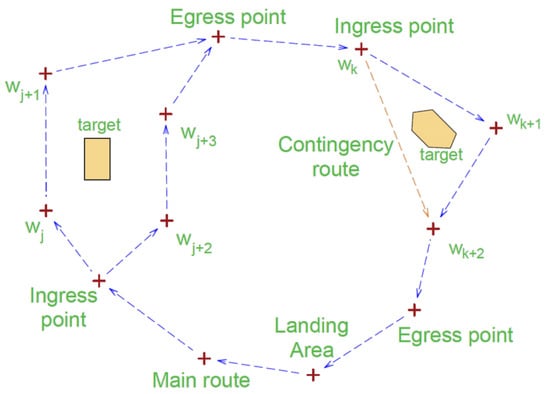
Figure 1.
Network model S, as presented in [20]. Two regions are visible for the UAV to recognize. These regions are colored brown. The route segments and waypoints, w, are drawn as blue arrows. Symbols j and k are indices of the vertices.
This article discusses a transportation network model represented as a graph that is used to solve mission planning tasks involving UAVs. The network, denoted as S, consists of edges representing UAV flight segments and vertices representing locations where flight parameters or equipment settings are adjusted. A vertex can also represent a recognizable object. It is assumed that the network remains unchanged during mission planning but can be modified if new obstacles emerge, requiring the algorithm to be restarted. The main focus is on the algorithm for constructing the S connection network and minimizing its size.
The method of the construction, S, of the networks used in this study is compatible with algorithms from the visibility graphs group of algorithms (see [21]). In computational geometry and robot motion planning, the visibility between field points is modeled with graphs. Each vertex represents a physical location in the terrain, and each edge between two vertices means that a vertex can see a vertex adjacent to it.
In order to determine the connection network with the minimum number of edges, the approach described in [1] is used. The algorithm consists of adding new vertices to the network, S, when there is an obstacle on the section modeled with the edge that the platform should avoid. It is worth adding that the vertices of the S network indicate not only the places where objects are recognized but also the places where the configuration parameters of sensors are changed or the places where the flight direction is changed due to the occurrence of threats or the planner’s operational decisions. The planner inserts vertices related to reconnaissance locations and changes in-flight directions when planning the mission.
The S network constructed in this way requires a reduction in the number of vertices. For each pair of vertices that the model object needs to recognize, the length of the route between these vertices is determined. A skillfully conducted process of building a connection network allows for a reduction in the set of vertices to those modeling the locations of object recognition or the most important places in the flight plan. In order to reduce the network, it is proposed to use the rapidly exploring random tree (RRT) algorithm shown in [22,23]. It lets the user determine the actual flight trajectories of UAVs based on the air platform dynamics model. When a time window is defined for each vertex of the S network in which the UAV should fly, the RRT algorithm confirms the possibility of flying between a given pair of vertices for which the flight time is calculated. If the calculations show that it is impossible to fly between the given vertices in a given time, a specific edge is removed from the S network. This is shown in Figure 2. The use of this algorithm in a large network allows for a reduction in the number of edges of the S network, especially when time windows related to reaching the vertices by UAVs are defined for the network.

Figure 2.
The network with vertices aggregating UAV activities during object recognition. The figure on the left shows the possible paths between the vertices modeling objects recognized during the mission. The use of the RRT algorithm presented in [22] allows for determining the admissibility of flying between individual vertices. The figure on the right shows the remaining arcs of the S network, which, after applying the RRT algorithm, ensure the ability to recognize objects. The vertices of the network S marked with circles remain in the network structure after the aggregation process. The vertices marked with crosses are removed. In some cases, after vertex aggregation, a network arc will be removed. This applies to the case when there is a time window of the VRPTW task in the optimization problem that does not let the UAV to fly between vertices due to the distance of these vertices.
When advanced reconnaissance sensors are used, their configuration is usually required during flight immediately before recognizing the object. During the reconnaissance of an object, the UAV mission computer (the main unit managing the air platform responsible for executing the mission in accordance with the plan) usually performs a series of preparatory activities, such as sensor calibration, etc. Then, the object is reconnoitered, the reconnaissance information is recorded, and the data are transmitted to the GCS (for example, when due to the requirements contained in the mission plan, there was no consent to transmit data online due to the security of the platform). If the above activities are performed in a small area, the network vertices should be grouped into one, as shown in Figure 3.
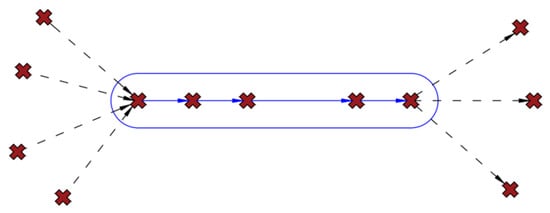
Figure 3.
A method of aggregating network vertices that are located close to each other and model sites that model activities on the same payload elements. The vertices enclosed in blue oval are aggregated according to the algorithm presented in [22].
The next sections of this article describe the problem of route planning belonging to the VRPTW task class. Due to the fact that this is a model in the form of an MILP formulation, finding a solution ensures that it is a feasible and optimal solution.
3.2. Constraints for UAVs without Co-operation
This section outlines a series of constraints relevant to modeling drone swarm flight. In order to maintain clarity, we have chosen to preserve certain constraints from our earlier works that remain unchanged in this article.
The model variables for each UAV () are the following:
- if the platform visits the vertex ; otherwise, it is 0;
- if the platform travels along an edge ; otherwise, it is 0;
- if the recognized object assigned to the edge is checked with the sensor ; otherwise, it is 0;
- is the arrival time of the platform to the waypoint ( means that UAV did not visit the vertex).
The basic constraints used in modeling the flight of an unmanned platform are described below. These constraints remain unchanged when modeling the flight of one or more drones. Some of them were presented in [1].
Route planning tasks in which time windows for reaching a waypoint are specified require determining the time to reach a specific vertex of the S network. This is modeled by constraint (1). Restrictions on the arrival time to a specific point, taking into account the time window, are defined by constraints (2) and (3). Note that for drone swarm mission planning tasks, time windows will only be defined for certain vertices. Therefore, the task of mission planning is much easier to solve if the above assumptions are taken into account, simplifying the structure of the connection network on which the routes are determined. It is a mistake to impose unnecessary or excessive time constraints on the optimization model. Constraint (1) contains a large M component used to model constraints as logical rules (see [24]).
Constraints (4)–(6) represent the model for target recognition by multiple UAVs flying along different route sections, as shown in Figure 1. The coefficient denotes the maximum number of platforms capable of reconnoitering a specific target. In this model, only two sections are defined to simplify the model without compromising its generality.
Constraint (7) ensures that the flight time of the designated UAV does not exceed its maximum possible flight length.
3.3. Flow Preservation Constraints
The flow preservation constraints must be maintained in each model using the directed network:
Constraint (8) prevents a UAV from flying within the same vertex. For UAV mission modeling, this constraint is critical. Banning the flight within one vertex forces the modeling of additional routes on which the UAV waits for the continuation of the mission when, after solving the optimization task, it appears that it would be too early in the next vertex. The take-off and landing areas are described by the different nodes of the S network.
In the model presented in this article, the UAV retranslator should be used first to perform the assigned reconnaissance tasks. Other UAVs may not be used if only one platform is enough to observe objects (assuming that the retranslator is the best-equipped platform). In fact, there is usually no need for all swarm platforms to start missions. The presented situation is modeled by the constraints (9) and (10), where is a retranslator.
The flow preservation constraint for S is presented in (11). It must be maintained for each UAV and each vertex.
Each UAV that has initiated its mission must return to the landing area (12). The take-off area is indexed as .
Constraint (13) ensures that each route segment can be visited multiple times but no more than . This modification was introduced to plan a swarm mission.
Constraint (14) lets be set to 1 when the platform moves from to . It means that when equals 1, then both vertices are visited (constraint (15)).
Constraint (16) describes the assignment of the sensor to the route segment. The constraint can only be met by UAVs equipped with sensors of the required type.
The constraints used to eliminate subtours were omitted. These constraints are presented in [1].
3.4. Constraints for the Swarm
This section presents three sets of constraints used to plan swarm routes. The first set involves planning the swarm’s flight so that each UAV remains within communication range.
The second set of constraints deals with determining the minimum and maximum flight times over a vertex. These constraints come into play when the analyst aims to minimize the difference between the maximum and minimum time it takes for the drone to reach the vertex.
The third set of constraints involves modeling the flight plans of UAVs along a directed network, where the vertices represent points at varying heights above the ground level.
These constraints are presented below.
3.4.1. The Flight of the Swarm within the Range of Data Link
In order to define these constraints, the position of the GCS that controls the swarm must be known. The GCS position is defined as . Thus, one may define the first constraint as
The safe distance, R, from the GCS ensures that the communication data link between the GCS and the UAV remains reliable even in adverse weather conditions. The indicates that the UAV serves as an information hub that collaborates with the GCS and other UAVs. Equation (17) is a quadratic equation. The methods for linearization of quadratic equations are presented in [25].
Now, let us consider a specific constraint from the constraint sets (17) to (21). Suppose the coefficients next to the variables in this constraint are subject to uncertainty. In the case of the discussed constraints, the analyst does not know whether it will be possible to maintain communication among the drones belonging to the swarm in the given weather conditions. Therefore, the formulation should be modified to provide the necessary “protection” by maintaining a gap between the two sides of this constraint.
For example, let . Then, the robust component of (17) may take the form:
where , , and is the gap protection for this constraint ( is usually not greater than 0.25). In this case, when (the information hub does not pass through the vertex of the net S), the variable . When the information hub traverses the vertex of this net, then . In this formulation, can also be binary. The technique based on robust components should, however, be used very carefully. The concept of adding gaps to the constraints that prevent an unacceptable solution from being designated also has its serious drawbacks. The introduction of such robust components to the constraints significantly limits the possibility of finding an acceptable solution. This is the price of necessary protection, as reported by Bertsimas et al. [3], which was first introduced by Soyster [26]. Therefore, in the robust model presented in the article, the robust component is only used for modeling the radio link.
The interested reader can learn about the method of modeling the communication range of drones in [22], which shows the method of finding the flight trajectory of UAVs based on the RRT algorithm.
3.4.2. Minimum and Maximum Flight Times over the Vertex
This set of constraints calculates the time when the first platform flies over the vertex and when the last platform flies over each vertex. When the time to fly through that vertex of the last UAV is determined for each vertex for which a flight time restriction is imposed, a target function can be defined that introduces a flight planning penalty outside the imposed time slot that is presented in function (27).
It is very important to compute and only for vertices with a flight time restriction to avoid unnecessary solver calculations.
The form of constraint (24) needs to be discussed. The must be much greater than the maximum path length in the directed network. In constraint (24), we actually determine the minimum flight time through the vertex of the network, but the use of this inequality is related to the fact that the values for are equal to 0 many times. Therefore, the possibility of the solver selecting 0 as the minimum value must be blocked.
3.5. Optimization Goals
The model employs the following optimization functions. The first function maximizes the profit obtained when the swarm visits the set of waypoints.
The optimization function presented in (25) consists of two parts. The first part is used to calculate the profit from the visited vertices, while the second part calculates the profit from the checked arcs. The second part is typically utilized when planning UAV maneuvers equipped with SAR (refer to [20]). In practice, the value of p in the objective function also corresponds to the recognition priority of a particular target, which is associated with the edge or vertex from which the target can be recognized.
An optimization function based on minimizing travel time, as presented in [1], was also used in the experiments.
The function, as presented in (26), is composed of two parts. The first part describes the travel times of the platforms. Parameter is an optimization coefficient (). The second part describes the profits from visiting the vertices with the highest priorities. An analyst planning UAV tasks determines whether they prefer to maximize the identified targets or whether they want to minimize the UAV flight time while simultaneously recognizing the targets.
The third function maximizes the profit from visiting the set of waypoints. The profit is reduced proportionally to the difference between the border times of entering a waypoint.
The form of the third component of the goal function results from constraint (24), which was discussed in Section 3.4.
4. Results
The experiments were conducted on a directed network, S, consisting of 10 to 40 vertices. The mission plans were generated for three different optimization models (see Table 1).

Table 1.
Optimization models used.
In order to increase the difficulty of the optimization task, it was assumed that any UAV could fly between any vertices of the S network. This means that the number of problem constraints has increased significantly. In real mission planning situations, when the S network size reduction methods are used (see [1]), the number of problem constraints may be several times smaller. This significantly affects the time needed to determine the solution.
Mission plans have been created for situations in which the UAV can observe all targets from an optimal flight altitude (refer to Table 2). The calculations were stopped when the solver found the best possible solution or a suboptimal solution. In the latter case, computation was stopped after a specified period if the solver did not find a better solution than the last one found. The calculations were performed on CPLEX 20.1 installed on Ubuntu 20. The workstation was equipped with an i7 processor.

Table 2.
Search times for the optimization problems for the predefined targets. The number of linear targets describes the number of route sections, the completion of which increases the profit from completing the mission. The parameter determines the permissible maximum number of flights along a specific section of the route by the UAV.
The vertices with the highest priority are marked in red in Figure 4 and Figure 5. For these vertices, the flight order was determined by defining the flight segments on which the platforms should fly. In case the target function maximizes the total profit and the UAVs are able to continue the flight, all vertices are recognized (see Figure 4). On the other hand, if it is important that all the most important targets are recognized and the UAV flight routes are minimized, only the most important vertices are recognized (see Figure 5). More computationally complex cases for the objective functions I (total profit maximization) and II (the number of recognized objects maximization) are shown in Figure 6 and Figure 7, respectively. The results for model III are presented in Figure 8.

Figure 4.
The route plan for a swarm with three UAVs calculated on net S with 10 vertices using model I (maximization of the profit). The figure shows the routes of all UAVs. The route of each UAV is marked with a different color. The path of the information hub UAV is marked with a dashed green line. The vertices of the S network with the highest priorities are marked in red.
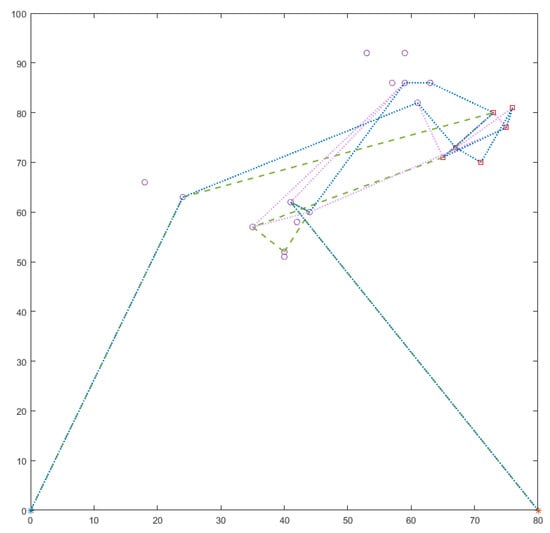
Figure 5.
The route plan for a swarm with three UAVs calculated on net S with 20 vertices using model II (minimization of the total route length and maximizing the total profit). The route of each UAV is marked in a different color. The vertices of the S network with the highest priorities are marked in red and the others in pink.

Figure 6.
The route plan for a swarm (four UAVs, net S, 30 vertices, and model I). The route of each UAV is marked in a different color. The vertices of the S network with the highest priorities are marked in red and the others in pink.

Figure 7.
The route plan for a swarm with four UAVs calculated on net S with 30 vertices using model II. The vertices of the S network with the highest priorities are marked in red and the others in pink.

Figure 8.
The route plan for a swarm (three UAVs, net S, 30 vertices, and model III). The path of the retranslator is marked with a dashed green line. The route of each UAV is marked in a different color. The vertices of the S network with the highest priorities are marked in red and the others in pink.
The mission plans have been prepared for situations where the UAV needs to observe one or more targets from an altitude higher than the optimal flight altitude. In such scenarios, model IV was utilized (refer to Table 2). The results are shown in Figure 9.
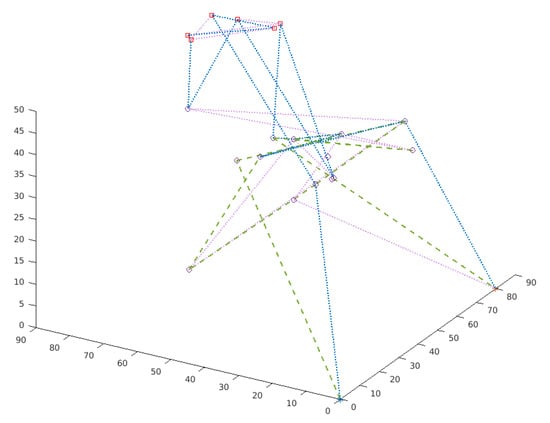
Figure 9.
The route plan for a swarm (three UAVs, net S, 20 vertices, and model IV). The path is presented in 3D. The route of each UAV is marked in a different color. The vertices of the S network with the highest priorities are marked in red and the others in pink.
The table shows the minimum time needed to find a solution that is close to the optimal and the so-called optimization gap—distance to the optimal solution—which is estimated at the current moment of the solver calculations. In practice, a gap of less than 5% means that an optimal solution has been found. When the gap is greater, it means that there is probably a better solution, but at a given stage of the calculations, it is impossible to say how much better. The experiments that were conducted show that with a given solver configuration, the optimal solutions did not significantly improve the suboptimal solutions found in the first few minutes. In the presented calculations, the constraints with robust modifications were applied.
There are many ways to increase the speed of obtaining a feasible solution that is optimal or very close to the optimal solution. Some of these techniques have been used in ongoing research. First, the way CPLEX looks for a solution has been changed. The standard method prefers obtaining feasible solutions for which their optimization gaps are precisely determined. Analysts usually put a greater emphasis on feasibility and less focus on proof of optimality. When the CPLEX parameter MIPEmphasis is set to 1, then the solver makes an effort to quickly find feasible solutions. Therefore, less computational effort is applied to analyses that aid proof of optimality. This behavior is described in the CPLEX User Manual on the IBM CPLEX website [27].
The important modification applied in this study was the use of the CPLEX solver method of modifying Branch&Cut tree building. The technique of changing the Branch&Cut tree construction method can be used in MILP tasks when the model has technical constraints that are not directly related to the substantive side of the optimization task being solved. In the presented model, such constraints are used to eliminate subtours in paths (see [1]). If these constraints were ignored, the problem would be solved, and the result would be optimal if there were no subtours in the solution. Therefore, it does not make sense to add these constraints as global constraints. If the solver finds a solution, and it is an integer feasible solution, then, in this case, it should be checked if it does not contain subtours. When there are no subtours in a solution, this solution becomes a potential optimal solution. On the other hand, when subtours are detected, the local constraints presented in [1] should be added to the vertex of the Branch&Cut tree. Due to the relatively large number of these technical constraints in relation to all the constraints of the optimization problem, the solver finds a solution in a shorter time. The results of CPLEX operation in the case of applying the Branch&Cut tree modification technique are shown in Table 3. The time needed to find a solution to a problem was reduced by approximately 10–15%.

Table 3.
Time needed to solve an optimization problem using the solver with Branch&Cut search improvement for predefined targets.
CPLEX has special mechanisms to support building solutions modifying the structure of the Branch&Cut tree by defining objects called GOALs (see the CPLEX User Manual and the description of advanced optimization techniques [27]). GOAL runs when the solver finds an acceptable solution. The user can then add new constraints for the given optimization problem. These can be local constraints (for one node only) or global (for the entire problem). The results of using the described technique are shown in Table 3.
The result of mission planning for optimization problem III is shown in Figure 8. For this problem, the maximum range of the information hub UAV was limited. The time intervals in which UAVs can fly to vertices with the highest priority (vertices marked in red) have also been limited. In the prepared plan, only one UAV flies through the vertices with the highest priority (marked in red). CPLEX was unable to find a solution that would allow other UAVs to fly over these vertices. Since the communication range of the UAV acting as a retranslator has been limited, the designated route of this UAV is similar to the routes of the UAV with which it is in contact.
The result shown in Figure 9 for model IV shows the routes of the platforms belonging to the swarm, where two platforms recognize the targets with the highest priority, and the retranslator is located at a distance from these objects. The retranslator, however, maintains a short distance from other platforms, which allows for maintaining radio communication. This example takes into account the flight altitude restrictions, as described in model IV.
5. Discussion
The presented results of the drone swarm planning algorithm require a detailed discussion due to the number of new elements in the model when compared to the standard VRPTW models and heuristic models for determining the flight routes of drone groups.
First, it is worth noting that constraints (17)–(22) that describe the requirements for maintaining communication between drones during a mission have been defined. These constraints do not allow any of the UAVs to fly out of communication range from the UAV managing the connection to the GCS. On the other hand, when taking into account the possibility of a temporary loss of radio link, modifications have been made to this constraint, which makes the model robust to interference. The applied method, based on Soyster’s algorithm [3], is sufficient for finding a suboptimal UAV route plan. The use of other methods of building robust models, in our case, does not bring much improvement in terms of minimizing the calculation time.
It is also worth discussing the presented form of the network for modeling the possible routes along which UAVs belonging to the swarm can fly. The concept of building an S network based on visibility graphs and the triangulation of route points determined using the visibility determination mechanism allows for the preparation of small-sized networks. On such a network, it is possible to efficiently determine the route plan of a swarm. In practice, without losing generality, a simplification of this net may be applied, consisting of indicating the route segments on which flight is prohibited due to the risk of moving along such segments. This kind of approach has a simple rationale. If an analyst does not want to estimate (in detail) the probability of losing the platform that flies on a dangerous route segment, then the arc modeling such a segment may be excluded from the set of E. This type of modeling is used in practice.
At this point, it is worth noting an important feature of the model that will simplify the form of the optimization task. If the analyst wants the designated swarm routes to include the most important terrain waypoints but the flight did not last too long, it is possible to limit the value of the UAV parameter, which is the maximum time spent in the air. This simple procedure, combined with the function of maximizing the profit from the flight (function no. I (25)), is enough to build a model that is practically used in air operations.
An important part of optimization is identifying the gap between the optimal solution and the solution that has been found. It is not usually justifiable to wait for the optimal solution because of the time required for the search. Figure 1 shows the convergence of the swarm route planning algorithm for the case illustrated in Figure 2. After about 36 s, a suboptimal solution was found that was within 12% of the optimal one. In this case, there is no need to wait for many minutes to search the entire solution space. Therefore, CPLEX_PARAM_MIPEMPHASIS was set to 5, allowing the solver to find an acceptable solution as quickly as possible using the implemented heuristics (see Figure 10).

Figure 10.
Convergence of the swarm route planning algorithm for 30 nodes of the S network and four UAVs (blue dashed line). Relative MIP gap tolerance is set to 15%. The processing time is shown on the horizontal axis. The blue squares represent the best integer solution found by CPLEX. The optimization function is presented in Equation (25).
CPLEX also found feasible solutions very quickly by using the control mechanism for adding constraints to nodes, which is presented in Section 4. If the constraints related to testing the occurrence of subtours are activated only when the solver finds acceptable solutions, the running time of the algorithm is significantly reduced.
Another important new element in this study is the form of the goal function in the model. In the literature, one can often find objective functions composed of several parts that are linked by weighting factors. This approach is very risky when an analyst considers the fact that VRPTW tasks are a specific class of scheduling problems. When facing problems with scheduling tasks on machines, complex multi-objective functions do not work and often produce results that are difficult to verify. An introduction to the construction of the objective function for these tasks is given by Brucker [28], and a more advanced version is given by Brucker et al. [29]. The presented model uses objective functions composed of one or, at most, two components. In particular, it is worth paying attention to objective function no. II (26), in which the lengths of the swarm’s flight paths are minimized. The flight on the segment where the UAV does not recognize the object means a penalty; i.e., the function increases its value. The flight over the segment where the UAV recognizes the object is a form of reward because it reduces the value of the goal function. The range of the lengths of the flight segments on which the UAVs fly is close to the value of profits from the flight on the reconnaissance segments, so the objective function can be treated as being composed of one part. In the case of objective function no. I (25), the situation is similar because the profits from the recognition of important route segments and the flight through the indicated terrain points are added up. This formulation of the objective function allows the model to be used on networks with different weights on the arcs.
The model presented in this article also shows the method of modeling the operation of the UAV by collecting data from individual UAVs and sending them to the GCS. In the opposite direction, it involves taking orders from the GCS and transmitting them to individual UAVs. As far as we know, there are no existing models in the literature that depict swarms of drones operating according to this particular scheme. In particular, it was not possible to find a model in which the UAV transmitting information between other UAVs and GCSs can independently carry out reconnaissance using the sensors it is equipped with. Knowing the characteristics of SARs, it can be said that the UAV retranslator can carry out reconnaissance from longer distances, for which SAR is very suitable.
6. Conclusions
This article discusses the planning of a drone swarm mission in a terrain using the MILP model. The terrain is represented using the S connection network. We provide a detailed explanation of how to construct this network and describe the objective functions that can be utilized in the optimization task. It also highlights the limitations of the optimization task, particularly those related to the co-operation principles of individual UAVs within the swarm.
Furthermore, this article introduces a version of the MILP model that incorporates an information hub UAV responsible for communication between the swarm and the GCS. The information hub UAV can also carry out reconnaissance tasks from greater distances, which is a feature commonly found in SAR-equipped systems.
The time required to solve the problem using the exact algorithm does not hinder its practical application with GCSs. Even small-sized GCSs are equipped with efficient computing systems capable of handling optimization tasks. While the use of approximate algorithms is feasible in practice, we do not delve into this topic due to the substantial existing literature on the subject. However, none of these articles referenced the swarm operation model presented in this article.
Author Contributions
Conceptualization, R.P. and W.S.; methodology, software, validation, W.S.; writing—original draft preparation, W.S.; writing—review and editing, R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This article was partly funded by the assistance of the Military University of Technology.
Data Availability Statement
All test data were generated.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| ANT | Ant colony optimization |
| EO/IR | Electro-optical/Infra-red |
| GA | Genetic Algorithm |
| GCS | Ground Control Station |
| PSO | Particle Swarm Optimization |
| RRT | Rapidly exploring Random Tree |
| SAR | Synthetic Aperture Radar |
| TS | Tabu Search |
| UAV | Unmanned Aerial Vehicle |
| VRP | Vehicle Route Planning |
| VRPTW | Vehicle Route Planning with Time Windows |
References
- Stecz, W.; Gromada, K. UAV Mission Planning with SAR Application. Sensors 2020, 20, 1080. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lu, D.; Zhang, Y.; Wang, X. A Complex Network Theory-Based Modeling Framework for Unmanned Aerial Vehicle Swarms. Sensors 2018, 18, 3434. [Google Scholar] [CrossRef] [PubMed]
- Bertsimas, D.; Sim, M. The Price of Robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Hu, C.; Lu, J.; Liu, X.; Zhang, G. Robust vehicle routing problem with hard time windows under demand and travel time uncertainty. Comput. Oper. Res. 2018, 94, 139–153. [Google Scholar] [CrossRef]
- Boskovic, J.; Prasanth, R.; Mehra, R. A multi-layer autonomous intelligent control architecture for unmanned aerial vehicles. J. Aerosp. Comput. Inf. Commun. 2004, 1, 605–628. [Google Scholar] [CrossRef]
- Zhou, Y.; Rao, B.; Wang, W. UAV Swarm Intelligence: Recent Advances and Future Trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Song, B.; Park, K.; Kim, J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Comput. Ind. Eng. 2018, 120, 418–428. [Google Scholar] [CrossRef]
- Chung, S.; Sah, B.; Lee, J. Optimization for drone and drone-truck combined operations: A review of the state of the art and future directions. Comput. Oper. Res. 2020, 123, 105004. [Google Scholar] [CrossRef]
- Brand, M.; Masuda, M.; Wehner, N.; Yu, X.H. Ant colony optimization algorithm for robot path planning. In Proceedings of the 2010 International Conference On Computer Design and Applications, Qinhuangdao, China, 25–27 June 2010; pp. 436–440. [Google Scholar] [CrossRef][Green Version]
- Butenko, S.; Murphey, R.; Pardalos, P. Cooperative Control: Models, Application and Alogorithms, 1st ed.; Kuwer Press: Noida, India, 2006. [Google Scholar]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Luo, R.; Zheng, H.; Guo, J. Solving the Multi-Functional Heterogeneous UAV Cooperative Mission Planning Problem Using Multi-Swarm Fruit Fly Optimization Algorithm. Sensors 2020, 20, 5026. [Google Scholar] [CrossRef]
- Singgih, I.; Lee, J.; Kim, B. Node and Edge Drone Surveillance Problem With Consideration of Required Observation Quality and Battery Replacement. IEEE Access 2020, 8, 44125–44139. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.; Geng, N. A memetic algorithm with iterated local search for the capacitated arc routing problem. Int. J. Prod. Res. 2013, 51, 3075–3084. [Google Scholar] [CrossRef]
- Chow, J. Dynamic UAV-based traffic monitoring under uncertainty as a stochastic arc-inventory routing policy. Int. J. Transp. Sci. Technol. 2016, 5, 167–185. [Google Scholar] [CrossRef]
- Schneider, M. The vehicle-routing problem with time windows and driver-specific times. Eur. J. Oper. Res. 2016, 250, 101–119. [Google Scholar] [CrossRef]
- Lu, F.; Jiang, R.; Bi, H.; Gao, Z. Order Distribution and Routing Optimization for Takeout Delivery under Drone–Rider Joint Delivery Mode. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 774–796. [Google Scholar] [CrossRef]
- Lu, F.; Chen, W.; Feng, W.; Bi, H. 4PL routing problem using hybrid beetle swarm optimization. Soft Comput 2023, 27, 17011–17024. [Google Scholar] [CrossRef]
- Amine Masmoudi, M.; Mancini, S.; Baldacci, R.; Kuo, Y.H. Vehicle routing problems with drones equipped with multi-package payload compartments. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102757. [Google Scholar] [CrossRef]
- Gromada, K.; Stecz, W. Determining UAV Flight Trajectory for Target Recognition Using EO/IR and SAR. Sensors 2020, 20, 5712. [Google Scholar] [CrossRef]
- Lee, W.; Choi, G.H.; wan Kim, T. Visibility graph-based path-planning algorithm with quadtree representation. Appl. Ocean Res. 2021, 117, 102887. [Google Scholar] [CrossRef]
- Kelner, J.; Burzynski, W.; Stecz, W. Modeling UAV swarm flight trajectories using Rapidly-exploring Random Tree algorithm. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 101909. [Google Scholar] [CrossRef]
- Burzynski, W.; Stecz, W. Trajectory planning with multiplatform spacetime RRT*. Appl. Intell. 2024, 54, 9524–9541. [Google Scholar] [CrossRef]
- Williams, H. Model Building in Mathematical Programming, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lin, M.; Carlsson, J.; Ge, D.; Shi, J.; Tsai, J. A Review of Piecewise Linearization Methods. Math. Probl. Eng. 2013, 11, 1–8. [Google Scholar] [CrossRef]
- Soyster, A. Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 1973, 21, 1154–1157. [Google Scholar] [CrossRef]
- IBM. CPLEX; IBM: Armonk, NY, USA, 2023. [Google Scholar]
- Brucker, P. Scheduling Algorithms, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Brucker, P.; Knust, S. Complex Scheduling, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).