YOLO-RWY: A Novel Runway Detection Model for Vision-Based Autonomous Landing of Fixed-Wing Unmanned Aerial Vehicles

Abstract

In scenarios where global navigation satellite systems (GNSSs) and radio navigation systems are denied, vision-based autonomous landing (VAL) for fixed-wing unmanned aerial vehicles (UAVs) becomes essential. Accurate and real-time runway detection in VAL is vital for providing precise positional and orientational guidance. However, existing research faces significant challenges, including insufficient accuracy, inadequate real-time performance, poor robustness, and high susceptibility to disturbances. To address these challenges, this paper introduces a novel single-stage, anchor-free, and decoupled vision-based runway detection framework, referred to as YOLO-RWY. First, an enhanced data augmentation (EDA) module is incorporated to perform various augmentations, enriching image diversity, and introducing perturbations that improve generalization and safety. Second, a large separable kernel attention (LSKA) module is integrated into the backbone structure to provide a lightweight attention mechanism with a broad receptive field, enhancing feature representation. Third, the neck structure is reorganized as a bidirectional feature pyramid network (BiFPN) module with skip connections and attention allocation, enabling efficient multi-scale and across-stage feature fusion. Finally, the regression loss and task-aligned learning (TAL) assigner are optimized using efficient intersection over union (EIoU) to improve localization evaluation, resulting in faster and more accurate convergence. Comprehensive experiments demonstrate that YOLO-RWY achieves ${\mathrm{AP}}_{50:95}$ scores of 0.760, 0.611, and 0.413 on synthetic, real nominal, and real edge test sets of the landing approach runway detection (LARD) dataset, respectively. Deployment experiments on an edge device show that YOLO-RWY achieves an inference speed of 154.4 FPS under FP32 quantization with an image size of 640. The results indicate that the proposed YOLO-RWY model possesses strong generalization and real-time capabilities, enabling accurate runway detection in complex and challenging visual environments, and providing support for the onboard VAL systems of fixed-wing UAVs.

1. Introduction

The approach and landing phase of flight is among the most challenging and hazardous, making a stable and safe landing process critical [1]. Successful landing requires precise alignment of the aircraft flight path with the runway centerline, ensuring passage through the designated touchdown point while maintaining the correct glide slope and descent rate [2]. To reduce pilot workload during landing and enhance safety, instrument approach procedures (IAPs) have been developed, supplementing visual landings where pilots must control the aircraft landing based on ground references [3]. The IAPs are categorized into three types: precision approaches (PAs), which provide both lateral and vertical guidance; approaches with vertical guidance (APV), which also offer guidance in both directions but do not meet PA standards; and non-precision approaches (NPAs), which provide only lateral guidance [4]. The PAs include systems such as the instrument landing system (ILS), microwave landing system (MLS), and ground-based augmentation system (GBAS) landing system (GLS). The APV include approaches like the localizer performance with vertical guidance (LPV). The NPAs include approaches such as the very-high frequency omnidirectional range (VOR) and non-directional beacon (NDB) approaches. During PA and APV procedures, aircraft are allowed to descend to the decision altitude/height (DA/H), whereas, during NPA procedures, aircraft are permitted to descend to the minimum descent altitude/height (MDA/H).

However, IAPs are heavily dependent on the proper functioning of ground-based radio navigation systems and global navigation satellite systems (GNSSs) [5]. These systems rely on active external signals, are typically expensive, and require complex installation and deployment. Moreover, IAPs are susceptible to obstacles and electromagnetic interference and can be misled by spoofing, potentially compromising the safety of the landing process [5]. Additionally, IAPs generally guide the aircraft only to a certain minimum altitude or height, after which the pilot must manually control the landing [6].

Given these limitations, the development of a vision-based autonomous landing (VAL) system, which provides real-time, accurate runway position and orientation guidance during landing, is essential and urgently needed to enhance the autonomy and intelligence of fixed-wing unmanned aerial vehicles (UAVs) [1]. VAL systems rely on visual sensors, such as visible light and infrared cameras, to perceive the environment, offering advantages like low cost, lightweight design, easy installation, rich visual features, and independence from external active signals. These systems significantly reduce the risk of signal interference and spoofing, thereby improving the safety of autonomous landing [7]. VAL systems can operate independently to enable fully autonomous landing using visual sensors or can be supplemented into existing integrated navigation systems [7]. By providing a vision-based virtual landing guidance path, VAL systems allow the UAV to assess runway alignment and determine whether the glide angle is appropriate [8]. As a crucial component of VAL, runway detection models provide the locations and sizes of runways in the pixel coordinate system, which can be used to further estimate the relative position and pose between the UAV and the runway [9].

Existing runway detection models for VAL applications can be broadly categorized into three types: image processing-based models, machine learning-based models, and deep learning-based models. Image processing-based models rely on techniques such as edge detection [10], line detection [11], template matching [12], feature extraction [13], feature matching [13], and their combinations. Machine learning-based models typically begin by extracting candidate regions where a runway might be present [14], treating runway detection as a classification task in which pretrained classifiers are used to identify the candidates [15].

However, image processing-based models generally require high image quality and are heavily dependent on expert knowledge and carefully designed parameters tailored to specific scenarios. While these models may be effective in certain situations, their applicability is limited. Overall, image processing-based models often suffer from poor robustness and generalization, severely limiting their broader applicability. Machine learning-based models rely on image processing techniques to construct handcrafted features and require repetitive classification, which limits their accuracy, generalization, and efficiency, rendering them insufficient for practical applications.

Deep learning, with its specifically designed architectures and high capacity, excels at autonomously learning task-specific feature representations from large-scale training datasets [16]. This capability has led to outstanding performance in autonomous systems. Deep learning-based models have been widely applied across various UAV domains, including human detection [17], vehicle detection [18], power grid inspection [19], drone detection [20], ship detection [21], smart agriculture [22], and more, covering a broad range of tasks in both civilian and industrial domains. Therefore, recent advancements in deep learning and edge devices have enabled the development and deployment of high-precision, high-reliability, and low-latency runway detection models for onboard VAL systems [1,2,5,6,7,23,24,25,26]. In addition, the recent release of several publicly available datasets for runway detection or segmentation during landing has further facilitated the development of deep learning-based runway detection models [1,2,7,27].

Although deep learning-based runway detection models have made notable progress, the specific requirements of runway detection for fixed-wing UAVs urgently present the following challenges that need to be addressed:

• With the ability to hover, rotary-wing UAVs utilize a relatively straightforward landing control strategy [6], therefore VAL has been successfully applied to rotary-wing UAVs [28,29,30]. In contrast, fixed-wing UAVs have much higher speeds, requiring the establishment of a stable landing configuration [31]. This results in a lower error tolerance, making the landing more challenging [32]. Moreover, in the safety-critical aviation field, runway detection models in VAL systems must meet rigorous requirements for robustness and safety. This necessitates sufficient stability, resistance to interference, and the ability to withstand potential adversarial attacks [26,33].
• Rotary-wing UAVs typically rely on downward-facing cameras to detect landing targets that are visually simple and specifically designed for easy recognition, often operating under favorable visual conditions [6]. In contrast, fixed-wing UAVs often operate in large-scale environments and perform long-endurance missions, where landing runways present complex textures, backgrounds, lighting conditions, perspectives, and weather, making accurate detection and positioning more difficult [23].
• Previous research primarily utilizes satellite remote-sensing runway datasets [34]. However, VAL systems require images captured by forward-looking cameras during landing, which is more vulnerable to challenges posed by complex lighting, atmospheric conditions, adverse weather, unique perspectives, and distortions [27]. Acquiring front-looking runway images is challenging due to flight management and safety considerations, leading to a lack of large-scale, high-quality, and diverse runway detection datasets. Although simulation engines can generate synthetic images, there is still a considerable disparity in diversity and feature distribution [27].
• Due to constraints on computational load, power consumption, and the weight of onboard embedded devices, VAL requires lightweight runway detection models that balance real-time performance and accuracy, thereby minimizing the impact on flight performance [24].

In conclusion, there is an urgent need for deep learning-based runway detection models to deliver high accuracy, low latency, and robust performance in complex environments, despite the limited availability of real-world samples and the insufficient realism of synthetic ones. This necessitates that runway detection models be capable of handling runway detection across different distances, scales, angles, and shapes under varying weather, lighting, and visual disturbance conditions.

To address these challenges, this paper proposes a novel deep learning-based runway detection model framework, YOLO-RWY. Experiments demonstrate that the proposed YOLO-RWY can accurately detect runways during landing, under various complex environments, exhibiting excellent real-time performance, accuracy, and robustness. Experiments on an edge device further show that the proposed YOLO-RWY achieves high inference speed, making it suitable for deployment on onboard edge devices of fixed-wing UAVs. The main contributions of this paper are summarized as follows:

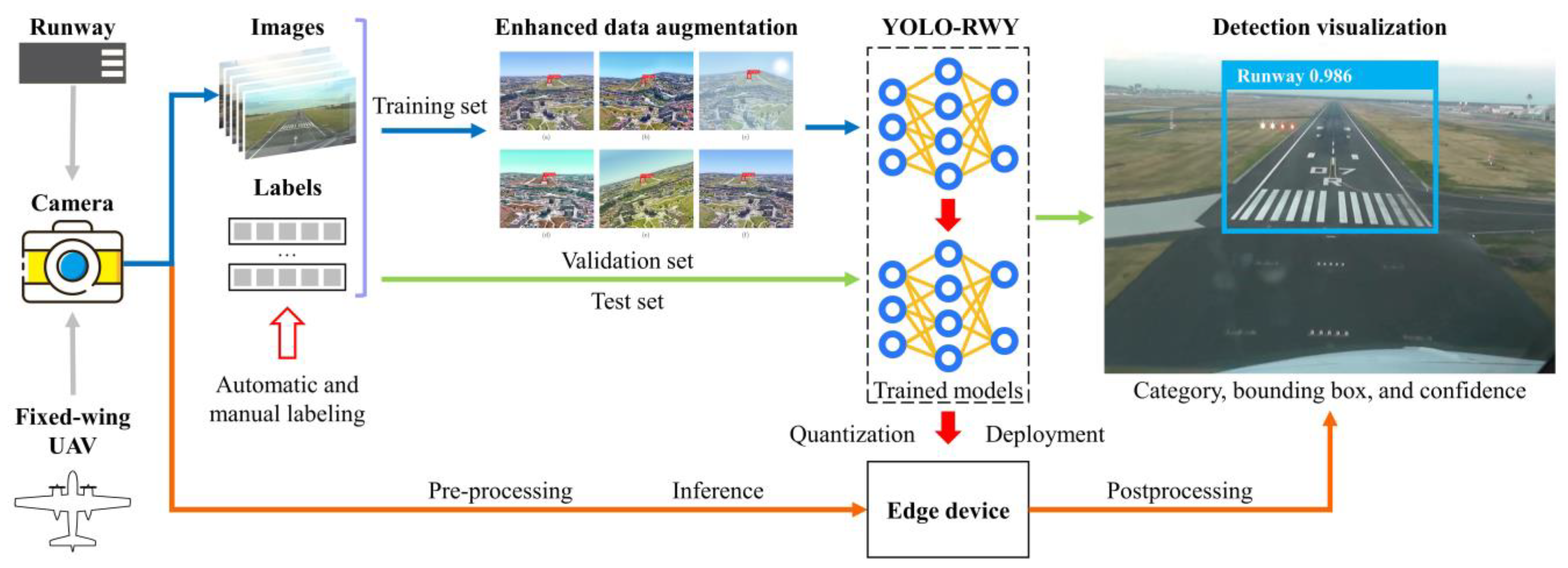
• The YOLO-RWY model is constructed based on the powerful single-stage, anchor-free, and decoupled you only look once v8 (YOLOv8) model architecture, with several key modules introduced to optimize the landing runway detection performance. The proposed model meets the requirements of the VAL system for accurate and real-time runway perception.
• Given the limitations of training images regarding representation diversity and the safety requirements in aviation applications for resisting disturbances, an enhanced data augmentation (EDA) module is proposed. EDA provides richer, more diverse, and more complex augmentations during training, including methods for augmenting color, geometry, blur, weather, and image quality. By randomly applying these augmentations, perturbations and enhancements are introduced, and the generalization, robustness, and safety of the model are improved, enabling accurate runway detection under various complex conditions.
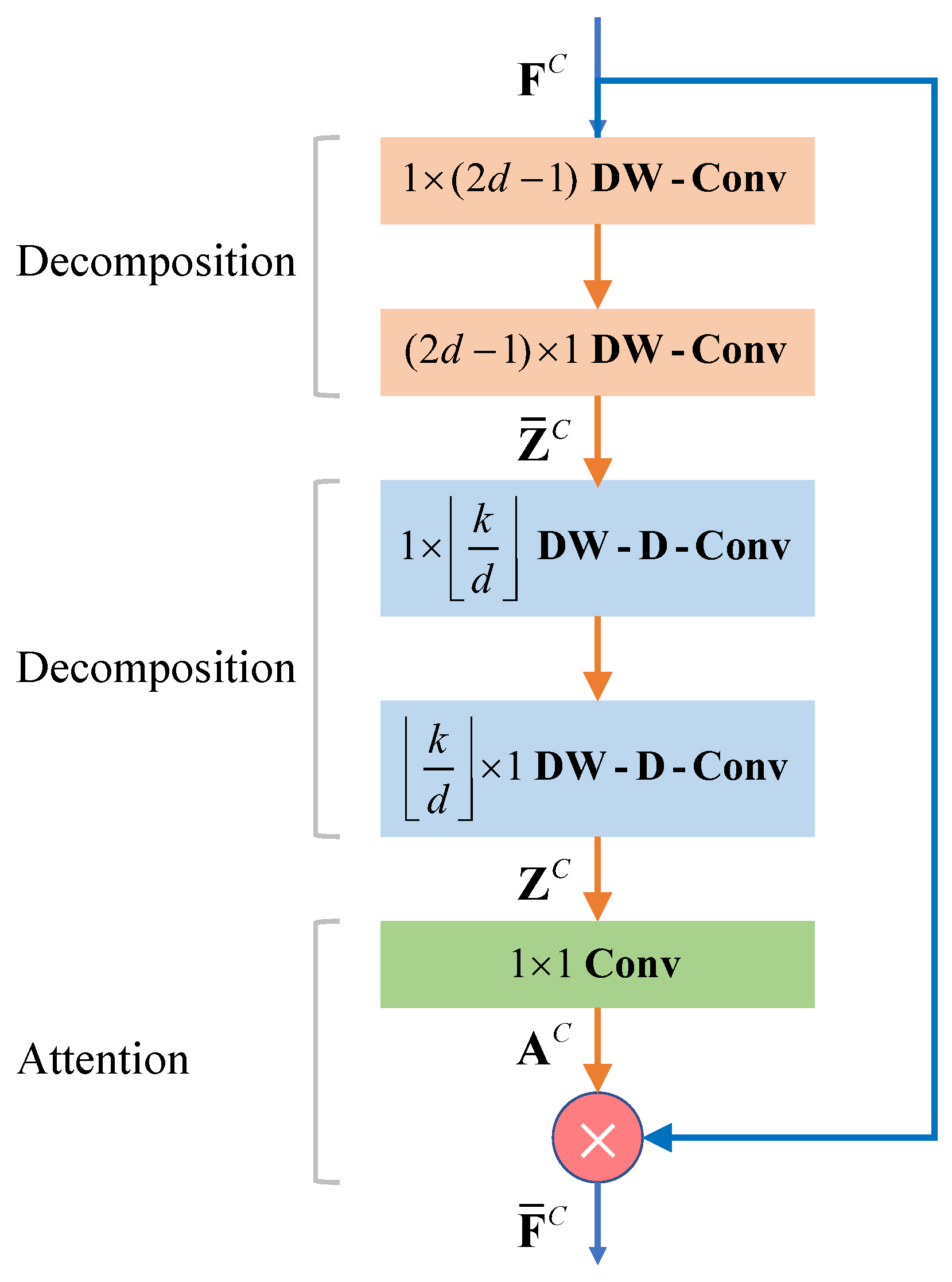
• To account for variations in runway scales, orientations, aspect ratios, textures, backgrounds, and visual disturbances, three key modules, namely large separable kernel attention (LSKA), bidirectional feature pyramid network (BiFPN), and efficient intersection over union (EIoU) are introduced to optimize the model structure and training. (a) LSKA enhances long-range dependency modeling capabilities using large kernels and encodes more shape-related information, aiding in detecting runways with varying shapes. (b) BiFPN offers lightweight, weighted multi-scale feature aggregation, beneficial for detecting runways of different scales and distances. (c) EIoU provides a more comprehensive and effective description of bounding box differences, optimizing both the sample assignment and regression loss, thereby improving model convergence and performance.
• Extensive experiments demonstrate the superior accuracy, speed, and robustness of the proposed YOLO-RWY model. Experiments show that the proposed model achieves an accuracy of 0.760, 0.611, 0.413, and 0.578 on the synthetic, real nominal, real edge, and overall real test sets, respectively, with improvements of 0.8%, 4.3%, 18.7%, and 6.1%, despite being trained solely on the training set composed of synthetic samples. When further finetuned with real-world data, the proposed model demonstrated a 40.2% performance improvement on the real edge test set, increasing from 0.413 to 0.579. These results demonstrate the superior performance of the proposed YOLO-RWY model. Experiments on the edge computing device Jetson AGX Orin show that the ${\mathrm{AP}}_{50:95}^{\mathrm{real}}$ and FPS are 0.578 and 154.4 for an input size of 640, and 0.707 and 46.0 for an input size of 1280. Both configurations show superior accuracy and real-time performance, and meet the practical requirements for onboard deployment of fixed-wing UAVs.

The remainder of this paper is organized as follows: Section 2 reviews related works on runway detection models. Section 3 presents the framework and architecture of YOLO-RWY, introducing the key improvement modules. Section 4 describes the datasets, evaluation metrics, experiment settings, and detailed experiments. Section 5 provides a comprehensive conclusion.

2. Related Works

2.1. Image Processing-Based Models

Ding et al. proposed a runway recognition method based on template matching [12]. The method first uses threshold segmentation to separate the runway from the background, followed by a search using binary templates to locate the runway. The location of the detected runway is then provided as an initial guess for subsequent searches to reduce search time. Experiments demonstrated that this method is both fast and accurate. Marianandam et al. introduced a runway line detection method utilizing Canny edge detection and Hough transform, aimed at runway alignment for fixed-wing UAVs [10]. Experiments confirmed that the method could successfully align the UAV with the runway using only visual input. Wu et al. proposed a visual runway detection method using forward-looking infrared (FLIR) images [11]. The method begins with line extraction using a line segment detector (LSD) and an improved line segment linking method, then extracting regions of interest (ROI) based on constraints. The ROI is then traced back based on texture distribution to identify the entire runway. Finally, similarity and contextual information are used to recognize the runway. Experiments showed that the method has good robustness and real-time performance. Tsapparellas et al. proposed an autonomous visual landing method for UAVs, combining scale-invariant feature transform (SIFT) and speeded-up robust features transform (SURF) for feature extraction, feature matching, and channel and spatial reliability tracker (CSRT) for runway tracking [13]. Experiments showed that the method achieves an accuracy of 94.89% under clear weather, with an average image processing time of 0.23 s, indicating real-time capability.

2.2. Machine Learning-Based Models

Liu et al. proposed a system based on regularized discriminant analysis (RDA) for recognizing airports using FLIR images [14]. The system first employs clustering segmentation to isolate candidate objects, followed by morphological filtering for processing. Invariant moments are then used as features, and a dual-parameter RDA classifier is utilized to identify airports. Experiments demonstrated that the system performs quite well. Fan et al. introduced a runway detection method using onboard front-looking camera images. The method first detects ROIs using saliency maps constructed with the spectral residual (SR) method, followed by feature extraction using sparse coding spatial pyramid matching (ScSPM). Finally, a trained linear support vector machine (SVM) is used to identify the ROIs [15]. Experiments confirmed the accuracy and effectiveness of the proposed method.

2.3. Deep Learning-Based Models

Deep learning-based runway detection models exhibit strong generalization capabilities, effectively addressing the issues of low accuracy and efficiency. These models can operate in various complex scenarios and demonstrate robustness against abnormal disturbances.

Table 1. Recent runway detection and segmentation literature based on deep learning.

Task	Ref.	Dataset Type	Dataset	Contributions
Det	[6]	Simulated (FlightGear)	-	1. Detection under low-light conditions at night; 2. Fusion of visible light and infrared images; 3. Improved Faster-RCNN runway detection model; 4. UAV relative pose estimation with respect to runway.
	[5]	Simulated (Vega Prime) and real	-	1. Enhanced YOLOX for coarse runway localization; 2. Precise runway line detection algorithm; 3. Vision-based localization and vision/inertial fusion navigation.
	[23]	Simulated (Prepar3D)	AIRport LAnding Dataset (AIRLAD)	1. Synthesizing adverse weather using vision-language models; 2. Mitigating visual degradations using distillation models; 3. Image transformation under crosswind landings using RuSTaN; 4. Detecting runway elements in images using YOLOv8.
	[24]	Simulated (UE platform) and real	Aerovista Runway Dataset (ATD)	1. Runway detection algorithm tailored for edge devices; 2. Combining YOLOv10 and MobileNetv3 for better performance; 3. Without the need for non-maximum suppression (NMS); 4. Runway keypoint detection and corresponding Wing loss.
	[25]	Simulated (Airsim)	-	1. Vision-based landing for carrier-based UAVs (CUAV); 2. Image dehazing model based on CNN and Transformer; 3. Ultra-fast lane detection (UFLD) for runway line detection; 4. Random sample consensus (RANSAC) for outlier removal.
	[26]	Simulated (Google Earth Studio) and real	Landing Approach Runway Detection (LARD)	1. Runway detection based on federated adversarial learning; 2. Enhanced data privacy and robustness against adversarial attacks; 3. Reduced communication using scale and shift deep features (SSF); 4. Fine-tuning based on lane detection vision transformer (ViT).
Seg	[7]	Simulated (Microsoft Flight Simulator 2020)	FS2020	1. Real-time efficient runway feature extractor (ERFE); 2. Both semantic segmentation and feature line probability maps; 3. Feature line reconstruction using weighted regression; 4. Improved benchmark for evaluating feature line error.
	[2]	Simulated (X-Plane 11)	Benchmark for airport runway segmentation (BARS)	1. Semi-automatic annotation pipeline for runway images; 2. Smoothing postprocessing module (SPM) for smoothing masks; 3. Contour point constraint loss (CPCL) for smoothing contours; 4. Average smoothness (AS) metric to evaluate the smoothness.
	[1]	Simulated (X-Plane 11) and real	Runway Landing Dataset (RLD)	1. Context enhancement module (CEM) for effective features; 2. Asymptotic feature pyramid network (AFPN) for semantic gaps; 3. Orientation adaptation module (OAM) for rotational information.

presents recent studies on deep learning-based runway detection (Det) and segmentation (Seg) models.

Deep learning-based runway detection models in Table 1 can be classified into two-stage and one-stage detection models.

For two-stage models, Wang et al. proposed a runway detection framework for automatic landing under low-light conditions at night [6]. The framework first fuses visible light and infrared images to overcome the challenges posed by low-light scenarios, followed by an improved faster region-based convolutional neural network (Faster R-CNN) for runway detection. Experiments showed that the model improves the detection accuracy. For one-stage models, Liu et al. introduced a runway line detection model and an integrated navigation method. The approach includes coarse runway ROI detection based on an improved you only look once X (YOLOX) model, followed by runway line detection, visual positioning, and integrated navigation [5]. Experiments demonstrated that the proposed algorithm significantly excels in accuracy, real-time performance, and generalization. Pal et al. proposed a runway detection framework to tackle challenges posed by adverse weather and crosswinds during landing. The framework includes a visual language weather diffusion model for synthesizing different meteorological conditions, a weather distillation model for mitigating meteorological impacts, a regularized spatial transformer network (RUSTAN) for geometric distortion calibration, and a YOLOv8 model for runway element detection [23]. Experiments indicated that the framework offers real-time situational awareness, meeting the requirements for visual landing. Dai et al. introduced a lightweight runway feature detection model specifically designed for edge devices, referred to as YOMO-Runwaynet [24]. The model combines the feature extraction capabilities of you only look once v10 (YOLOv10) model with the computational speed advantages of MobileNetV3 model, incorporating a lightweight attention module and enhancements to MobileNetV3. The model generates a single optimal prediction for each object, eliminating the need for postprocessing using non-maximum suppression (NMS) and therefore improving inference speed. Experiments demonstrated that the proposed model achieves high accuracy and real-time performance.

Several studies in Table 1 employ semantic and instance segmentation models for runway segmentation. Compared to object detection, these models provide pixel-level understanding and can accurately delineate runway regions instead of merely giving bounding boxes. Chen et al. proposed an efficient runway feature extractor (ERFE) based on a deep convolutional neural network, which provides runway semantic segmentation and runway lines for real-time detection [7]. Experiments showed that the model exhibits excellent performance and satisfactory generalization. Wang et al. developed a vision-based autonomous landing segmentation network (VALNet), combining a context enhancement module (CEM) and an orientation adaptation module (OAM) to overcome large-scale variations and significant image angle changes in runway instance segmentation [1]. Experiments demonstrated the effectiveness and interpretability of the model.

Deep learning-based models adaptively extract and learn complex and task-related feature representations from runway image samples, offering improved robustness and accuracy and enabling end-to-end landing runway detection. However, existing deep learning models still face numerous challenges in detecting runway targets of varying scales, shapes, and backgrounds in complex environments. To address these issues, this paper proposes the YOLO-RWY model.

3. Methodologies

3.1. Runway Detection Framework

The framework of the proposed YOLO-RWY consists of several stages: image acquisition, image annotation, data augmentation, model training and validation, model test, result visualization, and deployment, as illustrated in Figure 1. First, onboard cameras of fixed-wing UAVs capture runway images during landing. Next, the runway images are annotated either automatically or manually. The labeled dataset is then divided into training, validation, and test sets for model development. Following this, the online augmented training samples are used to train the YOLO-RWY model, with the validation set employed for validation during training. After training is completed, the model is evaluated on the test set. The detection results are visualized to intuitively demonstrate the effectiveness of runway detection. Finally, the trained model, after quantization, can be deployed on edge devices for onboard VAL applications of fixed-wing UAVs.

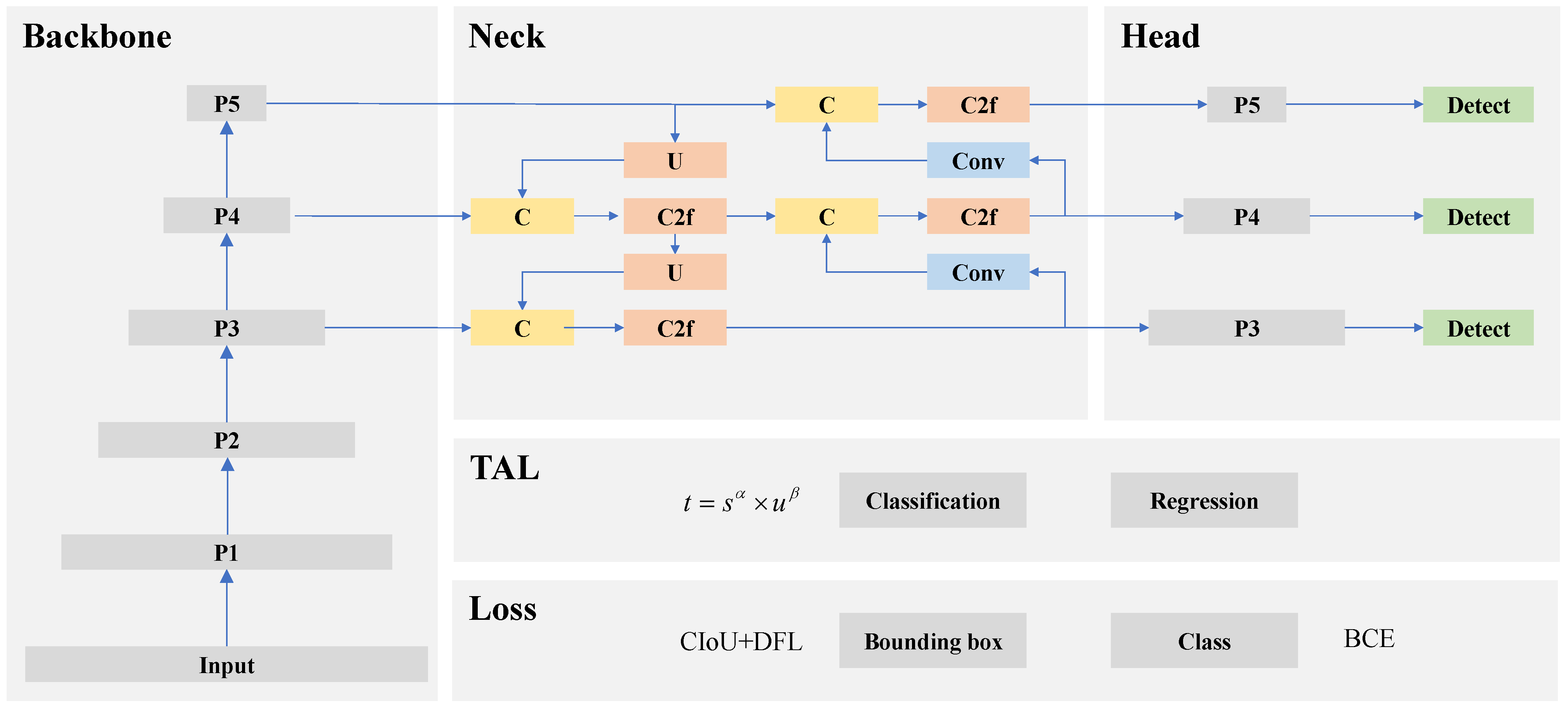
3.1.1. Object Detection Framework: You Only Look Once V8

YOLOv8 is a one-stage, anchor-free, and decoupled object detection framework that achieves high accuracy while maintaining a small size and excellent real-time performance [35]. The network structure of YOLOv8 consists of three main components: the backbone, neck, and head [1]. The backbone is designed based on the cross-stage partial network (CSPNet), which learns feature representations from images and produces feature maps with different resolutions and semantic information. The neck employs a path aggregation network and feature pyramid network (PAN-FPN) architecture [36], utilizing top-down and bottom-up pathways to perform multi-scale feature fusion. The improved C2f (faster implementation of CSP bottleneck with two convolutions) module is used in both the backbone and neck, reducing the number of parameters while introducing richer gradient flows, thereby enhancing both convergence speed and performance. The head adopts a decoupled architecture, separating the classification and regression tasks into distinct branches. Multiple detection heads provide candidate detections at different scales, improving the detection of objects at varying scales. The regression head employs an integral bounding box prediction strategy to address boundary ambiguity, which requires further decoding to obtain conventional coordinate representations.

The decoupled classification and regression heads focus on identifying salient features for classification and localization, respectively. Therefore, the learned features of the two heads may differ, leading to potential misalignment and inconsistency. To address this, YOLOv8 employs a task-aligned learning (TAL) assigner that selects positive samples based on weighted scores of classification and regression for dynamic sample assignment. The TAL assigner guides the model to predict bounding boxes that are highly consistent in classification and localization, thereby optimizing model convergence.

The loss function comprises regression loss and classification loss. The regression loss includes distribution focal loss (DFL) and complete intersection over union (CIoU) loss, while the classification loss is calculated using binary cross-entropy (BCE) loss. During training, an online data augmentation pipeline that includes Mosaic and Mixup augmentations is used, with Mosaic being turned off at the end of training for better performance. The schematic diagram of the YOLOv8 model is shown in Figure 2.

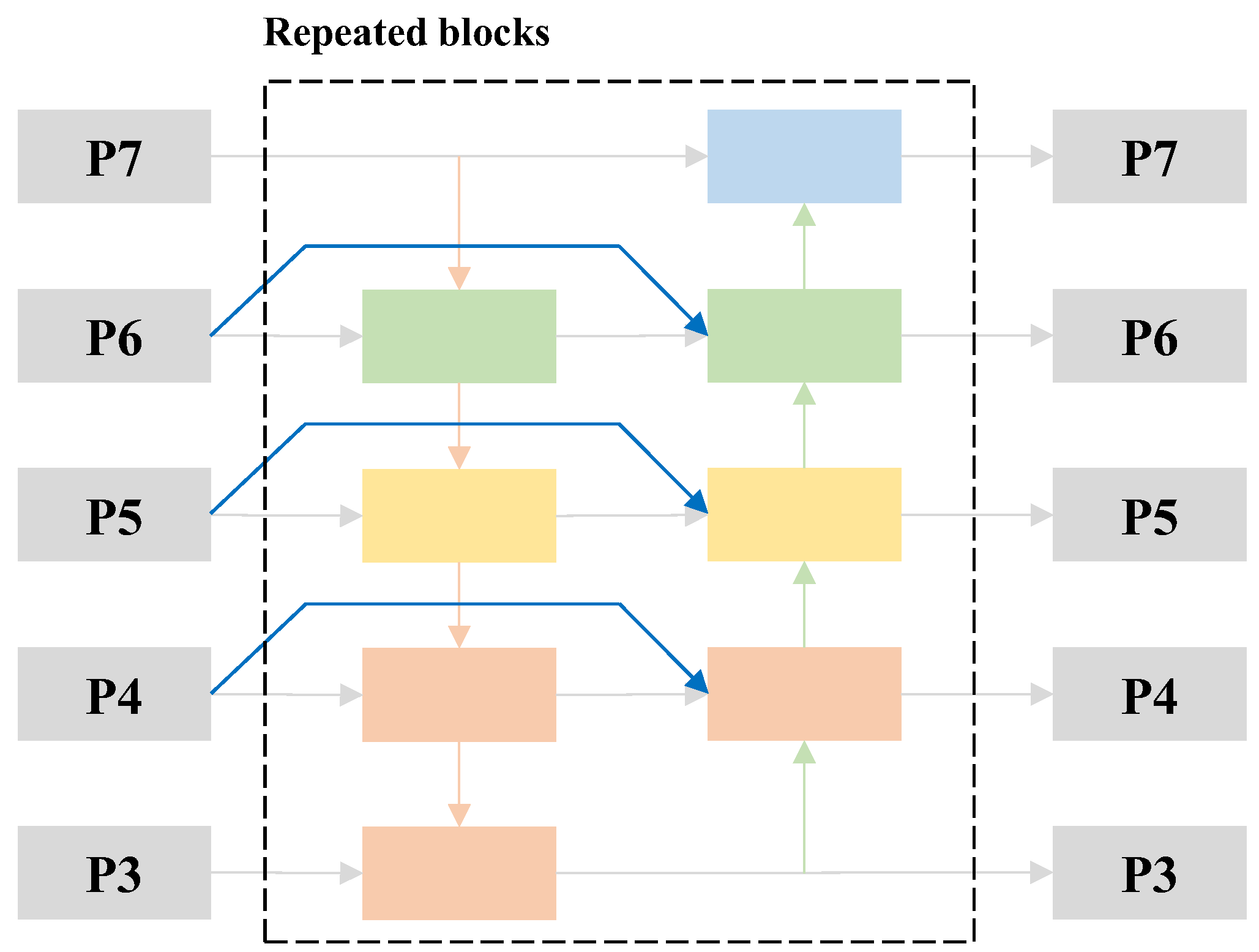
3.1.2. Structure of the Proposed YOLO-RWY Model

The proposed runway detection model, YOLO-RWY, is developed and improved based on the YOLOv8 framework. The following enhancements or modifications are introduced to optimize the runway detection performance:

• The enhanced data augmentation (EDA) module is employed during training to introduce more diverse images, thereby improving model generalization and safety.
• The large separable kernel attention (LSKA) module is integrated into the backbone structure to enhance feature representation by introducing a visual attention mechanism.
• The bidirectional feature pyramid network (BiFPN) module is introduced to reconfigure the neck structure and improve feature aggregation.
• The efficient intersection over union (EIoU) is integrated into the TAL assigner to form an efficient task-aligned learning (ETAL) assigner, optimizing sample assignment and accelerating convergence.
• The EIoU is also incorporated into the regression loss to form an EIoU loss, providing a more accurate bounding box description and better convergence guidance.

The schematic diagram of the proposed YOLO-RWY model is shown in Figure 3.

3.2. Key Improvement Modules of the Proposed Model

3.2.1. Enhanced Data Augmentation Module

Data augmentation creates new samples from existing images to enhance data diversity, thereby suppressing overfitting and improving generalization [37]. The EDA module is proposed to handle the specific challenges of landing runway detection. The necessity of the EDA module can be explained in detail from the following perspectives:

• High similarity among samples in runway detection datasets: The EDA module is essential for reducing redundancy due to the high similarity of samples within runway detection datasets. Numerous images are continuously captured and sampled during landing, resulting in highly similar adjacent images. Overall, the similarity in the runway detection datasets is much higher than in the conventional task datasets.
• Limitations and idealisms of synthetic runway detection datasets: Synthetic runway detection datasets are constructed using ideal camera imaging models and are often based on satellite maps captured under favorable weather conditions. This leads to a lack of representation of real-world scenarios, necessitating the EDA module to improve diversity.
• Safety considerations in applying deep learning in aviation: Numerous safety considerations arise when applying deep learning models in the aviation industry, necessitating the EDA module to introduce various perturbations and implicit regularization, thereby enhancing robustness and safety [38]. Deep learning models are susceptible to input perturbations, which can lead to unreliable detections. Additionally, these models may be vulnerable to adversarial attacks that are imperceptible to humans but significantly disruptive to models.

The EDA module is composed of pixel-level and spatial-level transformations. Pixel-level transformations alter images without affecting labels, enhancing diversity in terms of color, hue, brightness, contrast, sharpness, noise, blur, image quality, weather, and more. Spatial-level transformations modify both the images and labels, enhancing diversity in terms of position, orientation, scale, field of view, and distortion, among other factors. By applying these augmentation transformations, the overfitting to the training samples can be mitigated, significantly improving the model performance under adverse conditions such as complex lighting, weather, noise, and varying perspectives, thus enhancing the robustness and accuracy of runway detection.

The EDA module applies augmentations randomly, combined with the original augmentation pipeline of YOLOv8, to form a comprehensive augmentation pipeline. The structure of the EDA module is detailed in

Table A1. Structure of the EDA module.

Composition #1	Composition #2	Group	Transformation Methods
Compose	One of	Color	Random tone curve, Solarize, Posterize, Equalize, RGB shift, Random brightness contrast, Gauss noise, ISO noise, CLAHE, Channel shuffle, Invert image, Random gamma, To gray, To sepia, Downscale, Multiplicative noise, Fancy PCA, Color jitter, Sharpen, Emboss, Superpixels, Ringing overshoot, Unsharp mask, Pixel dropout, and Spatter.
	One of	Blur	Blur, Motion blur, Median blur, Gaussian blur, Glass blur, Advanced blur, Defocus, and Zoom blur.
	One of	Geometric	Shift scale rotate, Elastic transform, Perspective, Affine, Piecewise affine, Vertical flip, Horizontal flip, Flip, Optical distortion, Grid distortion, Channel dropout.
	One of	Weather	Random rain, Random snow, Random fog, Random shadow, and Random sun flare.
	One of	Quality	Image compression (JPEG) and Image compression (WEBP).

(Appendix A). Enhanced samples under different weather conditions and samples enhanced using the EDA module are shown in Figure A1 and Figure A2, respectively.

3.2.2. Large Separable Kernel Attention Module

LSKA is a visual attention module designed to address the quadratic increases in computation and memory usage as the kernel size of the large kernel attention (LKA) module increases [39]. LSKA can model long-range dependencies and exhibits strong spatial and channel adaptability, enabling it to scale to extremely large kernels, thereby providing a larger receptive field. The structure of the LSKA is shown in Figure 4.

By decomposing the 2D convolutional kernel into two sequential vertical and horizontal 1D convolutional kernels, LSKA achieves performance comparable to the LKA while reducing computational complexity and memory usage. This results in a well-balanced trade-off between kernel size, parameter size, and computational speed. Evidence also suggests that increasing the kernel size of LSKA allows the model to encode more shape information and less texture information, which is beneficial for detecting runways with different shapes across different landing segments.

The LSKA module can be mathematically expressed through Equations (1) to (4). The depth-wise convolution in Equation (1) captures local spatial information of the input and compensates for the gridding effect present in the depth-wise dilated convolution described in Equation (2). The depth-wise dilated convolution in Equation (2) then learns the global spatial information from the output of Equation (1). In both equations, the original 2D convolutional kernels in the depth-wise and depth-wise dilated convolutions are decomposed into two sequential separable 1D convolutional kernels that are perpendicular to each other.

$${\overline{Z}}^C={\displaystyle \sum _{H,W}{W}_{(2d-1)\times 1}^C}\ast \left({\displaystyle \sum _{H,W}{W}_{1\times (2d-1)}^C}\ast F^C\right)$$

(1)

where $\ast$ represents the convolution; $F^C\in {ℝ}^{C\times H\times W}$ is the input feature map with $C$ channels, height $H$, and width $W$; $W_{(2d-1)\times 1}^C$ is the vertical kernel with $C$ channels and a size of $(2d-1)\times 1$; $W_{1\times (2d-1)}^C$ is the horizontal kernel with $C$ channels and a size of $1\times (2d-1)$; $d$ is the dilation rate; and ${\overline{Z}}^C$ is the output feature map with $C$ channels of the depth-wise convolution.

$$Z^C={\displaystyle \sum _{H,W}{W}_{⌊\frac{k}{d}⌋\times 1}^C}\ast \left({\displaystyle \sum _{H,W}{W}_{1\times ⌊\frac{k}{d}⌋}^C}\ast {\overline{Z}}^C\right)$$

(2)

where $W_{⌊{\displaystyle \frac{k}{d}}⌋\times 1}^C$ is the vertical kernel with $C$ channels and a size of $⌊k/d⌋\times 1$; $W_{1\times ⌊{\displaystyle \frac{k}{d}}⌋}^C$ is the horizontal kernel with $C$ channels and a size of $1\times ⌊k/d⌋$; $⌊\cdot ⌋$ represents the floor operation; $k$ is the kernel size; and $Z^C$ is the output feature map with $C$ channels of the dilated depth-wise convolution.

The attention map $A^C$ can then be obtained by applying a $1\times 1$ convolutional kernel $W_{1\times 1}$ to the output $Z^C$, as expressed in Equation (3).

$$A^C=W_{1\times 1}\ast Z^C$$

(3)

Finally, the output ${\overline{F}}^C$ of the LSKA module is computed by combining $A^C$ and $F^C$ using the Hadamard product, as shown in Equation (4).

$${\overline{F}}^C=A^C\otimes F^C$$

(4)

where $\otimes$ represents the Hadamard product.

3.2.3. Bidirectional Feature Pyramid Network Module

BiFPN is a simple yet efficient multi-scale feature aggregation network that balances accuracy and efficiency [40]. Unlike previous feature pyramid networks (FPN), which merged different features indiscriminately, BiFPN introduces learnable weight coefficients to determine the importance of each feature. This enables BiFPN to account for the uneven contributions of features with varying resolutions. Additionally, BiFPN optimizes the network topology by introducing more diverse connections. The structure of BiFPN is illustrated in Figure 5.

BiFPN implements three key improvements to enhance performance from the perspective of cross-scale connections: First, nodes with only one input edge are removed due to their minimal contribution to feature fusion. Second, additional edges are added between nodes at the same level, allowing for the fusion of more features without significantly increasing computational load. Third, the top-down and bottom-up bidirectional paths are treated as an integrated block, which can be stacked to achieve higher-level feature fusion.

To address the unequal contributions of features with different resolutions, BiFPN assigns a weight to each input feature, allowing the network to learn the importance adaptively. To avoid potential instability from unbounded weights and to prevent a decrease in computational speed from using the Softmax function for normalization, BiFPN employs fast normalization fusion, as shown in Equation (5), in which the weights are constrained to be non-negative by applying the ReLU function.

$$\overline{F}={\displaystyle \sum _i\frac{w_i}{\epsilon +{\displaystyle \sum _j{w}_j}}}\cdot F_i$$

(5)

where $w_i$ is the learnable weight; $\epsilon$ is a small value for numerical stability; and $F_i$ and $\overline{F}$ are input and output features, respectively.

3.2.4. Efficient Intersection over Union Loss and Efficient Task-Aligned Learning Assigner

Compared to the standard intersection over union (IoU), the EIoU considers three key factors of the bounding boxes: overlapping area, center point distance, and side length differences [41]. EIoU loss more effectively captures the differences between the predicted and ground truth bounding boxes by introducing more reasonable penalty terms. The enhancement allows EIoU to accelerate convergence and improve regression accuracy.

The IoU between two bounding boxes can be calculated using Equation (6) [42].

$$IoU={\displaystyle \frac{|\mathrm{B}\cap {\mathrm{B}}^{\mathrm{gt}}|}{|\mathrm{B}\cup {\mathrm{B}}^{\mathrm{gt}}|}}$$

(6)

where $\mathrm{B}=\left(x, y, w, h\right)$ and ${\mathrm{B}}^{\mathrm{gt}}=\left(x^{\mathrm{gt}},y^{\mathrm{gt}},w^{\mathrm{gt}},h^{\mathrm{gt}}\right)$ are the predicted and ground-truth bounding boxes, respectively; $x$ and $y$ represent the coordinates of the bounding box center, while $w$ and $h$ denote the width and height of the bounding box.

EIoU is introduced into the regression loss of the proposed model, replacing the original CIoU loss. The modified loss function is referred to as EIoU loss, which consists of three components: IoU loss ${\mathcal{L}}_{\mathrm{IoU}}$, distance loss ${\mathcal{L}}_{\mathrm{dis}}$, and aspect ratio loss ${\mathcal{L}}_{\mathrm{asp}}$, as defined in Equation (7).

$$\begin{array}{cc}{\mathcal{L}}_{EIoU}\hfill & ={\mathcal{L}}_{\mathrm{IoU}}+{\mathcal{L}}_{\mathrm{dis}}+{\mathcal{L}}_{\mathrm{asp}}\hfill \\ & =1-IOU+{\displaystyle \frac{{\rho }^2(\mathrm{b},{\mathrm{b}}^{\mathrm{gt}})}{{(w^{\mathrm{c}})}^2+{(h^{\mathrm{c}})}^2}}+{\displaystyle \frac{d^2(w,w^{\mathrm{gt}})}{{(w^{\mathrm{c}})}^2}}+{\displaystyle \frac{d^2(h,h^{\mathrm{gt}})}{{(h^{\mathrm{c}})}^2}}\hfill \end{array}$$

(7)

where $\mathrm{b}$ and ${\mathrm{b}}^{\mathrm{gt}}$ are the center points of $\mathrm{B}$ and ${\mathrm{B}}_{\mathrm{gt}}$, respectively; $\rho$ is the Euclidean distance; $d$ is the difference; and $w^{\mathrm{c}}$ and $h^{\mathrm{c}}$ are the width and height of the smallest enclosing box ${\mathrm{B}}_{\mathrm{c}}$ that covers $\mathrm{B}$ and ${\mathrm{B}}_{\mathrm{gt}}$.

The schematic diagram of EIoU is shown in Figure 6.

The EIoU loss retains the effective characteristics of the CIoU loss in YOLOv8, such as guiding the maximization of IoU and the minimization of center point distance. Additionally, the EIoU loss directly guides the minimization of the width and height differences between the predicted and ground truth bounding boxes, rather than relying on the poorly defined aspect ratio difference in CIoU. This results in faster convergence and improved localization accuracy.

The TAL assigner in YOLOv8 dynamically assigns samples by evaluating the quality of predictions based on the combination of classification and localization scores, as shown in Equation (8).

$$t=s^{\alpha }\times u^{\beta }$$

(8)

where $s$ is the classification score and $u$ is the localization score calculated by IoU; $\alpha$ and $\beta$ are the corresponding weights.

To evaluate the localization score more accurately, EIoU is introduced into the TAL to replace IoU for calculating the localization score, forming the proposed ETAL assigner. ETAL assigner selects candidate samples with better alignments, guiding the model to predict bounding boxes that are highly consistent in classification and localization, thereby enabling faster and more accurate model convergence. The metric $t_{\mathrm{EIoU}}$ for measuring alignment in ETAL assigner is shown in Equation (9).

$$t_{\mathrm{EIoU}}=s^{\alpha }\times {u_{\mathrm{EIoU}}}^{\beta }$$

(9)

where the localization score $u_{\mathrm{EIoU}}$ is calculated using EIoU.

4. Experiments

4.1. Datasets

To evaluate model performance, the landing approach runway detection (LARD) dataset is used in this paper [27]. LARD provides aerial front-looking images of runways specifically designed for runway detection during landing. This dataset includes over 17,000 annotated synthetic image samples and more than 1800 annotated image samples extracted from real-world landing footage. The dataset is divided into one training set and three test sets. The training set exclusively contains a synthetic training set $D_{\mathrm{train}}^{\mathrm{synth}}$, while the test sets are composed of a synthetic test set $D_{\mathrm{test}}^{\mathrm{synth}}$, a real nominal test set $D_{\mathrm{test}}^{\mathrm{nominal}}$, and a real edge test set $D_{\mathrm{test}}^{\mathrm{edge}}$, respectively. Detailed information on LARD is provided in

Table 2. Overview of the LARD dataset.

Dataset	Type	${\mathit{N}}_{\mathbf{a}\mathbf{i}\mathbf{r}\mathbf{p}\mathbf{o}\mathbf{r}\mathbf{t}}$	${\mathit{N}}_{\mathbf{r}\mathbf{u}\mathbf{n}\mathbf{w}\mathbf{a}\mathbf{y}}$	${\mathit{N}}_{\mathbf{s}\mathbf{a}\mathbf{m}\mathbf{p}\mathbf{l}\mathbf{e}}$	Resolutions
Training	Synthetic	15	32	14,431	2448 × 2048
Test	Synthetic	40	79	2212	2448 × 2048
	Real nominal	95	115	4023	1280 × 720, 1920 × 1080, 3840 × 2160
	Real edge	34	40	1811	1280 × 720, 1920 × 1080, 3840 × 2160 1
Total	-	184 total (138 unique)	266	18,454	-

¹ Some sample sizes do not strictly adhere to 1920 × 1080 but are very close.

, where $N_{\mathrm{airport}}$, $N_{\mathrm{runway}}$, and $N_{\mathrm{sample}}$ represent the number of airports, the number of runways, and the number of samples, respectively.

Table 2 illustrates that the size of the synthetic dataset is significantly larger than that of the real dataset. This discrepancy arises from the relative ease of acquiring synthetic data, whereas the collection of real data is constrained by factors such as flight safety regulations and aviation management. In the LARD dataset, synthetic data are generated by applying perspective transformations to airport satellite images. Automatic data annotation is achieved by leveraging geographic information and artificially constructed virtual aircraft poses. This process can be repeated in a controlled environment to consistently produce a large volume of synthetic images. In contrast, the real data in LARD are derived from authorized flight recordings and manually annotated, making the process considerably more labor-intensive.

To reduce distribution similarity within the synthetic training set $D_{\mathrm{train}}^{\mathrm{synth}}$ and to provide validation during training, 20% of the training set is randomly selected as a validation set $D_{\mathrm{val}}^{\mathrm{synth}}$. The real nominal test set $D_{\mathrm{test}}^{\mathrm{nominal}}$ and real edge test set $D_{\mathrm{test}}^{\mathrm{edge}}$ are combined to form an overall real test set $D_{\mathrm{test}}^{\mathrm{real}}$ to comprehensively evaluate the real-world performance. To elucidate the attributes of LARD, the distributions of airport geospatial locations, aircraft positions in vertical and horizontal profiles, bounding box areas and aspect ratios, and normalized bounding box centers are visualized in Figure 7, Figure 8, Figure 9 and Figure 10, respectively.

The following conclusions can be drawn from Figure 7, Figure 8, Figure 9 and Figure 10:

• Figure 7 illustrates that the airports are primarily concentrated in Europe but are distributed worldwide across many countries and regions. The location diversity ensures that the runways cover various materials, geometric dimensions, surface markings, and surrounding terrain and landscapes, contributing to visual diversity.
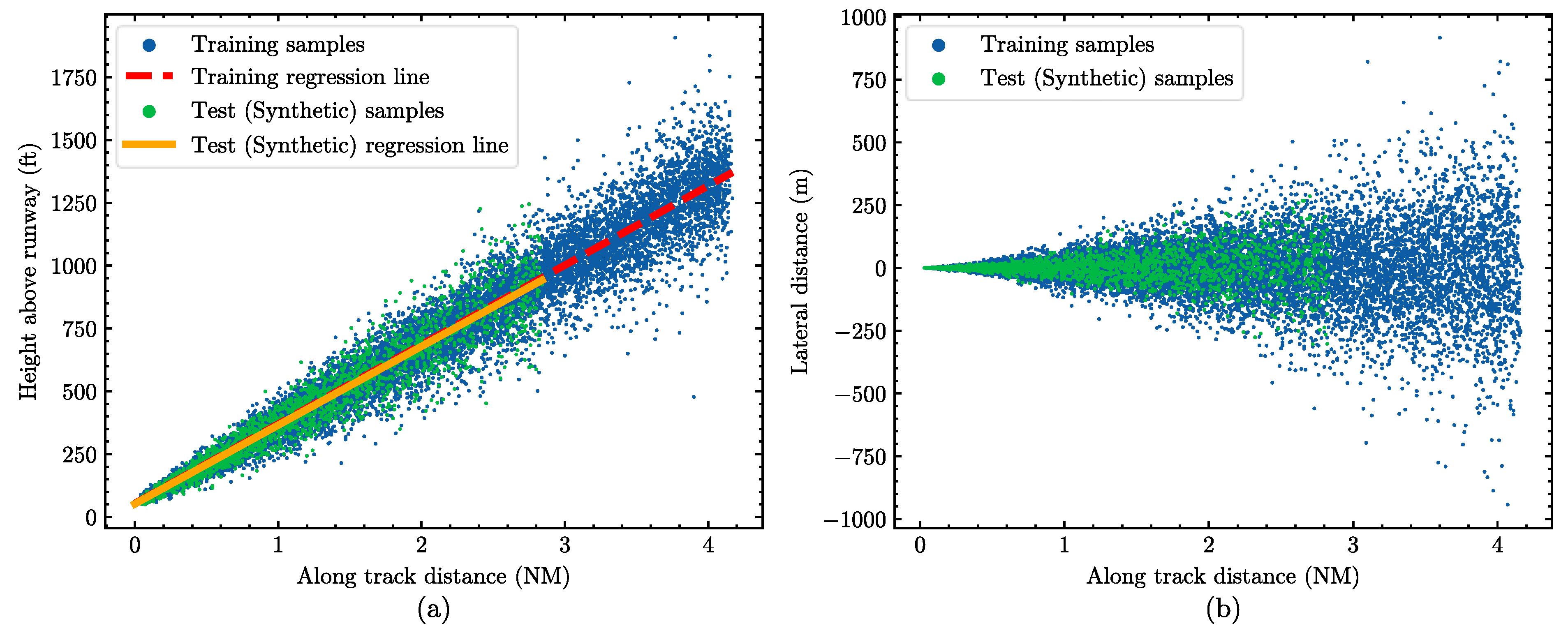
• Figure 8 shows that the camera positions (corresponding to aircraft positions) are distributed around both sides of the glide path, covering a variety of acceptable vertical deviations. Similarly, the samples are positioned along both sides of the localizer, covering a variety of acceptable lateral deviations.
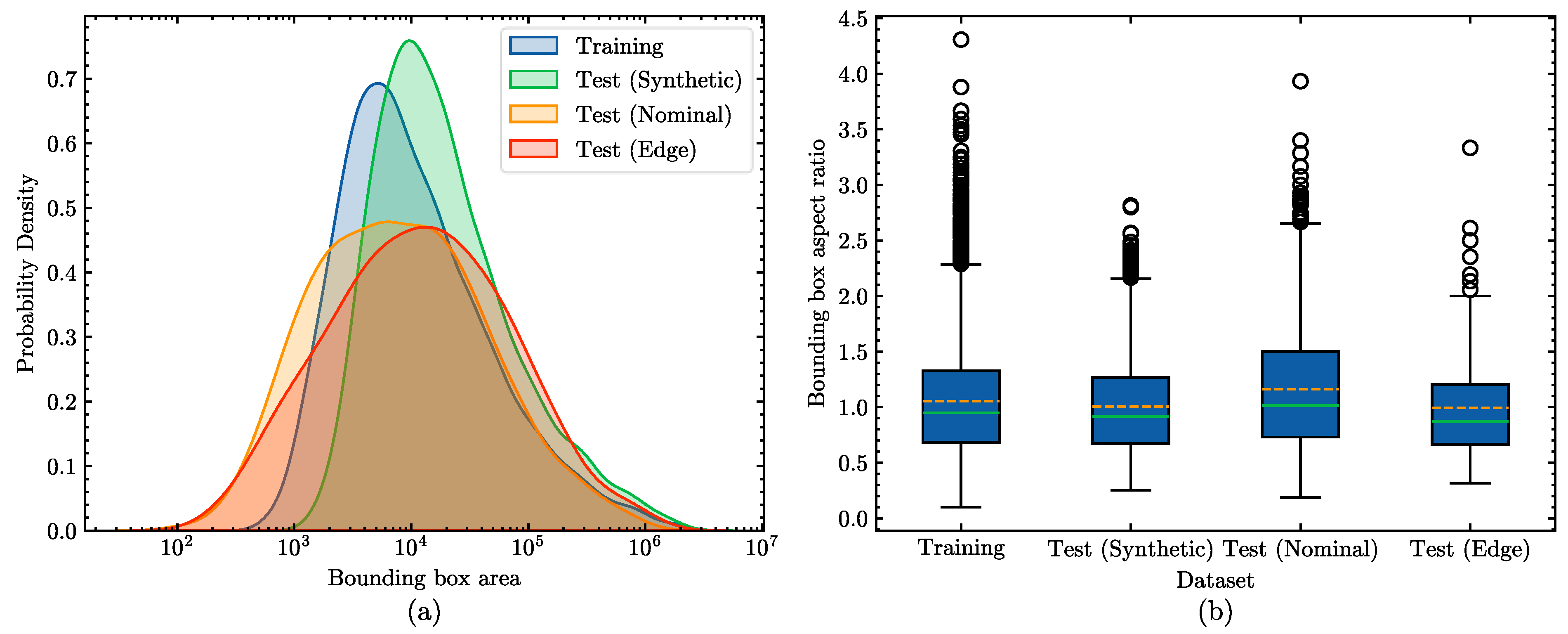
• Figure 9a indicates that the bounding box area distributions are similar across different datasets, encompassing visual features at various distances and scales. Compared to the synthetic datasets, the distribution of the real datasets is relatively more dispersed. Figure 9b indicates that the distributions of aspect ratios are also similar across different datasets, ensuring visual diversity under varying proportions.
• Figure 10 demonstrates that the bounding boxes are primarily concentrated in the center of the images. For the synthetic images, the horizontal distribution is relatively dispersed, while the vertical distribution is more concentrated, limited by the reasonable pitch range of UAVs. In contrast, real images exhibit a more balanced distribution in both directions due to variations in camera placements within the cockpits.

Four types of experiments are conducted in this paper:

In Experiments I, II, and III, all models are trained exclusively on the LARD training dataset, which consists solely of synthetic data, with 20% reserved as the validation set. The trained models are then tested on various test sets, including the synthetic test set, the real nominal test set, the real edge test set, and the overall real test set (comprising both the real nominal and real edge datasets).

In Experiment IV, to further explore the potential of the proposed model, additional datasets beyond the synthetic training set are introduced for fine-tuning the YOLO-RWY, including the validation set (composed entirely of synthetic data and derived from the 20% split of the original complete training set), the synthetic test set, and the real nominal test set. The fine-tuned models are evaluated on datasets that are not used in either the training or fine-tuning stages.

4.2. Evaluation Metrics

To accurately evaluate the precision and efficiency of the proposed YOLO-RWY, a comprehensive set of evaluation metrics is adopted [1], including mean average precision (mAP), frames per second (FPS), parameter size (Param.), and floating-point operations (FLOPs). Additionally, $t_{\mathrm{train}}$ is used to represent the overall training time.

Average precision (AP) is the metric used to evaluate the precision-recall trade-off for a specific class. For a given class and IoU threshold, the AP is calculated as the area under the precision-recall curve (PRC). The discrete calculation of the AP is shown in Equation (10).

$$\begin{array}{l}\mathrm{AP}={\displaystyle \sum _{i=1}^n\left(R_i-R_{i-1}\right)P_i^{\mathrm{interp}}}\\ P_i^{\mathrm{interp}}=\underset{\widehat{i}\ge i}{\max }{P}_{\widehat{i}}\end{array}$$

(10)

where $R_i$ is the recall under $i$-th confidence threshold; $P_i^{\mathrm{interp}}$ is the interpolated precision under $i$-th confidence threshold.

To evaluate the performance across multiple classes, the mAP is computed by averaging the AP values for each class, as defined in Equation (11).

$$\mathrm{mAP}={\displaystyle \frac{1}{C}}{\displaystyle \sum _{c=1}^C{\mathrm{AP}}_c}$$

(11)

where $C$ is the total number of classes; ${\mathrm{AP}}_c$ is the AP value for class $c$.

To comprehensively evaluate the performance under different IoU thresholds, ${\mathrm{AP}}_{50:95}$ is used, representing the average of the mAP values corresponding to 10 different IoU thresholds, as defined in Equation (12).

$${\mathrm{AP}}_{50:95}={\displaystyle \frac{1}{K}}{\displaystyle \sum _{k=1}^K{\mathrm{mAP}}^{{\mathrm{IoU}}_k}}$$

(12)

where $K=10$ is the number of the IoU thresholds; ${\mathrm{mAP}}^{{\mathrm{IoU}}_k}$ is the mAP at $k$-th IoU threshold. The IoU thresholds are sequentially taken from 0.50 to 0.95, with an interval of 0.05.

In the subsequent experiments, ${\mathrm{AP}}_{50:95}^{\mathrm{synth}}$, ${\mathrm{AP}}_{50:95}^{\mathrm{nominal}}$, ${\mathrm{AP}}_{50:95}^{\mathrm{edge}}$, and ${\mathrm{AP}}_{50:95}^{\mathrm{real}}$ are used to represent the ${\mathrm{AP}}_{50:95}$ values of the runway detection model on the synthetic, real nominal, real edge, and overall real test sets, respectively.

FPS describes the number of inferences executed per unit of time, as shown in Equation (13).

$$FPS={\displaystyle \frac{1}{t_{\mathrm{latency}}}}$$

(13)

where $t_{\mathrm{latency}}$ (measured in seconds) is the total time consumed for a single inference, including pre-processing, inference, and postprocessing, providing a comprehensive evaluation of inference speed.

4.3. Experiment Settings

4.3.1. Experimental Environments

The main experiments are conducted on an Ubuntu 22.04 system equipped with dual Intel(R) Xeon(R) Gold 5318Y CPUs, each with 48 cores running at 2.10 GHz, 10 NVIDIA RTX 3090 GPUs with 24 GB of VRAM each, and 256 GB of RAM. The deployment experiments are conducted on an Ubuntu 20.04 system equipped with an NVIDIA Jetson AGX Orin module, featuring a 12-core ARMv8 CPU running at 2.20 GHz, 32 GB of RAM, and an integrated GPU based on the NVIDIA Ampere architecture, with 2048 CUDA cores and 32 GB of VRAM.

The main experiments are conducted in an environment configured with Python 3.9.7, PyTorch 2.1.0+cu118, torchvision 0.16.0+cu118, CUDA 11.8, cuDNN 8.7.0, and Ultralytics 8.0.203. The deployment experiments are conducted in an environment configured with Python 3.8.18, PyTorch 1.13.0+nv22.10, torchvision 0.14.1, CUDA 11.4, cuDNN 8.3.2.49, TensorRT 8.4.0.11, and Ultralytics 8.0.203. The benchmark models in Experiments I are implemented using the MMDetection and MMYOLO frameworks. The proposed model and its variants are implemented using the Ultralytics framework.

4.3.2. Experimental Details and Parameters

In Experiments I, II, and III, the proposed models are trained from scratch without using pre-trained weights. In Experiment IV, the proposed models first load pre-trained weights and are subsequently fine-tuned. Both training and fine-tuning use all 10 available GPUs, with a batch size of 16 per GPU. During the test, only one GPU is used, with a batch size of 64 to fully utilize the GPU memory.

To better adapt the runway detection model to the input data distribution and improve performance, Mosaic augmentation is disabled during the final 20 epochs. Different from general object detection tasks, the maximum number of detections during a test is set to 8, considering the limited number of runways that can appear within the field of view during landing. The key parameters are detailed in

Table 3. Parameter settings of the proposed YOLO-RWY.

Phase	Parameter	Setup
Training and fine-tuning	Epochs	300
	Epoch (warming up)	3
	Epoch (closing Mosaic)	Last 20
	Batch size (per GPU)	16
	Workers (per GPU)	8
	Number of GPUs	10
	Optimizer	SGD
	Initial learning rate	0.0125
	Final learning rate	0.0125 × 0.01
	Momentum	0.937
	Weight decay	0.0005
	Image size 1	640
Test	Batch size	64
	Number of GPUs	1
	NMS confidence	0.001
	NMS IoU	0.6
	Max detections	8
	Image size 2	640

^1,2 The image size is set to 640 by default unless stated otherwise.

. The default values from the Ultralytics framework are used for parameters not explicitly listed.

4.4. Experiment I: Comparison with Benchmark Models

Extensive comparative experiments with benchmark models were conducted to comprehensively demonstrate the advantages of the proposed YOLO-RWY model in terms of accuracy and efficiency. The benchmark models include one-stage models such as YOLOv3 [43], YOLOv5n [32], YOLOv6n [44], YOLOv7t [45], SSD [46], and two-stage Faster R-CNN [47]. The results are presented in

Table 4. Evaluation metrics of benchmark models and the proposed model ¹.

Model	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Param. (M)	FLOPs (G)	FPS
YOLOv3	0.684	0.492	0.233	0.448	61.524	58.861	83.9
YOLOv6n	0.722	0.524	0.219	0.473	4.301	5.495	70.9
SSD	0.670	0.530	0.244	0.482	24.386	87.541	65.8
YOLOv7t	0.687	0.524	0.316	0.488	6.015	6.551	103.6
YOLOv5n	0.706	0.540	0.302	0.499	1.765	2.088	100.1
Faster RCNN	0.719	0.566	0.286	0.517	41.348	158.276	32.7
YOLOv8n	0.754	0.586	0.348	0.545	3.011	8.194	135.0
Proposed	0.760	0.611	0.413	0.578	3.106	8.308	125.3

¹ The bolded values represent the highest accuracy scores, and this convention is also followed in the subsequent tables.

.

Based on Table 4, the following conclusions can be drawn:

• YOLOv8n exhibits outstanding performance, significantly outperforming all benchmarks across all the test sets, with ${\mathrm{AP}}_{50:95}$ values of 0.754, 0.586, 0.348, and 0.545 on synthetic, real nominal, real edge, and overall real test sets, respectively. Additionally, YOLOv8n features a parameter size of 3.011 M, FLOPs of 8.194 G, and an FPS of 135.0. The superiority in accuracy and efficiency validates the selection of YOLOv8n as the baseline for the proposed model.
• The proposed YOLO-RWY model achieves the best accuracy metrics across all test sets, with ${\mathrm{AP}}_{50:95}$ values of 0.760, 0.611, 0.413, and 0.578 on the synthetic, real nominal, real edge, and overall real test sets, respectively. Compared to YOLOv8n, the proposed model shows a small improvement of 0.8% on the synthetic test set and significant improvements on all the real test sets, with increases of 4.3%, 18.7%, and 6.1%, respectively. This indicates the improved accuracy and strong generalization of the proposed model.
• The proposed model demonstrates excellent computational efficiency and speed, with only small differences compared to YOLOv8n. The parameter size is 3.106 M, and the FLOPs are 8.308 G, representing increases of 3.2% and 1.4%, respectively. The inference speed is 125.3 FPS, showing a slight decrease of 7.2%. Overall, the proposed model meets real-time requirements.

Figure 11 demonstrates the convergence of the proposed model, depicting various types of loss during the training and validation phases, along with the convergence of validation metrics. In Figure 11, the vertical axes of the loss plots are on a logarithmic scale to better illustrate the reduction in loss values over time.

As depicted in Figure 11, the model converges rapidly as training progresses. Initially, the training loss decreases sharply and then gradually levels off. A noticeable drop in training loss occurs upon deactivating the Mosaic augmentation, a predictable outcome given the restoration of the training sample distribution. Similarly, the validation loss quickly decreases, then stabilizes and converges. The metrics on the validation set also improve quickly before stabilizing. Overall, these observations confirm the stable convergence capabilities of the proposed YOLO-RWY model.

4.5. Experiment II: Module Comparisons and Ablation Experiments

Comprehensive comparative and ablation experiments were conducted to analyze the advantages of each introduced module and their overall contributions to the proposed model.

4.5.1. Comparison of Attention Modules

To verify the superiority of the LSKA module for feature extraction and enhancement, this experiment compares LSKA with various visual attention modules, including efficient multi-scale attention (EMA) [48], convolutional block attention module (CBAM) [49], large selective kernel (LSK) attention [50], efficient channel attention (ECA) [51], global attention mechanism (GAM) [52], squeeze-and-excitation (SE) attention [53], and channel prior convolutional attention (CPCA) [54]. The results are presented in

Table 5. Evaluation metrics of YOLOv8n with different attention modules.

Model	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Param. (M)	FLOPs (G)	FPS
YOLOv8n	0.754	0.586	0.348	0.545	3.011	8.194	135.0
YOLOv8n-EMA	0.754	0.561	0.323	0.521	3.012	8.215	122.0
YOLOv8n-CBAM	0.758	0.568	0.340	0.528	3.077	8.247	132.8
YOLOv8n-LSK	0.756	0.569	0.338	0.529	3.130	8.288	125.0
YOLOv8n-ECA	0.753	0.576	0.338	0.535	3.011	8.196	131.0
YOLOv8n-GAM	0.759	0.583	0.342	0.541	4.651	9.506	130.9
YOLOv8n-SE	0.751	0.584	0.353	0.544	3.019	8.201	127.3
YOLOv8n-CPCA	0.760	0.588	0.358	0.549	3.138	8.425	126.7
YOLOv8n-LSKA	0.751	0.590	0.366	0.552	3.089	8.256	132.3

.

Based on Table 5, the following conclusions can be drawn:

• Visual attention modules do not necessarily lead to improvements in accuracy. Modules such as EMA, CBAM, LSK, ECA, and GAM result in accuracy degradation on all the real test sets, even though the accuracy on the synthetic test set is either close to or slightly better than YOLOv8n. The SE module slightly improves accuracy on the real edge test set. The CPCA module achieves the best accuracy on the synthetic test set and shows improvements on all the real test sets. This may suggest that the enhanced feature learning capability brought by the attention modules could lead to overfitting on training sets.
• Introducing the LSKA module leads to the best accuracy on all the real test sets, although its accuracy on the synthetic test set is slightly lower. Compared to YOLOv8n, the ${\mathrm{AP}}_{50:95}$ values of YOLOv8n-LSKA on the synthetic, real nominal, real edge, and overall real test sets are 0.751, 0.590, 0.366, and 0.552, with changes of −0.4%, 0.7%, 5.2%, and 1.3%, respectively. The decrease in ${\mathrm{AP}}_{50:95}^{\mathrm{synth}}$ might indicate a reduction in overfitting, considering that the model is trained exclusively using the synthetic training set, which has a highly similar distribution to the synthetic test set. This suggests that the LSKA module effectively increases accuracy and generalization on real-world datasets, which is the focus of the VAL research in this paper.
• Compared to YOLOv8n, introducing the LSKA module does not significantly increase the parameter size and computational load. The inference speed is also minimally affected. The parameter size of YOLOv8n-LSKA is 3.089 M, and the FLOPs are 8.256 G, representing increases of 2.6% and 0.8%, respectively. The inference speed is 132.3 FPS, showing a slight decrease of 2.0%. Overall, the introduction of LSKA meets the requirements of real-time performance.

4.5.2. Comparison of Feature Pyramid Network Modules

To verify the superiority of the BiFPN module for feature aggregation, PAN-FPN (the FPN module of YOLOv8n) [36] and asymptotic feature pyramid network (AFPN) [55] are compared with BiFPN in this experiment. The results are shown in

Table 6. Evaluation metrics of YOLOv8n with different FPN modules.

Model	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Param. (M)	FLOPs (G)	FPS
YOLOv8n	0.754	0.586	0.348	0.545	3.011	8.194	135.0
YOLOv8n-AFPN	0.761	0.574	0.333	0.532	4.667	15.641	101.9
YOLOv8n-BiFPN	0.758	0.591	0.365	0.553	3.027	8.247	135.4

.

Based on Table 6, the following conclusions can be drawn:

• Although the AFPN module leads to the highest improvement in ${\mathrm{AP}}_{50:95}^{\mathrm{synth}}$, it results in decreased accuracy across all the real test sets. Due to the complex structure and powerful feature fusion capability, AFPN appears to overfit the synthetic training set. Additionally, AFPN significantly increases the parameter size and computational load, notably reducing inference speed.
• Compared to the YOLOv8n with PAN-FPN, the BiFPN module improves accuracy on all the test sets. The ${\mathrm{AP}}_{50:95}$ values of YOLOv8n-BiFPN on the synthetic, real nominal, real edge, and overall real test sets are 0.758, 0.591, 0.365, and 0.553, with improvements of 0.5%, 0.9%, 4.9%, and 1.5%, respectively. This suggests that BiFPN is effective in enhancing accuracy and generalization.
• With its simple structure, BiFPN has minimal impact on parameter size and computational load, remaining nearly consistent with YOLOv8n. The parameter size is 3.027 M, and the FLOPs are 8.247 G, with increases of 0.5% and 0.6%, respectively. The inference speed reaches 135.4 FPS, showing a slight increase attributed to experimental randomness. Therefore, the introduction of BiFPN continues to meet the real-time performance requirements.

4.5.3. Analysis of the Enhanced Data Augmentation Module

To demonstrate the indispensability of the EDA module, this experiment compares the detection performance under different augmentation probabilities of applying the EDA (EDA Prob.). The results are shown in

Table 7. Evaluation metrics of YOLOv8n with different EDA probabilities.

Model	EDA Prob.	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Param. (M)	FLOPs (G)	FPS	${\mathbf{t}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}$ (min)
YOLOv8n	0%	0.754	0.586	0.348	0.545	3.011	8.194	135.0	140.42
	1%	0.746	0.596	0.368	0.558	3.011	8.194	129.1	146.67
	5%	0.749	0.600	0.381	0.563	3.011	8.194	140.2	160.92

.

Based on Table 7, the following conclusions can be drawn:

• Under different probabilities of applying EDA, the ${\mathrm{AP}}_{50:95}^{\mathrm{synth}}$ values all decrease while ${\mathrm{AP}}_{50:95}$ values increase across all the real test sets. The EDA module reduces the distribution similarity between the synthetic training and synthetic test sets, thereby alleviating overfitting. This demonstrates that the EDA module effectively optimizes the detection performance on real-world datasets.
• At an EDA probability of 5%, the YOLOv8n model achieves the best improvements across all the real test sets. The ${\mathrm{AP}}_{50:95}$ values on the synthetic, real nominal, real edge, and overall real test sets are 0.749, 0.600, 0.381, and 0.563, with changes of −0.7%, 2.4%, 9.5%, and 3.3%, respectively. This indicates that the EDA module significantly improves generalization and accuracy across all the real test sets, with the most substantial improvement observed on the real edge test set. Therefore, an EDA probability of 5% is selected for the proposed model in this paper.
• The EDA module does not affect parameter size and computational load, as the EDA module is a pre-processing method and independent of the model network structure. The variations in FPS are attributed to experimental randomness. Nonetheless, as an online pre-processing algorithm, the EDA module inevitably extends the training duration. As the EDA probability increases, the overall training time correspondingly rises. Specifically, when the probability grows from 0% to 5%, the training time increases from 140.42 min to 160.92 min, an increase of 14.6%.

4.5.4. Ablation Experiments

Ablation experiments are conducted in this section to evaluate the contribution of each introduced module to the overall performance. The results are shown in

Table 8. Evaluation metrics of ablation experiments.

Model	Module				$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Param. (M)	FLOPs (G)	FPS	${\mathbf{t}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}$ (min)
	LSKA	BiFPN	EIoU	EDA
YOLOv8n					0.754	0.586	0.348	0.545	3.011	8.194	135.0	140.42
	√				0.751	0.590	0.366	0.552	3.089	8.256	132.3	141.50
		√			0.758	0.591	0.365	0.553	3.027	8.247	135.4	141.12
			√		0.757	0.572	0.338	0.532	3.011	8.194	132.4	139.33
	√	√			0.761	0.598	0.374	0.559	3.106	8.308	129.3	141.17
	√		√		0.756	0.576	0.339	0.536	3.089	8.256	135.8	139.18
		√	√		0.755	0.575	0.359	0.537	3.027	8.247	123.3	141.42
Proposed (w/o EDA) 1	√	√	√		0.762	0.600	0.393	0.563	3.106	8.308	131.4	141.53
Proposed	√	√	√	√	0.760	0.611	0.413	0.578	3.106	8.308	125.3	160.12

¹ w/o stands for ‘without’, and this convention is also followed in the subsequent tables.

.

Based on Table 8, the following conclusions can be drawn:

• When introducing LSKA alone, accuracy improves on all the real test sets while slightly decreasing on the synthetic test set. Introducing the BiFPN alone leads to accuracy improvements across all the test sets. However, introducing EIoU alone results in a slight accuracy improvement on the synthetic test set but a decrease in all the real test sets.
• The combination of LSKA and BiFPN improves accuracy on all the test sets, with greater improvements than using either module alone. This suggests that LSKA and BiFPN work synergistically to enhance feature learning across different levels. However, combining LSKA or BiFPN with EIoU improves accuracy on the synthetic test set but decreases accuracy on all the real test sets.
• When integrating LSKA, BiFPN, and EIoU, accuracy improves significantly across all the test sets. The values of the proposed (w/o EDA) model on the synthetic, real nominal, real edge, and overall real test sets are 0.762, 0.600, 0.393, and 0.563, with improvements of 1.1%, 2.4%, 12.9%, and 3.3%, respectively. This indicates that the combination of LSKA, BiFPN, and EIoU effectively enhances detection performance, even though EIoU performs less well in isolation.
• Further introducing the EDA module results in significant accuracy improvements across all the real test sets, with only small fluctuations on the synthetic test set. The values of the proposed model on the synthetic, real nominal, real edge, and overall real test sets are 0.760, 0.611, 0.413, and 0.578, with improvements of 0.8%, 4.3%, 18.7%, and 6.1%, respectively. This highlights the positive contribution of the EDA module to the proposed model, especially in challenging real edge cases where runway detection is more difficult compared to less complex cases.
• All models in the ablation experiments show no significant increase in parameter size or computational load, remaining nearly consistent with YOLOv8n. The inference speed of each model also remains largely unchanged. The FPS difference between the proposed (w/o EDA) and the proposed model is due to experimental randomness. Besides the EDA module, the introduction of various modules and their combinations does not significantly alter the training duration, further demonstrating that the proposed modifications to the network architecture are lightweight yet effective. The improvements in accuracy are achieved without incurring significant additional training costs. When the EDA module is introduced, it enables further enhanced performance with only a moderate and acceptable increase in training cost. Compared to the proposed (w/o EDA) model, the training time of the proposed model increases from 141.53 min to 160.12 min, an increase of 13.14%.

4.6. Experiment III: Performance Analysis under Different Conditions

To further evaluate runway detection performance under different experimental conditions and real-world scenarios, this experiment thoroughly analyzes the proposed YOLO-RWY model from various perspectives.

4.6.1. Performance under Different Target Sizes

This experiment categorizes runway objects into small, medium, and large objects to evaluate the accuracy of detecting runways of different sizes, according to the COCO dataset standards. The results are shown in

Table 9. Evaluation metrics for detecting runways with different target sizes.

Model	Metric	Test Sets
		${\mathbf{D}}_{\mathbf{test}}^{\mathbf{synth}}$	${\mathbf{D}}_{\mathbf{test}}^{\mathbf{nominal}}$	${\mathbf{D}}_{\mathbf{test}}^{\mathbf{edge}}$	${\mathbf{D}}_{\mathbf{test}}^{\mathbf{real}}$
YOLOv8n	${\mathrm{AP}}_{\mathrm{S}}$	-	0.188	0.110	0.174
	${\mathrm{AP}}_{\mathrm{M}}$	0.621	0.461	0.268	0.432
	${\mathrm{AP}}_{\mathrm{L}}$	0.813	0.784	0.439	0.715
Proposed (w/o EDA)	${\mathrm{AP}}_{\mathrm{S}}$	-	0.193 (+02.7%)	0.149 (+35.5%)	0.185 (+06.3%)
	${\mathrm{AP}}_{\mathrm{M}}$	0.632 (+01.8%)	0.473 (+02.6%)	0.319 (+19.0%)	0.450 (+04.2%)
	${\mathrm{AP}}_{\mathrm{L}}$	0.821 (+01.0%)	0.799 (+01.9%)	0.478 (+08.9%)	0.735 (+02.8%)
Proposed	${\mathrm{AP}}_{\mathrm{S}}$	-	0.205 (+09.0%)	0.191 (+73.6%)	0.201 (+15.5%)
	${\mathrm{AP}}_{\mathrm{M}}$	0.634 (+02.1%)	0.476 (+03.3%)	0.306 (+14.2%)	0.452 (+04.6%)
	${\mathrm{AP}}_{\mathrm{L}}$	0.817 (+00.5%)	0.815 (+04.0%)	0.521 (+18.7%)	0.759 (+06.2%)

, where ${\mathrm{AP}}_{\mathrm{S}}$, ${\mathrm{AP}}_{\mathrm{M}}$, and ${\mathrm{AP}}_{\mathrm{L}}$ represent average precision metrics on small, medium, and large targets, respectively.

Based on Table 9, the following conclusions can be drawn:

• The runway detection accuracy of each model decreases progressively from large to medium to small targets. Small runway objects occupy a smaller pixel area within the image, making accurate detection more challenging. Additionally, when the image is scaled down before being processed by the model, the small area becomes even smaller, further complicating detection.
• The proposed (w/o EDA) model shows improved accuracy for different runway sizes across all the test sets compared with YOLOv8n. The most significant improvement is observed on the real edge test set, where accuracy increases by 35.5% for small objects, 19.0% for medium objects, and 8.9% for large objects. The proposed (w/o EDA) model exhibits greater accuracy improvement for small objects than for medium and large objects across all the test sets. This proves the validity of the improved network structure of the proposed model.
• Introducing the EDA module further improves the detection accuracy. The proposed model shows better accuracy improvements than the proposed (w/o EDA) model for medium objects in the synthetic test set, all sizes in the real nominal test set, small and large sizes in the real edge test set, and all sizes in the overall real test set. The most significant improvement is again observed on the real edge test set, with accuracy increases of 73.6% for small objects, 14.2% for medium objects, and 18.7% for large objects compared with YOLOv8n. The results demonstrate that the EDA module is essential, and the proposed model is highly effective for detecting runways of varying sizes, particularly in challenging scenarios.

4.6.2. Performance under Different Distances

The previous experiment evaluated the accuracy of detecting runway objects of different sizes. However, the size classification defined by COCO is relatively coarse and not particularly intuitive for runway detection tasks. In this experiment, image samples are grouped based on landing distance or landing time intervals (along-track distance for synthetic images and time to landing for real images) to evaluate the accuracy variations throughout the landing process. The results are presented in

Table 10. Evaluation metric variations across different distance ranges.

Model	Metric	Range of Along-Track Distance (NM)
		0.0–0.5	0.5–1.0	1.0–1.5	1.5–2.0	2.0–2.5	2.5–3.0
YOLOv8n	${\mathrm{AP}}_{50:95}^{\mathrm{synth}}$	0.897	0.801	0.704	0.666	0.598	0.577
Proposed	${\mathrm{AP}}_{50:95}^{\mathrm{synth}}$	0.847 (−05.6%)	0.877 (+09.6%)	0.770 (+09.4%)	0.712 (+06.9%)	0.679 (+13.5%)	0.668 (+15.8%)

and

Table 11. Evaluation metric variations across different time ranges.

Model	Metric	Range of Time to Landing (s)
		0–10	10–20	20–40	40–80	80–160
YOLOv8n	${\mathrm{AP}}_{50:95}^{\mathrm{nominal}}$	0.824	0.659	0.441	0.279	0.044
	${\mathrm{AP}}_{50:95}^{\mathrm{edge}}$	0.536	0.300	0.207	0.066	0.034
	${\mathrm{AP}}_{50:95}^{\mathrm{real}}$	0.760	0.599	0.409	0.252	0.041
Proposed	${\mathrm{AP}}_{50:95}^{\mathrm{nominal}}$	0.884 (+07.3%)	0.825 (+25.3%)	0.657 (+49.0%)	0.496 (+77.6%)	0.343 (+683.3%)
	${\mathrm{AP}}_{50:95}^{\mathrm{edge}}$	0.689 (+28.5%)	0.498 (+66.1%)	0.378 (+82.4%)	0.252 (+279.8%)	0.020 (−40.4%)
	${\mathrm{AP}}_{50:95}^{\mathrm{real}}$	0.842 (+10.7%)	0.778 (+29.9%)	0.620 (+51.5%)	0.464 (+84.4%)	0.304 (+639.8%)

, respectively, and visualized in Figure 12.

Based on Table 10 and Table 11, and Figure 12, the following conclusions can be drawn:

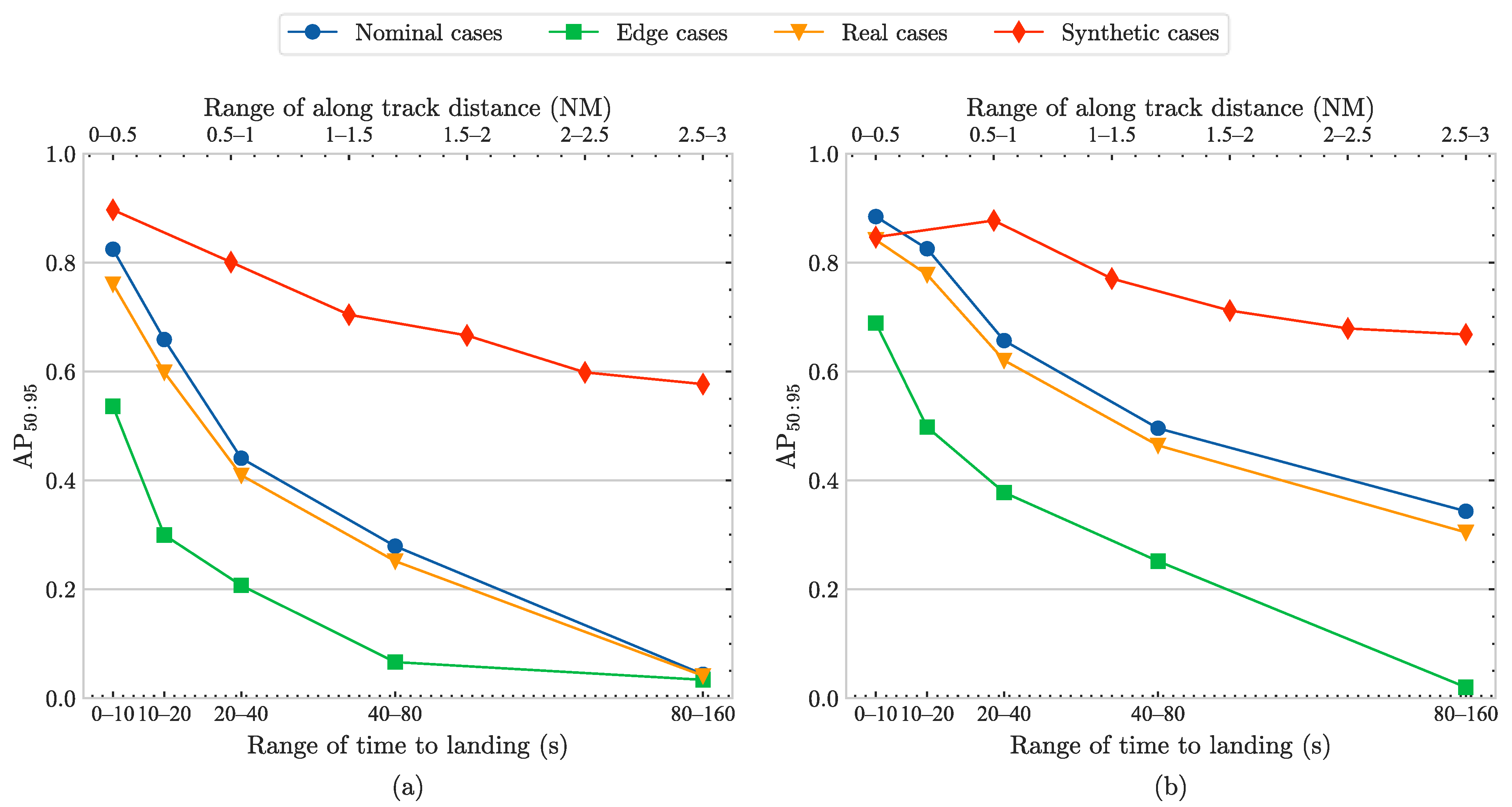
• Across all the test sets, the detection accuracy decreases rapidly as the time to landing increases and the along-track distance increases. When the time or distance is too long, the runway occupies too few pixels, reducing the likelihood of accurate detection. The detection accuracy on the synthetic test set is generally higher than on the real test sets, likely because the synthetic test set presents fewer challenging scenarios compared to the more complex real-world images in the real test sets.
• For the synthetic test set, the proposed model improves accuracy across all distance ranges except within the 0.0–0.5 NM range. The improvement is particularly pronounced at longer distance ranges, with accuracy increases of 13.5% and 15.8% in the 2.0–2.5 NM and 2.5–3.0 NM ranges, respectively.
• For all the real test sets, the proposed model improves accuracy across most conditions, except in the 80–160 s range for the real edge test set, where a slight decrease is observed. The proposed model shows significant improvements at longer time ranges, with accuracy increases of 77.6% and 683.3% in the 40–80 s and the 80–160 s ranges on the real nominal test set, which suggests that the proposed model is more effective for detecting runways at distant positions, enabling earlier detection during the initial landing phase.

4.6.3. Performance under Different Image Sizes

In all the previous experiments, both training and testing are conducted using an input size of 640. To evaluate the performance of the proposed model under different image sizes, this experiment conducts training and tests with input sizes of 640 and 1280. The results are shown in

Table 12. Evaluation metrics of the proposed model at various image sizes.

Model	Image Size		$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Param. (M)	FLOPs (G)	FPS	${\mathbf{t}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}$(min)
	Training	Test
Proposed	640	640	0.760	0.611	0.413	0.578	3.106	8.308	125.3	160.12
	640	1280	0.785 (+03.3%)	0.744 (+21.8%)	0.517 (+25.2%)	0.707 (+22.3%)	3.106 (+00.0%)	33.232 (+300.0%)	89.3 (−28.7%)	160.12
	1280	1280	0.848 (+11.6%)	0.750 (+22.7%)	0.489 (+18.4%)	0.709 (+22.7%)	3.106 (+00.0%)	33.232 (+300.0%)	90.9 (−27.5%)	346.58

.

Based on Table 12, the following conclusions can be drawn:

• With the training size kept at 640, and the test size increased to 1280, a significant accuracy improvement is observed across all the test sets. The ${\mathrm{AP}}_{50:95}$ values on the synthetic, real nominal, real edge, and overall real test sets are 0.785, 0.744, 0.517, and 0.707, with improvements of 3.3%, 21.8%, 25.2%, and 22.3%, respectively. Since the model size and scale remain unchanged, the parameter size stays at 3.106 M. However, the increased input resolution significantly raises the computational load, increasing FLOPs from 8.308 G to 33.232 G (an increase of 300.0%) and reducing FPS from 125.3 to 89.3 (a decrease of 28.7%). Furthermore, as retraining is not required, no additional training costs are incurred.
• Increasing both the training and test sizes to 1280 significantly improves the accuracy across all the test sets. The ${\mathrm{AP}}_{50:95}$ values on the synthetic, real nominal, real edge, and overall real test sets are 0.848, 0.750, 0.489, and 0.709, with improvements of 11.6%, 22.7%, 18.4%, and 22.7%, respectively. Compared to only increasing the test size, increasing both training and test size shows better performance on the synthetic, real nominal, and overall real test sets, though there is a slight accuracy decrease on the real edge test set. This might be due to the increased input size leading to further overfitting. Increasing the EDA probability may potentially alleviate this issue.
• When both the training and test sizes increase, the parameter size and computational load remain consistent with the configuration where only the test size is increased. The small differences in inference speed are due to experimental randomness. Moreover, setting the training size to 1280 significantly increases training costs due to the increased FLOPs. Specifically, the training time increased from 160.12 min to 346.58 min, representing a 116.45% rise. Therefore, the significant improvement in accuracy comes at the cost of a substantial increase in training time. However, considering that training is performed offline, such a trade-off is generally acceptable.

4.6.4. Performance under Different Quantization Precisions

All previous experiments were conducted on the GPU workstation. To validate the real-time performance in practical deployments, this experiment first evaluates the accuracy of the proposed model under different quantization precisions, specifically FP16 (half-precision floating-point) and FP32 (single-precision floating-point). Subsequently, the inference speed is tested on an edge device, the NVIDIA Jetson AGX Orin, using the TensorRT inference engine for acceleration. The results are presented in

Table 13. Evaluation metrics of the proposed model across different quantization precisions.

Model	Image Size		Quantization	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	Latency (ms)	FPS 1
	Training	Inference
Proposed	640	640	FP16	0.578	4.744	210.8
		640	FP32	0.578	6.475	154.4
		1280	FP16	0.704	15.419	64.9
		1280	FP32	0.707	21.762	46.0

¹ Jetson clocks enabled and power mode set to MAXN.

.

Based on Table 13, the following conclusions can be drawn:

• The proposed model meets real-time requirements across all the tested image sizes and quantization precisions. Under the least demanding conditions, with the smallest computational load (inference size 640 and FP16 quantization), the latency is 4.744 ms, and the FPS is 210.8. Under the most demanding conditions, with the largest computational load (inference size 1280 and FP32 quantization), the latency is 21.762 ms, and the FPS is 46.0.
• When the inference size remains constant, FP16 quantization effectively improves the inference speed while keeping accuracy basically unchanged or slightly decreased. For the input size of 640, FP16 quantization increases FPS by 36.5% with no significant change in accuracy (accurate to three decimal places). For the input size of 1280, FP16 quantization increases FPS by 41.1%, with a small accuracy reduction from 0.707 to 0.704, a decrease of only 0.4%.
• When quantization precision remains constant, increasing the input size significantly reduces the inference speed on the edge device. With FP16 quantization, increasing the input size from 640 to 1280 results in a 69.2% decrease in FPS. With FP32 quantization, the same increase in input size leads to a 70.2% decrease in FPS.

4.7. Experiment IV: Model Fine-Tuning and Detection Visualization

4.7.1. Performance Analysis of the Finetuned Proposed Model

The proposed model in previous experiments was trained using only the synthetic training set $D_{\mathrm{train}}^{\mathrm{synth}}$. Although the proposed model demonstrated significantly improved performance, there is still potential for further improvement when dealing with previously unseen real-world runway images. In this experiment, the proposed model pretrained on the $D_{\mathrm{train}}^{\mathrm{synth}}$ is further finetuned using the following datasets: synthetic validation set $D_{\mathrm{val}}^{\mathrm{synth}}$, synthetic test set $D_{\mathrm{test}}^{\mathrm{synth}}$, and real nominal test set $D_{\mathrm{test}}^{\mathrm{nominal}}$. All training parameters remained consistent with previous experiments. Additionally, EDA probabilities of 5% and 10% are both considered to explore any potential performance improvements. The experimental configurations and results are shown in

Table 14. Evaluation metrics of the finetuned proposed model.

Model	Fine-Tuning EDA Prob.	Fine-Tuning Datasets			Metrics
		${\mathbf{D}}_{\mathbf{val}}^{\mathbf{synth}}$	${\mathbf{D}}_{\mathbf{test}}^{\mathbf{synth}}$	${\mathbf{D}}_{\mathbf{test}}^{\mathbf{nominal}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{s}\mathbf{y}\mathbf{n}\mathbf{t}\mathbf{h}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{n}\mathbf{o}\mathbf{m}\mathbf{i}\mathbf{n}\mathbf{a}\mathbf{l}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{e}\mathbf{d}\mathbf{g}\mathbf{e}}$	$\mathbf{A}{\mathbf{P}}_{50:95}^{\mathbf{r}\mathbf{e}\mathbf{a}\mathbf{l}}$	${\mathbf{t}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}$(min) 2
Proposed	-	-	-	-	0.760	0.611	0.413	0.578	160.12
	5%	√			0.712 (−6.3%)	0.579 (−5.2%)	0.362 (−12.3%)	0.542 (−6.2%)	192.77
		√	√		-	0.615 (+0.7%)	0.381 (−7.7%)	0.576 (−0.3%)	215.30
		√	√	√	-	-	0.557 (+34.9%)	-	234.30
		√	√	√ 1	-	-	0.579 (+40.2%)	-	235.39
	10%	√			0.722 (−5.0%)	0.584 (−4.4%)	0.376 (−9.0%)	0.549 (−5.0%)	196.29
		√	√		-	0.627 (+2.6%)	0.401 (−2.9%)	0.590 (+2.1%)	221.55
		√	√	√	-	-	0.562 (+36.1%)	-	242.97
		√	√	√ 1	-	-	0.582 (+40.9%)	-	242.99

¹ The fine-tuning using a separate strategy. ² Including both training time and fine-tuning time.

.

Based on Table 14, the following conclusions can be drawn:

• Under the fine-tuning EDA probability of 5%, fine-tuning the proposed model with the synthetic validation set results in accuracy degradation across all the test sets. The reason may be that the synthetic validation set is randomly extracted from the original synthetic training set, and the distributions are highly similar, leading to increased overfitting. The degradation is predictable and demonstrates the effectiveness of reserving the validation set.
• When fine-tuning using both the synthetic validation and synthetic test sets, the accuracy improves on the real nominal test set, while the accuracy on the real edge and overall real test sets decreases. However, compared to fine-tuning with only the synthetic validation set, there is a slight improvement across all the available test sets. This is due to the limited but effective diversity introduced by the synthetic test set, which includes image samples from different airports, runways, and landings.
• When fine-tuning with the synthetic validation and synthetic test sets and further including the real nominal test set, two strategies are employed: (a) hybrid strategy: all three datasets are used for fine-tuning simultaneously; (b) separate strategy: the model is first pre-finetuned on the synthetic validation and synthetic test sets, and the model weights are saved, followed by further fine-tuning the pre-finetuned model with the real nominal test set. In both cases, the accuracy on the real edge test set improves significantly. The improvements are attributed to the model encountering real-world images for the first time, allowing it to learn the unseen characteristics of real-world runway samples and thereby enhance generalization. However, fine-tuning using a separate strategy achieves higher accuracy. The reason may be that the distributions of the synthetic and real datasets do not interfere with each other, leading to better convergence and more stable training.
• When the fine-tuning EDA probability increases to 10%, the accuracy in all scenarios across all the test sets surpasses corresponding experiments under the 5% probability. Fine-tuning with both the synthetic validation and synthetic test sets yields the best performance on the real nominal and overall real test sets, achieving accuracies of 0.627 and 0.590, with improvements of 2.6% and 2.1%, respectively. When the real nominal test set is further included using the separate strategy for fine-tuning, the model achieves the best performance on the real edge test set, with an accuracy of 0.582, an improvement of 40.9%.
• The training times presented in Table 14 include both the pre-training time and the fine-tuning time. With a 5% EDA probability, the training times for each model are 192.77 min, 215.30 min, 234.30 min, and 235.39 min, representing increases of 20.39%, 34.46%, 46.33%, and 47.01%, respectively, compared to the 160.12 min of the pertained YOLO-RWY. When the EDA probability is increased to 10%, the training times increase by 22.59%, 38.36%, 51.74%, and 51.75%, respectively, slightly higher than with the 5% probability. Given the additional fine-tuning datasets and increased training epochs, increases in training costs are to be expected.

4.7.2. Visualizations of the Runway Detections

To visually demonstrate the superior runway detection performance of the proposed YOLO-RWY model, this section presents the visualizations of the runway detection results. The fine-tuned model with the best accuracy is used for detection, with the input image size set to 1280 to showcase the strongest generalization capability. Additionally, assuming the number of airport runways to be detected is known, the maximum detection number is set to one during inference in this experiment.

Figure 13 illustrates the runway detections under different edge scenarios, including rain, snow, fog, backlight, and low light scenarios. Figure 14 shows the runway detections with corresponding enlarged views for details.

As shown in Figure 13 and Figure 14, the model demonstrates robust and accurate runway detections under various adverse conditions, effectively overcoming the challenges posed by unfavorable environments and weather conditions. However, due to the limited coverage of the training and fine-tuning datasets and the inherent limitations in model capacity, there are still instances of missed or false runway detections.

5. Conclusions

Vision-based autonomous landing is crucial for the intelligent and safe operation of fixed-wing UAVs during landing, providing an independent passive navigation source in the case of external navigation denial. Runway detection in VAL offers vital information about the runway position and orientation during landing, demanding high accuracy, efficiency, robustness, and lightweight design.

This paper proposes a high-precision and real-time runway detection model framework, YOLO-RWY, to address these challenges. The proposed YOLO-RWY is built on the single-stage, decoupled, and anchor-free YOLOv8 framework. First, to enhance generalization, disturbance resistance, and safety, the EDA module with a rich set of augmentation methods is designed for online sample augmentation. Second, the lightweight LSKA module is introduced into the backbone architecture to capture long-range dependencies through large receptive fields and attention mechanisms. Third, the neck architecture is restructured into the BiFPN module, offering more complex yet lightweight cross-scale feature aggregation with attention allocation. Finally, the EIoU loss and ETAL assigner are constructed to provide a more accurate evaluation of bounding box regressions, thereby guiding faster and better convergence during training.

Extensive experiments on the LARD dataset demonstrate that the proposed YOLO-RWY achieves ${\mathrm{AP}}_{50:95}$ scores of 0.760, 0.611, and 0.413 on the synthetic, real nominal, and real edge test sets, respectively. Further deployment experiments on an edge device show an inference latency of 6.475 ms and an FPS of 154.4. Visualization of runway detections further confirms the effectiveness of the proposed YOLO-RWY. In conclusion, the proposed YOLO-RWY significantly improves the accuracy and robustness while maintaining real-time performance. The model can accurately identify landing runways in various complex scenarios and meets the lightweight requirements of the fixed-wing UAV onboard devices, providing a reliable solution for the VAL systems.

Future research will focus on several key areas. First, the limited nighttime and adverse weather samples in the LARD dataset may affect the performance under extreme conditions. To address this, more diverse samples from adverse conditions can be introduced, and generative adversarial networks (GANs) for data augmentation can be employed, along with the development of feature enhancement modules to better handle the challenging environments. Additionally, the LARD dataset primarily consists of samples from large and medium-sized airports, which have standardized runway markings, materials, textures, and environments. In contrast, small airports often present more complex and diverse visual runway characteristics. Incorporating these unstructured runway samples will be essential to improve detection performance and broaden the applicability. Furthermore, target tracking can be integrated to compensate for missed or abnormal detections, potentially improving detection accuracy and enabling multi-runway detection and tracking. Finally, the integration of runway keypoint detection and semantic segmentation could support relative position and pose estimation and landing zone assessment, providing a foundation for more accurate and reliable VAL systems.