Autonomous Flight in Hover and Near-Hover for Thrust-Controlled Unmanned Airships
Abstract
:1. Introduction
2. A General Model for Airship Dynamics
2.1. Airship Flight Dynamics Model: General Formulation
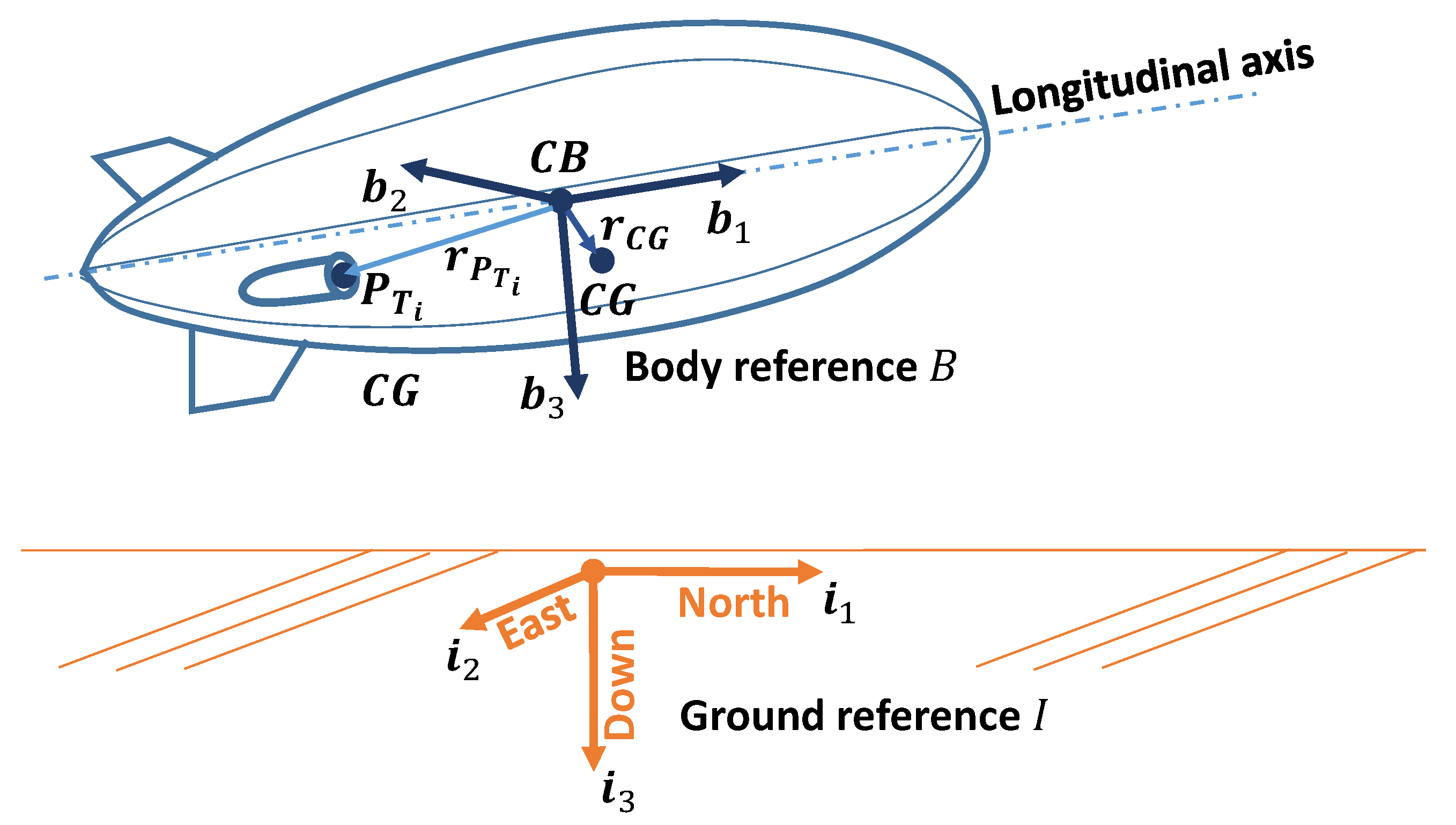
2.2. Representation of the Equations of Motion in Body Components
2.2.1. Aerodynamic Active and Reaction Terms
2.2.2. Buoyancy and Gravity
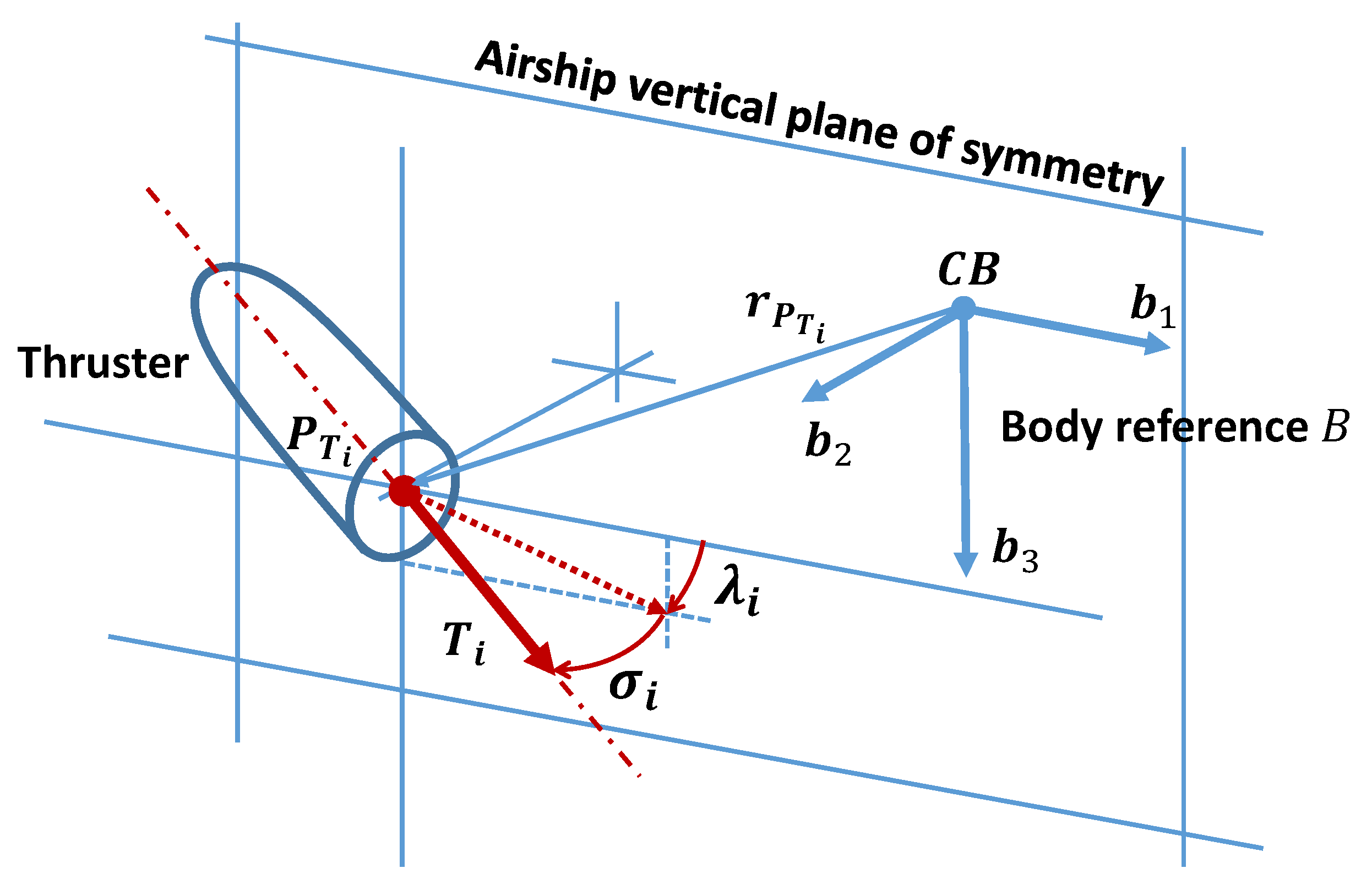
2.2.3. Thrust
3. Control Layers: Thrust for Hover Equilibrium and Near-Hover Steering
3.1. Control Solution for Static Equilibrium in Hovering Flight for a Thrust-Controlled Airship
- Thrusters: the body coordinates of the thrusters wrt. the center of buoyancy , and the attitude angles and of the thrusters with respect to the airship;
- Inertia: the mass m of the system and the body coordinates of the center of gravity wrt. the center of buoyancy ;
- Buoyancy: the volume of the envelope and the density of air at hovering altitude;
- The assigned pitch angle of the deck in hover .
3.2. Control Solution for Airship Steering in Hover and Near-Hover
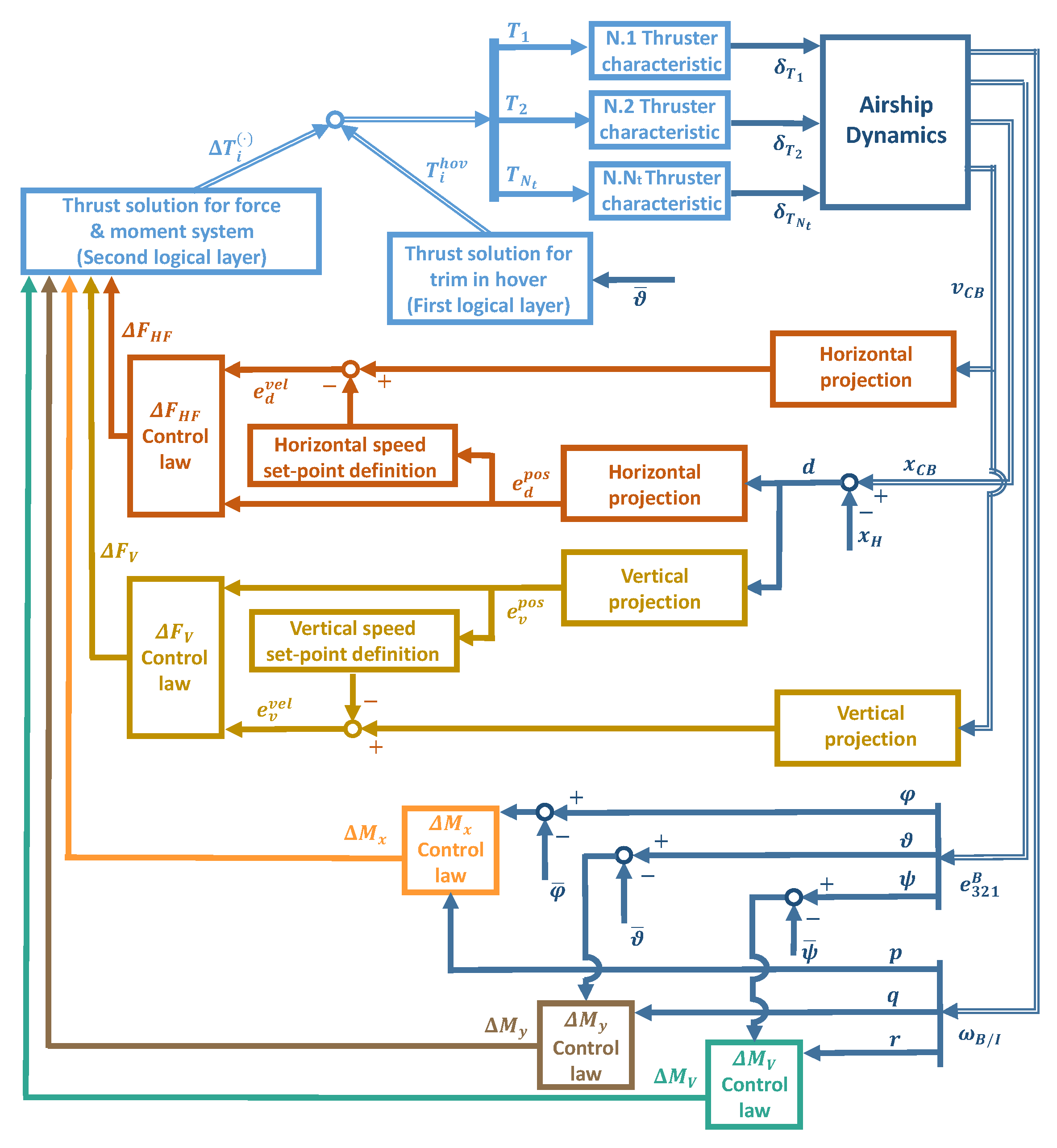
4. Control Schemes for Hover and Near-Hover
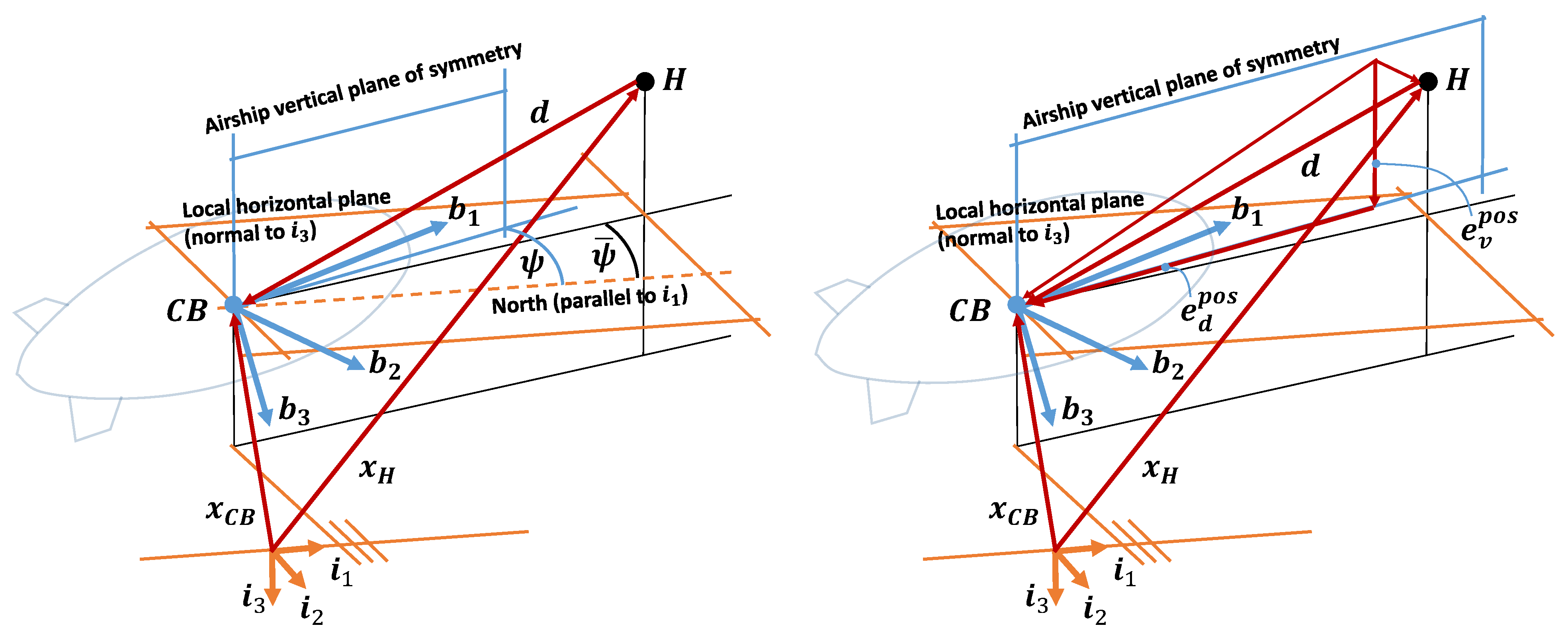
- Given the position of the airship wrt. the ground reference (i.e., the coordinates in three-dimensional space), the HNHC controller computes the relative position vector , between the target point for hover and the current position (see plots on Figure 4).
- Concurrently, the airship is pitched to a target deck angle by applying thrust components to obtain a suitable (the same conceptual procedure as the previous point).
- The airship is steered around the vertical inertial axis , to align the longitudinal body plane of symmetry with vector , through a set of values required for a suitable (the same conceptual procedure as the previous point).
- When alignment of the longitudinal plane of the airship with vector is reached within a certain tolerance, the airship is maneuvered through thrust force components and equivalent to prescribed and (the same conceptual procedure as the previous point), until the modulus of is satisfactorily small, i.e., the airship is sufficiently close to the target point . Then the airship is kept close to the target point by means of the same logic (i.e., horizontal-forward and vertical force).
4.1. Control Laws for Stabilization and Guidance
- The rolling moment demand is obtained through a proportional law on the roll angle and roll component of the rotational speed of the airship p, asIn Equation (12), the value of the reference roll can be set to zero, i.e., as stated, to take (and keep) the airship around a null roll value (the equivalent of a leveler function on most autopilots of common winged aircraft). The rate-proportional component takes the function of a roll damper, to induce stable behavior around the roll axis.
- The pitching moment demand is obtained through a proportional law, acting on the pitch angle and on the pitching component of the rotational speed q, yieldingwhere the value of is a target deck angle in hover, set by the mission planner, for instance based on requirements concerning the attitude of the payload. In particular, the component proportional to the rotational rate takes on the role of the pitch stability augmentation system deployed in FFC mode, increasing the damping around the pitch axis.
- The moment demand in the ground-horizontal plane is regulated through a proportional control law with respect to a heading signal and a yaw damping effect is added through a feed-back of the yaw rate signal r. The feed-back variable for heading control is the heading error, defined as in the left plot of Figure 4. The ensuing control law yieldswhere is the current heading of the airship.
- The values of and demanded for position control are computed according to two independent, yet structurally similar, laws. These are based on a position error and a velocity error. The concept behind these laws is that the preliminary action of the heading alignment control (previous point), reducing the absolute value of the error within a tolerance, will take the relative position vector on the longitudinal plane of the airship (or very close to this condition). From that condition, the horizontal-forward force should act on the distance from the target on the local horizon plane, whereas should act only on the corresponding vertical distance. As already pointed out, no action outside of the longitudinal plane of the airship is required in this scenario. Analytically, the two laws can be written asIn Equation (15), the position errors are the distance error and the vertical error , and they are pictorially defined on the right plot of Figure 4. Additionally, and are the velocity errors, respectively, between the velocity component on the local horizon plane or normal to it, and corresponding velocity set-points. The velocity set-points for horizontal and lateral speed are defined as functions of the corresponding position error, through a linear-bounded function. In particular, the velocity set-points are limited between a top and bottom value, which are reached for assigned values of the position errors, whereas the velocity set-points are null when the corresponding position errors are null.
4.2. Additional Remarks on Control Laws
4.3. From Force and Moment Demands to Thrust Settings
5. Case Study: A Five-Thruster Thrust-Controlled Airship
5.1. Assessment of Thruster Layout: Trim in Hover and Steering in Near-Hover
5.1.1. Control Solution for Trim in Hover
5.1.2. Steering Control in Near-Hover
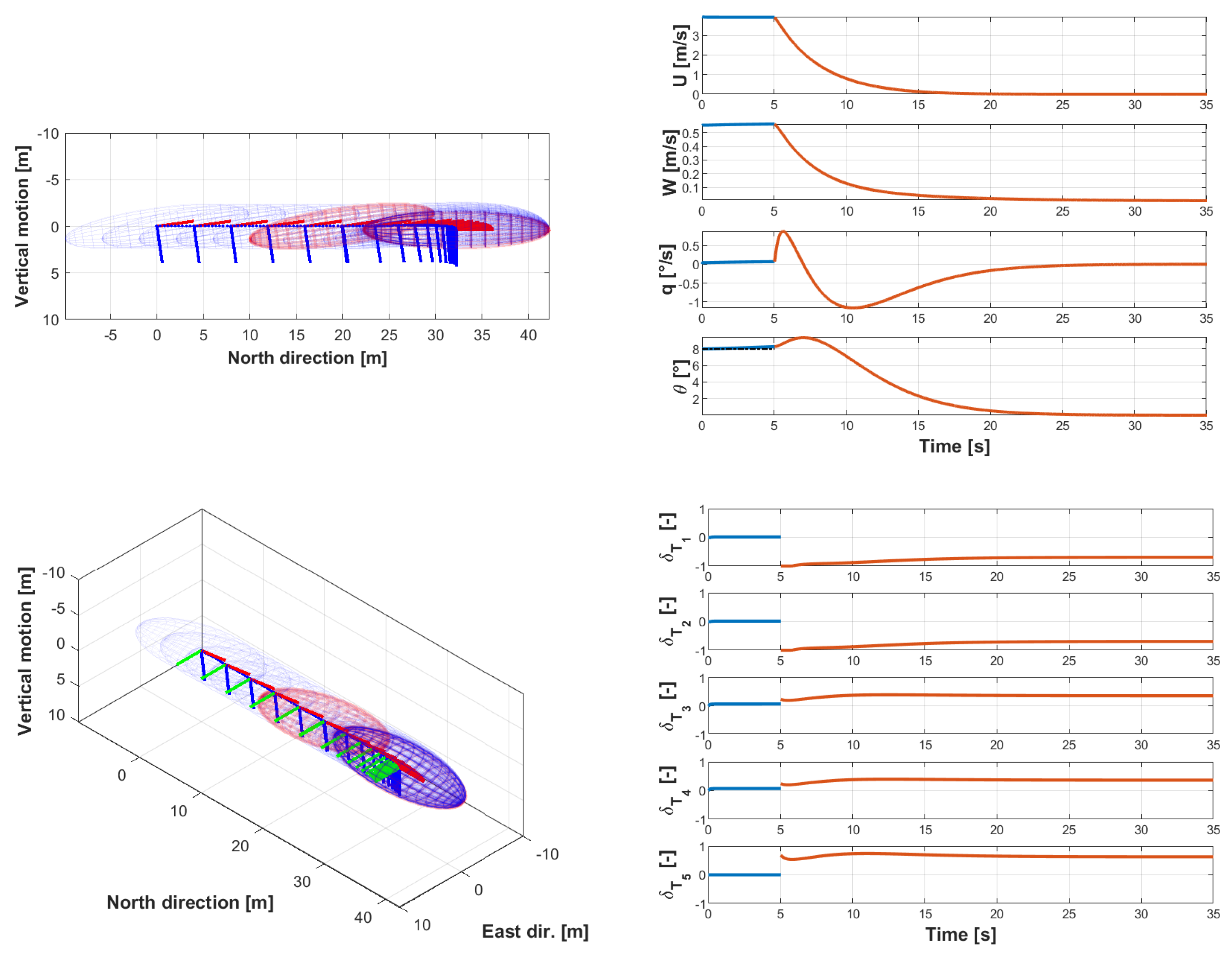
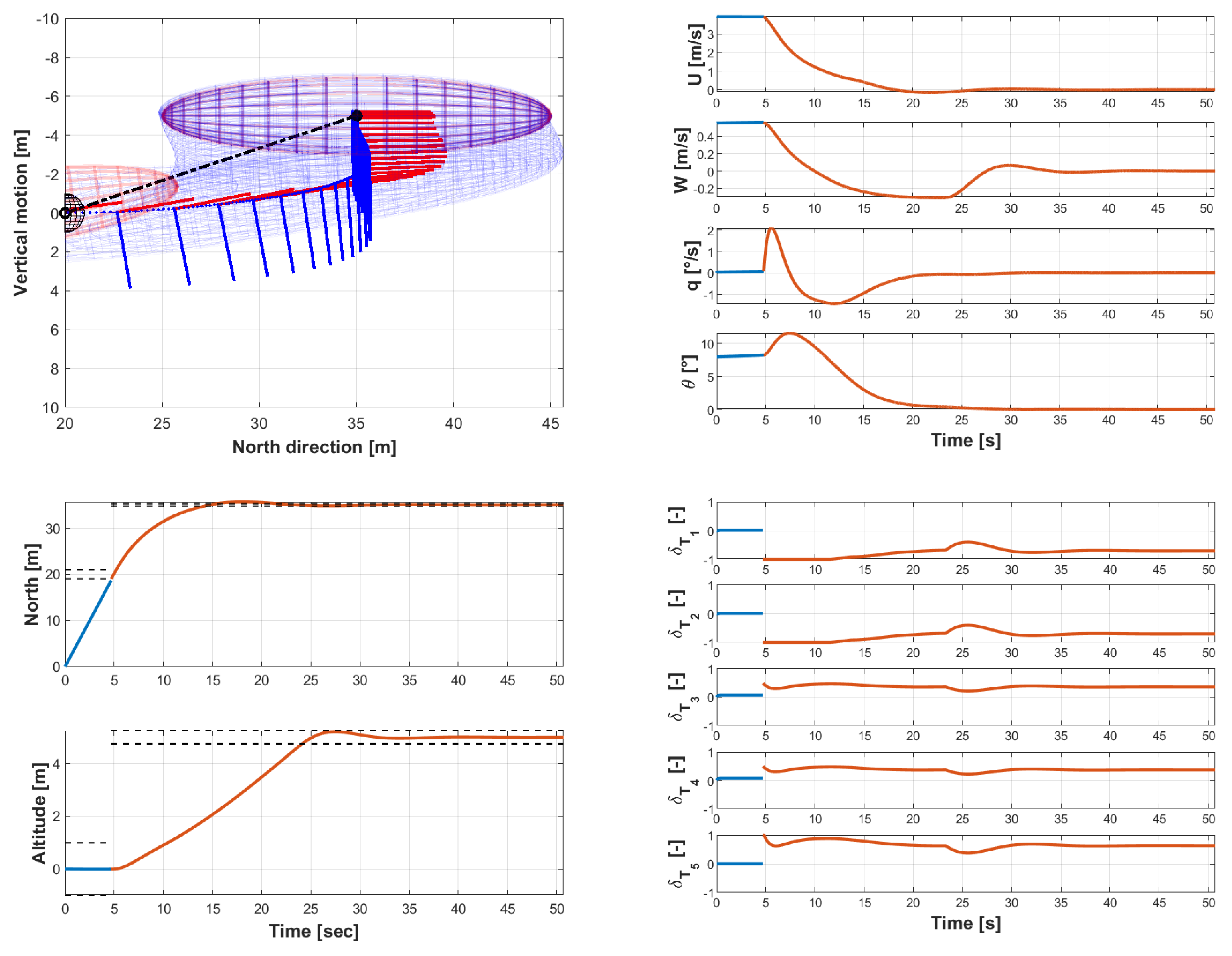
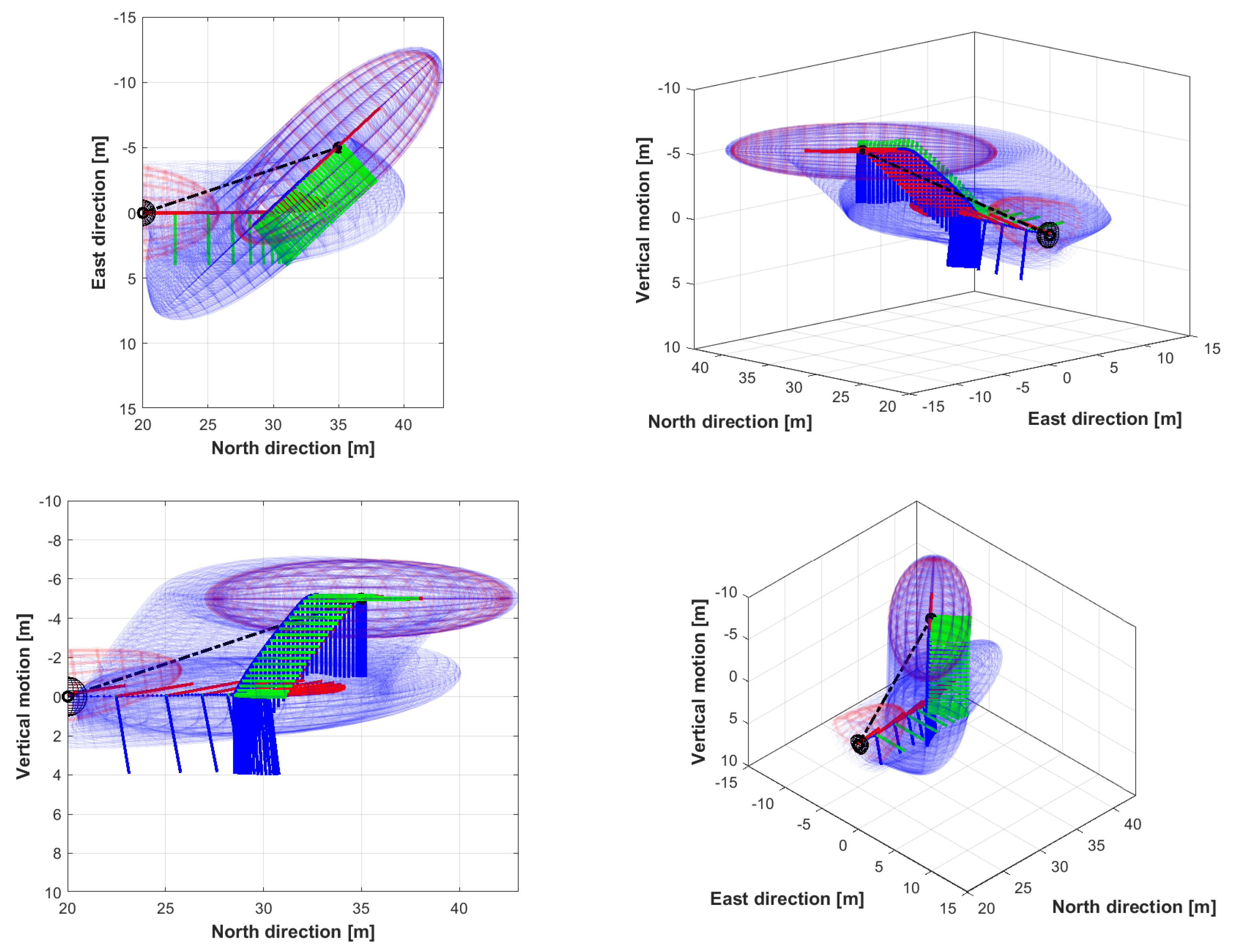
5.2. Numerical Results
5.2.1. Transition from Forward Flight to a Hovering Condition
5.2.2. From forward Flight to Hover at Assigned Position-Longitudinal Motion
5.2.3. From forward Flight to Hover at Assigned Position-Longitudinal and Lateral-Directional Motion
6. Conclusions
6.1. Proposed Control Strategy
6.1.1. First Control Layer: Static Equilibrium in Hover
6.1.2. Second Control Layer: Stabilization and Navigation in Near-Hover
6.1.3. Overall Control Algorithm: Hover and Near-Hover Flight Control Mode
6.2. Case Study
6.3. Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FFC | Forward flight control |
| HNHC | Hover and near-hover control |
| Body reference (supposed centered in in this paper) | |
| Inertia reference (ground in this paper) | |
| Volume of lifting gas on airship | |
| Center of buoyancy | |
| Center of gravity | |
| Inertia tensor in | |
| Generalized mass matrix in | |
| Static moment in | |
| Relative position of airship from target point | |
| Array of attitude angles | |
| Force vector | |
| Moment vector in | |
| Position of center of gravity from | |
| Position of point of application of i-th thrust force from | |
| Generalized forcing term vector in | |
| Aerodynamic forcing term vector in | |
| Active component of aerodynamic forcing term vector in | |
| Reactive component of aerodynamic forcing term vector in | |
| Buoyancy forcing term vector in | |
| Gravity forcing term vector in | |
| Thrust forcing term vector in | |
| Array of aerodynamic controls | |
| Array of thrust controls | |
| Velocity vector of | |
| Generalized velocity vector of | |
| Position vector of from the origin of reference | |
| Position vector of target point for hover from the origin of reference | |
| Rotational speed of body reference wrt. inertial reference | |
| Horizontal-forward force demand | |
| , | Horizontal-lateral force demand |
| Vertical force demand | |
| Modulating function of thrust vs. thrust setting for i-th thruster | |
| Moment demand in horizontal plane | |
| Rolling moment demand | |
| Pitching moment demand | |
| Number of thrusters | |
| Thrust from i-th thruster | |
| Thrust demand for horizontal-forward force from i-th thruster | |
| Thrust demand for horizontal-lateral force from i-th thruster | |
| Thrust demand for vertical force from i-th thruster | |
| Thrust demand for hover from i-th thruster | |
| Thrust demand for pitching moment from i-th thruster | |
| Thrust demand for rolling moment from i-th thruster | |
| Thrust demand for moment in horizontal plane from i-th thruster | |
| Nominal thrust intensity for i-th thruster | |
| U | First (longitudinal) component of in body ref. |
| V | Second (lateral) component of in body ref. |
| W | Third (vertical) component of in body ref. |
| Threshold distance from target point | |
| Horizontal error on position | |
| Error on horizontal velocity | |
| Vertical error on position | |
| Vertical error on velocity | |
| Control gain | |
| l.h.s | Left-hand side of expression |
| m | Mass of airship |
| p | First component of in body ref. |
| q | Second component of in body ref. |
| r | Third component of in body ref. |
| r.h.s | Right-hand side of expression |
| t | Time |
| Velocity threshold for HNHC activation | |
| Elevator deflection | |
| Aileron deflection | |
| Rudder deflection | |
| Thrust setting of i-th thruster | |
| Pitch attitude angle | |
| Tilt of i-th thrust line | |
| Density of air | |
| Lateral misalignment of i-th thrust line | |
| Roll attitude angle | |
| Yaw attitude angle | |
| Top bound of heading error |
References
- Elfes, A.; Bueno, S.; Bergerman, M.; Ramos, J. A semi-autonomous robotic airship for environmental monitoring missions. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No. 98CH36146), Leuven, Belgium, 20 May 1998; Volume 4, pp. 3449–3455. [Google Scholar]
- Jon, J.; Koska, B.; Pospíšil, J. Autonomous airship equipped with multi-sensor mapping platform. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. XL-5 W 2013, 1, 119–124. [Google Scholar] [CrossRef]
- Fedorenko, R.; Krukhmalev, V. Indoor autonomous airship control and navigation system. In MATEC Web of Conferences; EDP Sciences: Evry, France, 2016; Volume 42, p. 01006. [Google Scholar]
- Chu, A.; Blackmore, M.; Oholendt, R.G.; Welch, J.V.; Baird, G.; Cadogan, D.P.; Scarborough, S.E. A Novel Concept for Stratospheric Communications and Surveillance: Star Light. In Proceedings of the AIAA Balloon Systems Conference, Williamsburg, VA, USA, 21–24 May 2007. [Google Scholar] [CrossRef]
- Smith, I.; Lee, M.; Fortneberry, M.; Judy, R. HiSentinel80: Flight of a high altitude airship. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Including the AIAA Balloon Systems Conference and 19th AIAA Lighter-Than, Virginia Beach, VA, USA, 20–22 September 2011; p. 6973. [Google Scholar]
- Miller, S.H.; Fesen, R.; Hillenbrand, L.; Rhodes, J.; Baird, G.; Blake, G.; Booth, J.; Carlile, D.E.; Duren, R.; Edworthy, F.G. Airships: A New Horizon for Science. Technical report. arXiv 2014, arXiv:1402.6706. [Google Scholar]
- Riboldi, C.E.D.; Rolando, A.; Regazzoni, G. On the feasibility of a launcher-deployable high-altitude airship: Effects of design constraints in an optimal sizing framework. Aerospace 2022, 9, 210. [Google Scholar] [CrossRef]
- Young, M.; Keith, S.; Pancotti, A. An overview of advanced concepts for near space systems. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009; p. 4805. [Google Scholar]
- Manikandan, M.; Pant, R.S. Research and advancements in hybrid airships—A review. Prog. Aerosp. Sci. 2021, 127, 100741. [Google Scholar]
- Carichner, G.E.; Nicolai, L.M. Fundamentals of Aircraft and Airship Design; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2013. [Google Scholar]
- Kämpf, B. Flugmechanik und Flugregelung von Luftschiffen. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2004. [Google Scholar] [CrossRef]
- Kornienko, A. System Identification Approach for Determining Flight Dynamical Characteristics of an Airship from Flight Data. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2006. [Google Scholar] [CrossRef]
- Cai, Z.L. Research on Dynamical Modeling and Nonlinear Control of a Stratospheric Airship. Ph.D. Thesis, Shanghai JIAO TONG University, Shanghai, China, 2006. [Google Scholar]
- Li, Y.; Nahon, M.; Sharf, I. Dynamics modeling and simulation of flexible airships. AIAA J. 2009, 47, 592–605. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Zheng, W. Design, modeling and control for a stratospheric telecommunication platform. Acta Astronaut. 2012, 80, 181–189. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Thrust-Based Stabilization and Guidance for Airships without Thrust-Vectoring. Aerospace 2023, 10, 344. [Google Scholar] [CrossRef]
- Beji, L.; Abichou, A. Tracking control of trim trajectories of a blimp for ascent and descent flight manoeuvres. Int. J. Control 2005, 78, 706–719. [Google Scholar] [CrossRef]
- Cai, Z.; Qu, W.; Xi, Y.; Wang, Y. Stabilization of an underactuated bottom-heavy airship via interconnection and damping assignment. Int. J. Robust Nonlinear Control 2007, 17, 1690–1715. [Google Scholar] [CrossRef]
- Sangjong, L.; Haechang, L.; Daeyeon, W.; Hyochoong, B. Backstepping approach of trajectory tracking control for the mid-altitude unmanned airship. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 6319. [Google Scholar]
- Paiva, E.; Benjovengo, F.; Bueno, S.; Ferreira, P. Sliding mode control approaches for an autonomous unmanned airship. In Proceedings of the 18th AIAA Lighter-Than-Air Systems Technology Conference, Seattle, WA, USA, 4–7 May 2009. [Google Scholar]
- Liesk, T.; Nahon, M.; Boulet, B. Design and experimental validation of a nonlinear low-level controller for an unmanned fin-less airship. IEEE Trans. Control Syst. Technol. 2013, 21, 149–161. [Google Scholar] [CrossRef]
- Nagabhushan, B.L.; Tomlinson, N.P. Dynamics and control of a heavy lift airship hovering in a turbulent cross wind. J. Aircr. 1982, 19, 826–830. [Google Scholar] [CrossRef]
- Nagabhushan, B.L.; Tomlinson, N.P. Thrust-vectored takeoff, landing, and ground handling of an airship. J. Aircr. 1986, 23, 250–256. [Google Scholar] [CrossRef]
- Azinheira, J.R.; Moutinho, A.; De Paiva, E.C. Airship hover stabilization using a backstepping control approach. J. Guid. Control Dyn. 2006, 29, 903–914. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Zheng, W. Station-keeping control for a stratospheric airship platform via fuzzy adaptive backstepping approach. Adv. Space Res. 2013, 51, 1157–1167. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Zheng, W. Positioning control for an autonomous airship. J. Aircr. 2016, 53, 1638–1646. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Layout Analysis and Optimization of Airships with Thrust-Based Stability Augmentation. Aerospace 2022, 9, 393. [Google Scholar] [CrossRef]
- Pamadi, B.N. Performance, Stability, Dynamics, and Control of Airplanes; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Munk, M.M. The Aerodynamic Forces on Airship Hulls; Technical Report; Report No. 184; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1926. [Google Scholar]
- Lamb, H. Hydrodynamics; Dover Publications: New York, NY, USA, 1945. [Google Scholar]
- Jones, S.P.; DeLaurier, J.D. Aerodynamic estimation techniques for aerostats and airships. J. Aircr. 1982, 20, 120–126. [Google Scholar] [CrossRef]
- Mueller, J.; Paluszek, M.; Zhao, Y. Development of an aerodynamic model and control law design for a high altitude airship. In Proceedings of the AIAA 3rd “Unmanned Unlimited” Technical Conference, Workshop and Exhibit, Chicago, IL, USA, 20–23 September 2004; p. 6479. [Google Scholar]
- Trainelli, L.; Gennaretti, M.; Bernardini, G.; Rolando, A.; Riboldi, C.E.D.; Redaelli, M.; Riviello, L.; Scandroglio, A. Innovative helicopter in-flight noise monitoring systems enabled by rotor-state measurements. Noise Mapp. 2016, 3. [Google Scholar] [CrossRef]



| Parameter | Value | |
|---|---|---|
| Mass m (kg) | 137.28 | |
| Envelope volume (m3) | 107.42 | |
| Overall length (m) | 16.0 | |
| Horizontal displacement of from , (m) | 0.006 | |
| Vertical displacement of from , (m) | 0.455 | |
| Number of thrusters | 5 | |
| Nominal thrust (each unit) (N) | 250 | |
| Pos. of Nr. 1 thruster wrt. , (m) | ||
| Pos. of Nr. 2 thruster wrt. , (m) | ||
| Pos. of Nr. 3 thruster wrt. , (m) | ||
| Pos. of Nr. 4 thruster wrt. , (m) | ||
| Pos. of Nr. 5 thruster wrt. , (m) | ||
| Thruster tilt angle (deg) | 34.7 | |
| Thruster tilt angle (deg) | −38.7 | |
| Thruster tilt angle (deg) | 90 | |
| Thruster side angle (deg) | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riboldi, C.E.D.; Rolando, A. Autonomous Flight in Hover and Near-Hover for Thrust-Controlled Unmanned Airships. Drones 2023, 7, 545. https://doi.org/10.3390/drones7090545
Riboldi CED, Rolando A. Autonomous Flight in Hover and Near-Hover for Thrust-Controlled Unmanned Airships. Drones. 2023; 7(9):545. https://doi.org/10.3390/drones7090545
Chicago/Turabian StyleRiboldi, Carlo E. D., and Alberto Rolando. 2023. "Autonomous Flight in Hover and Near-Hover for Thrust-Controlled Unmanned Airships" Drones 7, no. 9: 545. https://doi.org/10.3390/drones7090545
APA StyleRiboldi, C. E. D., & Rolando, A. (2023). Autonomous Flight in Hover and Near-Hover for Thrust-Controlled Unmanned Airships. Drones, 7(9), 545. https://doi.org/10.3390/drones7090545








