Sliding Surface Designs for Visual Servo Control of Quadrotors
Abstract
1. Introduction
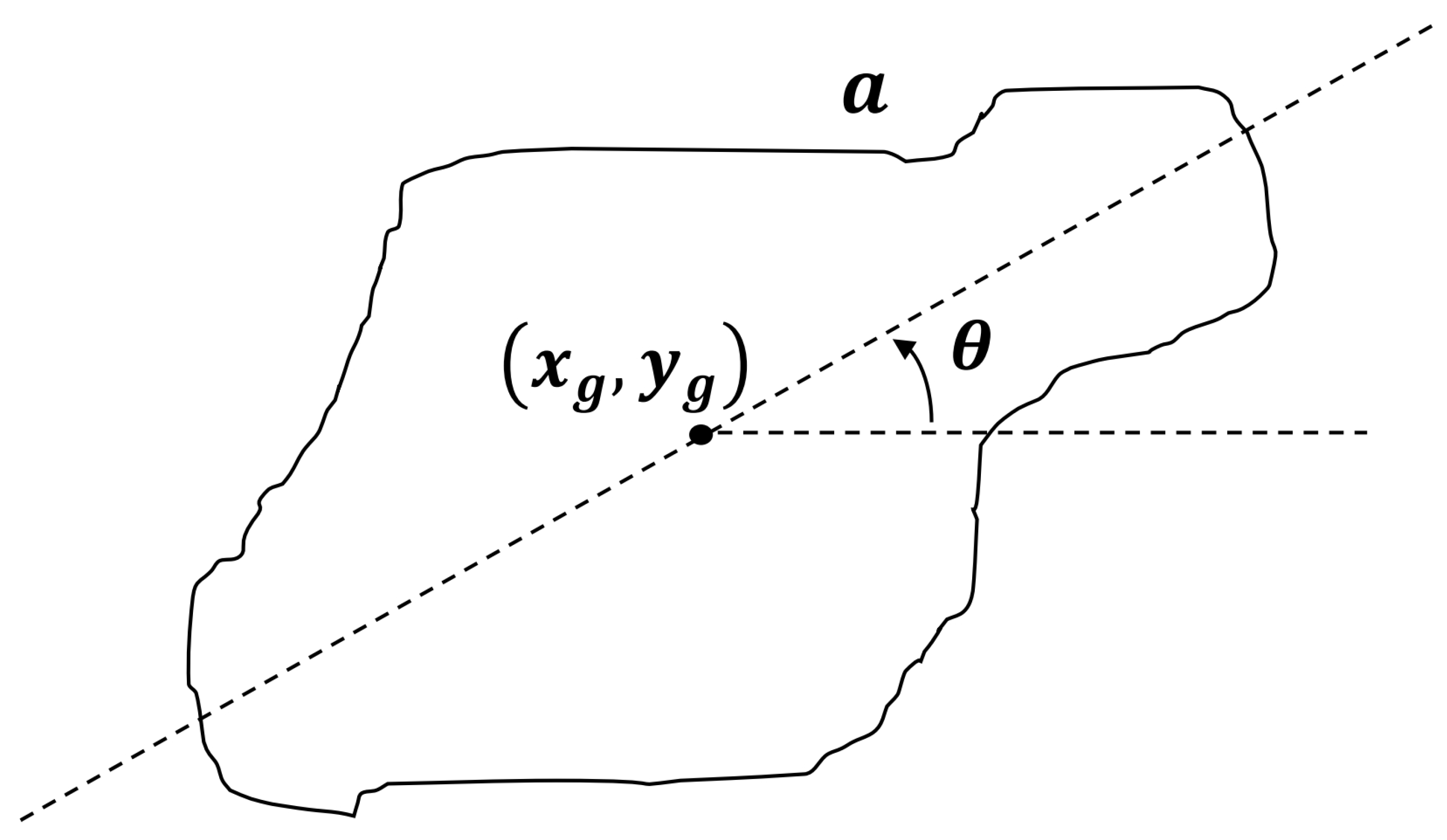
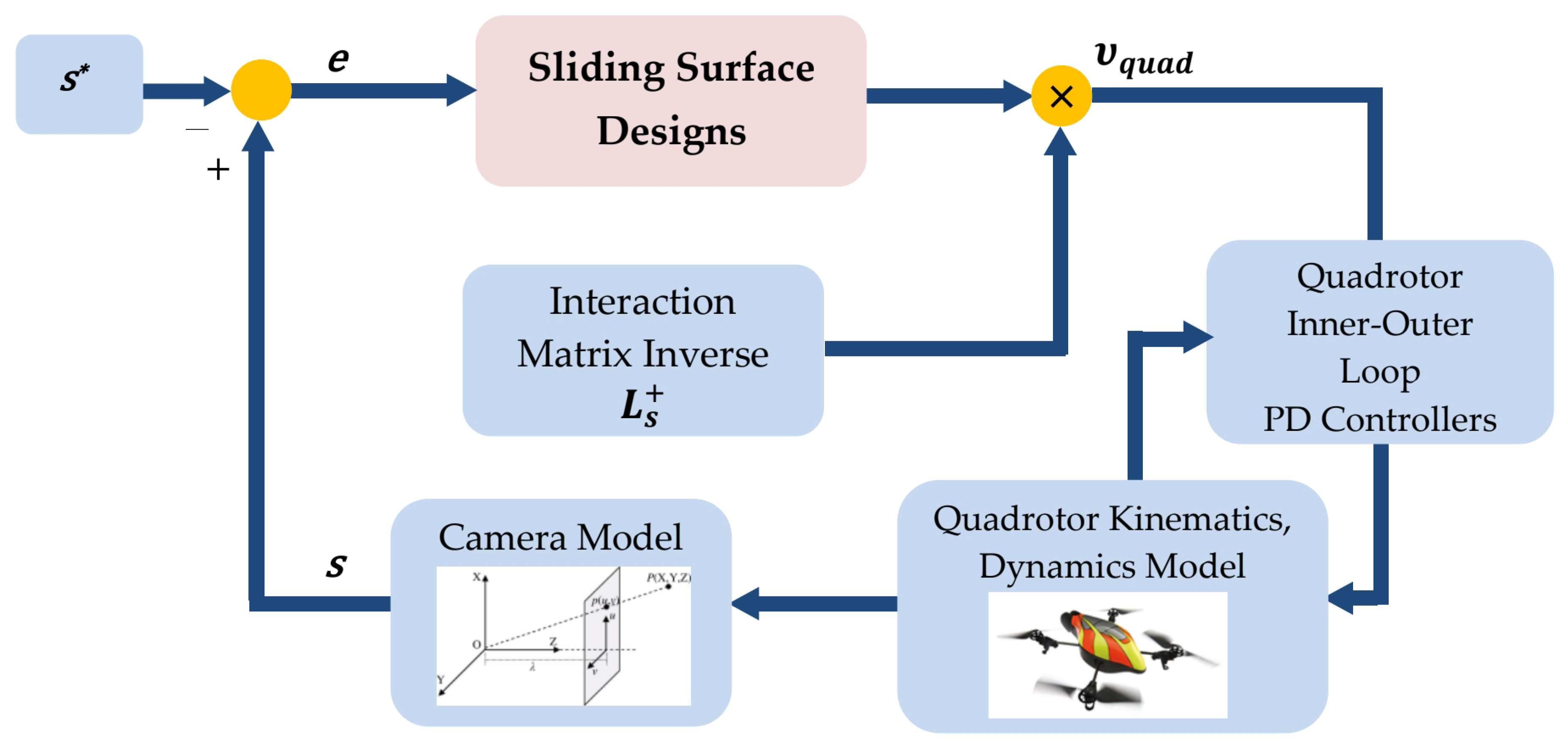
2. The Proposed IBVS System with Sliding Surface Designs
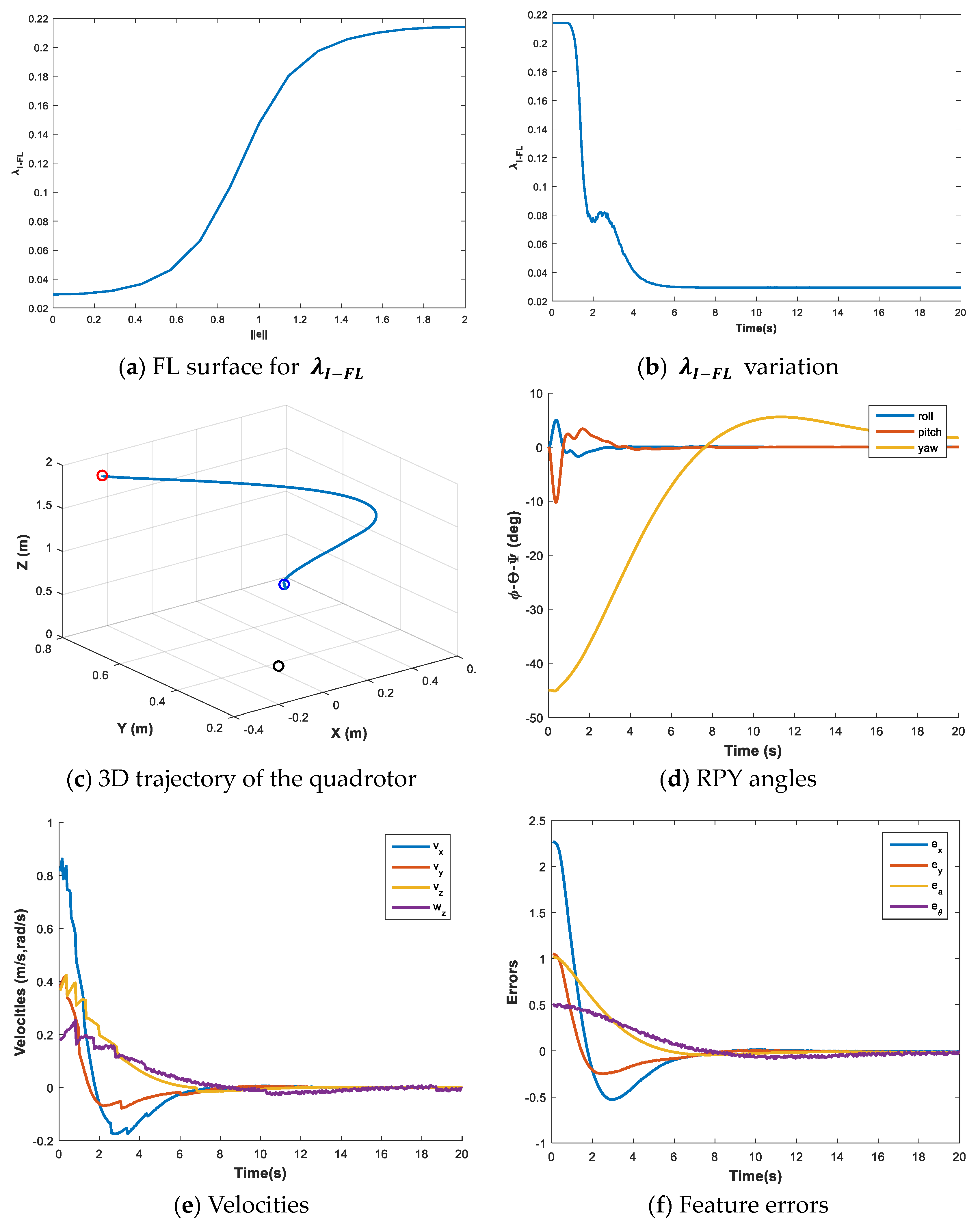
2.1. Fuzzy Logic for Linear Varying Sliding Surfaces
2.2. Fixed Accelerating Sliding Surface with Time Variation
2.3. Nonlinear Sliding Surface with Tangent Hyperbolic Function
2.4. Fuzzy Logic for Integral Sliding Surfaces
2.5. Nonlinear Sliding Surface with Time Variation
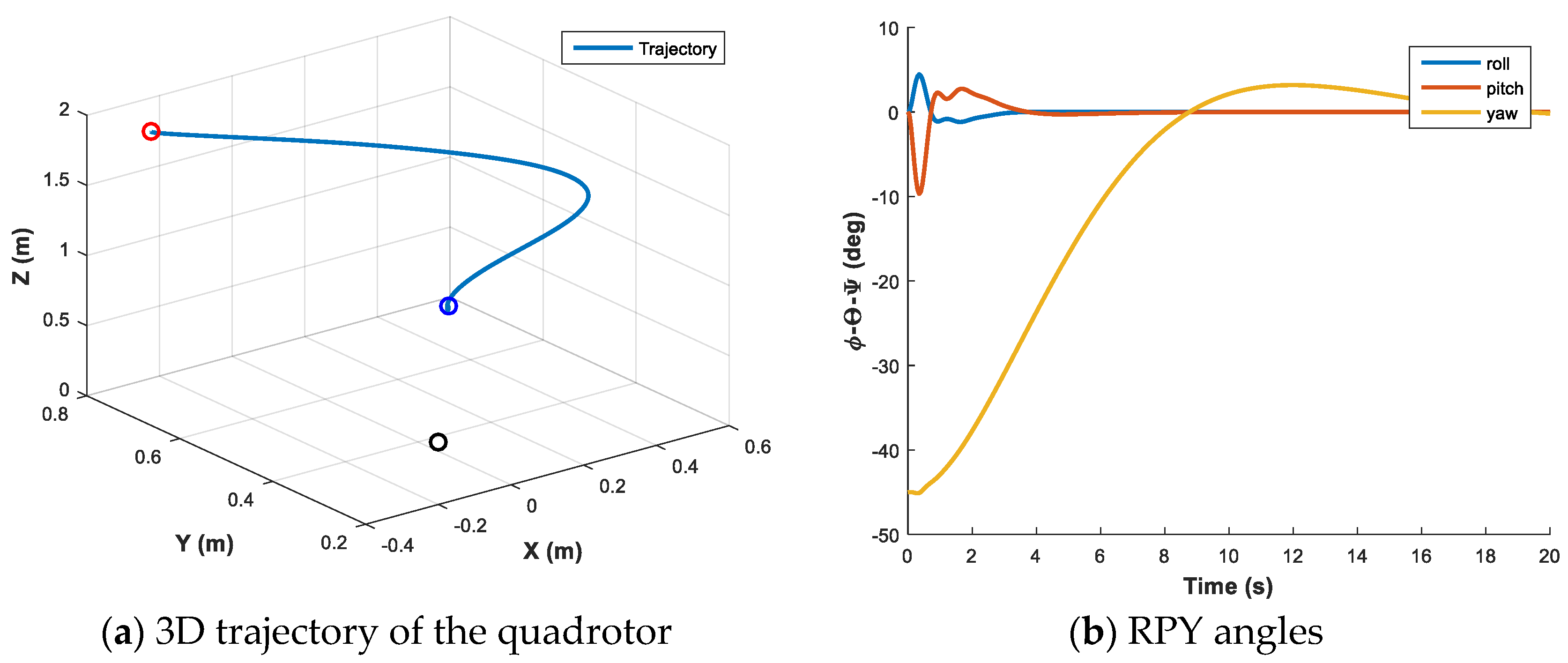
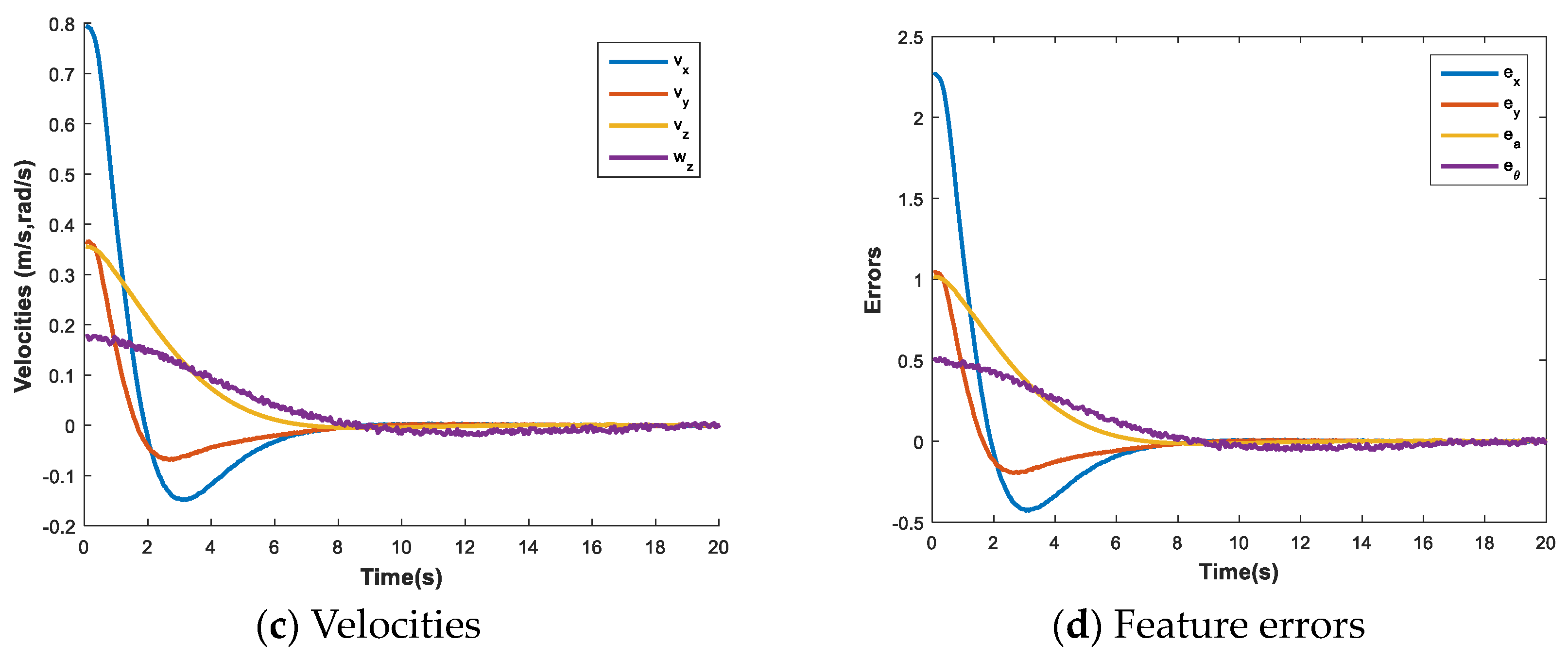
3. Simulation Results
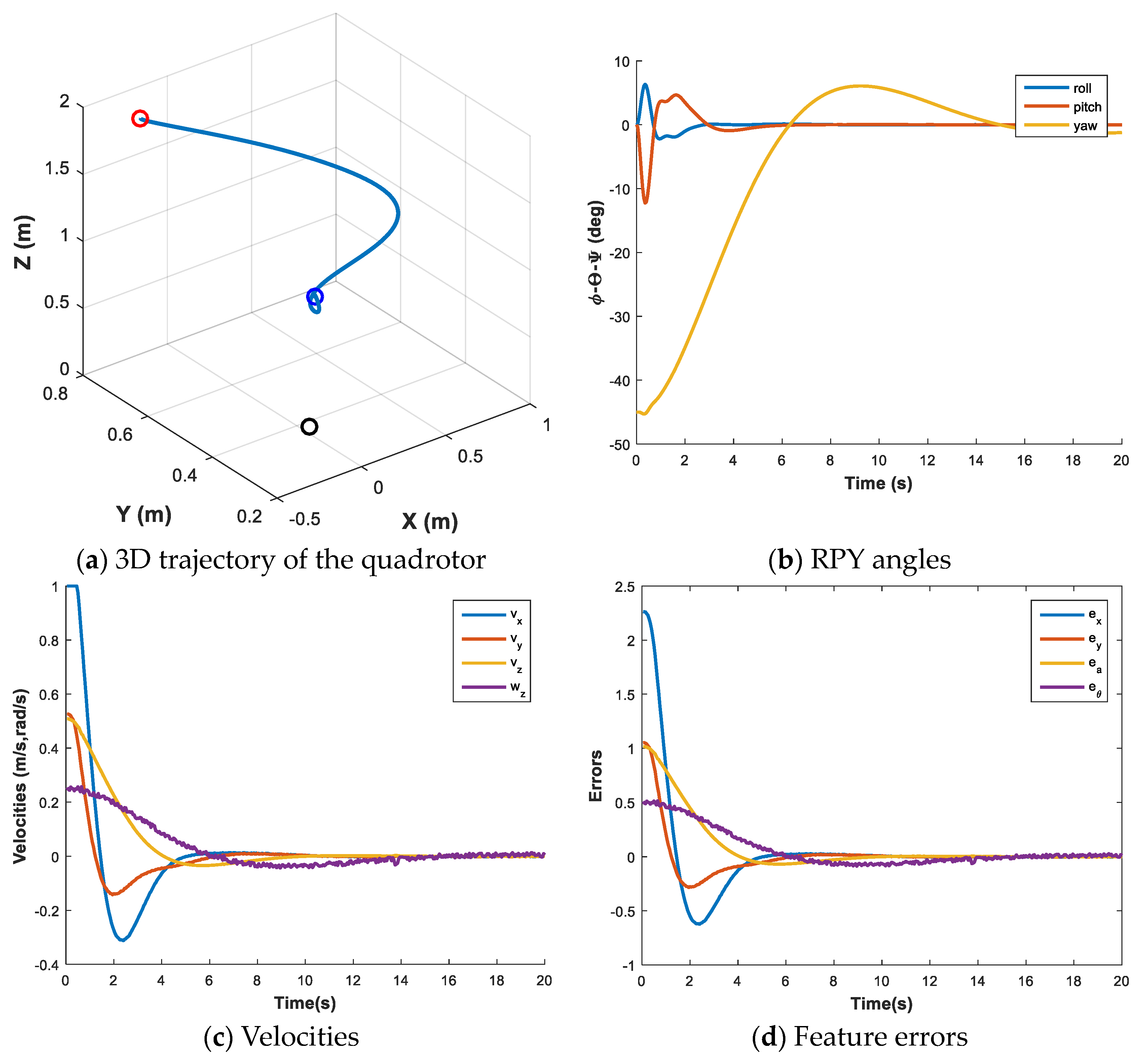
3.1. Classical IBVS with Fixed Sliding Slope
3.2. Design 1: IBVS with Fuzzy Logic for Linear Varying Sliding Surfaces
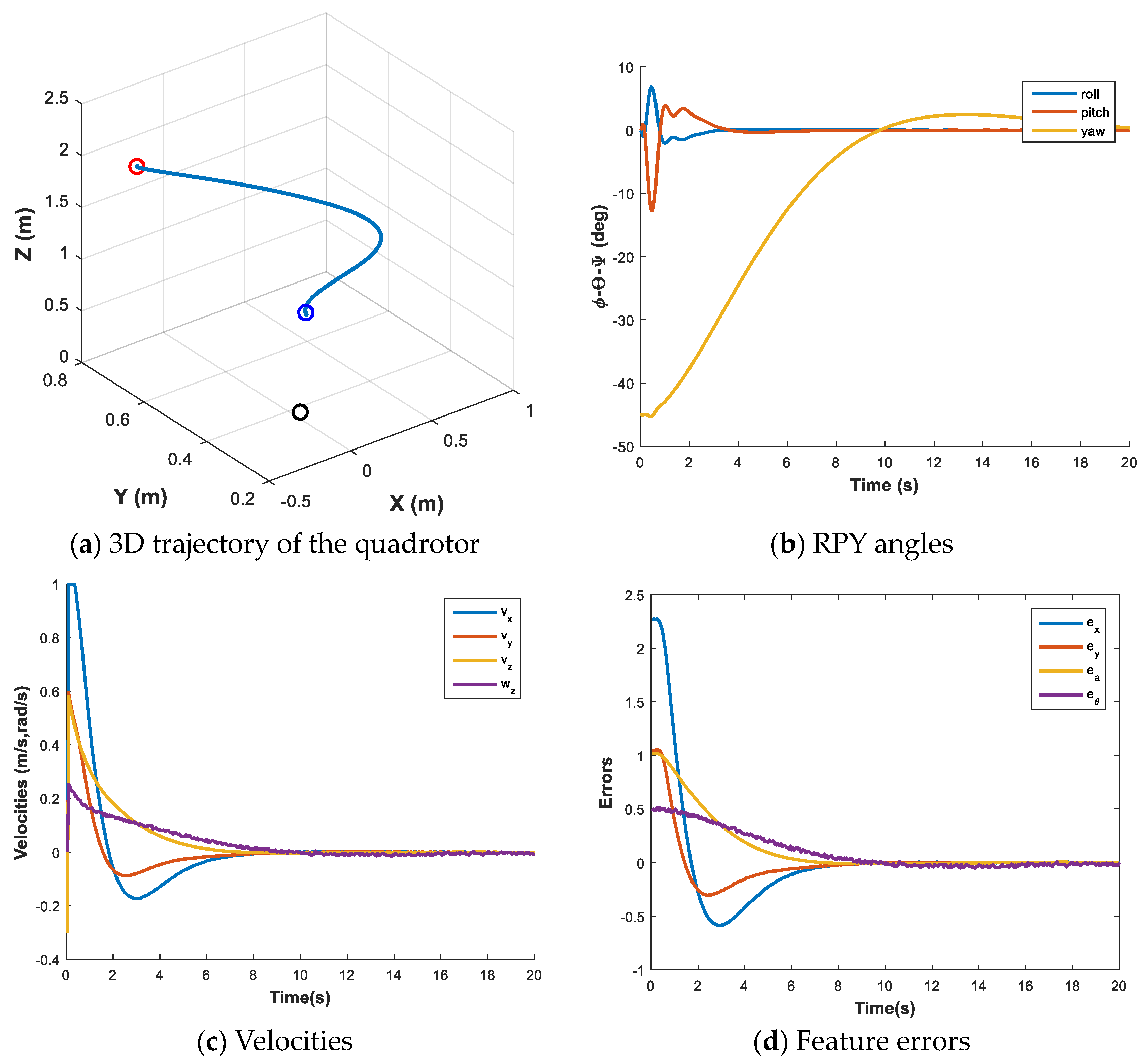
3.3. Design 2: IBVS with Fixed Accelerating Sliding Surface with Time Variations
3.4. Design 3: IBVS with Nonlinear Sliding Surface with Tangent Hyperbolic Function
3.5. Design 4: IBVS with Fuzzy Logic for Integral Sliding Surfaces
3.6. Design 5: IBVS with Nonlinear Sliding Surface with Time Variation
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roy, B.; DasGupta, A.; Paul, A. Impact of Space Weather Events on Satellite-Based Navigation. Sp. Weather 2013, 11, 680–686. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual Servo Control. I. Basic Approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Tahri, O.; Chaumette, F. Point-Based and Region-Based Image Moments for Visual Servoing of Planar Objects. IEEE Trans. Robot. 2005, 21, 1116–1127. [Google Scholar] [CrossRef]
- Bourquardez, O.; Mahony, R.; Hamel, T.; Chaumette, F. Stability and Performance of Image Based Visual Servo Control Using First Order Spherical Image Moments. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4304–4309. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual Servo Control. II. Advanced Approaches. IEEE Robot. Autom. Mag. 2007, 14, 109–118. [Google Scholar] [CrossRef]
- Yuksel, T. Intelligent Visual Servoing with Extreme Learning Machine and Fuzzy Logic. Expert Syst. Appl. 2017, 72, 344–356. [Google Scholar] [CrossRef]
- Chesi, G.; Hashimoto, K.; Prattichizzo, D.; Vicino, A. Keeping Features in the Field of View in Eye-in-Hand Visual Servoing: A Switching Approach. IEEE Trans. Robot. 2004, 20, 908–913. [Google Scholar] [CrossRef]
- Hamel, T.; Mahony, R. Visual Servoing of an Under-Actuated Dynamic Rigid-Body System: An Image-Based Approach. IEEE Trans. Robot. Autom. 2002, 18, 187–198. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T. Image-Based Visual Servo Control of Aerial Robotic Systems Using Linear Image Features. IEEE Trans. Robot. 2005, 21, 227–239. [Google Scholar] [CrossRef]
- Bourquardez, O.; Mahony, R.; Guenard, N.; Chaumette, F.; Hamel, T.; Eck, L. Kinematic Visual Servo Control of a Quadrotor Aerial Vehicle. IEEE Trans. Robot. 2007, 25, 833–838. [Google Scholar]
- Hamel, T.; Mahony, R. Image Based Visual Servo-Control for a Class of Aerial Robotic Systems. Automatica 2007, 43, 1975–1983. [Google Scholar] [CrossRef]
- Altug, E.; Ostrowski, J.P.; Taylor, C.J. Control of a Quadrotor Helicopter Using Dual Camera Visual Feedback. Int. J. Rob. Res. 2005, 24, 329–341. [Google Scholar] [CrossRef]
- Ceren, Z.; Altug, E. Image Based and Hybrid Visual Servo Control of an Unmanned Aerial Vehicle. J. Intell. Robot. Syst. 2012, 65, 325–344. [Google Scholar] [CrossRef]
- Metni, N.; Hamel, T. Visual Tracking Control of Aerial Robotic Systems with Adaptive Depth Estimation. Int. J. Control Autom. Syst. 2007, 5, 10. [Google Scholar]
- Sun, L.; Huang, Y.; Zheng, Z.; Zhu, B.; Jiang, J. Adaptive Nonlinear Relative Motion Control of Quadrotors in Autonomous Shipboard Landings. J. Frankl. Inst. 2020, 357, 13569–13592. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, X.; Yu, Y.; Yu, J.; Liu, X.; Zhou, C.; Tan, M. Image Dynamics-Based Visual Servoing for Quadrotors Tracking a Target with a Nonlinear Trajectory Observer. IEEE Trans. Syst. Man. Cybern. Syst. 2020, 50, 376–384. [Google Scholar] [CrossRef]
- Cunha, R.; Silvestre, C.; Hespanha, J.; Pedro Aguiar, A. Vision-Based Control for Rigid Body Stabilization. Automatica 2011, 47, 1020–1027. [Google Scholar] [CrossRef]
- Herissé, B.; Hamel, T.; Mahony, R.; Russotto, F.-X. Landing a VTOL Unmanned Aerial Vehicle on a Moving Platform Using Optical Flow. IEEE Trans. Robot. 2012, 28, 77–89. [Google Scholar] [CrossRef]
- Plinval, H.; Morin, P.; Mouyon, P.; Hamel, T. Visual Servoing for Underactuated VTOL UAVs: A Linear, Homography-Based Framework. Int. J. Robust Nonlinear Control 2014, 24, 2285–2308. [Google Scholar] [CrossRef]
- Asl, H.J.; Oriolo, G.; Bolandi, H. An Adaptive Scheme for Image-Based Visual Servoing of an Underactuated UAV. Int. J. Robot. Autom. 2014, 29, 92–104. [Google Scholar] [CrossRef]
- Thomas, J.; Loianno, G.; Daniilidis, K.; Kumar, V. Visual Servoing of Quadrotors for Perching by Hanging From Cylindrical Objects. IEEE Robot. Autom. Lett. 2016, 1, 57–64. [Google Scholar] [CrossRef]
- Mebarki, R.; Lippiello, V.; Siciliano, B. Nonlinear Visual Control of Unmanned Aerial Vehicles in GPS-Denied Environments. IEEE Trans. Robot. 2015, 31, 1004–1017. [Google Scholar] [CrossRef]
- Shi, H.; Hwang, K.S.; Li, X.; Chen, J. A Learning Approach to Image-Based Visual Servoing with a Bagging Method of Velocity Calculations. Inf. Sci. 2019, 481, 244–257. [Google Scholar] [CrossRef]
- Parsapour, M.; Taghirad, H.D. Kernel-Based Sliding Mode Control for Visual Servoing System. IET Comput. Vis. 2015, 9, 309–320. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, W.; Dong, H.; Ke, Y. Hybrid Visual Servoing for Rivet-in-Hole Insertion Based on Super-Twisting Sliding Mode Control. Int. J. Control Autom. Syst. 2020, 18, 2145–2156. [Google Scholar] [CrossRef]
- Miranda-Moya, A.; Castañeda, H.; Gordillo, J.L.; Wang, H. IBVS Based on Adaptive Sliding Mode Control for a Quadrotor Target Tracking under Perturbations. Mechatronics 2022, 88, 102909. [Google Scholar] [CrossRef]
- Yuksel, T. Intelligent Sliding Surface Design Methods Applied to an IBVS System for Robot Manipulators. In Applications from Engineering with MATLAB Concepts; Valdman, J., Ed.; IntechOpen: Rijeka, Croatia, 2016. [Google Scholar]
- Can, M.S.; Ercan, H. Real-Time Tuning of PID Controller Based on Optimization Algorithms for a Quadrotor. Aircr. Eng. Aerosp. Technol. 2022, 94, 418–430. [Google Scholar] [CrossRef]
- Palm, R.; Driankov, D.; Hellendoorn, H. Model Based Fuzzy Control Fuzzy Gain Schedulers and Sliding Mode Fuzzy Controllers; Springer: New York, NY, USA, 1996. [Google Scholar]
- Bartoszewicz, A.; Nowacka-Leverton, A. Time-Varying Sliding Modes for Second and Third Order Systems; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 9783540922162. [Google Scholar]
- Tokat, S.; Fadali, M.S.; Eray, O. A Classification and Overview of Sliding Mode Controller Sliding Surface Design Methods. In Recent Advances in Sliding Modes: From Control to Intelligent Mechatronics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Eker, I. Sliding Mode Control with PID Sliding Surface and Experimental Application to an Electromechanical Plant. ISA Trans. 2006, 45, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Kowalska, O.; Kamiński, M.; Szabat, K. Implementation of a Sliding-Mode Controller with an Integral Function and Fuzzy Gain Value for the Electrical Drive with an Elastic Joint. IEEE Trans. Ind. Electron. 2010, 57, 1309–1317. [Google Scholar] [CrossRef]
- Kim, J.-J.; Lee, J.-J.; Park, K.-B.; Youn, M.-J. Design of New Time-Varying Sliding Surface for Robot Manipulator Using Variable Structure Controller. Electron. Lett. 1993, 29, 195–196. [Google Scholar] [CrossRef]
- Corke, P.I. Robotics, Vision and Control: Fundamental Algorithms in MATLAB, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Pounds, P.E.I. Design, Construction and Control of a Large Quadrotor Micro Air Vehicle; The Australian National University: Canberra, Australia, 2007. [Google Scholar]
- Ercan, H.; Ulucan, H.; Can, M.S. Investigation of Wind Effect on Different Quadrotors. Aircr. Eng. Aerosp. Technol. 2022, 94, 1275–1288. [Google Scholar] [CrossRef]
- Colley, S.J. Vector Calculus; Pearson: London, UK, 2012. [Google Scholar]




| Low | Medium | High | |
|---|---|---|---|
| Low | High | High | High |
| Medium | Low | Low | High |
| High | Low | Low | Low |
| Parameters | Feature Conv. Time (s) | Path Length (m) | Maneuver Type | Computational Cost | |
|---|---|---|---|---|---|
| Classical | 16.25 | 1.7336 | Soft | Low | |
| Design 1 | 12.95 | 1.8009 | Aggressive (possible) | Medium | |
| Design 2 | 9.05 | 1.6269 | Aggressive (possible) | Low | |
| Design 3 | 12.65 | 1.97 | Soft | Low | |
| Design 4 | 17.3 | 1.83 | Aggressive (possible) | Medium | |
| Design 5 | 8.65 | 1.8237 | Soft | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuksel, T. Sliding Surface Designs for Visual Servo Control of Quadrotors. Drones 2023, 7, 531. https://doi.org/10.3390/drones7080531
Yuksel T. Sliding Surface Designs for Visual Servo Control of Quadrotors. Drones. 2023; 7(8):531. https://doi.org/10.3390/drones7080531
Chicago/Turabian StyleYuksel, Tolga. 2023. "Sliding Surface Designs for Visual Servo Control of Quadrotors" Drones 7, no. 8: 531. https://doi.org/10.3390/drones7080531
APA StyleYuksel, T. (2023). Sliding Surface Designs for Visual Servo Control of Quadrotors. Drones, 7(8), 531. https://doi.org/10.3390/drones7080531






