OwlFusion: Depth-Only Onboard Real-Time 3D Reconstruction of Scalable Scenes for Fast-Moving MAV
Abstract
1. Introduction
2. Related Work
2.1. Real-Time RGB-D Reconstruction
2.2. Pose Estimation of Fast Camera Motion
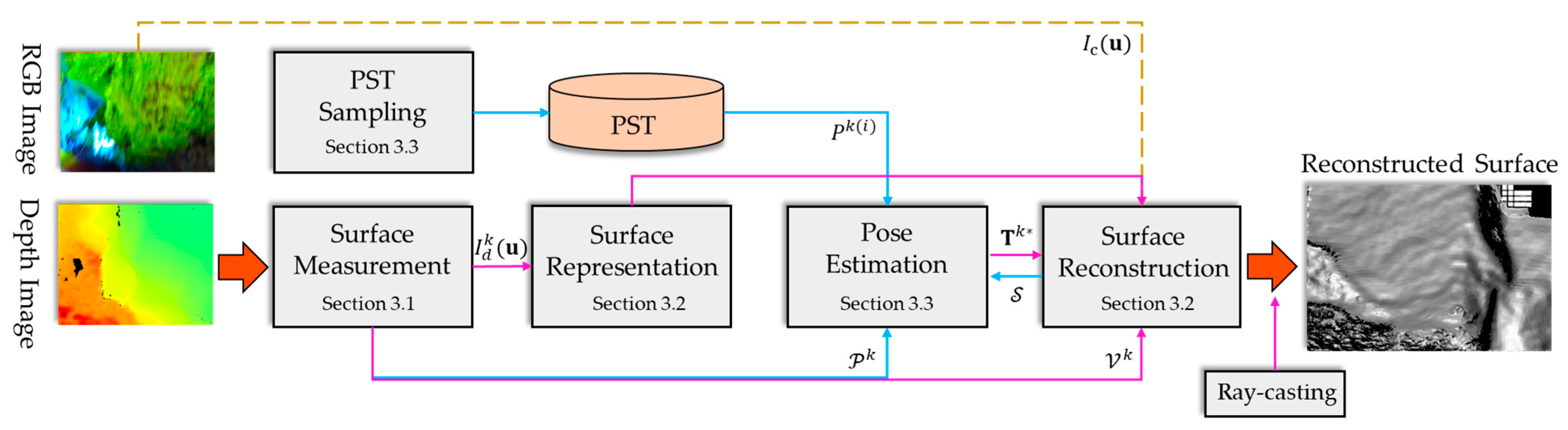
3. Methodology
3.1. Surface Measurement
3.2. Surface Reconstruction
3.3. Pose Estimation
4. Experiments
4.1. Performance and Parameters
4.2. Benchmark
4.3. Evaluation
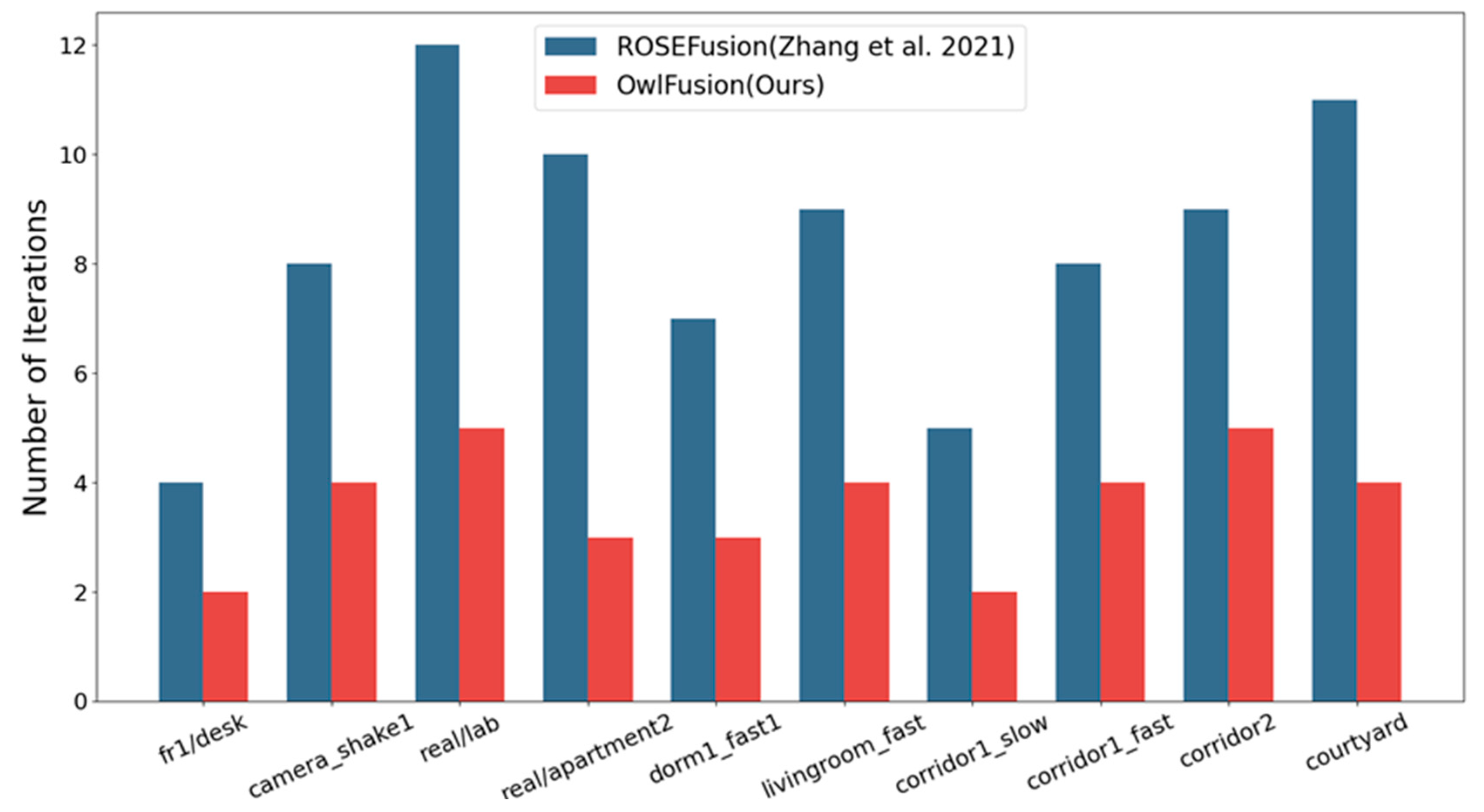
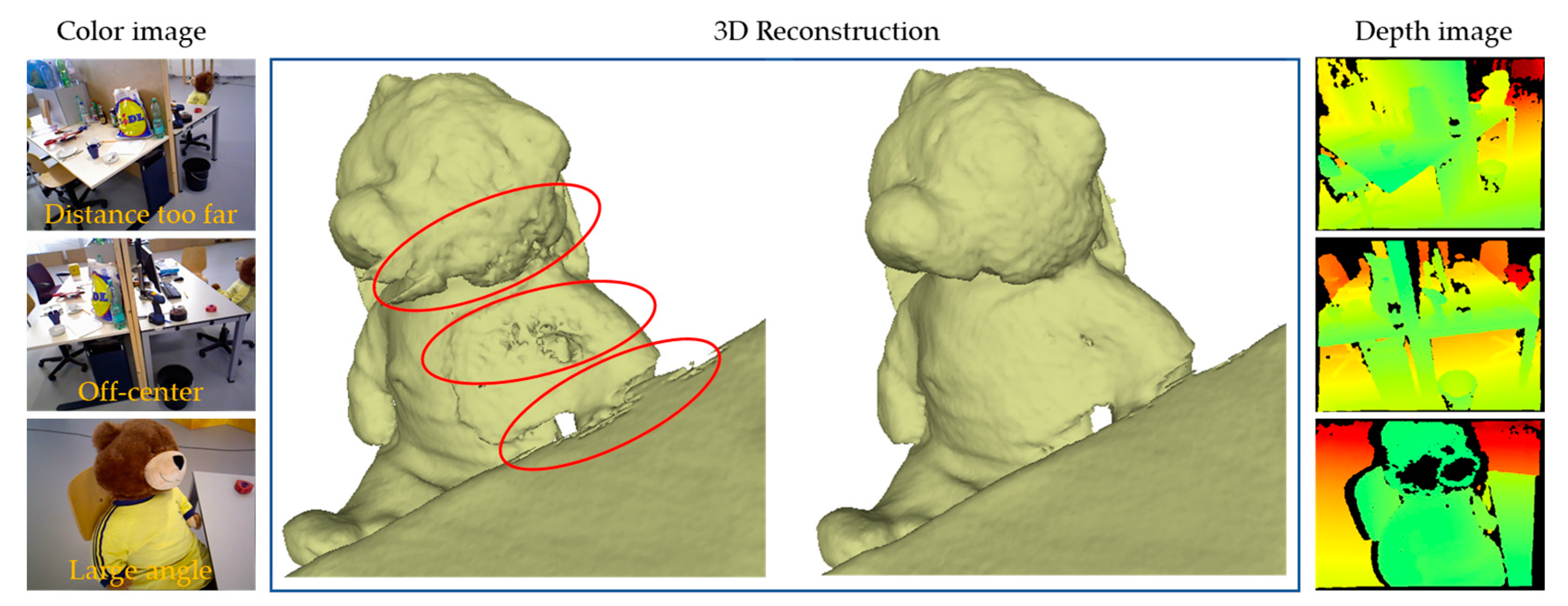
4.3.1. Random Optimization with Planar Constraint
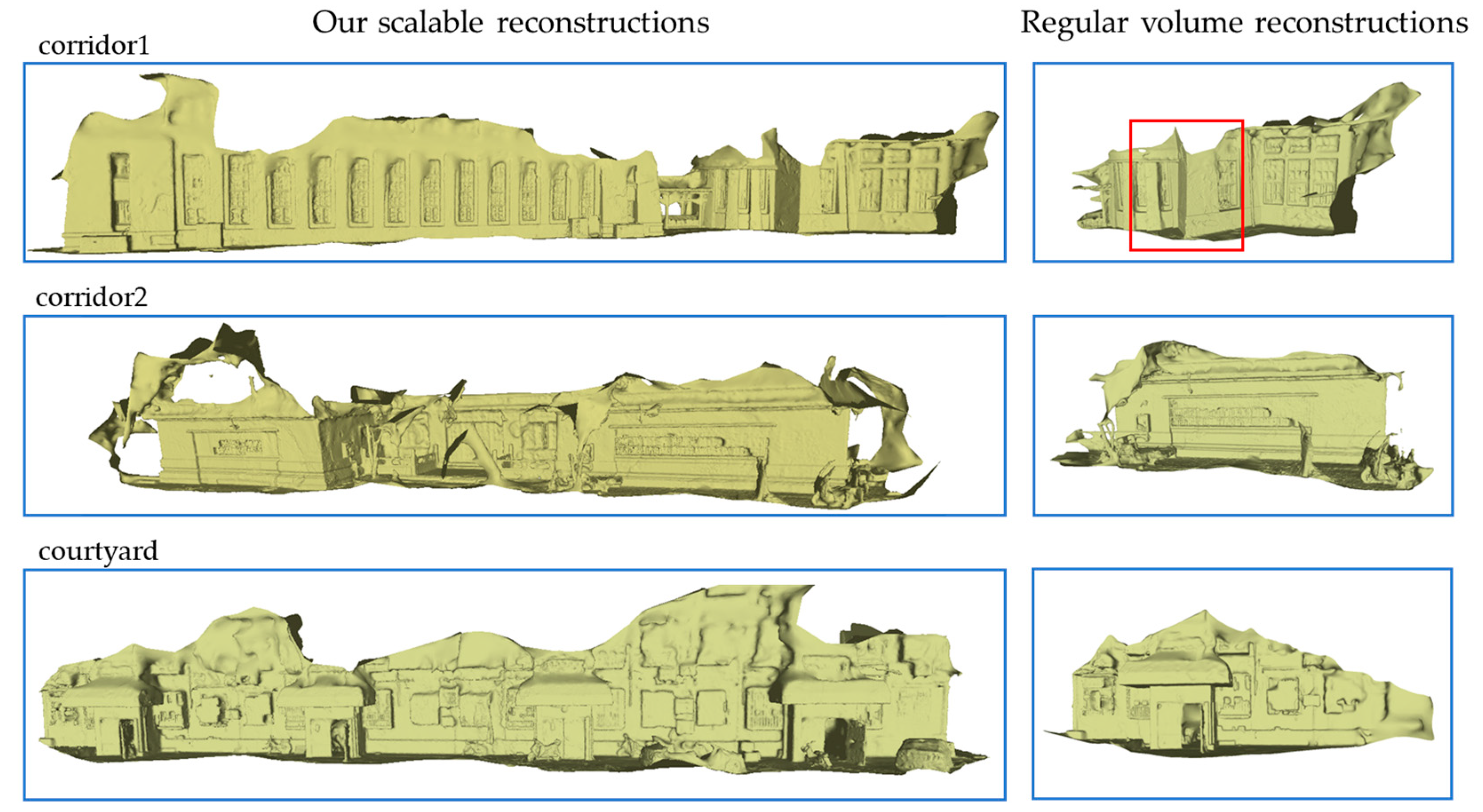
4.3.2. Scalability and Quality of Scene Reconstruction
4.3.3. System Efficiency
4.4. Comparison
4.4.1. Quantitative Comparison
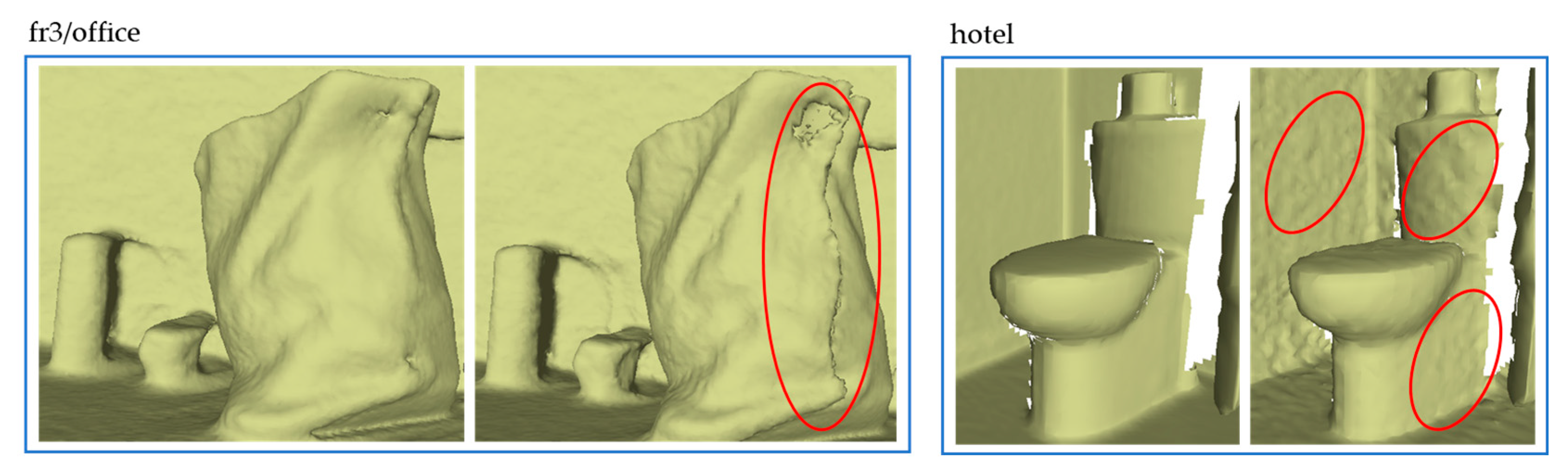
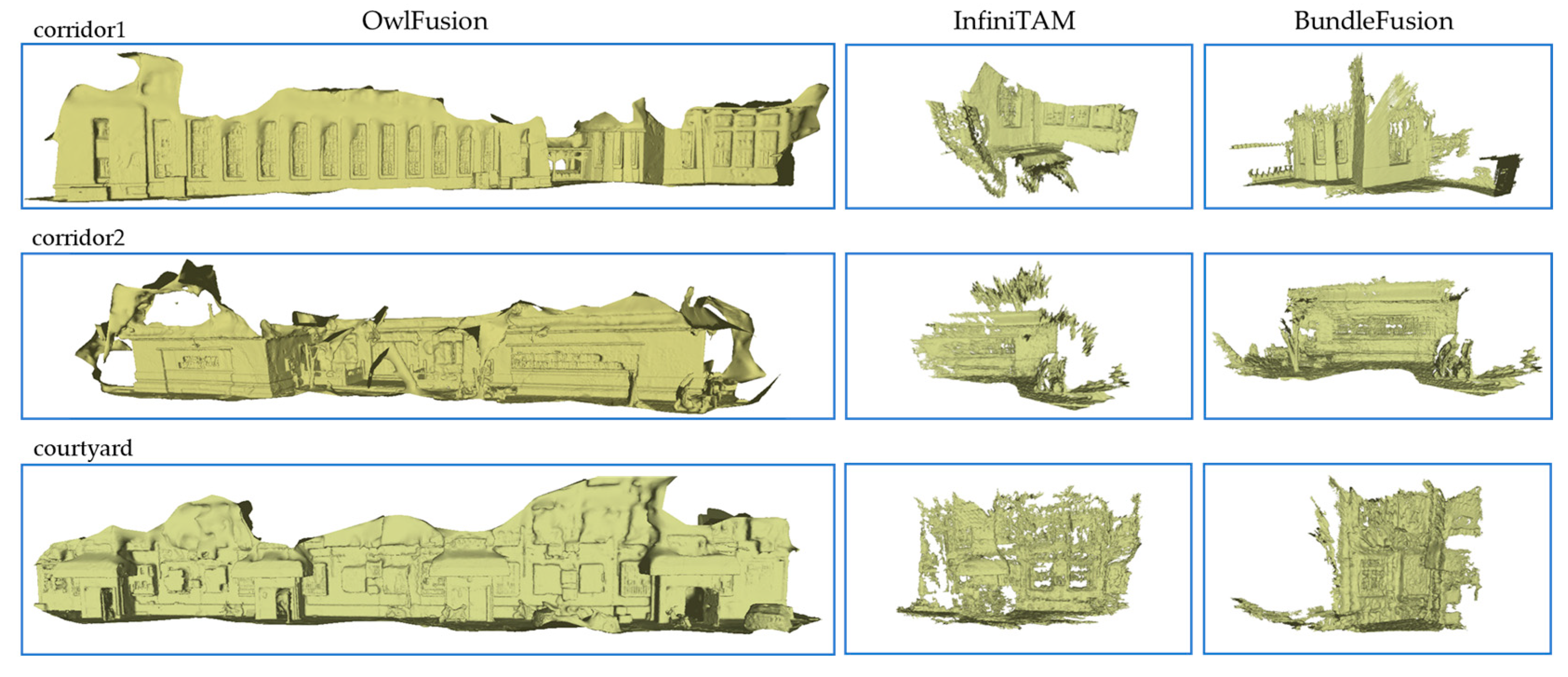
4.4.2. Qualitative Comparison
5. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohli, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A.W. KinectFusion: Real-time dense surface mapping and tracking. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, Switzerland, 26–29 October 2011; pp. 127–136. [Google Scholar]
- Whelan, T.; Kaess, M.; Fallon, M.F.; Johannsson, H.; Leonard, J.J.; McDonald, J.B. Kintinuous: Spatially Extended KinectFusion. In Proceedings of the AAAI Conference on Artificial Intelligence, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Dai, A.; Nießner, M.; Zollhöfer, M.; Izadi, S.; Theobalt, C. BundleFusion: Real-time globally consistent 3D reconstruction using on-the-fly surface re-integration. ACM Trans. Graph. 2016, 36, 1. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, C.; Zheng, L.; Xu, K. ROSEFusion: Random Optimization for Online Dense Reconstruction under Fast Camera Motion. ACM Trans. Graph. 2021, 40, 1–17. [Google Scholar]
- Newcombe, R.A.; Lovegrove, S.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the 2011 International Conference on Computer VIsion, Barcelona, Spain, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Curless, B.; Levoy, M. A volumetric method for building complex models from range images. In Proceedings of the 3rd Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 14–19 July 1996. [Google Scholar]
- Nießner, M.; Zollhöfer, M.; Izadi, S.; Stamminger, M. Real-time 3D reconstruction at scale using voxel hashing. ACM Trans. Graph. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Zeng, M.; Zhao, F.; Zheng, J.; Liu, X. Octree-based fusion for realtime 3D reconstruction. Graph. Model. 2013, 75, 126–136. [Google Scholar] [CrossRef]
- Chen, J.; Bautembach, D.; Izadi, S. Scalable real-time volumetric surface reconstruction. ACM Trans. Graph. 2013, 32, 1–16. [Google Scholar] [CrossRef]
- Steinbrücker, F.; Sturm, J.; Cremers, D. Volumetric 3D mapping in real-time on a CPU. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2021–2028. [Google Scholar]
- Dahl, V.A.; Aanæs, H.; Bærentzen, J.A. Surfel Based Geometry Reconstruction. In Proceedings of the TPCG, Sheffield, UK, 6–8 September 2010. [Google Scholar]
- Keller, M.; Lefloch, D.; Lambers, M.; Izadi, S.; Weyrich, T.; Kolb, A. Real-Time 3D Reconstruction in Dynamic Scenes Using Point-Based Fusion. In Proceedings of the 2013 International Conference on 3D Vision-3DV, Seattle, WA, USA, 29 June–1 July 2013; pp. 1–8. [Google Scholar]
- Salas-Moreno, R.F.; Glocker, B.; Kelly, P.H.J.; Davison, A.J. Dense planar SLAM. In Proceedings of the 2014 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Munich, Germany, 10–12 September 2014; pp. 157–164. [Google Scholar]
- Whelan, T.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J.; Leutenegger, S. ElasticFusion: Real-time dense SLAM and light source estimation. Int. J. Rob. Res. 2016, 35, 1697–1716. [Google Scholar] [CrossRef]
- Prisacariu, V.A.; Kähler, O.; Golodetz, S.; Sapienza, M.; Cavallari, T.; Torr, P.H.S.; Murray, D.W. InfiniTAM v3: A Framework for Large-Scale 3D Reconstruction with Loop Closure. arXiv 2017, arXiv:abs/1708.0. [Google Scholar]
- Mandikal, P.; Babu, R.V. Dense 3D Point Cloud Reconstruction Using a Deep Pyramid Network. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019; pp. 1052–1060. [Google Scholar]
- Mihajlović, M.; Weder, S.; Pollefeys, M.; Oswald, M.R. DeepSurfels: Learning Online Appearance Fusion. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2020; pp. 14519–14530. [Google Scholar]
- Kähler, O.; Prisacariu, V.A.; Ren, C.Y.; Sun, X.; Torr, P.H.S.; Murray, D.W. Very High Frame Rate Volumetric Integration of Depth Images on Mobile Devices. IEEE Trans. Vis. Comput. Graph. 2015, 21, 1241–1250. [Google Scholar] [CrossRef]
- Kähler, O.; Prisacariu, V.A.; Valentin, J.P.C.; Murray, D.W. Hierarchical Voxel Block Hashing for Efficient Integration of Depth Images. IEEE Robot. Autom. Lett. 2016, 1, 192–197. [Google Scholar] [CrossRef]
- Huang, A.S.; Bachrach, A.; Henry, P.; Krainin, M.; Maturana, D.; Fox, D.; Roy, N. Visual Odometry and Mapping for Autonomous Flight Using an RGB-D Camera. In Proceedings of the International Symposium of Robotics Research, Flagstaff, AZ, USA, 28 August–1 September 2011. [Google Scholar]
- Fraundorfer, F.; Heng, L.; Honegger, D.; Lee, G.H.; Meier, L.; Tanskanen, P.; Pollefeys, M. Vision-based autonomous mapping and exploration using a quadrotor MAV. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 4557–4564. [Google Scholar]
- Bachrach, A.; Prentice, S.; He, R.; Henry, P.; Huang, A.S.; Krainin, M.; Maturana, D.; Fox, D.; Roy, N. Estimation, planning, and mapping for autonomous flight using an RGB-D camera in GPS-denied environments. Int. J. Rob. Res. 2012, 31, 1320–1343. [Google Scholar] [CrossRef]
- Bylow, E.; Sturm, J.; Kerl, C.; Kahl, F.; Cremers, D. Real-Time Camera Tracking and 3D Reconstruction Using Signed Distance Functions. In Proceedings of the Robotics: Science and Systems, Berlin, Germany, 24–28 June 2013. [Google Scholar]
- Heng, L.; Honegger, D.; Lee, G.H.; Meier, L.; Tanskanen, P.; Fraundorfer, F.; Pollefeys, M. Autonomous Visual Mapping and Exploration With a Micro Aerial Vehicle. J. F Robot. 2014, 31, 654–675. [Google Scholar] [CrossRef]
- Burri, M.; Oleynikova, H.; Achtelik, M.; Siegwart, R.Y. Real-time visual-inertial mapping, re-localization and planning onboard MAVs in unknown environments. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1872–1878. [Google Scholar]
- Zhao, X.; Chong, J.; Qi, X.; Yang, Z. Vision Object-Oriented Augmented Sampling-Based Autonomous Navigation for Micro Aerial Vehicles. Drones 2021, 5, 107. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Z.; Gong, Z.; Cai, P.; Zhang, C.; Li, Y. Autonomous Navigation and Obstacle Avoidance for Small VTOL UAV in Unknown Environments. Symmetry 2022, 14, 2608. [Google Scholar] [CrossRef]
- Hao, C.K.; Mayer, N. Real-time SLAM using an RGB-D camera for mobile robots. In Proceedings of the 2013 CACS International Automatic Control Conference (CACS), Nantou, Taiwan, China, 2–4 December 2013; pp. 356–361. [Google Scholar]
- Nowicki, M.R.; Skrzypczyński, P. Combining photometric and depth data for lightweight and robust visual odometry. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013; pp. 125–130. [Google Scholar]
- Saeedi, S.; Nagaty, A.; Thibault, C.; Trentini, M.; Li, H. 3D Mapping and Navigation for Autonomous Quadrotor Aircraft. In Proceedings of the IEEE 29th Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016. [Google Scholar]
- Aguilar, W.G.; Rodríguez, G.A.; Álvarez, L.G.; Sandoval, S.; Quisaguano, F.J.; Limaico, A. Visual SLAM with a RGB-D Camera on a Quadrotor UAV Using on-Board Processing. In Proceedings of the International Work-Conference on Artificial and Natural Neural Networks, Cádiz, Spain, 14–16 June 2017. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2016, 33, 1255–1262. [Google Scholar] [CrossRef]
- Handa, A.; Newcombe, R.A.; Angeli, A.; Davison, A.J. Real-Time Camera Tracking: When is High Frame-Rate Best? In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012.
- Zhang, Q.; Huang, N.; Yao, L.; Zhang, D.; Shan, C.; Han, J. RGB-T Salient Object Detection via Fusing Multi-Level CNN Features. IEEE Trans. Image Process. 2019, 29, 3321–3335. [Google Scholar] [CrossRef] [PubMed]
- Saurer, O.; Pollefeys, M.; Lee, G.H. Sparse to Dense 3D Reconstruction from Rolling Shutter Images. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3337–3345. [Google Scholar]
- Gallego, G.; Delbrück, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.J.; Conradt, J.; Daniilidis, K.; et al. Event-Based Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 44, 154–180. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.S.; Kwon, J.; Lee, K.M. Simultaneous localization, mapping and deblurring. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1203–1210. [Google Scholar]
- Zhang, H.; Yang, J. Intra-frame deblurring by leveraging inter-frame camera motion. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–15 June 2015; pp. 4036–4044. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual--Inertial Odometry. IEEE Trans. Robot. 2015, 33, 1–21. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Li, Z. Robust Visual-Inertial Navigation System for Low Precision Sensors under Indoor and Outdoor Environments. Remote Sens. 2021, 13, 772. [Google Scholar] [CrossRef]
- Nießner, M.; Dai, A.; Fisher, M. Combining Inertial Navigation and ICP for Real-time 3D Surface Reconstruction. In Proceedings of the Eurographics, Strasbourg, French, 7–11 April 2014. [Google Scholar]
- Prisacariu, V.A.; Kähler, O.; Murray, D.W.; Reid, I.D. Real-Time 3D Tracking and Reconstruction on Mobile Phones. IEEE Trans. Vis. Comput. Graph. 2015, 21, 557–570. [Google Scholar] [CrossRef] [PubMed]
- Laidlow, T.; Bloesch, M.; Li, W.; Leutenegger, S. Dense RGB-D-inertial SLAM with map deformations. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6741–6748. [Google Scholar]
- Hansard, M.; Lee, S.; Choi, O.; Horaud, R. Time of Flight Cameras: Principles, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ji, C.; Zhang, Y.; Tong, M.; Yang, S. Particle Filter with Swarm Move for Optimization. In Proceedings of the Parallel Problem Solving from Nature, Dortmund, Germany, 13–17 September 2008. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Other Conferences, Boston, MA, USA, 30 April 1992. [Google Scholar]
- Kerl, C.; Sturm, J.; Cremers, D. Robust odometry estimation for RGB-D cameras. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3748–3754. [Google Scholar]
- Ginzburg, D.; Raviv, D. Deep Weighted Consensus: Dense correspondence confidence maps for 3D shape registration. arXiv 2021, arXiv:abs/2105.0. [Google Scholar]
- Lu, Y.; Song, D. Robust RGB-D Odometry Using Point and Line Features. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 1–13 December 2015; pp. 3934–3942. [Google Scholar]
- Yunus, R.; Li, Y.; Tombari, F. ManhattanSLAM: Robust Planar Tracking and Mapping Leveraging Mixture of Manhattan Frames. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 6687–6693. [Google Scholar]
- Zhu, Z.; Xu, Z.; Chen, R.; Wang, T.; Wang, C.; Yan, C.C.; Xu, F. FastFusion: Real-Time Indoor Scene Reconstruction with Fast Sensor Motion. Remote Sens. 2022, 14, 3551. [Google Scholar] [CrossRef]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Handa, A.; Whelan, T.; McDonald, J.B.; Davison, A.J. A benchmark for RGB-D visual odometry, 3D reconstruction and SLAM. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1524–1531. [Google Scholar]
- Schöps, T.; Sattler, T.; Pollefeys, M. BAD SLAM: Bundle Adjusted Direct RGB-D SLAM. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 134–144. [Google Scholar]
- Whelan, T.; Leutenegger, S.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J. ElasticFusion: Dense SLAM Without A Pose Graph. In Proceedings of the Robotics: Science and Systems, Rome, Italy, 17 July 2015. [Google Scholar]


 denotes the presence of the specific capability, while
denotes the presence of the specific capability, while  denotes the absence of the specific capability.
denotes the absence of the specific capability.
 denotes the presence of the specific capability, while
denotes the presence of the specific capability, while  denotes the absence of the specific capability.
denotes the absence of the specific capability.| Systems | Fast-Moving Tracking | Sparse Representation | Scalable Reconstruction | Onboard Performing |
|---|---|---|---|---|
| KinectFusion [1] | 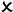 | 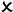 | 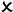 | 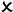 |
| Kintinuous [2] | 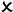 | 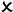 |  | 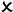 |
| Voxel Hashing [7] | 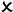 |  |  | 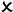 |
| InfiniTAM [15] | 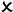 |  |  |  |
| Hierarchical voxels [19] | 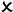 |  |  | 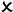 |
| BundleFusion [3] | 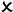 | 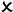 |  | 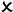 |
| RoseFusion [4] |  | 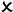 | 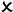 | 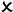 |
| Sequence | ||||
|---|---|---|---|---|
| TUM_fr1/desk | 0.41 | 0.66 | 0.41 | 0.94 |
| TUM_fr1/room | 0.33 | 0.76 | 0.52 | 0.85 |
| TUM_fr3/office | 0.25 | 0.36 | 0.18 | 0.35 |
| ICL_lr_kt0 | 0.13 | 0.27 | 0.16 | 0.33 |
| ICL_lr_kt1 | 0.05 | 0.09 | 0.10 | 0.40 |
| ICL_lr_kt2 | 0.28 | 0.40 | 0.23 | 0.46 |
| ICL_lr_kt3 | 0.27 | 0.38 | 0.12 | 0.41 |
| ETH3D_camera_shake1 | 0.46 | 0.64 | 1.88 | 2.65 |
| ETH3D_camera_shake2 | 0.33 | 0.48 | 1.90 | 3.27 |
| ETH3D_camera_shake3 | 0.37 | 0.51 | 2.16 | 3.43 |
| FastCaMo_real/lab | 0.98 | 3.62 | 0.91 | 5.20 |
| FastCaMo_real/apartment1 | 1.05 | 4.22 | 1.08 | 5.73 |
| FastCaMo_real/apartment2 | 1.71 | 3.73 | 1.38 | 4.21 |
| FastCaMo_synth/apartment1 | 1.53 | 3.88 | 0.92 | 2.08 |
| FastCaMo_synth/hotel | 1.66 | 3.94 | 1.13 | 2.23 |
| FMDataset_dorm1_fast1 | 0.52 | 0.92 | 1.24 | 2.59 |
| FMDataset_dorm2_fast | 0.75 | 1.60 | 1.23 | 2.16 |
| FMDataset_hotel_fast1 | 0.75 | 1.26 | 1.29 | 2.34 |
| FMDataset_livingroom_fast | 0.53 | 1.77 | 0.85 | 2.41 |
| FMDataset_rent2_fast | 0.83 | 1.54 | 1.31 | 2.27 |
| Ours_corridor1_slow | 0.40 | 0.73 | 0.55 | 0.89 |
| Ours_corridor1_fast | 0.92 | 1.44 | 1.31 | 3.03 |
| Ours_corridor2 | 0.87 | 1.95 | 1.42 | 2.89 |
| Ours_courtyard | 1.01 | 2.30 | 1.09 | 3.37 |
| Sequence | (ms) | ATE (cm) | MD (cm) | |||
|---|---|---|---|---|---|---|
| RoseFusion | OwlFusion | RoseFusion | OwlFusion | RoseFusion | OwlFusion | |
| fr1/desk | 218.38 | 23.35 | 2.48 | 1.93 | — | — |
| fr1/room | 219.04 | 24.20 | 4.86 | 4.32 | — | — |
| fr3/ office | 209.98 | 23.81 | 2.51 | 2.63 | — | — |
| lr_kt0 | 214.63 | 24.73 | 0.83 | 0.77 | — | — |
| lr_kt1 | 212.69 | 24.55 | 0.71 | 0.80 | — | — |
| camera_shake1 | 224.24 | 27.09 | 0.62 | 0.93 | — | — |
| camera_shake2 | 227.84 | 26.64 | 1.35 | 1.07 | — | — |
| camera_shake3 | 232.18 | 29.39 | 4.67 | 4.54 | — | — |
| synth/apartment1 | 228.93 | 29.60 | 1.10 | 1.32 | 4.52 | 4.37 |
| synth/hotel | 230.62 | 30.08 | 1.52 | 1.33 | 5.25 | 5.54 |
| real/lab | 230.24 | 30.27 | — | — | 4.86 | 4.50 |
| real/apartment1 | 230.75 | 30.51 | — | — | 4.88 | 5.45 |
| real/apartment2 | 228.69 | 24.20 | — | — | 4.23 | 5.01 |
| Sequence | FPS (Hz) | ||
|---|---|---|---|
| Comparison | Ours w/ Vis. | Ours w/o Vis. | |
| fr1/desk | 3.50 | 30.19 | 37.18 |
| fr1/room | 3.49 | 29.14 | 35.88 |
| fr3/ office | 3.64 | 29.60 | 36.46 |
| lr_kt0 | 3.56 | 28.51 | 35.11 |
| lr_kt1 | 3.60 | 28.72 | 35.37 |
| camera_shake1 | 3.41 | 26.02 | 32.05 |
| camera_shake2 | 3.36 | 26.46 | 32.59 |
| camera_shake3 | 3.29 | 23.99 | 29.54 |
| synth/apartment1 | 3.34 | 23.82 | 29.34 |
| synth/hotel | 3.32 | 23.44 | 28.87 |
| real/lab | 3.32 | 23.29 | 28.68 |
| real/apartment1 | 3.32 | 23.11 | 28.46 |
| real/apartment2 | 3.35 | 30.19 | 37.18 |
| Method | lr_kt0 | lr_kt1 | syn./apartment1 | syn./hotel |
|---|---|---|---|---|
| ORB-SLAM2 | 1.11 | 0.46 | — | — |
| ElasticFusion | 1.06 | 0.82 | 41.09 | 43.64 |
| InfiniTAM | 0.89 | 0.67 | 10.38 | — |
| BundleFusion | 0.61 | 0.53 | 4.70 | 65.33 |
| BAD-SLAM | 1.73 | 1.09 | — | — |
| OwlFusion | 0.83 | 0.72 | 1.08 | 1.47 |
| Sequence | InfiniTAM | BundleFusion | OwlFusion | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Compl. | Acc. | FPS | Compl. | Acc. | FPS | Compl. | Acc. | FPS | |
| syn./apartment1 | 21.74 | 7.32 | 31.87 | 39.82 | 5.48 | 0.67 | 93.65 | 4.37 | 29.34 |
| syn./hotel | 33.13 | 6.98 | 28.33 | 47.64 | 4.90 | 0.42 | 94.57 | 5.54 | 28.87 |
| real/lab | 11.21 | 9.24 | 30.75 | 16.88 | 5.42 | — | 92.81 | 4.50 | 28.68 |
| real/apartment1 | 9.83 | 8.73 | 29.37 | 34.23 | 6.39 | — | 87.23 | 5.45 | 28.46 |
| real/apartment2 | 15.07 | 8.68 | 32.92 | 25.17 | 5.23 | — | 89.65 | 5.01 | 37.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gou, G.; Wang, X.; Sui, H.; Wang, S.; Zhang, H.; Li, J. OwlFusion: Depth-Only Onboard Real-Time 3D Reconstruction of Scalable Scenes for Fast-Moving MAV. Drones 2023, 7, 358. https://doi.org/10.3390/drones7060358
Gou G, Wang X, Sui H, Wang S, Zhang H, Li J. OwlFusion: Depth-Only Onboard Real-Time 3D Reconstruction of Scalable Scenes for Fast-Moving MAV. Drones. 2023; 7(6):358. https://doi.org/10.3390/drones7060358
Chicago/Turabian StyleGou, Guohua, Xuanhao Wang, Haigang Sui, Sheng Wang, Hao Zhang, and Jiajie Li. 2023. "OwlFusion: Depth-Only Onboard Real-Time 3D Reconstruction of Scalable Scenes for Fast-Moving MAV" Drones 7, no. 6: 358. https://doi.org/10.3390/drones7060358
APA StyleGou, G., Wang, X., Sui, H., Wang, S., Zhang, H., & Li, J. (2023). OwlFusion: Depth-Only Onboard Real-Time 3D Reconstruction of Scalable Scenes for Fast-Moving MAV. Drones, 7(6), 358. https://doi.org/10.3390/drones7060358






