A Nonlinear Adaptive Autopilot for Unmanned Aerial Vehicles Based on the Extension of Regression Matrix
Abstract
1. Introduction
2. Problem Formulation
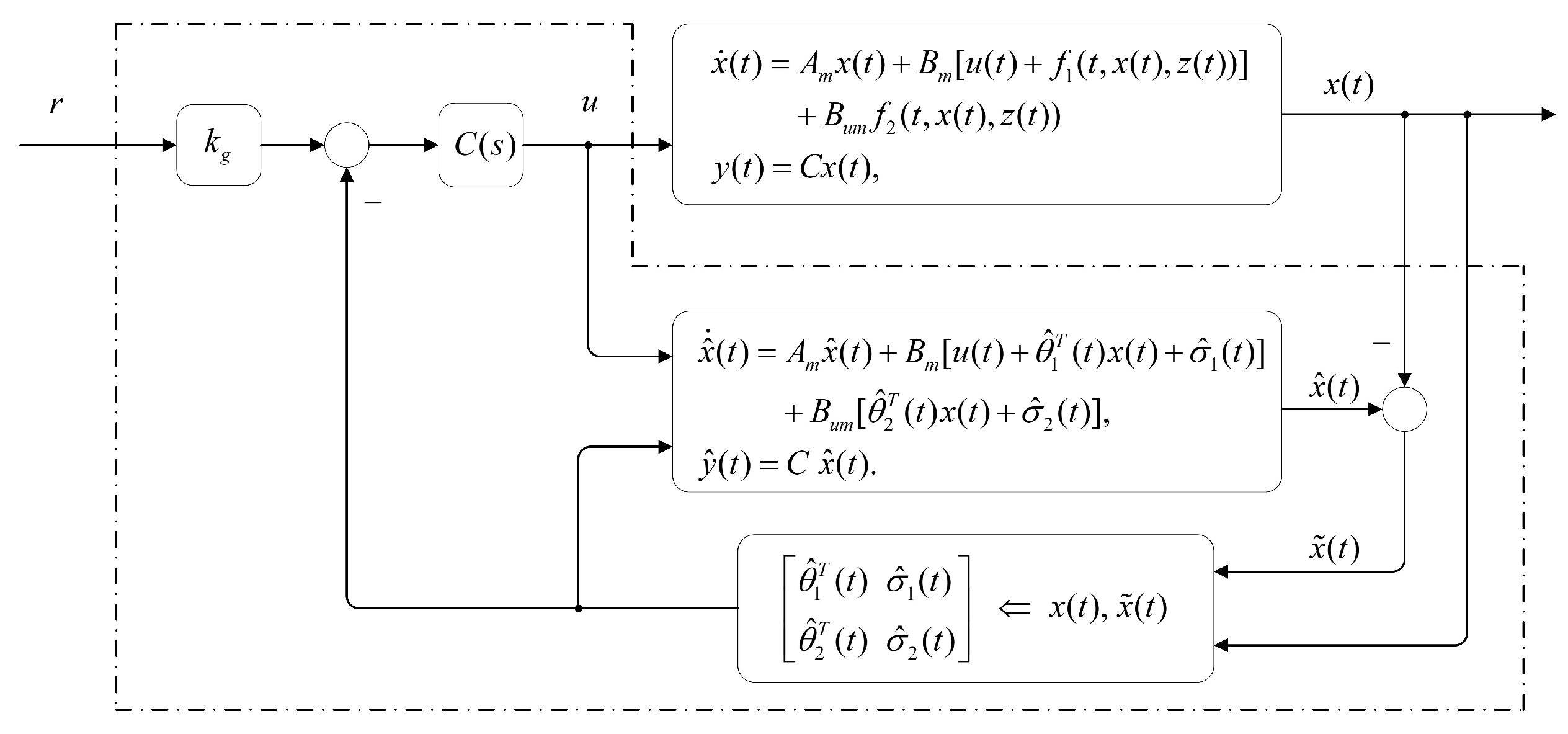
3. -PcEx Architecture
- State Predictor
- Adaptation laws
- Control Law
4. Analysis of the -PcEx
4.1. Assumptions and Definitions
4.2. Closed-Loop Reference System
4.3. Transient and Steady-State Performance
5. Simulation
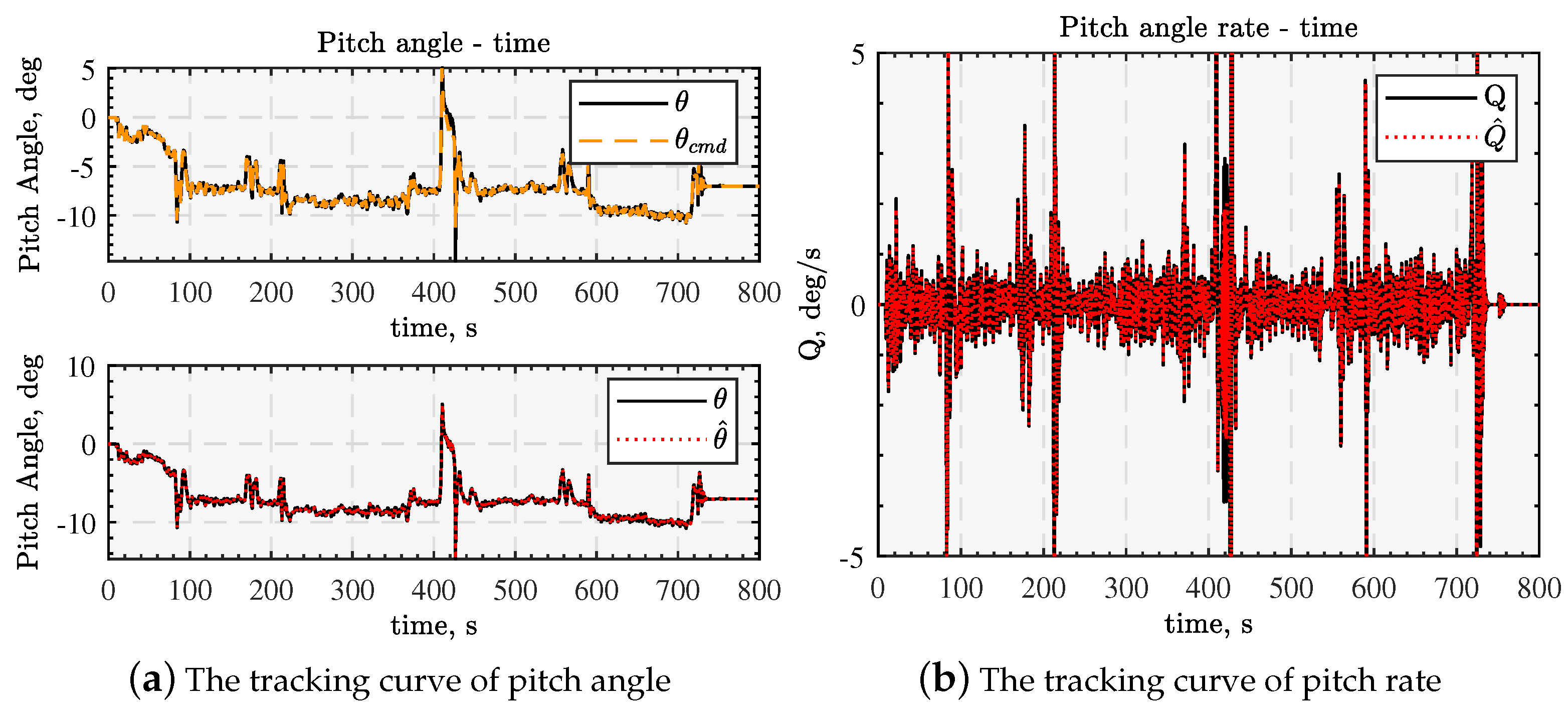
5.1. Flight Feasibility Simulation
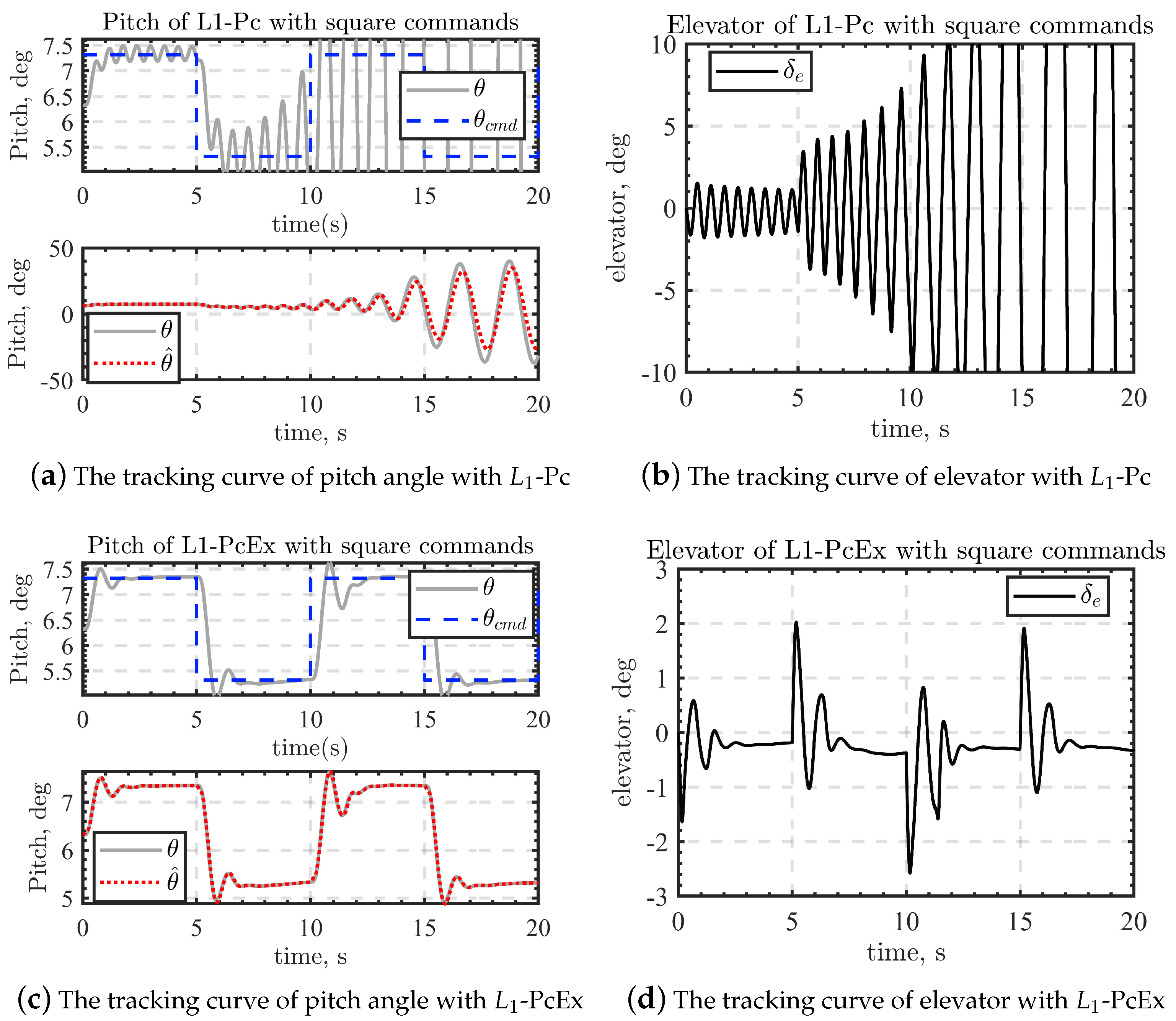
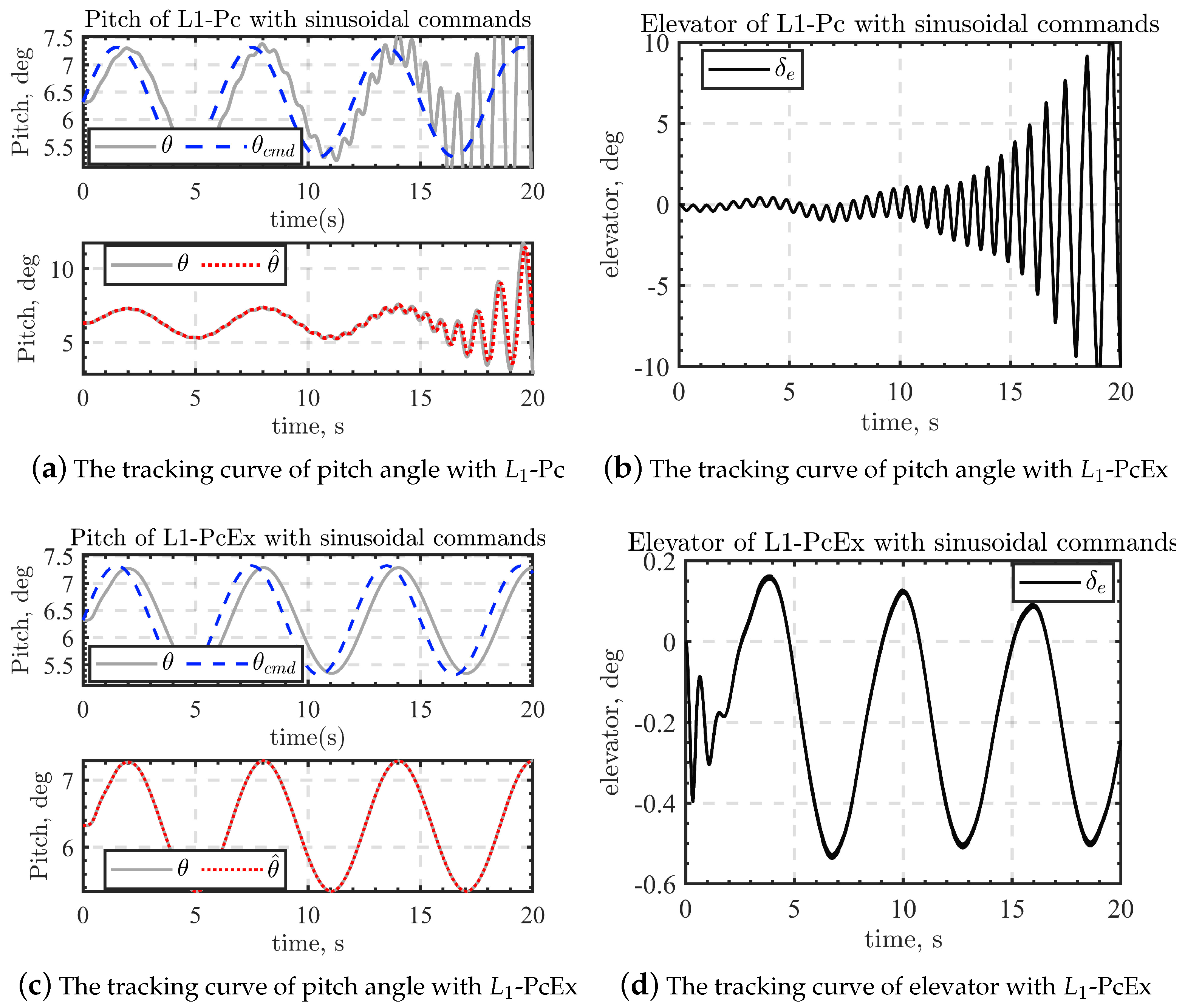
5.2. Comparison in the Presence of Uncertainties
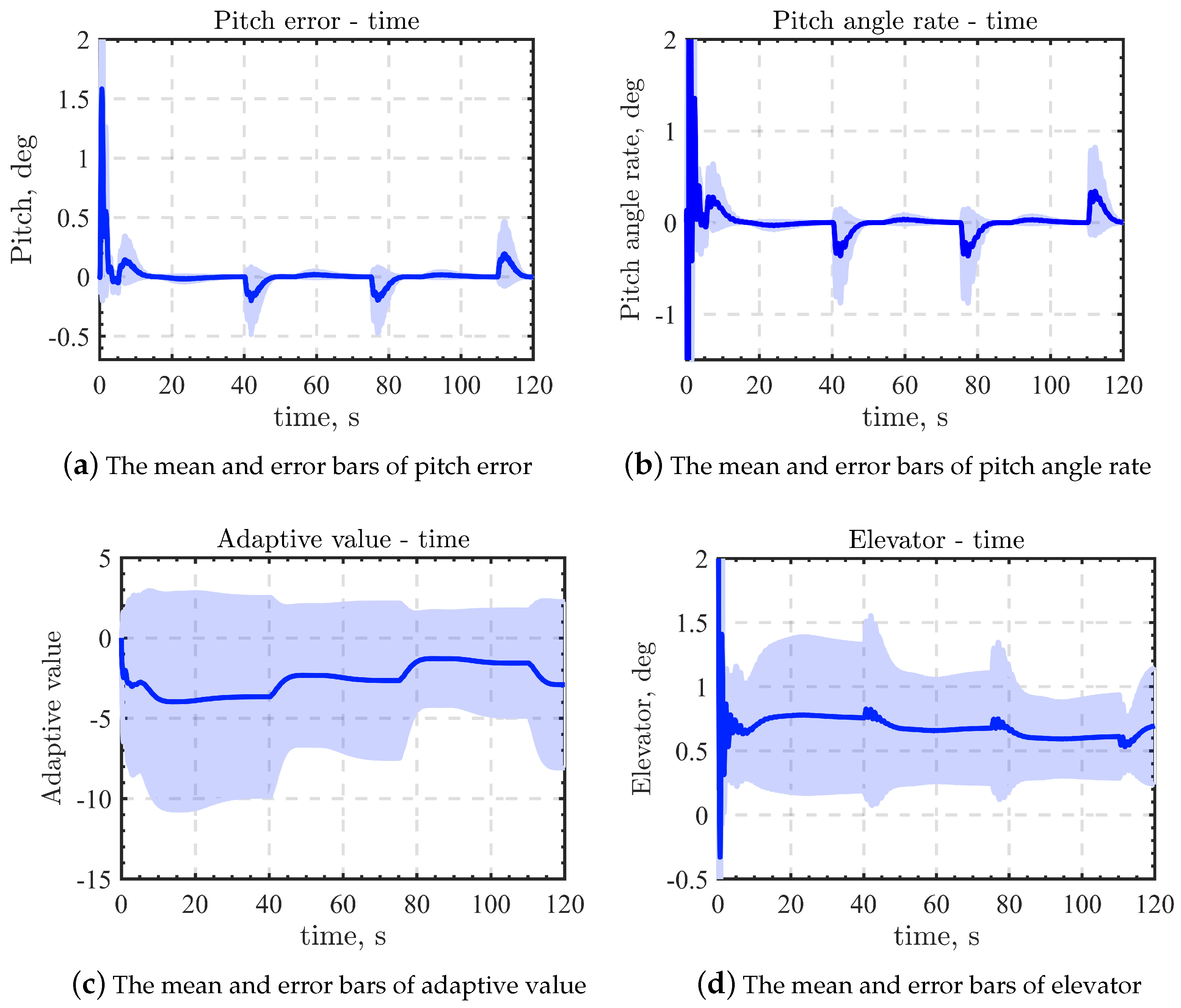
5.3. Monte Carlo Synthesis Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baldi, S.; Roy, S.; Yang, K.; Liu, D. An Underactuated Control System Design for Adaptive Autopilot of Fixed-Wing Drones. IEEE/ASME Trans. Mechatronics 2022, 27, 4045–4056. [Google Scholar] [CrossRef]
- Ale Isaac, M.S.; Luna, M.A.; Ragab, A.R.; Ale Eshagh Khoeini, M.M.; Kalra, R.; Campoy, P.; Flores Peña, P.; Molina, M. Medium-Scale UAVs: A Practical Control System Considering Aerodynamics Analysis. Drones 2022, 6, 244. [Google Scholar] [CrossRef]
- Ahmadi, K.; Asadi, D.; Nabavi-Chashmi, S.Y.; Tutsoy, O. Modified adaptive discrete-time incremental nonlinear dynamic inversion control for quad-rotors in the presence of motor faults. Mech. Syst. Signal Process. 2023, 188, 109989. [Google Scholar] [CrossRef]
- Blas, L.A.; Dávila, J.; Salazar, S.; Bonilla, M. Robust Trajectory Tracking for an Uncertain UAV Based on Active Disturbance Rejection. IEEE Control Syst. Lett. 2022, 6, 1466–1471. [Google Scholar] [CrossRef]
- Montoya-Morales, J.; Guerrero-Sánchez, M.; Valencia-Palomo, G.; Hernández-González, O.; López-Estrada, F.; Hoyo-Montaño, J. Real-time robust tracking control for a quadrotor using monocular vision. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 2023, 09544100231158265. [Google Scholar] [CrossRef]
- Gao, W.; Zhou, X.; Pan, M.; Zhou, W.; Lu, F.; Huang, J. Acceleration control strategy for aero-engines based on model-free deep reinforcement learning method. Aerosp. Sci. Technol. 2022, 120, 107248. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernández-González, O.; Valencia-Palomo, G.; López-Estrada, F.R.; Rodríguez-Mata, A.E.; Garrido, J. Filtered Observer-Based IDA-PBC Control for Trajectory Tracking of a Quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, M.E.; Hernández-González, O.; Valencia-Palomo, G.; Mercado-Ravell, D.; López-Estrada, F.R.; Hoyo-Montaño, J.A. Robust IDA-PBC for under-actuated systems with inertia matrix dependent of the unactuated coordinates: Application to a UAV carrying a load. Nonlinear Dyn. 2021, 105, 3225–3238. [Google Scholar] [CrossRef]
- Osburn, P.V.; Whitaker, H.P.; Kezer, A. New Developments in the Design of Model Reference Adaptive Control Systems; Institute of Aeronautical Sciences: New York, NY, USA, 1961; Volume 61. [Google Scholar]
- Butler, H. Model Reference Adaptive Control: From Theory to Practice; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Nguyen, N.T. Model-Reference Adaptive Control; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Zhi, Y.; Liu, L.; Guan, B.; Wang, B.; Cheng, Z.; Fan, H. Distributed robust adaptive formation control of fixed-wing UAVs with unknown uncertainties and disturbances. Aerosp. Sci. Technol. 2022, 126, 107600. [Google Scholar] [CrossRef]
- Anderson, R.B.; Marshall, J.A.; L’Afflitto, A. Constrained Robust Model Reference Adaptive Control of a Tilt-Rotor Quadcopter Pulling an Unmodeled Cart. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 39–54. [Google Scholar] [CrossRef]
- Van Heusden, K.; Talebian, K.; Dumont, G.A. Analysis of L1 adaptive state feedback control. Why does it approximate an implementable LTI controller? Eur. J. Control 2015, 23, 1–7. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Y.; Sun, Z.; Xi, B.; Wu, L. Robust modification of nonlinear L1 adaptive flight control system via noise attenuation. Aerosp. Sci. Technol. 2021, 117, 106938. [Google Scholar] [CrossRef]
- Adaptive control for linear parameter-varying systems with application to a VTOL aircraft. Aerosp. Sci. Technol. 2021, 112, 106621. [CrossRef]
- Ma, C.; Sun, D.; Hovakimyan, N. Modeling and Adaptive Control Law Design for a Bi-Tiltrotor Unmanned Aerial Vehicle. J. Aerosp. Eng. 2021, 34, 04021090. [Google Scholar] [CrossRef]
- Souanef, T. L1 Adaptive Path-Following of Small Fixed-wing Unmanned Aerial Vehicles in Wind. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3708–3716. [Google Scholar] [CrossRef]
- Ahmadian, H.; Lotfi, M.; Menhaj, M.B.; Talebi, H.A.; Sharifi, I. A novel L1 adaptive-hybrid control with guaranteed stability for a class of uncertain nonlinear systems: A case study on SA330 Puma. J. Frankl. Inst. 2022, 359, 9860–9885. [Google Scholar] [CrossRef]
- Souanef, T. L1 Adaptive Output Feedback Control of Small Unmanned Aerial Vehicles. Unmanned Syst. 2023, 11, 249–260. [Google Scholar] [CrossRef]
- Hovakimyan, N.; Cao, C. L1 Adaptive Control Theory: Guaranteed Robustness with Fast Adaptation; SIAM: Urbana, IL, USA, 2010. [Google Scholar]
- Li, Z.; Hovakimyan, N. L 1 adaptive controller for mimo systems with unmatched uncertainties using modified piecewise constant adaptation law. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 7303–7308. [Google Scholar] [CrossRef]
- Zhu, R.; Zhang, S.; Kang, J.; Guo, Z.; Tang, G. A Modified L1 Adaptive Output Feedback Control and its Application in Control of Wind Tunnel. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 5047–5054. [Google Scholar] [CrossRef]
- Wu, Z.; Cheng, S.; Ackerman, K.A.; Gahlawat, A.; Lakshmanan, A.; Zhao, P.; Hovakimyan, N. L1Adaptive Augmentation for Geometric Tracking Control of Quadrotors. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 1329–1336. [Google Scholar] [CrossRef]
- Leman, T.; Xargay, E.; Dullerud, G.; Hovakimyan, N.; Wendel, T. L1 adaptive control augmentation system for the X-48B aircraft. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 5619. [Google Scholar] [CrossRef]
- Gregory, I.; Xargay, E.; Cao, C.; Hovakimyan, N. Flight test of an L1 adaptive controller on the NASA AirSTAR flight test vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 8015. [Google Scholar] [CrossRef]
- Singh, L.; Miotto, P.; Breger, L.S. L1 Adaptive Control Design for Improved Handling of the F/A-18 class of Aircraft. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 5236. [Google Scholar] [CrossRef]
- Bhardwaj, P.; Akkinapalli, V.S.; Zhang, J.; Saboo, S.; Holzapfel, F. Adaptive augmentation of incremental nonlinear dynamic inversion controller for an extended f-16 model. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1923. [Google Scholar] [CrossRef]
- Pravitra, J.; Ackerman, K.A.; Cao, C.; Hovakimyan, N.; Theodorou, E.A. L1-Adaptive MPPI Architecture for Robust and Agile Control of Multirotors. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 7661–7666. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhao, P.; Wang, F.; Block, D.J.; Hovakimyan, N. Improving the Robustness of Reinforcement Learning Policies With L1Adaptive Control. IEEE Robot. Autom. Lett. 2022, 7, 6574–6581. [Google Scholar] [CrossRef]
- Hanover, D.; Foehn, P.; Sun, S.; Kaufmann, E.; Scaramuzza, D. Performance, Precision, and Payloads: Adaptive Nonlinear MPC for Quadrotors. IEEE Robot. Autom. Lett. 2022, 7, 690–697. [Google Scholar] [CrossRef]
- Zhao, P.; Guo, Z.; Hovakimyan, N. Robust Nonlinear Tracking Control with Exponential Convergence Using Contraction Metrics and Disturbance Estimation. Sensors 2022, 22, 4743. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Etkin, B.; Reid, L.D. Dynamics of Flight; Wiley: New York, NY, USA, 1959; Volume 2. [Google Scholar]
- Fang, Z. Dynamics of Airplane; Beihang University Press: Bejing, China, 2005. [Google Scholar]
- Schmidt, D.K. Modern Flight Dynamics; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Faleiro, L.; Lambregts, A. Analysis and tuning of a ‘Total Energy Control System’control law using eigenstructure assignment. Aerosp. Sci. Technol. 1999, 3, 127–140. [Google Scholar] [CrossRef]
- Jimenez, P.; Lichota, P.; Agudelo, D.; Rogowski, K. Experimental validation of total energy control system for UAVs. Energies 2019, 13, 14. [Google Scholar] [CrossRef]
- Dai, X.; Ke, C.; Quan, Q.; Cai, K.Y. RFlySim: Automatic test platform for UAV autopilot systems with FPGA-based hardware-in-the-loop simulations. Aerosp. Sci. Technol. 2021, 114, 106727. [Google Scholar] [CrossRef]

| Parameter | Scope |
|---|---|
| Lift coefficient | |
| Drag coefficient | |
| Pitching moment coefficient | |
| Pitching moment coefficient | |
| Pitching moment coefficient | |
| Center of gravity (m) | |
| Windx (m/s) | −10∼5 |
| Setting angle () | −1∼1 |
| Thrust line (m) | |
| Inertia | |
| Mass (kg) | |
| Steerage | |
| Uncertainties coefficient | |
| Uncertainties coefficient |
| Parameter | Pitch Angle Error | |
|---|---|---|
| Mean Value | Sample Variance | |
| Before sliding | ||
| Sliding for 0.5 s | ||
| Sliding for 5 s | ||
| Sliding for 10 s | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Feng, Y.; Wu, L.; Xi, B. A Nonlinear Adaptive Autopilot for Unmanned Aerial Vehicles Based on the Extension of Regression Matrix. Drones 2023, 7, 275. https://doi.org/10.3390/drones7040275
Hu Q, Feng Y, Wu L, Xi B. A Nonlinear Adaptive Autopilot for Unmanned Aerial Vehicles Based on the Extension of Regression Matrix. Drones. 2023; 7(4):275. https://doi.org/10.3390/drones7040275
Chicago/Turabian StyleHu, Quanwen, Yue Feng, Liaoni Wu, and Bin Xi. 2023. "A Nonlinear Adaptive Autopilot for Unmanned Aerial Vehicles Based on the Extension of Regression Matrix" Drones 7, no. 4: 275. https://doi.org/10.3390/drones7040275
APA StyleHu, Q., Feng, Y., Wu, L., & Xi, B. (2023). A Nonlinear Adaptive Autopilot for Unmanned Aerial Vehicles Based on the Extension of Regression Matrix. Drones, 7(4), 275. https://doi.org/10.3390/drones7040275






