Neural Network and Dynamic Inversion Based Adaptive Control for a HALE-UAV against Icing Effects
Abstract
1. Introduction
- We established a comprehensive fixed-wing icing model of HALE-UAV considering wind disturbance and sensor noise.
- We proposed an ice-tolerant control structure by combining multilayer perceptrons with the nonlinear dynamic inverse method (MLP-NDI controller) to provide robust compensation for the nonlinear and time-varying icing effects.
- We conducted extensive comparisons between the MLP-NDI controller and three typical controllers, demonstrating its superior performance in terms of stability, accuracy, and robustness.
- We explored the robustness and verified the effectiveness of an MLP-NDI controller under various icing scenarios.
2. Flight Dynamic Model
2.1. Icing Effects on Flight Dynamic
2.2. Nonlinear Dynamics
2.3. Disturbances and Measurement Noise
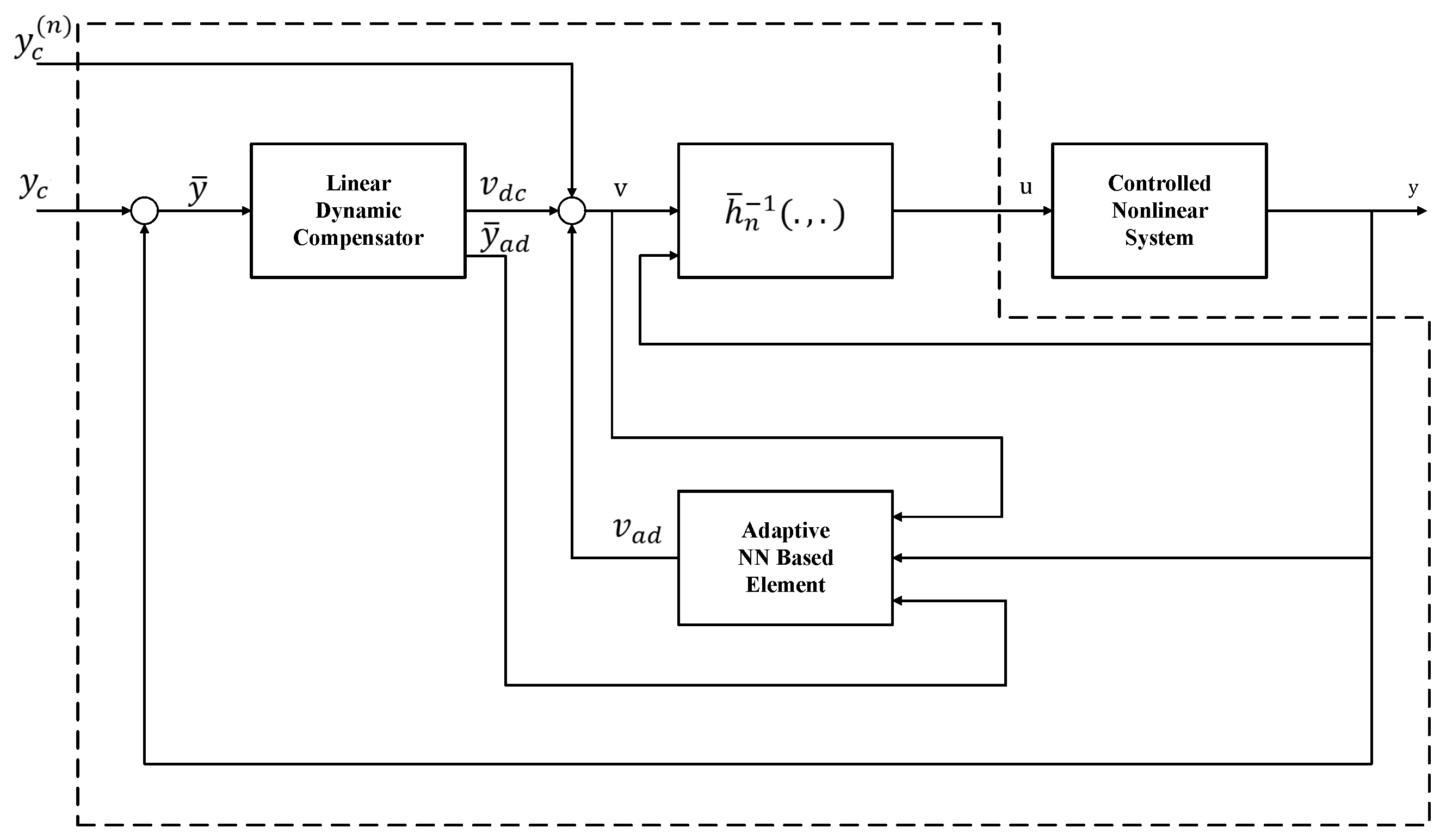
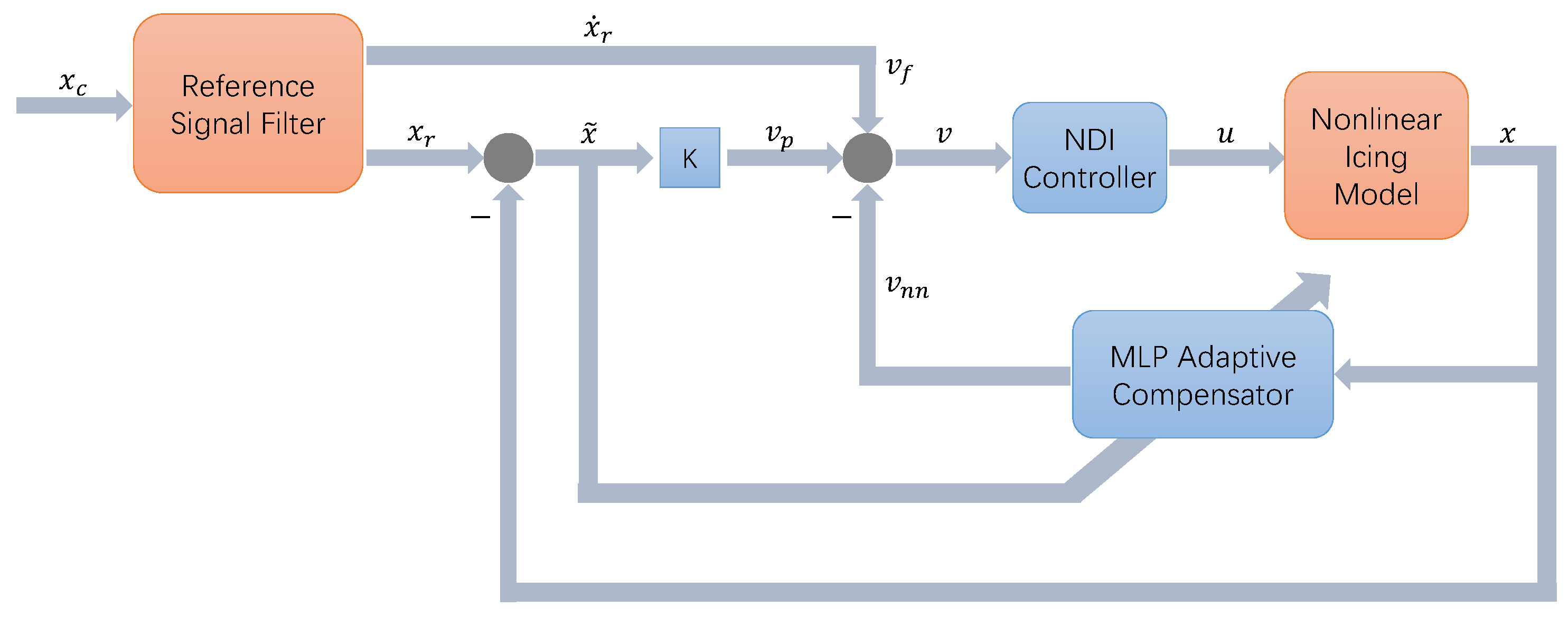
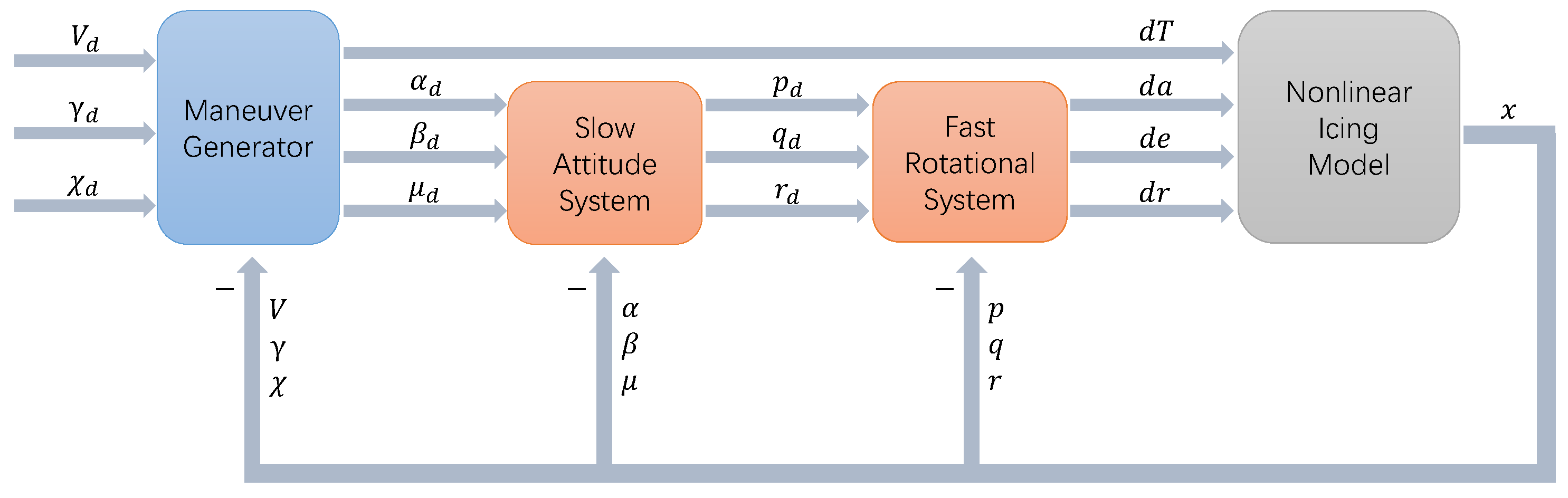
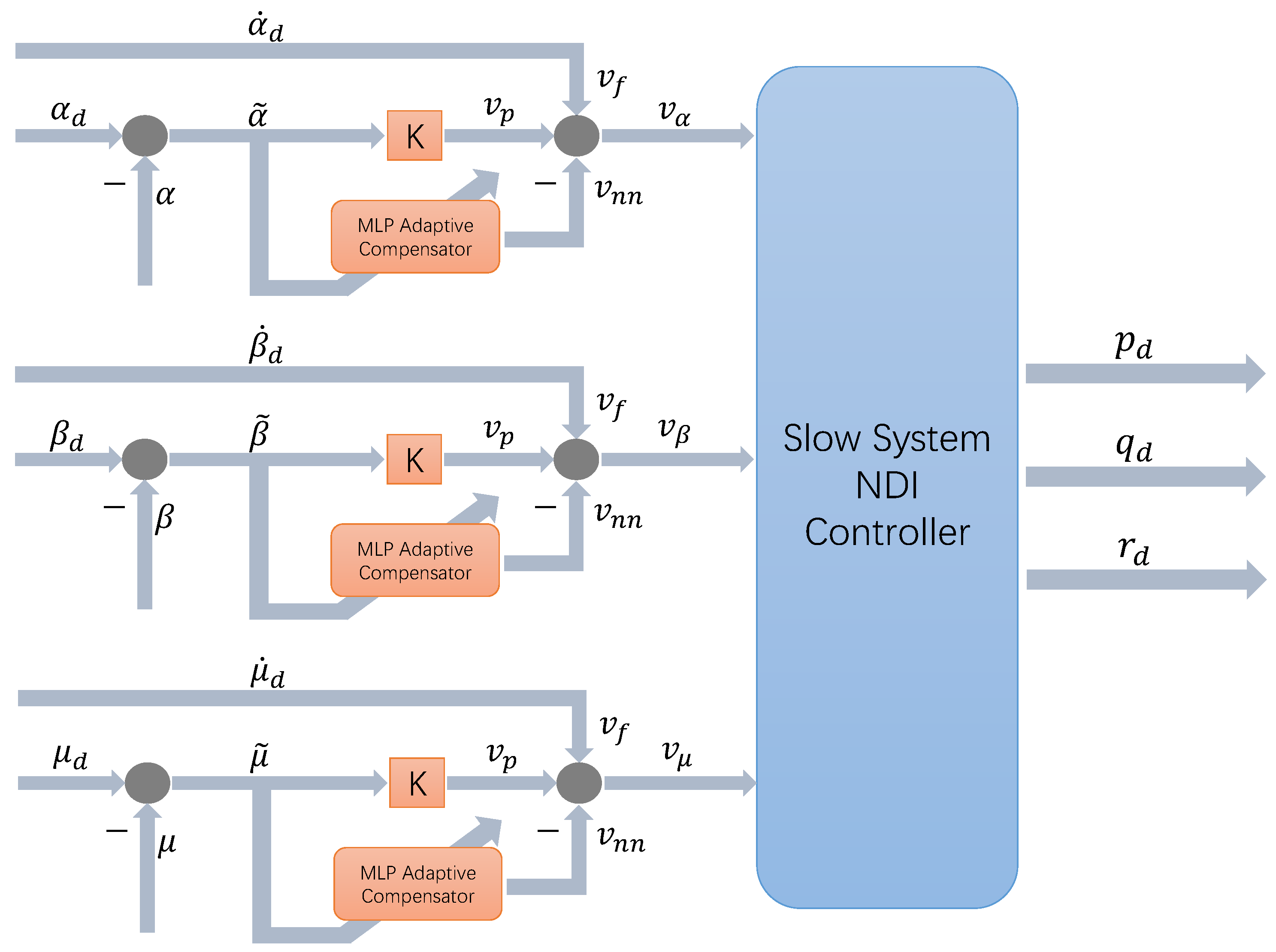
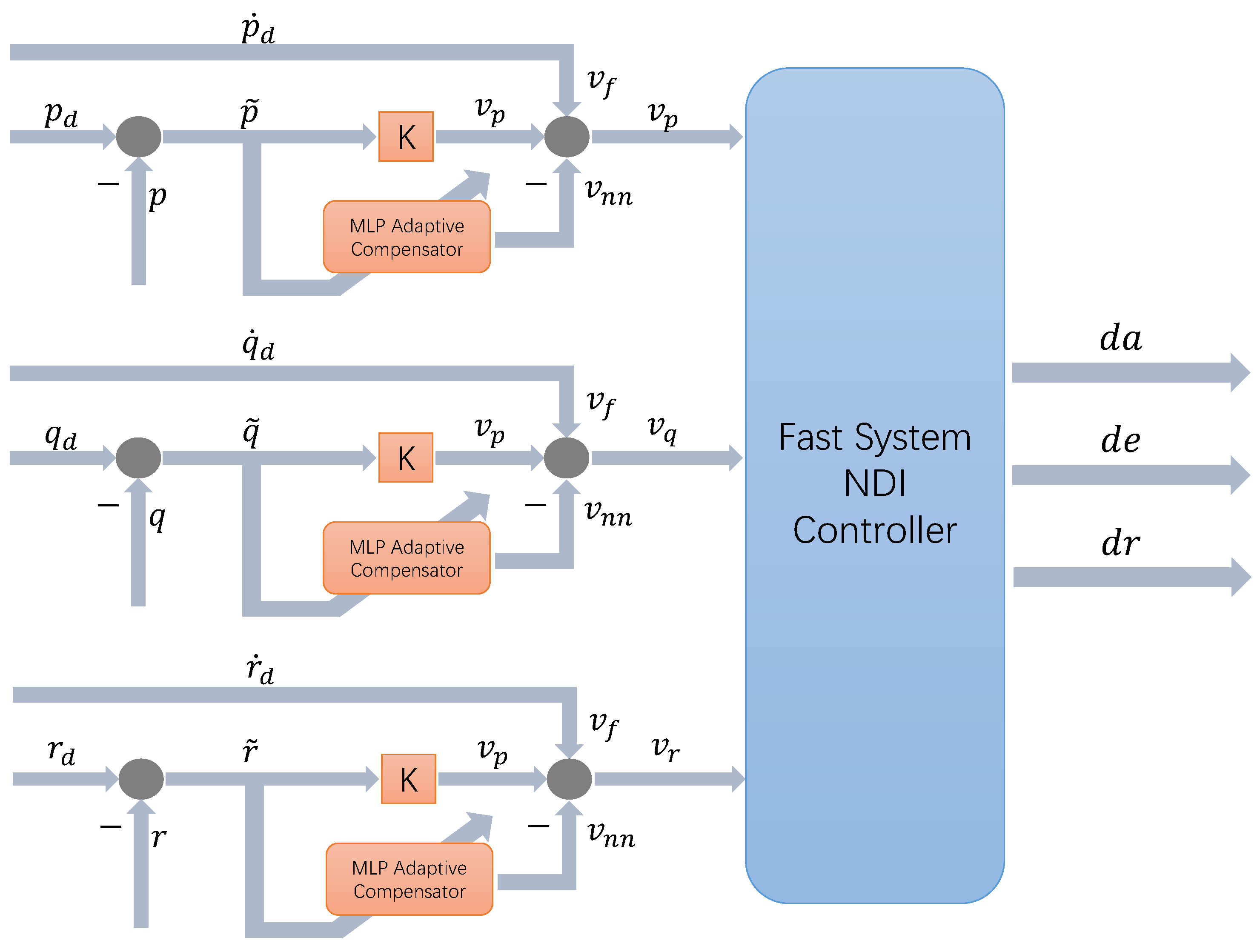
3. MLP-NDI Adaptive Control
3.1. Feedback Inversion
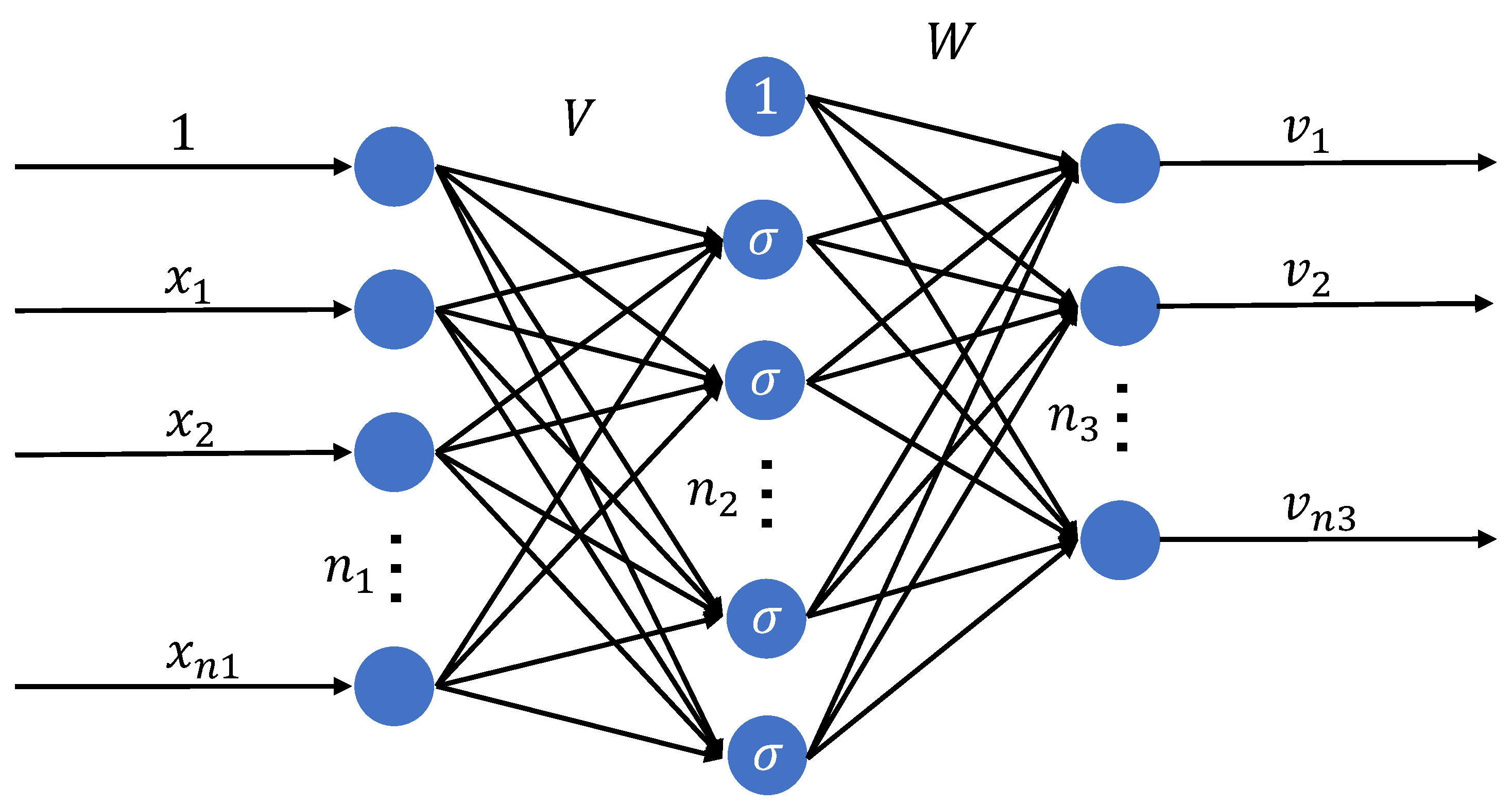
3.2. MLP-Based Adaptive Compensator
3.3. Application to Icing Flight Control
4. Experiment Evaluation and Comparison
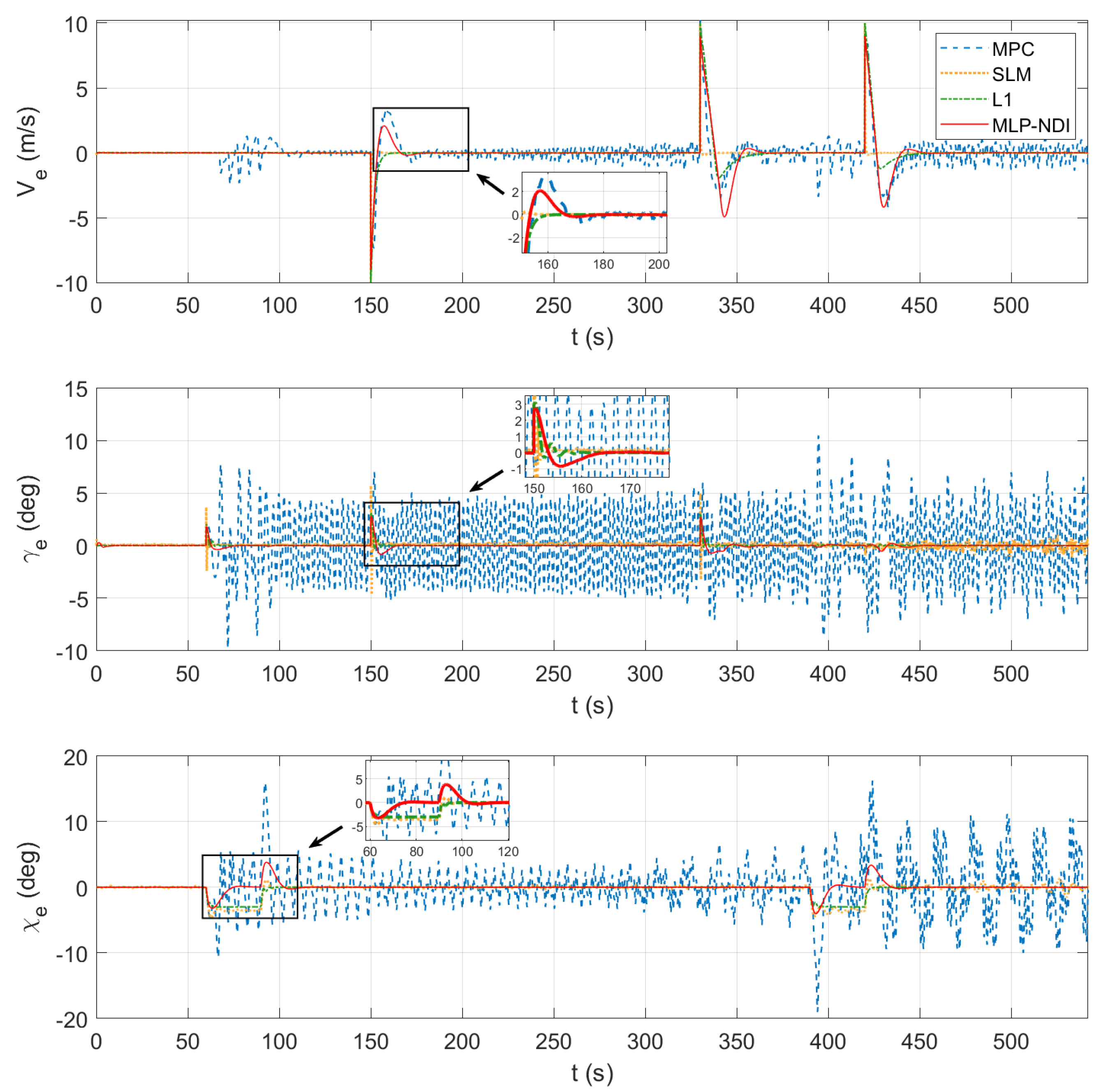
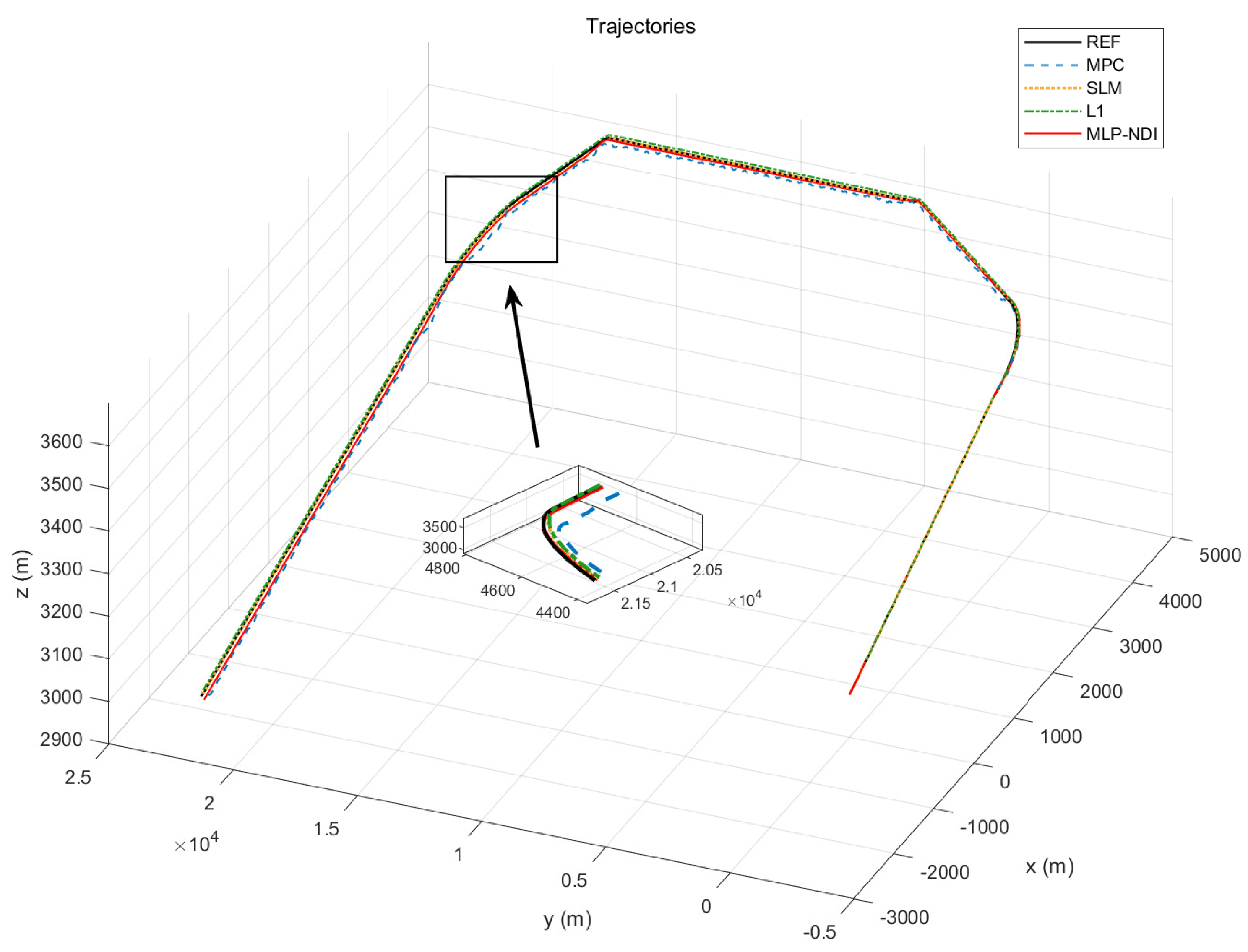
4.1. Scenario 1: Controllers Comparison
- MPC is widely recognized as a highly effective time domain controller due to its ability to predict the system’s future response and handle various process constraints in a systematic manner. Inspired by Wang [33], we utilized orthogonal basis functions such as Laguerre and Kautz function to establish the trajectory model of the control input signal . By doing so, we were able to obtain a concise cost function J, which could be optimized using quadratic programming (QP) to provide the optimal input series within each time horizon.
- The SMC method is a popular nonlinear control approach known for its robustness and ability to handle modeling error within a certain range [34,35]. In this paper, first- and second-order dynamic sliding mode technologies were employed to construct a sliding surface for the attitude control system [36], which was then used to derive the control law. In addition, a proportional control method with a low-pass filter was introduced outside the attitude loop to enable the tracking of velocity and track angles.
- L1 adaptive control is an adaptive method that can handle system uncertainty and parameter variation with sufficient robustness [37,38]. By designing a PI controller with a state observer using the linear quadratic regulator (LQR) technique, the L1 adaptive control is then applied to the traditional NDI framework to improve the system tracking performance under icing scenarios [39].
- The MLP-NDI controller described in Section 3.3 was tested here and initialed with random weights. The hidden layer consisted of 15 neurons and the adjustment factor of the learning rate was . The weight matrices were updated online according to Equation (36).
- In the case of the MPC controller, the disturbance and measurement noise were unable to be modeled, which led to oscillations during the optimization of Laguerre functions [33]. However, since the uncertainty was modeled with a zero-mean Gaussian function, the output of the MPC controller still remained close to the ideal output.
- In the SMC controller, the nonlinear system constructed is different on either side of the sliding mode region, leading to different paths towards the termination point [40]. This can result in buffeting due to the sensitivity of the system. The trajectory of SMC shows that the HALE-UAV experiences a long oscillation above the command signal, while on the other side of the sliding surface, the system performs more sensitively and is much quicker. As a result, the time accumulation of climbing is always larger than the time of descending, leading to a steady-state error in channel .
- Since the neural network of MLP-NDI was initialed with all random weights, it requires some time to update weights matrices before converging to a local optimum. Similarly, the adaptability of L1 also comes from its construction of the error system at each time moment; thus, both perform much slower than SMC, which mainly relies on the robustness of its default sliding surface.
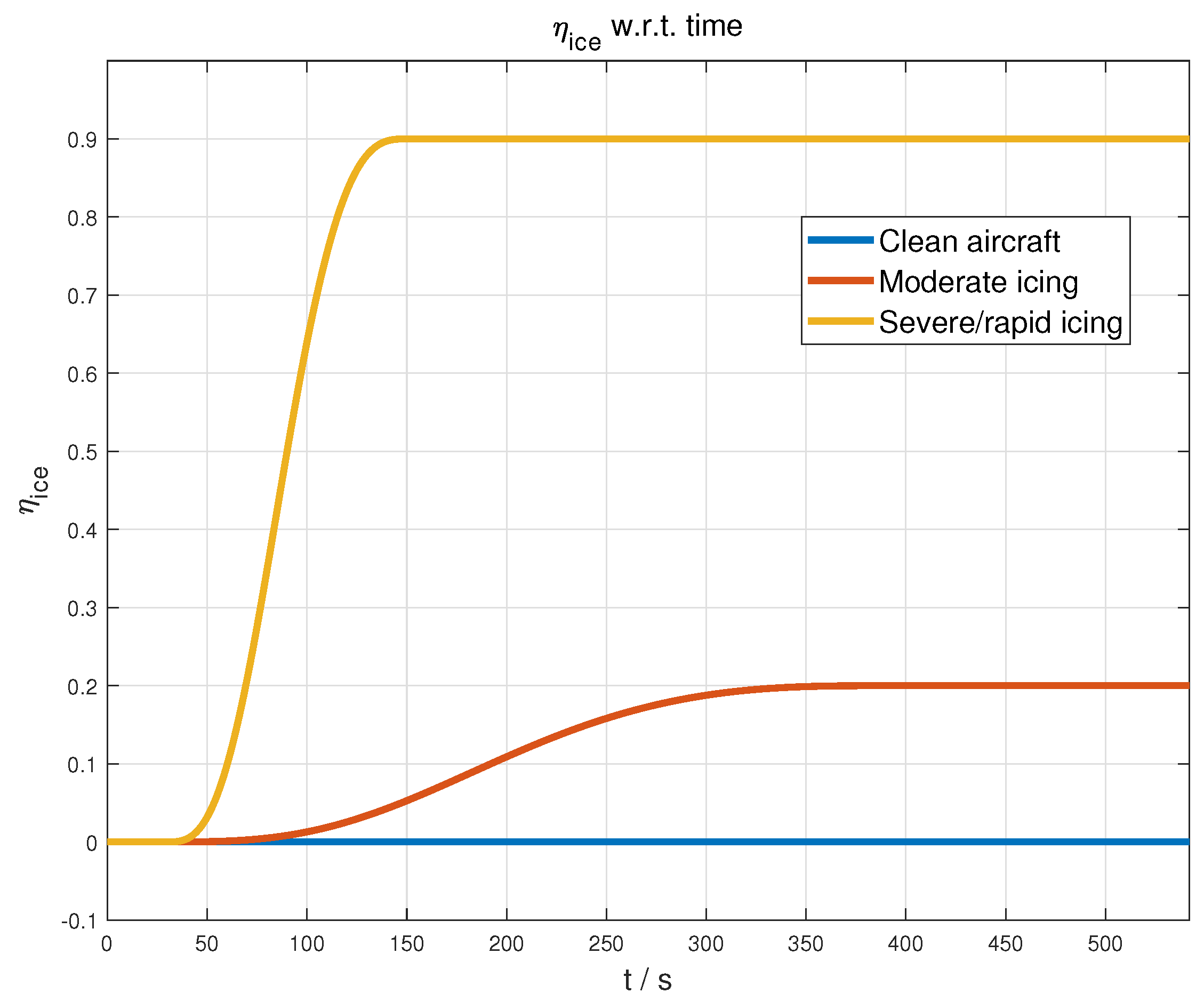
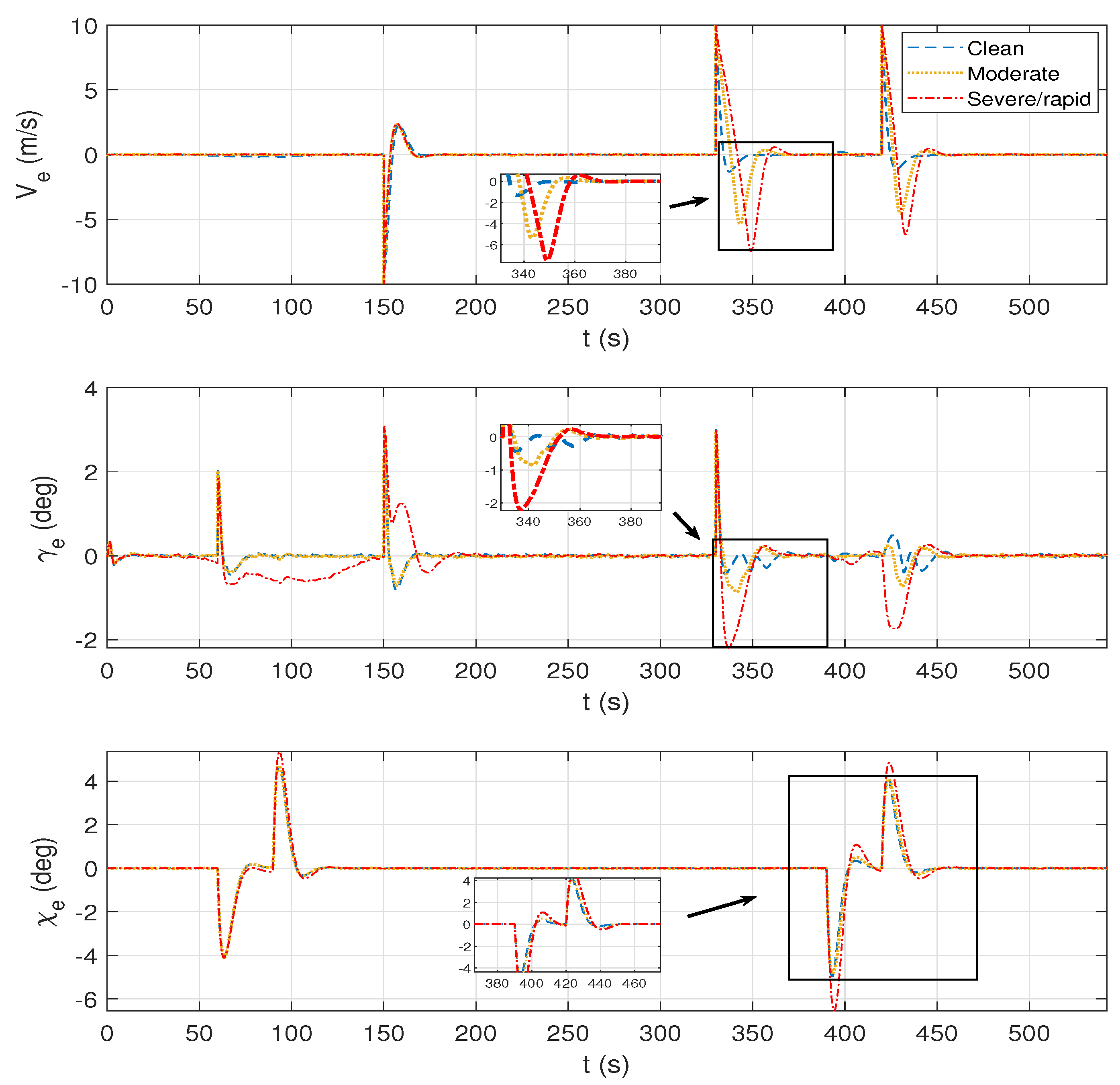
4.2. Scenario 2: Ice-Tolerant Robustness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HALE-UAV | high-altitude long-endurance unmanned aerial vehicle |
| MLP | Multilayer perceptron |
| NDI | Nonlinear dynamic inversion |
| IPS | Icing protection system |
| TIP | Tailplane icing program |
| IMS | Icing management system |
| FTC | Fault tolerant control |
| SMC | Sliding mode control |
| MPC | Model-predictive control |
| MIMO | Multi-input multi-output |
| DOF | Dimension of freedom |
| QP | Quadratic programming |
| LQR | Linear quadratic regulator |
References
- Bottyán, Z. Estimation of in-flight icing characteristics of UAVs during different meteorological conditions. In Proceedings of the 8th International Conference on Intelligent Unmanned Systems, Singapore, 22–24 October 2012; pp. 418–422. [Google Scholar]
- Bragg, M. Aircraft aerodynamic effects due to large droplet ice accretions. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996; p. 932. [Google Scholar]
- Cao, Y.; Wu, Z.; Su, Y.; Xu, Z. Aircraft flight characteristics in icing conditions. Prog. Aerosp. Sci. 2015, 74, 62–80. [Google Scholar] [CrossRef]
- Melody, J.W.; Başar, T.; Perkins, W.R.; Voulgaris, P.G. Parameter identification for inflight detection and characterization of aircraft icing. Control Eng. Pract. 2000, 8, 985–1001. [Google Scholar] [CrossRef]
- Dong, Y.; Ai, J. Inflight parameter identification and icing location detection of the aircraft: The time-varying case. J. Control Sci. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Aircraft Accident Report, Inflight Icing Encounter and Loss of Control, ATR Model 72-212, Roselawn, Indiana, 31 October 1994; Tech. Rep. NTSB/AAR-96/01; National Transportation Safety Board: Washington, DC, USA, 1996.
- Interim Report on the Accident on 1 June 2009 to the Airbus A330–203 Registered F-GZCP Operated by Air France Flight AF 447 Rio de Janeiro-Paris; Bureau d’Enquêtes et d’Analyses pour la Sécurité de l’Aviation Civile (BEA): Paris, France, 2009.
- Safety Investigation Following the Accident on 1st June 2009 to the Airbus A330-203, Flight AF 447-Summary, English ed. Bureau d’Enquêtes et d’Analyses pour la sécurité de l’Aviation civile (BEA): Paris, France, 2012.
- Ratvasky, T.; Van Zante, J.; Riley, J. NASA/FAA tailplane icing program overview. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999; p. 370. [Google Scholar]
- Bragg, M.; Perkins, W.; Sarter, N.; Basar, T.; Voulgaris, P.; Gurbacki, H.; Melody, J.; McCray, S. An interdisciplinary approach to inflight aircraft icing safety. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 95. [Google Scholar]
- Cheng, J.C.; Chen, Y.M. Investigation of fluid flow and heat transfer characteristics for a thermal anti-icing system of a high-altitude and long-endurance UAV. J. Mech. 2021, 37, 467–483. [Google Scholar] [CrossRef]
- Muhammed, M.; Virk, M.S. Ice Accretion on Fixed-Wing Unmanned Aerial Vehicle—A Review Study. Drones 2022, 6, 86. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, X. Fault-tolerant control systems: A comparative study between active and passive approaches. Annu. Rev. Control 2012, 36, 60–72. [Google Scholar] [CrossRef]
- Ding, D.; Che, J.; Qian, W.Q. Fault-tolerant flight control for aircraft wing icing based on icing detection method. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar]
- Ru, J.; Li, X.R. Variable-structure multiple-model approach to fault detection, identification, and estimation. IEEE Trans. Control Syst. Technol. 2008, 16, 1029–1038. [Google Scholar] [CrossRef]
- Verhaegen, M.; Kanev, S.; Hallouzi, R.; Jones, C.; Maciejowski, J.; Smail, H. Fault tolerant flight control-a survey. In Fault Tolerant Flight Control; Springer: Berlin/Heidelberg, Germany, 2010; pp. 47–89. [Google Scholar]
- Shtessel, Y.; Buffington, J.; Banda, S. Multiple timescale flight control using reconfigurable sliding modes. J. Guid. Control. Dyn. 1999, 22, 873–883. [Google Scholar] [CrossRef]
- Mignone, D. Control and estimation of hybrid systems with mathematical optimization. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2002. [Google Scholar]
- Funahashi, K.I. On the Approximate Realization of Continuous Mappings by Neural Networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Calise, A. Development of a reconfigurable flight control law for the X-36 tailless fighter aircraft. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Napoli, Italy, 13–16 June 2000; p. 3940. [Google Scholar]
- Idan, M.; Johnson, M.; Calise, A.J.; Kaneshige, J. Intelligent aerodynamic/propulsion flight control for flight safety: A nonlinear adaptive approach. In Proceedings of the 2001 American Control Conference (Cat. No. 01CH37148), Arlington, VA, USA, 25–27 June 2001; Volume 4, pp. 2918–2923. [Google Scholar]
- Hovakimyan, N.; Nardi, F.; Calise, A.; Kim, N. Adaptive output feedback control of uncertain nonlinear systems using single-hidden-layer neural networks. IEEE Trans. Neural Netw. 2002, 13, 1420–1431. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.H.; Kim, Y. Reconfigurable flight control system design using adaptive neural networks. IEEE Trans. Control Syst. Technol. 2004, 12, 87–100. [Google Scholar] [CrossRef]
- Bragg, M.; Hutchison, T.; Merret, J. Effect of ice accretion on aircraft flight dynamics. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000; p. 360. [Google Scholar]
- Ratvasky, T.; Ranaudo, R. Icing effects on aircraft stability and control determined from flight data-Preliminary results. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993; p. 398. [Google Scholar]
- Melody, J.W.; Hillbrand, T.; Başar, T.; Perkins, W.R. H∞ parameter identification for inflight detection of aircraft icing: The time-varying case. Control Eng. Pract. 2001, 9, 1327–1335. [Google Scholar] [CrossRef]
- Dong, Y.; Ai, J. Research on inflight parameter identification and icing location detection of the aircraft. Aerosp. Sci. Technol. 2013, 29, 305–312. [Google Scholar] [CrossRef]
- Fang, Z.; Chen, W.; Zhang, S. Aerospace Vehicle Dynamics, 1st ed.; Beihang University Press: Beijing, China, 2005. [Google Scholar]
- Pokhariyal, D.; Bragg, M.; Hutchison, T.; Merret, J. Aircraft flight dynamics with simulated ice accretion. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 541. [Google Scholar]
- Lewis, F.L.; Yesildirek, A.; Liu, K. Multilayer neural-net robot controller with guaranteed tracking performance. IEEE Trans. Neural Netw. 1996, 7, 388–399. [Google Scholar] [CrossRef]
- Snell, S.A.; Enns, D.F.; Garrard, W.L., Jr. Nonlinear inversion flight control for a supermaneuverable aircraft. J. Guid. Control. Dyn. 1992, 15, 976–984. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Jafarov, E.M.; Tasaltin, R. Robust sliding-mode control for the uncertain MIMO aircraft model F-18. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 1127–1141. [Google Scholar]
- Wang, T.; Xie, W.; Zhang, Y. Adaptive sliding mode fault tolerant control of civil aircraft with separated uncertainties. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 945. [Google Scholar]
- Pu, M.; Wu, Q.; Jiang, C.; Dian, S.; Wang, Y. Recursive terminal sliding mode control for higher-order nonlinear system with mismatched uncertainties. Acta Autom. Sin. 2012, 38, 1777–1793. [Google Scholar] [CrossRef]
- Hovakimyan, N.; Cao, C. L1 Adaptive Control Theory: Guaranteed Robustness with Fast Adaptation; SIAM: Urbana, IL, USA, 2010. [Google Scholar]
- Banerjee, S.; Boyce, R.; Wang, Z.; Baur, B.; Holzapfel, F. L1 augmented controller for a lateral/directional maneuver of a hypersonic glider. J. Aircr. 2017, 54, 1257–1267. [Google Scholar] [CrossRef]
- Chen, Q.; Wan, J.; Ai, J. L 1 adaptive control of a generic hypersonic vehicle model with a blended pneumatic and thrust vectoring control strategy. Sci. China Inf. Sci. 2017, 60, 32203. [Google Scholar] [CrossRef]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Hellmundt, F.; Wildschek, A.; Maier, R.; Osterhuber, R.; Holzapfel, F. Comparison of L1 adaptive augmentation strategies for a differential PI baseline controller on a longitudinal F16 aircraft model. In Advances in Aerospace Guidance, Navigation and Control; Springer: Berlin/Heidelberg, Germany, 2015; pp. 99–118. [Google Scholar]







| (a) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | ||||||||||||||
| Clean | −0.380 | −5.660 | −19.970 | −0.608 | −0.041 | 0.052 | 0.008 | −1.310 | −34.200 | −1.740 | ||||
| Wing | −0.380 | −5.342 | −19.700 | −0.594 | −0.050 | 0.053 | 0.008 | −1.285 | −33.000 | −1.709 | ||||
| Tail | −0.380 | −5.520 | −19.700 | −0.565 | −0.046 | 0.053 | 0.008 | −1.263 | −33.000 | −1.593 | ||||
| Both | −0.380 | −5.094 | −19.700 | −0.550 | −0.062 | 0.057 | 0.008 | −1.180 | −33.000 | −1.566 | ||||
| (b) | ||||||||||||||
| Clean | −0.60 | −0.20 | 0.40 | 0.150 | −0.080 | −0.50 | 0.06 | −0.150 | 0.0150 | 0.10 | −0.06 | −0.180 | −0.12 | −0.001 |
| Both | −0.48 | −0.20 | 0.40 | 0.135 | −0.072 | −0.45 | 0.06 | −0.135 | 0.0138 | 0.08 | −0.06 | −0.169 | −0.11 | −0.001 |
| r | V | H | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0167 | 0.0138 | 0.0293 | 0.0439 | 0.003 | 0.0391 | 2.4994 | 0.0091 | 0.0128 | 0.008 |
| Time (s) | V (m/s) | (deg) | (deg) |
|---|---|---|---|
| 0∼60 | 60 | 5 | 0 |
| 60∼90 | 60 | 3 | 0∼90 |
| 90∼150 | 60 | 3 | 90 |
| 150∼330 | 70 | 0 | 90 |
| 330∼390 | 60 | −3 | 90 |
| 390∼420 | 60 | −3 | 90∼180 |
| 420∼542 | 50 | −3 | 180 |
| CASE | V | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| PERF | 150 | 330 | 420 | 60 | 150 | 330 | 60 | 390 | |
| SMC | 0.56 | 0.42 | 0.30 | - | - | - | 23.33 | 26.09 | |
| L1 | 5.89 | 20.80 | 16.21 | 6.69 | 5.68 | 5.46 | 3.19 | 6.84 | |
| MLP-NDI | 13.72 | 21.30 | 17.19 | 14.07 | 12.24 | 14.94 | 13.26 | 18.92 | |
| SMC | 0.31 | 0.13 | 0.06 | 0.05 | 0.06 | 0.08 | - | - | |
| L1 | 4.25 | 6.38 | 5.13 | 0.96 | 0.91 | 1.02 | |||
| MLP-NDI | 3.02 | 7.37 | 5.69 | 2.37 | 2.75 | 2.73 | |||
| SMC | 2.6 | 1.98 | 2.22 | 137.82 | 164.99 | 115.67 | - | - | |
| L1 | 0 | 19.45 | 12.23 | 8.74 | 11.14 | 7.23 | |||
| MLP-NDI | 20.83 | 49.55 | 42.13 | 20.03 | 27.60 | 23.66 | |||
| SMC | 0.0085 | 0.0040 | 0.0294 | 0.1462 | 0.0964 | 0.0974 | 3.6277 | 3.6773 | |
| L1 | 0.0095 | 0.0029 | 0.0006 | 0.0002 | 0.00005 | 0.0003 | 2.9881 | 3.0091 | |
| MLP-NDI | 0.0041 | 0.0061 | 0.0119 | 0.0121 | 0.0117 | 0.0002 | 0.0294 | 0.0240 | |
| CASE | ERROR (m) | ||||
|---|---|---|---|---|---|
| max | min | mean | std | ||
| MPC | 0.13 | 0 | 0.08 | 0.04 | |
| SMC | 1.58 | 0 | 0.83 | 0.44 | |
| L1 | 0.02 | 0 | 0.01 | 0.01 | |
| MLP-NDI | 0.50 | 0 | 0.12 | 0.11 | |
| MPC | 137.79 | 0.04 | 86.97 | 34.58 | |
| SMC | 86.09 | 1.57 | 73.39 | 24.60 | |
| L1 | 111.96 | 0.04 | 90.28 | 32.94 | |
| MLP-NDI | 73.69 | 0.02 | 52.51 | 18.15 | |
| MPC | 167.99 | 109.03 | 136.42 | 13.30 | |
| SMC | 88.56 | 75.81 | 77.81 | 3.55 | |
| L1 | 94.48 | 53.80 | 64.81 | 11.64 | |
| MLP-NDI | 78.85 | 48.23 | 68.30 | 8.81 | |
| CASE | ERROR (m) | ||||
|---|---|---|---|---|---|
| max | min | mean | std | ||
| - | 42.04 | 0 | 23.25 | 13.20 | |
| clean | 0.50 | 0 | 0.12 | 0.11 | |
| icing | 73.69 | 0.02 | 52.51 | 18.15 | |
| iced | 78.85 | 48.23 | 68.30 | 8.81 | |
| clean | 0.50 | 0 | 0.12 | 0.11 | |
| icing | 77.52 | 0.04 | 49.03 | 31.79 | |
| iced | 106.28 | 59.99 | 85.08 | 11.80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Cheng, L.; Yuan, J.; Ai, J.; Dong, Y. Neural Network and Dynamic Inversion Based Adaptive Control for a HALE-UAV against Icing Effects. Drones 2023, 7, 273. https://doi.org/10.3390/drones7040273
Li Y, Cheng L, Yuan J, Ai J, Dong Y. Neural Network and Dynamic Inversion Based Adaptive Control for a HALE-UAV against Icing Effects. Drones. 2023; 7(4):273. https://doi.org/10.3390/drones7040273
Chicago/Turabian StyleLi, Yiyang, Lingquan Cheng, Jiayi Yuan, Jianliang Ai, and Yiqun Dong. 2023. "Neural Network and Dynamic Inversion Based Adaptive Control for a HALE-UAV against Icing Effects" Drones 7, no. 4: 273. https://doi.org/10.3390/drones7040273
APA StyleLi, Y., Cheng, L., Yuan, J., Ai, J., & Dong, Y. (2023). Neural Network and Dynamic Inversion Based Adaptive Control for a HALE-UAV against Icing Effects. Drones, 7(4), 273. https://doi.org/10.3390/drones7040273






