Abstract
An air-to-ground downlink communication network consisting of a reconfigurable intelligent surface (RIS) and unmanned aerial vehicle (UAV) is proposed. In conjunction with a resource allocation strategy, the system’s energy efficiency is improved. Specifically, the UAV equipped with a RIS starts from an initial location, and an energy-efficient unmanned aerial vehicle deployment (EEUD) algorithm is deployed to jointly optimize the UAV trajectory, RIS phase shifts, and BS transmit power, so as to obtain a quasi-optimal deployment location and hence improve the energy efficiency. First, the RIS phase shifts are optimized by using the block coordinate descent (BCD) algorithm to deal with the nonconvex inequality constraint, and then integrated with the Dinkelbach algorithm to address the resource allocation problem of the BS transmit power. Finally, for solving the UAV trajectory optimization problem, the complex objective function is transformed into a convex function, and the optimal UAV flight trajectory is obtained. Our simulation results show that the quasi-optimal deployment location obtained by the EEUD algorithm is superior to other deployment strategies in energy efficiency. Moreover, the instantaneous energy efficiency of the UAVs along the trajectory of searching the deployment location is better than other comparison trajectories. Furthermore, the RIS-assisted multi-user air-to-ground communication network can offer up to 145% improvement in energy efficiency over the traditional amplify-and-forward (AF) relay.
1. Introduction
Driven by the rapid development of global communication technology, wireless communication technology has been integrated into various fields of society, and has played a huge role in these fields and human life. The global communication network is showing a trend of continuous expansion, which makes the cost and the energy consumption of communication networks constantly increase. Adhering to the development concept of saving global energy and protecting the ecological environment is crucial to lowering the network’s overall energy consumption while meeting the growing service requirements. Therefore, green communication technology, as a new generation communication concept, is put forward in [1]. The aim of green communication is to reduce power consumption, improve energy efficiency, and achieve sustainable development. With the standardization of beyond-5G (B5G) wireless networks, 6G wireless networks are being developed by academia and industry alike. Meanwhile, energy efficiency has also become an important requirement of 6G wireless communications [2,3].
The reconfigurable intelligent surface (RIS), also known as the intelligent reflecting surface (IRS), a potential 6G wireless network technology, has been considered as an energy-efficient and low-cost way to increase the energy efficiency of wireless networks [4]. The RIS is essentially a new material composed of multiple discrete reflecting elements to form a planar structure. Each reflecting element of the RIS can change its phase shifts under the management of a microcontroller. Therefore, the RIS can achieve accurate three-dimensional reflection beamforming through flexible modification of each reflecting element’s phase shift [5]. As a passive relay, it is not necessary for the RIS to amplify and decode signals when reflecting the electromagnetic wave. Therefore, the RIS benefits from being low power and high energy-efficient. Compared to the conventional amplify-and-forward (AF) relay, the energy efficiency of communications networks assisted by the RIS can be greatly improved [6,7]. The intensive research efforts on the RIS greatly accelerate the 6G wireless communications networks to achieve the goal of green communications.
In practice, due to the limitation of network capacity and coverage, terrestrial communication networks cannot provide ubiquitous wireless connectivity with high data rates and reliability. To achieve network convergence and upgrade network capacity, traditional terrestrial networks have gradually evolved into air-ground integrated networks [8]. In recent years, it has attracted extensive attention in the air-to-ground communication network assisted by unmanned aerial vehicles (UAVs). The UAV can be considered as a base station (BS) or relay to provide a line-of-sight (LoS) dominant connection for ground users in blind spots [9]. Due to the characteristics of high mobility, a UAV can be quickly deployed as a communication node. Temporary emergency communications supported by the UAV can be a more practical and economical solution during political rallies, emergency events, or harsh environments such as woodlands, deserts, and disaster areas [10]. The UAV can also complete communication tasks effectively by adjusting the flight trajectory and deployment location. As one of the potential 6G key technologies, the RIS can be utilized as a UAV payload to achieve coverage enhancement, and further improve the network performance. In recent years, studies on air-to-ground communication networks assisted by the RIS and UAV have received extensive attention [11]. The performance of RIS-assisted UAV communication system has also been analyzed in detail [12].
1.1. Related Work
Due to its flexible deployment and low-cost characteristics, the RIS can be deployed on ground buildings or aerial UAVs, and some recent related works are summarized in Table 1. When the RIS is deployed on a ground building, the UAV usually acts as an aerial BS for cooperative transmission with the RIS. References [13,14,15] explored an air-to-ground network in which the RIS was deployed on a ground building to help communication between ground users and the UAV. The UAV followed a trajectory that can maximize the sum rate from the initial location to the final location, and communicated with ground users during the flight. Secure air-to-ground communication networks have also been extensively researched. The RIS can reduce the quality of eavesdropping while improving the quality of secure transmission, providing the RIS-assisted UAV network with a security transmission solution. The RIS deployed on the ground building was used to assist the UAV for secure communications with ground users in [16,17]. The UAV can also be an eavesdropper in RIS-assisted multi-user communications [18]. In addition, combining the UAV and RIS enables the expansion of wireless-powered communication networks (WPCNs). The RIS installed on a building was used to assist the UAV in transmitting energy to multiple ground sensors while flying along a trajectory that minimizes energy consumption, making WPCNs more energy efficient [19]. The RIS can also assist the UAV in mobile edge computing and minimizing system energy consumption [20]. Moreover, the deployment location and resource management of the UAV in RIS-assisted visible light communication networks was also presented in [21].

Table 1.
Comparison of related works.
Furthermore, the RIS can be deployed on the UAV. In this scenario, the UAV becomes an aerial relay. Reference [22] investigated a novel RIS-assisted air-to-ground system, where the aerial relay UAV was equipped with the RIS-supported BS to communicate with users and the system energy efficiency was improved. In addition, the classic three-node cooperative communication model was studied, in which the RIS-equipped UAV flew along the system throughput maximization trajectory to improve the system performance [23]. Reference [24] proposed an RIS-assisted UAV communication network in Terahertz bands, where an access point transmitted data to multiple ground user equipment (UE), aiming to expand signal coverage and reduce UAV energy consumption. Energy efficiency maximization of the RIS-assisted uplink network was proposed in [25], where the BS was associated with at most one user in any time slot. The system energy efficiency was maximized by jointly optimizing the user association, RIS phase shifts, UAV trajectory, and UE transmit power. Moreover, reference [26] maximized the energy efficiency in the WPCN, where the RIS-equipped UAV was deployed at fixed deployment locations. However, the above references [13,14,15,16,17,18,19,20,23,24,25] only studied UAV trajectory optimization, and did not consider the optimized deployment location of the UAV. References [15,16,17,23] only consider the single-user scenarios. References [16,17,23,24,25] consider multi-user scenarios; however, only one user is allowed to access the network in each time slot, and the scenario where multiple users communicate simultaneously is not considered. References [19,20,24] considered how to lower UAV energy consumption. However, only reducing UAV energy consumption cannot effectively improve the energy efficiency of the system. Although [22,26] consider improving system energy efficiency, the mobility of UAV is not utilized to optimize the location of UAV. Therefore, we consider the multi-user communication scenario and optimize the UAV deployment location and trajectory. We aim at improving energy efficiency and building an energy-efficient air-to-ground communication network.
1.2. Contributions
The RIS deployed on the UAV can provide 3D panoramic signal reflection for ground users. At the same time, the UAV makes RIS mobile, and the RIS can be flexibly relocated with the aid of the UAV to improve signal coverage enhancement. In order to realize energy-saving communications, it is imperative to enhance the system’s energy efficiency. Nevertheless, there is very limited research on UAVs equipped with the RIS with the objective of maximizing energy efficiency. Most previous studies have focused on maximizing network throughput or minimizing UAV energy consumption. This is because energy efficiency is related to both sum rate and energy consumption, and is much more difficult to optimize. Moreover, the UAV in [15,16,17,23,24,25] can be associated with only one user in each time slot; thus, it cannot realize multi-user communications. Furthermore, most RIS-related works in the literature are based upon traditional uniform linear arrays (ULAs), where the reflecting elements of the RIS maintain a uniform linear relationship with each other, and the phase shift of each reflecting element cannot be modified individually. To address these issues, the major contributions are summarized below.
- An energy-efficient air-to-ground communication network assisted by the RIS is proposed, in which the RIS-equipped UAV (RIS-UAV) assists the BS to communicate with multiple ground users simultaneously. The RIS-UAV adopts a non-ULA, where the reflecting elements of the RIS do not have a linear relationship among themselves, making the beamforming design of the RIS more flexible. By exploring the full potential of the RIS-UAV, the energy efficiency of the air-to-ground communication network is maximized;
- An energy efficiency optimization algorithm based on RIS-UAV deployment is proposed, which is termed the energy-efficient unmanned aerial vehicle deployment (EEUD) algorithm. By using the EEUD algorithm, the RIS phase shifts, the RIS-UAV trajectory, and the BS transmit power are optimized alternately to solve the complex multi-user energy efficiency maximization problem. In addition, we investigate the impact of varied numbers of users, RIS reflecting elements, and BS antennas on system energy efficiency;
- The proposed algorithm optimizes the RIS-UAV trajectory to ensure that the instantaneous system energy efficiency is maximized when the RIS-UAV flies along the optimal trajectory in each time slot. In the process of searching for the deployment location, the RIS-UAV maintains a simultaneous association with multiple users and BS to ensure network communications quality. Finally, simulation results are presented to demonstrate that the proposed solution outperforms other benchmark solutions.
The remainder of this paper is organized as follows. Section 2 describes the system model. Section 3 presents the EEUD algorithm that optimizes the system energy efficiency, and the simulation results are given in Section 4. Finally, concluding remarks are drawn in Section 5. The main symbols defined in this paper are listed in Table 2.

Table 2.
Main Notation.
Notation: In this paper, operators , , , , , and denote the -norm, Frobenius norm, pseudo-inverse, inverse, conjugate transpose, and transpose of a matrix, respectively. stacks all column vectors of matrix to form a vector, which is called the vectorization operator. represents a diagonal matrix with the elements of vector on the main diagonal. The Kronecker product is denoted by ⊗, and is the identity matrix.
2. System Model
Figure 1 illustrates the system model of the RIS-assisted multi-user air-to-ground downlink communications network under consideration in this paper.
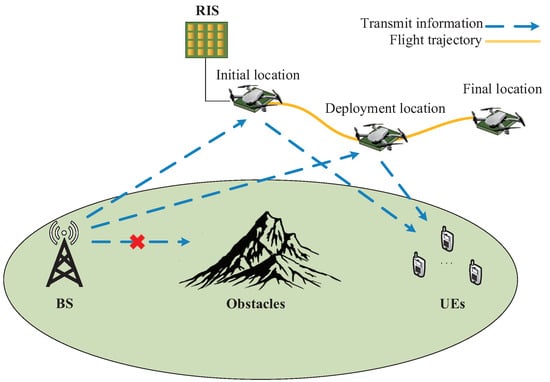
Figure 1.
System model of the RIS-assisted multi-user air-to-ground downlink communications network.
Due to the obstruction of obstacles, there exists no LoS link between K ground users and the BS. Therefore, the RIS-UAV is required to provide LoS connections between the BS and ground users to ensure non-interrupt communications. It is assumed that the RIS has N reflecting elements, the BS has M antennas, and each user is equipped with a single antenna. The RIS-UAV is usually deployed directly above obstacles to serve ground users. However, this is usually not the optimal deployment location. The RIS-UAV needs to find the best deployment location to improve system performance. The RIS-UAV under consideration in this system model starts from the location directly above the obstacles, and then searches for the best deployment location globally. During the searching processes, the RIS-UAV maintains connections with multiple users to ensure that communications are not interrupted. In addition, we assume that RIS-UAV maintains a fixed height and LoS connection with the BS during the flight. When the RIS-UAV finds the quasi-optimal deployment location, it will hover at that location. Until the communication mission is completed, the RIS-UAV will then leave the deployment location and fly to the final location.
2.1. Transmission Model
The channel gains from the BS to RIS-UAV and RIS-UAV to users are represented uniformly by , which is modeled as a combination of small-scale fading and large-scale path-loss. is modeled as a continuous distribution of two components, where R is the Rician factor, is the fast fading component of the LoS channel, is the fast fading component of the non-LoS (NLoS) channel, and is the matrix of the large-scale fading path loss [22]. Each element in can be denoted by , where is the path loss exponent, is the large-scale fading coefficient, and d is the propagation distance. is a Rayleigh channel when , while it becomes a Rician channel when .
Due to the effect of ground obstacles, there is an NLoS link between the BS and users. Assuming that there are LoS links between the BS and RIS-UAV, and between the RIS-UAV and users. The channel gains are represented by and (), respectively. In practical scenarios, both and are modeled as Rician channels. The RIS phase shifts are denoted by matrix . For the sake of fairness, each user is allocated the same bandwidth. denotes the transmitted downlink signal, where is the BS transmit power for user k [7]. Let be the unit-power complex-valued transmit symbol, and is the precoding vector at the BS. Thus, the discrete time signal received by user k can be written as
where is the cascaded channel between the BS and user k, and is the additive Gaussian white noise. Combined with (1), the received signal-to-interference-plus-noise ratio (SINR) at user k is
where denotes the power of the interference signal received by user k. In order to suppress the interference among users, it is assumed that ground users will not leave their locations for a period of time, andthe BS knows and , which can be achieved by the approaches given in, e.g., [27,28]. Therefore, the method of zero-forcing precoding is unitized at the BS to eliminate signal interference among users. Before applying the zero-forcing precoding, the channels , between the RIS-UAV and each user are merged into . In this case, the global channel matrix of the system can be expressed as . Supposing there exists a right inverse matrix for , based on the definition of the right inverse matrix, should satisfy the row full rank, which is . Then, the zero-forcing precoding matrix of the BS transmit signal is . Therefore, the product of the global channel matrix and the zero-forcing precoding matrix is an identity matrix, which can force the interference among users to be zero. At this time, the received SINR at user k can be converted into the signal-to-noise ratio (SNR):
2.2. Energy Efficiency Modeling and Optimization
Based on previous analysis, the system energy efficiency when the RIS-UAV is deployed at a fixed deployment location is
where B is the transmission bandwidth, is the reciprocal of the BS power amplifier efficiency, is the BS transmit power for user k, denotes the BS circuit power consumption, denotes flight power of the RIS-UAV at the deployment location, and denotes the circuit power consumption of each UE. denotes the power consumption of the RIS, where is the power consumption of each reflecting element. Therefore, the problem of maximizing the system energy efficiency can be formulated as :
The constraint (5a) is to ensure that the BS transmit power with zero-forcing precoding cannot exceed the maximum threshold , where the BS transmit power matrix . The constraint (5b) means that the rate of information transmission from the BS to user k cannot be less than the minimum threshold so as not to sacrifice the quality of service (QoS) of some users to improve the system energy efficiency, and ensure that each user can effectively communicate with the BS. The constraint (5c) ensures that the RIS only changes the phase shifts of the signal but not its amplitude. The constraint (5d) describes the initial location of the RIS-UAV, where is the coordinate of the initial location. Constraint (5e) indicates the flight distance of the RIS-UAV in each time slot, where is the maximum flight speed of the RIS-UAV when searching for the deployment location, T is the duration of each time slot, and j represents the j-th time slot. is the location of the RIS-UAV in the j-th time slot, and the RIS-UAV trajectory is composed of in all time slots. The three variables , , and are jointly optimized to maximize the system energy efficiency.
3. Energy-Efficient UAV Deployment Algorithm
In this section, the EEUD algorithm is designed to maximize the system energy efficiency by optimizing the RIS phase shifts , the RIS-UAV trajectory , and the BS transmit power alternately. The process of the EEUD algorithm is shown in Figure 2. The system energy efficiency in the objective function (5) is denoted by variable . However, since , , and co-exist in constraint (5a) under the effect of zero-forcing precoding, the values of and will affect the range of and thus the system energy efficiency. Therefore, and are optimized alternately first before , as shown in Figure 2 for steps 1 and 2. After taking steps 1 and 2 cyclically until the convergence of in (5a), and are fixed in step 3 to optimize . If the system energy efficiency converges, the EEUD algorithm is terminated and outputs the value of the system energy efficiency and RIS-UAV deployment location. Otherwise, the EEUD algorithm will iterate steps 1–3. The system energy efficiency increases with each iteration, and since (5) is upper-bounded on the feasible set, it eventually converges to a value that approximates the optimal energy efficiency.
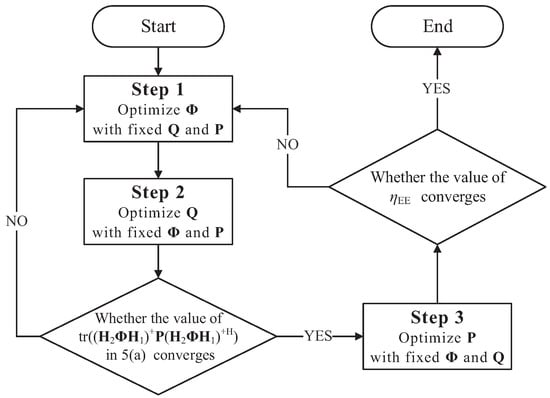
Figure 2.
Procedure of the EEUD algorithm.
The ultimate optimization problem in this paper is the optimization problem , which is to maximize the system’s energy efficiency. In order to solve this problem more efficiently, the objective function (5) will be transformed in the following subsections. The next three subsections describe steps 1–3 of the EEUD algorithm, respectively.
3.1. Step 1: Optimization of the RIS Phase Shifts
In this part, both the BS transmit power and RIS-UAV trajectory are fixed, while the RIS phase shift is optimized. The objective function reduces to a constant C since exists only in constraint (5a). The optimization problem is transformed into :
Since only appears in (6a), which means that the optimization of the RIS phase shifts is to make meet constraint (6a) as much as possible. Decreasing the value of in (6a) by optimizing can expand the feasible set of , which is conducive to increasing the value of the objective function (5). Therefore, constraint (6a) is regarded as the optimization objective to minimize . Therefore, the optimization goal is transformed into the optimization problem :
The optimization problem is non-convex, which is difficult to solve directly. To tackle this challenge, Equation (7) can be reduced to
The BS transmit power is decomposed in step I, where . Step II denotes . Step III is obtained by combining the pseudo-inverse law of matrix products and the property of the Frobenius norm. The vectorization operator in step IV is to transform a matrix into a vector. Therefore, calculating the Frobenius norm of a matrix becomes equivalent to calculating the norm of a vector. Finally, step V denotes , and simplifies the objective function. Then, problem is transformed into :
To solve the high-dimensional problem more effectively, we adopt the block coordinate descent (BCD) algorithm, which is a generalization of the coordinate descent. The BCD algorithm optimizes a subset of variables in each iteration, decomposing the original problem into multiple subproblems. in problem can be separated out of N variables denoted by (), where is the -th element of .
3.2. Step 2: Optimization of the RIS-UAV Trajectory
In this part, and are fixed when finding the deployment location by optimizing the RIS-UAV trajectory. As a result, the target optimization problem becomes
is the three-dimensional coordinate of the RIS-UAV in the j-th time slot. Since is included in both and of constraint (10a) and the objective function (10) is a constant, the optimization problem becomes
where can be decomposed into
where is a matrix denoting the distance between the BS and RIS-UAV, and indicates the distance between the BS and RIS-UAV. Similarly, can be treated in a similar manner as follows
where is a matrix denoting the distance between the RIS-UAV and users, and , denotes the distance from the RIS-UAV to user k. Therefore, the cascade channel matrix can further simplify to
Next, the objective function (11) becomes
Then, the optimization problem reduces to
The Hessian matrix in (16) is
where x and y are the coordinates of the x-axis and y-axis of the RIS-UAV in the Cartesian coordinate system, respectively. The objective function (16) is convex with regards to the coordinates in each time slot, due to the fact that its Hessian matrix is semi-positive definite. Therefore, this problem can be solved by a variety of convex optimization methods, such as the gradient descent method.
3.3. Step 3: Optimization of the BS Transmit Power
In this part, both the RIS phase shifts and RIS-UAV trajectory are fixed to optimize the BS transmit power . The optimization problem of the system is further transformed into the following :
The convex problem belongs to the 0–1 fractional programming problem, and it can be solved by using the Dinkelbach algorithm [29]. The Dinkelbach algorithm is essentially an iterative algorithm, which first starts with a random value, and then approximates the optimal solution iteratively. The process of using the Dinkelbach algorithm to solve problem is described as follows.
First, the objective function (18) is converted from a fraction into the following equation
Equation (19) is further reduced to
To apply the Dinkelbach algorithm, Equation (20) is converted to the following new function
In the n-th iteration of the Dinkelbach algorithm, function becomes
Before the Dinkelbach algorithm is iterated, the initial energy efficiency of the system with random values is given. Then, in the first iteration is
Next, the value of is maximized by adjusting the BS transmit power to user k, which falls under the category of linear programming problems. After the maximum of is obtained, , is used to update to . Similar operations are repeated in subsequent iterations. When the solutions in each iteration converge, the value of is taken as the optimal energy efficiency of the system.
3.4. Complexity Analysis
For the EEUD algorithm, its complexity is mainly determined by the number of iterations of its outer layer, denoted by . The complexity of optimizing the RIS phase shifts depends on the number of iterations of the BCD algorithm, denoted by . Note that the complexity of the convex problems is of polynomial complexity, and the maximum complexity is the fourth power of the number of optimized variables [30]. Since N variables of the RIS are divided into multiple subsets, the complexity of each subset is , where is the number of variables contained in the s-th subset and . The number of iterations between subsets is represented by . Thus, the complexity of the RIS phase shifts optimization by using EEUD algorithm is .
For the RIS-UAV trajectory optimization, the iteration times of the gradient descent method is required in each time slot, and depends on the partial derivatives and the step size of the objective function. Partial derivatives of the objective function with respect to and are calculated separately, and times are required in each time slot. For S time slots, the gradient descent algorithm has a complexity of . Therefore, the complexity of alternating and is .
Optimizing the BS transmit power depends on the iteration times of the Dinkelbach algorithm, denoted by . Since the convex problem solved by the Dinkelbach algorithm is the power allocation for K users, the complexity of the BS transmit power optimization is , where .
In conclusion, the overall complexity of the EEUD algorithm proposed in this paper can be shown as
4. Simulation Results
Figure 3 illustrates the 3D coordinate system of the RIS-assisted multi-user air-to-ground communication network, and the system parameters are given in Table 3 and Table 4, where is the location of the BS. The values of , , , , and in Table 3 are taken from [7]. The values B, , and in Table 3 are from [22]. The simulation is conducted in MatlabR2021a, and the argmax problem in this paper is solved by the fmincon function in Matlab, which is a powerful tool for solving extreme values of nonlinear multivariate functions.
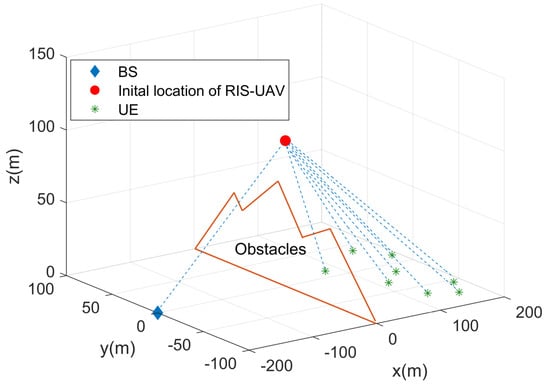
Figure 3.
Illustration of the 3D coordinate system, which includes a RIS-UAV network with N reflecting elements, a M-antenna BS, and K single-antenna ground users.

Table 3.
System parameters.

Table 4.
Distribution of user locations.
To validate the efficacy of the EEUD algorithm, three standard deployment locations are established, which are called benchmark locations 1, and 2. Benchmark location 1 (100 m, 50 m, 100 m) and benchmark location 2 (100 m, −50 m, and 100 m) are located on the perpendicular bisector between the initial location and the final location.
Figure 4 shows eight flight trajectories of the RIS-UAV. The deployment locations of the RIS-UAV in these eight paths are relatively independent and different, and the RIS-UAV will fly directly to the destination after completing the communication task at the different deployment locations. One path is the trajectory that the RIS-UAV uses the EEUD algorithm to find the quasi-optimal deployment location, whereas the other path is to use the majorization-minimization (MM) method in [18] to optimize the RIS phase shifts. The deployment location is the same for both the optimal path and the straight path. The difference between them is that the straight path does not optimize the trajectory of the RIS-UAV during the flying process, and the RIS-UAV keeps a straight line to the deployment location. As shown in Figure 4, when the RIS phase shifts are not optimized and fixed to a random value, the deployment location of the RIS-UAV is offset from the quasi-optimal location. The reason is that the EEUD algorithm does not optimize in this case, and do not need to be optimized alternately with , which results to the offset of deployment location. In addition, the paths of random phase 1 and random phase 2 almost coincide. The reason for this phenomenon is that when is not optimized, it is only necessary to minimize the objective function (11) when optimizing step 2 in the EEUD algorithm. Therefore, the optimization of the RIS phase shifts has a certain influence on the RIS-UAV trajectory and deployment location.
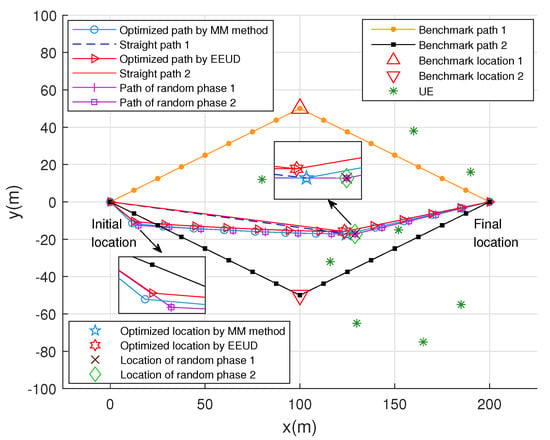
Figure 4.
Different trajectories of the RIS-UAV, where M = 8, N = 8, K = 8, and = 30 dBm.
Figure 5 shows the energy efficiency versus the maximum threshold , where the RIS-UAV is deployed at different locations and the BS transmit power is optimized. All curves are optimized for the RIS phase shifts except for the location of random phase 1 and random phase 2. For improving energy efficiency, the EEUD algorithm is better than both the MM method in [18] and the gradient descent (GD) method in [7], where [7] employs the GD method to optimize the RIS phase shifts. It is clear that when RIS-UAV is deployed at the location by using the EEUD algorithm, its energy efficiency is significantly higher than that of other deployment locations. In addition, the energy efficiency levels off around the taken at 30 dBm. The reason is that the variable is contained in both the numerator and the denominator of the objective function (5). For the numerator, exists in the logarithmic function. According to the characteristics of the logarithmic function, its growth rate will gradually decline. For the denominator, its value grows linearly according to . When the growth rate of the numerator is reduced to the same rate as that of the denominator, the system energy efficiency reaches a peak, which is the inflection point in Figure 5. Then, the BS will maintain at the inflection point to avoid reducing the system’s energy efficiency. The different curves in Figure 5 have different inflection points, which are related to the RIS phase shifts and the RIS-UAV deployment location, as they together constrain to satisfy the constraint (5a). It can be seen that when = 30 dBm, all curves reach their maximum values. Therefore, in the subsequent Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, we set the value of to 30 dBm. For the random phase, the maximum energy efficiency will be higher or lower than that of the RIS-UAV at benchmark location 1 or benchmark location 2, which is due to the different RIS phase shifts. Furthermore, the effect of the RIS and AF relay in improving system energy efficiency has been compared. To make the comparison more fairly, the number of AF relay antennae is kept the same as the number of RIS reflecting elements N, and the AF relay equipped on the UAV is deployed at the same quasi-optimal location as that of the RIS-UAV. As shown in Figure 5, compared with the AF relay, the RIS has a significant improvement in energy efficiency, which can provide up to 145% energy efficiency improvement.
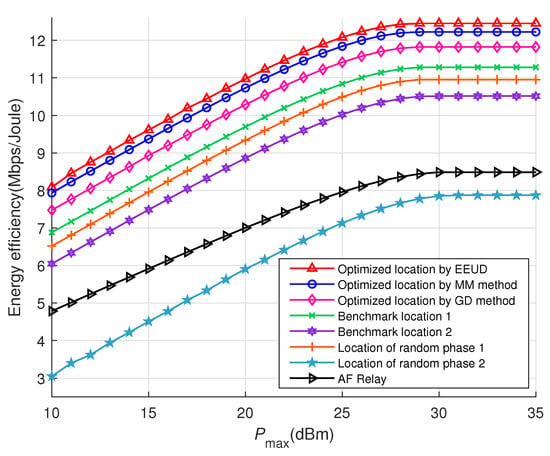
Figure 5.
Energy efficiency versus the maximum threshold for M = 8, N = 8, and K = 8. In addition, the circuit power consumption of the AF relay = 25 dBm.
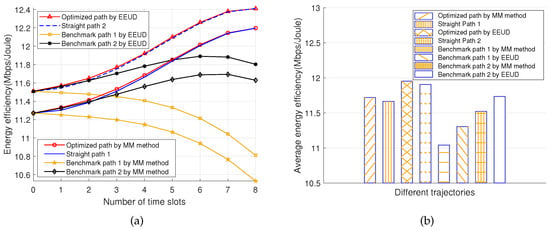
Figure 6.
System energy efficiency versus the number of time slots is shown in (a) and average energy efficiency versus different trajectories is shown in (b), where M = 8, N = 8, K = 8, and = 30 dBm.
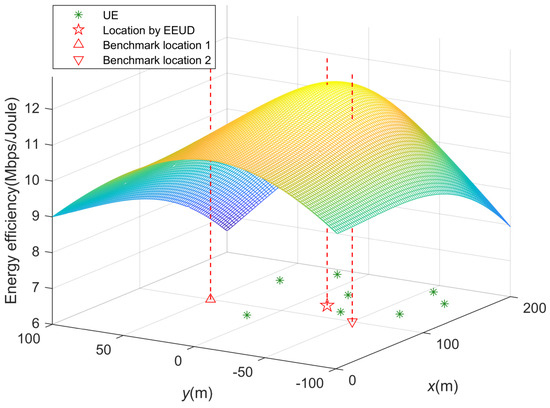
Figure 7.
System energy efficiency when the RIS-UAV is located at each point coordinate, where M = 8, N = 8, K = 8, and = 30 dBm.
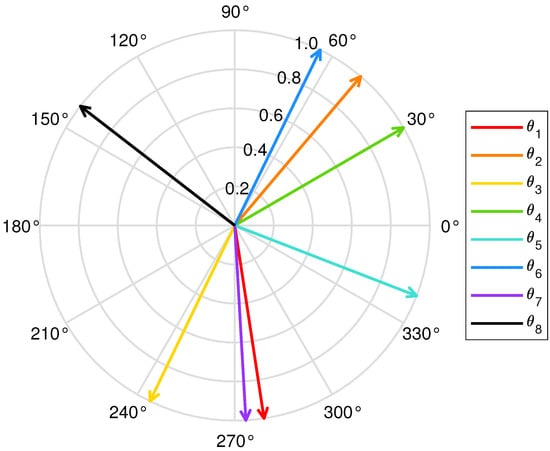
Figure 8.
Final phase distribution across the matrix of the RIS phase shifts when the RIS−UAV at the location by EEUD algorithm, where M = 8, N = 8, K = 8, and = 30 dBm.
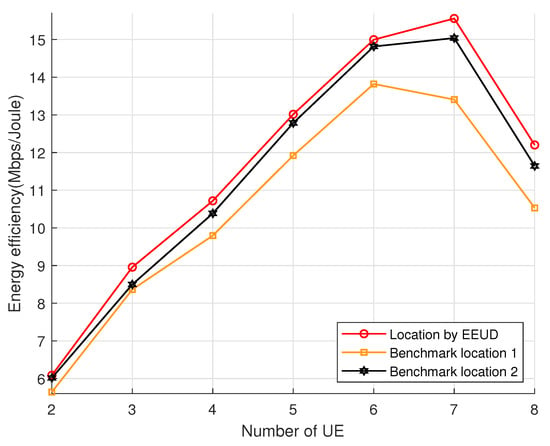
Figure 9.
Energy efficiency versus the user numbers, where M = 8, N = 8, and = 30 dBm.
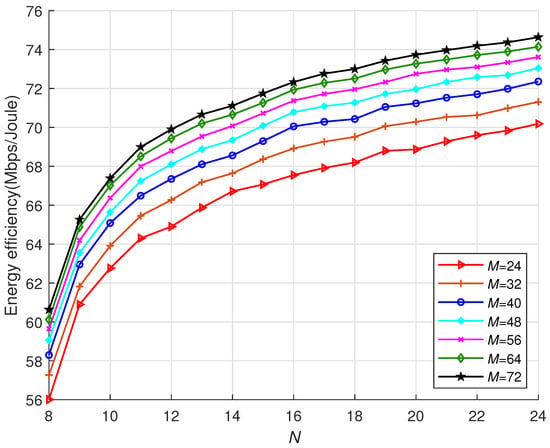
Figure 10.
Energy efficiency versus N, as well as M, where = 30 dBm.
Figure 6a characterizes the instantaneous system energy efficiency in each time slot and its average value in the full time slot when RIS-UAV follows different flight trajectories. The RIS phase shifts and BS transmit power in each time slot are optimized. For the instantaneous system energy efficiency, Figure 6a shows that when the RIS-UAV flies to the deployment location along the optimal path, the energy efficiency in each time slot is higher than that of the RIS-UAV flies along any other flight path. The reason is that the RIS-UAV follows the optimal path and can ensure high energy efficiency in each time slot. After the RIS-UAV reaches the deployment location, the optimal path and the straight path coincide, and their energy efficiency gradually becomes overlapped. For benchmark path 1, its energy efficiency rises initially and subsequently falls. The reason behind this is that the distance between the RIS-UAV and deployment location is inversely proportional to the system’s energy efficiency. Increasing the distance between the RIS-UAV and deployment location results in the decreased energy efficiency of the system. As shown in Figure 4, when the RIS-UAV flies along benchmark path 1, the distance between the RIS-UAV and deployment location first decreases and then increases. Therefore, for benchmark path 1, the system energy efficiency rises initially and subsequently falls. For benchmark path 2, the system energy efficiency keeps dropping because the RIS-UAV keeps moving far away from the deployment location during the flying path.
Moreover, the average energy efficiency of the RIS-UAV across all time slots along each flight path was calculated in Figure 6b. The average energy efficiency of the RIS-UAV flying along the optimal path is higher than that of any other path. The simulation results further verify that RIS-UAV flying to a quasi-optimal location along the optimal path is the best way to improve the system’s energy efficiency.
In order to explore the impact of different RIS-UAV deployment locations on system energy efficiency, we focus on the entire coordinate system, as shown in Figure 7. Assuming that each point coordinates on the entire coordinate system can be used as the deployment location of the RIS-UAV, and the RIS phase shifts and BS transmit power for each point coordinate are optimized to show the upper bound of the system energy efficiency. By combining the maximum energy efficiency of all the point coordinates on the whole coordinate system, a three-dimensional figure can be obtained that can visually reflect the impact of the RIS-UAV deployment location on system energy efficiency, as given in Figure 7. It is obvious that the system energy efficiency is almost the best when the RIS-UAV is at the quasi-optimal location identified found by the EEUD algorithm.
The final phase distribution across the RIS phase shifts is shown in Figure 8. As mentioned before, the RIS phase shifts are denoted by matrix , where corresponds to the phase of the n-th RIS reflecting element. The phase of each RIS reflecting element has a modulus of 1, which is determined by the characteristics of the RIS. The RIS does not change the amplitude of the reflected signal, but rather its phase shift. However, the traditional ULA RIS requires a fixed angle between each RIS reflecting element [15]. Compared with the ULA RIS, it can be clearly seen from Figure 8 that there is no linear relationship between each RIS reflecting element of the non-ULA RIS adopted in this paper, which makes the beamforming design of the RIS more flexible.
Figure 9 investigates the impact of different numbers of users on system energy efficiency, where the RIS phase shifts and BS transmit power are optimized. The RIS-UAV is deployed at the three different locations, and users are added to the system according to the coordinate in Table 4. It is obvious that the system’s energy efficiency increases with the user numbers at the beginning. However, when the user numbers further increase to a certain level, adding new users will instead reduce the system’s energy efficiency. The reason is that the system energy efficiency is the ratio of the sum rate to the total power consumption, and the growth rate of the total power consumption is faster than that of the sum rate. Adding new users will bring additional circuit power consumption to the system. When users continue to increase past the user numbers that can be accommodated by the system’s energy efficiency, it will cause a decrease in energy efficiency. In addition, compared with the quasi-optimal location, and benchmark location 2, when the RIS-UAV is deployed at benchmark location 1, the upper limit of the user number that can be accommodated by the system energy efficiency is small. The reason is that the benchmark location 1 is far away from the quasi-optimal location, resulting in large path loss during signal transmission, and the large path loss reduces the value of energy efficiency. Therefore, optimizing the deployment location of the RIS-UAV can increase the upper bound of the user numbers that the system can accommodate.
Figure 10 characterizes the effect of different numbers of BS antenna M and RIS reflecting element N on the system energy efficiency, where is 30 dBm. On the one hand, raising N improves the system energy efficiency since raising N can increase the channel numbers, and thereby improving the SNR. Nevertheless, when N continues to rise, the upward trend of the system energy efficiency begins to decelerate. The reason is that increasing SNR is nonlinear with regards to N, and the power consumption of RIS will rise with increasing N. On the other hand, when N is fixed, the increase in M can improve the system’s energy efficiency. This is because increasing M can improve the SNR. Because the increase in SNR is non-linear in relation to M, as M increases, the increasing trend of energy efficiency slows down progressively. As a result, the values of M and N should be chosen reasonably. If M or N is too large, the benefits of the system are limited and it will increase the cost and complexity of the hardware.
The convergence iterations of the EEUD algorithm are shown in Figure 11, including the number of the outer and inner layer iterations, where the inner layer refers to the RIS phase shifts optimization and the outer layer iteration executes steps 1–3 in the EEUD algorithm. It is clear that the outer layer of the EEUD algorithm converges quickly, and its improvement in system energy efficiency outperforms other solutions.
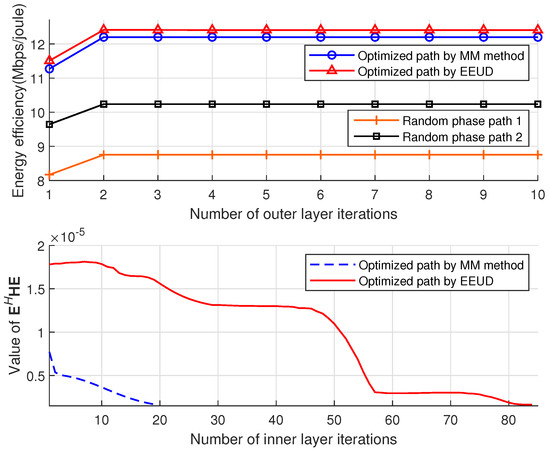
Figure 11.
Convergence analysis of the EEUD algorithms for M = 8, N = 8, K = 8, and = 30 dBm.
5. Conclusions and Future Work
In this paper, the RIS-UAV deployment location, RIS-UAV trajectory, and energy efficiency optimization in RIS-assisted multi-user air-to-ground communication system were investigated. We designed the EEUD algorithm, which jointly optimizes the RIS phase shifts, RIS-UAV trajectory, and BS transmit power to maximize the system energy efficiency. Moreover, a quasi-optimal deployment location was obtained and the trajectory to this deployment location was optimized. Based on both the theoretical and simulation results, the proposed EEUD algorithm was verified to improve the system energy efficiency, and the influence of the number of RIS reflecting elements, BS antennas, and different user numbers on energy efficiency was analyzed. Furthermore, compared to the traditional AF relay system, it was verified that the performance of an air-to-ground communication network based on RIS is more efficient. The introduction of RIS-UAV may create a new network paradigm, which brings new possibilities to the future network.
In future research, we will investigate another air-to-ground channel model, where the Rician factor R and the path loss exponent are modeled as a function of the elevation angle [31]. In addition, a new type of RIS, known as simultaneously transmitting and reflecting reconfigurable intelligent surface (STAR-RIS), and recent multiple-access technologies such as rate splitting multiple access (RSMA) and non-orthogonal multiple access (NOMA) will be considered in the future.
Author Contributions
Conceptualization, Y.Y. and K.L.; methodology, Y.Y. and K.L.; validation, Y.Y. and K.L.; formal analysis, Y.Y., K.L., S.H., X.L. and W.X.; investigation, Y.Y. and K.L.; resources, Y.Y.; writing—original draft preparation, Y.Y. and K.L.; writing—review and editing, Y.Y., K.L., S.H., X.L. and W.X.; supervision, S.H., X.L. and W.X.; project administration, Y.Y.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The works of the authors (except Wei Xiang) were funded by the Project of Cultivation for young top-notch Talents of Beijing Municipal Institutions (BPHR202203228) and Beijing Natural Science Foundation-Key project of Haidian Original Innovation Joint Fund (No. L222004).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this paper:
| 3D | 3 Dimensions |
| 6G | 6th Generation Mobile Networks |
| AF | Amplify-and-Forward |
| BS | Base Station |
| BCD | Block Coordinate Descent |
| B5G | Beyond-5th Generation Mobile Networks |
| CSI | Channel State Information |
| GD | Gradient Descent |
| EEUD | Energy-Efficient Unmanned Aerial Vehicle Deployment |
| IRS | Intelligent Reflecting Surface |
| LoS | Line-of-Sight |
| MM | Majorization-Minimization |
| NLoS | Non-Line-of-Sight |
| NOMA | Non-Orthogonal Multiple Access |
| QoS | Quality of Service |
| RSMA | Rate Splitting Multiple Access |
| RIS | Reconfigurable Intelligent Surface |
| RIS-UAV | Reconfigurable Intelligent Surface-equipped Unmanned Aerial Vehicle |
| STAR-RIS | Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surface |
| SINR | Signal-to-Interference-plus-Noise Ratio |
| SNR | Signal-to-Noise Ratio |
| ULAs | Uniform Linear Arrays |
| UAV | Unmanned Aerial Vehicle |
| UE | User Equipment |
| WPCNs | Wireless Powered Communication Networks |
References
- Bertin, E.; Crespi, N.; Magedanz, T. Future 6G Networks: Needs, Impacts, and Technologies; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2021; pp. 12–52. [Google Scholar]
- Hu, N.; Tian, Z.; Du, X.; Guizani, M. An Energy-Efficient In-Network Computing Paradigm for 6G. IEEE Trans. Green Commun. Netw. 2021, 5, 1722–1733. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards Smart and Reconfigurable Environment: Intelligent Reflecting Surface Aided Wireless Network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Kolb, J.F.; Elkashlan, M.; Chen, M.; Renzo, M.D.; Hao, Y.; Wang, J.; Swindlehurst, A.L.; et al. Reconfigurable Intelligent Surfaces for 6G Systems: Principles, Applications, and Research Directions. IEEE Commun. Mag. 2021, 59, 14–20. [Google Scholar] [CrossRef]
- Hum, S.V.; Perruisseau-Carrier, J. Reconfigurable Reflectarrays and Array Lenses for Dynamic Antenna Beam Control: A Review. IEEE Trans. Antennas Propag. 2014, 62, 183–198. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Shang, B.; Liu, L.; Ma, J.; Fan, P. Unmanned Aerial Vehicle Meets Vehicle-to-Everything in Secure Communications. IEEE Commun. Mag. 2019, 57, 98–103. [Google Scholar] [CrossRef]
- Agrawal, N.; Bansal, A.; Singh, K.; Li, C.-P. Performance Evaluation of RIS-Assisted UAV-Enabled Vehicular Communication System with Multiple Non-Identical Interferers. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9883–9894. [Google Scholar] [CrossRef]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.R.; Akyildiz, I.F. Help from the Sky: Leveraging UAVs for Disaster Management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Alsharif, M.H.; Uthansakul, P.; Solyman, A.A.A. Intelligent Reflecting Surfaces Assisted UAV Communications for Massive Networks: Current Trends, Challenges, and Research Directions. Sensors 2022, 22, 5278. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Li, P.; Meng, F.; Yu, S. Performance Analysis of RIS-Assisted UAV Communication Systems. IEEE Trans. Veh. Technol. 2022, 71, 9078–9082. [Google Scholar] [CrossRef]
- Li, J.; Liu, J. Sum Rate Maximization via Reconfigurable Intelligent Surface in UAV Communication: Phase Shift and Trajectory Optimization. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC), Chongqing, China, 9–11 September 2020; pp. 124–129. [Google Scholar]
- Zhang, X.; Zhang, H.; Du, W.; Long, K.; Nallanathan, A. IRS Empowered UAV Wireless Communication With Resource Allocation, Reflecting Design and Trajectory Optimization. IEEE Trans. Wirel. Commun. 2022, 21, 7867–7880. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Yuan, X.; Liang, Y.-C.; Di Renzo, M. Reconfigurable Intelligent Surface Assisted UAV Communication: Joint Trajectory Design and Passive Beamforming. IEEE Wirel. Commun. Lett. 2020, 9, 716–720. [Google Scholar] [CrossRef]
- Pang, X.; Zhao, N.; Tang, J.; Wu, C.; Niyato, D.; Wong, K.-K. IRS-Assisted Secure UAV Transmission via Joint Trajectory and Beamforming Design. IEEE Trans. Commun. 2022, 70, 1140–1152. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Renzo, M.D.; Tao, M.; Yuan, X. Robust Secure UAV Communications with the Aid of Reconfigurable Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2021, 20, 6402–6417. [Google Scholar] [CrossRef]
- Salem, A.A.; Ismail, M.H.; Ibrahim, A.S. Active Reconfigurable Intelligent Surface-Assisted MISO Integrated Sensing and Communication Systems for Secure Operation. IEEE Trans. Veh. Technol. 2022, in press. [CrossRef]
- Ren, H.; Zhang, Z.; Peng, Z.; Li, L.; Pan, C. Energy Minimization in RIS-Assisted UAV-Enabled Wireless Power Transfer Systems. IEEE Internet Things J. 2022, in press. [CrossRef]
- Mei, H.; Yang, K.; Shen, J.; Liu, Q. Joint Trajectory-Task-Cache Optimization with Phase-Shift Design of RIS-Assisted UAV for MEC. IEEE Wirel. Commun. Lett. 2021, 10, 1586–1590. [Google Scholar] [CrossRef]
- Cang, Y.; Chen, M.; Zhao, J.; Yang, Z.; Hu, Y.; Huang, C.; Wong, K. Joint Deployment and Resource Management for VLC-enabled RISs-assisted UAV Networks. IEEE Trans. Wirel. Commun. 2023, 22, 746–760. [Google Scholar] [CrossRef]
- Mohamed, Z.; Aissa, S. Leveraging UAVs with Intelligent Reflecting Surfaces for Energy-Efficient Communications with Cell-Edge Users. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Liu, X.; Yu, Y.; Li, F.; Durrani, T.S. Throughput Maximization for RIS-UAV Relaying Communications. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19569–19574. [Google Scholar] [CrossRef]
- Tatar Mamaghani, M.; Hong, Y. Aerial Intelligent Reflecting Surface-Enabled Terahertz Covert Communications in Beyond-5G Internet of Things. IEEE Internet Things J. 2022, 9, 19012–19033. [Google Scholar] [CrossRef]
- Long, H.; Chen, M.; Yang, Z.; Li, Z.; Shikh-Bahaei, M. Joint Trajectory and Passive Beamforming Design for Secure UAV Networks with RIS. In Proceedings of the 2020 IEEE Globecom Workshops (GC Wkshps), Virtual Event, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Yao, Y.; Lv, K.; Ma, N.; Yue, X.; Qin, X.; Yun, X. Energy efficient air-to-ground communication networks with reconfigurable intelligent surface. J. Commun. Netw. 2022, 24, 555–565. [Google Scholar] [CrossRef]
- An, J.; Xu, C.; Gan, L.; Hanzo, L. Low-Complexity Channel Estimation and Passive Beamforming for RIS-Assisted MIMO Systems Relying on Discrete Phase Shifts. IEEE Trans. Commun. 2022, 70, 1245–1260. [Google Scholar] [CrossRef]
- He, Z.-Q.; Yuan, X. Cascaded Channel Estimation for Large Intelligent Metasurface Assisted Massive MIMO. IEEE Wirel. Commun. Lett. 2020, 9, 210–214. [Google Scholar] [CrossRef]
- Dinkelbach, W. On Nonlinear Fractional Programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Azari, M.M.; Rosas, F.; Chen, K.-C.; Pollin, S. Ultra Reliable UAV Communication Using Altitude and Cooperation Diversity. IEEE Wirel. Commun. 2018, 66, 330–344. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).