Efficient Uncertainty Propagation in Model-Based Reinforcement Learning Unmanned Surface Vehicle Using Unscented Kalman Filter

Abstract

This article tackles the computational burden of propagating uncertainties in the model predictive controller-based policy of the probabilistic model-based reinforcement learning (MBRL) system for an unmanned surface vehicles system (USV). We proposed filtered probabilistic model predictive control using the unscented Kalman filter (FPMPC-UKF) that introduces the unscented Kalman filter (UKF) for a more efficient uncertainty propagation in MBRL. A USV control system based on FPMPC-UKF is developed and evaluated by position-keeping and target-reaching tasks in a real USV data-driven simulation. The experimental results demonstrate a significant superiority of the proposed method in balancing the control performance and computational burdens under different levels of disturbances compared with the related works of USV, and therefore indicate its potential in more challenging USV scenarios with limited computational resources.

1. Introduction

With the rapid development of machine learning technology in recent years, unmanned surface vehicles (USVs) are becoming more and more intelligent and have been widely deployed in various scenarios [1]. They not only improve the efficiency of the shipping industry but also alleviate the shortage of human resources. On the other hand, although USV has achieved impressive achievements in specific tasks, including position control [2,3,4,5], trajectory tracking [6,7,8,9,10,11,12], and obstacle avoidance [13,14], it is still a long-term goal in both industry and academia to develop a fully autonomous system that does not rely on human intervention and numerical models based on human prior knowledge to properly handle complex ocean disturbances  [15].

As an appealing approach to learning a fully autonomous system without human prior knowledge, reinforcement learning (RL) iteratively learns optimal and sub-optimal control policies that maximize the long-term reward function through trial-and-error interactions with unknown environments [16,17,18]. The traditional model-free RL approaches aim to directly learn the target task in the Markov decision process (MDP) without modeling the system. These methods have been extensively studied in USV simulations [19,20,21,22,23,24]. However, their implementation to the real-world USV remains limited due to the deteriorated control capability under real ocean environments, where the observation and prediction of the frequently changing disturbances are extremely difficult and expensive.

To address this issue, model-based reinforcement learning (MBRL) attempted to introduce the probabilistic model to properly process environmental disturbances as uncertainty. One of the most popular probabilistic MBRL, probabilistic inference for learning control (PILCO) [25], employs Gaussian processes (GP) [26] to model the system uncertainties as a collection of Gaussian distributions and learns its policy with a long-term propagation of uncertainties via analytic moment matching [27]. It successfully improved the control performance results under system uncertainties with great sample efficiency in robot control [28,29]. On the other hand, PILCO assumes that all disturbances are controllable and predictable in the full horizon of the rollout, which turns to a strenuous implementation of USV due to the heavy computational burden of the frequent decision making against the changing disturbances. To tackle the limitation of handling the real-time disturbances, GP-MPC integrates PILCO and model predictive control (MPC) in  [30]. This work optimizes its policy with an expanded dimensionality for a deterministic dynamical system with Lagrange parameters and state constraints under Pontryagin’s maximum principle (PMP), which resulted in heavy computational cost and therefore limited its application on simulated cart-pole and double pendulum tasks. Based on this work, probabilistic model predictive control (SPMPC) [31] is developed for better efficiency without expanded dynamics and PMP constraint. It is successfully implemented to USV with detailed evaluation in the real ocean environment. Its control capability is further improved in filtered probabilistic model predictive control (FPMPC) [32], where the state space is implicitly extended from MDP to partially observed MDP (POMDP). Although these works have demonstrated a great potential of probabilistic MBRL as a novel direction toward the fully autonomous USV, they are still limited by the bottleneck of computational complexity and are difficult to be widely applied in practice. The non-parametric characteristic of GP turned to a rapidly increasing computational burden with the expanding data size. It results in a difficult trade-off between the model expressiveness of GP and the control frequency of MPC based on long-term uncertainty propagation, especially with the limited computational resource on USV. Employing sparse GP [33] to balance the control performance and the computational complexity, the real-world USV in [31] was only controlled at $0.33$ Hz, which is insufficient for more challenging scenarios.

To tackle the computational efficiency issue of the uncertainty propagation of GP, unscented Kalman filter (UKF) [34,35] estimates the target distribution by the weighted $\sigma$ sampling rather than integrating the GP model over a Gaussian distribution input and therefore becomes an alternative solution besides analytic moment matching [27]. It achieved a superior computational efficiency from an engineering perspective in various applications of unmanned ground vehicles (UGVs) and unmanned aerial vehicles (UAVs) [36,37,38,39]. In the field of USV, UKF has been employed for the neural network controller [40] and model parameters estimation [41]. Despite successful applications of UKF in engineering, less work focused on using its efficient uncertainty propagation under RL’s trial-and-error framework. This prevents the engineering implementation of UKF when the human’s prior knowledge is unavailable.

In this work, we address the computational efficiency of uncertainty propagation in GP-based MBRL USV. Extending UKF to the MBRL system specific for USV, filtered probabilistic model predictive control with unscented Kalman filter (FPMPC-UKF) is proposed to alleviate the computational burden of GP uncertainty propagation, especially under larger sparse scales, i.e., the GP model is approximated by less sparse pseudo input. With the evaluation in position-keeping and target-reaching tasks on the simulation based on the real boat-driven data [31] under different ocean conditions, the proposed FPMPC-UKF demonstrated a significant superiority of the proposed method in the balance between the control capability and the computational cost compared with the related MBRL USV approach [32]. With a proper setting of the GP sparse pseudo input, it improved $20\%$ to $28\%$ computational efficiency while achieving $15\%$ to $29\%$ better control performance. Based on the relationship between the proposed method and other related approaches summarized in

Table 1. Relationship between the proposed approach and other related works, ◯ and × denote involve and uninvolved.

Approach	Uncertainty Propagation	MBRL	MPC	USV
PILCO [25]	analytic moment-matching	◯	×	×
GP-MPC [30]	analytic moment-matching	◯	◯	×
SPMPC [31], FPMPC [32]	analytic moment-matching	◯	◯	◯
RC-LB-NMPC [36]	UKF	×	◯	×
RBFNN-UKF [40]	UKF	×	×	×
FPMPC-UKF (proposed)	UKF	◯	◯	◯

, the contributions of this work are summarized as follows:

1.

Algorithmically, the proposed FPMPC-UKF first attempts to extend the potential of UKF uncertainty propagation to the GP-based MBRL. It not only contributes to a more effective solution to trade off the control performance and computational burden compared with the existing approaches with MPC-based policy [30,31,32] but also demonstrates the broad prospects of traditional optimal filtering methods in enhancing related MBRL approaches based on different prediction horizons [25] in more challenging control tasks.

2.

On the side of traditional optimal filtering technologies, this work can be seen as extending the current state-of-the-art optimal filtering implementations in unmanned systems [36,37,38,39] to the trial-and-error RL framework. It expanded the usage of optimal filters in unmanned systems by adaptively obtaining an efficient filter to propagate system uncertainties without human prior knowledge of the target model.

3.

On the side of the application of MBRL, a USV control system based on FPMPC-UKF was developed. We investigated the effect of sparse GP scales on both control capability and model prediction error in position-keeping and target-reaching tasks under different levels of disturbances. The proposed method significantly outperformed existing MBRL systems specific to USV [31,32] with over $15\%$ less offset while reducing more than $20\%$ computational burden. It enabled the higher control frequency in the existing work without damaging control performance and therefore expanded the practicability of probabilistic MBRL in the USV domain.

The remainder of this paper is organized as follows. The USV control problem and MBRL settings are introduced in Section 2. Section 3 explains the proposed FPMPC-UFK and the corresponding USV control system. The experimental results are demonstrated in Section 4. Section 5 presents the conclusions.

2. Preliminaries

2.1. Markov Decision Process of USV

The target USV dynamics is described in the bottom of Figure 1. The USV observation states include its position in GPS $(X_{\mathrm{usv}},Y_{\mathrm{usv}})$, orientation ${\mathrm{\Psi }}_{\mathrm{usv}}$, velocity $V_{\mathrm{usv}}$, the engine throttle ${\tau }_{\mathrm{usv}}$ and rudder angle ${\delta }_{\mathrm{usv}}$. The wind is defined as the observable disturbances in this study with direction ${\mathrm{\Psi }}_{\mathrm{wind}}$ and velocity $V_{\mathrm{wind}}$, while other disturbances, such as current, are considered unknown noises. The USV control problem is described as the Markov decision process (MDP) in the RL domain [16] with state space $\mathcal{S}$, action space $\mathcal{A}$ and reward function $\mathcal{R}$. The state vector is defined as $\mathit{x}=[X_{\mathrm{usv}},Y_{\mathrm{usv}},{\mathrm{\Psi }}_{\mathrm{usv}},V_{\mathrm{usv}},{\tau }_{\mathrm{usv}},{\delta }_{\mathrm{usv}},V_{\mathrm{wind}}·cos\left({\mathrm{\Psi }}_{\mathrm{wind}}\right),V_{\mathrm{wind}}·sin\left({\mathrm{\Psi }}_{\mathrm{wind}}\right)]$ in $\mathcal{S}$. The control signals to engine throttle and rudder angle are defined as a vector $\mathit{u}=[{\tau }_{\mathrm{action}},{\delta }_{\mathrm{action}}]$ in $\mathcal{A}$. Please note that the throttle and rudder signals ${\tau }_{\mathrm{usv}},{\delta }_{\mathrm{usv}}$ are the current states read from sensors, which are different from the current command sending to the throttle and rudder $[{\tau }_{\mathrm{action}},{\delta }_{\mathrm{action}}]$. A reward function $\mathcal{R}(\mathit{x},\mathit{u})$ is designed to evaluate the performance of USV in the target task.

2.2. Model-Based Reinforcement Learning

The goal of MBRL is to iteratively learn a policy $\pi :{\mathit{x}}_t\to {\mathit{u}}_t$ that maximizes the reward function in the long term by not only interacting with the environment but also approximating the following system transition model at time step t:

$$\begin{array}{c}\begin{array}{c}\hfill {\mathit{x}}_{t+1}=\widehat{f}({\mathit{x}}_t,{\mathit{u}}_t)+\mathit{w}\end{array}\end{array}$$

(1)

where $\mathit{w}$ represents the model error. Define a data set $\mathcal{D}$ to store the exploration sample for updating the policy and system model, and the interaction process of MBRL can be generalized as a loop: (1) execute control signals via the current policy ${\mathit{u}}_t^{*}\sim \pi \left({\mathit{x}}_t\right)$; (2) get the state in the next step ${\mathit{x}}_{t+1}$ and expand data set; and (3) move to the next step $t=t+1$, then return to 1.

As one appealing solution for alleviating the impact of complex and frequently changing disturbances, the MPC controller is widely utilized in several engineering MBRL systems [30,31,32]. At time step t, it plans a trajectory of control signals from the current state ${\mathit{x}}_t$ to maximize the expected long-term reward over a pre-defined horizon H:

$$\begin{array}{c}\begin{array}{cc}\hfill [{\mathit{u}}_t^{*},...,{\mathit{u}}_{t+H-1}^{*}]& =\underset{\begin{array}{c}{\mathit{u}}_t,...,{\mathit{u}}_{t+H-1}\end{array}}{arg\; max}\sum _{s=0}^{H-1}\mathcal{R}({\mathit{x}}_{t+s+1},{\mathit{u}}_{t+s}).\hfill \\ \hfill \mathrm{s}.\mathrm{t}.{\mathit{x}}_{t+s+1}& =\widehat{f}({\mathit{x}}_{t+s},{\mathit{u}}_{t+s})+\mathit{w}\hfill \\ \hfill {\mathit{x}}_{t+s+1}& \in \mathcal{S},{\mathit{u}}_{t+s}\in \mathcal{A}.\hfill \end{array}\end{array}$$

(2)

The nonlinear optimization approaches are applied to search for the optimal action sequence based on the approximated system model $\widehat{f}(·)$.

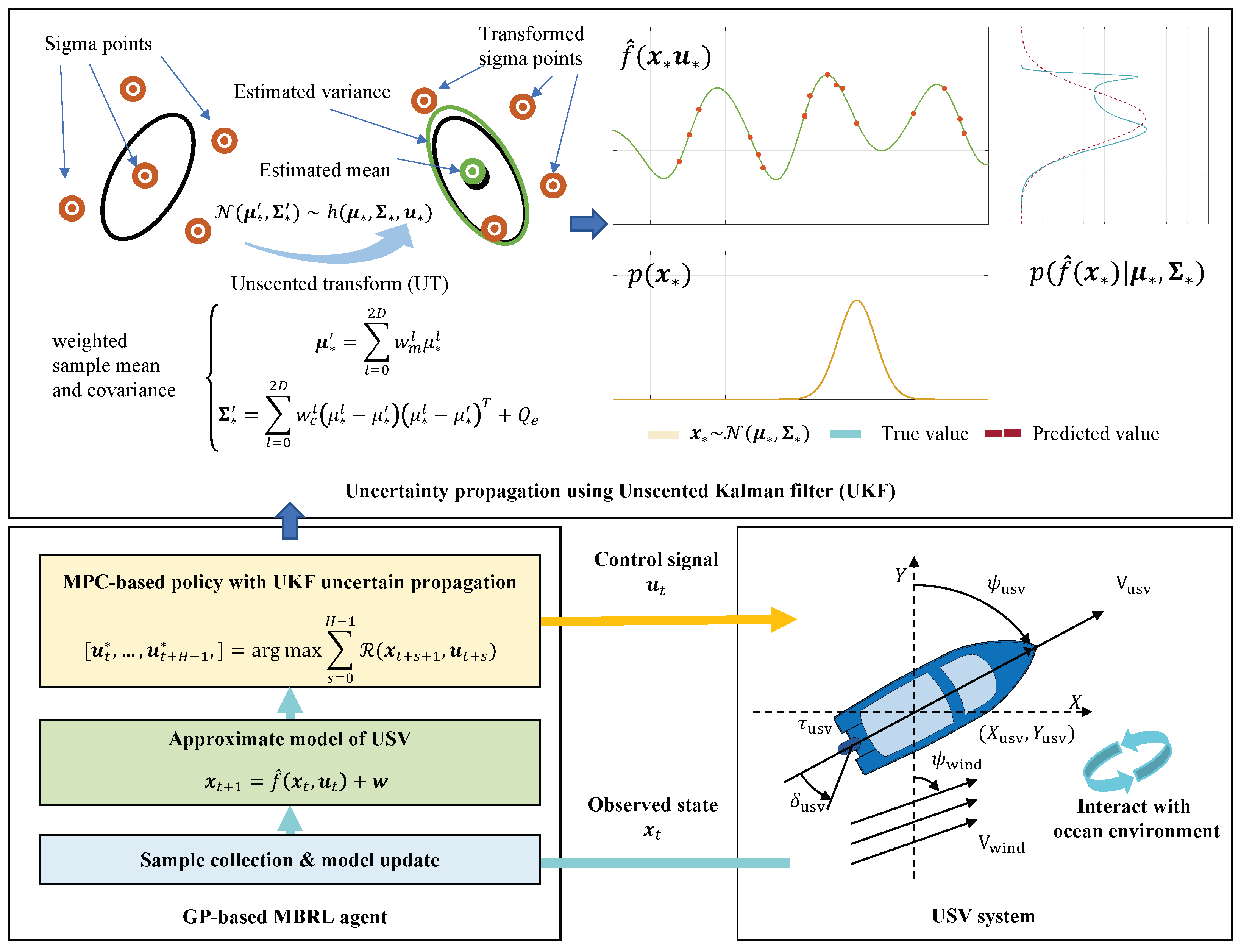
3. Approach

3.1. Probabilistic Model of USV

In this work, GP [26] is utilized to model the USV dynamics under a noisy environment in a probabilistic perspective. For each dimension of the state vector $a=1,...,D$, the approximated GP model of the target USV is as follows:

$$\begin{array}{c}\begin{array}{c}\hfill {\mathit{y}}_{a,t+1}={\widehat{f}}_a\left({\tilde{\mathit{x}}}_t\right)+w_a\end{array}\end{array}$$

(3)

where ${\tilde{\mathit{x}}}_t:=({\mathit{x}}_t,{\mathit{u}}_t)$ combines state and action vectors, and the unobservable noises in this dimension are simplified as one Gaussian noise $w_a\sim \mathcal{N}(0,{\sigma }_{w_a}^2)$. Since there is no assumption that the USV state must be fully observable or predicted, the output vector of model ${\mathit{y}}_{t+1}$ is defined by elements $X_{\mathrm{usv}},Y_{\mathrm{usv}},{\mathrm{\Psi }}_{\mathrm{usv}},V_{\mathrm{usv}},{\tau }_{\mathrm{usv}},{\delta }_{\mathrm{usv}}$ without unpredictable wind information. As a general model of USV, it is also free to expand the observable states with pitch, yaw, roll and wave information using the specific sensors or remove any state that cannot be easily accessed due to the limited hardware. In this work, the observable states of USV are defined following the existing work [31], which has been implemented in real-ocean boat with relatively limited observation states.

Let ${\tilde{\Lambda }}_a$ and ${\alpha }_{{\widehat{f}}_a}^2$ denote a diagonal matrix of squared characteristic length-scales and the noise variances of the target system, then the measurement of the distance of any two inputs $k_a({\tilde{\mathit{x}}}_i,{\tilde{\mathit{x}}}_j)$ is achieved by the squared exponential (SE) kernel function

$$\begin{array}{c}\begin{array}{c}\hfill k_a({\tilde{\mathit{x}}}_i,{\tilde{\mathit{x}}}_j)={\alpha }_{f_a}^2{e}^{\left(-\frac{{({\tilde{\mathit{x}}}_i-{\tilde{\mathit{x}}}_j)}^T{\tilde{\Lambda }}_a^{-1}({\tilde{\mathit{x}}}_i-{\tilde{\mathit{x}}}_j)}{2}\right)}.\end{array}\end{array}$$

(4)

Although the SE kernel is selected based on related works [30,31,32], it is also valuable and possible to investigate the power of other kernel functions [26] in modeling USV for challenging control tasks. We leave this issue as our future work.

Define the kernel function of one input ${\tilde{\mathit{x}}}_{*}$ as $k_{a**}=k_a({\tilde{\mathit{x}}}_{*},{\tilde{\mathit{x}}}_{*})$, the distance measurement of ${\tilde{\mathit{x}}}_{*}$ over the whole sample set as ${\mathit{k}}_{a*}=k_a(\tilde{\mathit{X}},{\tilde{\mathit{x}}}_{*})$, and the kernel matrix ${\mathit{K}}_a$ with $K_{a,i,j}=k_a\left({\tilde{\mathit{x}}}_i\right)$ as the distance measurement of each sample in the whole set. Setting ${\mathit{\beta }}_a={({\mathit{K}}_a+{\sigma }_{w_a}^2\mathit{I})}^{-1}{\mathit{Y}}_a$ as the irrelevant term to the input, its prediction is determined by the posterior mean $m_{{\widehat{f}}_a}\left({\tilde{\mathit{x}}}_{*}\right)$ and the corresponding variance ${\sigma }_{{\widehat{f}}_a}^2\left({\tilde{\mathit{x}}}_{*}\right)$:

$$\begin{array}{c}\begin{array}{c}\hfill m_{{\widehat{f}}_a}\left({\tilde{\mathit{x}}}_{*}\right):=\mathbb{E}\left[{\widehat{f}}_a\left({\tilde{\mathit{x}}}_{*}\right)\right|\tilde{\mathit{X}},{\mathit{Y}}_a]={\mathit{k}}_{a*}^T{({\mathit{K}}_a+{\sigma }_{w_a}^2\mathit{I})}^{-1}{\mathit{Y}}_a={\mathit{k}}_{a*}^T{\mathit{\beta }}_a,\end{array}\end{array}$$

(5)

$$\begin{array}{c}\begin{array}{c}\hfill {\sigma }_{{\widehat{f}}_a}^2\left({\tilde{\mathit{x}}}_{*}\right):=\mathrm{var}\left[{\widehat{f}}_a\left({\tilde{\mathit{x}}}_{*}\right)\right|\tilde{\mathit{X}},{\mathit{Y}}_a]=k_{a**}-{\mathit{k}}_{a*}^T{({\mathit{K}}_a+{\sigma }_{w_a}^2\mathit{I})}^{-1}{\mathit{k}}_{a*}.\end{array}\end{array}$$

(6)

Given a training data set $\tilde{\mathit{X}},\mathit{Y}$, the GP model’s hyper-parameters ${\alpha }_{f_a}^2,{\Lambda }_a,{\sigma }_{w_a}^2$ for each output dimension are determined by maximizing the log marginal likelihood via evidence maximization [26], which is called the training of the GP model:

$$\begin{array}{c}\begin{array}{cc}\hfill [{\tilde{\Lambda }}_a^{*},{\alpha }_{{\widehat{f}}_a}^{*},{\sigma }_{w_a}^{*}]& =arg\; maxlogp\left({\mathit{Y}}_a\right|\tilde{\mathit{X}},{\tilde{\Lambda }}_a,{\alpha }_{{\widehat{f}}_a},{\sigma }_{w_a})\hfill \\ \hfill p\left({\mathit{Y}}_a\right|\tilde{\mathit{X}},{\tilde{\Lambda }}_a,{\alpha }_{{\widehat{f}}_a},{\sigma }_{w_a})& =log\int p\left({\mathit{Y}}_a\right|{\widehat{f}}_a,\tilde{\mathit{X}},{\tilde{\Lambda }}_a,{\alpha }_{{\widehat{f}}_a},{\sigma }_{w_a})p\left({\widehat{f}}_a\right|\tilde{\mathit{X}},{\tilde{\Lambda }}_a,{\alpha }_{{\widehat{f}}_a},{\sigma }_{w_a})\mathrm{d}{\widehat{f}}_a\hfill \\ & =-\frac{1}{2}{\mathit{Y}}_a^T{({\mathit{K}}_a+{\sigma }_{w_a}^2\mathit{I})}^{-1}{\mathit{Y}}_a-\frac{1}{2}log|{\mathit{K}}_a+{\sigma }_{w_a}^2\mathit{I}|-\frac{D}{2}log\left(2\pi \right).\hfill \end{array}\end{array}$$

(7)

3.2. Uncertainty Propagation Using Unscented Kalman Filter

One core characteristic of existing probabilistic MBRL approaches, such as PILCO [25] and GP-MPC [30], is the characteristic of propagating the uncertainty predicted by GP in their policy. They employed analytic moment matching [27], which propagates the uncertainty by integrating the GP model over the Gaussian distribution input $p\left({\tilde{\mathit{x}}}_{*}\right)\sim \mathcal{N}({\tilde{\mathit{\mu }}}_{*},{\tilde{\Sigma }}_{*})$ rather than the deterministic state ${\mathit{x}}_{*}$:

$$\begin{array}{c}\begin{array}{c}\hfill p\left(\widehat{f}\left({\tilde{\mathit{x}}}_{*}\right)\right|{\tilde{\mathit{\mu }}}_{*},{\tilde{\Sigma }}_{*})=\int p\left(\widehat{f}\left({\tilde{\mathit{x}}}_{*}\right)|{\tilde{\mathit{x}}}_{*}\right)p\left({\tilde{\mathit{x}}}_{*}\right)\mathrm{d}{\tilde{\mathit{x}}}_{*},p\left({\tilde{\mathit{x}}}_{*}\right)\sim \mathcal{N}({\tilde{\mathit{\mu }}}_{*},{\tilde{\Sigma }}_{*}).\end{array}\end{array}$$

(8)

Since the resulting distribution is non-Gaussian without an analytical solution [25], it is estimated by a Gaussian distribution in analytic moment matching [27]:

$$\begin{array}{c}\begin{array}{cc}\hfill [{\mathit{\mu }}_{*}^{\prime },{\Sigma }_{*}^{\prime }]& =h({\mathit{\mu }}_{*},{\Sigma }_{*},{\mathit{u}}_{*})\hfill \\ \hfill \mathcal{N}({\mathit{\mu }}_{*}^{\prime },{\Sigma }_{*}^{\prime })& \approx \int p\left(\widehat{f}({\mathit{x}}_{*},{\mathit{u}}_{*})|{\mathit{x}}_{*},{\mathit{u}}_{*}\right)p\left({\mathit{x}}_{*}\right)\mathrm{d}{\mathit{x}}_{*}.\hfill \end{array}\end{array}$$

(9)

Although Equation (9) successfully captured uncertainties in various MBRL applications from the toy pendulum simulator to UGV and USV, it resulted in a heavy computational burden due to the frequent inversions of the kernel matrix over the full data set [31,42].

In this paper, we propose FPMPC-UKF to utilize UKF [34,35] to alleviate the computational burden of the uncertainty propagation of GP from an engineering perspective. Assuming the GP model’s input follows D-dimensional Gaussian distribution $p\left({\mathit{x}}_{*}\right)\sim \mathcal{N}({\mathit{\mu }}_{*},{\Sigma }_{*})$, where the action ${\mathit{u}}_{*}$ is deterministic following the setting of [31], SSUFK-MPC employs unscented transform (UT) to approximate the mean and variance of the target distribution by $2D+1$ sigma points, where D is the dimension of the GP input as demonstrated on the top of Figure 1. The first point is initialized as the current input mean ${\mathit{\chi }}_{*}^0={\mathit{\mu }}_{*}$. Other $2D$ points are selected by

$$\begin{array}{c}\begin{array}{c}\hfill {\mathit{\chi }}_{*}^l=\left\{\begin{array}{cc}\hfill {\mathit{\mu }}_{*}+{\left(\sqrt{(D+\lambda ){\Sigma }_{*}}\right)}_l& ,l=1,2,\dots ,D,\hfill \\ \hfill {\mathit{\mu }}_{*}-{\left(\sqrt{(D+\lambda ){\Sigma }_{*}}\right)}_l& ,l=D+1,D+2,\dots ,2D\hfill \end{array}\right.\end{array}\end{array}$$

(10)

where $\lambda ={\alpha }^2(D+\kappa )-N$ is the scale factor for reducing the prediction error. We set $\alpha =1$ for a common distribution of sigma points. $\kappa$ is set to 1 for the positive semi-definite of UKF. Calculating the GP prediction over these points,

$$\begin{array}{c}\begin{array}{c}\hfill {\mathit{\mu }}_{*}^l=m_{f_a}({\mathit{\chi }}_{*}^l,{\mathit{u}}_{*}),l=0,1,\dots ,2D.\end{array}\end{array}$$

(11)

The integration in Equation (9) can be approximated by $2D+1$ sigma points as follows:

$$\begin{array}{c}\begin{array}{cc}\hfill {\mathit{\mu }}_{*}^{\prime }& =\sum _{l=0}^{2D}{w}_m^l{\mathit{\mu }}_{*}^l,\hfill \\ \hfill {\Sigma }_{*}^{\prime }& =\sum _{l=0}^{2D}{w}_c^l\left({\mathit{\mu }}_{*}^l-{\mathit{\mu }}_{*}^{\prime }\right){\left({\mathit{\mu }}_{*}^l-{\mathit{\mu }}_{*}^{\prime }\right)}^T+Q_e\hfill \end{array}\end{array}$$

(12)

where $Q_e={10}^{-4}$ is an additional noise of variance for better robustness, and the weights of both predicting mean $w_m^l$ and variance $w_c^l$ for all $2D+1$ sigma points are calculated as

$$\begin{array}{c}\begin{array}{c}\hfill w_m^l=\left\{\begin{array}{cc}& \frac{\lambda }{D+\lambda },l=0,\hfill \\ & \frac{1}{2(D+\lambda )},l=1,\dots ,2D.\hfill \end{array}\right.\end{array}\end{array}$$

(13)

$$\begin{array}{c}\begin{array}{c}\hfill w_c^l=\left\{\begin{array}{cc}& \frac{\lambda }{D+\lambda }+\left(1-{\alpha }^2+\beta \right),l=0,\hfill \\ & \frac{1}{2(D+\lambda )},l=1,\dots ,2D\hfill \end{array}\right.\end{array}\end{array}$$

(14)

where $\beta =2$ is the weight coefficient.

According to [42], the computational complexity of analytic moment matching is $\mathcal{O}\left(D^3{M}^2\right)$, where D is the dimension number of the GP model, and M is the number of samples or sparse pseudo inputs. As a comparison, GP-based UKF achieved $\mathcal{O}\left(N^2{M}^2\right)$ in uncertainty propagation, which outperformed analytic moment matching, especially with large M. Despite the prediction error caused by the limited sampling of UKF, its superior computational efficiency resulted in wide engineering implementations [36,37,38,39]. With the equations above, we could efficiently calculate Equation (9) and employ it in the H steps prediction of Equation (2) to properly consider the propagated uncertainties in the MPC-based policy.

3.3. Filtered Probabilistic Model Predictive Control Using UKF

We detailed the workflow of the proposed method FPMPC-UKF for the USV control task in this subsection. Following the existing GP-based MBRL USV control system [31,32], the sample set $\mathcal{D}=(\tilde{X},Y)$, where $\tilde{X}$ collects the state and action $\mathit{x},\mathit{u}$ at the current time step t, $\tilde{Y}$ contains the controllable state $\mathit{x}=[X_{\mathrm{usv}},Y_{\mathrm{usv}},{\mathrm{\Psi }}_{\mathrm{usv}},V_{\mathrm{usv}},{\tau }_{\mathrm{usv}},{\delta }_{\mathrm{usv}}]$ in the next step $t+1$. The corresponding learning loop is shown in Algorithm 1. At the beginning, the GP model of USV was initially trained by a pre-prepared sample set $\mathcal{D}=(\tilde{X},Y)$ (usually generalized by random policy or human driver). The MBRL is updated in the $N_{trial}$ rollout during the learning. At the start of each rollout, the USV is reset to its initial state with $X_{\mathrm{usv}}=0,Y_{\mathrm{usv}}=0,{\mathrm{\Psi }}_{\mathrm{usv}}=0,V_{\mathrm{usv}}=0$. The initial observation at this moment was recorded as ${\mathit{\mu }}_{0|0}$ with an initial variance ${\Sigma }_{0|0}$, an empty control action that would be executed in the first step is set as ${\mathit{u}}_0^{*}=[0,0]$.

Algorithm 1:Learning loop of FPMPC-UKF USV control system

Following GPMPC [31] and FPMPC [32], the proposed method employs a double-prediction process by two separate CPU cores for swift control against the frequently changing environmental disturbances. At time step $t=1,...,L_{\mathrm{rollout}}$, two CPU parallelly worked. The first CPU core operated the pre-prepared control signal ${\mathit{u}}_{t-1}^{*}$ and stored the currently observed state ${\mathit{x}}_t^o$ to buffer. During the same period, the second CPU core first applied a Bayesian filter when $t>1$ for superior robustness under complex environmental disturbances [32]. Given the previous state and control signal $[{\mathit{\mu }}_{t-2|t-2},{\Sigma }_{t-2|t-2},{\mathit{u}}_{t-2}^{*}]$ at step $t-2$, the belief of the next step prediction was calculated by one-step prediction of Equations (11) and (12):

$$\begin{array}{c}\begin{array}{c}\hfill [{\mathit{\mu }}_{t-1|t-2},{\Sigma }_{t-1|t-2}]=h({\mathit{\mu }}_{t-2|t-2},{\Sigma }_{t-2|t-2},{\mathit{u}}_{t-2}^{*}).\end{array}\end{array}$$

(15)

Defining ${\mathit{y}}_{t-1}$ as the real observation ${\mathit{x}}_{t-1}^o$ without unpredictable information, such as wind, and ${\Sigma }_y$ as a constant observation variance, a Kalman filter based on the predicted belief was applied to estimate the posterior belief of the prediction with weights ${\mathit{W}}_f$ and ${\mathit{W}}_o$:

$$\begin{array}{c}\begin{array}{cc}\hfill {\mathit{\mu }}_{t-1|t-1}& ={\mathit{W}}_f{\mathit{\mu }}_{t-1|t-2}+{\mathit{W}}_o{\mathit{y}}_{t-1},\hfill \\ \hfill {\Sigma }_{t-1|t-1}& ={\mathit{W}}_f{\Sigma }_{t-1|t-2},\hfill \\ \hfill {\mathit{W}}_f& ={\Sigma }_y{({\Sigma }_{t-1|t-2}+{\Sigma }_y)}^{-1},\hfill \\ \hfill {\mathit{W}}_o& ={\Sigma }_{t-1|t-2}{({\Sigma }_{t-1|t-2}+{\Sigma }_y)}^{-1}.\hfill \end{array}\end{array}$$

(16)

Based on the posterior belief, which was reported as a more robust and accurate representation of the state in noisy environments [32] and previous control signal ${\mathit{u}}_{t-1}^{*}$, the USV state after executing the ${\mathit{u}}_{t-1}^{*}$ was estimated to compensate for the potential bias caused by the current action:

$$\begin{array}{c}\begin{array}{c}\hfill [{\widehat{\mathit{\mu }}}_t,{\widehat{\Sigma }}_t]=h({\mathit{\mu }}_{t-1|t-1},{\Sigma }_{t-1|t-1},{\mathit{u}}_{t-1}^{*})\end{array}\end{array}$$

(17)

which was achieved by one-step uncertainty propagation using UFK. The calculated state $[{\widehat{\mathit{\mu }}}_t,{\widehat{\Sigma }}_t]$ was set as the input state of searching the optimal actions of horizon H$[{\mathit{u}}_t^{*},...,{\mathit{u}}_{t+H-1}^{*}]$ following Equation (2). The first action ${\mathit{u}}_t^{*}$ is executed by the first CPU core in the next step. After each step, the sample set was expanded by $\tilde{\mathit{X}}=\{\tilde{\mathit{X}},({\mathit{x}}_{t-1}^o,{\mathit{u}}_{t-1}^{*})\},\mathit{Y}=\{\mathit{Y},{\mathit{y}}_t\}$, which is used for iteratively updating the GP model of USV at the end of each rollout.

4. Experimental Results

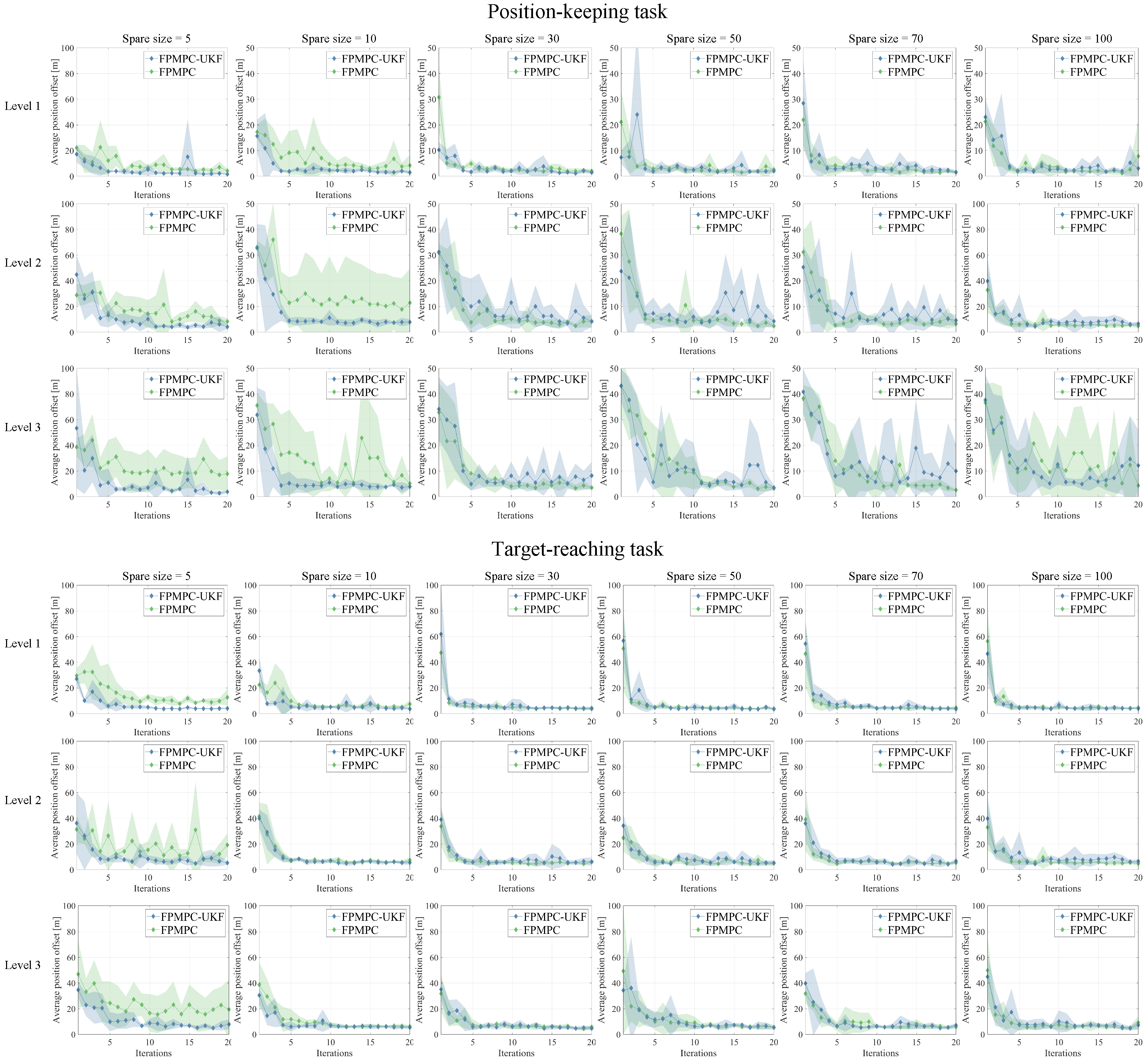
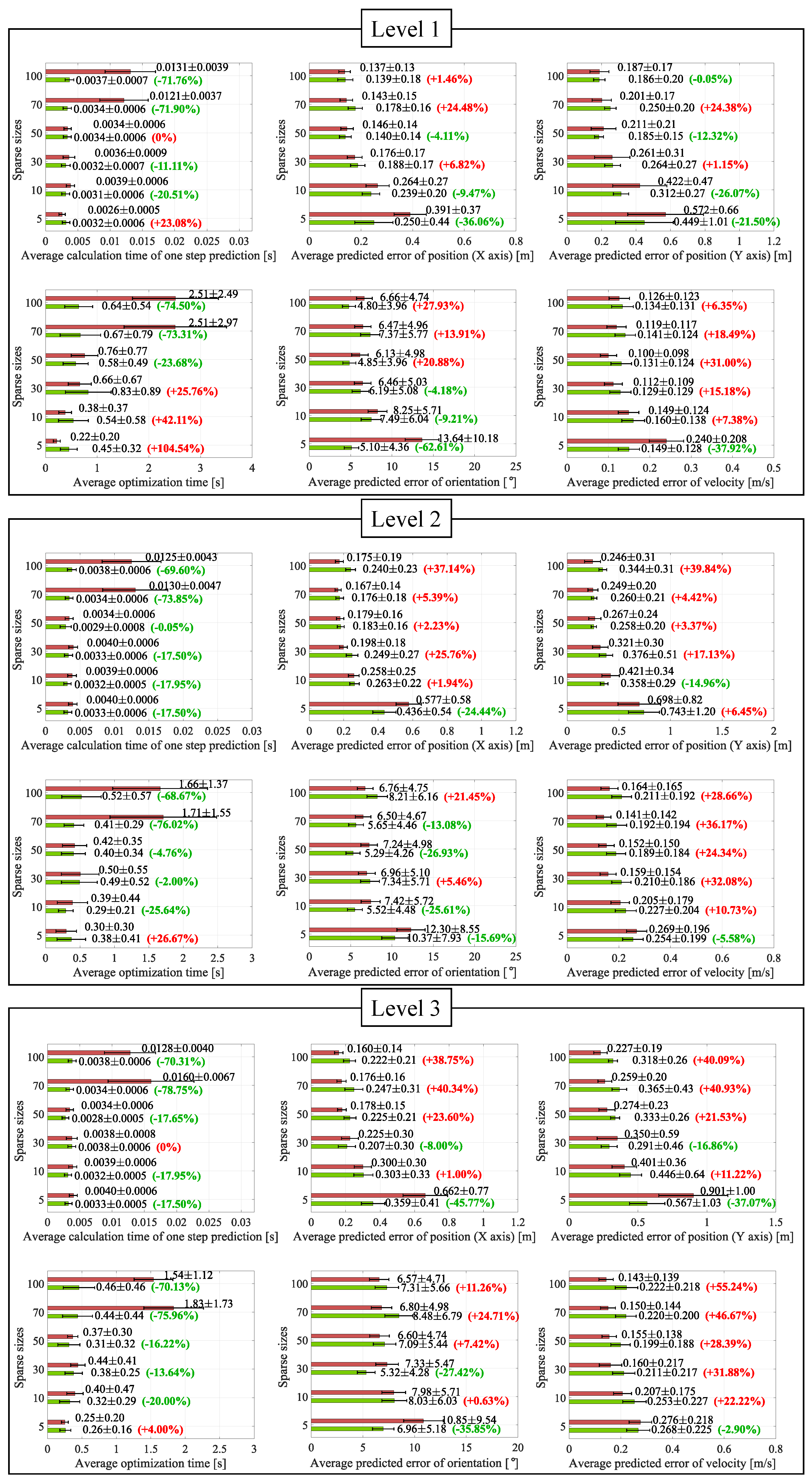
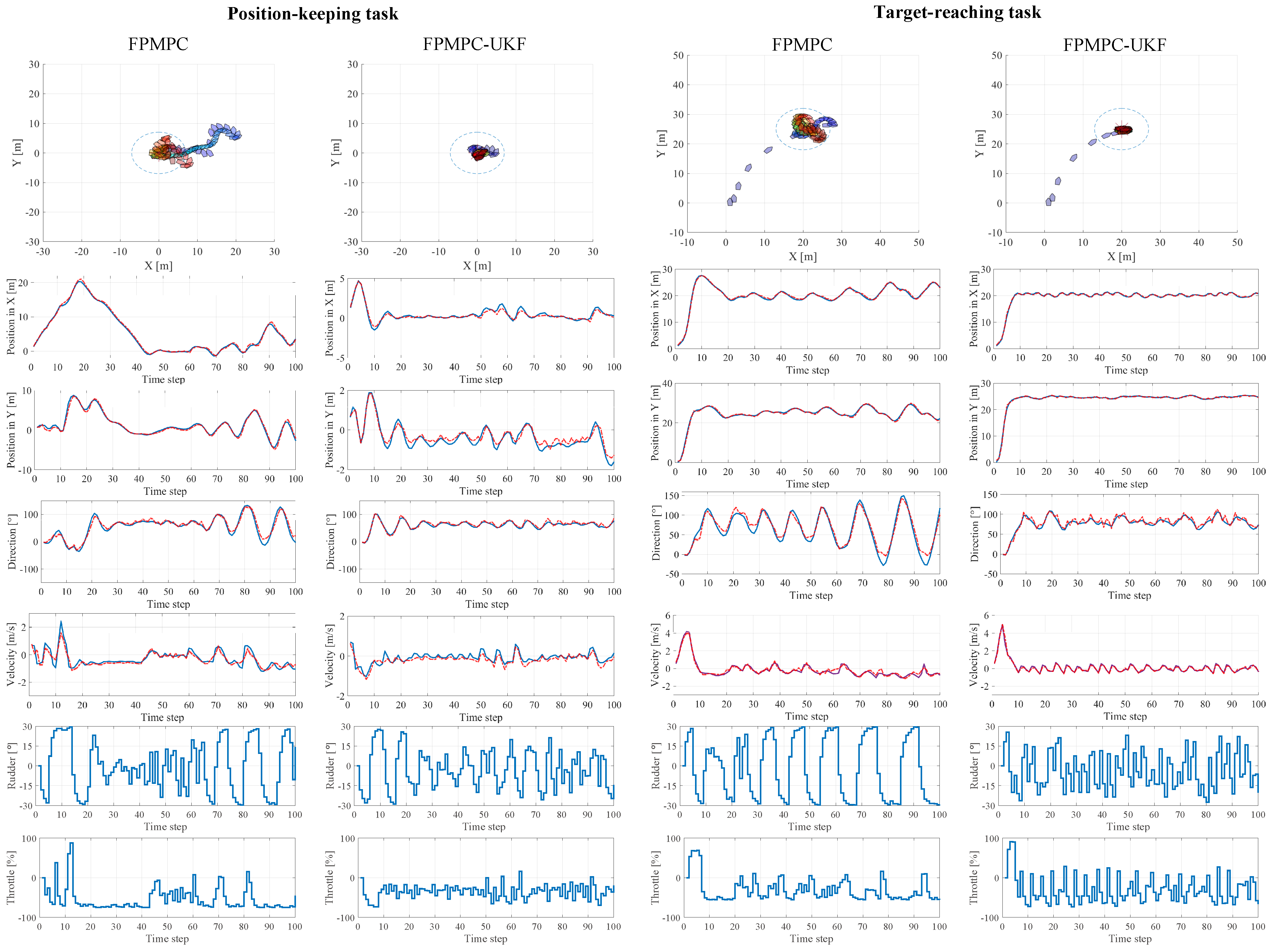
4.1. Simulation Settings

The proposed FPMPC-UKF was evaluated by the USV simulation developed based on the real boat-driven data under different ocean condition in [31], whose appendix detailed the parameters of dynamics. Three levels of disturbances, including observable wind (angle ${\psi }_{\mathrm{wind}}$ and velocity $v_{\mathrm{wind}}$) and unobservable current (angle ${\psi }_{\mathrm{current}}$ and velocity $v_{\mathrm{current}}$), were set to simulate increasing challenging ocean environments following the simulation settings in [31]:

∗

Level 1, $\left({\psi }_{\mathrm{wind}}\right)={37}^{\circ }+U{(-30,30)}^{\circ }$, ${\psi }_{\mathrm{current}}={100}^{\circ }+U{(-30,30)}^{\circ }$, $v_{\mathrm{wind}}=2.0+U(0,0.1)$ m/s, $v_{\mathrm{current}}=0.25+U(0,0.1)$ m/s,

∗

Level 2, ${\psi }_{\mathrm{wind}}={37}^{\circ }+U{(-30,30)}^{\circ }$, ${\psi }_{\mathrm{current}}={100}^{\circ }+U{(-30,30)}^{\circ }$, $v_{\mathrm{wind}}=4.0+U(0,0.1)$ m/s, $v_{\mathrm{current}}=0.5+U(0,0.1)$ m/s,

∗

Level 3, ${\psi }_{\mathrm{wind}}={37}^{\circ }+U{(-30,30)}^{\circ }$, ${\psi }_{\mathrm{current}}={100}^{\circ }+U{(-30,30)}^{\circ }$, $v_{\mathrm{wind}}=6.0+U(0,0.1)$ m/s, $v_{\mathrm{current}}=0.5+U(0,0.1)$ m/s.

The wind and current changedper step following uniform distributions U. The simulated boat had a single outboard engine with rudder range ${\delta }_{\mathrm{usv}}\in [-{30}^{\circ },+{30}^{\circ }]$, and the engine speed was mapped to ${\tau }_{\mathrm{usv}}\in [0\%,100\%]$ up to 800 rpm.

In this paper, we focused on two USV tasks: position keeping and target reaching. Define the reward function in Equation (2) as

$$\begin{array}{c}\begin{array}{c}\hfill \mathcal{R}\left({\mathit{p}}_{t+1}\right)=-\left|\right|{\mathit{p}}_{t+1}-{\mathit{p}}_{target}{\left|\right|}^2\end{array}\end{array}$$

(18)

where $\mathit{p}=[{\mathit{X}}_{\mathrm{usv}},{\mathit{Y}}_{\mathrm{usv}}]$ represents the location of USV at the corresponding time step. For the position-keeping task, the target position is set as ${\mathit{p}}_{target}=[0,0]$. For the target-reaching task, it is set to ${\mathit{p}}_{target}=[20,25]$. For the setting of the MPC-based policy, we select the prediction horizon as $H=3$, and the initial variance ${\Sigma }_{0|0}$ and observation variance ${\Sigma }_y$ are set as ${10}^{-4}$. The GP model of USV is initially trained with 500 samples with a random control policy. The agent is iteratively trained in $N_{trial}=20$ rollouts with length $L_{\mathrm{rollout}}=100$. Exploration noise was added to actions ${\mathit{w}}_e$, set to ${\Sigma }_e=0.1$. After the training process, it is evaluated by another 30 rollouts. For the baseline approach, we select FPMPC [32] based on its superior performance among related works. It can be treated as the proposed method without employing UKF uncertainty propagation. All approaches were developed GPflow [43], while the bound optimization by quadratic approximation [44] in NLopt (http://github.com/stevengj/nlopt accessed on 20 May 2021) was used to optimize the MPC-based policy. All experimental results were conducted on a computational server with an Intel Xeon(R) W-2275 CPU and 64 GB memory by five independent trials with different random seeds for statistical evidence.

4.2. Evaluation of Learning Capability

We first evaluated the learning capability of the proposed method in position keeping and target reaching with different sparse GP pseudo input sizes. According to the learning curves in Figure 2, both FPMPC-UKF and the baseline approach achieved convergence behaviors within 20 rollouts under various numbers of pseudo input in sparse GP. Compared with FPMPC using analytic moment matching, the proposed method enjoyed more stable learning curves with less standard deviation in the average position offset and usually converged faster with less sparse GP pseudo input ($\le 10$). These results indicate the superiority of FPMPC-UKF in convergence with less pseudo input in sparse GP. With the increasing level of disturbances and pseudo input, both methods achieved a larger standard deviation in the position-keeping task, while the learning curves of the target-reaching task are relatively flat. The main reason is the higher USV velocity in the target-reaching task, which resulted in better control capability against disturbances.

After training, the performance results of the proposed method in the testing procedures were studied, shown in

Table 2. Test result of the proposed method and baseline approach in the position-keeping.

Disturbances	Method	Sparse Sizes	Average Offset [m]	Median Offset [m]	Success Rate (Final)	Success Rate (Overall)
Level 1	FPMPC	5	$7.82\pm 14.35$	$4.25$	$62.67\%$	$11.33\%$
		10	$5.10\pm 5.66$	$3.20$	$80.00\%$	$20.00\%$
		30	$2.22\pm 2.90$	$1.54$	$96.00\%$	$72.00\%$
		50	$2.30\pm 4.31$	$1.26$	$92.67\%$	$77.33\%$
		70	$2.21\pm 2.20$	$1.56$	$95.33\%$	$69.33\%$
		100	$5.06\pm 11.06$	$1.42$	$85.33\%$	$67.33\%$
	FPMPC-UKF	5	$2.41\pm 4.79$$(-69.18\%)$	$1.47$$(-65.41\%)$	$97.33\%$$(+34.66\%)$	$78.00\%$$(+66.67\%)$
		10	$1.65\pm 1.21$$(-67.65\%)$	$1.35$$(-57.81\%)$	$99.33\%$$(+19.33\%)$	$90.67\%$$(+70.67\%)$
		30	$2.49\pm 5.11$$(+12.16\%)$	$1.47$$(-4.55\%)$	$94.67\%$$(-1.33\%)$	$77.33\%$$(+5.33\%)$
		50	$1.93\pm 2.34$$(-16.09\%)$	$1.34$$(+6.35\%)$	$95.33\%$$(+2.66\%)$	$80.67\%$$(+3.34\%)$
		70	$2.55\pm 3.13$$(+15.38\%)$	$1.67$$(+7.05\%)$	$92.00\%$$(-3.33\%)$	$52.67\%$$(-16.66\%)$
		100	$2.31\pm 1.77$$(-54.35\%)$	$1.86$$(+30.99\%)$	$97.33\%$$(+12.00\%)$	$62.67\%$$(-4.66\%)$
Level 2	FPMPC	5	$14.38\pm 19.20$	$9.01$	$26.00\%$	$1.33\%$
		10	$18.80\pm 33.99$	$4.88$	$64.67\%$	$4.00\%$
		30	$4.90\pm 8.99$	$3.05$	$88.00\%$	$18.00\%$
		50	$4.71\pm 7.21$	$3.03$	$88.67\%$	$24.67\%$
		70	$3.27\pm 3.47$	$2.34$	$94.67\%$	$37.33\%$
		100	$5.84\pm 10.48$	$3.26$	$85.33\%$	$10.00\%$
	FPMPC-UKF	5	$4.94\pm 6.43$$(-65.65\%)$	$3.73$$(-58.60\%)$	$77.33\%$$(+51.33\%)$	$13.33\%$$(+12.00\%)$
		10	$4.01\pm 4.20$$(-78.67\%)$	$3.35$$(-31.35\%)$	$95.33\%$$(+30.66\%)$	$24.67\%$$(+20.67\%)$
		30	$6.40\pm 10.56$$(+30.61\%)$	$3.36$$(+10.16\%)$	$78.67\%$$(-9.33\%)$	$15.33\%$$(-2.67\%)$
		50	$4.95\pm 5.94$$(+5.10\%)$	$3.05$$(+0.66\%)$	$82.00\%$$(-6.67\%)$	$12.67\%$$(-12.00\%)$
		70	$6.28\pm 8.44$$(+92.05\%)$	$3.44$$(+47.01\%)$	$75.33\%$$(-19.34\%)$	$8.00\%$$(-29.33\%)$
		100	$7.16\pm 13.32$$(+22.60\%)$	$3.60$$(+10.43\%)$	$74.00\%$$(-11.33\%)$	$5.33\%$$(-4.67\%)$
Level 3	FPMPC	5	$28.51\pm 35.60$	$14.59$	$18.67\%$	$0.00\%$
		10	$6.05\pm 5.37$	$4.98$	$70.67\%$	$1.33\%$
		30	$3.52\pm 2.64$	$2.95$	$94.00\%$	$20.97\%$
		50	$4.17\pm 6.98$	$2.86$	$90.67\%$	$19.33\%$
		70	$5.04\pm 7.84$	$3.44$	$86.00\%$	$13.33\%$
		100	$7.16\pm 11.99$	$4.04$	$76.00\%$	$1.33\%$
	FPMPC-UKF	5	$9.87\pm 34.20$$(-65.38\%)$	$4.27$$(-70.73\%)$	$85.33\%$$(+66.66\%)$	$14.67\%$$(+14.67\%)$
		10	$4.29\pm 2.69$$(-29.09\%)$	$3.88$$(-22.09\%)$	$82.00\%$$(+1.33\%)$	$18.67\%$$(+17.34\%)$
		30	$6.67\pm 10.09$$(+89.49\%)$	$4.02$$(+36.27\%)$	$70.00\%$$(-24.00\%)$	$12.00\%$$(-8.67\%)$
		50	$10.09\pm 16.18$$(+141.97\%)$	$4.07$$(+42.31\%)$	$72.00\%$$(-18.67\%)$	$9.33\%$$(-10.00\%)$
		70	$5.85\pm 5.91$$(+16.07\%)$	$4.13$$(+20.06\%)$	$78.67\%$$(-7.33\%)$	$2.67\%$$(-10.66\%)$
		100	$9.01\pm 12.12$$(+25.84\%)$	$4.89$$(+21.04\%)$	$67.33\%$$(-8.67\%)$	$0.67\%$$(-0.66\%)$

and

Table 3. Test result of the proposed method and baseline approach in the target-reaching.

Disturbances	Method	Sparse Sizes	Average Offset [m]	Median Offset [m]	Success Rate (Final)
Level 1	FPMPC	5	$10.91\pm 12.45$	$7.01$	$47.33\%$
		10	$5.99\pm 6.55$	$4.19$	$78.00\%$
		30	$3.53\pm 5.87$	$1.72$	$96.00\%$
		50	$3.19\pm 5.58$	$1.28$	$95.33\%$
		70	$3.57\pm 5.92$	$1.67$	$92.00\%$
		100	$4.27\pm 6.79$	$1.94$	$88.00\%$
	FPMPC-UKF	5	$4.89\pm 10.16$$(-55.18\%)$	$1.76$$(-74.89\%)$	$92.00\%$$(+44.67\%)$
		10	$3.33\pm 5.06$$(-44.41\%)$	$1.89$$(-54.89\%)$	$99.33\%$$(+21.33\%)$
		30	$2.87\pm 5.15$$(-18.70\%)$	$1.35$$(-21.51\%)$	$98.00\%$$(+2.00\%)$
		50	$3.40\pm 5.33$$(+6.58\%)$	$1.76$$(+37.50\%)$	$89.33\%$$(-6.00\%)$
		70	$3.45\pm 5.23$$(-3.36\%)$	$1.84$$(+10.18\%)$	$94.67\%$$(+2.67\%)$
		100	$3.22\pm 5.15$$(-24.59\%)$	$1.75$$(-9.79\%)$	$98.67\%$$(+10.67\%)$
Level 2	FPMPC	5	$15.43\pm 19.86$	$12.13$	$24.00\%$
		10	$5.85\pm 5.71$	$4.33$	$75.33\%$
		30	$4.48\pm 5.69$	$2.89$	$92.67\%$
		50	$5.42\pm 7.28$	$3.37$	$83.33\%$
		70	$4.49\pm 5.77$	$2.72$	$90.00\%$
		100	$5.90\pm 7.80$	$3.67$	$80.00\%$
	FPMPC-UKF	5	$7.64\pm 12.61$$(-50.49\%)$	$4.38$$(-63.89\%)$	$66.00\%$$(+42.00\%)$
		10	$5.15\pm 5.18$$(-11.97\%)$	$3.85$$(-11.09\%)$	$83.33\%$$(+8.00\%)$
		30	$6.53\pm 8.52$$(+45.76\%)$	$3.43$$(+18.69\%)$	$70.67\%$$(-22.00\%)$
		50	$4.62\pm 5.51$$(-14.76\%)$	$2.81$$(-16.62\%)$	$82.67\%$$(-0.66\%)$
		70	$6.52\pm 8.98$$(+45.21\%)$	$4.04$$(+48.53\%)$	$68.67\%$$(-21.33\%)$
		100	$6.09\pm 6.49$$(3.22\%)$	$4.17$$(+13.62\%)$	$72.67\%$$(-7.33\%)$
Level 3	FPMPC	5	$31.64\pm 39.31$	$16.15$	$27.33\%$
		10	$6.38\pm 10.04$	$3.93$	$77.33\%$
		30	$7.89\pm 19.91$	$2.86$	$84.67\%$
		50	$5.11\pm 5.52$	$3.47$	$78.67\%$
		70	$5.49\pm 6.68$	$3.39$	$87.33\%$
		100	$5.17\pm 6.07$	$3.66$	$80.67\%$
	FPMPC-UKF	5	$8.37\pm 14.42$$(-73.55\%)$	$5.46$$(-66.19\%)$	$62.00\%$$(+34.67\%)$
		10	$5.43\pm 6.41$$(-14.89\%)$	$3.94$$(+0.25\%)$	$81.33\%$$(+4.00\%)$
		30	$7.30\pm 11.61$$(-7.48\%)$	$3.76$$(+31.47\%)$	$78.00\%$$(-6.67\%)$
		50	$5.71\pm 6.22$$(+11.74\%)$	$4.15$$(+19.60\%)$	$72.00\%$$(-6.67\%)$
		70	$5.81\pm 5.71$$(+5.83\%)$	$4.22$$(+24.48\%)$	$72.67\%$$(-14.66\%)$
		100	$6.27\pm 6.59$$(+21.28\%)$	$4.22$$(+15.30\%)$	$68.00\%$$(-12.67\%)$

, respectively. Several terms are compared in these tables, including the average offsets, the median offsets and the average optimization time. The success rates (final) indicate the rates of successfully holding the USV near the target within 7 m at the end of each testing rollout. The success rates (overall), which are only for the position-keeping task, indicate the success rate of holding the USV during the whole rollout.

The result of the position-keeping task is shown in Table 2. The proposed FPMPC-UKF outperformed the baseline approach FPMPC under all three levels of disturbances with sparse GP pseudo input $\le 10$. With a 5 sparse size, despite its convergence in the training procedure, FPMPC had insufficient generalization capability to finish the test. With the increasing level of disturbances, it achieved very large average offsets (from 7 m to 28 m) with low success rates (from $18\%$ to $63\%$). As a comparison, FPMPC-UKF significantly outperformed the baseline; it achieved $65\%$ less average offset and $66\%$ higher success rate in the level 3 disturbances. Setting the sparse size to 10, FPMPC-UKF enjoyed better performance with significant superiority to FPMPC: it achieved $29\%$ to $78\%$ less average offsets and $17\%$ to $70\%$ higher success rates. With a sparse size larger than 10, the baseline approach usually outperformed the proposed method as the power of analytical moment matching in uncertainty propagation was fully released. However, it turned to heavy computational burdens, which are reported in the next section.

The result in the target-reaching task is shown in Table 3, which is close to the one in the position-keeping task. FPMPC-UKF outperformed the baseline approach at all three levels of disturbances with sparse GP pseudo input $\le 10$ in both average offset and success rate. With a 5 sparse size, FPMPC achieved large average offsets (from 10 m to 31 m) with low success rates (from $24\%$ to $47\%$) in all three levels of disturbances. As a comparison, FPMPC-UKF reduced more than $50\%$ average offset with $34\%$ to $44\%$ higher success rate. With 10 sparse size, FPMPC-UKF still outperformed FPMPC: it achieved $11\%$ to $44\%$ less average offsets and $4\%$ to $21\%$ higher success rates. On the other hand, it obtained less benefit from more sparse GP pseudo input compared with FPMPC using analytic moment matching.

4.3. Evaluation of Computational Efficiency and Model Quality

We further evaluate the computational efficiency (including one-step prediction time and the overall prediction time in the MPC policy) and quickly model the orientation and velocity, i.e., the model error of position, in one-step MPC prediction in this section. According to the results of the proposed and the baseline approaches (represented by green and red colors) in both position-keeping and target-reaching tasks, demonstrated in Figure 3 and Figure 4, the proposed FPMPC-UKF demonstrated a significant advantage in the average optimization time with sparse size $>5$, especially under larger environmental disturbances. With 5 sparse GP pseudo inputs, although the average optimization time of the proposed method was increased (up to $104\%$ in the target-research task with level 1 disturbances), it was limited within $0.5$ s, which is superior to the existing MBRL USV control system [31]. Meanwhile, FPMPC-UKF achieved great improvements in the model prediction error, which contributed to over $50\%$ decrease in the average offset and a significant increase in success rate, reported in Table 2 and Table 3.

Increasing the sparse GP pseudo inputs from 10 to 100, the baseline approach improved its model quality with heavy computational burdens (from $0.5$ s to more than 2 s). As a comparison, the proposed method still achieved close model prediction errors under these sparse sizes while enjoying a far faster optimization. Compared with FPMPC, which required over 2 s to search the optimal action with 100 sparse GP pseudo inputs, the proposed method only needs less than $0.5$ s (more than $70\%$ faster), which is more suitable in a real USV control system with a limited computational resource. Overall, the proposed method considerably outperformed the baseline approach in control performance and model prediction error, while enjoying a faster optimization time (about $0.3$ s) with less sparse GP pseudo input. With the increase in sparse GP pseudo input, the computational burden of the proposed method increased significantly less than the baseline approach, while maintaining close control performance and model prediction errors. These results demonstrated the great potential of FPMPC-UKF in balancing its learning capability and computational complexity and therefore contributed to a higher control frequency in MBRL USV.

Based on our experimental results, one proper balance between the control performance and computational efficiency was met when the sparse GP pseudo input was set to 10. In the position-keeping task, the proposed method achieved $67\%$, $78\%$, and $29\%$ less average offsets, and $70\%$, $20\%$, and $17\%$ higher success rates in three levels of disturbances, while achieving $28\%$ to $32\%$ superior computational efficiency, except for one tiny degradation in optimization time in level 1 disturbances compared with the baseline approach. In the target-reaching task, the proposed method achieved $15\%$, and $12\%$ less average offsets, and $21\%$, $8\%$, and $4\%$ higher success rates in three levels of disturbances while achieving $20\%$ to $25\%$ superior computational efficiency, except for one degradation in optimization ($42.11\%$ slower but still be close to $0.5$ s) time in level 1 disturbances compared with FPMPC.

Figure 5 illustrates the trajectories of USV in position-keeping and target-reaching tasks under level 3 disturbances during one test rollout of FPMPC and FPMPC-UKF with 10 sparse pseudo inputs as one case study. The environmental disturbances for all approaches were generated by the same random seed. It can be observed that in both tasks, the proposed FPMPC-UKF enjoyed better control performance. The fewer prediction errors in the orientation and velocity resulted in a more sophisticated control policy that smoothly drove the USV to hold its position/reach its target without over-large control signals in both the rudder and throttle. After reaching the target, the proposed method fully utilized uncertainty propagation to keep its position against disturbances. On the other hand, the analytic moment matching in the baseline approach did not work well in such a large GP sparse scale and therefore resulted in unstable driving trajectories and struggled with position keeping.

5. Conclusions

In this work, we proposed FPMPC-UKF, a novel GP-based MBRL approach specific for USV by introducing an efficient uncertainty propagation using UKF to the MPC-based policy for a superior control performance of USV against the real-time disturbances, especially with less sparse GP pseudo input. As a bridge connecting probabilistic MBRL and optimal filtering technologies toward fully autonomous USV, FPMPC-UKF naturally released the efficiency of the optimal filter in uncertainty propagation under the trial-and-error framework of RL with a system specific to USV. The proposed method was validated in both position-keeping and target-reaching tasks under different levels of environmental disturbances. The comprehensive comparisons with the related baseline approach in the learning capability, computation efficiency and model quality show the superiority of the proposed method in balancing the learning capability, control performance and computational burdens, which expands the potential of probabilistic MBRL in more challenging USV scenarios with limited computational resources.