Abstract
Mobile robots, including ground robots, underwater robots, and unmanned aerial vehicles, play an increasingly important role in people’s work and lives. Path planning and obstacle avoidance are the core technologies for achieving autonomy in mobile robots, and they will determine the application prospects of mobile robots. This paper introduces path planning and obstacle avoidance methods for mobile robots to provide a reference for researchers in this field. In addition, it comprehensively summarizes the recent progress and breakthroughs of mobile robots in the field of path planning and discusses future directions worthy of research in this field. We focus on the path planning algorithm of a mobile robot. We divide the path planning methods of mobile robots into the following categories: graph-based search, heuristic intelligence, local obstacle avoidance, artificial intelligence, sampling-based, planner-based, constraint problem satisfaction-based, and other algorithms. In addition, we review a path planning algorithm for multi-robot systems and different robots. We describe the basic principles of each method and highlight the most relevant studies. We also provide an in-depth discussion and comparison of path planning algorithms. Finally, we propose potential research directions in this field that are worth studying in the future.
1. Introduction
Mobile robots have been effectively used in various fields over the past few decades, including the military, industry, and security settings, to carry out important unmanned duties [1,2]. In recent years, robots have been given increasingly more applications, which can improve production efficiency, reduce manpower, and improve the working environment [3]. Ground robots are usually used to automate tasks, such as materials handling in warehouses, luggage picking up in airports, and mobile security inspection robots. Underwater robots are usually used to take samples, carry out testing, installation, maintenance, and overhaul of underground water environments, marine environments, and lake and river water environments. Aerial robots are usually used to conduct airborne search and rescue, search terrain data collection, aerial remote sensing, and other tasks [4,5]. The development of robot applications is bringing more and more innovations. The practicality of robots is dependent on their autonomous navigation planning capability. Hence, they need to not only understand the environment they face but also autonomously navigate and plan paths in given areas to meet task requirements. The capability of autonomous navigation and path planning is critical for robot applications, which can not only speed up the running speed of robots but also effectively avoid their blind spots and achieve more efficient task completion. One of the most fundamental issues that need to be resolved before mobile robots can move and explore on their own in complex surroundings is path planning [6]. According to a given robotic machine’s working environment, a mobile robot searches for an optimal or suboptimal path from the starting state to the goal state based on specific performance criteria. This is known as the path planning problem [7]. For mobile robots, effective path planning strategies can save significant time and minimize wear, tear, and capital expenditure. Therefore, the correct choice of a navigation technique is the most important step in robot path planning.
It is necessary to conduct a comprehensive investigation of mobile robot path planning owing to the recent technological progress and breakthroughs in the field. The purpose of this review is to summarize the path planning work of mobile robots and the technical details of some representative algorithms and discuss some open problems to be solved in this field. Articles on the path planning of the mobile robot were retrieved from the databases of Engineering Village and the Web of Science. The search terms during the data retrieval process were “path planning” and “mobile robot.” We selected well-known publications and articles from conferences in the field of robotics, with a focus on the path planning algorithms of mobile robots. In addition, we provide an in-depth discussion and comparison of path planning algorithms. Finally, we hope that this paper will provide a preliminary understanding of mobile robots and path planning for researchers who have just entered this field.
The remainder of this paper is organized as follows: Section 2 introduces the path planning algorithms for mobile robots. Section 3 introduces the path planning algorithms for multiple robots. Section 4 introduces a path planning algorithm for the cooperation of different robots. Section 5 discusses and summarizes the study. The conclusions are presented in Section 6.
2. Path Planning Algorithm
We will introduce the following different types of path planning algorithms: graph-based search, heuristic intelligence, local obstacle detection, artificial intelligence, sampling, path planners, constraint problem satisfaction algorithms, and other algorithms. For the classification of the above path planning algorithms, we consider that some traditional path planning algorithms can be applied to ground, underwater, and aerial robots. The following path planning algorithms [8] are then categorized based on how they work.
2.1. Algorithms Based on Graph Search
2.1.1. A* Algorithm
The A* algorithm, which is typically used for static global planning, is an efficient search method for obtaining the shortest paths and is also a typical heuristic algorithm. The effect of the A* algorithm is shown in Figure 1. The yellow box represents the starting point, the black box represents the obstacle, the pink box represents the end-point, and the blue polyline represents the path. The A* algorithm is used to realize the path planning from the starting point (yellow grid) to the ending point (pink grid) in an environment with obstacles.
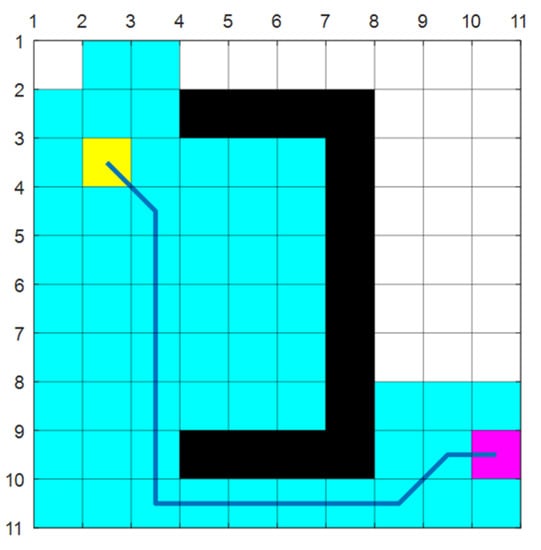
Figure 1.
Schematic diagram of the path planning algorithm based on the A*.
However, there are issues associated with the A* algorithm that limit its use. The system path planning has an excessive number of inflection points and turns, which makes it difficult for the robot to move in its actual surroundings. In [9], the T * algorithm, which combines the A* search algorithm with linear time logic path planning and uses the search process of the A* algorithm to generate the optimal path satisfying the time logic search, was proposed. The final experimental results reveal that the T * algorithm reduces the number of nodes and the generation time of the path compared with the existing algorithms when solving the temporal logical path planning problem in two- and three-dimensional spaces in a large workspace. In [10], the concept of optimality was introduced on a weighted color graph, which expresses the geometric and semantic information in the search space. On this basis, the class-ordered A (COA*) algorithm that finds the globally optimal path in the weighted color graph by heuristic construction of the optimal search tree was proposed. Compared with the traditional A* algorithm, this algorithm is better at finding uncertain paths. As the A* algorithm faces challenges in real-time path planning and collision-free path planning in a large-scale dynamic environment, in [11], the calculation of the distance cost of the risk cost function was simplified, key path points were extracted, and the number of nodes was reduced. Finally, combined with the adaptive window method, path tracking, and obstacle avoidance were achieved. The simulation results reveal that the algorithm can meet the real-time requirements of mobile robots in large–scale environments.
Owing to the low accuracy of existing terrain matching methods in areas with small eigenvalues, this study [12] proposed a seabed terrain matching navigation algorithm based on the A* algorithm, which mainly uses terrain information to analyze the area matching performance. It also proposed a search length and a dynamic matching algorithm to reduce time consumption. The simulations showed that this method can avoid obstacles with less-than-perfect matching and shorten the length of the path. As the traditional A* algorithm does not consider the turning cost and redundant path points, it cannot guarantee the safety of the mobile robot. The turning cost function was added in [13] to avoid the detour and frequent turning of the mobile robot. Additionally, the search points near the obstacles were reduced to ensure a safe distance, determine whether the point is redundant by judging whether there are obstacles around each path point, and optimize the generated trajectory. Compared to the traditional A* algorithm, it reduces the path length, search time, and several nodes.
To address the problem of global navigation satellite systems (GNSS) positioning map errors for unmanned aerial robots, an improved path planning algorithm based on the GNSS error distribution fusion A* was proposed [14]. The effectiveness of the improved A* algorithm was tested at different altitudes using a quadcopter in an actual urban environment. The experimental findings demonstrate that, compared to the traditional A* and artificial potential field (APF) algorithms, the revised A* algorithm offers safe pathways based on position error prediction at a low cost. The RiskA* algorithm was presented for unmanned aerial robot path planning optimization in urban environments [15]. The path length and risk cost are both considered while designing the cost function, and the final path minimizes the sum of these two costs. According to the simulation findings, the RiskA* algorithm performs well and can account for the risk posed by the ground population, a crucial element in urban areas, to determine the best solution. For rotary-wing unmanned aerial robots performing low-altitude missions in three-dimensional complex mountain environments, a fusion algorithm of the sparse A* algorithm and bio-inspired neurodynamic model was proposed [16]. This improved the A* algorithm in terms of the process structure and evaluation function. It also mitigated the computationally large problem of the A* algorithm in the three-dimensional (3D) trajectory planning process. Based on experimental findings, the fusion algorithm enables a rotary-wing unmanned aerial robot to design a safe, quick, and economical course in challenging mountainous terrain by reducing the complexity and time requirements of the A* algorithm.
In short, the A* algorithm is the most effective search algorithm in a static environment. However, it has many disadvantages, such as an excessive number of redundant nodes. Therefore, in recent years, scholars have mostly chosen to improve the cost function or reduce the number of nodes in its path. Moreover, it can meet the needs of different scenarios through different cost functions. However, in large environments, the A* algorithm still exhibits slow path planning. In [10,11], scholars also provided solutions to this problem. Therefore, in future research on the A* algorithm, enabling the A* algorithm to plan the optimal path in real-time in large environments is a possible direction.
2.1.2. Dijkstra’s Algorithm
Dijkstra’s algorithm was proposed by E.W. Dijkstra in 1959 [17]. It is a typical algorithm for solving the shortest-path problem in directed graphs. The algorithm sets the point where the mobile robot is located as the initial node and traverses the remaining nodes. It then adds the node with the closest distance to the initial node to the set of nodes, which spreads outward from the initial node in layers until all the nodes in the graph are traversed. Subsequently, it finds the shortest path from the initial node to the target node according to the magnitude of the path weight.
Owing to the uncertainty of odometer positioning, which offsets the path planning of a mobile robot [18], a path planning algorithm considering the minimum cumulative error of the sensor offset is proposed. Through statistical, qualitative, and quantitative analyses of the accumulated error of odometer positioning, the planning path with the minimum accumulated error is generated. Through simulations and comparative analysis, this method effectively reduces the cumulative error under complex conditions. Similarly, an improved Dijkstra algorithm was proposed for Dijkstra’s non-adaptation to complex environments. This introduces the concept of equivalent paths, analyzes the influencing factors and weights of equivalent paths, and finally obtains the conversion formula between equivalent paths and actual paths [19]. Combined with engineering examples, the shortest water avoidance path for a mine was calculated.
For dynamic obstacles in the ocean, the Dijkstra algorithm was improved by adding additional functions [20]. Furthermore, the algorithm alters the course according to the current dynamics.
The Dijkstra algorithm is a classic algorithm for finding the shortest path of a single source and is mainly used to find the optimal path of a geographic information system. However, with the massive growth of data, the operational efficiency of the classic Dijkstra algorithm has been unable to meet people’s needs, and it needs to be optimized from all aspects.
2.2. Heuristic Intelligent Search Algorithm
2.2.1. Genetic Algorithm
The genetic algorithm (GA), also known as the evolutionary algorithm, is a heuristic search algorithm. It generates an optimal solution to a problem by simulating the evolution of organisms using the principle of survival of the fittest. A population consists of a certain number of individuals, each carrying a certain number of coded genes, and the population is equivalent to a set of solutions to the problem. A diagram of the genetic algorithm is shown in Figure 2. It includes initializing the population randomly, selecting suitable individuals, carrying out the selection, crossover, and mutation genetic operations, and constantly updating the population.
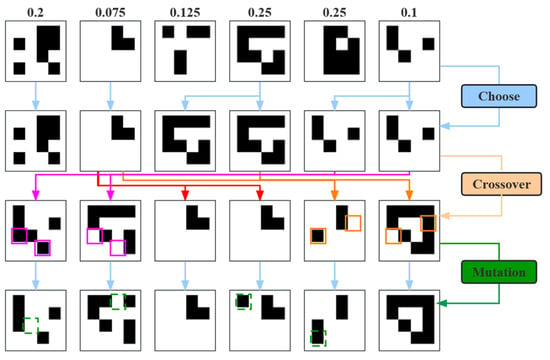
Figure 2.
Flow chart of genetic algorithm evolution [21].
Genetic algorithms have a low computational rate and consume a large number of computer resources in the process, which is also a major constraint to their development. A static global path planning method using a genetic algorithm was proposed, followed by dynamic obstacle avoidance using a Q-learning algorithm [21]. The entire method is an “offline” and then “online” hierarchical path planning method that successfully achieved the path planning of mobile robots. In [22], a new genetic modification operator was proposed to address the shortcomings of the GA algorithm, which has poor convergence and neglects inter-population cooperation. The improved algorithm can better avoid the local optimum problem and has a faster convergence speed. To address the multi-robot cooperation problem, a co-evolutionary mechanism is proposed to achieve collision-free obstacle avoidance planning for multiple robots. The efficiency of the algorithm is demonstrated by the experimental findings.
The GA was used [23] to generate offline optimal 3D paths, and the degree of path optimization was considered to provide a planning approach appropriate for 3D underwater environments. In [24], a path planner combining a GA and dynamic planning was proposed. In this algorithm, the random crossover operator from the traditional genetic algorithm is replaced by a crossover operator that is always the same and is based on dynamic planning. The path planner simultaneously optimized the path length, minimized the turning angle, and maximized the elevation rate. Compared to traditional genetic algorithms, this path planner is more adaptable and has a faster rate of convergence.
Reference [25] combined mixed integer linear programming (MILP) with genetic algorithms to propose a new method for improving unmanned aerial robot path planning in complex environments, and the effectiveness of the proposed method was validated using two, five, and seven unmanned aerial robots in urban and mountainous areas, respectively. The experimental findings demonstrate that in terms of cost-effectiveness and energy optimization environments, the proposed method outperforms the ant colony and genetic algorithms. Reference [26] proposed a dynamic genetic algorithm by optimizing the crossover and variation operators of the genetic algorithm to automatically adjust the crossover and variation probabilities using individual fitness. To quickly and effectively reject maladapted individuals and increase the search efficiency in the early phases of the algorithm, these operators are dynamically changed in real-time using individual fitness values. According to the experimental results, the GA optimization method can significantly increase search speed. Genetic algorithms and fuzzy logic have been combined [27] to increase path planning accuracy. This study interprets the path planning problem as a multi-traveler problem, solving the problem of returning each unmanned aerial robot to its starting point at the end of its action.
A GA can obtain multiple solutions through multiple runs. These solutions can be compared, and the best solutions can be selected. However, the operation process of GA is relatively complex, and it is necessary to select appropriate parameters. If inappropriate parameters are selected, the performance of the algorithm may deteriorate. Improvements can be made to its genetics. The future direction of improvement is still related to machine learning and other technologies to further improve the adaptive ability and intelligence level of the algorithm.
2.2.2. Ant Colony Algorithm
The ant colony algorithm (ACO) is a positive feedback mechanism algorithm proposed by the Italian scholar Dorigol in 1992, in which a pheromone-focused path has a heuristic influence on the search for the next node. Each ant produces a secretion as a reference along its walking path and senses the secretions generated by other ants when they are seeking food. This is the underlying concept behind the ACO algorithm. The mechanism of the ant colony algorithm is shown in Figure 3. The ants can communicate and make decisions based on this secretion, often referred to as pheromone. The colony migrates to a path where there are more pheromones than on other paths and releases more secretions as it moves, increasing the concentration of the pheromone and drawing more ants to the path, generating a positive feedback process. The pheromone concentration on the short road steadily increases over time, leading to an increase in the number of ants choosing it, whereas the pheromone concentration on other paths gradually diminishes until it disappears. The entire colony eventually focuses on the best route. The act of foraging by the ants is comparable to that of robotic path planning. The ants will choose the quickest route to the food if there are a sufficient number of them in the nest to overcome the barriers.
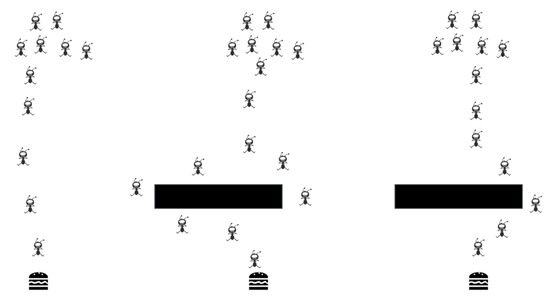
Figure 3.
The mechanism of the ant colony algorithm.
A new pheromone updating technique was proposed in a dynamic environment to avoid unnecessary loops and achieve faster convergence [28]. An improved algorithm with an adaptive search step size and pheromone waving strategy was proposed to address the problem of the ACO algorithm being prone to a local optimum and inefficient search [29]. For the path conflict problem caused by the over-concentration of multiple robot paths, a load-balancing strategy to avoid path conflict is proposed. Simulation results demonstrate that the proposed strategy is feasible and efficient. A hybrid approach based on the regression analysis-adaptive ant colony optimization (RA-AACO) humanoid robot navigation method was proposed [30], and a Petri net controller was designed to prevent multiple robots from colliding with one another in a re-simulation. The controller successfully implemented single and multi-robot navigation. This process can be applied as a reliable solution for humanoid robot navigation and other robotic applications.
An ant colony technique with particle swarm optimization was proposed [31] for the autonomous underwater robot to discover the ideal path through a complicated seafloor. To enhance the pheromone update rule, the particle swarm optimization technique was added to the path-length heuristic function. The strategy also restricts the initialization range of particular populations, considerably enhancing the search efficiency and preventing a series of superfluous pitches and undulations, considering how challenging it is for autonomous underwater robots to locate pathways in a three-dimensional space. Unlike the conventional “ant colony” algorithm, path optimization is significantly reduced. For the problem of autonomous underwater robots needing to traverse complex environments with dense obstacles, an ACO-A* algorithm was proposed by combining the ACO algorithm with the A* search algorithm [32]. Here, the ACO is responsible for determining the target travel order based on the cost map, and A* performs pairwise path planning based on the search map obtained from fine-grained modeling. Simulation results demonstrate that the time efficiency of the ACO-A* is verified.
An improved multi-objective swarm intelligence method was used to plan an accurate unmanned aerial robot 3D path (APPMS) [33]. The path planning problem is transformed in the APPMS approach into a multi-objective optimization task with numerous restrictions. In addition, a precise swarm intelligence search technique based on enhanced ant colony optimization was introduced to find the best unmanned aerial robot 3D flight path. This technique uses preferential search directions and a stochastic neighborhood search mechanism to enhance both global and local search capabilities. The simulation results demonstrate that the superiority of the proposed approach is supported by three sets of digital terrain (three, four, and eight threats) and genuine DEM data for the simulated disaster response missions. Another study suggested using [34] a 2-OptACO approach that builds on the 2-opt algorithm to enhance the ant colony optimization algorithm and is used to optimize the unmanned aerial robot path for search and rescue missions. According to the simulation findings, the 2-OptACO approach converges more quickly than the GA and ACO approaches. Better global optimal solutions are attained. Reference [35] presented a method based on ant colony optimization to determine the minimum time search path for multiple unmanned aerial robots (minimum time search-ant colony optimization MTS-ACO). Two different pheromone table encodings were proposed for MTS-ACO. A minimum–time search heuristic function was designed that enables the ant colony optimization algorithm to generate high-quality solutions at the initial stage and accelerate the convergence of the algorithm.
The ant colony algorithm can find the optimal path in a known static large-scale environment and is also suitable for multi-objective optimization problems. However, it easily falls into the local optimal solution, resulting in a slow convergence speed of the algorithm. Scholars have also improved its convergence speed. Nonetheless, its convergence speed and global searchability can be improved further.
2.2.3. Particle Swarm Optimization
The particle swarm optimization (PSO) algorithm mimics the behavior of birds in their search for food, sharing information regarding their current location as the flock forages. The entire flock can reach its final food source through proper communication between the individuals and group members. The basic principle is that individuals and groups collaborate and share information to obtain optimal solutions. This algorithm was proposed by Eberhart and Kennedy [36] in 1995 to determine the global optimum in terms of the current search for the optimum. It has the advantages of easy implementation, high accuracy, and quick convergence, and is not only suitable for multi-robot path planning but also capable of single-robot route planning. Figure 4 shows a schematic that mimics the behavior of birds seeking food. By communicating with the group, find the closest bird to the food and travel with it to find the ultimate largest food source. The circle represents the bird. The green vegetation represents food; most food is in the grove, and most food is in the forest.
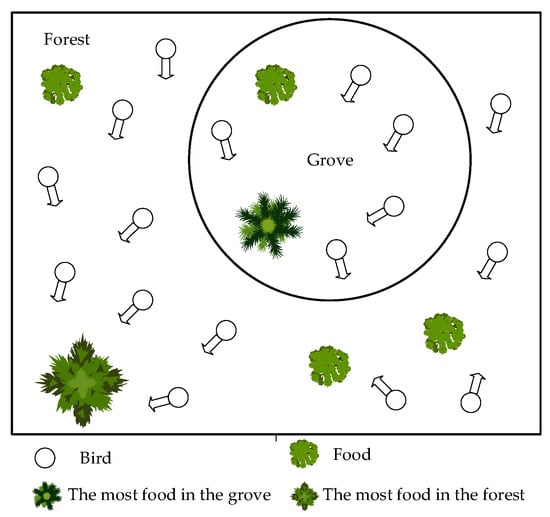
Figure 4.
The bird’s swarm searching for the optimal food source represents the particle swarm optimization process.
The performance of the proposed particle swarm algorithm depends on how its parameters are adjusted, managed, and changed. A robot path smoothing strategy was proposed to address the problem of unnecessary turns caused by unsmoothed paths generated by the PSO algorithm [37]. The strategy is based on the PSO algorithm, which introduces adaptive fractional-order velocities to improve the ability to search the space and increase the “smoothness” of the mobile robot path by using higher-order Bessel curves. Experiments show that the modified PSO algorithm is better than several existing PSO algorithms on several benchmark functions. The superiority of the new approach is supported by numerous thorough simulations of smooth path planning for mobile robots. A study [38] presented a new method for determining the optimal path of a multi-robot in a cluttered environment using a combination of the improved particle swarm optimization algorithm (IPSO) and the improved gravitational search algorithm (IGSA). The simulation results demonstrate that the proposed method outperforms other algorithms used for the navigation of multiple mobile robots.
To reduce energy usage for autonomous underwater robot path planning, a distance evolutionary nonlinear particle swarm optimization (DENPSO) algorithm was suggested [39]. The approach uses penalty functions to set the energy optimization goals under obstacles and in the ocean. It also changes linear inertial weight factors and learning factors into nonlinear ones so that the particles can fully explore the 3D underwater world during the evolution process. In the 3D simulated underwater environment, the simulation results demonstrate that DENPSO uses significantly less energy than the linear PSO algorithm. An evolutionary-based docking-path optimization technique was suggested [40]. The first step is the analysis and modeling of the ocean environment and its restrictions. The second design goal of the control points was to satisfy the model constraints. To accomplish global time optimization, adaptive rules, and quantum behavior were included in PSO. Finally, the proposed technique was assessed using Monte Carlo simulations. The experimental findings revealed considerable improvements to this approach.
A 3D path planning method based on adaptive sensitivity decision operators and particle swarm optimization was presented [41], where an adaptive sensitivity decision area was built to address the drawbacks of local optimality and slow convergence. To increase computational efficiency, alternative possibilities are eliminated, and prospective particle sites with a high probability are found by employing this defined region. In addition, the relative particle directionality obtained from the current position enhances the search accuracy. In terms of the path cost and path generation, the simulation results demonstrate that the upgraded PSO algorithm performs better than the GA and PSO approaches. For modern warfare, the ability of unmanned aerial robots to avoid enemy radar reconnaissance and artillery fire at the lowest cost has become an important research problem in unmanned aerial robot path planning. An algorithm (SHOPSO) combining a selfish herd optimizer (SHO) and a particle swarm optimizer (PSO) was proposed [42]. By combining SHO and PSO, the structure of SHO is simplified, and the SHO search capability is improved. In the simulation experiments, five two-dimensional complex battlefield environments and five three-dimensional complex battlefield environments were designed, and the proposed algorithm was compared with other algorithms that have better optimization performance. The results of the experiments demonstrate that this strategy offers the best path for unmanned aerial robots. For the 3D path planning issue of unmanned aerial robots in complex environments, an improved particle swarm optimization algorithm (called DCA*PSO) was proposed [43]. It is based on the dynamic divide-and-conquer (DC) strategy and the improved A* algorithm, and divides the entire path into multiple segments and evolves the paths of these segments using the DC strategy. The intricate, high-dimensional challenge is divided into numerous parallel, low-dimensional issues. According to the experimental results, the proposed DCA*PSO method can find workable pathways in complex landscapes with several waypoints.
Particle swarm optimization has no crossover or mutation operations and only requires the adjustment of some parameters. Additionally, it has a memory function that can find the best path in a short time. However, because of its randomness, a globally optimal solution cannot be guaranteed. Scholars have also improved their search abilities. Particle swarm optimization can be combined with a machine-learning algorithm to improve its performance and accuracy.
2.3. Algorithm Based on Local Obstacle-Avoidance
2.3.1. Dynamic Window Approach
The dynamic window approach (DWA) [44] is a technique that immediately samples the environment and determines the state of activity of the robot at the following instant. This approach permits quick access to the desired location while preventing robot collisions with objects in the search area. As shown in Figure 5, the surrounding circles represent walls, the inner circles represent dynamic obstacles, and the small circle represents a robot.
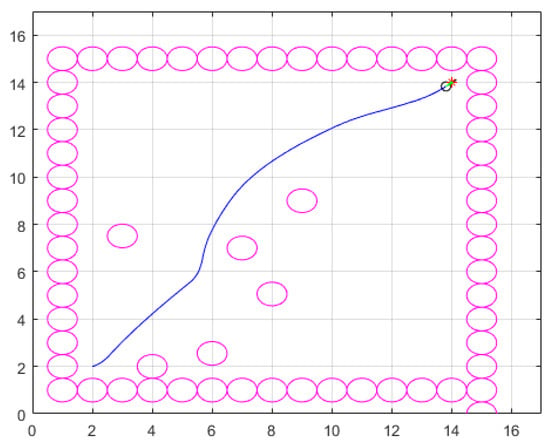
Figure 5.
Schematic diagram of the path planning algorithm based on the DWA.
An improved DWA algorithm based on Q-learning was proposed [45]. The method modified and extended the original evaluation function of the DWA, added two new evaluation functions, enhanced its global navigation capability, and adaptively de-adjusted the weights of the evaluation function through Q-learning. The experimental results demonstrate that the method has a high navigation efficiency and success rate in complex and unknown environments. A dynamic collision model that can predict future collisions with the environment by simultaneously considering the motion of other objects was designed [46]. According to experimental findings, this approach reduces the likelihood of robot collisions in dynamic environments. A global dynamic window navigation scheme based on model predictive control with unweighted objective functions was proposed in [47] to address the problem of most planning methods treating the robot as a single point, which leads to the inability of passing through narrow bands.
The dynamic window method is suitable for real-time path planning because of its speed, and it can also optimize the algorithm’s performance by adjusting the window parameters. However, it is sensitive to changes in the environment and requires frequent updates of obstacle information around the mobile robot. Therefore, in the future, it can be combined with a machine learning algorithm to predict the distribution of obstacles in an environment and optimize the accuracy and efficiency of path planning.
2.3.2. Artificial Potential Field Method
The physical concept of a potential field, which considers the motion of an object as the product of two forces, is the source of the idea of an artificial potential field [48]. As shown in Figure 6, the gravitational pull of a goal point pulls on a robot in the planning space, and an obstacle repels it. Under the combined influence of these two forces, the robot advances in the direction of the goal point and can successfully navigate around any obstacle in its path to reach its destination without incident. The black box represents the starting point, the red circle represents the ending point, and the green circle represents the obstacle.
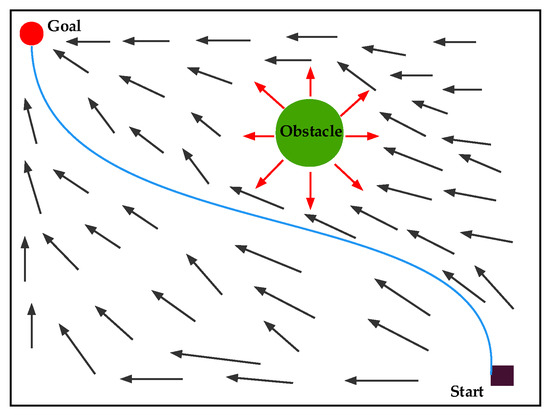
Figure 6.
Schematic diagram of the path planning algorithm based on APF.
Another study [49] presents a bacterial potential field method that ensures a feasible, optimal, and safe path for a robot in both static and dynamic environments. The bacterial potential field method combines an artificial potential field method with a bacterial evolutionary algorithm, thereby fully utilizing the APF method. According to experimental results, the bacterial potential field approach exhibits significant local and global controllability in dynamic and complex situations. To solve the problem of optimal motion planning, a continuous, deterministic, provable, and safe solution based on a parametric artificial potential field has been proposed [50]. Reinforcement learning was used to properly adjust the parameters of the artificial potential field to minimize the Hamilton–Jacobi–Bellman (HJB) error. In the simulation experiment, the cost function value and running time were better than with the fast search random tree algorithm.
A real-time path planning algorithm with an upgraded APF algorithm was proposed to solve the path planning problem for static and dynamic environments with unidentified obstacles (static and dynamic) [51]. This technique augments the repulsive potential field function with a distance adjustment factor to address the target unreachability issue based on the conventional APF. The relative velocity technique, which not only considers the relative distance but also the relative velocity between the autonomous underwater robot and moving objects, addresses the local minimum problem by combining the positive hexagonal guidance method and the APF. The experimental results demonstrate that this method reduces the computational effort required for navigation. To resolve the poor dynamic obstacle avoidance performance in the autonomous path of an underwater 3D autonomous underwater robot, a local obstacle avoidance technique based on the vectorial artificial potential field method was proposed [52], and the space vector method was employed to enhance the calculation of the direction of the combined force and the computational effectiveness of the algorithm. Eventually, by using the vector artificial potential field approach, the key path points were employed as local target locations to avoid nearby obstacles. The findings of the simulation demonstrate that the strategy can help the autonomous underwater robot efficiently avoid different obstacles and lower the cost.
Reference [53] provides a technique for avoiding local minima in an artificial potential field and maneuvering around the closest obstacle, allowing an unmanned aerial vehicle to successfully escape from the local minima without hitting any obstacles. The study suggests a parallel search technique that requires the unmanned aerial robot to navigate around the nearest obstacle to approach the target while detecting the obstacle between the current location and the target being too far away and having too many obstacles to reach it. Simulation results show that the path planning algorithm and controller that were suggested are useful. Reference [54] addresses the problem that most unmanned aerial robot path planning techniques do not consider, which is wind interference. A new 3D online APF path planning technique that enhances the sensitivity of the unmanned aerial robot to wind speed and direction was proposed. This is performed by presenting a new, improved attractor with a modified wind resistance gravitational function that considers any small changes in the relative displacement caused by the wind. This causes the unmanned aerial robot to drift in a certain direction. The proposed path planning technique is evaluated for various simulation scenarios. Its performance is superior in handling wind disturbances. Reference [55] describes an enhanced artificial potential field method incorporating the chaotic bat algorithm. It uses an artificial potential field to accelerate the convergence of bat position updates. It proposes an optimal success rate strategy with adaptive inertia weights and a chaotic strategy to prevent hitting a local optimum. The method is particularly robust for dealing with path planning issues, and the simulation results demonstrate that it considerably improves the success rate of discovering suitable planning paths and reduces the convergence time.
The artificial potential field method has great advantages in avoiding unknown obstacles. However, it can easily fall into the local minimum in complex environments, and it is also sensitive to noise interference. In the future, a complex artificial potential field could be designed to improve the adaptability of the algorithm.
2.3.3. Time Elastic Banding Algorithm
The timed elastic band algorithm (TEB) [56] is a classical local obstacle avoidance algorithm for two-wheeled differential robots. The method explicitly augments the “elastic band” with temporal information, thus allowing the dynamic constraints of the robot to be considered and the trajectory to be modified directly, transforming the traditional path planning problem into a graph optimization problem [57].
An active trajectory planning technique has been proposed for autonomous mobile robots operating in dynamic situations [58]. The proactive timed elastic band (PTEB) model, as suggested in this method, focuses on integrating the hybrid reciprocal velocity obstacle model (HRVO) into the goal function of the TEB algorithm. According to the simulation findings, the proposed motion planning model can control the mobile robot to actively avoid dynamic impediments and provide safe navigation. An improved TEB algorithm was proposed to address the anomalous behavior of the conventional TEB algorithm in cluttered scenarios where planning is prone to backward and large steering. Here, a hazard penalty factor constraint that can plan a safer motion trajectory, an acceleration jump suppression constraint to reduce large shocks in motion, and an end-smoothing constraint to reduce end shocks were added; the improved TEB achieved a smooth and accurate arrival of the target points [59]. The simulation findings demonstrate that the enhanced TEB algorithm may produce a more logical robot motion and create a safe and smooth course in challenging situations.
The time-elastic band algorithm considers the continuity of time, making the path smoother, but it cannot deal with complex scenes, such as large-scale scenes and high-dimensional space. In the future, it could be combined with a machine learning algorithm to improve the accuracy of path planning.
2.4. Algorithm Based on Artificial Intelligence
2.4.1. Neural Networks
An artificial neural network is an information processing system that mimics the structure and operation of a neural network in the brain. It is a complex network structure comprising several interconnected processing units (neurons) [60]. A typical artificial neural network has the following three components: input, hidden input, and hidden output. The input, hidden, and output layers are the first, intermediate, and last layers, respectively. The number of neurons in the input layer is determined by the input data, and the number of neurons in the other layers is altered to reflect the current condition. The concealed layers may have any number of layers, occasionally having multiple layers.
A guided autowave pulse coupled neural network (GAPCNN) was proposed to address the fact that most fast collision-free path planning algorithms cannot guarantee the superiority of paths, and it significantly improves the path query time by introducing a directed automatic wave control and accelerated discharge of neurons based on dynamic thresholding techniques [61]. The temporal effects of the algorithm demonstrate that it may be utilized for route planning in static as well as dynamic contexts. The simulation and testing findings demonstrate that the GAPCNN is a reliable and quick path planning technique. A multi-robot path planning algorithm based on a combination of Q-learning and convolutional neural network (CNN) algorithms was proposed for the problem of conflict-free path planning for multiple robots caused by practical tasks [62]. This technology enables many mobile robots to quickly design courses in various surroundings while successfully accomplishing the mission, according to experimental data. A new Fast Simultaneous Localization and Mapping (FastSLAM) algorithm based on the Jacobi-free neural network was proposed [63], which utilizes a multilayer neural network to compensate for the measurement error online and train the neural network online during Simultaneous Localization and Mapping (SLAM). The third integration rule of the Gaussian weighting method is also utilized to calculate the nonlinear leap density before the Gaussian third-order nonlinearity, estimate the state of the SLAM state (robot path and environment map), and train the neural network compensator online. According to simulation data, the mobile robot’s ability to navigate in unfamiliar areas and avoid collisions with objects was improved; SLAM performance was also improved.
An approach that combines a bio-inspired neural network and the potential field was suggested [64] to address the safety issue of autonomous underwater robot path planning in dynamic and uncertain situations. A bio-inspired neural network uses the environment to determine the best course for an autonomous underwater robot. The path of the bio-inspired neural network is modified by the potential field function such that the autonomous underwater robot can avoid obstructions. The experimental findings demonstrate that the strategy strikes a balance between autonomous underwater robot safety and path logic. The intended routes can accommodate the need for navigation in dynamic and unpredictable surroundings. Based on the excellent performance of deep learning, a hybrid recurrent neural network framework was proposed to estimate the position of an autonomous underwater robot [65]. In this approach, the raw sensor readings are processed in a single computational cycle using unidirectional and bidirectional long short-term memory networks (LSTM) with numerous memory units. The completely linked layer can then determine the displacement of the autonomous underwater robot using the output of the LSTM and the time interval of the previous cycle. The simulation results demonstrate that the approach presents significant navigational usefulness and high accuracy while minimizing sensor bias interference.
2.4.2. Reinforcement Learning
The basic principle of reinforcement learning [66] is that intelligence is continuously learned under the stimulus of environmental feedback rewards or punishments and continuously adjusts its strategy based on the feedback to eventually reach reward maximization or a specific goal. A deep Q-learning algorithm for experience replay and heuristic knowledge was proposed [67]. In this algorithm, neural networks are used to solve the problem of the dimensional catastrophe of Q-tables in reinforcement learning. This makes the most of the robot’s ability to collect data based on its experience as it moves. Heuristic knowledge helps avoid blind exploration by the robot and provides more efficient data for training the neural net for faster convergence on the optimal action strategy. Considering the local path planning problem in complicated dynamic environments, a fast extended random tree path planning method based on reinforcement learning SARSA(λ) optimization has been suggested [68]. This method increases the selection of expansion points, introduces the concept of biased goals, uses task return functions, goal distance functions, and angle constraints to improve the performance of the rapidly-exploring random tree (RRT) algorithm, decreases the number of invalid nodes, and ensures the randomness of the RRT algorithm. Reinforcement learning aims to train the intelligence to take action to maximize its reward with strong decision-making capabilities. Deep learning can extract high-level features from the raw mass of data and has a strong perceptual capability. Deep reinforcement learning [69] is an artificial intelligence program that combines the perceptual and decision-making abilities of reinforcement learning to make a more accurate model of the human mind. A learning-based map-free motion planner is proposed for obstacle-free maps and sparse distance information by considering the sparse ten-dimensional range results and the position of the target relative to the coordinate system of the mobile robot as the input and a continuous steering command as the output [70]. An asynchronous deep reinforcement learning technique can be used to train a mapless motion planner from one end to the other. This methodology is more reliable in excessively complex contexts.
For autonomous underwater robots to find a feasible collision-free path in complex underwater environments, the use of deep reinforcement learning algorithms to learn processed sonar data for autonomous underwater robot navigation in complicated situations has been proposed as an active sonar technique [71]. The process of switching the trajectory is accelerated by the addition of line-of-sight guidance. The performance of this approach was compared with that of genetic algorithms and deep learning algorithms in three environments: random static, hybrid static, and complicated dynamic, and it was found that the algorithm surpassed the other algorithms in terms of success rate, obstacle avoidance performance, and generalization capability. An enhanced deep deterministic policy gradient (DDPG) algorithm for real-time obstacle avoidance and 3D path tracking has also been suggested [72]. To address the problem of DDPG requiring a large training set to explore the strategy, a line-of-sight guidance-based approach is used to generate the target angle for path tracking and the error relative to the carrier coordinate system, which facilitates the filtering of irrelevant environmental information and generates the corresponding strategy. The method provides a more accurate approximation of the approach than the original DDPG algorithm, according to the simulation findings.
A deep reinforcement learning method for unmanned aerial robot path planning based on global situational information was proposed [73]. In this method, a situational evaluation model was developed based on the simulation environment provided by the Stage Scenario software. In this model, the probability of an unmanned aerial robot’s survival under enemy radar detection and missile attack was considered. Using a competing dual-depth Q network, the algorithm obtains a set of situational maps as input to approximate the Q values corresponding to all the candidate operations, which results in higher cumulative rewards and success rates compared to the dual-depth Q network. A distributed deep reinforcement learning framework that divides the unmanned aerial robot navigation task into two simple subtasks, each solved by a designed LSTM-based deep reinforcement learning network, was developed [74]. The simulation results demonstrate that the unmanned aerial robot performance of this method outperforms other state-of-the-art deep reinforcement learning methods in highly dynamic and uncertain environments. In [75], an interpretable deep neural network path planner was proposed for the automatic navigation problem of small unmanned aerial robots in unknown environments. The method models the navigation problem as a Markovian decision process that uses deep reinforcement learning to train the path planner in a simulation environment and proposes a feature attribute-based model interpretation method to better train the model. Based on experimental results in a genuine setting, the path planner can be directly used in a real environment. In reference [76], a 3D coverage map was first created, which stores the estimated disruption probability at each point to solve the communication interference from overhead buildings in unmanned aerial robot 3D path planning. Using the created coverage map, an approach based on multi-step dueling DDQN (multi-step D3QN) is suggested to build locally optimal unmanned aerial robot pathways. The unmanned aerial robot functions act as an agent in this algorithm, learning the proper course of action to perform the flight task.
Reinforcement learning can be used to learn the optimal strategy independently in a complex environment and can adaptively adjust the path planning scheme. However, reinforcement learning requires many calculations and also requires the adjustment of many parameters, which may have a significant impact on the final path. In the future, we will consider introducing this model to reinforcement learning. Additionally, to meet the interpretability of the reinforcement learning algorithm for path planning, we can investigate interpretable path planning.
2.4.3. Brain-like Navigation
As one of the research directions of artificial intelligence technology, brain-like navigation involves several interdisciplinary aspects such as brain science and control science. Brain-like navigation is a new navigation technology that mimics biological cognitive characteristics by sensing environmental information through multiple sensors and using intelligent and exogenous technologies to achieve navigation information fusion and cognitive map construction with knowledge memory, learning, and reasoning characteristics, as well as real-time intelligent path planning with cognitive characteristics [77]. Current studies regarding brain-like navigation have been conducted considering various aspects, including brain-like environmental perception, brain-like spatial cognition, and goal-oriented brain-like navigation. An integrated research system for modeling, simulations, and experimental validation has been initially formed. However, it remains in the exploration and improvement stage. Brain-like environmental perception mainly focuses on the extraction of multidimensional features from the navigation information of the carrier and the surrounding environment, drawing on the rich biological structures of the auditory, visual, olfactory, and sensory information processing mechanisms of animals. The University of California, Berkeley [78] designed an insect-like lightweight micro-unmanned aerial robot hardware platform for the US Defense Advanced Research Projects Agency (DAPPA) research. It also integrated multimodal bionic sensors such as compound eyes, insect balance bar gyroscopes, optical flow sensors, and U-shaped magnetometers. It has various advantages, such as retrieving rich environmental perception information, strong adaptation to the dynamic flight environment, accurate measurements, and energy savings. In 1948, Tolman [79] proposed a cognitive map by studying rats walking in a maze. In 1948, Tolman proposed the concept of a cognitive map by studying rats walking in mazes and suggested that rats use a certain spatial representation formed inside the brain to guide themselves in path planning, obstacle avoidance, and other navigational behaviors. The brain-inspired spiking neural network (SNN) is closer to the actual biological structure than other artificial neural network models. The output of its neurons has a pulse sequence encoded in the temporal dimension, and multiple neurons can achieve the ability to represent a two-dimensional space in time–space. Most of the connections of SNN-based brain-like spatial cognition models are predefined by brain structures, and less parameter learning is required to better model clusters of brain navigation cells, such as position cells, grid cells, and head orientation cells, which encode navigation information to map the environment [80]. The Google DeepMind team’s [81] dual-path deep reinforcement learning navigation architecture uses a two-path deep circulation neural network to remember the kernel of common navigation pathfinding strategies in different environments and present positions in different environments. Convolutional neural networks are then used to get visual input in real-time. The destination was successfully reached in an offline street view without reference to a map library and with only a few points (mission reward).
2.5. Sampling-Based Algorithms
2.5.1. Rapidly-Exploring Random Tree
The rapid-exploration random tree algorithm is built by randomly generating a tree starting from a starting point and connecting the generated tree to the trunk of the starting point to form a search tree. This continues until all of the branches of the tree lead to the target point. This algorithm is commonly used in the static path planning of mobile robots. In [82], based on the RRT* algorithm, a motion planning algorithm called Smooth RRT* that provided a smoother solution for robots with nonlinear dynamic constraints and could be used to reconnect two nodes in a given state was proposed. Compared with the traditional RRT algorithm and the Kinedynamic-RRT (Kino-RRT) [83] algorithm, the Smooth RRT* algorithm in this study is based on the number of nodes, and its path length and path smoothness are better than those of the previous two algorithms. In [84], the neural RRT* (NRRT*) algorithm, which is based on a convolutional neural network, was proposed as a new way to plan the best path. In this study, the optimal path and map information generated by the A* algorithm were used as datasets, and a large number of optimal paths generated by the A* algorithm were used to train the CNN model. Compared with the traditional RRT* algorithm and the informed RRT* [85] algorithm, the algorithm proposed in this paper is more effective with regard to path generation time and memory usage. As some path planning algorithms cannot guarantee the optimization memory and smoothness of the trajectory when a mobile robot completes a complex task, a bidirectional RRT (KB-RRT) algorithm based on kinematic constraints is proposed [86]. This algorithm limits the number of generated nodes without affecting its accuracy and uses kinematic constraints to generate a smoother trajectory. Compared to the bidirectional RRT [54] algorithm in three highly cluttered environments, the KB-RRT algorithm reduces the number of nodes and the running time and significantly improves memory utilization.
A Q-RRT* algorithm was suggested [87], which may be used with a sampling technique to further enhance the performance and demonstrates superior initial solution and convergence speed than the RRT* algorithm. A dual-tree expansion approach called Bi-RRT has been suggested [88] as being more effective than single-tree expansion. The initial and target points serve as the starting points for the expansion of the random tree by the algorithm. After choosing a random node, two trees are chosen one at a time, randomly extended on top of that, and their expansion orders are exchanged in the following iteration. A closed-loop stochastic dynamic path planning algorithm based on incremental sampling techniques was described in [89] as a closed-loop rapid exploration random tree (CL-RRT) algorithm. Here, in the autonomous underwater robot model, three fuzzy controllers were used to assess the scope of the search tree and whether the vertices satisfy the incomplete dynamic constraints of the autonomous underwater robot. The ability of CL-RRT to locate collision-free pathways in 3D environments with crowded obstacles was demonstrated using an Extended PC (xPC) target generator. According to the experimental results on terrain barriers and floating objects, AUVs can approach the ideal path considerably more quickly, and a study [90] suggests that a concentrated search employing heuristic ellipsoidal subset sampling improves the RRT* method.
An informed RRT* (IRRT*) algorithm was developed [91], which integrates the skewed cylindrical subset integration method into the RRT* algorithm for optimal unmanned aerial robot path planning. According to the experimental findings, the IRRT* algorithm is superior to the traditional RRT* method in terms of optimizing the path length and ensuring safe flying over a larger search region. A study [92] proposes a biased sampling potentially guided intelligent bidirectional RRT* (BPIB-RRT*) algorithm, which combines the bidirectional artificial potential field method with the idea of bi-directional biased sampling. This technique adapts the sample space with flexibility, considerably minimizing incorrect spatial sampling, and accelerating convergence. The advantage of the BPIB-RRT* algorithm suggested in this study is demonstrated by the simulation results.
The fast search random tree algorithm can efficiently explore the path and find the optimal solution in a complex environment, but its path quality is unstable, and there may be jitters. In the future, it can be combined with fuzzy control and machine learning to improve path stability.
2.5.2. Probabilistic Roadmap Method
The probabilistic roadmap method (PRM) algorithm is based on state–space sampling. It first uses random sampling to build a path network graph in the environment, converts continuous space into discrete space, and then performs path planning on the path network graph to solve the problem of low search efficiency in high-dimensional space. As it is difficult to use offline path planning to plan available paths in a dynamic and complex environment with narrow corridors when mobile robots perform tasks, a probabilistic path map algorithm based on obstacle potential field sampling strategy called the obstacle potential field probabilistic path map algorithm (OP-PRM) has been proposed [93]. The specific area of the obstacle is determined by introducing the potential field of the obstacle. The area of a certain range near the obstacle is taken as the target sampling area, and the number of sampling points in the narrow area is increased. After constructing the random road map, the incremental heuristic D* Lite algorithm is used to search for the shortest path between the starting point and target point on the road map. The simulation results reveal that this method can enable a robot to pass through a narrow corridor in a dynamic and complex environment. In [94], a hierarchical planning method for remote navigation tasks was proposed by combining PRM with reinforcement learning (PRM-RL). PRM-RL uses reinforcement learning to build a road map to ensure its connectivity instead of using collision-free linear interpolation in the C space of ships, and the road map built by PRM-RL follows robot dynamics and task constraints. This method can complete a planning task in a large environment.
Compared to the RRT algorithm, the PRM algorithm has a path that is less likely to jump around and is more stable. However, it takes a long time to calculate, so it is not good for real-time applications. In the future, we plan to develop methods that can quickly build a road map to reduce calculation time.
2.6. Planner-Based Algorithms
2.6.1. Covariant Hamilton Optimization Motion Planning
The covariance Hamiltonian optimal motion planning (CHOMP) is a gradient-based trajectory optimization program that makes many daily motion planning problems simple and trainable. Although most high-dimensional motion planners divide trajectory generation into different planning and optimization stages, the algorithm uses covariant gradient and functional gradient methods to design a motion planning algorithm that is completely based on trajectory optimization in the optimization stage. In [95], several methods for adapting CHOMP to vehicles with incomplete constraints were presented. These included using a separate objective function to constrain the curvature, integrating CHOMP with a smooth target, and introducing sliding and rolling constraints on the trajectory. In this study, experiments were carried out in real-world scenarios to help trucks with trailers avoid obstacles. In [96], an improved CHOMP algorithm was used for local path planning in automatic driving. An objective function that took into account the path’s deviation and the vehicle’s kinematic constraints was also added to create the right path. The research in this paper shows that, compared with traditional methods, the CHOMP algorithm has obvious advantages in terms of time and cost when used for path planning in automatic driving.
2.6.2. Trajectory Optimization for Motion Planning
Trajectory optimization (TrajOpt) is a sequential convex optimization algorithm for motion-planning problems. It relaxes non-convex, non-radial equality, and inequality constraints and uses approximate linearization and convexity to create an objective function. In [97], a new navigation framework was proposed that uses an enhanced version of TrajOpt for rapid 3D path planning of autonomous underwater vehicles. This study was also the first to apply TrajOpt to the 3D path planning of mobile robots.
2.7. Constraint Satisfaction Problem-Based Algorithms
2.7.1. Chance Constrained Programming
Chance–constrained programming is a method that achieves the best performance with a certain sense of probability. This is a random programming method that is suitable for a problem in which constraint conditions contain random variables and the decision must be made before the realization of the random variables is observed. In [98], a general chance–constrained trajectory planning formula was proposed that can deal with the non-Gaussian mixture distribution of the agent position. To strengthen the chance–constraint, a framework is proposed to generate an expression using a symbolic function. Based on the statistical moment of the basic distribution, the generated expression sets the upper limit of the polynomial chance–constraint. However, this study produced overly conservative results. In [99], a real-time method was proposed to solve a chance–constrained motion-planning problem with dynamic obstacles. The obstacles were considered to have uncertain locations, models, and interference in the form of additive Gaussian noise. In addition, this study developed a closed-form differentiable bound on the set probability to safely approximate the disjunction chance–constrained optimization problem to a nonlinear program. Experimental results revealed that, compared with other real-time methods, it reduces the degree of conservatism relatively and can still effectively control a mobile robot when considering multiple obstacles.
2.7.2. Model Predictive Control
Model predictive control is an advanced control method of the control process in process control that is mainly used for tracking the lane line in automatic driving to keep the vehicle track relatively stable when specific constraints are met. The MPC reconstructs the task of lane tracking into the problem of finding the optimal solution. The optimal solution to the optimization problem is the optimal trajectory. Every step we take will solve an optimal trajectory based on the current state, then the trajectory, and then the optimal trajectory will be solved again based on the new value from the sensor. This is performed to make sure that the trajectory and the lane line we want to track fit together as well as possible. Because autonomous vehicles exhibit poor performance in emergency obstacle avoidance, in [100], a new model predictive controller combined with a potential function was proposed to deal with complex traffic scenarios. To improve the security of the potential function, a sigmoid-based secure channel (SPMPC) was embedded in the MPC constraint, and a specific trigger analysis algorithm for monitoring traffic emergencies was designed. In two-lane and three-lane simulation experiments, the methods proposed in this study can successfully avoid obstacles that suddenly change lanes. In [101], an optimal guidance method based on MPC considering the current disturbance was proposed, and a path-tracking controller was designed by combining it with adaptive dynamic sliding mode control technology. This method can be applied not only to autonomous underwater vehicles but also to the path planning of other unmanned vehicles.
2.7.3. Quadratic Programming
Quadratic programming is used to solve nonlinear programming problems. The objective function is quadratic. The constraint conditions are the same as those of the linear programming problem, that is, linear or linear inequalities. As UAVs need to operate safely at high speeds in unknown environments, yet the realization of this operation usually leads to a slow and conservative trajectory, a fast and safe trajectory planner was proposed in [102] to solve these problems. The fast–safe trajectory planner obtains a high-speed trajectory by optimizing the local planner in known and unknown space and proposes a mixed integer quadratic programming formula. Finally, in the simulation flight experiment and an actual flight experiment, it was determined that the UAV successfully reached 3.6 m/s. In [103], an autonomous motion planning framework, including path planning and path generation, was proposed. In this framework, the PRM algorithm was used to first plan a safe path, and then the problem of minimizing the differential thrust and positioning clearance polynomial path was converted into unconstrained quadratic programming, which was solved in a two-step optimization. Compared with other methods, this method achieves higher computational efficiency and plans a safe trajectory.
2.7.4. Soft-Constrained Programming
The soft constraint generates a force on the robot to keep it away from obstacles. The most intuitive representation is the distance description. The Euclidean symbolic distance field (ESDF) is very important for evaluating the gradient size and direction in the gradient planner of a four-rotor UAV. However, it only covers a very limited subspace during trajectory optimization. In [104], a gradient-free programming framework based on ESDF was proposed. The collision term in the penalty function is established by comparing the collision trajectories and collision-free guidance paths. We introduce an anisotropic curve-fitting algorithm to change the high-order derivative of the trajectory without changing its shape. Experiments in the real world have verified its robustness and efficiency. In [105], a four-rotor UAV motion-planning system for rapid flight in a complex three-dimensional environment was proposed. The dynamic path search method was used to find a safe, dynamic, feasible, and minimum-time initial trajectory in the discrete control space. We improve the smoothness and clearance of the trajectory through B-spline optimization, which combines the gradient information and dynamic constraints of the Euclidean distance field and effectively utilizes the convex hull characteristics of the B-spline. Finally, by representing the final trajectory as a nonuniform B-spline, the iterative time adjustment method was adopted to ensure a dynamic, feasible, and nonconservative trajectory. This method was verified for real, complex scenes.
2.8. Other Algorithms
2.8.1. Differential Evolutionary Algorithm
Differential evolution (DE) is an effective global optimization approach. In addition, it uses a population-based heuristic search technique in which each member of the population represents a solution vector. This is similar to genetic algorithms. DE is another global optimization technique that comprises operations for selection, crossover, and compilation. DE also differs from genetic algorithms in that the variance vectors in the different evolution are generated from the variance vectors of the parents. Additionally, it directly chooses from the parent individuals and intersects the parent’s vectors to create a new individual vector. A new prediction-based path evaluator was designed to assess the fitness of possible paths by introducing a differential evolution algorithm as an optimizer [106]. The experimental results demonstrate that this method helps autonomous underwater robots make full use of ocean currents and effectively avoid collisions. Additionally, the control points produced by the B-spline were optimized using a differential evolutionary method [107]. This enables the autonomous underwater robot to successfully navigate a variety of obstacles in 3D space. The cost function used for methodology in this study accounted for the kinematic restrictions placed on the autonomous underwater robots’ sway, yaw, and pitch components. The results of the experiments were reported. The projected trend can be fully utilized for autonomous underwater robot path planning based on a differential evolutionary algorithm to address unforeseen perturbations.
The differential evolution algorithm has a strong global optimization ability and can find the global optimal solution or a solution close to the optimal solution. However, compared with those of other algorithms, its convergence speed is low. In the future, we need to focus on improving its efficiency and accuracy.
2.8.2. Biogeography Optimization Algorithm
Dan Simon proposed the Biogeography-Based Optimization (BBO) algorithm in 2008 [108], which has the same characteristics as other biology-based optimization methods (genetic algorithms and particle swarm optimization). Therefore, BBO can be used to solve many of the same problems that GA and PSO can, including high-dimensional problems with multiple local optima. A two-stage recursive task planning system for autonomous underwater robots based on the BBO algorithm was designed, and simulation experiments were conducted for three scenarios, which demonstrated that the algorithm is significantly effective in real-time [109].
2.8.3. Level Set Approach
The level set method (LSM) is a numerical technique for interface tracing and shape modeling [110]. The benefits of using the LSM are that evolving curved surfaces can be numerically calculated on a cartesian grid without the need to parameterize the surfaces, and the topological changes of an object can be easily tracked. Therefore, this approach can be utilized to address issues caused by underwater dynamics. LSM was used in studies [111,112] to reconcile the ocean-current problem with the planning time. A time-optimized LSM and a 3D ocean modeling optimization technique were combined [113]. This plan makes it possible to predict ocean currents and makes it easier to quickly coordinate autonomous underwater robot dynamic control plans. Stochastic dynamic orthogonal level set equations that can be used in dynamically varying current fields were derived, and a simplified form for numerical implementation was obtained [114]. The results demonstrate that the new algorithm is accurate and efficient. To address the problems of low computational efficiency and long planning times in autonomous underwater robot multiterminal route planning, the traditional level set function was localized, and a polynomial distance regularized (P-DRE) term was introduced to derive a new discrete iterative equation that improves the computational efficiency of the level set algorithm.
2.8.4. Fast Marching Method
The fast marching (FM) algorithm [115] is comparable to Dijkstra’s algorithm, except that Dijkstra’s algorithm updates with the Euclidean distance between two nodes, whereas the FM method updates a rough partial differential equation simplified by a non-linear Eikonal equation. The FM algorithm is applied in a large 3D environment for autonomous underwater robots and solves the pathfinding problems of autonomous underwater robots in terms of navigation, safety, and energy consumption. A hybrid search fast marching method (HSFM) based on the FM algorithm has been proposed [116]. The algorithm takes into account underwater undercurrents based on the relationship between the gradient lines and feature lines in a velocity profile. It also takes into account several constraints and decision criteria, such as currents, shoals, reefs, dynamic obstacles, and navigation rules, while reducing the paths and time. Thus, autonomous underwater robots are now more competitive in dynamic underwater obstacle avoidance. A novel FM method paired with the A* algorithm has been suggested [117] as a way to improve search precision and produce a finite curvature that can be used by autonomous underwater robots of all sizes.
2.8.5. Fuzzy Logic Method
By mimicking the ability of the human brain to evaluate uncertainty and make decisions based on environmental data and fuzzy rules, fuzzy logic can solve the path planning problem. To solve the problem of autonomous underwater robots being prone to receive sea-current interference when performing underwater path planning, a fuzzy optimization technique based on auto-disturbance rejection control (ADRC) was suggested to increase the adaptation of autonomous underwater robots to the marine environment by including ADRC to manage sea-current interference [118]. The findings of this trial demonstrate that the autonomous underwater robot can exert superior control in a challenging marine environment. An optimized fuzzy control algorithm was proposed for the autonomous underwater robot 3D path planning problem [119]. Horizontal and vertical sonar planes were used to collect the environmental data. A fuzzy system with an acceleration module was used to calculate the acceleration values, and an optimal fuzzy set was created by contrasting the two optimization techniques to determine the best course of action. The results of the experiments demonstrate that the method can complete the path planning of a 3D autonomous underwater robot. The change in distance between the autonomous underwater robot and obstacles was employed as an extra input to the fuzzy affiliation function [120] because it is challenging to determine the speed of obstacles moving in the actual world. When obstacles move quickly, the results demonstrate that the proposed method performs noticeably better than the conventional fuzzy logic algorithm.
The biggest advantage of the fuzzy logic algorithm is that it does not require an accurate mathematical model, and its operation principle is basically similar to human cognition. However, its definition of fuzzy rules depends on people’s experiences, and it cannot adapt to complex environments. Future research needs to focus on developing more intelligent path planning algorithms so that robots can adjust their paths intelligently according to environmental changes and user needs.
2.9. Discussion
Table 1 summarizes the advantages and disadvantages of each path planning algorithm. Both the A* and Dijkstra algorithms are classic algorithms based on graph search that are used to solve the shortest path problem. They can deal with path planning problems in a static environment, but the A* algorithm can find the optimal solution faster with the introduction of a heuristic function. Their disadvantage is that they cannot effectively address the path planning problem in a dynamic environment. Genetic algorithms typically perform many evolutionary operations. Therefore, they take up a considerable amount of storage space, and there are more parameters to be adjusted, resulting in a slower convergence speed. The advantage of the genetic algorithm is that it has a strong global search ability and can overcome the suboptimal solution of the A* algorithm. Similar to genetic algorithms, differential evolution algorithms also have genetic operators such as selective crossover mutations, which can be defined in different ways. The excellent robustness of differential evolution algorithms in a wide range of path planning applications has been proven in practice.

Table 1.
Summary of robot path algorithms.
The ant colony and particle swarm algorithms are bionic methods inspired by the behavior mechanisms of natural biological groups. They can adapt to the environment in a short time with the cooperation of individual organisms. The ant colony algorithm guides the search process by simulating the behavior of ants when searching for food through the role of pheromones and the process of pheromone volatilization, finally finding the optimal solution. The particle swarm algorithm simulates the collective behavior of birds and fish and finds the optimal solution by constantly adjusting the position of the particles. However, both the ant colony and particle swarm algorithms have their limitations, resulting in slow convergence. The RRT and PRM algorithms are sampling-based random algorithms that can be used to solve path planning problems in spaces with a lot of dimensions and complex shapes. Among them, the RRT algorithm leverages random sampling and can obtain feasible paths in a short time, but it is difficult to guarantee the quality of the paths. However, it can obtain better paths by building a road network; however, it requires a longer calculation time to achieve this.
The artificial potential field method is a path planning method based on a physical model that is suitable for path planning in a dynamic environment. It describes the environment and target location by defining the physical potential field to avoid obstacles and determine the optimal path. However, they can easily fall into a locally optimal solution in a complex environment. The dynamic window method is a path planning method based on control theory that can quickly give path planning results. It combines the motion model of the robot with the environment model and uses the window model to describe the motion state of the robot to evaluate the feasible motion trajectory. However, the calculation time increases with an increase in the dimensions of the robot’s state space. The TEB algorithm is based on time-space path planning and can deal with the motion and obstacle avoidance of robots in complex environments. Using the time expansion method, it changes the robot’s movement path into a time-space manifold. This makes it easier to optimize the path and avoid obstacles. However, this requires considerable computing resources and time. Reinforcement learning has a strong decision-making ability and can be used to plan an optimal path without any prior knowledge. Additionally, reinforcement learning exhibits strong adaptability and flexibility in complex and uncertain environments. Compared with other traditional path planning algorithms, such as the A* and Dijkstra algorithms, reinforcement learning does not require specific forms of objective functions. In addition, reinforcement learning can learn and adjust adaptively to optimize path planning. Traditional algorithms, such as swarm intelligence algorithms, typically need to set parameters manually and lack self-adaptability. However, reinforcement learning requires considerable training data, computing resources, and long training times.
3. Multi-Robot
Multi-robot collaboration technology remains of significant interest in robotics. When multiple robots share the same environment, collisions between them must be considered. To solve the problems of obstacle avoidance and collisions between the robots in multi-robot systems during formation, a method for obstacle avoidance and consistent formation control based on the improved artificial potential field method (IAPF) was proposed [121]. To solve the local minimum and target unreachability problems in the artificial potential field method, a rotating potential field was established. To avoid the collision problem between multi-robot systems, a repulsive potential function, and a robot priority model are set, and the consistency-based formation principle is used to design a stable topology for multi-robot formation control. The simulation results demonstrate that the method can effectively solve the obstacle avoidance problem of a multi-robot system during the formation process. To solve the control problem during multi-robot navigation, a shortest distance algorithm was proposed [122], which uses the current positions and directions of other robots to calculate collision-free trajectories and is based on the concept of relative orientation to ensure smooth and collision-free trajectories. To address the poor robustness and low exploration efficiency of traditional robotic collaborative exploration algorithms, a multi-robot collaborative spatial exploration method based on a rapidly expanding random tree-greedy frontier search (RRT-GFE) was proposed in [123]. The boundary points in the environment map were refined by proposing an improved boundary exploration algorithm to improve the maximum gain of exploring the target points. The exploration target points are dynamically assigned by introducing an improved task assignment algorithm, thus reducing the time required and improving the efficiency of multi-robot exploration. Simulations and prototype experiments were used to prove that the proposed method works and is reliable.
An elite group-based evolutionary algorithm (EGEA) that combines the key benefits of both approaches while integrating a group-based framework and an elite selection method for evolutionary path planning was proposed [124]. Due to the group-based architecture, each descendant of the evolutionary algorithm is allowed to provide its own set of novel solutions with a specified probability. The PSO and SA approaches are also presented to address the adaptive ocean sampling issue. According to the simulation results, the EGEA-based planner was superior and more reliable. A non-stop collision-free path planning system was proposed [125], which consists of a combination of a novel B-spline data frame and a particle swarm optimization-based solution engine. Using the unique B-spline data frame structure, candidate points can be intelligently sampled without having to suspend the sampling job. For several unmanned surface vehicles (USVs) to complete the sampling task from the starting point to the rendezvous point, the PSO-based solution engine creates optimal, smooth, constraint-aware path profiles. The applicability and reliability of the proposed path planning system for non-stop ocean sampling jobs are confirmed by simulation results.
A distributed velocity-aware algorithm and a method for avoiding collisions between multiple unmanned aerial robots have been proposed [126]. These are used to plan the paths of many unmanned aerial robots and prevent them from running into each other. The acceleration vectors on the pathways created by the velocity-aware algorithm converged at a preset location. When path conflicts are anticipated, the collision avoidance algorithm is activated to safeguard unmanned aerial robots from collisions. Compared to the hierarchical control model and the Lyapunov control method, this method improves the success rate of unmanned aerial robot mission execution and shortens the path. In [127], a time-stamped partitioning model was used to make it easier to process coordination costs between unmanned aerial robots. This was conducted to solve the problem of planning an optimal path for multiple unmanned aerial robots in a limited mission environment. A novel hybrid method (called HIPSO-MSOS) was subsequently proposed by fusing the improved particle swarm algorithm (IPSO) and modified symbiotic organisms research (MSOS). The experimental results demonstrate that the HIPSO-MSOS algorithm has considerable advantages in terms of accuracy, convergence speed, and stability and can successfully construct feasible and efficient pathways for each unmanned aerial robot. For the collaborative detection problem of avoiding collisions in three-dimensional space, a method based on adaptive DE and distributed model predictive control was proposed [128]. The control scheme incorporates an adaptive improvement of the DE algorithm and introduces an adaptive selection of the prediction range. In addition, the asymptotic convergence of the rolling optimization is analyzed. The simulation results demonstrate the effectiveness of the proposed control strategy. For the problem of path planning and formation control of multiple unmanned aerial robots in three-dimensional space, a multi-unmanned aerial robot path planning method based on an improved artificial potential field method [129] was proposed, which can effectively avoid local minima by introducing a rotating potential field. Using the leader-follower model, a formation controller based on the potential field function method is designed to ensure that the expected angle and distance between the follower unmanned aerial robot and the leader unmanned aerial robot are maintained. The simulation results demonstrate that the method is significantly effective in achieving path planning and formation control for multi-unmanned aerial robot systems. A multi-unmanned aerial robot path planning model with an energy constraint (MUPPEC) has been suggested [130] as a solution to the problem of multi-unmanned aerial robot energy consumption constraints when conducting monitoring activities. To reduce the monitoring time, MUPPEC primarily considers the unmanned aerial robot in various energy-consuming modes, such as accelerating and hovering. For the MUPPEC issue, a hybrid discrete grey wolf optimizer (HDGWO) based on grey wolf optimization is suggested. In HDGWO, a discrete grey wolf update operator is implemented, and the discrete problem space and grey wolf space are transformed using integer encoding and the greedy method. According to the experimental results, HDGWO can successfully solve the MUPPEC problem. In reference [131], a multi-objective optimization algorithm, called the angle-coded particle swarm optimization (θ-PSO), is proposed for multi-unmanned aerial robots performing infrastructure surface inspection tasks to find feasible obstacle-free paths for the entire formation by minimizing a cost function that combines multiple constraints on the shortest path and safe unmanned aerial robot operations. The experimental results demonstrate the effectiveness and feasibility of the method. A study [132] suggests a two-stage reinforcement-learning-based algorithm for collision-free path planning for many unmanned aerial robots. The policy is optimized using supervised training with a loss function that encourages the intelligence to follow a shared collision-free policy in the first stage. In the second stage, a policy gradient was used to hone the policy. The technique may produce time-effective and collision-free pathways in environments that are aware of uncertainty, according to the simulation data.
Table 2 summarizes the advantages and disadvantages of multi-robot cooperative path planning. In the field of robot technology, multi-robot cooperative path planning is an important area of research. In the future, multi-robot cooperative path planning may develop in the following aspects: Given the problems of high computational complexity and long running time in multi-robot cooperative path planning, it is necessary to study how to improve efficiency and real-time path planning in the future. Dynamic changes often occur in the working environment of robots, such as the emergence of new obstacles and the actions of other robots. Therefore, future multi-robot cooperative path planning needs to consider the dynamic changes of the environment and be able to respond and adapt in time. In addition to path planning, cooperation between robots is also a very important part of a multi-robot cooperation system. In the future, cooperation strategies among robots will need to be studied to achieve more efficient and intelligent multi-robot cooperation.

Table 2.
Summary of multi-robot path algorithms.
4. Ground Robot, Unmanned Aerial Robots Cooperative
Owing to the numerous applications in target tracking, intelligent surveillance, automated package delivery missions, and disaster rescue, research regarding unmanned aerial robot/ground robot cooperative detection systems has gained considerable momentum. For unmanned aerial robots and ground robots to simultaneously function in a system to complete missions, path planning for unmanned aerial robot/ground robot cooperative systems is a critical yet challenging problem. The path planning problem was modeled as a constrained optimization problem that attempted to minimize the overall execution time to complete an illegal urban building inspection task. Then, a two-level modal algorithm (called Two-MA) was proposed to solve the path planning problem for unmanned aerial robots and ground robots, finding the path with the shortest task execution time from both the node and cluster levels [133]. The experimental results validate that Two-MA outperforms classical algorithms in finding the path with the shortest task execution time to detect nonstandard buildings in cities. A collaborative unmanned aerial robot–ground robot system was developed [134] to implement unmanned aerial robot-assisted ground robot path planning. First, the unmanned aerial robot performs target detection by semantic segmentation, extracts information regarding ground obstacles, presents the obstacles in a circular approximation, and proposes an algorithm to derive the optimal collision avoidance trajectory for unattended ground robots using strict concave-convex planning techniques. According to the simulation findings, the path developed by the suggested path planning algorithm can successfully minimize ground robot collisions while attaining good energy efficiency. To decouple their routing based on air-ground cooperation, a two-step technique combining ant colony optimization and evolutionary algorithms was demonstrated [135] for the path planning problem of heterogeneous robotic systems used to deliver parcels in urban environments. ACO is utilized in the initial stage to identify the routes for the ground robots. Once the ground robot route has been predetermined in the first stage, the unmanned aerial robot route is solved using a genetic algorithm in the second stage. The simulation findings demonstrate the ability of the method to successfully address the issue of unmanned aerial robot heterogeneous distribution and choose the best course for unmanned aerial robots. A collaborative unmanned aerial robot-ground robot path planning method for dynamic environments was proposed by performing a semantic segmentation of images acquired from the perspective of an unmanned aerial robot through deep neural networks [136]. The method was evaluated in a car parking scenario to provide path planning for ground robots leading to empty parking spaces. For heterogeneous ground air robots, a tightly connected perception and navigation paradigm was suggested [137]. The primary contributions of this study are the derivation of high-level coordination methods and low-level goal-directed navigation in a completely integrated manner, as well as the provision of a unified framework for formulating collaborative navigation issues. The ability of the system to execute collaborative mapping and navigation in both structured and unstructured domains was demonstrated by the experimental findings.
5. Discussion
Path planning is an important research branch for improving the autonomy of mobile robots and has attracted the attention of researchers all over the world in recent decades. Although many path planning algorithms have been proposed and implemented in mobile robots, they have several drawbacks and limitations that need to be further explored.
(1) Although a variety of classical algorithms are widely used for traditional path planning, they have several shortcomings. Their adaptability to complex environments is unsatisfactory, and their ability to model and process an environment is limited to a certain extent. This is especially true in complex environments, which are hard to adapt to and process, which makes path planning less efficient and accurate. For example, in practical applications such as human–machine cooperation, multi-robot cooperation, and other scenarios, often involving a complex environment and a variety of different robots, the traditional A* and Dijkstra algorithms are not appropriate. Some traditional algorithms have problems such as endless cycles and perform repeated searches in the process of path search. This leads to low efficiency of the algorithm and affects its practical application. Traditional algorithms are often based on static environment modeling and path search. This means that they cannot be adaptively adjusted based on the actual environment and robot behavior, resulting in insufficient robustness and adaptability in path planning.
(2) Most of the current algorithms are based on improving their characteristics and demonstrating good results. However, the results are better when used with different algorithms as opposed to individual algorithm improvements. No single path planning algorithm can solve all the path planning problems in practical applications, especially in complex environments. Moreover, it is difficult to research new algorithms, so it is expected that more combined path planning algorithms will appear in the future to make up for each other’s deficiencies.
(3) The development of path planning techniques based on reinforcement learning and the derived deep reinforcement learning has important implications. Based on the current state of development and the needs for future development, the following are some possible directions for future research on path planning techniques based on reinforcement learning methods: designing reward functions, studying combinations with conventional path planning methods, and applying reinforcement learning to collaborative path planning for multiple intelligences. However, reinforcement learning, which involves trial-and-error learning and state generalization, consumes a lot of resources. Recently, brain science and brain-like intelligence have become hot spots for research and competition all around the world. Brain-like intelligence is capable of intelligent information acquisition, intelligent information processing and communication, and intelligent human–computer interaction. This meets the needs of intelligent path planning. By mimicking and interacting with the environment to carry out actions and plan, brain-like intelligence has the ability of autonomous development and can learn with a small number of samples, thus solving the defect of resource waste in reinforcement learning and making robots have the developmental capacity, gradually improving the intelligence level of path planning.
(4) Research on multi-robot cooperative path planning is gaining more attention as the robotic working environment is being extended, task complexity is increasing, and the application area is being enlarged. The system must efficiently, rapidly, and precisely coordinate several robots to cooperate and execute multiple tasks in tandem. This system entails not only path planning but also communication between each robot and the cooperative control, on the basis that members exchange messages.
(5) The possible future research directions and hotspots for mobile robot path planning are as follows: (1) Multi-robot cooperative path planning. With an increase in the number of robots, multi-robot cooperative path planning has become an important research direction. Future research will focus on cooperative actions among multiple robots, such as collaboration on industrial production lines and search and rescue missions in the wild; (2) performance improvement of path planning algorithms. Presently, many path planning algorithms take a long time to find the global optimal solution; thus, improving the efficiency of the algorithm has become a research hotspot. Future research will focus on improving the efficiency of the algorithm, reducing computation time, and adopting a new algorithm framework to solve this problem; (3) path planning based on reinforcement learning. Reinforcement learning has achieved great success in many fields and has great potential for use in mobile robot path planning. Future research will focus on how to use deep learning to plan routes and move from lab experiments to real-world applications; (4) planning routes by combining data from multiple sensors. The continuous development of sensor technology provides more information sources for robot path planning. Future research will pay more attention to how to fuse information from multiple sensors for path planning and verify its effect in practical applications.
6. Conclusions
With the development of intelligent techniques and industrial automation, path planning for mobile robots is one of the hot research topics in the field of robotics both domestically and internationally. This paper reviews the application fields of the current path planning algorithms and their improvement/optimization of them in four aspects, including ground robots, underwater robots, aerial robots, and collaborative robots. For each aspect, the path planning algorithms are analyzed, and their improvement measures, advantages, and disadvantages are discussed. Finally, a summary discussion is made to provide a reference for path planning for mobile robots.
Author Contributions
Conceptualization, S.S.; methodology, S.S. and H.Q.; investigation, H.Q.; resources, S.S. and T.W.; writing—original draft preparation, H.Q.; writing—review and editing, H.Q., S.S. and X.Y.; supervision, Y.J.; project administration, Z.C.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number U20A20201), the Natural Science Foundation of Liaoning Province (grant number 2021-MS-032), the Independent Project of the State Key Laboratory of Robotics (grant number 2022-Z02 and 2022-Z19).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tang, B.W.; Zhu, Z.X.; Luo, J.J. Hybridizing particle pswarm optimization and differential evolution for the mobile robot global path planning. Int. J. Adv. Robot. Syst. 2016, 13, 86. [Google Scholar] [CrossRef]
- Wahab, M.N.A.; Nefti-Meziani, S.; Atyabi, A. A comparative review on mobile robot path planning: Classical or meta-heuristic methods? Annu. Rev. Control 2020, 50, 233–252. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. A Review of Path-Planning Approaches for Multiple Mobile Robots. Machines 2022, 10, 773. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A Consolidated Review of Path Planning and Optimization Techniques: Technical Per-spectives and Future Directions. Electronics 2021, 10, 2250. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, J.; Sun, N. A Review of Collaborative Air-Ground Robots Research. J. Intell. Robot. Syst. 2022, 106, 60. [Google Scholar] [CrossRef]
- Klančar, G.; Zdešar, A.; Krishnan, M. Robot Navigation Based on Potential Field and Gradient Obtained by Bilinear Interpolation and a Grid-Based Search. Sensors 2022, 22, 3295. [Google Scholar] [CrossRef]
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328. [Google Scholar] [CrossRef]
- An, D.; Mu, Y.; Wang, Y.; Li, B.; Wei, Y. Intelligent Path Planning Technologies of Underwater Vehicles: A Review. J. Intell. Robot. Syst. 2023, 107, 22. [Google Scholar] [CrossRef]
- Khalidi, D.; Gujarathi, D.; Saha, I.T. A heuristic search based path planning algorithm for temporal logic specifications. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8476–8482. [Google Scholar]
- Lim, J.; Tsiotras, P. A generalized A* algorithm for finding globally optimal paths in weighted colored graphs. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May 2021–5 June 2021; pp. 7503–7509. [Google Scholar]
- Zhong, X.; Tian, J.; Hu, H.; Peng, X. Hybrid path planning based on safe A* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment. J. Intell. Robot. Syst. 2020, 99, 65–77. [Google Scholar] [CrossRef]
- Li, Y.; Ma, T.; Chen, P.; Jiang, Y.; Wang, R.; Zhang, Q. Autonomous underwater vehicle optimal path planning method for seabed terrain matching navigation. Ocean Eng. 2017, 133, 107–115. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Zhang, G.; Hsu, L.T. A new path planning algorithm using a GNSS localization error map for UAVs in an urban area. J. Intell. Robot. Syst. 2019, 94, 219–235. [Google Scholar] [CrossRef]
- Primatesta, S.; Guglieri, G.; Rizzo, A. A risk-aware path planning strategy for UAVs in urban environments. J. Intell. Robot. Syst. 2019, 95, 629–643. [Google Scholar] [CrossRef]
- Yewei, Z.; Jianhao, T.; Yaonan, W. Highly time-efficient trajectory planning strategy for rotorcraft in 3-dimensional complex mountain environment. Robotics 2016, 38, 727–737. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, C.; Yang, D.; Pan, G.; Zhang, F. Path Planning in Localization Uncertaining Environment Based on Dijkstra Method. Front. Neurorobotics 2022, 16, 821991. [Google Scholar] [CrossRef] [PubMed]
- Balado, J.; Díaz-Vilariño, L.; Arias, P.; Lorenzo, H. Point clouds for direct pedestrian pathfinding in urban environments. ISPRS J. Photogramm. Remote Sens. 2019, 148, 184–196. [Google Scholar] [CrossRef]
- Kirsanov, A.; Anavatti, S.G.; Ray, T. Path planning for the autonomous underwater vehicle. In Proceedings of the International Conference on Swarm, Evolutionary, and Memetic Computing, Chennai, India, 19–21 December 2013; Volume 8298, pp. 476–486. [Google Scholar]
- Naigong, Y.; Chen, W.; Fanfan, M. Dynamic environmental path planning based on Q-learning algorithm and genetic algorithm. J. Beijing Univ. Technol. 2017, 43, 1009–1016. [Google Scholar]
- Qu, H.; Xing, K.; Alexander, T. An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots. Neurocomputing 2013, 120, 509–517. [Google Scholar] [CrossRef]
- Ataei, M.; Yousefi-Koma, A. Three-dimensional optimal path planning for waypoint guidance of an autonomous underwater vehicle. Robot. Auton. Syst. 2015, 67, 23–32. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Fallahi, K.; Leung, H.; Tse, C.K. An AUVs path planner using genetic algorithms with a deterministic crossover operator. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2995–3000. [Google Scholar]
- Dai, R.; Fotedar, S.; Radmanesh, M.; Kumar, M. Quality-aware UAV coverage and path planning in geometrically complex environments. Ad Hoc Netw. 2018, 73, 95–105. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, P.; Ru, Y.; Wu, D.; Wang, S.; Yin, N.; Meng, F.; Liu, Z. A scheduling route planning algorithm based on the dynamic genetic algorithm with ant colony binary iterative optimization for unmanned aerial vehicle spraying in multiple tea fields. Front. Plant Sci. 2022, 13, 998962. [Google Scholar] [CrossRef] [PubMed]
- Sathyan, A.; Ernest, N.D.; Cohen, K. An efficient genetic fuzzy approach to UAV swarm routing. Unmanned Syst. 2016, 4, 117–127. [Google Scholar] [CrossRef]
- Rajput, U.; Kumari, M. Mobile robot path planning with modified ant colony optimisation. Int. J. Bio Inspired Comput. 2017, 9, 106–113. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, H.; Zheng, Y.; He, J. Research on path planning of mobile robot based on improved ant colony algorithm. Neural Comput. Appl. 2020, 32, 1555–1566. [Google Scholar] [CrossRef]
- Cheng, C.; Sha, Q.; He, B.; Li, G. Path planning and obstacle avoidance for AUV: A review. Ocean Eng. 2021, 235, 109355. [Google Scholar] [CrossRef]
- Che, G.; Liu, L.; Yu, Z. An improved ant colony optimization algorithm based on particle swarm optimization algorithm for path planning of autonomous underwater vehicle. J. Ambient Intell. Hum. Comput. 2020, 11, 3349–3354. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.N.; Gu, T.; Yuan, H.; Zhang, H.; Zhang, J. ACO-A*: Ant colony optimization plus A* for 3-D traveling in environments with dense obstacles. IEEE Trans. Evol. Comput. 2018, 23, 617–631. [Google Scholar] [CrossRef]
- Wan, Y.; Zhong, Y.; Ma, A.; Zhang, L. An accurate UAV 3-D path planning method for disaster emergency response based on an improved multiobjective swarm intelligence algorithm. IEEE Trans. Cybern. 2022, 53, 2658–2671. [Google Scholar] [CrossRef]
- Ji, X.; Hua, Q.; Li, C.; Tang, J.; Wang, A.; Chen, X.; Fang, D. 2-OptACO: An improvement of ant colony optimization for UAV path in disaster rescue. In Proceedings of the 2017 International Conference on Networking and Network Applications (NaNA), Kathmandu, Nepal, 16–19 October 2017; pp. 225–231. [Google Scholar]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; de la Cruz, J.M. Ant colony optimization for multi-UAV minimum time search in uncertain domains. Appl. Soft Comput. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Mhs95 Sixth International Symposium on Micro Machine & Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Panigrahi, B.K. A hybridization of an improved particle swarm optimization and gravitational search algorithm for multi-robot path planning. Swarm Evol. Comput. 2016, 28, 14–28. [Google Scholar] [CrossRef]
- Wu, J.; Song, C.; Fan, C.; Hawbani, A.; Zhao, L.; Sun, X. DENPSO: A distance evolution nonlinear PSO algorithm for energy-efficient path planning in 3D UASNs. IEEE Access 2019, 7, 105514–105530. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.; Gao, L.E.; Li, L.; Zhang, F. Path planning method for AUV docking based on adaptive quantum-behaved particle swarm optimization. IEEE Access 2019, 7, 78665–78674. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Guan, X.; Delahaye, D. Adaptive sensitivity decision based path planning algorithm for unmanned aerial vehicle with improved particle swarm optimization. Aerosp. Sci. Technol. 2016, 58, 92–102. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, Y.; Xiao, G.; Liu, C.; Hu, P.; Li, H. A method of path planning for unmanned aerial vehicle based on the hybrid of selfish herd optimizer and particle swarm optimizer. Appl. Intell. 2022, 52, 16775–16798. [Google Scholar] [CrossRef]
- Huang, C. A novel three-dimensional path planning method for fixed-wing UAV using improved particle swarm optimization algorithm. Int. J. Aerosp. Eng. 2021, 2021, 7667173. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Chang, L.; Shan, L.; Jiang, C.; Dai, Y. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment. Auton. Robot. 2021, 45, 51–76. [Google Scholar] [CrossRef]
- Missura, M.; Bennewitz, M. Predictive collision avoidance for the dynamic window approach. In Proceedings of the IEEE International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 8620–8626. [Google Scholar] [CrossRef]
- Kiss, D.; Tevesz, G. Advanced dynamic window based navigation approach using model predictive control. In Proceedings of the 17th International Conference on Methods & Models in Automation & Robotics, Miedzyzdroje, Poland, 27–30 August 2012. [Google Scholar]
- Kathib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots; Springer: New York, NY, USA, 1986. [Google Scholar]
- Montiel, O.; Orozco-Rosas, U.; Sepúlveda, R. Path planning for mobile robots using Bacterial Potential Field for avoiding static and dynamic obstacles. Expert Syst. Appl. 2015, 42, 5177–5191. [Google Scholar] [CrossRef]
- Rousseas, P.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Optimal robot motion planning in constrained workspaces using reinforcement learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 6917–6922. [Google Scholar]
- Fan, X.; Guo, Y.; Liu, H.; Wei, B.; Lyu, W. Improved artificial potential field method applied for AUV path planning. Math. Probl. Eng. 2020, 2020, 6523158. [Google Scholar] [CrossRef]
- Hao, K.; Zhao, J.; Li, Z.; Liu, Y.; Zhao, L. Dynamic path planning of a three-dimensional underwater AUV based on an adaptive genetic algorithm. Ocean Eng. 2022, 263, 112421. [Google Scholar] [CrossRef]
- Huang, T.; Huang, D.; Qin, N.; Li, Y. Path planning and control of a quadrotor UAV based on an improved APF using parallel search. Int. J. Aerosp. Eng. 2021, 2021, 5524841. [Google Scholar] [CrossRef]
- Jayaweera, H.M.P.C.; Hanoun, S. Path planning of unmanned aerial vehicles (UAVs) in windy environments. Drones 2022, 6, 101. [Google Scholar] [CrossRef]
- Lin, N.; Tang, J.; Li, X.; Zhao, L. A novel improved bat algorithm in UAV path planning. J. Comput. Mater. Contin. 2019, 61, 323–344. [Google Scholar] [CrossRef]
- Roesmann, C.; Feiten, W.; Woesch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the ROBOTIK 2012: 7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; Volume 2012. [Google Scholar]
- Rosmann, C.; Feiten, W.; Wosch, T.; Hoffmann, F.; Bertram, T. Efficient trajectory optimization using a sparse model. In Proceedings of the European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013. [Google Scholar]
- Lan, A.N.; Pham, T.D.; Ngo, T.D.; Truong, X.T. A proactive trajectory planning algorithm for autonomous mobile robots in dynamic social environments. In Proceedings of the 2020 17th International Conference on Ubiquitous Robots (UR), Kyoto, Japan, 22–26 June 2020. [Google Scholar]
- Wen, Y.; Jiangshuai, H.; Tao, J.; Xiaojie, S. Improved time-elastic band trajectory planning algorithm for safe smoothing. Control. Decis. Mak. 2022, 37, 2008–2016. [Google Scholar]
- Patle, B.K.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Syed, U.A.; Kunwar, F.; Iqbal, M. Guided Autowave Pulse Coupled Neural Network (GAPCNN) based real time path planning and an obstacle avoidance scheme for mobile robots. Robot. Auton. Syst. 2014, 62, 474–486. [Google Scholar] [CrossRef]
- Bae, H.; Kim, G.; Kim, J.; Qian, D.; Lee, S. Multi-robot path planning method using reinforcement learning. Appl. Sci. 2019, 9, 3057. [Google Scholar] [CrossRef]
- Li, Q.L.; Song, Y.; Hou, Z.G. Neural network based FastSLAM for autonomous robots in unknown environments. Neurocomputing 2015, 165, 99–110. [Google Scholar] [CrossRef]
- Cao, X.; Chen, L.; Guo, L.; Han, W. AUV global security path planning based on a potential field bio-inspired neural network in underwater environment. Intell. Autom. Soft Comput. 2021, 27, 391–407. [Google Scholar] [CrossRef]
- Mu, X.; He, B.; Zhang, X.; Song, Y.; Shen, Y.; Feng, C. End-to-end navigation for autonomous underwater vehicle with hybrid recurrent neural networks. Ocean Eng. 2019, 194, 106602. [Google Scholar] [CrossRef]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Jiang, L.; Huang, H.; Ding, Z. Path planning for intelligent robots based on deep Q-learning with experience replay and heuristic knowledge. IEEE CAA J. Autom. Sin. 2020, 7, 1179–1189. [Google Scholar] [CrossRef]
- Zou, Q.; Zhang, Y.; Liu, S. A path planning algorithm based on RRT and SARSA (λ) in unknown and complex conditions. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Tai, L.; Paolo, G.; Liu, M. Virtual-to-real deep reinforcement learning: Continuous control of mobile robots for maples navigation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; Volume 2017, pp. 31–36. [Google Scholar]
- Yuan, J.; Wang, H.; Zhang, H.; Lin, C.; Yu, D.; Li, C. AUV obstacle avoidance planning based on deep reinforcement learning. J. Mar. Sci. Eng. 2021, 9, 1166. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, P.; Du, B.; Dong, B.; Zhang, W. AUV path tracking with real-time obstacle avoidance via reinforcement learning under adaptive constraints. Ocean Eng. 2022, 256, 111453. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Towards real-time path planning through deep reinforcement learning for a UAV in dynamic environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Guo, T.; Jiang, N.; Li, B.; Zhu, X.; Wang, Y.; Du, W. UAV navigation in high dynamic environments: A deep reinforcement learning approach. Chin. J. Aeronaut. 2021, 34, 479–489. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Song, B. Explainable Deep Reinforcement Learning for UAV autonomous path planning. Aerosp. Sci. Technol. 2021, 118, 107052. [Google Scholar] [CrossRef]
- Xie, H.; Yang, D.; Xiao, L.; Lyu, J. Connectivity-aware 3D UAV path design with deep reinforcement learning. IEEE Trans. Veh. Technol. 2021, 70, 13022–13034. [Google Scholar] [CrossRef]
- Wu, D.; He, J.; Han, K.; Hui, L. Cognitive navigation and its thought of brain-inspired realization in unmanned combat platform. J. Air Force Eng. Univ. (Nat. Sci. Ed.). 2018, 19, 33–38. [Google Scholar]
- Wu, W.C. Biomimetic Sensor Modeling and Simulations for Flight Control of a Micromechanical Flying Insect; University of California Berkeley: Berkeley, CA, USA, 2006. [Google Scholar]
- Tolman, E.C. Cognitive maps in rats and men. Psychol. Rev. 1948, 55, 189–208. [Google Scholar] [CrossRef] [PubMed]
- Hwu, T.; Krichmar, J.; Zou, X. A complete neuromorphic solution to outdoor navigation and path planning. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017. [Google Scholar]
- Mirowski, P.; Grimes, M.; Malinowski, M.; Hermann, K.M.; Anderson, K.; Teplyashin, D.; Simonyan, K.; Kavukcuoglu, K.; Zisserman, A.; Hadsell, R. Learning to navigate in cities without a map. Adv. Neural Inf. Process. Syst. 2018, 31, 1–9. [Google Scholar]
- Kang, Y.; Yang, Z.; Zeng, R.; Wu, Q. Smooth-RRT*: Asymptotically Optimal Motion Planning for Mobile Robots under Kinodynamic Constraints. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8402–8408. [Google Scholar]
- Webb, D.J.; Van den Berg, J. Kinodynamic RRT*: Asymptotically optimal motion planning for robots with linear dynamics. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5054–5061. [Google Scholar]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M.Q.-H. Neural RRT*: Learning-based optimal path planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Ghosh, D.; Nandakumar, G.; Narayanan, K.; Honkote, V.; Sharma, S. Kinematic constraints based bi-directional RRT (KB-RRT) with parameterized trajectories for robot path planning in cluttered environment. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8627–8633. [Google Scholar]
- Jeong, I.B.; Lee, S.J.; Kim, J. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Bekris, K.E.; Chen, B.Y.; Ladd, A.M.; Plaku, E.; Kavraki, L.E. Multiple query probabilistic roadmap planning using single query planning primitives. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Taheri, E.; Ferdowsi, M.H.; Danesh, M. Closed-loop randomized kinodynamic path planning for an autonomous underwater vehicle. Appl. Ocean Res. 2019, 83, 48–64. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, L.; Chen, Z.; Wang, H.; Shen, J. Improved rrt* for fast path planning in underwater 3d environment. In Proceedings of the 2019 International Conference on Artificial Intelligence and Computer Science, Wuhan, China, 12–13 July 2019; pp. 504–509. [Google Scholar]
- Meng, J.; Pawar, V.M.; Kay, S.; Li, A. UAV path planning system based on 3d informed rrt* for dynamic obstacle avoidance. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; Volume 2018, pp. 1653–1658. [Google Scholar]
- Wu, X.; Xu, L.; Zhen, R.; Wu, X. Biased sampling potentially guided intelligent bidirectional RRT* algorithm for UAV path planning in 3D environment. Math. Probl. Eng. 2019, 2019, 5157403. [Google Scholar] [CrossRef]
- Ye, L.; Chen, J.; Zhou, Y. Real-time path planning for robot using OP-PRM in complex dynamic environment. Front. Neurorobot. 2022, 16, 910859. [Google Scholar] [CrossRef]
- Faust, A.; Oslund, K.; Ramirez, O.; Francis, A.; Tapia, L.; Fiser, M.; Davidson, J. PRM-RL: Long-range Robotic Navigation Tasks by Combining Reinforcement Learning and Sampling-Based Planning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5113–5120. [Google Scholar]
- David, J.; Valencia, R.; Philippsen, R.; Bosshard, P.; Iagnemma, K. Gradient based path optimization method for autonomous driving. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 4501–4508. [Google Scholar]
- Schitz, D.; Bao, B.; Rieth, D.; Aschemann, H. Shared autonomy for teleoperated driving: A real-time interactive path planning approach. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 999–1004. [Google Scholar]
- Xanthidis, M.; Karapetyan, N.; Damron, H.; Rahman, S.; Johnson, J.; O’Connell, A.; O’Kane, J.M.; Rekleitis, I. Navigation in the presence of obstacles for an agile autonomous underwater vehicle. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 892–899. [Google Scholar]
- Wang, A.; Jasour, A.; Williams, B.C. Non-gaussian chance-constrained trajectory planning for autonomous vehicles under agent uncertainty. IEEE Robot. Autom. Lett. 2020, 5, 6041–6048. [Google Scholar] [CrossRef]
- Castillo-Lopez, M.; Ludivig, P.; Sajadi-Alamdari, S.A.; Sanchez-Lopez, J.L.; Olivares-Mendez, M.A.; Voos, H. A real-time approach for chance-constrained motion planning with dynamic obstacles. IEEE Robot. Autom. Lett. 2020, 5, 3620–3625. [Google Scholar] [CrossRef]
- Lin, P.; Tsukada, M. Model predictive path-planning controller with potential function for emergency collision avoidance on highway driving. IEEE Robot. Autom. Lett. 2022, 7, 4662–4669. [Google Scholar] [CrossRef]
- Wang, X.; Yao, X.; Zhang, L. Path planning under constraints and path following control of autonomous underwater vehicle with dynamical uncertainties and wave disturbances. J. Intell. Robot. Syst. 2020, 99, 891–908. [Google Scholar] [CrossRef]
- Tordesillas, J.; Lopez, B.T.; How, J.P. FASTER: Fast and safe trajectory planner for flights in unknown environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1934–1940. [Google Scholar]
- Li, Y.; Liu, C. Efficient and safe motion planning for quadrotors based on unconstrained quadratic programming. Robotica 2021, 39, 317–333. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Z.; Ye, H.; Xu, C.; Gao, F. EGO-Planner: An ESDF-Free gradient-based local planner for quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 478–485. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, F.; Wang, L.; Liu, C.; Shen, S. Robust and efficient quadrotor trajectory generation for fast autonomous flight. IEEE Robot. Autom. Lett. 2019, 4, 3529–3536. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhang, S.; Zheng, R. AUV path planning based on differential evolution with environment prediction. J. Intell. Robot. Syst. 2022, 104, 23. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Powers, D.M.W.; Yazdani, A.M.; Sammut, K.; Atyabi, A. Efficient AUV path planning in time-variant underwater environment using differential evolution algorithm. J. Mar. Sci. Appl. 2018, 17, 585–591. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Zadeh, S.M.; Powers, D.M.; Sammut, K. An autonomous reactive architecture for efficient AUV mission time management in realistic dynamic ocean environment. Robot. Auton. Syst. 2017, 87, 81–103. [Google Scholar] [CrossRef]
- Kimmel, R.; Amir, A.; Bruckstein, A.M. Finding shortest paths on surfaces using level set methods. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 635–640. [Google Scholar] [CrossRef]
- Lolla, T.; Haley, P.J., Jr.; Lermusiaux, P.F.J. Path planning in multi-scale ocean flows: Coordination and dynamic obstacles. Ocean Model. 2015, 94, 46–66. [Google Scholar] [CrossRef]
- Lolla, T.; Ueckermann, M.; Yiğit, K.; Haley, P.J.; Lermusiaux, P.F. Path planning in time dependent flow fields using level set methods. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 166–173. [Google Scholar]
- Liang, S.; Qiu, Z.; Yu, S.; Jiao, J. A Novel Distance Regularized Hybrid Level Set Method for AUV Multi-destination Route Planning. Acta Armamentarii 2020, 41, 750–762. [Google Scholar]
- Subramani, D.N.; Lermusiaux, P.F.J. Energy-optimal path planning by stochastic dynamically orthogonal level-set optimization. Ocean Model. 2016, 100, 57–77. [Google Scholar] [CrossRef]
- Petres, C.; Pailhas, Y.; Petillot, Y.; Lane, D. Underwater path planing using fast marching algorithms. In Proceedings of the Oceans 2005-Europe, Brest, France, 20–23 June 2005; Volume 2, pp. 814–819. [Google Scholar]
- Yu, H.; Shen, A.; Su, Y. Continuous motion planning in complex and dynamic underwater environments. Int. J. Robot. Autom. 2015, 30, 192–204. [Google Scholar] [CrossRef]
- Petres, C.; Pailhas, Y.; Patron, P.; Petillot, Y.; Evans, J.; Lane, D. Path Planning for Autonomous Underwater Vehicles. Robot. IEEE Trans. 2007, 23, 331–341. [Google Scholar] [CrossRef]
- Li, H.; He, B.; Yin, Q.; Mu, X.; Zhang, J.; Wan, J.; Wang, D.; Shen, Y. Fuzzy optimized MFAC based on ADRC in AUV heading control. Electronics 2019, 8, 608. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Yang, S.X. An optimized fuzzy control algorithm for three-dimensional AUV path planning. Int. J. Fuzzy Syst. 2018, 20, 597–610. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Song, J.; Liu, D. Path planning for autonomous underwater vehicle in presence of moving obstacle based on three inputs fuzzy logic. In Proceedings of the 2019 IEEE 4th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Nagoya, Japan, 13–15 July 2019; pp. 265–268. [Google Scholar]
- Lei, F.; Yijie, Q.; Dingxin, H.; Wei, L. Multi-robot formation obstacle avoidance based on improved artificial potential field method. Control Eng. 2022, 29, 9. [Google Scholar]
- Ali, A.A.; Rashid, A.T.; Frasca, M.; Fortuna, L. An algorithm for multi-robot collision-free navigation based on shortest distance. Robot. Auton. Syst. 2016, 75, 119–128. [Google Scholar] [CrossRef]
- Yuming, N.; Uniting, L.I.; Cong, Y.A.O.; Jisheng, S. A collaborative multi-robot space exploration method based on fast extended random tree-greedy boundary search. Robotics 2022, 44, 708–719. [Google Scholar]
- Xiong, C.; Lu, D.; Zeng, Z.; Lian, L.; Yu, C. Path planning of multiple unmanned marine vehicles for adaptive ocean sampling using elite group-based evolutionary algorithms. J. Intell. Robot. Syst. 2020, 99, 875–889. [Google Scholar] [CrossRef]
- MahmoudZadeh, S.; Abbasi, A.; Yazdani, A.; Wang, H.; Liu, Y. Uninterrupted path planning system for Multi-USV sampling mission in a cluttered ocean environment. Ocean Eng. 2022, 254, 111328. [Google Scholar] [CrossRef]
- Hu, Y.; Yao, Y.; Ren, Q.; Zhou, X. 3D multi-UAV cooperative velocity-aware motion planning. Future Gener. Comput. Syst. 2020, 102, 762–774. [Google Scholar] [CrossRef]
- He, W.; Qi, X.; Liu, L. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning. Appl. Intell. 2021, 51, 7350–7364. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Adaptive differential evolution-based distributed model predictive control for multi-UAV formation flight. Int. J. Aeronaut. Space Sci. 2020, 21, 538–548. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.; Xia, Y.; Xiong, H.; Shao, X. An improved artificial potential field method for path planning and formation control of the multi-UAV systems. IEEE Trans. Circuits Syst. II 2021, 69, 1129–1133. [Google Scholar] [CrossRef]
- Huang, G.; Cai, Y.; Liu, J.; Qi, Y.; Liu, X. A novel hybrid discrete grey wolf optimizer algorithm for multi-UAV path planning. J. Intell. Robot. Syst. 2021, 103, 49. [Google Scholar] [CrossRef]
- Hoang, V.T.; Phung, M.D.; Dinh, T.H.; Ha, Q.P. Angle-encoded swarm optimization for UAV formation path planning. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; Volume 2018, pp. 5239–5244. [Google Scholar]
- Wang, D.; Fan, T.; Han, T.; Pan, J. A two-stage reinforcement learning approach for multi-UAV collision avoidance under imperfect sensing. IEEE Robot. Autom. Lett. 2020, 5, 3098–3105. [Google Scholar] [CrossRef]
- Li, J.; Sun, T.; Huang, X.; Ma, L.; Lin, Q.; Chen, J.; Leung, V.C.M. A memetic path planning algorithm for unmanned air/ground vehicle cooperative detection systems. IEEE Trans. Automat. Sci. Eng. 2021, 19, 2724–2737. [Google Scholar] [CrossRef]
- Niu, G.; Wu, L.; Gao, Y.; Pun, M. Unmanned aerial vehicle (UAV)-assisted path planning for unmanned ground vehicles (UGVs) via disciplined convex-concave programming. IEEE Trans. Veh. Technol. 2022, 71, 6996–7007. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Chen, Z.; Cheng, L.; Yang, Y.; Li, H. Delivery path planning of heterogeneous robot system under road network constraints. Comput. Electr. Eng. 2021, 92, 107197. [Google Scholar] [CrossRef]
- Vasić, M.K.; Drak, A.; Bugarin, N.; Kružić, S.; Musić, J.; Pomrehn, C.; Schöbel, M.; Johenneken, M.; Stančić, I.; Papić, V.; et al. Deep semantic image segmentation for UAV-UGV cooperative path planning: A car park use case. In Proceedings of the International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 17–19 September 2020; Volume 2020, pp. 1–6. [Google Scholar]
- Yue, Y.; Wen, M.; Putra, Y.; Wang, M.; Wang, D. Tightly-coupled perception and navigation of heterogeneous land-air robots in complex scenarios. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; Volume 2021, pp. 10052–10100. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).