Abstract
The demand for autonomous UAV swarm operations has been on the rise following the success of UAVs in various challenging tasks. Yet conventional swarm control approaches are inadequate for coping with swarm scalability, computational requirements, and real-time performance. In this paper, we demonstrate the capability of emerging multi-agent reinforcement learning (MARL) approaches to successfully and efficiently make sequential decisions during UAV swarm collaborative tasks. We propose a scalable, real-time, MARL approach for UAV collaborative navigation where members of the swarm have to arrive at target locations at the same time. Centralized training and decentralized execution (CTDE) are used to achieve this, where a combination of negative and positive reinforcement is employed in the reward function. Curriculum learning is used to facilitate the sought performance, especially due to the high complexity of the problem which requires extensive exploration. A UAV model that highly resembles the respective physical platform is used for training the proposed framework to make training and testing realistic. The scalability of the platform to various swarm sizes, speeds, goal positions, environment dimensions, and UAV masses has been showcased in (1) a load drop-off scenario, and (2) UAV swarm formation without requiring any re-training or fine-tuning of the agents. The obtained simulation results have proven the effectiveness and generalizability of our proposed MARL framework for cooperative UAV navigation.
1. Introduction
A UAV swarm is a cyber-physical system consisting of multiple, possibly heterogeneous, UAVs that cooperate to execute a particular mission. A significant amount of swarm applications involve making decisions on how the swarm members will maneuver to cooperatively achieve their objective, such as load delivery [1,2], area coverage [3], search and rescue [4], formation [5], path planning [6], and collision avoidance [7], among others. There are various benefits of deploying swarms of UAVs to carry out cooperative tasks as compared to a single agent, such as fault tolerance, task distribution, execution efficiency and effectiveness, and flexibility, to name a few. This has paved the way for further developments of swarms, particularly through artificial intelligence. As opposed to conventional approaches, learning-based decision-making involves less complex computations, requires neither prior nor global knowledge of the environment, and exhibits better scalability.
Deep reinforcement learning (DRL) [8] is a cutting-edge learning paradigm that accommodates sequential decision-making capabilities and has proved effective in a plethora of robotic applications. By interacting with the environment, a DRL agent controlling a robotic platform is able to learn a certain behavior through incentives and penalties provided by the environment as a result of certain actions decided by the agent. DRL can be extended to multiple agents through varying levels of centralization [9]. Centralized training and centralized execution (CTCE) is the most direct extension, where a single DRL agent is trained to control multiple platforms simultaneously. Although this approach exhibits high efficiency, it is computationally expensive, susceptible to failure upon communication loss, and hence is not robust. The second variant is the decentralized training and decentralized execution approach which is definitely more scalable and robust to a communication failure. This is attributed to the fact that a separate agent is trained to control every entity in the swarm which makes the approach less efficient and more computationally expensive. An alternative approach that combines the advantages of both levels of centralization is centralized training and decentralized execution (CTDE). In CTDE, agents are trained in a centralized manner and hence they exhibit collaborative behavior while maintaining the flexibility and scalability of the swarm. Various works in the literature have been carried out to employ multi-agent reinforcement learning (MARL) in various formulations to solve concurrent challenges concerning cooperative UAV applications. In the following section, a synopsis of the most recent related work on MARL-based UAV applications is presented.
1.1. Related Work
In reference [10], reinforcement learning-based path planning of muli-UAV systems is proposed using CTDE. A long short-term memory (LSTM) layer is used within a proximal policy optimization (PPO) agent, to facilitate making decisions based on current and past observations of the environment. Their reward function was designed as a weighted sum of the objectives that the agent is expected to achieve. Model validation was carried out in a simulated environment with three UAVs. By visualizing the reported results, the planned paths for the UAVs are not very smooth. This behavior may result due to various factors, such as oscillations in subsequent actions.
The work presented in [11] addresses the problem of flocking control of UAVs using a CTDE approach based on PPO. The approach aimed at maintaining a flocking behavior following the model suggested by Reynolds [12] and training was done using a simplified UAV model. The task was defined in such a way that the UAV swarm safely travels as fast as possible towards the goal with minimal distance to the swarm’s spatial center. The reward formulation was in terms of the Euclidean distances to the goal, the obstacles, and the swarm center. The UAVs in this work are assumed to fly at different altitudes and fixed speeds. The former condition simplifies exploration by excluding swarm collisions from the experiences, and the latter limits the control of the agent to the heading of the UAV. Controlling the speed or the position of the UAV using the reinforcement learning agent allows for more flexibility and efficiency, yet makes exploration much more challenging. This approach also requires communication between the UAVs in the swarm members, which makes the approach susceptible to communication failure. Simulation results were demonstrated with swarms including up to ten UAVs.
In reference [13], a multi-agent UAV navigation approach was developed using an extension of the original multi-agent deep deterministic policy gradient (MADDPG) [14]. The experiences collected by the agent during training are assigned priorities. Based on these priorities, the experiences are sampled out of the buffer to update the trainable parameters of the neural networks that constitute the MADDPG agent. This means that better experiences have a higher chance of being selected to update the network. However, it is also important for the agent to learn about undesired behaviors since it is highly likely that the agent will encounter previously unseen experiences during real-time deployment.
Another CTDE multi-agent reinforcement learning approach was presented in [15] for the application of collision avoidance of homogeneous UAVs. A PPO agent was adopted to decide on the acceleration of the UAVs in the swarm to maintain safety by avoiding collisions. Every UAV is aware of the positions and velocities of all other UAVs in the environment. This condition might be challenging to achieve in real-world scenarios and may require strong communication if some UAVs are out of the observation range of others in the environment. To circumvent the scalability issue, the algorithm uses an LSTM that encodes the states of all the agents in the swarm into a fixed-size vector. Quantitative results report a high success rate, however, the smoothness of the generated UAV trajectories could be improved. In reference [16], a hierarchy of reinforcement learning agents was used to achieve a multi-objective UAV swarm suppression of an enemy air-defense (SEAD) mission. The top-level agent is concerned about pinpointing the target location to be attacked, while the lower-level agent makes decisions on how the swarm will cooperatively attack the target. Training the agents was done in a decentralized manner, without any experience sharing between the two agent levels.
The work proposed in [17] addresses fixed-wing UAV formation using a leader–follower approach through deep reinforcement learning. The leader UAV makes decisions on how to maneuver, while the others (the followers) try to maintain a certain formation by executing the control commands specified by the leader and communicating the resulting states back. The swarm is rewarded based on defined relative positions between the UAVs respective to a certain formation. The proposed algorithm requires communication between the swarm members and for that, the authors proposed a communication protocol to ensure every UAV has a communication link with at least one member in the swarm. However, any loss of communication would result in undesired formation since the followers rely completely on the leader. An improvement to the original PPO algorithm was proposed to encourage better exploration.
A MARL-based multi-UAV decision making approach was proposed in [18]. A simple UAV model was used to train a multi-agent UAV system for an air-combat mission. A gated recurrent unit and an attention mechanism were used in the decentralized actor and centralized critic networks, respectively, to train a policy that is robust to environmental complexities. The action space combined continuous and discrete actions to make decisions concerning the UAV motion and the combat activity, respectively.
Several other multi-UAV flocking and navigation approaches were proposed using centralized reinforcement learning, such as [19,20]. However, such approaches require communication between the UAVs, rely on global information about the environment, and may not be flexible in terms of the size of the swarm.
An interesting research direction in MARL is credit assignment. When a reinforcement learning agent interacts with the environment, it receives a single scalar value as a reward/penalty for its action(s). In the case of cooperative tasks, multiple agents perform the learning task by taking actions to optimize a single reward that represents them all. This setting introduces a new challenge to MARL, in which agents become “lazy” [21]. In other words, some agents may not perform well as everyone else in the team, and yet receive the same reward collectively. Researchers have proposed several learning [21,22] and non-learning [23,24,25] approaches to tackle this issue by assigning credit to each agent based on their contribution to the success of the collaborative task. The learning-based methods rely on training agent-specific critic networks in addition to the global critic network to assist with factorizing the global reward into values that reflect the actual contribution of each agent in the team. The other non-learning methods use no additional networks; rather, they employ a difference-reward of various formulations to compute the advantage of each agent’s contribution to the collaborative outcome. For instance, the advantage function reflects the value of an agent’s actions [23,24] or the agent’s actions and observations [25]. Specifically, the approach in [25] implements a multi-agent collision avoidance approach using CTDE. Upon updating the network parameters, the advantage of each agent in the swarm is computed based on the contribution of their action and observation to the global state. The objects used to represent the UAVs in the swarm were defined using primitive kinematic equations, which are very simplistic and hard to transfer to reality. Furthermore, the action space is the heading of the UAV, where UAVs are assumed to fly at a fixed speed. This simplifies exploration, since the action space is bounded and varies along a single dimension.
1.2. Contributions
In this paper, a multi-agent reinforcement learning (MARL)-based cooperative navigation of a swarm of UAVs (as depicted in Figure 1) is developed through centralized training and decentralized execution (CTDE). Curriculum learning is used to facilitate and expedite convergence, in presence of various task complexities arising from partial environment observability, multi-agent training, and exploration in continuous state and action space scenarios. A reward function, combining positive and negative reinforcement, is formulated to encourage cooperative behavior and to ensure that agents achieve their individual goals simultaneously, although executed in a decentralized manner. The cooperative navigation approach is scaled-up to work with a large number of agents without requiring re-training or varying the number of agents during training, as opposed to the approaches in the literature, such as [25], where changing the swarm size requires retraining the agent since the observation space and hence the dimensions of the neural network inputs will differ. Scalability of the proposed approach was also achieved in terms of the swarm speed, and the size of the task environment. The generalizability of the proposed approach was demonstrated through a load delivery application, where the mass of the platform changes during the cooperative navigation task after the swarm drops off payloads (of variable mass per UAV). The swarm was shown to continue the task, and arrive at the final navigation goal (which is set during the task) at the same time, without fine-tuning the parameters of the MARL agent. Extensive testing of the proposed approach was carried out in simulations with varying swarm speeds, navigation goals, and environment sizes. Sample UAV swarm formation scenarios are also showcased and the convergence of the proposed approach is demonstrated.
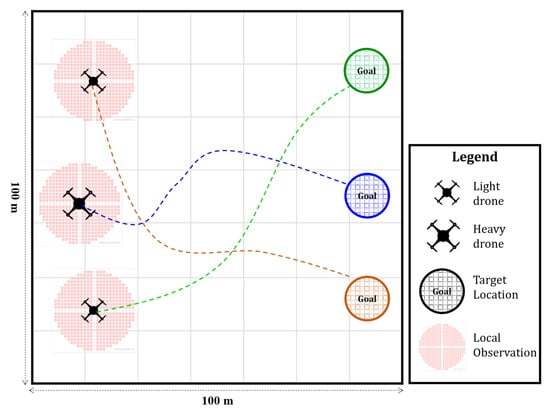
Figure 1.
UAV swarm cooperative navigation.
In summary, the contributions of this paper are listed below:
- The development of a scalable, real-time, autonomous MARL-based collaborative navigation approach for a swarm of UAVs using centralized training and decentralized execution.
- The training of the proposed collaborative navigation approach based on a combination of curriculum learning and early stopping using a reward formulation that encourages cooperative behavior during decentralized execution by means of positive reinforcement.
- Demonstration of the proposed collaborative navigation approach in a load delivery scenario and in swarm formation.
- Extensive testing of the proposed approach across various initial conditions, swarm sizes, UAV speeds, UAV loads, and environment sizes.
2. Methods
2.1. Task Description
The proposed MARL approach is designed for a cooperative navigation task in which a set of agents, in this case, UAVs, are expected to navigate to a set of locations in the task environment. Starting from an initial position, every UAV safely maneuvers to a specific target, within a certain period of time. UAVs are expected to simultaneously arrive at their target locations while operating independently in a decentralized manner. During execution, each agent will only obtain access to local observations within a certain range around the corresponding UAV. Cooperative behavior during decentralized execution is achievable because policies are obtained through centralized training, based on a reward formulation that encourages goal achievement at the individual and collaborative levels. Particularly, training is done with access to global observations collected by all members of the swarm and the parameters of the involved neural networks are updated based on the rewards pertaining to the collective swarm behavior. Collaborative navigation could be deployed in environments with various sizes, and consequently, the maximum allowable speeds may need to be adjusted based on the available space. In addition, the number of UAVs participating in the collaborative task varies based on the application. Flexibility and scalability of the swarm are essential and need to be accounted for in any swarm application.
2.2. Centralized Training and Decentralized Execution
Centralized training and decentralized execution (CTDE) [14] is an approach to MARL where the computational complexity is offloaded onto the training process rather than execution. A popular implementation of this approach is the centralized critic training and decentralized actor execution (as illustrated in Figure 2), which is an extension of the policy–gradient actor–critic model. Particularly, the critic network is trained offline, without constraints on real-time performance. The main purpose is to facilitate obtaining decentralized policies that could accomplish the cooperative multi-agent task through access to global information obtained by multiple agents during training, but not execution. In such a setting, every agent partially observes the environment and hence the problem could be modeled using an extension of Markov decision processes for multiple agents. This extension is referred to as a decentralized partially observable Markov decision process (Dec-POMDP) and is formulated as a five-tuple encapsulating:
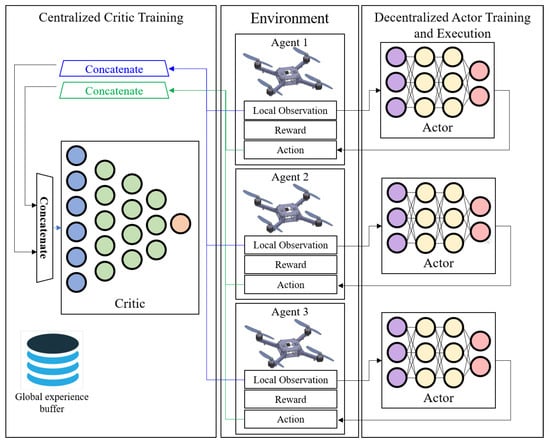
Figure 2.
Overall centralized training and decentralized execution (CTDE) multi-agent reinforcement learning (MARL) framework for collaborative UAV swarm navigation.
- State space (): the global setting of the environment including all the agents.
- Observation space (): the set of individual observations that agents perceive from the environment.
- Action space (): a set of actions that the agents execute in the environment.
- Reward (R): the incentives that agents receive upon acting in the environment.
- Transition function (): defines how agents transition from one state to another.
While operating, each agent attempts to maximize its expected return from the ongoing task, as defined in (1).
where T is the time horizon, and is a discount factor that determines the importance of future rewards and falls in the range .
In a policy gradient method where neural networks are used as policy estimators, the trainable parameters of the network are directly updated to maximize the objective of the optimization which in this case is the agent’s total return. The update is carried out by taking steps in the direction of the gradient of the objective function. The objective function and its gradient for a deterministic policy are formulated in (2) and (3).
where , is the state distribution, is an action, is a set of transitions collected through experiences and stored in the experience buffer, and is the action-value function associated with the deterministic policy .
For the case of CTDE-based MARL, the policy gradient algorithm could be extended to perform centralized critic training based on global observation () of N agents, each following a policy with a set of trainable parameters , where . The updated formulation of the policy gradient is shown in (4).
where is the observation of agent i. Every transition in the experience buffer in the multi-agent setting contains the current global state, the next global state, the individual actions per agent, and the corresponding rewards. In the current work, the deterministic policy and the corresponding value function and computed using neural networks, referred to as the actor and critic, respectively.
2.3. Proposed Model
2.3.1. Actor and Critic Architecture
An actor–critic agent is adopted to perform the cooperative navigation task. The critic is centralized and hence receives global input from the swarm, while the actor is decentralized where it processes local observations. Figure 3 shows a detailed description of the architecture of both the critic and actor. The critic consists of two input paths, one for the global state and the other for the swarm actions. The states are passed through seven hidden dense layers, activated using the rectified linear unit (ReLU), while the actions are passed through a single ReLU activated dense layer.
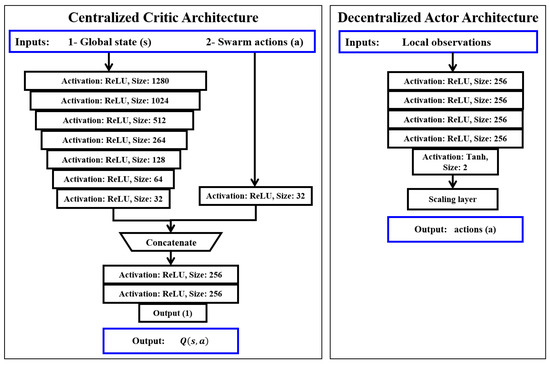
Figure 3.
Architecture of the proposed actor and critic networks.
The outputs of the two paths are then concatenated and passed into two ReLU activated dense layers. Finally, a single-neuron layer outputs the value of an action (a) taken in the state (s).
The actor-network, on the other hand, consists of four hidden dense layers activated using ReLU, followed by a two-neuron layer activated using hyperbolic-tan (tanh) to output actions in the range .
However, since it is sometimes desired to fly UAVs at higher speeds, particularly when the target locations are far apart, a scaling layer was used to set the maximum UAV speed per task.
It is worth noting that the actor-critic agent contains duplicate networks of the actor and critic, referred to as target actor and target critic, respectively. These networks are initialized to the same parameters as the actor and critic but are updated less frequently to achieve learning stability.
2.3.2. State Space and Action Space
At time step t, an agent i observes which represents its local surrounding; namely the relative distance to any other agent within the observation range, the speed of the observed neighbor, and the relative distance to the target location. It is worth noting that each agent is able to observe the environment up to certain spatial limits, and anything outside this range is not perceived by the agent and hence does not affect its decisions.
The action space used in the proposed approach is continuous and two-dimensional. More particularly, the actor-network outputs the reference velocities that will be passed to the UAV’s low-level controller to guide each UAV in the swarm from its initial position to its target location. At the time t, the action generated for agent i is denoted as .
2.3.3. Reward Formulation
Rewards are incentives that guide agent training to achieve a particular task, by praising actions taken towards the goal achievement and penalizing actions that hinder the completion of the task, such as collisions. For the cooperative navigation task, a major component of the reward function is concerned with reducing the Euclidean distance to the target location. This component was chosen to be continuous to ease exploration and facilitate convergence as defined in (7).
where is the position of the UAV controlled by the agent, and is the 2D target location set for this agent in the environment. It is assumed that UAVs fly at a fixed altitude.
To achieve cooperative behavior, a large positive reward () was granted to the UAV swarm if all agents arrived at the goal position at the same time. During training, it was observed that reaching the goal position was frequently achievable by the agents individually at different time instances during the episode. However, staying at the target location was challenging. To that end, positive reinforcement was used to reward individual agents that arrive at the goal position (). To maximize its own return, an agent will try to remain within the target area to collect as many rewards as possible. This component of the reward facilitated achieving the sought swarm objective, where all agents have to be at the target location at the same time. More specifically, the agent generates actions to reduce the speed of the UAV around the goal position. In case an action causes an agent to collide with other agents, a sparse negative penalty () is used to discourage this behavior.
The global reward associated with a set of actions taken in a certain state at time t is a weighted sum of these four components as indicated in (8).
where N is the number of agents, and was set to to scale down the value of the Euclidean distance since training was done in a 100 × 100 m environment.
2.4. Curriculum Learning
Curriculum learning is a training strategy in which a neural network is gradually exposed to task complexity as originally proposed in [26]. The concept behind this strategy is inspired by nature, where humans progressively learn the skills they need over their lifespan. Curriculum learning has two major advantages: (1) it facilitates fast convergence, and (2) it helps achieve better local minima when solving non-convex optimization. In the context of neural networks, curriculum learning guides training toward convergence in a timely manner.
In this work, training the proposed MARL framework was carried out in stages, in a way that supports exploration. UAVs were placed in an environment and were expected to navigate to a target position that required them to maneuver along a single dimension. Given the decentralized nature of the actor training/execution, each UAV receives an action based on its current local observation. Consequently, in every training step, every member in the swarm contributes a different experience towards achieving a common goal. In view of the fact that the action space is continuous, this has expedited the exploration of the action space and has facilitated convergence towards the required cooperative goal. The UAVs are considered to have achieved the goal if they arrive in the vicinity of the target location up to a certain radius. This spatial threshold was set to a large value in the first training stage (50 m) then gradually reduced to 2 m in the following stages.
The complexity of the task was then increased to require UAV control in two dimensions in order to arrive at the goal position. Instead of starting the training over, the neural networks were initialized using the weights from the previous stage. This has significantly accelerated convergence toward achieving the swarm goal. Due to the high variance of the training process, early stopping was also adopted to terminate training after the model had converged for a few hundred episodes.
2.5. UAV Dynamics
The UAV multirotor model that is used to train the proposed approach highly resembles the dynamics of a physical multicoptor to facilitate transferability to real experiments at later stages of this work. The model encapsulates various nonlinear dynamics [27], namely, (1) nonlinear drag dynamics for which a linearized drag model [28] was used, as verified in [29,30], (2) nonlinear propulsion dynamics for which electronic speed controllers (ESCs) are used to linearly map ESC inputs to corresponding thrust, (3) nonlinearities arising from motor saturation which are avoided through operation strictly in the non-saturation regime, and (4) nonlinear kinematics caused by under actuation and gravity, which are linearized using a geometric tracking controller [31] and hence a feedback linearization controller is obtained.
The adopted altitude and attitude dynamics are shown in (9)–(11) and a summary of the used transfer functions and symbols is provided in Table 1.

Table 1.
Linearized altitude and attitude dynamics.
The work presented in [27] demonstrates the high resemblance of the UAV behavior in simulations and experiments using this model. The lateral motion dynamics of the UAV are adopted from [32] to describe the change in attitude in the direction of motion. The equations are listed below (12)–(13) and explained in Table 2.

Table 2.
Linearized lateral motion dynamics.
The deep neural network and the modified relay feedback test (DNN-MRFT) identification approach [32] is used to experimentally identify the presented model parameters. First, a domain for the unknown time parameters is chosen for both the inner and lateral dynamic parameters as in [30,32], respectively. The selected domains are discretized to guarantee up to 10% performance sub-optimality. MRFT is then performed and the results are passed to the DNN which will select the best-suited model parameters. The corresponding controller parameters may then be obtained using the derivative-free Nelder–Mead simplex algorithm.
3. Results and Discussion
3.1. Model Training
The proposed model structure was developed using the TensorFlow [33] library on a Dell desktop, with Intel Xeon(R) W-2145 CPU @ 3.70 GHz × 16. The initial stage of training extended for 10,000 episodes, each consisting of a maximum of 3000 steps. Every step runs for 0.1 s, i.e., a new action is generated at the beginning of each step and the agent executes the action for the remaining time in that step. It is worth noting that during execution on a physical platform, the actor is capable of generating actions at 100 Hz by means of an Intel NUC onboard computer. The episode was selected to be long enough to allow sufficient exploration with various speeds in the task environment which spans 100 × 100 m. It is worth noting that the motion of the UAV swarm was restricted to the defined environment boundaries, where actions that lead to exiting the environment were ignored. In case the swarm goal is achieved or a collision occurs between the UAVs, the training episode is terminated. In subsequent training stages where the complexity of the task was increased, training was conducted with less exploration noise and a lower learning rate, and was suspended when convergence was observed. The training was repeated many times to ensure that the results are not affected by the initial random seed.
The plots depicted in Figure 4 show the cooperative navigation scenario on which the agent was trained. Three UAVs were guided through a 100 × 100 m environment to stop at the same time at set locations. The maximum speed of the swarm in this scenario was 1 m/s which is extremely slow for the total traveled distance per UAV. Hence, the swarm arrived at their goal positions, which are 80 m away from the initial position in 2600 steps.
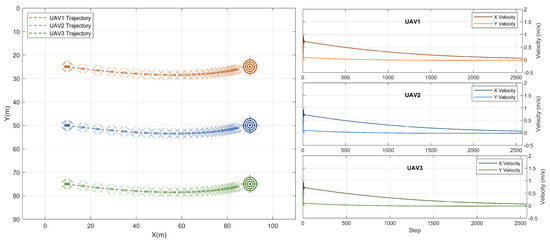
Figure 4.
Result: cooperative navigation training scenario.
One of the common problems in the reinforcement learning literature is the oscillatory behavior in consecutive actions generated by a trained agent [34]. Such oscillations may result in undesired behavior and may lead to damaging the platform in case of aggressive maneuvers. While testing the trained model, this behavior was not encountered in any of the scenarios across various speeds, various locations, and initial conditions, as will be shown in the next sections. Consecutive reference velocities generated by the MARL agent gradually decrease upon approaching the goal. This has resulted in smooth flights for all the members of the swarm.
The behavior exhibited by the agents upon approaching the goal is essential to achieving the swarm goal, particularly with decentralized execution, since agents are required to be at the target locations at the same time. The sparse positive reward used to incentivize individual agents for reaching their goal locations has contributed to this behavior, especially when agents have to traverse variable distances, as will be seen in the following sections.
3.2. Testing with Variable Swarm Speeds
In this section, the same scenario presented in the previous section is used, however, the swarm speed was much higher than in the training scenario. The maximum speed per UAV was 12 m/s which is 12 times the speed in the previous section. The decentralized policies were still able to successfully achieve the swarm goal and the three UAVs arrived at their target locations at the same time, after gradually and smoothly slowing down near the set locations. The swarm was at the target locations in less than 150 steps, which is equivalent to 15 s. The trajectories and the corresponding UAV speeds at each time step are shown in Figure 5.
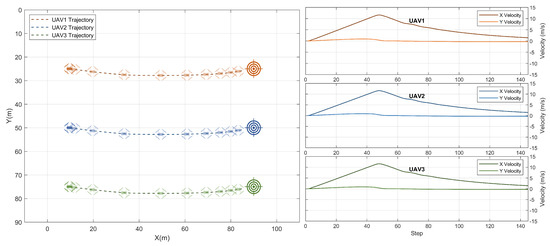
Figure 5.
Result: cooperative navigation with high swarm speed.
3.3. Testing with Different Goal Positions
In this example, the agents were assigned target locations at variable distances from the UAVs’ initial locations, in both dimensions (). Figure 6 shows the scenario and the obtained results using the proposed approach. UAV1 (in orange) has to travel the longest distance, followed by UAV2 (in green), and lastly UAV3 whose target location is the closest. Because of the centralized training nature, the decentralized policies exhibit collaborative behavior and are able to effectively achieve the goal of the swarm. In order for the three UAVs to arrive at their goal locations at the same time, the agents generated reference velocities based on each UAV’s distance from its target. Obviously, UAV1 was the fastest, followed by UAV3, and then UAV2. In the y dimension, the generated reference velocities were also different since the target locations were above, below, and along the initial location for UAV 1, 3, and 2 respectively. The maximum swarm speed was 8 m/s and the swarm goal was achieved after approximately 270 steps. The speed of each UAV was drastically reduced near the goal position.
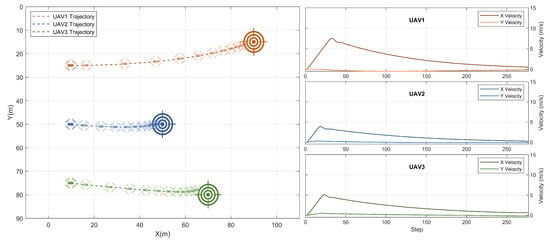
Figure 6.
Result: cooperative navigation with different goal Positions.
3.4. Load Drop-Off Scenario in a Large Environment
In this section, we demonstrate a load drop-off scenario using the proposed MARL-based cooperative navigation framework. The scenario is demonstrated in a larger environment than that used for training, involves changing the goal position during operation, and requires the ability to handle the change in the platform mass to achieve successful cooperative navigation, as depicted in Figure 7.
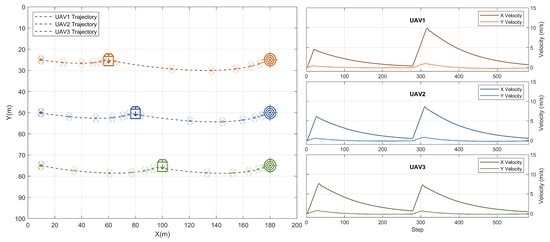
Figure 7.
Result: load drop-off scenario in a large environment.
Starting from their initial positions, every UAV is assumed to carry loads weighing 10%, 20%, and 30% of the platform mass, respectively. The three UAVs are expected to drop the load off simultaneously at locations 50 m, 70 m, and 90 m away from the initial positions. To achieve that, UAV3 commanded the highest reference velocity (approximately 8 m/s), while UAV1 traveled at the lowest speed among the other agents (approximately 5 m/s). The agents were able to drop their loads off simultaneously after about 28 s. Right then, the UAVs (with their reduced masses) were assigned updated target locations that are 120 m, 100 m, and 80 m apart from the drop-off locations of UAV 1, 2, and 3, respectively. It is worth noting that the UAVs were not completely stopped at the drop-off location. To arrive at the new target locations at the same time, the maximum speed for UAV1 was 10 m/s, while UAV2 and UAV3 traveled at lower speeds. All three UAVs arrived at the new target locations simultaneously and gradually slowed down in the target vicinity.
The results obtained in this test have proven the scalability of the proposed approach to a larger environment, its ability to handle changes in the platform mass in-flight, and its ability to cope with dynamic target locations during the mission.
3.5. Testing with Variable Swarm Sizes
The scenarios presented here show how the developed MARL cooperative navigation framework can be used for any number of UAVs in the swarm, given that it was trained to work for three only. In its original design, every agent observes its own distance to the goal, its own speed, and its relative distance to the other members of the swarm and their velocities if they fall within the observation range. Since the input to dense neural networks has to be of fixed size, the size of the observation vector of each agent was set to always fit the states of the two neighboring members of the swarm. In case they were out of the observation range, the corresponding values in the observation vector are set to zero. To make that work for a large swarm, we have added a function to check for the closest two neighbors to every agent in the swarm during operation then included their states in the observation vector of that agent. This has added flexibility to the number of allowable UAVs in the swarm and facilitated testing with larger numbers of UAVs without requiring retraining of the MARL agent. All agents demonstrated collaborative behavior and were able to achieve the swarm goal collectively.
The results illustrated in Figure 8 show an example scenario where six UAVs have maneuvered into a triangular formation starting from their initial positions where they were lined up at . The target locations were set at various distances in x and y dimensions. At any time instance, every UAV may observe the closest two members in the swarm. The velocity plots in the same figure show how each decentralized agent generated different reference velocities depending on the relative distance between the UAV and its corresponding target, to allow all UAVs to achieve their goals at the same time.
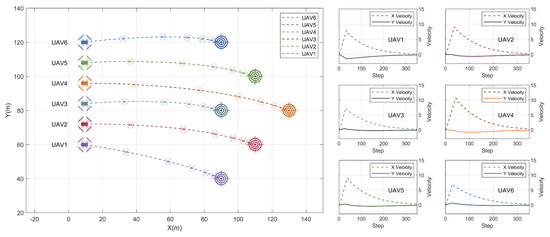
Figure 8.
Result: swarm formation example.
Figure 9 demonstrates another formation scenario where ten UAVs were assigned colinear target locations starting from opposite sides in the environment. In this example, the MARL agent was responsible for generating the magnitudes of the reference velocities and an external function was used to decide the direction of the velocity based on each agent’s relative position to its target. All ten UAVs were able to be within 2 m of the set target locations at the same time and all the flights show a high level of smoothness. The cooperative task was completed in 34 s.
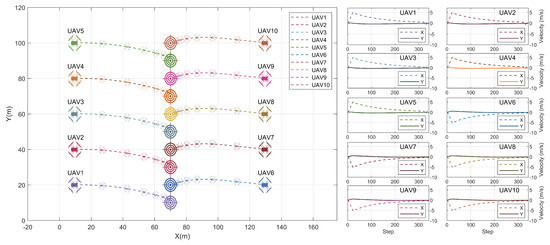
Figure 9.
Result: swarm formation in two directions.
3.6. Action Smoothness
In this section, a test with a swarm of 50 UAVs was conducted to demonstrate the ability of the proposed approach to generate smooth actions across consecutive steps. Every UAV started from a different position in the environment and was assigned a target location at a different distance than the other members in the swarm. This test shows the flexibility and the generalizability of the proposed approach and proves that oscillatory behavior is not encountered over a large range of states and actions. The trajectories followed by the UAVs are depicted in Figure 10 and the corresponding actions in the x direction are shown in Figure 11. The same test was repeated with much lower velocities and oscillations were not encountered at all.
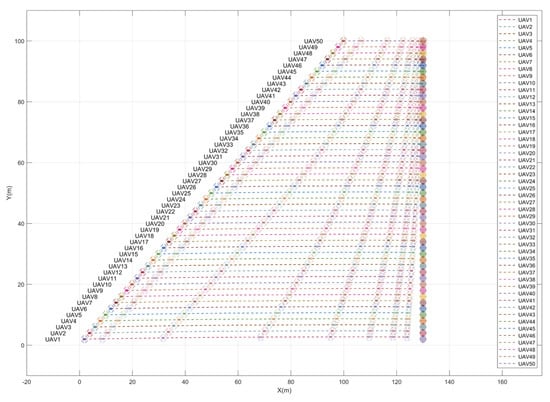
Figure 10.
Result: collaborative navigation of a swarm of 50 UAVs.
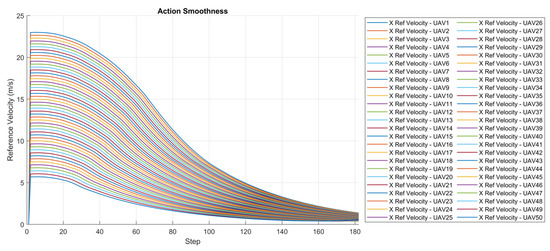
Figure 11.
Result: action smoothness with a swarm of 50 UAVs.
3.7. Training Convergence
Training the proposed approach was carried out in various stages starting from simple tasks to more difficult ones. During training, the performance of the model was evaluated based on the episodic reward, as well as the performance of the agents in the environment. Once the desired behavior was achieved by the proposed framework, training the model in that stage was halted (a training strategy referred to as early stopping). Afterward, the complexity of the problem was increased and the model retrained, where the neural networks were initialized into the values obtained in the previous stage. In later training stages, the learning rates of both the actor and critic are reduced to benefit more from what the model has already learned earlier. Figure 12 demonstrates the convergence of the model in the final training stages.
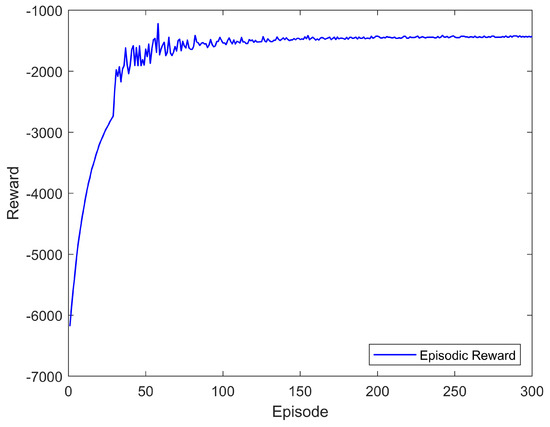
Figure 12.
Proposed MARL training convergence in final stages of curriculum learning.
The adopted training strategy has expedited converge to a policy that exhibits cooperative behavior although is executed in a decentralized manner. In addition, the actions generated by the policy resulted in smooth maneuvers as demonstrated in all the test results.
Without curriculum learning and early stopping, the convergence of the model is much more challenging due to the large environment size, continuous action and state spaces, multi-agent setting, limited observability, and the instability of the environment in presence of multiple dynamic entities at the same time. Figure 13a,b show examples of unstable training of the same model if exploration is performed in one shot. It is worth noting that positive rewards were achieved in these cases because of the positive component of the reward formulation that an agent receives when it arrives at its target location. Larger positive episodic rewards mean that one or two agents were at their target locations accumulating the positive rewards while waiting for the remaining two or one agent, respectively, to arrive at their target location. The latter agents in such cases would be exploring a different area in the environment and hence the episode was not terminated, until the specified number of steps ended. Furthermore, Figure 13c shows the episodic rewards of the same model with credit assignment as proposed in [25], where decentralized agents do not use the global reward to update their parameters, but rather a reward value that reflects their contribution to the success of the task. Every episode may extend to 3000 steps if no collisions between the UAVs happened. It is worth noting that the highest reward values, in this case, were achieved due to the early termination of the training episode, and hence the negative penalty corresponding to the Euclidean distance to the target location was not accumulated for a long time. A sample testing scenario with credit assignment where the collaborative navigation task was not achieved is shown in Figure 14. These examples demonstrate the importance of curriculum learning to the training convergence and task achievement.
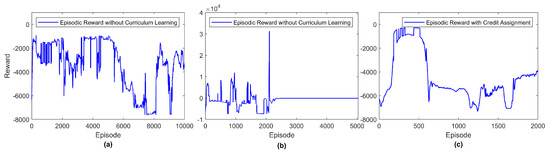
Figure 13.
(a,b): Sample learning curves by training the model without curriculum learning or early stopping, (c) Episodic reward with credit assignment as proposed in [25] without curriculum learning or early stopping.
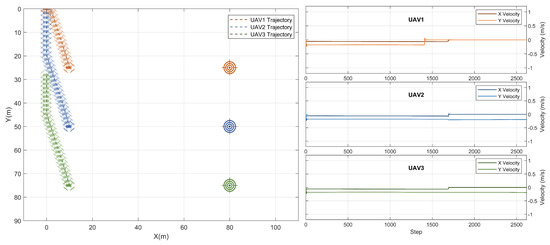
Figure 14.
Result: collaborative navigation with credit assignment.
In the future, the proposed MARL-based cooperative navigation approach will be tested in real-world experiments. It is anticipated that the policy will transfer well to the physical platforms in real environments. This was demonstrated in our previous work [35], in which a single agent was trained to perform a goal oriented task and the transferability to reality was seamless without any model retraining or finetuning. The same UAV model was used for training the current approach, and hence we conjecture that no additional tuning is required for simulation to reality transfer.
3.8. Centralized Collaborative Navigation
In this section, a centralized DDPG agent was trained to perform collaborative navigation in exactly the same settings as our proposed approach. The architecture of the actor and critic networks and the reward formulation were not altered. However, in the centralized approach, one actor network is used to generate the actions for all the UAVs in the swarm at the same time. The centralized agent was trained for more than 2 M steps but convergence was not achieved. The resulting behavior of the swarm after training is shown in Figure 15. One of the UAVs left the environment, while the other two collided. In addition, the actions demonstrate variations throughout the episode as opposed to the actions generated by our proposed approach which demonstrate much higher smoothness. Extensive exploration is yet needed for the centralized agent to achieve the sought performance. It is also worth noting that changes to the size of the swarm would require retraining the actor since the size of the output vector will change. Our proposed approach is more flexible since the decentralized nature of execution circumvents this problem.
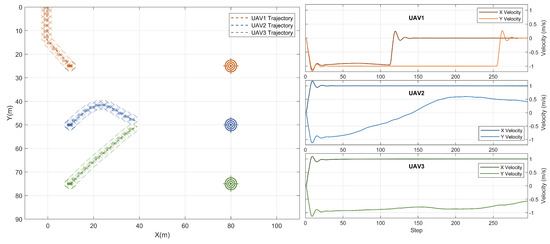
Figure 15.
Result: centralized collaborative navigation.
4. Conclusions
In this paper, a multi-agent reinforcement learning-based swarm cooperative navigation framework was proposed. The centralized training and decentralized execution approach was adopted with a reward formulation combining negative and positive reinforcement. The training was carried out using a high-fidelity UAV model to facilitate simulation to reality transfer. In order to achieve the desired behavior and reduce the complexity of exploration, training was performed in multiple stages where the difficulty of the swarm goal was gradually increased. The proposed framework was extensively tested in simulated scenarios which vary from the one used for training, and demonstrated remarkable performance. It generalized well to larger environment sizes, a large number of UAVs in the swarm, high speeds, various UAV masses, variable goal positions, and changes to the target locations in flight. The effectiveness and scalability of the multi-agent reinforcement-based UAV collaborative navigation were demonstrated through load drop-off and UAV formation scenarios. The training convergence of the proposed framework was demonstrated and the importance of curriculum learning was highlighted by analyzing the stability of the learning-in-one-shot of the same framework and another variant that uses credit assignment.
In the future, the proposed framework will be tested in real experiments and the complexity of the swarm goal will be increased to make the environment more challenging. In addition, navigation in 3D will be investigated to improve collision avoidance flexibility in presence of obstacles that could be avoided by flying at varying altitudes.
Author Contributions
Conceptualization: R.A., Y.Z. and I.B.; methodology, testing, validation, writing, original draft preparation, visualization: R.A.; review and editing, supervision, project administration, funding acquisition: Y.Z. and I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Khalifa University Grant CIRA-2020-082.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cavone, G.; Epicoco, N.; Carli, R.; Del Zotti, A.; Paulo Ribeiro Pereira, J.; Dotoli, M. Parcel Delivery with Drones: Multi-criteria Analysis of Trendy System Architectures. In Proceedings of the 29th Mediterranean Conference on Control and Automation (MED), Bari, Italy, 22–25 June 2021; pp. 693–698. [Google Scholar] [CrossRef]
- Saunders, J.; Saeedi, S.; Li, W. Autonomous Aerial Delivery Vehicles, a Survey of Techniques on how Aerial Package Delivery is Achieved. arXiv 2021, arXiv:2110.02429. [Google Scholar]
- Li, M.; Richards, A.; Sooriyabandara, M. Asynchronous Reliability-Aware Multi-UAV Coverage Path Planning. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10023–10029. [Google Scholar] [CrossRef]
- Alotaibi, E.T.; Alqefari, S.S.; Koubaa, A. LSAR: Multi-UAV Collaboration for Search and Rescue Missions. IEEE Access 2019, 7, 55817–55832. [Google Scholar] [CrossRef]
- Jiang, Y.; Bai, T.; Wang, Y. Formation Control Algorithm of Multi-UAVs Based on Alliance. Drones 2022, 6, 431. [Google Scholar] [CrossRef]
- Abichandani, P.; Lobo, D.; Muralidharan, M.; Runk, N.; McIntyre, W.; Bucci, D.; Benson, H. Distributed Motion Planning for Multiple Quadrotors in Presence of Wind Gusts. Drones 2023, 7, 58. [Google Scholar] [CrossRef]
- Huang, Y.; Tang, J.; Lao, S. Cooperative Multi-UAV Collision Avoidance Based on a Complex Network. Appl. Sci. 2019, 9, 3943. [Google Scholar] [CrossRef]
- Plaat, A. Deep Reinforcement Learning. arXiv 2022, arXiv:2201.02135. [Google Scholar]
- Zhang, K.; Yang, Z.; Basar, T. Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. arXiv 2019, arXiv:1911.10635. [Google Scholar]
- Chen, Y.; Dong, Q.; Shang, X.; Wu, Z.; Wang, J. Multi-UAV Autonomous Path Planning in Reconnaissance Missions Considering Incomplete Information: A Reinforcement Learning Method. Drones 2023, 7, 10. [Google Scholar] [CrossRef]
- Yan, P.; Bai, C.; Zheng, H.; Guo, J. Flocking Control of UAV Swarms with Deep Reinforcement Leaming Approach. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 592–599. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, Herds and Schools: A Distributed Behavioral Model. SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Wu, D.; Wan, K.; Tang, J.; Gao, X.; Zhai, Y.; Qi, Z. An Improved Method towards Multi-UAV Autonomous Navigation Using Deep Reinforcement Learning. In Proceedings of the 2022 7th International Conference on Control and Robotics Engineering (ICCRE), Beijing, China, 15–17 April 2022; pp. 96–101. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Thumiger, N.; Deghat, M. A Multi-Agent Deep Reinforcement Learning Approach for Practical Decentralized UAV Collision Avoidance. IEEE Control. Syst. Lett. 2022, 6, 2174–2179. [Google Scholar] [CrossRef]
- Yue, L.; Yang, R.; Zuo, J.; Zhang, Y.; Li, Q.; Zhang, Y. Unmanned Aerial Vehicle Swarm Cooperative Decision-Making for SEAD Mission: A Hierarchical Multiagent Reinforcement Learning Approach. IEEE Access 2022, 10, 92177–92191. [Google Scholar] [CrossRef]
- Xu, D.; Guo, Y.; Yu, Z.; Wang, Z.; Lan, R.; Zhao, R.; Xie, X.; Long, H. PPO-Exp: Keeping Fixed-Wing UAV Formation with Deep Reinforcement Learning. Drones 2023, 7, 28. [Google Scholar] [CrossRef]
- Li, S.; Jia, Y.; Yang, F.; Qin, Q.; Gao, H.; Zhou, Y. Collaborative Decision-Making Method for Multi-UAV Based on Multiagent Reinforcement Learning. IEEE Access 2022, 10, 91385–91396. [Google Scholar] [CrossRef]
- Wang, W.; Wang, L.; Wu, J.; Tao, X.; Wu, H. Oracle-Guided Deep Reinforcement Learning for Large-Scale Multi-UAVs Flocking and Navigation. IEEE Trans. Veh. Technol. 2022, 71, 10280–10292. [Google Scholar] [CrossRef]
- Shen, G.; Lei, L.; Li, Z.; Cai, S.; Zhang, L.; Cao, P.; Liu, X. Deep Reinforcement Learning for Flocking Motion of Multi-UAV Systems: Learn From a Digital Twin. IEEE Internet Things J. 2022, 9, 11141–11153. [Google Scholar] [CrossRef]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.F.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-Decomposition Networks For Cooperative Multi-Agent Learning. arXiv 2017, arXiv:1706.05296. [Google Scholar]
- Feng, L.; Xie, Y.; Liu, B.; Wang, S. Multi-Level Credit Assignment for Cooperative Multi-Agent Reinforcement Learning. Appl. Sci. 2022, 12, 6938. [Google Scholar] [CrossRef]
- Foerster, J.N.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual Multi-Agent Policy Gradients. arXiv 2017, arXiv:1705.08926. [Google Scholar] [CrossRef]
- Li, J.; Kuang, K.; Wang, B.; Liu, F.; Chen, L.; Wu, F.; Xiao, J. Shapley Counterfactual Credits for Multi-Agent Reinforcement Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Online, 14–18 August 2021; ACM: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, H.; Huang, Z. Multi-UAV Collision Avoidance Using Multi-Agent Reinforcement Learning with Counterfactual Credit Assignment. arXiv 2022, arXiv:2204.08594. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum Learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; Association for Computing Machinery: New York, NY, USA, 2009; Volume ICML ’09, pp. 41–48. [Google Scholar] [CrossRef]
- AlKayas, A.Y.; Chehadeh, M.; Ayyad, A.; Zweiri, Y. Systematic Online Tuning of Multirotor UAVs for Accurate Trajectory Tracking Under Wind Disturbances and In-Flight Dynamics Changes. IEEE Access 2022, 10, 6798–6813. [Google Scholar] [CrossRef]
- Pounds, P.; Mahony, R.; Corke, P. Modelling and control of a large quadrotor robot. Control. Eng. Pract. 2010, 18, 691–699. [Google Scholar] [CrossRef]
- Chehadeh, M.S.; Boiko, I. Design of rules for in-flight non-parametric tuning of PID controllers for unmanned aerial vehicles. J. Frankl. Inst. 2019, 356, 474–491. [Google Scholar] [CrossRef]
- Ayyad, A.; Chehadeh, M.; Awad, M.I.; Zweiri, Y. Real-Time System Identification Using Deep Learning for Linear Processes With Application to Unmanned Aerial Vehicles. IEEE Access 2020, 8, 122539–122553. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric tracking control of a quadrotor UAV on SE (3). In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; IEEE: PIscatway, NJ, USA, 2010; pp. 5420–5425. [Google Scholar]
- Ayyad, A.; Chehadeh, M.; Silva, P.H.; Wahbah, M.; Hay, O.A.; Boiko, I.; Zweiri, Y. Multirotors From Takeoff to Real-Time Full Identification Using the Modified Relay Feedback Test and Deep Neural Networks. IEEE Trans. Control. Syst. Technol. 2021, 1–17. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org (accessed on 15 September 2022).
- Ibarz, J.; Tan, J.; Finn, C.; Kalakrishnan, M.; Pastor, P.; Levine, S. How to Train Your Robot with Deep Reinforcement Learning; Lessons We’ve Learned. arXiv 2021, arXiv:2102.02915. [Google Scholar]
- Azzam, R.; Chehadeh, M.; Hay, O.A.; Boiko, I.; Zweiri, Y. Learning to Navigate Through Reinforcement Across the Sim2Real Gap. arXiv 2022, arXiv:20138960. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).