1. Introduction
Recently, with the complexity of unmanned aerial vehicle (UAV) flight environments and the diversification of mission load requirements, single UAVs with limitations of load and performance have been gradually replaced by multi-UAV cooperative systems with obvious advantages in scalability, applicability and robustness [
1]. The application of multi-UAV cooperative systems in civil and military fields (e.g., geophysical survey, wide-area personnel search and rescue, high-risk target penetration and multi-target detection and strike) has received widespread attention. Multi-UAV cooperative path planning (MUCPP) is one of the most basic and important problems to realize the application of multi-UAV system [
2].
This paper is devoted to the study of the MUCPP problem, which refers to planning collision-free paths from the start to the goal for multiple UAVs that satisfy the cooperative constraints [
3]. As multi-UAV cooperative systems are increasingly used in more complex tasks, such as single- and multiple-target cooperative attacks or multi-source information acquisition at the same time, all UAVs need the same minimum estimated time of arrival (ETA) on the basis of meeting the requirements of path collision avoidance, so as to meet the mission requirements [
4]. In other words, the path planning cooperative constraints that meet most of the mission requirements of UAVs need to be composed of both spatial and temporal constraints (i.e., time–space cooperative constraints), which makes it more difficult to deal with the MUCPP problem.
Since the configuration space is highly dimensional and the constraints are various (i.e., environmental, UAV performance and cooperative constraints), solving the MUCPP problem has become a challenging topic and has received widespread attention. In recent years, many different methods have been developed to solve this problem. These methods can be divided into two categories—reactive collision avoidance methods and active cooperative path generation methods. In reactive collision avoidance methods, each UAV only considers planning the optimal path that can avoid threats in the environment, without considering collision avoidance and time coordination with other UAVs. Then, when the risk of collision with other UAVs is detected, local re-planning is started to avoid collision [
5]. Many algorithms based on reactive collision avoidance methods have been proposed, such as optimal reciprocal collision avoidance (ORCA) [
6], distributed reactive collision avoidance (DRCA) [
7] and some intelligent algorithms (e.g., PRIMAL
2 [
8] and co-evolutionary genetic programming [
9]). The reactive collision avoidance method has been widely used in practice because of its fast calculation speed [
10]. However, it should be noted that such algorithms only plan the local collision avoidance path, so they may fall into the local optimal solution, meaning that the UAV cannot reach the goal. In addition, this local collision avoidance method struggles to meet the requirements of time–space constraints at the same time if the time coordination constraint is introduced.
Active cooperative path generation methods are divided into coupling methods and decoupling methods. Coupling methods usually design only one path planner for multiple UAVs. The planner includes the start and goal of all UAVs and can plan collision-free cooperative paths for all UAVs. Some coupling methods based on the reduction method obtain the cooperative path by simplifying the MUCPP problem to a problem that has been fully studied, such as linear programming (LP) [
11], constraint satisfaction problem (CSP) [
12], etc. In addition, some search-based coupling methods, such as the conflict-based search (CBS) [
13] and incremental cost tree search (ICTS) [
14], have also been proposed to transform the MUCPP problem into a global single-agent path search problem, and simultaneously generate the cooperative path of all UAVs. The coupling method can usually find the optimal path. However, with the increase in the number of collisions between UAVs and the increase in the dimensions and scope of the planning environment, the calculation time of the cooperative path obtained by the coupling method may increase exponentially. Furthermore, the coupling method has been proved to have a good effect when planning the conflict-free paths of multiple UAVs. However, if we want to deal with the MUCPP problem that meet the time–space cooperative constraints, the computational time of the algorithm will be further increased due to the introduction of time cooperative constraints. In addition, game theory-based optimal cooperative path planning has been deeply studied in recent years. The game-based particle swarm optimization (GPSO) algorithm [
15] develops a hierarchical method based on the framework of game theory to extend the spherical vector-based particle swarm optimization (SPSO) algorithm [
16]. Ref. [
17] combines the Stag Hunt game approach with GSPO. These two algorithms can efficiently find the optimal cooperative path with the formation being maintained and have good performance. However, we are not sure whether these two algorithms can still perform well in a large number of UAV formations due to the formation constraints.
On the other hand, decoupling methods plan the path for each UAV and coordinate the planning order of all UAVs through path coordination methods to obtain the collision free path, such as hierarchical cooperative A* algorithm (HCA*) [
18] and prioritized planning algorithm (PP) [
19]. Among them, the PP algorithm has been widely studied recently because of its ability to transform the MUCPP problem into the single UAV path planning problem to quickly and efficiently obtain the cooperative path [
20,
21]. In the PP algorithm, the upper planning coordinator assigns different priorities to all UAVs and then uses the single UAV path planner to plan the path from high priority to low priority. Although the classical PP algorithm can obtain the cooperative path quickly, the centralized framework of PP can be further improved to raise the computational efficiency. The authors of [
22,
23] proposed an asynchronous decentralized prioritized planning algorithm (ADRPP), which can make reasonable use of distributed computing resources to achieve faster algorithm convergence. Compared with the centralized prioritized planning algorithm (i.e., classical PP algorithm), the asynchronous decentralized prioritized planning algorithm (ADRPP) proposed in the literature [
22,
23] can usually complete the generation of cooperative paths with fewer cycles. In addition, compared with the synchronous decentralized prioritized planning algorithm (SDRPP) [
24], ADRPP can start the next round of planning without waiting for all UAVs to complete the planning, so it has higher planning efficiency. However, ADRPP algorithm does not provide a prioritization approach that can improve efficiency, so there is some room for improvement. However, the ADRPP and SDRPP algorithm does not provide a prioritization approach that can improve efficiency, so there is some room for improvement. In addition, none of the decoupling methods have been used in in-depth research on the cooperative problem of multiple unmanned aerial vehicles simultaneously. However, after transforming the cooperative path planning problem of multiple UAVs into a single path planning problem, the realization of time–space cooperative constraints is relatively easy and has little impact on the computational efficiency. In addition, decoupling methods have not been used in in-depth research on the MUCPP problem that meets the time–space cooperative constraints. However, it should be noted that after transforming the MUCPP problem into a single-UAV path planning problem, the realization of time–space cooperative constraints is relatively easy, and the computational efficiency is relatively high.
1.1. Motivation
It can be seen from the analysis that the above algorithms still have some room and possibility for improvement:
In order to meet the needs of most cooperative tasks of multiple UAVs, it is necessary to introduce the time–space cooperative constraints to deal with the MUCPP. The above algorithms focus more on spatial conflict avoidance but do not consider spatial and temporal cooperative constraints at the same time.
The reactive collision avoidance methods mainly focus on conflict avoidance in local areas and struggle to achieve time coordination. The coupling method adds the time coordination constraint to the path planner of multiple UAVs, which will further increase the calculation time and reduce the calculation efficiency. The decoupling method can simplify the MUCPP problem to the single-UAV path planning problem. Compared with the coupling method, the decoupling method has the possibility of introducing time-space coordination constraints by adding less computation.
In the PP algorithm, if the random prioritization method is adopted, or only the collision number based on the space cooperative constraint is considered for prioritization, the calculation efficiency of the algorithm will be reduced, and the calculation time will be increased.
The existing single-UAV path planning algorithms usually take the shortest path as the optimization standard. Additionally, the RRT* algorithm has been proved to be able to quickly obtain the optimal solution in high-dimensional planning space [
25]. However, the existing RRT* algorithm or its variant algorithms cannot meet the time–space coordination constraints of UAVs.
Therefore, in combination with the above motivations, this paper introduces the time–space cooperative constraints into the MUCPP problem so as to meet the needs of most multi-UAV systems to perform tasks. Meanwhile, the decentralized priority planning algorithm based on a decoupling method is further improved by combining the prioritization strategy suitable for time–space cooperative constraints. Furthermore, the RRT* algorithm is improved in the underlying single UAV planner to meet the time–space cooperative constraint, so that the path can be quickly planned for each UAV.
1.2. Contributions
In this paper, we propose the HDP-TSRRT* algorithm to solve the MUCPP problem based on time–space cooperative constraints. HDP-TSRRT* is a decoupled active cooperative path generation algorithm and adopts a hierarchical architecture. First, HDP-TSRRT* uses a synchronous decentralized architecture based on the RRT* algorithm to quickly plan the optimal pre-planning path for each UAV without considering cooperative constraints, which is the foundation for cooperative planning. Second, in the path coordination level, the heuristic decentralized prioritized planning algorithm (HDP) is proposed to coordinate the path planning priorities of the multi-UAV. The algorithm ranks the priority of UAVs by combining the number of potential collisions and the violation of the cooperative time into a performance evaluation function, which makes the priority allocation more reasonable and can improve the efficiency of cooperative planning. The algorithm also uses the asynchronous decentralized prioritized planning framework to coordinate the path planning of multiple UAVs to further improve the computational efficiency. Third, the RRT* algorithm based on time–space cooperative constraints (TSRRT*) is proposed as the execution algorithm of the underlying single-UAV cooperative path planner. The TSRRT* algorithm designs a cost function based on time constraints to gradually optimize the path. In the TSRRT* algorithm, the strategy of multiple sampling and cost function evaluation of optimal sampling proposed in this paper is used to expand the new node, and the time-constrained cost function is used to update the neighborhood nodes to quickly plan the path that meets the time–space cooperative constraint for each UAV.
Compared with the existing cooperative path planning algorithm for multi-UAV, the HDP-TSRRT* proposed in this paper mainly includes the following contributions:
A decoupled UAV cooperative path planning hierarchical framework is designed, which is composed of a synchronous decentralized pre-planner, an asynchronous decentralized prioritized planning path coordinator based on heuristic prioritization, and a single-UAV cooperative path planner based on time–space coordination constraint RRT*, to quickly plan a UAV’s time–space cooperative path.
In the path coordinator, a heuristic prioritization approach based on time–space coordination constraints is proposed to sort the UAVs, so as to ensure the rationality of the prioritization and reduce the calculation time of path coordination.
A cost function based on time coordination constraints is established to optimize the planned path of UAVs so as to ensure that the single-UAV cooperative path planner can find the path satisfying the time coordination constraint.
In the process of sampling and new node expansion of the single-UAV cooperative path planner, a multi-sampling and cost function evaluation strategy is proposed to expand the new node to improve the efficiency of cooperative path planning.
In the tree structure generation of the single-UAV cooperative path planner, a neighborhood node update method based on the time coordination cost function is proposed to guide the path generation meeting the time–space coordination constraints.
The rest of this paper is organized as follows: In
Section 2, we introduce the related works;
Section 3 describes the MUCPP problems based on the time–space coordination constraints;
Section 4 introduces the HDP-TSRRT* algorithm in three aspects;
Section 5 provides us with the simulation of the proposed algorithm and discusses the results; and
Section 6 describes some conclusions and future work.
3. Problem Formulation
Consider the UAVs group
composed of
UAVs flying in the planned space
composed of a three-dimensional battlefield environment. In a cooperative flight, all UAVs in
take off at the same time and reach the goal at the same time. Any
needs to start flying from its start node
and avoid all threats, including radar, anti-aircraft gun, missile and terrain in flight (the model of the threats is described in our previous work [
34]), as well as the remaining
, and finally reach its goal node
.
Since the start node or goal node of multiple UAVs may overlap, we assume that when different UAVs are at the same start node or goal node, their positions do not coincide, and there will be no conflict. In addition, we assume that each UAV in the group has an independent path planner and wireless communication equipment. Meanwhile, we assume that the communication equipment is completely reliable and has no delay.
3.1. Cooperative Path Planning Constraints of UAVs
The related constraints of UAV cooperative path planning are mainly divided into three categories, namely UAV performance constraints, planning space constraints and multi-UAV cooperative constraints. Firstly, the performance constraints of UAV are defined as follows.
Assume that the planned path
of
consists of a set of path node
. When planning the flight path of the UAV, it is necessary to take into account the maximum flight distance
, the maximum steering angle
and the climbing/diving angle
, as well as the shortest flight distance before steering
. Then, the performance constraints of
can be expressed as [
35]:
where
.
- 2.
Planning space constraints
The threat types set in the planning space include terrain threats, which is built by digital elevation model map (DEM, i.e., the digital expression of terrain surface morphology), radar, anti-aircraft guns and missiles. Then, the constraints of the planning space on UAVs can be expressed as:
where
represents the terrain threat level when the UAV is at
, and
represents other threats.
- 3.
Multi-UAV cooperative constraints
In this paper, we mainly study the MUCPP problem that simultaneously satisfies the time–space coordination constraints. We first describe the space coordination constraint.
If any two UAVs in
can maintain a certain safety distance
at any time in flight, then these two UAVs meet the space coordination constraint. Therefore, the space coordination constraint can be expressed as:
where
and
, respectively, represent the positions of
and
at any time
. In this paper, we assume that all UAVs pass through the planning space at the same velocity. The path of
is discretized according to the time information to obtain a group of discrete path nodes. In order to determine the safe distance between UAVs more accurately, this paper sets the time interval between two adjacent discrete path nodes of
as 0.01s. The potential collision between
and
is detected by comparing the distance between two path nodes (i.e.,
) and the minimum safety distance
at any same time
.
Meanwhile, in order to meet the mission requirements, UAVs need to take off at the same time and reach their respective goal at the same time to achieve time coordination. In this paper, we set all UAVs to fly at a constant speed and have the same speed range
—that is, the flight time of any UAV is
. The time coordination constraint that the
needs to meet is expressed as:
3.2. Cooperative Path Planning Formulation
When dealing with the MUCPP problem, not only the performance constraints and planning space constraints of a single UAV should be met, but also the coordination constraints of all UAVs. Firstly, the description of satisfactory path problem of is given.
Problem1.
(Satisfying Path Planning of ). In the planning space , for any in the , a satisfactory path is planned for the given start-goal set so that meets the constraint Equations (1) and (2).
If the satisfactory path and the satisfactory path of any in meet the space coordination constraint (i.e., Equation (3)), and are said to be collision-free. If and meet the time coordination constraint (i.e., Equation (4)), C and are said to be time-consistent. Then, Problem 2 can be described as follows.
Problem2.
(MUCPP Problem based on time–space coordination constraints). Given the planning space , and the start-goal set of , find the satisfactory path of all UAVs, and the and is collision-free and time-consistent.
4. HDP-TSRRT* Algorithm
In this paper, the HDP-TSRRT* algorithm is proposed to quickly plan the path satisfying the time–space cooperative constraint of multi-UAV. As a decoupled path coordination algorithm, the algorithm realizes the path planning of a single UAV and the path coordination of multiple UAVs in a hierarchical manner. On the basis of finding the pre-planned path, the heuristic prioritization-based asynchronous decentralized prioritized planning algorithm (HDP) is used to allocate the cooperative path planning order of all UAVs. Then, the cooperative path planning of each UAV from high priority to low priority is completed by using the proposed TSRRT* algorithm so that the path can meet the time–space constraints at the same time. The HDP-TSRRT* algorithm will be introduced in detail through the overall framework of the HDP-TSRRT* algorithm, the HDP algorithm and the TSRRT* algorithm in the following subsections.
4.1. Overall Framework
The algorithm is mainly divided into three levels, i.e., the pre-planning level, the planning coordination level and the single-UAV cooperative path planning level. The pseudocode of HDP-TSRRT* is shown in Algorithm 3.
| Algorithm 3: HDP-TSRRT* Algorithm |
|
The definitions of some symbols appearing in Algorithm 3 are as follows. is the tree structure of any . is the tree structure of with priority of . is the current path of any . is the current path of with priority of . is the time–space occupied area set occupied by UAVs . is the length of the path , which is calculated by function . and are the path set and ETA set of UAVs, respectively. the minimum ETA of the UAVs group. represents the priority ranking set of all UAVs obtained through the function . The function contains the path information of the with priority . and are defined in Equations (3) and (4).
Figure 1 shows the overall framework of HDP-TSRRT * algorithm. As shown in
Figure 1, the HDP-TSRRT * algorithm can be divided into three levels.
This level mainly includes the synchronous decentralized pre-planning process, which plans the initial optimal path for each UAV to obtain the shortest ETA and the initial parameters of the HDP algorithm. In this part, the UAVs do not need to consider the time–space coordination constraints when planning the path, and instead, only consider the performance constraints and planning space constraints of UAVs and use the RRT* algorithm (i.e., Algorithm 1) for optimal path planning. After each UAV obtains its optimal path, the path length is obtained through the function, and then the flight time set of all UAVs is obtained. It should be noted that all UAVs use the RRT* algorithm for optimal path planning, which means that all UAVs obtain the shortest flight time. However, for the MUCPP based on time–space coordination constraints, if the shortest flight time of is less than the shortest flight time of the , only by increasing the to make it the same as the can the two UAVs achieve time coordination. Therefore, it is necessary to take the maximum time in the flight time set as the ETA, , and set the UAV mapped by as the UAV with the highest priority to avoid repeated planning of the same path.
- 2.
The planning coordination level
This level mainly includes the coordination process of multi-UAV path planning priorities, which uses the proposed HDP algorithm to improve the efficiency of path coordination. First, the priority assignment process from 2 to of all UAVs based on the heuristic prioritization approach is completed through the function. Since the cooperative constraints of UAVs are divided into two aspects, space and time, a priority performance evaluation function composed of potential collision times and cooperative time violations is designed in the algorithm. After outputs the priority order of all UAVs, the asynchronous decentralized prioritized planning is used to coordinate the generation of time–space cooperative paths. In the asynchronous decentralized prioritized planning, each low-priority UAV needs to avoid the time–space occupied area set occupied by the high-priority UAV. In other words, the time–space area set of low-priority UAVs should contain high-priority paths to avoid collision with them.
- 3.
The single-UAV cooperative path planning level
This level mainly includes the process of cooperative path planning for a single UAV, which is realized by the TSRRT* algorithm. Under the framework of the HDP algorithm, UAVs regard the time–space occupied area occupied by other UAVs as threats and use the TSRRT* to plan the path satisfying the time–space coordination constraint for each UAV. The TSRRT* algorithm evaluates the generated path through the cost function based on the time coordination constraint so that the planned path can meet the time coordination constraint on the basis of no collisions. In addition, we effectively reduce the computational loss through the proposed multiple sampling and cost function evaluation strategy.
4.2. HDP Algorithm
This section describes the HDP algorithm from two aspects: the heuristic prioritization approach and the framework of the HDP algorithm.
4.2.1. Heuristic Prioritization Approach
The priority level of a UAV affects the robustness and efficiency of cooperative path generation. When the prioritized planning algorithm is used for the path coordination of multiple UAVs, the inappropriate priority order will not only reduce the efficiency of cooperative path planning but also cause the failure of cooperative path planning. To solve this problem, the heuristic prioritization approach is proposed in this paper.
Since the algorithm proposed in this paper is mainly used for path planning of multiple UAVs that satisfy the time-space coordination constraints, the design of heuristic prioritization approach should take into account the impact of both time and space coordination constraints. For the time coordination constraint, if the pre-planned path of is significantly different from the minimum ETA time to be met, it is obvious that the cooperative re-planning path of the will also change more. Furthermore, because the re-planning path of the changes greatly, the change of its space and time occupied area set will be greater, and the impact on other UAVs will be greater. Therefore, we need to set the priority of the higher, so that the can carry out cooperative re-planning before other UAVs to reduce the impact on other UAVs. For the space coordination constraints, which are similar to the time coordination constraints, if the number of potential collisions between the pre-planned paths of and other UAVs is more, the path of the will change more during the collaborative re-planning, which means that more other UAVs will be affected. Therefore, if the priority of the is assigned higher, the less other UAVs will be affected by its re-planning. It can be seen from the analysis that the heuristic prioritization approach based on time–space coordination constraints can improve the planning efficiency.
In the heuristic prioritization approach, we designed a performance evaluation function consisting of the number of potential collisions and the amount of cooperative time violations of the pre-planned path to assign reasonable priority to all UAVs. The evaluation function is defined as follows:
where
is the space cost function, representing the normalized potential collision number cost between
and other UAVs.
is the time cost function, i.e., the normalized violation of
and cooperative ETA
. The final priority performance score of
is
.
and
are weights.
The purpose of the heuristic prioritization approach is to allocate the priority for each UAV reasonably, and the performance evaluation function designed will be used to evaluate the priority level. In addition, it is not difficult to find that the of any is positively correlated with the number of collisions and the cost of cooperation time violation. Therefore, we give the prioritization definition of UAVs based on performance evaluation function as follows.
Definition1.
(Prioritization evaluation based on performance evaluation function) Given a group of and any group of weights , the performance evaluation function set of is ranked from largest to smallest to generate the set , whose elements map the priority of of in turn.
First, we analyze the calculation process of
. Based on the space coordination constraint (Equation (3)), the potential collision number
between the
and any other
based on the pre-planned path can be calculated as follows:
Obviously, the number of collisions of the same UAV is zero. In addition, if the number of collisions between
and
is
, the number of collisions between
and
is
, where
. From this, the total number of collisions of
can be determined as:
Then, the
of
can be expressed as:
For the calculation of cooperative time violation cost
based on the time coordination constraint of
, the path length
needs to be obtained through the pre-planned path, so as to calculate the ETA time
. Then, the
is:
It should be noted that there may be a specific situation, i.e., when the performance evaluation function of some UAVs may be equal, in which the priority of UAVs with equal can be randomly assigned.
Then, the heuristic prioritization approach framework is shown in Algorithm 4.
| Algorithm 4: Heuristic prioritization approach (i.e., ) |
|
4.2.2. The Framework of HDP Algorithm
This paper proposes the HDP algorithm, which improves the ADRPP algorithm. The HDP algorithm introduces a heuristic prioritization approach based on time–space coordination constraints, which can reasonably prioritize UAVs, thus improving the efficiency and robustness of path coordination. In addition, in order to deal with the MUCPP problem based on time–space cooperative constraints, we propose the TSRRT* algorithm in the single-UAV cooperative path planner of the HDP algorithm, which will be described in
Section 4.3.
The framework of the HDP algorithm is shown in Algorithm 3. First, the priority of the UAV is ranked by the heuristic prioritization approach (i.e., function ). Then, any with a priority of only needs to receive and process the path change message of the with higher priority and response. If receiving the path change message from the , will update the information of the time–space occupied area to the current path information of . After that, checks whether the planned path based on the current can meet the space–time coordination constraints. If not, uses the TSRRT* algorithm to re-plan the path that meets the time–space coordination constraints in combination with the current . Otherwise, does not need to re-plan the path and keeps the communication silent. The algorithm stops until all UAVs plan paths that meet the time–space cooperation constraints.
4.3. TSRRT* Algorithm
As a decoupled cooperative path planning algorithm, the HDP-TSRRT* algorithm needs to carry out path planning for each UAV that meets the time–space cooperative constraints after using the HDP algorithm to coordinate the planning of multi-UAV. In addition, it is noted that when the HDP algorithm is used for planning coordination, many rounds of path re-planning may be required for a single UAV to ensure that all UAVs can meet the coordination constraints, which is a great challenge to the efficiency of the path planning algorithm for a single UAV. If the efficiency of path planning is low, it will greatly increase the planning time of the cooperative path.
Therefore, this paper proposes the TSRRT* algorithm as the single-UAV cooperative path planning algorithm. The TSRRT* algorithm will be introduced in four parts, i.e., the cost function based on time–space coordination constraints, the tree expansion based on multi-sampling strategy, the neighborhood node optimization approach and the framework of TSRRT*.
4.3.1. Evaluation of the Cost Function Based on Time-Coordination Constraint
After obtaining the shortest cooperative ETA (i.e., ), we can obtain the path length of any meeting the time cooperative constraint according to , where . Therefore, in the TSRRT* algorithm, we introduce a new cost function that can constrain the length of the planned path, i.e., the cost function based on the time coordination constraint, so as to ensure that the planned path meets the time coordination constraint.
The cost function based on the time coordination constraint is no longer aimed at minimizing the path length but at minimizing the difference between the actual path length and the constrained path length. The cost function is defined as follows:
where
.
represents the actual distance from the start node
to the current tree node
.
represents the estimated distance from the
to the goal node
, and
is the estimated distance coefficient. This paper takes the Euclidean distance between two nodes as the estimated distance
, where
.
4.3.2. Node Expansion Based on Multi-Sampling Strategy
In the tree structure of the classical RRT* algorithm, the expansion of a new node is only completed through one sampling. However, due to the large flight environment of UAVs, even though the generation of sampling points is guided by some offset sampling methods [
36,
37,
38], there is still great randomness in the expansion, which affects the efficiency of path planning. For the decoupled cooperative path planning algorithm, the path planning efficiency of a single UAV is crucial.
Therefore, in order to ensure the efficiency of planning, this paper proposes a multi-sampling strategy, which directly selects the goal as the sampling point during sampling or selects a batch of sampling points for pre-expansion so as to reduce the probability of adding low-quality sampling nodes to the tree for expansions to improve efficiency. Algorithm 5 shows the process of the new node expansion approach based on a multiple sampling strategy.
| Algorithm 5: Node expansion based on multi-sampling strategy () |
|
When
, the multi-sampling process is executed. First, we select a group of
sampling nodes from the planning space, and any potential sampling point is
, where
. Then, we calculate the corresponding potential expansion nodes
for all potential sampling points, and the calculation formula for any potential expansion node
is as follows:
where
,
,
are UAV position coordinates. For potential expansion nodes that meet UAV performance constraints, planning space constraints and space coordination constraints, the expansion length of nodes is determined by the expansion step
. Then, we use the sampling node
and the nearest node
from
in the tree to determine the potential expansion node
. If
does not meet the above constraints, it will be discarded.
After obtaining the potential expansion nodes set
that meet the constraints, the cost function based on time constraints is used to select the optimal potential expansion node as the new node
for expansion, that is,
It can be seen that the new node expansion method based on multiple sampling and cost function evaluation strategy is divided into three steps. First, we select the expansion method of the new node—that is, we select the target point as the sampling point or conduct multi-sampling. If multi-sampling is selected, a batch of nodes are randomly sampled through multi-sampling strategy for pre-expansion to ensure the randomness of tree structure expansion. Then, all potential expansion nodes that meet the constraints are evaluated using the cost function based on the time coordination constraint to obtain the optimal expansion node as a new node. This method can reduce the randomness of the expansion of new nodes to a certain extent and ensure that the expansion of the tree structure can meet the solution of the time coordination constraint so as to improve the planning efficiency and make the planned path close to the optimal path under the current cost function. In addition, the evaluation process directly discards some sampling points with poor performance so that these nodes will not be subject to subsequent neighborhood node updates and other operations with high computational complexity, which can also reduce the planning time.
4.3.3. Neighborhood Nodes Update Approach Based on the Cost Function of Time Coordination Constraint
It should be noted that the key to ensuring the progressive optimality of the traditional RRT* algorithm is the introduction of neighborhood node optimization. Therefore, in the TSRRT* algorithm, in order to plan a path that meets the time–space coordination constraints, on the basis of obtaining the of the new node, the cost function based on the time coordination constraint should also be used in the neighborhood node update to guide the parent node’s updating and rewiring of the new node to ensure that the planned path gradually meets the time coordination constraint.
Because the neighborhood node update includes the parent node update process and the rewiring of the new node
, the two processes are basically the same. Therefore, Algorithm 6 gives a general framework for neighborhood node optimization of the TSRRT* algorithm.
| Algorithm 6: Neighborhood node update (i.e.,) |
|
First, we analyze the process of performing
for the first time—that is, the process of selecting the parent node with less cost based on the time cooperation constraint in the neighborhood for
. Firstly, it is determined whether the edge
composed of any node
in the neighborhood, and
meets the UAV performance constraints, planning space constraints and space coordination constraints. If the constraints are met, the distance between two nodes is calculated. Note that all nodes in the neighborhood have been added to the tree, so we can directly obtain the actual path length from the start node
to
in the tree. Then, the estimated distance
from
to the goal node
is calculated. Then, the cost
based on time coordination constraint from
through
to
is
After calculating the cost of all neighborhood nodes, the node with the lowest cost is selected as the parent node of .
The process of the second is basically similar to that of the first. The only difference is that this operation takes as the potential parent node of all nodes in the neighborhood to optimize the neighborhood nodes.
4.3.4. The Framework of TSRRT* Algorithm
This section mainly analyzes the overall framework of the TSRRT* algorithm, which is shown in Algorithm 7. After designing the cost function based on the time coordination constraint as the evaluation standard in TSRRT*, the multiple sampling and cost function evaluation strategy is designed in the tree node expansion process to improve the planning efficiency. Then, the cost function based on time coordination constraint is used to guide the updating and rewiring of nodes in the neighborhood.
| Algorithm 7: TSRRT* algorithm |
|
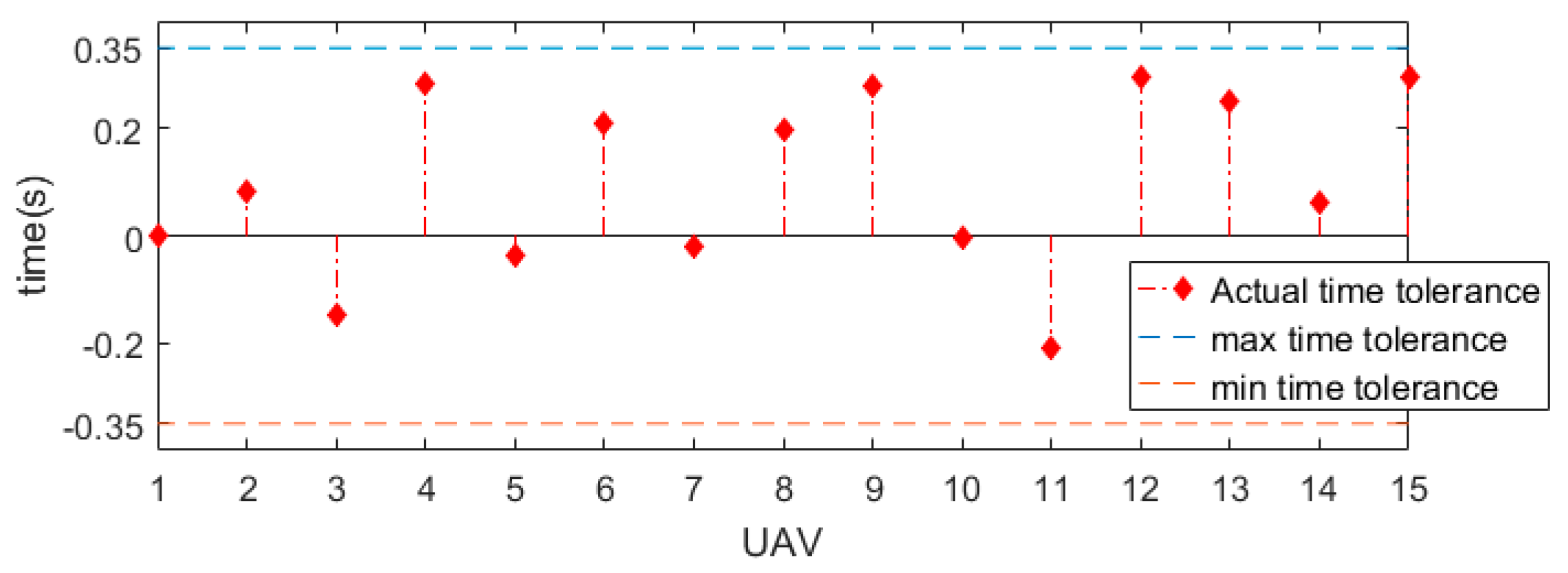
When the new node extends into the goal region, a path can be found. If the deviation between the path length of and the is greater than or equal to the given tolerance , the tree structure is updated using the Algorithm 7, Line 3–12 to optimize the . When , the path satisfying the time–space coordination constraints is output.
6. Conclusions
In this paper, a decoupling cooperative path planning algorithm named HDP-TSRRT* is proposed to solve the MUCPP based on the time–space cooperative constraints. Each UAV shares the same arrival time, and there is no conflict or threat avoidance among them. The proposed algorithm adopts a hierarchical architecture. The first is the pre-planning level, which aims to obtain the relevant parameter information and lay the foundation of cooperative path planning. Then, at the coordination planning level, an HDP algorithm is proposed, which introduces the heuristic prioritization approach based on time–space coordination constraints so as to assign reasonable priority to each UAV to improve the planning efficiency and robustness. Lastly, at the single-UAV cooperative path planning level, we propose the TSRRT* algorithm, which can quickly and stably plan a path that meets the time–space cooperative constraints for a single UAV.
In future work, we plan to expand the HDP-TSRRT* algorithm to the multi-UAV system with local communication to complete the real outdoor experiment. In real experiments, the proposed algorithm requires each UAV to have a separate communication unit to achieve real-time information reception and broadcast. However, ensuring the reliability and real-time of communication between UAVs is also a difficult problem to be faced in the implementation of this algorithm. In addition, we plan to use the decoupling prioritized planning algorithm or its derivative algorithm to deal with the MUCPP problem in a dynamic environment.