Fault Tolerant Control of Drone Interceptors Using Command Filtered Backstepping and Fault Weighting Dynamic Control Allocation
Abstract
:1. Introduction
2. Nonlinear Model of the Interceptor
3. Fault Weighting Dynamic Control Allocation
3.1. Fault Weighting Dynamic Control Allocation Strategy
3.2. Fault Estimation
3.3. Desired Steady State Control Input
4. Nonlinear Virtual Control Law Design
4.1. Virtual Control Law
4.2. Stability Analysis
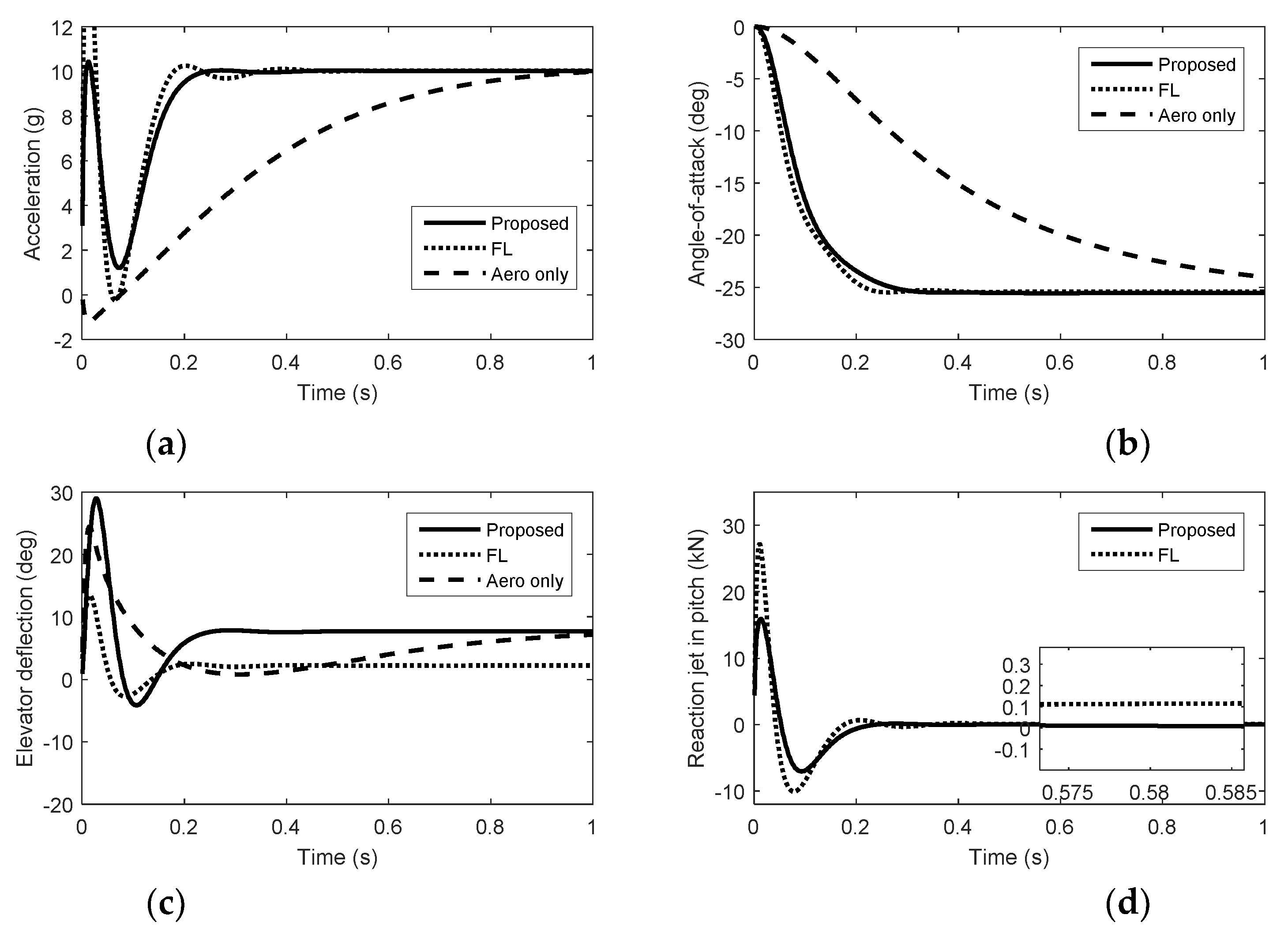
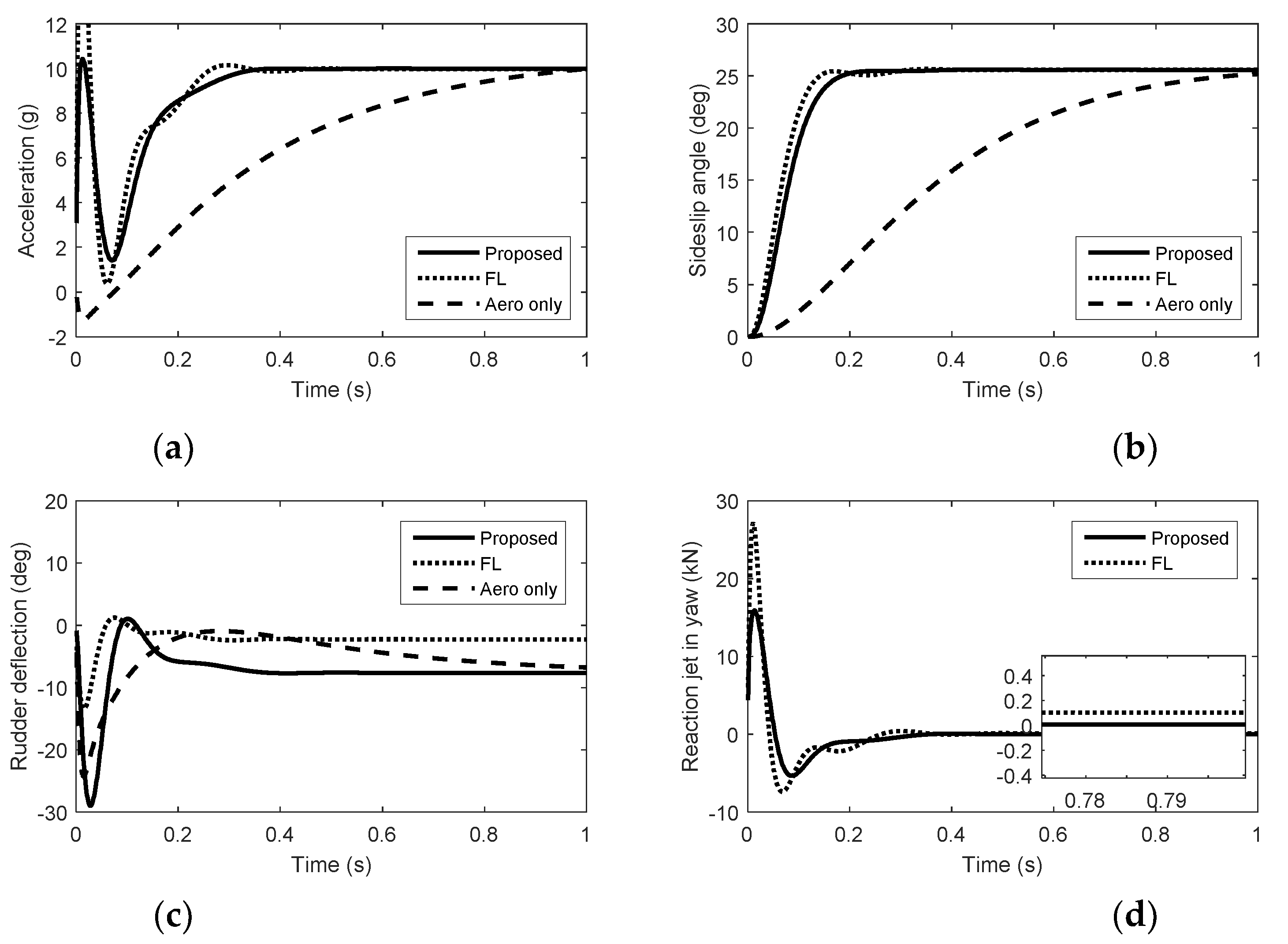
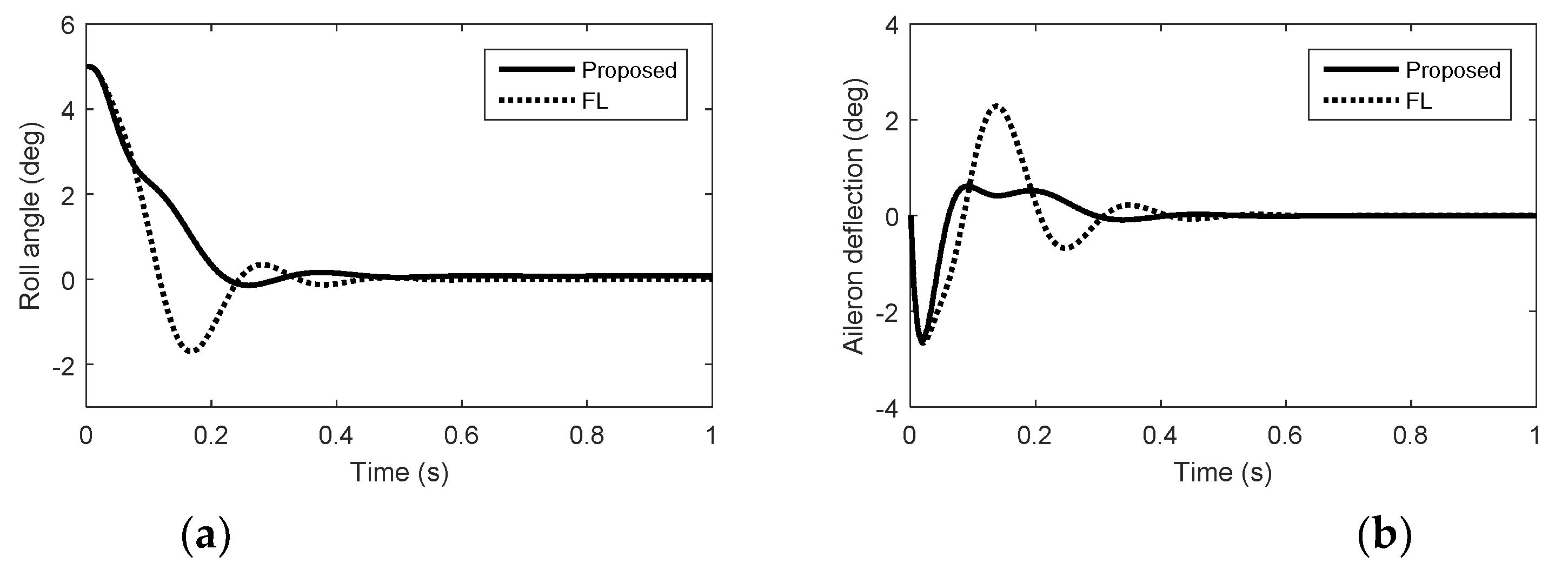
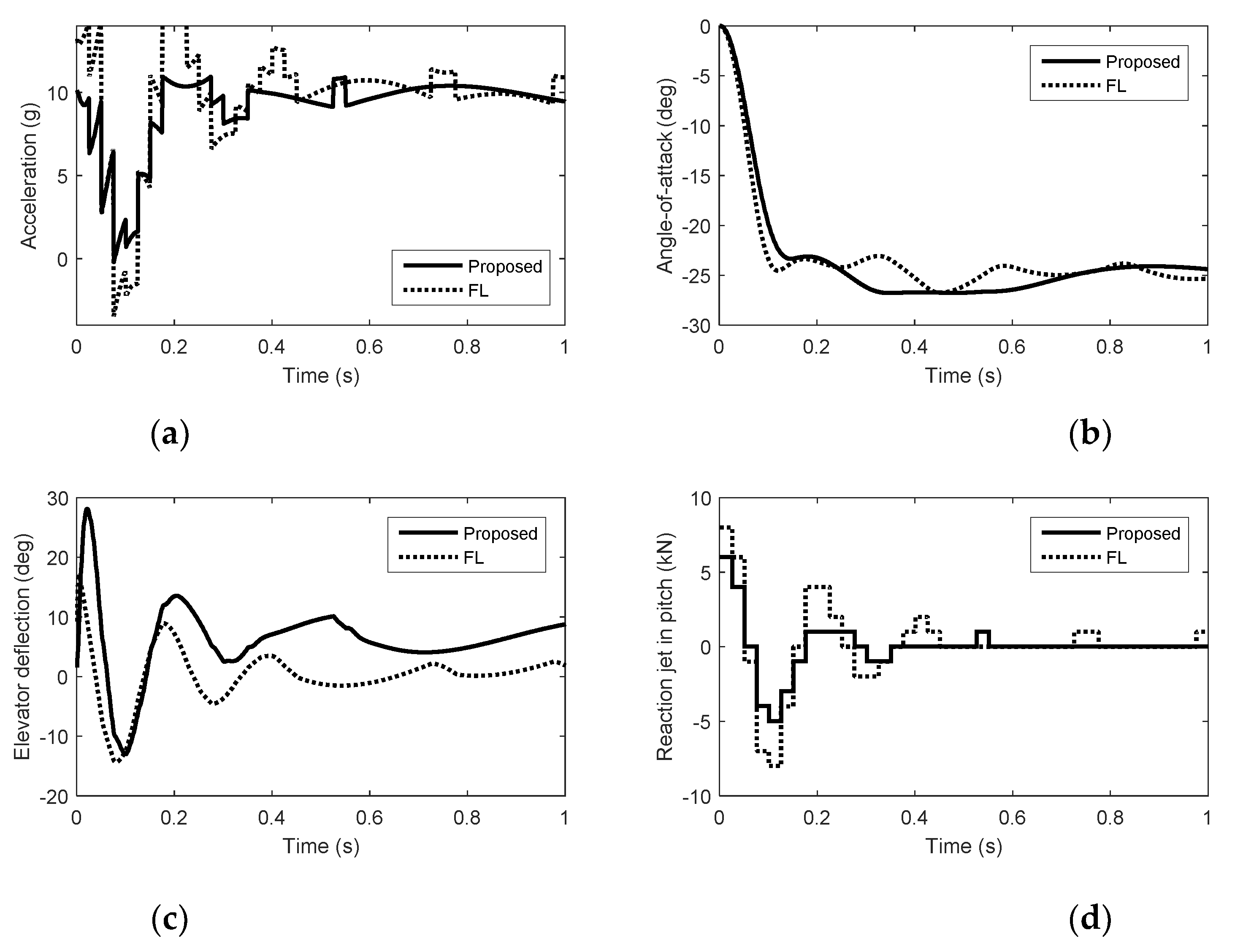
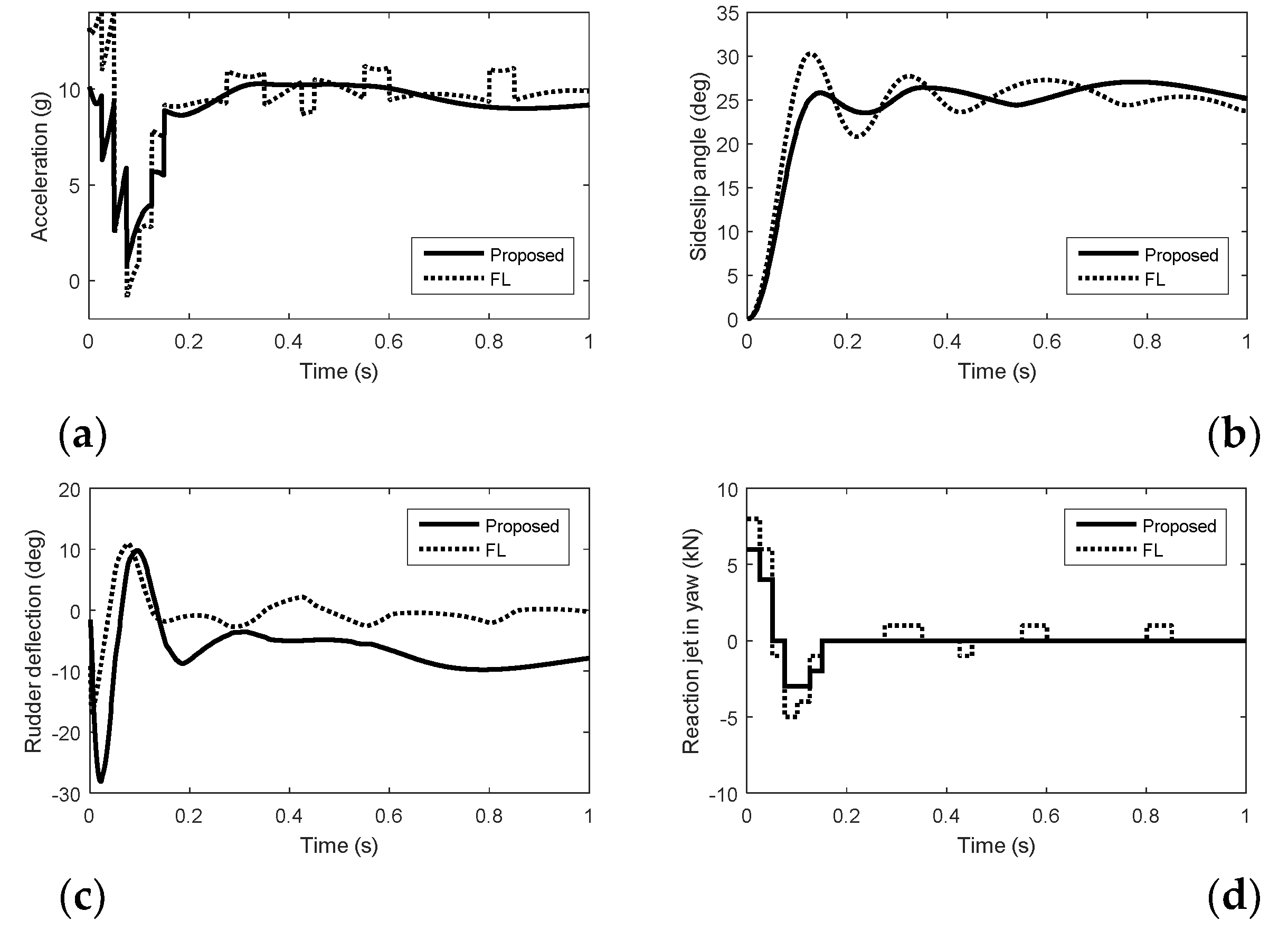
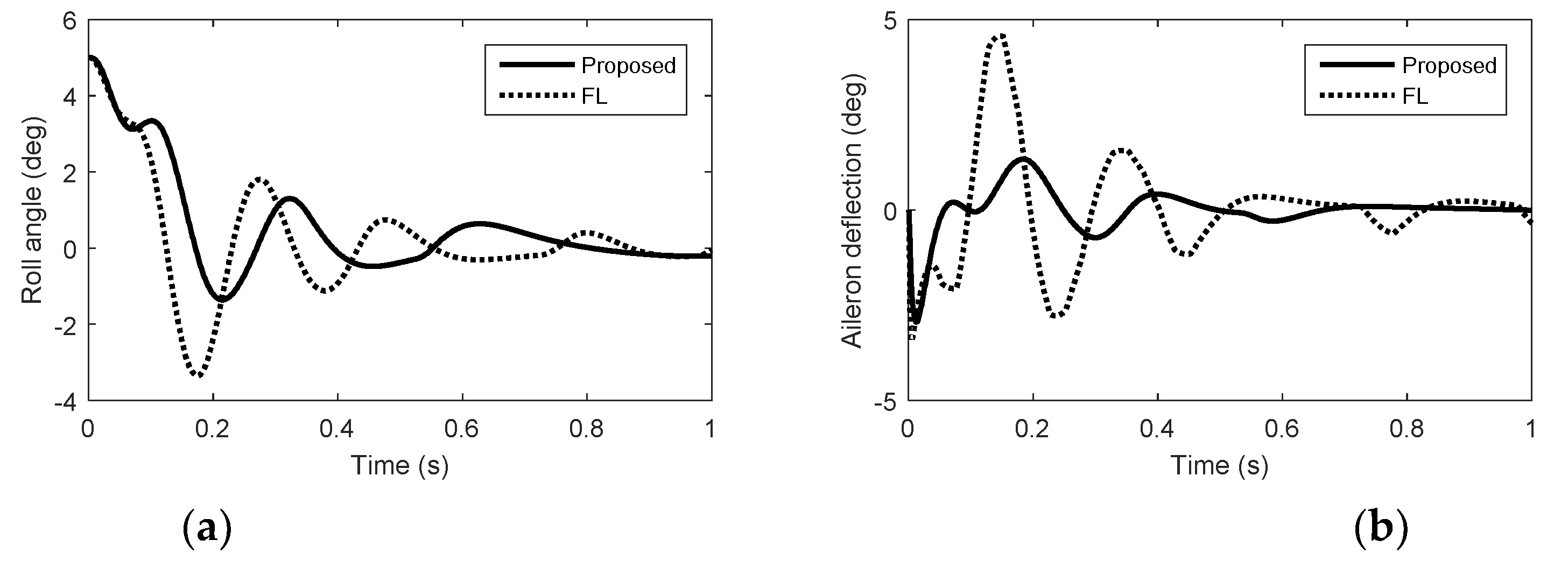
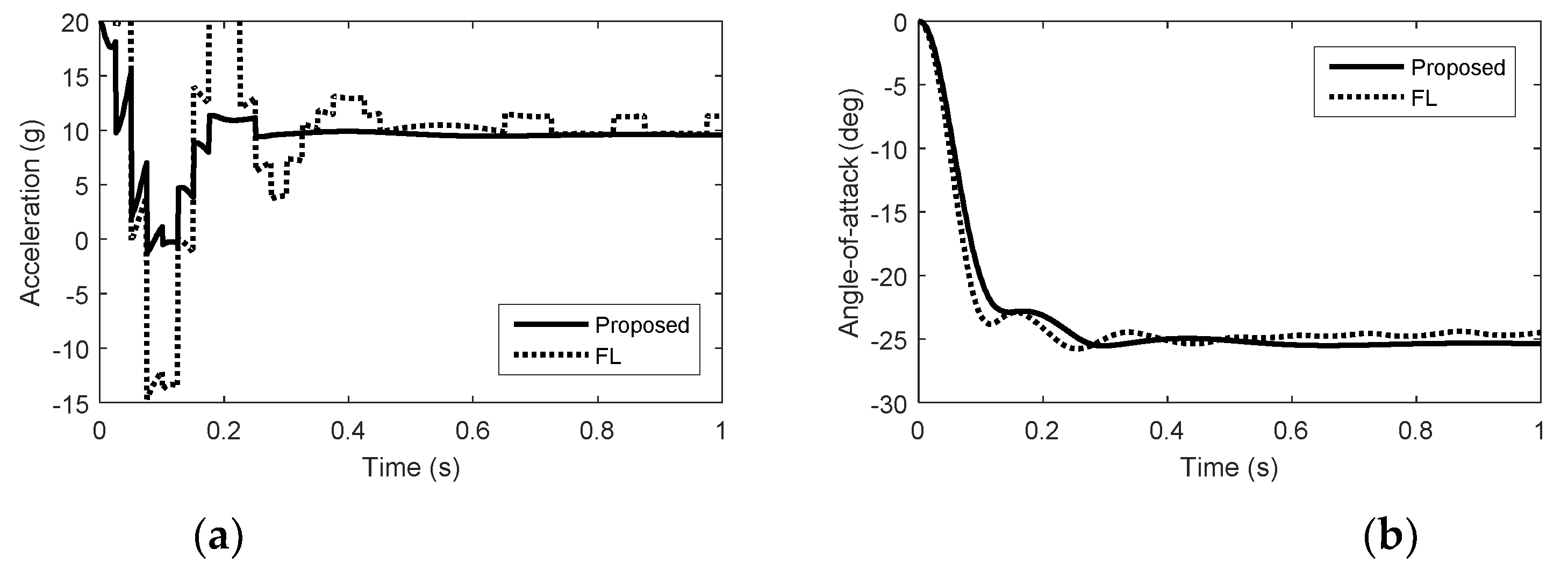
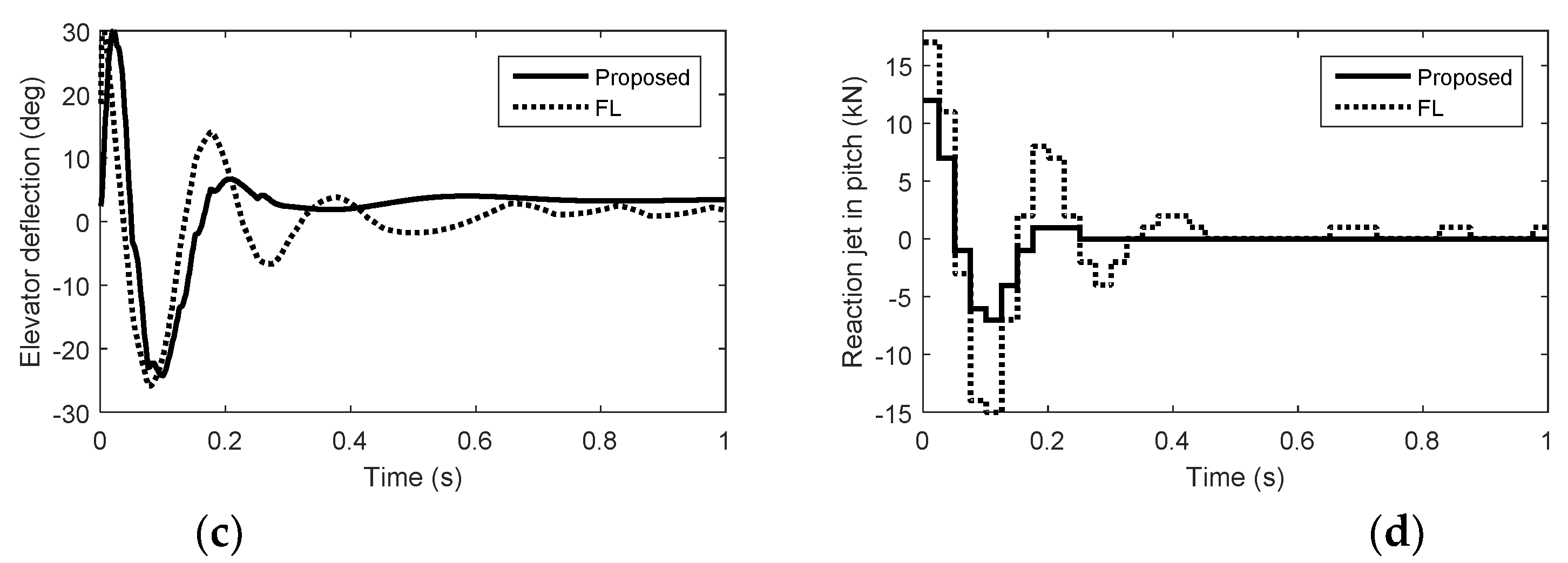
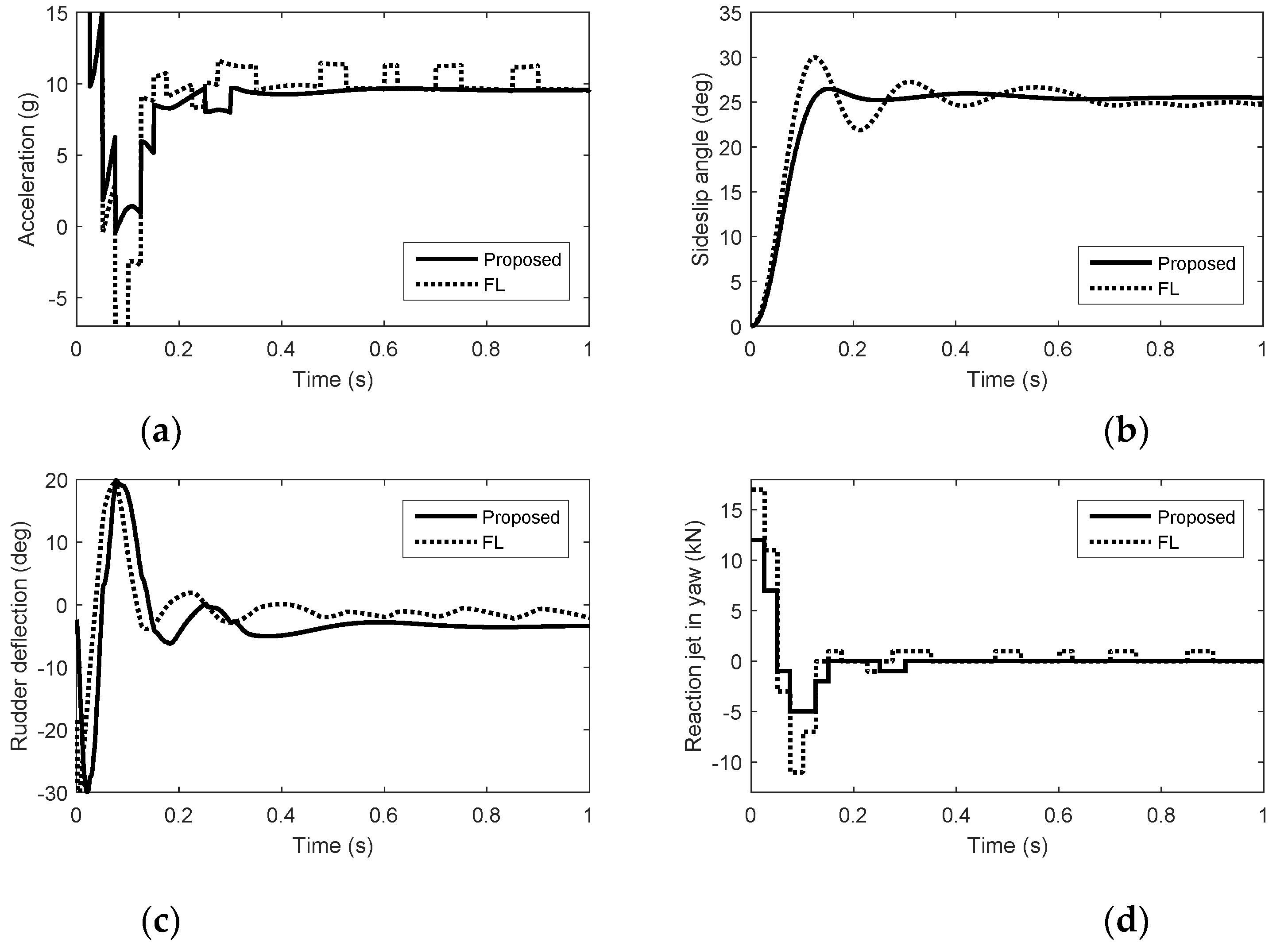
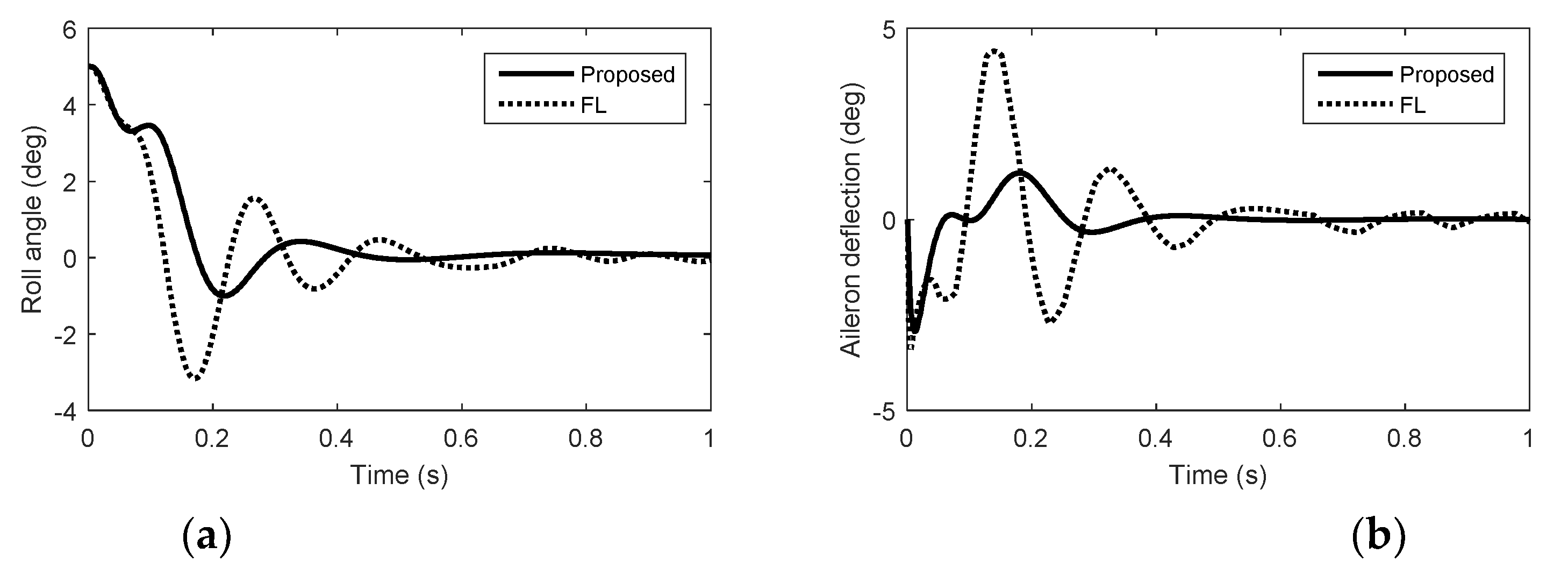
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, D.; Xu, B. Adaptive dynamic surface guidance law with input saturation constraint and autopilot dynamics. J. Guid. Control Dyn. 2016, 39, 1152–1159. [Google Scholar] [CrossRef]
- Xu, B.; Zhou, D.; Liang, Z.; Zhou, G. Robust adaptive sliding sector control and control allocation of a missile with aerodynamic control surfaces and reaction jets. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2017, 231, 397–406. [Google Scholar] [CrossRef]
- Puchalski, R.; Giernacki, W. UAV fault detection methods, state-of-the-art. Drones 2022, 6, 330. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, K.; Wang, S. Sliding mode disturbance observer-based adaptive dynamic inversion fault-tolerant control for fixed-wing UAV. Drones 2022, 6, 295. [Google Scholar] [CrossRef]
- Härkegard, O.; Glad, S.T. Resolving actuator redundancy—Optimal control vs. control allocation. Automatica 2005, 41, 137–144. [Google Scholar] [CrossRef]
- Thukral, A.; Innocenti, M. Sliding mode missile pitch autopilot synthesis for high angle of attack maneuvering. IEEE Trans. Control Syst. Technol. 1998, 6, 359–371. [Google Scholar] [CrossRef]
- Han, T.; Hu, Q. Robust autopilot design for STT missiles with multiple disturbances using twisting control. Aerosp. Sci. Technol. 2017, 70, 428–434. [Google Scholar] [CrossRef]
- Mohammadi, M.R.; Jegarkandi, M.F.; Moarrefianpour, A. Robust roll autopilot design to reduce couplings of a tactical missile. Aerosp. Sci. Technol. 2016, 51, 142–150. [Google Scholar] [CrossRef]
- Mattei, G.; Monaco, S. Nonlinear autopilot design for an asymmetric missile using robust backstepping control. J. Guid. Control Dyn. 2015, 37, 1462–1476. [Google Scholar] [CrossRef]
- Xin, M.; Balakrishnan, S.N. A new method for suboptimal control of a class of non-linear systems. Optim. Control Appl. Methods 2005, 26, 55–83. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, D. Nonlinear autopilot design for interceptors with tail fins and pulse thrusters via θ-D approach. J. Syst. Eng. Electron. 2014, 25, 273–280. [Google Scholar] [CrossRef]
- Xin, M.; Balakrishnan, S.N. Nonlinear H∞ missile longitudinal autopilot design with θ-D method. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 41–56. [Google Scholar] [CrossRef]
- Choi, B.; Kang, S.; Kim, H.J.; Jun, B.E.; Lee, J.I.; Tahk, M.J.; Park, C. Roll-pitch-yaw integrated μ-synthesis for high angle-of-attack missiles. Aerosp. Sci. Technol. 2012, 23, 270–279. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Hu, Q.; Li, B.; Zhang, Y. Robust attitude control design for spacecraft under assigned velocity and control constraints. ISA Trans. 2013, 52, 480–493. [Google Scholar] [CrossRef]
- Zhou, D.; Shao, C. Dynamics and autopilot design for endoatmospheric interceptors with dual control systems. Aerosp. Sci. Technol. 2009, 13, 291–300. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Autom. 2013, 49, 1087–1103. [Google Scholar] [CrossRef]
- Chang, Y.; Yuan, R.; Tan, X.; Yi, j. Observer-based adaptive sliding mode control and fuzzy allocation for aero and reaction jets’ missile. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2016, 230, 498–511. [Google Scholar] [CrossRef]
- Xing, L.; Zhang, K.; Chen, W. Optimal Control and Output Feedback Considerations for Missile with Blended Aero-fin and Lateral Impulsive Thrust. Chin. J. Aeronaut. 2010, 23, 401–408. [Google Scholar]
- Lei, R.; Chen, L. Adaptive fault-tolerant control based on boundary estimation for space robot under joint actuator faults and uncertain parameters. Def. Technol. 2019, 15, 964–971. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C. Fault tolerant control using sliding modes with on-line control allocation. Autom. 2008, 44, 1859–1866. [Google Scholar] [CrossRef]
- He, J.; Qi, R.; Jiang, R.; Zhai, R. Fault-tolerant control with mixed aerodynamic surfaces and RCS jets for hypersonic reentry vehicles. Chin. J. Aeronaut. 2017, 30, 780–795. [Google Scholar] [CrossRef]
- Härkegard, O. Dynamic control allocation using constrained quadratic programming. J. Guid. Control Dyn. 2004, 27, 1028–1034. [Google Scholar] [CrossRef]
- Brierley, S.D. and Longchamp, R. Application of sliding-mode control to air-air interception problem. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 306–325. [Google Scholar] [CrossRef]
- Manchester, I.R.; Savkin, A.V. Circular navigation missile guidance with incomplete information and uncertain autopilot model. J. Guid. Control Dyn. 2004, 27, 1078–1083. [Google Scholar]
- Reisner, D. and Shima, T. Optimal guidance-to-collision law for an accelerating exoatmospheric interceptor missile. J. Guid. Control Dyn. 2013, 36, 1695–1708. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A.; Polycarpou, M.M.; Djapic, V.; Sharma, M. Command filtered adaptive backstepping. IEEE Trans. Cotrol Syst. Technol. 2012, 20, 566–580. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Ma, Q.; Feng, J.; Zhang, J. Fault Tolerant Control of Drone Interceptors Using Command Filtered Backstepping and Fault Weighting Dynamic Control Allocation. Drones 2023, 7, 106. https://doi.org/10.3390/drones7020106
Xu B, Ma Q, Feng J, Zhang J. Fault Tolerant Control of Drone Interceptors Using Command Filtered Backstepping and Fault Weighting Dynamic Control Allocation. Drones. 2023; 7(2):106. https://doi.org/10.3390/drones7020106
Chicago/Turabian StyleXu, Biao, Qingfeng Ma, Jianxin Feng, and Jinpeng Zhang. 2023. "Fault Tolerant Control of Drone Interceptors Using Command Filtered Backstepping and Fault Weighting Dynamic Control Allocation" Drones 7, no. 2: 106. https://doi.org/10.3390/drones7020106
APA StyleXu, B., Ma, Q., Feng, J., & Zhang, J. (2023). Fault Tolerant Control of Drone Interceptors Using Command Filtered Backstepping and Fault Weighting Dynamic Control Allocation. Drones, 7(2), 106. https://doi.org/10.3390/drones7020106



