A Computational Investigation of the Hover Mechanism of an Innovated Disc-Shaped VTOL UAV
Abstract
:1. Introduction
2. The Disc-Shaped VTOL UAV at a Glance
3. Computational Method
3.1. Mathematical Modeling and Governing Equations
3.2. Generating Computational Mesh
3.3. Boundary Conditions and Physical Modeling
4. Results
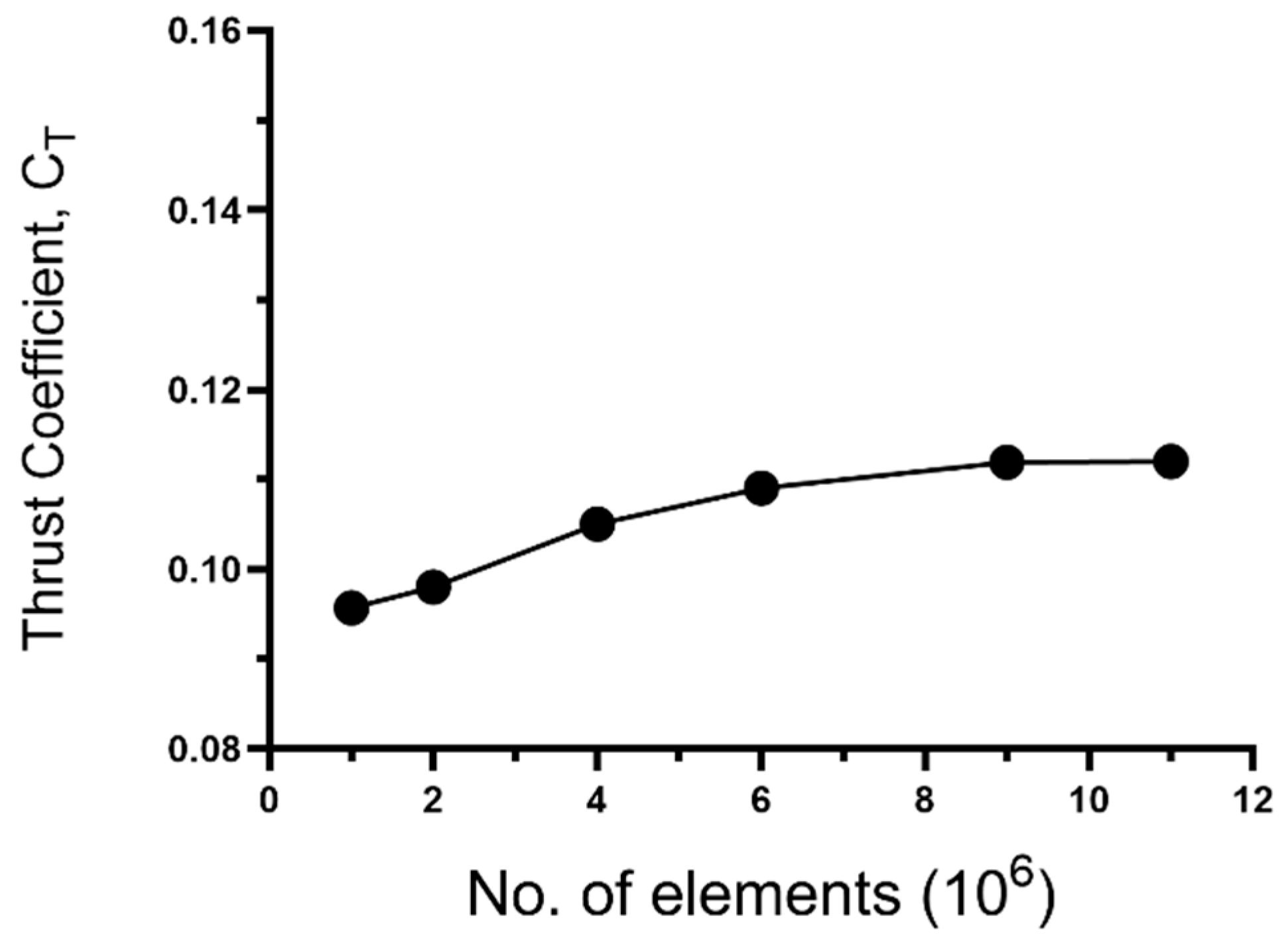
4.1. Mesh Sensitivity Analysis
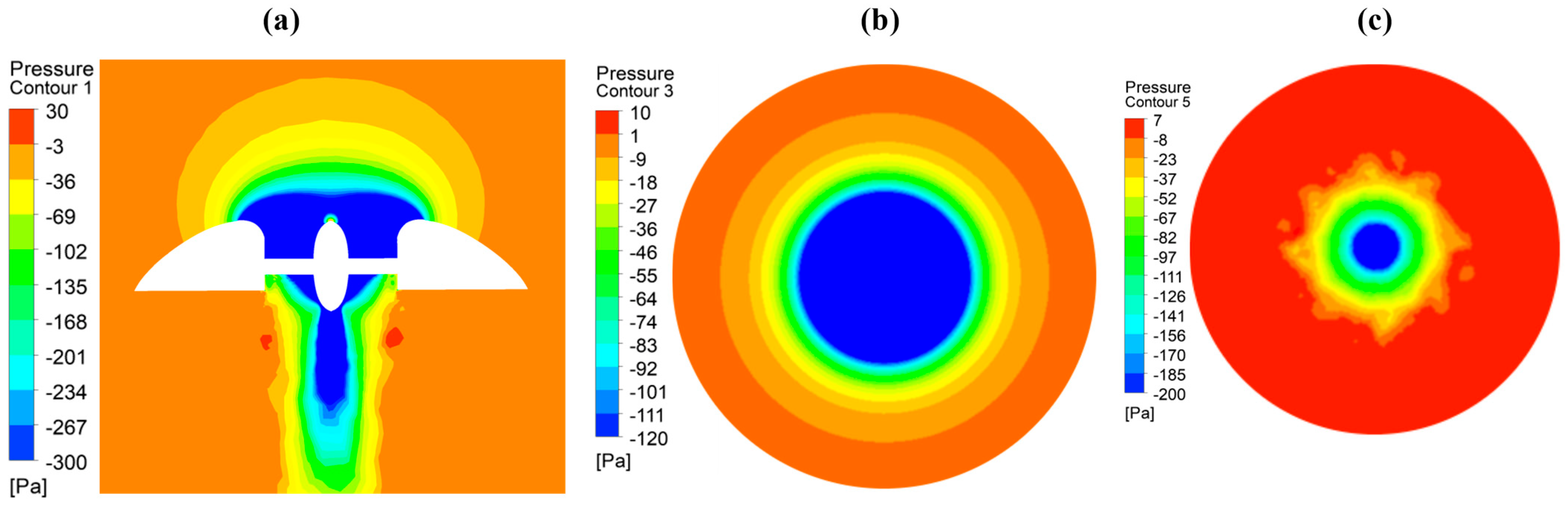
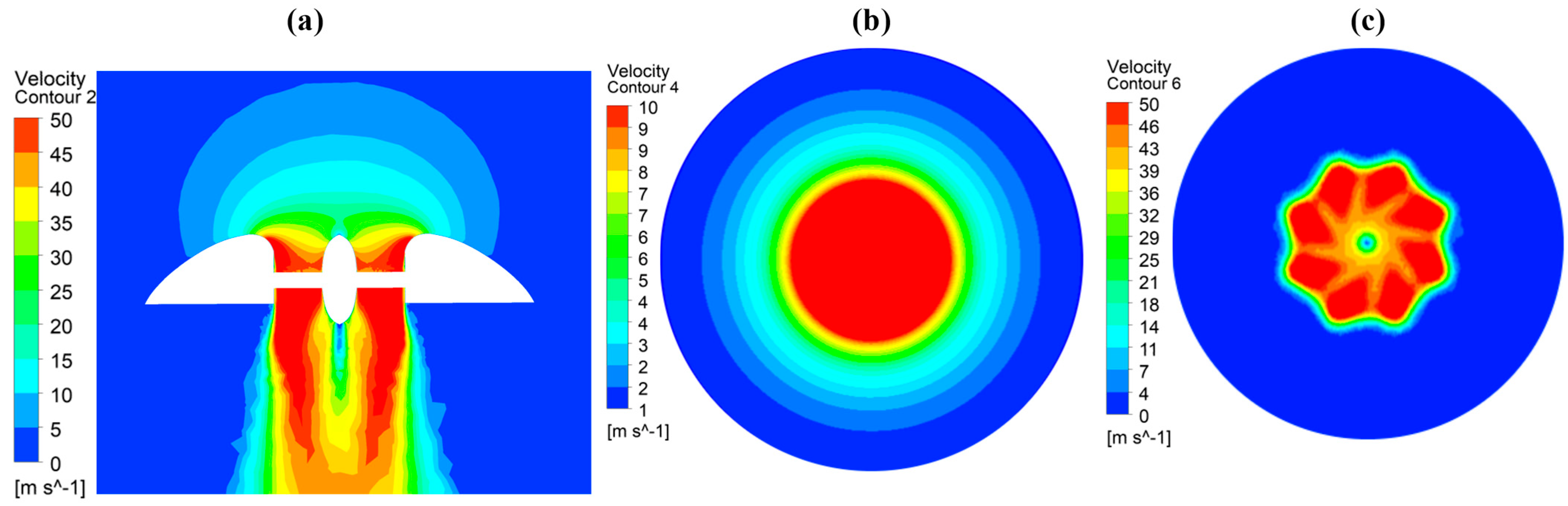
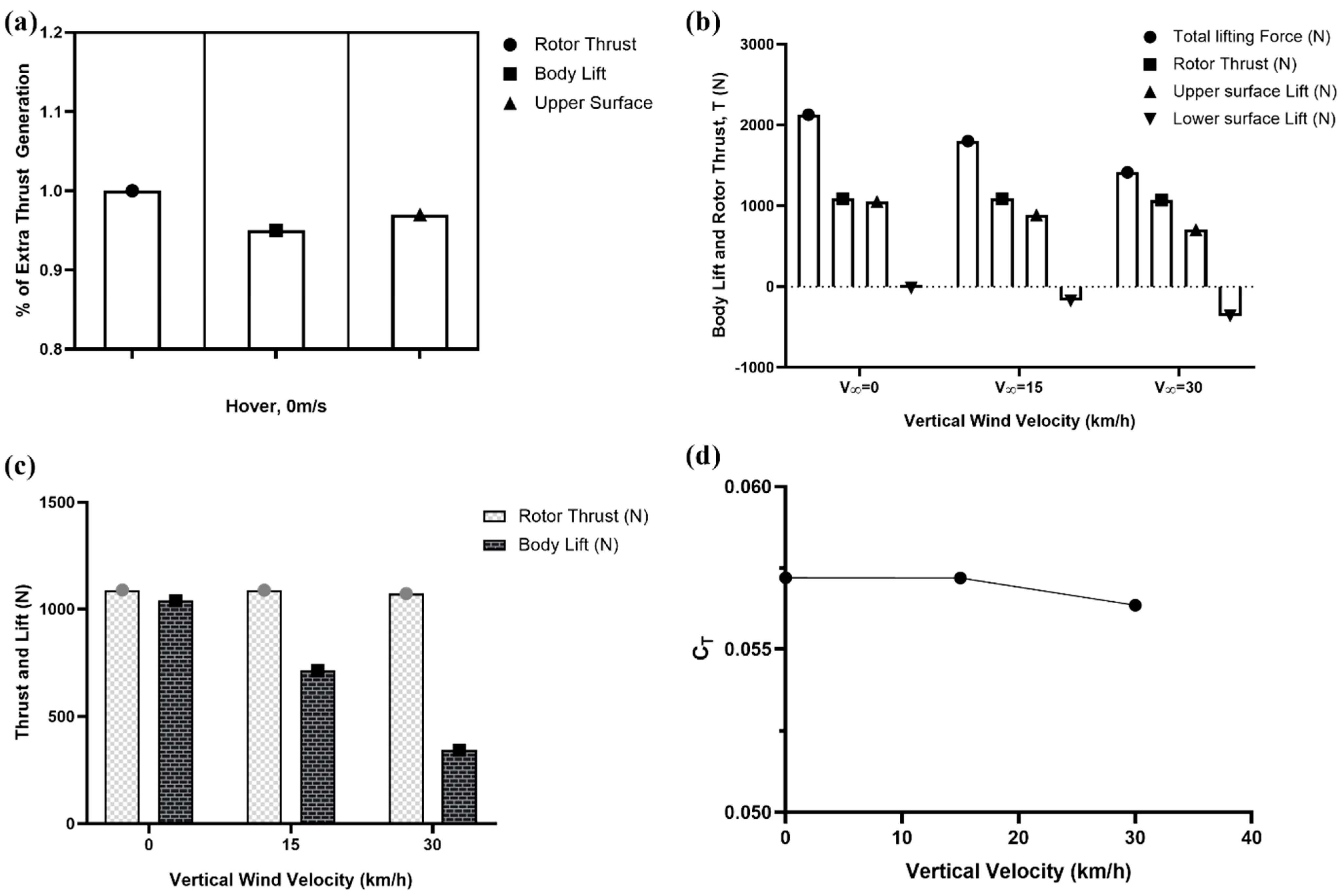
4.2. Hover and Vertical Flight Results
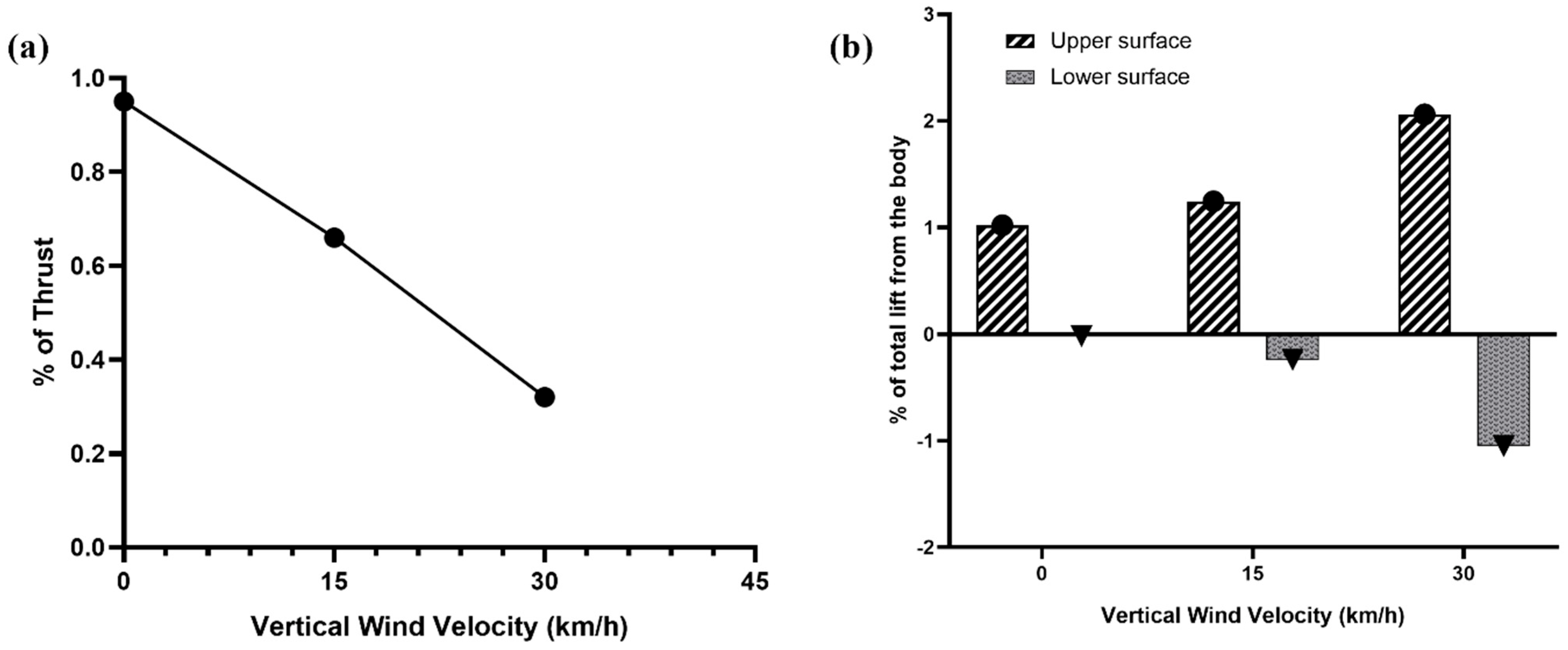
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- González-Jorge, H.; Martínez-Sánchez, J.; Bueno, M.; Arias, P. Unmanned Aerial Systems for Civil Applications: A Review. Drones 2017, 1, 2. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Austin, R. Unmanned Aircraft Systems: UAVS Design, Development and Deployment; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 54. [Google Scholar]
- Aleksandrov, D.; Penkov, I. Energy Consumption of Mini UAV Helicopters with Different Number of Rotors. In Proceedings of the 11th International Symposium” Topical Problems in the Field of Electrical and Power Engineering, Estonia, Pärnu, 16–21 January 2012; pp. 259–262. [Google Scholar]
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Towards Autonomous Indoor Micro VTOL. Auton. Robot. 2005, 18, 171–183. [Google Scholar] [CrossRef]
- Diaz, P.V.; Yoon, S. Computational Analysis of Urban Air Mobility Vehicles. In Proceedings of the 8th European Conference for Aeronautics and Aerospace Sciences (EUCASS), NASA Ames Research Center, Moffett Field, Santa Clara, CA, USA, 1–4 July 2019; p. 359. [Google Scholar]
- Lei, Y.; Huang, Y.; Wang, H. Aerodynamic Performance of an Octorotor SUAV with Different Rotor Spacing in Hover. Processes 2020, 8, 1364. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Jung, M.K.; Kwon, O.J. Numerical Study of Aerodynamic Performance of a Multirotor Unmanned-Aerial-Vehicle Configuration. J. Aircr. 2015, 52, 839–846. [Google Scholar] [CrossRef]
- Giljarhus, K.E.T.; Porcarelli, A.; Apeland, J. Investigation of Rotor Efficiency with Varying Rotor Pitch Angle for a Coaxial Drone. Drones 2022, 6, 91. [Google Scholar] [CrossRef]
- Kolaei, A.; Barcelos, D.; Bramesfeld, G. Experimental Analysis of a Small-Scale Rotor at Various Inflow Angles. Int. J. Aerosp. Eng. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Byham, G.M. The future of rotorcraft. Aeronaut. J. -New Ser. 2003, 107, 377–388. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B.; Huang, T. CFD Study of an Annular-Ducted Fan Lift System for VTOL Aircraft. Aerospace 2015, 2, 555–580. [Google Scholar] [CrossRef]
- Hatton, G. Thrust Generating Apparatus. US0213090A1, 4 September 2008. [Google Scholar]
- Nedelcut, F. Coanda Effect UAV—A New Born Baby in the Unmanned Aerial Vehicles Family. Rev. Air Force Acad. 2010, 17, 21–28. [Google Scholar]
- Ahmed, R.I.; Abu Talib, A.R.; Rafie, A.S.M.; Djojodihardjo, H. Aerodynamics and flight mechanics of MAV based on Coandă effect. Aerosp. Sci. Technol. 2017, 62, 136–147. [Google Scholar] [CrossRef]
- Hibbeler, R. Fluid Mechanics, 2nd ed.; Pearson: London, UK, 2015. [Google Scholar]
- Siddiqi, Z.; Lee, J.W. Experimental and numerical study of novel Coanda-based unmanned aerial vehicle. J. Eng. Appl. Sci. 2022, 69, 76. [Google Scholar] [CrossRef]
- Lopez, O.D.; Escobar, J.A.; Pérez, A.M. Computational Study of the Wake of a Quadcopter Propeller in Hover. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, Colorado, 5–9 June 2017. [Google Scholar] [CrossRef]
- Henricks, Q.; Wang, Z.; Zhuang, M. Small-Scale Rotor Design Variables and Their Effects on Aerodynamic and Aeroacoustic Performance of a Hovering Rotor. J. Fluids Eng. 2020, 142, 081209. [Google Scholar] [CrossRef]
- Barlow, C.; Lewis, D.; Prior, S.D.; Odedra, S.; Erbil, M.A.; Karamanoğlu, M.; Collins, R. Investigating the Use of the Coanda Effect to Create Novel Unmanned Aerial Vehicles. In Proceedings of the International Conference on Manufacturing and Engineering Systems, Huwei, Yunlin, Taiwan, 17–19 December 2009; pp. 386–391. [Google Scholar]
- Cycon, J.P.; Scott, M.W.; DeWitt, C.W. Method of Reducing a Nose-Up Pitching Moment on a Ducted Unmanned Aerial Vehicle. US6170778B1, 9 January 2001. [Google Scholar]
- Petrolo, M.; Carrera, E.; D'Ottavio, M.; Visser, C.C.d.; Pátek, Z.; Janda, Z. On the development of the Anuloid, a disk-shaped VTOL aircraft for urban areas. Adv. Aircr. Spacecr. Sci. 2014, 1, 353–378. [Google Scholar] [CrossRef]
- Stajuda, M.; Karczewski, M.; Obidowski, D.; Jóźwik, K. Development of a CFD model for propeller simulation. Mech. Mech. Eng. 2016, 20, 579–593. [Google Scholar]
- van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Xu, H.; Ye, Z.-Y.; Shi, A.-M. Numerical Study of Propeller Slipstream Based on Unstructured Dynamic Overset Grids. J. Aircr. 2012, 49, 384–389. [Google Scholar] [CrossRef]
- Ryu, M.; Cho, L.; Cho, J. Aerodynamic Analysis of the Ducted Fan for a VTOL UAV in Crosswinds. Trans. Jpn. Soc. Aeronaut. Space Sci. 2016, 59, 47–55. [Google Scholar] [CrossRef]
- Blocken, B.; Defraeye, T.; Koninckx, E.; Carmeliet, J.; Hespel, P. CFD simulations of the aerodynamic drag of two drafting cyclists. Comput. Fluids 2013, 71, 435–445. [Google Scholar] [CrossRef]
- Kim, W.-Y.; Senguttuvan, S.; Kim, S.-M. Effect of Rotor Spacing and Duct Diffusion Angle on the Aerodynamic Performances of a Counter-Rotating Ducted Fan in Hover Mode. Processes 2020, 8, 1338. [Google Scholar] [CrossRef]
- Thouault, N.; Breitsamter, C.; Adams, N.A. Numerical and Experimental Analysis of a Generic Fan-in-Wing Configuration. J. Aircr. 2009, 46, 656–666. [Google Scholar] [CrossRef]
- Kutty, H.A.; Rajendran, P. 3D CFD Simulation and Experimental Validation of Small APC Slow Flyer Propeller Blade. Aerospace 2017, 4, 10. [Google Scholar] [CrossRef]
- Pérez Gordillo, A.M.; Villegas Santos, J.S.; Lopez Mejia, O.D.; Suárez Collazos, L.J.; Escobar, J.A. Numerical and Experimental Estimation of the Efficiency of a Quadcopter Rotor Operating at Hover. Energies 2019, 12, 261. [Google Scholar]
- Jiang, Y.; Zhang, B. Numerical Investigation of Effect of Parameters on Hovering Efficiency of an Annular Lift Fan Aircraft. Aerospace 2016, 3, 35. [Google Scholar] [CrossRef]
- Min, K.-M.M.K.-M.; Tjprc. Design and CFD Analysis of A Low-Altitude VTOL UAV. Int. J. Mech. Prod. Eng. Res. Dev. (IJMPERD) 2019, 9, 555–562. [Google Scholar]
- Prisacariu, V. CFD Analysis of UAV Flying Wing. Incas Bull. 2016, 8, 65–72. [Google Scholar] [CrossRef]
- John Seddon, S.N. Rotor in Vertical Flight: Momentum Theory and Wake Analysis. In Basic Helicopter Aerodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 23–61. [Google Scholar] [CrossRef]
- Crivoi, O.; Doroftei, I. Some experimental results on Coanda effect with application to a flying vehicle. IOP Conf. Ser. Mater. Sci. Eng. 2016, 147, 012082. [Google Scholar] [CrossRef]
- Najafi, M.; Jahanmiri, M. An Innovative Technique to Increase Lift of a Coanda UAV. IOSR J. Mech. Civ. Eng. 2017, 14, 27–35. [Google Scholar] [CrossRef]
- Shin, D.; Kim, H.; Gong, J.; Jeong, U.; Jo, Y.; Matson, E.T. Stealth UAV through Coandă Effect. In Proceedings of the 2020 Fourth IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 9–11 November 2020; pp. 202–209. [Google Scholar]
- Gad-el-Hak, M.; Bushnell, D. Separation Control: Review. J. Fluids Eng. 1991, 113, 5–30. [Google Scholar] [CrossRef]
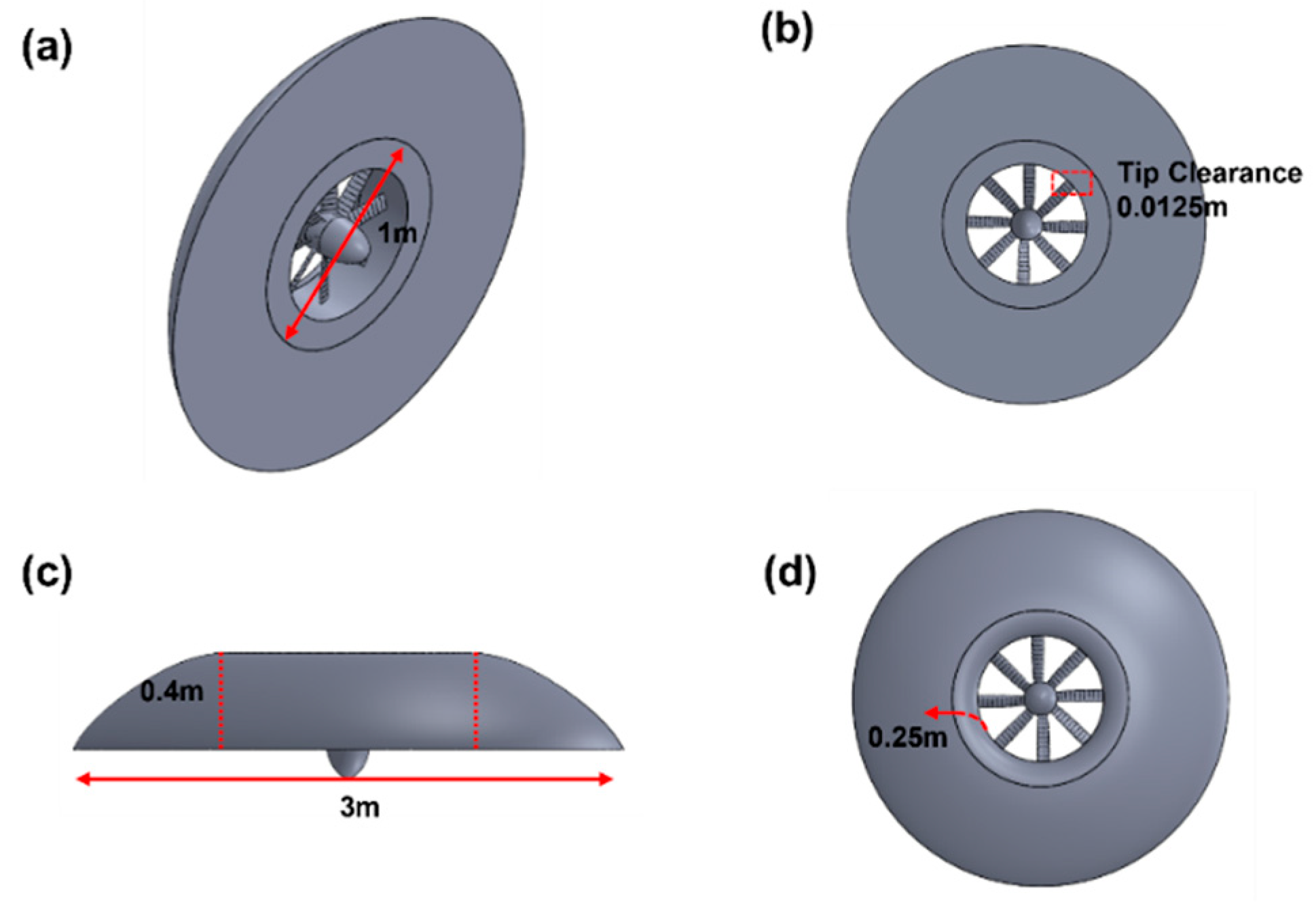

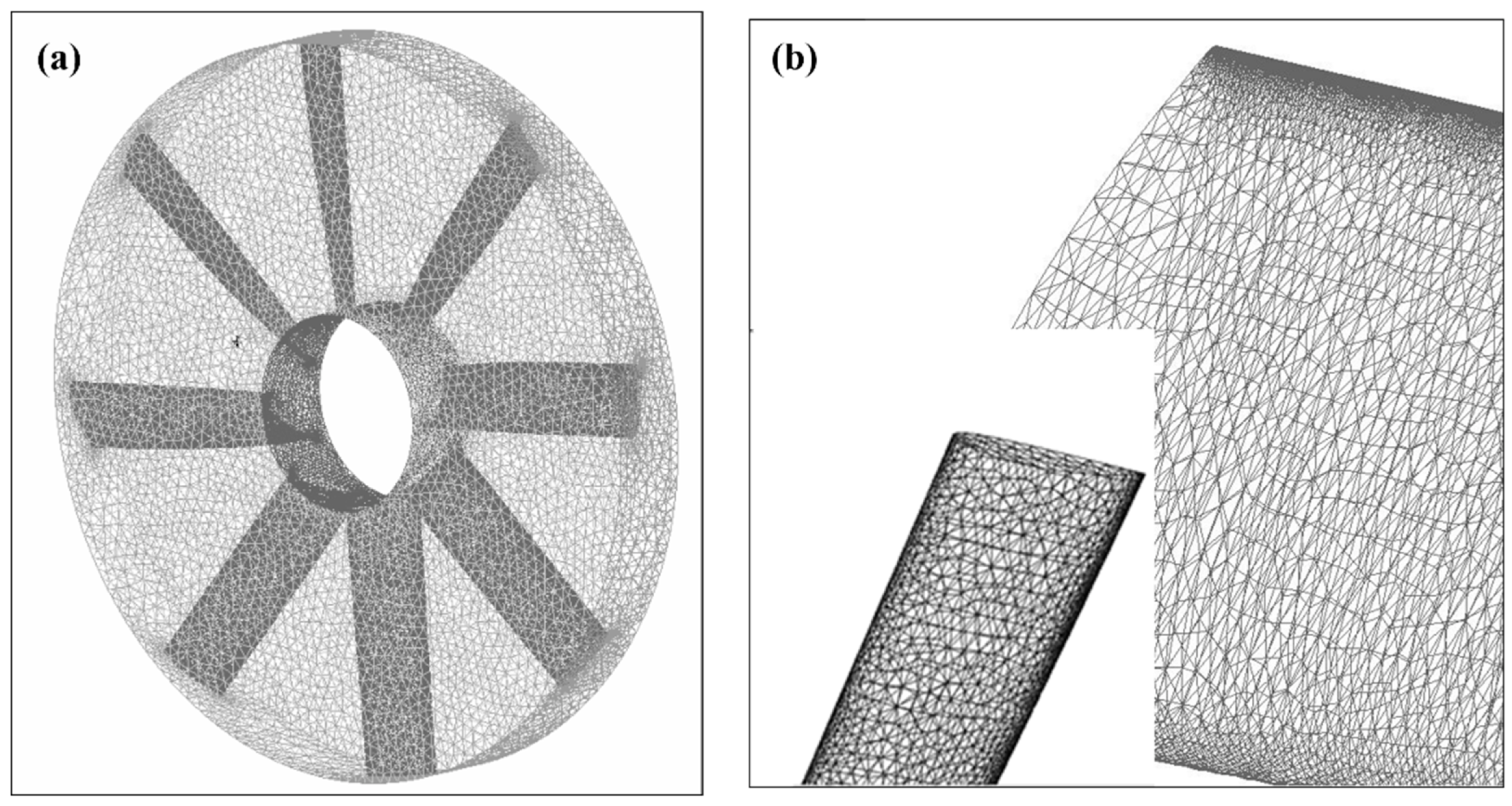
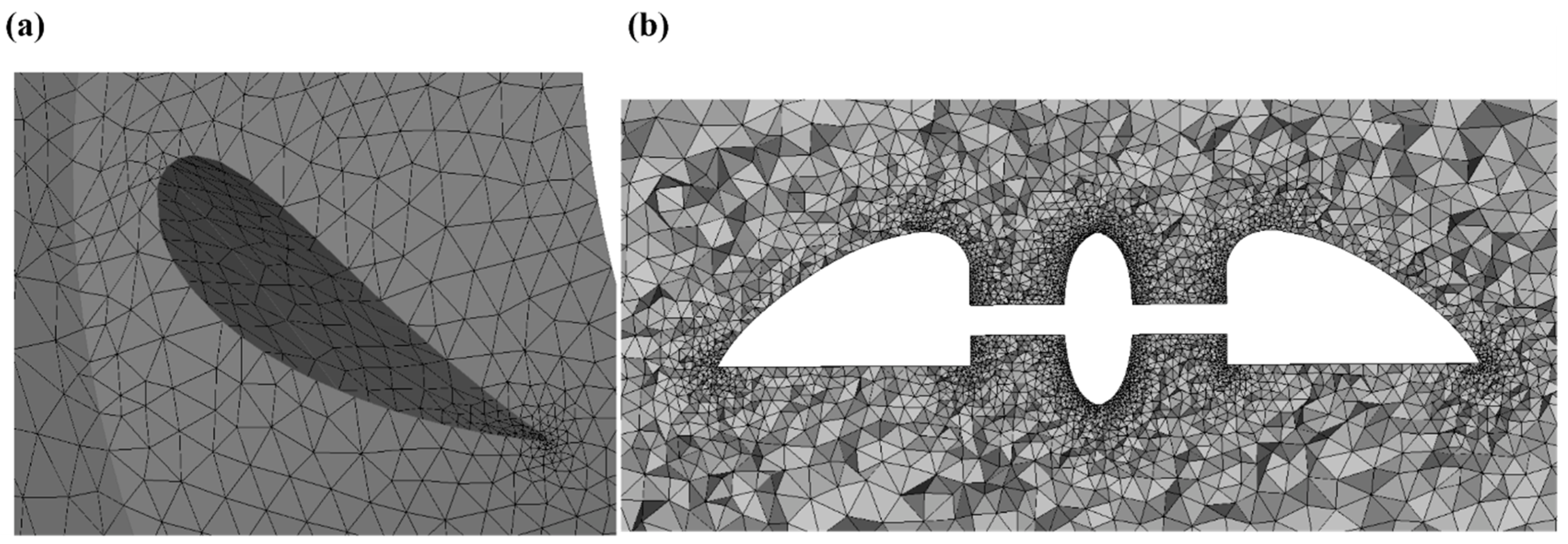
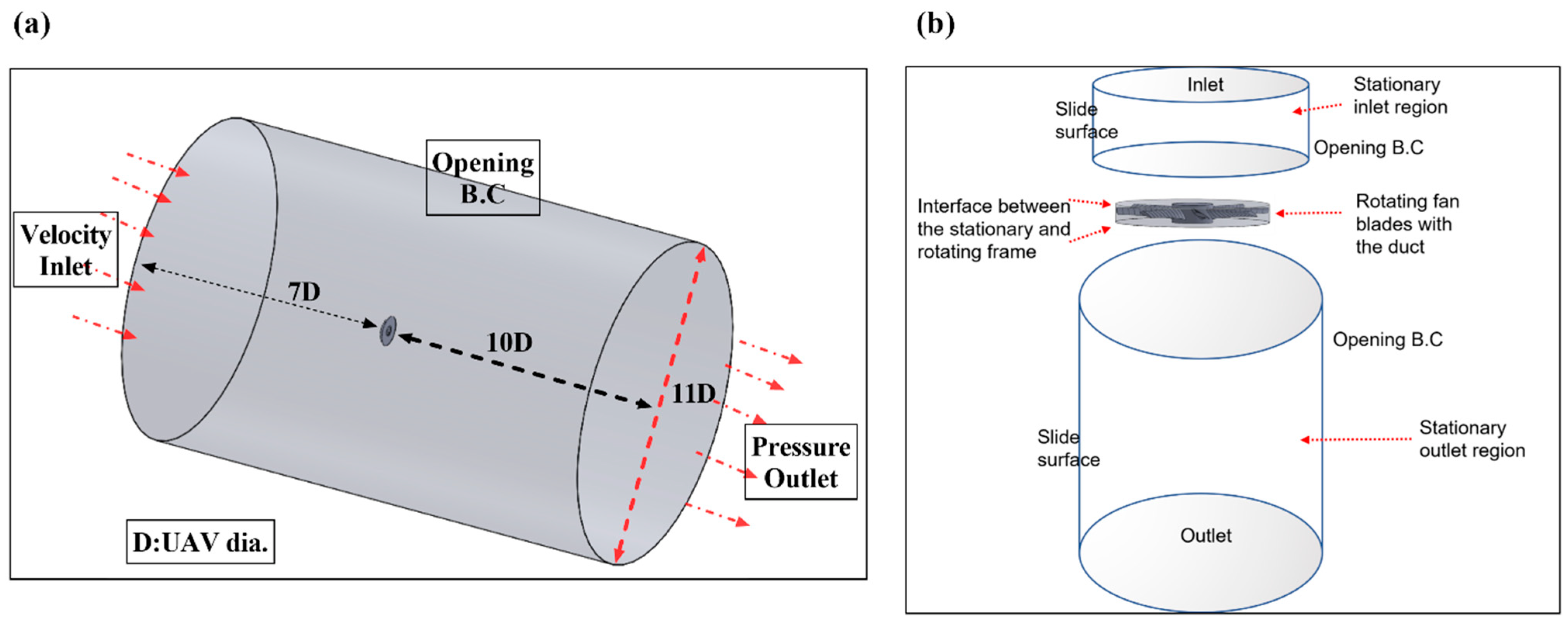

| Component | Feature | Details |
|---|---|---|
| ANSYS CFX—Pre | Simulation type | Steady state |
| Fluid type | Air ideal gas | |
| Domain type | Multiple domain Rotating frame of reference Stationery frame of reference | |
| Turbulence model | SST | |
| Heat transfer | Total energy | |
| Boundary conditions | Velocity inlet (Subsonic) Pressure outlet (Subsonic) Wall: no-slip Wall: adiabatic Far-field: opening | |
| Domain interfaces | General connection Frozen rotor Specified pitch angles (360o) | |
| Timestep | Physical timescale: | |
| ANSYS CFX—Solver Manager | Start | Double Precision |
| ANSYS CFX—Post | Plots | Contour: pressure, and velocity Streamlines Velocity vector |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed Snikdha, S.S.; Chen, S.-H. A Computational Investigation of the Hover Mechanism of an Innovated Disc-Shaped VTOL UAV. Drones 2023, 7, 105. https://doi.org/10.3390/drones7020105
Ahmed Snikdha SS, Chen S-H. A Computational Investigation of the Hover Mechanism of an Innovated Disc-Shaped VTOL UAV. Drones. 2023; 7(2):105. https://doi.org/10.3390/drones7020105
Chicago/Turabian StyleAhmed Snikdha, Samia Shahrin, and Shih-Hsiung Chen. 2023. "A Computational Investigation of the Hover Mechanism of an Innovated Disc-Shaped VTOL UAV" Drones 7, no. 2: 105. https://doi.org/10.3390/drones7020105
APA StyleAhmed Snikdha, S. S., & Chen, S.-H. (2023). A Computational Investigation of the Hover Mechanism of an Innovated Disc-Shaped VTOL UAV. Drones, 7(2), 105. https://doi.org/10.3390/drones7020105







