Research on Data Link Channel Decoding Optimization Scheme for Drone Power Inspection Scenarios
Abstract
:1. Introduction
- Firstly, we incorporate the concept of the model-driven approach and leverage the advantages of neural networks and Tanner graphs to expand the iterative decoding process of checking the update and propagation of messages between nodes and variable nodes in the minimum sum algorithm (NMS) into a deep feed-forward neural network. We use a novel method of sharing network parameters to improve the NNMS network, which is distinct from the shared-parameter method proposed in [31]. This approach improves the BER performance by reasonably reducing network parameters.
- Furthermore, to further improve the novel LDPC decoding algorithm, we introduce a weight quantization method based on a codebook. This approach not only reduces the precision of each weight but also decreases the number of weight types required for training the network, leading to reduced computational complexity and resource consumption. The reasonable selection of the quantization schemes can even have a positive impact on the decoding performance.
- Finally, to validate the BER performance of the proposed improved LDPC decoding algorithm, we demonstrate a performance and complexity analysis under a Rician channel in the context of drone communication scenarios.
2. Materials and Methods
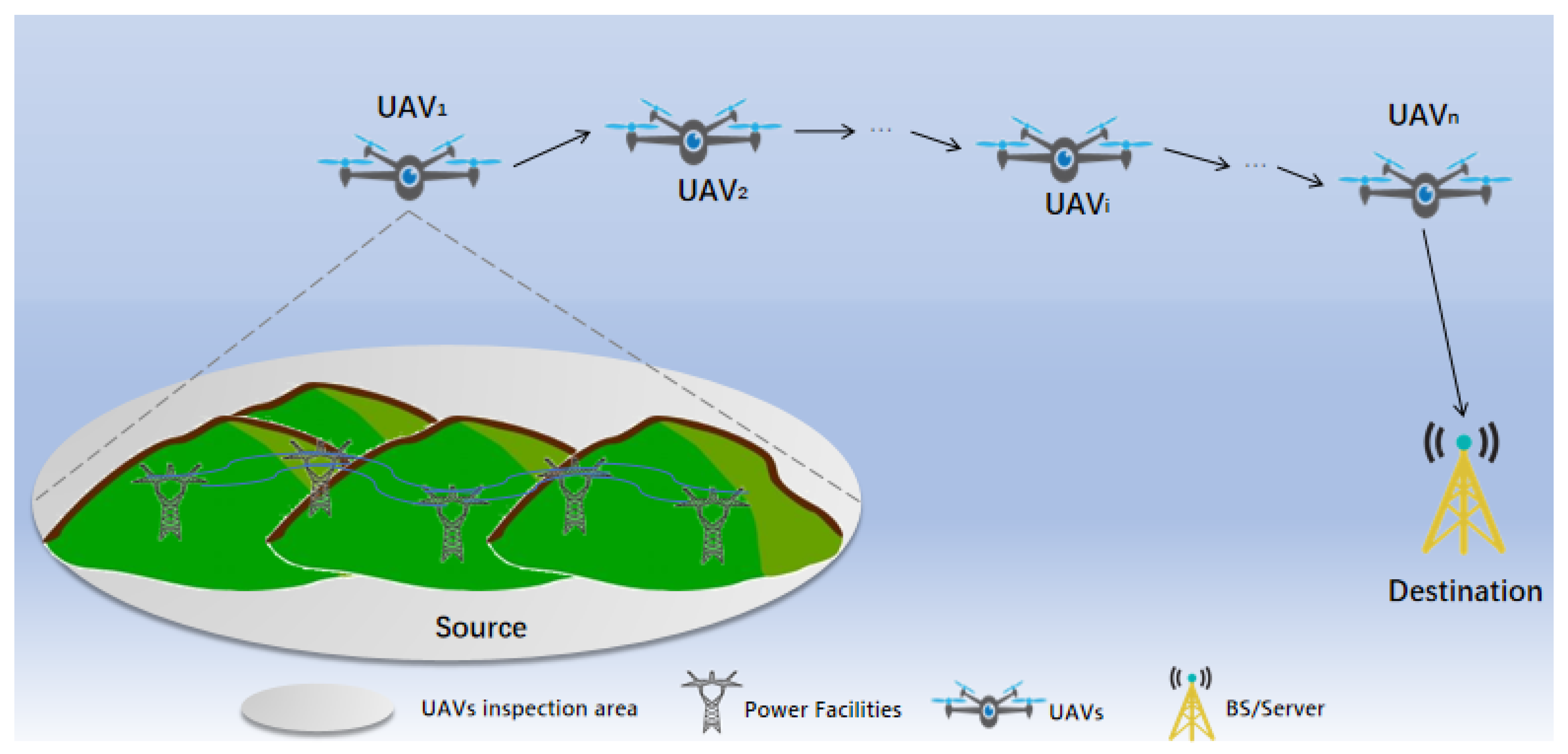
2.1. System Model
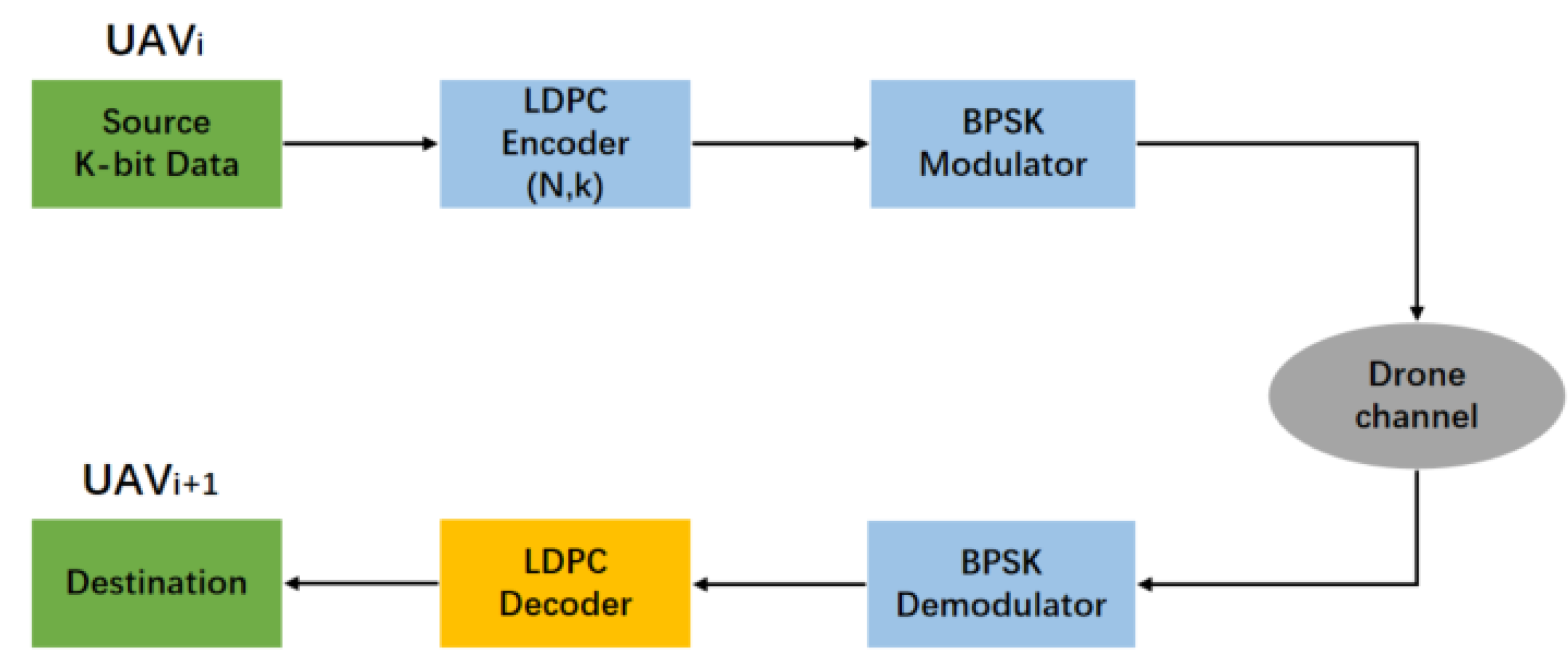
2.2. Air-to-Air Data Transmission Link Model
2.3. Prior Work
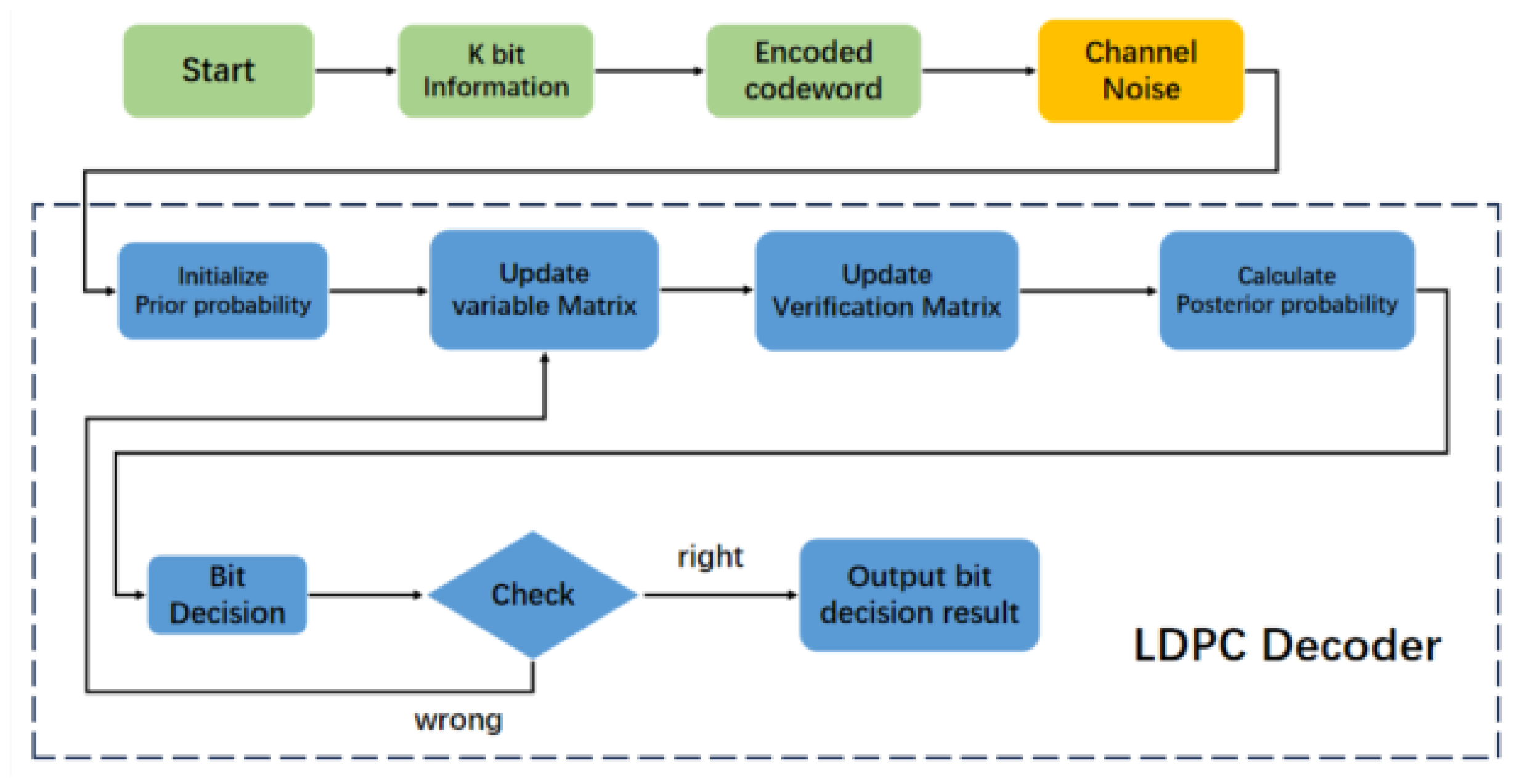
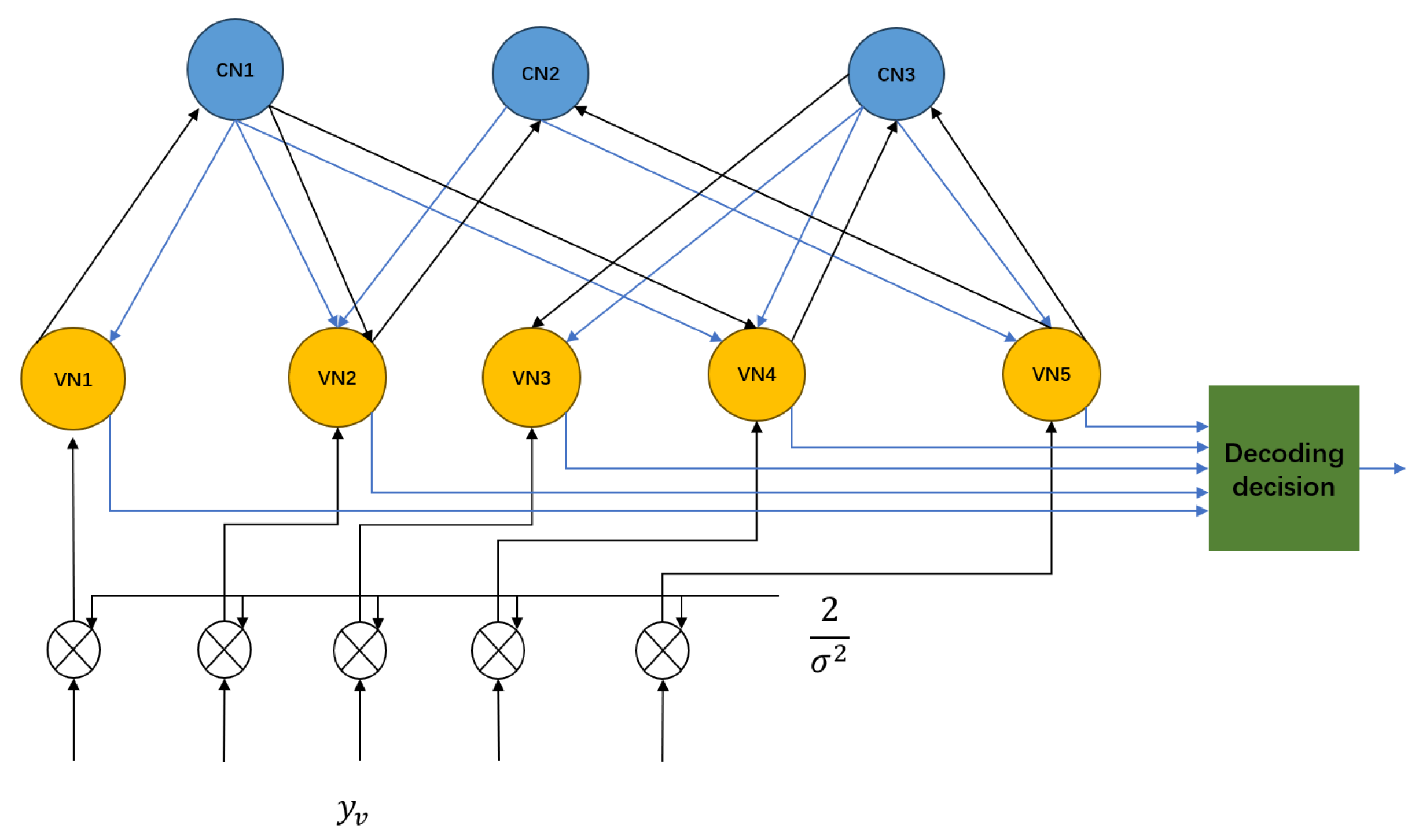
2.3.1. Normalized Minimum Sum Algorithm (NMS) and Model-Driven Methods
2.3.2. Codebook-Based Quantization Method
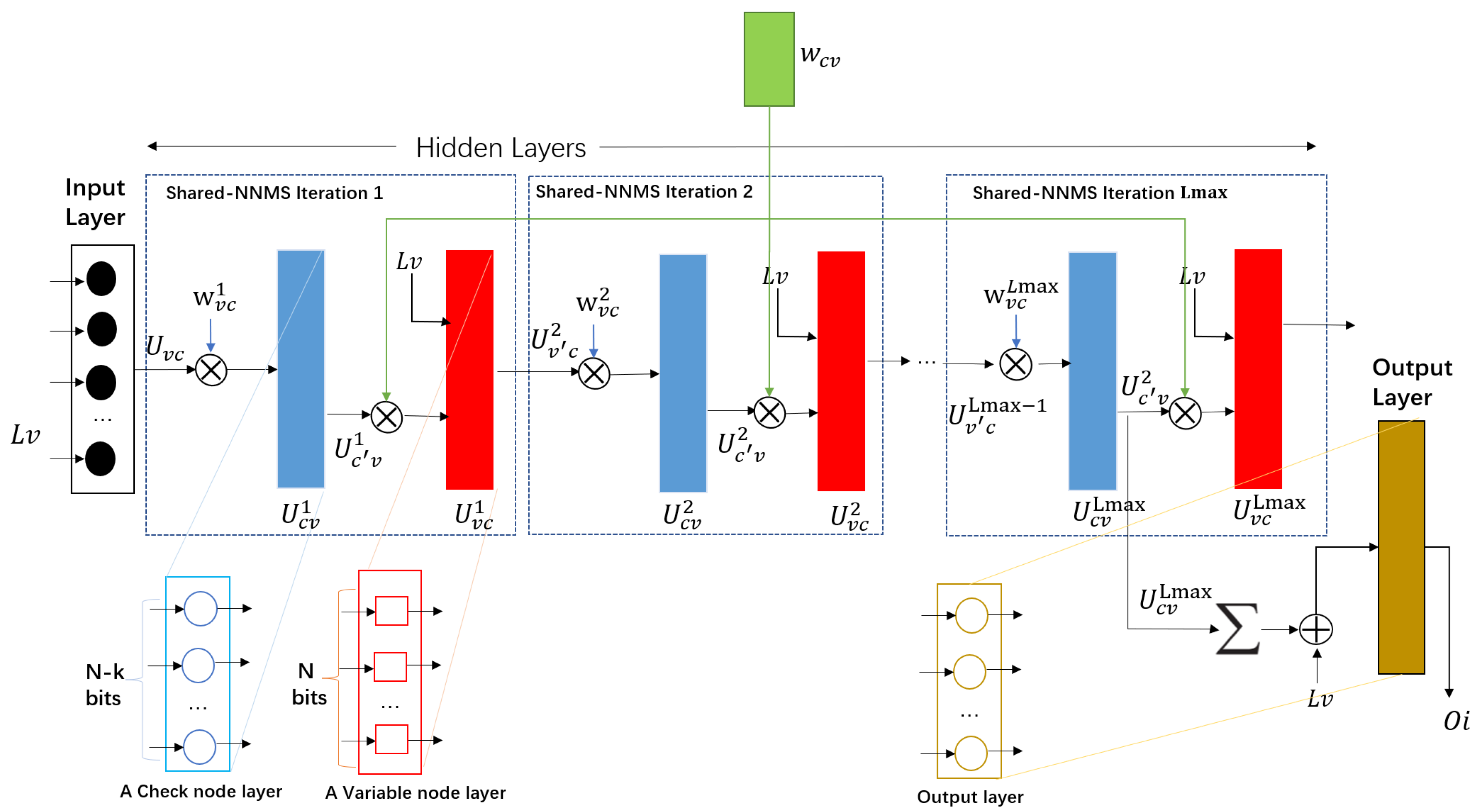
2.4. The Proposed Shared-Parameter Neural-Network-Normalized Minimum Sum Decoding Algorithm Based on Codebook Quantization (Shared-NNMS-CQ)
- Shared neural network trainable parameters: A novel new shared-parameter NNMS (new-SNNMS) LDPC decoding is proposed. The weights and are independent and learnable. The weight vector is shared across different iterations, and different weights are assigned to the check node messages in each iteration. The correction factor is shared among all variable node messages in each iteration. This sharing mechanism reduces the number of correction factors and network weights, thereby reducing the computational complexity.
- Codebook-based weight parameter quantization: In the proposed new-SNNMS LDPC decoding neural network, the parameters in the network are quantized. First, the decimal places of float32 floating-point weights are quantized to q bits. Then, a codebook-based weight quantization method is used to reduce the number of weight types to . This approach decreases the precision of each weight and reduces the variety of network weight values.
3. Results
3.1. Experimental Setup
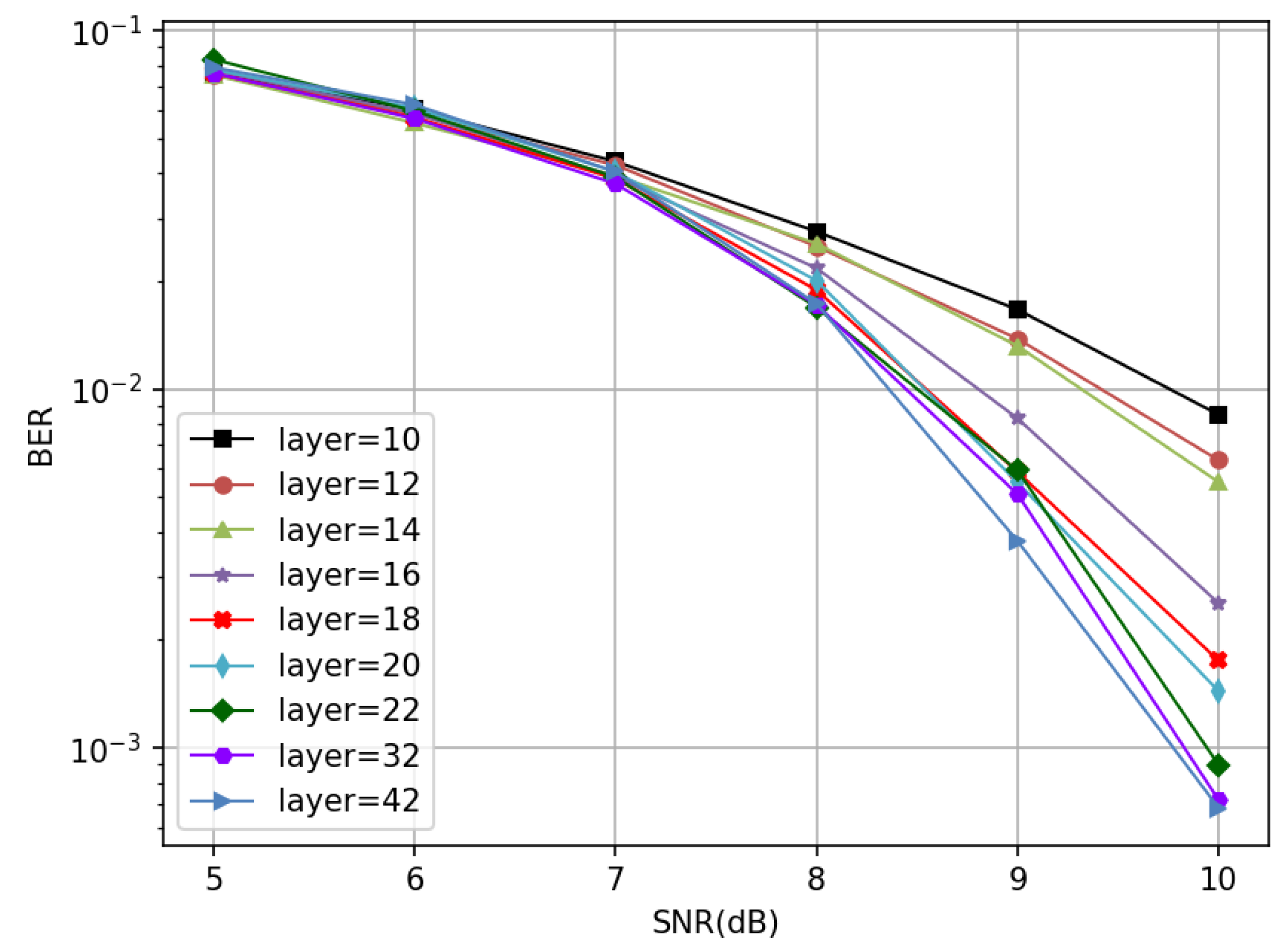
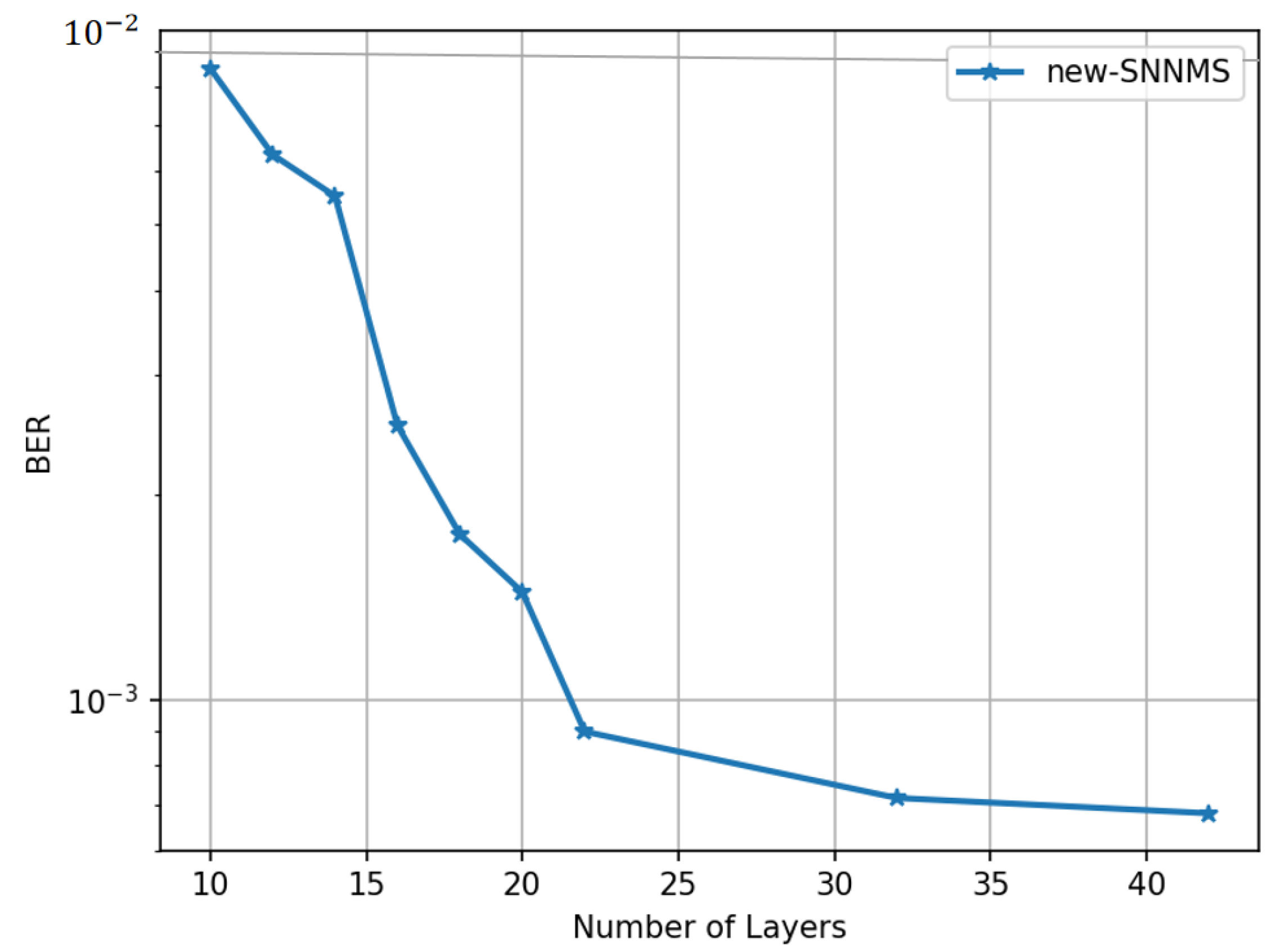
3.2. BER Performance vs. Number of Network Layers
3.3. BER Performance Comparison among NNMS, SNNMS, and New-SNNMS
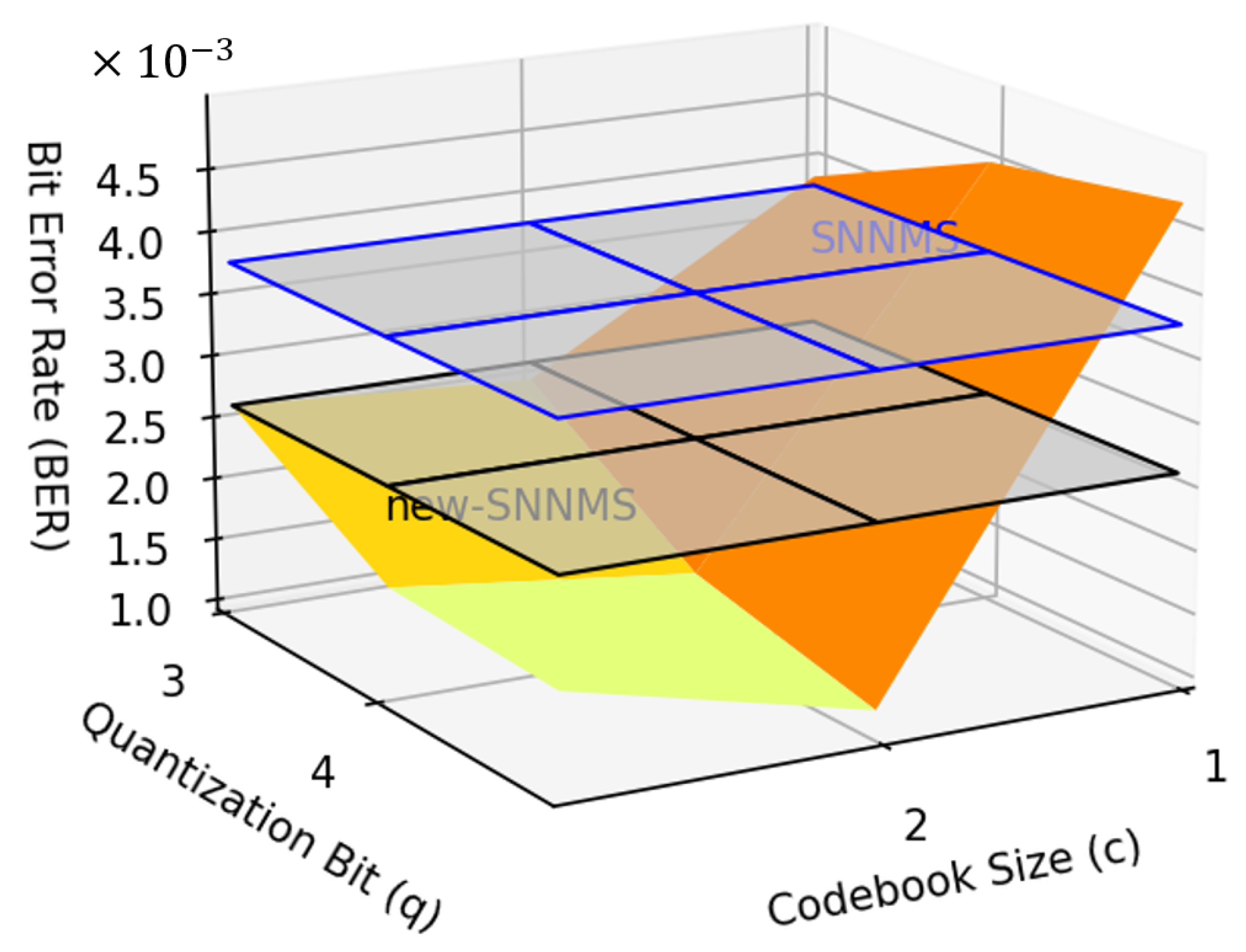
3.4. Quantization
3.5. Complexity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, L.; Fan, J.; Liu, Y.; Li, E.; Peng, J.; Liang, Z. A review on state-of-the-art power line inspection techniques. IEEE Trans. Instrum. Meas. 2020, 69, 9350–9365. [Google Scholar] [CrossRef]
- Du, Q.; Dong, W.; Su, W.; Wang, Q. UAV Inspection Technology and Application of Transmission Line. In Proceedings of the 2022 IEEE 5th International Conference on Information Systems and Computer Aided Education (ICISCAE), Dalian, China, 23–25 September 2022; IEEE: New York, NY, USA, 2022; pp. 594–597. [Google Scholar]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, C.; Wei, Z.; Pan, C.; Zhang, H.; Ren, Y. Joint UAV hovering altitude and power control for space-air-ground IoT networks. IEEE Internet Things J. 2018, 6, 1741–1753. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; He, Q.; Bian, K.; Song, L. Joint trajectory and power optimization for UAV relay networks. IEEE Commun. Lett. 2017, 22, 161–164. [Google Scholar] [CrossRef]
- Jaziri, A.; Nasri, R.; Chahed, T. Congestion mitigation in 5G networks using drone relays. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; IEEE: New York, NY, USA, 2016; pp. 233–238. [Google Scholar]
- Horiuchi, M.; Nishiyama, H.; Kato, N.; Ono, F.; Miura, R. Throughput maximization for long-distance real-time data transmission over multiple UAVs. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; IEEE: New York, NY, USA, 2016; pp. 1–6. [Google Scholar]
- Li, X.; Guo, D.; Yin, H.; Wei, G. Drone-assisted public safety wireless broadband network. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), New Orleans, LA, USA, 9–12 March 2015; IEEE: New York, NY, USA, 2015; pp. 323–328. [Google Scholar]
- Chen, Y.; Zhao, N.; Ding, Z.; Alouini, M.S. Multiple UAVs as relays: Multi-hop single link versus multiple dual-hop links. IEEE Trans. Wirel. Commun. 2018, 17, 6348–6359. [Google Scholar] [CrossRef]
- Berrou, C.; Glavieux, A. Near optimum error correcting coding and decoding: Turbo-codes. IEEE Trans. Commun. 1996, 44, 1261–1271. [Google Scholar] [CrossRef]
- Heegard, C.; Wicker, S.B. Turbo Coding; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- MacKay, D.J. Good error-correcting codes based on very sparse matrices. IEEE Trans. Inf. Theory 1999, 45, 399–431. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Z.; Liu, Y. High-throughput layered LDPC decoding architecture. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 582–587. [Google Scholar]
- Gallager, R. Low-density parity-check codes. IRE Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Chen, J.; Dholakia, A.; Eleftheriou, E.; Fossorier, M.P.; Hu, X.Y. Reduced-complexity decoding of LDPC codes. IEEE Trans. Commun. 2005, 53, 1288–1299. [Google Scholar] [CrossRef]
- Zhao, J.; Zarkeshvari, F.; Banihashemi, A.H. On implementation of min-sum algorithm and its modifications for decoding low-density parity-check (LDPC) codes. IEEE Trans. Commun. 2005, 53, 549–554. [Google Scholar] [CrossRef]
- Oh, D.; Parhi, K.K. Min-sum decoder architectures with reduced word length for LDPC codes. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 105–115. [Google Scholar]
- Nurbani, C.A.; Anwar, K.; Cahyadi, W.A. Hybrid multikernel-constructed polar codes for short blocklength transmissions. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; IEEE: New York, NY, USA, 2021; pp. 724–728. [Google Scholar]
- Gefei, Y.; Zhenhua, W.; Ying, L.; Hui, H. Channel coding in the data link of unmanned aerial vehicle. J. Chongqing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2014, 26, 845–849. [Google Scholar]
- Wang, F.; Guo, M.; Wang, P. Research on Waveform Design of Physical Layer of UAV Cluster Data Link. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 23–25 October 2020; IEEE: New York, NY, USA, 2020; pp. 542–546. [Google Scholar]
- Wang, F.; Liu, J.; Wang, S. LDPC code design for quadrature-quadrature phase shift keying. In Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), Guangzhou, China, 6–8 May 2017; IEEE: New York, NY, USA, 2017; pp. 15–19. [Google Scholar]
- Zhu, T.-L.; Qin, F.; Li, F.-X.; Wen, J.-M. Q-LDPC Code for UAV TT&C Transmission System. Telecommun. Eng. 2014, 54, 1622–1626. [Google Scholar]
- Liang, F.; Shen, C.; Wu, F. An iterative BP-CNN architecture for channel decoding. IEEE J. Sel. Top. Signal Process. 2018, 12, 144–159. [Google Scholar] [CrossRef]
- Gruber, T.; Cammerer, S.; Hoydis, J.; Ten Brink, S. On deep learning-based channel decoding. In Proceedings of the 2017 51st annual conference on information sciences and systems (CISS), Baltimore, MD, USA, 22–24 March 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Zhang, Z.; Wu, F.; Lee, W.S. Factor graph neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 8577–8587. [Google Scholar]
- Satorras, V.G.; Welling, M. Neural enhanced belief propagation on factor graphs. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; pp. 685–693. [Google Scholar]
- Nachmani, E.; Marciano, E.; Lugosch, L.; Gross, W.J.; Burshtein, D.; Be’ery, Y. Deep learning methods for improved decoding of linear codes. IEEE J. Sel. Top. Signal Process. 2018, 12, 119–131. [Google Scholar] [CrossRef]
- Nachmani, E.; Be’ery, Y.; Burshtein, D. Learning to decode linear codes using deep learning. In Proceedings of the 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; IEEE: New York, NY, USA, 2016; pp. 341–346. [Google Scholar]
- Abotabl, A.; Bae, J.H.; Song, K.B. Offset min-sum optimization for general decoding scheduling: A deep learning approach. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Xu, W.; Wu, Z.; Ueng, Y.L.; You, X.; Zhang, C. Improved polar decoder based on deep learning. In Proceedings of the 2017 IEEE International workshop on signal processing systems (SiPS), Lorient, France, 3–5 October 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Wang, Q.; Wang, S.; Fang, H.; Chen, L.; Chen, L.; Guo, Y. A model-driven deep learning method for normalized min-sum LDPC decoding. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Wang, L.; Chen, S.; Nguyen, J.; Dariush, D.; Wesel, R. Neural-network-optimized degree-specific weights for LDPC minsum decoding. arXiv 2021, arXiv:2107.04221. [Google Scholar]
- Lian, M.; Carpi, F.; Häger, C.; Pfister, H.D. Learned belief-propagation decoding with simple scaling and SNR adaptation. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; IEEE: New York, NY, USA, 2019; pp. 161–165. [Google Scholar]
- Wang, Q.; Liu, Q.; Wang, S.; Chen, L.; Fang, H.; Chen, L.; Guo, Y.; Wu, Z. Normalized min-sum neural network for LDPC decoding. IEEE Trans. Cogn. Commun. Netw. 2022, 9, 70–81. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Qingle, W.; Su-Kit, T.; Liang, Y.; LAM, C.T.; Yan, M. A low complexity model-driven deep learning ldpc decoding algorithm. In Proceedings of the 2021 IEEE 6th International Conference on Computer and Communication Systems (ICCCS), Chengdu, China, 23–26 April 2021; IEEE: New York, NY, USA, 2021; pp. 558–563. [Google Scholar]
- Teng, C.F.; Wu, C.H.D.; Ho, A.K.S.; Wu, A.Y.A. Low-complexity recurrent neural network-based polar decoder with weight quantization mechanism. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; IEEE: New York, NY, USA, 2019; pp. 1413–1417. [Google Scholar]
- Tanner, R. A recursive approach to low complexity codes. IEEE Trans. Inf. Theory 1981, 27, 533–547. [Google Scholar] [CrossRef]
- Liu, J.; Jing, S.; You, X.; Zhang, C. A merged BP decoding algorithm for polar-LDPC concatenated codes. In Proceedings of the 2017 22nd International Conference on Digital Signal Processing (DSP), London, UK, 23–25 August 2017; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar]
- Yang, N.; Jing, S.; Yu, A.; Liang, X.; Zhang, Z.; You, X.; Zhang, C. Reconfigurable decoder for LDPC and polar codes. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar]
- Wang, J.; Jiang, C.; Zhang, H.; Ren, Y.; Chen, K.C.; Hanzo, L. Thirty years of machine learning: The road to Pareto-optimal wireless networks. IEEE Commun. Surv. Tutor. 2020, 22, 1472–1514. [Google Scholar] [CrossRef]
- He, H.; Jin, S.; Wen, C.K.; Gao, F.; Li, G.Y.; Xu, Z. Model-driven deep learning for physical layer communications. IEEE Wirel. Commun. 2019, 26, 77–83. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Zhang, L.; Zhang, Y.; Li, Q.; Chen, K.C. Reliable transmission for NOMA systems with randomly deployed receivers. IEEE Trans. Commun. 2022, 71, 1179–1192. [Google Scholar] [CrossRef]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized neural networks: Training neural networks with low precision weights and activations. J. Mach. Learn. Res. 2017, 18, 6869–6898. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for Large-Scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Helmling, M.; Scholl, S.; Gensheimer, F.; Dietz, T.; Kraft, K.; Ruzika, S.; Wehn, N. Database of Channel Codes and ML Simulation Results. 2019, pp. 0733–8716. Available online: www.uni-kl.de/channel-codes (accessed on 10 August 2023).


| Performance | LDPC Code | Turbo Code | Convolutional Code |
|---|---|---|---|
| Error correction ability | Pretty strong | Pretty strong | Strong |
| Fragrance limit difference | 0.0045 dB | 0.5 dB | >4 dB |
| Encoding and decoding complexity | Medium | Complex | Simple |
| Anti-interference ability | Strong | Strong | Average |
| Throughput | >100 Mbps | 1–100 Mbps | >100 Mbps |
| Calculation | Parallel | Parallel | Parallel |
| Parameters | Values |
|---|---|
| Encoding | LDPC code (576,432) |
| Coding Rate | 3/4 |
| SNR | 5,6,7,8,9,10 |
| Batch Size | 240 |
| Optimizer | Adam |
| Learning Rate | 0.001 |
| Channel Model | Rician |
| Item | NMS | NNMS | SNNMS | Shared-NNMS-CQ |
|---|---|---|---|---|
| CMP/XOR | ||||
| ADD | ||||
| ML | T | 2T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Zhang, K.; Zhao, X.; Zhang, Y.; Cui, B.; Sun, S.; Liu, G.; Yu, B.; Ma, C.; Liu, Y.; et al. Research on Data Link Channel Decoding Optimization Scheme for Drone Power Inspection Scenarios. Drones 2023, 7, 662. https://doi.org/10.3390/drones7110662
Yu H, Zhang K, Zhao X, Zhang Y, Cui B, Sun S, Liu G, Yu B, Ma C, Liu Y, et al. Research on Data Link Channel Decoding Optimization Scheme for Drone Power Inspection Scenarios. Drones. 2023; 7(11):662. https://doi.org/10.3390/drones7110662
Chicago/Turabian StyleYu, Haizhi, Kaisa Zhang, Xu Zhao, Yubing Zhang, Bingfeng Cui, Shujuan Sun, Gengshuo Liu, Bo Yu, Chao Ma, Ying Liu, and et al. 2023. "Research on Data Link Channel Decoding Optimization Scheme for Drone Power Inspection Scenarios" Drones 7, no. 11: 662. https://doi.org/10.3390/drones7110662
APA StyleYu, H., Zhang, K., Zhao, X., Zhang, Y., Cui, B., Sun, S., Liu, G., Yu, B., Ma, C., Liu, Y., & Gao, W. (2023). Research on Data Link Channel Decoding Optimization Scheme for Drone Power Inspection Scenarios. Drones, 7(11), 662. https://doi.org/10.3390/drones7110662






